Sample and population exponents of generalized Taylor’s law

Significance

Taylor’s law (TL) has been verified very widely in the natural sciences, information technology, and finance. The widespread observation of TL suggests that a context-independent mechanism may be at work and stimulated the search for processes affecting the scaling of population fluctuations with population abundance. We show that limited sampling may explain why TL is often observed to have exponent $b=2$. Abrupt transitions in the TL exponent associated with smooth changes in the environment were recently discovered theoretically and comparable real-world transitions could harm fish populations, forests, and public health. Our study shows that limited sampling hinders the anticipation of such transitions and provides estimates for the number of samples required to reveal early warning signals of abrupt biotic change.

Abstract

Taylor’s law (TL) states that the variance V of a nonnegative random variable is a power function of its mean M; i.e., $V=a{M}^b$. TL has been verified extensively in ecology, where it applies to population abundance, physics, and other natural sciences. Its ubiquitous empirical verification suggests a context-independent mechanism. Sample exponents b measured empirically via the scaling of sample mean and variance typically cluster around the value $b=2$. Some theoretical models of population growth, however, predict a broad range of values for the population exponent b pertaining to the mean and variance of population density, depending on details of the growth process. Is the widely reported sample exponent $b\simeq 2$ the result of ecological processes or could it be a statistical artifact? Here, we apply large deviations theory and finite-sample arguments to show exactly that in a broad class of growth models the sample exponent is $b\simeq 2$ regardless of the underlying population exponent. We derive a generalized TL in terms of sample and population exponents $b_{jk}$ for the scaling of the kth vs. the jth cumulants. The sample exponent $b_{jk}$ depends predictably on the number of samples and for finite samples we obtain $b_{jk}\simeq k/j$ asymptotically in time, a prediction that we verify in two empirical examples. Thus, the sample exponent $b\simeq 2$ may indeed be a statistical artifact and not dependent on population dynamics under conditions that we specify exactly. Given the broad class of models investigated, our results apply to many fields where TL is used although inadequately understood.

Taylor’s law (TL) (1), also known as fluctuation scaling in physics, is one of the most verified patterns in both the biological (2–6) and physical (7–12) sciences. TL states that the variance of a nonnegative random variable $V=\text{Var}\left[X\right]$ is approximately related to its mean $M=\mathbb{E}\left[X\right]$ by a power law; that is, $\text{Var}\left[X\right]=a\mathbb{E}{\left[X\right]}^b$, with $a>0$ and $b\in \mathrm{ℝ}$. In ecology, the random variable of interest is generally the size or density N of a censused population and TL can arise in time (i.e., the statistics of N are computed over time) or in space (i.e., the statistics are computed over space). The widespread verification of TL has led many authors to suggest the existence of a universal mechanism for its emergence, although there is currently no consensus on what such a mechanism would be. Various approaches have been used in the attempt, ranging from the study of probability distributions compatible with the law (13–15) to phenomenological and mechanistic models (16–20). Although most empirical studies on spatial TL report an observed sample exponent b in the range 1–2 (1, 21), mostly around $b\simeq 2$ (21) [figure 10(g) in ref. 22], population growth models (5, 23–26) can generate TL with any real value of the exponent. Moreover, theoretical investigations of multiplicative growth models in correlated Markovian environments (24, 25) have shown that the exponent b can undergo abrupt transitions following smooth changes in the environmental autocorrelation.

Here, we distinguish between values of b derived from empirical fitting (sample exponents) and values obtained via theoretical models that pertain to the probability distribution of the random variable N (population exponents). We show that in a broad class of multiplicative growth models, the sample and population exponents coincide only if the number of observed samples or replicates is greater than an exponential function of the duration of observation. Among the relevant consequences, we demonstrate that the sample TL exponent robustly settles on $b\simeq 2$ for any Markovian environment observed for a duration that is larger than a logarithmic function of the number of replicates. Accordingly, when the number of observations is limited, abrupt transitions in the sample TL exponent can be observed only within relatively short time windows.

Results

Let us consider multiplicative growth models in Markovian environments (24, 25). Let $N\left(t\right)$ be the density of a population at time t and assume that the initial density is $N_0>0$. $N\left(t\right)$ is assumed to undergo a multiplicative growth process such that

$$N\left(t\right)=N_0\hspace{0.17em}{\displaystyle \prod _{n=1}^t{A}_n}.$$ [1]

The values of the multiplicative growth factors $A_i$ are determined via a two-state homogeneous Markov chain with state space $\chi =\left\{r,s\right\}$ (we assume, without loss of generality, $r>s$ and $N_0=1$) and transition matrix $\mathrm{\Pi }$ with $\mathrm{\Pi }\left(i,j\right)>0$ for all $i,j\in \chi$ (Methods). In our notation, $\mathrm{\Pi }\left(i,j\right)$ is the one-step probability to go from state i to state j; i.e., $\mathrm{\Pi }\left(i,j\right)=\text{Prob}\left(A_{n+1}=j|A_n=i\right)$. For the sake of clarity, we restrict our discussion to symmetric transition matrices, with $\mathrm{\Pi }\left(i,j\right)=\lambda$ for $i\ne j$. We derive (Methods) exact results on both sample and population TL exponents for a broad class of multiplicative processes, including state spaces with size higher than 2 and nonsymmetric transition matrices (SI Methods).

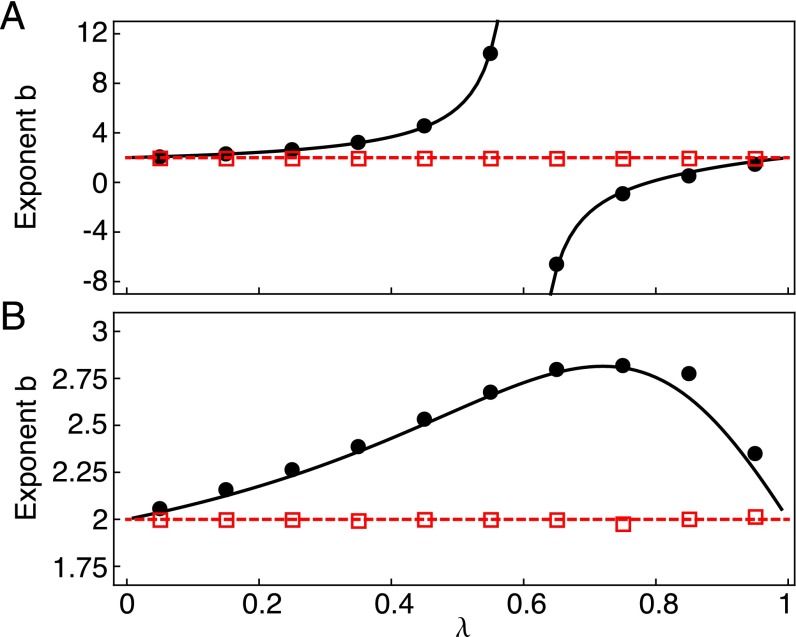
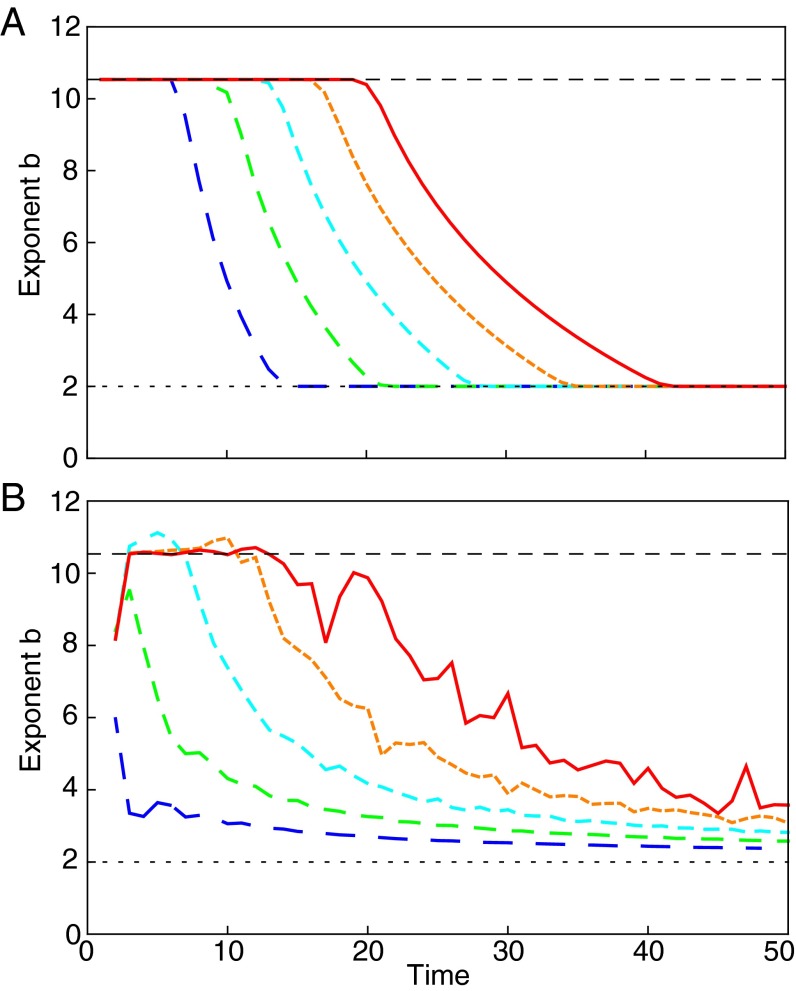
By adopting large deviation theory techniques (27, 28) and finite sample size arguments (29), we show (Methods) that for any choice of $\mathrm{\Pi }$ and χ, the sample mean and variance in a finite set of R independent realizations of the process obey TL asymptotically as $t\to \infty$ with an exponent that may differ from the corresponding population exponent. More precisely, our analysis reveals two regimes ($t\gg \log R$ and $1\ll t\ll \log R$, respectively—all logarithms here are to the base e) where the sample TL holds with different exponents. In the former regime, sample exponents inevitably tend to $b\simeq 2$ independently of model specifications. In the latter, sample exponents accurately approximate population ones, which can be computed analytically and may differ from $b=2$. Fig. 1 shows that simulation results and theoretical predictions in the two regimes are in excellent agreement. Fig. 2 shows the temporal evolution of the sample TL exponent, which crosses over from the approximate value of the population exponent (Eq. 9) at small times to the asymptotic prediction $b\simeq 2$ at larger times (Eq. 13).

Fig. 1.

TL exponent b for different values of the transition probability λ. The sample exponents computed in R simulations of a two-state multiplicative process with symmetric transition matrix in the two regimes $1\ll t\ll \log R$ (black solid circles, $R={10}^6$ up to time $t=10$) and $t\gg \log R$ (red open squares, $R={10}^4$ up to time $t=400$) are in good agreement with predictions for the asymptotic population (black solid line, Eq. 9) and sample (red dashed line, $b=2$) exponents. In the simulations, the sample exponent b was computed by least-squares fitting of $\log \mathrm{Var}\left[N\left(t\right)\right]$ as a function of $\log \mathbb{E}\left[N\left(t\right)\right]$ for the last 6 (black circles) and 200 (red squares) time steps. In A, which has the plotted theoretical result from ref. 24, $\chi =\left\{r,s\right\}=\left\{2,1/4\right\}$ (b displays a discontinuity); in B, $\chi =\left\{r,s\right\}=\left\{4,1/2\right\}$ (in such a case, b displays no discontinuity). Fig. S1 shows the generalized TL exponent $b_{23}$ in the same simulations.

Fig. 2.

Time evolution of the sample TL exponent. The sample exponent {computed as the slope of the curve $\log \mathbb{E}\left[N{\left(t\right)}^2\right]$ vs. $\log \mathbb{E}\left[N\left(t\right)\right]$} crosses over from the approximate population exponent (Eq. 9, dashed upper horizontal line) at small times to $b\simeq 2$ (dotted lower horizontal line) at larger times. The number of simulations $R={10}^n$ increases exponentially from ${10}^2$ (blue dashed lines) to ${10}^6$ (red solid lines), whereas the crossover time increases approximately linearly. Here, $\chi =\left\{r,s\right\}=\left\{2,1/4\right\}$ and the transition probability (with $\mathrm{\Pi }$ symmetric) is $\lambda =0.55$. (A) Theoretical prediction computed via Eq. 15. (B) Simulation results. Curves are averaged over ${10}^8/R$ simulations (except for the blue curve, averaged over ${10}^5$ simulations). Mismatches between A and B are due to the necessity to have t and R not too large to keep simulations feasible, whereas Eqs. 8 and 13 hold true asymptotically in t.

We derive a generalized TL that involves the scaling of the kth moment vs. the jth moment of the distribution of $N\left(t\right)$. Exact results (Methods) show that the generalized TL,

$$\mathbb{E}\left[N^k\left(t\right)\right]=a_{jk}\mathbb{E}{\left[N^j\left(t\right)\right]}^{b_{jk}},$$ [2]

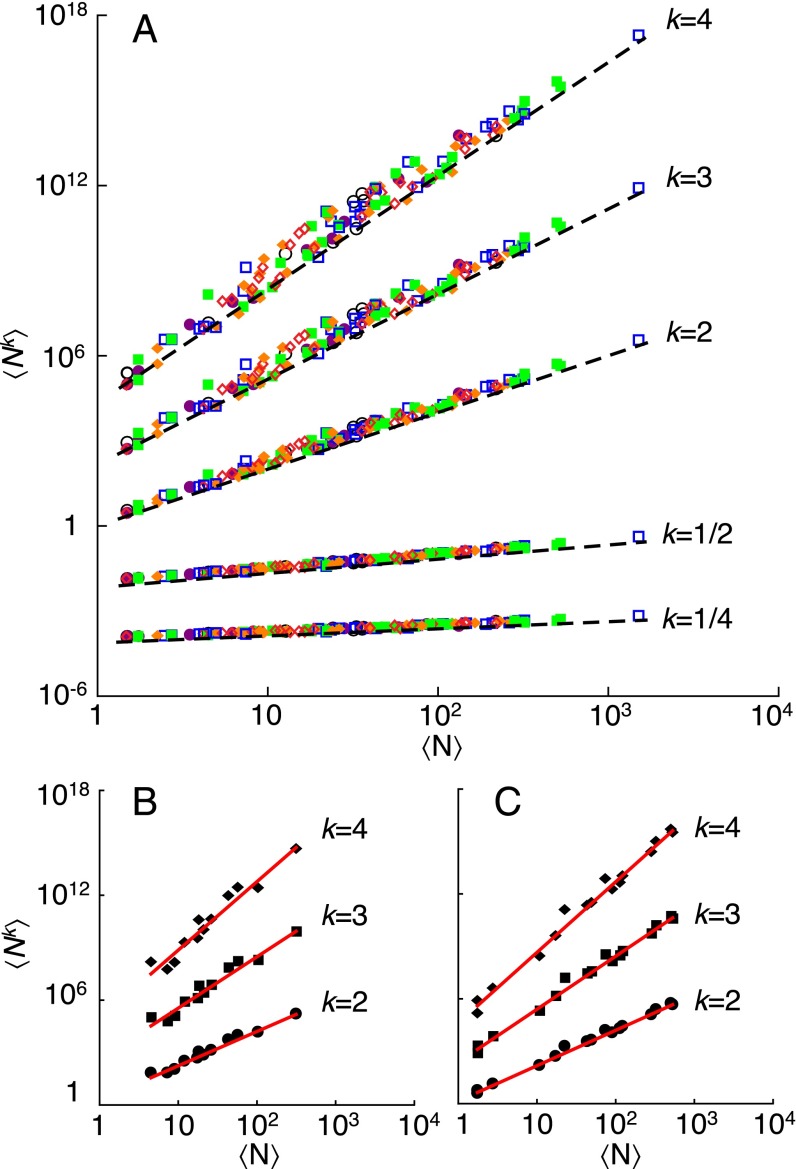
holds asymptotically in t for any choice of j and k (including noninteger values), both for population and for sample moments (the positivity of $\mathrm{\Pi }$ ensures that the same scaling relationship holds between the kth and jth cumulants) (SI Methods). In accordance with the above results on the conventional TL (recovered in this framework with the choice $j=1$, $k=2$), two regimes exist: If $1\ll t\ll \log R$, sample moments and cumulants accurately approximate population ones (and the value of $b_{jk}$ can be computed analytically); if $t\gg \log R$, the generalized TL exponent approximates $b_{jk}\simeq k/j$ (Fig. S1 C and D).

In ecological contexts, the number of realizations R that determine the possible convergence of sample and population TL exponents could refer, for instance, to independent patches experiencing different realizations of the same climate (24). In an established ecosystem, species have been present for several generations, and one might assume that the system is in the asymptotic regime $t\gg \log R$. Within this perspective, we tested the prediction that for large t sample exponents satisfy the relation $b_{jk}=k/j$ (including the conventional TL) on two datasets.

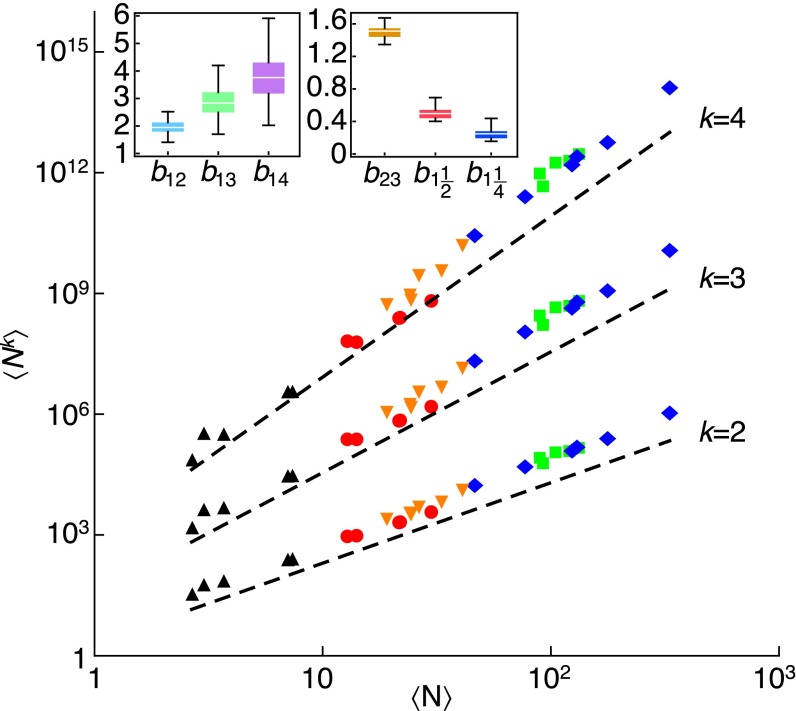
A first example is drawn from a long-term census of plots within the Black Rock Forest (BRF) (5). It was shown that the Lewontin–Cohen model (a particular case of the multiplicative model studied here) describes the population dynamics of trees in BRF and provides an interpretation of the TL exponent (5). The interpretation of the six plots as distinct and independent replicates of the Lewontin–Cohen model is supported by statistical analysis (5) and allowed relating the model predictions to the spatial TL. Here, we computed, for each year t, the spatial sample moments $\langle N^k\rangle \left(t\right)$ of tree abundance across plots and we found that the least-squares slopes $b_{jk}$ of $\log \langle N^k\left(t\right)\rangle$ vs. $\log \langle N^j\left(t\right)\rangle$ (Table 1) are compatible with the asymptotic model prediction $b_{jk}=k/j$ (Methods).

Table 1.

Sample exponents for the generalized TL in the Black Rock Forest dataset, data from ref. 5

$j,k$	$k/j$	$b_{jk}\pm$SE	$R^2$
1, 2	2	$2.14\pm 0.12$	0.991
1, 3	3	$3.33\pm 0.32$	0.973
1, 4	4	$4.54\pm 0.58$	0.954
2, 4	2	$2.15\pm 0.16$	0.984
2, 3	1.5	$1.57\pm 0.07$	0.995
3, 4	1.333	$1.37\pm 0.04$	0.997
1, 1/2	0.5	$0.48\pm 0.02$	0.997
1, 1/4	0.25	$0.23\pm 0.01$	0.993
1, 2/3	0.667	$0.65\pm 0.01$	0.999

A second example uses the data collected by P. den Boer (30), who measured abundances of carabid beetles in various sites across The Netherlands within a 200-km² area for 8 consecutive years. The dataset was shown to support the conventional spatial TL (16). We computed the sample moments of carabid beetles abundance, $\langle N^k\left(t\right)\rangle$, across similar sites (either woodland or heath), for each species separately and year t. In the intraspecific analysis (Fig. 3), linear regressions of $\log \langle N^k\left(t\right)\rangle$ vs. $\log \langle N^j\left(t\right)\rangle$ for $t=1,\dots ,Y$ (Y is the total number of years) gave the estimate of the sample exponent $b_{jk}$ for each species separately (different species are identified by different colors in Fig. 3). Frequency histograms of empirical exponents $b_{jk}$ are shown in Fig. S2 (also the box-whisker plots in Fig. 3, Insets); for every integer choice of j and k (here, up to $k=4$), the histogram is centered in $k/j$, as the asymptotic model predicted. A one-sample t test does not reject the null hypothesis that the sample mean of the values of $b_{jk}$ does not differ significantly from the theoretically predicted mean $k/j$ (Fig. S2). In the interspecific analysis (Fig. 4), we calculated the least-squares slope $b_{jk}$ (for $j=1$) of $\log \langle N^k\rangle$ vs. $\log \langle N\rangle$ across all species at a given year and site type (Tables S1 and S2). Each data point in Fig. 4 refers to a single species. The empirical exponents $b_{jk}$ for all years are compatible with the asymptotic model prediction $b_{jk}=k/j$, as are the mean (across years and site type) exponents $b_{jk}$ (Table 2).

Fig. 3.

Generalized TL for intraspecific patterns of carabid beetles abundance. Shown is a double logarithmic plot of $\langle N^k\rangle$ vs. $\langle N\rangle$ for different species (identified by different colors and symbols), for consecutive years (each symbol refers to a single year t). For visual clarity, only five species are shown. Dashed black lines of slopes $b_{1k}=k$ (asymptotic model prediction) are shown. Vertical offsets are introduced to aid comparison of slopes. (Insets) Box and whisker plots for the empirical distribution of intraspecific generalized TL exponents $b_{jk}$, showing the median (white horizontal line) and the $25\text{\%}$ and $75\text{\%}$ quantiles.

Fig. 4.

Generalized TL for interspecific patterns of abundance of carabid beetles. (A) Double logarithmic plot of $\langle N^k\rangle$ vs. $\langle N\rangle$ for all species, years, and site types. Each data point refers to a single species in 1 y and site type. The color and symbol code identifies data relative to the same year: 1961 (black open circles), 1962 (purple solid circles), 1963 (blue open squares), 1964 (green solid squares), 1965 (orange solid diamonds), and 1966 (red open diamonds). Dashed black lines of slope $b_{1k}=k$ (asymptotic model prediction) are plotted next to the corresponding data series. Vertical offsets are introduced to aid comparison of slopes. (B and C) Examples of interspecific moments scaling (each data point refers to a single species) for a single year and site type (B, woodland 1964; C, heath 1964) used for the statistical analysis (SI Methods, Table 2, Tables S1 and S2, and Fig. S5). The red lines are the least-squares regressions of $\log \langle N^k\rangle$ vs. $\log \langle N\rangle$ across species.

Table 2.

Statistics of estimated sample exponents in the interspecific generalized TL on carabid beetles abundances

$j,k$	$k/j$	$b_{jk}$	$2.5\text{\%}$ percentile	$97.5\text{\%}$ percentile
1, 2	2	2.005	1.984	2.025
1, 3	3	3.005	2.961	3.042
1, 4	4	3.994	3.936	4.057

The column $k/j$ gives the asymptotic model prediction for the exponent $b_{jk}$. The point estimate $b_{jk}$ is computed as the average $b_{jk}$ across years and site type, not by pooling all of the data from different years and site types to calculate means and variances. The confidence intervals are obtained via bootstrapping with ${10}^6$ bootstrap samples from the set of $b_{jk}$.

The empirical confirmation and the finding that other demographic models predict the generalized TL with $b_{jk}=k/j$ (SI Text) indicate that these predictions are probably insensitive to the details of the dynamics, just as the original TL is quite robust (3, 15, 31).

Discussion

Understanding to what extent widely reported macroecological patterns are the result of statistical instead of ecological processes is one of the main challenges in ecology (32). Here, we have uncovered a general mechanism that yields TL with the widely observed sample exponent $b\simeq 2$, which may be attributable to the finite size of both ecosystems and sampling efforts. For a broad range of parameters within the class of multiplicative models, and other demographic processes, the generalized TL describes the scaling of moments and cumulants with the sample exponent $b_{jk}$ asymptotically equal to $k/j$. Our theoretical predictions are supported by two empirical examples and invite further testing, also outside the field of ecology. When the number of samples is limited, TL may not reflect (or depend on) the underlying population dynamics and the empirically measured sample exponent may be a statistical artifact that is not representative of the population distribution of abundances. Our investigation provides a tool to discern whether the observed patterns of population abundance depend on the underlying population dynamics.

Limited sampling efforts might hinder the observation of abrupt transitions in population exponents that were recently discovered for theoretical multiplicative growth processes. Because fluctuations in population abundances strongly affect ecological dynamics, in particular extinction risk, comparable real-world transitions may harm fish populations, forests, and public health. Our calculation of the minimum number of samples required to observe such transitions may help to identify early signals of abrupt biotic change following smooth changes in the environment.

Methods

Theoretical Analysis.

Let $\mathrm{\Pi }$ be a $2\times 2$ symmetric matrix. The stationary distribution π of the chain is unique and in the symmetric case satisfies $\pi \left(i\right)=1/2$, $i\in \chi$, for all $\lambda \in \left(\mathrm{0,1}\right)$. We assume that the chain starts at equilibrium. We introduce the empirical mean $L_t\left(z\right):\chi \to \left[\mathrm{0,1}\right]$, defined as

$$L_t\left(z\right)=\frac{1}{t}{\displaystyle \sum _{n=1}^t{\delta }_{A_n,z}},$$ [3]

where δ is Kronecker’s delta. The random measure $L_t\left(r\right)$ gives the fraction of times that r appears in a realization of the Markov chain up to time t. $L_t$ satisfies a large deviation principle (LDP) (27) with rate function

$$I_{\mathrm{\Pi }}\left(x\right)=\underset{u>0}{\text{sup}}\left[x\log \left(\frac{u_1}{{\left(\mathrm{\Pi }u\right)}_1}\right)+\left(1-x\right)\log \left(\frac{u_2}{{\left(\mathrm{\Pi }u\right)}_2}\right)\right],$$ [4]

where x ($x\in \left[\mathrm{0,1}\right]$) is the proportion of r in a realization of the Markov chain up to time t (correspondingly, the proportion of s is $1-x$) and u is a strictly positive vector in ${\mathrm{ℝ}}^2$ (i.e., $u_1,u_2>0$). Stating that $L_t$ satisfies a LDP means that ${\lim }_{t\to \infty }\left(1/t\right)\log \mathrm{\mathbb{P}}\left(L_t\left(r\right)\in \left[x,x+dx\right]\right)=-I_{\mathrm{\Pi }}\left(x\right)$. The rate function $I_{\mathrm{\Pi }}\left(x\right)$ is convex ($d^2{I}_{\Pi }/d{x}^2>0$), attains its minimum at $x_{\text{min}}=1/2$ with $I_{\mathrm{\Pi }}\left(x_{\text{min}}\right)=0$, and is symmetric around $x_{\text{min}}$ (lemma IV.10 of ref. 27, theorems 3.1.2 and 3.1.6 of ref. 33, and section 4.3 of ref. 28). The subscript $\mathrm{\Pi }$ is used to indicate that the rate function depends on the transition matrix. Additionally, Eq. 4 depends on $u_1$ and $u_2$ only through $u\equiv u_2/u_1$; thus, by standard one-variable calculus, a long but explicit form of $I_{\mathrm{\Pi }}\left(x\right)$ can be computed,

$$\begin{array}{c}{I}_{\mathrm{\Pi }}\left(x\right)=\left(x-1\right)\log \left\{1-\lambda \left[\frac{2\left(\lambda -1\right)x}{S_{\lambda }\left(x\right)-2\lambda x}+1\right]\right\}\\ -\hspace{0.17em}x\log \left[1-\frac{\lambda \left(S_{\lambda }\left(x\right)-2x\right)}{2\left(\lambda -1\right)x}\right],\end{array}$$ [5]

where

$$S_{\lambda }\left(x\right)=\lambda +\sqrt{{\lambda }^2+8\lambda \left(x-1\right)x-4\left(x-1\right)x}.$$ [6]

The rate function does not depend on the values of the multiplicative factors r and s. As in ref. 25, we consider the ratio between $t^{-1}\log \mathrm{Var}\left[N\left(t\right)\right]$ and $t^{-1}\log \mathbb{E}\left[N\left(t\right)\right]$, but here we exploit the LDP, adopting Varadhan’s lemma (theorem III.13 of ref. 27), to perform such computation. First, because $\mathrm{\Pi }$ is positive and $r\ne s$, it holds true that

$$\underset{t\to \infty }{\lim }{t}^{-1}\log \mathrm{Var}\left[N\left(t\right)\right]=\underset{t\to \infty }{\lim }{t}^{-1}\log \mathbb{E}\left[N{\left(t\right)}^2\right].$$ [7]

See the appendix in ref. 25 for a proof. Then, for the population moments of the population density $N\left(t\right)$, applying Varadhan’s lemma, we have

$$\underset{t\to \infty }{\lim }{t}^{-1}\log \mathbb{E}\left[N{\left(t\right)}^k\right]=\underset{x\in \left[\mathrm{0,1}\right]}{\sup }\left[kG\left(x\right)-I_{\mathrm{\Pi }}\left(x\right)\right],$$ [8]

where $G\left(x\right)=x\log r+\left(1-x\right)\log s$. The population TL exponent b (which depends on λ) can thus be computed as

$$b\left(\lambda \right)=\frac{{\sup }_{x\in \left[\mathrm{0,1}\right]}\left[2G\left(x\right)-I_{\mathrm{\Pi }}\left(x\right)\right]}{{\sup }_{x\in \left[\mathrm{0,1}\right]}\left[G\left(x\right)-I_{\mathrm{\Pi }}\left(x\right)\right]}.$$ [9]

For certain values of r and s, $b\left(\lambda \right)$ can show a discontinuity at a critical value of the transition probability λ (black line in Fig. 1A). The existence of such discontinuity was discovered and discussed in ref. 24. An analysis of the critical transition probability is available in SI Methods (Figs. S3 and S4). A generalized TL can be derived by adapting Eq. 8 to compute the scaling exponent for any pair of population moments as

$$b_{jk}\left(\lambda \right)=\frac{{\lim }_{t\to \infty }{t}^{-1}\log \mathbb{E}\left[N{\left(t\right)}^k\right]}{{\lim }_{t\to \infty }{t}^{-1}\log \mathbb{E}\left[N{\left(t\right)}^j\right]}=\frac{{\sup }_{x\in \left[\mathrm{0,1}\right]}\left[kG\left(x\right)-I_{\mathrm{\Pi }}\left(x\right)\right]}{{\sup }_{x\in \left[\mathrm{0,1}\right]}\left[jG\left(x\right)-I_{\mathrm{\Pi }}\left(x\right)\right]}.$$ [10]

Discontinuities can also arise for these population exponents (SI Methods).

Eqs. 9 and 10 hold true when one considers an infinite number of realizations of the multiplicative process, which ensures visiting the whole region $x\in \left[\mathrm{0,1}\right]$. We now estimate the sample exponent b that is based on the sample mean and variance calculated over a finite set of R realizations of the multiplicative process. We present here a heuristic derivation of the sample exponent. A more rigorous calculation is given in SI Methods. We define $x_{+}$ as the value in $\left[\mathrm{0,1}\right]$ such that the probability of a larger frequency x of r in R runs of the Markov chain up to time t is $1/R$:

$$\mathrm{\mathbb{P}}\left(L_t\left(r\right)\in \left(x_{+},1\right]\right)=\frac{1}{R}.$$ [11]

With this definition, $x_{+}$ can be interpreted (29) as the typical maximum frequency of r in R realizations of the chain. Analogously, we define $x_{-}$ as the value such that smaller values of the frequency of r are observed with probability $1/R$, namely $\mathrm{\mathbb{P}}\left(L_t\left(r\right)\in \left[0,x_{-}\right)\right)=1/R$. For large t, one can adapt Varadhan’s lemma (or Laplace’s method of integration) to obtain, as a function of t, the approximate number of replicas R needed to explore rare events [i.e., to compute $\mathrm{\mathbb{P}}\left(L_t\left(r\right)\in \left(x_{+},1\right]\right)=R^{-1}$]. Approximately

$$R\simeq \exp \left[t{I}_{\mathrm{\Pi }}\left(x_{\pm }\right)\right].$$ [12]

Inversion of this formula (by taking the logarithm on both sides and expanding $I_{\mathrm{\Pi }}$ in Taylor series around $x=x_{\text{min}}$) gives $x_{\pm }\simeq 1/2\pm \sqrt{\left(\left(1-\lambda \right)/2\lambda \right)\left(\left(\log R\right)/t\right)}$. Consequently, the sample TL exponent in an ensemble of R realizations of the process can be approximated as

$$b\left(\lambda ,t\right)\simeq \frac{{\sup }_{x\in \left[x_{-},x_{+}\right]}\left[2G\left(x\right)-I_{\mathrm{\Pi }}\left(x\right)\right]}{{\sup }_{x\in \left[x_{-},x_{+}\right]}\left[G\left(x\right)-I_{\mathrm{\Pi }}\left(x\right)\right]},$$ [13]

where the dependence on t is through $x_{+}$ and $x_{-}$. The zero of the rate function, $x_{\text{min}}=1/2$, corresponds to the most probable value of the product in Eq. 1. Because $x_{\pm }\simeq 1/2\pm \sqrt{\left(\left(1-\lambda \right)/2\lambda \right)\left(\left(\log R\right)/t\right)}$, for fixed R the suprema in Eq. 13 are computed over an increasingly narrower set around $x_{\text{min}}$ [with $I_{\mathrm{\Pi }}\left(x_{\text{min}}\right)=0$] as t increases (Fig. 5). Thus, for any finite number of realizations R, the sample exponent will approximate ${\lim }_{t\to \infty }b\left(\lambda ,t\right)\simeq 2$ after a time $t^{\ast }$ that increases only logarithmically with R (Eq. 12 and Fig. 2), for any choice of λ, r, and s. For example, with $\lambda =0.5$, when $t=100$, to access the extreme event $x_{+}=0.9$ (and $x_{-}=0.1$) one needs about $R\simeq {10}^{13}$ replicates of the process. More precisely, the sample exponent is close to the population exponent if the arguments of the two suprema in Eq. 9 are included in $\left[x_{-},x_{+}\right]$. Using $x_{\pm }\simeq 1/2\pm \sqrt{\left(\left(1-\lambda \right)/2\lambda \right)\left(\left(\log R\right)/t\right)}$, if the largest argument of the suprema in Eq. 9 is $\tilde{x}>1/2$, the sample exponent approximates accurately the population exponent for $t<\left(\left(1-\lambda \right)/\lambda \right){\left(\tilde{x}-1/2\right)}^{-2}\log R$ and tends to $k/j$ for $t>\left(\left(1-\lambda \right)/\lambda \right){\left(\tilde{x}-1/2\right)}^{-2}\log R$ (Figs. 1 and 2). If r and s are such that the population TL exponent b displays a discontinuity at $\lambda ={\lambda }_c$ [in which case ${\lambda }_c=\left(1-r-s+rs\right)/\left(-r-s+2rs\right)$] (SI Methods), then the above results give the minimum number of replicates required to observe such discontinuity also in the sample TL exponent.

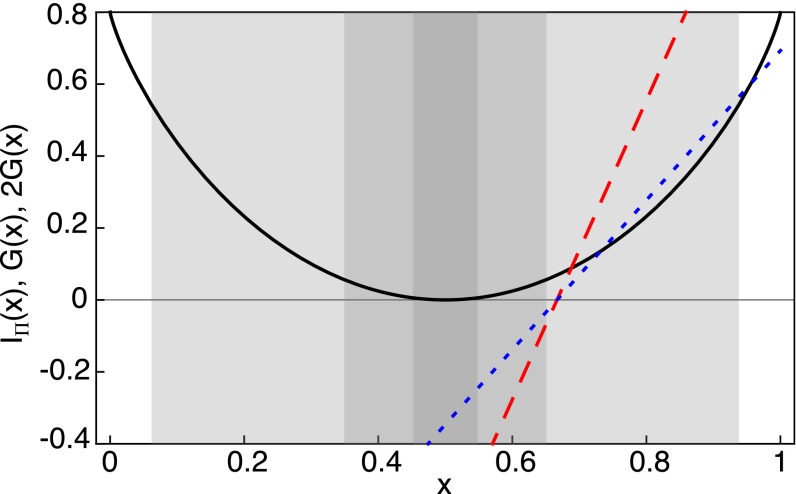
Fig. 5.

Plot of $I_{\mathrm{\Pi }}\left(x\right)$ (black curve), $G\left(x\right)$ (dotted blue line), and $2G\left(x\right)$ (dashed red line). Marked in gray are the regions $\left[x_{-},x_{+}\right]$ at times $t=10$, 100, and 1,000 (from light to dark gray) for fixed $R=100$. These gray regions are the intervals over which the supremum in Eq. 13 is computed. In this example, $r=2$, $s=1/4$, $\lambda =0.55$. The quantities $x_{+}$ and $x_{-}$ are computed by solving numerically Eq. 12.

Analogous considerations hold for the asymptotic sample exponent describing the scaling of the sample moments $\mathbb{E}\left[N{\left(t\right)}^k\right]$ with $\mathbb{E}\left[N{\left(t\right)}^j\right]$, which can be approximated as

$$b_{jk}\left(\lambda ,t\right)\simeq \frac{{\sup }_{x\in \left[x_{-},x_{+}\right]}\left[kG\left(x\right)-I_{\mathrm{\Pi }}\left(x\right)\right]}{{\sup }_{x\in \left[x_{-},x_{+}\right]}\left[jG\left(x\right)-I_{\mathrm{\Pi }}\left(x\right)\right]},$$ [14]

which is the analog of Eq. 13 for any pair of sample moments. Fig. S1 C and D shows that simulation results and theoretical predictions for $b_{jk}$ show excellent agreement in the two regimes $t\gg \log R$ and $1\ll t\ll \log R$.

A standard saddle-point calculation suggests that the limiting growth rate of the variance is equal to the limiting growth rate of the second moment also for ergodic transition matrices, apart from peculiar cases (see ref. 25 for a discussion of a counterexample). The same argument suggests that the limiting growth rate of the kth cumulant equals that of the kth moment ($t^{-1}\log \mathbb{E}\left[N{\left(t\right)}^k\right]$) for large t. The suggested equivalence between the scaling exponents of cumulants and moments for ergodic $\mathrm{\Pi }$ would allow extending the result on the sample TL ($b=2$) and generalized TL ($b=k/j$) to the scaling of cumulants in m-step Markov chains, whose transition matrix is ergodic but not twofold irreducible. However, pathological counterexamples may exist.

Eq. 13 gives the estimated sample exponent of TL asymptotically, ignoring the constant term in the scaling of the variance V vs. the mean M as $\log V=b\log M+\log a$. For small t, $\log a$ can be of the same order of magnitude as $\log V$. Fig. 2 shows the crossover of the sample exponent (for fixed R, λ, r, and s) from the population exponent $b=b\left(\lambda \right)$ as in Eq. 9 (observed when $t\ll \log R$) to $b\simeq 2$ (when $t\gg \log R$), where the sample exponent is calculated as the slope of the curve $\log \mathbb{E}\left[N{\left(t\right)}^2\right]$ vs. $\log \mathbb{E}\left[N\left(t\right)\right]$ at time t (thus not neglecting the constant term $\log a$). The sample moments are computed as

$$t^{-1}\log \mathbb{E}\left[N{\left(t\right)}^k\right]\simeq \underset{x\in \left[x_{-},x_{+}\right]}{\sup }\left[kG\left(x\right)-I_{\mathrm{\Pi }}\left(x\right)\right]$$ [15]

(compare Eq. 8) in Fig. 2A and as the sample moments in simulations in Fig. 2B.

See SI Methods for further details and generalizations.

Empirical Analysis.

We used the BRF dataset to show that the generalized TL holds with sample exponent $b_{jk}=k/j$. We computed the moment ratios $\langle {\left[N\left(t\right)/N_0\right]}^k\rangle$, where the symbol $\langle \cdot \rangle$ identifies the sample mean across the six plots of BRF and $N_0$ is the number of trees at the start of the census in 1931. Following ref. 5, we tested whether the moments of the spatial density ratio $N\left(t\right)/N_0$ in the five most recent censuses satisfied TL and the generalized TL with $b_{jk}=k/j$. Table 1 reports the slopes of the least-squares linear regressions of $\langle {\left[N\left(t\right)/N_0\right]}^k\rangle$ vs. $\langle {\left[N\left(t\right)/N_0\right]}^j\rangle$, which are all compatible with the model prediction $b_{jk}=k/j$. The BRF dataset thus provides an empirical example where the multiplicative model satisfactorily describes the underlying dynamics and the generalized TL holds asymptotically as the model predicts.

The intraspecific form of TL and the generalized scaling relationship between higher moments (Eq. 2) were tested using abundance data from 26 species of carabid beetles. We have limited the analysis of the intraspecific TL to the set of species that were present in all sites in each given year. We have followed the researchers who collected the carabid beetles abundance data (30) in excluding species with year samples with zero individuals in at least one of the sites from the statistical analysis. The authors of ref. 30 declared that they were unable to differentiate sites where a species was not present from sites where the density of such species was so low that no catches were realized. For each species, we selected data from a minimum of three to a maximum of six sites (all either woodland or heath) (30) and from a minimum of 4 to a maximum of 6 consecutive years. The precise number of sites and years varied for each species, depending on the number of sites and years in which at least one individual of such species was found in each site. The moments of species abundance were calculated separately for each species and for each available year. Linear regressions of $\log \langle N^k\left(t\right)\rangle$ vs. $\log \langle N^j\left(t\right)\rangle$ for $y=\mathrm{1,2},\dots ,Y$ [where Y is the total number of available years for the selected species and $\langle N^k\left(t\right)\rangle$ is the kth spatial sample moment in year t] gave the estimate of the sample exponent $b_{jk}$ for the selected species (Fig. 3).

The interspecific form of TL and the generalized scaling relationship for statistical moments (Eq. 2) were investigated following ref. 16, using the carabid beetles dataset, computing spatial sample moments across similar sites. Data from sites labeled B, C, X, and AE in ref. 30, collected between 1961 and 1966, were used to calculate spatial moments across woodland sites. Data from sites labeled AT, N, Z, and AG in ref. 30, collected between 1963 and 1966, were used to calculate spatial moments across heath sites. As for the intraspecific TL analysis, we have limited the analysis of the interspecific TL to the set of species that were present in all sites in each given year. Spatial moments of carabid beetles abundance were computed for each species individually and separately for each year and site type (woodland or heath). For each year, we calculated the least-squares slope of $\log \langle N^k\rangle$ vs. $\log \langle N\rangle$ across all species at a given year and site type. Tables S1 and S2 show the summary statistics for all years and site types. Fig. 4A and Fig. S5 M and N show the scaling of the kth sample moment $\langle N^k\rangle$ with $\langle N\rangle$ when data for all years and site types are plotted together; each data point in Fig. 4 and in Fig. S5 refers to the spatial moments of a single species in one year and site type. Fig. S5 A–L shows the scaling of the kth sample moment $\langle N^k\rangle$ with $\langle N\rangle$ for each year and site type separately. The least-squares exponents $b_{jk}$ computed in the linear regression of $\log \langle N^k\rangle$ vs. $\log \langle N^j\rangle$ are compatible with the asymptotic model prediction $b_{jk}=k/j$ (Tables S1 and S2), as are the mean exponents $b_{jk}$ (Table 2).

See SI Methods and Tables S3 and S4 for further details.