Development and validation of a comprehensive model for map of fruits based on enzyme kinetics theory and arrhenius relation

Abstract

MAP is a dynamic system where respiration of the packaged product and gas permeation through the packaging film takes place simultaneously. The desired level of O₂ and CO₂ in a package is achieved by matching film permeation rates for O₂ and CO₂ with respiration rate of the packaged product. A mathematical model for MAP of fresh fruits applying enzyme kinetics based respiration equation coupled with the Arrhenious type model was developed. The model was solved numerically using MATLAB programme. The model was used to determine the time to reach to the equilibrium concentration inside the MA package and the level of O₂ and CO₂ concentration at equilibrium state. The developed model for prediction of equilibrium O₂ and CO₂ concentration was validated using experimental data for MA packaging of apple, guava and litchi.

Introduction

Modified-atmosphere packaging (MAP) of fresh commodity refers to the technique of sealing actively respiring produce in polymeric film packages to modify the O₂ and CO₂ levels within the package atmosphere. It is often desirable to generate an atmosphere low in O₂ and/or high in CO₂ to influence the metabolism of the product being packaged, or the activity of decay-causing organisms to increase storability and/or shelf life (Kader et al. 1989; Mangaraj et al. 2009). In addition to atmosphere modification, MAP vastly improves moisture retention, which can have a greater influence on preserving quality than O₂ and CO₂ levels (Mangaraj and Tripathi 2013). Furthermore, packaging isolates the product from the external environment and helps to ensure conditions that, if not sterile, at least reduce exposure to pathogens and contaminants (Mahajan et al. 2007).

MAP is a dynamic system during which respiration and permeation occur simultaneously. In a properly designed MAP, after a period of transient state an equilibrium state is established. At equilibrium, the amount of O₂ entering into the package and that of CO₂ permeating out of the package become equal to the amount of O₂ consumed and that of CO₂ evolved by the packaged fruit, respectively (Yam and Lee 1995; Del Nobile et al. 2007). Respiration rate of the commodity, permeability of packaging film, mass of the produce packed inside the package, area of the packaging film, surrounding gas composition, optimum level of O₂ and CO₂ concentration, storage temperature etc. affect the equilibrium gas concentration (Yam and Lee 1995; Jacxsens et al. 2000; Mangaraj et al. 2013a) and they are taken as input parameters for developing mathematical model.

Different mathematical models were developed to describe the mass balance of O₂ and CO₂ concentration inside the package during storage. These model parameters were considered for theoretical design of MAP of commodity. Cameron et al. (1989) employed O₂ depletion method for determining O₂ consumption in a closed system for tomatoes and optimized the package parameters based on the gas exchange model. Christie et al. (1995) proposed a material balance equation that relates the package film permeability and produce metabolism to the in-package gas concentrations. Song et al. (2002) developed a MAP model based on mass balances and the transport phenomenon across the package and solved it numerically using Adams-Moulton’s numerical technique. The reasons for choosing the Adams-Moulton's numerically technique in this MAP model is due to the fact that it is useful for the solution of the differential equation to calculate and predict the variation of oxygen and carbon dioxide concentration with time. This method is very accurate for solving the higher order differential equation that form in MAP modeling process.

Rocculi et al. (2006) developed the models applying Michaelis-Menten’s equation and Arrehnius’s type expression to describe the mass balance of O₂ and CO₂ concentration inside the MA package for minimally processed apple packed in multilayer pouches. Torrieri et al. (2007) studied the effect of temperature, oxygen, red coloration process and post-harvest storage time on the respiration rate of fresh-cut Annurca apples for developing suitable MAP. Mahajan et al. (2007) developed software for MAP design of fresh and fresh-cut produce for selecting suitable packaging materials. Techavises and Hikida (2008) developed a mathematical model based on Fick’s law for predicting O₂, CO₂, N₂, and water vapor exchange in film packaging with macroscopic perforations.

A systematic theoretical design and modeling is needed to establish conditions for the success and benefit of MAP for a particular produce (Exama et al. 1993; Mahajan et al. 2007). Such a design and analysis could provide closely the characteristic of the commodity, film properties and optimized packaging parameters. Simulation of a MAP system is the most appropriate method to allow a correct MAP design and consequently obtain a successful commercial product (Cameron et al. 1989; Makino and Iwasaki 1997; Del Nobile et al. 2007).

Considering these approaches in mind a global model for MA packaging of fruits was proposed. The proposed model coupled to the principle of enzyme kinetics equation that describes the dependence of respiration rate on gas composition, temperature (and eventually time) and models that describes the dependence of packaging material on temperature; with the mass balance equations that describes the gaseous exchange in MAP. Using this model the variation of O₂ and CO₂ inside the MA package and the time to reach equilibrium level could be predicted accurately at any storage temperature.

Materials and methods

Respiration rate model

The Michaelis-Menten type equation based on principle of enzyme kinetics with uncompetitive type of inhibition, wherein CO₂ does not bind with the enzyme but reacts with enzyme substrate complex (Lee and Wicker 1991), was the model fitted to the experimental respiration data (Peppelenbos and Leven 1996; Mangaraj and Goswami 2011a, b). The relevant enzyme kinetics models are shown Eqs. (1) and (2).

$${\mathrm{R}}_{\mathrm{O}2}=\frac{{\mathrm{V}}_{\mathrm{m}\left(\mathrm{O}2\right)}\times {\mathrm{Y}}_{\mathrm{O}2}}{{\mathrm{k}}_{\mathrm{m}\left(\mathrm{O}2\right)}+\left\{1+\left(\left[{\mathrm{Z}}_{\mathrm{CO}2}\right]\right)/{\mathrm{k}}_{\mathrm{i}\left(\mathrm{O}2\right)}\right\}{\mathrm{Y}}_{\mathrm{O}2}}$$ 1

$${\mathrm{R}}_{\mathrm{CO}2}=\frac{{\mathrm{V}}_{\mathrm{m}\left(\mathrm{CO}2\right)}\times {\mathrm{Y}}_{\mathrm{O}2}}{{\mathrm{k}}_{\mathrm{m}\left(\mathrm{CO}2\right)}+\left\{1+\left(\left[{\mathrm{Z}}_{\mathrm{CO}2}\right]/{\mathrm{k}}_{\mathrm{i}\left(\mathrm{CO}2\right)}\right)\right\}{\mathrm{Y}}_{\mathrm{O}2}}$$ 2

The temperature dependence of the model parameters of the above Michaelis-Menten equations was quantified using an Arhhenius model (Mangaraj and Goswami 2008).

$${\mathrm{R}}_{\mathrm{m}}={\mathrm{R}}_{\mathrm{p}}exp\left[\frac{{\mathrm{E}}_{\mathrm{a}}}{\mathrm{R}\times {\mathrm{T}}_{\mathrm{abs}}}\right]$$ 3

Model for gas transmission rates

The gas transmission rates (OTR/CTR) of polymeric film are temperature dependent and hence Arrhenius-equations of the following type were fitted to the experimental data to depict the relationship of GTR with temperature (Exama et al. 1993).

$$\mathrm{GTR}=\mathrm{GT}{\mathrm{R}}_{\mathrm{p}}exp\left[\frac{-{\mathrm{E}}_{\mathrm{aGTR}}}{\mathrm{R}{\mathrm{T}}_{\mathrm{abs}}}\right]$$ 4

Design variables in MAP

The variables involved in the MA package design are: the surrounding gases composition (Y_O2^a and Z_CO2^a), temperature (T), O₂ consumption rate and CO₂ production rate (R_O2 and R_CO2), the optimum gas composition to be attained in the package (Y_O2^eq and Z_CO2^eq), weight of the fruits in package (W_p), surface area of the packaging film (A_p), free volume of the package (V_fp), thickness of the film (x), gas transmission rates of film to O₂ and CO₂ (OTR and CTR). The ultimate aim of this design was to select suitable films for a 1 ± 0.1 kg fill weight so that the equilibrium concentrations of O₂ and CO₂ are reached within shortest possible time and these concentrations lie within the range required for maximum shelf life of stored fruits (Das 2005; Mangaraj et al. 2009; Mangaraj et al. 2011). The package size of 1 ± 0.1 kg was considered based on survey conducted at the local market.

Target level of MA package air composition for fruits

The recommended level of gas concentration in CA/MA storage of apple, guava and litchi for maintaining quality and extending shelf-life are 1–3 and 3–5 %; 2–5 and 2–5 %; 3–5 and 3–5 % O₂ and CO₂, respectively (Mangaraj and Goswami 2009a, b; Singh and Pal 2008; Shivakumar et al. 2007) with N₂. On the basis of preliminary investigations and the sub-optimal package air composition it was found appropriate for designing the optimal MA packages for apple, guava and litchi with target air composition of 3 %O₂ and 3 % CO₂; 5 %O₂ and 4 % CO₂; 5 %O₂ and 5 % CO₂ in N₂, respectively.

Development of MAP model for fruits

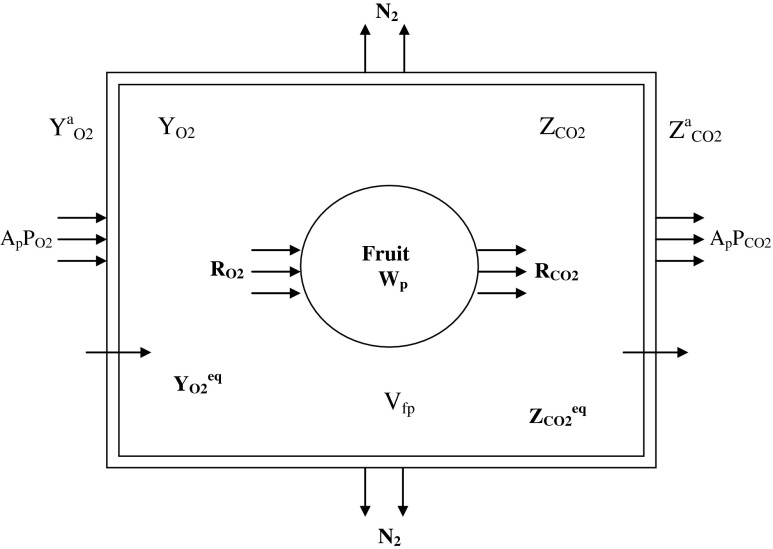
Respiration of the fruits and the gas permeation through the packaging film takes place simultaneously during MA packaging. In general, the relative humidity in the internal package atmosphere is higher than the external atmosphere. Hence some amount of water vapor may permeate out of the package, depending upon the WVTR of the polymeric film. The mathematical modeling of gaseous exchange for respiratory gases (O₂ and CO₂) has been attempted here. The diagrammatic representation of the gaseous exchange in MAP is shown in Fig. 1.

Fig. 1.

Diagrammatic representation of gaseous exchange in MAP system

The concept is that once the fruit is sealed inside the package the O₂ and CO₂ concentration gradients develop due to the fruit respiration and the polymeric film serves as the regulator of O₂ flow into the package and the flow of CO₂ out of the package. At a given temperature and for a considerably small length of transient period, the rates of O₂ consumption (R_O2) and the rate of CO₂ evolution (R_CO2) of the packaged fruits depend greatly on O₂ concentration (Y_O2) and CO₂ concentration (Z_CO2). Considering that there is no gas stratification inside the packages and that the total pressure is constant (Mahajan et al. 2007; Mangaraj et al. 2011), the differential mass balance equations that describe the O₂ concentration changes in a package containing respiring product are:

Rate of O₂ entry into package space—Rate of O₂ consumed by product

= Rate of O₂ accumulation inside package space

$$\mathrm{That}\mathrm{is,}{\mathrm{A}}_{\mathrm{p}}{\mathrm{P}}_{\mathrm{O}2}\left({\mathrm{Y}}_{\mathrm{O}2}^{\mathrm{a}}-{\mathrm{Y}}_{\mathrm{O}2}\right)-{\mathrm{W}}_{\mathrm{p}}{\mathrm{R}}_{\mathrm{O}2}={\mathrm{V}}_{\mathrm{fp}}\left(\frac{\mathrm{d}{\mathrm{Y}}_{\mathrm{O}2}}{\mathrm{dt}}\right)$$ 5

$$\mathrm{Or}\left(\frac{\mathrm{d}{\mathrm{Y}}_{\mathrm{O}2}}{\mathrm{dt}}\right)=-\left(\frac{{\mathrm{W}}_{\mathrm{p}}}{{\mathrm{V}}_{\mathrm{fp}}}\right){\mathrm{R}}_{\mathrm{O}2}+\left(\frac{{\mathrm{A}}_{\mathrm{p}}{\mathrm{P}}_{\mathrm{O}2}}{{\mathrm{V}}_{\mathrm{fp}}}\right)\left({\mathrm{Y}}_{\mathrm{O}2}^{\mathrm{a}}-{\mathrm{Y}}_{\mathrm{O}2}\right)$$ 6

Similarly, the CO₂ concentration changes in a package can be written as,

Rate of CO₂ generated by the fruits—Rate of CO₂ leaving out of the package space

= Rate of accumulation CO₂ inside package space

That is,

$${\mathrm{W}}_{\mathrm{p}}{\mathrm{R}}_{\mathrm{CO}2}-{\mathrm{A}}_{\mathrm{p}}{\mathrm{P}}_{\mathrm{Co}2}\left({\mathrm{Z}}_{\mathrm{CO}2}-{\mathrm{Z}}_{\mathrm{CO}2}^{\mathrm{a}}\right)={\mathrm{V}}_{\mathrm{fp}}\left(\frac{\mathrm{d}{\mathrm{Z}}_{\mathrm{CO}2}}{\mathrm{dt}}\right)$$ 7

$$\mathrm{Or}\left(\frac{\mathrm{d}{\mathrm{Z}}_{\mathrm{CO}2}}{\mathrm{dt}}\right)=\left(\frac{{\mathrm{W}}_{\mathrm{p}}}{{\mathrm{V}}_{\mathrm{fp}}}\right){\mathrm{R}}_{\mathrm{CO}2}-\left(\frac{{\mathrm{A}}_{\mathrm{p}}{\mathrm{P}}_{\mathrm{CO}2}}{{\mathrm{V}}_{\mathrm{fp}}}\right)\left({\mathrm{Z}}_{\mathrm{CO}2}-{\mathrm{Z}}_{\mathrm{CO}2}^{\mathrm{a}}\right)$$ 8

The Eqs. 6 and 8 were coupled to the enzyme kinetics models that describes the dependence of respiration rate on gas composition, temperature (and eventually time) i.e. Eqs. 1, 2 and 3 and models that describes the dependence of packaging film on temperature, i.e. Eq. 4 constitute the basic of development MAP models. Now substituting the Eqs. 1, 2, 3 and 4 appropriately in Eqs. 6 and 8 we have:

$$\left(\frac{\mathrm{d}{\mathrm{Y}}_{\mathrm{O}2}}{\mathrm{dt}}\right)=-\left(\frac{{\mathrm{W}}_{\mathrm{p}}}{{\mathrm{V}}_{\mathrm{fp}}}\right)\times 〈\frac{\left({\mathrm{R}}_{\mathrm{pvmO}2}\times exp\left[\frac{-{\mathrm{E}}_{\mathrm{avmO}2}}{\mathrm{R}\times {\mathrm{T}}_{\mathrm{abs}}}\right]\right)\times {\mathrm{Y}}_{\mathrm{O}2}}{\left({\mathrm{R}}_{\mathrm{pvmO}2}\times exp\left[\frac{-{\mathrm{E}}_{\mathrm{akmO}2}}{\mathrm{R}\times {\mathrm{T}}_{\mathrm{abs}}}\right]\right)+\left\{1+\left[\left[{\mathrm{Z}}_{\mathrm{CO}2}\right]÷\left({\mathrm{R}}_{\mathrm{pkiO}2}\times exp\left[\frac{-{\mathrm{E}}_{\mathrm{akiO}2}}{\mathrm{R}\times {\mathrm{T}}_{\mathrm{abs}}}\right]\right)\right]\right\}\times {\mathrm{Y}}_{\mathrm{O}2}}〉+\left(\frac{{\mathrm{A}}_{\mathrm{p}}\times \left(\mathrm{OT}{\mathrm{R}}_{\mathrm{p}}\times exp\left[\frac{{\mathrm{E}}_{\mathrm{aOTR}}}{\mathrm{R}{\mathrm{T}}_{\mathrm{abs}}}\right]\right)}{{\mathrm{V}}_{\mathrm{fp}}}\right)\times \left({\mathrm{Y}}_{\mathrm{O}2}^{\mathrm{a}}-{\mathrm{Y}}_{\mathrm{O}2}\right)$$ 9

$$\begin{array}{l}\left(\frac{\mathrm{d}{\mathrm{Z}}_{\mathrm{CO}2}}{\mathrm{dt}}\right)=\left(\frac{{\mathrm{W}}_{\mathrm{p}}}{{\mathrm{V}}_{\mathrm{fp}}}\right)\times 〈\frac{\left({\mathrm{R}}_{\mathrm{pvmCO}2}\times exp\left[\frac{-{\mathrm{E}}_{\mathrm{avmCO}2}}{\mathrm{R}\times {\mathrm{T}}_{\mathrm{abs}}}\right]\right)\times {\mathrm{Y}}_{\mathrm{O}2}}{\left({\mathrm{R}}_{\mathrm{pkmCO}2}\times exp\left[\frac{-{\mathrm{E}}_{\mathrm{akmCO}2}}{\mathrm{R}\times {\mathrm{T}}_{\mathrm{abs}}}\right]\right)+\left\{1+\left[\left[{\mathrm{Z}}_{\mathrm{CO}2}\right]÷\left({\mathrm{R}}_{\mathrm{pkiCO}2}\times exp\left[\frac{-{\mathrm{E}}_{\mathrm{akiCO}2}}{\mathrm{R}\times {\mathrm{T}}_{\mathrm{abs}}}\right]\right)\right]\right\}\times {\mathrm{Y}}_{\mathrm{O}2}}〉-\left(\frac{{\mathrm{A}}_{\mathrm{p}}\times \left(\mathrm{CT}{\mathrm{R}}_{\mathrm{P}}\times \left[\frac{{\mathrm{E}}_{\mathrm{aCTR}}}{\mathrm{R}{\mathrm{T}}_{\mathrm{abs}}}\right]\right)}{{\mathrm{V}}_{\mathrm{fp}}}\right)\times \left({\mathrm{Z}}_{\mathrm{CO}2}-{\mathrm{Z}}_{\mathrm{CO}2}^{\mathrm{a}}\right)\\ \end{array}$$ 10

Numerical analysis

Simultaneous solution of above differential equations would give variation of O₂ concentration, Y_O2 (volume fraction), CO₂ concentration, Z_CO2 (volume fraction) as a function of time, t (h). The typical functional relationship for R_O2 and R_CO2 as a function of Y_O2 and Z_CO2 is carried out numerically, using Adams numerical method, which is based on Taylor’s formula (Piskunov 1981).

The estimated values of respiration model parameters R_p and E_a for O₂ consumption and CO₂ evolution, along with the weight of fruits (W_p) constitute the product parameters. The GTR_p, E_aOTR and E_aCTR of selected films were used as film parameters. Total surface area of film package (A_p) and the package head space (V_fp) served as input for package parameters, whereas, initial in-pack O₂ and CO₂ concentration (Y_O2, Z_CO2) and outside atmosphere (Y_O2^a and Z_CO2^a) served as environment parameters. As the MA package initially contained air, initial O₂ and CO₂ (Y_O2 and Z_CO2) concentration were taken as 21 % (0.21 cm³/cm³ of air) and 0.03 % (0.0003 cm³/cm³ of air) respectively.

MA Packaging of selected fruits

Apple, guava and litchi of medium size harvested at commercial maturity were collected from the orchard and number-labeled for MA packaging (Mangaraj and Goswami 2009c). Five types of packages (PKG-LFR1, PKG-LFR2, PKG-LFR3, PKG-LFR4 and PKG-LFR5) of required size i.e. 24 × 19 cm for apple; 19 × 19 cm for guava and 28 × 22 cm for litchi for 1 ± 0.1 kg fill weight were developed. Fruits were packaged and heat sealed. Impulse time was adjusted for different films for obtaining a clean seal. Silicon rubber septums were glued to the packages to facilitate gas sampling. The MA packages were labeled marked and kept in the incubator for subsequent storage study at 10, 15, 20 and 25 ºC (Mangaraj et al. 2005; Mangaraj et al. 2012a, b; Mangaraj et al. 2013b).

The samples of package air were analyzed on Gas Chromatograph (Mangaraj and Goswami 2009a, b) for determining the variation of O₂ and CO₂ concentration in the package with time. The equilibrium concentration of O₂ (Y_O2^eq) and CO₂ (Z_CO2^eq) were subsequently determined. From the mathematical model of gaseous exchange in MAP, the values of Y_O2, Z_CO2, Y_O2^eq, Z_CO2^eq and t_eq were predicted by employing MATLAB Programme. The predicted and the experimental values of Y_O2, Z_CO2, Y_O2^eq, Z_CO2^eq and t_eq were compared for validation of the developed model.

Results and discussions

MAP modelling and analysis

With the objective of meeting MAP requirements of fruit the polymeric high, medium and low barrier hydrophilic films namely, low density polyethylene (LDPE), biaxially oriented polypropylene (BOPP), polyvinyl chloride (PVC), polyvinyledene chloride (PVDC) were procured from Reliance Food Industry, Kolkata considering various film characteristics (Exama et al. 1993; Mangaraj et al. 2009; Costa et al. 2011). Two different films were com-bined through the tailoring of film laminates to bring the gas transmission requirement of the laminates close to the required values (Mangaraj et al. 2012a, b; Mangaraj and Tripathi 2013, a, ba,b). Three types of film packages i.e. PCG-LFR-1 (BOPP-30 μ + PVC−50 μ) for apple; PCG-LFR-3 (BOPP-45 μ + PVC−25 μ) for guava; and PCG-LFR-5 (BOPP-30 μ + PVC−25 μ) for litchi of package size 24 cm × 19 cm; 19 cm × 19 cm and 28 cm 22 cm, respectively were chosen for experimental validation of proposed MAP model (Mangaraj et al. 2012a, b; Mangaraj and Tripathi 2013, a, b). The activation energy and pre-exponential factor of Arrhenius-type equation for different model parameters of enzyme kinetics of uncom-petitive inhibition is presented in Table 1; moreover the activation energy and pre-exponential factor of Arrhenius-type equation for selected polymeric films is given in Table 2. These values were used for validating the developed global MAP model (Mangaraj and Goswami 2008, 2011a, b).

Table 1.

Activation energy and pre-exponential factor of Arrhenius-type equation for different model parameters of uncompetitive inhibition

Arrhenius parameter	vm (O2)	vm (CO2)	km (O2)	km (CO2)	ki (O2)	ki (CO2)
Apple
Ea (kJ/g-mole)	30.06	25.10	20.45	11.88	−20.23	−16.84
Rp (ml [O2] kg−1 h−1)	5.2 × 106	9.1 × 105	3.8 × 104	1.7 × 103	1.7 × 10−3	9.2 × 10−3
Guava
Ea (kJ/g-mole)	27.89	26.69	14.58	18.02	−17.54	−16.40
Rp (ml [O2] kg−1 h−1)	3.7 × 106	1.9 × 106	4.5 × 103	1.4 × 104	5.0 × 10−3	7.0 × 10−3
Litchi
Ea (kJ/g-mole)	42.24	39.45	17.76	16.36	−18.17	−10.44
Rp (ml [O2] kg−1 h−1)	2.59 × 109	6.17 × 108	2.33 × 104	9.19 × 103	2.9 × 10−3	1.1 × 10−1

Table 2.

Activation energy and pre-exponential factor of Arrhenius-type equation for selected polymeric films

Parameters for Arrhenious equations	Polymeric films with their thickness
	BOPP-30 μ		BOPP-45 μ		PVC-25 μ		PVC-35 μ		PVC-50 μ		LDPE-40 μ		LDPE-60 μ		PVDC-40 μ
	OTR	CTR	OTR	CTR	OTR	CTR	OTR	CTR	OTR	CTR	OTR	CTR	OTR	CTR	OTR	CTR
Ea (kJ/g-mole)	50.09	53.36	52.96	66.84	49.65	51.40	51.89	53.84	51.65	53.99	51.61	54.01	51.40	54.38	46.84	50.82
GTRp (cm3/m2 h ΔC)	7.58 × 1010	1.34 × 1012	1.55 × 1011	2.06 × 1014	9.52 × 1011	1.22 × 1013	1.57 × 1012	2.18 × 1013	9.90 × 1011	1.58 × 1013	5.52 × 1011	8.51 × 1012	3.34 × 1011	6.38 × 1012	1.54 × 108	2.94 × 109

In this study a generalized global model was developed and verified against the MAP storage study data for apple, guava and litchi for 1 ± 0.1 kg fill weight. The output obtained from this model was compared with the experimental data and used for predicting the equilibrium level of O₂ and CO₂ in MA packaging of different commodity carried out by some researchers.

Equilibrium concentrations of O₂ and CO₂ in MA packages

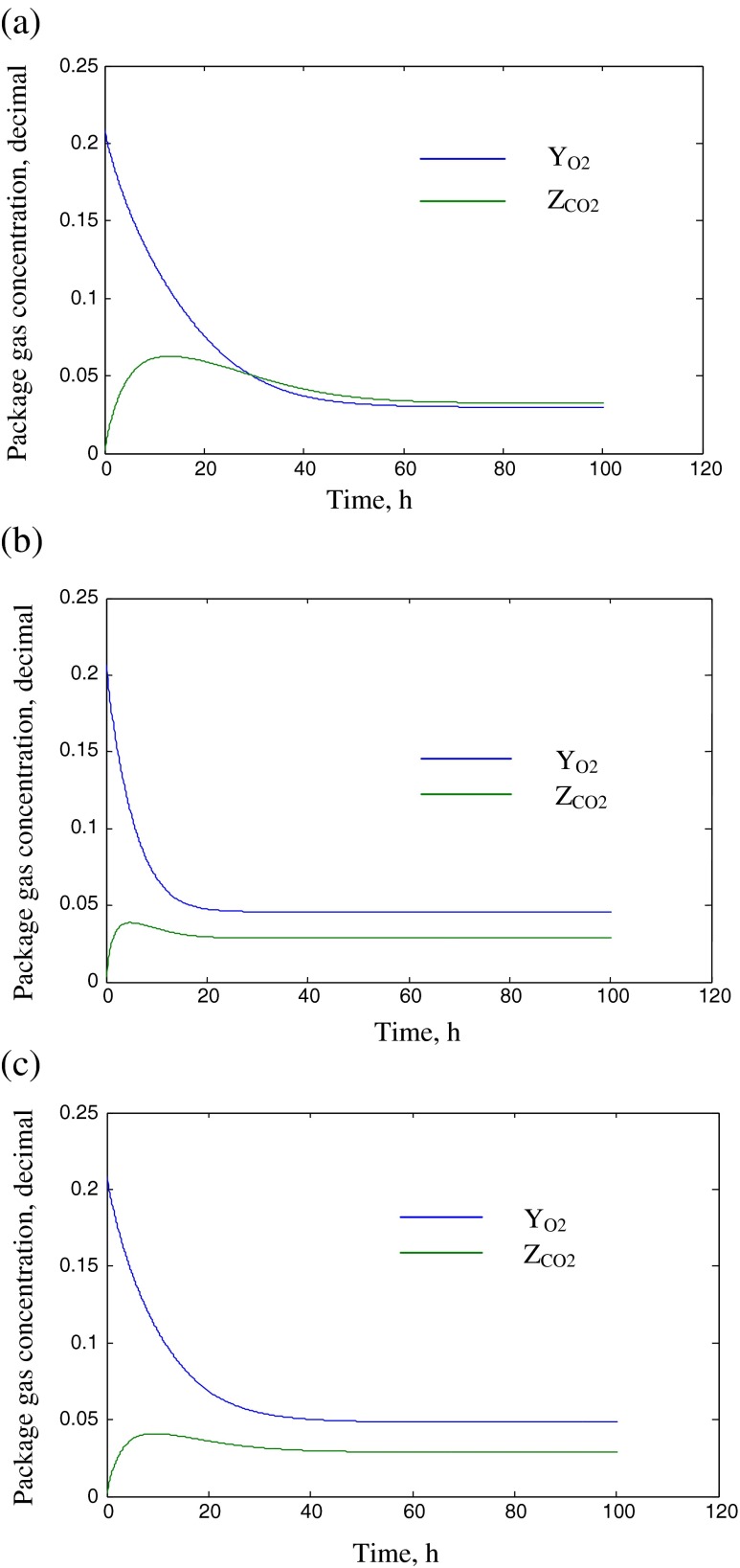
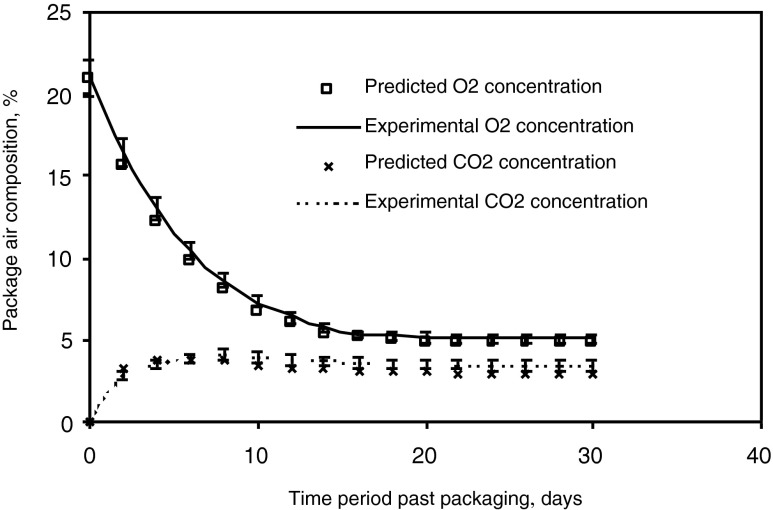
The predicted as well as experimental values of Y_O2^eq, Z_CO2^eq and t_eq for various MA packages for 1 ± 0.1 kg fill weight at different storage temperatures have been presented in Table 3. The profile of package air com-position with time predicted by the modelling of gas-eous exchange in MAP for the packages PCG-LFR-1, PCG-LFR-3 and PCG-LFR-5 for apple, guava and li- tchi, respectively at 15 ºC has been depicted in Fig. 2. Most of the packages have established equilibrium at such levels of O₂ and CO₂, which were fairly close to the target levels. The predicted and experimental values of Y_O2^eq, Z_CO2^eq were found to be higher than the target levels for all the MA packages. There was good agreement between predicted as well as experimental values of Y_O2^eq and Z_CO2^eq. The experimental values of Y_O2^eq varied between 3.10–3.31 % (0.031–0.033 cm³ per cm³ of air); 5.00–5.37 % (0.05–0.054 cm³ per cm³ of air); 4.95–5.28 % (0.049–0.053 cm³ per cm³ of air) whereas those of Z_CO2^eq varied between 3.34–4.17 % (0.0334–0.0417 cm³ per cm³ of air); 3.14–3.72 % (0.0314–0.0372 cm³ per cm³ of air); 3.56–4.20 % (0.0356–0.0420 cm³ per cm³ of air) for all types of MA packages for apple, guava and litchi, respectively at all the reference temperature levels. The equilibrium O₂ and CO₂ concentration obtained from the model was verified against the experimental data for MA packages of fruits. The mean relative deviation moduli between the equilibrium concentration of O₂ and CO₂ as predicted by the developed model and that obtained through experiments were found to be in the range of 5.92–8.6 % and 7.14–9.35 %, respectively. This indicated that, the developed model is in good agreement with the experimental data. The experimental as well as predicted variation of O₂ and CO₂ levels in MA packages PCG-LFR-3 at 15 ºC storage temperatures has been shown in Fig. 3. During steady state period, the experimental values of O₂ and CO₂ were found to be nearly constant for an extended period of storage. By and large all types of MA packages have established dynamic equilibrium state without causing any unfavorable deviation from the target levels of O₂ and CO₂ at all the reference storage temperatures.

Table 3.

Equilibrium concentration of O₂ and CO₂ predicted by the model and experimental observations for apple (PCG-LFR-1), guava (PCG-LFR-3) and litchi (PCG-LFR-5) packages

MA package fill weight of 1.00 kg
Temperature (ºC)	YO2 eq-pre (%)	YO2 eq-exp (%)	ZCO2 eq-pre (%)	ZCO2 eq-exp (%)	teq-pre (h)	teq-exp (h)
Apple
10	3.11	3.17	3.53	3.74	60.00	66.00
15	3.14	3.22	3.51	3.68	54.00	58.00
20	3.31	3.24	3.59	3.74	46.00	50.00
25	3.30	3.17	3.90	4.17	40.00	42.00
Guava
10	4.97	5.20	2.91	3.34	24.00	26.00
15	4.86	5.13	2.97	3.45	22.00	24.00
20	4.82	5.00	2.93	3.39	18.00	20.00
25	5.11	5.27	2.86	3.27	16.00	16.00
Litchi
10	4.93	5.16	3.32	3.96	44.00	48.00
15	5.01	5.24	3.20	3.75	40.00	42.00
20	4.90	5.19	3.14	3.63	30.00	28.00

Fig. 2.

(a, b, c): Predicted variation of O₂ and CO₂ with time by the model in MA packed apple, guava and litchi at 15 ºC

Fig. 3.

Experimental and predicted variation in package air composition with time for guava (PCG-LFR-3) at 15 ºC storage temperatures

Equilibrium time

The length of time taken by the MA package to establish dynamic equilibrium from the time of packaging is considered as equilibrium time. For various packages, the predicted values of equilibrium time were found to have varied between 36–72 h; 12–30 h; and 26–50 h, whereas those of experimental values varied between 34–80 h; 10–34 h and 24–56 for all types of MA packages for apple, guava and litchi, respectively at all the reference storage temperatures as given in Table 3. The mean relative deviation moduli for the equilibrium time as predicted by the developed model and that obtained through experiments were found to be 7.77, 7.17 and 2.47 % for apple, guava and litchi, respectively. This indicated that, the developed model is in good agreement with the experimental data. There was some deviation of experimental values from the predicted ones. The development of quasi-equilibrium conditions and the variations in the free volume in the package (V_fp), because of the varying fill weight, were probably the cause of such deviations in equilibrium time (t_eq) values. In fact, small variations in V_fp are always possible in a flexible package. Hence, it is unrealistic to expect a constant value of V_fp in the flexible packages. It has been seen that the variation in O₂ affects both R_O2 and R_CO2 significantly. With the variation in R_O2 and R_CO2, the O₂ consumption as well as the CO₂ evolution of the package varies which in turn affects O₂ and CO₂ level in the internal atmosphere of the package. Thus, as O₂ decreases, R_CO2 reduces which in turn reduces CO₂ in the internal atmosphere of the package.

Reduction in CO₂ level tends to retrieve R_CO2 slightly. However, the amount of reduction in CO₂ due to decrease in O₂ is greater than the amount of retrieved. As such, with the decrease in O₂ level CO₂ level also decreases, though by small amounts. Thus, though the equilibrium condition for CO₂ level appears to be approaching earlier than that of O₂ level but in true sense, CO₂ level becomes stable only when O₂ level attains equilibrium (Fig. 2 and 3). It implies that the equilibrium for both, O₂ and CO₂ is attained simultaneously in MA packaging. Also, in view of the fact that O₂ level has more pronounced effect on respiration rates than CO₂ level, the equilibrium time (t_eq) for O₂ level assume greater importance. The single equilibrium time (t_eq) approach advocated in this study is in agreeance with the study of (Rocculi et al. 2006; Torrieri et al. 2007; Gonzalez-Buesa et al. 2009; Tariq et al. 2009; Mangaraj et al. 2011).

Validation of model with other’s work

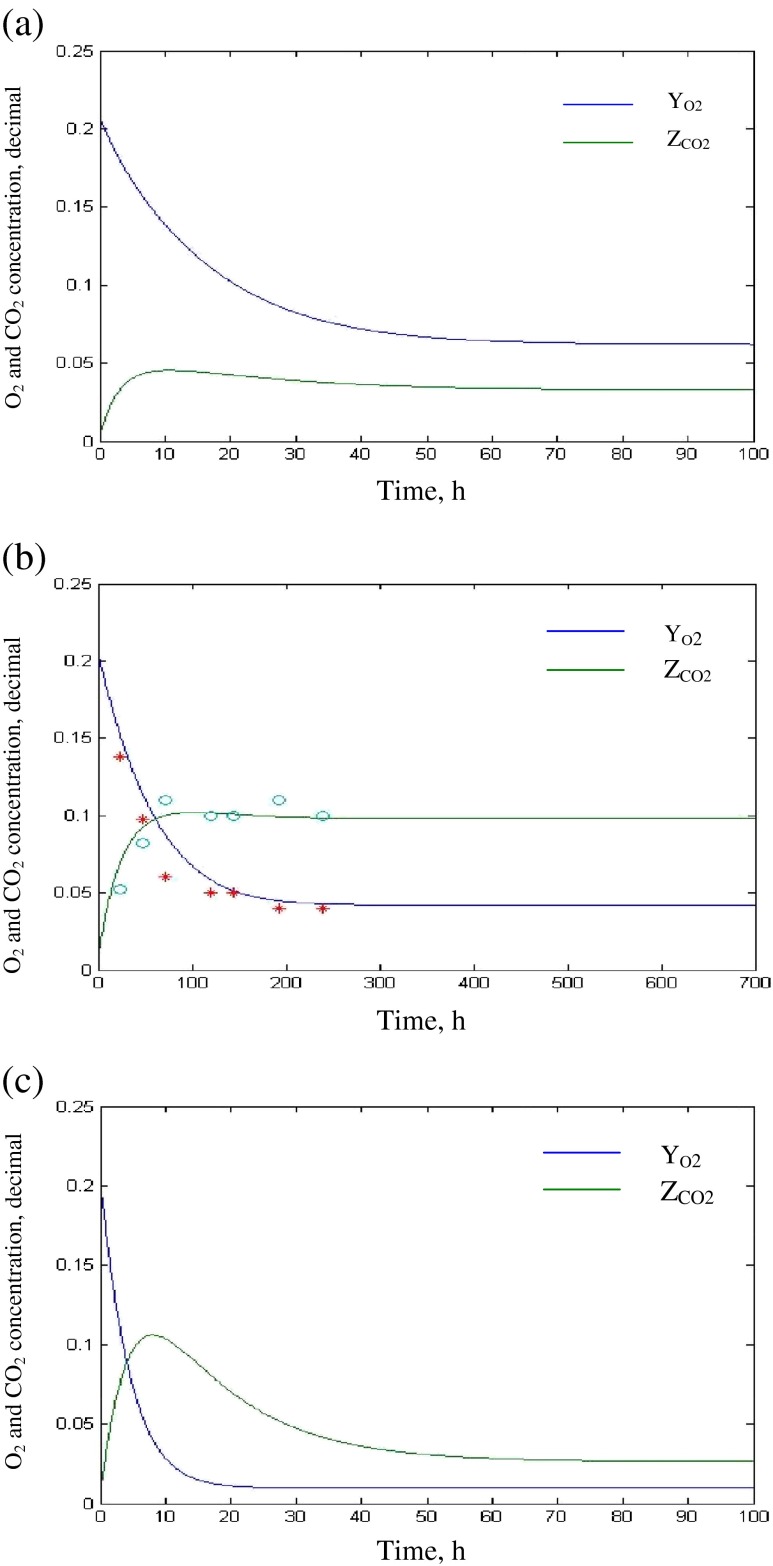
Mahajan and Goswami (2001) has developed enzyme kinetics respiration model for red delicious apple. Using the values of model parameters the activation energy and respiration pre-exponential factor for O₂ consumption and CO₂ evolution was obtained. Substituting these values in Eqs. 9 and 10, with area of packaging film (A_p) as 0.11 m², mass of apple (W_p) of 1.00 kg, void volume of the package (V_fp) of 1,000 cm³ the variation of O₂ and CO₂ with time plot was obtained (Fig. 4a). It shows that (Fig. 4a) the model has achieved an equilibrium concentration of 6 % O₂ (0.06 cm³ per cm³ of air) and 4 % CO₂ (cm³ per cm³ of air) at 40 h and remains in equilibrium for 100 h. Geeson et al. (1985) conducted MA packaging study with tomato of weighing 390 g using 15 μ polyvinylchloride film having void volume of 550 cm³ at a temperature of 10 °C. The equilibrium concentration of O₂ (4 %) and CO₂ (10 %) achieved inside the film package in 200 h using the developed model (Fig. 4b). Similarly, Rai and Paul (2007) worked on design and modelling of gaseous exchange in MAP for button mushrooms. They stored mushrooms of weight 500 g inside a 57 μLDPE film having a void volume of 545 cm³ and area of packaging film of 0.11 m² at a temperature of 15 °C. They recorded the variation of O₂ concentration and CO₂ concentration with time inside the MA package. They found that O₂ concentration decreased and CO₂ concentration increased inside the package as the storage period progressed (Fig. 4c). The model suggested, that the dynamic equilibrium attained at 2 % oxygen and 4 % carbon dioxide level (Fig. 4c) and it maintained till 96 h of packaging. The mean relative deviation modulus for equilibrium gas concentration and time as predicted by the developed model and experimental values varied in the range of 4.7–8.5 % and 3.9–6.4 %, respectively indicating the good predictability of the developed MAP model.

Fig 4.

a Plot between O₂ and CO₂ with time for red delicious apple b Plot between O₂ and CO₂ with time for tomato c Plot between O₂ and CO₂ with time for button mushroom

Conclusions

A mathematical model for MA packaging of apple, guava and litchi applying enzyme kinetics based respiration equation coupled with the Arrhenious model was developed. The model was used to determine the time to reach to the equilibrium concentration inside the MA package and the level of O₂ and CO₂ concentration at equilibrium state. The equilibrium O₂ and CO₂ concentration obtained from the model was verified against the experimental data for MA packages of fruits. The mean relative deviation moduli between the equilibrium concentration of O₂ and CO₂ as predicted by the developed model and that obtained through experiments were found to be in the range of 5.92–8.60 % and 7.14–9.35 %, respectively for apple, guava and litchi fruits. This indicated that, the developed model is in good agreement with the experimental data. There were some deviations of equilibrium time between the predicted and experimental values may be attributed to the development of quasi-equilibrium conditions and the variations in the free volume in the package due to the varying fill weight. In fact, small variations in free volume are always possible in a flexible package. It has been seen that the equilibrium time for both, O₂ and CO₂ attained simultaneously in MA packaging. The model has been used for predicting the equilibrium level of O₂ and CO₂ in MA packaging of different commodity carried out by some researchers. These results further strengthen the model for its validation and wide application for fresh fruits and vegetables.

Notations

A_p

Surface area of the packaging film, m²

E

Mean relative deviation modulus, %

E_a

Activation energy, kJ g⁻¹ mol⁻¹

E_ap

Activation energy of gas transmission rates for O₂ and CO₂ (kJ/kg-mole)

GTR

Gas transmissions rates of films (cm³/m² h ΔC) at temperature T_abs

GTR_p

Gas transmission rates pre-exponential factor for O₂ and CO₂ (cm³/m² h ΔC)

K_m(O2)

Michaelis-Menten constant for O₂ consumption, % O₂

K_m(CO2)

Michaelis-Menten constant for CO₂ evolution, % O₂

K_i (O2)

Inhibition constants for O₂ consumption, % CO₂

K_i (CO2)

Inhibition constants for CO₂ evolution, % CO₂

R_O2

Respiration rate, ml [O₂] kg⁻¹ h⁻¹

R_CO2

Respiration rate, ml [CO₂] kg⁻¹ h⁻¹

Y_O2

O₂ concentration inside the package (cm³ per cm³ of air)

Z_CO2

CO₂ concentration inside the package (cm³ per cm³ of air)

T

Storage time in h

Δt

Time difference between two gas measurements

V_f

Free volume of the respiration chamber in ml

W

Weight of the fruit in kg

R

Universal gas constant, 8.314 kJ kg⁻¹ mol⁻¹ K⁻¹

R_CO2

Respiration rate, ml [CO₂] kg⁻¹ h⁻¹

R_exp

Experimental respiration rate, ml kg⁻¹ h⁻¹

R_m

Model parameter of enzyme kinetic

R_pre

Predicted respiration rate, ml kg⁻¹ h⁻¹

R_O2

Respiration rate, ml [O₂] kg⁻¹ h⁻¹

R_p

Respiration pre-exponential factor

T

Storage temperature, °C

T_abs

Storage temperature, K

t

Storage time, h

Δt

Time difference between two gas measurements

V_f

Free volume of the respiration chamber, ml

V_m (CO2)

Maximum respiration rate for CO₂ evolution, ml/kg-h

V_m (O2)

Maximum respiration rate for O₂ consumption, ml/kg-h

Y_O2^a

O₂ concentration in the atmospheric air (cm³ per cm³ of air)

Z_CO2^a

CO₂ concentration in the atmospheric air (cm³ per cm³ of air)

Y_O2^eq

Equilibrium/optimum O₂ concentration attained in the package

Z_CO2^eq

Equilibrium/optimum CO₂ concentration attained in the package

W_p

Weight of the fruits in MA package, kg

V_fp

Free volume in the package, cm³

X

Thickness of the film, cm

OTR

Oxygen transmission rates

CTR

Carbon dioxide transmission rates

P_O2

O₂ permeability of packaging material (cm³. m⁻² . h⁻¹. [Conc. diff. of O₂ in volume fraction]⁻¹)

P_CO2

CO₂ permeability of packaging material (cm³. m⁻². h⁻¹. [Conc. diff. of O₂ in volume fraction]⁻¹)

dY_O2/dt

Rate of change of O₂ concentration ‘Y_O2’ within the package at time ‘t’ of storage (cm³ per cm³ of air. h⁻¹)

dZ_CO2/dt

Rate of change of CO₂ concentration ‘Z_CO2’ within the package at time ‘t’ of storage (cm³ per cm³ of air. h⁻¹) respectively

N

Number of respiration data points