Semiparametric Relative-risk Regression for Infectious Disease Transmission Data

Abstract

This paper introduces semiparametric relative-risk regression models for infectious disease data. The units of analysis in these models are pairs of individuals at risk of transmission. The hazard of infectious contact from i to j consists of a baseline hazard multiplied by a relative risk function that can be a function of infectiousness covariates for i, susceptibliity covariates for j, and pairwise covariates. When who-infects-whom is observed, we derive a profile likelihood maximized over all possible baseline hazard functions that is similar to the Cox partial likelihood. When who-infects-whom is not observed, we derive an EM algorithm to maximize the profile likelihood integrated over all possible combinations of who-infected-whom. This extends the most important class of regression models in survival analysis to infectious disease epidemiology. These methods can be implemented in standard statistical software, and they will be able to address important scientific questions about emerging infectious diseases with greater clarity, flexibility, and rigor than current statistical methods allow.

1 INTRODUCTION

Infectious diseases are an important threat to human health and commerce, and understanding the transmission of disease is crucial to the design of public health interventions. The statistical analysis of infectious disease data is complicated by the fact that infections are inherently dependent, especially when they are transmitted directly from person to person (Becker, 1989; Andersson and Britton, 2000). Epidemiologists have dealt with this problem in three ways. The most common approach is to model susceptibility to disease using standard statistical methods such as logistic or Cox regression, ignoring disease transmission. A second approach is to use chain binomial models (Rampey et al., 1992), which estimate the probability of escaping infectious contact from infected members of groups such as households, classrooms, or hospital wards. The third approach is to model the spread of disease as a branching process where infectees are the o spring of their infectors (Wallinga and Teunis, 2004; White and Pagano, 2008). The time between the infections of an infector and an infectee is called a generation interval. In this approach, the generation intervals are assumed to be independent and identically distributed (iid).

To understand transmission, it is crucial to separate the e ects of covariates on infectiousness and susceptibility from their association with exposure to infected people (Rhodes et al., 1996). Regression models that ignore transmission cannot do this. When disease transmission is modeled as a branching process, uninfected people do not exist and cannot be exposed to infected people. The failure to account for uninfected person-time and competing risks of infection cause several problems with this approach (Svensson, 2007; Kenah et al., 2008). The assumption that generation intervals are iid is di cult to relax, making estimation of covariate e ects di cult (Kenah, 2013). Chain binomial models are a statistically sound response to the problem of dependence and can be used to estimate covariate e ects. However, their use is limited in two ways: First, they are not implemented in standard statistical software—a problem solved partially by the publicly-available package TranStat (www.epimodels.org/midas/transtat.do). Second, they use discrete time. Since infectious disease data are usually recorded by the day or week, this is not unnatural. However, continuous-time models corrected for ties may o er a more flexible modeling framework.

Kenah (2011) extended parametric methods from survival analysis to infectious disease data by modeling the contact interval. In the ordered pair ij, the contact interval τ_ij is the time between the onset of infectiousness in i and the first infectious contact from i to j, where infectious contact is a contact sufficient to infect a susceptible individual. It is right-censored if the infectious period of i ends before i makes infectious contact with j or if j is infected by someone other than i. These methods solve the problem of dependence by treating ordered pairs of individuals, not the individuals themselves, as the units of analysis. Kenah (2013) showed that the contact interval distribution could be estimated nonparametrically by adapting the Nelson-Aalen estimator from standard survival analysis. These methods assume a homogeneous population where the contact interval distribution is the same for all pairs ij in which transmission from i to j is possible. They are unable to estimate covariate e ects on transmission, which is a primary goal of vaccine trials, outbreak investigations, and many other studies of infectious disease.

The goal of this paper is to extend the methods of Kenah (2013) to develop a relative-risk regression model similar to that of Cox (1972). This model will allow semiparametric estimation of the e ects of covariates on the hazard of infectious contact in pairs of individuals. For the ordered pair ij, the covariate vector can include infectiousness covariates for i, susceptibility covariates for j, and pairwise covariates. This semiparametric regression model will allow many of the most important scientific questions in infectious disease epidemiology to be addressed with greater clarity, flexibility, and rigor.

1.1 Stochastic S(E)IR epidemic model

Consider a closed population of n individuals assigned indices 1 . . . n. Each individual is in one of four states: susceptible (S), exposed (E), infectious (I), or removed (R). Person i moves from S to E at his or her infection time t_i, with t_i = ∞ if i is never infected. After infection i has a latent period of length ε_i, during which he or she is infected but not infectious. At time t_i + ε_i, i moves from E to I, beginning an infectious period of length _i. At time t_i + ε_i + l_i, i moves from I to R. Once in R, i can no longer infect others or be infected. The states and notation are illustrated at the top of Figure 1. The latent period is a nonnegative random variable, the infectious period is a strictly positive random variable, and both have finite mean and variance.

Figure 1.

Notation for the stochastic SEIR model natural history (top) and infectious contact process (bottom). In the bottom diagram, the infectious contact interval ${\tau }_{ij}^{\ast }$ is equal to the contact interval τ_ij because τ_ij ≤ l_i. Otherwise, we would have ${\tau }_{ij}^{\ast }=\infty$ and no infectious contact from i to j would occur.

An epidemic begins with one or more persons infected from outside the population, which we call imported infections. The methods in this paper require that the set of imported infections is known. For simplicity, we assume that epidemics begin with one or more imported infections at time 0 and there are no other imported infections.

After becoming infectious at time t_i + ε_i, person i makes infectious contact with j ≠ i at time $t_{ij}=t_i+{\epsilon }_i+{\tau }_{ij}^{\ast }$, where the infectious contact interval ${\tau }_{ij}^{\ast }$ is a strictly positive random variable with ${\tau }_{ij}^{\ast }=\infty$ if infectious contact never occurs. Since infectious contact must occur while i is infectious or never, ${\tau }_{ij}^{\ast }\in (0,{\iota }_i]$ or ${\tau }_{ij}^{\ast }=\infty$. We define infectious contact to be a contact sufficient infect a susceptible person, so t_j ≤ t_ij for all i ≠ j. The infectious contact interval is illustrated at the bottom of Figure 1.

For each ordered pair ij, let C_ij = 1 if infectious contact from i to j is possible and C_ij = 0 otherwise. These C_ij could be the entries in an adjacency matrix for a static contact network. We assume that the infectious contact interval ${\tau }_{ij}^{\ast }$ is generated in the following way: A contact interval τ_ij is drawn from a distribution with hazard function λ_ij(τ). If τ_ij ≤ l_i and C_ij = 1, then ${\tau }_{ij}^{\ast }={\tau }_{ij}$. Otherwise, ${\tau }_{ij}^{\ast }=\infty$. In this paper, we assume the contact intervals in all ordered pairs ij are independent and have finite mean and variance.

1.2 Observation and censoring

Our population has size n, and we observe the times of all S → E (infection), E → I (onset of infectiousness), and I → R (removal) transitions in the population between time 0 and time T . For all ordered pairs ij such that i is infected, we observe C_ij. We first consider the case where who-infects-whom is observed and then consider the more realistic case where it is not.

We assume that we can observe τ_ij only if j is infected by i at time t_i+ε_i+τ_ij. Clearly, τ_ij can be observed only if C_ij = 1. We also have right-censoring of τ_ij:

1. Since infectious contact can occur only while i is infectious, τ_ij can be right-censored by the infectious period l_i of i. Let ${\mathcal{I}}_i\left(\tau \right)=1_{\tau \in (0,{\iota }_i]}$ indicate whether i remains infectious at infectious age τ.

2. Since j is susceptible to infection by i only if he or she has not been infected by anyone else, τ_ij can be right-censored by t_i′j − t_i − ε_i for i′ ≠ i. Let ${\mathcal{S}}_{ij}\left(\tau \right)=1_{t_i+{\epsilon }_i+\tau \le t_j}$ indicate whether j remains susceptible at infectious age τ of i.

Let T denote the time at which observation ends. Then τ_ij can be right-censored by the end of observation at infectious age T − t_i − ε_i of i. Let ${\mathcal{Y}}_i\left(\tau \right)=1_{t_i+{\epsilon }_i+\tau \le T}$ indicate whether observation is ongoing when i reaches infectious age τ.

Since ${\mathcal{I}}_i\left(\tau \right)$, ${\mathcal{S}}_{ij}\left(\tau \right)$, and ${\mathcal{Y}}_{ij}\left(\tau \right)$ are left-continuous,

$$Y_{ij}\left(\tau \right)=C_{ij}{\mathcal{I}}_i\left(\tau \right){\mathcal{S}}_{ij}\left(\tau \right){\mathcal{Y}}_i\left(\tau \right)$$ (1)

is a left-continuous process that indicates the risk of an observed infectious contact from i to j at infectious age τ of i. The assumptions made in the stochastic S(E)IR model above ensure that ${\mathcal{I}}_i\left(\tau \right)$ and ${\mathcal{S}}_{ij}\left(\tau \right)$ independently censor τ_ij. We also require that T is a stopping time with respect to the observed data such that, for all i, ${\mathcal{Y}}_i\left(\tau \right)$ independently censors τ_ij for each j exposed to infectious contact from i. The possible censoring scenarios are illustrated in Figure 2.

Figure 2.

The three censoring processes for the contact interval τ_ij. The onset of infectiousness in i occurs at time t_i + ε_i, and the infection of j occurs at t_j. At the top, τ_ij is censored because ${\mathcal{I}}_i(t_j-t_i-{\epsilon }_i)=0$. In the middle, τ_ij is observed if ${\mathcal{S}}_{ij}(t_j-t_i-{\epsilon }_i)=1$ and censored otherwise. At the bottom, τ_ij is censored because ${\mathcal{Y}}_i(t_j-t_i-{\epsilon }_i)=0$.

1.3 Transmission trees and infectious sets

Following Wallinga and Teunis (2004), let v_j denote the index of the person who infected person j, with v_j = 0 for imported infections and v_j = ∞ for persons not infected prior to the end of observation. The transmission tree is the directed network with an edge from v_j to j for each j such that t_j ≤ T . It can be represented by a vector v = (v₁, . . . , v_n). Let ${\mathcal{V}}_j=\{i:C_{ij}{\mathcal{I}}_i\left(t_j\right)=1\}$ denote the set of possible infectors of person j, which we call the infectious set of j. Let $\mathcal{V}$ denote the set of all v consistent with the observed data. A $\mathbf{v}\in \mathcal{V}$ can be generated by choosing a $v_j\in {\mathcal{V}}_j$ for each non-imported infection j.

2 METHODS

Kenah (2013) described the nonparametric estimation of the contact interval distribution for a homogeneous population. Here, we consider a semiparametric relative-risk model like that of Prentice and Self (1983). Let

$${\lambda }_{ij}\left(\tau \right)=r\left({\beta }_0^{\mathsf{T}}{X}_{ij}\left(\tau \right)\right){\lambda }_0\left(\tau \right),$$ (2)

where λ₀(τ) is an unspecified baseline hazard function, $r:\mathbb{R}\to (0,\infty )$ is a relative risk function, β₀ is an unknown b × 1 coefficient vector, and X_ij(τ) is a b × 1 predictable covariate process taking values in a set $\mathcal{X}$. The covariates X_ij(τ) can include individual-level covariates predicting the infectiousness of i or the susceptibility of j as well as pairwise covariates (e.g., membership in the same household) that predict the hazard of infectious contact from i to j.

We assume that r has continuous first and second derivatives, r(0) = 1, and ln r(β^TX) is bounded on $\mathcal{X}$. Letting r(x) = exp(x) gives us a loglinear relative risk regression model like that of Cox (1972), and letting r(x) = 1 + x gives us a linear relative risk regression model. To fit these semiparametric models, we adapt the nonparametric estimators from Kenah (2013) to account for the relative risk function.

2.1 Who-infects-whom is observed

Let N_ij(τ) = 1_τij ≤_τ indicate whether an observed infectious contact from i to j has occurred by infectious age τ in i, and let $N\left(\tau \right)={\sum }_{j=1}^n{\sum }_{i\ne j}{N}_{ij}\left(\tau \right)$. Note that we must observe who-infected-whom in order to calculate N(τ).

Let ${\Lambda }_0\left(\tau \right)={\int }_0^{\tau }{\lambda }_0\left(u\right)\mathrm{d}u$. Given β, the Breslow estimator (Breslow, 1972) of Λ₀(τ) is

$$\widehat{\Lambda }(\beta ,\tau )={\int }_0^{\tau }\frac{1}{Y(\beta ,u)}\mathrm{d}N\left(u\right),$$ (3)

where

$$Y(\beta ,u)=\sum _{j=1}^n\sum _{i\ne j}r\left({\beta }^{\mathsf{T}}{X}_{ij}\left(u\right)\right)Y_{ij}\left(u\right).$$ (4)

The Breslow estimator has two desirable properties. First, $\widehat{\Lambda }({\beta }_0,\tau )$ is an unbiased estimator of Λ₀(τ). Let

$$M(\beta ,\tau )=N\left(\tau \right)-{\int }_0^{\tau }Y(\beta ,u){\lambda }_0\left(u\right)\mathrm{d}u.$$ (5)

Then for all τ such that Y (τ) > 0,

$$\widehat{\Lambda }({\beta }_0,\tau )-{\Lambda }_0\left(\tau \right)={\int }_0^{\tau }\frac{1_{Y\left(u\right)>0}}{Y({\beta }_0,u)}\mathrm{d}M({\beta }_0,u)$$ (6)

is a mean-zero martingale when β = β₀. Second, $\widehat{\Lambda }(\beta ,\tau )$ maximizes the log likelihood

$$\ell (\beta ,\Lambda )=\sum _{j=1}^n\sum _{i\ne j}\ln \left(r\left({\beta }^{\mathsf{T}}{X}_{v_{j}j}\left({\tau }_{v_{j}j}\right)\right)\mathrm{d}\Lambda \left({\tau }_{v_{j}j}\right)\right)-{\int }_0^{\infty }Y(\beta ,u)\mathrm{d}\Lambda \left(u\right)$$ (7)

over all step functions Λ(τ). Substituting $\widehat{\Lambda }(\beta ,\tau )$ into l(β, Λ) profile likelihood

$$\ell (\beta ,\widehat{\Lambda })=\left(\sum _{j=1}^n\ln \frac{r\left({\beta }^{\mathsf{T}}{X}_{v_{j}j}\left({\tau }_{v_{j}j}\right)\right)}{Y(\beta ,{\tau }_{v_{j}j})}\right)-\tau ,$$ (8)

where $\mathcal{T}=\max \{\tau :Y\left(\tau \right)>0\}$. The first term is similar to the log partial likelihood from Cox (1972) and the second term does not depend on β. Dropping the second term, let

$$pl\left(\beta \right)=\sum _{j=1}^n\ln \frac{r\left({\beta }^{\mathsf{T}}{X}_{v_{j}j}\left({\tau }_{v_{j}j}\right)\right)}{Y(\beta ,{\tau }_{v_{j}j})}$$ (9)

be the log partial likelihood for β. This derivation of the partial likelihood as a profile likelihood follows that of Johansen (1983). Let $\widehat{\beta }$ denote the value of β that maximizes pl(β), and let ${\widehat{\Lambda }}_0\left(\tau \right)=\widehat{\Lambda }(\widehat{\beta },\tau )$ denote the corresponding Breslow estimate of the baseline cumulative hazard.

2.2 Partial likelihood score process

We can rewrite pl(β) as a sum of stochastic integrals:

$$pl\left(\beta \right)=\sum _{j=1}^n\sum _{i\ne j}{\int }_0^{\infty }\ln \frac{r\left({\beta }^{\mathsf{T}}{X}_{ij}\left(u\right)\right)}{Y(\beta ,u)}\mathrm{d}{N}_{ij}\left(u\right).$$ (10)

The corresponding score process is

$$U(\beta ,\tau )=\sum _{j=1}^n\sum _{i\ne j}{\int }_0^{\tau }\frac{\partial }{\partial \beta }\ln r\left({\beta }^{\mathsf{T}}{X}_{ij}\left(u\right)\right)-E(\beta ,u)\mathrm{d}{N}_{ij}\left(u\right),$$ (11)

where

$$E(\beta ,u)=\frac{{\sum }_{j=1}^n{\sum }_{i\ne j}r\left({\beta }^{\mathsf{T}}{X}_{ij}\left(u\right)\right)Y_{ij}\left(u\right)\frac{\partial }{\partial \beta }\ln r\left({\beta }^{\mathsf{T}}{X}_{ij}\left(u\right)\right)}{{\sum }_{j=1}^n{\sum }_{i\ne j}r\left({\beta }^{\mathsf{T}}{X}_{ij}\left(u\right)\right)Y_{ij}\left(u\right)}.$$ (12)

is the expected value of $\frac{\partial }{\partial \beta }\ln r\left({\beta }^{\mathsf{T}}{X}_{ij}\left(u\right)\right)$ over the risk set at u when each pair is weighted by its hazard of infectious contact at u. By the Doob-Meyer decomposition, there is a mean-zero martingale M_ij(u) for each ij such that

$$\mathrm{d}{N}_{ij}\left(u\right)=r\left({\beta }_0^{\mathsf{T}}{X}_{ij}\left(u\right)\right){\lambda }_0\left(u\right)Y_{ij}\left(u\right)\mathrm{d}u+\mathrm{d}{M}_{ij}\left(u\right).$$ (13)

Expanding equation (11) using this decomposition and simplifying, we get

$$U({\beta }_0,\tau )=\sum _{j=1}^n\sum _{i\ne j}{\int }_0^{\tau }\frac{\partial }{\partial \beta }\ln \frac{r\left({\beta }_0^{\mathsf{T}}{X}_{ij}\left(u\right)\right)}{Y({\beta }_0,u)}\mathrm{d}{M}_{ij}\left(u\right).$$ (14)

Since it is a sum of integrals of predictable processes with respect to martingales, U(β₀, τ) is a mean-zero martingale.

2.3 Observed and expected information

Let $v^{\otimes 2}=v{v}^{\mathsf{T}}$ for a column vector v. Since the N_ij(τ) do not jump simultaneously in continuous time, the predictable variation process of U(β₀, τ) is

$$\langle U\left({\beta }_0\right)\rangle \left(\tau \right)={\int }_0^{\tau }V({\beta }_0,u)Y({\beta }_0,u){\lambda }_0\left(u\right)\mathrm{d}u,$$ (15)

where

$$V(\beta ,u)=\sum _{j=1}^n\sum _{i\ne j}{\left(\frac{\partial }{\partial \beta }\ln \frac{r\left({\beta }^{\mathsf{T}}{X}_{ij}\left(u\right)\right)}{Y(\beta ,u)}\right)}^{\otimes 2}\frac{r\left({\beta }^{\mathsf{T}}{X}_{ij}\left(u\right)\right)Y_{ij}\left(u\right)}{Y(\beta ,u)}$$ (16)

is the variance of $\frac{\partial }{\partial \beta }\ln r\left({\beta }^{\mathsf{T}}{X}_{ij}\left(u\right)\right)$ over the risk set at u when each pair ij is weighted by its hazard of infectious contact at u.

Let $I\left(\beta \right)=-\frac{{\partial }^2}{\partial {\beta }^2}pl\left(\beta \right)$ be the observed information. Then

$$I\left(\beta \right)=\sum _{j=1}^n\sum _{i\ne j}{\int }_0^{\infty }{\left(\frac{\partial }{\partial \beta }\ln r\left({\beta }^{\mathsf{T}}{X}_{ij}\left(u\right)\right)\right)}^{\otimes 2}-E{(\beta ,u)}^{\otimes 2}\mathrm{d}{N}_{ij}\left(u\right)-\sum _{j=1}^n\sum _{i\ne j}{\int }_0^{\infty }\frac{\frac{{\partial }^2}{\partial {\beta }^2}r\left({\beta }^{\mathsf{T}}{X}_{ij}\left(u\right)\right)}{r\left({\beta }^{\mathsf{T}}{X}_{ij}\left(u\right)\right)}-\frac{\frac{{\partial }^2}{\partial {\beta }^2}Y(\beta ,u)}{Y(\beta ,u)}\mathrm{d}{N}_{ij}\left(u\right).$$ (17)

Expanding I(β₀) via the Doob-Meyer decomposition (13) and simplifying, we get

$$I\left({\beta }_0\right)={\int }_0^{\infty }V({\beta }_0,u)Y({\beta }_0,u){\lambda }_0\left(u\right)\mathrm{d}u+\sum _{j=1}^n\sum _{i\ne j}{\int }_0^{\infty }\frac{{\partial }^2}{\partial {\beta }^2}\ln \frac{r\left({\beta }_0^{\mathsf{T}}{X}_{ij}\left(u\right)\right)}{Y({\beta }_0,u)}\mathrm{d}{M}_{ij}\left(u\right).$$ (18)

The second term has expectation zero, so I(β₀) is an unbiased estimate of Var(U(β₀, ∞)).

Another estimate Var(U(β₀, ∞)) is obtained by substituting the increments of the Breslow estimator (3) for λ₀(u) du in equation (15). This gives us the estimated expected information

$$\mathcal{I}\left(\beta \right)={\int }_0^{\infty }V(\beta ,u)\mathrm{d}N\left(u\right).$$ (19)

Expanding $\mathcal{I}\left({\beta }_0\right)$ using the Doob-Meyer decomposition and simplifying, we get

$$\mathcal{I}\left({\beta }_0\right)={\int }_0^{\infty }V({\beta }_0,u)Y({\beta }_0,u){\lambda }_0\left(u\right)\mathrm{d}u+{\int }_0^{\infty }V({\beta }_0,u)\mathrm{d}M\left(u\right),$$ (20)

where $M\left(\tau \right)={\sum }_{j=1}^n{\sum }_{i\ne j}{M}_{ij}\left(\tau \right)$. The second term has expectation zero, so $\mathcal{I}\left({\beta }_0\right)$ is also an unbiased estimate of the variance of U(β₀, ∞). $\mathcal{I}\left({\beta }_0\right)$ may be a better estimator of Var(U(β₀, ∞)) than I(β₀) because it is guaranteed to be positive semidefinite (Prentice and Self, 1983) and it depends only on aggregates over risk sets (Aalen et al., 2009).

When r(x) = exp(x) as in the Cox model, $I\left(\beta \right)=\mathcal{I}\left(\beta \right)$ for all β. For general r(x), I(β₀) and $\mathcal{I}\left({\beta }_0\right)$ are asymptotically equivalent under weak regularity conditions (see Appendix A online).

2.4 Large-sample estimation of β₀ and Λ₀(τ)

Appendix A, available online, outlines sufficient conditions for the asymptotic normality of U(β₀, τ) and $\widehat{\beta }$ as m → ∞, where m is the number of pairs ij at risk of transmission. Under these conditions, hypothesis tests and confidence intervals for β₀ can be obtained using score, Wald, or likelihood ratio statistics. These conditions are very similar to those for the standard Cox model (Prentice and Self, 1983) except for the additional requirement that both the number of susceptibles and the number of pairs be large such that each susceptible is exposed to a number of infectors < < m. When a given susceptible j is infected, all pairs ij are censored. If there were many pairs but few susceptibles, each susceptible would be exposed to a very high hazard of infection and most pairs would be censored very quickly. To take an extreme case, imagine a single susceptible exposed to m infecteds. The number of pairs at risk of transmission is m but the susceptible will be infected almost immediately when m is large. After this, there are no more pairs at risk of transmission and we can learn nothing further about β₀ or Λ₀(τ).

Given $\widehat{\beta }$ the Breslow estimator of ${\Lambda }_0\left(\tau \right)\text{is}{\widehat{\Lambda }}_0\left(\tau \right)={\widehat{\Lambda }}_0(\widehat{\beta },\tau )$. Its variance is consistently estimated by

$${\widehat{\sigma }}_0^2\left(\tau \right)={\left(\frac{\partial }{\partial \beta }\widehat{\Lambda }(\widehat{\beta },\tau )\right)}^{\mathsf{T}}I{\left(\widehat{\beta }\right)}^{-1}\left(\frac{\partial }{\partial \beta }\widehat{\Lambda }(\widehat{\beta },\tau )\right)+{\int }_0^{\tau }\frac{1}{Y{(\widehat{\beta },u)}^2}\mathrm{d}N\left(u\right),$$ (21)

which is derived in Appendix B.1. $I\left(\widehat{\beta }\right)$ can be replaced by $\mathcal{I}\left(\widehat{\beta }\right)$. Using the martingale central limit theorem and a log transformation, we get the approximate pointwise 1 − α confidence limits

$${\widehat{\Lambda }}_0\left(\tau \right)\exp \left(\pm \frac{{\widehat{\sigma }}_0\left(\tau \right)}{{\widehat{\Lambda }}_0\left(\tau \right)}{\Phi }^{-1}\left(1-\frac{\alpha }{2}\right)\right).$$ (22)

Point and interval estimates for the baseline survival function can be obtained using the relationship S₀(τ) = exp (− Λ₀(τ)

2.5 Who-infects-whom is not observed

When we do not observe who-infected-whom, we do not know which contact intervals are observed and which are censored. It impossible to calculate the partial likelihood pl(β) or the Breslow estimate $\widehat{\Lambda }(\beta ,\tau )$. In this section, we show how an EM algorithm similar to that of Kenah (2013) can be used to obtain consistent and asymptotically normal estimates of β₀ and Λ₀(τ).

Given β, λ(τ), and the observed information, the probability that j was infected by i is

$$p_{ij}(\beta ,\lambda )=\frac{r\left({\beta }^{\mathsf{T}}{X}_{ij}(t_j-t_i-{\epsilon }_i)\right)\lambda (t_j-t_i-{\epsilon }_i)1_{i\in {\mathcal{V}}_j}}{{\sum }_{k\in {\mathcal{V}}_j}r\left({\beta }^{\mathsf{T}}{X}_{kj}(t_j-t_k-{\epsilon }_k)\right)\lambda (t_j-t_k-{\epsilon }_k)},$$ (23)

and the infectors of different infected persons can be chosen independently (Kenah et al., 2008). The probability of a transmission network v = (v₁, . . . , v_n) given β, λ(τ), and the observed data is

$$\mathrm{Pr}(\mathbf{v}\mid \beta ,\lambda ,\text{observed data})=\prod _{j:0<v_j<\infty }{p}_{v_{j}j}(\beta .\lambda ).$$ (24)

Note that the last two equations assume a continuous contact interval distribution, so simultaneous infectious contacts have probability zero.

Let pl_v(β) be the log partial likelihood that we would have calculated had we observed the transmission network v. Given a coefficient vector β^* and a baseline hazard function λ^*(τ), the expected log likelihood is

$${\widetilde{pl}}_{{\beta }^{\ast },{\lambda }^{\ast }}\left(\beta \right)=\sum _{\mathbf{v}\in \mathcal{V}}p{l}_{\mathbf{v}}\left(\beta \right)\mathrm{pr}(\mathbf{v}\mid {\beta }^{\ast },{\lambda }^{\ast },\text{observed data})=\sum _{j=1}^n\sum _{i\ne j}{\int }_0^{\mathcal{T}}\ln \frac{r\left({\beta }^{\mathsf{T}}{X}_{ij}\left(u\right)\right)}{Y(\beta ,u)}\mathrm{d}{\tilde{N}}_{ij}(u\mid {\beta }^{\ast },{\lambda }^{\ast }),$$ (25)

where Ñ_ij(τ|β^*, λ^*) = p_ij(β^*, λ^*)1_τ≥_tj−_ti−_εi. Now let N(τ|v) be the value of N(τ) that we would have calculated had we observed the transmission network v. The corresponding Breslow estimate is

$${\widehat{\Lambda }}_{\mathbf{v}}(\beta ,\tau )={\int }_0^{\tau }\frac{1}{Y(\beta ,u)}\mathrm{d}N(u\mid \mathbf{v}).$$ (26)

The marginal Breslow estimate given β^* and λ^* (τ) is

$${\tilde{\Lambda }}_{{\beta }^{\ast },{\lambda }^{\ast }}(\beta ,\tau )=\sum _{\mathbf{v}\in \mathcal{V}}{\widehat{\Lambda }}_{\mathbf{v}}(\beta ,\tau )\mathrm{Pr}(\mathbf{v}\mid {\beta }^{\ast },{\lambda }^{\ast },\text{observed data})={\int }_0^{\tau }\frac{1}{Y(\beta ,u)}\mathrm{d}\tilde{N}(u\mid {\beta }^{\ast },{\lambda }^{\ast }),$$ (27)

where $\tilde{N}(\tau \mid {\beta }^{\ast },{\lambda }^{\ast })={\sum }_{j=1}^n{\sum }_{i\ne j}{\tilde{N}}_{ij}(\tau \mid {\beta }^{\ast },{\lambda }^{\ast })$.

For the relative risk function r(x) = exp(x), the expected log partial likelihood ${\widetilde{pl}}_{{\beta }^{\ast },{\lambda }^{\ast }}\left(\beta \right)$ is the log partial likelihood of a weighted Cox regression model (Therneau and Grambsch, 2000) with two copies of each pair ij: an uncensored copy with weight p_ij(β^* , λ^*) and a censored copy with weight 1 − p_ij(β^* , λ^*). The baseline hazard estimate from this model is the marginal Breslow estimate ${\tilde{\Lambda }}_{{\beta }^{\ast },{\lambda }^{\ast }}(\tilde{\beta },\tau )$, where $\tilde{\beta }=\arg {\max }_{\beta }{\widetilde{pl}}_{{\beta }^{\ast },{\lambda }^{\ast }}\left(\beta \right)$.

2.6 EM algorithm

When who-infects-whom is not observed, the semiparametric regression model can be fit using the ECM algorithm of Meng and Rubin (1993), which is an extension of the EM algorithm of Dempster et al. (1977). In each iteration, we first estimate β₀ using the expected log partial likelihood and then calculate the marginal Breslow estimator of Λ₀(τ). We use these new estimates to re-weight the possible v. The entire process is described in Algorithm 1.

Algorithm 1 ECM algorithm for semiparametric estimation of β₀ and Λ₀(τ).

To show that this is an ECM algorithm, we must show that the CM1 and CM2 steps are conditional maximizations of the expected log likelihood. The CM1 step is a conditional maximization by definition, so it remains to show that the CM2 step is a conditional maximization. Given a coefficient vector β^* and a hazard function λ^*, the expected log likelihood is

$${\tilde{\ell }}_{{\beta }^{\ast },{\lambda }^{\ast }}(\beta ,\Lambda )=\sum _{j=1}^n\sum _{i\ne j}{p}_{ij}({\beta }^{\ast },{\lambda }^{\ast })\ln \left(r\left({\beta }^{\mathsf{T}}{X}_{ij}(t_j-t_i-{\epsilon }_i)\right)\mathrm{d}\Lambda (t_j-t_i-{\epsilon }_i)\right)-{\int }_0^{\infty }Y(\beta ,u)\mathrm{d}\Lambda \left(u\right).$$ (28)

Differentiating with respect to dΛ(t_j − t_i − ε_i) for each i and j shows that, for a fixed β, l̃β^*,_λ^* (β, Λ) is maximized over all step functions Λ(τ) by setting

$$\mathrm{d}\Lambda (t_j-t_i-{\epsilon }_i)=\frac{p_{ij}({\beta }^{\ast },{\lambda }^{\ast })}{Y(\beta ,t_j-t_i-{\epsilon }_i)},$$ (29)

exactly as in the marginal Breslow estimator ${\tilde{\Lambda }}_{{\beta }^{\ast },{\lambda }^{\ast }}(\beta ,\tau )$. Therefore, Algorithm 1 is an ECM algorithm. When it is known that β = 0, it reduces to the EM algorithm in Kenah (2013). Therefore, the convergence of both β^(k) and Λ^(k)(τ) should be monitored.

2.7 Large-sample estimation of β₀

Let $\tilde{\beta }$ denote the estimate of β₀ to which the ECM algorithm converges, and let $\tilde{\lambda }\left(\tau \right)$ denote the corresponding estimate of λ₀(τ). Let U_v(τ, β) and I_v(β) denote the score and the observed information that we would have calculated had we observed the transmission network v. Using the methods of Louis (1982), the observed information is

$$\tilde{I}\left(\tilde{\beta }\right)={\mathbb{E}}_{\tilde{\beta },\tilde{\lambda }}\left[I_{\mathbf{v}}\left(\tilde{\beta }\right)\right]-{\mathbb{E}}_{\tilde{\beta },\tilde{\lambda }}\left[U_{\mathbf{v}}{(\tilde{\beta },\infty )}^{\otimes 2}\right],$$ (30)

where ${\mathbb{E}}_{\beta ,\lambda }[\cdot ]$ denotes an expectation taken under the assumption that the true coefficient vector is β and the true baseline hazard function is λ(τ). The first term in (30) is

$$-\sum _{j=1}^n\sum _{i\ne j}{\int }_0^{\tau }\frac{{\partial }^2}{\partial {\beta }^2}\ln \frac{r\left({\tilde{\beta }}^{\mathsf{T}}{X}_{ij}\left(u\right)\right)}{Y(\beta ,u)}\mathrm{d}{\tilde{N}}_{ij}\left(u\right),$$ (31)

where ${\tilde{N}}_{ij}\left(u\right)={\tilde{N}}_{ij}(u\mid \tilde{\beta },\tilde{\lambda })$. This is the observed information matrix from a weighted regression model where each ij has an uncensored copy with weight $p_{ij}(\tilde{\beta },\tilde{\lambda })$ and a censored copy with weight 1 − $1-p_{ij}(\tilde{\beta },\tilde{\lambda })$. To evaluate the second term in (30), let

$${\tilde{U}}_{.j}(\beta ,\tau )=\sum _{i\ne j}{\int }_0^{\tau }\frac{\partial }{\partial \beta }\ln \frac{r\left({\beta }^{\mathsf{T}}{X}_{ij}\left(u\right)\right)}{Y(\beta ,u)}\mathrm{d}{\tilde{N}}_{ij}\left(u\right),$$ (32)

be the expected score contribution from all pairs with j as a susceptible. Since ${\sum }_{j=1}^n{\tilde{U}}_{.j}(\tilde{\beta },\infty )=0$, each infected person j has only one infector in any v, and the infectors of different individuals can be chosen independently, we have

$${\mathbb{E}}_{\tilde{\beta },\tilde{\lambda }}\left[U{(\tilde{\beta },\infty )}^{\otimes 2}]\right]=\sum _{j=1}^n\sum _{i\ne j}{\int }_0^{\infty }{\left(\frac{\partial }{\partial \beta }\ln \frac{r\left({\tilde{\beta }}^{\mathsf{T}}{X}_{ij}\left(u\right)\right)}{Y(\tilde{\beta },u)}\right)}^{\otimes 2}\mathrm{d}{\tilde{N}}_{ij}\left(u\right)-\sum _{j=1}^n{\tilde{U}}_{.j}{(\tilde{\beta },\infty )}^{\otimes 2}$$ (33)

2.8 Large-sample estimation of Λ₀(τ)

Let ${\tilde{\Lambda }}_0\left(\tau \right)$ be the marginal Breslow estimate obtained after convergence of the ECM algorithm. Appendix B.2, available online, derives the variance estimate

$${\tilde{\sigma }}_0^2\left(\tau \right)={\left(\frac{\partial }{\partial \beta }{\tilde{\Lambda }}_{\tilde{\beta },\tilde{\lambda }}(\tilde{\beta },\tau )\right)}^{\mathsf{T}}\tilde{I}{\left(\tilde{\beta }\right)}^{-1}\left(\frac{\partial }{\partial \beta }{\tilde{\Lambda }}_{\tilde{\beta },\tilde{\lambda }}(\tilde{\beta },\tau )\right)$$ (34)

$$+2{\int }_0^{\tau }\frac{1}{Y{(\tilde{\beta },u)}^2}\mathrm{d}\tilde{N}\left(u\right)-\sum _{j=1}^n{\left({\int }_0^{\tau }\frac{1}{Y(\tilde{\beta },u)}\mathrm{d}{\tilde{N}}_{.j}\left(u\right)\right)}^2,$$ (35)

where Ñ_.j(u) = Σ_i≠j Ñ_.j(u). Using the martingale central limit theorem and a log transformation, we get the approximate pointswise 1 − α confidence limits

$${\tilde{\Lambda }}_0\left(\tau \right)\exp \left(\pm \frac{{\tilde{\sigma }}_0\left(\tau \right)}{{\tilde{\Lambda }}_0\left(\tau \right)}{\Phi }^{-1}\left(1-\frac{\alpha }{2}\right)\right).$$ (36)

Point and interval estimates for the baseline survival function can be obtained using the relationship S₀(τ) = exp (− Λ₀(τ)

3 SIMULATIONS

The performance of the methods from Section 2 was tested with a series of 12000 network-based epidemic simulations. All epidemics took place on a Watts-Strogatz small-world network (Watts and Strogatz, 1998), which mimics the high clustering and low diameter of real human contact networks. Starting with a ring of 50000 nodes, each node was connected to its 10 nearest neighbors and each edge was rewired to a randomly chosen node with probability 0.1. A new contact network was built for each simulation.

All epidemic models were written in Python 2.7 (www.python.org) using the packages NetworkX 1.6 (networkx.lanl.gov), NumPy 1.6, and SciPy 0.9 (www.scipy.org). Statistical analysis was done in in R 2.15 (www.r-project.org) via the Rpy2 2.2 package (rpy.sourceforge.net). The code for the models is available as Online Supplementary Information.

3.1 Transmission model

The transmission model had a latent period of zero and an exponential infectious period with mean one. The baseline contact interval distribution was Weibull(α, γ), where α is the shape parameter and γ is the rate parameter. 6000 simulations had a Weibull(0.5, 0.2) distribution, which has Λ₀(τ) = (0.2τ)^0.5. The other 6000 had a Weibull(2, 0.6) distribution, which has Λ₀(τ) = (0.6τ)². These distributions gave a basic reproduction number (expected number of infectious contacts made by a typical infectious person) R₀ ≈ 3 in a null model.

In the transmission model, each person i had an infectiousness covariate $X_i^{\inf }$ and a susceptibility covariate $X_i^{\mathrm{sus}}$. Each pair ij connected by an edge had a pairwise covariate $X_{ij}^{\mathrm{pair}}$. All covariates were independent Bernoulli(.5) random variables. For a connected pair ij, the hazard of infectious contact from i to j at infectious age τ of i was

$${\lambda }_{ij}\left(\tau \right)=\exp \left({\beta }_{\inf }{X}_i^{\inf }+{\beta }_{\mathrm{sus}}{X}_j^{\mathrm{sus}}+{\beta }_{\mathrm{pair}}{X}_{ij}^{\mathrm{pair}}\right){\lambda }_0\left(\tau \right)$$ (37)

For each parameter β, there were 4000 simulations where its true value was chosen from a uniform distribution on (−1, 1). Of these, 2000 simulations used the Weibull(0.5, 0.2) baseline hazard and 2000 used the Weibull(2, 0.6) baseline hazard. Of the 2000 simulations for each baseline hazard, 1000 had the other two β set to 0 and 1000 had the other two β set to 1.

Each simulated epidemic began with a single person infected at time 0. Data from the next 1000 infections was used to fit two regression models, one using information on who-infected-whom as in Section 2.1 and one using an EM algorithm as in Section 2.5. The EM algorithm used a minimum of 2 and a maximum of 25 iterations. At each iteration, a weighted Cox model was run using the last parameter estimates as the initial parameter estimates. Convergence was defined as a change less than 0.002 in the expected log likelihood (tighter convergence criteria yielded nearly identical parameter estimates). After convergence, a Cox model was run using the final weights and initial parameters β_inf = β_sus = β_pair = 0.

After each simulation, we recorded the true value, estimate, and 95% confidence interval endpoints for each in the model and the baseline hazard at the 10^th, 25^th, 50^th, 75^th, and 90^th percentiles of all censored and observed contact intervals. We also recorded the α and γ of the baseline hazard function and the number of EM iterations.

3.2 Results

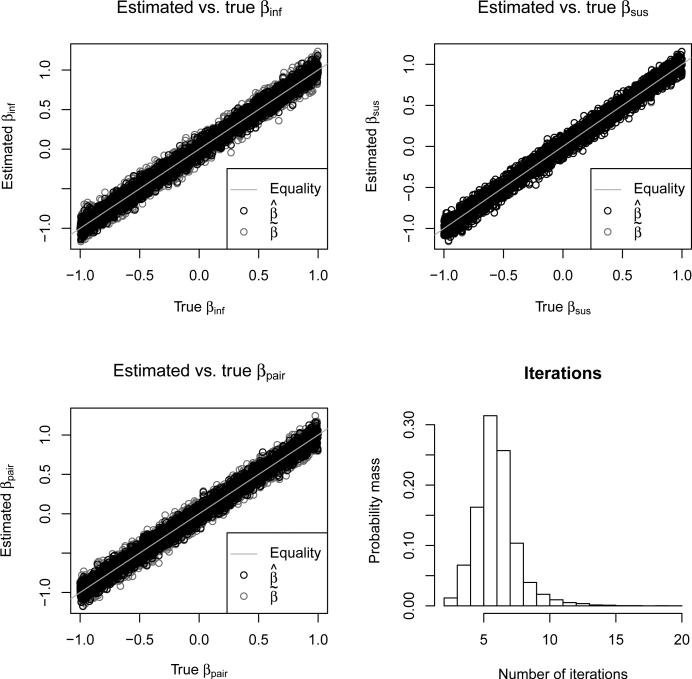
Figure 3 shows good agreement between the estimated and true β_inf, β_sus, and β_pair for both $\widehat{\beta }$ (who-infects-whom observed) and $\tilde{\beta }$ (who-infects-whom unobserved). Table 1 shows excellent 95% confidence interval coverage probabilities for all combinations of baseline hazards and parameters. The $\tilde{\beta }$ estimates had slightly lower coverage probabilities than the $\widehat{\beta }$ estimates. The lower right panel of Figure 3 shows that this was achieved with relatively few iterations. The median number of iterations was 6, and 98% of simulations required ≤ 10 iterations. Only 2 out of 12000 simulations failed to converge within 25 iterations.

Figure 3.

The top two panels and the bottom left panel show $\widehat{\beta }$ (black circles) and $\tilde{\beta }$ (gray circles) versus true β for β_inf, β_sus, and β_pair. The bottom right panel shows a histogram of the number of EM iterations required for convergence.

Table 1.

Hazard ratio 95% confidence interval coverage probabilities in simulations. Each probability is based on the results of 1000 simulations.

Baseline hazard	Parameter: βinf
	βsus=βpair=0		βsus=βpair=1
	β inf	β inf	β inf	β inf
α = .5	.952	.937	.937	.945
α = 2	.955	.952	.957	.941
Baseline hazard	Parameter: βsus
	βinf = βpair = 0		βinf = βpair = 1
	β sus	β sus	β sus	β sus
α = .5	.951	.950	.939	.939
α=2	.952	.948	.945	.946
Baseline hazard	Parameter: βpair
	βinf = βsus = 0		βinf = βsus = 0
	β pair	β pair	β pair	β pair
α = .5	.942	.927	.955	.946
α=2	.942	.929	.951	.951

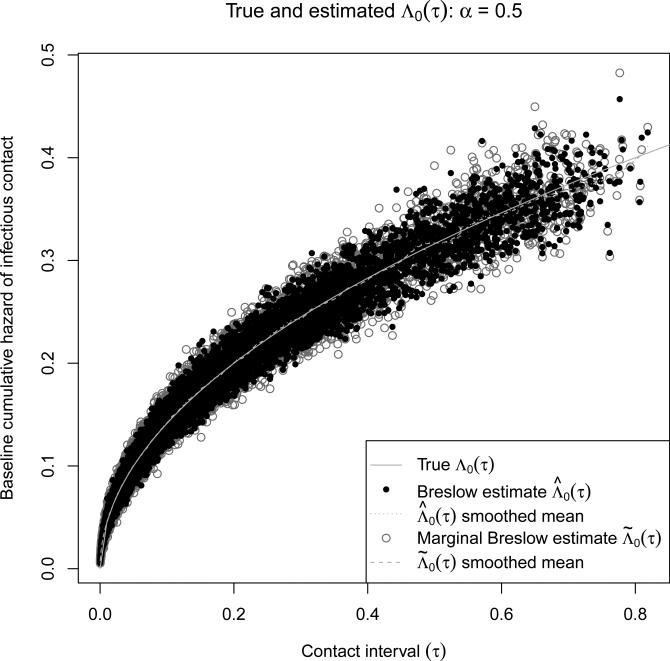
Figures 4 and 5 show good agreement between the estimated and true base-line hazard for both ${\widehat{\Lambda }}_0\left(\tau \right)$ (who-infects-whom observed) and ${\tilde{\Lambda }}_0\left(\tau \right)$ (who-infects-whom unobserved). The smoothed means show almost no bias in ${\widehat{\Lambda }}_0\left(\tau \right)$ or ${\tilde{\Lambda }}_0\left(\tau \right)$. Table 2 shows good 95% confidence interval coverage probabilites for both base-line hazards and all percentiles except for α = 2 at the 10^th and 25^th percentiles. When α = 2, the baseline hazard of infectious contact is λ₀(τ) = 1.2τ. At low values of τ, the hazard of infectious contact is very small, so almost all of the contact intervals will be censored. Since the percentiles are calculated for all censored and observed contact intervals, there may be too few observed intervals at the 10^th and 25th percentiles when α = 2 for the large-sample normal approximation to be valid.

Figure 4.

${\widehat{\Lambda }}_0\left(\tau \right)$ and ${\tilde{\Lambda }}_0\left(\tau \right)$ versus true Λ₀(τ) for the 6000 simulations with a Weibull(0.5, 0.2) baseline contact interval distribution. For each simulation and each estimator, a circle is shown for the 10^th, 25^th, 50^th, 75^th, and 90^th percentiles of all possible contact intervals. The smoothed means were calculated using cubic smoothing splines.

Figure 5.

${\widehat{\Lambda }}_0\left(\tau \right)$ and ${\tilde{\Lambda }}_0\left(\tau \right)$ versus true Λ₀(τ) for the 6000 simulations with a Weibull(2, 0.6) baseline contact interval distribution. For each simulation and each estimator, a circle is shown for the 10^th, 25^th, 50^th, 75^th, and 90^th percentiles of all possible contact intervals. The smoothed means were calculated using cubic smoothing splines.

Table 2.

95% confidence interval coverage probabilities in simulations. Each probability is based on the results of 6000 simulations.

Baseline hazard Quantile	α = .5		α=2
	${\widehat{\Lambda }}_0\left(\tau \right)$	${\tilde{\Lambda }}_0\left(\tau \right)$	${\widehat{\Lambda }}_0\left(\tau \right)$	${\tilde{\Lambda }}_0\left(\tau \right)$
10%	.949	.938	.957	.875
25%	.949	.940	.951	.905
50%	.950	.941	.955	.934
75%	.949	.936	.949	.939
90%	.949	.941	.953	.939

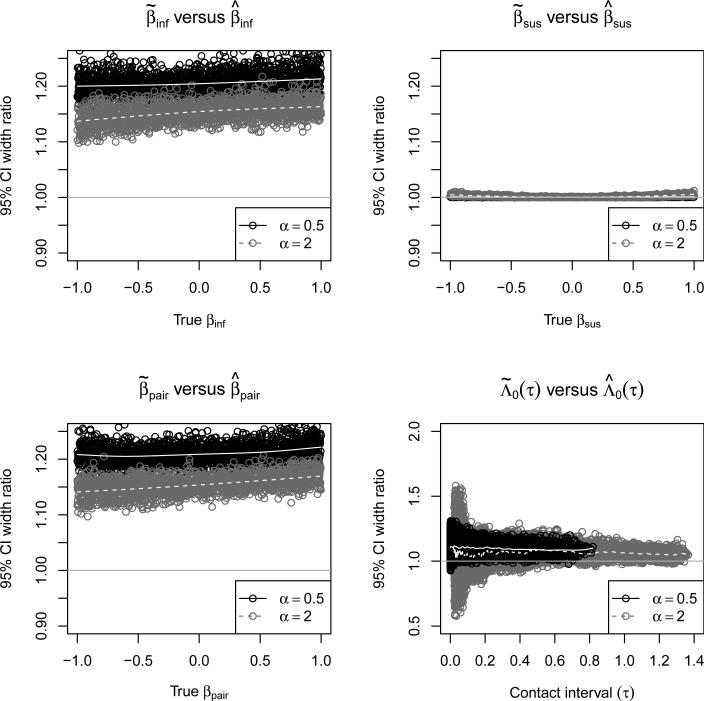
Figure 6 shows the widths of the confidence intervals when who-infects-whom is not observed in terms of the width of the confidence interval when who-infects-whom is observed for β_inf, β_sus, β_pair, and Λ₀(τ). For β_inf and β_pair, the precision gained by observing who-infects-whom is roughly equivalent to a 20-40% increase in sample size. The baseline hazard plays an important role in how much precision is gained, with a larger gain for α = 0.5 than for β = 2. There is no gain in precision for β_sus because observing who-infects-whom does not add to our knowledge of who was infected. Seeing who-infects-whom only slightly improves the precision of baseline hazard estimates.

Figure 6.

The width of 95% confidence intervals when who-infects-whom is not observed divided by its width when who-infects-whom is observed for β_inf, β_sus, β_pair, and Λ₀(τ). The solid gray lines show smoothed means for α = 0.5 and dashed gray lines show smoothed means for α = 2. The smoothed means were calculated using cubic smoothing splines.

Observing who-infects-whom allows point estimates that are closer to the truth and interval estimates with better coverage probabilities. However, the EM algorithm can recover a great deal of information when who-infects-whom is not observed, making the iterative regression model of Section 2.5 a promising tool for infectious disease epidemiology.

4 DATA ANALYSIS

To show how the methods of Section 2 can be applied, we will look at the effect of antiviral prophylaxis and age on the transmission of pandemic influenza A(H1N1) in Los Angeles County in 2009. The Los Angeles County Department of Public Health (LACDPH) collected household surveillance data between April 22 and May 19 according to the following protocol (Sugimoto et al., 2011):

1. Nasopharyngeal swabs and aspirates were taken from individuals who reported to the LACDPH or other health care providers with acute febrile respiratory illness (AFRI), defined as a fever ≥ 100°F plus cough, core throat, or runny nose. These specimens were tested for influenza, and the age, gender, and symptom onset date of the AFRI patient were recorded.

2. Patients whose specimens tested positive for pandemic influenza A(H1N1) or for influenza A of undetermined subtype were enrolled as index cases. Each of them was given a structured phone interview to collect the following information about his or her household contacts: age, gender, type of contact (household, intimate, in-home daycare, non-home daycare), and high risk status (pregnant, child on long-term aspirin therapy, immuno-suppressed, or history of a chronic cardiac, pulmonary, renal, liver, or neurologic condition). The interviewer also recorded whether prophylactic antiviral medication was being taken by the household contacts. They were asked to report the symptom onset date of any AFRI episodes among their household contacts.

3. When necessary, a follow-up interview was given 14 days after the symptom onset date of the index case to assess whether any additional AFRI episodes had occurred in the household, including their illness onset date.

There were 58 households with a total of 299 members. There were 99 infections, of which 62 were index cases (4 of the 58 households had co-primary cases) and 27 were household contacts with an AFRI. For simplicity, we assume these were all influenza A(H1N1) cases and that all household members were susceptible to infection.

Our natural history assumptions were adapted from Yang et al. (2009) and are identical to those in Kenah (2013). In the primary analysis, we assumed an incubation period of 2 days, a latent period of 0 days, and an infectious period of 6 days. Under these assumptions, a person j with symptom onset at time $t_j^{\mathrm{sym}}$ was infected at time $t_j=t_j^{\mathrm{sym}}-2$ and will stop being infectious at time $t_j+6=t_j^{\mathrm{sym}}+4$. Under these assumptions, person j can transmit infection on days t_j + 1 to t_j + 6. In a sensitivity analysis, we vary the latent period from 0 to 1 days, and the infectious period from 5 to 7 days.

We modeled influenza transmission within households, not between households or from outside the observed households. In each household, infected household members who had no possible infector within the household according to our natural history assumptions were assumed to be imported infections. We assumed that any infected household member could infect any susceptible household member. We used the regression model of Section 2.5 to estimate influenza transmission hazard ratios for the following covariates:

• age_inf = 0 if the infectious person is < 18 years old and 1 otherwise,

• age_sus = 0 if the susceptible is < 18 years old and 1 otherwise,

• proph_sus = 0 if the susceptible is not on antiviral prophylaxis and 1 otherwise.

Since antiviral prophylaxis was initiated after the initial case in each household, it was considered only as a susceptibility covariate. All statistical analysis was done in R 2.15 (www.r-project.org).

4.1 Results

There were 114 people aged < 18 years and 185 aged ≥ 18 years, with no missing age data. There were 91 people taking antiviral prophylaxis and 152 not taking prophylaxis, with missing prophylaxis data for 56 people. When who-infects-whom is not observed, a complete-case analysis requires the removal of all rows corresponding to infectious-susceptible pairs ij where $i\in {\mathcal{V}}_j$ and any member of ${\mathcal{V}}_j$ is missing data. Otherwise, the remaining members of ${\mathcal{V}}_j$ get too much credit for the infection of j.

In the main analysis, there were 70 people infected from outside the household (i.e., no possible infector in the household), 16 with 1 possible infector, 7 with 2 possible infectors, 4 with 4 possible infectors, and 2 with 8 possible infectors, giving us 1¹⁶ × 2⁷ × 4⁴ × 8² = 2097152 possible transmission trees. The pairwise data contains 443 infectious-susceptible pairs with a total of 2455 pair-days at risk of infection. Of these, 16 × 1 + 7 × 2 + 4 × 4 + 2 × 8 = 62 rows represent possible infection events. All models used the Efron approximation (Efron, 1977) for the partial likelihood with tied failure times.

The top panel of Table 3 shows the results of seven models. All of the models including prophylaxis suggested that antiviral prophylaxis reduced the hazard of infectious contact by about 60%, with low p-values. Hazard ratio point estimates for the main effects of age in all models suggest that adults are more infectious and less susceptible than children. However, evidence for this result is very weak. Only one of the age effects was statistically significant in univariable models, and none were significant in any multivariable model. Multivariable and stratified models with interaction terms for age and antiviral prophylaxis suggest a stronger effect of antiviral prophylaxis on transmission to and from adults than on transmission to and from children. However, the evidence for this result is also weak; these coefficients had high p-values and wide confidence intervals. The bottom panel of Table 3 shows the results of a sensitivity analysis using the multivariable model without interaction. Varying the latent and infectious periods has little effect on the results of the model.

Table 3.

Hazard ratios with 95% con dence intervals and p-values for different models of the 2009 pandemic inuenza A(H1N1) household surveillance data from Los Angeles County. Likelihood ratio p-values comparing models with and without interaction terms are also given. The multivariable and stratied models without interaction were used as the final models.

	Main effects			Interactions
	ageinf	agesus	prophysus	Variables	HR (p-value)
Regression model
Univariable	1.53 (0.66, 3.54) p = .321	0.41 (0.20, 0.85) p = .016	0.43 (0.18, 1.02) p = . 057
Multivariable	1.78 (0.69, 4.62) p = .234	0.69 (0.29, 1.64) p= .399	0.41 (0.17, 0.98) p = . 046
Multivariable + interaction	1.59 (0.32, 7.84) p = . 570	0.63 (0.14, 2.73) p= .532	0.04 (0.00, 9.62) p = . 253	ageinf:agesus ageinf :prophsus agesus :prophsus	0.66 (p = .71) 9.28 (p= .45) 2.72 (p = .36) LR p = .101
Stratified	strata	0.69 (0.29, 1.64) p = . 401	0.41 (0.17, 0.99) p = . 047
Stratified + interaction	strata	0.52 (0.29, 1.64) p = .219	0.23 (0.05, 1.16) p = . 075	ageinf :prophsus	2.37 (p = .38) LR p = .353
Sensitivity analysis (multivariable model without interaction)
Latent period 1 day	1.44 (0.64, 3.26) p = .378	0.83 (0.36, 1.93) p = . 670	0.35 (0.15, 0.80) p = .013
Infectious period 5 days	1.59 (0.60, 4.20) p = . 348	0.64 (0.27, 1.55) p = .322	0.45 (0.18, 1.07) p = .073
7 days	1.45 (0.62, 3.40) p = .378	0.89 (0.38, 2.04) p = . 670	0.34 (0.17, 0.87) p = .013

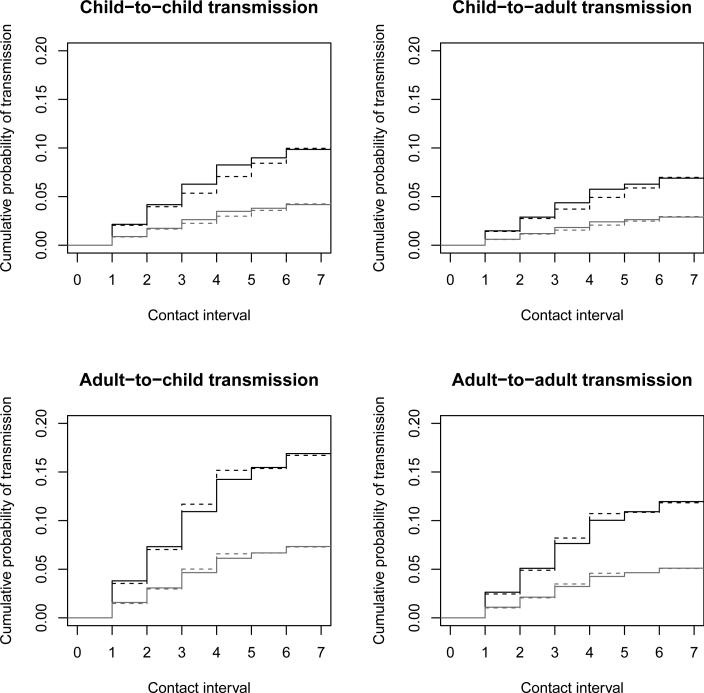
Figure 7 shows estimates of the cumulative transmission probability based on the multivariable and stratified models without interaction. The results of the two models are similar, but the stratified model showed lower probabilities of transmission from children and higher probabilities of transmission from adults. All four panels clearly show the estimated effect of antiviral prophylaxis. All curves show bigger jumps on the first four days after infection than on days 5 and 6, which is consistent with the results of Kenah (2013). Comparing the top and bottom rows shows that children are estimated to be less infectious than adults. Comparing the left and right columns shows that children are estimated to be more susceptible than adults. As noted above, these differences are not statistically significant.

Figure 7.

Household transmission of 2009 pandemic influenza A(H1N1) in Los Angeles County. Each panel shows separate curves for susceptible contacts with (gray lines) and without (black lines) antiviral prophylaxis. The solid lines are based on the multivariable model, and the dotted lines are based on the model stratified by age_inf.

This data analysis has been intended primarily to illustrate the flexibility of the regression modeling framework for analyzing transmission data. There are several important limitations of the analysis itself. With only 29 within-household transmissions, the large-sample normal approximations may not hold and there is limited power to estimate the effects of age and antiviral prophylaxis. The age classification is crude, so it may not accurately capture the effects of age. The prophylaxis variable was missing for many pairs and was binary, allowing no consideration of the timing of prophylaxis relative to exposure. Analyses of the household transmission of influenza A(H3N2) found greater child-to-child than adult-to-adult transmission (Addy et al., 1991). In our analysis of influenza A(H1N1), children appeared less infectious and more susceptible than adults, but these differences were not statistically significant. If not due to random noise, such a result could reflect a difference between the H3N2 and H1N1 subtypes of influenza A or a bias caused the failure to account for infection from outside the household. In any case, this analysis shows that the model needs to be extended to model infection from outside the household and to handle missing data.

5 DISCUSSION

The semiparametric relative-risk regression model proposed here has several important advantages over the chain binomial model. It can be fit using standard statistical software with parameter interpretations that resemble the Cox model. Standard software can be used to convert the results into curves representing the cumulative probability of transmission in pairs of individuals with specific characteristics. It does not make any parametric assumptions about the baseline hazard of infectious contact, and it allows many of the same extensions as the Cox model, including stratification, interaction, and time-dependent covariates. This flexibility and ease of use will make it an important tool for infectious disease epidemiology. To realize this potential, there are several limitations that remain to be addressed.

We assumed that the set of imported infections is known. The chain binomial model handles unknown imported infections by including a per-time-unit probability of escaping infection from outside the household. In the semipara-metric regression model, this could be achieved by fitting two models in each step of the EM algorithm: a pairwise contact interval model within the household and an individual-level model in absolute time for infection from outside the household. At each step, the weights would be recalculated based on covariates, coefficient estimates, the baseline hazard of the contact interval distribution, and the baseline hazard of infection from outside the household.

We assumed that infection times, latent periods, and infectious periods were all observed. We can usually observe only the clinical course of the disease, so these times must be imputed. In Section 4, we had missing data on covariates. Simple missing data (such as antiviral prophylaxis) could be handled by extending the EM algorithm to calculate the expected log likelihood over the possible values of the missing data as well as who-infected-whom. More complex missing data (such as infection and removal times) could be handled using data augmentation in a profile sampler (Lee et al., 2005), getting a posterior distribution for the model coefficients while treating the baseline hazards as a nuisance parameter.

We assumed that all possible infectors of each person were observed. Unobserved infectors could occur because of incomplete contact tracing or asymptomatic infection. The possible bias caused by unobserved sources of infection needs to be studied, and methods for controlling it analytically or assessing its severity in a sensitivity analysis need to be developed.

We assumed a static contact network where the C_ij were binary and constant. In reality, people are exposed to close contacts at home, at work, at school, and at other locations in a dynamic process. The extension of these methods to dynamic contact networks is possible but nontrivial. We could allow C_ij(τ) to be a time-dependent process in the infectious age τ of i. The contact interval distribution would then be defined as the distribution of the contact interval that would occur if C_ij(τ) = 1 for all τ. For estimation, we would have to observe the process C_ij(τ) for each ij.

Some of our assumptions must be relaxed to capture the natural history of complex diseases. We assumed an SEIR framework best suited to acute, immunizing diseases that spread directly from person to person. Many foodborne and waterborne diseases, pneumococcal and meningococcal diseases, and other infectious diseases of major public health importance do not fit easily into this framework. To extend the proposed regression model to complex diseases, we could allow individuals to experience multiple events (e.g., first infection, second infection) or to experience different types of events (e.g., colonization, infection, relapse). We assumed that contact intervals were independent of infectious periods even though both are a ected by the same host-pathogen interaction. In some cases, there may be a covariate process X(τ) such that I_i(τ) and ${\mathcal{N}}_{ij}\left(\tau \right)$ are conditionally independent given X(τ⁻). Otherwise, infectious contact and the infectious period must be modeled as a multivariate survival process.

Several technical issues need further attention. The smoothing step is crucial to the fitting the regression model when who-infects-whom is not observed. Here, we used cubic smoothing splines because they were convenient and worked well. However, these do not guarantee that the smoothed hazard function is monotonically increasing and lack a convenient interpretation in terms of the likelihood. A penalized likelihood estimator that guarantees monotonicity, such as that of Anderson and Senthilselvan (1980), would be more consistent with the EM algorithm. Model diagnostics, goodness-of-fit tests, and small-sample methods for point and interval estimation need to be developed, and a more rigorous study of the model asymptotics needs to be done.

Despite these limitations, the semiparametric relative-risk regression model presented here is a powerful new framework for the analysis of infectious disease transmission data. Placing statistical methods for infectious disease epidemiology on the broad and deep theoretical foundation of survival analysis will help clarify study design and causal inference for communicable diseases and allow statistical methods to develop in concert with advances in molecular biology. Ultimately, these improvements may lead to more efficient vaccine trials and a better-informed public health response to future outbreaks and epidemics.