Mapping fast protein folding with multiple-site fluorescent probes

Significance

Fast–protein-folding experiments and molecular-dynamics simulations can nowadays be compared on the same timescale. The comparison is limited by the lack of time-resolved structural information from experiment, which usually provides only information on global kinetics or stability. Structural data from microsecond folding experiments enables more rigorous testing of the detailed predictions available from simulations, which will in turn make future simulations more reliable. Here, we tackled this long-standing problem by measuring tertiary contact formation between three helices in a fast-folding protein. The folding of this protein is not as simple as it seems but matches up nicely with a long all-atom simulation trajectory that monitors multiple folding and unfolding events.

Abstract

Fast protein folding involves complex dynamics in many degrees of freedom, yet microsecond folding experiments provide only low-resolution structural information. We enhance the structural resolution of the five-helix bundle protein λ_6–85 by engineering into it three fluorescent tryptophan–tyrosine contact probes. The probes report on distances between three different helix pairs: 1–2, 1–3, and 3–2. Temperature jump relaxation experiments on these three mutants reveal two different kinetic timescales: a slower timescale for 1–3 and a faster one for the two contacts involving helix 2. We hypothesize that these differences arise from a single folding mechanism that forms contacts on different timescales, and not from changes of mechanism due to adding the probes. To test this hypothesis, we analyzed the corresponding three distances in one published single-trajectory all-atom molecular-dynamics simulation of a similar mutant. Autocorrelation analysis of the trajectory reveals the same “slow” and “fast” distance change as does experiment, but on a faster timescale; smoothing the trajectory in time shows that this ordering is robust and persists into the microsecond folding timescale. Structural investigation of the all-atom computational data suggests that helix 2 misfolds to produce a short-lived off-pathway trap, in agreement with the experimental finding that the 1–2 and 3–2 distances involving helix 2 contacts form a kinetic grouping distinct from 1 to 3. Our work demonstrates that comparison between experiment and simulation can be extended to several order parameters, providing a stronger mechanistic test.

The mechanism of protein folding is one of the central questions in biological science (1). The first all-atom simulation to capture substantial protein-refolding dynamics, which lasted 1 μs, was published in 1998 (2). Since then, the timescales of protein folding achieved experimentally and computationally have met (3). Advances in computation now produce distributed (4) and single-trajectory (5) protein-folding simulations on the same nanosecond-to-millisecond timescale as the fastest folding experiments.

With rich computational data becoming available, experimental testing of simulations is now hampered by the difficulty of acquiring experimental structural data with microsecond or faster time resolution. Fast ensemble and single-molecule experiments commonly probe only one order parameter such as the fluorescence lifetime of a single tryptophan residue, a broad infrared (IR) spectral response, or one Förster resonant energy transfer (FRET) efficiency (3). Fortunately, a quantitative comparison of such experimental order parameters with simulations is now possible: for example, solvent-accessible surface area of tryptophan can serve as a proxy for experimentally detected fluorescence (6), or computed 2D-IR spectra can track secondary structure (7). Still, a single-order parameter, even when compared accurately, cannot capture the complexity of folding on a funneled energy landscape (3). It becomes essential to capture experimental information along several coordinates that are amenable to straightforward modeling. One way of achieving this is through the use of multiple probes in a single protein.

The problem of multiple probes reporting on several order parameters of protein folding has been addressed previously. For example, stopped-flow experiments have been combined with multiple fluorescent probes to study slow protein folding or membrane insertion processes (8, 9). Noninvasive equilibrium NMR experiments, including some coupled with molecular dynamics simulations, have evaluated two-state fits and provided high resolution folding landscapes by using multiple probe nuclei (10–12). Notable progress in multiprobe analysis of folding kinetics has been achieved by using nonnatural amino acid IR probes (13) in combination with T-jump relaxation spectroscopy (14, 15). Comparisons between fast protein folding kinetics probed by fluorescence and/or IR spectroscopy identified heterogeneous folding of trpzip2 (16), λ repressor (17), and α₃D (18). Tryptophan fluorescence probes local solvent exposure, whereas the amide I IR fingerprint probes global backbone hydrogen bonding. In downhill or incipient downhill folders, a free-energy landscape with a single-order parameter cannot reproduce both fluorescence and IR results because downhill folding is defined by a rapid interconversion between various conformational subpopulations.

Here, we approached the problem of multiple structural coordinates for fluorescence-detected fast kinetics by designing new fluorescence-quenching mutants capable of detecting site-specific tertiary contact formation in the five-helix bundle λ_6–85. The required conservative amino acid side-chain mutations fall between extrinsic dye labeling (e.g., FRET detection) and isotope labeling (IR spectroscopy) in their intrusiveness, so simulations will be critical for interpreting them. Our hypothesis, to be tested by comparison with simulation, is that the probes are sufficiently nonintrusive to reveal a common mechanism.

Many folding studies of λ_6–85 have been performed by using the fluorescence of a tryptophan (Trp) engineered into position 22 of helix 1 (19), quenched by a tyrosine (Tyr) (20) engineered into position 33 of helix 2. Trp-22 and Tyr-33 form a contact pair in the crystal structure (21). When Tyr-33 is absent, Trp-22 fluorescence increases slightly upon folding; with Tyr-33 present, Trp fluorescence is strongly quenched upon folding.

We expand the use of Trp–Tyr pairs to probe contact formation between three helix pairs during the folding of λ_6–85 (Fig. 1). In addition to helices 1–2 probed by Trp-22 and Tyr-33, we generate two new mutants whose fluorescence quenching links helices 1–3 and 2–3. These mutants are thermally stable α-helical proteins with high expression yield and strong Trp quenching by Tyr. Temperature jump measurements on the helix 1–2, 1–3, and 3–2 mutants allowed us to compare experimental kinetics with the corresponding autocorrelation analysis of long molecular-dynamics (MD) trajectories published previously (5). We find agreement between the experimental and computational interhelix contact formation in the helix triad 1–2–3, suggesting that a common mechanism underlies the three different mutants. Both experiments and computational analysis suggest that the free-energy landscape of λ_6–85 includes a transiently populated trap at a free energy of about 3.5–4.5 k_BT that involves helix 2, altering the kinetics of the 1–2 and 3–2 probes relative to the 1–3 probe. Our results show that the match between fast-folding experiments and MD simulations can advance in its structural resolution into the regime of secondary structural building blocks.

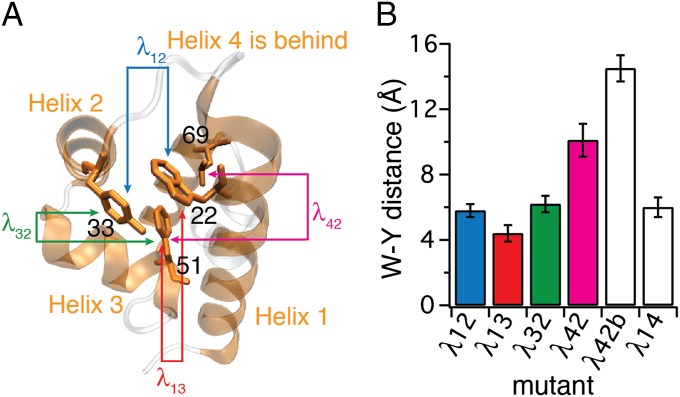
Fig. 1.

Construction of λ_6–85 mutants. (A) Crystal structure of the template mutant λ₁₂ (PDB ID code 3KZ3) with residues 22, 33, 51, and 69 highlighted in helices 1, 2, 3, and 4, respectively. Helices 1 through 4 in which mutations were made are shown in orange; the rest of the sequence is shown in gray. Arrows between pairs of residues and mutant names λ_ij follow the coloring and naming scheme used throughout the paper. Mutants λ_ij are named according to the helix pair contact probed. (B) Tryptophan–tyrosine (W-Y) distances calculated for six λ_6–85 mutants. Error bars represent the SD from fluctuations of the protein structures in the 100 ns of native-state MD simulations (SI Appendix, Fig. S1 and Table S2). All sequences are in SI Appendix, Fig. S1.

Results

Design of Mutants.

Our goal was to engineer new mutants of λ_6–85, such that several helix contact formations could be probed by Trp–Tyr fluorescence quenching. We started with the mutant Y22W, Q33Y, G46A, G48A. Its crystal structure is known [Protein Data Bank (PDB) ID code 3KZ3] (21). We name mutants according to the nomenclature “λ_ij,” where the subscripts stand for the helices in which tryptophan and tyrosine residues are positioned. Thus, we call the above mutant ${\mathrm{\lambda }}_{12}$ because in this mutant Trp is in helix 1 and Tyr is in helix 2.

Fig. 1A illustrates the crystal structure of ${\mathrm{\lambda }}_{12}$, with residues in positions 22, 33, 51, and 69 highlighted to indicate positions that were mutated in helices 1, 2, 3, and 4. We designed five additional mutants to probe other pairs of helices by Trp–Tyr contact (Fig. 1B and SI Appendix, Fig. S1). We mutated large hydrophobic amino acids to accommodate the probes, targeting Trp–Tyr distances <7 Å to obtain quenching upon folding of the protein. In helix 4, positions 62, 66, and 69 were considered for mutations. Position 66 was not pursued because a previous report indicated that such mutations can substantially decrease the thermal stability of the protein (22). Therefore, we tried mutating the remaining two hydrophobic-core–facing residues in positions 62 and 69. Mutations in helix 5 were not attempted because helix 5 is believed to be relatively unstructured in solution based on previously published mutational analysis and MD simulations (22–24). We ran 100-ns MD calculations of the proposed mutants in the native state (SI Appendix, Fig. S1) to ensure that the distances between probes would be short (<7 Å)—a necessary requirement for quenching of tryptophan fluorescence by tyrosine in the native state (Fig. 1B). Expression of mutants that showed larger interprobe distances in MD simulations, ${\mathrm{\lambda }}_{42}$ and λ_42b, was attempted as nonquenching controls.

Expression and Validation of Mutants.

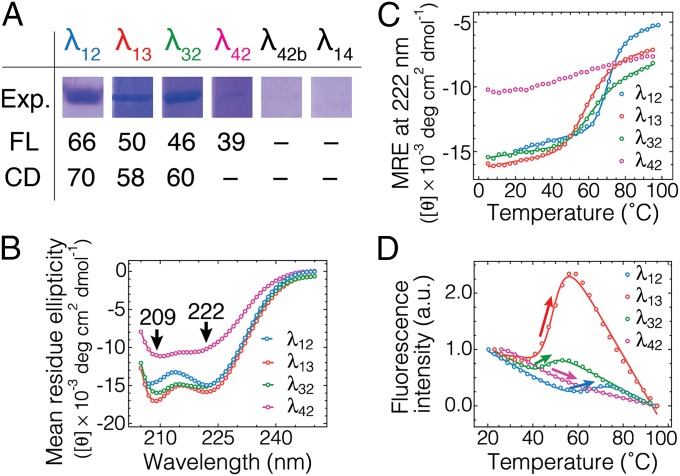
We attempted to express five new mutants of λ_6–85 using standard protein overexpression in BL21 Escherichia coli cells (Materials and Methods and SI Appendix, Fig. S1). Images of acrylamide gels containing corresponding chromatography fractions of each mutant are shown in Fig. 2A. Mutants λ₁₂, λ₁₃, and λ₃₂ showed a good expression yield of several milligrams of protein per liter of culture. Mutant λ₄₂ had a 10× lower expression yield. The other two mutants, λ_42b and λ₁₄, did not show detectable expression.

Fig. 2.

Expression and thermodynamic validation of engineered mutants. (A) Corresponding fractions of the protein purification gels for each mutant showing the relative expression yield. The midpoint denaturation temperatures in °C as determined by fluorescence intensity analysis (D; SI Appendix, Table S1) and circular dichroism (CD) at 222 nm as a proxy for α-helical content (C; SI Appendix, Table S1) are also shown. (B) CD spectra of four λ_6–85 mutants collected at 23 °C. Negative peaks at 209 and 222 nm are characteristic of α-helical content. Data are in SI Appendix, Fig. S2 and Table S1. (C) Equilibrium temperature denaturation of four λ_6–85 mutants monitored by CD at 222 nm as a proxy for α-content. Solid lines are two-state thermodynamic fits, which were used to determine the midpoint denaturation temperatures CD-T_m in A. λ₄₂ was not fitted. (D) Equilibrium temperature denaturation of four λ_6–85 mutants as monitored by fluorescence intensity integrated from 290 to 450 nm. The traces are normalized to begin at unity and end at zero. Solid lines are two-state fits, which were used to determine the midpoint denaturation temperatures FL-T_m in A. An increase in fluorescence intensity (arrows) is characteristic of the disruption of the Trp–Tyr interaction. Data are in SI Appendix, Fig. S3 and Table S1. Linear baselines are clearly a good approximation over our temperature range.

Mutants with detectable expression were analyzed for secondary structure content by circular dichroism (CD) (Fig. 2B and SI Appendix, Fig. S2). All mutants showed a characteristic signature of α-helical secondary structure as evidenced by negative peaks at 209 and 222 nm. We used the CD peak at 222 nm to monitor the equilibrium unfolding of λ repressor mutants as a function of temperature (Fig. 2C). All mutants showed an unfolding transition except λ₄₂. Note that λ₄₂ also had the least helical CD signal (Fig. 2B). λ₁₂ was most stable with a midpoint of unfolding at 70 ± 1 °C by CD (Fig. 2 A and C, and SI Appendix, Fig. S2 and Table S1). The other two mutants with high expression yield, λ₁₃ and λ₃₂, were also thermally stable with midpoint temperatures of 58 ± 1 and 60 ± 1 °C.

We also assessed protein thermal stability and quenching upon folding by fluorescence spectroscopy (Fig. 2D and SI Appendix, Fig. S3 and Table S1). λ₁₂ was again the most stable mutant with a midpoint of unfolding at 66 ± 1 °C by fluorescence (Fig. 2 A and D, and SI Appendix, Fig. S3 and Table S1). λ₁₃ and λ₃₂ showed midpoint temperatures of 50 ± 1 and 46 ± 1 °C, respectively. Mutant λ₄₂ showed the lowest midpoint temperature of 39 ± 1 °C. Only the most stable and well-expressed mutants (λ₁₂, λ₁₃, λ₃₂) showed an increase in fluorescence intensity upon denaturation (Fig. 2D). This observation is expected because in the native state, the Trp–Tyr distance for these mutants is short (∼5 ± 1 Å in Fig. 1B) and tryptophan is quenched by tyrosine.

As a control, increased fluorescence intensity upon denaturation is not observed for λ₄₂, a mutant with too large a Trp–Tyr distance for Dexter quenching (20) (∼10 Å; Fig. 1B). As mentioned above, λ₄₂ also showed a lower expression yield, lower secondary structure content, and lower midpoint unfolding temperature compared with the other three mutants. Thus, only the helix 1–2–3 triad of mutants λ₁₂, λ₁₃, and λ₃₂ was retained for further analysis.

Different Relaxation Times for Different Helix Pairs.

We measured the temperature jump relaxation (Materials and Methods) of the three mutants that showed fluorescence quenching upon folding. To compare mutants at similar melting temperatures, we adjusted the melting temperature of λ₁₂ as measured by CD to a value similar to the other two mutants, λ₁₃ and λ₃₂, by using 2.2 M guanidine hydrochloride (GuHCl) (SI Appendix, Fig. S4). We call this sample λ₁₂*. Temperature jumps of 8–9 °C were performed in a range close to the unfolding transition midpoint temperature for each protein [57 ± 1 °C for λ₁₂*, 58 ± 1 °C for λ₁₃, and 60 ± 1 °C for λ₃₂]. Higher temperature data for λ₁₂ without GuHCl extrapolates well to the λ₁₂* data in Fig. 3A (SI Appendix, Figs. S6–S8). The λ₁₂* trace in Fig. 3A does not include a 10% correction for the viscosity of GuHCl, which would make the blue trace even slightly faster than the green trace.

Fig. 3.

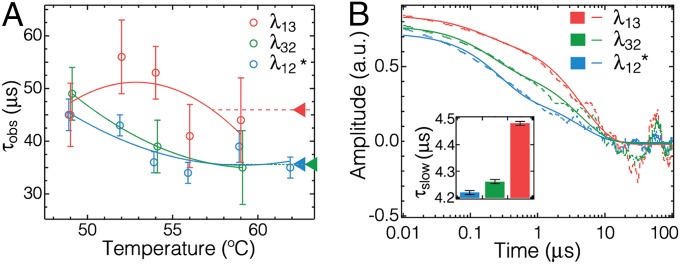
T-jump relaxation experiments and comparison with MD simulations. (A) Relaxation times of three λ_6–85 mutants as a function of final T-jump temperature. λ₁₂* was measured in 2.2 M GuHCl to reduce its stability to that of λ₁₃ and λ₃₂. Higher T measurements of λ₁₂ without GuHCl extrapolate well to the data shown here (SI Appendix, Figs. S6–S8 and Tables S2 and S3). Parabolic curves are guides for the eye. Triangular pointers on the Right highlight the observed time constants at the approximate region of equilibrium transition midpoints for each mutant. (B) Autocorrelations from a single MD trajectory (dashed lines) and double-exponential fits (solid lines) of the Dexter-weighted distances δ_ij between positions where Trp and Tyr are located in the experimental mutants. The slow phases are λ₁₃: 4.48 ± 0.01 μs; λ₃₂: 4.26 ± 0.01 μs; and λ₁₂: 4.22 ± 0.01 μs (see SI Appendix, Fig. S10, for details, and analysis of unweighted distances Δ_ij that produce the same ordering). The same trend as in experiment can be seen (Inset), although the simulated kinetics are faster by approximately a factor of 10.

The kinetic traces shown in SI Appendix, Figs. S6 and S7 were fitted to an exponential function FI(t) = A₁exp(−t/τ_obs), where τ_obs is the observed relaxation time constant. Kinetics faster than 2 μs associated with activated protein population (downhill folding) were not fitted for the present purpose, and for high-concentration measurements (Materials and Methods), a minor slow phase A₂exp(−t/τ₂) was added to account for a small amount of protein aggregation (SI Appendix, Fig. S5) observed previously (25). All fitting parameters are listed in SI Appendix, Tables S2 and S3. The temperature dependence of the relaxation time τ_obs for the three mutants from final T-jump temperature ranging from 49 to 59 °C are shown in Fig. 3A. Our results show that λ₁₃ has a slower observed relaxation time, whereas λ₃₂ and λ₁₂* (even without viscosity correction) have faster relaxation times, which are similar within the experimental error in the 50–60 °C range. Measurements over a wider temperature range and without denaturant (SI Appendix, Fig. S8) show that the λ₁₂ relaxation could become the slowest at high temperature.

Comparison with MD Simulations.

We compared the results of kinetics experiments with a previously published single-trajectory full-atom MD simulation (λ_Shaw in SI Appendix, Fig. S1, total of 161-μs simulation dataset courtesy of D. E. Shaw Research) (5). This simulation differs from our template protein λ₁₂ by an additional D14A mutation and residues at the N and C terminus (SI Appendix, Fig. S1). Such single-trajectory MD simulations are commonly analyzed in terms of global order parameters such as the contact order (Q) or the root-mean-square deviation of α-carbons from the crystal structure (C_α-RMSD) (SI Appendix, Fig. S9).

Instead, we used the distance ${\mathrm{\Delta }}_{ij}$ between sidechains of amino acids located at the positions of our experimental probes as three order parameters that are directly related to our experimental fluorescence quenching observables. To match computed and experimental observables as accurately as possible, the computed distances were weighted by the Dexter energy transfer efficiency ${\delta }_{ij}=\text{exp}[-{\mathrm{\Delta }}_{ij}/(5\hspace{0.17em}\mathrm{\AA })]$ responsible for Tyr–Trp quenching (20). This weighting function is monotonic with distance and does not affect the computed ordering (Fig. 3B and SI Appendix, Fig. S10); neither does varying the screening length from 4 to 7 Å. We calculated autocorrelation functions of the weighted distances ${\delta }_{ij}$ as a function of time (Fig. 3B) to compare the ordering of relaxation times between trajectory calculations and relaxation experiments (Fig. 3A). In the linear response regime (where the fluctuation–dissipation theorem is valid) (26), such autocorrelations of trajectories (equilibrium data) correspond directly to the decay signal in a kinetic jump experiment (relaxation data) probing the same variable. We observed that the decay times of computed autocorrelation functions follow the same ordering as the experimentally measured kinetic traces (Fig. 3), grouped into a slower Δ₁₃ distance and faster Δ₁₂ and Δ₂₃ distances near T_m. The slowest phases of the computed decays are about a factor of 10 faster than the experimental kinetics.

Discussion

Comparing fast protein folding experiments and MD simulations at a more detailed structural level is one of the current goals of the protein-folding field. Such comparisons can lead to the detailed mechanistic understanding of protein folding and misfolding, and they are important for further refinement of MD force fields to eventually make them mechanistically accurate. To facilitate such comparisons at higher resolution, microsecond folding experiments with more structural information content are needed. An example directly relevant here is the folding of λ₁₂ monitored by global IR spectroscopy (amide I′ band, reporting on secondary structure) and local tryptophan fluorescence (reporting on the helix 1–2 contact via Trp–Tyr quenching) (17). We found that the two probes relax with different timescales.

To introduce more structural information from fluorescence measurements, we generated three mutants of λ_6–85 probing all pairwise combinations of the helix triad 1–2–3 by Trp–Tyr Dexter quenching. In one helix, we substituted a hydrophobic side chain that had little solvent exposure by a tryptophan side chain, to ensure its partial burial and a potentially large change in its fluorescence. Into a neighboring helix, we engineered a contact quencher (Tyr) (20). The 100-ns simulations of all mutants were used to calculate the distance distribution between tryptophan and tyrosine (Fig. 1B). Based on the Trp–Tyr Dexter quenching properties (20), we expected that mutants with average distance ≤7 Å would quench, and longer distance mutants would not. This expectation was borne out by all mutants whose expression yield was sufficient to measure fluorescence quenching (Fig. 2). The fluorescence enhancement upon denaturation is thus an indicator of Trp–Tyr contact formation in the native state.

The variants do not exhibit the exact same thermal stability and identical secondary structure content (Fig. 2). These differences could influence the observed kinetics. However, the ranking of relaxation rates is robust by two different experimental approaches between 50 and 60 °C, a temperature range consistent with the MD simulation when accounting for a global stability shift of the simulated protein due to imperfect solvent modeling (5). In one experimental approach, GuHCl was used to bring the melting temperatures in line for a direct comparison (Fig. 3A), and in the other approach the higher melting mutant data were extrapolated to lower temperature in absence of GuHCl (SI Appendix, Fig. S8). In each case, the helix 1–3 probe has a slower relaxation time than the two helix 1–2 and 3–2 probes involving helix 2.

The MD simulation produces the same ranking of contact formation rate as experiment, albeit 10 times faster (Fig. 3). The lower solvent viscosity of the force field, also reported by others (27, 28), accounts for about a factor of 3. The origin of the remaining factor of 3–4 is not clear at present. Perhaps force field imperfections (e.g., collective behavior of water during the “drying” transition that forms the native state) are responsible; solvation effects are known to increase the computed T_m over the experimental value for λ repressor and other proteins (5).

Comparison of the computed helix 1–3 vs. 1–2 and 3–2 kinetics from the single all-atom simulation with the experiment yields the same order of rates, supporting the hypothesis that the perturbation induced by the probes does not affect the free-energy landscape of the protein under similar free-energy conditions (extrapolated, or achieved by denaturant). We hope that our data encourage long-trajectory simulations of mutants made as site-specific probes, so that such perturbations can be assessed directly. Computational expense is rapidly reaching a point where such direct comparisons are realistic.

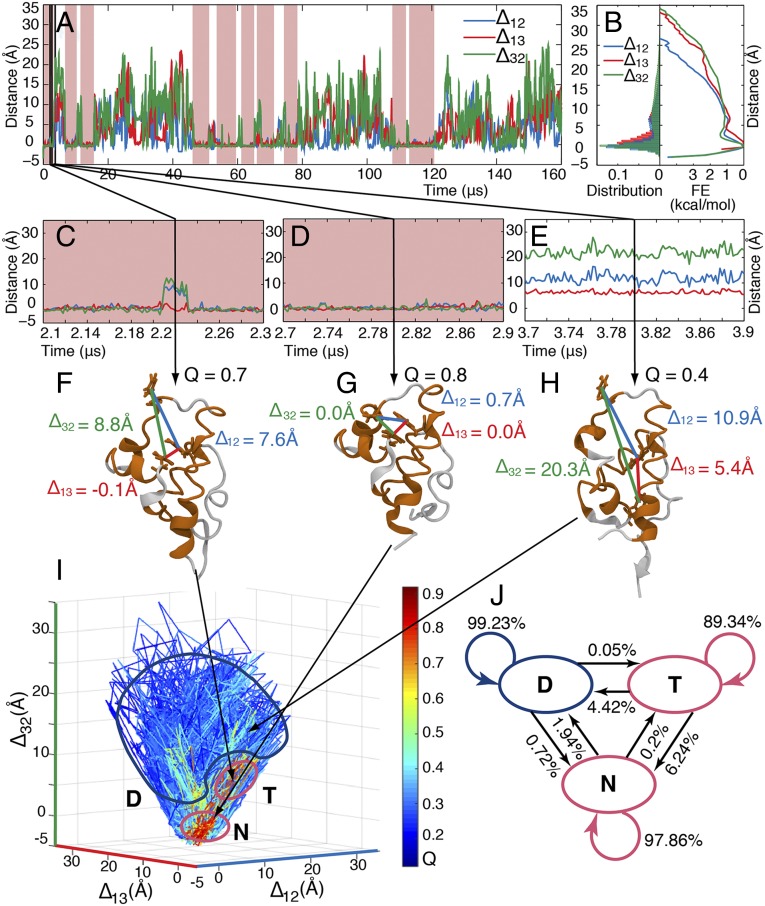
The most probable order of events that eventually leads to complete folding/unfolding relaxation, at least as far as helices 1/2/3 are concerned, is as follows: helix 1–3 contact formation occurs more slowly, whereas helix 2 more frequently forms/dissolves contacts with the other two helices. This agreement of experiment and computation suggests that the all-atom trajectories can tell us about the microscopic origin of the difference between the contact probes. Therefore, we further analyzed the single-trajectory MD simulation that we used for autocorrelation analysis (Fig. 4). In particular, we plotted the simulated trajectory in the coordinate space of the three probe distances Δ₁₂, Δ₁₃, and Δ₃₂ with respect to the crystallographic native state, such that Δ₁₃ = Δ₁₂ = Δ₃₂ = 0 for the crystal structure (Fig. 4A and SI Appendix, Fig. S11, for a raw time traces plot).

Fig. 4.

Analysis of the folding MD simulations (161-μs simulation data sampled at 0.2 ns; courtesy of D. E. Shaw Research) (5). (A) Smoothed time traces of distances (with respect to the native-state values) between side chains of the simulated mutant where Trp and Tyr are located in λ₁₂, λ₁₃, and λ₃₂. (Raw distance time traces are in SI Appendix, Fig. S11.) Pink background indicates high Q states (folded). (B) Histogram of populations (Left) and corresponding estimates of the free-energy profiles (Right) with respect to interhelical distances for the time trace in A; the three order parameters differ slightly. (C–E) Close-up of interhelical distances within the time trace in A. (F–H) Sample structures of (F) a trapped state (T) with high Q, short distance between helices 1 and 3 (Δ₁₃), but long distances between helices 1 and 2 (Δ₁₂) and helices 3 and 2 (Δ₃₂); of (G) a native state (N) with high Q and short distances between all three probe pairs; and of (H) denatured structure (D) with low Q and long interhelical distances. (I) Time trace plotted in the coordinates of interhelical distances and color-coded by the Q values (color scale is on the Right). Three states are circled: the native state (N), where Q is high and all interhelical distances are native-like (i.e., close to the origin in this coordinate system); the denatured state (D), where Q is low and all interhelical distances are long; and the trap (T), where Q is high (Q > 0.6), Δ₁₃ is short (<3 Å), but Δ₁₂ and Δ₃₂ are long (>5 Å). (J) Three-state Markov model based on the complete simulation data for the system in I (data are in SI Appendix, Tables S5–S7).

Fig. 4B shows the corresponding histograms of populations and also estimated potentials of mean force (PMFs) for the three order parameters. The mean first-passage times of folding on the three PMFs follow the trend captured by the autocorrelation functions (SI Appendix, Table S8). This result reinforces the notion that our chosen 1D order parameters self-consistently describe the folding process as captured by the MD simulations and experiments. Fig. 4 C–E shows highlights from the trajectory; in particular, Fig. 4C shows one of the many excursions that make Δ₁₂ and Δ₃₂ “faster” than Δ₁₃ in the autocorrelation of Fig. 3B.

Fig. 4I shows the trajectory in the space of Δ₁₂, Δ₁₃, and Δ₃₂ (color represents contact order Q; see SI Appendix for details.) The visualization in Fig. 4I allowed us to identify three distinct states: a native state (denoted N; structure shown in Fig. 4G), a denatured state (denoted D; sample structure shown in Fig. 4H), and a transiently populated trap (denoted T; structure shown in Fig. 4F). The trapped state showed a high, folded-like Q and short distance between helices 1 and 3 (Δ₁₃), but a long distance between helix 2 and the other two helices (Δ₃₂ and Δ₁₂ > Δ₁₃). Helix 2 is not properly docked in this otherwise native-like but short-lived trap (about 0.3-μs residence time in the example in Fig. 4C). The existence of a short-lived trap is consistent with a previous two-probe experimental study (17) of λ_6–85, and with more recent computational results suggesting that λ_6–85 is not a perfect two-state folder (23, 29). Recent pressure-jump experiments and simulations also show that helix 2 lags by ∼0.5 μs during the transition from U to N, and that traps exist during pressure-jump refolding (24). The short-lived trap is also consistent with previous single-probe downhill folding experiments on λ₁₂ and its variants that show (k_m)⁻¹ ∼ 1- to 2-μs transit times between N and D attributed to landscape roughness (=short-lived traps) in the folding free-energy surface (25). However, these single-probe analyses are intrinsically limited. Identification of transient nonnative states requires a significant separation of timescales with a single probe, which is not necessary when independent probes are used.

We used the MD simulation from D. E. Shaw Research to generate a three-state Markov model (Fig. 4J and SI Appendix, Tables S5–S7) based on the N, T, and D states observed in the simulation. A single major trap state is consistent with our experimental data (Fig. 3A). If the rates of λ₁₂ and λ₃₂ were also significantly different near T_m (three interconversion timescales), one would expect to observe at least one additional trap or intermediate state (four states). The transition matrix revealed that the native protein N is almost 10 times more likely to convert to the denatured state D directly without visiting trap T, and the denatured state D is 14 times more likely to convert back to the native state N before being trapped in T. The trap is thus a high free-energy state rarely visited from D and N. T lies at about k_BTln(4.42/0.05) ∼ 4.5 k_BT above the average free energy of D, and 3.4 k_BT above the average free energy of N at the temperature sampled by the trajectory in Fig. 4. T is best characterized as a short-lived high-energy intermediate only occasionally populated in transit between the native and denatured states, and thus requiring two order parameters, as proposed by Bieri and Kiefhaber (30) for the much slower lysozyme folding process. SI Appendix, Tables S6 and S7 show that trapping is also very rarely observed when helices 1 or 3 are not properly docked, indicating further traps at free energies at least 9 k_BT above the state N. When a protein like λ_6–85 is biased toward downhill folding, such excited states are the source of free-energy landscape roughness that limits the molecular timescale (or transition state transit time) to ≥1 μs (21).

According to our Markov model, T lies neither on a highly populated parallel path, nor is it completely off the N–D path. Its accessibility from N is four times greater than its accessibility from D, but not much larger (as required for a strict off-pathway trap accessible only from the native state). This observation illustrates that “the glass is half empty,” when it comes to classifying nonnative states exclusively as traps, parallel pathways, or productive intermediates.

In conclusion, we have investigated more deeply the folding mechanism of λ_6–85 with conservative mutants that probe contacts between three different helix pairs using Dexter fluorescence quenching. A nonquenching mutant experimentally confirmed the design. We analyzed single-trajectory full-atom MD simulations of λ_6–85 to gain a microscopic understanding of the experimentally observed kinetics and discovered a native-like trap with helix 2 unraveled a few k_BT above the native and denatured states. The trap is populated transiently from both the native and the denatured states, but to different extent. The T-jump experiments show that helix 2 undocks from 1 and 3 faster than 1 does from 3, consistent with a short-lived state without helix 2 properly folded into place. This result shows that multiprobe mapping of protein folding can be combined successfully with state-of-the-art MD simulations to gain a higher resolution picture of apparent two-state folding.

Materials and Methods

Protein Expression and Purification.

The gene of interest subcloned into a pET-15b vector was obtained from GenScript. BL21(DE3)-RipL cells (Agilent) were transformed with the plasmid and grown on selective media. The cells were then grown in liquid culture at 37 °C to OD₆₀₀ of 0.6, and the cultures were induced with 1 mM isopropyl β-d-1-thiogalactopyranoside overnight at 23 °C. The cells were pelleted and lysed using sonication in a solution containing 1 mM phenylmethylsulfonyl fluoride for protease inhibition. The supernatant was filtered with 0.45-μm syringe filters and applied to a Ni:NTA column (Qiagen). The column was eluted using an imidazole gradient. Fractions containing the protein of interest were dialyzed against 50 mM K₃PO₄, pH 7.0, at 4 °C. Mutations were done using QuikChange site-directed mutagenesis (Stratagene). All chemicals were purchased from Sigma-Aldrich and used without further purification.

Equilibrium Experiments and Data Analysis.

CD experiments were done using a Jasco-715 spectropolarimeter (Jasco). Each measurement consisted of three accumulations of spectra, which were collected between 200 and 250 nm. The temperature was controlled using a Peltier element. The temperature was incremented by 3 °C starting with 5 °C and increasing to 95 °C. Protein concentration was 2.5 μM. Fluorescence experiments were done using a Cary Eclipse (Varian) spectrophotometer equipped with a Peltier heating stage. Tryptophan was excited at 280 nm, and fluorescence was collected between 290 and 450 nm. Temperature was incremented in the same way as in CD measurements. Protein concentration was 10 μM. Starna cuvettes (Starna Cells) were used for both measurements. Igor Pro (Wavemetrics) and Matlab (MathWorks) were used for data analysis. Fluorescence intensity was calculated by integrating the entire spectrum at a specific temperature: I_total(T) = ∫I(λ,T)dλ. The mean wavelength was calculated according to the formula: 〈I(T)〉 = ∫ λ I(λ,T) dλ/∫I(λ,T) dλ. Two-state thermodynamic fits had the form: F(T) = [F_D/(1 + K_eq)] + [F_NK_eq/(1 + K_eq)], where K_eq = exp[−ΔG(T)/RT]; F_i = b_i + m_i(T − T_m); and ΔG(T) ≅ ΔG(T_m) + ΔS(T_m)T_m – ΔS(T_m)T. We note that a linear temperature dependence of Trp fluorescence intensity is an approximation used here for simplicity (10).

Kinetics Experiments and Data Analysis.

Temperature jumps were performed using an in-house built instrument, which was described in detail previously (31). Briefly, a sample consisting of the tested protein in 50 mM K₃PO₄ buffer at pH 7 was placed in a cuvette made out of a rectangular capillary (Vitrocom) welded on one side. The sample concentrations were 309, 373, and 50 μM, for ${\mathrm{\lambda }}_{12}^{\ast }$, λ₁₃, and λ₃₂, respectively. Low concentration was used in λ₃₂ because a significant amount of sample aggregation was visually observed during the measurements in high concentration. The equilibrium temperature of the sample was maintained using a water flow system. The temperature of the solution was suddenly jumped using a nanosecond pulse of a Q-switched Nd:YAG laser (Continuum). The fundamental wavelength of 1,064 nm of the laser was Raman-shifted to 1.9 μm using a 1-m-long chamber with hydrogen compressed to 300 psi. The beam was split using a 50% reflective mirror, and the sample was illuminated from both sides to achieve uniform heating. Tryptophan was excited every 12.5 ns using light centered at 280 nm from a frequency-tripled mode-locked Ti:sapphire laser (KMLabs). The repetition period of the Ti:sapphire laser (12.5 ns) puts a limit on the time resolution of our kinetics data even in the absence of noise. Fluorescence was collected at 90° angle using an optical waveguide (Oriel), filtered from incident radiation with a bandpass filter (B370; Hoya), and detected by a photomultiplier tube (R7400U-03; Hamamatsu). The signal was digitized with a period of 100 ps (10 GHz; 125 points per fluorescence decay) and a bandwidth of 2.5 GHz using an oscilloscope (DPO7254; Tektronix). The data were analyzed using Igor Pro (Wavemetrics) and Matlab (MathWorks). One-hundred kinetic traces were averaged at each temperature unless stated otherwise. The decays were normalized to yield a parameter χ(t) such that χ(t) = a₁/(a₁ + a₂), where each fluorescence decay is represented as a linear combination of a decay before the temperature jump (f₁) and a decay at the very end of the kinetic trace (f₂), f = a₁f₁ + a₂f₂. Thus, every trace begins with χ(t = 0) = 1 and ends with χ(t = 1 ms) = 0. The resulting kinetic traces were then fit to a single- or a double-exponential function of the forms FI(t) = A exp(−t/τ) and FI(t) = A₁ exp(−t/τ₁) + A₂ exp(−t/τ₂), respectively.

MD Simulations.

The coordinates of wild-type protein were obtained from a crystal structure (PDB ID code 3KZ3; resolution of 1.64 Å). Mutants were prepared using the Mutator plugin of Visual Molecular Dynamics (VMD) software (32). Each system was minimized for 1,000 time steps, and equilibrium MD was performed for 100 ns using NAMD2 software (33) with the CHARMM27 force field (34), the TIP3P model of water (35), and the CMAP corrections (36) for proteins in the NPT ensemble. Langevin dynamics with a 0.5 ps⁻¹ damping coefficient and the Langevin piston Nosé–Hoover procedure was used to maintain temperature and pressure to constant values (300 K and 1 atm, respectively) (37, 38). The particle mesh Ewald (PME) method (39) was used to calculate long-range electrostatic forces without truncation, using a grid density of 1 Å⁻³ . The van der Waals interaction cutoff value was 12 Å, whereas the integration time steps for bonded, nonbonded, and PME calculations were 2, 1, and 2 fs, respectively. Trajectory geometry analysis was performed using Tcl scripts within VMD (32).

D. E. Shaw Research MD Simulation Data Analyses.

We obtained the all-atom λ-repressor simulation dataset from D. E. Shaw Research. Simulations were performed by D. E. Shaw Research in the CHARMM22* force field, and the frames were saved every 200 ps (5). The simulations data were analyzed using scripts for VMD (32) and Matlab.