Iterative experiment design guides the characterization of a light-inducible gene expression circuit

Significance

System identification addresses the problem of identifying unknown model parameters from measured data of a real system. In the case of biochemical reaction networks, the available measurements are typically sparse because of technical and/or economic reasons. Therefore, it is of paramount importance to maximize the information that can be gained by each experiment. Here, we apply a systematic design scheme for single-cell experiments based on information theoretic criteria. For the considered light-inducible gene expression circuit, we show that this scheme allows one to precisely identify model parameters that were practically unidentifiable from data measured in random experiments. This result provides evidence that optimal experiment design is a key requirement for the successful identification of biochemical reaction networks.

Abstract

Systems biology rests on the idea that biological complexity can be better unraveled through the interplay of modeling and experimentation. However, the success of this approach depends critically on the informativeness of the chosen experiments, which is usually unknown a priori. Here, we propose a systematic scheme based on iterations of optimal experiment design, flow cytometry experiments, and Bayesian parameter inference to guide the discovery process in the case of stochastic biochemical reaction networks. To illustrate the benefit of our methodology, we apply it to the characterization of an engineered light-inducible gene expression circuit in yeast and compare the performance of the resulting model with models identified from nonoptimal experiments. In particular, we compare the parameter posterior distributions and the precision to which the outcome of future experiments can be predicted. Moreover, we illustrate how the identified stochastic model can be used to determine light induction patterns that make either the average amount of protein or the variability in a population of cells follow a desired profile. Our results show that optimal experiment design allows one to derive models that are accurate enough to precisely predict and regulate the protein expression in heterogeneous cell populations over extended periods of time.

The use of quantitative mathematical models to investigate biochemical reaction networks is nowadays common practice. Typically, models are built based on the available biological knowledge and used to generate hypotheses, which are then refined or invalidated through experimentation. For this process to be successful, it is of paramount importance to design and perform experiments that yield the information required to identify the model under consideration. Optimal experiment design techniques have been extensively studied for ordinary differential equation models (1–5), which are typically used to describe the average behavior of cell populations (6–8). With the development of high-throughput measurement techniques, such as flow cytometry, it has, however, become evident that restricting the attention only to the average population behavior neglects the potentially valuable information contained in the full population distribution (9–11). This additional information can be captured by stochastic models. Recently, methods for parameter inference (12–15) and optimal experiment design (16, 17) for stochastic models have been developed and applied to a number of biological systems (12, 18). However, a systematic characterization procedure that exploits the information gained from each performed experiment has not yet been fully developed or experimentally validated.

Here, we provide the first study, to our knowledge, in which a noisy biochemical reaction network is characterized and ultimately also controlled through iterations of optimally designed flow cytometry experiments and stochastic modeling. Specifically, we consider a gene expression circuit in yeast that has been engineered such that the expression of the gene can be induced and inhibited by exposure of the cells to red and far-red light (19, 20). We use optimal experiment design to ensure that the light induction pattern yielding the most informative output is administered to the cells and that the most informative measurement times are chosen. The collected data are then used in a Bayesian parameter inference scheme to improve the quality of the model. The updated model, in turn, serves as the basis for designing additional optimal experiments in an iterative fashion until the outcome of future experiments can be predicted with low uncertainty. Ultimately, we obtain a stochastic model that is capable of predicting the response of the entire cell population to arbitrary light induction patterns with high precision. This result allows us to in silico plan light induction patterns that regulate statistics of the protein population distribution to desired profiles. Our experimental results show that different reference profiles can be successfully tracked over long time horizons. In contrast to previous studies, the use of a stochastic model allows us to regulate not only population averages as done in refs. 20–23 or individual cells as in ref. 24 but also the variability across the population.

Results

Stochastic Modeling of the Light-Inducible Gene Expression Circuit.

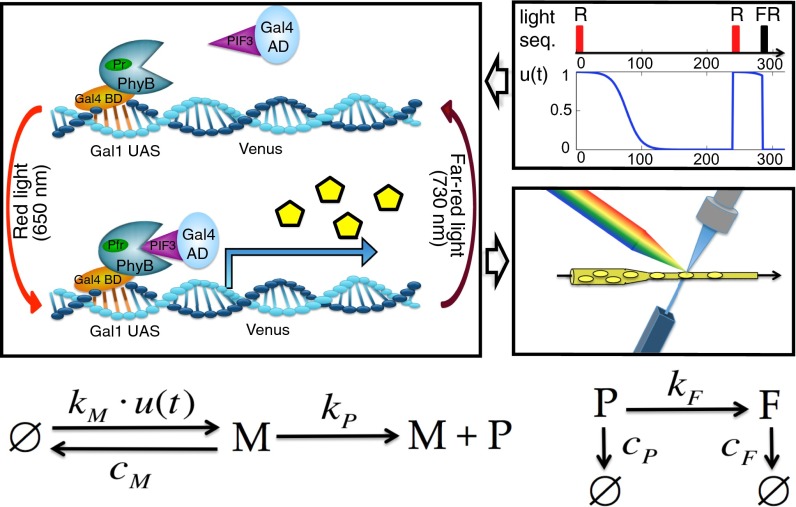
We consider the engineered gene expression circuit presented in ref. 20. The main component of this system is a light-responsive Phytochrome/Phytochrome-Interacting Factor (Phy/PIF) module (19) that can be used to drive the expression of a YFP reporter by shining red and far-red light on a population of yeast cells. Fig. 1 shows the stochastic reaction network that we propose as model of the system.

Fig. 1.

Stochastic modeling of the light-inducible gene expression circuit. (Top Left) The binding and unbinding of PhyB-PIF3 caused by the light pulses is modeled by multiplying the mRNA production rate by the signal $u\left(t;\gamma ,L\right)=U\frac{e^{-d_r\left(t-t_c\right)}}{e^{-d_r\left(t-t_c\right)}+h}$ (Top Right). When a pulse is applied, $t_c$ is reset to the current time, and U is set to one (red pulse) or zero (far-red); $d_r$ and h are unknown parameters that capture the natural decay of the signal after a red pulse because of dark reversion (20). When the signal is active, mRNA (M) is produced with a rate $k_M\cdot u\left(t;\gamma ,L\right)$. To capture cell to cell variability in the light-responsive module, we assume that $k_M$ varies between different cells according to a gamma distribution $P_{k_M}$ with unknown mean $M_{k_M}$ and variance $V_{k_M}$. When mRNA is present, protein P is produced with rate $k_P$ and becomes fluorescent with rate $k_F$. All of the species degrade: the mRNA (M) with rate $c_M$ and the dark (P) and fluorescent (F) protein with rate $c_P=c_F$ as detailed in the reaction network at the bottom. The empty set notation is used whenever a certain species is produced or degrades without involving the other species. We assume that each fluorescent protein molecule emits an unknown but deterministic amount r of fluorescence. The fluorescence distribution in the cell population is recorded over time using flow cytometry (Middle Right). In total, the model (Bottom) comprises three species, six reactions, and nine unknown parameters $\gamma ={\left[M_{k_M}\hspace{0.17em}{V}_{k_M}\hspace{0.17em}{k}_P\hspace{0.17em}{k}_F\hspace{0.17em}{c}_M\hspace{0.17em}{c}_P\hspace{0.17em}{d}_r\hspace{0.17em}h\hspace{0.17em}r\right]}^{\mathrm{\top }}$ (SI Appendix, section S2). AD, activation domain; BD, binding domain; FR, far-red pulse; Pfr, far-red-absorbing phytochrome form; PhyB, phytochrome B; PIF3, phytochrome-interacting factor 3; Pr, red-absorbing phytochrome form; R, red pulse; UAS, upstream activating sequence.

The effect of the light on the expression of the gene is modeled by multiplying the mRNA production rate $k_M$ by a function $u\left(t;\gamma ,L\right)$ that depends on some of the unknown model parameters γ and the applied sequence of light pulses L, as detailed in Fig. 1 and SI Appendix, section S2.1. To capture the variability of the light-responsive module, we model the mRNA production rate $k_M$ as a random variable that is distributed according to a gamma distribution $P_{k_M}$ with unknown mean $M_{k_M}$ and variance $V_{k_M}$ (SI Appendix, section S2.2) (16). Therefore, the time evolution of the amount of molecules in each cell is described by a conditional chemical master equation (SI Appendix, section S2.2) that depends on the particular realization of $k_M$ in the cell. Statistics of the entire population can be computed from this family of master equations by deriving a system of moment equations (12)

$$\frac{d}{dt}\tilde{\mu }\left(t;\gamma \right)=A\left(\gamma ,u\left(t;\gamma ,L\right)\right)\tilde{\mu }\left(t;\gamma \right)+B\left(\gamma ,u\left(t;\gamma ,L\right)\right),$$ [1]

which, given a parameter vector γ, describes the time evolution of the population moments $\tilde{\mu }\left(t;\gamma \right)$ up to a desired order. For the moments up to order four, which are required in the sequel, Eq. 1 is a system of 65 coupled ordinary differential equations. For our model, the population moment equations are nonlinear, because the moment evolution depends on the product between the input signal $u\left(t;\gamma ,L\right)$ and some of the moments, but they are closed in the sense that they do not depend on moments of higher order.

Systematic Characterization Procedure.

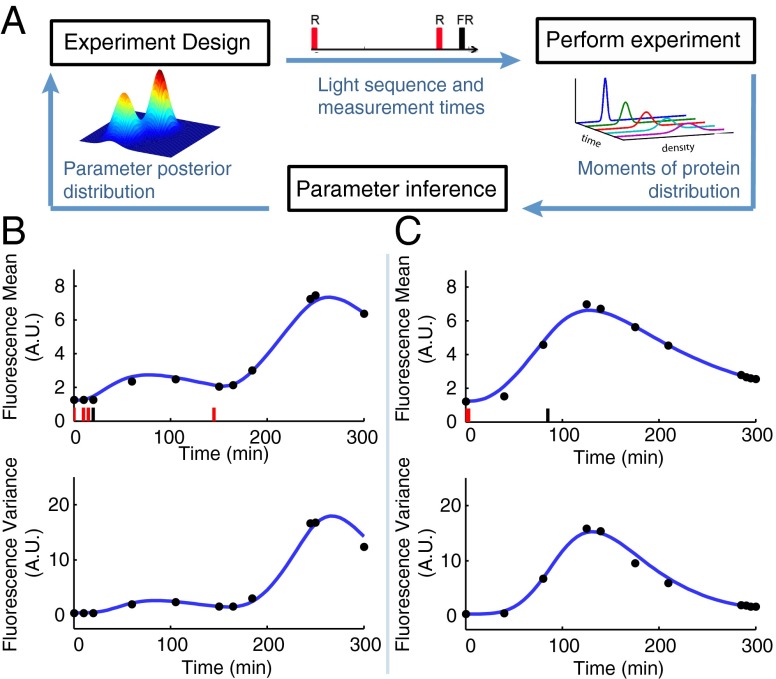
To optimally identify the model parameters, we propose an iterative characterization procedure that comprises three steps (Fig. 2A). The key ingredients are an algorithm that searches for the most informative light induction pattern and measurement times, an experimental setup to perform the selected experiment based on the precomputed input light pattern and output measurements collected at the predetermined times, and a Bayesian moment-based inference scheme to compute posterior distributions of the model parameters from the measured data.

Fig. 2.

Optimal characterization of the light-inducible gene expression circuit. (A) Illustration of the iterative experiment design scheme. (B) Applied light induction pattern (red and black bars) and measured means and variances (black dots) in the first optimal experiment. The blue line is the model output with the maximum a posteriori estimate ${\widehat{\gamma }}^1$ obtained from the data of this experiment. (C) Applied light induction pattern and measured means and variances in the second optimal experiment. The blue line is the model output with the maximum a posteriori estimate ${\widehat{\gamma }}^2$ obtained from the data of the two optimal experiments. FR, far-red pulse; R, red pulse.

The optimal experiment design algorithm aims at finding the most informative experiment. To this end, we use as information measure the determinant of the Fisher information matrix (FIM), whose inverse provides a lower bound for the variance of any unbiased parameter estimator (Cramér–Rao inequality) (25). To evaluate the FIM, the solution of the population moment equations (Eq. 1) and its partial derivatives with respect to the model parameters are computed for each candidate experiment using the best available estimate $\widehat{\gamma }$ of the model parameter vector γ (more details on the optimization algorithm and the choice of the experiments’ length are given in Materials and Methods and SI Appendix, section S3).

The solution of the population moment equations (Eq. 1) is also used to determine the likelihood of means and variances of the measured fluorescence distributions given a vector of model parameters. This likelihood is used in the Bayesian inference algorithm to draw samples from the parameter posterior distribution using a Sequential Monte Carlo algorithm (SI Appendix, section S4) (26).

Using this procedure, we designed a first optimal experiment (Fig. 2B) based on an initial estimate of the parameters ${\widehat{\gamma }}^0$ taken from the literature (SI Appendix, Table S5). We then administered the resulting light induction pattern to the cells using a custom-built LED-based light delivery system and measured by flow cytometry the resulting fluorescence intensity at the optimal measurement times. Subsequently, the data were processed and used in the inference algorithm to determine the parameter posterior distribution. Fig. 2B shows that the model output computed using the corresponding maximum a posteriori estimate ${\widehat{\gamma }}^1$ agrees well with the means and variances of the measured fluorescence distributions. This result, however, does not guarantee that the maximum a posteriori estimates can be used to predict the outcome of new experiments. Indeed, the parameter posterior distribution (SI Appendix, Fig. S4) is flat in some dimensions, indicating that some of the parameters are practically unidentifiable from the data measured in the first experiment only.

Based on these considerations, we concluded that one experiment is not sufficient to characterize the system. Consequently, we designed a second experiment that, according to the FIM computed with the maximum a posteriori estimate ${\widehat{\gamma }}^1$, optimally complements the already performed one (SI Appendix, section S3.2). The resulting light induction pattern and measurement times are shown in Fig. 2C.

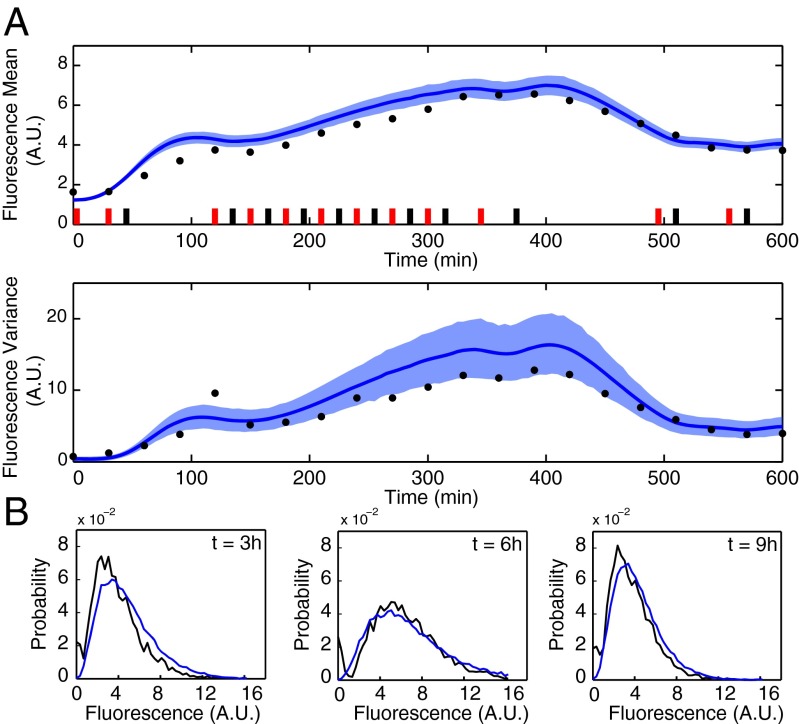
After performing the second experiment, we again used Bayesian moment-based inference to update the parameter posterior distribution. The resulting distribution shows (SI Appendix, Fig. S4) that additional certainty about the model parameters was gained from the second experiment. To determine whether the residual prediction uncertainty is sufficiently small to terminate the iterative procedure, we used the obtained model to predict the outcome of a 10-h experiment with a randomly chosen light pattern. In particular, to quantify how the uncertainty in the posterior distribution of the model parameters influences the prediction of future experiments, we computed the posterior predictive distribution (SI Appendix, section S5.1). Fig. 3A shows the $98\%$ confidence region for both fluorescence mean and variance computed from the obtained posterior predictive distributions. We judged these confidence regions to be sufficiently tight to terminate the iterative procedure. The parameter posterior distribution thus obtained (SI Appendix, Fig. S4) corresponds to our final model.

Fig. 3.

Validation of the identified model. (A) Measured and predicted (Upper) mean and (Lower) variance of the fluorescence distribution in a validation experiment. Model predictions are visualized in terms of the means (solid lines) and 98% confidence regions (shaded regions) of the posterior predictive distributions. (B) The measured fluorescence distributions (black) agree very well with simulated distributions (blue) obtained with the maximum a posteriori estimate ${\widehat{\gamma }}^2$.

To validate the obtained model, we performed the experiment in Fig. 3A and verified that the means and variances of the fluorescence distributions measured every 30 min are within or very close to the precomputed confidence regions. We further validated the model by comparing the entire predicted fluorescence distribution with the measured one at different times (Fig. 3B); the model predictions were obtained by simulating the system using the stochastic simulation algorithm by Gillespie (27) with the maximum a posteriori estimate ${\widehat{\gamma }}_2$. The results agree very well with the experimentally measured distributions, indicating that the model is capable of predicting entire population distributions, although only measured means and variances were used in the identification.

Random Experiments Cannot Be Used to Characterize the System.

The results above show that our iterative characterization procedure leads to a predictive model after only two experiments. To show that optimal experiment design is necessary to obtain this result, we performed two experiments of the same duration (5 h) and with the same number of measurements (10 equally spaced) as the optimal experiments but randomly chosen light induction patterns (SI Appendix, section S7.1). The parameter posterior distribution computed from the resulting data shows that the random experiments convey much less information than the optimal ones, leading to large residual uncertainty about the parameter values (SI Appendix, Fig. S8).

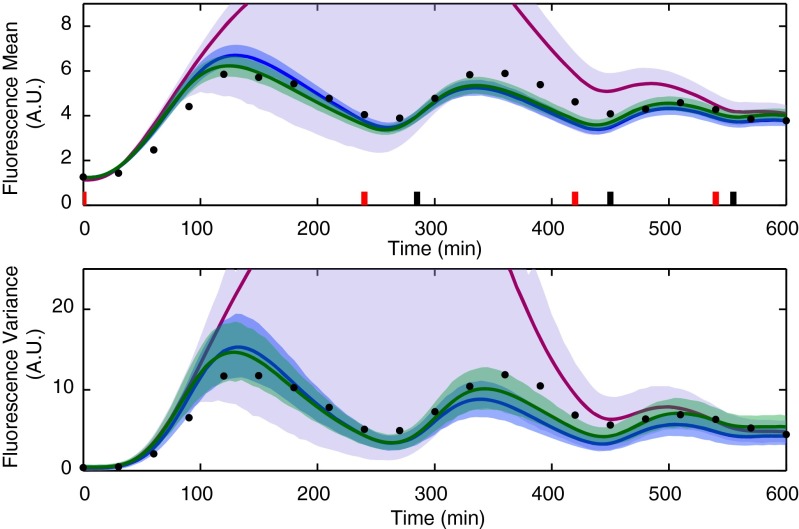
Fig. 4 shows that the model identified from the two random experiments cannot adequately predict the outcome of other experiments (that is, the large uncertainty remaining in the parameter posterior distribution propagates to the predictive distributions of the fluorescence mean and variance). Adding a third random experiment improves the situation only marginally (SI Appendix, Figs. S8 and S9). According to our experience, a large number of random experiments would be required to obtain an accurate model of this system.

Fig. 4.

Comparison of the posterior predictive distributions computed using the parameter posterior distribution obtained from the two optimally designed (blue), the best pair of experience-based (green), and the two random (magenta) experiments for a second validation experiment. Model predictions are visualized in terms of the means (solid lines) and 98% confidence regions (shaded regions) of the posterior predictive distributions. The light sequence was chosen to produce damped oscillations of the mean fluorescence. The means and variances of the measured fluorescence distributions are shown with black dots.

Because the light-inducible gene expression circuit is a relatively simple system, it is also reasonable to design experiments based on intuition/experience only. It is obviously a subjective matter what kind of experiments should be termed intuitively good for the characterization of this system. We decided that the most objective choice was to use the experiments performed for the identification of this system in ref. 20. Hence, we chose three of the experiments shown in figure 1 of ref. 20 (one for each panel), applied the corresponding light induction patterns to the cell population, and measured the fluorescence for 5 h every 30 min, equivalently to what was done for the random experiments. The parameter posterior distribution computed from the resulting data (SI Appendix, Fig. S11) and the corresponding model predictions (SI Appendix, Fig. S12) show that any combination of only two experience-based experiments leads, on average, to worse results than the two optimal experiments. Table 1 gives a summarizing comparison of how well a number of different experiments are predicted by the models obtained from the optimal, the random, and two different pairs of experience-based experiments. From Table 1, it can be seen that the performance of the experience-based approach depends strongly on the particular choice of the pair of experiments. Furthermore, the model identified from the two optimal experiments outperforms the one identified from the best pair of experience-based experiments in five out of six cases. We conclude that, for this system, experimental effort can be saved if optimal experiment design is used.

Table 1.

Comparison of optimal, random, and experience-based experiments

	Optimal	Best experience based	Worst experience based	Random
Fig. 5A	−44.7*	−125.1	−356.5	−225.6
Fig. 5B	−174.4*	−210.0	−342.3	−310.7
Fig. 5C	−67.7*	−135.9	−315.1	−261.4
Fig. 5D	−67.1*	−71.2	−131.5	−143.6
Fig. 3	−28.8*	−123.0	−335.0	−206.2
Fig. 4	−69.6	30.6*	20.2	−115.9

For each performed experiment, the log of the mean likelihood of the measured data according to the different parameter posterior distributions is computed.

^*The best model (that is, the one with highest expected likelihood).

Regulating Statistics of the Cell Population.

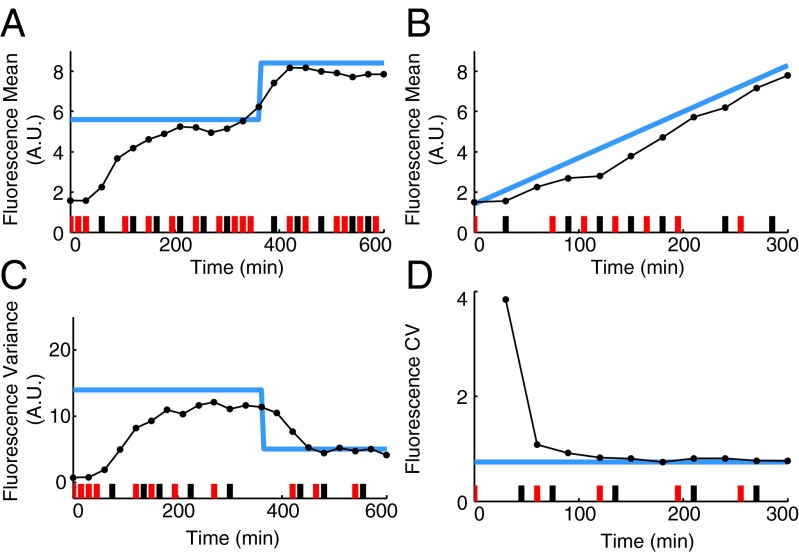
Our final model of the gene expression circuit seems to be sufficiently accurate to predict moments of the fluorescence distribution for any light induction pattern. Consequently, we can use it to regulate statistics of the amount of fluorescent protein in the population. To illustrate this point, we used the maximum a posteriori estimate ${\widehat{\gamma }}^2$ identified from the two optimal experiments to compute two light induction patterns that make the mean of the fluorescence distribution follow two different reference profiles (SI Appendix, section S8.2). Fig. 5 A and B shows that a very good tracking of the reference is achieved in both experiments.

Fig. 5.

Regulation of population statistics. Light blue lines are the reference time courses, and the black dots are the measured data. (A) The mean of the fluorescence distribution is made to follow a piecewise constant reference. (B) The mean of the fluorescence distribution is made to follow a ramp. (C) The variance of the fluorescence distribution is made to follow a piecewise constant reference. (D) The coefficient of variation (CV) of the fluorescence distribution is regulated to a constant value.

Given that our stochastic model can be used to predict higher order statistics of the fluorescence distribution, we can also choose reference time courses for other population statistics. Fig. 5 C and D shows two experiments in which references for the variance and the coefficient of variation of the fluorescence distribution are tracked. For the model under consideration, we found that, with the red and far-red light as the only control inputs, it is practically impossible to independently regulate the mean and the variance of the fluorescence distribution, which is in line with the results reported in refs. 28 and 29 (SI Appendix, section S8.1).

Discussion

Stochastic models of biochemical reaction networks have become a widely used tool for understanding the role of randomness in molecular biology (30, 31). The main goal of our study was to show that optimally designed experiments can be a key ingredient for the successful identification of such models. This point was shown by the fact that random experiments did not provide sufficient information to obtain precise estimates of all of the model parameters (Fig. 4 and SI Appendix, Fig. S8). The main reason for this is that, to be informative, an experiment should have an input tailored to the properties of the system under study, such as its frequency spectrum (32), which are, of course, unknown a priori. Intuition about the modeled process can be used to derive nearly optimal inputs; however, this guess becomes more difficult with increasing system complexity. Iterative experiment design allows one to overcome this problem by encoding implicitly the input requirements in the FIM.

The validity of our model is ultimately certified by the fact that the regulation results in Fig. 5 were obtained by applying precomputed light induction patterns in an open loop fashion. Although the use of feedback control (20, 24) is always recommended to compensate for unpredictable disturbances or unknown initial conditions, the success of our open loop experiments is proof that the remaining mismatch in our model is practically negligible, contrary to what was observed for the deterministic model used in ref. 20. As noted therein, the mismatch between the real system and deterministic models is mainly caused by the presence of “inevitable intracellular fluctuations.” Our results show that very accurate models that capture these fluctuations can be obtained by using a stochastic approach.

As a side contribution, the regulation results serve also to experimentally show that, with an accurate stochastic model obtained through optimal experiment design, it is possible to regulate not only the average gene expression, as done in previous studies (20–23), but also higher order statistics (for instance, the variance or the coefficient of variation of the produced protein). It can be envisioned that this will be useful for further investigating the role of stochasticity in biological systems.

Materials and Methods

Strains, Growth Conditions, and Experiment Protocol.

The yeast strain used in this study was described previously in ref. 20. For all experiments, cells were grown in SDC (synthetic defined complete) media with Trp and Leu dropouts (SDC-Trp-Leu) at 30 °C in the dark. The cultures were grown in exponential phase for a minimum of 13 h before all experiments. They were then diluted to an OD (optical density at 600 nm) of 0.1 in media supplemented with phycocyanobilin (catalog no. P14137; Frontier Scientific) at a saturating concentration (50 μM). The cells were then incubated in the dark for an additional 20 min.

For each inference experiment, 17 mL cell culture was placed in a glass tube inside a custom-built turbidostat with a hotplate magnetic stirrer. The turbidostat was operated inside a custom-built light delivery system using the 650- and 730-nm high-power LED (light emitting diode) sources described in ref. 20. Density was kept constant at an OD of 0.1 using growth media with the same saturating chromophore concentration as described above. For each validation and control experiment, 3 mL cell culture was kept in 15-mL light-shielded plastic culture tubes (BD Falcon) in the incubator at 30 °C with a shaking speed of 230 rpm. For these experiments, a 1:2 manual dilution was applied every 90 min, which was approximately the doubling time of our strain under the used experimental conditions. The tubes were briefly placed inside the light delivery system for light pulse application and returned to the incubator afterwards.

For all experiments, light pulses of ∼30 sec duration were applied. Cell fluorescence was measured on a BD Accuri Flow Cytometer. YFP was excited at 488 nm, and the fluorescence was collected through a 533/30 filter. Cells were measured at slow flow speed for ∼3 min for each time point.

Data Analysis and Noise Model.

The measured flow cytometry data were gated by forward and side scatter to remove aberrant cells and other unwanted particles from the sample. The remaining fluorescence intensities were then normalized by the forward scatter of each cell to reduce variability stemming from different cell sizes. Analysis of the data showed that this procedure leads to fluorescence distributions that are similar to the distributions that would have been obtained with a smaller gate on the forward scatter. The advantage of larger gates is that more cells are kept inside the gate, which is desirable for the accuracy of the computed population statistics. Let ${\left\{y_n\left(t_s\right)\right\}}_{n=1}^N$ be the final sample of the processed data at time $t_s$. We assume that these fluorescence measurements are affected by additive noise terms caused by autofluorescence artifacts and technical errors that are modeled as realizations of a random variable A, which has a distribution that is time-invariant and independent from the gene expression process (SI Appendix, section S2.3). As a consequence, time-dependent and process-correlated variabilities coming, for example, from the fact that the cells are not well mixed are allowed only through the parameter $k_M$. Details are provided in SI Appendix, section S2.4, where we report results suggesting that the noise assumed in our model suffices to explain the observed variability in replicates of the same experiment (SI Appendix, Fig. S2) and discuss alternatives. Finally, we compute the sample means ${\widehat{\mu }}_1\left(t_s\right)=1/N{\displaystyle {\sum }_{n=1}^N{y}_n\left(t_s\right)}$ and the centered sample moments ${\widehat{\mu }}_i\left(t_s\right)=1/N{\displaystyle {\sum }_{n=1}^N{\left(y_n\left(t_s\right)-{\widehat{\mu }}_1\left(t_s\right)\right)}^i}$ of order $i=\mathrm{2,3,4}$.

Population Moment Equations.

The time evolution of the amounts of molecules in a single cell is described by a chemical master equation conditioned on the particular realization of the mRNA production rate parameter $k_M$ for that cell. Let $x\in {\mathrm{\mathbb{N}}}^3$ be a vector containing the molecule counts of the different chemical species, and let $p\left(x,t|k_M\right)$ denote the probability that x molecules are present in the cell at time t given the particular realization of $k_M$. Then,

$$\begin{array}{c}\frac{d}{dt}p\left(x,t|k_M\right)={\displaystyle \sum _{k=1}^6-p\left(x,t|k_M\right)a_k\left(x;\gamma \right)}+{\displaystyle \sum _{k=1}^{6}p\left(x-{\nu }_k,t|k_M\right)a_k\left(x-{\nu }_k;\gamma \right)},\end{array}$$ [2]

where ${\nu }_k\in {\mathrm{\mathbb{Z}}}^3$ and $a_k\left(x;\gamma \right):\hspace{0.17em}{\mathrm{\mathbb{N}}}^3\mapsto {\mathrm{ℝ}}_0^{+},\hspace{0.17em}k=1,\dots ,6$ are the stoichiometric transition vectors and the propensity functions of the six reactions given in Fig. 1, respectively. The dependence of the mRNA production propensity function on $k_M$ and $u\left(t;\gamma ,L\right)$ is omitted for simplicity. From Eq. 2, we can derive a system of population moment equations (SI Appendix, section S2.2):

$$\frac{d}{dt}{\tilde{\mu }}^e\left(t;\gamma \right)=A\left(\gamma ,u\left(t;\gamma ,L_e\right)\right){\tilde{\mu }}^e\left(t;\gamma \right)+B\left(\gamma ,u\left(t;\gamma ,L_e\right)\right),$$ [3]

where ${\tilde{\mu }}^e\left(t;\gamma \right)$ is a vector that comprises the moments up to a desired order (in our case four) of the joint distribution of the molecule counts and the parameter $k_M$ at time t for an experiment e characterized by the light sequence $L_e$. From the vector ${\tilde{\mu }}^e\left(t;\gamma \right)$, we can extract the mean ${\mu }_1^{eF}\left(t;\gamma \right)$ and the centered moments ${\mu }_i^{eF}\left(t;\gamma \right),\hspace{0.17em}i=2,\dots ,4$ of the marginal distribution of the fluorescent protein $F\left(t\right)$ and convert them to moments that are compatible with the moments of the measured distributions through multiplication with the scaling parameter r and convolution with the distribution of the noise A (SI Appendix, section S2.3). For instance, mean and variance of the fluorescence intensities are obtained as

$${\mu }_i^e\left(t;\gamma \right)=r^i\cdot {\mu }_i^{eF}\left(t;\gamma \right)+{\mu }_i^A,i=\mathrm{1,2},$$ [4]

where ${\mu }_1^A$ and ${\mu }_2^A$ are the mean and the variance of A.

Experiment Design.

As a result of a tradeoff between being able to properly excite the system and updating the parameter estimates as frequently as possible in the iterative identification procedure, we fix the maximal duration of each designed experiment to $T_{max}=5$ h (SI Appendix, section S3.4). To determine the informativeness of each candidate experiment $e=\left\{L_e,t_1,\dots ,t_S\right\}$ characterized by a light induction pattern $L_e$ and S measurement times $t_1,\dots ,t_S\in \left[0,T_{max}\right]$, we compute the determinant of the FIM $I\left(\gamma ,e\right)$ (25). The entries of the FIM are computed from the solution of the population moment equations (Eq. 3) and the partial derivatives with respect to all components of the parameter vector γ according to the formula derived in ref. 16:

$$\begin{array}{c}I\left(\gamma ,e\right)={\displaystyle \sum _{s=1}^S{I}_{t_s}^e},\hspace{0.17em}\text{where}\\ {\left[I_{t_s}^e\right]}_{k,l}=N\frac{\frac{\partial {\mu }_1^e}{\partial {\gamma }_k}\frac{\partial {\mu }_1^e}{\partial {\gamma }_l}}{{\mu }_2^e}+N\frac{\left({\mu }_2^e\frac{\partial {\mu }_2^e}{\partial {\gamma }_k}-\frac{\partial {\mu }_1^e}{\partial {\gamma }_k}{\mu }_3^e\right)\left({\mu }_2^e\frac{\partial {\mu }_2^e}{\partial {\gamma }_l}-\frac{\partial {\mu }_1^e}{\partial {\gamma }_l}{\mu }_3^e\right)}{{\left({\mu }_2^e\right)}^2\left({\mu }_4^e-{\left({\mu }_2^e\right)}^2\right)-{\mu }_2^e{\left({\mu }_3^e\right)}^2},k,l=1,\dots ,9.\end{array}$$ [5]

Here, N is the number of cells measured at every sample time, ${\mu }_1^e={\mu }_1^e\left(t_s;\gamma \right)$ is the mean, and ${\mu }_i^e={\mu }_i^e\left(t_s;\gamma \right),\hspace{0.17em}i=\mathrm{2,3,4}$ are the centered moments of the fluorescence intensity distribution at time $t_s$ computed from Eqs. 3 and 4 (SI Appendix, section S3.1). The summation goes over all measurement time points $t_s,\hspace{0.17em}s=1,\dots ,S$. Note that the FIM depends on the model parameters γ that are to be estimated. These parameters are obviously unknown; hence, we replace them by the estimate $\widehat{\gamma }$. To design the first experiment, we use the parameter vector ${\widehat{\gamma }}^0$ taken from the literature (SI Appendix, section S3.2), whereas the second experiment is designed using the maximum a posteriori estimate ${\widehat{\gamma }}^1$ obtained from the data collected in the first experiment. Using Eq. 5, we can compute the FIM for any candidate experiment. We define the optimal experiment as the solution of the following optimization problem:

$$e^{*}=\underset{e\in \mathrm{ℰ}}{\text{arg}\hspace{0.17em}\text{max}}\left\{\det \hspace{0.17em}I\left(\widehat{\gamma },e\right)\right\},$$ [6]

where $\mathrm{ℰ}$ is the set of all candidate experiments (SI Appendix, section S3.2). Because of computational limitations, the optimization problem in Eq. 6 cannot be solved exactly. Consequently, the use of the term optimal experiment has to be understood in light of the simplifications made in the optimization algorithm (SI Appendix, sections S3.3 and S3.4).

Moment-Based Inference.

After performing the characterization experiments $e_d$, $d=1,\dots ,D$, we compute an empirical estimate of the means ${\widehat{\mu }}_1^{ed}=\left[{\widehat{\mu }}_1^{ed}\left(t_1\right)\dots {\widehat{\mu }}_1^{ed}\left(t_S\right)\right]$ and variances ${\widehat{\mu }}_2^{ed}=\left[{\widehat{\mu }}_2^{ed}\left(t_1\right)\dots {\widehat{\mu }}_2^{ed}\left(t_S\right)\right]$ of the fluorescence distribution from the measured samples. These estimates are then used as noisy data, $\mathcal{D}={\left\{\left({\widehat{\mu }}_1^{ed},{\widehat{\mu }}_2^{ed}\right)\right\}}_{d=1}^D$, in a Bayesian moment-based inference scheme (12) to compute the parameter posterior distribution:

$$p\left(\gamma \mathrm{\mid }\mathcal{D}\right)=\frac{p\left(\mathcal{D}\mathrm{\mid }\gamma \right)p\left(\gamma \right)}{p\left(\mathcal{D}\right)}=\frac{\left({\displaystyle {\prod }_{d=1}^{D}p}\left({\widehat{\mu }}_1^{ed},{\widehat{\mu }}_2^{ed}\mathrm{\mid }\gamma \right)\right)p\left(\gamma \right)}{p\left(\mathcal{D}\right)}$$ [7]

where $p\left(\gamma \right)$ is the parameter prior, and for each experiment, $e_d$, the likelihood of the measured data according to the parameter vector γ, is given by

$$p\left({\widehat{\mu }}_1^{ed},{\widehat{\mu }}_2^{ed}|\gamma \right)={\displaystyle \prod _{s=1}^S{p}_{t_s}\left({\widehat{\mu }}_1^{ed}\left(t_s\right),{\widehat{\mu }}_2^{ed}\left(t_s\right)|\gamma ,L_d\right)}.$$ [8]

According to the central limit theorem, in the limit of $N\to \infty$, $p_{t_s}\left(\cdot ,\cdot |\gamma ,L_d\right)$ follows a Gaussian distribution $\mathcal{N}\left({\mu }^{ed}\left(t_s,\gamma \right),{\mathrm{\Sigma }}^{ed}\left(t_s,\gamma \right)\right)$ centered around the output evolution, ${\mu }^{ed}\left(t_s;\gamma \right)={\left[{\mu }_1^{ed}\left(t_s;\gamma \right){\mu }_2^{ed}\left(t_s;\gamma \right)\right]}^{\mathrm{\top }}$, computed from the solution of Eqs. 3 and 4 with light induction pattern $L_d$ and variance

$${\mathrm{\Sigma }}^{ed}\left(t_s;\gamma \right)=\frac{1}{N}\left[\begin{array}{cc}{\mu }_2^{ed}\left(t_s;\gamma \right)& {\mu }_3^{ed}\left(t_s;\gamma \right)\\ {\mu }_3^{ed}\left(t_s;\gamma \right)& {\mu }_4^{ed}\left(t_s;\gamma \right)-\frac{N-3}{N-1}{\left({\mu }_2^{ed}\left(t_s;\gamma \right)\right)}^2\end{array}\right],$$

(SI Appendix, section S4.1). To draw samples from the posterior distribution, we use a Sequential Monte Carlo algorithm described in SI Appendix, section S4.2 and in ref. 26.

Posterior Predictive Distributions.

To determine how well new experiments can be predicted by the model, we compute the posterior predictive distributions for the means and variances of the fluorescence distribution in a future experiment $e_v$ characterized by the sequence $L_v$. These distributions describe how likely different measurements of means and variances ${\widehat{\mu }}^{ev}\left(t_s\right)={\left[{\widehat{\mu }}_1^{ev}\left(t_s\right){\widehat{\mu }}_2^{ev}\left(t_s\right)\right]}^{\mathrm{\top }},s=1,\dots ,S$ are a priori for the new experiment given all of the previously measured data $\mathcal{D}$. They can be computed from the parameter posterior distribution $p\left(\gamma |\mathcal{D}\right)$ according to

$$p_{t_s}^{pred}\left({\widehat{\mu }}_1^{ev}\left(t_s\right),{\widehat{\mu }}_2^{ev}\left(t_s\right)|\mathcal{D},L_v\right)={\displaystyle \underset{\gamma }{\int }{p}_{t_s}}\left({\widehat{\mu }}_1^{ev}\left(t_s\right),{\widehat{\mu }}_2^{ev}\left(t_s\right)|\gamma ,L_v\right)p\left(\gamma |\mathcal{D}\right)d\gamma ,$$ [9]

where $p_{t_s}\left(\cdot ,\cdot |\gamma ,L_v\right)$ is the distribution of ${\widehat{\mu }}^{ev}\left(t_s\right)$ given that the light induction pattern $L_v$ is applied to the population and that γ is the vector of model parameters. These predictive distributions $p_{t_s}^{pred}\left(\cdot ,\cdot |\mathcal{D},L_v\right),s=1,\dots ,S$ can be approximately computed by replacing the integral over γ with a sum over samples ${\gamma }_q,q=1,\dots ,Q$ drawn from the parameter posterior distribution $p\left(\gamma |\mathcal{D}\right)$. Since $p_{t_s}\left(\cdot ,\cdot |\gamma ,L_v\right),s=1,\dots ,S$ are approximately two-variate Gaussian distributions that can be computed from the solution of the population moment equations, we obtain a Gaussian mixture approximation of the predictive distributions at every measurement time (SI Appendix, section S5.1):

$$p_{t_s}^{pred}\left(\cdot ,\cdot |\mathcal{D},L_v\right)\approx \frac{1}{Q}{\displaystyle \sum _{q=1}^Q\mathcal{N}\left({\mu }^{ev}\left(t_s;{\gamma }_q\right),{\mathrm{\Sigma }}^{ev}\left(t_s;{\gamma }_q\right)\right)}.$$ [10]