Abstract
Extracting biologically meaningful information from the continuing flood of genomic data is a major challenge in the life sciences. Codon usage bias (CUB) is a general feature of most genomes and is thought to reflect the effects of both natural selection for efficient translation and mutation bias. Here we present a mechanistically interpretable, Bayesian model (ribosome overhead costs Stochastic Evolutionary Model of Protein Production Rate [ROC SEMPPR]) to extract meaningful information from patterns of CUB within a genome. ROC SEMPPR is grounded in population genetics and allows us to separate the contributions of mutational biases and natural selection against translational inefficiency on a gene-by-gene and codon-by-codon basis. Until now, the primary disadvantage of similar approaches was the need for genome scale measurements of gene expression. Here, we demonstrate that it is possible to both extract accurate estimates of codon-specific mutation biases and translational efficiencies while simultaneously generating accurate estimates of gene expression, rather than requiring such information. We demonstrate the utility of ROC SEMPPR using the Saccharomyces cerevisiae S288c genome. When we compare our model fits with previous approaches we observe an exceptionally high agreement between estimates of both codon-specific parameters and gene expression levels ( in all cases). We also observe strong agreement between our parameter estimates and those derived from alternative data sets. For example, our estimates of mutation bias and those from mutational accumulation experiments are highly correlated (). Our estimates of codon-specific translational inefficiencies and tRNA copy number-based estimates of ribosome pausing time (), and mRNA and ribosome profiling footprint-based estimates of gene expression () are also highly correlated, thus supporting the hypothesis that selection against translational inefficiency is an important force driving the evolution of CUB. Surprisingly, we find that for particular amino acids, codon usage in highly expressed genes can still be largely driven by mutation bias and that failing to take mutation bias into account can lead to the misidentification of an amino acid’s “optimal” codon. In conclusion, our method demonstrates that an enormous amount of biologically important information is encoded within genome scale patterns of codon usage, accessing this information does not require gene expression measurements, but instead carefully formulated biologically interpretable models.
Keywords: synonymous codon usage, translation efficiency, mutation bias, population genetics, selection coefficient, codon usage bias
Introduction
Genomic sequences encode a trove of biologically important information. Over 49,600 genomes are currently available from the Genomes OnLine Database (Pagani et al. 2012) alone and the flow of newly sequenced genomes is expected to continue far into the future. As a result, developing ways to turn these data into useful information is one of the major challenges in the life sciences today. Although great strides have been made in extracting this information, ranging from the simple, for example, identification of protein-coding regions, to the more difficult, for example, identification of regulatory elements (Hughes et al. 2000; Wasserman and Sandelin 2004; Dunham et al. 2012; Kundaje et al. 2015), much of this information remains untapped. To address one aspect of this challenge, we present a method to estimate the expression levels of every gene, codon-specific selection coefficients, and mutation biases solely from patterns of codon usage bias (CUB) in protein-coding sequences within a genome.
One of the earliest arguments against neutrality between synonymous codon usages was given by Clarke (1970). Since then, evidence for selection acting on CUB has been repeatedly observed. CUB clearly varies systematically within and between open-reading frames (ORFs) within a species as well as across species (Grantham et al. 1980; Ikemura 1981, 1985; Bennetzen and Hall 1982; Sharp and Li 1987; Andersson and Kurland 1990; Qin et al. 2004; Gilchrist and Wagner 2006; Chamary et al. 2006; Hershberg and Petrov 2008; Plotkin and Kudla 2011). These patterns in CUB are driven by two evolutionary forces: Mutation bias and natural selection (Ikemura 1981; Bulmer 1988, 1991). Current evidence supports multiple selective forces contributing to the evolution of CUB. Most of these hypothesized selective forces affect the efficiency and efficacy of ORF translational through factors, such as ribosome pausing times (Andersson and Kurland 1990; Bulmer 1991; Sørensen and Pedersen 1991; Plotkin and Kudla 2011; Shah and Gilchrist 2011), missense and nonsense errors (Kurland 1987, 1992; Akashi 1994; Gilchrist 2007; Drummond and Wilke 2008, 2009), cotranslational protein folding (Thanaraj and Argos 1996; Kimchi-Sarfaty et al. 2007; Tsai et al. 2008; Pechmann and Frydman 2013), equalizing tRNA availability (Qian et al. 2012), and the stability and/or accessibility of mRNA secondary structures (Kudla et al. 2009; Tuller et al. 2010; Gu et al. 2012; Bentele et al. 2013). The relative importance of each of these selective forces is expected to vary both within and between genes. The effects of these forces can be unified within a single framework by considering how the codon usage of a given ORF alters the ratio of the expected cost of protein synthesis over the expected benefit of protein synthesis, or the cost–benefit ratio η for short (Gilchrist et al. 2009) (see Materials and Methods).
One likely way different synonymous codons lead to changes in a gene’s cost–benefit ratio η results from differences in the abundances of cognate and near cognate tRNAs and the stability of the Watson–Crick base pairing between a given codon and tRNA anticodons (Ikemura 1981; Zaher and Green 2009; Plotkin and Kudla 2011). These differences, in turn, are predicted to lead to differences in ribosome pausing times and error rates between codons. Specifically, codons with higher abundances of cognate and near-cognate tRNAs are thought to have both shorter pausing times and lower error rates than codons with lower abundances of cognate and near-cognate tRNA (Ikemura [1981]; Kurland [1992], though see Shah and Gilchrist [2010] for a more nuanced view).
The assumption that natural selection favors codon usage which reduces the protein synthesis cost–benefit ratio η implies that the strength of this selection should scale with the gene’s protein synthesis rate: Highly expressed genes should show the strongest bias for codons with shorter pausing times and error rates (Ikemura 1981, 1985; Sharp and Li 1986, 1987). As a result, given sufficiently large effective population size Ne, such that high expression genes contain some signal of adaptation, the patterns of CUB observed within a genome should contain a significant amount of information about the average protein synthesis rate for a given gene. Further, because low expression genes are under very weak selection to reduce η, their patterns of CUB should provide information on the mutational biases experienced within a genome.
Accessing this information held within CUB patterns of an organism’s genome has been the focus of several decades of research in molecular evolution. However, most approaches examine mutation bias and selection in isolation and ignore their possible interactions. The strength of mutation bias has typically been investigated by comparing the differences in GC content of synonymous sites of codons with the rest of the gene (Galtier et al. 2001; Knight et al. 2001; Palidwor et al. 2010).
Numerous methods have been used to quantify or describe selection on synonymous codon usage. For example, Sharp and Li (1987) relied on the codon usage in a set of highly expressed genes to identify the “optimal” codon for a given amino acid as these genes are under stronger selection to be translated efficiently and accurately. Approaches that focus on a subset of high expression genes in this way implicitly assume the contribution of mutation bias to CUB is overwhelmed by natural selection and, therefore, can be ignored. As our results show, because this view lacks an explicit population genetics framework it is likely overly simplistic and may lead to the misidentification of optimal codons.
Phylogenetic models of protein evolution, some of which are derived from population genetics models, have also been used to generate estimates of codon-specific selection coefficients and mutation biases (Tamuri et al. 2012; Rodrigue et al. 2010; Yang and Nielsen 2008). Other approaches have relied on intraspecific variation to make similar types of inferences (Keightley and Eyre-Walker 2007; Lawrie et al. 2013) or a combination of interspecific divergence and intraspecific variation (Akashi 1995). However, all of these approaches fail to disentangle how the contributions of mutation bias and natural selection change with gene expression. Furthermore, these models are either fitted independently across genes and thus estimate a large number of gene-specific parameters from a relatively small amount of data or assume that the magnitude of selection is uniform across genes.
We, along with others, have previously worked to link gene expression levels to patterns of CUB by nesting a mechanistic model of protein translation into a population genetics model of allele fixation in order to estimate codon-specific mutation and selection parameters (Gilchrist and Wagner 2006; Gilchrist 2007; Shah and Gilchrist 2011; Wallace et al. 2013). Although these methods represent significant advances in estimating codon-specific mutation biases and selection coefficients from genomic data, they are limited to genomes with independent measurements of gene-specific protein synthesis rates or a close proxy. Historically, mRNA abundances have been used as such a proxy due to the fact that generating reliable genome scale measurements of protein synthesis is an expensive undertaking (e.g., Arava et al. 2005; Ingolia et al. 2009; Li et al. 2014). In contrast, the method proposed here does away with the necessity of having protein synthesis rate estimates (or their proxy) and provides estimates of the average protein synthesis rate for each gene, . Importantly, our method also provides estimates of codon-specific mutation biases and translational inefficiencies, which is the additive contribution of a codon to the cost of protein synthesis.
Furthermore, we can combine our gene-specific estimates of protein synthesis rates and codon-specific translational inefficiencies to produce estimates of the strength of natural selection on synonymous substitutions on a gene-by-gene and codon-by-codon basis. Estimating gene-specific selection coefficients on synonymous codons is critical to determining whether a gene is evolving under purifying or positive selection. Current models to identify the selection regime under which a gene evolves rely on estimates of the rates of nonsynonymous changes to rates of synonymous changes (dN/dS) (Li et al. 1985; Nei and Gojobori 1986; Yang and Nielsen 2000). However, the commonly made assumption that all synonymous changes within a gene are neutral can bias values of dN/dS toward overestimating the number of genes evolving under positive selection (Spielman and Wilke 2015). By accurately estimating strength of selection on synonymous changes, researchers can begin to explicitly incorporate these effects into methods for identifying purifying and positive selection.
In order to extract information from the genome-wide patterns of CUB using our Stochastic Evolutionary Model of Protein Production Rate (SEMPPR) (Gilchrist 2007; Shah and Gilchrist 2011), we build on the Bayesian statistical advances of Wallace et al. (2013). Because the costs in our model can be interpreted as proportional differences in ribosome overhead costs (ROC) due to ribosome pausing, for simplicity we refer to the model formulated here as ROC SEMPPR (see Materials and Methods).
Using the Saccharomyces cerevisiae S288c genome as an example, we demonstrate that ROC SEMPPR can be used to accurately estimate differences in codon-specific mutation biases and contributions to the protein synthesis cost–benefit function η without the need for gene expression data. ROC SEMPPR’s codon-specific estimates of mutation biases and translational inefficiencies generated without gene expression data match almost exactly those generated with gene expression data (Pearson correlation coefficient for both sets of parameters). In the end, we observe a Pearson correlation coefficient of between our predicted protein synthesis rates and the mRNA abundances from Yassour et al. (2009) (which was identified as the most reliable data set out of five different mRNA abundance data sets by Wallace et al. [2013]). The variation between our predictions and Yassour et al. (2009)’s measurements is on par with the variation observed between mRNA abundance measurements from different laboratories (Wallace et al. 2013). Further, our predictions show strong and significant correlations with measurements of mRNA abundance from four other labs and estimates of protein synthesis rates based on ribosome-profiling (RPF) data from three other labs (supplementary figs. S4 and S5, Supplementary Material online).
By releasing our work as a standalone package in R (see Chen et al. 2014), researchers can potentially take the genome of any microorganism and obtain accurate, quantitative information on the effect of synonymous substitutions on protein translation costs, gene expression levels, and the strength of selection on CUB.
Results
The posterior means estimated from our Bayesian Markov chain Monte Carlo (MCMC) simulation of ROC SEMPPR demonstrate two key facts: 1) We are able to estimate the strength of selection on synonymous CUB from the patterns of codon usage observed within a genome and 2) we can attribute this selection to the interaction of two underlying biological traits: Difference between synonymous codons in their contribution to the cost–benefit ratio η for protein synthesis and the protein synthesis rate of the ORF averaged across its various environments and life-stages.
For this study, we scale our codon-specific translational inefficiencies relative to the strength of genetic drift, ,
| (1) |
where q described the proportional decline in fitness per ATP wasted per unit time. More specifically, describes the difference in the contribution of synonymous codons i and j to the protein synthesis cost–benefit ratios of an ORF, , scaled by effective population size and the relative fitness cost of expending an extra ATP per unit time, q. The greater the contribution of a codon to η, the greater its inefficiency. For a set of synonymous codons, by convention, we define codon 1 as the codon with the lowest inefficiency, that is, the codon which makes the smallest additive contribution to η and is most favored by selection. Thus, for i = 1 and for i > 1. For notational simplicity, we will only include the subscripts when needed for clarity.
At equilibrium, under the weak-mutation regime (Sella and Hirsh 2005; Shah and Gilchrist 2011b; McCandlish and Stoltzfus 2014), the expected frequency of observing a synonymous codon i (pi) of an amino acid in a gene with an average protein synthesis rate follows a multinomial logistic distribution. Specifically, for a given amino acid a with na unique codons
| (2) |
where is a unitless measure of codon-specific mutation bias. Note that, as with for i = 1 but, unlike with can be positive or negative. Further, because it relies on the stationary probability of observing a synonymous codon, ROC SEMPPR can only detect variation in mutation bias, not variation in absolute mutation rates. Additional model details can be found in the Materials and Methods.
The utility of equation (2) is that it allows us to probabilistically link ROC SEMPPR’s parameters of interest, that is, codon-specific differences in mutation biases, , translational inefficiencies , and gene-specific protein synthesis rates, , to the CUB patterns observed within and between ORF of a given genome. The term represents the number of amino acids that use multiple codons, whereas ng represents the number of genes in the genome.
Because moving between the synonymous codon groups (TCA, TCC, TCG, TCT) and (AGC, AGT) for Ser requires at least one nonsynonymous nucleotide substitution, we treated these two groups as if they were different amino acids, Ser4 and Ser2, respectively. So while strictly speaking, 18 of the canonical 20 amino acids use more than one codon, because we treat Ser as two separate amino acids, Ser2 and Ser4, for our purposes . Assuming a log-normal distribution (LogN) with a mean of 1 as the prior for allows us to employ a random walk Metropolis chain to estimate the posteriors for , and without the need for any laboratory measurements of gene expression, . This ability to fit our ROC SEMPPR model without data is the major advance of our work over Wallace et al. (2013). Tables with estimates of gene-specific protein synthesis rates, , mutation biases, ΔM, and translational inefficiencies, Δη, based on ROC SEMPPR’s posterior sampling for the S. cerevisiae genome can be found in the supplementary material, Supplementary Material online.
Evaluating Model Parameter Estimates
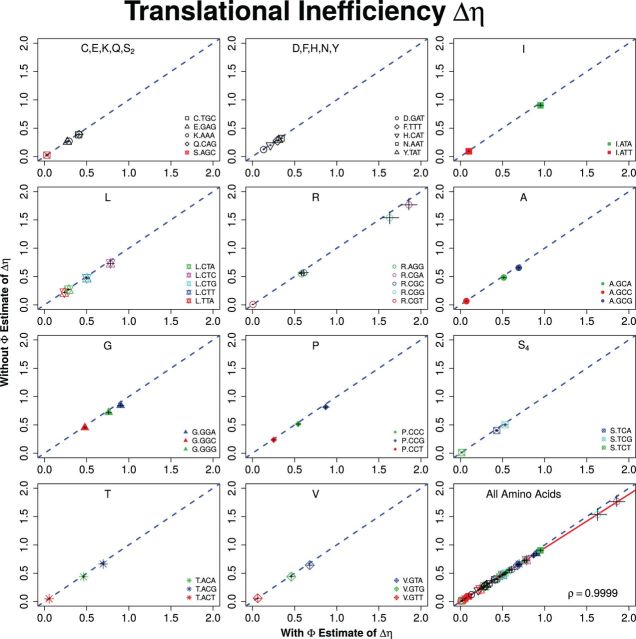
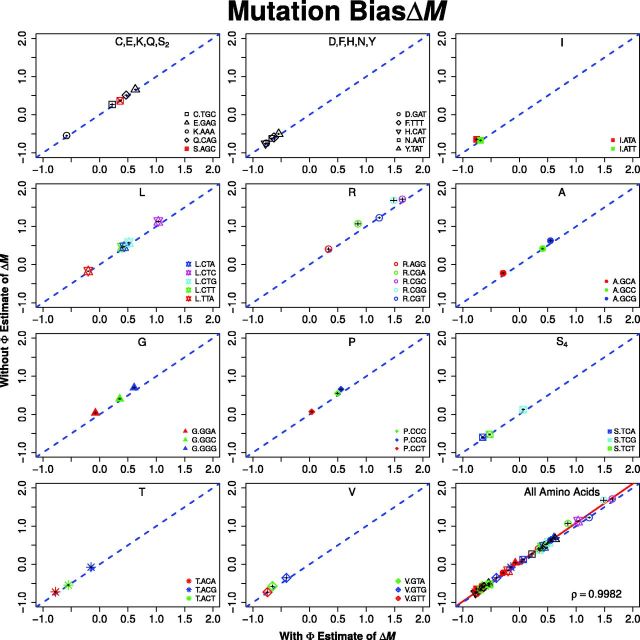
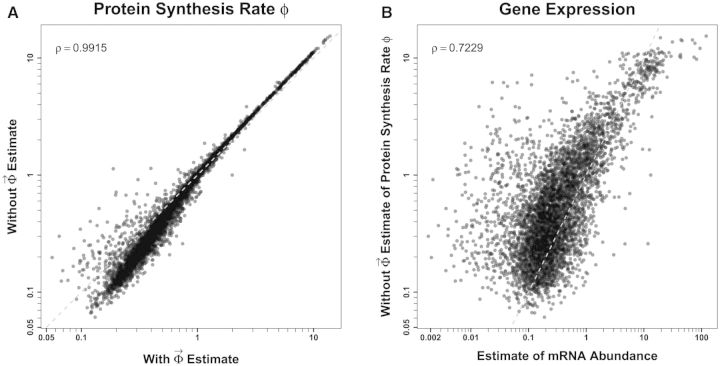
Briefly, when fitted to the S. cerevisiae S288c genome, we find nearly perfect agreement between ROC SEMPPR’s with and without estimates for codon-specific protein synthesis translational inefficiencies, Δη, and mutation bias, ΔM (Pearson correlation for both sets of parameters, see figs. 1 and 2). We note that, with the exception Arginine’s , the central 95% credibility intervals (CIs) for ROC SEMPPR’s Δη and ΔM parameters do not overlap with zero (see supplementary tables S1–S4, Supplementary Material online). These results indicate that information on the genome scale parameters, and are robustly encoded and estimable from CUB patterns and that provides little additional information.
Fig. 1.—
Comparison of with and without ROC SEMPPR estimates for codon-specific differences in translational efficiencies Δη which have units where the units of time are set such that the average protein synthesis rate across the genome, , equals 1. To improve legibility of the plots, the two codon amino acids have been combined into two plots and all of the amino acids with greater than two codons into separate plots. The dashed blue line represents the 1:1 line between axes and error bars indicate the 95% posterior CIs for each parameter. For both the with and without fits of ROC SEMPPR, all codons but one, Arg codon CGT, have CIs that do not overlap with 0. As illustrated in the last plot, a linear regression between estimates of for all codons produces a correlation coefficient .
Fig. 2.—
Comparison of with and without ROC SEMPPR estimates for codon-specific differences in mutation biases terms ΔM which are unitless. Specifically, equals the natural logarithm of the ratio of the frequencies of synonymous codon 1 to i in the absence of natural selection. To improve legibility of the plots, the two codon amino acids have been combined into two plots and all of the amino acids with greater than two codons into separate plots. The dashed blue line represents the 1:1 line between axes and error bars indicate the 95% posterior CIs for each parameter. For both the with and without fits of ROC SEMPPR, all codons have CIs that do not overlap with 0. As illustrated in the last plot, a linear regression between estimates of for all codons produces a correlation coefficient .
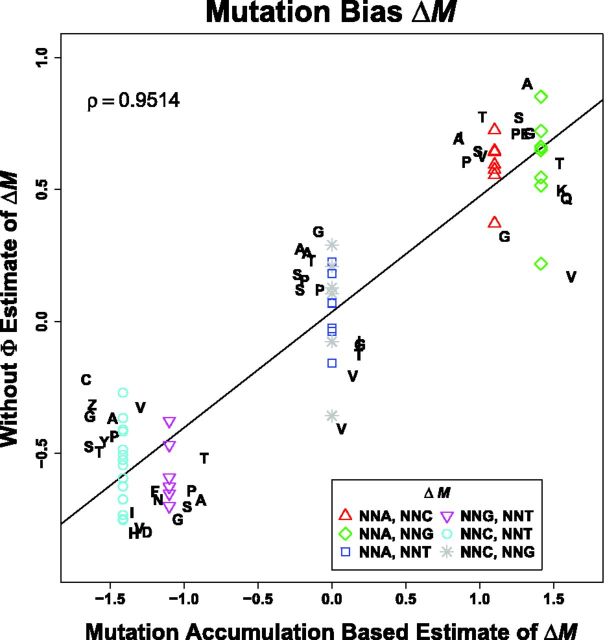
Instead of simply comparing our ROC SEMPPR model’s without estimates of ΔM and Δη to its with estimates, we can also compare these parameters with other data. Due to the detailed balance requirement of the stationary distribution of our population genetics model (Sella and Hirsh 2005), differences in ΔM values between codons that can directly mutate to one another will equal the log of the ratio of their mutation rates. Thus, our estimates of ΔM provide testable hypotheses about the ratio of mutation rates in S. cerevisiae. We use estimates of per base-pair mutation rates from a recent high-throughput mutation accumulation experiment in S. cerevisiae (Zhu et al. 2014). These experimental estimates of mutation bias, , are calculated as
| (3) |
where is the number of mutations observed per ni bases in the genome. As mutations in mutation accumulation experiments are strand agnostic, that is, they do not distinguish between the coding and template strand nucleotides, we cannot distinguish between the mutations NNCNNG and NNGNNC nor NNANNT and NNTNNA. As a result, our empirical estimates of and are set to 0. We find that our estimates of codon-specific mutation rates correlate highly with empirical mutation rates in S. cerevisiae (, fig. 3).
Fig. 3.—
Comparison of without estimates of codon-specific mutation biases ΔM and estimates generated from mutation accumulation experiments (Zhu et al. 2014). For each amino acid the codon with the shortest pausing time is used as a reference and is not shown because, by definition their values are 0. Pearson correlation coefficient ρ for all of the codons is given. The solid line represents the best fit linear regression.
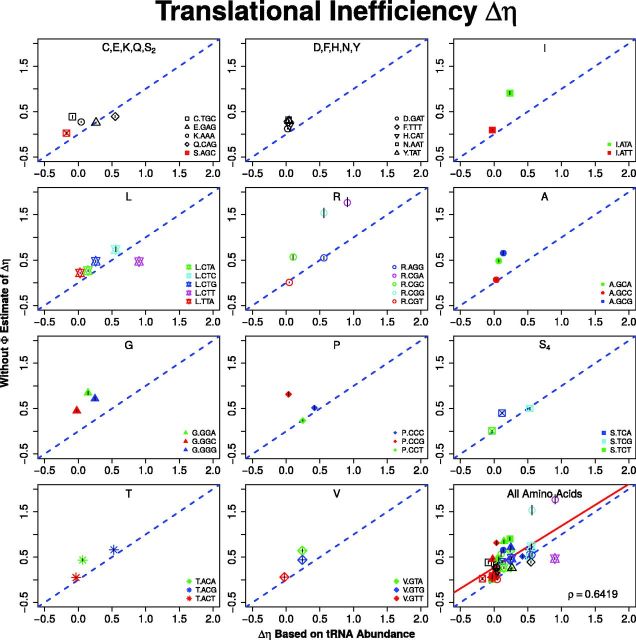
Unlike mutation bias parameters, empirical estimates of the codon-specific differences in translational efficiencies do not exist. However, one of the simplest ways of linking a codon to η is based on the indirect cost of codon-specific ribosome pausing during translation. That is, where ti is the average time a ribosome pauses when translating codon i. We calculate empirical estimates of pausing times based on a simple model of translation where pausing times at a codon depend only on its cognate tRNA abundances and associated wobble parameters (Ikemura 1981; Andersson and Kurland 1990; Sørensen and Pedersen 1991; Kanaya et al. 1999; Gilchrist and Wagner 2006; Zaher and Green 2009; Shah et al. 2013).
| (4) |
Specifically, tRNAi is the gene copy number of the tRNA that recognize codon i and wi is the wobble term between the anticodon of and codon i. When a codon is recognized by its canonical tRNA, we set wi = 1. We assume a purine–purine (RR) or pyrimidine–pyrimidine (YY) wobble term to be and a purine–pyrimidine (RY/YR) wobble term to be based on Curran and Yarus (1989) and Lim and Curran (2001). We find that our genome-wide estimates of Δt are positively correlated with empirical estimates of Δt in S. cerevisiae (, fig. 4).
Fig. 4.—
Comparison of without estimates of codon-specific translational inefficiencies Δη and estimates of differences in ribosome pausing times, based on tRNA gene copy number and wobble inefficiencies. For each amino acid, the codon with the shortest pausing time is used as a reference and is not shown because, by definition their values are 0. Pearson correlation coefficient ρ for all of the codons is given. The dashed blue line represents the 1:1 line and the red line represents the best fit linear regression line.
Predicting Protein Synthesis Rates
Given the strong correlation between ROC SEMPPR’s with and without estimates of the codon-specific mutation biases and translational inefficiencies , it is not surprising that with and without estimates of from ROC SEMPPR are highly correlated (, fig. 5a). More importantly, the without based estimates of show substantial correlation with the mRNA abundance based estimates of values from Yassour et al. (2009) (, fig. 5b). To be clear, these values are the same values used as inputs to the with model fits.
Fig. 5.—
Evaluation of predicted gene expression levels between models and empirical measurements from Yassour et al. (2009). (a) Comparison of with and without ROC SEMPPR estimates of protein synthesis rates, . The units for are proteins/t and time t is scaled such that the prior for satisfies . Note the very strong correlation between the with and without estimates of for the high expression genes. (b) Comparison of without estimates of and empirical measurements of mRNA abundances, . The empirical mRNA abundance measurements, [mRNA], are being used here as a proxy for protein synthesis rates, that is, [mRNA] proteins/t. The measurements are scaled such that the mean [mRNA] value is 1. Pearson correlation coefficients ρ are given and the dashed gray line indicates 1:1 line.
Supplementary figures S4 and S5, Supplementary Material online, explore this issue further by plotting ROC SEMPPR’s posterior mean estimates of produced with and without against eight sets of experimental data. These data include three genome-wide estimates based on RPF measurements (Ingolia et al. 2009; Artieri and Fraser 2014; McManus et al. 2014) and five other genome-wide estimates of mRNA abundances (Arava et al. 2003; Nagalakshmi et al. 2008; Holstege et al. 1998; Sun et al. 2012). The with posterior estimates are generated using mRNA abundance measurements from Yassour et al. (2009) and are, therefore, independent of the measurements from other labs. Correlation between estimates for the without ROC SEMPPR fits and measured mRNA abundances ranges from 0.534 to 0.707, and measured RPF reads ranges from 0.629 to 0.742. The correlation between estimates for the with fits and mRNA provides only a 7–15% increase in explanatory power over the without ROC SEMPPR predictions of . Similarly, correlation between estimates for ROC SEMPPR’s with fits and RPF reads provides a 6–12% increase in explanatory power over its without predictions of .
Changes in CUB with Protein Synthesis Rate
As first shown in Shah and Gilchrist (2011), the relationship between codon usage and protein synthesis rate can range from simple and monotonic to complex. Figure 6 illustrates how codon usage changes across approximately 2 orders of magnitudes of for each of the multicodon amino acids. Both ROC SEMPPR’s with and without model fits accurately predict how CUB changes with protein synthesis rates (fig. 6). Indeed, the predicted changes in CUB between the with and without ROC SEMPPR model fits are almost indistinguishable from one another, reflecting the strong agreement between their estimates of ΔM and Δη across models as discussed above.
Fig. 6.—
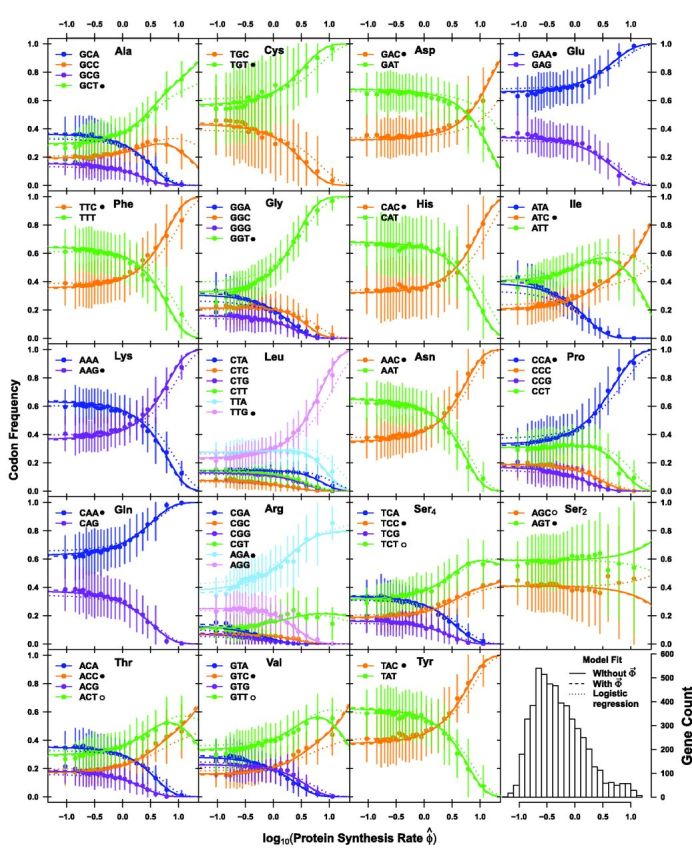
Model predictions and observed codon usage frequencies as a function of estimated protein synthesis rate for the S. cerevisiae S288c genome. The units for are proteins/t and time t is scaled such that the prior for satisfies . Each amino acid is represented by a separate subplot. Solid, dashed, and dotted lines represent the without , with ROC SEMPPR model fits, and a simple logistic regression approach where the estimation error in is ignored, respectively. None of the parameter estimates’ 95% CIs overlaps with 0 except . Genes are binned by their expression levels with solid dots indicating the mean codon frequency of the genes in the respective bin. Error bars indicate the standard deviation in codon frequency across genes within a bin. For each amino acid, the codon favored by natural selection for reducing translational inefficiency is indicated by a . The four indicate codons that have been previously identified as optimal but our ROC SEMPPR model fits indicate these codons actually are the second most efficient codons. A histogram of the values is presented in the lower right corner. Estimates of protein synthesis rates are based on the with ROC SEMPPR model fits, thus representing our best estimate of their values.
Changes in codon frequency with are the result of a subtle interplay between natural selection for reducing η and mutation bias (Figure 6). The simplest cases involve two codon amino acids where the same codon is favored by both selection and mutation bias, that is, Cys, Glu, and Ser2. In these three cases, the selectively and mutationally favored codon 1 is used preferentially across all protein synthesis rates and the frequency of the preferred codon increases monotonically with . The next simplest cases involve two codon amino acids where codon 1 is favored by selection and codon 2 is favored by mutation bias, for example, Asp, Asn, and Phe. In these cases, the mutationally favored codon 2 is used preferentially at low values and the selectively favored codon 1 is used preferentially used in genes at high values. Nevertheless, as before the codon frequencies change monotonically with .
More complex, nonmonotonic changes in codon frequencies can occur in amino acids that use three or more codons. For example, the Ile codon ATC has the lowest translational inefficiency Δη and, therefore, is the most favored codon by natural selection whereas ATT has the second lowest translational inefficiency. As a result, both codons initially increase in frequency with increasing at the expense of the most inefficient codon ATA. However, once the frequency of ATA approaches 0, selection for ATC begins driving the frequency of ATT down. These nonmonotonic changes in codon frequency is most notable in Ala, Ile, Thr, and Val. Examining the derivative of with respect to indicates that if , a given codon i will increase in frequency with , if , that is, if the sum of the derivatives of the selective advantage of codon i over the other codons is positive. For the reference codon 1 where, by definition, , we see that this inequality always holds. This criterion can only be met by the nonreference codon in amino acids with more than two synonyms and when there are other nonreference codons with lower fitnesses at appreciable probabilities. In the S. cerevisiae S288c genome, these conditions can occur when the codon most favored by natural selection is strongly disfavored by mutation. Although this nonlinear quality of multinomial logistic regression is well known among statisticians, the fact that nonoptimal codons can increase with production rate has not been widely recognized by biologists.
If we ignore the noise in the data, our with model fitting simplifies to the standard logistic regression model applied in Shah and Gilchrist (2011). This simplification results in a slight distortion of ΔM estimates and a general attenuation of our estimates of Δη (Wallace et al. 2013). The effect of this attenuation can be seen in figure 6 where the changes in CUB predicted from the standard logistic regression model fit lag behind the predicted changes when either the error in is accounted for or the data are not used. In the case of Ser2, controlling for error leads to a change in the codon identified as being favored by natural selection. Although Shah and Gilchrist (2011) predicted codon AGC would be favored by selection over AGT, both of ROC SEMPPR’s with and without fits predict the opposite. Although, this switch in order is “significant” in that the 95% CI for is less than 0, the amino acid Ser2 is used at very low frequency in high expression genes and its 97.5% CI boundary lies very close to 0. (The upper boundary lies at 0.00387 and 0.000634 for the with and without ROC SEMPPR fits, respectively.) As a result, this discrepancy is not strongly supported and warrants further investigation.
In summary, for genes with protein synthesis rates substantially lower than the average, that is, , codon usage is largely determined by mutation bias terms . For about half of the amino acids (e.g., Cys, Lys, and Pro), in genes with protein synthesis rates ten or more times greater than average, that is, , codon usage is largely determined by selection for the codon with the smallest translational inefficiency . This result is largely consistent with the frequent assumption that in the set of genes with the highest expression levels the most translationally efficient codon dominates. However, for the amino acids (e.g., Ala, Ile, and Arg) selection for reducing η in high expression genes is substantially tempered by the force of mutation bias.
Estimating Selection on Synonymous Codon Usage
The assumptions of the ROC SEMPPR model imply that the codon-specific translational inefficiencies are independent of codon position within a sequence. As a result, the relative strength of purifying selection on synonymous codon j in comparison to codon i in a gene with an average protein synthesis rate is
| (5) |
We remind the reader that includes the effective population size, , in its definition. As a result, our selection coefficients S are measured relative to the strength of genetic drift, , as is commonly done. The distribution of S across all genes for each alternative to an amino acid’s reference codon is illustrated in figure 7 and summarized in table 1. Tables with genome-wide gene and codon-specific estimates of S can be found in the supplementary material, Supplementary Material online. Recall that S is scaled by and that the distribution of values across genes appears to follow a heavy tailed distribution. As a result even though, by definition, the average value of is 1, the large majority of genes have values less than 1. As a result, although purifying selection on synonymous codons is universal, its selection coefficients are usually quite small (i.e., ). Nevertheless, because our framework utilizes information on CUB held across genes, we can clearly detect the signature of selection at the genome level, specifically in the form of values whose posterior CIs differ from 0, whereas other approaches might fail.
Fig. 7.—
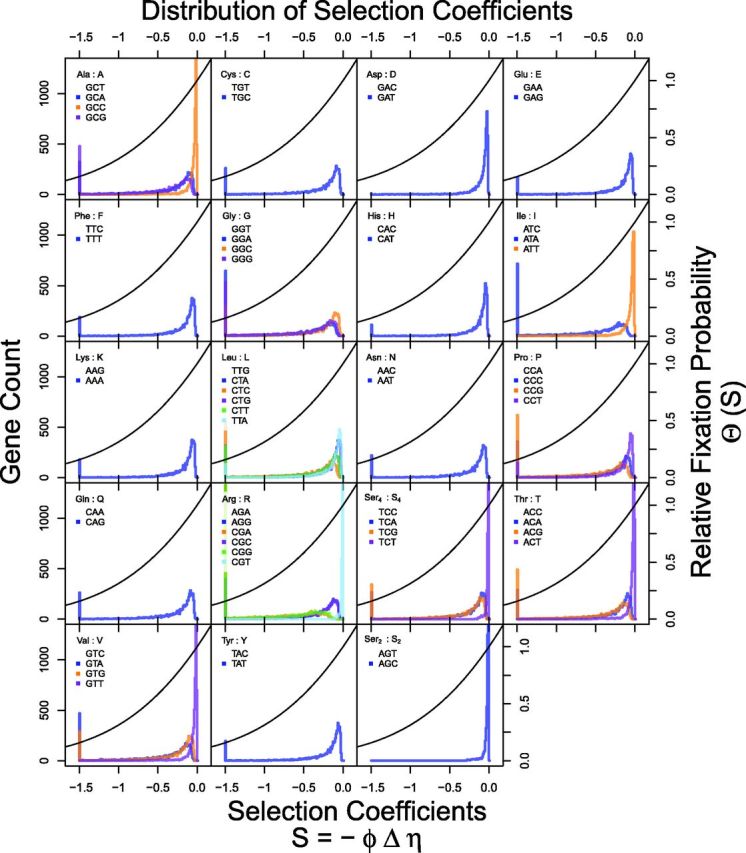
Distribution of gene-specific selection coefficients on synonymous codon usage from the without model fit to the S. cerevisiae genome. Selection coefficient S was calculated on a gene-by-gene basis and relative to reference codon, which is most favored by selection and for which, by definition, S = 0, and is listed first within the legend of each panel. Genes with were combined together into a single bin. For reference, the fixation probability of a codon relative to a pure drift process, , is also plotted (–line). Summary statistics can be found in table 1.
Table 1.
Summary Statistics for Gene-Specific Selection Coefficients on Synonymous Codon Usage from the without ROC SEMPPR Model Fit to the Saccharomyces cerevisiae Genome
| Quantile | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| AA | Codon | 1% | 5% | 25% | 50% | 75% | 95% | 99% | ||
| A | GCA | −0.4743 | 0.6171 | −4.3994 | −1.7817 | −0.4715 | −0.2096 | −0.1135 | −0.0620 | −0.0466 |
| A | GCC | −0.0648 | 0.0115 | −0.6014 | −0.2436 | −0.0645 | −0.0287 | −0.0155 | −0.0085 | −0.0064 |
| A | GCG | −0.6420 | 1.1306 | −5.9551 | −2.4117 | −0.6382 | −0.2837 | −0.1536 | −0.0839 | −0.0631 |
| C | TGC | −0.3777 | 0.3913 | −3.5032 | −1.4187 | −0.3754 | −0.1669 | −0.0903 | −0.0493 | −0.0371 |
| D | GAT | −0.1201 | 0.0396 | −1.1142 | −0.4512 | −0.1194 | −0.0531 | −0.0287 | −0.0157 | −0.0118 |
| E | GAG | −0.2527 | 0.1752 | −2.3440 | −0.9493 | −0.2512 | −0.1117 | −0.0605 | −0.0330 | −0.0248 |
| F | TTT | −0.2741 | 0.2061 | −2.5425 | −1.0297 | −0.2725 | −0.1211 | −0.0656 | −0.0358 | −0.0269 |
| G | GGA | −0.8286 | 1.8834 | −7.6861 | −3.1127 | −0.8237 | −0.3662 | −0.1982 | −0.1083 | −0.0815 |
| G | GGC | −0.4436 | 0.5398 | −4.1149 | −1.6664 | −0.4410 | −0.1960 | −0.1061 | −0.0580 | −0.0436 |
| G | GGG | −0.7052 | 1.3641 | −6.5412 | −2.6490 | −0.7010 | −0.3116 | −0.1687 | −0.0921 | −0.0693 |
| H | CAT | −0.1966 | 0.1060 | −1.8233 | −0.7384 | −0.1954 | −0.0869 | −0.0470 | −0.0257 | −0.0193 |
| I | ATA | −0.8874 | 2.1604 | −8.2318 | −3.3337 | −0.8822 | −0.3922 | −0.2123 | −0.1159 | −0.0872 |
| I | ATT | −0.0906 | 0.0225 | −0.8403 | −0.3403 | −0.0901 | −0.0400 | −0.0217 | −0.0118 | −0.0089 |
| K | AAA | −0.2661 | 0.1943 | −2.4686 | −0.9997 | −0.2646 | −0.1176 | −0.0637 | −0.0348 | −0.0262 |
| L | CTA | −0.2636 | 0.1906 | −2.4452 | −0.9902 | −0.2620 | −0.1165 | −0.0631 | −0.0344 | −0.0259 |
| L | CTC | −0.7185 | 1.4162 | −6.6650 | −2.6991 | −0.7143 | −0.3175 | −0.1719 | −0.0939 | −0.0706 |
| L | CTG | −0.4662 | 0.5961 | −4.3242 | −1.7512 | −0.4634 | −0.2060 | −0.1115 | −0.0609 | −0.0458 |
| L | CTT | −0.4601 | 0.5807 | −4.2679 | −1.7284 | −0.4574 | −0.2033 | −0.1101 | −0.0601 | −0.0452 |
| L | TTA | −0.2128 | 0.1242 | −1.9741 | −0.7995 | −0.2116 | −0.0941 | −0.0509 | −0.0278 | −0.0209 |
| N | AAT | −0.3164 | 0.2746 | −2.9347 | −1.1885 | −0.3145 | −0.1398 | −0.0757 | −0.0413 | −0.0311 |
| P | CCC | −0.5061 | 0.7027 | −4.6948 | −1.9013 | −0.5031 | −0.2237 | −0.1211 | −0.0661 | −0.0498 |
| P | CCG | −0.8002 | 1.7567 | −7.4230 | −3.0061 | −0.7955 | −0.3537 | −0.1914 | −0.1046 | −0.0787 |
| P | CCT | −0.2319 | 0.1476 | −2.1513 | −0.8712 | −0.2306 | −0.1025 | −0.0555 | −0.0303 | −0.0228 |
| Q | CAG | −0.3840 | 0.4046 | −3.5624 | −1.4427 | −0.3818 | −0.1697 | −0.0919 | −0.0502 | −0.0378 |
| R | AGG | −0.5378 | 0.7935 | −4.9890 | −2.0204 | −0.5347 | −0.2377 | −0.1287 | −0.0703 | −0.0529 |
| R | CGA | −1.7330 | 8.2391 | −16.0757 | −6.5103 | −1.7228 | −0.7659 | −0.4146 | −0.2264 | −0.1704 |
| R | CGC | −0.5568 | 0.8504 | −5.1646 | −2.0915 | −0.5535 | −0.2461 | −0.1332 | −0.0727 | −0.0547 |
| R | CGG | −1.5092 | 6.2486 | −13.9999 | −5.6696 | −1.5003 | −0.6670 | −0.3611 | −0.1972 | −0.1484 |
| R | CGT | −0.0080 | 0.0002 | −0.0744 | −0.0301 | −0.0080 | −0.0035 | −0.0019 | −0.0010 | −0.0008 |
| S | TCA | −0.3942 | 0.4264 | −3.6571 | −1.4810 | −0.3919 | −0.1742 | −0.0943 | −0.0515 | −0.0388 |
| S | TCG | −0.4927 | 0.6660 | −4.5705 | −1.8509 | −0.4898 | −0.2178 | −0.1179 | −0.0644 | −0.0484 |
| S | TCT | −0.0121 | 0.0004 | −0.1120 | −0.0454 | −0.0120 | −0.0053 | −0.0029 | −0.0016 | −0.0012 |
| T | ACA | −0.4278 | 0.5020 | −3.9679 | −1.6069 | −0.4252 | −0.1890 | −0.1023 | −0.0559 | −0.0421 |
| T | ACG | −0.6503 | 1.1603 | −6.0327 | −2.4431 | −0.6465 | −0.2874 | −0.1556 | −0.0850 | −0.0639 |
| T | ACT | −0.0482 | 0.0064 | −0.4468 | −0.1810 | −0.0479 | −0.0213 | −0.0115 | −0.0063 | −0.0047 |
| V | GTA | −0.6310 | 1.0922 | −5.8529 | −2.3703 | −0.6272 | −0.2789 | −0.1509 | −0.0824 | −0.0620 |
| V | GTG | −0.4308 | 0.5092 | −3.9966 | −1.6185 | −0.4283 | −0.1904 | −0.1031 | −0.0563 | −0.0424 |
| V | GTT | −0.0570 | 0.0089 | −0.5288 | −0.2142 | −0.0567 | −0.0252 | −0.0136 | −0.0074 | −0.0056 |
| Y | TAT | −0.2857 | 0.2239 | −2.6501 | −1.0732 | −0.2840 | −0.1263 | −0.0683 | −0.0373 | −0.0281 |
| Z | AGC | −0.0248 | 0.0017 | −0.2297 | −0.0930 | −0.0246 | −0.0109 | −0.0059 | −0.0032 | −0.0024 |
Note.—The selection coefficient S was calculated relative to the most translationally efficient codon for a given amino acid on a gene-by-gene basis.
Figure 8 compares our without ROC SEMPPR-based estimates of S with those estimated using the FMutSel phylogenetic model of Yang and Nielsen (2008) using PAML (Yang 2007) for the 106 genes in the Rokas et al. (2003) data set. Overall, we observe reasonable qualitative agreement between the two models with the majority of codon-specific predictions having correlation coefficients . Unfortunately, although PAML provides maximum-likelihood point estimates of parameters, it does not provide any confidence intervals for these parameters. Given the large number of parameters (>60) estimated from each coding sequence by FMutSel, the confidence intervals for each parameter are likely to be large and, hence, could explain much of the variation we observe between ROC SEMPPR and FMutSel parameter estimates. Nonetheless, for 85% of the codons examined (34/40), we observe is a significant (P < 0.05) and positive linear relationship between the ROC SEMPPR and the FMutSel estimates of S (see supplementary table S11, Supplementary Material online). Of the remaining six codons, half exhibit a positive, but nonsignificant relationship between ROC SEMPPR and FMutSel’s estimates of S, whereas the other half exhibit a negative, but again nonsignificant, relationship between estimates of S. Thus for 92% of the codons, both the ROC SEMPPR and FMutSel estimates of S agree qualitatively.
Fig. 8.—
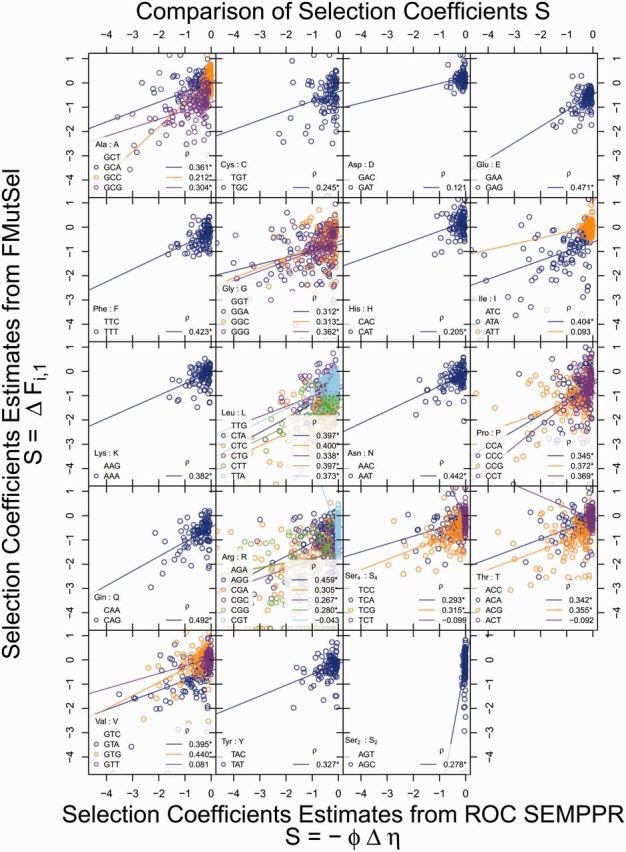
Comparison of gene-specific selection coefficients on synonymous codon usage from the without model fit to the S. cerevisiae genome and those from fitting the FMutSel model from Yang and Nielsen (2008) for 106 yeast genes used in Rokas et al. (2003) as estimated by Kubatko LS, Shah P, Herbei R, Gilchrist M (unpublished data). For more details, see the main text. Selection coefficient S was calculated on a gene-by-gene basis and relative to the most translationally efficient codon for a given amino acid (which is the codon listed first in the legend). Lines indicate linear regression line best fit and the corresponding correlation coefficients are listed as well with an indicating model fits with P < 0.05. Under the FMutSel model, monomorphic sites across species can lead to estimates of S = −∞, these observations are plotted on the x axis.
The three exceptions to this qualitative agreement are codons CGT (Arg), TCT (Ser4), and ACT (Thr) and it is worth noting two points. First, the central 95% CI for CGT (Arg) overlaps with 0 in both the with and without ROC SEMPPR model fits. Second, the Ser4 codon TCT and Thr codon ACT are two of the four codons that ROC SEMPPR indicates have been misidentified as optimal codons in the past. Relative to the ROC SEMPPR reference codons, TCT and ACT have small Δη values, approximately 0.01 and approximately 0.05, respectively, and large ΔM values, approximately −0.5 for both. Thus, it appears in these last two cases the FMutSel model is misattributing the CUB toward these codons to selection rather than mutation (see figure 6).
Discussion
Recent advances in technology have led a remarkable and continuing decrease in the cost of genome sequencing. What is now needed are robust models and computational tools that allow researchers to access the information encoded within these genomes. Several models have been proposed that estimate selection coefficients of all 61 sense codons either on a whole gene basis or on a site-by-site basis (Tamuri et al. 2012; Rodrigue et al. 2010; Yang and Nielsen 2008). While important advances, these models fail to leverage information on CUB encoded across genes. In contrast, ROC SEMPPR estimates selection coefficients and other key parameters by assuming a common direction of selection on CUB, but where the strength of selection varies with protein synthesis rate.
As a result, ROC SEMPPR provides a modeling framework which can quickly extract information on codon-specific translational inefficiencies Δη, mutation biases ΔM, and gene-specific estimates of protein synthesis rates , using only genome-wide patterns of CUB. This ability stems from the hypotheses that the intergenic variation in patterns of CUB observed within a genome reflects a lineage’s evolutionary responses to selection against inefficient protein translation as well as mutation bias. Our results clearly show that these CUB patterns contain remarkably large amounts of useful quantitative information and the use of carefully constructed, mechanistically driven mathematical models can greatly improve our ability to access and interpret this information. Indeed, we find that for S. cerevisiae ROC SEMPPR’s without estimates of ΔM, Δη, and Φ⃗ values match almost exactly with the with estimates of these parameters. By removing the need for gene expression data and, instead, providing reliable predictions of their average protein synthesis rates , the methods developed here should be especially helpful for molecular-, systems-, and microbiologists for whom genomic sequence data are both abundant and inexpensive to obtain. For example, the protein translation rates we estimate should contain useful information about the physiology and ecology of the organism. Indeed, for the large number of sequenced microorganisms that cannot be easily cultured in the laboratory, their genome sequence may become the primary source of information about their biology for the near future.
Of course, ROC SEMPPR may not work for all organisms. For example, some organisms may evolve under Ne values too small for adaptation in CUB to occur. Under these conditions, our method should fail to confidently identify the selectively preferred codon (i.e., our CIs for our Δη parameters will overlap with 0). However, because our estimates of Δη are based on the analysis of the entire genome simultaneously rather than the combination of independent assessments of individual genes, our method may be able to detect the signature of selection on CUB in organisms where it previously went undetected. Alternatively, there may be organisms where Ne is so large that, as a result, there is not enough variation in CUB to reliably estimate our parameters. Assuming we retain our flat priors on Δη, in these cases we expect our estimates of Δη for the most selectively favored codons to continually increase in magnitude during the MCMC simulation rather than eventually stabilizing. Such behavior reflects a lack of information in the data rather than a flaw in our model and has been observed in other approaches, such as those using inter- and intraspecific variation (Yang and Nielsen [2008] and Lawrie et al. [2013], respectively). ROC SEMPPR may also fail to work with organisms whose adaptation in CUB is driven by more complex or less consistent selective forces. If these forces are uncorrelated across amino acids within a gene or varied greatly with position within a gene, then our method should not be able to confidently identify the selectively preferred codons, similar to the case with of organisms with small Ne.
Although direct, codon-specific estimates of and do not exist, data from mutation accumulation lines and tRNA copy number can be used as proxies. Reassuringly, we observe strong and consistent agreement between ROC SEMPPR’s parameter estimates and these proxies. In addition, when comparing ROC SEMPPR’s estimates of S with the FMutSel model we observe general agreement between our estimates with the three key exceptions likely due to relatively small differences in translational inefficiencies between these synonymous codons and their most efficient alternative and strong mutation bias against the most efficient, which is misinterpreted by FMutSel as selection. In contrast, the selective values S on synonymous codon usage we estimate using ROC SEMPPR are substantially smaller than those estimated by Lawrie et al. (2013) based on intraspecific variation in 4-fold degenerate sites for Drosophila melanogaster. Although we have no immediate explanation for these differences we do note that Lawrie et al. (2013) acknowledge that the high S values they estimate are the exception rather than the rule for population genetic studies, including those looking at nonsynonymous substitutions.
Because of ROC SEMPPR’s derivation from population genetics, it should be possible to take any observed intraspecific variation into account by expanding our codon counts likelihood function in equation (8) to be calculated across the polymorphic alleles in proportion to their frequencies. Further, given that the direction of selection in ROC SEMPPR is estimated using information from across the genome, our ability to detect site-specific violations of the model should be much greater than when analyzing the CUB of each gene separately. Expanding ROC SEMPPR to utilize interspecific variation, however, is more complex and will require expanding the model to include the effects of nonsynonymous substitutions and phylogenetic history.
For organisms that can be cultured in the laboratory, researchers can utilize experimental techniques to measure mRNA, ribosome profiles, and protein abundances. Even though impressive gains have been made in our ability to measure these quantities at a genome scale, abundance data still have limitations. For example, mRNA abundance measurements have been shown to vary substantially between labs using the same strain and the same general conditions (Wallace et al. 2013). Indeed, our posterior mean estimate of the error in mRNA abundance measurement () indicates that the error in a given measurement ranges over an order of magnitude. In terms of protein abundance measurements, most proteomic studies have difficulty quantifying membrane bound proteins (Durr et al. 2004; Babu et al. 2012; Chen et al. 2013). Furthermore, both transcriptomic and proteomic measurements are, by their very nature, restricted to the specific growth conditions used. Unfortunately, the frequency with which organisms outside of the lab encounter such conditions is generally unknown. This is particularly important for understanding a pathogenic organism, where expression of genes involved in its persistence and spread is highly dependent on their hosts and is difficult to mimic in vitro.
The predictions of protein synthesis rates generated by ROC SEMPPR contain independent and complementary information to that found in mRNA or protein abundance measurements. As a result, this information can be used on its own or in combination with other measures of gene expression. For example, our work provides estimates of protein production based on the average environment that an organism’s lineage has experienced. These estimates of average gene expression can be used to further contextualize gene expression measurements in different environments. For example, comparing the values for proteins involved in different, environment-specific pathways should give researchers an understanding of the relative importance of these environments in the lineage’s evolutionary history. At a finer scale, gene-specific incongruences between mRNA abundance measurements and estimates may indicate genes undergoing extensive posttranscriptional regulation, a hypothesis that can be evaluated experimentally.
The fact that the additional information provided by the data from Yassour et al. (2009) leads to a relatively small increase in the quality of our predictions of data from other labs may seem surprising.
However, we believe this behavior indicates that the information in about gene-specific protein synthesis rates is largely redundant with the information held within the CUB patterns within a gene and across a genome.
Of course a skeptic might proffer a different interpretation, that is, the model is somehow ignoring or insensitive to the information in . We, however, believe this is not the case for the following reasons. First, ROC SEMPPR was carefully formulated to combine the information from independent measurements and the CUB of each gene in a straightforward and logical manner (see supplementary material: Fitting of Model to Genomic Data and Noisy Measurements and eq. S1 in particular, Supplementary Material online). Instead of a priori assuming one source of information is better than the other, ROC SEMPPR actually evaluates the relative quality of each source of information in explaining the observed bias in codon usage for a gene across the naa amino acids. Next, given the fact that the 95% posterior CIs for Δη differ for at least one pair of codons for each amino acid indicates that the information held within the CUB patterns is reliable. In contrast, ROC SEMPPR’s estimate of the error in indicates that the empirical measurements are noisy, consistent with the findings from other studies. For example, Wallace et al. (2013) looked at the correlation in measurements between independent labs and found nontrivial disagreement in their values. Finally, and perhaps most convincingly, the without version of ROC SEMPPR treats the values as missing values and is able to predict their values to a similar level of accuracy observed between empirical measurements from different laboratories and using different platforms (supplementary figs. S4 and S5, Supplementary Material online).
Accessing information on using a mechanistic, model-based approach as developed here has additional, distinct advantages over more ad-hoc approaches frequently used by other researchers. Quantifying selection on synonymous codons is important for phylogenetic inference. Classical codon substitution models of protein evolution typically assume that synonymous codons of an amino acid are selectively neutral. In contrast, our estimates of codon-specific translation inefficiencies Δη and expression levels provide an independent measure of selection on synonymous codons from a single genome. By incorporating these measures in codon substitution models, researchers would be able to measure selection on nonsynonymous changes either within a gene or on a site-by-site basis.
In addition, current measures to identify the selective regime in which a gene evolves, for example, positive, negative or nearly neutral, are based on estimating the number of nonsynonymous to synonymous changes (dN/dS) (Li et al. 1985; Nei and Gojobori 1986; Yang and Nielsen 2000) or polymorphism data (McDonald and Kreitman 1991). These tests generally assume that synonymous changes are neutral. However, Spielman and Wilke (2015) have recently shown that ignoring selection on synonymous changes can lead to a false positive signal of a gene evolving in response to diversifying selection. By using our codon-specific estimates of translation inefficiencies, researchers will now be able to explicitly account for biases in estimates of dS due to selection on synonymous changes (Spielman and Wilke 2015).
Estimates of codon-specific translation inefficiencies are also important for practical applications such as codon-optimization algorithms that are used to increase heterologous gene expression, for example, insulin expression in Escherichia coli. When heterologous genes are expressed in a particular model organism such as E. coli or S. cerevisiae, their codon usage is “optimized” by assuming that the most frequently used codon in a set of highly expressed genes is the optimal one. This approach implicitly assumes that natural selection against translational inefficiencies overwhelms any mutation bias. In several amino acids that use more than two synonymous codons, for example, Ser4, Thr and Val, genes with highest expression are more often encoded by the mutationally favored, second-best codon rather than the mutationally disfavored optimal codon. As a result, relying on the codon usage of highly expressed genes appears to be overly simplistic in the case of the S. cerevisiae genome and, if our inferences are correct, has led to misidentification of the optimal codon.
In addition to codon-specific translation inefficiencies Δη, we also estimate codon-specific mutation biases ΔM. We find that the direction of mutation biases between synonymous codons is consistent across all amino acids and in the same direction as genomic AT content. However, as we documented in Shah and Gilchrist (2011), ΔM for similar sets of nucleotides differs significantly between amino acids. For instance, in the case of two-codon amino acids with C-T wobble, we find that ranges from 0.27 to 0.75. For genes with low expression levels (i.e., ), this corresponds to ratios of T-ending codons to C-ending codons between amino acids ranging from 1.3 to 2.1. One possible explanation for this wider than expected range of mutation biases could be context-dependence of mutation rates. Recent high-throughput mutation accumulation experiments in yeast support this idea, estimating that the mutation rate at a particular nucleotide depends on the context of surrounding nucleotides: The C nucleotide in the context of CCG has several fold higher mutation rate than in the context of CCT (Zhu et al. 2014).
Despite the numerous advances outlined above, our work is not without its limitations. One important limitation stems from our assumption that codons contribute to the cost–benefit ratio of protein translation in an additive manner. Although this assumption is consistent with certain costs of protein translation, such as ribosome pausing, it ignores many others selective forces potentially shaping the evolution of CUB. For example, the cost of nonsense errors, that is, premature termination events, is generally expected to increase with codon position along an ORF and, thus, leads to a nonadditive contribution of a given codon to the cost–benefit ratio η (Gilchrist et al. 2009). Similarly, if one assumes that the main effect of missense errors is to reduce the functionality of the protein produced, then the cost of these errors is expected to depend greatly on specific details such as the structural and functional role of the amino acid at which the error occurs and the physiochemical differences between the correct and the erroneously incorporated amino acids. Finally, the pausing time at a codon is also influenced by several factors such as downstream mRNA folding (Yang et al. 2014), presence of polybasic stretches (Brandman et al. 2012) as well as cotranslational folding of the growing polypeptide (Thanaraj and Argos 1996; Pechmann and Frydman 2013). Although the contributions of these factors to ribosomal pausing times are often idiosyncratic and vary widely between genes, they can all influence the cost–benefit ratio η. The situation becomes even more complex and nonlinear when considering how nonsense and missense errors along with various factors influencing pausing time costs combine to affect η. In all of these situations, the nonlinear mapping between a codon sequence and η makes direct evaluation of the likelihood function difficult. In such situations alternative, approximate methods and simulation techniques, such as those developed by Murray et al. (2006), will become necessary. Expanding our approach to include these additional selective forces should allow us to quantitatively evaluate the separate contributions of ribosome pausing time, nonsense errors, and missense errors have made to the evolution of CUB for a given species. Doing so will allow us to address the long held goal in molecular and evolutionary biology of accurately quantifying the factors contributing to the evolution of CUB within a coding sequence and across a genome.
Materials and Methods
Modeling Natural Selection on Synonymous Codons
Following the notation and framework introduced in Gilchrist (2007) and Shah and Gilchrist (2011), we assume that for each gene, the organism has a target, average protein synthesis rate . Protein synthesis rates have units of 1/time; for convenience and ease of interpretation, we define our time units such that the average or expected protein synthesis rate across the genome is one, that is, . The cost–benefit ratio represents the expected cost, in ATPs, to produce one functional protein from the coding sequence where ci represents the codon used at position i in a protein of length n. In its most general form, , where is the expected direct and indirect energetic costs incurred by a cell when a ribosome initiates translation of a transcript containing c⃗. Similarly, is the expected benefit, relative to a complete and error free protein, received by a cell when a ribosome initiates translation of a transcript containing c⃗. By definition, in the absence of translation errors, ribosomes will only produce complete and error free proteins, that is, for ROC SEMPPR . Thus any differences in η are the result of differences in between alternative c⃗’s and E(Cost) simplifies to where a1 is the direct and indirect cost of translation initiation, a2 is the direct cost of peptide elongation (four ATPs/amino acid), is the average pausing time a ribosome takes to translate codon ci, and v scales this indirect cost of ribosome pausing from units of time to ATPs. Based on these definitions, represents the average energy flux an organism must expend to meet its target production rate for a given protein. If we assume that every ATP/time spent leads to a small, proportional reduction in genotype fitness q, then the fitness of a given genotype is
| (6) |
In the simplest scenarios, such as when there is selection to minimize ribosome pausing during protein synthesis, a synonymous codon i makes an additive, position-independent contribution to η. In this scenario, the evolution of the codons in is independent between positions. As a result, the information held within c⃗ can be summarized by the number of times each synonymous codon is used within c⃗. Given these assumptions, within the ORF of a given gene the stationary probability of observing a set of codon counts for a given amino acid with na synonymous codons within c⃗ will follow a multinomial distribution with the probability vector . Here, for ,
| (7) |
where is a measure of codon-specific mutation bias and is a measure of translational inefficiency. Specifically, , that is the natural logarithm of the ratio of the frequencies of synonymous codon 1 to i in the absence of natural selection. Following the detailed balance assumptions in our population genetics model, in the specific cases where codons i and 1 can mutate directly between each other, is also equal to the log of the ratio of the mutation rates between the two codons (Sella and Hirsh 2005; Shah and Gilchrist 2011; Wallace et al. 2013). Following Sella and Hirsh (2005), for , for both a haploid and diploid Fisher–Wright populations, we scale the differences in the contribution two synonymous codons make to η relative to genetic drift, that is, . Because the reference codon 1 is determined by pausing time values, values can be both negative and positive, unlike .
Fitting the Model to Genomic Data
Our main goal is to estimate codon-specific differences in mutation bias, , translational inefficiencies, , and protein synthesis rates for all genes, from the information encoded in the codon usage patterns found across a genome. To test our approach, we used the S. cerevisiae S288c genome file orf_coding.fasta.gz which was posted on February 3, 2011 by Saccharomyces Genome Database http://www.yeastgenome.org/ (last accessed April 4, 2015) (Engel et al. 2014). These data contain 5,887 genes and consist of the ORFs for all “Verified” and “Uncharacterized” genes as well as any transposable elements. To fit the with model, we used RNA-seq-derived mRNA abundance measurements from Yassour et al. (2009). We combined the abundance measures from the four samples, YPD0.1, YPD0.2, YPD15.1, and YPD15.2, taken during log growth phase and used the geometric mean of these values as a proxy for relative protein synthesis rates . As is commonly done by empiricists, we rescaled our values such that they summed to 15,000. Because our with model fits estimate the scaling term, , the only effect of this rescaling is on our estimate of . To reduce noise in the data, we only used genes with at least three nonzero measurements. The intersection of 5,887 DNA ORF sequences and 6,303 mRNA abundance measurements produced 5,346 ORFs in common to both data sets. These 5,346 genes made up the final data set used for ROC SEMPPR’s with and without model fits.
Using an MCMC approach we sample from the posterior distribution, according to the equation
| (8) |
where the likelihood of the codon counts, , are naturally modeled as a multinomial distribution (Multinom) for the amino acid i in the ORF of gene j as defined in equation (7), is an inverse multinomial logit function () of , , and , and is the prior for the protein synthesis rate . In order to enforce the restriction that for all genes, we include the constraint that . As a result there is only one free parameter for the distribution . Further, we propose a flat prior for , that is, for .
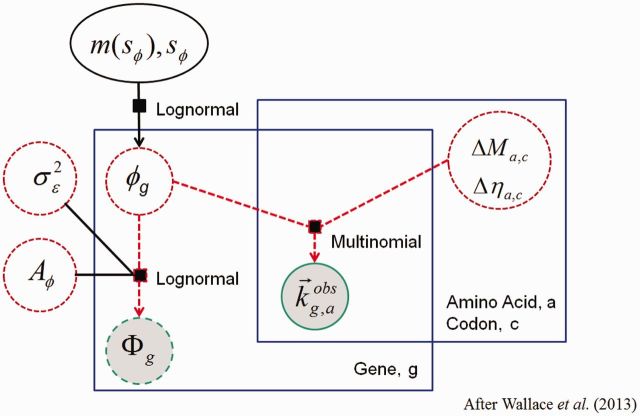
Figure 9 presents an overview of the structure of our approach, but to summarize,
Our MCMC routine provides posterior samples of the genome-wide parameters , , and and the gene-specific, protein synthesis parameters Φ⃗. We refer to this model as the ROC SEMPPR without model.
Fig. 9.—
Dependence graph of with and without ROC SEMPPR methods. Shaded circles and represent observed data. Dashed circles represent key random model parameters, whereas the solid oval represents a random hierarchical parameter. Solid black squares provide information on the distributional relationships between quantities. Large rectangular boxes represent replication of each model component across both amino acids and genes, for example, pausing, and mutation parameters differ across amino acids but are common across genes, whereas counts differ across both amino acids and genes.
We refer to the more general model which incorporates information on from noisy protein synthesis measurements or their proxy, such as mRNA abundances, as the with model. This model differs from that of Wallace et al. (2013) in that 1) we assume is drawn from a log-normal distribution rather than an asymmetric Laplace distribution, 2) we include and estimate an explicit empirical scaling term for the data, and 3) as in the without approach, we force the prior for , to have instead of rescaling estimates of as a postprocessing step. This prevents the introduction of additional biases in our parameter estimates. See the supplementary material, Supplementary Material online, for more details.
Model Fitting Details
We briefly describe the model fitting procedure here; full details can be found in Chen W-C, Zaretzki R, Gilchrist MA (unpublished data). The code was originally based on a script published by Wallace et al. (2013), which was modified extensively and expanded greatly. Unless otherwise mentioned, all model fits were carried out using R version 3.0.2 (R Core Team 2013) using standard routines, specifically developed routines, and custom scripts. All code was run on a multicore workstation with AMD Opteron 6378 processors. For both ROC SEMPPR’s with and without model fits, it takes less than 30 min and less than 3 GB of memory to run 10,000 iterations of a chain when using 5,346 genes of S. cerevisiae S288c genome. Each MCMC sampling iteration was divided into three parts:
Conditional on a new set of parameters, propose new and values independently for each amino acid.
Conditional on the updates of (1), propose a new value for the prior distribution of .
Conditional on the updates of (2), propose new values independently for each gene. Update the new set of parameters and return to (1).
In all three phases, proposals were based on a random walk with step sizes normally or log-normally distributed around the current state of the chain.
In order to generate reasonable starting values for in the without version of ROC SEMPPR, we first calculated the SCUO value for each gene (Wan et al. 2006) and then ordered the genes according to these corresponding values. We then simulated a random vector of equal dimension to from a distribution where represents the initial value of and controls the standard deviation of . Next, these random variates were rank ordered and assigned to the corresponding gene of the same SCUO rank. As a result, the rank order of a gene’s initial value, , was the same as the rank order of its SCUO value. We tried a variety of values and they all converged to similar parameter values. For the with model, we tried both the SCUO-based approach and using the data to initialize our values of . In this second scenario, we set where represents the geometric mean of the observed mRNA abundances for gene j. As in the without ROC SEMPPR model fit, we found the with chains consistently converged to the same region of parameter space independent of the initial values. It is worth noting that the structure of the probability function defined in equation (7) is such that if the rank order of were reversed from their true order, the model would converge to a similar quality of model fit and the signs of the parameters would change. Thus it is recommended that model fits be checked to ensure that the final estimates of for housekeeping genes, such as and ribosomal proteins, are much greater than 1.
Treating our initial protein synthesis rates for the entire genome as explanatory variables, the initial values for and were generated through multinomial logistic regression using the vglm() function of the VGAM package (Yee 2013). We also used the covariance matrix returned by vglm() as the proposal covariance matrix for and for each amino acid. In order to make our random walk more efficient, we used an adaptive proposal function for all parameters in order to reach a target range of acceptance rates between 20% and 35%. For example, the covariance matrix of the step sizes was multiplied by a scalar value that was then increased or decreased by 20% every 100 steps when the acceptance rate of a parameter set was greater than 35% or less than 20%, respectively. The variance terms of the random walks for the and the global parameter were also adjusted in a similar manner.
The results presented here were generated by running the MCMC algorithm for 10,000 iterations and, after examining the traces of the samples for evidence of convergence, selecting the last 5,000 iterations as our posterior samples. The arithmetic means of the posterior samples were used as point estimates based on the mean of our posterior samples. Posterior CIs are generated by excluding the lower and upper 2.5% of samples. Additional details on the model fit can be found in the supplementary material, Supplementary Material online, and in Chen W-C, Zaretzki R, Gilchrist MA (unpublished data). The code is implemented in an R package “cubfits” (Chen et al. 2014) which is freely available for download at http://cran.r-project.org/package=cubfits (last accessed April 4, 2015).
Estimating Selection Coefficients Using FMutSel
In order to evaluate the consistency of our estimates of with other approaches, we used the data set from Rokas et al. (2003) which consisted of 106 aligned genes from 8 yeast species. Details of the model fitting can be found in Kubatko LS, Shah P, Herbei R, Gilchrist M (unpublished data) (available at bioRxiv doi: http://dx.doi.org/10.1101/007849, last accessed May 28, 2015), but briefly, we used the maximum-likelihood tree found by Rokas et al. (2003) and then generated maximum likelihood estimates of the stationary probability of a given codon under the FMutSel model from Yang and Nielsen (2008) using CODONML in PAML 4.4 (Yang 2007). Using the same notation as in Yang and Nielsen (2008) we have
where, for a given gene, πJ represents the stationary probability of observing codon J given nucleotide-specific mutational bias terms and where . It follows that the comparable selection coefficient on synonymous codon usage relative to our reference codon 1 is
| (9) |
A list of these parameter estimates can be found in the supplementary material, Supplementary Material online.
Supplementary Material
Supplementary material, figures S1–S5, and tables S1–S11 are available at Genome Biology and Evolution online (http://www.gbe.oxfordjournals.org/).
Acknowledgments
The authors acknowledge financial support for this project from NSF grants MCB-1120370 (M.A.G. and R.Z.) and EOB-1355033 (Brian O’Meara, M.A.G., and R.Z.). P.S. was supported by Burroughs Wellcome Fund, the David and Lucile Packard Foundation, and US Army Research Office Grant W911NF-12-1-0552 awarded to Joshua Plotkin. Additional support was also provided by the National Institute for Mathematical and Biological Synthesis (NSF:DBI-1300426 with additional support from the University of Tennessee). They are grateful to the RDAV group at the National Institute for Computational Sciences: George Ostrouchov, Drew Schmidt, and Pragnesh Patel who contributed to an earlier attempt to address this problem. They also thank W. Preston Hewgley, Brian O’Meara, Ivan Erill, and Patrick O’Neill for their helpful discussions and suggestions and Laura Kubatko for providing the FMutSel output. Finally, they thank their two anonymous reviewers whose comments and suggestions greatly improved the quality of this article.
Literature Cited
- Akashi H. 1994. Synonymous codon usage in Drosophila melanogaster: natural selection and translational accuracy. Genetics 136(3):927–935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Akashi H. 1995. Inferring weak selection from patterns of polymorphism and divergence at silent sites in drosophila DNA. Genetics 139:1067–1076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andersson SGE, Kurland CG. 1990. Codon preferences in free-living microorganisms. Microbiol Rev. 54(2):198–210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arava Y, et al. 2003. Genome-wide analysis of mRNA translation profiles in Saccharomyces cerevisiae. Proc Natl Acad Sci U S A. 100:3889–3894. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arava Y, Boas FE, Brown PO, Herschlag D. 2005. Dissecting eukaryotic translation and its control by ribosome density mapping. Nucleic Acids Res. 33:2421–2432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Artieri CG, Fraser HB. 2014. Evolution at two levels of gene expression in yeast. Genome Res. 24(3):411–421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Babu M, et al. 2012. Interaction landscape of membrane-protein complexes in Saccharomyces cerevisiae. Nature 489(7417):585–589. [DOI] [PubMed] [Google Scholar]
- Bennetzen JL, Hall BD. 1982. Codon selection in yeast. J Biol Chem. 257(6):3026–3031. [PubMed] [Google Scholar]
- Bentele K, Saffert P, Rauscher R, Ignatova Z, Blüthgen N. 2013. Efficient translation initiation dictates codon usage at gene start. Mol Syst Biol. 9:675. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brandman O, et al. 2012. A ribosome-bound quality control complex triggers degradation of nascent peptides and signals translation stress. Cell 151(5):1042–1054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bulmer M. 1988. Are codon usage patterns in unicellular organisms determined by selection-mutation balance? J Evol Biol. 1(1):15–26. [Google Scholar]
- Bulmer M. 1991. The selection-mutation-drift theory of synonymous codon usage. Genetics 129(3):897–907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chamary JV, Parmley JL, Hurst LD. 2006. Hearing silence: non-neutral evolution at synonymous sites in mammals. Nat Rev Genet. 7(2):98–108. [DOI] [PubMed] [Google Scholar]
- Chen F, et al. 2013. High-mass matrix-assisted laser desorption ionization-mass spectrometry of integral membrane proteins and their complexes. Anal Chem. 85(7):3483–3488. [DOI] [PubMed] [Google Scholar]
- Chen W-C, et al. 2014 cubfits: codon usage bias fits. R Package. Available from: http://cran.r-project.org/package=cubfits. [Google Scholar]
- Clarke B. 1970. Darwinian evolution of proteins. Science 168:1009–1011. [DOI] [PubMed] [Google Scholar]
- Curran JF, Yarus M. 1989. Rates of aminoacyl-tRNA selection at 29 sense codons in vivo. J Mol Biol. 209(1):65–77. [DOI] [PubMed] [Google Scholar]
- Drummond DA, Wilke CO. 2008. Mistranslation-induced protein misfolding as a dominant constraint on coding-sequence evolution. Cell 134(2):341–352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drummond DA, Wilke CO. 2009. The evolutionary consequences of erroneous protein synthesis. Nat Rev Genet. 10(10):715–724. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dunham I, et al. 2012. An integrated encyclopedia of DNA elements in the human genome. Nature 489(7414):57–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Durr E, et al. 2004. Direct proteomic mapping of the lung microvascular endothelial cell surface in vivo and in cell culture. Nat Biotechnol. 22(8):985–992. [DOI] [PubMed] [Google Scholar]
- Engel SR, et al. 2014. The reference genome sequence of Saccharomyces cerevisiae: then and now. G3 4(3):389–398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galtier N, Piganeau G, Mouchiroud D, Duret L. 2001. GC-content evolution in mammalian genomes: the biased gene conversion hypothesis. Genetics 159(2):907–911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilchrist M, Shah P, Zaretzki R. 2009. Measuring and detecting molecular adaptation in codon usage against nonsense errors during protein translation. Genetics 183:1493–1505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilchrist MA. 2007. Combining models of protein translation and population genetics to predict protein production rates from codon usage patterns. Mol Biol Evol. 24:2362–2373. [DOI] [PubMed] [Google Scholar]
- Gilchrist MA, Wagner A. 2006. A model of protein translation including codon bias, nonsense errors, and ribosome recycling. J Theor Biol. 239:417–434. [DOI] [PubMed] [Google Scholar]
- Grantham R, Gautier C, Gouy M, Mercier R, Pave A. 1980. Codon catalog usage and the genome hypothesis. Nucleic Acids Res. 8:R49–R62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gu WJ, Wang XF, Zhai CY, Xie XY, Zhou T. 2012. Selection on synonymous sites for increased accessibility around miRNA binding sites in plants. Mol Biol Evol. 29:3037–3044. [DOI] [PubMed] [Google Scholar]
- Hershberg R, Petrov DA. 2008. Selection on codon bias. Annu Rev Genet. 42:287–299. [DOI] [PubMed] [Google Scholar]
- Holstege FC, et al. 1998. Dissecting the regulatory circuitry of a eukaryotic genome. Cell 95(5):717–728. [DOI] [PubMed] [Google Scholar]
- Hughes JD, Estep PW, Tavazoie S, Church GM. 2000. Computational identification of cis-regulatory elements associated with groups of functionally related genes in Saccharomyces cerevisiae. J Mol Biol. 296(5):1205–1214. [DOI] [PubMed] [Google Scholar]
- Ikemura T. 1981. Correlation between the abundance of Escherichia-coli transfer-RNAs and the occurrence of the respective codons in its protein genes—a proposal for a synonymous codon choice that is optimal for the Escherichia-coli translational system. J Mol Biol. 151:389–409. [DOI] [PubMed] [Google Scholar]
- Ikemura T. 1985. Codon usage and transfer-RNA content in unicellular and multicellular organisms. Mol Biol Evol. 2:13–34. [DOI] [PubMed] [Google Scholar]
- Ingolia NT, Ghaemmaghami S, Newman JRS, Weissman JS. 2009. Genome-wide analysis in vivo of translation with nucleotide resolution using ribosome profiling. Science 324(5924):218–223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kanaya S, Yamada Y, Kudo Y, Ikemura T. 1999. Studies of codon usage and tRNA genes of 18 unicellular organisms and quantification of Bacillus subtilis tRNAs: gene expression level and species-specific diversity of codon usage based on multivariate analysis. Gene 238(1):143–155. [DOI] [PubMed] [Google Scholar]
- Keightley PD, Eyre-Walker A. 2007. Joint inference of the distribution of fitness effects of deleterious mutations and population demography based on nucleotide polymorphism frequencies. Genetics 177:2251–2261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimchi-Sarfaty C, et al. 2007. A “silent” polymorphism in the MDR1 gene changes substrate specificity. Science 315(5811):525–528. [DOI] [PubMed] [Google Scholar]
- Knight RD, Freeland SJ, Landweber LF. 2001. A simple model based on mutation and selection explains trends in codon and amino-acid usage and GC composition within and across genomes. Genome Biol. 2(4):RESEARCH0010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kudla G, Murray AW, Tollervey D, Plotkin JB. 2009. Coding-sequence determinants of gene expression in Escherichia coli. Science 324(5924):255–258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kundaje A, et al. 2015. Integrative analysis of 111 reference human epigenomes. Nature 518:317–330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kurland CG. 1987. Strategies for efficiency and accuracy in gene expression. Trends Biochem Sci. 12:126–128. [Google Scholar]
- Kurland CG. 1992. Translational accuracy and the fitness of bacteria. Annu Rev Genet. 26:29–50. [DOI] [PubMed] [Google Scholar]
- Lawrie DS, Messer PW, Hershberg R, Petrov DA. 2013. Strong purifying selection at synonymous sites in D. melanogaster. PLoS Genet. 9:e1003527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li GW, Burkhardt D, Gross C, Weissman JS. 2014. Quantifying absolute protein synthesis rates reveals principles underlying allocation of cellular resources. Cell 157:624–635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li W-H, Wu CI, Luo CC. 1985. A new method for estimating synonymous and nonsynonymous rates of nucleotide substitution considering the relative likelihood of nucleotide and codon changes. Mol Biol Evol. 2(2):150–174. [DOI] [PubMed] [Google Scholar]
- Lim VI, Curran JF. 2001. Analysis of codon:anticodon interactions within the ribosome provides new insights into codon reading and the genetic code structure. RNA 7(7):942–957. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCandlish DM, Stoltzfus A. 2014. Modeling evolution using the probability of fixation: history and implications. Q Rev Biol. 89(3):225–252. [DOI] [PubMed] [Google Scholar]
- McDonald JH, Kreitman M. 1991. Adaptive protein evolution at the Adh locus in Drosophila. Nature 351(6328):652–654. [DOI] [PubMed] [Google Scholar]
- McManus CJ, May GE, Spealman P, Shteyman A. 2014. Ribosome profiling reveals post-transcriptional buffering of divergent gene expression in yeast. Genome Res. 24(3):422–430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murray I, Ghahramani Z, MacKay DJC. 2006. MCMC for doubly-intractable distributions. In: Proceedings of the 22nd Annual Conference on Uncertainty in Artificial Intelligence (UAI-06). AUAI Press; p. 359–366. [Google Scholar]
- Nagalakshmi U, et al. 2008. The transcriptional landscape of the yeast genome defined by RNA sequencing. Science 320(5881):1344–1349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nei M, Gojobori T. 1986. Simple methods for estimating the numbers of synonymous and nonsynonymous nucleotide substitutions. Mol Biol Evol. 3(5):418–426. [DOI] [PubMed] [Google Scholar]
- Pagani I, et al. 2012. The genomes online database (gold) v.4: status of genomic and metagenomic projects and their associated metadata. Nucleic Acids Res. 40(D1):D571–D579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palidwor GA, Perkins TJ, Xia X. 2010. A general model of codon bias due to GC mutational bias. PLoS One 5(10):e13431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pechmann S, Frydman J. 2013. Evolutionary conservation of codon optimality reveals hidden signatures of cotranslational folding. Nat Struct Mol Biol. 20(2):237–243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Plotkin JB, Kudla G. 2011. Synonymous but not the same: the causes and consequences of codon bias. Nat Rev Genet. 12(1):32–42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qian W, Yang J-R, Pearson NM, Maclean C, Zhang J. 2012. Balanced codon usage optimizes eukaryotic translational efficiency. PLoS Genet. 8(3):e1002603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qin H, Wu WB, Comeron JM, Kreitman M, Li WH. 2004. Intragenic spatial patterns of codon usage bias in prokaryotic and eukaryotic genomes. Genetics 168:2245–2260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Core Team. 2013. R: a language and environment for statistical computing. Vienna (Austria): R Foundation for Statistical Computing. [Google Scholar]
- Rodrigue N, Philippe H, Lartillot N. 2010. Mutation-selection models of coding sequence evolution with site-heterogeneous amino acid fitness profiles. Proc Natl Acad Sci U S A. 107(10):4629–4634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rokas A, Williams BL, King N, Carroll SB. 2003. Genome-scale approaches to resolving incongruence in molecular phylogenies. Nature 425:798–804. [DOI] [PubMed] [Google Scholar]
- Sella G, Hirsh AE. 2005. The application of statistical physics to evolutionary biology. Proc Natl Acad Sci U S A. 102(27):9541–9546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shah P, Ding Y, Niemczyk M, Kudla G, Plotkin JB. 2013. Rate-limiting steps in yeast protein translation. Cell 153(7):1589–1601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shah P, Gilchrist MA. 2010. Effect of correlated tRNA abundances on translation errors and evolution of codon usage bias. PLoS Genet. 6(9):e1001128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shah P, Gilchrist MA. 2011. Explaining complex codon usage patterns with selection for translational efficiency, mutation bias, and genetic drift. Proc Natl Acad Sci U S A. 108(25):10231–10236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharp PM, Li WH. 1986. An evolutionary perspective on synonymous codon usage in unicellular organisms. J Mol Evol. 24:28–38. [DOI] [PubMed] [Google Scholar]
- Sharp PM, Li WH. 1987. The codon adaptation index—a measure of directional synonymous codon usage bias, and its potential applications. Nucleic Acids Res. 15:1281–1295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sørensen MA, Pedersen S. 1991. Absolute in vivo translation rates of individual codons in Escherichia coli. The two glutamic acid codons GAA and GAG are translated with a threefold difference in rate. J Mol Biol. 222(2):265–280. [DOI] [PubMed] [Google Scholar]
- Spielman SJ, Wilke CO. 2015. The relationship between dn/ds and scaled selection coefficients. Mol Biol Evol. 32:1097–1108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun M, et al. 2012. Comparative dynamic transcriptome analysis (cDTA) reveals mutual feedback between mRNA synthesis and degradation. Genome Res. 22(7):1350–1359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tamuri AU, dos Reis M, Goldstein RA. 2012. Estimating the distribution of selection coefficients from phylogenetic data using sitewise mutation-selection models. Genetics 190(3):1101–1115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thanaraj TA, Argos P. 1996. Ribosome-mediated translational pause and protein domain organization. Protein Sci. 5(8):1594–1612. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsai C-J, et al. 2008. Synonymous mutations and ribosome stalling can lead to altered folding pathways and distinct minima. J Mol Biol. 383(2):281–291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tuller T, Waldman YY, Kupiec M, Ruppin E. 2010. Translation efficiency is determined by both codon bias and folding energy. Proc Natl Acad Sci U S A. 107(8):3645–3650. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wallace EWJ, Airoldi EM, Drummond DA. 2013. Estimating selection on synonymous codon usage from noisy experimental data. Mol Biol Evol. 30:1438–1453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wan XF, Zhou J, Xu D. 2006. Codono: a new informatics method for measuring synonymous codon usage bias within and across genomes. Int J Gen Syst. 35:109–125. [Google Scholar]
- Wasserman WW, Sandelin A. 2004. Applied bioinformatics for the identification of regulatory elements. Nat Rev Genet. 5(4):276–287. [DOI] [PubMed] [Google Scholar]
- Yang J-R, Chen X, Zhang J. 2014. Codon-by-codon modulation of translational speed and accuracy via mRNA folding. PLoS Biol. 12(7):e1001910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang ZH. 2007. Paml 4: phylogenetic analysis by maximum likelihood. Mol Biol Evol. 24:1586–1591. [DOI] [PubMed] [Google Scholar]
- Yang ZH, Nielsen R. 2000. Estimating synonymous and nonsynonymous substitution rates under realistic evolutionary models. Mol Biol Evol. 17:32–43. [DOI] [PubMed] [Google Scholar]
- Yang ZH, Nielsen R. 2008. Mutation-selection models of codon substitution and their use to estimate selective strengths on codon usage. Mol Biol Evol. 25:568–579. [DOI] [PubMed] [Google Scholar]
- Yassour M, et al. 2009. Ab initio construction of a eukaryotic transcriptome by massively parallel mRNA sequencing. Proc Natl Acad Sci U S A. 106:3264–3269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yee T. 2013. VGAM: vector generalized linear and additive models. R Package version 0.9-3. [Google Scholar]
- Zaher HS, Green R. 2009. Fidelity at the molecular level: lessons from protein synthesis. Cell 136:746–762. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu YO, Siegal ML, Hall DW, Petrov DA. 2014. Precise estimates of mutation rate and spectrum in yeast. Proc Natl Acad Sci U S A. 111(22):E2310–E2318. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.