Abstract
The development of synthetic gene oscillators has not only demonstrated our ability to forward engineer reliable circuits in living cells, but it has also proven to be an excellent testing ground for the statistical behavior of coupled noisy oscillators. Previous experimental studies demonstrated that a shared positive feedback can reliably synchronize such oscillators, though the theoretical mechanism was not studied in detail. In the present work, we examine an experimentally motivated stochastic model for coupled degrade-and-fire gene oscillators, where a core delayed negative feedback establishes oscillations within each cell, and a shared delayed positive feedback couples all cells. We use analytic and numerical techniques to investigate conditions for one cluster and multicluster synchrony. A nonzero delay in the shared positive feedback, as expected for the experimental systems, is found to be important for synchrony to occur.
Introduction
In the past decade, remarkable progress has been achieved in the new field of synthetic biology [1]. Along with developing synthetic biological systems for novel therapeutical and bioengineering applications, synthetic biology serves as a tool for elucidating fundamental principles of biology using forward engineering of relatively simple systems amenable to thorough theoretical and experimental analysis. One particular area of rapid progress has been the design and implementation of synthetic gene oscillators. A number of intracellular oscillators mimicking natural genetic clocks have been constructed since the seminal repressilator [2], including those using interlocked positive and negative feedback loop oscillators in bacteria [3] and mammalian cells [4], and those leveraging quorum sensing systems [5].
The robust gene oscillator designs used in Refs. [3,5], and explored in Refs [6–8], were determined to depend on a core negative feedback loop. It was shown that even a small feedback delay is capable of generating long-period oscillations in a strongly nonlinear regime through a so-called degrade-and-fire (DF) mechanism [9]. In this regime, a short (on the order of the time delay) but strong burst of repressor protein synthesis is followed by the long period of enzymatic protein degradation, which largely determines the oscillation period.
Degrade-and-fire oscillations are especially sensitive to noise since their period and amplitude are primarily determined by the short transcriptional burst when the number of repressor protein molecules is small and therefore stochasticity is strong [10]. Thus, a population of noninteracting cells with genetically identical DF oscillator circuits rapidly loses synchronization even if set to the same phase initially. However, it has been well known since Huygens that sufficiently strong coupling between oscillators may lead to their synchronization even in the presence of unavoidable stochastic variability. In Ref. [5], we first demonstrated the synchronization of synthetic gene oscillators though quorum sensing and developed a detailed mechanistic model that demonstrated good agreement with the experiment. In order to develop deeper insight into the mechanism of synchronization, we also studied a simple mathematical model of synchronization of discontinuous DF oscillators in which firing of individual oscillators was controlled a repressive interaction [11,12]. However, this model qualitatively different from the experimental setup in which the oscillators were synchronized by a common activator [5,8]. Furthermore, the finite time required for the production of proteins associated with activation also implies a delay in the positive feedback, which is known to influence synchronization phenomena [13–16].
In this Letter, we introduce and analyze a model for the synchronization via delayed mutual activation of DF oscillators that is general and simple enough to permit a thorough analytical and numerical investigation. Within this model, conditions for the synchronization of noisy DF oscillations are reduced to finding roots of two transcendental equations for the eigenvalues. In particular, a finite time delay in the global positive feedback loop is found to be critical for the robust single cluster synchronization. It is worth mentioning that our study is distinct from similar work on pulse-coupled integrate-and-fire oscillators [17–21]. For instance, while integrate-and-fire “neurons” are typically assumed to be continually affected by an (often discontinuous) coupling field, the oscillators in our DF model are affected by a continuous coupling field only during brief firing events.
Mathematical model
Near the Hopf bifurcation, any weakly nonlinear oscillator can be well characterized by a single phase variable, and the dynamics of coupled phase oscillators is governed by the seminal Kuramoto model or its direct generalizations which have been studied in great detail [22]. Here we are interested in gene oscillators far from the Hopf bifurcation, in the strongly nonlinear DF regime where classical results are not applicable. The deterministic model of an isolated DF oscillator is based on a single delay-differential equation for the concentration of the repressor protein x [9],
| (1) |
in which the first and second terms describe the synthesis and enzymatic degradation of x(t), respectively. The synthesis rate F(xτ1) depends on the delayed concentration xτ1= x(t − τ1), and since x is an autorepressor, dF(x)/dx < 0. An example of such an autorepressing synthesis function is the Hill-type function considered in Ref. [9]. When first taking K infinitesimal but positive, and assuming F(x) remains non-negative but decreases with x sufficiently quickly, then for τ1 → 0 while the product F(0)τ1 remains fixed, it can be shown for a wide range of parameter regimes that this model generates quasisawtooth oscillations with approximate period T = F(0)τ1/γ [9]. Thus, the model (1) can be replaced by a discontinuous system where x decays linearly with rate γ until it reaches x = 0, when it instantaneously is reset to x = X0 = F(0)τ1. By also including the noise in the synthesis of repressor proteins that is intrinsic to gene circuits, we arrive at the following dynamical equation for the repressor protein concentration in a single DF oscillator:
| (2) |
where Ĩ(x, X0) is a stochastic impulse function such that x → x + X0 + ξ̃ when x = 0, where ξ̃ is a random variable with average 〈ξ̃〉 = 0. We choose for convenience of analysis that ξ̃ is independently and uniformly distributed in [−η/2, η/2], though the physical situation can be more complicated [see Supplemental Material (SM) [23] for more background and motivation for approximations]. Furthermore, in the following we will treat η as an independent parameter; however, in reality it is likely dependent on the synthesis rate and therefore related to X0. Thus, when we keep X0 fixed in our results, varying η may be interpreted as adjusting the physically meaningful relative noise strength.
The solution of Eq. (2) has a discontinuous sawtooth shape. If ti is the time of the last “firing,” i.e., impulse, and if ξ̃i are independent uniform random variables distributed in [−η/2, η/2], then the concentration of the repressor x after time ti decays linearly, x(t) = X0 + ξ̃i − γ(t − ti), until it reaches x = 0 at time ti+1 = ti + (X0 + ξ̃i)/γ, after which x is instantaneously mapped to X0 + ξi+1, and the process repeats. That the amplitude of the bursts varies from firing to firing is typical of the synthetic gene oscillators under study.
Now we extend the model and consider a system of N DF oscillators with repressor concentrations xn, n = 1,…, N coupled to a single scalar activator concentration A that provides global coupling. All oscillators contribute to synthesis of this activator, and the activator A, in turn, increases the amplitude of firing. This model is a direct generalization of Eq. (2), but with one additional equation describing collective activator synthesis by all oscillators. These N + 1 variables obey the following equations:
| (3) |
| (4) |
where β is the degradation rate of the activator and Aτ = A(t − τ), since we allow for a delay between synthesis of the activator A and the commencement of activation. Here, for simplicity, we assume a linear rate of activator synthesis by individual xn.
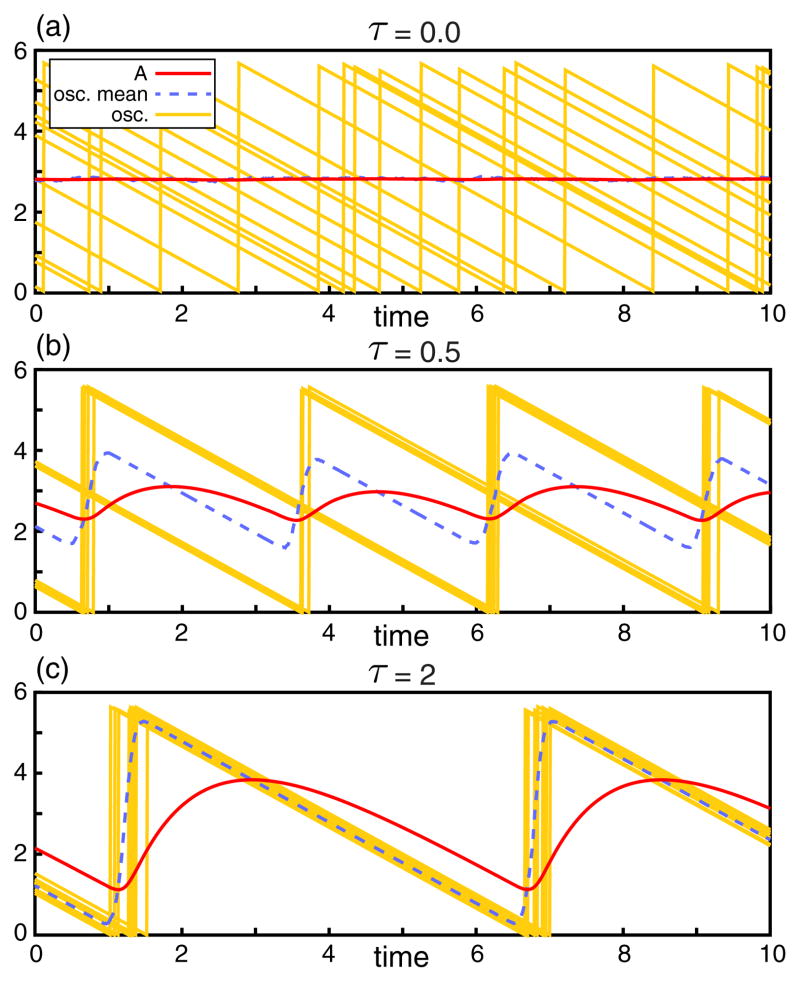
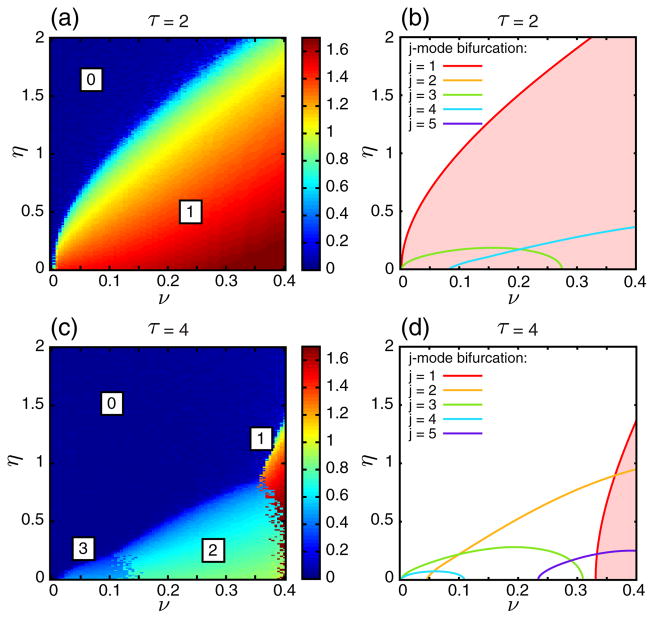
Straightforward simulation of the model (see SM [23] for details) leads to a variety of behaviors. Strong noise (large η) is found to generate the asynchronous or homogenous state, where the xn amplitudes are approximately uniformly distributed at any given time. However, one or more synchronized clusters may form for sufficiently small η, where a cluster is roughly defined as a set of oscillators having a small dispersion in their firing times (see Fig. 1 for examples of tight clusters). Within this regime, numerical simulation supports that an appropriate choice for τ can robustly generate a single cluster, as demonstrated in Fig. 2(a), while other choices for τ lead to the formation of two- or even three-cluster populations, as demonstrated in Fig. 2(c). Furthermore, Fig. 2(c) illustrates the coexistence of metastable clusters, e.g., as indicated by the “speckled” boundary between the one-cluster and two-cluster regions.
FIG. 1.
(color online). Different synchronization regimes for a set of 1000 noisy DF oscillators. Pictured are the values of global activator A (red line), the mean oscillator value 〈x〉 (dashed blue line), and ten randomly selected oscillator trajectories xn(t) (yellow lines). (a) Absence of synchronization for τ = 0. Other parameters are η = 0.2, ν = 0.2, γ = 1, β = 1, and X0 = 5. (b) Two-cluster regime for τ = 0.5 and other parameters the same as above. (c) Single-cluster regime for τ = 2.
FIG. 2.
(color online). (a) For τ = 2, the standard deviation (over time) of the mean oscillator value 〈x〉 for 1000 oscillators as a function of parameters (see SM for simulation details [23]). Note that the time variation of 〈x〉 is essentially zero in the asynchronous regime. Boxed numerals indicate the number of clusters associated with the given region of parameter space. Other parameters are γ = 1.0, β = 1.0, and X0 = 5.0. These results do not appear to be sensitive to the initial conditions of simulation (see SM [23]). (b) Associated linear stability analysis of the continuum asynchronous state with respect to the mode j, derived from numerical solution of Eqs. (11) and (12). Regions below the presented lines are unstable to growing oscillations of the density function. This is indicated for the one-mode instability by a red shaded region. Notice the correspondence with (a): the boundary between the blue region (asynchronous regime) and the clustered region corresponds to the first mode bifurcation line in (b). Panels (c) and (d) are the same as (a) and (b), respectively, but for τ = 4. In different regions of parameters, different modes become unstable (d) and lead to formation of multiclustered states in (c) as labeled. The “speckling” between boundaries in (c) is consistent with multistability, as suggested by the coexistence of several unstable modes in (d).
Continuum limit
Analysis of parameter regimes leading to various modes of synchronization in our model becomes somewhat simpler when we take the thermodynamic limit N → ∞. For an infinite number of oscillators we can introduce a continuum probability density distribution function f(x, t) for the repressor concentration x in different cells at time t. It is easy to see that the set of discrete equations for the individual repression concentrations can now be replaced by the Liouville equation
| (5) |
that is coupled to the integro-differential equation for A,
| (6) |
Here the function g(x, Aτ) characterizes the distribution of firing magnitudes (the jumps from 0 to the maxima in the beginning of each period), and it has to be normalized to conserve probability
| (7) |
As before, we assume that firing magnitudes are distributed uniformly within (X0 + νAτ − η/2, X0 + νAτ + η/2), such that
| (8) |
where Θ is the Heaviside function. The asynchronous solution to Eqs. (5) and (6) corresponds to time-independent f0(x) and A0. With the choice for g in Eq. (8), the asynchronous solution for f0(x) can be shown to be piecewise linear, and the value for A0 only depends on the solution to a quadratic equation (see SM for further details [23]).
The stability of the asynchronous solution with respect to small perturbations is useful when discussing synchronization, since it turns out that the corresponding bifurcation diagram predicts surprisingly well the results from direct numerical simulation of Eqs. (3) and (4). Seeking the solution in the form
| (9) |
| (10) |
and after rescaling time by setting γ = 1, a straightforward calculation leads to a pair of transcendental equations for the complex eigenvalue λ (see SM for details [23]),
| (11) |
| (12) |
where P = X0 + νA0 and ζ ≡ A1/f1(0). Notice that first solving for ζ is straightforward, but solving for λ can be highly nontrivial for general parameter values. We solve this eigenvalue problem numerically by continuing solutions for ν = 0 and η small but finite, where these root solutions can be labeled by an index corresponding to the number of oscillations in the eigenfunction (see SM [23]). This index corresponds to the number of clusters for full nonlinear synchronization.
Figure 2 compares direct simulation of Eqs. (3) and (4) to this linear stability analysis. The ability for the linear theory to predict global dynamics is quite good, including the prediction of clusters of definite size (e.g., two clusters), and including regions of multistability, where multiple cluster solutions coexist. We find that positive delay τ is important for synchronization, since we find numerically that the asynchronous solution is stable when τ = 0. Thus, the delay in the global positive feedback plays a crucial role in the synchronization of these DF oscillators, as was suggested in Ref. [5]. Figure 3 shows that there exists a wide range of parameters when the first mode is the only unstable solution corresponding to a single synchronized cluster. However, in other parameter domains, higher-order modes can also become unstable and lead to multicluster solutions and multistability.
FIG. 3.
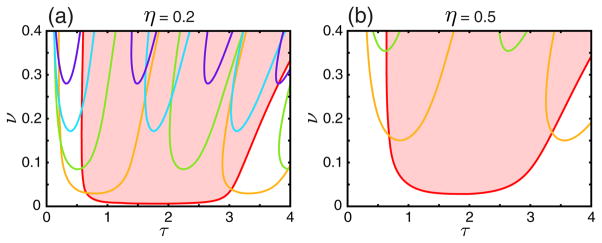
(color online). The linear stability bifurcation diagrams of the asynchronous state with respect to different modes as a function of τ and ν for two values of η [η = 0.2 in part (a), η = 0.5 in part (b)],, with instability of a mode occurring above each line. This is indicated for the one-mode instability by a red shaded region. The colors of each curve correspond to the mode numbers indicated in the legend in Figs. 2(a) and 2(b). Details of calculations are similar to Figs. 2(a) and 2(b). In particular, we find that the asynchronous state is stable when τ = 0 and most unstable when τ = 2 (which roughly corresponds to the half of the oscillator period) with respect to one-mode (single cluster).
As mentioned above, in this analysis we consider the noise strength η to be the independent parameter while keeping the mean firing amplitude X0 fixed. However, in reality both η and X0 are determined by the biochemical details of the repressor protein synthesis. In the SM [23] we present the results of simulations and the stability analysis for the simple example of “multiplicative noise” in which η ∝ X0.
Highly synchronized regime
Now we consider the opposite limit of strong coupling ν, when nearly all oscillators are periodic and synchronized by the common activator field. In this case, the activator field A(t) oscillates strongly with the bulk of the oscillators. For small disorder (η → 0), the periodic solution over the first period (0 ≤ t < T) has the form
| (13) |
| (14) |
with Ps ≡ X0 + νAs(−τ). It holds that As(−τ) = As(T − τ) due to periodicity of the solution. Consistency requires that the period T = Ps/γ and As(T) = As(0), from which the periodic solution can be determined.
To address the stability of this periodic solution, we consider the interaction of a single noiseless DF oscillator with this synchronized cluster. Since we operate in the limit of large N, the influence of the test oscillator x on the activator field can be neglected, and so we can consider the “bulk” periodic solution As(t) given and independent of x. The dynamics of x is only affected by the values of the activator field at the time τ before firing events: As(ti − τ), where ti denotes times when x = 0, enumerated by the index i. The dynamics of a deterministic test oscillator reduces to a map between the consecutive firing times ti,
| (15) |
We can linearize this map with respect to the small deviation of ti from the times when the bulk of the oscillators fire, shifted to be iT for integer i. Introducing δti = ti − iT and linearizing Eq. (15), we obtain
| (16) |
By periodicity, the condition for cluster stability is
| (17) |
Since A(t) in the synchronized regime always has a minimum at the firing times (see Fig. 1), the derivative dA/dt for sufficiently small (but nonzero) τ is robustly negative, and therefore the synchronized regime is linearly stable. This observation may explain the tendency to reliably form a synchronous oscillation in the experimental context [5,8].
In the presence of noise (η > 0), we find that this single mode may be only metastable. We discuss this and related phenomena in the SM [23]; e.g., see Figs. S1 and S2.
Discussion
In this Letter we introduced an analytically treatable model for a population of noisy degrade-and-fire oscillators coupled through a common activator. Using this model in the thermodynamic limit of infinitely many oscillators, we derived conditions for the instability of the asynchronous state and formation of one or multiple clusters of synchronized DF oscillators. In particular, we demonstrated the role of the activation delay τ. Too short or too long of a delay can lead to multiple clusters, but a moderate delay was found to robustly form a single cluster. This trend was demonstrated in three different ways: numerical simulation, stability analysis of the asynchronous state, and the stability analysis of a single coherent cluster.
Our model is similar in spirit to the model of harmonic oscillators diffusively coupled through external medium [16]. However, due to a very different nature of individual oscillators (degrade-and-fire versus harmonic), we do not find the phenomenon of “dynamical amplitude death,” while the model of Ref. [16] does not describe multicluster regimes and bistability.
In this work we assumed that all oscillators have the same parameters, and only may dephase due to stochasticity in the magnitude of individual firing events. It would also be interesting to study the dynamics of oscillators with randomized parameters X0 and/or γ (“quenched disorder”), in analogy with the Kuramoto model of phase oscillators with distributed frequencies [22]. One can expect a similar phase transition to a synchronous regime at a certain minimal coupling strength ν. On the other hand, we assumed global coupling, whereas networks of coupled oscillators with nonglobal coupling often exhibit complex “chimera” states in which synchronized and nonsynchronized phases coexist [21,24]. However, we leave the analysis of these systems to future work.
Supplementary Material
Acknowledgments
We are grateful to the San Diego Center for Systems Biology (NIH Grant No. P50-GM085764), NIGMS (NIH Grant No. RO1-GM069811), and NSF (NSF Grant No. 1330180) for financial support.
References
- 1.Purnick PE, Weiss R. Nat Rev Mol Cell Biol. 2009;10:410. doi: 10.1038/nrm2698. [DOI] [PubMed] [Google Scholar]
- 2.Elowitz MB, Leibler S. Nature (London) 2000;403:335. doi: 10.1038/35002125. [DOI] [PubMed] [Google Scholar]
- 3.Stricker J, Cookson S, Bennett MR, Mather WH, Tsimring LS, Hasty J. Nature (London) 2008;456:516. doi: 10.1038/nature07389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Tigges M, Marquez-Lago TT, Stelling J, Fussenegger M. Nature (London) 2009;457:309. doi: 10.1038/nature07616. [DOI] [PubMed] [Google Scholar]
- 5.Danino T, Mondragón-Palomino O, Tsimring L, Hasty J. Nature (London) 2010;463:326. doi: 10.1038/nature08753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Hasty J, Dolnik M, Rottschäfer V, Collins JJ. Phys Rev Lett. 2002;88:148101. doi: 10.1103/PhysRevLett.88.148101. [DOI] [PubMed] [Google Scholar]
- 7.Mondragón-Palomino O, Danino T, Selimkhanov J, Tsimring L, Hasty J. Science. 2011;333:1315. doi: 10.1126/science.1205369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Prindle A, Samayoa P, Razinkov I, Danino T, Tsimring LS, Hasty J. Nature (London) 2011;481:39. doi: 10.1038/nature10722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Mather W, Bennett MR, Hasty J, Tsimring LS. Phys Rev Lett. 2009;102:068105. doi: 10.1103/PhysRevLett.102.068105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Tsimring LS. Rep Prog Phys. 2014;77:026601. doi: 10.1088/0034-4885/77/2/026601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Fernandez B, Tsimring LS. Phys Rev E. 2011;84:051916. doi: 10.1103/PhysRevE.84.051916. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Fernandez B, Tsimring LS. J Math Biol. 2014;68:1627. doi: 10.1007/s00285-013-0680-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Stephen Yeung MK, Strogatz SH. Phys Rev Lett. 1999;82:648. [Google Scholar]
- 14.Choi MY, Kim HJ, Kim D, Hong H. Phys Rev E. 2000;61:371. doi: 10.1103/physreve.61.371. [DOI] [PubMed] [Google Scholar]
- 15.Atay FM. Phys Rev Lett. 2003;91:094101. doi: 10.1103/PhysRevLett.91.094101. [DOI] [PubMed] [Google Scholar]
- 16.Schwab DJ, Baetica A, Mehta P. Physica (Amsterdam) 2012;241D:1782. doi: 10.1016/j.physd.2012.08.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Mirollo RE, Strogatz SH. SIAM J Appl Math. 1990;50:1645. [Google Scholar]
- 18.van Vreeswijk C. Phys Rev E. 1996;54:5522. [Google Scholar]
- 19.Mohanty PK, Politi A. J Phys A. 2006;39:L415. [Google Scholar]
- 20.Zillmer R, Livi R, Politi A, Torcini A. Phys Rev E. 2007;76:046102. doi: 10.1103/PhysRevE.76.046102. [DOI] [PubMed] [Google Scholar]
- 21.Wildie M, Shanahan M. Chaos. 2012;22:043131. doi: 10.1063/1.4766592. [DOI] [PubMed] [Google Scholar]
- 22.Kuramoto Y. Chemical Oscillations, Waves, and Turbulence. Dover; New York: 2003. [Google Scholar]
- 23.See Supplemental Material at http://link.aps.org/supplemental/10.1103/PhysRevLett.113.128102 for further details concerning simulation and analysis.
- 24.Sethia GC, Sen A, Atay FM. Phys Rev Lett. 2008;100:144102. doi: 10.1103/PhysRevLett.100.144102. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.