Abstract
There is a compelling need for early, accurate diagnosis of Parkinson’s disease (PD). Various magnetic resonance imaging modalities are being explored as an adjunct to diagnosis. A significant challenge in using MR imaging for diagnosis is developing appropriate algorithms for extracting diagnostically relevant information from brain images. In previous work, we have demonstrated that individual subject variability can have a substantial effect on identifying and determining the borders of regions of analysis, and that this variability may impact on prediction accuracy.In this paper we evaluate a new statistical algorithm to determine if we can improve accuracy of prediction using a subjects left-out validation of a DTI analysis. Twenty subjects with PD and 22 healthy controls were imaged to evaluate if a full brain diffusion tensor imaging-fractional anisotropy (DTI-FA) map might be capable of segregating PD from controls. In this paper, we present a new statistical algorithm based on bootstrapping. We compare the capacity of this algorithm to classify the identity of subjects left out of the analysis with the accuracy of other statistical techniques, including standard cluster-thresholding. The bootstrapped analysis approach was able to correctly discriminate the 20 subjects with PD from the 22 healthy controls (area under the receiver operator curve or AUROC 0.90); however the sensitivity and specificity of standard cluster-thresholding techniques at various voxel-specific thresholds were less effective (AUROC 0.72–0.75). Based on these results sufficient information to generate diagnostically relevant statistical maps may already be collected by current MRI scanners. We present one statistical technique that might be used to extract diagnostically relevant information from a full brain analysis.
Keywords: Parkinson disease, Diffusion tensor imaging, Diagnosis, Data analysis methods
Introduction
There is a compelling need for early and accurate diagnosis of Parkinson’s disease (PD). Various MR imaging modalities are being explored to enhance diagnosis (Skidmore et al. 2011a, b, c; Gorell et al. 1995; Shalom Michaeli et al. 2007; Vaillancourt et al. 2009; Péran et al. 2010; Ma et al. 2010; Brodoehl et al. 2012; Focke et al. 2011; Haller et al. 2012). Methodologies for developing predictions from imaging datasets vary. For example, some groups focus on individual regions, ignoring the vast majority of the image in order to focus on, for example, regions such as the substantia nigra (Gorell et al. 1995; Vaillancourt et al. 2009), or olfactory regions (Brodoehl et al. 2012). In some cases, multiple modalities are used to look at a single regions or a small number of regions to boost diagnostic yield (Péran et al. 2010). These region-specific approaches assume consistency of effects amongst all PD patients, which may not be a valid assumption. A few groups have attempted to perform full brain analyses to evaluate group differences using all the available imaging information (Skidmore et al. 2011a, b, c; Ma et al. 2010; Focke et al. 2011; Haller et al. 2012). However, while multiple methods show robust group-level differences between individuals with PD and individuals without PD, prediction of diagnosis on an individual level is usually less robust, and only a few studies are attempting to examine sensitivity or specificity for diagnosis (Skidmore et al. 2011a, b, c; Haller et al. 2012).
One possible limitation for generating predictive imaging maps may relate to the statistical techniques used for the analysis of imaging data. For example, cluster thresholding is a longstanding and accepted technique used to evaluate significance in imaging datasets (Forman et al 1995). Methods used by Forman et al. have been generally adopted for statistical testing of imaging data for the purposes of hypothesis-testing, and this method is still in widespread use (Leunissen et al. 2013; Monti et al. 2013; Junger et al. 2013; Gallivan et al. 2013). However, the variability of the results derived by this technique to the voxel-wise thresholding criteria is well recognized (Nichols and Hayasaka 2003; Nichols and Hayasaka 2003; Bennet et al. 2009; Smith and Nichols 2009). Our earlier work disclosed that individual subject variability within an imaging dataset can additionally have a significant effect. Specifically, leaving out individual subjects from modest sized analyses can result in substantial changes in the probability of individual voxels exceeding a statistical threshold. In addition, reliability on a regional basis of voxels to exceed a statistical threshold has an effect on the ability of a region to predict group membership of individuals within a given dataset (Skidmore et al. 2011a, b, c).
Univariate techniques have long assumed that physical proximity (as judged by the size of a region of interest exceeding a certain statistical threshold) has an intrinsic value in distinguishing signal from noise in large imaging datasets (Forman et al. 1995). Multivariate techniques such as principal component analysis (e.g. see Eidelberg 2009) examine the spatial covariance of the whole brain data structure for the purposes of identifying characteristic disease specific patterns rather than isolated anatomical deviations (e.g. see Eidelberg 2009). These methods have been primarily successful when applied to steady-state functional data such as in Positron Emission Tomography (PET) imaging, but have had limited success in DTI data thus-far (see e.g., Caprihan et al. 2008), possibly because of difference in signal to noise ratio on a voxel-by-voxel basis between PET images and DTI imaging. Since regional averaging effects might improve signal-tonoise issues in DTI imaging, we wished to explore alternative techniques that explicitly allowed regional statistical relationships (e.g. Regions of Interest) to continue to play a role in selection of the voxels for the purposes of developing a statistical map, while controlling for individual subject effects.
Bootstrapping, using a univariate region-based approach, is a procedure that may be well suited for this purpose. Bootstrapping refers to a class of statistical methods that use resampling to generate an empirical estimate of population distribution. Classical bootstrapping, as defined by Efron et al. (Efron 1979) is similar but not identical to other permutation methods, which merely provide the probabilities of an occurrence. Bootstrapping may be distinguished from other permutation methods methodologically by two factors: 1) relative robustness as a measure, (bootstrapping can be applied with minimal assumptions to even complex datasets), and 2) generating as a principal output estimates of confidence intervals and standard error within the dataset (see DiCiccio and Romano 1989).
In this paper, we estimate the capacity of a bootstrapped analysis approach to generate a predictive map using real imaging data by comparing a straightforward bootstrapped process (using confidence intervals to define our regions of interest for the purposes of prediction), compared to a standard statistical mapping technique (Forman et al 1995). We also compare our previous predictive mapping strategy (Skidmore et al. 2011a, b, c) and discuss problems with this strategy that this bootstrapping procedure corrects. We generate this analysis in a dataset of clinical interest—evaluating how well we can distinguish PD from healthy controls in a DTI data set.
Materials and Methods
Subjects
In this study we initially recruited 20 subjects with PD and 23 healthy controls. After enrollment but before data analysis, one healthy control was excluded after developing a resting tremor that was levodopa responsive, leading to a diagnosis of PD, and thus, the final subject pool included 20 subjects with PD and 22 healthy controls (Demographics, Table 1). Disease severity and cognitive profile for all subjects with PD are evaluated 12–18 h after the last levodopa dose, in a practically defined “off” state. All PD subjects in the analyzed dataset had been followed clinically for two or more years and retained the same clinical diagnosis of levodopa-responsive Parkinson disease.
Table 1.
Demographics of sample
| Controla | PDa | P | |
|---|---|---|---|
| Number | 22 | 20 | |
| Age | 61±13 | 64±9 | P=0.40 |
| Gender (F/M) | 8 F/14 M | 3 F/17 M | P=0.22 |
| Cognitive profile | |||
| MMSE | 28±2 | 26±3 | p=0.02 |
| MOCA | 27±3 | 24±5 | p=0.04b |
| Trail making test | |||
| Part A | 28±8 | 59±36 | p=0.001b |
| Part B | 90±54 | 159±105 | p=0.01b |
| Stroop | |||
| Word | 97±5 | 92±11 | p=0.04b |
| Color | 76±14 | 64±22 | p=0.05b |
| Interference | 39±15 | 31±17 | p=0.11 |
| JLO | 26±5 | 23±6 | p=0.08 |
| Mood/Emotion | |||
| Marin apathy scale | 24±4 | 23±4 | p=0.47 |
| Hamilton depression | 8±5 | 13±7 | p=0.01 |
| Disease severity | |||
| H/Y(Off Med) | 3(1.5–5) | ||
| H/Y (On Med) | 2(1.5–3) | ||
| UPDRS-OffMed | |||
| Part I | 4±3 | ||
| Part II | 12±6 | ||
| Part III | 34±14 | ||
| Part IV | 3±2 | ||
| Total (Sum of I-IV) | 52±21 |
H/Y Hoehn/Yahr
UPDRS Unified Parkinson Disease Rating Scale
Continuous Data and Discrete Data (such as age or values on scored tests) are displayed as mean value or score with standard deviation. Display of gender data is self-explanatory. Hoehn and Yahr score is a form of categorical data, and is displayed as median score and range. UPDRS score was obtained In an “off medication” state for all subjects
Unequal sample variance
Imaging and Data Preprocessing
Imaging was performed on a Philips Achieva 3.0 T scanner (Phillips Medical systems, Best, The Netherlands) using a 2-dimensional acquisition with the parameters: b-value= 1000 s/ mm3, TE = 55 ms, TR = 11,304 ms, 32 directions, 66 slices with slice thickness = 2 mm, image matrix =112 × 112, with FOV of 224 mm and in-plane voxel-wise resolution of 2 mm × 2 mm. Currently, most common spatial normalization method used in the field is to calculate the diffusion tensor metrics in the native space then use FA or bo images to register to a common template (Theilmann et al. 2013; Melzer et al. 2013). There is no accepted method to use all tensor components (a vector field) for registration (Lauzon et al. 2013). In the case that the subjects studied considerably differ from the normal population (such as a pediatric population of certain age range—see Villalon et al. 2013) a population specific atlas can be used. We specifically recruited individuals with Parkinson disease without cognitive decline, a group not expected to differ significantly from a healthy population (Melzer et al. 2013). In this case a subject specific atlas would not be necessary nor useful.
Pre-processing was therefore performed to calculate fractional anisotropy (FA) for each subject. Specifically, the diffusion weighted images of the DTI dataset images were corrected for eddy current induced distortions using the eddy current correction routine in FSL (www.frnrib.ox.ac.uk/fsl/). The non-brain tissue was removed using brain extraction routine (BET2) in the FSL package. The FA maps were then calculated using the FSL routine DTIFIT for all subjects. We first registered b0 images to the Montreal Neurological Institute template (MNI-152: 1 × 1 × 1 mm3 ) using a 12-parameter affine transformation (FLIRT in FSL package). We then applied the same transformation to the FA maps to register them to MNI template space. The FA maps were then transformed to a format (“BRIK” and “HEAD” files) relevant to the Analysis of Functional Neuroimaging (AFNI - Cox 1996) program, which was used for further analysis, and the FA images were smoothed using a kernel of 5 mm (FWHM) in AFNI.
Statistical Analysis
We evaluated here the hypothesis that a bootstrapped analysis may generate a better predictive map. To accomplish this, we performed 42 analyses three times, using three different techniques. In each analysis, one subject, or one control, was left out once. We used the 42 analyses to generate sensitivity and specificity estimates, and a receiver-operator curve (ROC) for each of the three techniques. Our comparative measure for evaluation of various methods was predictive accuracy—specifically in this case area under the ROC curve (AUROC) compared as correlated curves. We can compare accuracy of each technique because each analysis is based on the same cases. We analyzed which approach generated the best statistical map to predict left out subjects. The three mapping strategies compared were:
Standard Cluster-Thresholding (Forman et al 1995).
The RMRD method, described previously (Skidmore et al 2011a,b).
A bootstrapped analysis (described in more detail below).
Two general considerations were important in generating our analyses. First, each type of analysis resulted in an identification of a Region or Regions of Interest that were significantly different in the comparison between the PD subjects and controls. Each of the three mapping strategies, however, while often agreeing on a general region of analysis, selected a different size and shape considered key or the basis of the Region of Interest. Differences in the size and shape of the regions chosen related in some part to the voxel-wise criteria (e.g.p<0.05, p<0.01, p<0.001)used in the selection, as well as the specific method (#1,2, and 3 above) used. The RMRD method and the bootstrapped method were designed to improve reliability in determining the borders of specific regions of interest used to develop prediction; the RMRD improved reliability by using the full analysis to constrain the regions used for prediction (and we discuss limitations of this approach later), while the bootstrapped method was model-free at the level of each individual analyses (e.g. a full analysis did not inform any of the results of the 42 independent leave one out, analyses).
Secondly, in order to make a relevant comparison, a uniform measure was needed to compare the accuracy of techniques. Each method selected regions of interest; the regions, as developed by the specific method, were then used to generate a prediction. The uniform technique we use follows the following steps:
Identification of Regions (Method Specific).
Normalization
Regional Averaging
Variable Thresholding
Comparison with Left Out Subject Value in Defined Regions
Prediction and calculation of ROC and AUROC
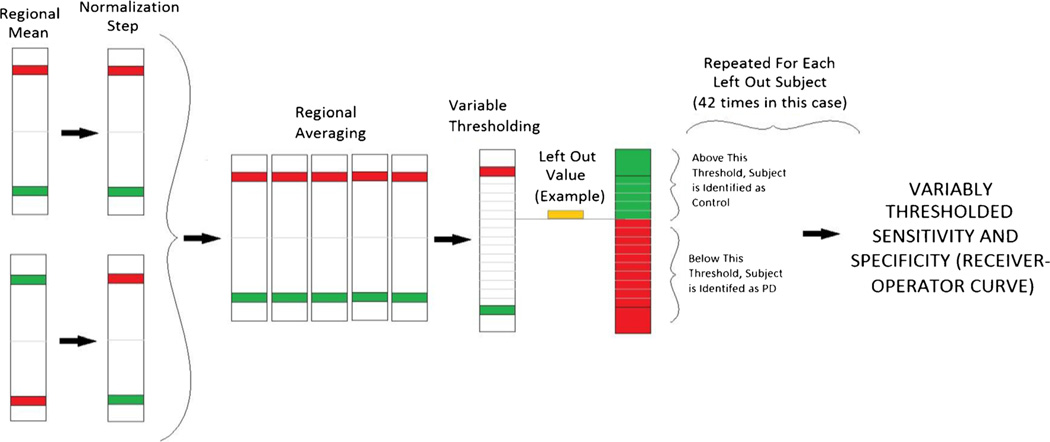
These steps are recapitulated in Fig. 1. Each analysis method generates distinct regions of interest for analysis. Once regions are selected, we use an identical method to define predictive accuracy across all methods. For the purposes of visual display, assume red band represents the PD regional mean; the green band represents the control regional mean. There is a normalization step to normalize the direction of prediction for each region. We can then evaluate the capacity of the selected region to predict the identity of the subject (illustrated as an orange rectangle). On the far left, note we demonstrate a generated regional mean (take in this case “Red” to be the PD mean, and “Green” to be the control mean) for a particular Region of Interest. With respect to the normalization step, once we select Regions of Interest, the selected regions may differ in one of two fashions. Either, the mean fractional anisotropy may be DECREASED in the region in individuals with PD with respect to healthy controls, OR, the mean fractional anisotropy may be INCREASED in the region in individuals with PD compared to the controls. In order to use all the available information, we must therefore adjusted for the direction of difference. We therefore normalize the difference of the means to create a unidirectional relationship (equivalent to taking the absolute value of the difference—see Normalization Step).
Fig. 1.
Uniform method for analyzing regions of interest. Each analysis method generates distinct regions of interest for analysis. Once regions are selected, we use an identical methods to define predictive accuracy across all methods. For the purposes of visual display, assume red band represents the PD regional mean; the green band represents the control regional mean. There is a normalization step to normalize the direction of prediction. Variable thresh-holding allows us to evaluate the capacity of the selected region to predict the identity of the subject (illustrated as an orange rectangle). In this case, the prediction favors a diagnosis of PD (red) at many thresholds but adopting a more stringent threshold results in identification as a control subject (green). Accuracy of the prediction compared to the known identification of the left out subject allows us to generate sensitivity and specificity across multiple thresholds. With multiple subjects, this allows us to generate a receiver operator characteristic curve
Combining regional findings, for each analysis we generated a prediction. We have in most cases generated multiple Regions of Interest to be used for our prediction. Mean values for each calculated region are calculated for each left out subject. A number of distance measures could be considered to define our prediction, but pragmatically for this study we simply average all the normalized Regions of Interest to generate a single metric. Thus, no region is weighted more heavily than another, since the method choses regions that are presumed to contribute information equally to discrimination. Using variable thresholding, we generate an estimate at each threshold as to whether the subject would be rated as a PD subject, or as a control subject. In the case illustrated in Fig. 1 (with the small Orange box represents the mean normalized FA value of the left out subject), the subject’s mean value would result in the subject being rated as PD subject at many thresholds, but as a control if we allow the threshold to more closely approach the PD mean (varying this threshold would therefore allow one to increase the specificity or sensitivity of diagnosis). As we repeat this analysis 42 times, we then are able to generate a Sensitivity measure (the likelihood that an individual with PD is accurately diagnosed with PD), and a Specificity measure (the likelihood that a Control subject is accurately identified as a control or not PD), for each analysis method, across all thresholds.
Our three methods differed primarily in the way that they select Regions of Interest, and the precise voxels considered part of each Region of Interest; we discuss this in more detail below.
Standard Cluster-Thresholding
Cluster-thresholding is a longstanding and accepted technique used to evaluate significance in imaging datasets (Forman et al 1995). The method used by Forman et al. is still in common use (Leunissen et al. 2013; Monti et al. 2013; Junger et al. 2013; Gallivan et al. 2013), although the non-linear sensitivity of the results derived by this technique to the voxel-wise thresholding criteria is well recognized (Nichols and Hayasaka 2003; Nichols and Hayasaka 2003; Bennet et al. 2009; Smith and Nichols 2009). We used a straightforward adaption of this technique. Following the general processes outlined by Forman et al. and using a Monte-Carlo analysis, we defined significant cluster size on a brain-wide basis for the following voxel-wise thresholds: p<0.05, p<0.01, and p<0.001. We then left out each subject once, resulting in 42 independent analyses. A single, voxel-wise t-test was then performed for each of the 42 analyses. Thresholding was performed at each voxel-wise statistical threshold, with each voxel being characterized as above, or below, threshold. Regions were then selected based on whether they were above or below the cluster-size threshold. In order to keep our technique as simple as possible, clustering was performed using a nearest-neighbor method—e.g. voxels had to be directly contacting each other in order to be assumed to be a cohesive entity from the perspective of clustering, and no adjustment for the size or shape of the cluster was performed (e.g., two cohesive globular or ovoid clusters joined by a relatively narrow “neck” could be considered a single cluster in this approach). A simplified clustering method was performed in part because we wished to avoid post-hoc adjustments to the analysis. We selected Regions of Interest for analysis as follows:
For the voxel-wise threshold of p<0.05, the largest single Region of Interest that met cluster size threshold (based on our Monte-Carlo evaluation, our cluster size threshold was 3971 voxels) was selected develop the mean for each PD and Control group, and assessed for the left out subject.
For the voxel-wise threshold of p< 0.01, we selected up to five Regions of Interest (the largest five) meeting the cluster size threshold (in this case, 771 voxels).
For a voxel-wise threshold of p<0.001, we allowed up to 50 Regions of Interest meeting the cluster-size threshold (233 voxels) to be selected (at this threshold, however, in all cases we identified only 1–3 Regions of Interest meeting both the voxel-wise and cluster-size threshold criteria).
Each identified Region of Interest was used to develop a mean FA value, which was then normalized as described above (Fig. 1) and used to generate an ROC curve for the Cluster Thresholding method, at each voxel-wise threshold.
Regional Mapping of Reliable Difference (RMRD) Method
We fully discuss the RMRD method in previous publications (Skidmore et al. 2011a, b, c). Briefly, in this study we first generated a full, two sample t-test, using standard cluster-thresholding to identify regions of interest in which the two samples differed. Subsequently, each subject was left out once, and a 2-sample t-Test was once again performed. Rather than threshold by cluster size, within these iterative maps, Regions of Interest were identified in accordance with degree of overlap with the center of mass of Regions of Interest identified in the primary analysis. In this case, we evaluated two voxel-wise thresholds (p<0.01 and p<0.001) to define potential regions of difference in the full sample, and these thresholds were also used within each “left out” analysis to create the predictive maps for predicting the left-out subjects. As with 2.3a, the selected regions were used to generate Sensitivity and Specificity estimates at each threshold and an ROC curve.
Bootstrap Analysis
We developed a new statistical algorithm using bootstrapping to evaluate if we could improve prediction compared to a standard Cluster Thresholding approach and our previous RMRD algorithm evaluated using leave one out approaches. With a bootstrapping, we assume that an inference about a population distribution S from sample data can be modeled by resampling the data. Formally, with bootstrapping we expect that the true probability distribution within a full population, S, given the original data, is analogous to the empirical distribution of the resampled data, Ŝ, determined from the resampled data. Since we know the distribution of Ŝ, we can generate confidence intervals, and use these to make an inference about the true sample distribution S. The bootstrap analysis described by Efron does not require a null hypothesis, but does make one important assumption embedded in many statistical models—that the distribution of the true sample can be approximated by a normal distribution. With a bootstrapped analysis, we posit that, under the normality assumption, bootstrapping will better approximate the true sample distribution, allowing us to better define the borders of regions of interest that might accurately identify left out subjects.
Creating an Individual Bootstrapped Analysis
Bootstrapping uses selection with replacement to generate a new sample. The technique can obviously be used with any number of subjects, but works best when the sampling frame is large. In our case, starting with our full sample, H, comprised of n subjects (in this case 20 subjects with PD and 22 healthy controls), we created a new sample H using random selection with replacement. The new sample in this case is also comprised of 20 PD images and 22 control images. However, with random selection and replacement approximately 11 (standard deviation~+/−2) subjects with PD and approximately 12 (standard deviation again~+/−2) healthy controls are used to generate this new sample H, with some subjects deleted and others duplicated one or more times within the new sample. In each case, subjects that are within the analysis, and subjects excluded from the analysis, are recorded for the purposes of validation (see 2.3c.4 below). In a larger sample, of course there is less overlap amongst samples, but process and concepts are the same.
Defining the Statistical Measure to be Bootstrapped
Any statistical measure can be the target of a bootstrapped analysis, however the technique is intensive from a computational and memory or storage perspective. For the purposes of our analysis, we performed a t-test with each new sample on each voxel; let us represent the 3-dimensional map generated by this statistical analysis by the term Ĥ. In this case, Ĥ represented, in aggregate, the set comprised of each individual voxel within the 3-dimensional map, as identical statistical operations are performed in parallel to each voxel, and no analysis is performed across voxels until the clustering step. Each t-test was then thresholded, defining voxels in which the PD group differs from the control group at stringency of p<0.05. A binary map, Ĥb comprising all voxels statistically significant at the defined stringency level for each analysis “n”, which we can define as Ĥb(n) for each analysis “n”, are generated. We term this map a binary map because our threshold defines each voxel in the map either as 0 (below threshold) or 1 (above threshold).
Defining the Number of Bootstrapped Iterations
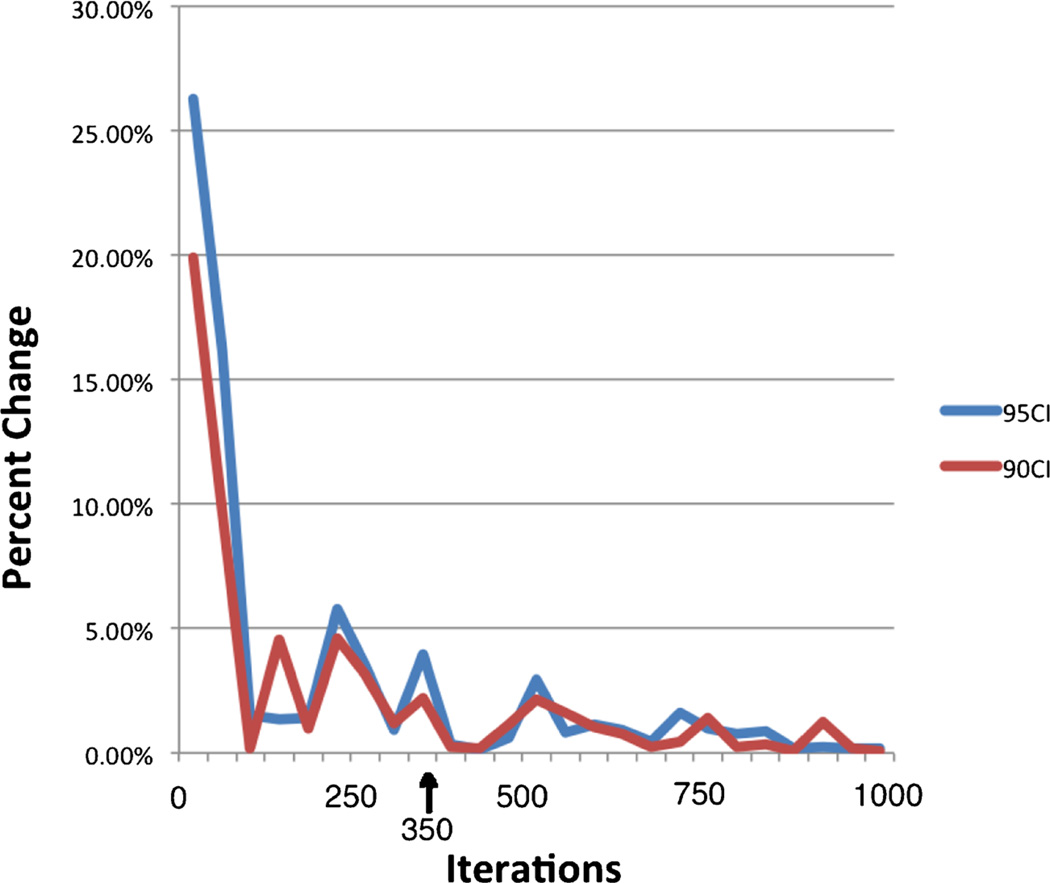
The number of iterations required for an optimal bootstrapping operation is undefined, and is dependent on the desired level of estimate precision. We wished to perform sufficient iterations to obtain a stable regional estimate of the shape and size of Regions of Interest, and as a surrogate measure of this defined that a shift in the estimated number of voxels meeting criteria of <+/−5 % should be sufficient to allow us to evaluate our hypothesis. Empirically, we find that in all cases by approximately 350 iterations we develop stability in the number of voxels estimated to meet our confidence interval criteria at both the 90 % and the 95 % confidence interval (Fig. 2) and this would vary with the size of the underlying sampled population of cases and homogeneity amongst those cases and size of the resultant population. We required about 50 iterations per subject (a total of 2100 iterations) to obtain sufficient samples in which all 42 subjects were left out of at least 350 analyses (range ~350 to 1,050). Our bootstrapped sample is therefore based on 2100 iterations.
Fig. 2.
Percent change in predicted “Significant” area by number of bootstrapped iterations. Within this dataset, and using a cutoff of 95 and 90 % voxel-wise confidence interval, area predicted to be “above threshold” stabilized markedly over the first 100 iterations. Approximately 350 iterations were required to stabilize predictions to an arbitrarily defined baseline with change of <+/−5 %. Arrow marks approximate lower limit of iterations among “left out” subjects
Creating the Bootstrapped Statistical and Validation Maps
A full sample bootstrapped map, ŜF, including all subjects, is created for the purposes of displaying results, and includes a summation of all individual Ĥb(n) binary maps, formally:
In addition, for each subject, a bootstrapped map comprising only those maps in which a particular individual is left out of the all analyses can also be generated. Formally, we can define, given the 42 subjects in our data pool, for individual i in the set a = {1, 2, 3, … 42}, the specific bootstrapped map Ŝj comprises all bootstrapped results bi, with the number of iterations in which i is not present being defined as the set ni = {0, 1 … x}, formally:
These summary maps can be normalized to a percentile rank per voxel for each map, which essentially gives us our confidence interval that a particular voxel is significantly above the defined threshold, given the assumption of normality of the fractional anisotropy signal distribution within each subject grouping (e.g. the PD group and the control group).
Selecting Regions in Order to Test Bootstrap Validity
To estimate the validity of the bootstrapped method to predict left-out subjects, we use a confidence interval (rather than a t-statistic) to define the borders of our Region(s) of Interest. There are no specific criteria for selecting the number of regions in a bootstrapped model to accept for the purposes of prediction, and we selected the number empirically. In this paper, we elected to use the largest 5 Regions of Interest (comparable to the number of Regions of Interested selected using standard Cluster thresholding and using the RMRD method) for the purposes of generating a prediction of left out subjects The borders of each Region of Interest for each of the 42 individual subject bootstraps was generated using a confidence interval of 90 %, and 95 %.
Results
Prediction of Left Out Subjects
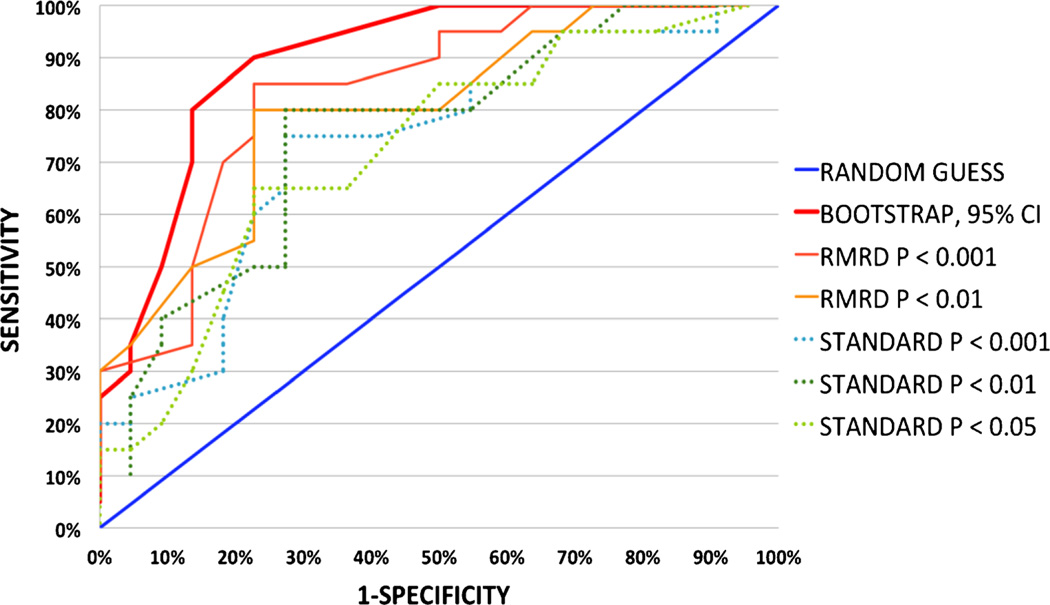
Using variable thresholding, a Receiver-Operator Characteristic Curve was determined for each method (Fig. 3). Accuracy of prediction for the bootstrapped analysis at both the 90 % confidence interval and the 95 % confidence interval essentially overlap; the ROC curve for the 95 % confidence interval is presented. Area under the receiver-operator curve (AUROC) for each method is shown in Table 3. Summarizing the table, AUROC for the bootstrap analysis is 0.897 at a confidence interval of 90 % and 0.901 at a confidence interval of 95 %. AUROC for the RMRD and for standard cluster-thresholding is less as is shown in Table 2.
Fig. 3.
Receiver-operator characteristic curve derived from DTI-FA maps of 20 PD & 22 healthy controls left-out of analysis pool. Receiver operator characteristic curve derived from DTI-FA maps of 20 PD & 22 healthy controls for detection of subjects left out of analysis. Cluster-thresholding at various voxel-wise thresholds (dotted) provide marginal prediction in our hands. The PI’s RMRD method had improved accuracy (dashed lines). A bootstrapping approach (heavy solid red line) was the most predictive
Table 3.
Number/Proportion of voxels deemed “Significant” by voxel-wise and cluster-wise thresholding, by analysis method
| Method | Voxel-wise stringency requirement |
Cluster-size stringency requirement |
Cluster numberΨ actual (Maximum) |
Mean # voxels “Significant” |
Percent of total voxels |
|---|---|---|---|---|---|
| Cluster-Threshold | P<0.05 | 3971 (each analysis) | 1 (1) | 25,964 | 1.4% |
| P<0.01 | 771 (each analysis) | 4–5 (5) | 9826 | 0.5 % | |
| P< 0.001 | 233 (each analysis) | 3 (50) | 1714 | 0.09 % | |
| RMRD | P<0.01 | 771 (full analysis) | 5 (5) | 8668 | 0.45 % |
| P< 0.001 | 233 (full analysis) | 3 (50) | 1300 | 0.068 % | |
| Bootstrap | >90 % of T-Tests | None | 5 (N/A) | 6784 | 0.35 % |
| >95 % of T-Tests | None | 5 (N/A) | 4265 | 0.22 % |
In both cluster-threshold analysis and the RMRD method clusters are selected on both a voxel-wise and cluster size stringency requirement. There is at present no defined cluster-size stringency requirement for a bootstrapped process; five regions were selected empirically to test prediction accuracy
Table 2.
Effectiveness, by method, of predictive mapping for detection of left out subjects
| Method | AUROC for detection of “left out” subject |
|---|---|
| Bootstrap, 95 % Confidence Interval | 0.901 |
| Bootstrap, 90 % Confidence Interval | 0.897 |
| RMRD Method, threshold p<0.001 | 0.83 |
| RMRD Method, threshold p<0.01 | 0.82 |
| Standard Cluster-Thresholding, p<0.001 | 0.73 |
| Standard Cluster-Thresholding, p<0.01 | 0.75 |
| Standard Cluster-Thresholding, p<0.05 | 0.72 |
Map Characteristics
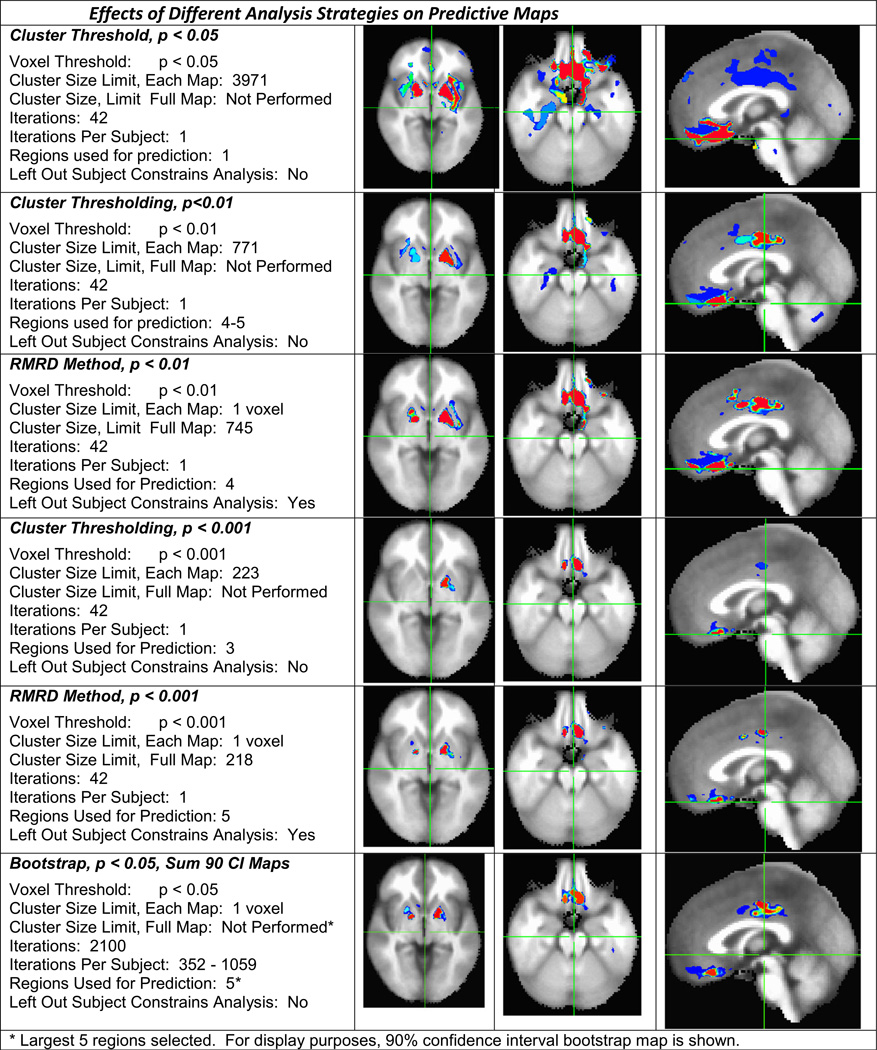
Each method resulted in differences in the number and location of voxels selected for the purposes of generating a prediction (see Table 3 for summary). Statistical maps using each method were developed and are displayed in Fig. 4. It can be readily appreciated, first, that none of the methods we use “invent” data—that is to say happily that there is a remarkable consistency among analysis techniques in the location of regions defined as significant. It is however also notable from an examination of the figure that both individual voxels and regions are emphasized, or de-emphasized, depending on the analysis threshold, and method chosen. We note that, in our hands, increasing statistical stringency of standard cluster-thresholding from p<0.05 to p<0.001 did not improve prediction of left out subjects although the sample size itself is small. Conversely, the bootstrapped analysis best selected those voxels associated with regions that were predictive of the “left out” subject.
Fig. 4.
Effects of different analysis strategies on predictive maps
Differences Between PD and Control Sample
Since the bootstrapped analysis generated Regions of Interest that best predicted the left-out subject, we used this analysis to define regional differences between the samples. Table 4 delineates results of bootstrapping. Turning to Table 4, we note that, using our algorithm, sensitivity and specificity of individual selected regions met or exceeded the best results of all regions generated using standard cluster-thresholding (e.g. AUROC > 0.75 for each region), and combining regions resulted in AUROC = 0.901 at a confidence interval of 95 %. In regions selected using our bootstrapping algorithm, it is notable that fractional anisotropy is increased in individuals with PD in our sample. This finding is likely related to a significant distinction in our preprocessing strategy and goals compared to other groups, and we will discuss this in more detail in the discussion Section.
Table 4.
Significant regions defined by bootstrapped analysis (Bilateral)
| Locationa | Sizea | Mean fractional anisotropya | Sensitivity/Specificity | ||||
|---|---|---|---|---|---|---|---|
| Region | RL | AP | IS | Voxels (mm3) | PD | Control | Regional AUROC |
| Rectal GyrusŦ | 1 | −25 | −21 | 1457 | 0.24+/−0.03 | 0.20+/−0.02 | 0.82 |
| Middle CingulateŦ | 1 | 18 | 38 | 1093 | 0.20+/−0.05 | 0.15+/−0.04 | 0.75 |
| Left Putamen | 18 | −6 | −3 | 1066 | 0.30+/−0.04 | 0.24+/−0.03 | 0.82 |
| Right Putamen | −18 | −10 | −6 | 411 | 0.26+/−0.04 | 0.20+/−0.03 | 0.82 |
| Left Thalamus | 9 | 21 | 7 | 238 | 0.28+/−0.02 | 0.25+/−0.02 | 0.80 |
| Mean of Regionsb | 0.25+/−0.02 | 0.21+/−0.02 | 0.901 | ||||
Raw results involved creating 42 separate renditions of the above tables. However, for the sake of clarity, we present location and size of regions derived from the full analysis (generated by taking the 90 % confidence interval from a map comprised of adding all 2,100 bootstrapped analyses). Similarly, mean and standard deviation of fractional anisotropy are shown based on the full bootstrapped analysis. Conversely, sensitivity and specificity (AUROC) is based on each of the 42 individual “left out” analysis
Mean value of each region, rather than mean of individual voxels (which would have weighted predictions to favor larger regions) was used to generate a “mean of regions” for the purposes of prediction
Discussion
The goal of our study was twofold. First, we had an overall goal of evaluating the feasibility of using diffusion tensor imaging for the purposes of identifying the presence of PD. In this specific work, we use a region of interest based approach to distinguish PD from a control sample, and we evaluate if a bootstrapped analysis allows us to better define the borders of our regions of interest from the perspective of identifying left-out subjects for validation. We find that a bootstrapped approach can generate more robust predictive maps (AUROC 0.901 at our 95 % confidence interval). We would interpret the improved prediction using our bootstrapped methodology as evidence that the bootstrapping constrained selection, shape, and precise localization of regions to maximize identification of those voxels within the selected regions that would be most likely to be predictive of the shape, size, and location of a similar identifying region in a new subject. The approach improves on standard cluster-thresholding, and also provides an improved prediction compared to our previously published RMRD method (Skidmore et al 2011a, b, c). In addition, unlike the RMRD method, we do not constrain our results by an initial analysis, removing some a feature in the RMRD method that could lead to circularity in the analysis and over-optimistic estimates of the effectiveness of the RMRD method to predict new data. We find again in this analysis that significance and reliability are dissociated properties in brain images, and that focusing on defining what regions of an image are reliably different leads to better prediction of new data. We accordingly propose consideration of a general standard in statistical analysis of brain imaging data, focusing on clinically relevant criteria of reliability of prediction of new data.
Our findings of increased fractional anisotropy in several regions are ostensibly distinct from the findings of other laboratories that have evaluated white matter integrity in Parkinson disease. For example, both Zhang et al., and Zhan et al. studied white matter integrity in PD using voxel-based morphometry, and found decreased FA in a number of regions throughout the brain (Zhang et al 2011; Zhan et al. 2012). A close examination of the papers in question, however, reveals that our analytical goals were quite different from those of Zhan and Zhang. In their studies, performed on high-performance 4T MRIs, rigid thresholding was used to remove gray matter (for example, voxels with signal <0.20 were excluded from analysis). To maintain precise localization of often narrowly defined white matter tracts, smoothing of the data was not performed. The principal goal of the research of these two groups was the valuable, and valid goal of specifically evaluating white matter integrity in PD. However in removing large regions of the image to isolate only white matter tracts much information that might be useful for differentiating the samples may also have been removed.
In our case, we were not specifically focused on the goal of understanding white matter integrity in PD, but rather on the more prosaic goal of determining whether we could use an FA map to predict group identity. Our results may differ from those of Zhan and Zhang, due to the simple fact that we retained a significant amount of fractional anisotropy data within our images, information that was discarded by Zhan and Zhang. It can be noted, for example, that the mean FA value of several of our regions of largest FA difference (including the rectal gyrus and the supplementary motor cortex) were in healthy controls below the predetermined threshold of both labs (e.g. the regions would have been discarded and not included in their analyses). It would be reasonable to posit that in these regions FA values represented a mixture of gray and white matter signal. It is therefore entirely possible that the “increases” in FA in PD discerned by our analysis might represent a decrease in gray matter in the regions identified in at least some cases. Further study will be required to determine the nature of the underlying structural differences that might be responsible for the FA differences within our sample.
A further limitation of our study is our sample size, and the nature of our sample. Our PD sample pool included only 20 individuals with late mild to moderate PD, with disease duration between 5 and 12 years. All subjects clearly had defined PD under chronic treatment with dopaminergic agents, that would be identifiable by brief clinical examination by any qualified neurologist. An additional interest in collection of the dataset was the causes of apathy in PD (Skidmore et al 2011c), and so the presence of apathy is relatively enriched in our data pool. Nevertheless, unless there is a method by PD interaction, our use of all three methods applied to the same individuals should still allow valuable conclusions. The validity of a map generated by such a population to identify PD in unmedicated individuals early in disease (an eventual goal of analysis) is open to question, but it is likely that sensitivity and specificity will suffer, perhaps dramatically.
We further are limited by the nature of our goals in this study—we show that we can segregate PD from healthy controls, but do not show that we can differentiate PD from other forms of parkinsonism. More specifically, we show we can segregate individuals with well-defined clinical disease from individuals who do not have PD; as we will discuss below, the clinical population we study is therefore quite distinct from a clinical population that would be of general clinical relevance—individuals in early stages of symptoms, where differential diagnosis and prognosis is a clinical question of significant relevance.
Finally, our study was a single-site study, performed using a specific 3 T Phillips MRI, with a defined obsolescence date. As is common in the field, we standardized our data according to a uniform atlas, and we face the usual issue of variability in size and shape of the brain of each subject. We used an established and valid method of mapping to the atlas that may however be distinct from methods used by other laboratories. Our laboratory is not alone in managing these types of difficulties, which are common features in a field of study in which individual variability in the analytical approach dramatically colors research output.
Given the above caveats, it would be inappropriate to conclude that we have discovered a “diagnostic map” for PD. Rather, we present an approach to analysis of imaging that may begin to lead towards better standardization and yields results that are more closely aligned with clinically relevant outcomes (prediction). Given that we show excellent sample segregation using only one aspect of the DTI image— fractional anisotropy (FA), we also show that full brain analysis of DTI images may be a fruitful area of study for developing biomarkers for PD. However, a larger sample group, collected across multiple sites will likely be required to generate predictive maps relevant across sites, and showing that PD can be differentiated from parkinsonism would be an important additional step. If identification of individuals with early-stage disease is a goal, then maps should be generated in a dataset of individuals with early disease. We present a proof of concept therefore; further optimization is likely to occur over time.
Our brute force approach (bootstrapping) applied here works as a univariate voxel based algorithm, and may suggest that bootstrapping can also be extended to multivariate covari-ance network based analysis of voxel interconnectivity such as SSM-PCA where bootstrapping has been previously used to validate predictive network pattern maps in PET images (Tang et al 2010a, b; Eidelberg 2009; Mure et al. 2011; Huang et al. 2007, 2008; Habeck et al. 2008). Combined approaches, using bootstrapping to constrain regions selected for analysis, might also bear fruit. Further, while in this initial analysis, we used a “one-voxel, one vote” analysis, creating averages for each region based on equal weighting of all voxels in the identified cluster, our current approach creates complex maps that are amenable to weighting. Finally, with respect to the choice of imaging technique, we evaluated the DTI FA signal, however FA is only a small fragment of information available in DTI images, and other imaging types, including cortical thickness maps, resting fMRI, p-CASL images, and a host of new and developing techniques for imaging brain iron and other characteristics will likely all contribute to improving the direct clinical relevancy of brain imaging.
In summary, we show that it is possible, using an iterative, full brain, bootstrapped analysis, to generate robust DTI brain maps that are predictive of new data that was generated and processed in a similar fashion. We propose that methods of statistical analysis focused on reliability of prediction of new data may over time be more useful than standard statistical methods in advancing brain imaging towards the goal of improved clinical relevancy.
Information Sharing Statement
The full de-identified dataset used to develop these research results is available for research purposes. Access must be approved and is generally limited to use for the following purposes: new hypothesis generated research, replication of results, or research collaboration. Unrestricted use of this data is available to individuals associated with a University or research center. General public access of this data is not generally available but exceptions can be made on a case by case basis with justification. Please leave a comment on our website to make arrangements to obtain the data: http://blogs.uabgrid.uab.edu/dti/ or contact the principal author at fskidmor@uab.edu
Acknowledgments
Funding for this project was provided by the nonprofit fund Hawg Wild for the Cure with special thanks to Capital City Harley Davidson and Gainesville Harley Davidson, as well as by the National Center for Advancing Translational Sciences of the National Institutes of Health under award number UL1TR00165. Additional funding for this project came from the Micanopy Doc Hollywood Fund.
References
- Bennet CM, Wolford GL, Miller MB. The principled control of false positives in neuroimaging. Social Cognitive and Affective Neuroscience. 2009;4(4):417–422. doi: 10.1093/scan/nsp053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brodoehl S, Klingner C, Volk GF, Bitter T, Witte OW, Redecker C. Decreased olfactory bulb volume in idiopathic Parkinson’s disease detected by 3.0-Tesla magnetic resonance imaging. Movement Disorders. 2012;27(8):1019–1025. doi: 10.1002/mds.25087. [DOI] [PubMed] [Google Scholar]
- Caprihan A, Pearlson GD, Calhoun VD. Application of principal component analysis to distinguish patients with schizophrenia from healthy controls based on fractional anisotropy measurements. Neurolmage. 2008;42(2):675–682. doi: 10.1016/j.neuroimage.2008.04.255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cox RW. AFNI: software for analysis and visualization of functional magnetic resonance neuroimages. Computers and Biomedical Research. 1996;29:162–173. doi: 10.1006/cbmr.1996.0014. [DOI] [PubMed] [Google Scholar]
- DiCiccio TJ, Romano JP. A review of bootstrap confidence intervals. Journal of the Royal Statistical Society, Series B. 1989;50:338–354. [Google Scholar]
- Efron B. Bootstrap methods: another look at the jackknife. Annals of Statistics. 1979;7:1–26. [Google Scholar]
- Eidelberg D. Metabolic brain networks in neurodegenerative disorders: a functional imaging approach. Trends in Neurosciences. 2009;52(10):548–557. doi: 10.1016/j.tins.2009.06.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Focke NK, Helms G, Scheewe S, Pantel PM, Bachmann CG, Dechent P, et al. Individual voxel-based subtype prediction can differentiate progressive supranuclear palsy from idiopathic Parkinson syndrome and healthy controls. Human Brain Mapping. 2011;52(11):1905–1915. doi: 10.1002/hbm.21161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Forman SD, Cohen JD, Fitzgerald M, Eddy WF, Mintun MA, Noll DC. Improved assessment of significant activation in functional magnetic resonance imaging (fMRI): use of a cluster-size threshold. Magnetic Resonance in Medicine. 1995;55(5):636–647. doi: 10.1002/mrm.1910330508. [DOI] [PubMed] [Google Scholar]
- Gallivan JP, McLean DA, Flanagan JR, Culham JC. Where one hand meets the other: limb-specific and action-dependent movement plans decoded from preparatory signals in single human frontoparietal brain areas. The Journal of Neuroscience. 2013;30(5):1991–2008. doi: 10.1523/JNEUROSCI.0541-12.2013. 33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gorell JM, Ordidge RJ, Brown GG, Deniau JC, Buderer NM. Helpern. Increased iron-related MRI contrast in the substantia nigra in Parkinson’s disease. Neurology. 1995;459(6):1138–1143. doi: 10.1212/wnl.45.6.1138. [DOI] [PubMed] [Google Scholar]
- Habeck C, Foster NL, Perneczky R, Kurz A, Alexopoulos P, Koeppe RA, et al. Multivariate and univariate neuroimaging biomarkers of Alzheimer’s disease. Neurolmage. 2008;40:1503–1515. doi: 10.1016/j.neuroimage.2008.01.056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haller S, Badoud S, Nguyen D, Barnaure I, Montandon ML, Lovblad KO, et al. Differentiation between Parkinson disease and other forms of Parkinsonism using support vector machine analysis of susceptibility-weighted imaging (SWT): Initial results. European Radiology. 2012 doi: 10.1007/s00330-012-2579-y. http://us.datscan.com/patient/support-resources/locate-datscan-imaging-center. [DOI] [PubMed]
- Huang C, Mattis P, Tang C, Perine K, Carbon M, Eidelberg D. Metabolic brain networks associated with cognitive function in Parkinson’s disease. Neurolmage. 2007;34(2):714–723. doi: 10.1016/j.neuroimage.2006.09.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang C, Mattis P, Perine K, Brown N, Dhawan V, Eidelberg D. Metabolic abnormalities associated with mild cognitive impairment in Parkinson disease. Neurology. 2008;70(16 pt 2):1470–1477. doi: 10.1212/01.wnl.0000304050.05332.9c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Junger I, Pauly K, Brohr S, Birkholz P, Neuschaefer-Rue C, Kohler C, et al. Sex matters: neural correlates of voice gender perception. Neurolmage. 2013;79:275–287. doi: 10.1016/j.neuroimage.2013.04.105. [DOI] [PubMed] [Google Scholar]
- Lauzon, et al. Simultaneous analysis and quality assurance for diffusion tensor imaging. PLOS One. 2013;8(4):e61737. doi: 10.1371/journal.pone.0061737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leunissen I, Coxon JP, Geurts M, Caeyenberghs K, Michiels K, Sunaert S, et al. Disturbed cortic-subcortical interactions during motor task switching in traumatic brain injury. Human Brain Mapping. 2013;34:1254–1271. doi: 10.1002/hbm.21508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma Y, Huang C, Dyke IP, Pan H, Alsop D, Feigin A, et al. Parkinson’s disease spatial covariance pattern: noninvasive quantification with perfusion MRI. Journal of Cerebral Blood Flow and Metabolism. 2010;30(3):505–509. doi: 10.1038/jcbfm.2009.256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Melzer, et al. White matter micro structure deteriorates across cognitive stages in Parkinson disease. Neurology. 2013;80:1841. doi: 10.1212/WNL.0b013e3182929f62. [DOI] [PubMed] [Google Scholar]
- Monti MM, Pickard ID, Owen AM. Visual cognition in disorders of consciousness: from VI to top-down attention. Human Brain Mapping. 2013;34:1245–1253. doi: 10.1002/hbm.21507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mure H, Hirano S, Tang CC, Isaias IU, Antonini A, Ma Y, et al. Parkinson’s disease tremor-related metabolic network: characterization, progression, and treatment effects. Neurolmage. 2011;54:1244–1253. doi: 10.1016/j.neuroimage.2010.09.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nichols T, &Hayasaka S. Controlling the family wise error rate in functional neuroimaging: a comparative review. Statistical Methods in Medical Research. 2003;12(5):419–446. doi: 10.1191/0962280203sm341ra. [DOI] [PubMed] [Google Scholar]
- Péran P, Cherubini A, Assogna F, Piras F, Quattrocchi C, Peppe A, et al. Magnetic resonance imaging markers of Parkinson’s disease nigrostriatal signature. Brain. 2010;33(11):3423–3433. doi: 10.1093/brain/awq212. [DOI] [PubMed] [Google Scholar]
- Shalom Michaeli S, Oz G, Sorce DI, Garwood M, Ugurbil K, Majestic S, et al. Assessment of brain iron and neuronal integrity in patients with Parkinson’s disease using novel MRI contrasts. Movement Disorders. 2007;22(3):334–340. doi: 10.1002/mds.21227. [DOI] [PubMed] [Google Scholar]
- Skidmore FM, Yang M, Baxter L, von Deneen KD, Collingwood J, He G, et al. Reliability analysis of the resting state can sensitively and specifically identify the presence of Parkinson disease. Neurolmage. 2011a;75:249–261. doi: 10.1016/j.neuroimage.2011.06.056. [DOI] [PubMed] [Google Scholar]
- Skidmore FM, Spetsieris P, Yang M, Gold M, Heilman KM, Collingwood J, et al. Diagnosis of Parkinson’s disease using resting state fMRI. Poster LB22, Movement Disorders, Toronto. 2011b Jun [Google Scholar]
- Skidmore FM, Yang M, Baxter L, von Deneen K, Collingwood J, He G, et al. Apathy, depression, and motor symptoms have distinct and separable resting activity patterns in idiopathic Parkinson disease. Neurolmage. 2011c;81:484–495. doi: 10.1016/j.neuroimage.2011.07.012. [DOI] [PubMed] [Google Scholar]
- Smith SM, Nichols TE. Threshold-free cluster enhancement: addressing problems of smoothing, threshold dependence and localisation in cluster inference. Neurolmage. 2009;44(1):83–98. doi: 10.1016/j.neuroimage.2008.03.061. [DOI] [PubMed] [Google Scholar]
- Tang CC, Poston KL, Dhawan V, Eidelberg D. Abnormalities in metabolic network activity precede the onset of motor symptoms in Parkinson’s disease. Journal of Neuroscience. 2010a;30(3):1049–1056. doi: 10.1523/JNEUROSCI.4188-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang CC*, Poston KL*, Eckveer T, Feigin A, Frucht S, Gudesblatt M, et al. Differential diagnosis of Parkinsonism: a metabolic imaging study using pattern analysis. Lancet Neurology. 2010b;9:149–158. doi: 10.1016/S1474-4422(10)70002-8. *Equal first author contribution. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Theilmann, et al. White-matter changes correlate with cognitive functioning in Parkinson’s disease. Frontiers in Neurology. 2013;4:37. doi: 10.3389/fneur.2013.00037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vaillancourt DE, Spraker MBBS, Prodoehl J, Abraham I, Corcos DM, Zhou XI, et al. High-resolution diffusion tensor imaging in the substantia nigra of de novo Parkinson disease. Neurology. 2009;72(16):1378–1384. doi: 10.1212/01.wnl.0000340982.01727.6e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Villalon D, et al. White matter microstructural abnormalities in girls with chromosome 22q11.2 deletion syndrome. Neurolmage. 2013 doi: 10.1016/j.neuroimage.2013.04.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhan W, Kang GA, Glass GA, Zhang Y, Shirley C, Millin R, et al. Regional alterations of brain micro structure in Parkinson’s disease using diffusion tensor imaging. Movement Disorders. 2012;27(1):90–97. doi: 10.1002/mds.23917. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang K, Yua C, Zhang Y, Wu X, Zhuc C, Chan P, et al. Regional alterations of brain microstructure in Parkinson’s disease using diffusion tensor imaging. European Journal of Radiology. 2011;77:269–273. [Google Scholar]