A surrogate-primary replacement algorithm for response-adaptive randomization in stroke clinical trials

Abstract

Response-adaptive randomization (RAR) offers clinical investigators benefit by modifying the treatment allocation probabilities to optimize the ethical, operational, or statistical performance of the trial. Delayed primary outcomes and their effect on RAR have been studied in the literature; however, the incorporation of surrogate outcomes has not been fully addressed. We explore the benefits and limitations of surrogate outcome utilization in RAR in the context of acute stroke clinical trials. We propose a novel surrogate-primary (S-P) replacement algorithm where a patient’s surrogate outcome is used in the RAR algorithm only until their primary outcome becomes available to replace it. Computer simulations investigate the effect of both the delay in obtaining the primary outcome and the underlying surrogate and primary outcome distributional discrepancies on complete randomization, standard RAR and the S-P replacement algorithm methods. Results show that when the primary outcome is delayed, the S-P replacement algorithm reduces the variability of the treatment allocation probabilities and achieves stabilization sooner. Additionally, the S-P replacement algorithm benefit proved to be robust in that it preserved power and reduced the expected number of failures across a variety of scenarios.

1 Introduction

In randomized clinical trials, adaptive designs can be used to alter trial characteristics in response to accumulating information within the trial itself. In particular, response-adaptive randomization (RAR) procedures shift the treatment allocation probabilities in favor of the treatment that appears more successful based on the outcome of participants already treated in the trial, in order to achieve a certain objective, such as maximizing the chance of identifying the best treatment arm among several arms, maximizing the power, minimizing the total number of failures, or minimizing the total treatment cost. The use of RAR may lead to reduced exposure of trial subjects to ineffective experimental arms, more efficient and accurate dose finding, and more rapid identification of drugs and devices lacking clinically important benefit.¹ RAR is especially advantageous in early phase trials where little is currently known about the estimates of treatment efficacy. With RAR, it is generally assumed that participants enter the trial sequentially, the outcome variable is stable over time, and that the primary outcome variable can be determined quickly relative to the length of the enrollment period.²

Some clinical trials have a short participant enrollment period relative to the time required to obtain the primary outcome. Delayed primary outcomes and their effect on standard RAR have been studied in the literature under the assumption of a random-time delay.^3–5 The standard RAR approach is to wait and update the treatment allocation probabilities whenever a primary outcome becomes available. These studies indicate that when the delay is moderate (when 60% or more of already randomized participants’ outcomes become available), the power of the trial is negligibly affected while the allocation skewness is reduced with reduced variability.⁶ This body of work currently assumes that only a primary outcome is available for updating the allocation probabilities and that the time delay is random. Yet many biomedical applications, acute stroke treatment trials for example, have surrogate outcomes that can be measured sooner than the primary clinical outcome. However, the incorporation of surrogate outcomes into RAR has not been fully explored.

Surrogate and primary outcomes were utilized in an adaptive, phase II trial to efficiently identify the dose of L-carnitine in the treatment of septic shock.⁷ This study incorporated both the change in Sequential Organ Failure Assessment (SOFA) score at 48-hour post-treatment (surrogate) and the 28-day mortality (primary) endpoints. However, the allocation of subjects to doses and hence the RAR aspect of the study was determined only by the observed change in SOFA score (surrogate); while the stopping rules and interpretation of the trial results were based on the mortality (primary) benefit seen with the most-promising L-carnitine dose. Thus the surrogate and primary endpoints were both used, but for different adaptive aspects of the trial. The use of short-term and long-term responses in RAR was explored in the setting of survival clinical trials.⁸ Here complete remission and survival were both utilized to ‘‘speed up’’ the adaptation of the randomization procedure through a Bayesian model. We present a detailed investigation into the benefits and limitations of an alternative surrogate outcome utilization RAR design.

2 Background

Our illustrative example is the NINDS rt-PA Stroke Study,⁹ which evaluated the effectiveness of intravenous recombinant tissue plasminogen activator (rt-PA) for acute ischemic stroke when treatment can be initiated within 3 h of stroke onset. A primary outcome of interest was the 90-day modified Rankin scale (mRS).¹⁰ The mRS is a commonly used measure of functional disability or dependence at 3 months post-randomization in stroke clinical trials (ordinal score ranging from 0 = no symptoms to 5 = severe disability and 6 = dead). The mRS is typically dichotomized, but the cutoff scores distinguishing favorable and unfavorable outcome are highly variable between various acute stroke trials.^11,12 We chose a dichotomization for the mRS that was utilized in the NINDS rt-PA Stroke Study: 0–1 versus 2–6 representing success and failure, respectively. The NINDS rt-PA Stroke Study also collected a neurological function measure known as the National Institute of Health Stroke Scale (NIHSS). NIHSS is a systematic assessment tool that provides a quantitative measure (integer scale ranging from 0 = no deficit to 42 = extreme deficit) of neurologic deficit, and is often assessed at baseline, 24-hours and 90-days post-randomization.¹² We propose the use of the clinically utilized 24-hour NIHSS score as a surrogate outcome for the 90-day mRS. This is done based on the strong predictive capabilities of the baseline NIHSS¹³ on outcome. To be clinically useful, the NIHSS is also typically dichotomized. Utilizing the Interventional Management of Stroke (IMS¹⁴ and IMS II¹⁵) Studies data, an ROC curve analysis was performed to identify a cut-point in the NIHSS that simultaneously maximized both sensitivity and specificity with respect to the dichotomized 90-day mRS. This identified the NIHSS cut-point of 10 (83% sensitivity and 81% specificity) where less than 10 and greater than or equal to 10 represents a success and failure, respectively.

A delay time is the time from the intervention to obtaining the outcome measure. The current literature focuses on random primary outcome delay times^4,16 where it is unknown when the outcome will occur. However, in the NINDS rt-PA Stroke Study this delay time was fixed at 90 days in that the study protocol required mRS assessment 90 days post treatment. Hence, our interest in the length of the delay can equivalently be represented by the length of the enrollment period. For a fixed delay time, a long enrollment period (relative to the delay) translates into a large percentage of the primary outcomes becoming available during that enrollment period; whereas, a short enrollment period (relative to the delay) translates into a small percentage of primary outcomes becoming available during that enrollment period reducing the RAR scheme’s ability to skew the treatment allocation probabilities.

RAR schemes can be classified as either a design-driven urn model or an optimal allocation.¹⁷ The urn model approach employs intuitive rules to adapt the allocation probabilities as each participant enters the trial. Examples are Zelen’s play-the-winner² (which is response-adaptive but not randomized), Wei and Durham’s¹⁸ randomized play-the-winner, and Ivanova’s¹⁹ drop-the-loser methods. The asymptotic properties of these designs are provided in detail in Rosenberger and Lachin.²⁰ Urn models asymptotically target the urn allocation proportion

$$\rho =\frac{n_A}{n}\to \frac{q_B}{q_A+q_B}$$ (1)

almost surely,²⁰ where ρ denote the proportion of participants assigned to Treatment A, n_i is the number of participants assigned to Treatment i (n = n_A + n_B) and q_i = 1 − p_i is the probability of failure on Treatment i for i = A, B.

Alternatively, some RAR schemes were developed that focus on optimization criteria.¹⁷ Optimization may be based on several operating characteristics, including power, total expected sample size, expected number of treatment failures, expected number of participants assigned to the inferior treatment, total expected cost, etc.²¹ If the main objective is to identify for fixed sample size, the allocation that maximizes power, the solution is to target the Neyman allocation proportion

$$\rho =\frac{\sqrt{p_A{q}_A}}{\sqrt{p_A{q}_A}+\sqrt{p_B{q}_B}}$$ (2)

The major drawback of Neyman allocation is that it solely focuses on statistical aspects by assigning the majority of participants to the treatment having higher variability without regard for the treatment’s effectiveness.²⁰ Alternatively, if the main objective is to identify for fixed variance of the test, the allocation that minimizes the expected number of failures, then the solution is to target the allocation proportion

$$\rho =\frac{\sqrt{p_A}}{\sqrt{p_A}+\sqrt{p_B}}$$ (3)

which we refer to as optimal allocation.²² Analogous optimal allocation proportions exist for continuous outcomes based on μ_A, μ_B, σ_A, and σ_B.¹⁷ Zhang and Biswas²³ propose a broad family of allocation rules for RAR that contain Neyman and optimal allocation as special cases. Other target allocations exist which are not optimal in the formal sense, but are of specific clinical interest. One attribute that all target allocations have in common is that they are all functions of unknown population parameters.

Since the optimal allocations, ρ, involves unknown parameters of the population model, one cannot implement them in practice. This issue can be resolved in one of two ways: operate under the null hypothesis, which will result in equal allocation or operate under a best guess of the parameter values, i.e. a sequential estimation procedure (SEP). The latter approach was employed by Melfi and Page²⁴ in their sequential maximum likelihood estimation (SMLE) procedure. As the trial progresses, unknown parameters are replaced by current values of parameter estimates. SMLE was further improved upon by Eisele²⁵ and Eisele and Woodroofe²⁶ and called the doubly-adaptive biased coin design (DBCD). Later, Hu and Zhang²⁷ updated the conditions of DBCD and proposed a bivariate function g (r_current, r_target) (for γ ≥ 0) which represents the probability of assigning the current participant to Treatment A

$$\text{Prob}(\mathrm{T}\mathrm{r}\mathrm{t}\mathrm{A})=\mathrm{g}(r_{\text{current}},r_{\text{target}})=\frac{r_{\text{target}}{\left(\frac{r_{\text{target}}}{r_{\text{current}}}\right)}^{\gamma }}{r_{\text{target}}{\left(\frac{r_{\text{target}}}{r_{\text{current}}}\right)}^{\gamma }+(1-r_{\text{target}})+{\left(\frac{(1-r_{\text{target}})}{(1-r_{\text{current}})}\right)}^{\gamma }}$$ (4)

where r_current is the current proportion of participants assigned to Treatment A and r_target is the current estimate of the target allocation. If the current proportion of participants assigned to Treatment A, r_current, is less/more than the current target proportion of participants assigned to Treatment A, r_target, then the probability that the next participant will be assigned to Treatment A is greater/less than a half. Sequential estimation procedures, as the name infers, are iterative in that whenever new information becomes available (a treatment allocation or an outcome), the parameter estimates must be recalculated. That is, when a subject is randomized to a treatment arm, the r_current parameter is updated. When an outcome is observed, the success proportions (p_A and p_B) are updated and thus the target allocation r_target is updated. Therefore, the Treatment A allocation probability, Prob(Trt A), is sequentially estimated and utilizes all previously observed information. DBCD is the most favorable procedure due to its flexibility in terms of targeting any desired allocation; it is only slightly less powerful than the drop-the-loser rule; and one can fine tune the parameter γ in g (r_current, r_target) to reflect the degree of randomization desired.²⁸ At the most extreme, when γ = 0, DBCD simplifies to the sequential maximum likelihood procedure, which has the highest variability of the allocation proportions arising from the randomized procedure. As γ tends to ∞, DBCD assigns the patient to treatment with probability one and thus is deterministic (but with the smallest variability). Thus, as γ becomes smaller there is more randomization but also more variability. It has been shown that the DBCD with γ = 2 tends to have very good convergence for moderate sample sizes²⁹ and thus we utilized the DBCD (γ = 2) throughout this study.

3 Methods

3.1 RAR using primary outcome only

Consider a simple clinical trial with two Treatments A and B, a binary primary outcome and a binary surrogate outcome. Define T_i as the treatment assignment for participant i where T_i = A if participant i is assigned Treatment A and T_i = B if participant i is assigned Treatment B. Let P_i ~ h(Θ, T_i), where i = 1, 2, …, n, be the primary outcome of interest with a distribution based on unknown population parameters Θ and the assigned treatment. Since the primary outcome is binary, Θ = {p_AP, p_BP} where p_AP and p_BP are the population proportion of successful primary outcomes on Treatments A and B, respectively. Let S_i ~ h(Ω, T_i), where i = 1, 2, …,n, be the binary surrogate outcome with a distribution based on unknown population parameters Ω = {p_AS, p_BS} and the assigned treatment where p_AS and p_BS are the population proportion of successful surrogates on Treatments A and B, respectively. Ideally for RAR, the probability that participant k + 1 is assigned to Treatment A is a function of the treatment assignments and primary outcomes of the previous participants 1 through k.

$$\text{Prob}[T_{k+1}=A]=f(T_1,P_1,T_2,P_2,\dots ,T_k,P_k)$$ (5)

Here, RAR is based solely on the primary outcomes (no surrogates) and is referred to as standard RAR. The true allocation proportion (based on Θ) is specified and the sequentially estimated allocation proportion approaches the true allocation proportion as n increases.

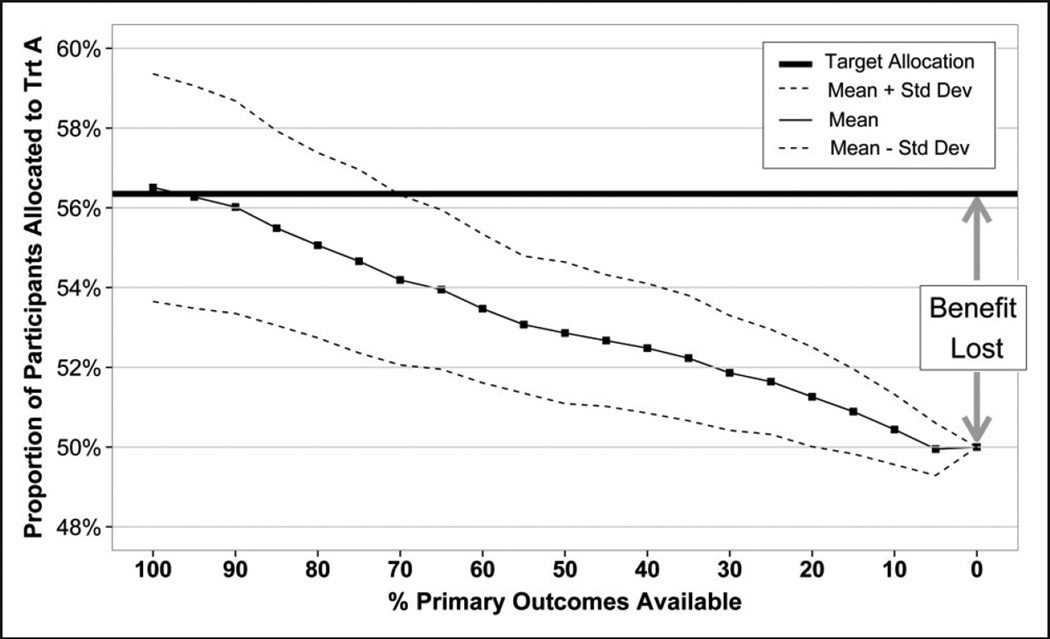
This approach performs best when the primary outcome of interest is available quickly relative to the enrollment period. In practice, however, most clinical trials involve long-term follow up to obtain the primary outcome. In our example of acute stroke trials, the final assessment of treatment benefit traditionally occurs 90 days after the start of treatment, and the surrogate measure (the NIHSS score) at 24 h. It is important to note that for fixed-time delays (i.e. 90 days), depending on the enrollment period, only a fraction of the primary outcomes will become available for the adaptation of the allocation probabilities during the enrollment period. The shorter the enrollment period, the fewer primary outcomes available and the further the observed mean allocation will be from the target allocation (Figure 1). The skewness of the allocation proportion increases as more primary outcomes become available (assuming a treatment effect). However, the variance of the allocation proportion is also larger because the allocation probability changes whenever a new participant enrolls. The distance from the target allocation line to the 50% proportion of participants assigned to Treatment A line can be viewed as the benefit of RAR. Since we have illustrated binary outcomes with optimal allocation (which minimizes failures), this can be interpreted as potential lives saved (additional successes). As the percent of primary outcome availability decreases, the benefit of RAR decreases.

Figure 1.

The effect of outcome delay on treatment allocation when utilizing standard RAR. N = 250. DBCD (γ = 2). Optimal allocation. Simulations = 1000. p_A = 0.5, p_B = 0.3. Treatment allocation moves from the target toward the 50% line when the percentage of available primary outcomes decreases from 100% to 0% for RAR based solely on primary outcomes.

If all primary outcomes are ‘instantaneously’ available (a participant’s primary outcome is obtained before the next participant enrolls), then the observed mean allocation achieves the target allocation. Here, the maximum RAR benefit is realized. When none of the primary outcomes becomes available during the enrollment period, no information exists to skew the allocation, thereby simplifying the RAR to simple randomization (equal allocation). Here, none of the RAR benefit is realized. Figure 1 illustrates the drawback of the standard RAR approach that waits until the primary outcomes become available and then updates the allocation probabilities, losing the benefit of RAR.

3.2 Proposed method

We propose a surrogate-primary replacement algorithm (S-P replacement algorithm) which utilizes both the surrogate and the primary outcomes. The parameter estimates are based on the surrogate outcome only until the primary outcome for the corresponding subject becomes available. Thus, the surrogate outcome is replaced with the primary outcome in the target allocation estimation. This approach is consistent with the goal of RAR, which is to utilize all available information.

The probability that participant k + 1 is assigned to Treatment A is a function of the treatment assignments and primary outcomes of the previous participants 1 through t and the surrogate outcomes of the previous participants t + 1 through k for whom the primary outcome is not yet available

$$\text{Prob}[T_{k+1}=A]=f(T_1,P_1,T_2,P_2,\dots ,T_t,P_t,T_{t+1},S_{t+1},T_{t+2},S_{t+2},T_k,S_k)$$ (6)

The S-P replacement algorithm is detailed in Figure 2. Like standard RAR, this method requires tracking the following for each treatment group: (1) the number of subjects assigned to each treatment group; (2) the number of subjects with a primary outcome available; (3) the number of primary outcome successes; and (4) the Treatment A allocation proportion. The S-P replacement algorithm additionally requires tracking the number of subjects with only a surrogate response available and the number of surrogate outcome successes for each treatment group. To begin implementation, we incorporate the option of an initial block (not required) of pre-specified size (typically 5–10% of total sample size) where participants are randomly allocated in equal numbers to Treatments A and B to force a balance. Initial blocks are a useful way to obtain initial parameter estimates required in a sequential estimation procedure such as the DBCD. Whether it is after the initial block or after a surrogate outcome becomes available in each treatment arm, one begins by calculating the weighted current total number of subjects assigned to each treatment and the current total number of response successes for each treatment. For this, we introduce the surrogate outcome weight (w_s) which represents the weight assigned to a surrogate outcome compared to a primary outcome. Generally, one would weight the surrogate outcome less than the primary, hence 0 ≤ w_s ≤ 1. When w_s = 1, the surrogate and the primary outcomes are of equal value. When w_s = 0, the surrogate outcome is not utilized and the algorithm simplifies to the standard RAR approach of waiting and updating whenever the primary outcomes become available. Our simulations utilize a surrogate outcome weight of w_s = ½; however, the selection of w_s is dependent on confidence in your surrogate outcome (close to 1 = very confident, close to 0 = little confidence) and is context specific. Next, the current response success and failure rates are calculated for each treatment group. These rates are then plugged into the desired target allocation (e.g. Neyman, optimal) to obtain the current Treatment A target allocation. Using both the current Treatment A allocation proportion and the current Treatment A target allocation proportion, the Treatment A allocation probability for the next subject is calculated using a sequential estimation procedure (e.g. DBCD). The next subject is randomized and all counts are updated. The process is repeated until reaching the desired sample size. Ultimately, the idea of the S-P replacement algorithm is that RAR is performed based on all available data, whether that is a surrogate or primary outcome. So for participant i, once his/her primary outcome becomes available, the participants enrolled after this event will use RAR with the ith participant’s primary outcome, while the participants enrolled before this event will use RAR with the ith participant’s surrogate outcome.

Figure 2.

Surrogate-primary replacement algorithm.

3.3 Simulation study

Computer simulation investigates RAR with delayed primary outcomes both when a surrogate outcome is (the proposed S-P replacement algorithm) and is not (the standard RAR method) utilized. To compare these two approaches, we apply them to bootstrapped samples (phases I and II combined, n = 624) of the NINDS rt-PA Stroke Study⁹ database. Direct comparisons are valid as this sample size yields simulated power of approximately 99% under both complete randomization and DBCD targeting optimal allocation randomization. Assume a random enrollment rate, where the time between participants enrollments is distributed uniformly (0, δ). The parameter δ represents the estimated maximum time between subject enrollments and can be selected according to the specific application under investigation. The lower bound of 0 allows more than one participant to enroll on any given day. Here, we investigate the effects of each method on the treatment allocation probabilities (the probability of each participant being assigned to the treatment rt-PA) and the treatment allocation (the actual proportion of participants assigned to the treatment rt-PA). In addition, we present another simulation study comparing complete randomization, standard RAR and S-P replacement algorithm with respect to power and expected number of failures under various treatment success scenarios and primary outcome delays (0%, 25%, 50%, and 75%). First, this is performed under the ideal situation where the surrogate and primary outcome have the same underlying distribution. Then, the investigation is repeated with various discrepancies (Δ = 10%, 20%, and 30%) among the two distributions. Without loss of generality, we assume a constant enrollment rate (a moving window). Therefore, for example, suppose that during the time it takes to obtain a primary outcome from the first participant in the study, 20 additional participants enroll. Then, when the 21st participant enrolls, the primary outcome becomes available for the 1st participant; when the 22nd participant enrolls, the primary outcome becomes available for the 2nd participant, etc. We implement Biswas and Hwang’s³⁰ formulation of a bivariate binomial distribution in the sense that marginally each of the two random variables (surrogate and primary outcome) has a binomial distribution and they have some nonzero correlation in the joint distribution.

4 Results

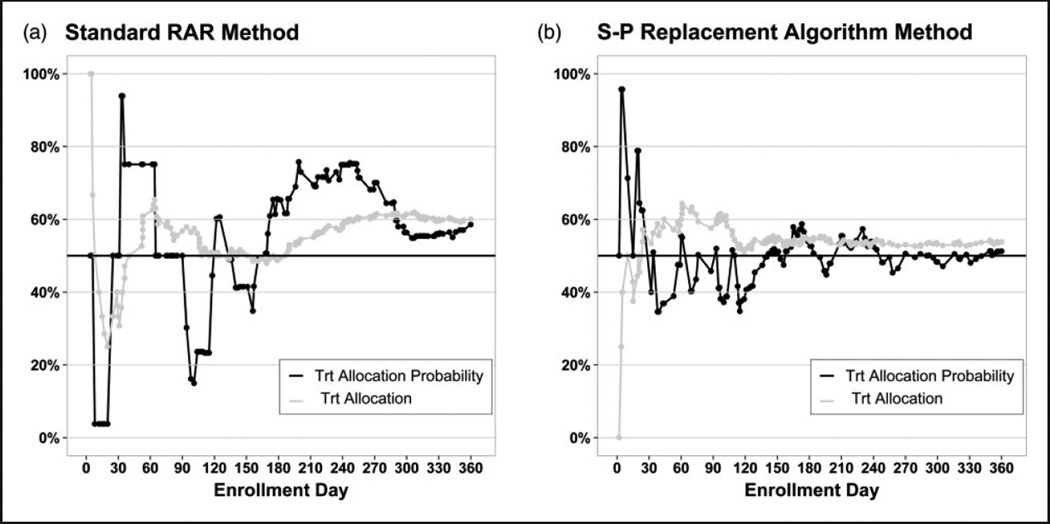
One realization of the standard RAR method and the S-P replacement algorithm are illustrated in Figure 3(a) and (b), respectively, for a 1-year enrollment period. The S-P replacement algorithm outperforms the standard RAR method by reducing the variability of the treatment allocation probabilities and stabilizing the treatment allocation sooner. Also, the S-P replacement algorithm achieves the correct target allocation of 56%, whereas the standard RAR method overshoots due to the limited data available to skew the allocation. When the enrollment period decreases, fewer primary outcomes become available and the advantages of the S-P replacement algorithm are magnified. As the enrollment period increases, more primary outcomes become available and eventually the two methods perform equivalently. These single realizations are presented to highlight the advantages of the S-P replacement algorithm; however, the variability of these designs is also of interest.

Figure 3.

Comparison of the standard RAR method for handling delayed primary outcomes and the S-P replacement algorithm on the NINDS rt-PA Stroke Study data (N = 160, one realization). Primary outcome is the 90-day mRS, the surrogate outcome is the 24-hour NIHSS with a 1-year enrollment period.

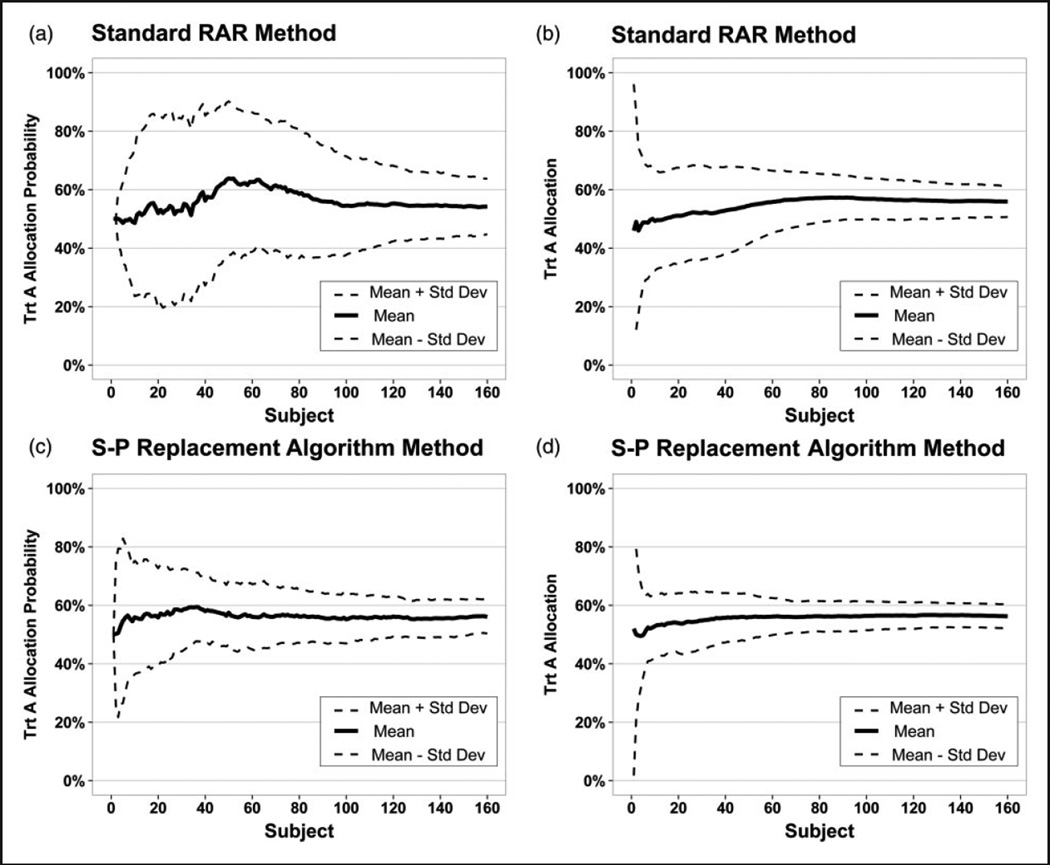
Figure 4 compares the performance of the standard RAR method (a, b) and the S-P replacement algorithm (c, d) with regard to the treatment allocation probabilities and treatment allocation, respectively. The mean and standard deviation are presented. The S-P replacement algorithm reduces the variability and stabilizes much quicker than the standard RAR method with regard to both aspects. Hence, there is benefit in utilizing surrogate information when available.

Figure 4.

Comparison of the variation of the standard RAR method for handling delayed primary outcomes and the S-P replacement algorithm on the NINDS rt-PA Stroke Study data (N = 160, simulations = 100). Primary outcome is the 90-day mRS, the surrogate outcome is the 24-hour NIHSS with a 1-year enrollment period.

To investigate the performance of the S-P replacement algorithm, it was compared in a simulation study to both complete randomization and standard RAR with respect to power and expected number of failures when targeting optimal allocation (Table 1). When there is no delay in obtaining the primary outcome, both the S-P replacement algorithm and standard RAR yield approximately the same power as complete randomization, with a smaller expected number of treatment failures. This is consistent with findings of Rosenberger and Hu²⁹ that the sample size required by DBCD is often comparable or slightly smaller than that required for complete randomization. Complete randomization is not affected by the delay in obtaining the primary outcome as it does not utilize the responses and thus its performance remains unchanged as the delay increases. The benefit of the standard RAR in terms of reducing treatment failures decreases as the delay in the primary outcomes increases; however, the power remains comparable. The S-P replacement algorithm maintains the benefit of reducing treatment failures as the delay in the primary outcome increases (while maintaining power) as it additionally utilizes the surrogate outcome information. While the magnitude of the reduced number of failures may not appear dramatic, one must consider that if the true optimal allocation was achieved, this would only shift 3, 5, 6, 29, and 46 subjects to Treatment A in each of these five scenarios, respectively. This, however, is optimal performance for S-P replacement algorithm as the surrogate distribution equals the primary distribution.

Table 1.

The effect of primary outcome delay on power and expected treatment failures (standard deviation) for complete randomization, standard RAR, and the S-P replacement algorithm.

				Complete		Treatment A Optimal allocation	Standard RAR		S-P Replacement algorithm
	pA	pB	N	Power	Failures		Power	Failures	Power	Failures
Delay = 0%	0.9	0.3	24	91	10 (2.4)	63%	90	7 (2.7)	90	7 (2.7)
	0.9	0.7	162	91	32 (5.0)	53%	91	31 (4.7)	91	31 (4.7)
	0.7	0.3	62	90	31 (3.9)	60%	91	28 (3.6)	91	28 (3.6)
	0.5	0.4	1036	90	570 (16.0)	53%	90	567 (15.8)	90	567 (15.8)
	0.2	0.1	532	90	452 (8.2)	59%	90	447 (8.4)	90	447 (8.4)
Delay = 25%	0.9	0.3	24	91	10 (2.4)	63%	92	9 (2.1)	90	8 (2.0)
	0.9	0.7	162	91	32 (5.0)	53%	91	31 (4.7)	91	31 (4.8)
	0.7	0.3	62	90	31 (3.9)	60%	90	30 (3.8)	91	28 (3.5)
	0.5	0.4	1036	90	570 (16.0)	53%	90	567 (16.0)	90	567 (15.9)
	0.2	0.1	532	90	452 (8.2)	59%	91	450 (8.2)	90	447 (8.5)
Delay = 50%	0.9	0.3	24	91	10 (2.4)	63%	92	9 (2.1)	90	8 (2.3)
	0.9	0.7	162	91	32 (5.0)	53%	91	31 (4.7)	91	31 (4.9)
	0.7	0.3	62	90	31 (3.9)	60%	90	30 (3.7)	90	28 (3.6)
	0.5	0.4	1036	90	570 (16.0)	53%	90	568 (16.0)	90	567 (15.8)
	0.2	0.1	532	90	452 (8.2)	59%	90	450 (8.3)	90	447 (8.4)
Delay = 75%	0.9	0.3	24	91	10 (2.4)	63%	92	10 (1.9)	90	7 (2.3)
	0.9	0.7	162	91	32 (5.0)	53%	91	31 (4.8)	91	31 (4.9)
	0.7	0.3	62	90	31 (3.9)	60%	91	31 (3.7)	90	28 (3.6)
	0.5	0.4	1036	90	570 (16.0)	53%	90	569 (16.0)	90	567 (15.9)
	0.2	0.1	532	90	452 (8.2)	59%	90	451 (8.3)	90	448 (8.5)

RAR: response-adaptive randomization; DBCD: doubly-adaptive biased coin design.

The sample size was selected that yielded simulated power of approximately 90% under complete randomization. Both RAR methods implemented DBCD (γ = 2) and targeted optimal allocation. Simulations = 10,000 replications (α = 0.05, two-sided). Surrogate distribution equals primary distribution. Surrogate weight w_s = 0.5.

In practice, the surrogate distribution is close to the primary outcome distribution, but typically does not equal it. Hence, in Table 2 we explore the impact of discrepancies among the two distributions. When this occurs, the target allocation based on the surrogate responses differs from that based on the primary responses and the resulting target allocation is a weighted combination of the two. The weight is determined by the selected surrogate weight, w_s, as well as the delay in obtaining the primary outcome. When both treatment arms over/under estimate the primary outcome success rates equally, the expected number of failures is preserved. When the discrepancy overestimates the superior Treatment A and underestimates the inferior Treatment B, the expected number of failures decreases. When the discrepancy underestimates the superior Treatment A and overestimates the inferior Treatment B, the expected number of failures increases. However, even in these suboptimal scenarios, the expected number of failures remains lower than that from complete or standard RAR. It is only when the distributional discrepancy is so large that the surrogate incorrectly identifies the better performing treatment arm (unlikely in practice) that the number of failures increases to the level of complete randomization. Power remains relatively constant in all scenarios with the one exception being when the surrogate distribution assigns subjects almost deterministically to one treatment arm. Here, the power dips to around 85% due to the extreme inequalities. Thus, the S-P replacement algorithm is rather robust with respect to both distributional discrepancies and delays in obtaining primary outcomes in terms of preserving both power and reducing the expected number of treatment failures.

Table 2.

The effect of surrogate distributional discrepancy and delay in obtaining primary outcomes on power and expected treatment failures (standard deviation) for the S-P replacement algorithm.

			S-P Replacement algorithm
			pPA = pSA pPB = pSB	pSA ↑ Δ pSB ↑ Δ	pSA ↓ Δ pSB ↓ Δ	pSA ↑ Δ pSB ↓ Δ	pSA ↓ Δ pSB ↑ Δ
Δ = 10%	Trt A surrogate success probability (pSA) =		0.70	0.80	0.60	0.80	0.60
	Trt B surrogate success probability (pSB) =		0.30	0.40	0.20	0.20	0.40
	Optimal allocation Trt A target =		0.60	0.59	0.63	0.67	0.55
	Delay = 25%	Power	91	90	90	90	90
		Failures (std dev)	28.4 (3.6)	28.3 (3.6)	28.5 (3.7)	28.2 (3.7)	28.8 (3.6)
	Delay = 50%	Power	91	90	89	89	91
		Failures (std dev)	28.4 (3.6)	28.5 (3.6)	28.2 (3.6)	27.7 (3.6)	29.2 (3.6)
	Delay = 75%	Power	90	91	90	90	90
		Failures (std dev)	28.3 (3.6)	28.6 (3.5)	27.8 (3.7)	27.2 (3.6)	29.5 (3.7)
Δ = 20%	Trt A surrogate success probability (pSA) =		0.70	0.90	0.50	0.90	0.50
	Trt B surrogate success probability (pSB) =		0.30	0.50	0.10	0.10	0.50
	Optimal allocation Trt A target =		0.60	0.57	0.69	0.75	0.50
	Delay = 25%	Power	91	90	90	90	91
		Failures (std dev)	28.4 (3.6)	28.3 (3.6)	28.7 (3.6)	28.1 (3.7)	29.1 (3.6)
	Delay = 50%	Power	91	90	90	88	90
		Failures (std dev)	28.4 (3.6)	28.5 (3.8)	28.5 (3.9)	27.6 (3.9)	29.8 (3.8)
	Delay = 75%	Power	90	90	89	88	90
		Failures (std dev)	28.3 (3.6)	28.8 (3.7)	27.8 (3.9)	26.7 (3.9)	30.4 (3.7)
Δ = 30%	Trt A surrogate success probability (pSA) =		0.70	0.99	0.40	0.99	0.40
	Trt B surrogate success probability (pSB) =		0.30	0.60	0.01	0.01	0.60
	Optimal allocation Trt A target =		0.60	0.56	0.86	0.91	0.45
	Delay = 25%	Power	91	90	90	89	91
		Failures (std dev)	28.4 (3.6)	28.1 (3.6)	29.5 (3.7)	28.2 (3.8)	29.4 (3.6)
	Delay = 50%	Power	91	89	89	88	90
		Failures (std dev)	28.4 (3.6)	27.6 (4.2)	30.7 (4.6)	28.2 (4.3)	30.6 (3.8)
	Delay = 75%	Power	90	87	86	84	90
		Failures (std dev)	28.3 (3.6)	27.4 (4.6)	30.7 (6.0)	28.5 (5.6)	31.2 (3.8)

The sample size (N = 62) was selected that yielded simulated power of approximately 90% under complete randomization. S-P replacement algorithm method implemented doubly-adaptive biased coin design (γ = 2). Simulations = 5000 replications (α = 0.05, two-sided). Surrogate weight w_s = 0.5.

5 Discussion

5.1 Outcome measures

For stroke trials specifically, there has been a recent push to analyze the full scale of the mRS. In the context of RAR designs, the outcomes of interest can be of the same or different types of measures. Thus, depending on the nature of the surrogate outcome and the primary outcome, four cases arise: (1) binary–binary; (2) continuous–continuous; (3) continuous–binary; (4) binary–continuous. We have addressed the simpler cases where the measures are the same, but the other cases are more complex and require further investigation.

5.2 Multiple surrogates

The proposed method of updating the surrogate outcomes as the primary outcome becomes available can be extended to include multiple surrogate outcomes. This assumes that a number of surrogate outcomes are obtained over the course of the study and that surrogate outcomes become better predictors as their measurements are taken closer in time to the primary outcome assessment time. Thus, the outcome is updated with the most recently available surrogate until the primary outcome becomes available.

We return to our example, the NINDS rt-PA Stroke Study⁹ where the NIHSS was assessed at 2 h, 24 h, and 7–10 days post treatment as well as at 90 days. The first three measures could serve as surrogate outcomes for the 90-day score. Naturally, these surrogates increase in their strength of correlation with the primary outcome (0.60, 0.70, and 0.83 respectively) and become an ideal candidate for the multiple surrogate version of the proposed method. Alternatively, some stroke trials have begun to collect the mRS at day 7 and/or discharge in addition to the 90-day primary outcome time point. Thus the NIHSS or mRS early measurements (either separate or in combination) would be examples of ideal candidates for the multiple surrogate version of the proposed method.

The S-P replacement algorithm is not without limitations. First, this approach assumes that a surrogate outcome is available, which is not always the case. The best performing surrogates are the ones with distributions closely resembling that of the primary outcome, not necessarily the surrogates most predictive of the primary. Second, as mentioned, this approach currently is only suitable when the surrogate and primary outcomes are of the same type of measure (binary–binary or continuous–continuous). Third, not specific to the S-P replacement algorithm, but to all RAR designs, is the issue of power. The simulations presented here utilized sample sizes large enough that RAR and equal allocation designs were adequately powered; however, this is not always the case and depends heavily on the target allocation selected. Particularly when RAR is selected solely for an ‘ethical benefit’, when the power is fixed, the total number of failures may actually increase under RAR mainly due to the extra samples needed to cover the power loss owing to the allocation ratio shifting. When RAR is selected for other purposes, to add/drop treatment arms or dose-finding, this becomes less of an issue. Lastly, any adaptive design adds complexity in implementation and requires greater planning and simulation along with more advanced administrative infrastructure.

Despite these limitations, RAR designs in general have a niche and are developing a presence. In the Adaptive Designs Accelerating Promising Trials Into Treatments (ADAPT-IT) project, a group of researchers are applying adaptive clinical trial principles and studying the process of collaboration necessary to design and implement adaptive clinical trials.¹ This group identified RAR as one of five possible types of adaptations having significant promise for confirmatory trials. With recent computation advances, complex models can be integrated into both Bayesian and frequentist designs. Meurer et. al. highlight that the choice of method should be based on operating characteristics of the design and the experience of the team.

6 Conclusions

In RAR, the probabilities for assigning eligible participants to different treatments are influenced by the observed outcomes among participants previously enrolled. When RAR is based solely on primary outcomes (standard RAR), any delay in obtaining the primary outcome will result in an observed mean allocation differing from the target allocation. With a long delay, very few primary outcomes become available to skew the allocation probabilities and all potential benefit of the RAR design is lost. Our proposed S-P replacement algorithm utilizes surrogate outcomes only until the primary outcome becomes available. Thus, it shifts the estimation of parameters from the surrogate to the primary outcome distribution. Even with modest delays in obtaining the primary outcomes and distributional discrepancies among the surrogate and primary outcome, the S-P replacement algorithm has shown an advantage over both standard RAR and complete randomization. Therefore, for fixed-time surrogate and primary outcomes, the S-P replacement algorithm outperforms the standard RAR approach by reducing probability variability and increasing convergence of the treatment allocation toward its target.