Pathways to dewetting in hydrophobic confinement

Significance

Dewetting in hydrophobic confinement plays an important role in diverse phenomena, ranging from protein folding and assembly, to the heterogeneous nucleation of vapor bubbles and superhydrophobicity. Using molecular simulations, we find that dewetting proceeds through the formation of isolated cavities adjacent to one of the confining surfaces. These isolated cavities are stabilized by enhanced water density fluctuations, and their growth is uphill in free energy. Upon growing to a certain size, the isolated cavities transition abruptly into supercritical vapor tubes that span the confined region, and grow spontaneously. Consequently, this nonclassical pathway results in lower free energy barriers than anticipated by macroscopic theory, with important implications for the kinetics of dewetting and hence for water-mediated self-assembly.

Abstract

Liquid water can become metastable with respect to its vapor in hydrophobic confinement. The resulting dewetting transitions are often impeded by large kinetic barriers. According to macroscopic theory, such barriers arise from the free energy required to nucleate a critical vapor tube that spans the region between two hydrophobic surfaces—tubes with smaller radii collapse, whereas larger ones grow to dry the entire confined region. Using extensive molecular simulations of water between two nanoscopic hydrophobic surfaces, in conjunction with advanced sampling techniques, here we show that for intersurface separations that thermodynamically favor dewetting, the barrier to dewetting does not correspond to the formation of a (classical) critical vapor tube. Instead, it corresponds to an abrupt transition from an isolated cavity adjacent to one of the confining surfaces to a gap-spanning vapor tube that is already larger than the critical vapor tube anticipated by macroscopic theory. Correspondingly, the barrier to dewetting is also smaller than the classical expectation. We show that the peculiar nature of water density fluctuations adjacent to extended hydrophobic surfaces—namely, the enhanced likelihood of observing low-density fluctuations relative to Gaussian statistics—facilitates this nonclassical behavior. By stabilizing isolated cavities relative to vapor tubes, enhanced water density fluctuations thus stabilize novel pathways, which circumvent the classical barriers and offer diminished resistance to dewetting. Our results thus suggest a key role for fluctuations in speeding up the kinetics of numerous phenomena ranging from Cassie–Wenzel transitions on superhydrophobic surfaces, to hydrophobically driven biomolecular folding and assembly.

The favorable interactions between two extended hydrophobic surfaces drive numerous biomolecular and colloidal assemblies (1–5), and have been the subject of several theoretical, computational, and experimental inquiries (6–22). Examples include the association of small proteins to form multimeric protein complexes, of amphiphlic block copolymers, dendrimers, or proteins to form vesicular suprastructures, and of patchy colloidal particles into complex crystalline lattices (23–27). When two such hydrophobic surfaces approach each other, water between them becomes metastable with respect to its vapor at a critical separation, $d_c$, that can be quite large (8, 9, 28–30). For nanometer-sized surfaces at ambient conditions, $d_c$ is proportional to the characteristic size of the hydrophobic object, whereas for micron-sized and larger surfaces, $d_c\sim 1\hspace{0.17em}\mu$m (29, 30). However, due to the presence of large kinetic barriers separating the metastable wet and the stable dry states, the system persists in the wet state, and a dewetting transition is triggered only at much smaller separations ($\sim 1$ nm) (13, 22, 28, 30).

To uncover the mechanism of dewetting, a number of theoretical and simulation studies have focused on the thermodynamics as well as the kinetics of dewetting in the volume between two parallel hydrophobic surfaces that are separated by a fixed distance, $d<d_c$ (8, 10–16, 18–21). These studies have highlighted that the bottleneck to dewetting is the formation of a roughly cylindrical, critical vapor tube spanning the region between the surfaces (11, 14, 15). A barrier in the free energetics of vapor tube formation as a function of tube radius is also supported by macroscopic interfacial thermodynamics, wherein the barrier arises primarily from a competition between the favorable solid–vapor and unfavorable liquid–vapor surface energies (Eq. 1 and Fig. 1). Thus, the classical mechanism for the dewetting transition prescribes that a vapor tube that spans the volume between the two surfaces must first be nucleated, and if the vapor tube is larger than a certain critical size, it will grow until the entire confined volume is dry (9).

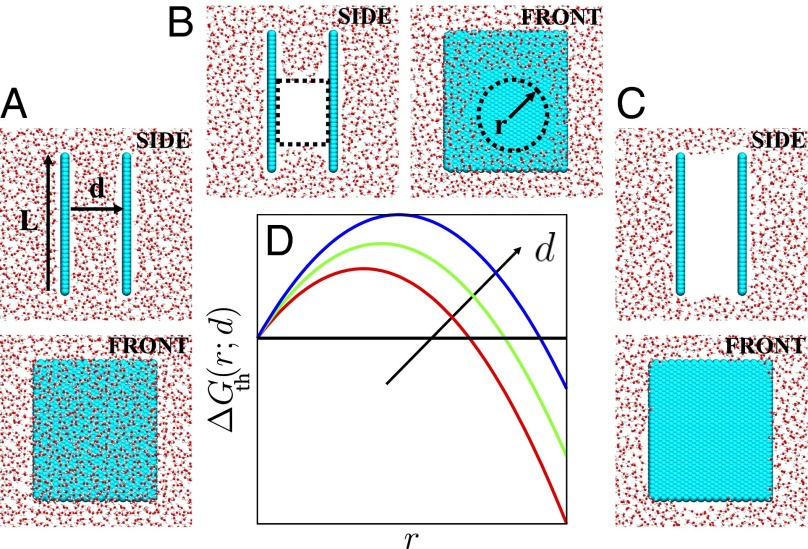
Fig. 1.

(A–C) Simulation snapshots of water (shown in red/white) in confinement between two square hydrophobic surfaces (shown in cyan) of size $L=4$ nm that are separated by a distance of $d=20$ Å; configurations highlighting (A) the liquid basin, (B) a cylindrical vapor tube of radius, r, that spans the confined region, and (C) the vapor basin are shown. In the front views, only one of the confining surfaces is shown. (D) Macroscopic theory predicts a free energetic barrier to vapor tube formation (Eq. 1), suggesting that a vapor tube larger than a critical size must be nucleated before dewetting can proceed.

Although it has been recognized that water density fluctuations must play a crucial role in nucleating vapor tubes (14, 15), the precise mechanism by which these tubes are formed is not clear. To understand how vapor tubes are formed and to investigate their role in the dewetting process, here we use molecular simulations in conjunction with enhanced sampling methods (31, 32) to characterize the free energetics of water density fluctuations in the region between two nanoscopic hydrophobic surfaces. Such a characterization of water density fluctuations in bulk water and at interfaces has already provided much insight into the physics of hydrophobic hydration and interactions (5, 13, 31–44). In particular, both simulations and theory have shown that the likelihood of observing low-density fluctuations adjacent to extended hydrophobic surfaces is enhanced relative to Gaussian statistics (13, 31, 36–38, 42). Further, the intricate coupling between enhanced solvent fluctuations and dewetting kinetics has been highlighted by both coarse-grained (45–47) and atomistic simulations (48–51).

Here we show that such enhanced water density fluctuations influence the pathways to dewetting in hydrophobic confinement by stabilizing isolated cavities adjacent to one of the confining surfaces with respect to vapor tubes. As the density in the confined region is decreased, the stability of isolated cavities relative to vapor tubes also decreases, and at a particular density, isolated cavities abruptly transition to vapor tubes. Surprisingly, for $d\mathrm{\lesssim }{d}_c$, that is, separations for which dewetting is thermodynamically favorable, we find that the nascent vapor tubes formed from the isolated cavities are already larger than the corresponding critical vapor tubes predicted by classical theory. Because the newly formed vapor tube is supercritical, it grows spontaneously. Importantly, because the formation of this supercritical vapor tube involves a nonclassical pathway that circumvents the critical vapor tube altogether, the process entails a smaller free energetic cost. Our results thus point to smaller kinetic barriers to dewetting than predicted by macroscopic theory.

Macroscopic Theory

According to classical interfacial thermodynamics, the free energy for creating a cylindrical vapor tube of radius r, which spans the volume between two surfaces separated by a distance d, is given by:

$$\mathrm{\Delta }{G}_{\text{th}}\left(r;d\right)=\pi \left[r^{2}d\mathrm{\Delta }P+2rd\mathrm{\gamma }+2r^2\mathrm{\gamma }\cos \mathrm{\theta }+4r\mathrm{\lambda }\right],$$ [1]

where $\mathrm{\Delta }P$ is the difference between the system pressure and the saturation pressure, γ is the liquid–vapor surface tension, θ is the contact angle, and λ is the line tension. For nanoscopic surfaces, the pressure-volume contribution is negligible at ambient conditions (29, 52, 53), whereas the line tension contribution can be important (20, 54). The term containing $\cos \mathrm{\theta }$ is negative for hydrophobic surfaces and favors dewetting, whereas the term corresponding to formation of the vapor–liquid area is unfavorable. The functional form of $\mathrm{\Delta }{G}_{\text{th}}\left(r;d\right)$ given in Eq. 1 is illustrated in Fig. 1D for three d values. In each case, a barrier separates the liquid $\left(r=0\right)$ and vapor (large r) basins, supporting the notion of dewetting mediated by the nucleation and growth of a vapor tube; both the critical vapor tube radius and the barrier height increase with increasing d.

Density-Dependent Free Energy Profiles Feature a Kink

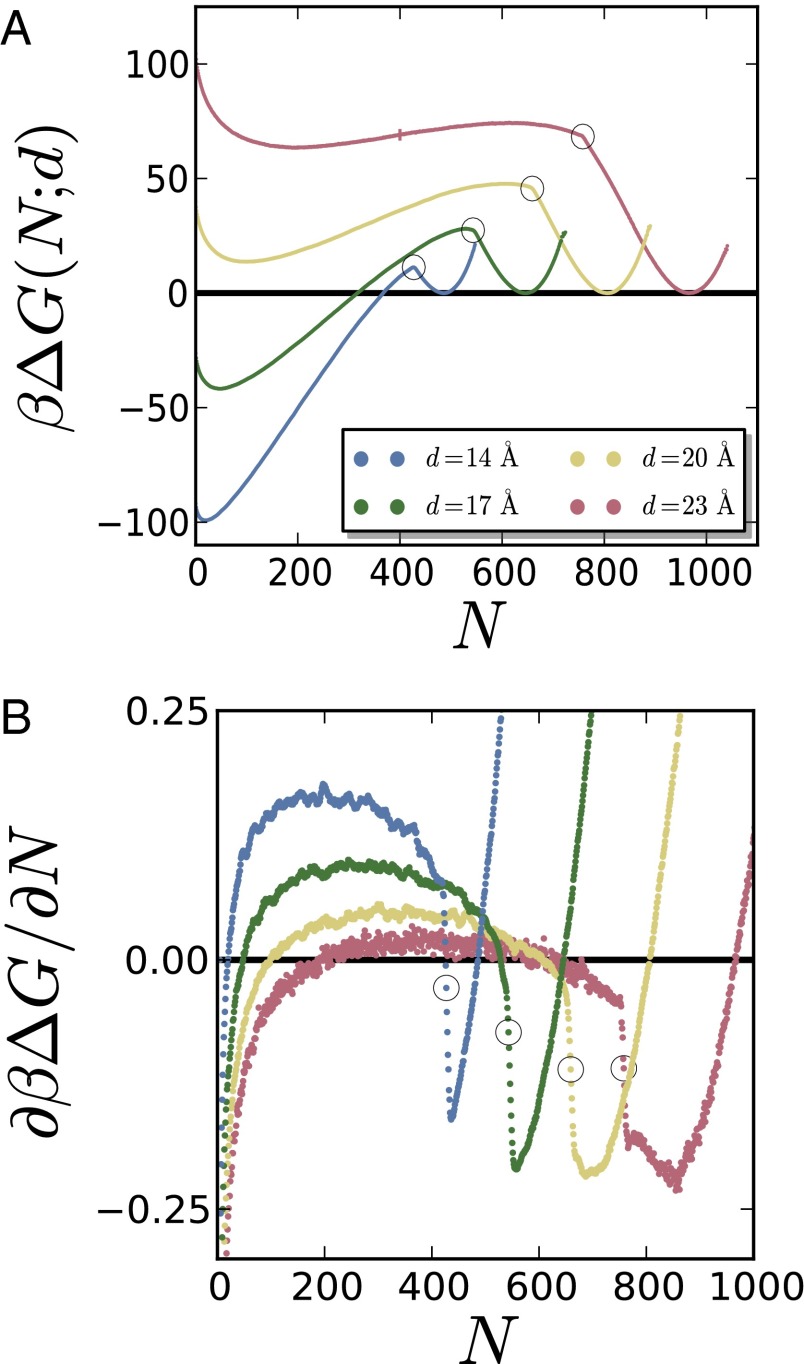
To investigate how water density fluctuations influence the mechanism of dewetting in hydrophobic confinement, here we perform molecular dynamics simulations of water confined between two roughly square hydrophobic surfaces of size $L=4$ nm, separated by a distance, d, as shown in Fig. 1A. Water in the confined region is in equilibrium with a reservoir of water, which in turn is in coexistence with its vapor $\left(\mathrm{\Delta }P=0\right)$ (31, 48). We characterize the statistics of water density fluctuations in the confined volume using indirect umbrella sampling (INDUS) (31, 32); that is, we estimate the free energy, $\mathrm{\Delta }G$, of observing N water molecules in that volume. The free energy, $\mathrm{\Delta }G\left(N;d\right)$, thus estimated is shown in Fig. 2A for a range of separations, d, with the free energy of the liquid basin, $N=N_{\text{liq}}$, being set to zero in each case. Over the entire range of separations considered, the free energy profile displays distinctive liquid (high N) and vapor (low N) basins with barriers separating them. Interestingly, the free energy profiles also feature a kink, that is, an abrupt change in the slope of $\mathrm{\Delta }G\left(N;d\right)$ is observed at a particular value of N between the liquid and vapor basins; we refer to this value of N as $N_{\text{kink}}$. This discontinuity in slope is seen more clearly in the derivatives of the free energy, shown in Fig. 2B. Small errors in $\mathrm{\Delta }G$ are amplified if simple finite differences are used to evaluate the derivatives; we therefore smooth the free energy profiles before evaluating the derivatives. Details of the smoothing procedure as well as the unsmoothed derivatives are shown in the SI Appendix.

Fig. 2.

(A) The simulated free energy profiles, $\beta \mathrm{\Delta }G\left(N;d\right)$, as a function of the number of water molecules between the surfaces, N, display marked kinks (highlighted by circles). Here, $\beta =1/k_{\text{B}}T$, with $k_{\text{B}}$ being the Boltzmann constant and T being the temperature. The size of the largest error bar is also shown for $d=23$ Å and $N=400$. (B) The kinks are also apparent in the smoothed derivatives of the free energy profiles, which display a sharp decrease in the vicinity of $N_{\text{kink}}$.

Kink Separates the Vapor Tube and Isolated Cavity Ensembles

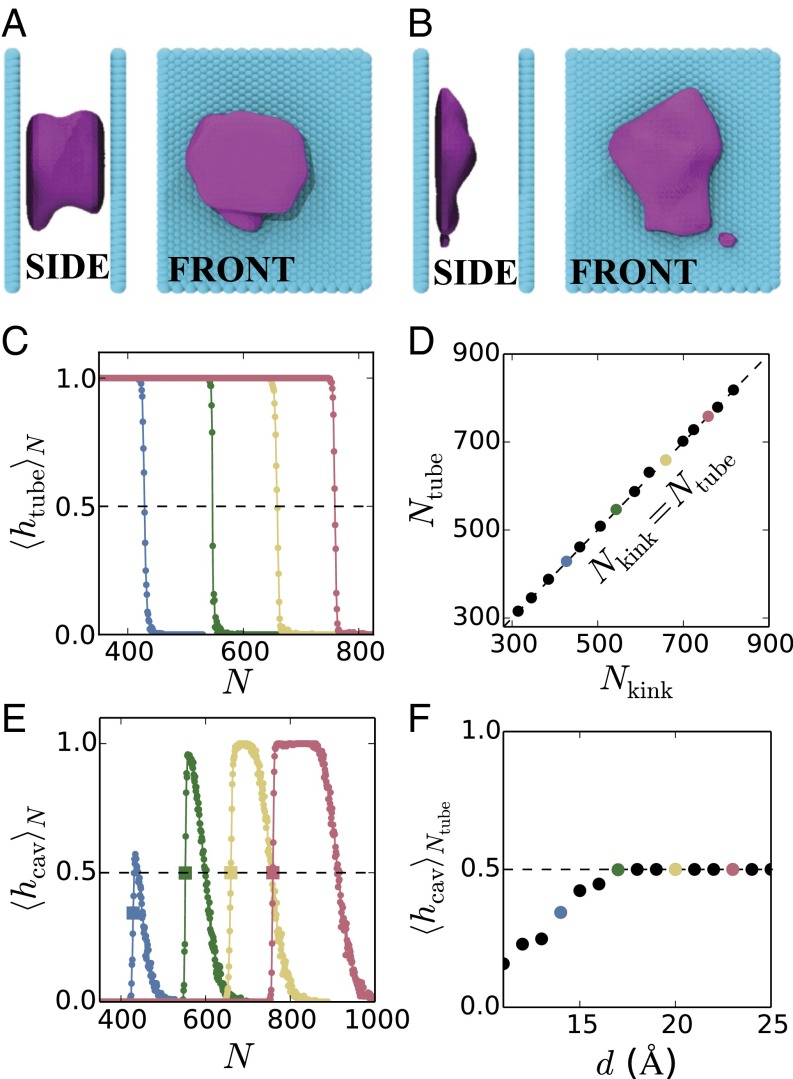
To investigate the significance of the kink in the free energy, we characterize configurations corresponding to N on either side of $N_{\text{kink}}$. We do so by building upon the instantaneous interface method of Willard and Chandler (55) to identify isosurfaces that encompass the dewetted regions, that is, the regions from which water is absent. The details of the method are included in the SI Appendix. As illustrated in Fig. 3A for $d=20$ Å and $N=N_{\text{kink}}-12$, characteristic configurations with $N\mathrm{\lesssim }{N}_{\text{kink}}$ contain a vapor tube, that is, the dewetted region (in purple) clearly spans the confined volume between the two surfaces (side view, left). Water molecules (not shown for clarity) occupy the entire region between the surfaces not shown in purple and are also present outside the confinement region. In contrast, for configurations with $N\mathrm{\gtrsim }{N}_{\text{kink}}$, isolated cavities are observed adjacent to one surface or the other; however, as seen in Fig. 3B for $N=N_{\text{kink}}+3$, the cavities do not span the region between the surfaces to form vapor tubes. Movies corresponding to the configurations shown in Fig. 3 A and B are included in the Supporting Information as Movies S1–S4.

Fig. 3.

Instantaneous interfaces encompassing dewetted regions (shown in purple) between the hydrophobic surfaces (shown in cyan) separated by $d=20$ Å highlight the presence of (A) a vapor tube for $N=N_{\text{kink}}-12$, and (B) an isolated cavity for $N=N_{\text{kink}}+3$. Water molecules not shown for clarity. (C) Average of the binary vapor tube indicator function, $h_{\text{tube}}$, conditioned on the number of waters in confinement being N, displays a sharp transition from 1 to 0 as N is increased. The color scheme is the same as that in Fig. 2. The value of N corresponding to ${\langle h_{\text{tube}}\rangle }_N=0.5$ (dashed line) is defined as $N_{\text{tube}}$. (D) $N_{\text{tube}}$ is identical to the location of the kink in the free energy profiles, $N_{\text{kink}}$, as shown by the agreement between the simulation data and a straight line (dashed). This agreement confirms that the kink demarcates conformations with and without vapor tubes. (E) Conditional average of the isolated cavity indicator function, ${\langle h_{\text{cav}}\rangle }_N$, shows a sharp increase in the vicinity of $N_{\text{kink}}$ (the square symbols correspond to $N_{\text{tube}}$), followed by a gradual decrease at larger N values, and eventually vanishes around $N=N_{\text{liq}}$. (F) For the larger d values, ${\langle h_{\text{tube}}\rangle }_{N_{\text{tube}}}={\langle h_{\text{cav}}\rangle }_{N_{\text{tube}}}=0.5$. However, for the smaller d values, ${\langle h_{\text{cav}}\rangle }_{N_{\text{tube}}}<0.5$, suggesting the possibility of direct vapor tube nucleation without isolated cavities as intermediates.

The configurations shown in Fig. 3 A and B suggest that $N=N_{\text{kink}}$ marks the boundary between the vapor tube and isolated cavity ensembles. To put this notion on a quantitative footing, we define indicator functions, $h_{\text{tube}}$ and $h_{\text{cav}}$, which are 1 if a given configuration has a vapor tube or an isolated cavity, respectively, and 0 otherwise. The average value of the indicator function ${\langle h_{\text{tube}}\rangle }_N$, subject to the constraint that the number of water molecules in confinement is N, is shown in Fig. 3C for the entire range of N values, and for several separations, d. Because the configurations were generated in the presence of biasing potentials, care must be exercised in evaluating the averages shown in Fig. 3C; details of the averaging procedure as well as the criteria used in the definition of the indicator functions can be found in the SI Appendix. For a given separation, ${\langle h_{\text{tube}}\rangle }_N$, which is the probability of observing a vapor tube conditional on the number of waters in confinement being N, is a sigmoidal function of N, decreasing sharply from 1 at low N to 0 for high N. We define $N_{\text{tube}}$ to be the value of N at which ${\langle h_{\text{tube}}\rangle }_N$ undergoes a sharp transition; in particular, where ${\langle h_{\text{tube}}\rangle }_N$ crosses 0.5. As shown in Fig. 3D, for the entire range of d values studied here $\left(11\hspace{0.17em}\AA \le d\le 25\hspace{0.17em}\AA \right)$, $N_{\text{tube}}$ is equal to $N_{\text{kink}}$, formalizing the notion that the kink in $\mathrm{\Delta }G\left(N;d\right)$ demarcates configurations that display vapor tubes and those that do not.

Analogous to ${\langle h_{\text{tube}}\rangle }_N$, the conditional average ${\langle h_{\text{cav}}\rangle }_N$ quantifies the fraction of configurations with N confined waters, which feature isolated cavities. For all separations, ${\langle h_{\text{cav}}\rangle }_N$ displays a sharp increase, followed by a gradual decrease; see Fig. 3E. The sharp increase occurs in the vicinity of $N=N_{\text{kink}}$ as vapor tubes give way to isolated cavities, whereas the gradual decrease corresponds to a crossover from isolated cavities to uniform configurations. To specify the location of this crossover, we define $N_{\text{cav}}$ to be the value of N where ${\langle h_{\text{cav}}\rangle }_N$ crosses 0.5 (with a negative slope). Despite these common features in the functional form of ${\langle h_{\text{cav}}\rangle }_N$, there are subtle differences in ${\langle h_{\text{cav}}\rangle }_N$ at small and large separations, which nevertheless have interesting consequences. For the largest separations, a well-defined plateau at ${\langle h_{\text{cav}}\rangle }_N=\hspace{0.17em}1$ separates the sharp increase in ${\langle h_{\text{cav}}\rangle }_N$ and its gradual decrease; this plateau demarcates the range of N values, which reliably feature isolated cavities. In contrast, the plateau at ${\langle h_{\text{cav}}\rangle }_N=\hspace{0.17em}1$ is absent for the smaller separations. Instead, the sharp increase in ${\langle h_{\text{cav}}\rangle }_N$ and its gradual decrease overlap in their range of N values. This overlap suggests that configurations corresponding to $N=N_{\text{kink}}$ are not limited to those with vapor tubes or isolated cavities, but could also be uniform. Given that ${\langle h_{\text{tube}}\rangle }_N=0.5$ at $N=N_{\text{tube}}$ by definition, a value of ${\langle h_{\text{cav}}\rangle }_{N_{\text{tube}}}<\hspace{0.17em}0.5$ would correspond to a nonzero likelihood of observing uniform configurations with $N=N_{\text{tube}}=N_{\text{kink}}$. As shown in Fig. 3F, that is indeed the case for $d\le 16$ Å, suggesting that although the nucleation of a vapor tube must proceed through the formation of isolated cavities for $d>16$ Å, vapor tubes may be nucleated directly from uniform configurations for smaller separations.

Free Energetics of Vapor Tubes and Isolated Cavities

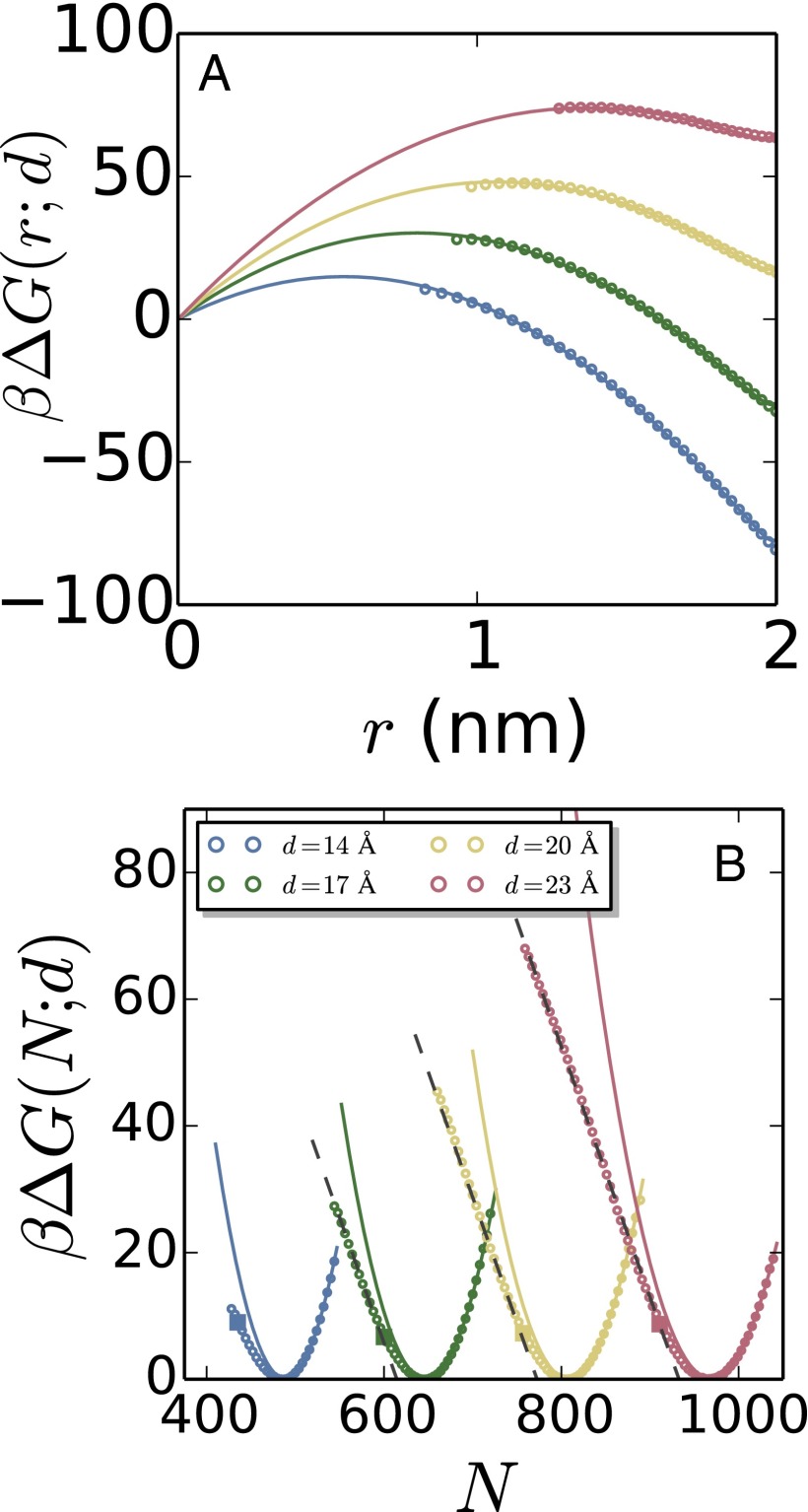
Given the abrupt change in the dewetted morphologies at $N\hspace{0.17em}=\hspace{0.17em}{N}_{\text{kink}}$, we expect the functional form of the free energetics for $N>N_{\text{kink}}$ and $N<N_{\text{kink}}$ to be different. Fig. 3 C and D collectively show that configurations with $N\mathrm{\lesssim }{N}_{\text{kink}}$ feature a vapor tube spanning the confined region, consistent with classical arguments. Although the vapor tube undergoes extensive shape fluctuations, we find its average shape to be roughly cylindrical. Coarse-grained density maps of select configurations reflecting the average vapor tube shape are included in the SI Appendix. To compare the free energetics of the vapor tubes obtained from our simulations to macroscopic theory, we first transform the number of waters in the confined region, N, to an approximate vapor tube radius, r, using the simple relation, $\pi r^2/L^2=\left(N_{\text{liq}}-N\right)/N_{\text{liq}}$. The values of vapor tube radii thus obtained are consistent with the average radii of the vapor tubes observed in our simulations for $N<N_{\text{kink}}$, as shown in the SI Appendix. Having a one-to-one relation between N and r allows us to transform the simulated free energies, $\mathrm{\Delta }G\left(N;d\right)$, into r-dependent free energies, $\mathrm{\Delta }G\left(r;d\right)$ in the region $r_{\text{kink}}<r<L/2$; the corresponding free energies are shown as symbols in Fig. 4A. The lines are fits to the $\mathrm{\Delta }G\left(r\right)$ data using the macroscopic expectation, $\mathrm{\Delta }{G}_{\text{fit}}\left(r\right)=\mathrm{\Delta }{G}_{\text{th}}\left(r\right)+2k_{\text{B}}T\ln \left(1-2r/L\right)$, where the logarithmic term corresponds to the translational entropy of the vapor tube. $\mathrm{\Delta }G\left(r\right)$ is fit separately for each d value and yields values of γ and λ that are reasonable. Values of γ are in the range of $12.2-15.8\hspace{0.17em}{k}_{\text{B}}T/{\text{nm}}^2$, comparable to the reported value of $14.5\hspace{0.17em}{k}_{\text{B}}T/{\text{nm}}^2$ for the water model that we use (56). Our fits yield $-\mathrm{\lambda }/\mathrm{\gamma }$ in the $6.5-7.5\hspace{0.17em}\AA$ range, in accord with a recently reported experimental value of $\mathrm{\lambda }=-30$ pN (54), which yields $-\mathrm{\lambda }/\mathrm{\gamma }=4.2\hspace{0.17em}\AA$. These agreements are remarkable considering the simplicity of the model that we use as well as the assumptions that we make (cylindrical vapor tube shape, constant surface tension independent of vapor tube curvature, etc.), and suggest that the energetics of the vapor tube are well-described by classical macroscopic theory. Further details of our fitting procedure, the values of the fit parameters for each d, as well as our attempts to fit the simulation data to other reasonable expressions of $G_{\text{th}}\left(r\right)$ can be found in the SI Appendix.

Fig. 4.

(A) $\beta \mathrm{\Delta }G\left(N\le N_{\text{kink}};d\right)$ is recast as $\beta \mathrm{\Delta }G\left(r;d\right)$, the free energy to form a vapor tube of radius, r. The points were obtained from the simulated free energy profiles by using the relation $\pi r^2/L^2=\left(N_{\text{liq}}-N\right)/N_{\text{liq}}$ in the region $r_{\text{kink}}<r<L/2$, and the lines are fits to macroscopic theory. (B) The portion of the free energy corresponding to the liquid basin $\left(N\ge N_{\text{kink}}\right)$ is parabolic at high N (Gaussian fluctuations), but linear at low N (fat tails in water number distributions). The crossover is gradual and occurs in the vicinity of $N_{\text{cav}}$ (square symbols), that is, the value of N for which ${\langle h_{\text{cav}}\rangle }_N$ is 0.5 with a negative slope. The linear regions have roughly the same slope for all separations.

To investigate the free energetics of the isolated cavity ensemble, in Fig. 4B, we focus on $\mathrm{\Delta }G\left(N>N_{\text{kink}};d\right)$. In the liquid basin, that is, in the vicinity of $N=N_{\text{liq}}$, the free energy (symbols) is parabolic (solid lines), indicating that the underlying density fluctuations are Gaussian. Although $\mathrm{\Delta }G$ remains harmonic for $N>N_{\text{liq}}$, it crosses over to being roughly linear (dashed lines) for $N<N_{\text{liq}}$. Such a crossover from parabolic to linear has also been observed adjacent to single extended hydrophobic surfaces (31, 41, 42), and corresponds to the interfacial water undergoing a collective dewetting transition to expel water from a nanometer-sized cavity (13, 38, 42). Indeed, as shown in Fig. 4B, the location of the crossover agrees well with the corresponding $N_{\text{cav}}$ values (squares) discussed in the previous section. Interestingly, the slopes of the linear fat tails are similar for all d values (in the range of $N_{\text{kink}}+20\le N\le N_{\text{liq}}-50$); the dashed lines shown in Fig. 4B are linear fits with a slope of $-0.396\hspace{0.17em}\hspace{0.17em}{k}_{\text{B}}T$ per water. Additional details of the fitting procedure and the values of the parameters obtained are provided in the SI Appendix. The difference between the values of $N_{\text{liq}}$ and the x intercepts of the linear fits is also approximately the same for all d values, and is equal to $30\hspace{0.17em}\pm \hspace{0.17em}5$ waters. Thus, the free energy for forming an isolated cavity of a given size (as quantified by the number of waters displaced from the confined region, $N_{\text{liq}}-N$), is independent of the separation between the surfaces; that is, the free energetics of isolated cavity formation adjacent to one hydrophobic surface are largely unaffected by the presence of the other confining surface. In contrast, the free energetics of vapor tube formation clearly depend on the intersurface separation, d. As a result, the location of the kink, where isolated cavities become metastable with respect to vapor tubes, also depends on d.

Nonclassical Dewetting Mechanism Reduces Barriers

Fig. 5A summarizes our findings for the dewetting mechanism presented thus far; in addition to the simulated $\mathrm{\Delta }G\left(N;d\right)$ for $d=15\hspace{0.17em}\AA$, it highlights the metastable branches of the vapor tube and isolated cavity ensemble free energies, anticipated from the fits shown in Fig. 4. It is clear that the system minimizes its free energy at all times by staying on the branch with the lower free energy; at $N=N_{\text{kink}}$, where the two free energy profiles intersect, the system jumps from the isolated cavity to the vapor tube ensemble. Importantly, the nonclassical path leading up to the formation of nascent vapor tubes $\left(N>N_{\text{kink}}\right)$ can result in smaller barriers to dewetting than anticipated by classical theory, as shown in Fig. 5B. For $d=14\hspace{0.17em}\AA$, the classical barrier (critical vapor tube) appears in the metastable segment of the free energy profile. The system thus circumvents the classical barrier, and instead adopts the path involving isolated cavities, which give way to vapor tubes only at $N=N_{\text{kink}}$; these nascent vapor tubes are larger than the critical vapor tube, so their subsequent growth is downhill in energy. Thus, the barrier to dewetting is the free energetic cost for forming these nascent, supercritical vapor tubes, which is clearly smaller than the classical barrier. In Fig. 5C, we illustrate that the nascent vapor tubes are not supercritical for all separations; for $d=23\hspace{0.17em}\AA$, the classical barrier appears in the stable segment of the free energy profile. Thus, although the kink in $\mathrm{\Delta }G\left(N;d\right)$ again marks the formation of a vapor tube for $d=23\hspace{0.17em}\AA$, the vapor tube formed is smaller than the critical vapor tube, and must grow further in a process that is uphill in energy, before dewetting can proceed. As a result, the barrier to dewetting coincides with that predicted by macroscopic theory.

Fig. 5.

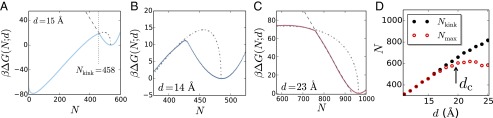
(A) The simulated $\beta \mathrm{\Delta }G\left(N;d\right)$ for $d=15\hspace{0.17em}\AA$ (solid) is shown along with the expected metastable branches of the free energies corresponding to the vapor tube (dot-dashed) and isolated cavity (dashed) ensembles. The metastable branches are anticipated from the fits shown in Fig. 4. The system minimizes its free energy by localizing to the ensemble with the lower free energy. (B) For $d=14$ Å, the nascent vapor tube formed at the kink is larger than the critical vapor tube anticipated by macroscopic theory, and therefore grows spontaneously. As a result, the corresponding barrier to dewetting is smaller than that predicted by macroscopic theory. (C) For larger separations, here $d=23$ Å, the newly formed vapor tube is subcritical, and has to grow larger for dewetting to proceed. (D) Comparison of the location of the kink, $N_{\text{kink}}$, with the location of the barrier between the liquid and vapor basins, $N_{\text{max}}$. For small d, the barrier (point of highest $\mathrm{\Delta }G$) occurs at the kink, so that $N_{\text{max}}\approx N_{\text{kink}}$. In contrast, for larger d values, the barrier occurs in the vapor tube segment of the simulated free energy profile and corresponds to the classical critical vapor tube, so that $N_{\text{max}}<N_{\text{kink}}$. The transition from nonclassical to classical behavior occurs in the vicinity of the coexistence separation, $d_{\text{c}}$.

To uncover the separation at which the system transitions from a supercritical to a subcritical nascent vapor tube, in Fig. 5D, we plot $N_{\text{kink}}$ and $N_{\text{max}}$ as a function of d. Here, $N_{\text{max}}$ corresponds to the value of N between the liquid and vapor basins where $\mathrm{\Delta }G\left(N;d\right)$ is the highest. For small values of d, $N_{\text{max}}=N_{\text{kink}}$, indicating that $\mathrm{\Delta }G\left(N;d\right)$ is the highest at the kink, consistent with the formation of supercritical nascent vapor tubes. For larger values of d, there is an additional maximum in $\mathrm{\Delta }G$ at $N_{\text{max}}<N_{\text{kink}}$, suggesting that the newly formed vapor tubes are smaller than the corresponding critical vapor tubes. Interestingly, the separation at which the system transitions from nonclassical to classical dewetting barriers is close to the separation, $d_{\text{c}}$, at which there is coexistence between the liquid and vapor. Thus, for the separations with a thermodynamically favorable driving force for dewetting, the mechanism for dewetting is manifestly nonclassical, corresponding to the formation of supercritical vapor tubes from isolated cavities, and requiring a smaller free energetic barrier than anticipated by macroscopic theory.

Discussion and Outlook

Our results highlight that water density fluctuations can play a central role in determining the pathways to dewetting in hydrophobic confinement. Enhanced water density fluctuations in the vicinity of hydrophobic surfaces stabilize isolated cavities relative to vapor tubes for $N>N_{\text{kink}}$; the system resides in the classical vapor tube ensemble only for $N<N_{\text{kink}}$. Our results thus highlight a breakdown of classical nucleation theory that stems from the stabilization of a nonclassical species (isolated cavities) and leads to an alternative pathway with a lower barrier. Similar findings have been reported for crystal nucleation, wherein a nonclassical pathway is stabilized by liquidlike solute clusters, which results in a reduced barrier (57, 58).

Although the free energetics of both the isolated cavity and vapor tube ensembles are well described by the number of waters in confinement, N, this simple order parameter may not be sufficient to describe the transition from one ensemble to the other. Indeed, $\mathrm{\Delta }G\left(N;d\right)$ represents a projection of a complex free energy landscape onto the single parameter, N, and a kink in $\mathrm{\Delta }G\left(N;d\right)$ strongly suggests that the transition from an isolated cavity to a vapor tube involves order parameter(s) that are orthogonal to N. Although beyond the scope of the present work, it would be interesting to uncover these order parameters that define the transition state ensemble along with N. Determining these additional parameters will require path sampling techniques in conjunction with a characterization of commitment probabilities (14); it is conceivable that additional barriers may present themselves in these order parameters.

Dewetting in nanoscopic hydrophobic confinement plays an important role in biology; ranging from the assembly of multimeric proteins and the collapse of the hydrophobic protein core, to the vapor-lock gating of ion channels and the specific binding of ligands to hydrophobic grooves on their binding partners. In particular, recent work has highlighted the importance of including the solvent coordinate, N, in describing the kinetics of hydrophobically driven collapse and assembly (49–51, 59). Our results show that water density fluctuations stabilize nonclassical pathways, which reduce the barriers along the N coordinate, and should therefore enhance the kinetics of dewetting-mediated biophysical phenomena.

Dewetting in hydrophobic confinement can also be important in a host of nonbiological phenomena, ranging from heterogeneous nucleation of vapor bubbles and contact line pinning, to the Cassie–Wenzel transitions on textured surfaces (60). These phenomena involve intricate confinement geometries, which could result in complex pathways involving one or more transitions between various dewetted morphologies, akin to the transition between isolated cavities and vapor tubes observed here. Fluctuation-mediated pathways ought to also reduce dewetting barriers associated with these diverse phenomena.

Materials and Methods

We simulate the SPC/E (extended simple point charge) model of water in confinement between two square hydrophobic surfaces of size $L=4$ nm, for a range of separations, d (Fig. 1A), ranging from 11 to 25 Å, chosen to span the entire range of d values with both liquid and vapor basins. The surfaces are composed of 1,008 atoms each, which are arranged on a hexagonal lattice with a spacing of 1.4 Å. The surface atoms interact with the water oxygens through the Lennard–Jones potential with the parameters, $\sigma =$ 3.283 Å and $\mathrm{ϵ}=0.121$ kJ/mol (see refs. 20, 21 for further details). As shown in the SI Appendix, this well depth was chosen so that a water droplet on the hydrophobic surface makes a contact angle, $\mathrm{\theta }\approx 120°$, which is characteristic of alkyl-terminated self-assembled monolayer surfaces (37). For water, we have chosen the SPC/E model (61) because it adequately captures the experimentally known features of water such as surface tension, compressibility, and vapor–liquid equation of state near ambient conditions, which are important in the study of hydrophobic effects (5, 62). Our simulations contain roughly 10,000–15,000 water molecules and were performed in the canonical ensemble, thermostated at $T=300$ K using the canonical velocity rescaling thermostat (63). We use a periodic simulation box with the hydrophobic surfaces of interest fixed at the center of the box, and a buffering liquid–vapor interface nucleated at the top of the box with the help of a wall of purely repulsive particles. The buffering interface ensures that the system is at the saturation pressure of SPC/E water at 300 K (31, 48); free energies obtained with such a construct have been shown to be nearly indistinguishable from those obtained in the NPT ensemble at a pressure of $1$ bar (32). Short-ranged interactions were truncated at 1 nm; whereas, long-ranged electrostatic interactions were computed using the particle mesh Ewald method (64). The bonds in water were constrained using the SHAKE algorithm (65). To study the free energetics of dewetting, we select the cuboid shaped $\left(L\times L\times d\right)$ observation volume between the hydrophobic surfaces, and estimate the free energies, $\mathrm{\Delta }G\left(N;d\right)$, using the INDUS method (31, 32). Each biased simulation was run for 6 ns and the first 1 ns was discarded for equilibration.