Effective approach for calculations of absolute stability of proteins using focused dielectric constants

Abstract

The ability to predict the absolute stability of proteins based on their corresponding sequence and structure is a problem of great fundamental and practical importance. In this work, we report an extensive, refinement and validation of our recent approach (Roca et al., FEBS Lett 2007;581:2065–2071) for predicting absolute values of protein stability ΔG_fold. This approach employs the semimacroscopic protein dipole Langevin dipole method in its linear response approximation version (PDLD/S-LRA) while using the best fitted values of the dielectric constants ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }$ and ${\mathrm{\epsilon }}_{\text{eff}}^{\prime }$ for the self energy and charge–charge interactions, respectively. The method is validated on a diverse set of 45 proteins. It is found that the best fitted values of both dielectric constants are around 40. However, the self energy of internal residues and the charge–charge interactions of Lys have to be treated with care, using a somewhat lower values of ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }$ and ${\mathrm{\epsilon }}_{\text{eff}}^{\prime }$. The predictions of ΔG_fold reported here, have an average error of only 1.8 kcal/mole compared to the observed values, making our method very promising for estimating protein stability. It also provides valuable insight into the complex electrostatic phenomena taking place in folded proteins.

INTRODUCTION

The ability to predict physical and chemical properties of proteins, given their sequence and folded tertiary structure, is of crucial importance for the study of enzymes.^1–3 Computational approaches for predicting the thermal stability of proteins, the difference of free energy between their folded and unfolded state, have yet to emerge and validate. That is, despite the progress in the development of models for studying the folding of proteins^4–12 there are still major problems in predicting protein stability by either microscopic or macroscopic models. For example, we lack a clear understanding of the magnitude of electrostatic contributions to thermal stability and to the overall folding free energy. Similarly, the values of the dielectric constants to be used and the contribution of the ionizable residues to the stability of a folded protein are only a few of the questions still unanswered.

Discretized continuum studies^13,14 have suggested that charged and polar groups lead to destabilization of a folded protein. Other studies, however, have indicated that protein stability is far more complicated than originally thought, and that charged residues do not necessarily destabilize the protein core. Quite the opposite, they tend to increase protein stability.^15–18 Even the general idea in continuum studies that internal ionizable residues tend to destabilize the protein core is now under reevaluation.¹⁹ Overall there is a growing realization that electrostatic energy is related to stability in general, and that electrostatic interactions usually stabilize the native states of proteins quite significantly. However, the exact role of electrostatic interactions in protein stability is obscured by the competition between desolvation penalties, stabilization by local protein dipoles, and charge–charge interaction.

Recently, we introduced an approach²⁰ that evaluates the electrostatic contribution to protein stability by selecting relatively high values of dielectric constants for charge–charge interactions (ε_eff) and for self energy (ε_p). This approach determines the absolute stability of a given protein based on (a) the use of the semimacroscopic protein dipole Langevin dipole (PDLD/S) in its linear response approximation version (the PDLD/S-LRA method) for self energy and (b) the usage of high values ε_p and ε_eff. Our preliminary studies²⁰ indicated that a major part of the absolute folding energy is reproduced by the electrostatic energy evaluated with large ε_eff and more surprisingly by a large ε_p. The contribution of the screened charge–charge interactions is consistent with the recent findings (e.g., Makhatadze and coworkers^21–23 as well as Garcia Moreno and coworkers^24,25 and Pace and coworkers^26–28), as far as the relative contribution of surface groups is concerned. However, our finding appeared to be more general with implications about the energetics of internal groups. The corresponding physical picture appeared to be quite intriguing but more validation is essential. Moreover, the predictive value of our approach has not been fully validated. The present work explores this model in a much more extensive and systematic way and establishes its general validity. We focus on the challenge of finding the best fitted values for the dielectric constants and on the effectiveness of the method in predicting protein stability.

METHODS

The method described in this work focuses on the electrostatic contribution to the folding free energy, assuming that this is the main contribution. The method was described previously by Roca et al.,²⁰ and we consider below the main points.

Our starting point is the folding paths of Figure 1, where the system can move from the unfolded state (A) to the folded state (E) in two pathways. In one of them (A) → (B) → (C) → (D) → (E), the unfolded protein becomes uncharged (transferring the charges to solution on the proper proton transfer process), folds to its neutral folded form (C), and then move to the final folded charged form (E) through an uncharged structure that is similar to that of (E). In the second path, the charged protein folds directly by moving from (A) to (E). The electrostatic contributions to folding, $\mathrm{\Delta }{G}_{\text{fold}}^{\text{elec}}$, of a given protein at a specific ionization state and at a given pH, is evaluated by²⁹:

$$\mathrm{\Delta }{G}_{\text{fold}}^{\text{elec}}=\mathrm{\Delta }{G}_{\mathrm{f}}^{\text{elec}}-\mathrm{\Delta }{G}_{\mathrm{u}\mathrm{f}}^{\text{elec}}=-2.3RT\sum _i{Q}_i^{(\mathrm{f})}(\mathrm{p}{K}_{i,\text{int}}^p({\mathrm{\epsilon }}_{\mathrm{p}})-\mathrm{p}\mathrm{H})+166\sum _{i\ne j}\frac{Q_i^{(\mathrm{f})}{Q}_j^{(\mathrm{f})}}{r_{ij}^{(\mathrm{f})}{\mathrm{\epsilon }}_{\text{eff}}(r_{ij}^{(\mathrm{f})})}+2.3RT\sum _i{Q}_i^{(\mathrm{u}\mathrm{f})}(\mathrm{p}{K}_{a,i}^w-\mathrm{p}\mathrm{H})-166\sum _{i\ne j}\frac{Q_i^{(\mathrm{u}\mathrm{f})}{Q}_j^{(\mathrm{u}\mathrm{f})}}{{\mathrm{\epsilon }}_{\text{water}}{r}_{ij}^{(\mathrm{u}\mathrm{f})}}$$ (1)

where uf and f designate, the unfolded and folded states, Q_i is the charge of the ith residue, in the folding (f) or the unfolding (uf) state, ε_p is the dielectric constant used in the semimacroscopic calculation of intrinsic pK_a, $\mathrm{p}{K}_{i,\text{int}}^p({\mathrm{\epsilon }}_{\mathrm{p}})$ is the intrinsic pK_a of the ith residue in its given protein state when all other residues are neutral, at a given ε_p. Finally r_ij is the distance between residues i and j, while ε_eff is the effective dielectric for charge–charge interactions inside the protein and ε_water is the effective dielectric constant for charge–charge interactions in water.

Figure 1.

The thermodynamic cycle for the folding of a charged protein. Steps A → B and B →C correspond, respectively, to the uncharging of the unfolded protein and the folding of the uncharged protein. Step C → D corresponds to the change of the unfolded protein from its equilibrium structure to the structure of the folded charged protein. Step A → E corresponds to a direct folding of the ionized protein. The figure defines the free energy terms used in this work.

As clarified elsewhere,^29,30 ε_p determines the “self energy” and the corresponding intrinsic pK_a of each charged group. This parameter is not related to the response of the protein to electric field but to the method used in the calculations and to the elements included explicitly in the simulation system. Basically, ε_p reflects all the effects that are not included explicitly in the calculations of the self energy.³⁰ Similarly, ε_eff is a parameter that reflects the compensation of the gas phase charge–charge interaction by the reorganization of the solvent and the protein.²⁹

The folding free energy also includes non-electrostatic contributions such as configuration entropy and hydrophobic contributions. These contributions depend on the path used in Figure 1. For example, we can write according to Figure 1,

$$\mathrm{\Delta }{G}_{\text{fold}}=\mathrm{\Delta }{G}_{\mathrm{f}}^{\text{elec}}-\mathrm{\Delta }{G}_{\mathrm{u}\mathrm{f}}^{\text{elec}}+\mathrm{\Delta }{G}_{\mathrm{u}\mathrm{f}\to \mathrm{f}}^{\text{uncharged}}=\mathrm{\Delta }{G}_{\text{fold}}^{\text{elec}}+\mathrm{\Delta }{G}_{\mathrm{u}\mathrm{f}\to \mathrm{f}}^{\text{uncharged}}$$ (2)

In this description, the electrostatic terms represent the charging process in the folded state and the uncharging in the unfolded state, while the non-electrostatic is entirely associated with the folding of the fully uncharged protein. The use of this equation for mutations of ionized residues of a given protein allows us to focus only on $\mathrm{\Delta }{G}_{\text{fold}}^{\text{elec}}$.

Eq. (1) describes the electrostatic contribution to the folding energy of the given protein, and the corresponding value depends, of course, upon the choice of ε_p and ε_eff. Concerning the non-electrostatic term $\mathrm{\Delta }{G}_{\mathrm{u}\mathrm{f}\to \mathrm{f}}^{\text{uncharged}}$, it may well be of different value for different proteins, and there is no current computational method that can provide a reliable estimate of the quantities. However, if we use the direct (A) → (E) path of Figure 1 we get a different picture of the calculate ΔG_fold, since now the entire folding process can be described in terms of the corresponding change in charge–charge interactions, using

$$\mathrm{\Delta }{G}_{\text{fold}}\cong 166\sum _{i\ne j}\frac{Q_i{Q}_j}{{\mathrm{\epsilon }}_{\text{eff}}(r_{ij})}[\frac{1}{r_{ij}^{(\mathrm{f})}}-\frac{1}{r_{ij}^{(\mathrm{u}\mathrm{f})}}]$$ (3)

That is, now the non-electrostatic effects may be absorbed in the effective dielectric for the work of bringing the charged groups from the unfolded to the folded state in the (A) → (E) path of Figure 1. In other words, the (B) → (D) step involves non-electrostatic contributions that may be significant, while the step (D) → (E) is formally a well defined electrostatic step, which includes, of course, structural reorganization. The dielectric that reflects the structural reorganization in the (D) → (E) step may be modified by considering the free energy of the (B) → (D) step and requiring that this free energy will be reproduced by Eq. (1). Now if the effect of the (B) → (D) step is not large or if it is somehow correlated with the trend in the electrostatic free energy, we will have a uniform dielectric that works for all proteins. Conversely, if this is not the case we will not be able to use such approximation. It is this philosophy, though with some assumptions, that leads us to the next important step of our method. Since our concept of a dielectric constant is somewhat complex we refer the reader to Refs. ^29–31 for further clarification.

If the $\mathrm{\Delta }{G}_{\mathrm{u}\mathrm{f}\to \mathrm{f}}^{\text{uncharged}}$ term is somehow small, reflecting compensation between the entropy and the hydrophobic effect, we may examine the approximation:

$$\mathrm{\Delta }{G}_{\text{fold}}\approx \mathrm{\Delta }{G}_{\text{fold}}^{\text{elec}}({\mathrm{\epsilon }}_{\mathrm{p}}^{\prime },{\mathrm{\epsilon }}_{\text{eff}}^{\prime })$$ (4)

where ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime },{\mathrm{\epsilon }}_{\text{eff}}^{\prime }$ is the set of ε_p and ε_eff that successfully reproduce the folding energy. In this case we obtain:

$$\mathrm{\Delta }{G}_{\text{fold}}^{\text{elec}}=\mathrm{\Delta }{G}_{\text{fold}}^{\text{elec}}({\mathrm{\epsilon }}_{\mathrm{p}}^{\prime },{\mathrm{\epsilon }}_{\text{eff}}^{\prime })\approx -2.3RT\sum _i{Q}_i(\mathrm{p}{K}_{i,\text{int}}^p({\mathrm{\epsilon }}_p^{\prime })-\mathrm{p}{K}_{i,w}^w)+166\sum _{i\ne j}{Q}_i{Q}_j[\frac{1}{r_{ij}^{(\mathrm{f})}{\mathrm{\epsilon }}_{\text{eff}}^{\prime (\mathrm{f})}}-\frac{1}{80r_{ij}^{(\mathrm{u}\mathrm{f})}}]$$ (5)

Where: uf and f designate, the unfolded and folded states, Q_i is the charge of the ith residue, in the folding (f) state only, $\mathrm{p}{K}_{i,\mathit{\text{int}}}^p({\mathrm{\epsilon }}_{\mathrm{p}}^{\prime })$ is the intrinsic pK_a of the ith residue calculated from the chosen ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }$ and not the original ε_p, and $\mathrm{p}{K}_{i,w}^w$ is the pK_a of the i residue in water. Rigorously, we should use $Q_{\mathrm{i}}^{(\mathrm{f})}$ but since the contribution from the unfolded state will be neglected here we leave the notation Q_i. We also use 80 instead of the ε_water since the difference is trivial and the effect of this term is small. Finally, r_ij is the distance between residues i and j, in the folding (f) and unfolding (uf) state. Here, ${\mathrm{\epsilon }}_{\text{eff}}^{\prime (\mathrm{f})}$ is the chosen dielectric effective constant for the charge–charge interactions. It should be pointed out that ${\mathrm{\epsilon }}_{\text{eff}}^{\prime (\mathrm{f})}$ in Eq. (5) is taken here as independent of the distance r_ij. In later sections, we discuss exceptions, where the choice of ${\mathrm{\epsilon }}_{\text{eff}}^{\prime (\mathrm{f})}$ for certain cases is affected by both the residues i and j as well as its distance r_ij. At any rate, the first term in Eq. (5) represents the change of self energy upon moving a charge from water to its site in the folded protein: That is,

$$-2.3RT\sum _i{Q}_i(\mathrm{p}{K}_{i,\text{int}}^p({\mathrm{\epsilon }}_{\mathrm{p}}^{\prime })-\mathrm{p}{K}_{i,w}^w)=\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{sol}}^{\mathrm{w}\to \mathrm{p}}(Q_i=0\to Q_i=Q_i^0)$$ (6)

The second term in Eq. (5) represents the effect of charge–charge interaction.

Adopting the approximation of Eq. (5) reduces the complicated and difficult problem of calculating absolute folding energy of a protein, to the finding of the proper, best fitted values of ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }$ and ${\mathrm{\epsilon }}_{\text{eff}}^{\prime (\mathrm{f})}$, which provides the best estimate of ΔG_fold. This idea is based on the fact that semimacroscopic models can represent implicitly physical and chemical properties even though they lack explicit representation of the phenomena taking place. Of course, such an approach can work only if the given model retains the main physics of the real system. Overall, we expect the best fitted values of ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }$ and ${\mathrm{\epsilon }}_{\text{eff}}^{\prime (\mathrm{f})}$ to be higher than the values of 4 to 8, values used for example to calculate accurate values of pK_a’s in proteins.³²

Equation (5) can be further simplified, by assuming that $r_{\mathrm{i}\mathrm{j}}^{(\mathrm{u}\mathrm{f})}$ is in general much larger than $r_{ij}^{(\mathrm{f})}$, and that ${\mathrm{\epsilon }}_{\text{eff}}^{\prime (\mathrm{f})}$ is smaller than 80. Thus, Eq. (5) is finally approximated by:

$$\mathrm{\Delta }{G}_{\text{fold}}^{\text{elec}}({\mathrm{\epsilon }}_{\mathrm{p}}^{\prime },{\mathrm{\epsilon }}_{\text{eff}}^{\prime (\mathrm{f})})=-2.3RT\sum _i{Q}_i(\mathrm{p}{K}_{i,\text{int}}^p({\mathrm{\epsilon }}_{\mathrm{p}}^{\prime })-\mathrm{p}{K}_{i,w}^w)+166\sum _{i\ne j}{Q}_i{Q}_j\left[\frac{1}{r_{ij}^{(\mathrm{f})}{\mathrm{\epsilon }}_{\text{eff}}^{\prime (\mathrm{f})}}\right]=2.3RT\sum _i{Q}_i(\mathrm{p}{K}_{i,\text{int}}^p({\mathrm{\epsilon }}_p^{\prime })-\mathrm{p}{K}_{i,w}^w)+166\sum _{i\ne j}{Q}_i{Q}_j\left[\frac{1}{r_{ij}{\mathrm{\epsilon }}_{\text{eff}}^{\prime }}\right]$$ (7)

In Eq. (7) we drop the notation (f) from the variables $r_{ij}^{(\mathrm{f})}$ and ${\mathrm{\epsilon }}_{\text{eff}}^{\prime (\mathrm{f})}$, and we will use r_ij and ${\mathrm{\epsilon }}_{\text{eff}}^{\prime (\mathrm{f})}$ as the distance and the corresponding dielectric constant for interactions between residues i and j in the folding state. This simplification may overlook cases where the contribution from the unfolded protein is significant. This might be the case when the unfolded protein has a compact structure, as implied by the studies of Raleigh and coworkers³³ or when electrostatic interaction in the unfolded state play a significant role for folding kinetics as suggested by Pace, Trefethen, and coworkers.^26,27 However, it is possible that the contribution from the unfolded configuration is relatively small and the best way to judge this issue is to explore the validity of Eq. (7) in a large number of test cases.

The evaluation of the intrinsic pK_a’s were done by using the PDLD/S-LRA method according to standard protocol using the POLARIS module and the ENZYMIX force field of MOLARIS program.^20,36 Each protein studied in this work was first solvated by the surface constrained all atom solvent (SCAAS) model,^35,36 and all the ionizable groups (Asp, Glu, Lys, Arg, but not His) at pH = 7 were assigned a charge which is 50% of their full charge at the ionized state (this was considered as the best procedure for the initial relaxation). The resulting system (protein and waters) was equilibrated by running a 100 ps molecular dynamics simulation with 1 fs time step at 300 K. The subsequent PDLD/S-LRA calculations of the $\mathrm{p}{K}_{i,\text{int}}^p({\mathrm{\epsilon }}_{\mathrm{p}}^{\prime })$ of each ionizable residue started with 10 ps equilibration run, followed by 25 2 ps runs (starting from different configurations) on both the charged and uncharged state of the given residue. The resulted calculated pK_i,int were then averaged to evaluate the final $\mathrm{p}{K}_{i,\text{int}}^p({\mathrm{\epsilon }}_{\mathrm{p}}^{\prime })$. The total simulation time depends on the size and the number of ionizable groups of the given protein. For example it took 22 hours on 4 dual core nodes (Dual Intel P4 3.0 GHz, 2 GB Memory) to evaluate all the $\mathrm{p}{K}_{i,\text{int}}^p({\mathrm{\epsilon }}_{\mathrm{p}}^{\prime })$ of snase (protein 1EY0, size 136 residues, which contains 48 ionizable residues).

Once the intrinsic pK_a’s were evaluated, the ionization states of the protein residues at pH = 7 were determined, by using a Monte Carlo approach described previously.³⁶ This procedure was repeated at different ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime },{\mathrm{\epsilon }}_{\text{eff}}^{\prime }$ and provides the charges (the Q_i) of the ionized residues as a function of the given dielectric constants. Using the $\mathrm{p}{K}_{i,\mathit{\text{int}}}^p({\mathrm{\epsilon }}_{\mathrm{p}}^{\prime })$ and the Q_i in Eq. (7) provided $\mathrm{\Delta }{G}_{\text{fold}}^{\text{elec}}({\mathrm{\epsilon }}_{\mathrm{p}}^{\prime },{\mathrm{\epsilon }}_{\text{eff}}^{\prime })$ as a function of ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }$ and ${\mathrm{\epsilon }}_{\text{eff}}^{\prime }$.

RESULTS

Initial estimate of the best fitted values of ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }$ and ${\mathrm{\epsilon }}_{\text{eff}}^{\prime }$

In this work, we moved to a much more extensive benchmark than the one used in our previous work,²⁰ considering all the proteins listed in Table I. Our test set included 45 proteins with various sequence sizes, folds, and function.

Table I.

The benchmark considered in this work

No.	Name	PDB ID	Number of residues	Type	Source
1	SSO7d	1SSO	62	monomer	37
2	Thioredoxin	2TRX	108	monomer	37
3	Barstar	1A19	89	monomer	37
4	Apoflavodoxin	1FTG	168	monomer	37
5	λ-Repressor	1LMB	87	monomer	37
6	Snase	1EY0	136	monomer	37
7	BsHpr, Phosphotransferase	2HID	87	monomer	37
8	FeCyt b562	1QPU	106	monomer	37,38
9	Arc Repressor	1ARQ	53	dimer	37,39
10	Aspartate Amilotransferase	1VPE	398	monomer	3
11	Chey	1TMY	118	monomer	3
12	GDH Domain II	1B26 (A02)	234	monomer	2,3,37
13	Histidine Phosphocarrier	1Y4Y	87	monomer	3
14	Phosphotransferase, Histidine containing protein	2HPR	87	monomer	3
15	Ribosomal	1H7M	99	monomer	34
16	RNase H*	1JXB	147	monomer	3,40
17	Ferridoxin	1VJW	59	monomer	3
18	O-Methyl Guanine DNA methyltransferase	1MGT	169	monomer	3
19	Sac7d	1WD0	66	monomer	2,3
20	aHistone	1BFM	134	dimer	2,41
21	PFRD-XC4	1QCV	53	monomer	42
22	aStaphylococcal Nuclease I92K	1TR5	130	monomer	43
23	Staphylococcal Nuclease I92E	1TR5	130	monomer	43
24	aStaphylococcal Nuclease	1TR5	130	monomer	43
25	Bs CSP	1CSP	67	monomer	20,44
26	Bc CSP	1C9O	66	monomer	20,45
27	Tm CSP	1G6P	61	monomer	2,20
28	aUbiquitin D21N	1AAR	76	monomer	20,46
29	Ubiquitin F45W	1AAR	76	monomer	20,47
30	aUbiquitin K27A	1AAR	76	monomer	20,46
31	Tm DHFR	1CZ3	164	dimer	20,48
32	Ec DHFR	1RX2	159	monomer	20
33	Ribonuclease	1X1P	212	monomer	2,49
34	Glucanase C	1CX1	153	monomer	50
35	Phospholipid A2	1P2P	124	monomer	51
36	Trypsin Proteinase	2CI2	65	monomer	52
37	Interleukin	1IOB	153	monomer	53
38	aAdhesion transferase Y92E	1K40	126	monomer	54
39	Complement	1GKG	136	monomer	4
40	Cytochrome b5 Rat	1B5M	84	monomer	55
41	Gene V DNA Binding	1VQB	86	monomer	56
42	Glu Transferase	1GSD	208	dimer	57
43	Growth Factor	1FGA	124	monomer	58
44	Isomerase	1HTI	248	dimer	59
45	Ribosomal S6	1RIS	97	dimer	60

^aThe structure used to calculate $\mathrm{\Delta }{G}_{\text{fold}}^{\text{elec}}$, was obtained by mutating the corresponding PDB structure reported in the third column of this table.

We started with a rough estimate of the best fitted set of ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime },{\mathrm{\epsilon }}_{\text{eff}}^{\prime }$ for the prediction of ΔG_fold. This was done first for a single protein (L-Repressor, PDB ID 1LMB) by the approach illustrated in Figure 2.

Figure 2.

The calculated values of $\mathrm{\Delta }{G}_{\text{fold}}^{\text{elec}}$ as a function of ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }$ and ${\mathrm{\epsilon }}_{\text{eff}}^{\prime }$ for L-Repressor. The best fitted values of ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }$ and ${\mathrm{\epsilon }}_{\text{eff}}^{\prime }$ are taken as the values that give the best agreement between $\mathrm{\Delta }{G}_{\text{fold}}^{\text{elec}}({\mathrm{\epsilon }}_{\mathrm{p}}^{\prime },{\mathrm{\epsilon }}_{\text{eff}}^{\prime })$ and the observed ΔG_fold. Observed stability for this protein is −4.6 kcal/mole. As seen from the figure, these values are around $35\le {\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }\le 45$ and $35\le {\mathrm{\epsilon }}_{\text{eff}}^{\prime }\le 45$.

In order to clarify the nature of Figure 2, it is useful to start, for example, with the evaluation of $\mathrm{\Delta }{G}_{\text{fold}}^{\text{elec}}({\mathrm{\epsilon }}_{\mathrm{p}}^{\prime },{\mathrm{\epsilon }}_{\text{eff}}^{\prime })$ at a specific point (e.g., ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }=20$ and ${\mathrm{\epsilon }}_{\text{eff}}^{\prime }=30$). In this case, we first used ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }=20$ and evaluate the intrinsic pK_a values for all the ionizable residues. In the next step, we used Eq. (7) with ${\mathrm{\epsilon }}_{\text{eff}}^{\prime }=30$ and obtained $\mathrm{\Delta }{G}_{\text{fold}}^{\text{elec}}({\mathrm{\epsilon }}_{\mathrm{p}}^{\prime },{\mathrm{\epsilon }}_{\text{eff}}^{\prime })=\mathrm{\Delta }{G}_{\text{fold}}^{\text{elec}}(20,30)=-4.27\mathrm{k}\mathrm{c}\mathrm{a}\mathrm{l}/\mathrm{m}\mathrm{o}\mathrm{l}$. This value was then assigned in the corresponding point in Figure 2. Now the same procedure was repeated for other values of ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }$ and ${\mathrm{\epsilon }}_{\text{eff}}^{\prime }$ and the figure was completed. Next, we identified the set of $\mathrm{\Delta }{G}_{\text{fold}}^{\text{elec}}({\mathrm{\epsilon }}_{\mathrm{p}}^{\prime },{\mathrm{\epsilon }}_{\text{eff}}^{\prime })$ that gave the best agreement with the observed ΔG_fold (around −4.6 kcal/mole for L-Repressor) and identified the optimal dielectric constants. In the case of Figure 2, the best fitted values were found to be in the vicinity of ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }={\mathrm{\epsilon }}_{\text{eff}}^{\prime }=40$.

After applying the above approach to all the 45 proteins of our test case, we considered several alternative ways of analyzing the corresponding results. The first and simplest analysis which is summarized in Figure 3, was based on allowing both ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }$ and ${\mathrm{\epsilon }}_{\text{eff}}^{\prime }$ to be either 35 or 40, and choosing the value of $\mathrm{\Delta }{G}_{\text{fold}}^{\text{elec}}({\mathrm{\epsilon }}_{\mathrm{p}}^{\prime },{\mathrm{\epsilon }}_{\text{eff}}^{\prime })$ that minimizes the difference $|\mathrm{\Delta }{G}_{\text{fold}}^{\text{elec}}({\mathrm{\epsilon }}_{\mathrm{p}}^{\prime },{\mathrm{\epsilon }}_{\text{eff}}^{\prime })-\mathrm{\Delta }{G}_{\text{fold}}^{\text{obs}}|$. The corresponding results were used to generate Figure 3(A). This type of treatment will be referred here as getting the “best fitted” $\mathrm{\Delta }{G}_{\text{fold}}^{\text{elec}}({\mathrm{\epsilon }}_{\mathrm{p}}^{\prime },{\mathrm{\epsilon }}_{\text{eff}}^{\prime })$. The same procedure was followed in the generation of Figure 3(B), but this time with $8\le {\mathrm{\epsilon }}_p^{\prime }\le 20$ and $8\le {\mathrm{\epsilon }}_{\text{eff}}^{\prime }\le 20$.

Figure 3.

The correlation between the best fitted $\mathrm{\Delta }{G}_{\text{fold}}^{\text{elec}}({\mathrm{\epsilon }}_{\mathrm{p}}^{\prime },{\mathrm{\epsilon }}_{\text{eff}}^{\prime })$ and ΔG_fold for best fitted values of ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }$ and ${\mathrm{\epsilon }}_{\text{eff}}^{\prime }$ in a restricted range. The calculations considered all the proteins in the benchmark of Table I and take the value of $\mathrm{\Delta }{G}_{\text{fold}}^{\text{elec}}({\mathrm{\epsilon }}_{\mathrm{p}}^{\prime },{\mathrm{\epsilon }}_{\text{eff}}^{\prime })$ that gives best fitted results for the two allowed values of ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }$ and ${\mathrm{\epsilon }}_{\text{eff}}^{\prime }$ (see text for the procedure used for selecting the best fitted values). The two values considered in Figure 3(A) are ε_p, ε_eff = 35, 40 whereas in Figure 3(B) we consider ε_p, ε_eff = 8, 20. As discussed in the text, the calculated best fitted values of $\mathrm{\Delta }{G}_{\text{fold}}^{\text{elec}}({\mathrm{\epsilon }}_{\mathrm{p}}^{\prime },{\mathrm{\epsilon }}_{\text{eff}}^{\prime })$ diverge greatly from the corresponding observed values. The average error between observed ΔG_fold and best fitted $\mathrm{\Delta }{G}_{\text{fold}}^{\text{elec}}({\mathrm{\epsilon }}_{\mathrm{p}}^{\prime },{\mathrm{\epsilon }}_{\text{eff}}^{\prime })$ is 3.5 kcal/mole, and 7.3 kcal/mole for Figure 3(A) and 3(B), respectively. Some points of Figure 3(B) are outside the scale of this figure.

As seen from both Figures 3(A) and 3(B), there is significant disagreement between the best fitted $\mathrm{\Delta }{G}_{\text{fold}}^{\text{elec}}({\mathrm{\epsilon }}_{\mathrm{p}}^{\prime },{\mathrm{\epsilon }}_{\text{eff}}^{\prime })$ and observed ΔG_fold for many proteins. However, from these initial trials it appears that with the use of high values of ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }$ and ${\mathrm{\epsilon }}_{\text{eff}}^{\prime }$ of around 40, the absolute difference between observed and calculated stability $|\mathrm{\Delta }{G}_{\text{fold}}^{\text{elec}}({\mathrm{\epsilon }}_{\mathrm{p}}^{\prime },{\mathrm{\epsilon }}_{\text{eff}}^{\prime })-\mathrm{\Delta }{\mathrm{G}}_{\text{fold}}|$ is significantly smaller than the difference obtained with other dielectric constants (see example demonstrated in Figure 3(B), where the discrepancy is much larger at the region when $8\le {\mathrm{\epsilon }}_p^{\prime }\le 20,8\le {\mathrm{\epsilon }}_{\text{eff}}^{\prime }\le 20$).

Improving the model

In the next stage of the refinement of our model, we tried to further search for the best fitted values for the dielectric constants. This was done by considering the dielectrics that minimize the function

$$F_{\text{error}}({\mathrm{\epsilon }}_{\mathrm{p}}^{\prime },{\mathrm{\epsilon }}_{\text{eff}}^{\prime })=\sum _i\left|\mathrm{\Delta }{G}_{(i)\text{fold}}^{\text{elec}}\right({\mathrm{\epsilon }}_{\mathrm{p}}^{\prime },{\mathrm{\epsilon }}_{\text{eff}}^{\prime })-\mathrm{\Delta }{G}_{(i)\text{fold}}^{\text{obs}}|$$ (8)

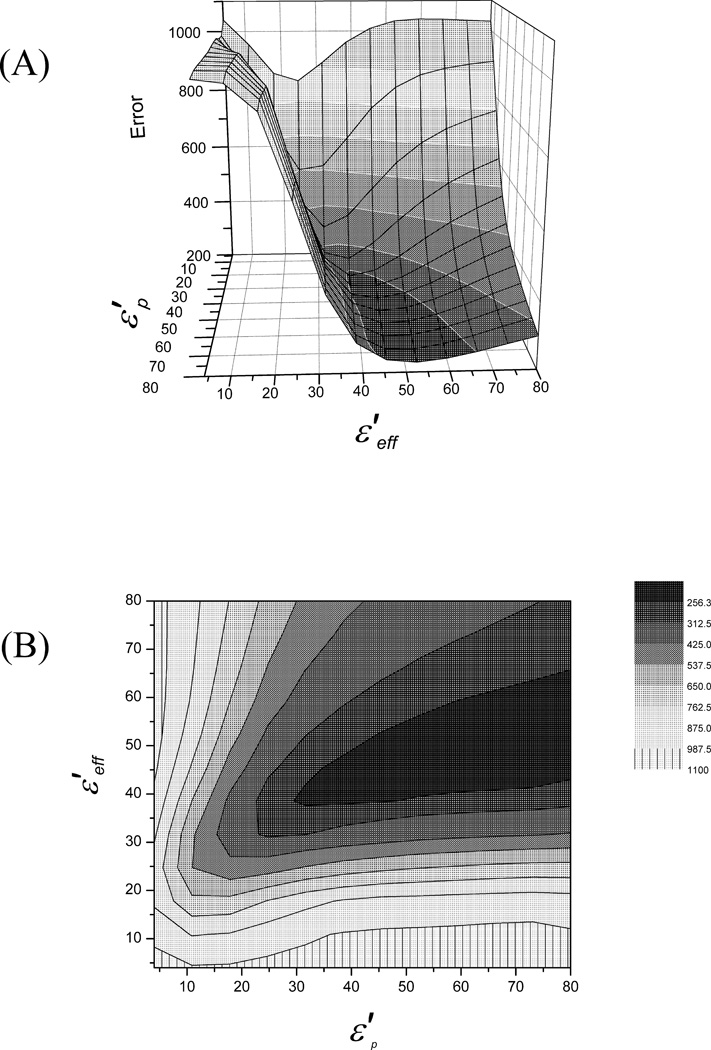
Where i runs on all 45 test proteins, and $F_{\text{error}}({\mathrm{\epsilon }}_{\mathrm{p}}^{\prime },{\mathrm{\epsilon }}_{\text{eff}}^{\prime })$ is the sum of the absolute value of errors between calculated and observed stabilities, for a specific value of ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }$ and ${\mathrm{\epsilon }}_{\text{eff}}^{\prime }$. The resulting surface is shown in Figures 4(A) and 4(B).

Figure 4.

The surface (A) and contour plots (B) of $F_{\text{error}}({\mathrm{\epsilon }}_{\mathrm{p}}^{\prime },{\mathrm{\epsilon }}_{\text{eff}}^{\prime })$. In these plots it is clearly shown that the best fitted values for the dielectric constants follow approximately the line ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }={\mathrm{\epsilon }}_{\text{eff}}^{\prime }$, and that for ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }={\mathrm{\epsilon }}_{\text{eff}}^{\prime }=40$ and above, the error reaches its minimum plateau.

As seen from the figures, the best fitted values of ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }$ and ${\mathrm{\epsilon }}_{\text{eff}}^{\prime }$ follow approximately a line where ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }={\mathrm{\epsilon }}_{\text{eff}}^{\prime }$, and the global minimum occurs approximately where ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }={\mathrm{\epsilon }}_{\text{eff}}^{\prime }=40$. Thus, it is concluded that the best fitted dielectrics needed for prediction of protein stability is the one around ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }={\mathrm{\epsilon }}_{\text{eff}}^{\prime }=40$.

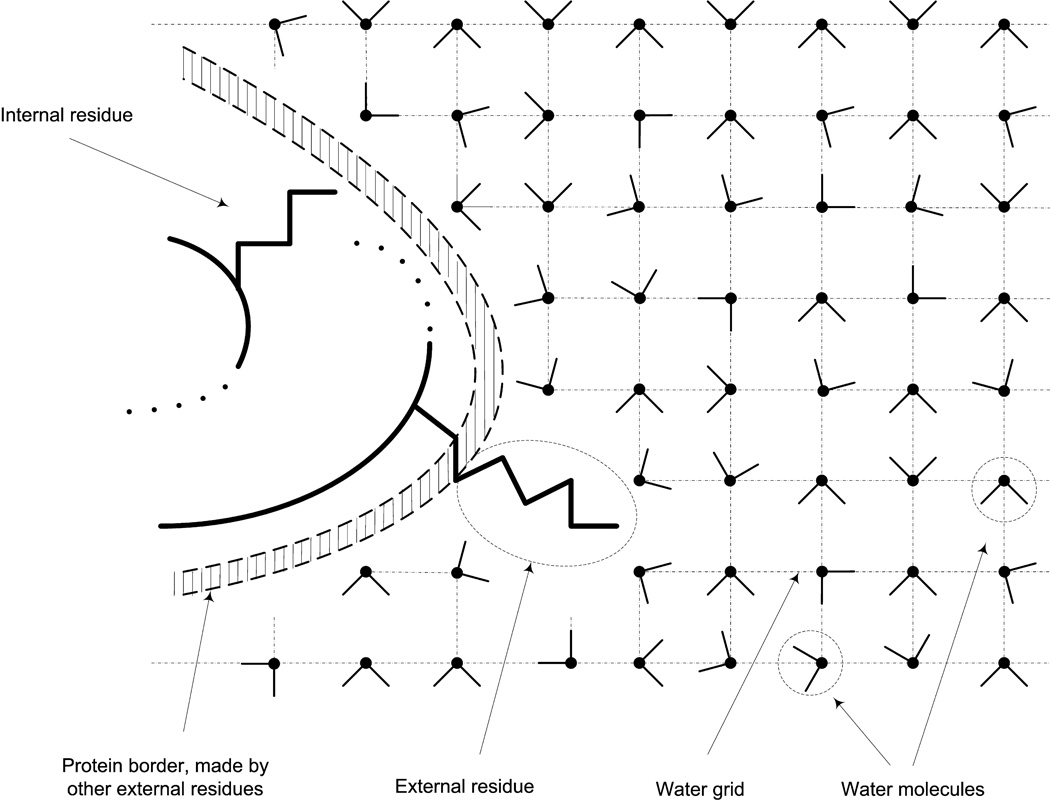
To improve the performance of our model, we started with a global analysis of the reasons for the disagreement between the calculated and observed values shown in Figure 3. This analysis focused first on the location of the ionized residues in the cases that have not produced satisfactory results. This was done by evaluating the distance between the ionized groups to the closest water molecule using the grid created by MOLARIS in the initial process of generating the SCAAS water sphere (see Refs. ²⁹ and ³⁶ for earlier studies along this line). The use of water grid in the identification of the internal/external residues is illustrated in Figure 5.

Figure 5.

Illustrating our procedure for defining internal groups. The protein is surrounded by a cubic grid of water molecules and the distance between the water oxygen and the given group is used to determine whether the group is internal or external.

The above grid analysis indicated that the main problem is associated with internal groups, and led us to modify our approach, with the working hypothesis that in the case of truly internal groups it is better to use lower ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }$ while still using a large ${\mathrm{\epsilon }}_{\text{eff}}^{\prime }$. This was done by defining an internal residue when the following conditions occur: (a) the shortest distance between a grid point and a heavy atom of the given residue is higher or equal to the threshold value reported in Table II, depending upon the type of the residue, and (b) the given residue has a low number of water molecules within a radius of 5 Å (five or less water molecules) from its geometrical center. Condition (b) was used mainly as a verification of condition (a).

Table II.

The Threshold Distances Between the Terminal Heavy Atom of the Given Amino Acid and the Closest Grid Point (The Closest Water Molecule)

Residue type	Threshold (Å)
ASP	5.0
GLU	5.2
HIS	5.2
LYS	5.5
ARG	5.7

For example, a Glu residue is considered to be internal when there are five or less water molecules within a distance of 5 Å from its geometrical center, and the closest water is 5.2 Å or more from its furthest heavy atom, which in this case is one of the two oxygen atoms off its side chain.

If a single ionizable residue is identified as an internal residue, then the intrinsic pK_a for this residue is chosen to take a value between the calculated $\mathrm{p}{K}_{i,\text{int}}^p$ for ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }=8$ and the $\mathrm{p}{K}_{i,\text{int}}^p$ for ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }=20$. For example, if a tested protein has 20 ionizable residues, and residue 17 is identified as internal, then in Eq. (7), for residue i = 17 the pK_a value used will be:

$$\mathrm{p}{K}_{17,\text{int}}^p({\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }=\text{fixed})\simeq \frac{\mathrm{p}{K}_{17,\text{int}}^p({\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }=8)+\mathrm{p}{K}_{17,\text{int}}^p({\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }=20)}{2}$$ (9)

Now Eq. (7) for this case (protein with 20 ionizable residues and one internal residue) becomes:

$$\mathrm{\Delta }{G}_{\text{fold}}^{\text{elec}}({\mathrm{\epsilon }}_{\mathrm{p}}^{\prime },{\mathrm{\epsilon }}_{\text{eff}}^{\prime })=-2.3RT\sum _{\begin{array}{c}\hfill i=1\hfill \\ \hfill i\ne 17\hfill \end{array}}^{20}{Q}_i(\mathrm{p}{K}_{\mathrm{i},\text{int}}^p({\mathrm{\epsilon }}_{\mathrm{p}}^{\prime })-\mathrm{p}{K}_{\mathrm{i},\mathrm{w}}^{\mathrm{w}})-2.3RT{Q}_{17}(\mathrm{p}{K}_{17,\text{int}}^{\mathrm{p}}({\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }=\text{fixed})-\mathrm{p}{K}_{17,\mathrm{w}}^{\mathrm{w}})+166\sum _{i\ne j}{Q}_i{Q}_j\left[\frac{1}{r_{ij}{\mathrm{\epsilon }}_{\text{eff}}^{\prime }}\right]$$ (10)

In some cases we identified internal ionizable residues with a very large difference between calculated $\mathrm{p}{K}_{i,\text{int}}^p({\mathrm{\epsilon }}_{\mathrm{p}}^{\prime })$ and $\mathrm{p}{K}_{i,w}^w$. In these cases we found it useful to use an even lower value of ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }$. Thus we further refined our procedure and used an intrinsic pK_a subscript that corresponds to ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }=8$ when the difference $\mathrm{p}{K}_{i,\text{int}}^p({\mathrm{\epsilon }}_{\mathrm{p}}^{\prime })-\mathrm{p}{K}_{i,w}^w$ for values of ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }$ between 4 and 8 was positive and higher than 4 for Asp and Glu, and negative and lower than −3 for Lys and Arg.

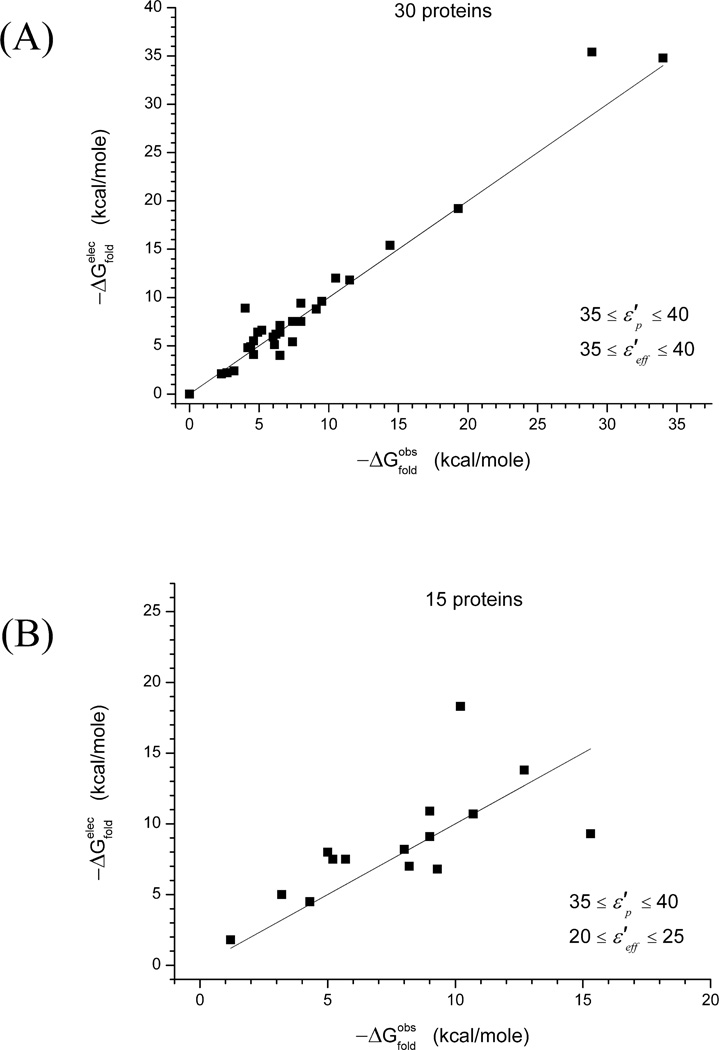
Assigning lower ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }$ values and using the corresponding $\mathrm{p}{K}_{i,\text{int}}^p({\mathrm{\epsilon }}_{\mathrm{p}}^{\prime })$ for the internal ionizable residues, resulted in a significant increase in the accuracy of the calculated ΔG_fold for our protein test set. Now the majority of the proteins were showing excellent ΔG_fold predictions for dielectrics of ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }={\mathrm{\epsilon }}_{\text{eff}}^{\prime }\approx 40$. However, we also observed that a significant fraction of the tested proteins give more accurate results for $35\le {\mathrm{\epsilon }}_p^{\prime }\le 40$ and $20\le {\mathrm{\epsilon }}_{\text{eff}}^{\prime }\le 25$. The result for both cases are shown in Figures 6(A) and 6(B), respectively.

Figure 6.

The correlation between $\mathrm{\Delta }{G}_{\text{fold}}^{\text{elec}}$ and $\mathrm{\Delta }{G}_{\text{fold}}^{\text{obs}}$ after using lower ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }$ for the internal residues. Both Figures 6(A) and 6(B) use the same representation as in Figure 3. In this case, the test proteins fall into two main categories: (a) the one shown in Figure 6(A) where the best fitted $\mathrm{\Delta }{G}_{\text{fold}}^{\text{elec}}({\mathrm{\epsilon }}_{\mathrm{p}}^{\prime },{\mathrm{\epsilon }}_{\text{eff}}^{\prime })$ is in the range of $35\le {\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }\le 40,35\le {\mathrm{\epsilon }}_{\text{eff}}^{\prime }\le 40$, and (b) the one shown in Figure 6(B) where the best fitted $\mathrm{\Delta }{G}_{\text{fold}}^{\text{elec}}({\mathrm{\epsilon }}_{\mathrm{p}}^{\prime },{\mathrm{\epsilon }}_{\text{eff}}^{\prime })$ is in the range $35\le {\mathrm{\epsilon }}_p^{\prime }\le 40,20\le {\mathrm{\epsilon }}_{\text{eff}}^{\prime }\le 25$. The majority of the test proteins fall into the first category.

Some of the results obtained after the specialized treatment of the internal residues were still puzzling. That is, although the majority of the proteins tests were giving excellent results for ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }={\mathrm{\epsilon }}_{\text{eff}}^{\prime }=40$, there was still a significant number of proteins where $\mathrm{\Delta }{G}_{\text{fold}}^{\text{elec}}({\mathrm{\epsilon }}_{\mathrm{p}}^{\prime },{\mathrm{\epsilon }}_{\text{eff}}^{\prime })$ was substantially lower than ΔG_fold, (see Fig. 6B). However, the fact that in both cases the value of ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }$ was around 40, indicated that the problem is due to ${\mathrm{\epsilon }}_{\text{eff}}^{\prime }$, that produced — in certain cases—the underestimation of ΔG_fold. To decipher this non obvious behavior of ${\mathrm{\epsilon }}_{\text{eff}}^{\prime }$, we concentrated on proteins cases where point mutation resulted in “shifting” the best fitted values of ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }$ and ${\mathrm{\epsilon }}_{\text{eff}}^{\prime }$ from the $35\le {\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }\le 40$ and $35\le {\mathrm{\epsilon }}_{\text{eff}}^{\prime }\le 40$ range to the $35\le {\mathrm{\epsilon }}_p^{\prime }\le 40$ and $20\le {\mathrm{\epsilon }}_{\text{eff}}^{\prime }\le 25$ range, and vice versa. This was found in the case of the CSP where we examined examined three proteins with high sequence similarities and only a few point mutations. In the case of bs-CSP we obtained the best results in the $35\le {\mathrm{\epsilon }}_p^{\prime }\le 40$ and $20\le {\mathrm{\epsilon }}_{\text{eff}}^{\prime }\le 25$ range, in the case of bc-CSP we obtained the best results in the $35\le {\mathrm{\epsilon }}_p^{\prime }\le 40$ and $25\le {\mathrm{\epsilon }}_{\text{eff}}^{\prime }\le 30$ range, while in the case of tm-CSP we obtained the best results in the $35\le {\mathrm{\epsilon }}_p^{\prime }\le 40$ and $35\le {\mathrm{\epsilon }}_{\text{eff}}^{\prime }\le 40$ range. The analysis of this data indicated that the interaction of Lys residue with charged residues at 10 Å or less leads to the above shift. Thus, we modified the ${\mathrm{\epsilon }}_{\text{eff}}^{\prime }$ for the interaction of Lys with negatively charged residues by using:

$${({\mathrm{\epsilon }}_{\text{eff}}^{\prime })}_{\text{shifted}}=0.8{\mathrm{\epsilon }}_{\text{eff}}^{\prime }$$ (11)

for a distance r_ij ≤ 10 Å.

This special treatment is rationalized by the fact that Lys residues can move their center quite easily and thus can adjust their interaction with counter ions (see analysis in our previous work⁶¹).

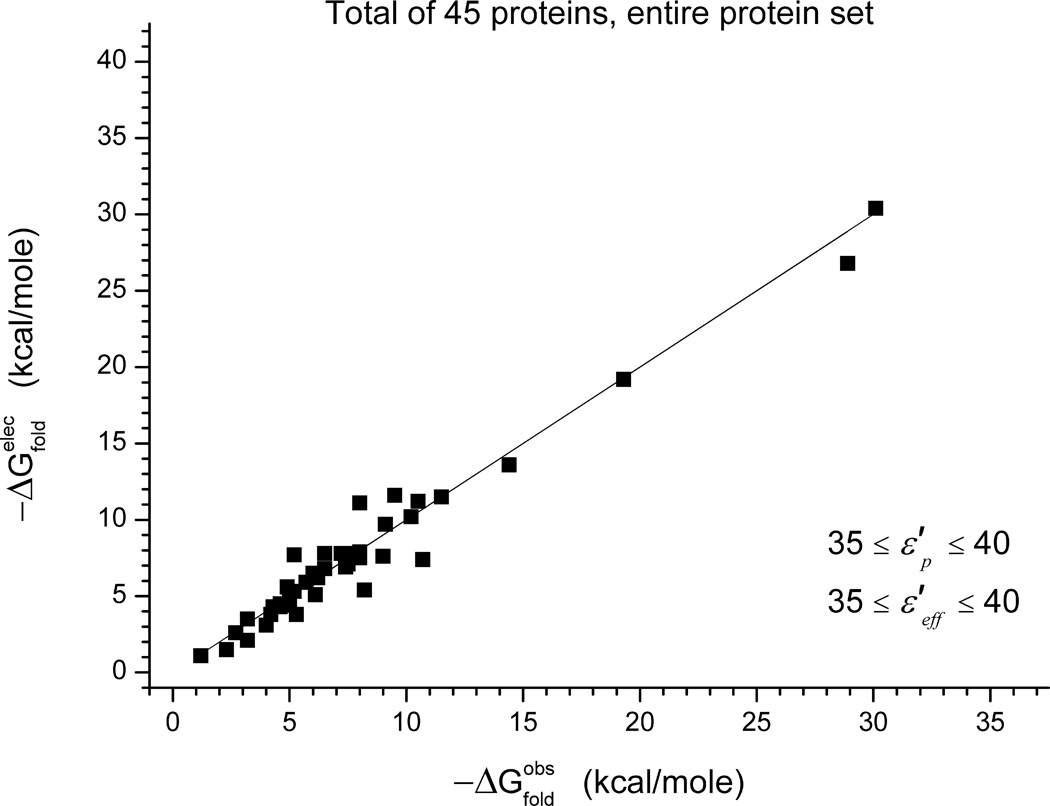
Using both the modified ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }$ and ${\mathrm{\epsilon }}_{\text{eff}}^{\prime }$ for Lys allowed us finally to obtain much better results, as shown in Figure 7, and in the corresponding columns in Table III. Now the agreement between the best fitted $\mathrm{\Delta }{G}_{\text{fold}}^{\text{elec}}({\mathrm{\epsilon }}_{\mathrm{p}}^{\prime },{\mathrm{\epsilon }}_{\text{eff}}^{\prime })$ and ΔG_fold is excellent.

Figure 7.

The best fitted $\mathrm{\Delta }{G}_{\text{fold}}^{\text{elec}}({\mathrm{\epsilon }}_{\mathrm{p}}^{\prime },{\mathrm{\epsilon }}_{\text{eff}}^{\prime })$ and observed ΔG_fold for the tested proteins, after the use of lower ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }$ for the internal residues and lower ${\mathrm{\epsilon }}_{\text{eff}}^{\prime }$ for the Lys with r_ij ≤ 10 Å. In this case, all proteins show best fitted values of $\mathrm{\Delta }{G}_{\text{fold}}^{\text{elec}}({\mathrm{\epsilon }}_{\mathrm{p}}^{\prime },{\mathrm{\epsilon }}_{\text{eff}}^{\prime })$ when dielectric constants are in the range of $35\le {\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }\le 40,35\le {\mathrm{\epsilon }}_{\text{eff}}^{\prime }\le 40$. The difference between best fitted $\mathrm{\Delta }{G}_{\text{fold}}^{\text{elec}}({\mathrm{\epsilon }}_{\mathrm{p}}^{\prime },{\mathrm{\epsilon }}_{\text{eff}}^{\prime })$ and observed ΔG_fold has significantly decreased, compared to the previous cases of Figures 3 and 5. (For 45 proteins, the average difference is reduced to 0.7 kcal/mole.)

Table III.

Predicted ΔG_fold for the Series of Proteins Considered in this Work^a

No.	Protein	$-\mathrm{\Delta }{G}_{\text{fold}}^{\text{elec}}$	$-\mathrm{\Delta }{G}_{\text{fold}}^{\text{obs}}$	|Error|	Best εp	Best εeff	$-{\overline{\mathrm{D}\mathrm{G}}}_{\text{fold}}^{\text{calc}}$	|Error|
1	SSO7d	7.9	8.0	0.1	40	40	8.5	0.5
2	Thioredoxinb	4.4	9.0	4.6	40	35	3.1	5.9
3	Barstar	5.9	5.7	0.2	35	35	4.9	0.8
4	Apoflavodoxin	4.3	4.3	0.0	35	40	5.0	0.7
5	λ-Repressor	4.5	4.6	0.1	40	40	4.8	0.2
6	Snase	6.3	6.2	0.1	35	40	8.0	1.8
7	BsHpr, Phosphotransferase	3.1	4.0	0.9	40	35	2.1	1.9
8	FeCyt b562	7.7	5.2	2.5	35	40	9.7	4.5
9	Arc Repressor	4.3	4.6	0.3	40	35	1.7	2.9
10	Aspartate Amilotransferase	26.8	28.9	2.1	40	40	31.0	2.1
11	Chey	11.6	9.5	2.1	35	40	13.5	4.0
12	GDH Domain II	5.6	4.9	0.7	35	35	4.2	0.7
13	Histidine Phosphocarrier	5.4	8.2	2.8	40	35	4.5	3.7
14	Phosphotransferase, Histidine containing protein	5.3	5.2	0.1	40	35	4.0	1.2
15	Ribosomal	7.4	10.7	3.3	40	35	6.4	4.3
16	RNase H*	7.1	7.5	0.4	40	35	6.5	1.0
17	Ferridoxinb	3.8	9.3	5.5	40	35	3.2	6.1
18	O-Methyl Guanine DNA methyltransferase	10.2	10.2	0.0	35	35	9.1	1.1
19	Sac7d	7.8	7.4	0.4	40	40	9.0	1.6
20	Histone	7.8	7.2	0.6	40	35	7.6	0.4
21	PFRD-XC4	2.1	3.2	1.1	40	35	1.2	2.0
22	Staphylococcal Nuclease I92K	1.5	2.3	0.8	40	40	2.8	0.5
23	Staphylococcal Nuclease I92E	3.8	4.2	0.4	40	35	2.2	2
24	Staphylococcal Nuclease	11.5	11.5	0.0	35	35	10.3	1.2
25	Bs CSP	1.1	1.2	0.1	35	35	0.8	0.4
26	Bc CSP	5.2	5.0	0.2	40	35	4.2	0.8
27	Tm CSP	6.8	6.5	0.3	35	40	8.0	1.5
28	Ubiquitin D21N	5.1	6.1	1.0	40	35	3.9	2.2
29	Ubiquitin F45W	6.9	7.4	0.5	40	35	5.9	1.5
30	Ubiquitin K27A	4.3	4.4	0.1	40	40	4.8	0.4
31	Tm DHFR	30.4	30.1	0.3	40	35	25.9	4.2
32	Ec DHFR	6.5	6.0	0.5	35	35	4.9	1.1
33	Ribonuclease	11.2	10.5	0.7	40	40	13.1	2.6
34	Glucanase Cb	0.0	0.0	0.0	–	–	0.0	0.0
35	Phospholipid A2	7.8	6.5	1.3	35	40	9.1	2.6
36	Trypsin Proteinase	7.7	7.5	0.2	35	35	6.8	0.7
37	Interleukin	9.7	9.1	0.6	35	35	8.9	0.2
38	Adhesion transferase Y92E	7.5	8.0	0.5	40	40	8.4	0.4
39	Complement	2.6	2.7	0.1	35	35	2.5	0.2
40	Cytochrome b5 Rat	3.5	3.2	0.3	35	35	2.3	0.9
41	Gene V DNA Binding	7.6	9.0	1.4	40	35	6.6	2.4
42	Glu Transferase	13.6	14.4	0.8	35	35	10.2	4.2
43	Growth Factor	0.0	0.0	–	–	–	0.0	0.0
44	Isomerase	19.2	19.3	0.1	40	35	13.7	5.6
45	Ribosomal S6	11.1	8.0	3.1	35	40	12.9	4.9

^aAll free energies reported are in kcal/mol. The third column reports the experimental values of the absolute stabilities of the tested proteins. The last two columns give the predicted stability according to Eq. (12) and the corresponding error. The sources of the observed values are given in Table I.

^bProteins containing a disulfide bond (which is not treated by the present method) where the corresponding “missing” energy is around 5 kcal/mole.

Using the results described in Figure 7 to calculate the sum of errors $F_{\text{error}}({\mathrm{\epsilon }}_{\mathrm{p}}^{\prime },{\mathrm{\epsilon }}_{\text{eff}}^{\prime })$ introduced in Eq. (8), we evaluated again the best fitted values for the dielectric constants by determining the region of $({\mathrm{\epsilon }}_{\mathrm{p}}^{\prime },{\mathrm{\epsilon }}_{\text{eff}}^{\prime })$ where $F_{\text{error}}({\mathrm{\epsilon }}_{\mathrm{p}}^{\prime },{\mathrm{\epsilon }}_{\text{eff}}^{\prime })$ is minimized. This treatment led to the surface described in Figures 8(A) and 8(B). The best fitted region follows again an approximate line where ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }={\mathrm{\epsilon }}_{\text{eff}}^{\prime }$. The main difference between Figures 4 and 8 is that the region with ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }={\mathrm{\epsilon }}_{\text{eff}}^{\prime }$ corresponds to much deeper valley (indicating a minimum in the function $F_{\text{error}}({\mathrm{\epsilon }}_{\mathrm{p}}^{\prime },{\mathrm{\epsilon }}_{\text{eff}}^{\prime })$).

Figure 8.

The surface (A) and contour plots (B) of $F_{\text{error}}({\mathrm{\epsilon }}_{\mathrm{p}}^{\prime },{\mathrm{\epsilon }}_{\text{eff}}^{\prime })$ obtained after refinement of ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }$ for internal groups and ${\mathrm{\epsilon }}_{\text{eff}}^{\prime }$ for Lys. The plots show clearly that the best fitted values for the dielectric constants follow approximately the line ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }={\mathrm{\epsilon }}_{\text{eff}}^{\prime }$, with a global minimum of around $({\mathrm{\epsilon }}_{\mathrm{p}}^{\prime },{\mathrm{\epsilon }}_{\text{eff}}^{\prime })=(40,40)$. This means that values of $\mathrm{\Delta }{G}_{\text{fold}}^{\text{elec}}({\mathrm{\epsilon }}_{\mathrm{p}}^{\prime },{\mathrm{\epsilon }}_{\text{eff}}^{\prime })$ proximal to ΔG_fold can be acquired when ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime },{\mathrm{\epsilon }}_{\text{eff}}^{\prime }$ have high values, and ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }={\mathrm{\epsilon }}_{\text{eff}}^{\prime }$.

Table III summarizes the calculated results for the best fitted dielectric constants. As seen from the Table, we obtained quite accurate results. Most of the protein tested show error of around 1 kcal/mole, and only a few have errors above 2 kcal/mole, while still not exceeding 3 kcal/mole. The average error for the best fitted values of $\mathrm{\Delta }{G}_{\text{fold}}^{\text{elec}}({\mathrm{\epsilon }}_{\mathrm{p}}^{\prime },{\mathrm{\epsilon }}_{\text{eff}}^{\prime })$ (shown on the forth column of Table III) is only 0.7 kcal/mole.

The ΔG_fold values reported in Table III for Glucanase C is zero, since the protein is unstable according to Ref. 50. In this case, it is found experimentally that without the Cys6–Cys27 disulfide bond, the protein is unstable, thus our finding that $\mathrm{\Delta }{G}_{\text{fold}}^{\text{elec}}({\mathrm{\epsilon }}_{\mathrm{p}}^{\prime },{\mathrm{\epsilon }}_{\text{eff}}^{\prime })$ is positive for all dielectric constants, is consistent with the experimental observation, since our calculations do not include the disulfide bond. Protein acidic fibroblast growth factor is also unstable under physiological conditions. It is reported^62,63 that the protein without certain polyanions, remains relatively unstable.

Concerning the two proteins of Thioredoxin^64,37 and Ferridoxin,^3,65 our method underestimated the observed stability by 5 kcal/mole. However, those two proteins contain one disulfide bond, and since a disulfide bond stabilizes a protein with an amount of approximately 5 kcal/mole,^66,67 we consider our method to be successful in predicting their absolute stabilities.

Predicting absolute stabilities of proteins

This work so far has shown that the calculated absolute stability of a protein can be correlated quite accurately with the corresponding observed value, by choosing best fitted values of ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }$ and ${\mathrm{\epsilon }}_{\text{eff}}^{\prime }$ in the region $35\le {\mathrm{\epsilon }}_p^{\prime }\le 40;35\le {\mathrm{\epsilon }}_{\text{eff}}^{\prime }\le 40$.

This however is not fully unbiased since the “best fitted” values are taken as the values that give the best result. Thus, it is important to select a well defined scheme for actually predicting the relevant stability. After considering several options, we concluded that a reasonable prediction can be obtained by using:

$${\overline{\mathrm{\Delta }G}}_{\text{fold}}^{\text{calc}}=\frac{\mathrm{\Delta }{G}_{\text{fold}}^{\text{elec}}(35,35)+\mathrm{\Delta }{G}_{\text{fold}}^{\text{elec}}(35,40)}{4}+\frac{\mathrm{\Delta }{G}_{\text{fold}}^{\text{elec}}(40,35)+\mathrm{\Delta }{G}_{\text{fold}}^{\text{elec}}(40,40)}{4}$$ (12)

The corresponding result for ${\overline{\mathrm{\Delta }G}}_{\text{fold}}^{\text{calc}}$ are shown on the right columns of Table III and in Figure 9. As seen from the figure, the agreement is reasonable (an average error of 1.8 kcal/mole) although less impressive than that of Figure 7. However, in this case, we are not selecting any best fitted values and have a robust way of predicting protein stability.

Figure 9.

Calculated and observed folding energies for all our benchmark. The calculations are done using Eq. (12), rather than by choosing the best fitted values of $\mathrm{\Delta }{G}_{\text{fold}}^{\text{elec}}({\mathrm{\epsilon }}_{\mathrm{p}}^{\prime },{\mathrm{\epsilon }}_{\text{eff}}^{\prime })$, as was in Figure 7.

Dependence of absolute stabilities on the size and fold of the protein

During the validation of our model we examined the possibile influence/dependence of factors such as protein size and fold on absolute stability. To investigate such dependence, we chose the protein test set that included proteins of largely different size and fold. Comparisons of both the observed and the calculated stability with size and fold of proteins didn’t show any particular correlation. For example, there are many small proteins in the test set shown in Table I, which have relatively large values of observed and calculated absolute stabilities (for example SSO7D, Histidine Phosphocarrier and Sac7d) but at the same time there are many that show low values (for example Barstar, PFRD-X64, and Bs CSP). The same trend is observed for large proteins (for example staphylococcal nuclease, isomerase, Tm DHFR, and aspartate amilotransferase show large values of absolute stability, while GDH Domain II, staphylococcal nuclease I92K, and Ec DHFR have low values for absolute stability). Comparison of fold and absolute stability also has not showed any correlation, i.e., whether the structures were mainly alpha, mainly beta, amorphous, or alpha-beta, didn’t show an important difference in absolute stability.

Finally, no correlation between best fitted values of ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }$ and ${\mathrm{\epsilon }}_{\text{eff}}^{\prime }$ and the size or fold has been observed.

A practical and powerful approach for stabilizing proteins

The present approach should provide a powerful new way of stabilizing proteins by systematic mutations and this is expected to help augmenting existing strategies (e.g., Reetz et al.⁶⁸). We can of course just use Eq. (7) and examine systematically different mutant. This is done as a demonstration in Table IV. However, a more effective approach is obtained by differentiating Eq. (7) and evaluating the gradient of the free energy with regards to the charges of the protein residues.

$$\frac{\partial \mathrm{\Delta }{G}_{\text{fold}}^{\text{elec}}}{\partial Q_i}\approx -2.3RT(\mathrm{p}{K}_{i,\text{int}}^{\mathrm{p}}-\mathrm{p}{K}_{i,w}^w)+332\sum _{i\ne j}{Q}_j\left[\frac{1}{r_{ij}{\mathrm{\epsilon }}_{ij}^{\prime }}\right]$$ (13)

Table IV.

Calculated $\mathrm{\Delta }{G}_{\text{fold}}^{\text{elec}}$ for the Set of Dielectrics ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }=40$ and ${\mathrm{\epsilon }}_{\text{eff}}^{\prime }=40$ for Different Proposed Mutations in the Wild Type Lip A^a

Ionized to non polar mutations of the wild type Lip A
Structures	$\mathrm{\Delta }{G}_{\text{fold}}^{\text{elec}}$
Wild type	−7.62b
Arg142Ala	−9.27
Lys23Ala	−9.61
Lys70Ala	−9.65
Lys88Ala	−9.80
Arg107Ala	−10.15
Arg33Ala	−10.31
Lys23Ala//Arg33Ala	−10.64
Lys23Ala//Arg33Ala//Arg107Ala	−12.43
Non polar to ionized mutations of the wild type Lip A
Structures	$\mathrm{\Delta }{G}_{\text{fold}}^{\text{elec}}$
Wild type	−7.62b
Ala38Asp	−8.53
Ala132Asp	−8.96
Ala105Asp	−9.39
Ala15Asp	−9.52
Ala75Asp	−9.77
Ala81Asp	−9.97
Ala20Asp	−10.78
Ala68Asp	−10.89
Ala146Asp	−11.03
Ala97Asp	−11.21
Ala113Asp	−11.63
Charged to non polar mutations of the most stable mutant (variant XI) of Lip A
Structures	$\mathrm{\Delta }{G}_{\text{fold}}^{\text{elec}}$
Variant XI	−10.30b
Lys32Ala	−10.71
Asp133Ala	−11.08
Lys70Ala	−11.16
Lys23Ala//Lys70Ala	−11.32

^aEnergies in kcal/mol.

^bTaken from Ref. 69.

The gradient can then be used in predicting the change of charges that will stabilize the protein, using

$$\mathrm{\Delta }{Q}_i=-\alpha \left(\frac{\partial \mathrm{\Delta }{\mathrm{G}}_{\text{fold}}^{\text{elec}}}{\partial Q_i}\right)$$ (14)

(where α is a scaling factor) and repeating the procedure iteratively we can predict the charge configurations that will increase the stability. Our preliminary validations of the above approach included a demonstration that we can reproduce the energetics of known mutants starting from the native protein, or from other mutants. Experimental validation of our approach should be extremely useful.

DISCUSSION

This work attempted to develop and validate a method for predicting absolute folding free energies. The main idea behind our approach is the hypothesis that the folding free energy is mainly determined by electrostatic free energies. Thus, the working hypothesis is that fitting the relevant dielectric constants will give a highly predicted model. The specific strategy involved evaluation of the intrinsic pK_a by the PDLD/S–LRA method with a given ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }$ and evaluating charge–charge interactions with a dielectric ${\mathrm{\epsilon }}_{\text{eff}}^{\prime }$.

The overall best fitted dielectric constants were found to be in the range of 35–40 for both ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }$ and ${\mathrm{\epsilon }}_{\text{eff}}^{\prime }$. However, a significant improvement was obtained by using a lower value of ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }$ for internal groups and by reducing ${\mathrm{\epsilon }}_{\text{eff}}^{\prime }$ for Lys groups.

As seen from Figure 9, the agreement between calculated and observed stability is reasonable although slightly less impressive than those of Figure 7. However, in this case, we are not selecting any best fitted values of ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }$ and ${\mathrm{\epsilon }}_{\text{eff}}^{\prime }$, and we have a robust way of predicting protein stability. In fact, it is quite possible that the present method can be further improved by, for example, reducing ${\mathrm{\epsilon }}_{\text{eff}}^{\prime }$ for internal ion pairs, or by other physically based refinements.

The validity of our method can be best judged from its performance on the diverse test case used. To the best of our knowledge, such a performance in prediction of absolute folding energies has not been obtained by other approaches. Here, one can argue that the method is empirical and thus may reflect effects that are not related to the electrostatic free energy. We believe, however, that the method captures consistently electrostatic effects and discusses these issues in our previous work (Ref. ²⁰). That is, using Figure 1 we rationalize the high ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }$ even for internal groups by pointing out that going on A → E path corresponds to a folding of polyelectrolyte where the energetics of buried ionized group in the protein interior is reflected in the effective dielectric for charge–charge interactions. We also note that using a large ${\mathrm{\epsilon }}_{\text{eff}}^{\prime }$ is fully consistent with our previous concepts.²⁹ Furthermore, we addressed the puzzling finding that ε_p for calculating pK_a’s is small (when evaluated consistently while considering the local protein relaxation³⁰) while ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }$ for folding calculations is relatively large. This issue was explored in the specific case of ubiquitin where it was concluded that ε_p in pK_a calculations reflects only the relaxation in the D → E step (the protein is near its structure in the charged configuration). On the other hand, ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }$ should reflect implicitly the compensating protein pre-organization in the C → E process (see Figure 5 in Ref. 20). Apparently, since this effect is not included explicitly, we have to use a large value of ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }$.

The present work involved much more extensive benchmark than the one used in Ref. 20 and thus allowed us to refine our ideas about ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }$ and ${\mathrm{\epsilon }}_{\text{eff}}^{\prime }$. We found that the idea of using large dielectrics is confirmed as much as surface groups are concerned. However, for internal groups, it appears that a compromise that involves ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }$ ≤ 20 (which is still quite large) is required.

One may argue that the identification of our calculated folding free energy with electrostatic energy is not fully justified since the effective dielectric reflects non-electrostatic contributions. However, this argument overlooks the logical definition of energy contributions in biophysics. That is, if a given effect scales according to the charges of the system, it can and should be defined as an electrostatic contribution. For example, the free energy change associated with turning a charge on or off (e.g., in redox and pK_a processes) is rigorously defined as electrostatic free energy, despite the fact that the corresponding charging process is associated with a response of the system that reflects all the forces and interactions in the system. The same is true for the charging of an ion in water, which reflects the reorientation of the water molecules and even the water–water Van der Walls interactions. On the other hand, if the folding energy is due to the size of different residues, rather than their charges, it would be logical to state that the folding energy reflects steric repulsion. Alternatively, if we will be able to correlate the absolute folding free energy with the hydrophobicity of the residues, we will be able to say that the folding free energy is determined by the hydrophobic effect. The same is true with regards to configurational entropy effects. This does not mean that hydrophobic and entropic effects do not contribute to the folding free energy. However, the present study indicates that theses contributions may cancel each other in some way. More specifically, it has been long argued that hydrophobic effects contribute in a major way to protein stability (e.g., Refs. ^{70, 71}). While there are overwhelming evidences that such effects are a crucial part of the folding free energy, we are not aware of any clear correlation between the number or position of the hydrophobic residues and the observed absolute protein stability. Thus, although the reason for the luck of correlation is unclear (it may be due to a compensation by configuartional entropy) it seems to us that (until proved otherwise) we should accept the fact that the absolute protein stability is not correlated with the markers of hydrophobic free energy.

One may also claim that our effective dielectric reflect non-electrostatic contributions such as the hydrophobic contributions in the (B) → (D) step of our cycle. This argument is reasonable as much as the cycle (A) → (E) is concerned but less reasonable when Eq. (3) captures the trend in the observed folding energy. At any rate, as long as we cannot establish correlation between hydrophobic markers and absolute stability it would be hard to attribute the folding energy to such effects.

It must be stated here that the present work has not established that the correlation with the electrostatic free energy is perfect. Obvious examples are the effects of SS bonds in the proteins thioredoxin, ferredoxin, and glucanace C. Cases of interaction with the ligand were not explored here carefully by considering the relevant electrostatic contributions. Another interesting case is observed for example in the case of residues of staphylococcal nuclease,⁴³ where the deviation between calculated and observed folding energy is due most probably to the hydrophobic contribution. However, the overall trend is clearly best and overwhelmingly correlated with the electrostatic free energy.

We would also like to mention that it is very likely that we will identify cases where the dielectric constant will not follow our idealized roles. For example, there could be cases where we will have to use higher ${\mathrm{\epsilon }}_{\text{eff}}^{\prime }$, when we have a large number of neighboring charge residues, that will create the equivalent of a high ionic strength. There could be also cases where ${\mathrm{\epsilon }}_{\text{eff}}^{\prime }$ at close distance will have to be decreased (this may be handled by employing a distance dependent dielectric³⁰). To explore and analyze such cases, we will have to focus on more comparative mutational studies, in particular between thermophile and mesophile enzymes. Obviously, further experiments and theoretical studies are clearly needed. Fortunately, recent experimental studies provide remarkable benchmark for such detailed studies.¹⁹ At any rate, regardless of the formal justification of our approach, its power can be exploited in predicting and analyzing protein stabilities.

As mentioned in the results-section, we have not found a correlation between the ΔG_fold and the size of the protein or other characteristic properties. We did observe, however, that regardless of the size or the fold of a protein, a single mutation that turns a charge on or off may have a large impact on stability. This is clearly shown in the case of the staphylococcal nuclease mutations,⁴³ where a single mutation of a non-charged residue into Lysine, reduced the protein’s stability by the enormous amount of around 9 kcal/mole. Therefore, we consider the charges of a protein as a more important factor in determining the overall stability, than the size or the fold. Obviously, various protein sizes and folds may reflect the amount and type of certain ionizable residues within a protein, but in the end it is the charges of those ionizable residues that define the stability.

It may be useful to point out here that Gurd and coworkers⁷² invoked the idea that the stability of proteins could be evaluated by considering the ΔG_ij obtained with ${\mathrm{\epsilon }}_{\text{eff}}^{\prime }$ of 40 or larger. However, this was an almost obvious conclusion for those who accepted the Tanford Kirkwood model⁷³ which overlooked the self energy term and the destabilization expected from this term in non polar regions of the protein (see discussion in Warshel et al.⁷⁴). The interesting finding that seems to emerge from the present and other works is the observation that despite the fact that charges should not be stable in non polar environments the effective environment around charges in proteins behave as a relatively polar environment.

It is significant, however, to note that Eq. (3) does not produce perfect results [and the same is true for Eq. (7)] when ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }$ and ${\mathrm{\epsilon }}_{\text{eff}}^{\prime }$ are equal. In some cases, we had to use ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }$, which is significantly smaller that 40 and this reflects the effect of the self energy. Yet this effect is much smaller than what would be deduced from the assumption that the charged groups are in partially non polar environment. In fact, as established in our previous work (Ref. ²⁰) and the present work the best fitted ${\mathrm{\epsilon }}_{\mathrm{p}}^{\prime }$ is much larger than the one that is requires to obtain the observed pK_a’s. The reasons for this have been discussed in great length in Ref. 20 and it is associated with the compensation in the (D) → (E) step in Figure 1.

Another interesting issue is the acid unfolding effect.⁷⁵ Here, again we are dealing with a full electrostatic effect exactly as is the case in redox processes since the unfolding upon charging of ionizable residues reflects exactly the free energy of the charging process, which always involves structural rearrangements. In other words, it does not matter that the unfolding process is opposed by hydrophobic forces, the overall energetics is rigorously the charging free energy and thus electrostatic free energy. This is very different than the (B) → (D) free energy which is a non-electrostatic energy as it does not involve any change in charge. At any rate, predicting the energetics of the acid unfolding is clearly a task that should be accomplished by our formulation.

The present approach focuses in absolute folding energy and is likely to work well on the less challenging problem of exploring mutational effects. The limited test cases of mutational effects examined in this present work provides encouraging results, but further studies are needed. Here, we have a very extensive set of relevant experiments (e.g., Ref. 43–46, 58).