Emergence of upstream swimming through a hydrodynamic transition

Abstract

We demonstrate that upstream swimming of sperm emerges via an orientation disorder-order transition. The order parameter, the average orientation of the sperm head against the flow, follows a 0.5 power law with the deviation from the critical flow shear rate (γ − γ_c). This transition is successfully explained by a hydrodynamic bifurcation theory, which extends the sperm upstream swimming to a broad class of near surface micro-swimmers that possess front-back asymmetry and circular motion.

Micro-swimmers, including bacteria, copepods, and sperm, swim against fluid flows when seeking food or in order to reproduce [1–3]. For a successful fertilization, sperm must travel a long and complex female reproductive tract to reach the egg. Although much of the work on directed sperm migration has been focused on chemotaxis [4], recent developments show that physical forces actively regulate sperm migration [5–7]. Notably, Ref. [5] demonstrated that sperm migrate against fluid flows both ex vivo and in vitro, and Ref. [7] showed that hydrodynamic forces are responsible for sperm upstream swimming behavior. In this Letter, we report the existence of a finite shear rate required for the onset for upstream swimming in the context of a hydrodynamic bifurcation theory. We also showed that hydrodynamic interactions of a front-back asymmetric swimmer with the wall is a sufficient criterion for upstream rotation.

Experiments were carried out in a wide microfluidic channel, and fluid flows were driven by a syringe pump [see Fig. 1(a)]. Swimming bull sperm were used as a model system in our experiments. In low viscosity fluids, bull sperm swim with a self-rolling [counter-clockwise (CCW) seen from in front of the sperm head] (SMovie1 in [8]) along the long axis of the sperm head [22,23] with a rolling rate of approximately 10 Hz at 38.5°C (bovine core body temperature). Images of the swimming sperm [Fig. 1(b), also SMovie2 in [8]] were recorded and post-processed to obtain sperm trajectories [Fig. 1(c)] and orientations. Figure 1(c) shows that most sperm execute clockwise (CW) circular trajectories on the bottom surface of the channel (viewed from above). For consistency, all the near surface sperm swimming movies were taken from above the surface.

FIG. 1.

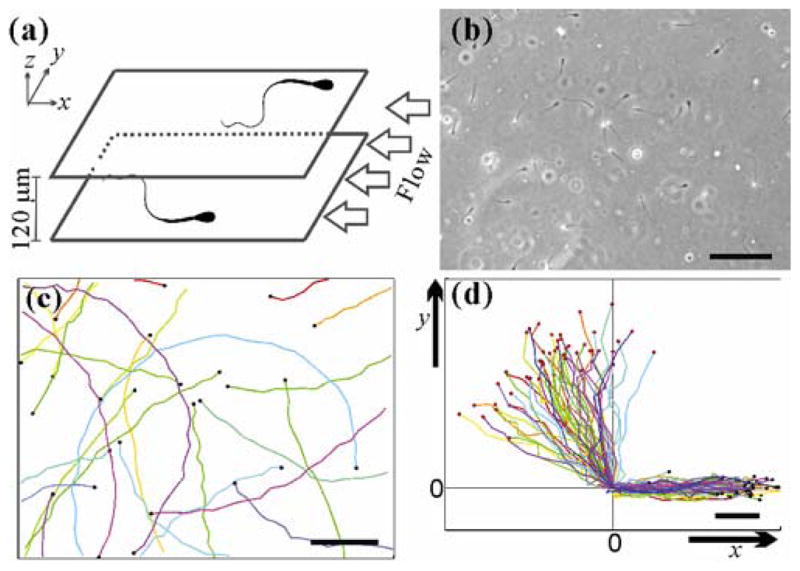
Sperm structure, trajectory chirality, and near-surface swimming. (a) Schematic of experimental setup. Each bull sperm has a paddle-shape head, with approximate dimensions of 10 μm long, 5 μm wide, and roughly 1 μm thick. The head is directly connected to a single flagellum that is about 50 – 60 μm long and tapers from 1 μm in diameter at the connection to 200 nm at the tail end. Mean swimming speed is close to 120 μm/s. Sperm travelling along the surfaces of a microfluidic channel with 2.47 mm width and 120 μm height. Fluid flow is applied in −x direction. (b) A micrograph (570 × 426 μm) of sperm swimming along the lower surface of the central portion of the microfluidic channel. Scale bar: 100 μm. (c) Trajectories (1–6.30s long) of sperm in the absence of the flow. Each colored line is a sperm track that ends at the black dot. CW chirality is seen in the trajectories. Scale bar: 100 μm. (d) Trajectories (1.78 s long) of 30 sperm swimming toward the side wall of the microfluidic channel, and the coordinate (0,0) marks the point where the sperm hits the side wall. The sperm continue to move along the sidewall (or x-axis). Red/black dots are starting/ending positions of the tracks. Scale bar: 25 μm.

Sperm, along with many other ‘pusher micro-swimmers’ such as Escherichia coli [24–26] or Caulobacter crescentus [27], have the tendency to swim near surfaces [28] and sidewalls in microfluidic channels [6,29,30]. This is clearly seen in Fig. 1(d) and SMovie 3&4 in supplemental materials [8], where sperm are shown to swim along a sidewall regardless of the angle at which they hit the wall. In our experiments, sperm rapidly contacted and continued swimming along the upper or lower surface when introduced into a wide microfluidic channel [Fig. 1(a)]. For consistency, all data presented here were taken from the sperm swimming along the lower surface of the channel [6].

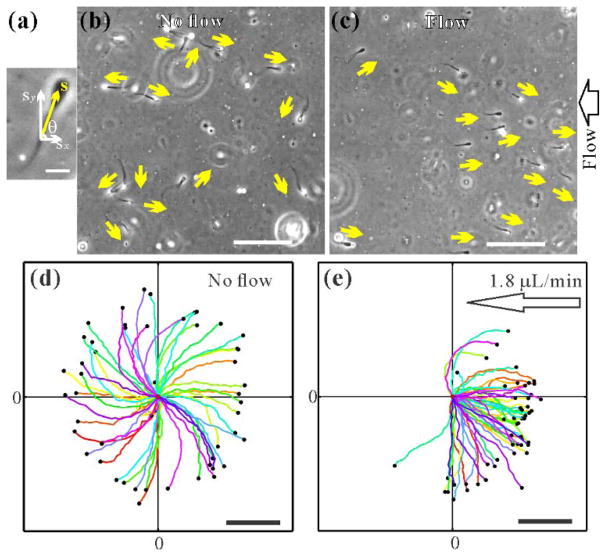
Sperm were seen to re-orient and swim against the flow as the flow rate exceeded a critical value (Fig. 2). This is clearly demonstrated by the sperm head orientations [Figs. 2(b) and (c)], the sperm swimming trajectories at various flow rates [Figs. 2(d) and (e)] and SMovie2&5 in [16]. In the absence of the flow or when the shear rate was below the critical value, sperm swam in all directions [Figs. 2(b) and (d)], and each sperm followed a clockwise (CW, viewed from above) circling trajectory. When the shear rate exceeded the critical value, sperm swam predominantly upstream in nearly straight lines [Fig. 2(e)]. It should be noted that near surface sperm were seen to swim in CW circles with a characteristic curvature (3.0 ± 0.4) × 10⁻³ μm⁻¹ below the flow onset shear rate (Fig. 1(c), Fig. 2(d) and SMovie 2 in [8]). This observation is consistent with previous reports for sea urchin, bovine and human sperm when swimming near surface [5,7,31,32]. In rare cases [e. g. 3 trajectories out of 53 in Fig. 2(d)], sperm circled with a CCW chirality, and those were found to swim via planar beating of the flagellum, a phenomenon that is commonly observed in sperm swimming in viscous fluids [7,23,31]. In this Letter, we focus on the self–rolling sperm motility in Newtonian fluids, although the theory proposed here can be applied to the planar beating sperm in viscous fluids as well.

FIG. 2.

Emergence of upstream swimming and CW swimming chirality. (a) Sperm head orientation is represented by the unit vector, s, where θ is the angle with respect to x-axis. Scale bar: 15 μm. (b) and (c) Micrograph (422.5 × 422.5 μm) of sperm swimming in the absence/presence of the flow (4.5 μL/min). Yellow arrows denote the sperm head orientation. Scale bar: 100 μm. (d) and (e) Trajectories of ~ 50 sperm, each is sampled at 8.91 Hz and 2.81 s long, when there is no flow (d), and when a critical flow rate is exceeded (e). Clockwise (CW) chirality (with an exception of ~6 % of the sperm) is demonstrated in (d). Emergence of directional swimming pattern is clearly shown in (c) and (e). Flows are applied in the −x direction. Scale bar: 100 μm.

The onset of upstream swimming can be understood based on the hydrodynamic model presented in the Supplemental Materials [8]. Based on the linearity of Stokes flow we can superimpose the swimming induced rotation with that due to the imposed fluid flow. Using linearity, symmetry, the observation that sperm swim parallel to the wall, and the fact that the imposed flow on the scale of a sperm is a simple shear flow, the change of sperm orientation s can be written as

$${\stackrel{.}{s}}_i=\omega {\epsilon }_{\mathit{ijk}}{s}_j{n}_k-\nu \left({\delta }_{ij}-s_i{s}_j\right)n_k\frac{\partial u_j}{\partial x_k},$$ (1)

where ν is a dimensionless constant related to the front-back asymmetry of the swimmer [33], u(x) is the imposed flow field, and n is the unit vector normal to the surface. Eq. (1) yields:

$$\stackrel{.}{\theta }=-\omega -\gamma \nu sin\theta ,$$ (2)

where θ is the angle of the sperm relative to the upstream direction and γ is the shear rate at the wall. For a given channel geometry, the volumetric flow rate q and the flow speed at a fixed distance from the wall u are proportional to the shear rate γ.

The physical mechanism leading to sperm rotation is illustrated in Fig. 3(a). In the absence of flow, the sperm body experiences a net resistive force due to the interaction with the wall, F_R, near the wall as a result of self-rolling. A special case can be lubrication force. This force leads to a torque that is responsible for the sperm right hand circling trajectory [Fig. 2(d)] with a constant angular velocity ω [34]. In the presence of the flow (but no cell propulsion), the sperm head and flagellum are carried downstream by the flow, but the head experiences a larger resistive force, F_F, due to the hydrodynamic interaction with the wall, than does the flagellum. This larger resistance leads to a torque orienting the cell upstream. Based on linear superposition, the rotations due to F_R and F_F can be superimposed to yield Eq. (2). A calculation for a simple model swimmer [8] consisting of a spherical head and straight cylindrical flagellum leads to a rotational parameter ν = 0.07 which is within a factor of two of the experimental value of ν = 0.118 ± 0.005. Ref. [7] derived a flow-induced rotation rate consistent with Eq. (2) by considering the shear-induced rotation of a spiral flagellum with one end fixed at the wall, although they did not specify a physical mechanism (e. g. cell-wall resistance) for this constraint.

FIG. 3.

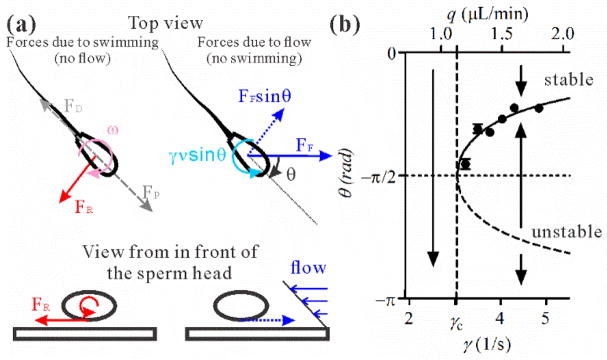
A hydrodynamic model for upstream micro-swimmers. (a) Force diagram of a near surface swimmer subjected to shear flow. Left: Forces due to swimming. When rolling near a surface, the sperm head experiences a net resistive force (e. g. lubrication force) that creates a torque responsible for the CW trajectories observed in Fig. 2(d). Note the propulsion force (F_P) and the drag (F_D) due to the sperm swimming motion do not contribute to the torque. Right: Forces due to fluid flow. Sperm experiences a near wall resistive force that is opposite to the direction of the flow. Due to the front – back asymmetry of the sperm, the head experiences a larger force than its tail, which leads to a torque that orients the sperm upstream. Note that shear is required because both the fluid flow and the no-slip boundary condition are needed for the near wall resistive force to exist. (b) Diagram for a saddle-node bifurcation. No fixed point solution can be found when γ <γ_c. At γ = γ_c, a neutral fixed point solution first shows at θ = −π/2. When γ > γ_c, two fixed point solutions emerge symmetrically on both sides of θ = −π/2 line, one stable θ₀ which falls in the range −π/2<θ₀ <π/2 and one unstable −π − θ₀.

Interestingly, the above equation is an over-damped and forced oscillator equation (also known as Adler equation) [35,36]. The solution to the above equation is a classical saddle-node bifurcation [Fig. 3(b)]. Using Eq. (2), we show that there exists a critical shear γ_c, where γ_c = ω/ν. Below γ_c, no steady state solution exists. The CW circling bias dominates, the sperm swim clockwise following right hand circles, and stay in bound states. Above γ_c, there exists two steady states (or fixed points), θ₀ and −π − θ₀, where sinθ₀ = −ω/γν and −π/2 < θ₀ < π/2. Linear stability analysis (see the next section) around the two fixed points shows that θ₀ is a stable fixed point [37], while −π − θ₀ is an unstable fixed point. This means that the system stays on the fixed point θ₀ above the onset point, which predicts an emergence of the orientation order of upstream swimming at the critical shear rate.

The saddle-node bifurcation described above is verified in our experiments [Fig. 3(b)]. Using the images [Figs. 2(b), (c)], we made precise measurements of sperm head orientation, θ, as a function of flow rate near the transition point [Fig. 3(b)]. A random orientation is seen from the distribution of θ, p(θ), for flow shear rates below γ_c and a preferred swimming direction θ₀, in the form of a peak in p(θ), emerges when shear rate is above a critical value [8]. For those showing a preferred swimming direction, we then fit the distribution p(θ) to a Gaussian curve near the peak region [8], which provides us the measured θ₀. The experimentally measured 1/sinθ₀ is proportional to the volume flow rate q or wall shear γ as predicted by Eq. (2) [8]. A linear fit to the data gives us the experimental onset point q_c =1.13 ± 0.03 μL/min, or γ_c = 3.03 ± 0.08 1/s for upstream swimming. It remains to be explored whether female reproductive tract uses this transition to selectively orient sperm upstream during estrus, as there are as yet no reported flow rate measurements within the bovine reproductive tract.

Further characterizing the transition behavior, we found that the emergence of upstream swimming is continuous [Fig. 4(a)], following a 0.5 power law scaling both in experiments and theory. Here, we define an order parameter, 〈s_x〉, the x-component of the average orientation vector of each sperm 〈s〉 [38], which varies from 0 for isotropic orientation distribution to 1 for perfect alignment in the upstream orientation. Our experimental data shows that 〈s_x〉 ~ (γ − γ_c)^β with an exponent β of 0.53 ± 0.05 [Fig. 4(a)], a value typically found in supercritical bifurcations of dynamic systems [39]. We note here that the sperm orientation |〈s〉| also exhibits an orientation disorder-order transition [8].

FIG. 4.

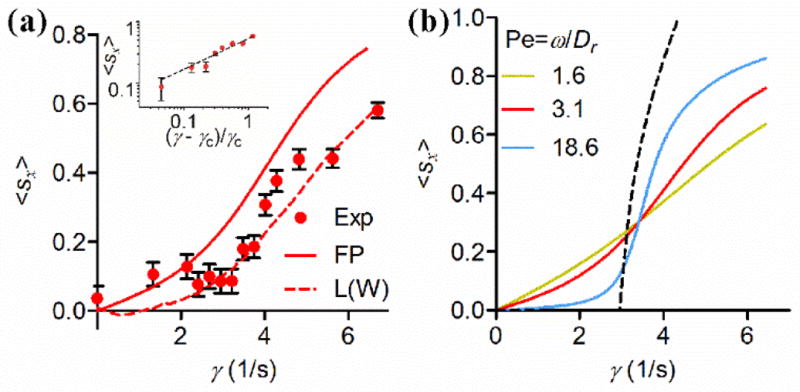
Onset of upstream swimming via a saddle-node transition. (a) The average value of sperm head orientation unit vector along the x-direction (or against the flow direction) 〈s_x〉 versus shear rate γ. Red dots are experimental measurements, red solid line is the solution of the Fokker-Planck equation, and dashed line is the results of Langevin simulation taking into account the wiggling motion. Error bars show standard errors of the mean. Inset: a power law with exponent of 0.53 ± 0.05 is observed above γ_c for measured 〈s_x〉 versus γ curve. The black dashed line is a guideline with an exponent of 0.5. (b) Numerical solution of the Fokker-Planck equation showing that the transition curve becomes steeper with increasing Péclet number (Pe). In the high Pe asymptotic limit, it approaches the black dashed line described by $\sqrt{2}{(\gamma -{\gamma }_c)}^{1/2}$.

The hydrodynamic equation [Eq. (2)] can describe the 0.5 power scaling law shown in Fig. 4. At high Peclet numbers Pe = ω/D_r, rotary diffusion is negligible, and Eq. (2) provides a dynamic equation for the sperm orientation. Here, we perform a linear stability analysis around the fixed point, θ′ =θ₀ + ε, where ε is small, Eq. (2) can be written as

$$\frac{d\epsilon }{dt}=-\gamma \nu cos{\theta }_0\epsilon$$

In order for the fixed point to be stable, γνcosθ₀ needs to be greater than 0. Since γ and ν are both positive, cosθ₀ > 0 in the range of −π/2<θ₀ < 0. The stable solution θ₀ predicts that sperm swim against the flow.

We next examine how 〈s_x〉 will scale with a shear rate around the transition point. We assume γ = γ_c + δ. At high Pe,

$$s_x=cos{\theta }_0={\left(1-\frac{{\omega }^2}{{\gamma }^2{\nu }^2}\right)}^{1/2}={\left[1-\frac{{\omega }^2}{{\gamma }_c^2{\nu }^2}{(1+\delta )}^{-2}\right]}^{1/2}\cong {(2\delta )}^{1/2}$$

Therefore the separation of the fixed points and their distance from the symmetry plane (plane perpendicular to the flow direction) are proportional to (γ−γ_c )^0.5. This scaling accounts for the dependence of the order parameter on the flow shear.

A more complete description of the transition is obtained using the stochastic Adler equation, i.e., Eq. (2) with the addition of a noise term that takes into account a rotational diffusivity D_r [8]. The sperm orientation distribution can be obtained from numerical solutions of the Fokker-Plank (FP) equation or stochastic Langevin simulations for various value of the Peclet number Pe = ω/D_r [8,40]. The two methods yield comparable results [8], and the transition curve from the FP equation is shown in Figs. 4(a) and (b), which predicts the 0.5 power law at the high Pe asymptotic limit, reminiscent of avoided critical behaviors [41]. This solution neglects the wiggling motion of the sperm head, which increases the stability of the swimming as shown by the result from Langevin simulations [dashed red line in Fig. 4(a)].

We note here that the experiments and theory of Ref. [7] like those in our Letter show that sperm upstream swimming is caused by hydrodynamic effects. However, there are two important differences between our work and Ref. [7]. First, by considering the competition between the circling motion of the cells and the rotation induced by the flow induced near wall resistive force, we have identified a critical shear rate needed for upstream swimming to occur. The theory of Ref. [7] considered the sperm swimming to be random in the absence of the flow and did not lead to an onset point from circling to directed upstream swimming. Second, we have that upstream rotation will occur for any front-back asymmetric micro-swimmers interacting hydrodynamically with a surface, so that upstream swimming would be a general phenomenon not requiring the chiral flagellum shape assumed in Ref. [15] [1–3,5–7,42].

We have demonstrated that the onset of upstream swimming can be described by a saddle-node bifurcation in both experiments and theory. The hydrodynamic theory proposed here revealed a simple physical mechanism responsible for upstream swimming, that is - the near wall resistive forces experienced by the near surface swimmers in the presence of flow. The bifurcation theory brings two important insights into the problem of upstream swimming. First, it extends the phenomena of sperm upstream swimming to a broad class of micro-swimmers (e. g. bacteria) that possess front-back asymmetry and execute circular motion near surface. They will all swim against the flows with an onset. Second, it links the onset of upstream swimming to a large class of critical behavior problems through Adler equation, which arises in many fields of engineering and science; they include phase locking of electronic signals in electronics [35], synchronization of flagella beating in biology [36], and current occurrence in Josephson junctions in condensed matter physics [43]. Knowledge gained in learning the physical science system now can be applied for the studies of upstream swimmers [35].

From a physical science perspective, this work provides the first example in a living system where an orientationally ordered state emerges via a saddle-node bifurcation when subjected to a shear flow. This is in contrast to the class of nonlinear pattern forming systems such as Taylor-Couette fluid flows where bifurcation theories have been used successfully [39]. In both cases, shear stress leads to the emergence of order. We emphasize that the emergence of the order reported here comes from the hydrodynamic interaction of each sperm cell with the flow shear at the wall and it differs fundamentally from collective behavior arising in some systems due to particle-particle interactions. From a biology perspective, this work highlights the importance of physical forces and the existence of a hydrodynamic transition in regulating sperm upstream swimming events. It suggests that the co-evolution of sperm and the female reproductive tract may have fine-tuned the motility parameters of sperm and flow rate in the female tract, such that the female tract gains control over sperm migration and directs sperm to fertilization site during estrus. No mechanosensing is necessary for sperm upstream swimming. Such understanding will help the development of novel assisted reproductive technologies and contraceptives.