The Cusp Catastrophe Model as Cross-Sectional and Longitudinal Mixture Structural Equation Models

Abstract

Catastrophe theory (Thom, 1972, 1993) is the study of the many ways in which continuous changes in a system’s parameters can result in discontinuous changes in one or several outcome variables of interest. Catastrophe theory–inspired models have been used to represent a variety of change phenomena in the realm of social and behavioral sciences. Despite their promise, widespread applications of catastrophe models have been impeded, in part, by difficulties in performing model fitting and model comparison procedures. We propose a new modeling framework for testing one kind of catastrophe model — the cusp catastrophe model — as a mixture structural equation model (MSEM) when cross-sectional data are available; or alternatively, as an MSEM with regime-switching (MSEM-RS) when longitudinal panel data are available. The proposed models and the advantages offered by this alternative modeling framework are illustrated using two empirical examples and a simulation study.

Psychologists are often interested in phenomena that change, adapt, manifest, or behave in nonlinear, discontinuous ways. Examples include discontinuities in infant motor skill acquisition (Adolph, Robinson, Young, & Gill-Alverez, 2008), sudden reduction in depression symptoms in the treatment of depression (T. Z. Tang & DeRubeis, 1999) and relapse to alcohol use after a period of successful abstinence (Witkiewitz, van der Maas, Hufford, & Marlatt, 2007). The notion that psychological concepts and behavior could be mapped as discontinuous dynamic systems was initially proposed nearly 80 years ago in Kurt Lewin’s book on topological psychology (Lewin, 1936). Numerous dynamical approaches to understanding and describing psychological systems have been proposed since Lewin’s book (e.g., Smith & Thelen, 1993; Vallacher & Nowak, 1994), but few have been as appealing to a broad audience of psychologists and also rife with controversy (Kolata, 1977) as the catastrophe theory.

Initially proposed in the early 1970s by the mathematician Rene Thom (Thom, 1972, 1993), catastrophe theory is the study of the many ways in which continuous changes in a system’s control parameters/variables can result in discontinuous changes in one or several outcome variables of interest. There are seven types of catastrophe models, each with an increasing number of control variables, behavioral dimensions, and corresponding mathematical functions. The cusp catastrophe model, which has two control variables and one behavioral outcome, has been the most commonly applied in the social sciences, and will be the focus of this paper. Zeeman (1976) used this model to describe a dog’s abrupt shifts in behavioral response between attacking (fight) and retreating (flight) with continuous changes in rage and fear (i.e., the control variables; see Figure 1). Several features of the cusp catastrophe model are evident in Figure 1, including biomodality (i.e., two modes of behavioral response, either fight or flight), divergence (increasing extremeness in the behavioral modes with increasing rage), hysteresis, and bifurcation. Hysteresis refers to the differences in the value of fear that triggers a sudden change in behavior from retreating to attacking (i.e., path B), vs. a sudden change from attacking to retreating (i.e., path C) depending on previous values of the system. That is, while it only takes a slight increase in fear to bring the dog from attacking to retreating if the dog is located at the tipping point of path C, a much lower level of fear is needed to bring the dog from retreating to attacking again once the dog has settled into the lower layer of the folded region (i.e., it would now follow path B, as opposed to path C). Bifurcation, another key feature of the cusp catastrophe system, occurs when continuous changes in one of the independent variables (e.g., rage) yield sudden, qualitative changes in behavior (e.g., a shift from a single mode of outcome to the coexistence of two modes; as shown in the scatterplot of the dog’s behavioral responses against rage in the top left corner of Figure 1). These relations cannot be adequately described using linear equations, thus the introduction of nonlinear differential equations.

Figure 1.

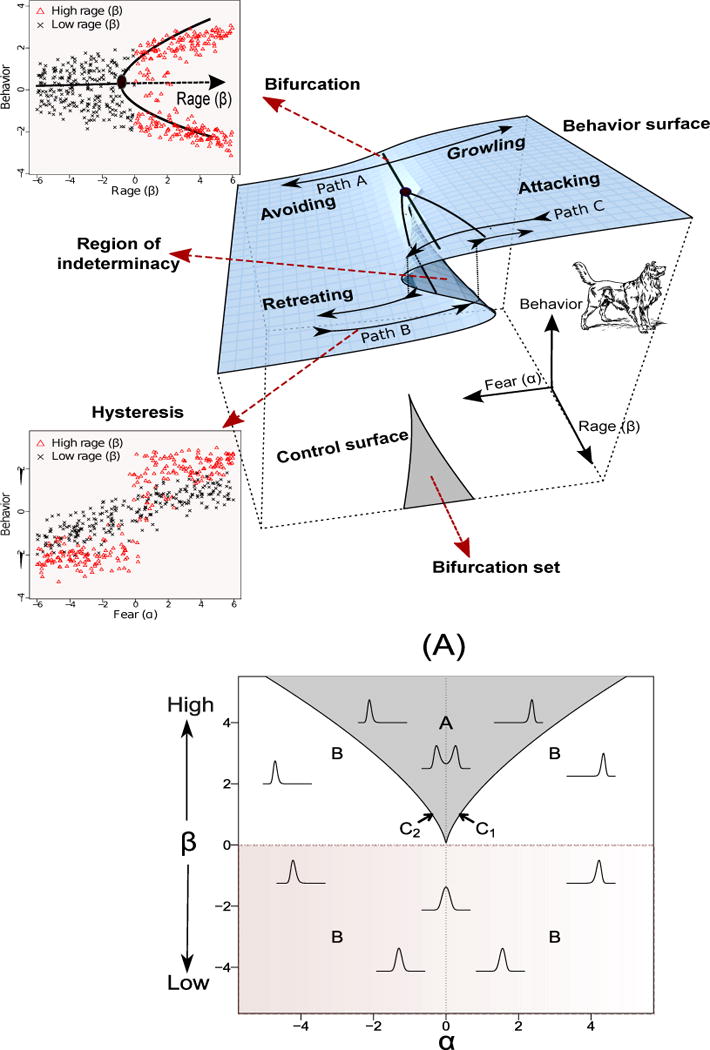
(A) Zeeman’s (1976) use of the cusp catastrophe model to represent the ways in which a dog might undergo sudden transition between attacking and retreating with continuous changes in fear and rage. A plot summarizing the broad categories of behaviors in the cusp system as a function of α and β is shown in subplot (A). The densities overlaid on the α-β plane represent the equilibrium points of y at different values of α and β.

The popularity of catastrophe theory has evidenced some ebbs and flows, as well as a fair share of criticism. Substantively, catastrophe theory has inspired myriad applications in modeling human driving speed (Poston & Stewart, 1978), attitude (Flay, 1978; Latané & Nowak, 1994; Wimmers, Savelsbergh, & van der Kamp, 1998), affective states (Allen & Carifo, 1995; Strahan & Conger, 1999), alcohol use (Clair, 1999; Witkiewitz & G. A. Marlatt, 2004), and developmental discontinuities (Freedle, 1977; Klahr & Wallace, 1976; Preece, 1980; van der Maas & Molenaar, 1992). Despite its conceptual appeal and contribution, widespread applications of such models have been impeded by unresolved difficulties in utilizing current approaches of fitting the cusp catastrophe with empirical data (for more thorough descriptions of the catastrophe models and the empirical challenges in fitting these models see Dultilh, Wagenmakers, Visser, & van der Maas, 2010; Hartelman, Van der Maas, & Molenaar, 1998; van der Maas & Molenaar, 1992; Wagenmakers, Molenaar, Hartelman, & van der Maas, 2005; Witkiewitz et al., 2007). We provide a synopsis of these problems after a brief overview of the mathematical foundation behind the cusp catastrophe system.

Mathematical Background on the Cusp Catastrophe System

In catastrophe systems, changes in a system over time are governed by a deterministic potential function, V (y; θ), written as:

$$\frac{d\mathit{y}}{\mathit{dt}}=-\frac{\partial V(\mathit{y};\mathbf{\theta })}{\partial \mathit{y}},$$ (1)

where y is a vector of dependent variables of interest, usually referred to as the behavioral variables in the catastrophe literature, and θ is a vector of control parameters. Equation 1 indicates that the instantaneous changes in the behavioral variables with each unit of increase in time (as the increments in time get infinitely small), $\frac{d\mathit{y}}{\mathit{dt}}$, are negatively related to changes in the potential function with respect to each of the behavioral variables contained in the vector, $\frac{\partial V(\mathit{y};\mathbf{\theta })}{\partial \mathit{y}}$. If the change in the potential function with respect to the pth behavioral variable, $\frac{\partial V(\mathit{y};\mathbf{\theta })}{\partial y_p}$, is positive, the potential function increases with increase in that behavioral variable; if this value is negative, the potential function decreases with increase in the behavioral variable. If $\frac{\partial V(\mathit{y};\mathbf{\theta })}{\partial \mathit{y}}=0$, then all the dependent variables are “static” or do not manifest any changes over time. Thus, the equilibrium points of the cusp catastrophe systems are values of y for which $\frac{\partial V(\mathit{y};\mathbf{\theta })}{\partial \mathit{y}}=0$. Finding the equilibrium points of a catastrophe system and understanding the dynamics of the system around each of the equilibrium points is a key step toward deducing the long-term behaviors of the system.

One of the simplest forms of catastrophe is the cusp catastrophe (see Figure 1) in which

$$-V(y;\mathbf{\theta })=\frac{1}{2}\beta y^2+\alpha y-\frac{1}{4}{y}^4,$$ (2)

where there is only one behavioral variable and θ = [α β]′ consists of the two control parameters in the system (Gilmore, 1981; Stewart & Peregoy, 1983). In practice, these parameters are often expressed as linear, fixed functions of one or more covariates (e.g., Cobb & Zacks, 1985; Grasman, Van der Maas, & Wagenmakers, 2009; Guastello, 1984; van der Maas & Molenaar, 1992). Thus, the control parameters are sometimes referred to as control variables. The parameter α is referred to as the normal variable or asymmetry variable, whereas β is often referred to as the splitting or bifurcation variable. They are responsible for driving hysteresis and bifurcation, respectively, in the system (Gilmore, 1981; Grasman et al., 2009; Poston & Stewart, 1978). The equilibrium points of the cusp catastrophe system can be obtained by differentiating Equation 2 with respect to y and setting it to zero as

$$\beta y+\alpha -y^3=0.$$ (3)

That is, the roots of (3) depict the equilibrium points of the system under different values of α and β. A stable equilibrium is defined as a point into which a system settles in the long run. The different combinations of α and β values, together with their associated equilibrium points, constitute a 3-dimensional landscape – referred to as the cusp landscape – as depicted in Figure 1. The nature of the equilibrium points that arise under different values of α and β can be deduced from the Cardan’s discriminant of Equation 3 (Grasman et al., 2009; Poston & Stewart, 1978), defined as:

$$D=27{\alpha }^2-4{\beta }^3.$$ (4)

The Cardan’s discriminant, D, conveys information about the nature of the roots of Equation 3 and thus, helps classify the behaviors of the system under different α and β values into 4 broad categories or sets (A, B, C₁ and C₂), which are shown in subplot (A) in Figure 1.¹ Figure 1A, denoted herein as the α-β plane, is a cross-section of the cusp landscape in Figure 1 consisting of different values of α and β. The peaks of the densities superimposed on the plot show the equilibrium points of y conditional on specific values of α and β.

The shaded region labeled as “A” arises when D < 0: it corresponds to the folded region of the cusp landscape, in which multiple equilibrium points — or multimodality — exist for each combination of α and β values. The precise equilibrium point the system settles into depends both on the values of α and β, as well as where the system was located previously. Values of α and β in this range constitute the “bifurcation set” in Figure 1. The areas labeled as “B” outside of the shaded region all correspond to D > 0 and in these areas, there is only one stable equilibrium point for each value of α and β (indicated by the single peak in each conditional density).² The origin represents a bifurcation point at which β = α = 0 and only one equilibrium exists at y = 0; bifurcation – qualitative changes in the number of equilibrium points with continuous changes in β – occurs when this bifurcation point is crossed.

The two branches or borders of the shaded region (C₁ and C₂ in Figure 1A), for which D = 0, constitute the last set of values. These branches correspond to the two sets of “tipping points” in the folded region of the cusp landscape. On each of these branches, the system is characterized by one unstable equilibrium and a stable equilibrium. The precise value of the stable equilibrium depends on whether the system crosses the branch that brings the system from the top layer of the cusp landscape to the bottom layer, or the branch the brings the system from the bottom layer up to the top layer. The more interesting point to note is that these branches give rise to the feature of hysteresis – that is, the dynamics of the system near these branches depend on previous history of the system, or in other words, whether the system was previously located on the top or bottom layer of the cusp landscape. Thus, it can be seen from the scatterplot in the lower left corner of Figure 1 that while a particular level of fear (at around .5 to 1.0) is enough to cause a dog to go from attacking to retreating, a much lower level of fear (at around −.5 to −1.0) is needed to restore the dog from retreating to attacking again.

The scatterplot also highlights the differential changes in the behavioral variable with high versus low β values (i.e., positive vs. negative values of β, respectively). Specifically, with low β, linear increases in α are associated with smooth and linear increases in the behavioral variable; in contrast, with high β, increases in α would result in sudden jumps in the values of the behavioral variable near the origin. This discontinuity in the behavioral variable constitutes the region of indeterminacy on the cusp landscape. Relatedly, this discontinuity also leads to increase in variance in the behavioral variable near the points of sudden transition, another catastrophe flag known as anomalous variance.

Divergence is another flag manifested by the cusp catastrophe system. In the context of the aggression example, divergence means that with increased values of rage, the dog would manifest more extreme transitions in the behavioral variable—namely, showing abrupt transition between retreating and attacking (paths B and C), as opposed to more graduated changes between avoiding and growling (e.g., path A in Figure 1). This tendency further attests to the complex roles of β in instigating bifurcation and divergence. On the one hand, β serves as a categorical indicator of when the cusp system changes from having one (when β < 0) to multiple (when β > 0) equilibrium points (see the top-left plot in Figure 1). On the other hand, as part of the divergence flag, if the system settles into the top bifurcation branch, increasing values of β are associated with increases in the values of the behavioral variable. In contrast, in the lower branch, increasing β values are associated with decreasing values of the behavioral variable. This is reflected in the slight upward versus downward tilt in the cusp landscape with increasing values of β.

Closely associated with divergence are the two remaining catastrophe flags of Divergence of linear response and critical slowing down. These flags are only evident when slight changes are induced in the control variables – either mathematically or experimentally. These flags occur when changes in α and β values near the tipping points of the cusp landscape lead to larger fluctuations in the system (divergence of linear response), and longer time for the system to settle into an equilibrium (critical slowing down).

Limitations of Current Approaches for Fitting the Cusp Catastrophe Models

Current approaches for fitting this model are plagued by several practical and potentially severe methodological limitations. One of the most widely utilized methods, Guastello’s (1982, 1992) approach to fitting the catastrophe models as polynomial regression model, utilizes empirical difference scores as the dependent variable in model fitting. Thus, while this approach is convenient and can be readily implementable with standard statistical packages, it suffers from the same unreliability issues known to plague empirical difference scores (Harris, 1963). The same unreliability issue is inherent in another approach proposed by Browne (1995), who used nonlinear least squares with a Runge-Kutta integration procedure to fit catastrophe models to empirical difference scores. In addition, when Guastello’s approach is used, specialized relationships exist among the parameters from the polynomial regression model and those from the catastrophe models; however, such nonlinear constraints as well as other distributional assumptions are not explicitly imposed in Guastello’s polynomial regression approach. Thus, a researcher may unknowingly interpret the estimates from model fitting assuming that they are linked to parameters from the cusp catastrophe model although, in fact, these estimates are linked to parameters from a completely different model. This issue has been discussed previously by other researchers in the context of fitting linear stochastic differential equation models (Singer, 1992, 1993).

Other approaches for fitting catastrophe models include Oliva’s (1987) least-squares extension, which allows for multiple manifest measures via principal component analysis and factor analysis in a two-step model-fitting process, Cobb’s (Cobb, 1981; Cobb, Koppstein, & Chen, 1983) likelihood approach to fitting a stochastic formulation of the catastrophe models, and related computational improvements (e.g., Grasman et al., 2009; Hartelman et al., 1998). These modified approaches are still characterized by other practical data analytic challenges. First, none of these current approaches readily account for heterogeneities and uncertainties in the timing of switches between behavioral modes, either within or across subjects. Second, model fitting is not performed at the latent variable level, therefore rendering it difficult to distinguish process noise from measurement noise. Third, none of these approaches accommodate longitudinal panel data with multiple subjects, missing data or categorical indicators. Finally, there lacks a straightforward mechanism for comparing the fit of the cusp catastrophe model to alternative models given that: (1) it is unclear what a reasonable comparison model might be, (2) indices such as R² can take on negative values in the presence of skewed data (Grasman et al., 2009), and (3) some of the proposed comparison models (e.g., linear and logistic regression models) have very different probability density functions, and thus, distinct parameter sets, than those associated with the cusp system. Such discrepancies may violate some of the asymptotic conditions needed to derive information criterion (IC) measures such as the Akaike Information Criterion and their correction terms (Bozdogan, 1987; Witkiewitz et al., 2007). More elaborate discussions of the difficulties in fitting the cusp catastrophe model can be found elsewhere (Hartelman et al., 1998; Rosser, 2007; van der Maas, Kolstein, & van der Pligt, 2003; Wagenmakers et al., 2005).

To circumvent the aforementioned modeling and practical limitations, several researchers have begun to consider approximations to the cusp catastrophe models that are more amenable to real-life modeling contexts but still capture selected features of the cusp catastrophe model. Examples include the Hidden Markov Model considered by Dultilh et al. (2010) and a mixture structural equation Model with regime switching (to be detailed in the next section) considered by Chow, Witkiewitz, Grasman, Hutton, and Maisto (2014). Still, these models were designed to capture only limited aspects of the cusp system. For instance Chow et al. (2014) only focused on representing the sudden transitions between the extreme modes of behavior in the cusp catastrophe system (e.g., the transitions between attacking and retreating), while bypassing the fact that with low (or negative) β values, changes in the behavioral variable with changes in α are smooth and do not show sudden jumps. In addition, no formal study has been conducted to evaluate on how well conventional model fit indices and diagnostic tools can help detect cusp-related features when such approximation models are used. Our goals in this paper were to (1) present a formal framework for reformulating the cusp catastrophe model as a mixture structural equation model (MSEM) for use with cross-sectional data, and a mixture structural equation model with regime-switching (MSEM-RS) for use with longitudinal data; and (2) evaluate the extent to which evidence for cusp-related features can be detected using conventional model fit indices and diagnostic tools when these “misspecified” approximation models are used.

The remainder of the article is organized as follows. We first present the general MSEM-RS framework, followed by cross-sectional and longitudinal special cases designed to circumvent some of the practical difficulties associated with fitting the cusp catastrophe model. The new models are then tested and illustrated using a simulation study and two empirical examples. We conclude by discussing the implications of our results, as well as the strengths and limitations of the proposed modeling framework.

Mixture Structural Equation Models with Regime Switching

Structural Equation Modeling (Jöreskog, 1973) is a statistical technique for representing multivariate relationships involving both observed and latent variables. A mixture SEM (MSEM; Dolan & van der Maas, 1998; Jedidi, Jagpal, & DeSarbo, 1997; Vermunt & Magidson, 2005) is an extension of SEM that allows for heterogeneities in the mean and covariance structures of a SEM model conditional on individual i’s unobserved group membership, C_i0, (i = 1, …, n), typically referred to as the individual’s latent class.

In a MSEM, the measurement and structural models for an individual i in latent class h, namely, C_i0 = h, can be expressed, respectively as

$$\begin{array}{cc}({\mathbf{z}}_i|C_{i0}=h)={\mathit{\nu }}_h+{\mathbf{\Lambda }}_h{\mathit{\eta }}_i+{\mathit{\epsilon }}_i,& ({\mathit{\epsilon }}_i|C_{i0}=h)\end{array}~\mathcal{N}(0,{\mathbf{\Psi }}_{\mathit{\epsilon },h}),$$ (5)

$$\begin{array}{cc}({\mathit{\eta }}_i|C_{i0}=h)={\mathbf{\tau }}_h+{\mathbf{\Gamma }}_h{\mathit{\eta }}_i+{\mathbf{\zeta }}_i,& ({\mathbf{\zeta }}_i|C_{i0}=h)\end{array}~\mathcal{N}(0,{\mathbf{\Psi }}_{\zeta ,h}),$$ (6)

where z_i is a p × 1 vector of continuous observed variables for individual i, η_i is a w × 1 vector of latent variables, ν_h and τ_h are, respectively, a p × 1 and a w × 1 vector of intercepts, Λ_h is a p × w matrix of factor loadings, ε_i is a p × 1 vector of measurement errors, Γ_h is a w × w matrix of class-dependent regression effects among the latent variables and ζ_i is a w × 1 vector of disturbances. The subscript h highlights the class-specific nature of the parameters and the index of “0” in C_i0 is used to highlight the time-invariant nature of the latent class membership in MSEM in contrast to the MSEM-RS to be described later. In cases involving discrete or categorical indicators, the corresponding elements in z_i are unobserved and appropriate link functions are used to relate these unobserved continuous variables to their observed indicators (see e.g., Jöreskog & Moustaki, 2001). For instance, with ordinal observed variables, the lth unobserved continuous variable, z_il, is linked to the corresponding manifest ordinal response, $z_{\mathit{il}}^{\ast }$, as (Jöreskog & Moustaki, 2001; B. O. Muthén, 1984)

$$z_{\mathit{il}}^{\ast }=s\iff {\kappa }_{l,s-1}<z_{\mathit{il}}\le {\kappa }_{l,s},s=1,\dots ,S,$$ (7)

where κ_l,h, is a set of threshold values for variable l that is held invariant across individuals.

A multinomial logistic regression model is typically used to represent the class probabilities as

$$\mathrm{Pr}(C_{i0}=h|{\mathit{x}}_{i0})\triangleq {\pi }_{h,i0}=\frac{\exp (a_{h_0}+{{\mathit{b}}^{\prime }}_{h_0}{\mathit{x}}_{i0})}{{\displaystyle {\sum }_{s_0=1}^{K_0}\exp (a_{s_0}+{{\mathit{b}}^{\prime }}_{s_0}{\mathit{x}}_{i0})}},$$ (8)

where a_h0 is the logit intercept for class h; x_i0 is a vector of covariates used to predict class membership, ${\mathit{b}}_{h_0}$ is the associated vector of logit slopes and K₀ is the number of latent classes. For identification purposes, one of the classes has to be designated to be the reference class, with $a_{K_0}$ and ${\mathit{b}}_{K_0}$ set to zeros.

Mixture structural equation models with regime switching (MSEMs-RS) are longitudinal extensions of MSEMs in which individuals are allowed to transition among different latent classes over time (Chow, Grimm, Guillaume, Dolan, & McArdle, 2013; Kaplan, 2008; B. O. Muthén & Asparouhov, 2011; Nylund-Gibson, Muthén, Nishina, Bellmore, & Graham, 2013). These different latent classes can be conceived as distinct phases of a process over time and are commonly referred to as regimes in the time series and econometric literature (Hamilton, 1994; Kim & Nelson, 1999). Here, we use the terms latent class and regime interchangeably, and refer to within-person switches between latent classes as regime switching.

To deal with repeated measures in SEM, z_i and η_i are expanded to include ${\mathbf{z}}_i=[{{\mathbf{z}}^{\prime }}_{i1}\dots {{\mathbf{z}}^{\prime }}_{iT}]\prime$ and ${\mathit{\eta }}_i=[{{\mathit{\eta }}^{\prime }}_{i1}\dots {{\mathit{\eta }}^{\prime }}_{iT}]\prime$. The sizes of all other components in Equations 5–6 are also expanded accordingly to accommodate the presence of multiple time points (e.g., ν_h is now of size pT × 1, as opposed to p × 1; Λ_h is of size pT × wT, etc.). The C_i0 in Equation 8 may then be conceptualized as an indicator of membership in an initial (baseline) class. A separate multinomial logistic regression model is used to describe each individual i’s class membership at time t, denoted as C_it, conditional on membership at time t-1. In the general MSEM-RS framework, the transition in class membership can depend on all previous class membership information (e.g., including C_i0; Asparouhov & B. O. Muthén, 2011). One of the simpler special cases is a first-order Markov specification, which allows the class membership at time t to only depend on the class membership at time t − 1 as

$$\mathrm{Pr}(C_{\mathit{it}}=k|C_{i,t-1}=j,{\mathit{x}}_{\mathit{it}})\triangleq {\pi }_{jk,it}=\frac{\exp (a_{k_t}+{{\mathit{b}}^{\prime }}_{j{k}_t}{\mathit{x}}_{\mathit{it}})}{{\displaystyle {\sum }_{s_t=1}^{K_t}\exp (a_{s_t}+{{\mathit{b}}^{\prime }}_{j{s}_t}{\mathit{x}}_{\mathit{it}})}},$$ (9)

where π_jk,it is individual i’s transition probability of moving from class j at time t-1 to class k at time t; K_t denotes the number of classes at time t, highlighting the possibility that latent classes may emerge or diminish over time. The parameter $a_{k_t}$ is the logit intercept for the kth class at time t, x_it is a vector of fixed covariates for predicting the transition probabilities, with an associated vector of logit slopes, ${\mathit{b}}_{j{k}_t}$. Included in x_it are K_t−1 − 1 binary constants reflecting the deviation in log-odds of switching into latent class k at time t from latent class j (i.e., C_i,t−1 = j, C_it = k), as compared to switching into C_it = k from the reference class, i.e., C_i,t−1 = K_t−1. Note that no binary constants are included in x_i0 in Equation 8 because at time 1, there are no transition probabilities to be predicted, only class probabilities. In addition, time index is included in elements such as K_t, $a_{k_t}$ and ${\mathit{b}}_{j{k}_t}$ to allow the possibility for them to vary over time. Similar to the need to select a reference class among the initial latent classes for model identification purposes, a reference class also has to be selected for each time point and all the logit-related parameters for the reference class have to be set to zeros. This has the effect of setting each row of person i’s K_t−1 × K_t transition probability matrix at time t to sum to 1.

Maximum likelihood estimates of the parameters in the MSEM and MSEM-RS can be obtained via the Expectation-Maximization (EM; Dempster, Laird, & Rubin, 1977; Everitt & Hand, 1981; Titterington, Smith, & Makov, 1985) algorithm. The estimation details have been documented elsewhere (see e.g., Asparouhov & B. O. Muthén, 2011; B. O. Muthén & Shedden, 1999) and are not reiterated here. All model fitting presented herein was performed using a commercial structural equation modeling software, Mplus (L. K. Muthén & B. O. Muthén, 2001).

Cusp Catastrophe-Inspired MSEM and MSEM-RS

In this section, we describe one possible way of circumventing the methodological difficulties behind fitting the nonlinear cusp catastrophe model by approximating it using variations of MSEM/MSEM-RS composed of multiple regimes within which the system’s dynamics are all linear, but differ in meaningful and measurable ways. In this way, we are approximating the multimodal density of y by combining a series of conditional distributions of y that are assumed to be normal within a regime. This approach is similar in rationale to those adopted by others to approximate non-normal data using mixture of normal distributions (e.g., Dolan & van der Maas, 1998), or to approximate nonlinear functions using mixture of linear functions (e.g., Bauer, 2005). Thus, conditional on (i.e., within) a particular regime, a linear structural equation model can be used, and the presence of selected cusp-related features can be tested by means of model fit indices and diagnostic tools designed for use with MSEM and MSEM-RS.

As described earlier, the β variable in the cusp system plays a dual-role: on the one hand, it controls, in a categorical way, when the system bifurcates from a single (when β < 0) to multiple (when β > 0) equilibrium points; on the other hand, higher positive values of β also give rise to increasingly divergent changes in the behavioral variable in a continuous fashion (see Figure 1). In behavioral sciences, however, it is difficult to pinpoint the precise point at which a system undergoes a bifurcation (if at all), unless a researcher has perfect knowledge on the true model, which is never the case in practice. To deal with this challenge, we consider both the scenario that β_i is available as an observed, person-specific covariate, as well as the case that β_i is a latent factor indicated by a number of manifest variables. Furthermore, to capture the emergence of multimodality at high values of β (> 0 in the cusp system), we define an initial class indicator, C_i0, that consists of K₀ = 2 regimes, representing, respectively a high- and a low-β regime as:

$$({\beta }_{\mathit{it}}|C_{i0}=\text{high}\beta )~N({\mu }_{\beta ,\mathit{high}},{\psi }_{\beta ,\mathit{high}}),\text{and}({\beta }_{\mathit{it}}|C_{i0}=\text{low}\beta )~N({\mu }_{\beta ,\mathit{low}},{\psi }_{\beta ,\mathit{low}}).$$ (10)

In this case, membership in the β regimes is latent, as opposed to observed, as is β itself. α_i is assumed in the context as an observed, person- and time-specific covariate, but this assumption can also be relaxed in other applications. Next, we describe ways to test cusp-related characteristics separately for the cases in which the behavioral variable is available cross-sectionally vs. longitudinally. In both scenarios, we assume that data from multiple subjects are available (n > 1).

Cusp-Inspired MSEM

Many applications of the cusp catastrophe model utilize cross-sectional data. In this case, η_i in Equations 5 and 6 reduce to a scalar, y_i. We define three latent classes corresponding, respectively, to a medium (the cusp region in which β < 0 and the distribution of the behavioral variable is unimodal), low (the “retreating” region in Figure 1 with β > 0) and high (the “attacking” region in Figure 1) behavioral regime. These three regimes, denoted respectively as R_med, R_low and R_high, are further defined as showing the following properties:

$$\begin{array}{lll}\underset{¯}{\text{Regime}}\hfill & \underset{¯}{\text{Model}}\hfill & \hfill \\ R_{\mathit{high}}:\text{High}y\hfill & y_i={\tau }_{\mathit{high}}+b_{\alpha ,\mathit{high},\mathit{low}}{\alpha }_i+b_{\beta ,\mathit{high}}{\beta }_i+{\zeta }_i,\hfill & {\zeta }_i~N(0,{\psi }_{\zeta ,\mathit{high}\&\mathit{low}}),\hfill \\ R_{\mathit{med}}:\text{Medium}y\hfill & y_i={\tau }_{\mathit{med}}+b_{\alpha ,\mathit{med}}{\alpha }_i+b_{\beta ,\mathit{med}}{\beta }_i+{\zeta }_i,\hfill & {\zeta }_i~N(0,{\psi }_{\zeta ,\mathit{med}}),\hfill \\ R_{\mathit{low}}:\text{Low}\hfill & y_i={\tau }_{\mathit{low}}+b_{\alpha ,\mathit{high},\mathit{low}}{\alpha }_i+b_{\beta ,\mathit{low}}{\beta }_i+{\zeta }_i,\hfill & {\zeta }_i~N(0,{\psi }_{\zeta ,\mathit{high}\&\mathit{low}}).\hfill \end{array}$$ (11)

where τ_high, τ_med and τ_low denote respectively, the intercept of the high, medium and low behavioral regimes. b_β,high, b_β,med and b_β,low represent the effects of β_i — either as a latent factor or an observed covariate — on y_i, for the high, medium and low regime, respectively. The term b_α,high,low denotes the effect of α_i on y_i in both the high and low behavioral regimes, while b_α,med is the effect of α_i on y_i in the medium regime. This was motivated by the cusp-based characteristic that the effect of α_i on y_i is of comparable magnitude in the high and low behavioral regime (i.e., the top and bottom layers of the fold), but not in the medium behavioral regime. In a similar vein, the residual, ζ_i, is assumed to be normally distributed with zero mean and variance, ψ_ζ,med, for the medium regime, and ψ_ζ,high&low for both the high and low behavioral regimes. Of course, these invariance constraints between the high and low regimes may also be relaxed as needed.

The tendency for the cusp system to show bifurcation with continuous increase in β beyond β = 0 is captured in the MSEM through the specification of two, as opposed to one regime for individuals with high β. The related phenomenon of divergence, namely, the increasingly extreme modes of behavior with increasing β, is operationalized by having regime-specific regression weight of β on y_i. In particular, in the medium regime, corresponding to cases with β < 0, the regression coefficient for β (i.e., b_β,med) may be fixed at zero based on characteristics of the cusp system, or freely estimated as a testable hypothesis. For those in the high behavioral regime (i.e., those who bifurcate into the top branch), the regression weight for β is expected to be positive. In contrast, those in the low behavioral regime are expected to have a negative regression weight for β.

When group membership with regard to β is known and observed, the model is a multiple-group latent class model with 2 known β groups and 3 latent classes (as defined in Equation 11). When β_i is unobserved, the model has 2 latent class indicators: one indicating membership in the β regimes (see Equation 10), and another indicating the 3 behavioral regimes a shown in Equation 11. Furthermore, the log odds of being in the high- vs. low-β class, and the log odds of being in the 3 behavioral regimes given membership in the β regimes, are specified respectively as:

$$\begin{array}{l}\begin{array}{cc}\underset{¯}{\text{Log odds}(C_{i0}=h)}& \underset{¯}{\text{Log odds}(C_{i1}=k|C_{i0}=h,{\alpha }_i)}\end{array}\\ \begin{array}{cc}& \begin{array}{lll}\text{High}y& \text{Low}y& \text{Medium}y\end{array}\end{array}\\ \begin{array}{cc}\begin{array}{c}\text{High}\beta \\ \text{Low}\beta \end{array}\left[\begin{array}{c}{a}_{1_0}\\ 0\end{array}\right]& \begin{array}{c}\text{High}\beta \\ \text{Low}\beta \end{array}\left[\begin{array}{ccc}{a}_{1_1}+b_{{11}_1,\mathrm{\Delta }}+b_{{11}_1,\alpha }{\alpha }_i& a_{2_1}+b_{{12}_1,\mathrm{\Delta }}+b_{{12}_1,\alpha }{\alpha }_i& 0\\ a_{1_1}+b_{{21}_1,\alpha }{\alpha }_i& a_{2_1}+b_{{22}_1,\alpha }{\alpha }_i& 0\end{array}\right]\end{array}\end{array}$$ (12)

The first matrix is the log odds form of Equation 8, which shows the probability of being in a particular regime h at time 0, π_h,i0. Here, a₁₀ indicates the logit intercept associated with being in β regime 1 (i.e., the high β regime) at time 0 (baseline); the log-odds of the last β regime (i.e., the low β regime, the reference class) is set to zero for identification purposes. If β is observed and membership in the β regime is known, $a_{1_0}$ is no longer a modeling parameter but can be obtained using the observed proportions of cases that have positive versus negative values of β.

The second matrix in (12) shows the log odds form of Equation 9, indicating the log odds of being in each of the three behavioral regimes given initial membership in the two β regimes, whether membership in the β regime is known (observed) or unobserved. The rows of the matrix reflect β membership at baseline, while the columns of the matrix denote the event C_i1 = k. In this case, $a_{k_1}$ represents the logit intercept associated with being in behavioral regime k (e.g., 1 = the high y regime and 2 = the low y regime) at time 1, and $b_{1k_1,\mathrm{\Delta }}$ represents the deviation in log odds of switching into the kth behavioral regime given initial membership in the first (i.e., the high) β regime compared to switching into the kth behavioral regime given initial membership in the reference β regime (i.e., the low-β regime). The null elements in the matrix represent elements that are fixed at zero for identification purposes.

The cusp-inspired MSEM provides several possibilities for testing cusp-related properties. For instance, based on the tendency of the cusp system to only bifurcate into the high and low behavioral regimes with positive β value, one may impose the constraints that $a_{1_1}=a_{2_1}=-10$, and that $b_{{21}_1,\alpha }=b_{{22}_1,\alpha }=0$. In this way, the log odds of appearing in the two extreme behavioral models are extremely low given membership in the low-β regime regardless of the values of α.³ Alternatively, these values may be freely estimated. In addition, to evaluate the cusp-related constraint that sudden jumps in behavioral tendency due to α tend to occur only in the high-β region and not in the low-β region, one may evaluate whether the values of $b_{{21}_1,\alpha }$ and $b_{{22}_1,\alpha }$ are significantly different from zero by means of a Wald test or a likelihood ratio test (LRT).

The covariate α_i is used as a person-specific predictor of elements of the transition matrix to allow continuous changes in α to yield sudden jumps in the values of the behavioral variable conditional on membership in the β regimes. As noted earlier, evidence of hysteresis is revealed in part by having distinct probabilities of appearing in the high and low behavioral regimes given initial membership in the high-β regime. As also mentioned earlier, because of the tendency of the cusp catastrophe system to only move into the high or low behavioral regimes with positive β values, one may set the values of $a_{1_1}$ and $a_{2_1}$ to equal to some large negative constant (e.g., −10). In addition, according to the cusp catastrophe model, individuals with high β can only transition between the high and low behavioral regimes. Thus, it may be reasonable to also impose the constraint that $b_{{11}_1,\alpha }=-b_{{12}_1,\alpha }$ so that the log odds of moving into the high behavioral regime increases (decreases) at the same rate as the decrease (increase) in the log odds of moving into the low behavioral regime with changes in α. Consequently, controlling for α, unequal probabilities of appearing in the high and low behavioral regimes are attained when $b_{{11}_1,\mathrm{\Delta }}\ne b_{{12}_1,\mathrm{\Delta }}$ (see similar postulate by Dultilh et al., 2010). As we will demonstrate using a simulation study and two empirical examples, however, whether one can find asymmetry in these class probabilities depends largely on whether there are sufficient cases that are more likely to show sudden jumps in one direction than the other (e.g., cases with β and α values that are closely clustered around the tipping point of the top layer of the cusp so that the the system is much more likely to show a sudden drop, as opposed to a sudden increase, in the behavioral variable). When only cross-sectional data are available, sudden jumps are simply manifested as between-person differences in transition patterns. We next consider a longitudinal cusp-inspired MSEM-RS that can be used to represent within-person sudden jumps in the behavioral variable.

Longitudinal Extension: A Cusp-Inspired MSEM-RS

Longitudinal data afford researchers the opportunity to test postulates of within-person transitions among the behavioral regimes. In this case, a t subscript would have to be added to the terms, y_i, α_i and ζ_i in Equation 11 to highlight their time-varying nature. The bifurcation variable, β_i, can also be time-varying, but we focus herein on time-invariant β. As in Chow, Witkiewitz, et al. (2014), we assume that the transition between regimes from time t-1 to time t depends both on the operating regimes at time t-1, as well as the initial β regime. As distinct from Chow, Witkiewitz, et al., however, we impose additional constraints to eliminate some of the less prevalent regime transition patterns to reduce computational costs.⁴ In particular, we capitalize on features of the cusp model to specify the presence of two behavioral regimes – a high and a low behavioral regime – only for the high-β group/class. For those in the low-β class, only one behavioral regime – the medium behavioral regime – is present. One possible way to implement this specification is to define a higher-order Markov dependency in the transition probability equation as:

$$\mathrm{Pr}(C_{\mathit{it}}=k|C_{i,t-1}=j,C_{i0}=h,{\mathit{x}}_{\mathit{it}})\triangleq {\pi }_{jk,h,it}=\frac{\exp (a_{h,k_t}+{{\mathit{b}}^{\prime }}_{h,j{k}_t}{\mathit{x}}_{\mathit{it}})}{{\displaystyle {\sum }_{s_t=1}^{K_t}\exp (a_{h,s_t}+{{\mathit{b}}^{\prime }}_{h,j{s}_t}{\mathit{x}}_{\mathit{it}})}},$$ (13)

to capture the dependency of the current regime on the regime at time t-1, as well as the initial β regime. In this way, while the matrix of log odds for the initial β regime is identical to the first matrix in (12), only two regimes exist for t = 1, …, T. The critical point here is that the characteristics of these regimes are dependent on an individual’s initial β membership. The log odds of transitioning into the behavioral regimes (the second log odds matrix in (12) then becomes:

$$\begin{array}{c}\underset{¯}{\text{Log odds}(C_{i1}=k|C_{i0}=h,{\alpha }_{\mathit{it}})}\\ \begin{array}{c}\text{High}\beta \\ \\ \text{Low}\beta \end{array}\stackrel{\begin{array}{cc}\text{High}y& \text{Low}y\end{array}}{[\begin{array}{cc}{\mathbf{a}}_{{\mathbf{1}}_{\mathbf{1}}}+b_{{11}_1,\mathrm{\Delta }}+b_{{11}_1,\alpha }{\alpha }_{\mathit{it}}& 0\\ \text{Medium}y& \text{Medium}y\\ {\mathbf{a}}_{{\mathbf{1}}_{\mathbf{1}}}& 0\end{array}]}\\ \begin{array}{c}\text{High}\beta \\ \\ \text{Low}\beta \end{array}\stackrel{\begin{array}{cc}\text{High}y& \text{Low}y\end{array}}{\left[\begin{array}{cc}\mathbf{10}+b_{{11}_1,\mathrm{\Delta }}+b_{{11}_1,\alpha }{\alpha }_{\mathit{it}}& 0\\ \text{Medium}y& \text{Medium}y\\ \mathbf{10}& 0\end{array}\right]}\end{array}$$

and there are two additional 2 × 2 transition matrices conditional on β membership that are parameterized as:

$$\begin{array}{l}\begin{array}{l}\underset{¯}{\text{Log odds}(C_{\mathit{it}}=k|C_{i,t-1}=j,C_{i0}=\text{high}\beta ,{\alpha }_{\mathit{it}})}\\ \begin{array}{c}\text{High}y\\ \text{Low}y\end{array}\stackrel{\begin{array}{cc}\text{High}y& \text{Low}y\end{array}}{\left[\begin{array}{cc}{\mathbf{a}}_{\mathbf{2},{\mathbf{1}}_{\mathit{t}}}+a_{1,1_t}+b_{1,{11}_t,\mathrm{\Delta }}+b_{1,{11}_t,\alpha }{\alpha }_{\mathit{it}}& 0\\ {\mathbf{a}}_{\mathbf{2},{\mathbf{1}}_{\mathit{t}}}+a_{1,1_t}+b_{1,{21}_t,\alpha }{\alpha }_{\mathit{it}}& 0\end{array}\right]\text{and}}\end{array}\\ \begin{array}{l}\underset{¯}{\text{Log odds}(C_{\mathit{it}}=k|C_{i,t-1}=j,C_{i0}=\text{low}\beta ,{\alpha }_{\mathit{it}})}\\ \begin{array}{cc}\begin{array}{c}\text{Medium}y\\ \text{Medium}y\end{array}\stackrel{\begin{array}{cc}\text{Medium}y& \text{Medium}y\end{array}}{\left[\begin{array}{cc}{\mathbf{a}}_{\mathbf{2},{\mathbf{1}}_{\mathit{t}}}+{\mathit{b}}_{\mathbf{1},\mathbf{1}{\mathbf{1}}_{\mathit{t}},\mathbf{\Delta }}& 0\\ {\mathbf{a}}_{\mathbf{2},{\mathbf{1}}_{\mathit{t}}}& 0\end{array}\right]=}& \begin{array}{c}\text{Medium}y\\ \text{Medium}y\end{array}\end{array}\stackrel{\begin{array}{cc}\text{Medium}y& \text{Medium}y\end{array}}{\left[\begin{array}{cc}\mathbf{10}& 0\\ -\mathbf{10}& 0\end{array}\right].}\end{array}\end{array}$$ (14)

As defined previously, the zeros in the last column of all the log odd matrices are needed for identification purposes. A few other constraints (highlighted in bold font) are unconventional but theoretically-driven constraints that are imposed to improve computational costs. First, we define the two regimes that arise under low β to possess identical distributional and behavioral characteristics, and including additional constraints to specify one of the two to be a spurious regime by: (1) setting the log odds of transitioning from the low-β regime to the first medium behavioral regime at $a_{1_1}=10$ to dictate that individuals in the low β regime to always transition into the first of the two medium regimes; and (2) requiring individuals to always stay within either one of the medium regimes by setting $a_{2,1_t}=-10$, and $b_{2,{11}_t,\mathrm{\Delta }}=20$ so the log odds of staying within the first medium regime is $a_{2,1_t}+b_{2,{11}_t,\mathrm{\Delta }}=10$. In addition, parameters such as $a_{1,1_t}$, $a_{2,1_t}$, $b_{1,{11}_t,\mathrm{\Delta }}$and $b_{1,{11}_t,\alpha }$ now allow us to study the prevalence of different within-person transition patterns in targeted ways. For instance, for those in the high-β regime, $a_{1,1_t}$ indicates the deviation in log odds of showing sudden jump from the low to the high behavioral regime relative to $a_{2,1_t}$, and $b_{1,{21}_t,\alpha }$ indicates the extent to which this jump is related to the value of α_it at that specific time point. In a similar vein, $b_{1,{11}_t,\mathrm{\Delta }}$ reflects the deviation in log odds of staying within the high behavioral regime whereas $b_{1,{11}_t,\alpha }$ captures the extent to which this deviation is driven by α_it. Similar to the cusp-inspired MSEM, the MSEM-RS may be used to detect evidence for hysteresis through asymmetry in the probability of transitioning from the high to the low behavioral regime, as compared to transition in the reverse direction (see e.g., Dultilh et al., 2010).

Other specification details pertaining to the behavioral variable while in the high, low and medium behavioral regimes are identical to those specified in the cross-sectional model. We further assume longitudinal invariance by constraining all parameters to be invariant over time. Although the formulation in Equation 11 does not postulate any additional within-person over-time changes in the behavioral variable, or any lagged dependencies of the current behavioral variable on previous values of the behavioral variable, Equation 11 can be modified to accommodate other within-person trends. For instance, as will be illustrated in one of the empirical examples, autoregressive processes can be included by allowing values of y_i,t−q from more distant time points (e.g., from q = 1, 2, and so on) to influence the current y_it. Secular trends such as the weekend and time of the day effects can be included in the structural model by adding exogenous binary indicators at appropriate time points to capture deviations in levels on weekends and specific times of the day. Exogenous variables may also be included in the multinomial logistic regression equations in (8), (9) and (13) as needed. Examples may include extraneous events, age and lifespan developmental changes, gender and other possible determinants of intraindividual change.

Simulation Study

The proposed cusp-inspired MSEM and MSEM-RS are approximations to the cusp catastrophe model and as such, they may be regarded as “misspecified” models. This simulation study was designed to illustrate and evaluate the extent to which standard model selection and comparison indices used within the MSEM and MSEM-RS literature – which were developed on the basis that the true model is among the models considered, or that the degree of misspecification is mild (e.g., no larger than sampling error; Browne, 1984) – can be used to detect evidence for cusp-like characteristics.

Using the cusp package in R (Grasman et al., 2009), we simulated data using the cusp catastrophe model in Equation 2 to yield (1) cross-sectional data with T = 1, observed vs. unobserved group membership, and n = 200 or 500; (2) longitudinal data with T = 6, observed vs. unobserved group membership, and n = 200 or 500. With two designs (cross-sectional vs. longitudinal), each with 2 sample size conditions and two β membership conditions, there were 2 × 2 × 2 = 8 conditions. The conditions considered were by no means exhaustive; our goal is simply to showcase how the MSEM and MSEM-RS models may be used to evaluate selected cusp-based features as testable hypotheses, as opposed to assuming them as true and irrevocable. The sample size configurations were selected to be comparable to the sample sizes in studies utilizing MSEM and MSEM-RS (e.g., Chow et al., 2013), including those utilized in our empirical illustrative examples. The decision to compare conditions with observed vs. unobserved β group membership, in contrast, was motivated by fact that the bifurcation variable β in social/behavioral sciences is often a latent construct and it is of interest to evaluate the viability of the proposed approaches in such scenarios. Five hundred Monte Carlo (MC) replications were run for each condition to provide insights into the asymptotic performance of the proposed approaches. All variations of MSEM and MSEM-RS considered were fitted using Mplus (L. K. Muthén & B. O. Muthén, 2001). Sample Mplus scripts for fitting cusp-inspired MSEM and MSEM-RS to simulated data are available in the supplementary material.⁵

For the cross-sectional conditions, values of α were drawn from a uniform distribution with a range of [−6, 6]. For conditions with observed β membership, we also generated β values from a uniform distribution with range [−6, 6]. These observed β values were used to define an observed group membership (with β group = 0 if β < 0, and β group = 1 otherwise), and also included as an observed continuous predictor of the behavioral variable, y_i, as shown in Equation (11). For conditions with latent β membership, we generated β values from a mixture of two normal distributions with equal probability, with means of −2.5 and 2.5, respectively, and the same standard deviation of .7. We further assumed that these β values were not available directly but rather, were identified using three manifest indicators, with factor loadings λ_β,1 = 1.0, λ_β,2 = 1.2, and λ_β,3 = .9, respectively, and measurement error variances, ${\psi }_{{\beta }_1}^2={\psi }_{{\beta }_2}^2={\psi }_{{\beta }_3}^2=0.09$, respectively. These values were selected to yield relatively reliable manifest indicators for β. In fitting each cusp-inspired model, λ_β,1, was set to 1.0 to identify the model.

For each cross-sectional condition, we fitted 8 MSEM models and examined whether conventional model comparison indices such as LRTs (in cases involving nested models), and IC measures such as the Akaiki Information Criterion (AIC; Akaike, 1973), Bayesian Information Criteria (BIC; Schwarz, 1978) and sample-size adjusted BIC (aBIC; Sclove, 1987) can be used to detect evidence for specific properties of the cusp system. The eight models considered and the research questions to answer are summarized in Table 1.

Table 1.

Summary of Models Used in the Simulation Study.

MSEM	Descriptions	Questions to address
Model 1	The cusp-inspired MSEM in Eqs 11–12, with $a_{1_1}=a_{2_1}=-10$ and $b_{{21}_1,\alpha }=b_{{22}_1,\alpha }=0$ to prevent cases in the low-β regime from moving into the high and low regimes.
Model 2	Same specifications as Model 1, with the exceptions that the values of $a_{1_1}$, $a_{2_1}$, $b_{{21}_1,\alpha }$ and $b_{{22}_1,\alpha }$ were all freely estimated.	Q1: Can the MSEM be used to detect the unique transition patterns of the cusp system? What proportion of MC replications shows significant LRT results in comparing Model 1 to Model 2?
Model 3	A 2-regime model with no explicit constraint.	Q2: Can IC measures detect the existence of 3 regimes?
Model 4	Same specifications as Model 2, with the exception that bβ,high = bβ,low in Eq (11).	Q3: Can evidence of bifurcation be detected? What proportion of MC replications shows significant LRT results comparing Model 2 to Model 4?
Model 5–Model 8	Identical to Models 1–4, respectively, but β was latent; membership in the high- vs. low-β regime was unknown.	Relative differences in performance between Models 1–4 (with known β membership) compared to Models 5–8.
MSEM-RS
Model 1	The cusp-inspired MSEM-RS described in Eqs 11 (with time index to denote repeated measurements), 13 and 14
Model 2	Less restrictive 3-R model: same specifications as MSEM-RS Model 1, with the exception that bα,high,low = bα,med in Eq (11).	Q4: Can the differential effects of α on yit be detected? What proportion of MC replications shows significant LRT results in comparing MSEM-RS Model 1 to 2?
Model 3	The longitudinal analog of the 2-regime MSEM Model 3	Q5: Can IC measures detect the higher-order Markov dependency on Ci0?
Model 4	The longitudinal analog of MSEM Model 4, with bβ,high = bβ,low in Eq. (11).	Q6: Can evidence of bifurcation be detected? What proportion of MC replications shows significant LRT results comparing Model 1 to Model 4?
Model 5–Model 8	Identical to Models 1–4, respectively, but β was latent; membership in the high- vs. low-β regime was unknown.	Relative differences in performance between Models 1–4 compared to Models 5–8 when longitudinal data are used.

For the longitudinal conditions, we generated all β values from a mixture of two normal distributions with equal probability, with means of −2.5 and 2.5, respectively, and the same standard deviation of .7. These β values were either available directly as an observed variable, or were contaminated with measurement errors to yield three manifest indicators, $z_{{\beta }_1}-z_{{\beta }_3}$, with the same measurement specifications as the cross-sectional models. To ensure that there were sufficient instances of sudden jumps between the high and the low behavioral regimes, we drew independent samples of α_it for each individual and time point from a uniform distribution with a slightly narrower range (i.e., Unif[−4, 4]) to yield cases that were more closely clustered around the bifurcation set (see Figure 1). As described earlier, in the interest of improving computational efficiency, we imposed the higher-order Markov transition patterns specified in (14) in the longitudinal MSEM-RS to preclude transition into the two extreme behavioral regimes given membership in the low-β regime. The resultant list of MSEM-RS models considered and the research questions we sought to address are summarized in Table 1.

Simulation Results

Plots of IC and entropy measures obtained from model fitting, as averaged across the 500 MC runs, are shown in Figures 2A–D and 3A–D, respectively, for the two β membership and sample size configurations considered. Entropy values may range between 0 and 1, with values approaching 1 indicate clear delineation of classes, and the value of .90 being a commonly adopted “rule of thumb” for indicating reasonable class separation in empirical studies (Celeux & Soromenho, 1996). Further details pertaining to testing questions 1–6 are summarized in Tables 2–3. Due to space constraints, we only show the summary statistics of the parameter estimates from MSEM Model 6 and MSEM-RS Model 5, the least restrictive MSEM and MSEM-RS models with unknown β membership of the models considered, for the condition where n = 500 (see Tables 4–5). Parameter estimates from fitting these two models to data with n = 200 and their corresponding variations with known β membership are available as online supplementary materials. To aid interpretation, the logit intercept and slope parameter estimates obtained from model fitting were used in conjunction with Equations 8, 9 and 13 to yield the transition probability estimates shown in the tables.

Figure 2.

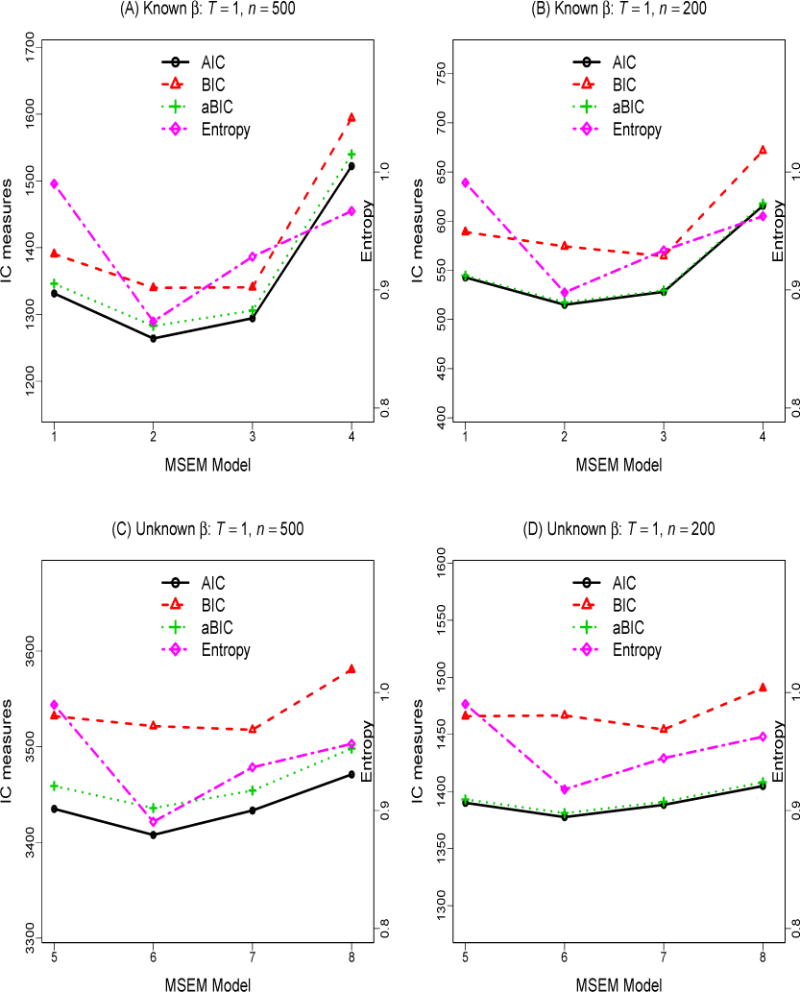
IC measures obtained from fitting different cross-sectional MSEM models (T = 1) across 2 parameter conditions (with known and unknown β), and 2 sample sizes (n = 500 and 200). The eight models considered were: (1) Models 1 and 5: cusp-inspired models with special constraints on transition between regimes, with known and unknown β membership; (2) Models 2 and 6: cusp-inspired models with no constraints on the transition between regimes, with known and unknown β membership; (3) Models 3 and 7: 2-regime models, with known and unknown β membership; (4) Models 4 and 8: models with equal β regression weight on y_i, with known and unknown β membership.

Figure 3.

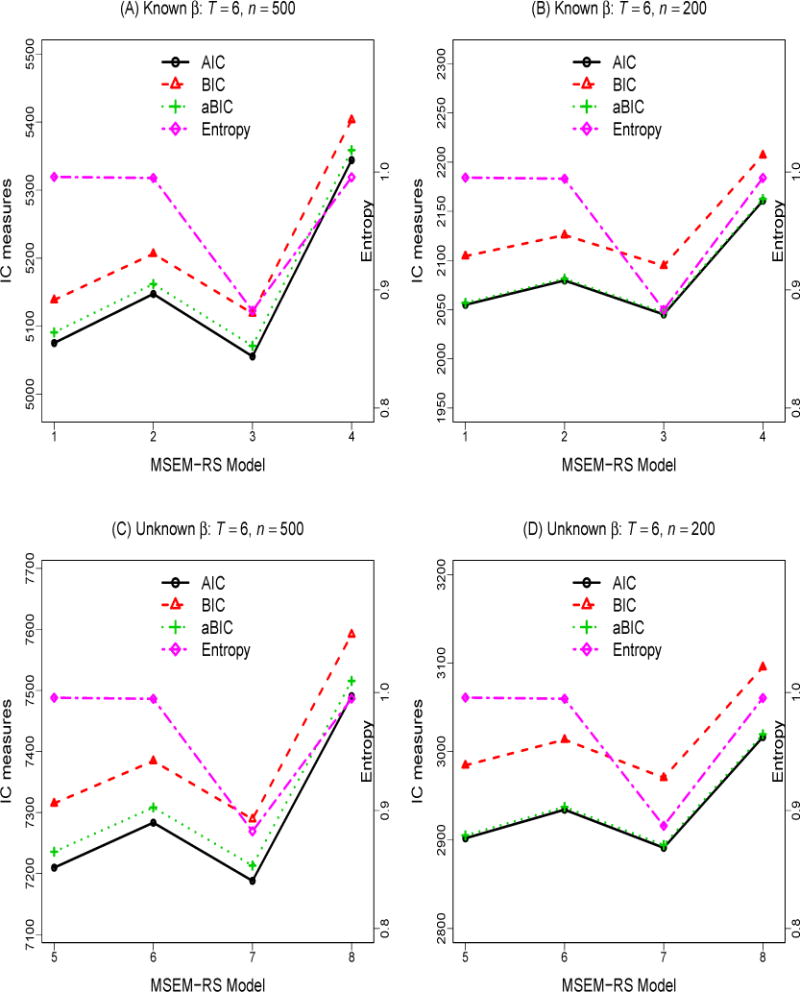
IC measures obtained from fitting different longitudinal MSEM-RS models (T = 6) across 2 parameter conditions (with known and unknown β), and 2 sample sizes (n = 500 and 200). The eight models considered were: (1) Models 1 and 5: cusp-inspired models with special constraints on transition between regimes, with known and unknown β membership; (2) Models 2 and 6: cusp-inspired models with equal regression weight of α_it on y_it, with known and unknown β membership; (3) Models 3 and 7: 2-regime models, with known and unknown β membership; (4) Models 4 and 8: models with equal β regression weight on y_it, with known and unknown β membership.

Table 2.

Summary Statistics of Results from Testing Questions 1–3 Using MSEMs as Highlighted in the Simulation Design Section.

Known β membership, T = 1 and n = 500

Q1: Proportion of MC runs with significant LRT from freeing LO(low β → high) and LO(low β → low) = 1.00

Q2:

Proportion (AIC favors less restrictive 3-R Model to 2-R Model) = 1.00

Proportion (BIC favors less restrictive 3-R Model to 2-R Model) = .51

Proportion (aBIC favors less restrictive 3-R Model to 2-R Model) = .95

Proportion (Entropy favors cusp-inspired 3-R model among all models considered) = .97

Q3: Proportion of MC runs with significant LRT with equal bβ across regimes = 1.00

Proportion (cases free of SE estimation problems for logit parameters in Model 2) =.94

Known β membership, T = 1 and n = 200

Q1: Proportion of MC runs with significant LRT from freeing LO(low β → high) and LO(low β → low) = .96

Q2:

Proportion (AIC favors less restrictive 3-R Model to 2-R Model) = .93

Proportion (BIC favors less restrictive 3-R Model to 2-R Model) = .17

Proportion (aBIC favors less restrictive 3-R Model to 2-R Model) = .90

Proportion (Entropy favors cusp-inspired 3-R model among all models considered) = .89

Q3: Proportion of MC runs with significant LRT with equal bβ across regimes = 1.00

Proportion (cases free of SE estimation problems for logit parameters in Model 2) =.54

Unknown β membership, T = 1 and n = 500

Q1: Proportion of MC runs with significant LRT from freeing LO(low β → high) and LO(low β → low) = .97

Q2:

Proportion (AIC favors less restrictive 3-R Model to 2-R Model) = .99

Proportion (BIC favors less restrictive 3-R Model to 2-R Model) = .35

Proportion (aBIC favors less restrictive 3-R Model to 2-R Model) = .93

Proportion (Entropy favors cusp-inspired 3-R model among all models considered) = .88

Q3: Proportion of MC runs with significant LRT with equal bβ across regimes = 1.00

Proportion (cases free of SE estimation problems for logit parameters in Model 2) =.69

Unknown β membership, T = 1 and n = 200

Q1: Proportion of MC runs with significant LRT from freeing LO(low β → high) and LO(low β → low) = .68

Q2:

Proportion (AIC favors less restrictive 3-R Model to 2-R Model) = .87

Proportion (BIC favors less restrictive 3-R Model to 2-R Model) = .06

Proportion (aBIC favors less restrictive 3-R Model to 2-R Model) = .84

Proportion (Entropy favors cusp-inspired 3-R model among all models considered) = .82

Q3: Proportion of MC runs with significant LRT with equal bβ across regimes = .99

Proportion (cases free of SE estimation problems for logit parameters in Model 2) =.38

Table 3.

Summary Statistics of Results from Testing Questions 4–6 Using MSEM-RSs as Highlighted in the Simulation Design Section.

Known β membership, T = 6 and n = 500

Q4: Proportion of MC runs with significant $\mathrm{\Delta }\alpha =b_{{\alpha }_{\mathit{high},\mathit{low}}}-b_{{\alpha }_{\mathit{med}}}=1.00$

Q5:

Proportion (AIC favors cusp-inspired 3-R Model to 2-R Model) = .24

Proportion (BIC favors cusp-inspired 3-R Model to 2-R Model) = .24

Proportion (aBIC favors cusp-inspired 3-R Model to 2-R Model) = .24

Proportion (Entropy favors cusp-inspired 3-R model among all models considered) = .97

Q6: Proportion of MC runs with significant LRT with equal bβ across regimes = 1.00

Proportion (cases free of SE estimation problems for logit parameters in Model 2) = 1.00

Known β membership, T = 6 and n = 200

Q4: Proportion of MC runs with significant $\mathrm{\Delta }\alpha =b_{{\alpha }_{\mathit{high},\mathit{low}}}-b_{{\alpha }_{\mathit{med}}}=.97$

Q5:

Proportion (AIC favors cusp-inspired 3-R Model to 2-R Model) = .32

Proportion (BIC favors cusp-inspired 3-R Model to 2-R Model) = .32

Proportion (aBIC favors cusp-inspired 3-R Model to 2-R Model) = .32

Proportion (Entropy favors cusp-inspired 3-R model among all models considered) = .86

Q6: Proportion of MC runs with significant LRT with equal bβ across regimes across regimes = 1.00

Proportion (cases free of SE estimation problems for logit parameters in Model 2) =.93

Unknown β membership, T = 6 and n = 500

Q4: Proportion of MC runs with significant $\mathrm{\Delta }\alpha =b_{{\alpha }_{\mathit{high},\mathit{low}}}-b_{{\alpha }_{\mathit{med}}}=.98$

Q5:

Proportion (AIC favors cusp-inspired 3-R Model to 2-R Model) = .24

Proportion (BIC favors cusp-inspired 3-R Model to 2-R Model) = .21

Proportion (aBIC favors cusp-inspired 3-R Model to 2-R Model) = .24

Proportion (Entropy favors cusp-inspired 3-R model among all models considered) = .73

Q6: Proportion of MC runs with significant LRT with equal bβ across regimes = 1.00

Proportion (cases free of SE estimation problems for logit parameters in Model 2) = 1.00

Unknown β membership, T = 6 and n = 200

Q4: Proportion of MC runs with significant $\mathrm{\Delta }\alpha =b_{{\alpha }_{\mathit{high},\mathit{low}}}-b_{{\alpha }_{\mathit{med}}}=.97$

Q5:

Proportion (AIC favors cusp-inspired 3-R Model to 2-R Model) = .30

Proportion (BIC favors cusp-inspired 3-R Model to 2-R Model) = .24

Proportion (aBIC favors cusp-inspired 3-R Model to 2-R Model) = .29

Proportion (Entropy favors cusp-inspired 3-R model among all models considered) = .62

Q6: Proportion of MC runs with significant LRT with equal bβ across regimes = 1.00

Proportion (cases free of SE estimation problems for logit parameters in Model 2) = .99

Table 4.

Summary Statistics of Parameter Estimates from MSEM Model 6, T = 1 and n = 500 across 500 MC Replications.

	True θ	Mean $\widehat{\theta }$	SD	2.5 %tile	97.5%tile	$a\widehat{SE}$
λβ,1	1.20	1.20	0.01	1.19	1.22	0.01
λβ,2	0.90	0.90	0.01	0.89	0.91	0.01
${\psi }_{\mathit{\epsilon },{\beta }_1}^2$	0.09	0.09	0.01	0.07	0.11	0.01
${\psi }_{\mathit{\epsilon },{\beta }_2}^2$	0.09	0.09	0.01	0.07	0.11	0.01
${\psi }_{\mathit{\epsilon },{\beta }_3}^2$	0.09	0.09	0.01	0.08	0.10	0.01
μβ,high	2.50	2.50	0.05	2.41	2.59	0.05
ψβ,high	0.49	0.49	0.05	0.40	0.58	0.05
μβ,low	−2.50	−2.50	0.05	−2.60	−2.41	0.05
ψβ,low	0.49	0.49	0.05	0.39	0.59	0.05
τhigh		1.06	0.10	0.83	1.21	0.07
bα,high&low		0.12	0.01	0.09	0.15	0.01
bβ,high		0.20	0.03	0.17	0.27	0.02
ψζ,high&low		0.12	0.01	0.09	0.14	0.01
τlow		−1.06	0.10	−1.22	−0.84	0.07
bβ,low		−0.20	0.03	−0.28	−0.16	0.02
τmed		−0.00	0.24	−0.52	0.47	0.15
bα,med		0.18	0.08	0.01	0.31	0.06
ψζ,med		0.19	0.07	0.04	0.31	0.06
$a_{1_0}$, logit intercept for Rhigh β	0.00	−0.00	0.00	−0.01	0.01	0.09
$b_{{11}_1,\mathrm{\Delta }}$, Δ LO(high β → high)		2.84	3.99	−2.02	13.93	2.24
$b_{{12}_1,\mathrm{\Delta }}$, Δ LO(high β → low)		2.74	3.76	−2.21	11.84	2.34
$a_{1_1}$, logit intercept for LO(low β → high)		−1.99	3.84	−11.75	2.93	2.09
$a_{2_1}$, logit intercept for LO(low β → low)		−1.93	3.63	−10.85	3.02	2.23
$b_{{11}_1,\alpha }$, α → ΔLO(high β → high)		1.74	1.01	0.48	4.17	0.65
$b_{{12}_1,\alpha }$, α → ΔLO(high β → low)		−1.75	1.11	−3.94	−0.45	0.66
$b_{{21}_1,\alpha }$, α → LO(low β → high)		1.01	1.12	−0.69	3.95	0.69
$b_{{22}_1,\alpha }$, α → LO(low β → low)		−0.88	1.10	−3.72	0.81	0.69
Pr(high β → high)a		0.41	0.11	0.18	0.60	0.10
Pr(high β → low)		0.39	0.11	0.19	0.58	0.10
Pr(high β → med)		0.20	0.09	0.05	0.42	0.09
Pr(low β → high)		0.19	0.15	0.00	0.55	0.12
Pr(low β → low)		0.20	0.16	0.00	0.55	0.12
Pr(low β → med)		0.62	0.24	0.02	0.98	0.18

MSEM-RS = mixture structural equation model with regime-switching; MC = Monte Carlo; True θ = True parameter values; Mean $\widehat{\theta }$ = Average point estimate for each parameter across MC runs; 2.5%tile and 97.5%tile = 2.5th and 97.5th percentiles for each parameter across MC runs; $a\widehat{SE}=\mathrm{SE}$ estimate for a parameter across MC runs.

^aThe class and transition probabilities were computed using Equations 8, 9 and 12 with α_i set to 0.

Table 5.

Summary Statistics of Parameter Estimates from MSEM-RS Model 5, T = 6 and n = 500 across 500 MC Replications.

	True θ	Mean $\widehat{\theta }$	SD	2.5 %tile	97.5%tile	$a\widehat{SE}$
λβ,1	1.20	1.20	0.01	1.18	1.22	0.01
λβ,2	0.90	0.90	0.01	0.89	0.91	0.01
${\psi }_{\mathit{\epsilon },{\beta }_1}^2$	0.09	0.09	0.01	0.07	0.11	0.01
${\psi }_{\mathit{\epsilon },{\beta }_2}^2$	0.09	0.09	0.01	0.07	0.11	0.01
${\psi }_{\mathit{\epsilon },{\beta }_3}^2$	0.09	0.09	0.01	0.07	0.11	0.01
μβ,high	2.50	2.50	0.05	2.41	2.60	0.05
ψβ,high	0.49	0.50	0.05	0.40	0.61	0.05
μβ,low	−2.50	−2.50	0.04	−2.59	−2.42	0.05
ψβ,low	0.49	0.48	0.05	0.40	0.58	0.05
τhigh		0.58	0.12	0.03	0.73	0.06
bα,high&low		0.24	0.01	0.23	0.26	0.01
bβ,high		0.27	0.04	0.22	0.46	0.02
ψζ,high&low		0.18	0.01	0.17	0.20	0.01
τlow		−0.57	0.13	−0.72	−0.02	0.06
bβ,low		−0.27	0.05	−0.47	−0.22	0.02
τmed		−0.00	0.01	−0.03	0.03	0.01
bα,med		0.24	0.01	0.23	0.26	0.01
ψζ,med		0.26	0.01	0.24	0.28	0.01
$a_{1_0}$, logit intercept for Rhigh β	0.00	0.00	0.01	−0.00	0.02	0.09
$b_{{11}_1,\mathrm{\Delta }}$, Δ LO(high β → high)		−10.00	0.33	−10.60	−9.38	0.31
$a_{{11}_1,\mathrm{\Delta }}$, α → ΔLO(low → high| high β)		9.99	0.18	9.63	10.38	0.19
$b_{{11}_t,\mathrm{\Delta }}$, Δ LO(high → high|high β)		0.01	0.25	−0.47	0.50	0.26
$b_{{11}_1,\alpha }$, α → Δ LO(high β → high)		2.67	0.67	1.92	4.17	0.48
$b_{{11}_t,\alpha }$, α → LO(high → high)		2.57	0.30	2.07	3.31	0.29
$b_{{21}_t,\alpha }$, α → LO(low → high)		2.56	0.31	2.06	3.24	0.29
Pr(high → high|high β, low α)a		0.00	0.00	0.00	0.01	0.00
Pr(high → low|high β, low α)		1.00	0.00	0.99	1.00	0.00
Pr(low → high|high β, low α)		0.00	0.00	0.00	0.01	0.00
Pr(low → low|high β, low α)		1.00	0.00	0.99	1.00	0.00
Pr(high → high|high β, high α)		1.00	0.00	0.99	1.00	0.00
Pr(high → low|high β, high α)		0.00	0.00	0.00	0.01	0.00
Pr(low → high|high β, high α)		1.00	0.00	0.99	1.00	0.00
Pr(low → low|high β, high α)		0.00	0.00	0.00	0.01	0.00
Pr(high → high|high β, avg α)		0.50	0.04	0.42	0.59	0.05
Pr(high → low|high β, avg α)		0.50	0.04	0.41	0.58	0.05
Pr(low → high|high β, avg α)		0.50	0.05	0.41	0.59	0.05
Pr(low → low|high β, avg α)		0.50	0.05	0.41	0.59	0.05

True θ = True parameter values; Mean $\widehat{\theta }$ = Average point estimate for each parameter across MC runs; 2.5%tile and 97.5%tile = 2.5th and 97.5th percentiles for each parameter across MC runs; $a\widehat{SE}=\mathrm{SE}$ estimate for a parameter across MC runs.

^aThe transition probabilities were computed using Equations 13 and 14. Avg α = value of α was set to 0; high α = value of α was set to 1 SD above the mean of 0; low α = value of α was set to 1 SD below the mean of 0.

Across all the cross-sectional conditions considered, the less restrictive MSEM Model 2 and Models 6, which allowed cases from the low-β regime to appear in the two extreme behavioral regimes, were found to yield the best fit among the models considered based on AIC and aBIC. The initial transition probability estimates shown in Table 4 suggested that on average, even though cases with low values of β were more likely (with .62 probability) to transition into the medium behavioral regime and cases with high values of β were likely to move into the two extreme behavioral regimes (combined probability = .80), some cases still deviated from such patterns. LRTs comparing MSEM Models 1 and 2, conducted to answer Q1, further confirmed that significant improvements in model fit were found in 68—100% of the MC runs when the logit intercept parameters enabling cases with low β values to transition into the high and low behavioral regimes, $a_{1_1}$ and $a_{2_1}$, were freely estimated, as opposed to fixed at −10 (see Table 2).

In answering Q2, we found that the IC measures were able to detect the medium behavioral regime, but not all low-β cases were correctly classified to only transition into the medium regime. When β membership was known, the AIC and aBIC almost always (≥ 84% of the time) favored the less restrictive 3-regime Model (MSEM Models 2 and 6) to the 2-regime model (MSEM Models 3 and 7) across both sample size conditions (see Table 2). The more conservative BIC, in contrast, tended to favor the 2-regime model. In the conditions with unknown β membership, which was characterized by more pronounced separation in β values between cases in the high- and low-β regimes, differences in the IC values across models were relatively small. The best entropy, in contrast, almost always favored the cusp-inspired 3-regime model (i.e., MSEM Models 1 and 5) to all other models considered. This indicates the utility of using multiple fit indices and model selection criteria to determine the best approximation model, even if the approximation model is a misspecified model. More post-hoc explorations indicated that, in terms of IC measures, the extent to which the 2-regime model was favored over the cusp-inspired 3-regime model decreased with: (1) clearer separation in β values between the low- and high-β regimes, and (2) less extreme values of α — both of which reduced the tendency for cases from the low-β regime to be classified into the two extreme behavioral regimes. The very wide range of α values (from −6 to 6) considered in this particular simulation study led to notable instances of extreme behavioral values even in the low-β region, and consequently, reduced need for a third, medium behavioral regime.

The less restrictive 3-regime model was associated with other challenges. Specifically, due to the unique transition patterns of the cusp system and their linkages to the β values, some of the logit transition parameters were close to their boundary values (e.g., due to the scarcity of cases with low β values that appeared in the extreme behavioral regimes). Thus, the point estimates for some of the logit transition parameters were highly variable in the n = 200 conditions (e.g., parameters such as $a_{1_1}$, $a_{2_1}$, $b_{{11}_1,\mathrm{\Delta }}$, and $b_{{12}_1,\mathrm{\Delta }}$). SE estimates could not be obtained in many replications on these logit parameters. These estimation issues were greatly alleviated in the n = 500 as compared to the n = 200 conditions. With the exception of the logit parameters, the SE estimates of other parameters in the MSEM models generally mirrored the variability of the parameters across MC runs. Furthermore, in the models with unknown β membership, factor loading and mean/covariance parameters involving the latent variable distribution of β were all characterized by high accuracy, precision, and close correspondence between the estimated SEs and the empirical SEs (SDs of these parameter estimates across MC runs; see Table 4). Finally, the power for detecting evidence of bifurcation and divergence by means of LRTs (i.e., Q3) was consistently high (100%) throughout all sample size and β membership conditions.

In the longitudinal conditions, it is possible to detect within-person instances of sudden jumps, in addition to interindividual differences in the tendency to show sudden jumps in the behavioral variable. The estimated transition probabilities obtained from fitting the cusp-inspired MSEM-RS Model 5 (see Table 5) help convey the role of α_it in driving the cusp system to show sudden jumps between the high and low behavioral regimes with changes in α_it. By parameterizing the model to explicitly preclude the possibility for cases with high β values to transition into the medium regime and cases with low β values to transition into the two extreme behavioral regimes, noticeably fewer estimation problems arose. The average standard error estimates from MSEM-RS Model 5 across MC runs also appeared to be close to the MC SDs for all the parameters, particularly the logit parameters (see Table 5).

The power for detecting the differential continuous effects of α_it on y_it in the high/low versus the medium behavioral regime (Q4) was high, as indicated by the high proportions of MC runs that showed significant LRTs when the regression weight for α was constrained to be invariant across the three regimes (≥ .97). To address Q5, we found that the differences in fit between the 3-regime models (MSEM-RS Models 1 and 5) and 2-regime models (MSEM-RS Models 3 and 7) were relatively minor when longitudinal panel data were used. In addition, not only was the entropy notably higher in the 3-regime model than in the 2-regime model, entropy of the 2-regime MSEM-RS actually fell below .90, the commonly adopted “rule of thumb” for indicating clarity in class assignment (Celeux & Soromenho, 1996). This demonstrates the utility of using longitudinal panel data to investigate cusp-related properties. Finally, as in the cross-sectional conditions, the power for detecting evidence of bifurcation and divergence by means of LRTs (i.e., Q6) was also very high (close to 100%).

Overall, results from the present simulation study illustrated that the proposed cusp-inspired MSEM and MSEM-RS model can in fact be used to capture selected features of the cusp catastrophe model. The results are especially encouraging for two reasons. First, the proposed models are not really the true model, but rather, a mixture approximation to the true cusp model. Second, the means of the conditional distributions of y in the three regimes we sought to identify were extremely close to one another due to the skewed nature of these distributions. Cases that appear in the bifurcation set are especially prone to being assigned to the wrong regimes given the co-existence of multiple equilibrium points. Of note is that some of the key differences in the three regimes lie in how individuals transition into and out of their previous regimes — an aspect of model testing and assumption falsification that we have shown to be greatly facilitated by the availability of longitudinal data. For instance, using IC measures as well as entropy, stronger evidence in favor of the cusp-inspired 3-regime models (as opposed to their 2-regime counterparts) was found with longitudinal than cross-sectional data. The power for detecting bifurcation, divergence, and differential roles of α on the behavioral variable were also high for the simulation settings considered.

Illustrative Examples

Example 1: Sudden Transition in Attitude

The first example involves the reanalysis of a set of cross-sectional data collected by Felling, Peters, and Schreuder (1985), for which van der Maas et al. (2003) previously analyzed using the cusp catastrophe model and subsequently made available as part of the R library “cusp” (Grasman et al., 2009). The dependent variable consisted of 3000 Dutch respondents’ levels of agreement with respect to the statement, “The government must force companies to let their workers benefit from the profit as much as the shareholders do,” as measured on a 5-point scale (1 = totally agree to 5 = totally disagree). Thus, higher values on the behavioral variable correspond to greater disagreement toward the attitude statement. Political orientation, as measured on a 10-point scale from 1 = left wing to 10 = right wing, was used as the asymmetry variable (α). The total score on a 12-item political involvement scale was used as the bifurcation variable (β), with higher values indicating higher political involvement.

Consistent with Grasman et al. (2009), we only present results (see Figure 4A) from fitting the cusp catastrophe model in which the bifurcation factor is determined exclusively by political engagement, while the asymmetry factor is determined by political orientation. In this model, political involvement loaded positively on β, suggesting greater divergence in opinions toward social cultural developments among individuals with high political involvement. The positive loading of political orientation on α suggests that among those with low political involvement (β), one’s advocacy for right-wing perspectives at the moment (i.e., higher α) was associated with greater disagreement (again, note the negative coding of the behavioral variable such that higher values indicate higher disagreement) with the attitude statement, but slight changes in political orientation near the bifurcation region may propel individuals to show sudden transition in attitude. This variation of cusp catastrophe model yielded lower AIC and BIC than a linear regression model and a logistic regression model, providing some evidence that the cusp catastrophe model was a better-fitting model among the three models considered.

Figure 4.

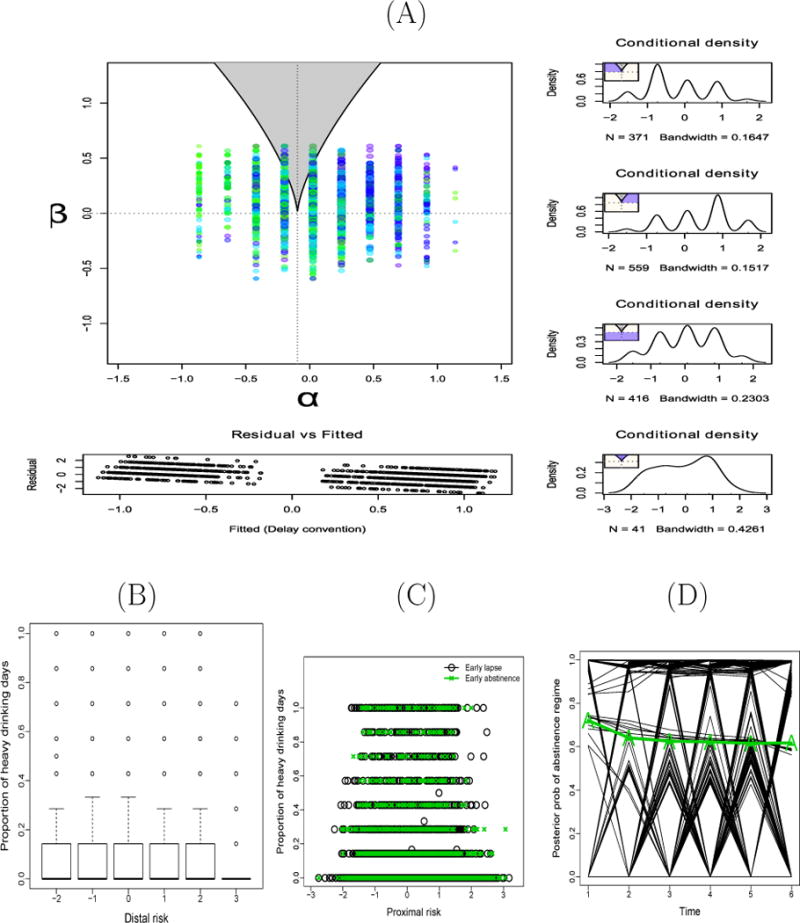
Selected plots from illustrative examples I (panel A) and II (panels B–D). (A) Classification of cases into the respective regions of the α-β plane based on results from fitting the cusp SDE to Felling et al’s (1985) data. At the bottom, a scatter plot of the residuals versus fitted values is displayed. In the cusp region with multimodality, each fitted value was computed post-hoc based on the mode that gave the smallest residual (hence the label “Delay convention”). Shown in the right are empirical kernel density plots whose shapes are similar to the theoretical densities depicted in Figure 1(A). (B) A plot of the biweekly PHD scores over the course of the treatment program against the distal risk composite score; (C) a plot of the biweekly PHD scores against proximal risk and (D) a plot of the estimated posterior probabilities of being in the abstinence regime (R_abs) and the estimated proportion of participants in the complete abstinence regime at any single time point (as a thick solid line marked with “A.”)

Several unresolved issues remained. For one, the cusp model and other comparison models assume very different probability density functions for y, with distinct and non-overlapping parameter sets. It remains unclear whether the asymptotic conditions required to obtain the correction term in the IC measures (see e.g., Bozdogan, 1987) are met in this case. For another, we obtained a negative R² value when the cusp SDE was fitted due to the skewed nature of the distribution of y (as discussed e.g. in Grasman et al., 2009). These issues lead to direct difficulties in falsifying features of the cusp model against other alternatives. In addition, both the behavioral variable (agreement toward the statement concerning government intervention in company policy) and α were ordinal items, but were assumed to be continuous in fitting the cusp SDE.

To provide some comparisons to the cusp SDE-based results, we first fitted the cusp-inspired 3-regime MSEM model specified in Equations 11–12 to the data as if they were continuous, and subsequently reran the analysis by specifying the attitude variable as ordinal.⁶ As distinct from our simulation results, the 3-regime cusp-inspired MSEM yielded better model fit in terms of IC measures as well as entropy value (AIC = 7446.01; BIC = 7555.95; aBIC = 7489.24; entropy = .66 with 21 parameters) than the 2-regime model (AIC = 7545.66; BIC = 7644.12; aBIC = 7583.77; entropy = .44 with 19 parameters). This may be related to the narrower range of α values (between −1.0 and 1.2) for this empirical example (see Figure 4A). The intercept value of the high and medium agreement regimes were indistinguishable from each other⁷ (τ_high = 0.52 (SE = .03), τ_med = 0.52 (SE = .03), while τ_low = −1.11 (SE = .02)), with residual variances ${\psi }_{\mathit{high}}^2=0.02(\mathrm{SE}=0.006)$; ${\psi }_{\mathit{medium}}^2=0.40(\mathrm{SE}=0.03)$, and ${\psi }_{\mathit{low}}^2=0.18(\mathrm{SE}=0.02)$, respectively.

To ease presentation, we denote the third regime as the low disagreement regime, and the first two regimes as the “avid supporter” regime and ‘avid antagonist” regime, for reasons that are to be elaborated next. Specifically, even though α was found to show a significant positive relationship with the behavioral variable in all three regimes, the symmetry in the regression effect of alpha evidenced in the “high” and “low” behavioral regimes evidenced in the simulation study was no longer present (b_{α,avid supporter} = 0.64 (SE = 0.03); b_α,low = 0.06 (SE = 0.03); b_{α,avid antagonist} = 0.19 (SE = 0.03)). Evidence of bifurcation was found, however. Greater political engagement (i.e., higher β) was associated with less disagreement with government intervention (b_{β,avid supporter} = −0.82 (SE = 0.03) in the avid supporter regime), but increased disagreement among those in the avid antagonist regime b_{β,avid antagonist} = 0.14 (SE = 0.03). In the low disagreement regime, while increased right-wingedness (i.e., higher α) was also associated with greater disagreement with government intervention, the effect of political involvement on agreement was not statistically significant. Thus, results from fitting the MSEM to the attitude data under continuous data specification already revealed some discrepancies between features of the empirical data and those manifested by the cusp system.

We fit the 3-regime model again with level of disagreement specified as ordinal data. We set the residual variances of y (i.e., the ψ parameters) in all regimes to be 1.0 and freely estimated the intercepts in all regimes. The four threshold parameters for the attitude question were estimated to be −1.44 (fixed based on the observed proportion of participants who endorsed the lowest category of disagreement to aid convergence), −0.49 (SE = 0.04), 0.32 (SE = 0.04) and 1.43 (also fixed using observed proportion of responses). The threshold values suggest that while it was relatively easy for the participants to express some level of agreement/disagreement with the attitude question, extreme levels of agreement/disagreement were relatively rare.

Consistent with results from continuous data modeling, the intercepts of the “high” and “medium” regime were also not clearly distinguishable from one another. Besides the differences in the magnitudes of the parameter estimates due to scaling differences with the ordinal specification, several differences can be noted in the results from using the ordinal specification. First, the entropy for the model was higher (.75 compared to .66 with continuous specification, with 21 parameters in both models). Second, while an “avid supporter” regime (in which the regression effects associated with political orientation and political engagement were positive and negative, respectively) was still identified, the sign of the regression coefficient for political orientation in the “avid antagonist” regime was flipped. In this regime, although greater political engagement (β) was still associated with more disagreement with the attitude question (b_{β,avid antagonist} = 0.65; SE = 0.19), increased right-wingedness (i.e., higher α) was associated with less disagreement (i.e., more agreement) with the statement (b_{α,avid antagonist} = −0.53; SE = 0.29). In other words, although evidence of bifurcation in attitude due to political engagement was still found, the effect of right-wingedness was reversed.

Finally, in the regime with the lowest intercept, the effects of political engagement and orientation were both positive and statistically significant. This is consistent largely with the results seen in the continuous data for the lowest disagreement regime, although the marginally significant effect of political involvement in the continuous case now became statistically significant with the ordinal specification (b_β,low = 0.06, SE = 0.03, p = .06; in contrast to b_β,low = 0.16, SE = 0.04, p < .001 in the ordinal case). There was also an increase in the effect size associated with political orientation in the ordinal case (b_α,low = 0.06, SE = 0.03, p = .03; in contrast to b_α,low = 0.41, SE = 0.05, p < .001 in the ordinal case). The estimated proportion of participants who resided in each of the regimes also differed substantially (e.g., for participants in the high political engagement class, approximately 23.5% of them were assigned to the “avid supporter” regime in the ordinal model, compared to only 4.0% in the continuous case).

In sum, consistent with findings in the literature, which suggest that misspecifying ordinal data as continuous can, in some cases (e.g., with very irregularly spaced thresholds), lead to biases in parameter estimates and incorrect inference results (Babakus, Ferguson, & Jöreskog, 1987; Mooijaart, 1983; B. O. Muthén & Kaplan, 1992), we found discrepancies in modeling results between the continuous and ordinal models. The MSEM framework offers a way to accommodate ordinal and other types of responses (e.g., binary, censored, and Poisson distributed responses) and thus offers considerable gain in flexibility in testing cusp-related hypotheses in empirical settings.

Example 2: Nonlinear Shifts in Alcohol Use Tendency

Following alcohol treatment, individuals with alcohol use disorders often undergo sudden, nonlinear transitions between periods of abstinence/non-problem drinking and periods of heavy drinking (Skinner, 1989; Witkiewitz, 2008; Witkiewitz, Maisto, & Donovan, 2010, 2007). Such nonlinear transitions are associated with hysteresis-like characteristics, as suggested by the distinctly higher prevalence rate of lapses in comparison to prolapses (i.e., returning to abstinence after heavy drinking). Witkiewitz and G. A. Marlatt (2004) represented such transitions using the cusp catastrophe model, in which distal and proximal processes serve as β and α, respectively, to affect drinking outcomes (i.e., the behavioral variable). Distal risks may be conceived as background or relatively stable characteristics (e.g., previous history of alcohol dependence). Proximal risks, in contrast, encompass transient precipitants that change an individual’s tendency to drink on a moment-to-moment basis (e.g., momentary stress). Witkiewitz and colleagues (Witkiewitz & G. A. Marlatt, 2004; Witkiewitz & G. Marlatt, 2007; Witkiewitz et al., 2007) stipulated that for individuals with low distal risk, drinking changes linearly with changes in proximal risk (path A in Figure 1). However, for those with high distal risk, the associated alcohol use pathways may resemble paths B and C in Figure 1 more closely: a small increase in proximal risk may push an individual “over the edge,” leading to an episode of lapse. A prolapse then requires a substantially larger reduction in proximal risk to help the individual regain abstinence.

Thus far, the cusp-based analyses conducted by Witkiewitz and colleagues were restricted to cross-sectional analyses due to the inability of current software routines to handle longitudinal panel data as well as missing values. As demonstrated in our simulation study, longitudinal panel data contain valuable information about within-person instances of sudden jumps that are not available in cross-sectional data. In addition, not all empirical data sets conform to every mathematical premise of the cusp model. This example serves to demonstrate the flexibility of the MSEM-RS framework in adapting to specific features of alcohol use data.

Data from Project Matching Alcohol Treatments to Client Heterogeneity < Project MATCH; >MATCH97a were used. Participants in Project MATCH (n = 1,726) were recruited from nine research units and randomly assigned to one of three treatments: cognitive-behavior therapy, 12-step facilitation, or motivation enhancement therapy. For the current study, only those treated in the outpatient condition were included in the analyses.

Perceived stress (Cohen, Kamarck, & Mermelstein, 1983), difficulty abstaining from alcohol, and alcohol craving (Anton, Moak, & Latham, 1995) were used to derive a composite indicator of proximal risk. As a measure of distal risk (β), we considered a composite score derived by averaging the participants’ self-reported alcohol dependence severity using the Alcohol Dependence Scale < ADS; >Skinner84a, previous history of psychiatric problems as measured using the Global Severity Index of the Brief Symptom Inventory < BSI; >Derogatis93a,Hufford03a and family support (reverse coded based on scores on the original 0–7 scale). However, preliminary graphical analyses suggested no categorical divergence in drinking patterns as a function of this distal composite score. We thus used early treatment proportion of heavy drinking days (at week 1) to define a grouping factor such that the high-β group was defined as participants who showed early lapses at the start of the treatment program (approximately 35% of the participants), while the low-β group comprised those who maintained early abstinence. This was motivated by an emphasis in previous research on the importance of maintaining abstinence or preventing early lapses after the start of a treatment program. That is, early individual differences in responsiveness to the treatment effects may be regarded as a source of distal risk, as opposed to individual differences in drinking dynamics. The composite distal risk score was still retained as a continuous indicator of β in Equation 15 (to appear next).

We used each participant’s Proportion of Heavy Drinking Days (PHD; defined as 4 or more drinks per day for women and 5 or more drinks per day for men) since the last assessment occasion as our key dependent variable of interest. For model fitting purposes, we aggregated data every two weeks from week 2 to week 12, yielding a set of longitudinal panel data with 6 equally-spaced time points. Plots of the PHD scores of the participants against their composite distal and proximal risk scores are shown in Figures 4B–C. It can be seen that a large number of abstainers were present at each time point. Thus, the low behavioral regime as posited in the cusp system may not be adequate to capture the limited drinking variability shown by of this group of abstainers. This motivated us to reformulate our cusp-inspired MSEM-RS so the low behavioral regime corresponded to an abstinence regime with no alcohol consumption. Thus, we modified Equation 11 to yield:

$$\begin{array}{ll}\underset{¯}{\text{Regime}}\hfill & \underset{¯}{\text{Model}}\hfill \\ R_{\mathit{high}}:\text{High drinking}\hfill & (y_{\mathit{it}}-{\tau }_{\mathit{high}})={\varphi }_{\mathit{high}}(y_{i,t-1}-{\tau }_{\mathit{high}})+b_{\alpha ,\mathit{high}}{\alpha }_i+b_{\beta ,\mathit{high}}{\beta }_i+{\zeta }_{\mathit{it}}\hfill \\ R_{\mathit{med}}:\text{Mediumdrinkin g}\hfill & (y_{\mathit{it}}-{\tau }_{\mathit{med}})={\varphi }_{\mathit{med}}(y_{i,t-1}-{\tau }_{\mathit{med}})+b_{\alpha ,\mathit{med}}{\alpha }_i+b_{\beta ,\mathit{med}}{\beta }_i+{\zeta }_{\mathit{it}},\hfill \\ R_{\mathit{ads}}:\text{Complete abstinence}\hfill & 0,\hfill \end{array}$$ (15)

The regime denoted as R_abs was specified to be a complete abstinence regime, with no variability in drinking level and no effect of α or β. The two remaining regimes were distinguished by within-person, over-time fluctuations in y_it around two different baseline levels, τ_high, and τ_med, with the constraint that τ_high > τ_med. In both the high and medium drinking regime, deviations in drinking level around τ_high and τ_med were modeled as an autoregressive process of order 1 (i.e., an AR(1) process) with AR weight ϕ_high and ϕ_med, respectively, and as subjected to regime-specific effects of α and β. An AR(1) value that is significantly different from zero would suggest some continuity or regularity in how individuals manifested drinking from occasion to occasion. The process noise variable, ζ_it, was assumed to be normally distributed with mean 0 and variances ${\psi }_{\mathit{high}}^2$ and ${\psi }_{\mathit{medium}}^2$, respectively, for the high and medium drinking regimes.

The cusp-inspired 3-regime model (with low, medium, and high regimes) with early lapses as a known grouping variable did not yield better fit (AIC = −3311.51; BIC= −3249.72; aBIC = −3303.62 with 17 parameters) than a 2-regime model with a drinking and a complete abstinence regime (AIC = −9264.21, BIC = −9220.05 and aBIC = −9258.11 with 12 parameters). Entropy value for the 2-regime model was estimated to be .96, indicating clear classification of participants into their respective classes (Celeux & Soromenho, 1996). Based on the parameter estimates from the 2-regime model, the two regimes may be interpreted as a complete abstinence and a (moderate) drinking regime, with an estimated intercept of τ = 0.32 (SE = .035), and an AR(1) coefficient of 0.65 (SE = 0.08). The magnitude of the AR coefficient, given that it is less than 1 in absolute value, indicated that any deviations away in drinking level from τ were expected to diminish over time at a moderate pace. Contrary to our expectation, continuous changes in composite distal risk did not have a statistically significant effect on drinking (b_β = 0.03, SE = 0.02).

Composite distal risk and proximal risk were used as predictors of initial class probability at week 2. Proximal risk, but not composite distal risk, was found to have a statistically significant effect on the initial class probabilities. The corresponding estimates of the log odds parameters and the initial class/transition probabilities are given by (with SEs included in parentheses):

$$\begin{array}{l}\begin{array}{ll}\underset{¯}{\text{Log odds}(C_{i1}=k)}& \underset{¯}{\mathrm{Pr}(C_{i1}=k|\text{avg proximal risk level})}\end{array}\\ \begin{array}{cc}\begin{array}{c}\text{Drink}\\ \text{Abs}\end{array}\left[\begin{array}{c}-1.62(0.16)+0.42(0.12){\text{Prox}}_{i1}-0.19(0.15){\text{Distal}}_i\\ 0\end{array}\right]& \begin{array}{c}\text{Drink}\\ \text{Abs}\end{array}\left[\begin{array}{c}.17(0.02)\\ .83(0.02)\end{array}\right]\end{array}\\ \begin{array}{cc}\underset{¯}{\text{Log odds}(C_{i1}=k|C_{i,t-1}=j,{\text{Prox}}_i)}& \end{array}\\ \begin{array}{cc}\begin{array}{cc}\text{Drink}& \text{Abs}\hfill \end{array}& \end{array}\\ \begin{array}{cc}\begin{array}{c}\text{Drink}\\ \text{Abs}\end{array}\left[\begin{array}{cc}-2.56(0.14)+3.37(0.26)-0.12(0.18){\text{Prox}}_{\mathit{it}}& 0\\ -2.56(0.14)+0.63(0.18){\text{Prox}}_i& 0\end{array}\right]& \end{array}\end{array}$$

We found that the participants were 1.62 times more likely to be in the abstinence than in the drinking regime at time 1. Proximal risk was found to play a statistically significant role in increasing the log odds of being in the drinking regime at week 2, as well as the log odds of transitioning from abstinence to drinking. However, it did not show a significant effect on the log odds of staying within the drinking regime, or a significant continuous effect on drinking (b_α = 0.04; SE = 0.02). Overall, the abstinence regime was characterized by a higher staying probability (.93; SE = 0.01) than the drinking regime (.69; SE = 0.04).

The posterior probabilities from model fitting (see Figure 4D) – namely, each individual’s estimated probability of being in a particular regime (e.g., the complete abstinence regime) at each time point conditional on the data — indicated that the participants continued to show ongoing transitions into and out of the abstinence regime throughout the treatment period. The proportion of participants assigned to the complete abstinence regime at each time point based on their highest posterior probabilities is also included in the plot as a thick solid line marked with “A.” On average, the prevalence of the complete abstinence regime remained relatively stable over time. A small but relatively constant proportion of individuals continued to be assigned to the drinking regime throughout the three-month treatment period.

In sum, results from model fitting suggested that the 2-regime model provided a more parsimonious representation of individuals’ recovery pathways following alcohol treatment than the adapted cusp-inspired 3-regime model. In particular, participants with high distal risk did not appear more susceptible to a lapse at week 2 post-treatment, nor did they show recovery pathways that were clearly distinct from the pathways of participants with low distal risk (e.g., showing sudden jumps between extreme drinking modes with changes in proximal risk). In addition, although changes in proximal risk did not give rise to smooth, proportionate changes in the participants’ drinking patterns, increased proximal risk was associated with significant increase in the log odds of a lapse. As a whole, the general MSEM-RS framework offers enough flexibility for model explorations, evaluations and comparisons to allow us to detect the ways in which the data deviate from the theoretically hypothesized model.

Discussion

Researchers well versed to the tradition of a linear regression or structural equation modeling framework may be accustomed to transforming away skewness or other non-normalities in the data prior to model fitting. Few researchers have asked or tested whether such transformations are warranted, or whether the non-normalities are indeed part of the intrinsic dynamics of the system, as is the case with the cusp catastrophe system. In this article, we proposed a MSEM/MSEM-RS framework for capturing selected characteristics of the cusp catastrophe model in exchange for greater flexibility in handling practical data analytic and model comparison issues. A simulation study and two empirical examples were included to illustrate the strengths and limitations of the proposed approach in detecting catastrophe flags. Structuring the cusp catastrophe model as an MSEM or MSEM-RS has some clear advantages. First, the proposed models can be readily fitted using available software programs with built-in options for handling incomplete and categorical data, and a variety of fit indices for model comparison purposes. Second, measurement noise can be distinguished from process noise. Third, lagged effects among the behavioral and control variables can be readily accommodated, and the model can be expanded, as needed, to test multivariate extensions involving other dependent variables of interest. Fourth, by using person- and time-specific covariates to predict the probabilities of transitioning between regimes, the new approach also allows for heterogeneous timing of sudden jumps within and across subjects. Other advantages we demonstrated in the contexts of our empirical examples include the added flexibility offered by the MSEM/MSEM-RS framework to capture data characteristics that deviate from those posited in the cusp framework, such as the presence of the zero-inflation phenomenon in the MATCH reanalysis example.

We have shown how postulates concerning the number and nature of the different equilibrium systems can be tested as hypotheses concerning the number of regimes in an MSEM/MSEM-RS using standard model comparison indices such as entropy and IC measures. Other more complicated catastrophe models may also be structured in a similar vein. Of course, the validity of the cusp-inspired MSEM-RS still depends on the tenability of the normality assumptions imposed on the behavioral variable within regimes. We only managed to test a selected set of assumptions in our simulation study and empirical examples. There are many other possible assumptions that can be relaxed or evaluated in other empirical applications, as deemed appropriate by the researchers. Some examples might include testing the tenability of measurement invariance, evidence for between-class heterogeneities in measurement structure (e.g., measurement error variance), and possible between-person or between-group differences in the transition probabilities or other modeling components. In addition, one alternative way in which researchers can test the stability of the latent classes/regimes is to use different covariates to predict class membership and assess whether the model parameters and conclusions change in anyway when different covariates are used. If they do, researchers may want to impose additional constraints to facilitate the extraction of substantively meaningful latent classes/regimes.

The present article is not the first application of MSEM-RS (see e.g., Chow et al., 2013; Dolan, Schmittmann, Lubke, & Neale, 2005). By including an explicit longitudinal model within each regime or class, MSEM-RS as a whole differs from another class of well known longitudinal models of discrete changes—the Hidden Markov Models (HMMs; Elliott, Aggoun, & Moore, 1995), or the related latent transition models (LTA; which emphasize categorical indicators; L. M. Collins & Wugalter, 1992; Lanza & Linda M. Collins, 2008). HMM may be regarded as a generalization of latent class/mixture models due to the inclusion of a Markov chain that governs the transition between classes over time. It is worth noting that in HMMs, there is no continuous latent variable vector, η, or any longitudinal model specifying lagged dependencies between the current η_it and those from previous time points. The specification of a continuous model of change within each regime allows the intra-person dynamics within regimes in an MSEM-RS to be continuous in nature, even though the shifts between regimes or classes are discrete. In this way, MSEM-RS models are more suited to representing processes wherein the changes that unfold within regimes are continuous, and of central interest to the researcher. In addition, a first-order Markov chain is typically assumed in HMMs. As a result, algorithms for estimating HMMs, such as the Baum-Welch algorithm⁸ (Baum, Petrie, Soules, & Weiss, 1970; Welch, 2003) can reasonably assume that the density of the observations in y_it only depends on the latent regime at time t namely, C_it, and not on other earlier regime information (see e.g., p. 10, Welch, 2003). The computational costs are thus greatly reduced. This assumption generally does not hold in regime-switching models with continuous latent variables that show lagged dependencies (e.g., in Equation 15 and in other regime-switching state-space models; see discussion on p. 69 of Kim & Nelson, 1999), or in models where the first-order Markov assumption is relaxed, such as the general MSEM-RS framework implemented in Mplus.

It is worth noting, however, that all exact likelihood approaches, including the EM algorithm implemented in Mplus, requires the storage of the entire regime history for estimation purposes, unless simplifying assumptions are made, such as in the case of estimating HMMs. In fact, the full Markov dependency built into the MSEM-RS is consistent with the modeling conventions in the SEM framework, in which repeated measurement occasions of y_it, η_it and C_it are included as separate variables within y_i, η_i and C_i, respectively. When T is small, this modeling framework provides great flexibility, for instance, in allowing the number of latent classes to vary for each time point. However, when T is large, considerable increase in computational costs may be observed. In this case, alternative regime-switching estimation techniques commonly adopted in the time series/state–space literature (e.g., the Kim filter; Kim & Nelson, 1999; Yang & Chow, 2010) may be used.

Several unresolved methodological challenges associated with the proposed modeling approach should be noted. Models with multiple regimes are notorious for their large numbers of local maxima. The use of multiple starting values to check the sensitivity of the estimation results to different starting values can help detect possible local maxima. Sample size consideration is also a critical issue, because sufficient observations have to be available from every regime to adequately model the dynamics within regimes and differences across regimes (Chow et al., 2013; Chow & Zhang, 2013; Tueller & Lubke, 2010). Influence analysis in the context of MSEM/MSEM-RS and related models is another important topic that warrants further investigation. In particular, it is possible to develop diagnostics similar to those considered elsewhere (Chow, Hamaker, & Allaire, 2009) to identify outlying cases (i.e., individuals) and measurement occasions that are influential to the modeling results and perform data processing procedures as needed.

Fixed covariates were used in the multinomial logistic regression models shown in Equations 8, 9 and 13 to predict the initial class and transition probabilities. When missingness is present in the covariates, such missingness in the covariates cannot be handled directly using full-information maximum likelihood approaches. If the bifurcation and asymmetry variables are incorporated into the model as other key variables with distributional assumptions, data that are missing at random can be readily accommodated. However, new computational challenges may arise with the added modeling complexity, particularly when categorical predictors are involved. In this application, cases with missing covariates were removed from model fitting as the default option in Mplus. Future applications should consider multiple imputation or other approaches that model the missingness in the covariates explicitly (e.g., Greenland & Finkle, 1995; Ibrahim, Chen, & Lipsitz, 1999; Lee & N.-S. Tang, 2006).

Model identification in MSEM/MSEM-RS is another key issue that warrants more attention from researchers. When the number of regimes is large or the distinctions between regimes are not pronounced, researchers may want to impose more than the necessary number of constraints to aid estimation. The regime-switching models considered in this study are highly constrained compared to other conventional mixture models. That is, in addition to the constraints imposed to avoid the well-known problem of “label switching” (McLachlan & Peel, 1995; Tueller & Lubke, 2010), we also incorporated many theoretically and model-driven constraints. Such constraints allow us to explicitly represent the continuous changes that unfold within regimes and offer a useful alternative to models such as HMMs. While such constraints may help aid model identification, researchers also have to be wary of whether such constraints put some of the parameters on the boundary of the parameter space over which optimization is done, thereby violating one of the regularity conditions for standard LRTs (Savalei & Kolenikov, 2008). In the examples considered in the simulation study and empirical examples in which LRTs were used, we did not have this problem. However, in other situations, such as in cases where the more restrictive model (the null hypothesis) involves restrictions on the transition probability patterns (e.g., the probability of transitioning into a particular regime is zero), other model comparison indices will have to be used (e.g., bootstrapped LRTs, which are currently available in Mplus for cross-sectional but not mixture models; Nylund, Asparouhov, & Muthén, 2007).

In closing, we note that, although the proposed models were able to retain some of their features, our intention is not to discount the roles of the cusp catastrophe or other related catastrophe models. Using a mixture model to approximate the differing pathways of change also did not fully capture the distinctions between the linear and the nonlinear pathways of change posited in the cusp catastrophe model. Whereas the proposed MSEM/MSEM-RS framework helps to circumvent several challenges in the analysis of empirical data, we still acknowledge the general appeal of the catastrophe models as possible ways of representing change.