Significance
Fingerprint recognition, which is considered to be a reliable means for human identification, has been used in many applications ranging from law enforcement and forensics to unlocking mobile phones. Despite its successful deployment, the fundamental premise of fingerprint-based identification—persistence and uniqueness of fingerprints—has not yet been well studied, resulting in challenges to the admissibility of friction ridge evidence in courts of law. This study investigates the tendency of fingerprint similarity scores and recognition accuracy with respect to covariates characterizing properties of fingerprint impressions and demographics of subjects, including time interval between two fingerprints being compared in regard to the persistence of fingerprints. A multilevel statistical analysis is conducted with a longitudinal dataset of fingerprint records from 15,597 subjects.
Keywords: biometrics, fingerprint recognition, persistence of fingerprints, longitudinal data analysis, multilevel statistical model
Abstract
Human identification by fingerprints is based on the fundamental premise that ridge patterns from distinct fingers are different (uniqueness) and a fingerprint pattern does not change over time (persistence). Although the uniqueness of fingerprints has been investigated by developing statistical models to estimate the probability of error in comparing two random samples of fingerprints, the persistence of fingerprints has remained a general belief based on only a few case studies. In this study, fingerprint match (similarity) scores are analyzed by multilevel statistical models with covariates such as time interval between two fingerprints in comparison, subject’s age, and fingerprint image quality. Longitudinal fingerprint records of 15,597 subjects are sampled from an operational fingerprint database such that each individual has at least five 10-print records over a minimum time span of 5 y. In regard to the persistence of fingerprints, the longitudinal analysis on a single (right index) finger demonstrates that (i) genuine match scores tend to significantly decrease when time interval between two fingerprints in comparison increases, whereas the change in impostor match scores is negligible; and (ii) fingerprint recognition accuracy at operational settings, nevertheless, tends to be stable as the time interval increases up to 12 y, the maximum time span in the dataset. However, the uncertainty of temporal stability of fingerprint recognition accuracy becomes substantially large if either of the two fingerprints being compared is of poor quality. The conclusions drawn from 10-finger fusion analysis coincide with the conclusions from single-finger analysis.
Friction ridge skin on fingers and palms has been purportedly known to be a physical characteristic of an individual that does not change over time (i.e., persistence or permanence of friction ridge pattern) and can be used as a person’s “seal” or “signature” (i.e., uniqueness or individuality of ridge pattern). Starting with the first known case where the latent fingerprints found at a crime scene in Argentina in 1893 were officially accepted as evidence to convict a suspect (1), friction ridge analysis has become one of the most crucial methods in crime scene investigations worldwide. The decision made in Frye v. United States in 1923 (2) was widely cited as the basis for the admissibility of forensic evidence, including friction ridge pattern; Frye standard states that a scientific principle or discovery that has gained a general acceptance in the relevant field is admissible in the courts.
In Daubert v. Merrell Dow Pharmaceuticals, Inc., in 1993 (3), however, the general acceptance test of Frye was superseded by the Federal Rules of Evidence. The Daubert ruling established a guideline for admitting forensic evidence, which consists of the following factors: (i) empirical testing, (ii) peer review and publication, (iii) known or potential error rate, (iv) standards controlling the operation, and (v) the Frye standard of general acceptance. The Daubert standard provoked challenges to admissibility of friction ridge evidence in the courts. Although all of about 40 such challenges resulted in a decision that friction ridge analysis is acceptable as forensic evidence, the Daubert case highlighted a lack of scientific basis of persistence and uniqueness of fingerprints and standards that can be universally referred to in friction ridge analysis.
Along with the development of standards and guidelines for friction ridge analysis (4) and retraining of latent examiners (5) as a result of the Daubert ruling, a body of research to demonstrate uniqueness and persistence of friction ridge patterns has emerged. Although the uniqueness of fingerprints has been studied by (i) estimating the probability of a random correspondence (i.e., two different fingerprints selected at random will be sufficiently similar to be claimed as a mate) (6–8) or (ii) measuring the evidential value§ of latent fingerprint comparisons (9) (terminologies indicated with § are defined in SI Appendix, section S2), the persistence of fingerprints has been generally accepted based on anecdotal evidence, including case studies conducted by Herschel (10) and Galton (11) (SI Appendix, section S4), and the anatomical structure of friction ridge skin—the ridge pattern formed in the inner (dermal) layer during gestation remains unchanged with the protection of the outer (epidermal) layer (12).
The persistence of fingerprints typically refers to the invariance of friction ridge pattern itself. However, the pertinent question of interest is whether the fingerprint recognition methodology (SI Appendix, section S3) maintains high recognition accuracy as the time interval between two fingerprints being compared increases. The 2009 National Research Council report Strengthening Forensic Science in the United States: A Path Forward (13) pointed out, “Uniqueness and persistence are necessary conditions for friction ridge identification to be feasible, but those conditions do not imply that anyone can reliably discern whether or not two friction ridge impressions were made by the same person.” Fingerprint recognition exhibits two types of comparison errors: (i) false rejection: two impressions of the same finger (a genuine fingerprint pair) are declared as a nonmatch due to large “intrafinger” variability, and (ii) false acceptance: impressions from two distinct fingers (an impostor fingerprint pair) are declared as a match due to large “interfinger” similarity. The intrafinger variability is observed due to changes in intrinsic skin condition (e.g., finger skin dryness, cuts, and abrasions) and extrinsic acquisition process (e.g., finger pressure and placement), and sensing technology (e.g., interoperability among various fingerprint sensors). The interfinger similarity is observed when the ridge patterns from two distinct fingers coincide partially.
The biometric recognition literature has reported a phenomenon called template aging, which refers to an increase in the error rate in biometric recognition with respect to the time gap between a query and a template (or reference) (14). A study comparing groups of fingerprint pairs with respect to time gap reported that the fingerprint comparisons with less than a 5-y time gap show lower error rate than comparisons with a larger time gap (15). However, cross-sectional analysis used in ref. 15 is valid only if the longitudinal data§ are balanced§ and time structured§; this condition is not typically satisfied in most biometrics data, including the dataset used in ref. 15. Longitudinal studies on fingerprint, face, and iris biometrics published in the literature are summarized in SI Appendix, section S4.
Study Objectives and Caveats
A longitudinal dataset of fingerprints from 15,597 subjects apprehended by Michigan State Police (MSP) is analyzed, which consists of five or more fingerprint records over a time span varying from 5 to 12 y for each subject. Multilevel statistical models with covariates characterizing properties of fingerprint impressions and demographics of subjects are designed to analyze the longitudinal dataset, which is unbalanced and time unstructured. Specifically, our study aims to address the following issues:
-
•
Trend of fingerprint match scores of genuine and impostor pairs with respect to the following covariates: time interval between fingerprints in comparison, subject’s demographic factors (age, sex, and race), and fingerprint image quality;
-
•
Assessment and comparison of the multilevel models with various combinations of the covariates;
-
•
Correlations and interactions among covariates;
-
•
Temporal trend of fingerprint recognition accuracy in terms of probabilities of true acceptance and false acceptance;
-
•
Trend of fingerprint match scores and recognition accuracy when all 10 of a subject’s fingers are used for recognition, a prevailing practice in law enforcement.
The results and conclusions made in this paper should be interpreted with the following caveats:
-
i)
Any variability appearing in fingerprint images collected over time may be induced by either physical changes in friction ridge structure or changes in imaging condition and subject’s behavior during fingerprint acquisition. No distinction between the two sources of variability is made in the analysis presented in this paper.
-
ii)
The inferences and conclusions presented in this paper are drawn from 10-print analysis and do not suggest the same conclusions for latent fingerprint (or finger mark) analysis.
The detailed explanations about the caveats can be found in SI Appendix, section S1.
Longitudinal Fingerprint Dataset
A longitudinal dataset of fingerprints was collected from the records of repeat offenders apprehended by the MSP. SI Appendix, Fig. S3 shows an example of six fingerprint impressions of the right index finger of a subject in the dataset acquired between June 2001 and October 2008. A total of 15,597 subjects were randomly extracted from the MSP fingerprint archive, such that each subject has at least five acquisitions from all 10 fingers on a formatted fingerprint card (called 10-print card) over a minimum of 5-y time span. The 10-print cards of a subject are ordered according to the time sequence; a set of 10-print cards of subject i (; N is the total number of subjects in the dataset) is labeled as follows: , such that , where is the jth 10-print card of subject i, is the time stamp of , and denotes the number of 10-print cards belonging to subject i.
A summary of the dataset is below, and the data statistics are shown in SI Appendix, Fig. S4.
-
•
Each of the 15,597 subjects has at least five 10-print cards, providing 122,685 10-print cards in total. The average number of 10-prints per subject in the dataset is 8, and the maximum is 26 cards.
-
•
The 10-print impressions of a subject have a minimum of 5-y time span (the time difference between the first and the last fingerprint acquisitions of a subject); that is, y for , where . The average time span is 9 y, and the maximum time span in the dataset is 12 y.
-
•
Any two consecutive 10-print impressions of a subject are obtained with at least a 2-mo time gap; mo for for subject i.
-
•
Along with 10-print images, the following demographic information is also available for each subject: sex (male or female), race (white/Hispanic, black, American Indian/Eskimo, or Asian/Pacific Islander), and age at the time of 10-print acquisition (the youngest subject’s age at the time of the first impression is 8 y; the oldest subject’s age at the time of the last impression is 78 y).
Two commercial off-the-shelf (COTS) fingerprint matchers (denoted as COTS-1 and COTS-2) are used to compute match scores. For subject i with fingerprint impressions, we conduct all pairwise comparisons; that is, genuine match scores are generated from each matcher. This is because law enforcement agencies often store all of the 10-print records for every subject and compare a query fingerprint to all records in the database. Note that the pairwise comparisons of the fingerprint records of a subject result in correlations among the genuine match scores of the subject. On the other hand, the impostor scores are obtained by comparing subject i’s fingerprint impressions to the first impressions from all other subjects. For each finger position, 481,181 genuine match scores and 1,913,395,260 impostor match scores are obtained by each of the COTS matchers.
Multilevel Statistical Model
For balanced and time-structured longitudinal dataset, cross-sectional analysis can be readily applied by grouping the data according to cohort (for example, short-term and long-term fingerprint comparison groups) under the assumption of compound symmetry.§ In reality, however, it is not feasible to collect longitudinal fingerprint data by following an identical measurement schedule over a large number of subjects in the sample satisfying the compound symmetry. Multilevel statistical model (16, 17) is one of several statistical models that can handle the unbalanced and/or time-unstructured longitudinal data.
As a fingerprint comparison essentially involves two fingerprint impressions to generate a single match score, a simple linear two-level model with a single covariate for continuous match scores can be represented by the following:
Level 1 model (intrasubject variability):
| [1] |
Level 2 model (intersubject variability):
| [2] |
The level 1 model in Eq. 1 is regressed to the repeated measurements taken from each subject, and accounts for the intrasubject variability. In case of genuine fingerprint comparisons, the variables and parameters in the level 1 model are defined as follows: is the subject i’s observed response of match score when the jth and kth fingerprints are compared, is the explanatory variable (or covariate), and are the true parameters representing the intercept and slope of the linear model for subject i, and is the error in the observed response from the model fit. The error is assumed to be normally distributed with a zero mean and a variance of .
In the level 2 model in Eq. 2, where the population-mean tendency and deviations of subjects from the mean trend are modeled to account for the intersubject variability, the true parameters for subject i ( and ) can be modeled by a mixture of fixed and random effects: fixed-effects parameters and represent the grand means of intercept and slope across all N subjects in the data, and random-effects parameters and represent the deviations of subject i’s intercept and slope from and . The random effects are assumed to follow a normal distribution.
To determine whether two fingerprint impressions are from the same finger, a binary decision for a fingerprint pair is made by applying a predetermined decision threshold to the match score. If the match score of a fingerprint pair is greater than the threshold, the two fingerprints are determined to be a genuine match; otherwise, they are determined to be an impostor match. If a fingerprint pair determined to be a genuine match is indeed from the same finger, the binary decision is a true acceptance. If a genuine-match decision is made on two fingerprints that are in fact from different fingers, the decision is a false acceptance. In multilevel modeling, a binary response is viewed as a Bernoulli trial with the probability of true (or false) acceptance , and the expected is modeled after being transformed by a logit link function.
| [3] |
where is a logit link function: .
The maximum likelihood (ML) and generalized least-squares (GLS) estimations are widely used to estimate parameters in a multilevel model (17). Under the assumption that the residuals are normally distributed, the ML estimates of the parameters are typically obtained by iterative GLS (16).
With multilevel modeling for longitudinal data analysis, we investigate the following observed responses:
-
•
Case I: A single finger (right index finger of the subjects that is typically chosen as the primary finger in fingerprint recognition with one finger) is used for recognition.
–Normalized genuine match score obtained by the following:
| [4] |
where is the genuine match score between the jth and kth fingerprint impressions of the right index finger of subject i, and μ and σ are the mean and SD of , respectively.
–Normalized impostor match score between the kth fingerprint impression of the right index finger of subject i and the right index fingerprint in the first 10-print card of subject j for and .
–Binary identification decision made on a genuine pair with match score of by applying a decision threshold :
| [5] |
–Binary identification decision made on an impostor pair with match score of by applying the decision threshold .
-
•
Case II: All 10 fingers are used for recognition.
Similar to Case I, normalized genuine and impostor fusion scores ( and ) and binary identification decisions made on genuine and impostor pairs of subjects ( and ) are obtained based on the match score fused by a sum rule (SI Appendix, section S5).
The following covariates are investigated in the multilevel models for genuine fingerprint pairs:
-
•
: Time interval between the jth and kth fingerprint impressions of subject i; for ;
-
•
: Age of subject i when the latter of the jth and kth 10-print impressions was made; the subject i’s age at for ;
-
•
: The value corresponding to the lower of the qualities of the jth and kth fingerprint impressions of subject i. In this study, the National Institute of Standards and Technology Fingerprint Image Quality (NFIQ) measure (18) is used, which assigns one of the five discrete values ranging from 1 (the highest quality) to 5 (the lowest quality), to define fingerprint image quality. According to the definition of NFIQ, , where is the NFIQ value of the jth fingerprint impression of subject i;
-
•
: A binary indicator of sex of subject i; 1 for male, and 0 for female;
-
•
: A binary indicator of race of subject i; 1 for whites, and otherwise 0.
Multilevel models for impostor pairs are designed with the following covariates:
-
•
: Time elapsed since the first 10-print of subject i was obtained; , ;
-
•
and : Age of subject i when the kth 10-print impression was made, and the age of impostor subject j at the time of the first 10-print acquisition, respectively.
The two-level linear models investigated in our study are listed in Table 1 and SI Appendix, section S6.
Table 1.
Multilevel models for genuine match score analysis
| Model | Level 1 model | Level 2 model |
| Model A | ||
| Model | , | |
| Model | , | |
| Model | , | |
| Model | , | |
| Model | , | |
| Model D | , , , | |
| Model E | , , , , , |
Results
Population-Mean Trend of Genuine Fingerprint Match Scores.
Given that the normality assumptions of the residuals and random effects in the multilevel model fit to the data are violated (SI Appendix, section S7), the parameters in the multilevel models are estimated by a fully nonparametric bootstrap (16). We generate 1,000 bootstrap samples for genuine match score analysis, where each bootstrap sample is obtained by a cluster bootstrap—N subjects are resampled with replacement at level 1, and all of the level 2 data belonging to those subjects are included in the sample—to preserve the hierarchy in the longitudinal data.
SI Appendix, Tables S2 and S3 report the mean of the parameter estimates of the bootstrap samples and the percentile confidence intervals for the genuine match score models. The population-mean trends of models , , and based on the fixed-effects parameter estimates ( and ) show that the genuine match scores tend to decrease when , , and increase (Fig. 1 and SI Appendix, Fig. S6). The null hypothesis— in models , , and (i.e., the slope of the linear model is zero)—is rejected for all three models at a significance level of 0.05 because the 95% confidence interval for does not contain zero.
Fig. 1.
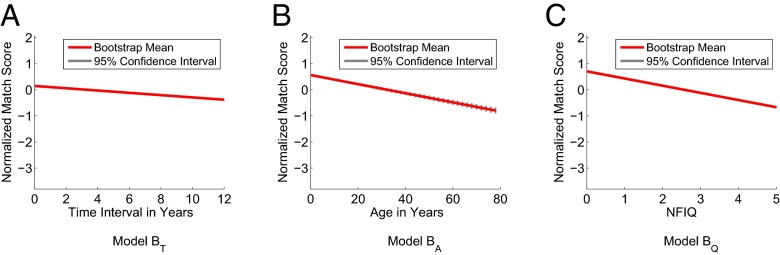
Population-mean trends of genuine match scores obtained by COTS-1 matcher along with 95% confidence intervals with respect to (A) , (B) , and (C) when a single finger is used for recognition. The confidence intervals for models and are too tight along the means to be visible.
Models D and E incorporate all three covariates (, , and ) into the model; model E includes interaction terms ( and ), whereas model D does not. The covariance matrix in model D shows that the correlations (i) between and and (ii) between and are very small. Also, the population-mean trends of models D and E and their 95% confidence intervals, illustrated in SI Appendix, Fig. S7, indicate that the impact of the interactions (i) between and and (ii) between and on genuine match scores is not significant (see SI Appendix, section S8, for the detailed analysis with models D and E).
Outlying Subjects in Model .
The parameter estimates of for each subject in model are shown in SI Appendix, Fig. S10, in addition to the population-mean trend . Several outlying subjects whose genuine match score trend markedly deviates from the population-mean trend in terms of Mahalanobis distance are identified. SI Appendix, Figs. S11–S15 show the individual trends of the outlying subjects and their fingerprint impressions.
-
•
Outlying subject 1 (SI Appendix, Fig. S11): The estimated intercept of this subject is very small. The subject consistently gives low genuine match scores because his fingerprints are severely scarred.
-
•
Outlying subject 2 (SI Appendix, Fig. S12): The intercept of the fitted model for this subject is rather large, although the slope is negative. This subject consistently gives high genuine match scores because his fingerprint impressions are of good quality.
-
•
Outlying subject 3 (SI Appendix, Fig. S13): This subject shows a very sharp decrease in genuine match scores as a function of time interval. In SI Appendix, Fig. S13A, the genuine match scores involving the first fingerprint impression are very low. This fingerprint impression is indeed an impostor fingerprint (SI Appendix, Fig. S13B); it is of tented arch type whereas the actual pattern of this finger is a right loop. After inspection of the subject’s 10-print cards, it turned out that the subject’s left and right hands were swapped at the time of the first 10-print card acquisition; the first impression came from the subject’s left index finger, instead of right index finger. This shows that operational fingerprint data can be mislabeled.
-
•
Outlying subject 4 (SI Appendix, Fig. S14): This subject also has a steep slope. It turned out that the fingerprint impressions of this subject were collected during his adolescence (starting at the age of 11 until the age of 21). This explains the sharp decrease in genuine match scores due to growth in finger size (19).
-
•
Outlying subject 5 (SI Appendix, Fig. S15): A positive slope is observed for this subject because the comparisons involving a lower quality fingerprint were made over a shorter time interval than the comparisons with higher quality fingerprints. This example illustrates that the fingerprint image quality does not necessarily vary with respect to time elapsed.
Model Assessment and Comparison.
Goodness-of-fit of a model evaluates how well the model fits the data. Furthermore, the impact of covariates on the observed responses can be assessed by comparing the goodness-of-fits of different models. The following three criteria are used to measure the goodness-of-fit: (i) deviance, (ii) Akaike information criterion (AIC), and (iii) Bayesian information criterion (BIC). The deviance measure is used to compare nested models, whereas AIC and BIC add a constant term to the deviance for the sake of comparing nonnested models (SI Appendix, section S9). The smaller the deviance (AIC or BIC), the better the model fit.
SI Appendix, Table S1 shows the goodness-of-fit measures of the multilevel models fit to genuine match scores obtained by the two COTS matchers. The model comparisons based on the goodness-of-fit lead to the following observations:
-
•
A decrease in deviance is observed when models , , and are compared with model A (unconditional mean model or empty model). This means that each individual covariate used in model B (, , or ) can explain some of the variation in genuine match scores.
-
•
Model provides a better fit to the data than models and . This implies that fingerprint quality explains better the variation in genuine match scores than time interval or subject’s age.
-
•
Sex and race are not important factors to explain the variation in genuine match scores because the deviance barely decreases from model to models or .
-
•
Models D and E show significantly smaller goodness-of-fit values than the other models. In other words, including all of the three covariates (, , and ) in the multilevel model better explains the trend in genuine match scores compared with including only a single covariate. The additional interaction terms in model E slightly improve the model fit.
Population-Mean Trend of Impostor Fingerprint Match Scores.
For impostor score analysis, 1,000 bootstrap samples are constructed to accurately capture the variability among distinct fingers, maintain the size of bootstrap sample feasible for model fitting, and avoid data dependency. The rth bootstrap sample contains a set of impostor scores for subject i , , where is a random set with indices of 10 impostor subjects for subject i. is sampled such that (i) and , for , are independent, and (ii) , where , does not include subject i.
The impact of time elapsed and subjects’ ages ( and ) on impostor match scores is evaluated in models and , respectively. Note that model in SI Appendix, Eq. S4, has two covariates associated with the age of two subjects involved in an impostor comparison: age of the subject of interest for longitudinal analysis and an impostor subject’s age as a control .
Although the null hypothesis is rejected in both models and at a significance level of 0.05 (SI Appendix, Table S4 and Figs. S16–S18), (i) the decrease in the population-mean trend of impostor match scores is negligible for both COTS matchers as time elapsed since the first fingerprint acquisition increases up to 12 y, the maximum time span in the dataset, and (ii) subject’s age appears to have marginal impact on impostor match scores in that the tendencies observed in two COTS matchers do not coincide (i.e., for COTS-1 matcher and for COTS-2 matcher), and the changes in impostor match score with the increase of subject’s age up to 78 y are small. For a similar reason to (ii), the impostor subject’s age has an insignificant impact on the impostor match scores.
Population-Mean Trend of Probability of True Acceptance.
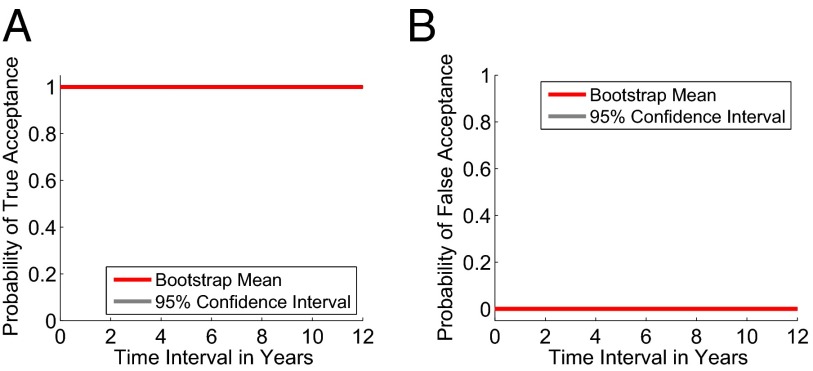
The population-mean trend of probability of true acceptance with respect to in model in SI Appendix, Eq. S5 is investigated at various false acceptance rates (FARs) (0.01%, 0.00001%, and empirical 0%). The decision thresholds are determined based on the impostor score distribution obtained by making all pairwise comparisons among the first fingerprint impressions of N subjects. The threshold corresponding to FAR of p is determined by a maximum of match score x satisfying , where is the cumulative distribution function of impostor match scores. The threshold corresponding to empirical 0% FAR is set to the maximum value in the impostor score set. The expected value of at the operational FAR range between 0.01% and 0.00001% remains close to 1.0 for the both COTS matchers even though the time interval between two fingerprints in comparison increases up to 12 y (Fig. 2A and SI Appendix, Figs. S19 and S20 and Table S5). At empirical 0% FAR, an extreme FAR point, the expected for COTS-1 matcher still remains close to 1.0, whereas COTS-2 matcher, which delivers inferior recognition accuracy compared with COTS-1 matcher, exhibits a considerable degradation in with increase in .
Fig. 2.
Population-mean trend of fingerprint recognition accuracy along with 95% confidence interval with respect to . (A) Probability of true acceptance ( in model ) and (B) probability of false acceptance ( in model ). Match scores are obtained by COTS-1 matcher when a single finger is used for recognition. The confidence intervals are too tight along the means to be visible in the plots.
To understand the joint impact of , , and on the probability of true acceptance, model D* in SI Appendix, Eq. S6 is fit to the binary decisions on genuine fingerprint pairs when the threshold corresponding to 0.00001% FAR is applied to COTS-1 match scores. The population-mean trend of with respect to is shown in Fig. 3 and SI Appendix, Fig. S21, at various and values. The bootstrap mean trend remains close to 1.0 across all age groups and fingerprint image quality levels. Interestingly, whereas 95% confidence intervals of are consistent among different age groups at fixed , 95% confidence interval of increases substantially when the fingerprint quality decreases (recall, the higher the , the lower the fingerprint quality) regardless of subject’s age group. This indicates that the tendency of with respect to has a considerable uncertainty when either of two fingerprints in comparison is of poor quality. It conforms to the model assessment analysis that fingerprint image quality, rather than time interval between fingerprints in comparison or subject’s age, explains well the variation in genuine match scores, and the large confidence intervals observed in models D and E fit to genuine match scores.
Fig. 3.
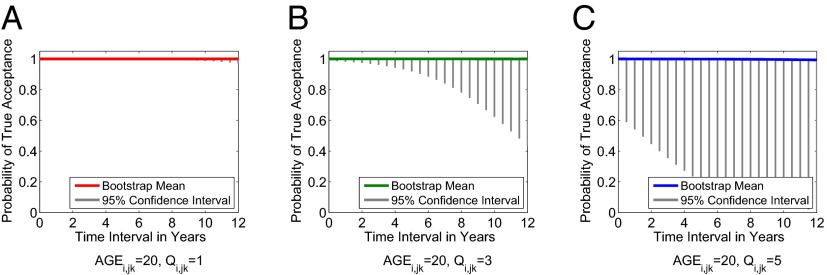
Population-mean trend and 95% confidence interval of probability of true acceptance with respect to when is 20 and is (A) 1, (B) 3, and (C) 5 in model D*. The decision threshold is set to the value corresponding to FAR of 0.00001%. Match scores are obtained by COTS-1 matcher when a single finger is used for recognition.
Population-Mean Trend of Probability of False Acceptance.
The population-mean trend of probability of false acceptance is also investigated at various FARs (0.01%, 0.1%, and 1%). Fig. 2B and SI Appendix, Figs. S22 and S23 and Table S5 show that the predicted value of remains close to 0.0 regardless of within 12 y. This implies that the binary decisions made on impostor fingerprint comparisons over time are not likely to be affected by the time elapsed.
Results When Using All 10 Fingers for Recognition.
Ten-finger fusion results of genuine match scores (SI Appendix, Table S6 and Fig. S24) and impostor match scores (SI Appendix, Table S7 and Figs. S25–S27) conform to the results in the single-finger experiments. It is noteworthy that the probability of true acceptance remains 1.0 for both matchers when match scores from 10 fingers are fused, even at the extreme FAR point of 0% (SI Appendix, Table S8 and Figs. S28 and S29). The probability of false acceptance stays close to 0.0 with the increase in time elapsed (SI Appendix, Table S8 and Figs. S30 and S31).
Conclusions
Since ancient times, fingerprints have been accepted as persistent and unique to an individual. Early scientific studies on fingerprint recognition in the late 19th century claimed that there is no significant change in the friction ridge structure over time by examining small sets of genuine fingerprint pairs captured over a large time interval. Although fingerprint recognition is now prevalent in distinguishing a large number of individuals—for example, Federal Bureau of Investigation’s Next Generation Identification searches a fingerprint database holding 106 million criminal and civil files (20)—acceptance of the persistence of fingerprints has been mostly based on anecdotal evidence.
To understand the behavior of fingerprint match score and recognition accuracy, multiple fingerprint records of 15,597 subjects apprehended by the MSP over a time span varying from 5 to 12 y were investigated. The genuine and impostor match scores obtained by two COTS fingerprint matchers were analyzed by linear multilevel statistical models with various covariates, including time interval between two fingerprints being compared, subject’s demographic factors such as age, sex, and race, and fingerprint image quality. The longitudinal study of fingerprint recognition reported in this paper leads to the following conclusions:
-
•
The hypothesis test for the slope of a linear model indicates that genuine match scores tend to decrease as the time interval between two fingerprints being compared increases. Furthermore, genuine match scores tend to decrease as the subject’s age increases or when the fingerprint image quality decreases.
-
•
Despite the downward trend in genuine match scores over time, the probability of true acceptance, at operational FAR settings, remains close to 1.0 (up to 12 y, the maximum time span in the dataset). However, if either of two fingerprints in comparison is of poor quality, the uncertainty in the expected probability of true acceptance becomes considerably large.
-
•
The changes in impostor match scores with respect to time elapsed and subject’s age are negligible. Hence, the probability of false acceptance remains close to 0.0 regardless of the time interval between two fingerprints.
-
•
A comparison among the models with different covariates fit to the genuine match scores shows the following:
–Time interval, subject’s age, and fingerprint image quality can explain the variation in genuine match scores, whereas subject’s sex and race have marginal impact.
–Fingerprint image quality explains the variation in genuine match scores better than time interval and subject’s age.
–The correlations (i) between time interval and fingerprint image quality and (ii) between subject’s age and fingerprint image quality are negligibly small in the population-mean trend analysis.
–The impact of the interactions (i) between time interval and fingerprint image quality and (ii) between subject’s age and fingerprint image quality on genuine match scores is not significant.
-
•
Outlying subjects in the dataset who do not conform to the population-mean trend as determined by model fit are examined. These outlying subjects illustrate (i) a case where a COTS matcher consistently provides high genuine match scores due to high-quality fingerprints from the same finger, (ii) an example where the matcher generates low genuine match scores due to the scarring of a finger, (iii) a degradation in genuine match scores when a juvenile fingerprint is compared with the corresponding adult fingerprint, and (iv) presence of labeling errors in the operational fingerprint databases.
-
•
The inferences from single (right index) finger analysis conform to the inferences from 10-finger score fusion analysis.
-
•
The results from two different COTS fingerprint matchers used in the study coincide, except the tendency of impostor match scores with respect to subject’s age and the temporal tendency of probability of true acceptance at empirical 0% FAR in the single-finger analysis.
Our future work will include the following: (i) given that we make all pairwise comparisons of the fingerprint impressions from each subject, the correlation among the genuine match scores of a subject needs to be reflected in the model; and (ii) nonlinear multilevel models will be investigated and compared with the linear models presented in this study.
Supplementary Material
Acknowledgments
We thank Prof. Joseph Gardiner (Department of Epidemiology and Biostatistics, Michigan State University) and Karthik Nandakumar (IBM, Singapore) for helpful discussions and suggestions. We also acknowledge the help of Capt. Greg Michaud, Director of Forensic Science Division at the Michigan State Police, in providing us the fingerprint dataset used in this study. This research was supported by a grant from the National Science Foundation Center for Identification Technology Research.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
Data deposition: The dataset used in this paper can be made available to interested researchers for longitudinal study under appropriate nondisclosure agreement dictated by the Michigan State Police.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1410272112/-/DCSupplemental.
References
- 1.Hawthorne MR. Fingerprints: Analysis and Understanding. CRC; Boca Raton, FL: 2009. [Google Scholar]
- 2. Frye v. United States (1923) 54 App. D.C. 46, 293 F. 1013.
- 3. Daubert v. Merrell Dow Pharmaceuticals, Inc. (1993) 509 U.S. 579, 113 S. Ct. 2786.
- 4. Scientific Working Group on Friction Ridge Analysis, Study and Technology (SWGFAST) (2013) Standards for Examining Friction Ridge Impressions and Resulting Conclusions (Latent/Tenprint). Available at www.swgfast.org/documents/examinations-conclusions/130427_Examinations-Conclusions_2.0.pdf. Accessed May 12, 2015.
- 5.Vanderkolk JR. 2011. Examination process. Fingerprint Sourcebook (National Institute of Justice, Washington, DC), Chap 9.
- 6.Pankanti S, Prabhakar S, Jain AK. On the individuality of fingerprints. IEEE Trans Pattern Anal Mach Intell. 2002;24(8):1010–1025. [Google Scholar]
- 7.Zhu Y, Dass SC, Jain AK. Statistical models for assessing the individuality of fingerprints. IEEE Trans Inform Forensics Secur. 2007;2(3):391–401. [Google Scholar]
- 8.Chen Y, Jain AK. 2009. Beyond minutiae: A fingerprint individuality model with pattern, ridge and pore features. Third IAPR/IEEE International Conference on Biometrics, Lecture Notes in Computer Science, eds Tistarelli M, Nixon MS (Springer, Berlin), Vol 5558, pp 523–533.
- 9.Neumann C, et al. Computation of likelihood ratios in fingerprint identification for configurations of any number of minutiae. J Forensic Sci. 2007;52(1):54–64. doi: 10.1111/j.1556-4029.2006.00327.x. [DOI] [PubMed] [Google Scholar]
- 10.Herschel WJ. The Origins of Finger-Printing. Oxford Univ Press; Oxford: 1916. [Google Scholar]
- 11.Galton F. Finger Prints. Macmillan; London: 1892. [Google Scholar]
- 12.Cummins H, Midlo M. Finger Prints, Palms and Soles: An Introduction to Dermatoglyphics. Dover Publications; New York: 1961. [Google Scholar]
- 13.National Research Council . Strengthening Forensic Science in the United States: A Path Forward. National Academies Press; Washington, DC: 2009. [Google Scholar]
- 14.Mansfield AJ, Wayman JL. Best Practices in Testing and Reporting Performance. Center for Mathematics and Scientific Computing, National Physical Laboratory; Teddington, UK: 2002. [Google Scholar]
- 15. Federal Office for Information Security (BSI) (2004) Evaluation of fingerprint recognition technologies–BioFinger. Available at https://www.bsi.bund.de/SharedDocs/Downloads/EN/BSI/Publications/Studies/BioFinger/BioFinger_pdf.pdf?__blob=publicationFile. Accessed May 12, 2015.
- 16.Goldstein H. Multilevel Statistical Models. 4th Ed Wiley; Chichester, UK: 2010. [Google Scholar]
- 17.Singer JD, Willett JB. Applied Longitudinal Data Analysis: Modeling Change and Event Occurrence. Oxford Univ Press; Oxford: 2003. [Google Scholar]
- 18.Tabassi E, Wilson CL, Watson CI. 2004. Fingerprint image quality. National Institute of Standards and Technology Interagency Report 7151 (National Institute of Standards and Technology, Gaithersburg, MD)
- 19.Gottschlich C, et al. Modeling the growth of fingerprints improves matching for adolescents. IEEE Trans Inform Forensics Secur. 2011;6(3):1165–1169. [Google Scholar]
- 20. Federal Bureau of Investigation (2014) Next Generation Identification (NGI). Available at www.fbi.gov/about-us/cjis/fingerprints_biometrics/ngi. Accessed May 12, 2015.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.