Dynamical malaria models reveal how immunity buffers effect of climate variability

Significance

We apply recently developed inference techniques to disentangle the relative impacts of extrinsic climatic and intrinsic immunological forcing on the epidemiology of lethal human malaria, Plasmodium falciparum, for two adjacent cohorts in Senegal. For the cohort in which transmission is limited by mosquito existence by rainfall, the pattern of cases is driven by climate forcing. On the contrary, in the village where mosquitoes are present year-round, the impact of climate on incidence is largely buffered by clinical immunity. Our models, which are capable of simulating reported cases over two decades, open the possibility of forecasting malaria from climate in endemic regions but only after accounting for the interaction between climate and immunity.

Abstract

Assessing the influence of climate on the incidence of Plasmodium falciparum malaria worldwide and how it might impact local malaria dynamics is complex and extrapolation to other settings or future times is controversial. This is especially true in the light of the particularities of the short- and long-term immune responses to infection. In sites of epidemic malaria transmission, it is widely accepted that climate plays an important role in driving malaria outbreaks. However, little is known about the role of climate in endemic settings where clinical immunity develops early in life. To disentangle these differences among high- and low-transmission settings we applied a dynamical model to two unique adjacent cohorts of mesoendemic seasonal and holoendemic perennial malaria transmission in Senegal followed for two decades, recording daily P. falciparum cases. As both cohorts are subject to similar meteorological conditions, we were able to analyze the relevance of different immunological mechanisms compared with climatic forcing in malaria transmission. Transmission was first modeled by using similarly unique datasets of entomological inoculation rate. A stochastic nonlinear human–mosquito model that includes rainfall and temperature covariates, drug treatment periods, and population variability is capable of simulating the complete dynamics of reported malaria cases for both villages. We found that under moderate transmission intensity climate is crucial; however, under high endemicity the development of clinical immunity buffers any effect of climate. Our models open the possibility of forecasting malaria from climate in endemic regions but only after accounting for the interaction between climate and immunity.

Climate plays a key role in driving the seasonal outbreaks of malaria in areas of low or unstable malaria transmission (1–4). Recent studies have shown the possibility of forecasting malaria outbreaks on the basis of climate information and disease features in these low-transmission settings (3, 5). For instance, in highland malaria the role of warming temperatures is vividly debated (4, 6–8) and in desert-epidemic fringes early studies reported predictions of a widespread increase in malaria transmission (9–12). Recent malaria models also predict a global net increase of the population at risk (13); however, others suggest a shift in spatial distribution rather than a large net increase in total malaria incidence worldwide (14, 15). In epidemic fringes, variation in the incidence of disease is largely determined by the seasonal variation of the mosquito population’s occurrence and density, which are essentially modulated by local rainfall [e.g., if water limited (3, 16)] or temperature [e.g., if altitude limited (2, 4, 8)]. This is not the case in holoendemic transmission settings, where incidence of disease is determined not only by external forces, but also by the development of clinical and antiparasite immunity. Under intense transmission, clinical immunity develops during childhood after many infections (17, 18), whereby the individual can tolerate nonnegligible parasite densities without showing symptoms. Subsequently, antiparasite immunity, which enables control of parasite density, develops much more slowly (19), leading to a state of premunition, whereby individuals harbor chronic, potentially subpatent infections (20). Continued exposure to the parasite is seemingly required to maintain such premunition (21). Complete protection from further infections is rarely, if ever, achieved. In such high-transmission regions, the relationship between local climate and disease is difficult to disentangle.

In this study, two unique long-term cohort datasets from villages separated by 5 km but with markedly different malaria transmission intensity (Fig. 1, Upper) enable us to showcase the relative roles of internal and external factors in malaria epidemiology, assess the potential degree of predictability emanating from climatic variability, and generate estimates of key parameters in determining malaria population dynamics. To this end, we use a recently developed inference methodology for nonlinear stochastic dynamical systems, successfully applied to epidemic dynamics (3, 16) but never applied to endemic settings. A general coupled mosquito–human compartment model that includes possible key mechanisms common to both villages serves our aim of disentangling differences related to immunity, infectivity, superinfection, and asymptomatic infections as well as to measure the relevance of local climate for each village.

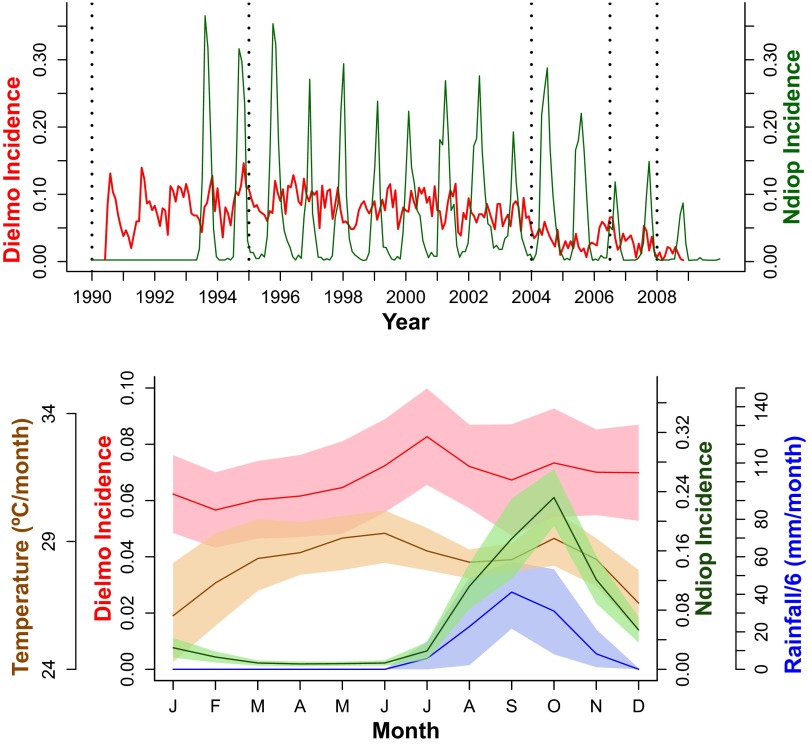
Fig. 1.

(Upper) P. falciparum malaria incidence for Dielmo (red) and Ndiop (green). Vertical dotted black lines separate the four different drug regimes (from left to right: Quinine, Chloroquine, Fansidar, and ACT). Incidence units are episodes per person per month. (Lower) Average annual cycles computed as the average month by month for the whole time series of P. falciparum monthly incidence for Dielmo (red) and Ndiop (green), local rainfall (blue), and temperature (orange). Shaded regions correspond to the SD.

Dynamic Malaria Transmission Model

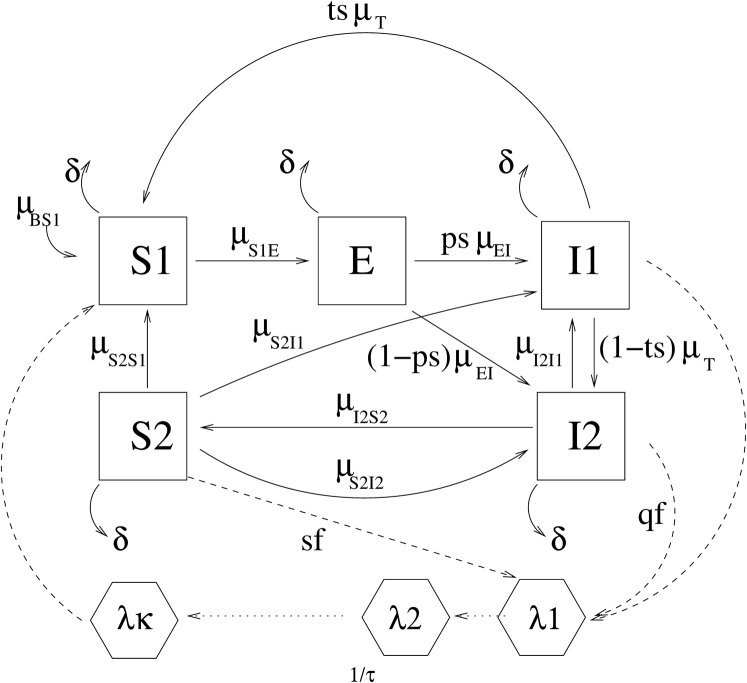
We classify humans into five distinct classes: $S1$, susceptible to infection; E, exposed (i.e., carrying a latent infection but not yet infectious); $I1$, infected symptomatic and infectious; $I2$, infected asymptomatic and infectious; and $S2$, recovered but with a subpatent load of parasites (not completely cleared) and potentially infectious to mosquitoes (Fig. 2). Reinfection, which here includes both superinfections and recrudescent infections that were formerly subpatent, but not new infections, was included as transitions from $S2$ to $I1$ and $I2$ classes. The force of reinfection was considered as a constant proportion, $s_i$, of the force of infection ${\mu }_{S1E}$ (SI Text). Given that the higher the transmission intensity is, the slower the recovery rate (4, 22), immunity and recovery were considered as functions of the transmission intensity as explained in SI Text. Drug periods were modeled as constant functions for the corresponding period (see SI Text for details), and treatment success probability was considered through a parameter $t_s$. We do not explicitly model mosquito abundance, survival, or parasite development. Instead, we model vector dynamics through a delayed equation for the force of infection ${\mu }_{S1E}\left(t\right)$, taking into account the fact that the parasite has an extrinsic incubation period, τ, within the mosquito, during which time the parasite passes through its sporogonic cycle (SI Text). Transmission was modeled as proportional to the entomological inoculation rate (EIR). Alternatively we replaced mosquito population variability by a set of functions as explained in SI Text to account for yearly periodic forces, together with rainfall and temperature anomalies to take into account intrayear variability. The same model was applied to both villages to compare both fitted sets of parameters and infer possible differences in the mechanisms underlying the model. Environmental noise was also included in the transmission term (SI Text). We took into account the yearly change in the total human population (Table S1) and the mortality rate was assessed by fitting population data for each of the villages as explained in SI Text (see also Fig. S1). Fittings and simulations were performed using open source code for statistical inference for partially observed Monte Carlo processes (23).

Fig. 2.

Flow diagram of the SDE model. Human classes are $S1$ (susceptible), E (exposed, carrying a latent infection), $I1$ (symptomatic infected and infectious), $I2$ (asymptomatic infected and infectious), and $S2$ (recovered subpatent, i.e., having some resistance to reinfection). Mosquito–parasite classes are ${\lambda }_1$ (force of infection at previous time t − s) and ${\lambda }_{\kappa }$ (force of infection at current time t). The possibility of transition between classes X and Y is denoted by a solid arrow, with the corresponding rate written as ${\mu }_{XY}$. The dotted arrows represent interactions between the human and mosquito stages of the parasite. The model is formalized by Eqs. S1–S5 and Eqs. S9–S11.

Results and Discussion

Plasmodium falciparum incidence time series for Ndiop and Dielmo are shown in Fig. 1, Upper. Ndiop, an area with scarce vegetation and temporary surface water bodies supplied by seasonal rainfalls (see figure 1, Ndiop, in ref. 24), shows mesoendemic seasonal dynamics. On the contrary, Dielmo, situated on the marshy bank of a small permanent stream (see figure 1, Dielmo, in ref. 24) exhibits perennial malaria transmission leading to a holoendemic type of dynamics. The EIR time series for Dielmo and Ndiop are shown in Fig. S2 classified according to mosquito species. The EIR variability of Anopheles gambiae sensu lato is clearly more seasonal than that of Anopheles funestus as previously observed (25). Interestingly, there was a significant positive correlation ($r_{xy}$) between Dielmo cases and Dielmo’s EIR of A. funestus (Pearson’s $r_{xy}=0.36$, $P\hspace{0.17em}\text{value}=2.921e-08$), but not with Dielmo’s EIR of A. gambiae s.l.. On the contrary for the case of Ndiop there was a significant positive correlation ($r_{xy}$) between cases and Ndiop’s EIR of A. gambiae s.l. (Pearson’s $r_{xy}=0.37$, $P\hspace{0.17em}\text{value}=3.791e-07$), but not with Ndiop’s EIR corresponding to A. funestus.

In light of the knowledge about these species’ ecology and larval habitat, where A. gambiae s.l. breeds in surplus surface water and A. funestus prefers to breed in stagnant water at the edge of rivers (25–27), one would expect A. gambiae s.l. dynamics to be more dependent on rainfall variability (Fig. S3). We did find a significant correlation between rainfall and Dielmo’s EIR of A. gambiae s.l. (Pearson’s $r_{xy}=0.42$, $P\hspace{0.17em}\text{value}=3.844e-11$) as well as between rainfall and Ndiop’s EIR of A. gambiae s.l. (Pearson’s $r_{xy}=0.33$, $P\hspace{0.17em}\text{value}=3.844e-3$) whereas none was obtained between rainfall and EIR of A. funestus either for Dielmo or for Ndiop. It is therefore reasonable to expect that rainfall acts as a pacemaker of A. gambiae s.l. population variability affecting in a more direct way Ndiop malaria dynamics.

Averaged malaria incidence in Dielmo and Ndiop together with both mean local rainfall and temperature are shown in Fig. 1, Lower (see also Figs. S3 and S4). For the case of Dielmo we observe a steady increase of malaria cases from March, reaching a peak around the month of July, and then staying more or less stationary with barely a second increase in October. This last minor increase in Dielmo agrees with the timing of the Ndiop single peak in malaria cases also occurring around October. Rainfall peaks around August–September and temperature is maximal around the month of July. Therefore, rainfall and temperature are good candidates to influence Ndiop cases variability. However, unlike Ndiop there is no clear picture of the influence of rainfall on the fluctuations of malaria cases in Dielmo’s first peak, unless the lower-amplitude anomalies were sufficient to stimulate a large increase in mosquito population and/or to significantly alter EIR values.

We found highly significant correlation values between Ndiop cases and rainfall in the previous month (Pearson’s $r_{xy}=0.75$, $P\hspace{0.17em}\text{value}=2.2e-16$), which suggests that rainfall plays an important role in Ndiop malaria dynamics, in agreement with the fact that local climate variability drives malaria outbreaks in low-transmission epidemic fringes (3, 4, 16). In the case of Dielmo, a high-transmission perennial site, the second peak is seen to be significantly modulated by rainfall in the previous month (Dielmo second peak: Pearson’s $r_{xy}=0.24$, $P\hspace{0.17em}\text{value}=0.6e-3$) albeit to a lesser extent than in Ndiop. Dielmo’s second peak of cases shows a significant negative correlation with temperature (Dielmo second peak: Pearson’s $r_{xy}=-0.4$, $P\hspace{0.17em}\text{value}=0.7e-10$). Dielmo’s first peak of cases is presumably related to the stream dynamics (permanent water availability) and temperature as indicated by the significant correlation with temperature (Dielmo first peak: Pearson’s $r_{xy}=0.36$, $P\hspace{0.17em}\text{value}=0.3e-7$) and between A. funestus EIR (strongly depending on the stream flow dynamics) and malaria first peak cases in Dielmo (Pearson’s $r_{xy}=0.2$, $P\hspace{0.17em}\text{value}=4.4e-3$). All these associations suggest that climate variability plays an important role in malaria dynamics and indicate that climate covariates should be included in the malaria models.

Transmission variability was modeled in four different ways: (i) only by means of the EIR, (ii) with a seasonal flexible function [seasonal splines (Sp)], and (iii) with a combination of a seasonal flexible function and climatic covariate anomalies in two alternative ways [seasonal splines plus linear combination of temperature and rainfall (SpTR)] and SpROT (same as before plus rainfall over temperature) as explained in SI Text. Likelihoods of these transmission models for each of the drug periods are shown in Table 1 together with second-order Akaike information criterion (${\text{AIC}}_c$) values; AIC_c is a likelihood-based criterion that penalizes for higher number of parameters as well as for size of dataset (28). For both Dielmo and Ndiop the fit improves when rain and temperature anomalies are included in the models (${\text{AIC}}_c$ values in Table 1 and Tables S2–S4). Values of ${\text{AIC}}_c$ for each of the drug periods (Table 1) show that the average seasonal variation in climate (and therefore in the mosquito population), represented by a flexible function not specified a priori and emerging freely from the fitting procedure, is necessary to describe observed cases. Overall the best performance corresponds to the SpTR model that takes into account rainfall and temperature contributions in a simplest parsimonious way, as an indicator of humidity conditions. The sensitivity of these results with the inclusion of each of the climate covariates is reported in SI Text, giving more support to the tight association between rainfall and temperature to fluctuations in mosquito population and parasite development and ultimately to malaria dynamics.

Table 1.

Maximum likelihood of fits for different drug periods and different transmission dependence

		Ndiop								Dielmo
		Quinine, $n=26$		Chloroquine, $n=95$		Fansidar, $n=30$		ACT, $n=21$		Quinine, $n=57$		Chloroquine, $n=106$		Fansidar, $n=31$		ACT, $n=27$
Model	p	$\ell$	${\text{AIC}}_c$	$\ell$	${\text{AIC}}_c$	$\ell$	${\text{AIC}}_c$	$\ell$	${\text{AIC}}_c$	$\ell$	${\text{AIC}}_c$	$\ell$	${\text{AIC}}_c$	$\ell$	${\text{AIC}}_c$	$\ell$	${\text{AIC}}_c$
EIR	4	−141	292	−433	874	−143	296	−94	198	−227	463	−398	804	−134	277	−121	252
Sp	3	−113	233	−381	768	−124	255	−90	187	−223	452	−399	804	−128	263	−122	251
SpTR	5	−109	231	−378	766	−121	254	−86	186	−223	457	−391	792	−121	254	−115	243
SpROT	6	−117	250	−521	1055	−119	254	−87	192	−222	458	−392	797	−121	257	−115	246

For each drug period transmission was modeled by means of the entomological inoculation rate (EIR), only with splines (Sp) and with splines and anomalies of rain and temperature (SpTR and SpROT). The p-labeled column corresponds to the number of free parameters. The rest of the parameters were fixed at the maximum-likelihood estimated values listed in Tables S3 and S4. The second-order Akaike information criterion (${\text{AIC}}_c$) is computed as ${\text{AIC}}_c=-2\ell +2p+\left(2p\left(p+1\right)\right)/\left(n-p-1\right)$ with n the number of observations. The best fits are shown in boldface type. Overall the fit improves when temperature and rainfall anomalies are considered (SpTR model).

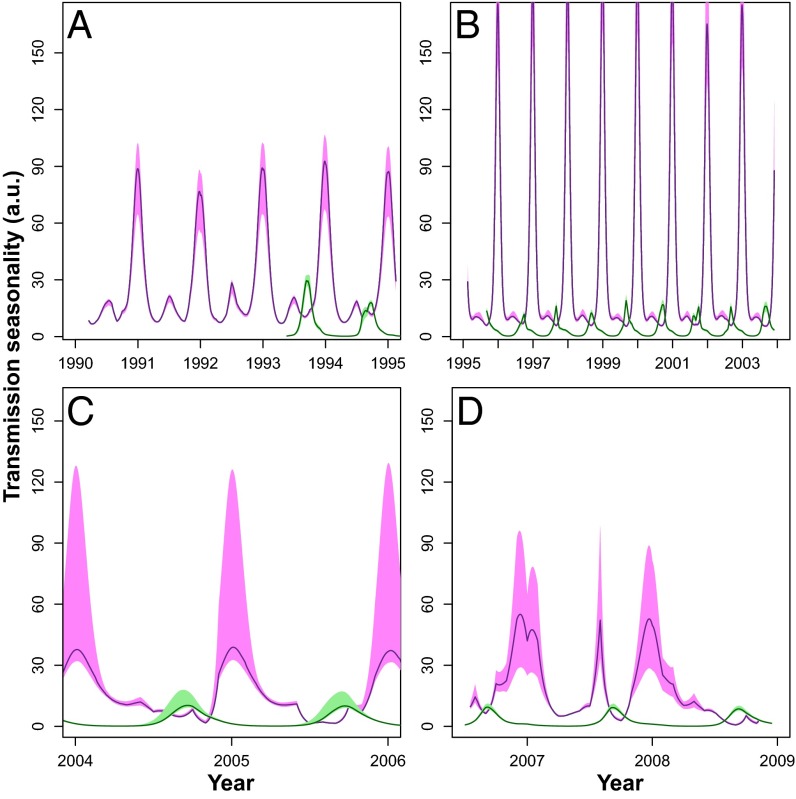
For Dielmo, fitted transmission with the SpTR model exhibits two maxima as shown in Fig. 3. A smallest peak in transmission occurs around June and a second peak in transmission starts to rise in October, reaching its maximum around December. If we accept some seasonality in Dielmo transmission, then people will have been less exposed to new infections from January to June, losing some short-term clinical immunity and responding more clinically to the rise in infectious bites in July. Following the onset of increased transmission intensity in July (due to the seasonal increase in A. gambiae s.l.), by the time December arrives, individuals will have had their clinical immunity boosted by renewed increased exposure to infection and hence have reduced clinical expression. Thus, even when transmission increases in December, the development of short-term clinical immunity would reduce the tendency to have clinical episodes toward the end of the year as can be seen in Fig. 1, Lower. For the case of Ndiop, fitted transmission with the SpTR model exhibits a single peak in the seasonal cycle that attains its maximum during August (Fig. 3). According to the SpTR model, transmission intensity is on average 10 times higher in Dielmo (Fig. 3, violet line/shading) than in Ndiop (Fig. 3, green line/shading). This result is independent of our previous knowledge that the number of infectious bites is 10-fold lower in Ndiop than in Dielmo (SI Text), validating our modeling approach. School holidays and harvest time coincide with the rainy season and hence lead to temporary intraannual increases in population size, although this variation is minimal and short-lived (Fig. S5) and therefore was not considered in our model.

Fig. 3.

Fitted transmission seasonality with the SpTR model for each of the drug periods for Dielmo (violet) and Ndiop (green). Lines correspond to the mean of 500 fits, and shaded regions correspond to the 10th and 90th percentiles of all fits. Transmission was modeled as a seasonal spline basis and climatic covariates are explained in SI Text. Between years variability in transmission reflects the variability in rainfall and temperature anomalies. (A) Quinine period. (B) Chloroquine period. (C) Fansidar period. (D) Artemisinin combination therapies (ACT) period.

To be able to compare resulting parameter values between Ndiop and Dielmo, we fitted malaria dynamics of both villages with the same dependence of transmission on climate covariates [as explained in SI Text (see also Figs. S6 and S7)]. Parameter values are shown in column SpTR in Tables S3 and S4. Average times from exposed latent to infected were similar in Ndiop and Dielmo ($1/m{u}_{EI}\approx 10\hspace{0.5em}\text{d}$). By contrast, the probability of developing symptoms was much smaller in Dielmo ($P_s\approx 0.04$) than in Ndiop ($P_s\approx 0.8$). To our knowledge, this result is in agreement with a faster development of clinical immunity in Dielmo due to the cumulative exposure to the parasite (29–32). The average time spent as an asymptomatic but infectious individual ($t_{I2S2}$) is ∼3 mo for Ndiop and 1 mo for Dielmo. In other words, it takes longer to clear the parasite in Ndiop than in Dielmo, reflecting the higher level of antiparasite immunity in the area of higher transmission intensity. Similarly, the time needed to completely clear the parasite ($t_{S2S1}$) is longer for Ndiop than for Dielmo.

Given that passive as well as active surveillance is performed in both villages (as explained in SI Text), all of the infected symptomatic people, i.e., people in the $I1$ class, receive drug treatment. According to our model 90% of the people in $I1$ ($t_s\approx 0.9$) recover in ∼11 d after drug treatment. However, we considered the possibility of drug treatment failure due for example to parasite resistance, in which case it would take between 3 mo and 5 mo to go from the symptomatic ($I1$) to the asymptomatic class ($I2$) without any treatment. This result is in agreement with recent epidemiological observations in sub-Saharan Africa where the average duration of infection was brought down from 270 d to 14 d by administration of drugs (33).

Interestingly for both villages the infectiousness of the asymptomatic ($I2$) and subpatent ($S2$) classes is not negligible (Ndiop, $s_f\approx q_f\approx 0.5$; Dielmo, $s_f\approx 0.6,q_f\approx 0.8$) where the infectivity of the $I1$ class was set to one for comparison. Thus, the proportion of the asymptomatic class infecting mosquitoes is higher in Dielmo than in Ndiop. The reasons for this are not clear, but may reflect differences in the immune state of asymptomatic individuals in the two villages: i.e., despite all broadly belonging to an asymptomatic class, the higher transmission intensity and hence more rapid acquisition of clinical and antiparasite immunity in Dielmo may contribute to differences in infectiousness. Children tend to have higher gametocyte prevalence rates (34), thus potentially making the younger asymptomatics (in Dielmo) more infectious.

We found that the overall force of reinfection needed for an individual to pass from asymptomatic ($I2$) to symptomatic ($I1$) is comparable between both villages. This result is surprising given that individuals from Dielmo have higher levels of clinical immunity. As for this transition we are taking into account not only superinfection but also recrudescent infections; the use of an age-dependent threshold in Dielmo for asymptomatics may lead to more immediate changes of infected category following superinfection and cumulative parasite densities than in Ndiop. Differences in the parasite density criteria defining the symptomatic class in both villages may likewise lead to a rapid change of state simply on the basis of within-host parasite population dynamics.

Finally, the force of infection needed to change from subpatent ($S2$) to symptomatic ($I1$) in Dielmo is 20 times higher than the one needed in Ndiop. This transition represents pure superinfection in the sense that humans with ultralow parasite densities flip to the symptomatic state. Recent mouse model studies have suggested that superinfection is impaired by the first infection, but only when the blood-stage parasite density exceeds a certain threshold (35); however, the presence of a blood-stage infection can suppress liver-stage immunity (36). Our findings are consistent with these observations. In particular, the force of reinfection needed for transition from subpatent ($S2$) to symptomatic ($I1$) was virtually equal to the overall force of infection in Dielmo. This suggests that subpatent infections in Dielmo are unlikely to recrudesce and generate symptomatic infections, reflecting the high levels of antiparasite and clinical immunity. It is notable that the relative force of infection necessary for the transition from the subpatent to asymptomatic states ($S2$ to $I2$) in Dielmo was lower, consistent with there being greater levels of clinical than antiparasite immunity. In Ndiop, the relative forces of infections necessary for subpatent infections to transit to either asymptomatic or symptomatic infections were similar, confirming our observations on the relative absence of clinical immunity in this population. Notably, however, the presence of an infection or a subpatent infection per se overall increases the risk of a symptomatic (or asymptomatic) infection than if the individual was not infected at all.

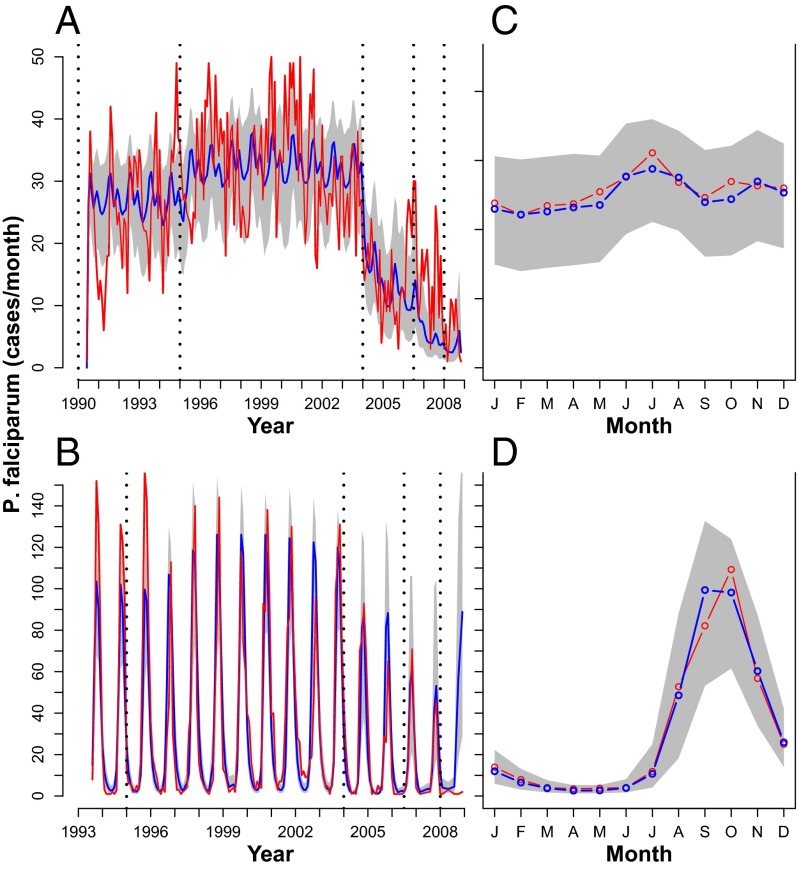
Simulations performed for the whole time series period by setting initial conditions and parameters only from the fitting procedure with the SpTR model (Tables S3 and S4) are shown in Fig. 4. Remarkably, they are not next step predictions but 18-y trajectories starting from initial conditions in the 1990s with no posterior readjustment (Fig. 4). In this sense, they reproduce not only the annual average cycles of cases for both villages (Fig. 4, Lower), but also the dynamics of the whole time series for both villages (Fig. 4, Upper). This remarkable agreement indicates that with the appropriate set of parameters the same structural model can be used to describe Ndiop epidemic as well as Dielmo endemic dynamics.

Fig. 4.

(A and C) Dielmo. (B and D) Ndiop. (A and B) Red, P. falciparum cases; blue, the mean of 1,000 simulations; gray shading, the 10th and 90th percentiles of the simulations. Simulations were done with parameters extracted from 500 fits, weighting them according to their likelihood. All of the simulations were done from the also fitted initial conditions, simulating all of the time series ahead (i.e., with no readjustment of any parameter at any point in time during the simulation). Model used: SpTR. (A) Dielmo; (B) Ndiop. (C and D) Monthly average of the curves in A and B. Simulations are shown in blue/gray and data in red. (C) Dielmo; (D) Ndiop.

Conclusions

The implementation of dynamical models in conjunction with recently developed statistical inference methods allowed us to determine some unknown epidemiological malaria parameters as well as to confirm some of the known ones. Furthermore, it enabled us to extract information on important unobserved variables, such as transmission variability, and most significantly to infer the relative importance of different covariates (e.g., climate variability) pertinent to the mechanisms underlying malaria epidemiology. The emerging set of epidemiological parameters consistent with some relevant field observations allowed us to better understand important differences between high- and low-transmission settings, related to parasite immunity, clinical immunity, and reinfection. The dynamic model for P. falciparum transmission applied to Dielmo and Ndiop showed that the role of climatic covariates clearly differs in both villages. Whereas in Ndiop rainfall and temperature are key drivers of transmission determining most of the interannual variability in malaria cases, in Dielmo those climate covariates only partially account for the seasonal variation of the force of infection. Climate plays an important role in the increase in malaria cases in Dielmo around July, contributing to the increase in clinical immunity. However, toward the end of the year, clinical immunity reduces the number of clinical cases in the face of an increase in transmission intensity. This new supporting evidence on the interaction between climate and immunity in Dielmo, not observed in Ndiop, suggests for the first time to our knowledge that clinical immunity to malaria might buffer or even halt the effect of climate on transmission intensity in endemic settings in general. For instance, if clinical immunity decreases (e.g., after bed net policies or insecticide campaigns), the distribution of recorded malaria cases throughout the year would change accordingly, making climate and immunity intertwined drivers of variation in incidence of malaria. Recent multimodel approaches addressed the potential expansion of malaria to currently uninfected areas by performing predictions mainly based on climate (13). This study shows that such extrapolation is valid only along the fringes where the disease is unstable but has to be carefully addressed for endemic places where intrinsic factors such as immunity, reinfection, and asymptomatics should be taken into account to reproduce the observed temporal patterns. Our approach opens the possibility to forecast also in malaria endemic regions and could be useful for other datasets from very different epidemiological dynamics as well as for other vector-borne diseases.

Materials and Methods

This program is supported by three different institutions: the Institut Pasteur (Dakar, Senegal), the Institut de Recherche pour le Développement (Marseille, France), and the Senegalese Ministry of Health and Prevention. An agreement between these institutions defines all research activities conducted in this program. The longitudinal surveys were approved by the Ministry of Health of Senegal and the assembled population of the two villages (as explained in SI Text). Written informed consent was obtained from all participants. We studied two extensive long-term epidemiological datasets of daily P. falciparum confirmed malaria cases, probably among the best malaria records worldwide, recorded for 19 y (1990–2008) in Dielmo and for 16 y (1993–2008) in Ndiop (see SI Text for more details) (37). Although these western Senegalese villages are situated only 5 km apart, the epidemiology of both villages is strikingly different. Dielmo village is situated on the marshy bank of a small permanent stream (see figure 1, Dielmo, in ref. 24), where anopheline mosquitoes breed year-round (31, 38) and malaria transmission is intense and perennial, with a mean 258 infected bites per person per year (during 1990–2006) (27). Transmission is on average 10-fold lower in Ndiop (see figure 1, Ndiop, in ref. 24) but highly variable, increasing during the rainy season from July to October (39). Exposure to infection and acquisition of immunity therefore markedly differ in the villages (31, 32, 38, 40). This difference is most evident in the higher P. falciparum prevalence rates of infection in Dielmo (80+%) compared with the seasonal rates in Ndiop that change from 20% in the dry season to 70% in the rainy season (31). Mosquitoes of the A. gambiae s.l. species complex are the main vectors in both Ndiop and Dielmo. However, notably, A. funestus is also present in Dielmo, largely because of the stream that provides a suitable larval habitat. The intensity of malaria transmission was monitored during the whole study period; night-time collections of mosquitoes landing on volunteers were carried out monthly and the sporozoite rate was determined. It was thus possible to estimate the EIR, i.e., the number of infective bites per person per night, for every month of the whole period (see ref. 41 for more information). From 1990 to 2008 four different drug regimes were implemented: Quinine from 1990 to 1994, Chloroquine from 1995 to 2003, Fansidar from 2004 to mid-2006, and Artemisinin-based combination therapy (ACT) from mid-2006 to 2008. Insecticide campaigns were not performed until the implementation of bed nets starting from July 2008 in both villages (37). Rainfall time series from Dielmo (13,685662N, 16,38463W) and Ndiop (13,724620N, 16,409324W) come from a meteorological ground-based manually operated station in each village. Temperature was extracted from National Oceanic and Atmospheric Administration National Climate Data Center Global Hydrology and Climatology Network v2 (42) averaged from the four nearest villages (Cap Skirring, Kaolack, Diourbel, and Ziguinchor).