Properties of precise firing synchrony between synaptically coupled cortical interneurons depend on their mode of coupling

Abstract

Precise spike synchrony has been widely reported in the central nervous system, but its functional role in encoding, processing, and transmitting information is yet unresolved. Of particular interest is firing synchrony between inhibitory cortical interneurons, thought to drive various cortical rhythms such as gamma oscillations, the hallmark of cognitive states. Precise synchrony can arise between two interneurons connected electrically, through gap junctions, chemically, through fast inhibitory synapses, or dually, through both types of connections, but the properties of synchrony generated by these different modes of connectivity have never been compared in the same data set. In the present study we recorded in vitro from 152 homotypic pairs of two major subtypes of mouse neocortical interneurons: parvalbumin-containing, fast-spiking (FS) interneurons and somatostatin-containing (SOM) interneurons. We tested firing synchrony when the two neurons were driven to fire by long, depolarizing current steps and used a novel synchrony index to quantify the strength of synchrony, its temporal precision, and its dependence on firing rate. We found that SOM-SOM synchrony, driven solely by electrical coupling, was less precise than FS-FS synchrony, driven by inhibitory or dual coupling. Unlike SOM-SOM synchrony, FS-FS synchrony was strongly firing rate dependent and was not evident at the prototypical 40-Hz gamma frequency. Computer simulations reproduced these differences in synchrony without assuming any differences in intrinsic properties, suggesting that the mode of coupling is more important than the interneuron subtype. Our results provide novel insights into the mechanisms and properties of interneuron synchrony and point out important caveats in current models of cortical oscillations.

precise (sharp) firing synchrony, with action potentials of two or more neurons occurring within a few milliseconds of each other, has been observed in various brain regions and cell types, but the mechanisms for such synchrony, and what role(s) it may or does play in processing, transmitting and encoding information by the brain, are still unresolved (Atencio and Schreiner 2013; Bruno 2011; Diba et al. 2014; Doucette et al. 2011; Hatsopoulos et al. 1998; Histed and Maunsell 2014; Riehle et al. 1997; Stanley et al. 2012). Of particular interest is precise synchrony between inhibitory cortical interneurons, proposed to drive various cortical rhythms such as gamma oscillations (Bartos et al. 2007; Cardin et al. 2009; Fries et al. 2007; Penttonen et al. 1998; Sohal et al. 2009). Gamma oscillations, in turn, are suggested to be the neural correlates of conscious perception and cognition (Jensen et al. 2007; Melloni et al. 2007; Ward 2003).

Two network “motifs” can drive interneuron synchrony: shared excitatory inputs, via pyramidal-interneuron connections, and mutual coupling, via interneuron-interneuron connections. Cortical interneurons share excitatory inputs with specific subsets of other excitatory or inhibitory cortical neurons (Otsuka and Kawaguchi 2013; Yoshimura and Callaway 2005), and such shared excitatory postsynaptic potentials (EPSPs) may drive sharp synchrony between neocortical interneurons in vivo (Constantinidis and Goldman-Rakic 2002; Swadlow et al. 1998). Mutual interneuron-interneuron coupling can be chemical, through inhibitory synapses, electrical, through gap junctions, or both, and all three modes can generate highly precise synchrony in vitro (Galarreta and Hestrin 1999; Gibson et al. 2005, 1999; Hu et al. 2011; Merriam et al. 2005; Tamas et al. 2000). Thus cortical interneurons can potentially synchronize through several distinct mechanisms. This begs several questions. First, do different subtypes of cortical interneurons preferentially synchronize through some of these mechanisms and not others? Second, is firing synchrony driven by these different mechanisms distinguishable in any way, qualitatively or quantitatively? Last, are these mechanisms consistent with current models of gamma oscillations?

In the present study we examined precise interneuron synchrony in vitro driven by mutual coupling. To address the above questions, we recorded intracellularly from over 150 homotypic pairs of mouse somatostatin-containing (SOM) and parvalbumin-containing, fast-spiking (FS) interneurons, characterized their coupling mode as chemical, electrical, or dual, and quantified their firing synchrony using a novel synchrony index. We then tested the dependence of the synchrony on firing rate and quantified the temporal precision of synchrony. We report that chemical coupling between FS interneurons gave rise to synchrony that was strongly firing rate dependent, requiring firing rates of 80 Hz or higher. FS-FS synchrony, driven by either chemical or dual connectivity, was also significantly more precise than SOM-SOM synchrony, driven by electrical coupling. To determine if the differences in synchrony properties depended on differences in intrinsic properties between the two interneuron subtypes, we performed computer simulations of pairs of neurons with identical intrinsic properties but different modes of connectivity. Our results reveal that the properties of interneuron synchrony depend on the mode of synaptic connectivity and pose specific constraints on interneuron-based models of cortical oscillations.

MATERIALS AND METHODS

Animals.

All experimental protocols were approved by the West Virginia University Animal Care and Use Committee. Experiments were conducted on juvenile mice of either sex (postnatal days 15–22; see results for justification of this age range). SOM pairs were recorded either in X94 mice (Ma et al. 2006), in which a subset of layers 4–5 SOM interneurons express green fluorescent protein (GFP), or in progeny of SOM-IRES-Cre (Taniguchi et al. 2011) and Ai9 reporter mice (Madisen et al. 2010), in which all SOM interneurons express tdTomato, a red fluorescent protein (SOM-RFP mice). FS pairs were recorded in X94 animals, in which they were targeted by their cell body shape and size; in G42 mice (Chattopadhyaya et al. 2007), in which a subset of FS interneurons express GFP; or in progeny of PV-Cre (Hippenmeyer et al. 2005) and Ai9 mice, in which all FS interneurons express tdTomato (PV-RFP mice). All mouse lines are available from the Jackson Laboratory (Bar Harbor, ME). Mouse lines were maintained as hemizygotes by breeding mutant males with outbred wild-type females; as a result, the four genotypes used did not have a homogeneous genetic background.

Electrophysiological recordings.

For preparation of brain slices, mice were anesthetized deeply with isoflurane and decapitated. The brains were removed and submerged in ice-cold artificial cerebrospinal fluid (ACSF) bubbled with 95% O₂-5% CO₂; ACSF was composed of (in mM) 126 NaCl, 3 KCl, 1.25 NaH₂PO₄, 2 CaCl₂, 1.3 MgSO₄, 26 NaHCO₃, and 20 d-glucose. With the use of a Vibroslicer (World Precision Instruments), 350-μm-thick coronal slices were cut, transferred into a holding chamber filled with recirculated ACSF, and incubated for 30–45 min at 32°C and then at room temperature until used. For recording, slices were transferred to the recording chamber and continuously superfused at a rate of 2–3 ml/min with ACSF at 32°C. Glass micropipettes (typically 5–8 MΩ in resistance) were filled with (in mM) 134 K-gluconate, 3.5 KCl, 0.1 CaCl₂, 10 HEPES, 1.1 EGTA, 4 Mg-ATP, 10 phosphocreatine-Tris, and 2 mg/ml biocytin, adjusted to pH 7.25 and ∼290 mosM. Neurons were visualized under differential interference contrast and fluorescence illumination using an Olympus BX50WI microscope equipped with a ×40 water-immersion objective and a Hamamatsu Orca camera. Simultaneous current-clamp whole cell recordings were performed from pairs of (mostly) layer 4 interneurons in somatosensory (barrel) cortex, using an AxoClamp 2B amplifier (Molecular Devices). To block GABA_A, AMPA, and NMDA receptors, gabazine, 6-cyano-7-nitroquinoxaline-2,3-dione disodium (CNQX), and d-(−)-2-amino-5-phosphonopentanoic acid (APV; Tocris) were added to the ACSF at a final concentration of 10, 20, and 20 μM, respectively.

Electrophysiological parameters.

Intrinsic electrophysiological parameters were defined and measured as previously described (Ma et al. 2006). The electrical coupling coefficient (ECC) was defined as the ratio of the voltage deflection in the noninjected cell to the voltage deflection in the injected cell just before offset of a 600-ms, −30-mV hyperpolarizing step and was averaged between the two directions of connectivity. Pairs with ECC ≥0.5% in at least one direction were considered electrically coupled. Synaptic connections were tested by eliciting action potentials in the presynaptic cell every 8 s while holding the postsynaptic cell at a depolarized potential (typically −50 mV); 10–15 responses were averaged. The one-way connection probability was calculated as (u + 2r)/2n, and the reciprocation probability was calculated as 2r/(u +2r), where u is the number of unidirectionally connected pairs, r is the number of reciprocally connected pairs, and n is the total number of pairs. To test for bias toward reciprocal connectivity, the unidirectionally connected FS pairs were nominally defined as either A→B or B→A, and the 2 × 2 contingency table (reciprocal, A→B, B→A, not connected) was tested using Fisher's exact test.

Synchrony analysis.

Synchrony was quantified using the Jitter-Based Synchrony Index (JBSI) (Agmon 2012). The JBSI is a normalized measure of the rate of synchrony above (or below) that expected by chance; it can assume values from −1 (least possible synchrony) to 1 (maximum possible synchrony), with 0 indicating chance-level synchrony. To calculate the JBSI, a synchrony window ± S (S = 2 ms) was centered on each of the spikes of the faster spike train, and the number SYN(S) of spikes in the slower spike train occurring within synchrony windows was counted. A jitter window ± J (J = 2S) was then centered on each of the N spikes of the slower spike train, and the probability that a jittered spike would fall within a synchrony window was computed analytically, rather than by Monte Carlo simulations as in previous implementations of jitter methods (Amarasingham et al. 2012). The number of coincidences expected after a random jitter of ± J, 〈SYN^J(S)〉, is given by the sum of these probabilities; the JBSI is then defined as JBSI = 2[SYN(S) − 〈SYN^J(S)〉]/N. This definition differs somewhat from the Jitter-Sensitive Synchrony Index (JSSI) used in our previous study (Hu et al. 2011), but the two indexes are strongly correlated (r² > 0.97 in the current data set); the JBSI is preferable to the JSSI because of its robustness against firing rate differentials between the two neurons. Unlike commonly used synchrony measures, the JBSI is independent of firing rates and is not sensitive to slow comodulations in firing rates (Agmon 2012).

Simulations.

We constructed an integrate-and-fire model of two neurons based on a minimal number of assumptions. At any given time point the membrane potential of each neuron was assumed to relax with a time constant τ (typically set at 10 ms) toward an asymptotic value determined by the experimenter. A spike was fired whenever firing threshold was crossed from below and was followed by an absolute refractory period of 2 ms. A low level of random noise (0.5 mV peak to peak) was added to the membrane potential to generate realistic-looking spike trains; noise was added independently to each cell at each integration step (0.1 ms), so no spurious correlations were introduced. After a spike, the presynaptic neuron's membrane potential decremented instantaneously by a fixed value (representing the afterhyperpolarization, AHP), and after a delay d a synaptic conductance G was activated in the postsynaptic neuron for a duration RT, representing the rise time of the PSP (typically set at 2 ms). This synaptic conductance caused the postsynaptic membrane potential to relax toward a predefined synaptic reversal potential with a time constant proportional to 1/G. Inhibitory postsynaptic potentials (IPSPs) were modeled as PSPs with a reversal potential of −60 mV and a 1-ms delay, and electrical synapses were modeled as PSPs with a reversal potential of 0 mV and 0 delay; minor variations in these parameters did not affect our conclusions (see results). The subthreshold effects of electrical coupling were not included in the model. Computations were done in Mathcad (PTC).

Statistics.

Other than multiple regression, all statistical tests were done in Mathcad, using in-house algorithms, by comparing the observed value of the statistic with the distribution of 10,000 values computed from random permutations of the data; in cases where 10,000 permutations yielded no more extreme values, the P value is listed as <0.0001. Comparisons of means were two-tailed; comparisons of correlation coefficients and cumulative distributions were one-tailed. Multiple linear regression was done in Statistica (StatSoft). Data are means ± SE unless indicated otherwise.

RESULTS

Electrophysiological characteristics of SOM and FS interneurons.

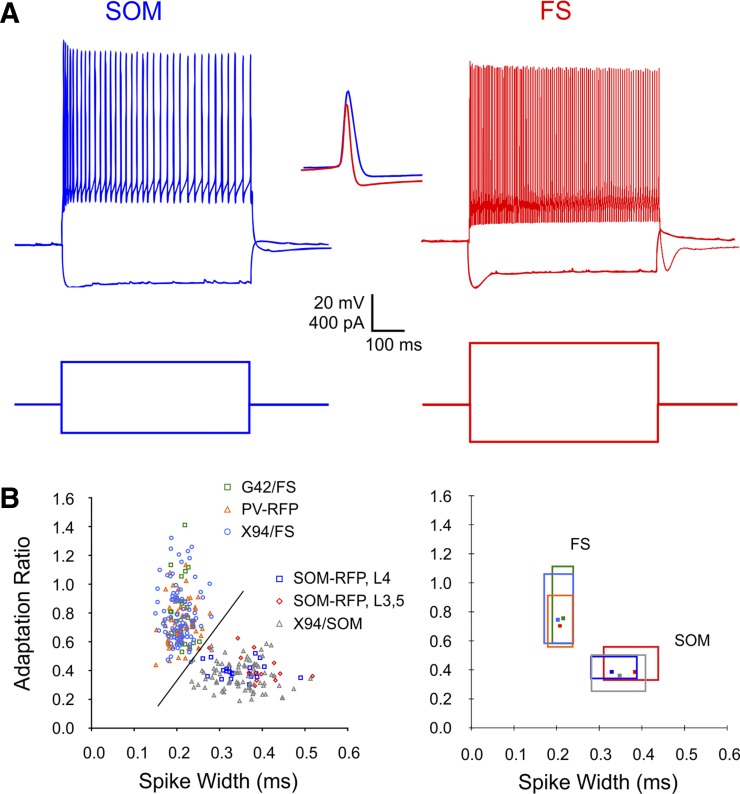
To examine the relative contributions of electrical coupling, inhibitory synapses, and shared inputs to synchronous firing of cortical interneurons, we conducted simultaneous whole cell current-clamp recordings from pairs of interneurons in the somatosensory (“barrel”) cortex in brain slices from juvenile mice. Our data set consisted of 60 SOM pairs and 54 FS pairs, which were pooled with 40 additional FS pairs recorded in a previous study (Hu et al. 2011) and which we reanalyzed for this study. With the exception of 8 SOM pairs recorded in layers 3 and 5, all pairs were recorded in cortical layer 4, typically from the same barrel. The largest center-to-center separations between paired cells were 83 and 105 μm for SOM and FS pairs, respectively. We used four different mouse genotypes to target SOM or FS interneurons for recording (see materials and methods); the majority of recorded neurons were targeted by their fluorescence, but FS cells in X94 mice were nonfluorescent and were targeted by their cell body size and shape. The identity of each neuron as FS or SOM was further verified by its characteristic firing pattern (Fig. 1A); this was especially important when recording from SOM-RFP mice, because about 15% of tdTomato-expressing neurons in these animals were found to be FS interneurons (Hu et al. 2013) and were excluded from analysis. We measured seven basic electrophysiological parameters for each neuron (Table 1); with the exception of resting potential, differences in these parameters between the two groups were both highly significant and large. When the two parameters with the most pronounced differences, spike width and adaptation ratio, were plotted against each other, FS and SOM interneurons segregated nearly perfectly, whereas interneurons of the same subtype but different genotypes had largely overlapping distributions (Fig. 1B), suggesting that electrophysiological characteristics of an interneuron are strongly dependent on its subtype but, at most, weakly dependent on its genotype.

Fig. 1.

Electrophysiological characteristics of somatostatin-containing (SOM) and parvalbumin-containing, fast-spiking (FS) interneurons. A: voltage responses (top) to negative and positive intracellular current steps (bottom). Compare the adaptation in both firing frequency and spike height in the SOM cell to the nearly constant firing rate and spike height in the FS cell. Inset shows spike waveforms at a faster time base (scale bar: 20 mV, 0.5 ms); note the wider and taller waveform of the SOM spike and the deeper afterhyperpolarization (AHP) of the FS spike. B, left: scatter plot of adaptation ratio vs. spike width for 119 SOM and 185 FS interneurons included in our data set, color coded by mouse line and layer. The diagonal line separates the 2 subtypes nearly perfectly, with only 1 cell per subtype misclassified. Right, the same data plotted as boxes spanning the 10–90 percentile ranges for each subgroup; the 2-dimensional median of each subgroup is indicated by a marker. Note that the ranges for data points from different mouse lines but belonging to the same subtype (SOM or FS) nearly totally overlap, with the exception of layer 3 (L3) and L5 SOM interneurons, which had somewhat wider spikes and weaker adaptation compared with L4 SOM neurons (Ma et al. 2006). See materials and methods for details of mouse lines.

Table 1.

Intrinsic membrane parameters of FS and SOM interneurons

	SOM		FS
Parameter	Mean	SD	Mean	SD	P Value
Age, postnatal days	18.5	2.2	18.7	1.9	0.48
Vrest, mV	−64.7	1.7	−64.3	1.8	0.07
Vthreshold, mV	−38.4	4.1	−35.6	5.2	<10−4
AHP, mV	11.0	2.1	17.9	3.5	<10−4
Rin, MΩ	104.8	28.8	69.5	13.9	<10−4
Spike height, mV	72.4	8.6	67.5	9.4	<10−4
Spike width, ms	0.35	0.06	0.21	0.03	<10−4
Adaptation ratio	0.38	0.09	0.77	0.18	<10−4

Values are parameters in fast-spiking (FS; N = 185) and somatostatin-containing (SOM; N = 119) interneurons. V_rest, resting potential; V_threshold, threshold potential; AHP, afterhyperpolarization; R_in, input resistance.

Electrical and chemical connectivity in SOM and FS pairs.

In each interneuron pair, we used subthreshold current steps to measure the steady-state ECC (see materials and methods) and recorded the synaptic response of one cell to an action potential elicited in the other. As previously observed (Gibson et al. 1999; Hu et al. 2011; Pfeffer et al. 2013), SOM pairs were never connected by chemical synapses; however, 93% of SOM pairs were coupled electrically (Fig. 2A; Table 2), with ECCs ranging from our detection limit of ∼0.5% to 24% (median ECC: 6.0%). Within our data set, there was a weak negative correlation between ECC and cell-cell distance (r² = 0.09, P = 0.03). In strongly coupled pairs, an action potential fired by one neuron elicited a depolarizing junctional PSP (JPSP) in the paired neuron [Fig. 2B; JPSPs are also referred to in the literature as “electrical PSPs” (Gibson et al. 2005), “gap junction potentials” (Tamas et al. 2000), or “spikelets” (MacVicar and Dudek 1981)]. JPSP amplitudes (median: 0.6 mV, range: 0.2–3.0 mV, N = 38) were strongly correlated with the ECC (r² = 0.66, P < 0.0001). Note that we recorded JPSPs at a depolarized holding potential (typically −50 mV), so their time course and amplitude were likely enhanced by intrinsic subthreshold conductances (Curti and Pereda 2004; Gibson et al. 2005; Mann-Metzer and Yarom 1999).

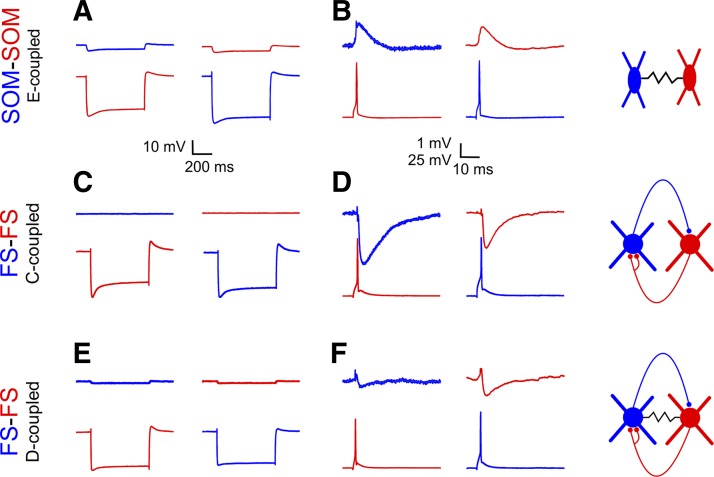
Fig. 2.

Electrical and chemical connectivity of SOM and FS pairs. Response of 1 cell (top trace) to a hyperpolarizing current step (A, C, E) or to an action potential (B, D, F) in the paired cell (bottom trace). Schematics at right illustrate the respective mode of coupling: electrical (E-coupled; top), chemical (C-coupled; middle) or dual (D-coupled; bottom). In E- or D-coupled pairs (A and E), a hyperpolarizing step induced by current injection in 1 cell was reflected by a passively conducted, smaller hyperpolarization in the paired cell. In strongly E-coupled pairs (B), an action potential in 1 cell was followed by a passive slower depolarizing potential (JPSP) in the paired cell. In C-coupled pairs (D), an action potential in the presynaptic cell was followed by an inhibitory postsynaptic potential (IPSP) in the paired cell. In some D-coupled pairs (F), an action potential in the presynaptic cell was followed by a biphasic, electrical-chemical postsynaptic response in the paired cell.

Table 2.

Summary of chemical and electrical coupling of FS and SOM pairs

	No Chemical Connection	One-Way IPSP	Reciprocal IPSP	Total
FS pairs
Not electrically coupled	11 (12%)	18 (20%)	24 (26%)	53 (58%)
Electrically coupled	3 (3%)	18 (20%)	18 (20%)	39 (42%)
Total	14 (15%)	36 (39%)	42 (46%)	92 (100%)
SOM pairs
Not electrically coupled	4 (7%)			4 (7%)
Electrically coupled	56 (93%)			56 (93%)
Total	60 (100%)			60 (100%)

Values are numbers of interneuron pairs, with percentages given in parentheses. IPSP, inhibitory postsynaptic potential.

In contrast to SOM pairs, 85% of FS pairs were connected chemically by one-way or reciprocal inhibitory synapses (Fig. 2D; Table 2); the distribution between one-way, reciprocal, and no connectivity (39%, 46%, and 15%, respectively) was similar to that previously reported in adult mice (Galarreta and Hestrin 2002). The one-way connection probability was 0.64, but the reciprocation probability (the probability that a synapse from A→B will be reciprocated by a synapse from B→A; see materials and methods) was 0.70, suggesting that a synaptic connection in one direction slightly increases the probability of a connection in the reciprocal direction; however, this bias did not reach statistical significance (P = 0.12, Fisher's exact test, 2-tailed). Unitary IPSP (uIPSP) amplitudes, measured at a holding potential of −50 mV, ranged from our noise limit of about 0.2 mV to 4.7 mV, with one outlier of 8.1 mV (median: 1.2 mV, N = 121). The uIPSP reversal potential in our recordings (not corrected for the liquid junction potential introduced by the micropipette) was −76.2 ± 0.8 mV (N = 6). As measured for all uIPSPs ≥1.4 mV (N = 46), the synaptic latency (from peak presynaptic spike to uIPSP onset) was 0.61 ± 0.02 ms, and the effective IPSP duration (from peak presynaptic spike to 10% of the IPSP peak) was 20.4 ± 0.7 ms.

Also in contrast to SOM pairs, only 42% of FS pairs in our data set were coupled electrically, and the great majority of these were also coupled chemically (Fig. 2, E and F; Table 2). ECCs of electrically coupled FS pairs were markedly small, ranging from the noise limit of ∼0.5% to 5.0% (median of detectable ECCs: 1.5%). Thus FS pairs were 0.4 times as likely as SOM pairs to be electrically coupled, and if coupled, they were 4 times less strongly so, implying that electrical coupling between FS interneurons was only ∼10% as effective as between SOM cells. An identical probability of FS-FS electrical coupling (42%) was reported in juvenile mice (Pangratz-Fuehrer and Hestrin 2011), and identical average coupling strength was reported in adult mice (Galarreta and Hestrin 2002). Within our data set, neither chemical nor electrical connectivity of FS pairs was correlated with cell-to-cell distance. Chemically connected FS pairs, whether connected one-way or reciprocally, were more than twice as likely to be electrically coupled as nonconnected pairs (0.43, 0.50, and 0.21 coupling probability in reciprocally, one-way, and nonconnected pairs, respectively; P = 0.054, Fisher's exact test, 2-tailed). In contrast, electrically coupled FS pairs were only slightly more likely to also be connected chemically, compared with noncoupled pairs (0.92 vs. 0.79). Similar enrichment of electrical coupling in chemically connected compared with nonconnected pairs has been noted before in adult mice (Galarreta and Hestrin 2002) and juvenile rats (Gibson et al. 2005); this suggests that chemical connectivity between two interneurons is linked in some manner (causal or otherwise) to formation or stabilization of gap junctions.

In this article, we refer to paired interneurons communicating only through chemical synapses, whether one-way or reciprocal, as chemically coupled, or C-coupled; to pairs communicating only through electrical synapses as electrically coupled, or E-coupled; and to pairs communicating through both types of synapses as dually coupled, or D-coupled. Pairs with neither chemical nor electrical connections are referred to as noncoupled. By these definitions, 45% of FS pairs were C-coupled and 38% were D-coupled, but only 3% were E-coupled. A similar scarcity of E-coupled FS pairs was previously reported in adult mice (4%; Galarreta and Hestrin 2002) and juvenile rats (7%; Gibson et al. 2005).

Age-dependent changes in intrinsic and synaptic properties were minor.

Rodent cortical interneurons are still developing during the third and early fourth postnatal weeks, the age range represented by our data set (Angulo et al. 1999b; Doischer et al. 2008; Goldberg et al. 2011; Okaty et al. 2009; reviewed by Le Magueresse and Monyer 2013); we therefore examined our data for age-dependent changes in intrinsic and synaptic properties of SOM and FS interneurons. Most membrane and spike parameters showed no significant correlations with age, and those that did changed only slightly over the age range of our sample. In SOM cells, the only parameter that showed a statistically significant age-dependent changes was spike width, with the trend line decreasing over the sampled age range by about 0.08 ms (r² = 0.18, P < 0.0001). In FS cells, the spike height trendline increased by ∼5 mV (r² = 0.03, P = 0.03) and spike threshold became more negative by ∼3 mV (r² = 0.04, P = 0.009). Importantly, neither subtype exhibited any statistically significant age-dependent changes in uIPSP or ECC amplitudes. These findings are consistent with previous studies showing that by the beginning of the third postnatal week, the developmental trend in most intrinsic and synaptic properties of FS interneurons has leveled out, or nearly so (Doischer et al. 2008), FS-FS connection probability has stabilized (Pangratz-Fuehrer and Hestrin 2011), SOM interneurons have acquired their ability to synchronize (Long et al. 2005), and the process of programmed interneuron death is over (Southwell et al. 2012). This justifies pooling data over the postnatal day 15–22 age range and suggests that the major phase in postnatal interneuron development is over (or nearly so) by the third postnatal week, although we cannot rule out a second, late phase of maturation beyond the ages we examined.

SOM and FS pairs displayed long-lasting, stable firing synchrony.

To examine firing synchrony and compare it between E-, C-, and D-coupled pairs, we evoked firing in interneuron pairs by injecting periodic currents steps (600-ms steps at 5-s intervals) into one cell (the “driver”; Figs. 3, A and B, and 4, A–C, red traces) and constant current into the other (the “follower”; blue traces); in C- or D-coupled FS pairs, the cell eliciting the stronger IPSP was selected as driver. The firing rates of both driver and follower cells varied over a wide range (see below); however, the driver cell always fired ∼1.5 to 4 times faster than the follower. We quantified firing synchrony using a novel index, the JBSI, which is a normalized measure of the fraction of follower spikes synchronous with any driver spikes (see materials and methods and Agmon 2012 for computational details). The JBSI is derived by subtracting out any synchrony that survives a virtual jitter of spike times; it therefore depends on both the chosen synchrony window (the maximum lag between 2 spikes considered synchronous) and the jitter window. Unless stated otherwise, these two parameters were ±2 ms and ±4 ms, respectively. A by-product of the JBSI computation is an estimate of the statistical significance of the observed synchrony, in the form of a Z score; we considered Z scores >2.6 (i.e., >2.6 SD from the mean, equivalent to P < 0.01) to indicate nonrandom synchrony. In general, pairs with JBSI ≥ 0.08 displayed statistically significant synchrony. The two pairs illustrated in Fig. 3, A and B, had JBSI values of 0.40 and 0.67 and Z scores of 8.6 and 14.4, respectively, calculated from the first 400 follower spikes in the train. For comparison, the conventional cross-correlogram representations of the same spike trains are shown in Fig. 3, C and D. Note that the cross-correlogram peaks were symmetric around 0 lag, indicating that within each synchronous spike pair there was no systematic firing order to the two neurons.

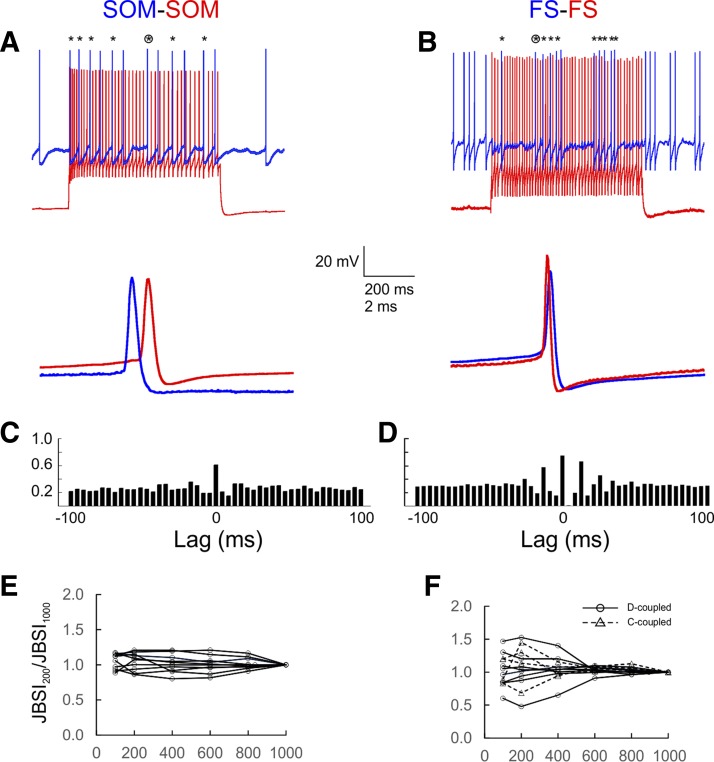
Fig. 3.

SOM and FS pairs displayed long-lasting, stable firing synchrony. A and B: the basic protocol used to identify and estimate synchrony. One cell in the pair (driver cell; red traces) was strongly activated by 600-ms current steps repeated every 5 s, whereas the other (follower cell; blue traces) was depolarized above threshold by constant current; the red and blue traces are displaced vertically for clarity. Asterisks at top indicate synchronous spikes (peaks within 2 ms of each other); the circled asterisk indicates the spike pair shown at a faster time base at bottom. C and D: a traditional cross-correlogram representation of the same pairs, computed from 400 spikes in the follower cell; bins are 4 ms wide. The height of the central bin indicates the fraction of follower spikes that are within ±2 ms of a driver spike. E and F: a synchrony index (JBSI) was calculated for 10 representative SOM and 12 FS pairs from increasingly longer segments of the full spike train and normalized to its value at 1,000 spikes (JBSI₁₀₀₀); note the short-term fluctuations, especially in FS pairs, but the long-term stability of the JBSI.

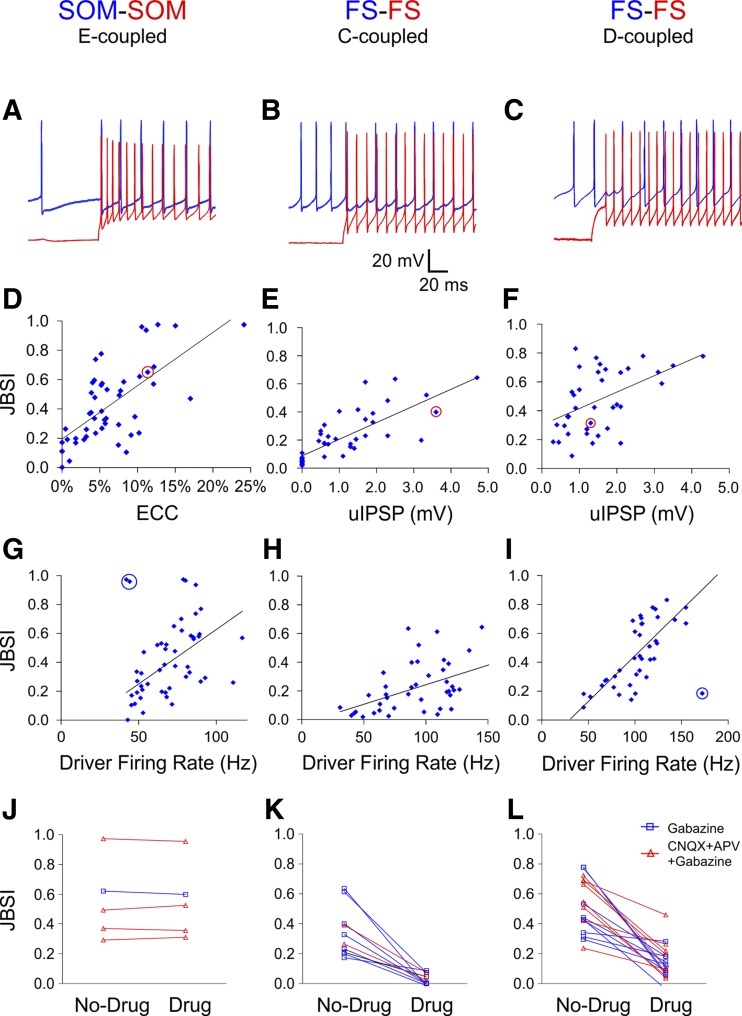
Fig. 4.

Interneuron synchrony depends on electrical synapses, chemical synapses, and firing rate. A–C: to test for firing synchrony, paired spike trains were elicited by suprathreshold current steps in the driver cell (red traces) and by tonic suprathreshold depolarization in the follower cell (blue traces). D–F: strength of synchrony (as quantified by the JBSI) was well correlated with the electrical coupling coefficient (ECC) in E-coupled SOM pairs (r² = 0.45) and with the unitary IPSP (uIPSP) in C-coupled FS pairs (r² = 0.58) and not as well correlated with the uIPSP in D-coupled FS pairs (r² = 0.27). Data points corresponding to the example pairs are circled in red. G–I: the JBSI correlated with the firing rate of the driver cell (r² = 0.29, 0.20, and 0.58, respectively), but not the follower cell (not shown). The regression lines and correlation coefficients were calculated after exclusion of the 3 outlier data points circled in blue in G and I. J–L: blocking GABA_A receptors, with or without blocking ionotropic glutamate receptors, had no effect on synchrony between E-coupled SOM pairs (J), abolished synchrony between C-coupled FS pairs (K), and suppressed but did not abolish synchrony between D-coupled FS pairs (L). CNQX, 6-cyano-7-nitroquinoxaline-2,3-dione disodium; APV, d-(−)-2-amino-5-phosphonopentanoic acid.

Because synchrony computation required long spike trains, we were concerned that the JBSI might not be a stable parameter but would decay with time or with the number of spikes due to rundown of electrical or synaptic connections. To test for such rundown, we compared the JBSI calculated from the first 1,000 follower spikes (JBSI₁₀₀₀) with that calculated from the first 200 spikes (JBSI₂₀₀) for all pairs with JBSI > 0.4 (N = 12 SOM pairs and 26 FS pairs). With the exception of 5 SOM pairs (below), the ratio JBSI₂₀₀/JBSI₁₀₀₀ varied between 0.86–1.22 (geometric mean: 1.06) and 0.48–1.65 (geometric mean: 1.03) for SOM and FS pairs, respectively, and was not significantly different from 1 (P = 0.06 and P = 0.29). (In 5 SOM pairs recorded sequentially using the same batch of intracellular solution, there was a clear rundown of synchrony, with a JBSI₂₀₀/JBSI₁₀₀₀ ratio of 2–3; these pairs were excluded from further analysis.) For 10 representative SOM and 12 FS pairs, we also calculated the JBSI for an increasing number of follower spikes, from 100 to 1,000, at 200-spike increments. JBSI values of SOM pairs remained within ∼20% of their JBSI₁₀₀₀ (Fig. 3E). JBSI values of FS pairs fluctuated relative to JBSI₁₀₀₀, but these fluctuations were in general symmetric between different pairs, and with increasing number of spikes the JBSI approached a steady value (Fig. 3F). Beyond simply a manifestation of the law of large numbers, this analysis suggested that synchrony was a stable parameter and that deviations from the long-term value at lower spike counts were statistical fluctuations rather than a systematic shift. On the basis of this analysis, we selected 200 follower spikes as a minimum requirement for computing synchrony; in actuality, synchrony in most pairs was calculated from many more spikes (on average ∼800, typically collected over a 5-min period).

Interneuron synchrony depended on electrical coupling, chemical connectivity, and driver firing rate.

As expected from their strong electrical coupling, 96% of all SOM pairs tested with current steps (N = 49) exhibited nonrandom synchrony. JBSI values of SOM pairs (0.43 ± 0.04) were well correlated with the ECC (r² = 0.45, P < 0.0001; Fig. 4D) and even better correlated with the JPSP (r² = 0.65, N = 38). The majority (89%) of all FS pairs similarly tested (N = 79) also fired synchronously. As previously demonstrated (Gibson et al. 2005; Hu et al. 2011), synchrony between interneurons can be driven by one-way or reciprocal inhibitory synapses, and indeed JBSI values of C-coupled FS pairs (0.22 ± 0.03, N = 42) were well correlated with the amplitude of the uIPSP (r² = 0.58, P < 0.0001; Fig. 4E; for reciprocal connections, the JBSI is plotted against the larger of the two uIPSPs). Even though the average uIPSP was not significantly different between C-coupled and D-coupled FS pairs (P = 0.30), the average JBSI in D-coupled pairs (0.48 ± 0.04, N = 36) was more than twice as high as in C-coupled pairs (P < 0.0001). Moreover, the JBSI in D-coupled pairs was not as well correlated with the uIPSP (r² = 0.27, P = 0.0002; Fig. 4F), suggesting that synchrony was only partially attributable to chemical synapses and that electrical coupling also contributed to the observed synchrony. As an estimate of the contribution of chemical vs. electrical synapses to firing synchrony, we used the regression equation derived from C-coupled FS pairs (Fig. 4E) to predict the JBSI expected in D-coupled pairs based on their chemical connectivity alone. The actual JBSI was, on average, 1.66 times higher than that predicted from the IPSP alone, suggesting that electrical coupling contributed, on average, 40% of the synchrony in D-coupled FS pairs.

In pairs of cortical neurons, correlations in the number of spikes (counted over tens or hundreds of milliseconds) fired in response to repeated stimuli have been shown to increase with firing rate (de la Rocha et al. 2007; Greenberg et al. 2008); we therefore asked whether millisecond-scale synchrony between coupled interneurons was also firing rate dependent. Unlike some commonly used measures of synchrony (Turker and Powers 2002), the JBSI is intrinsically independent of firing-rate (Agmon 2012) and can therefore report correctly any firing rate dependency of synchrony. To test for correlation between synchrony and firing rate, we computed for each pair the average firing rate of the driver (phasically driven) and follower (tonically driven) cell from the same spike trains used for computing the JBSI. Synchrony in all three groups was correlated with the driver firing rate (Fig. 4, G–I; r² = 0.29, 0.20, and 0.58, P = 0.0001, 0.003, and <0.0001 for SOM, C-coupled FS, and D-coupled FS pairs, respectively, after exclusion of the 3 outliers circled in Fig. 4, G–I), but only SOM pair synchrony was correlated with the follower firing rate, and weakly at that (r² = 0.16, 0.001, and 0.09, P = 0.003, 0.19, and 0.08, respectively), thus justifying the terms “driver” and “follower.”

To estimate the relative contributions of electrical coupling, inhibitory synaptic connections, and driver firing rate to pairwise interneuron synchrony, we performed multiple linear regression of the JBSI on these three variables (Table 3). More than half the variance in JBSI (R² = 0.54 and 0.60 for SOM and FS pairs, respectively) was explained by these variables. The relative contribution of each variable to pairwise synchrony was estimated from its standardized multiple regression coefficient (β). In SOM pairs, the contribution of the ECC was more than twice as strong as that of the firing rate, and in FS pairs the contribution of the uIPSP was >1.5 times stronger than either firing rate or the ECC (Table 3). Interestingly, replacing the ECC in FS cells with a categorical variable (“coupled/not-coupled”) increased the R² value to 0.64 while approximately equalizing the contributions of electrical and chemical coupling (Table 3), suggesting that even weak coupling between chemically connected FS cells can have a significant effect on synchrony and that electrical and chemical synapses interact in a nonlinear manner to promote firing synchrony, as predicted theoretically (Traub et al. 2001).

Table 3.

Multiple linear regression of the JBSI on uIPSP, ECC, and driver firing rate

	Value	SE	P Value
SOM pairs
R2	0.54	0.18	<10−6
Intercept	−0.10	0.11	0.36
ECC β	0.65	0.10	<10−6
Driver rate β	0.30	0.10	0.005
FS pairs
R2	0.60	0.15	<10−6
Intercept	−0.07	0.06	0.24
uIPSP β	0.53	0.08	<10−6
ECC β	0.31	0.08	0.0001
Driver rate β	0.27	0.08	0.002
FS pairs
R2	0.64	0.14	<10−6
Intercept	−0.10	0.05	0.07
uIPSP β	0.45	0.07	<10−6
Coupled Y/N? β	0.38	0.07	1×10−6
Driver rate β	0.30	0.08	0.0002

Multiple linear regression of the Jitter-Based Synchrony Index (JBSI) shows relative contributions of electrical coupling (ECC, electrical coupling coefficient), inhibitory synaptic connections (unitary IPSP, uIPSP), and driver firing rate to pairwise synchrony in SOM (N = 49 pairs) and FS (N = 80 pairs) interneurons. Replacing the ECC in FS cells with a categorical variable (coupled/not coupled; 2nd set of data for FS pairs) increased the R² value and approximately equalized the contributions of electrical and chemical coupling (see text).

Although the analysis above indicates that synchrony was correlated with the strength of the electrical and/or chemical coupling and with the driver firing rate, correlations do not necessarily imply causation. To test for causality between inhibitory synapses and synchrony, we compared JBSI values in 33 pairs before and after pharmacologically blocking fast GABAergic neurotransmission (GABA_A receptors were blocked in isolation or together with ionotropic glutamate receptors). As expected, blocking GABA_A receptors in E-coupled SOM pairs left JBSI values unchanged (increased by 0.9 ± 2.4%, N = 5; Fig. 4J), whereas JBSI values in C-coupled FS pairs were reduced by 90 ± 5.3% (N = 10; Fig. 4K), confirming that GABAergic synapses were necessary for synchrony between C-coupled FS interneurons (see also Hu et al. 2011). In D-coupled FS pairs, blocking GABA_A receptors reduced JBSI values by 69 ± 5.8% (N = 18; Fig. 4L), implying that electrical coupling contributed about 30% of firing synchrony in this subset.

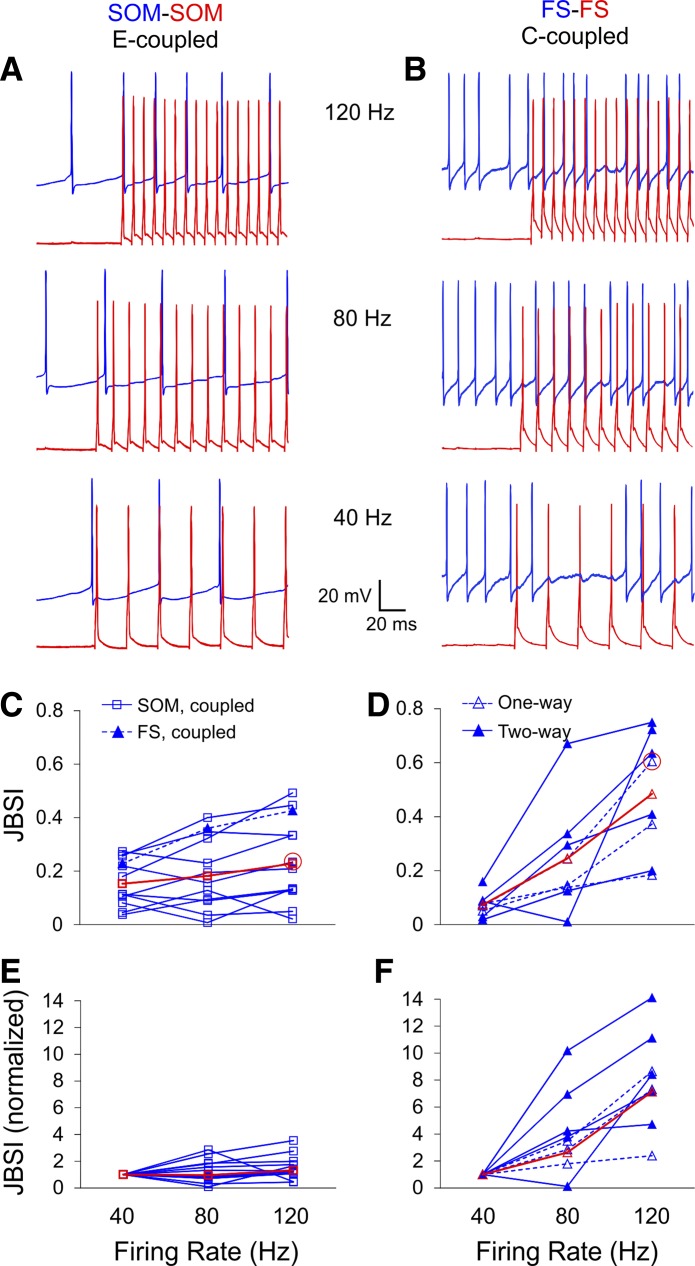
Next, we tested for causality between firing rate and synchrony in a subset of SOM pairs and FS pairs by firing the driver cell at predetermined frequencies of 40, 80, and 120 Hz with brief current steps while depolarizing the follower cells tonically with constant current (Fig. 5, A and B). The follower firing rates in these experiments were allowed to co-vary with the driver rates but were two to four times slower. This protocol, in which the precise spike times of the driver cell were predetermined by the experimenter, resulted in considerably lower JBSI values compared with the protocol illustrated in Fig. 4, especially in SOM pairs. To avoid floor and ceiling effects, we excluded from this analysis pairs in which JBSI values at all frequencies remained ≤0.1 (3 FS and 4 SOM pairs) or ≥0.9 (1 SOM pair). Within the remaining pairs, synchrony between E-coupled SOM interneurons (N = 11) increased modestly with the firing rate of the driver cell, with the average JBSI increasing by 0.08 ± 0.03 between 40 and 120 Hz (Fig. 5C). In contrast, synchrony in C-coupled FS pairs (N = 8) was strongly firing rate dependent, with JBSI values increasing by 0.41 ± 0.07 over the same range of firing rates, 5 times more than in SOM cells (P = 0.0006; Fig. 5D). Comparing the degree of increase (fold increase) in JBSI values between 40 and 120 Hz yielded a similar result: a 1.32 ± 0.28-fold increase in SOM pairs (geometric mean) compared with a 7.13 ± 1.27-fold increase in FS pairs (Fig. 5, E and F; P < 0.0001). The fold increase in JBSI was not correlated with the JBSI (r² < 0.01). Importantly, half of the FS pairs showed no statistically significant synchrony at 40 Hz (Fig. 5D), which is notable in light of the proposed role for FS interneurons in generating 40-Hz oscillations (see discussion). Interestingly, the one E-coupled FS pair tested (blue triangles in Fig. 5C) exhibited a 1.9-fold increase in JBSI, from ∼0.2 at 40 Hz to ∼0.4 at 120 Hz, and thus resembled E-coupled SOM pairs rather than C-coupled FS pairs in its frequency dependence.

Fig. 5.

Chemically driven, but not electrically driven, synchrony is strongly firing rate dependent. A and B: firing at predefined rates (40, 80, 120 Hz) was elicited in the driver cell (red traces) by trains of 20 brief current pulses repeated every 3 s, and tonic firing was elicited in the follower cell (blue traces) by constant current injection. C and D: summary plots of JBSI at each firing rate for all pairs tested; red symbols are group averages. Data points corresponding to the 2 example pairs are circled in red. E and F: the same data normalized to the JBSI value at 40 Hz. Synchrony was strongly dependent on driver firing rate in C-coupled FS pairs (D and F) and only weakly so in E-coupled SOM pairs (C and E). One E-coupled FS pair (filled triangles) is included with the SOM pairs in C; it resembled E-coupled SOM pairs rather than C-coupled FS pairs.

Chemically driven synchrony is more precise than electrically driven synchrony.

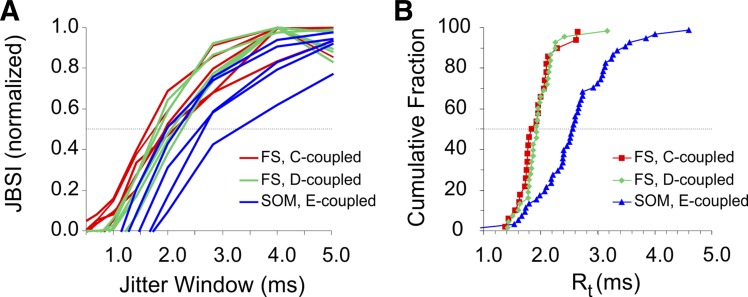
Firing synchrony has two distinct attributes: strength and precision. Strength (for example, as measured by the JBSI) reflects the rate of synchronous firing above chance level, whereas precision is a measure of how “sharp” the synchrony is, or how small are the time lags between synchronous or near-synchronous spikes. For illustration, when the well-known cross-correlogram method is used, synchrony strength is estimated from the height of the central peak of the cross-correlogram, whereas precision is estimated from the width of this peak. Precision of synchrony can be regarded as a measure of the relevant time scale used by the neural system under study, i.e., its temporal resolution (Amarasingham et al. 2012; Hatsopoulos et al. 2003). It was therefore of interest to determine and compare precision of synchrony between pairs of interneurons of different subtypes and different modes of connectivity. Because the JBSI is a measure of the difference between the observed synchrony count and the expected count after a random jitter, and because jitter by less than the temporal resolution of the system should not affect the synchrony count, the JBSI should rapidly fall to zero once the jitter window falls below the system's temporal resolution. One can therefore estimate the system's temporal resolution by plotting the JBSI for decreasing jitter windows and determining the point where the plot drops off sharply to the left (Agmon 2012); intuitively, this point represents the maximal spike time jitter that would not be noticed by a downstream observer counting the rate of synchronous spikes. (Note that the JBSI will also fall off to the right, i.e., for longer jitter windows, because at jitter windows larger than the interspike interval (ISI) of the paired neuron, there is an increased probability that a spike which was originally synchronous with a given spike in the paired train will fall after the jitter into the synchrony window of another spike. This JBSI decline to the right was always much slower than the drop-off to the left.) We plotted the JBSI for jitter windows decreasing from 16 to 0.5 ms in multiples of √2/2, keeping the synchrony window at half the jitter window, and defined the temporal resolution (R_t) of a pair as the (interpolated) point at which the JBSI dropped to half its maximal value (Fig. 6A). Thus, lower R_t values correspond to higher precision of synchrony. Because this calculation became noisy at low JBSI values, we included in the analysis only pairs with JBSI ≥ 0.15 (N = 44, 25, and 34 for SOM, C-coupled FS, and D-coupled FS pairs, respectively). Superimposed normalized plots of JBSI vs. jitter window for five representative pairs from each group are shown in Fig. 6A, and cumulative histograms of R_t for each group are plotted in Fig. 6B. As evident from these histograms, there was no significant difference between the cumulative R_t distributions of C-coupled and D-coupled FS pairs (red and green data points in Fig. 6B; medians = 1.84 and 1.92 ms, respectively; P = 0.36). There was, however, a highly significant difference between R_t of FS pairs and that of SOM pairs (blue data points in Fig. 6B; median = 2.54; P < 0.0001). R_t of FS pairs was independent of the JBSI (r² < 0.03, P = 0.22), but R_t of SOM pairs was inversely correlated with the JBSI (r² = 0.42, P < 0.0001), likely because higher JBSI resulted from larger and faster-rising JPSPs, and the latter evoked spikes in the coupled interneuron with less jitter. We conclude that firing synchrony in E-coupled SOM pairs was about 25% less precise than synchrony in C- or D-coupled FS pairs.

Fig. 6.

Chemically driven synchrony was more precise than electrically driven synchrony. A: normalized JBSI values computed for decreasing jitter windows, from pairs tested by current steps, are plotted against the jitter window for 5 representative pairs from each group (blue lines for E-coupled SOM pairs, red and green lines for C- and D-coupled FS pairs, respectively). The jitter window for which the JBSI drops to half its maximum (crossing the horizontal dotted line) is defined as the temporal resolution (R_t) of that pair and is inversely related to firing precision. B: cumulative histograms of R_t for pairs tested by current steps; only pairs with peak JBSI ≥ 0.15 are included. Precision of C- and D-coupled FS pairs was similar to each other but significantly better (by about ⅓) than precision of E-coupled SOM pairs (note the differences in medians, the points intersecting the horizontal dotted line).

Simulations reproduced the observed differences between electrically and chemically driven synchrony.

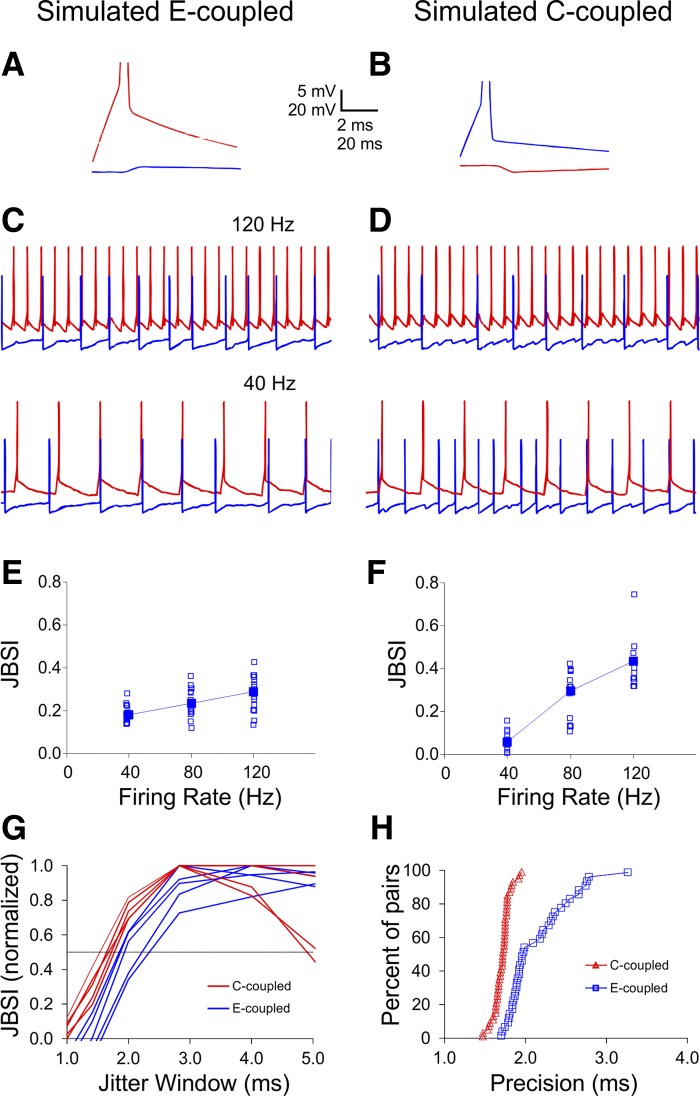
The two major differences we observed between FS-FS and SOM-SOM synchrony, the stronger firing rate dependence and the higher precision of FS-FS synchrony, could be explained in two different ways. They could result from the mode of connectivity (electrical vs. chemical synapses) or they could reflect the well-documented differences in intrinsic properties between these two interneuron subtypes, including shorter membrane time constants, faster EPSP and IPSP kinetics, and presence of autapses, characteristic of FS interneurons (Angulo et al. 1999a; Bacci and Huguenard 2006; Bartos et al. 2002; Beierlein et al. 2003; Fricker and Miles 2000; Galarreta and Hestrin 2001; Tan et al. 2008). Our observations were based on comparison of E-coupled SOM pairs to C- or D-coupled FS pairs; because we found no C-coupled SOM pairs and very few E-coupled FS pairs, we could not differentiate between connectivity-based and intrinsic properties-based factors experimentally. We therefore addressed this question with computer simulations. We implemented a reduced integrate-and-fire model of pairs of neurons with identical intrinsic parameters, divided into two groups differing only in their mode of connectivity being electrical or chemical, so an action potential in one cell was followed by a JPSP or an IPSP, respectively, in the paired cell (Fig. 7, A and B; see materials and methods for details). JPSPs were depolarizing and occurred with 0 latency, whereas IPSPs were hyperpolarizing and occurred after a 1-ms latency. Both types of responses had a 1- to 2-ms rise time and decayed with the time constant of the membrane, set to 10 ms; with these settings the duration of simulated uIPSPs was about 20 ms, similar to experimental ones. Notably, the results were robust to realistic variations in most parameters (see below). Subthreshold electrical coupling was not incorporated into the model, and neither was dual connectivity. We tested the modeled pairs for firing rate dependence of synchrony as we did in our experiments, stimulating the driver neuron (in FS pairs, the presynaptic) with trains of brief current steps at three different frequencies, and depolarizing the follower neuron with constant current (Fig. 7, C and D). The firing rate of the follower cell and the amplitudes of JPSPs and IPSPs were allowed to vary within experimentally observed values. The results of a set of 90 runs of the simulation (15 runs per firing rate per group) are plotted in Fig. 7, E and F. Clearly, the simulation reproduced the strong firing rate dependence of C-coupled pairs and the much weaker dependency of E-coupled pairs observed experimentally without assuming any intrinsic differences between the neurons (compare Fig. 7, E and F, to Fig. 5, C and D, respectively). To test for differences in precision of synchrony, we ran simulations in which both neurons were depolarized tonically and the firing rates of both neurons, as well as the JPSP and IPSP amplitudes, were varied within experimentally observed ranges. We then calculated the JBSI of each run for a range of jitter windows, as shown in Fig. 6 for the experimental pairs. Normalized JBSI vs. Jitter Window curves for 5 representative runs from each group are superimposed in Fig. 7G, and cumulative R_t histograms from 50 representative runs from each group are plotted in Fig. 7H. Again, the simulation reproduced the experimentally observed difference in temporal precision between E-coupled and C-coupled pairs without assuming any intrinsic differences between the two groups (compare Fig. 7, G and H, to Fig. 6, A and B, respectively).

Fig. 7.

Simulations reproduced the observed differences between electrically and chemically driven synchrony. A reduced integrate-and-fire model was used to simulate paired spike trains from interconnected neurons with identical intrinsic properties. A and B: electrical coupling was simulated by a JPSP following a spike in the paired neuron with 0 latency, and chemical coupling was simulated by an IPSP following a spike in the presynaptic neuron with 1-ms latency. Both postsynaptic potentials decayed at the membrane time constant, assumed to be 10 ms. C: simulated paired spike trains in which 1 neuron (red traces) was induced to fire at predefined frequencies while the other (blue traces) was tonically depolarized, as in our experiments; the level of tonic depolarization was varied within experimental values, as were the JPSP and IPSP amplitudes. E and F: JBSI plotted against firing rate for 15 simulated pairs from each group. Filled symbols indicate medians. Synchrony by E-coupling was weakly firing rate dependent, but synchrony by C-coupling was strongly firing rate dependent, similarly to our experiments (compare with Fig. 5, C and D). G: JBSI plotted at decreasing jitter windows for 5 representative simulated pairs from each group (compare with Fig. 6A). H: cumulative firing precision for 50 simulated pairs from each group (compare with Fig. 6B).

To further explore the origin of the difference in precision between the two modes of connectivity, and also to test the robustness of our conclusions to variations in the assumed parameters of the model, we conducted additional simulations in which we varied the synaptic delay and rise time of the JPSP and the IPSP. Increasing either the rise time of the JPSP (from the assumed 1 ms) or its synaptic delay (from the assumed 0) shifted the cumulative histogram of E-coupled pairs to the right, i.e., reduced the precision of E-coupled pairs even further. In contrast, increasing the rise time of the IPSP (from the assumed 1 ms) had negligible effect on precision of synchrony in C-coupled pairs, but reducing IPSP latency (from the assumed 1 ms toward the experimentally observed values of ∼0.6 ms) shifted the R_t histogram to the left, i.e., increased the precision of C-coupled pairs. We conclude that our simulations, if anything, underestimated the difference in precision between E-coupled and C-coupled pairs, and that the precision of synchrony in E-coupled pairs was constrained mainly by the rise time of the JPSP, whereas the precision of synchrony in C-coupled pairs was constrained mainly by the synaptic delay.

DISCUSSION

The goals of this study were to characterize firing synchrony between pairs of mouse neocortical interneurons and to relate its properties to the subtype identity (SOM or FS) and synaptic connectivity (electrical, chemical, or dual) of the paired interneurons. Our data set included over 150 homotypic pairs of interneurons induced to fire in isolation, on the background of quiescent brain slices, so network effects beyond mutual synaptic interactions (e.g., common excitatory or inhibitory inputs originating in the surrounding network) were presumably absent. Our main findings were that 1) when driven to fire at relatively high rates, pairs of interneurons exhibited strong and stable synchrony that depended on electrical coupling in SOM pairs and on chemical or dual coupling in FS pairs; 2) whereas electrically driven SOM-SOM synchrony was only weakly dependent on firing rate, chemically driven FS-FS synchrony required high firing rates (≥80 Hz) in the presynaptic (driver) cell and was not evident at the prototypical 40-Hz gamma frequency (see also Gibson et al. 2005); 3) precision of synchrony was about one-third higher in C- and D-coupled FS pairs compared with E-coupled SOM pairs; and 4) a minimal integrate-and-fire model, in which intrinsic properties were identical in all neurons, captured the differences in firing rate dependence and precision of synchrony observed experimentally between electrically and chemically coupled interneurons, implying that the mode of coupling was sufficient to account for these difference.

Limitations of our methods.

Our conclusions are obviously constrained by our use of a reduced in vitro preparation. Extracellular recordings in vivo would have the dual advantage of studying an intact brain while recording from a large number of neurons simultaneously, but could not resolve subthreshold responses, crucial for quantifying chemical and electrical coupling, and could not classify the recorded neurons by morphological and electrophysiological criteria beyond the limited distinction possible from extracellular spike waveforms. Although these disadvantages can in principle be overcome by paired intracellular recordings in vivo, such experiments are extremely difficult and rarely reported (Lampl et al. 1999; Poulet and Petersen 2008; Steriade et al. 1998). Our slices did not maintain long-range connections from thalamus or from other cortical areas and may have lost a considerable fraction of local connectivity, as well (Levy and Reyes 2012; Stepanyants et al. 2009). Specifically, incidence and strength of inhibitory FS-FS connections in the slice are likely to be an underestimate of their values in vivo. This implies that the reported JBSI values of FS pairs could have been underestimated; however, such an underestimate should not have affected conclusions 2) and 3) above, about frequency dependence or precision of synchrony, because these properties were not correlated with the JBSI. Finally, our recordings were limited to pairs of interneurons and thus may have missed higher-order interactions in the network (Ohiorhenuan et al. 2010); however, much of the collective behavior of multineuron networks may be satisfactorily captured by sampling these interactions pairwise (Schneidman et al. 2006).

How chemical inhibitory synapses drive synchrony.

That mutual inhibitory connections alone can generate precise spike synchrony has been demonstrated experimentally in cerebellar Purkinje cells (de Solages et al. 2008) and cortical interneurons (Gibson et al. 2005; Hu et al. 2011; Merriam et al. 2005). How can inhibition drive precise synchrony? When a presynaptic inhibitory neuron fires repetitively with ISIs shorter than the IPSP time course (which was ∼20 ms in our data set), firing probability in the postsynaptic neuron will follow the time course of the IPSP; it will be highest just before the onset of the next IPSP, when inhibition is at a local minimum. Onset of the next IPSP will occur one synaptic delay after the next presynaptic spike; this represents the closing of the “window of opportunity” for the postsynaptic cell to fire in that cycle, which explains why in our simulations precision was increased when synaptic delay was decreased. The onset of the window of opportunity will depend on the driver firing rate; because the decay of the IPSP follows an exponential time course, the shorter the presynaptic ISI, the steeper will be the postsynaptic membrane trajectory and the narrower the window of opportunity for firing. This explains the increase in synchrony with the presynaptic (driver) firing rate. Note that the postsynaptic cell needs to be driven strongly enough to occasionally overcome the IPSP but not strongly enough to fire more than once per presynaptic cycle; in other words, synchrony by chemical inhibition cannot be maintained if the follower cell fires at a higher rate than the driver cell, a situation that was avoided in our experiments. The follower cell can, however, fire at arbitrarily slow rates, because the JBSI depends on the relative fraction of synchronous follower spikes, not on their absolute number. This explains why the JBSI of C-coupled FS pairs in our data set was not dependent on the follower firing rate. Last and perhaps most importantly, if the driver firing rate falls below ∼50 Hz, the IPSP will decay to baseline before the next presynaptic spike has arrived and the window of opportunity will be broadened considerably, resulting in loss of synchrony.

Repetitively activated inhibitory synapses made by FS cells on excitatory neurons or on interneurons undergo rate-dependent short-term depression (Beierlein et al. 2003; Galarreta and Hestrin 1998; Gonzalez-Burgos et al. 2005; Ma et al. 2012; Varela et al. 1999). Short-term depression was evident in our recordings (e.g., Fig. 3B), but was not likely to have affected our conclusions for three reasons. First, as shown in Fig. 3F, we did not observe a systematic time- or spike-dependent rundown in synchrony in our recordings. More importantly, any depression of IPSPs would have decreased synchrony more at higher presynaptic firing rates, opposite to the observed effect. Last, synaptic depression was not incorporated into our computer model, and yet the simulations reproduced the main experimental observations.

How electrical and dual synapses drive synchrony.

Electrical synapses are widely observed in the central nervous system and promote both subthreshold and spike synchrony (reviewed in Bennett and Zukin 2004; Connors and Long 2004). In the neocortex, electrical coupling synchronizes interneurons of various subtypes (Beierlein et al. 2003; Caputi et al. 2009; Deans et al. 2001; Galarreta et al. 2004; Galarreta and Hestrin 1999; Gibson et al. 1999). Stronger coupling generates larger JPSPs, which are more likely to fire the follower interneuron, explaining the dependence of the JBSI on the ECC. We found that synchrony by electrical coupling, although strong, was considerably less precise than synchrony by chemical or dual connectivity (Fig. 6B). Our simulations suggest that precision of electrically driven synchrony is constrained by the rise time of the JPSP: the faster the rise time, the faster it will bring the follower cell to firing threshold and the shorter the time lag between the presynaptic and postsynaptic spikes. In many pairs, the JPSP was relatively weak and slow rising, allowing a broader and less precise window of opportunity and thus generating lower precision synchrony, compared with chemically connected pairs. Note however that this conclusion is based only on E-coupled SOM pairs and may not necessarily be generalizable to E-coupled FS pairs, because we found very few of the latter. As previously observed, JPSPs between E-coupled FS pairs have biphasic waveforms, with a second, negative phase reflecting the presynaptic AHP (Galarreta and Hestrin 2001; Gibson et al. 2005); this may result in more precise synchrony compared with the monophasic JPSPs observed in SOM interneurons.

Dual connectivity, electrical and chemical, has also been described in a variety of cortical interneuron subtypes (Blatow et al. 2003; Chu et al. 2003; Galarreta et al. 2004; Galarreta and Hestrin 1999; Gibson et al. 1999; Olah et al. 2007; Szabadics et al. 2001; Tamas et al. 2000), and its role in synchronizing firing has received considerable theoretical attention, sometimes with conflicting conclusions. We found that the relatively weak electrical coupling of D-coupled FS pairs resulted in a twofold increase in synchrony compared with C-coupled pairs with comparable chemical connectivity strength (Fig. 4, E and F). This is consistent with models suggesting that addition of weak electrical coupling to strong inhibitory coupling promotes a large, supralinear increase in synchrony, possibly because electrical coupling keeps the subthreshold membrane trajectories of the two neurons from diverging (Kopell and Ermentrout 2004; Pfeuty et al. 2005, 2007; Traub et al. 2001).

Role of interneuron synchrony in gamma oscillations.

The activated state of the cortical network is often manifested as “40 Hz,” or more generally 30–90 Hz, field potential spectral components known as gamma oscillations (reviewed in Buzsaki and Wang 2012; Fries et al. 2007), thought to be indicative of conscious cognitive processes such as memory, attention, and perception (Jensen et al. 2007; Melloni et al. 2007; Ward 2003). Synchronous firing of FS interneurons is proposed as the major driver of gamma oscillations (reviewed in Bartos et al. 2007), and two classes of models, so-called ING and PING, invoke either purely interneuron-interneuron connections or pyramidal-interneuron connections, respectively, in generating this synchrony (Tiesinga and Sejnowski 2009; Whittington et al. 2011). Our results imply that FS interneurons are not likely to synchronize at ∼40 Hz through mutual inhibition alone, putting in question ING-like mechanisms as generators of slower gamma rhythms. Consistent with this conclusion, genetic removal of FS-FS inhibitory synapses does not affect gamma oscillations (Wulff et al. 2009), and hippocampal FS cells are only weakly modulated at ∼40-Hz gamma frequencies (Tukker et al. 2007). Note that our results do not rule out PING-like mechanisms (Atallah and Scanziani 2009; Mann et al. 2005; Oren et al. 2006); nor do they rule out contribution of coupled FS interneurons to oscillation frequencies ≥80 Hz such as fast gamma or sharp-wave-associated ripples (Colgin et al. 2009; Sohal and Huguenard 2005; Tukker et al. 2013; Vida et al. 2006).

GRANTS

This work was supported by National Institute of Neurological Disorders and Stroke Grant NS050437.

DISCLAIMER

The authors of this manuscript are fully and solely responsible for its content.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

H.H. performed experiments; H.H. and A.A. analyzed data; H.H. and A.A. interpreted results of experiments; H.H. and A.A. approved final version of manuscript; A.A. conception and design of research; A.A. prepared figures; A.A. drafted manuscript; A.A. edited and revised manuscript.