Abstract
Background and Aims In mountain ecosystems, predicting root density in three dimensions (3-D) is highly challenging due to the spatial heterogeneity of forest communities. This study presents a simple and semi-mechanistic model, named ChaMRoots, that predicts root interception density (RID, number of roots m–2). ChaMRoots hypothesizes that RID at a given point is affected by the presence of roots from surrounding trees forming a polygon shape.
Methods The model comprises three sub-models for predicting: (1) the spatial heterogeneity – RID of the finest roots in the top soil layer as a function of tree basal area at breast height, and the distance between the tree and a given point; (2) the diameter spectrum – the distribution of RID as a function of root diameter up to 50 mm thick; and (3) the vertical profile – the distribution of RID as a function of soil depth. The RID data used for fitting in the model were measured in two uneven-aged mountain forest ecosystems in the French Alps. These sites differ in tree density and species composition.
Key Results In general, the validation of each sub-model indicated that all sub-models of ChaMRoots had good fits. The model achieved a highly satisfactory compromise between the number of aerial input parameters and the fit to the observed data.
Conclusions The semi-mechanistic ChaMRoots model focuses on the spatial distribution of root density at the tree cluster scale, in contrast to the majority of published root models, which function at the level of the individual. Based on easy-to-measure characteristics, simple forest inventory protocols and three sub-models, it achieves a good compromise between the complexity of the case study area and that of the global model structure. ChaMRoots can be easily coupled with spatially explicit individual-based forest dynamics models and thus provides a highly transferable approach for modelling 3-D root spatial distribution in complex forest ecosystems.
Keywords: Heterogeneous forest ecosystems, plant growth modelling, tree root density, fine root, coarse root, root system architecture, logistic function, Weibull distribution, log-normal distribution, Gompertz distribution, Abies alba, silver fir, Picea abies, Norway spruce.
INTRODUCTION
Tree roots can constitute >60 % of total biomass in forest ecosystems (Vogt et al., 1996). To evaluate below-ground ecosystem services, a reliable characterization of the spatial distribution of root density is fundamental. However, determining root density can be challenging, especially in remote locations or protected areas where root excavation is difficult or limited, e.g. at high altitudes or in naturally regenerated forests. These forests also possess particularly heterogeneous distributions of roots in both space and time (Soethe et al., 2006; Schwarz et al., 2010; Mao et al., 2012, 2013), and therefore reliable data remain scarce. Developing an accurate model that could predict root density from above-ground tree dimensions would be highly useful in complex forest ecosystems and could likely be applied to other types of forest.
In naturally regenerated montane and subalpine forests, trees commonly grow in clusters named tree islands, i.e. canopy-closed zones surrounded by clusters of trees. Between the clusters are gaps, i.e. canopy-open zones (Mao et al., 2012). In each cluster there is usually more than one species, tree ages are different and there is an irregular distribution of tree locations. Soil is also spatially heterogeneous, due, for example, to a high presence of stones that can obstruct root extension. Root growth of trees might also be in competition with that of shrubby and herbaceous understorey plants, rendering more difficult the modelling of root density distribution.
Models of tree root spatial distribution have been developed for the last 40 years (Böhm, 1979; Coutts, 1983; Schenk and Jackson, 2002; Zianis et al., 2005; Picard et al., 2012). The distribution of root density, either horizontal (e.g. along a gradient of canopy openness) or vertical (e.g. along a gradient of soil depth), is supposed largely to be a consequence of intrinsic and ontogenic traits and environmental factors (Picard et al., 2012). Different tree species possess different root system architectures, which change throughout the life of a tree. Environmental factors affecting root density distribution can be (1) abiotic, including climatic, e.g. altitudinal trends (Hertel and Schöling, 2011; Mao et al., 2015), edaphic, e.g. water and nutrient availability in soil (Coutts et al., 1999), soil texture and compaction level (Dexter, 2004) and topographic, e.g. the presence of physical obstructions such as stones (Hoffmann and Usoltsev, 2001; Soethe et al., 2006) and slope angle (Di Iorio et al., 2005; Chiatante and Scippa, 2006), and (2) biotic, e.g. interactions between trees and between trees and understorey species (van Noordwijk et al., 1996; Cardinael et al., 2015). Existing models have been developed on the basis of the above sources of effects. Most models are allometric relationship-based (ARB) models, in which root density varies as a function of dendrometric properties of aerial tree organs and spatial distance [horizontal and/or vertical (for reviews see Hoffmann and Usoltsev, 2001; Schenk and Jackson, 2002; Zianis et al., 2005; Day et al., 2010)]. The ARB models generally have a simple and empirical structure and a small number of easy-to-measure parameters, and thus are easy to operate. However, most ARB models are developed at the scale of the plant individual and do not take into account the effects of interactions between trees. Thus, the relevance of up-scaling and applying tree individual-based ARB models to the whole-forest scale remains questionable, especially for heterogeneous mountain forests.
Another group of models developed at the plant individual scale aims at simulating spatio-temporal root growth dynamics. These models can be either (1) pseudoroot system architecture (RSA) models, which simulate the spatio-temporal distribution details of root density in a given soil volume as a proxy of RSA via diffusion or carbon allocation processes (Mulia et al., 2010), or (2) true RSA models, which simulate RSA skeletons via stochastic approaches (Doussan et al., 2003). Compared with ARB models, both pseudo-RSA and true RSA models are more sophisticated because they are more mechanistic, considering both root proliferation and certain biological parameters. The RSA models are more dynamic in time and space (i.e. root growth can be integrated) and can simulate two-dimensional (2-D) or three dimensional (3-D) root architecture skeletons or proxies of RSA that are highly realistic. Such models also have a strong potential to take into account interactions between trees (Pagès et al., 2004) and between trees and understorey species (Collet et al., 2006), although most RSA models have not considered these interactions yet. Nevertheless, the existing RSA models are mostly designed for agricultural crops or agroforest trees, which constitute relatively regular and homogeneous ecosystems in both above- and below-ground compartments (Mulia et al., 2010). Thus, the applicability of RSA models to naturally regenerated trees within highly heterogeneous mountain ecosystems remains uncertain. Furthermore, most models require many complex parameters related to root traits and development. These parameters are either unavailable for natural species or are time-consuming to estimate.
High-altitude, mixed, naturally regenerated forest ecosystems are complex in vegetation distribution and environmental conditions and therefore new models for predicting the spatial distribution of root density are needed. It is preferable that these models possess the advantages of both ARB and RSA approaches and comprise simple equations with easy-to-measure inputs for forest and environmental characteristics. Models should also combine mechanistic processes and ecologically meaningful parameters. It is also desirable that model predictions are spatially explicit and can be used for up-scaling. Such models are lacking, especially for highly heterogeneous forest ecosystems. Nevertheless, some modelling studies on root distribution exist (Gersani et al., 2001; Müller and Wagner, 2003; Roering et al., 2003; O’Brien et al., 2007), as they are simple and include plant interactions. For example, Müller and Wagner (2003) and Roering et al. (2003) developed models whereby they hypothesized that root density at a given point was affected by the presence of roots from the surrounding trees and that density varied between this point and the tree stem. On the basis of game theory, Gersani et al. (2001) and O’Brien et al. (2007) considered that a plant produces fewer roots when in competition with its neighbour than if it is isolated. Root overlapping was also taken into account. These models appear suitable to capture some features of complex forest stands (e.g. spatial heterogeneity of trees and tree interactions), although several were not initially developed for modelling forest ecosystems (e.g. Gersani et al., 2001; O’Brien et al., 2007).
We developed a model based on the hypothesis that root density at a given point is affected by the presence of roots of surrounding trees forming a polygon shape, with a possible saturating effect depending on the total density of surrounding trees. The effect of tree size and distance to a given point, species, presence of rocks and competition with roots of the understorey vegetation was investigated. Data to test the model were collected in the French Alps. The root density indicator was root interception density (RID, number of roots m–2), which is one of the most commonly used root indicators characterizing root density (Van Noordwijk et al., 2000; Maurice et al., 2010; Mao et al., 2012, 2013). RID can be used in the calculation of root area ratio (i.e. total root cross-sectional area per soil area) and is a key input for assessing the role of roots in reinforcing soils against shallow landslides (Stokes et al., 2009; Mao et al., 2012, 2013). RID is also considered a suitable proxy to evaluate above- and below-ground carbon allocation at a stand level (Mao et al., 2015). As RID is easy to measure, it has been frequently used for estimating root length density (RLD) (Van Noordwijk et al., 2000; Chopart et al., 2008; Maurice et al., 2010; Cardinael et al., 2015). Root length density is often used as a proxy to characterize plant water and nutrition uptakes in forest or agricultural systems (Chopart et al., 2008). The potential of our model is discussed with regard to its more widespread use in several types of forest ecosystems.
MATERIALS AND METHODS
Description of the model
The model, called ChaMRoots (Characterisation of Mountain forest Roots) comprises three sub-models for predicting the following parameters (Note: according to the international standard ISO 31–11, ]x, y] denotes a left half-open interval from x (excluded) to y (included)):
Spatial heterogeneity of tree roots. The sub-model predicts the RID of roots ]0, 1] mm in diameter within the top 0·2 m of soil as a function of tree species, tree dimension [e.g. basal area at breast height (g)], tree position [i.e. the distance between the tree and a given point (D)] and the presence/absence of obstacles (e.g. stones) in soil that emerge on the ground (O).
Diameter spectrum. The distribution of RID as a function of root diameter class for roots ≥1 mm in diameter is predicted by the second sub-model.
Vertical profile. The vertical distribution of RID as a function of soil depth (z) is predicted by the third sub-model.
Sub-model of spatial heterogeneity of tree roots
The fundamental principle of the first sub-model is that a tree contributes more to total root density at a given point when it is large, close to that point and no obstacles are present between the tree and the given point. The higher potential production of roots also depends on species and site conditions. The contribution of roots to total density is implicitly modulated by the presence of other trees due to inter-tree competition. Distance, tree size, obstacles and species were therefore selected as the main factors influencing tree root density (Hoffmann and Usoltsev, 2001).
The core of the first sub-model of root spatial heterogeneity is based upon root production efficiency (E) at a given point, which depends on the surrounding trees. E is defined by:
| (1) |
where p is the potential of trees to grow roots at a given point in the soil. The term ‘tree root potential’ or p will be used hereafter. The value of p depends on the dimension and position of the surrounding trees. p differs from E, which measures the capacity of trees to convert a unit of p to root density. RIDt,0–1 is the RID of the finest tree roots; dRIDt,0–1/dp is the production of RIDt,0–1 per p metric.
p at a given point is defined by the following general form:
| (2) |
Ns is the number of tree species around the target point (Ns ≥ 0, s ∈ [0, Ns]). Ne is the number of tree individuals of a given species s around the target point (Ne ≥ 0, e ∈ [0, Ne]). pe,s is the tree root potential contributed by a tree (e, s). ge,s is the basal area at a height of 1·3 m of an individual tree e of species s (m2). De,s is the horizontal distance from the centre of a tree (e, s) to the target point (m) and has a value ≥0. Oe,s is the absence of emerged obstacles (diameter >∼30 cm) on the ground between the target point and tree e of species s. The value of Oe,s can be either binary (1 = yes, absence of obstacles; 0 = no, presence of obstacles) or unique (1 = yes, indifferent to the absence or presence of obstacles), depending whether the effect of obstacles is considered. α and β are scaling parameters of the surrounding trees’ influence on p, while λs and φs are RSA parameters (see below). These four parameters are fitted parameters.
α and β are generic coefficients (α and β ≥0) accounting for the effect of intrinsic tree allometry regardless of tree species, as they allow an alteration of the weight of De,s relative to ge,s. When β = 0, both pe,s and p ∈ [0, +∞[, if De,s tends to approach 0, i.e. the given point is situated at the centre of the tree (e, s), then p tends to infinity. When β > 0, β is effectively limiting the ratio between gi and Di, without the drawback of pulling pe,s towards infinity. To estimate α and β, we tested the following cases:
α, β ∈ [0, +∞[
α ∈ [0, +∞[, β = 0
α ∈ [0, +∞[, β = 1
λs and φs are specific coefficients (λs, φs ≥ 0) accounting for the effect of RSA. Species that differ in architecture may possess variable capacities for root extension, which results in a disparity in the spatial distribution of roots in the soil. We divided species into three groups according to the morphology of the root system, using the classification of Köstler et al. (1968), as follows.
Plate-like morphology, with a greater superficial, horizontal root extension compared with that of the vertical roots, e.g. Picea abies. In this case, λs = λp, φs = φp.
Taproot morphology (λs = λa), with a greater extension of vertical roots compared with the extension of horizontal and lateral roots, e.g. Abies alba. In this case, λs = λa, φs = φa.
Heart-like morphology, where the root system is a mixture of the above two types, e.g. Fagus sylvatica, Sorbus aucuparia, Acer pseudoplatanus. In this case, λs = λb, φs = φb.
To facilitate the estimation of coefficients, we consider P. abies as the reference species and let λp = 1 and φp = 1. The p of A. alba and broadleaves based on λa, φa and λb φb can be considered as relative p compared with P. abies. In this study, due to a small population of broadleaves, pb was forced to share the same coefficient with either pp or pa, i.e. Ns = 2. The following two cases were tested:
λp = 1; φp = 1; λa = λb∈ [0, +∞[, φa = φb∈ [0, +∞[
λp = λb = 1, φp = φb = 1, λa∈ [0, +∞[, φa ∈ [0, +∞[
where broadleaves were grouped together with A. alba and P. abies, respectively.
To estimate λs and φs, we tested the following cases:
λs ∈ [0, +∞[, φs = 1
λs = 1, φs ∈ [0, +∞[
λs ∈[0, +∞[, φs ∈ [0, +∞[, λs = φs
These three cases represent different biological phenomena concerning the effect of species on tree root extension. Options (1) and (2) assume that the effect of species on p is uniquely effective with regard to tree size and the distance between the tree and the target point, respectively; while (3) assumes that the effect of species on p is effective with regard to ge,s and De,sα, i.e. both tree size and position.
We modelled E using two approaches. Firstly, in a semi-mechanistic approach, E was assumed to be dependent on two factors: (1) the ‘root-providing pool’, which represents the existing quantity of roots from which the finest roots can be borne; (2) the ‘restraining pool’, representing the upper limit of the finest root production due to root competition, which can be both intra- and inter-species specific. Therefore, E can be written as a derived form of the logistic function:
| (3) |
Here, K is the maximum density of RID0–1 of both tree and understorey species that the soil can support, RIDu,0–1 is the RID of understorey species and θ is the coefficient describing the relationship between understorey species' roots and tree roots. If θ = 0, there is a neutral relationship of root growth between tree and understorey species, and E is uniquely determined by the RID of the trees. If θ > 0, understorey species' roots are in competition with tree roots; for a given K, a higher θ value reflects a greater detrimental effect of understorey species' roots on tree roots. Theoretically, θ can be negative, suggesting that roots of understorey species are in a mutualistic relationship with tree roots, but this phenomenon might be rarely observed in reality. r is the average branching rate for the production of RID0–1, and RIDt,x–y is the RID of tree roots in the class of root diameter ]x, y] mm from which fine roots can be borne.
Preliminary regression analyses based on our monolith data (see section Tree and root data) revealed that RIDu,0–1 had no significant effect on RIDt,0–1 (P > 0·40, data not shown), suggesting a low competitive effect between understorey species' roots and tree roots in our study sites. Hence, we set θ = 0, simplifying eqn (3) by removing the non-significant interactions between RID of trees and that of the understorey species:
| (4) |
where K in eqn (4) is replaced by Kt, which denotes the maximum density of RID0–1 of tree roots.
Field observations from rhizotrons at the same field sites showed that roots ]0, 1] mm in diameter could be branches initiated on roots of ]1, 5] mm or those of ]0, 1] mm (Mao et al., 2013). Hence, we have:
| (5) |
Here we chose to use a linear relationship between RIDt,1–5 and RIDt,0–1 regardless of site rather than non-linear curves or fitting one curve per site, as a linear relationship leads to a more simple integral equation, i.e. eqn (5).
| (6) |
where a and b are the slope and intercept coefficients of the linear univariate equation a ≥ 0; b >0.
By linking eqns (1), (5) and (6), the integrated form of eqn (4) (see Supplementary Data S1 for details of deduction) is:
| (7a) |
where:
| (7b) |
According to eqns (7a) and (7b), we see that when p = 0 (no tree), RIDt,0–1 = 0, and when p → +∞ (no limitation of the maximum tree inclusion zone), RIDt,0–1 → Kt.
Alternatively, we modelled E and RIDt,0–1 in an empirical approach using a power function, which is one of the most commonly attempted functions when exploring a relationship between two variables:
| (8) |
| (9) |
where m and n are the two coefficients of the power function. Such a comparison allowed us to discuss the efficiency of different approaches.
Sub-model of diameter spectrum.
We modelled the cumulative frequency Cd (dimensionless) of RID as a function of the upper boundary of root diameter class (d). Compared with absolute values of RID, Cd enabled us to reduce the irregular jump of data points from one diameter class to another. We tested four types of function for the optimum fit of the sub-model of diameter spectrum, including a one-parameter cumulative distribution function (CDF) of exponential distribution [eqn (10a), ‘exponential’]:
| (10a) |
and three two-parameter functions, i.e. a Weibull distribution [eqn (10b), ‘Weibull’], Gompertz distribution [eqn (10c), ‘Gompertz’] and log-normal distribution [eqn (10d), ‘log normal’], respectively:
| (10b) |
| (10c) |
| (10d) |
where Cd is the cumulative frequency of RID from the finest roots to those of root class diameter d mm (dimensionless), d ∈ ]0, 50] mm; Cd ∈ [0, 1], ζ, γ, κ, η, δ, μ and σ are the coefficients of root of diameter spectrum in the CDFs, and erf is the Gauss error function.
Sub-model of vertical profile.
Root density varies significantly with soil depth, which has, in turn, commonly been used as a key parameter when modelling vertical root distribution (Gale and Grigal, 1987; King et al., 2003). To facilitate comparison with previous studies, we modelled the root distribution along a vertical soil profile using the following one-parameter exponential model:
| (11) |
where Cz is the cumulative frequency of RID from ground surface to the soil depth z (m); Cz ∈ [0, 1·0], with z ∈ ]0, zmax] and ε is the coefficient of root profile shape, with ε ∈[0, 1[. The closer ε approaches 1, the more roots tend to be less concentrated at the soil surface. We fixed maximum soil depth at 1·0 m according to field observations from the same field site (Mao et al., 2013). This equation is derived from the model of Gale and Grigal (1987) for estimating the vertical distribution of roots.
Tree and root data
Characteristics of study sites.
Our study sites were located near the village of Chamrousse, Isère, France (45°07'7N, 5°52' E) and comprised two mixed, mature, naturally regenerated forests of Norway spruce (P. abies), silver fir (A. alba) and European beech (F. sylvatica) growing at altitudes of 1400 m a.s.l. (Prémol forest) and 1700 m a.s.l. (Bachat-Bouloud forest). Mean monthly air temperature was lowest in January or February (–5·2 °C at 1400 m, –3·6 °C at 1700 m) and highest in July (13·7 °C at 1400 m, 12·0 °C at 1700 m). Average annual precipitation is 1530 mm at 1400 m and 1710 mm at 1700 m. Soils are acidic at both sites. According to the World Reference Base (IUSS Working Group WRB, 2007) for soil resources, the soil is classified as Cambisols (Hyperdystric) at Prémol and as Cambisols (Humic, Hyperdystric) at Bachat-Bouloud. A high presence of coarse elements (rocks and stones) was found at both sites. More details about the site characteristics are available in Mao et al. (2012).
Plot settings for tree and root data.
Two 25 m × 25 m plots were set at each site for forest inventories, except for one plot at 1400 m, which was 25 m × 30 m. Within each plot, two locations were randomly selected for excavating roots: one in a tree island and the other in a tree gap (see Fig. 1 for examples of trench location within two chosen plots). Each root trench had a dimension of 1·0 m (length) × 0·6 m (width) × 1·0 m (depth, i.e. maximum rooting depth). Sets of data on forest inventories for global site descriptions and those for root density and growth dynamics in each trench are available in Mao et al. (2012, 2013).
Fig. 1.
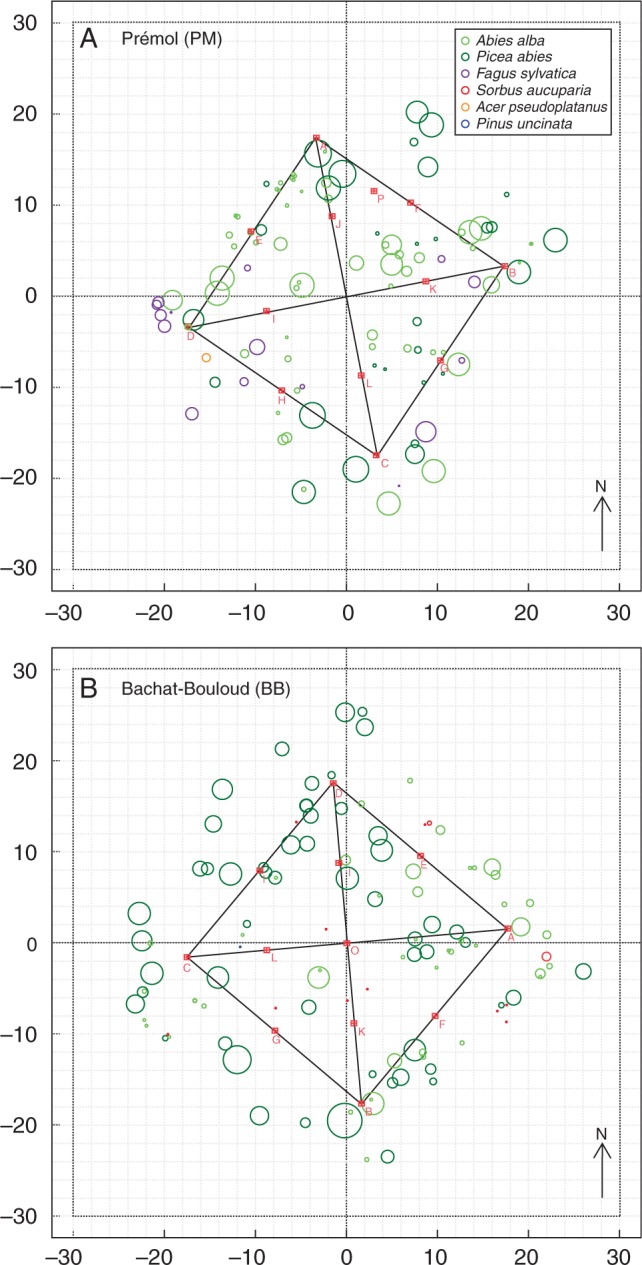
Mapping of mini-monoliths (squares) and tree trunks of different species (circles of different colours) based on forest inventories in 2009 and 2010. x- and y-axes are distances in metres. The diameter of each tree trunk has been enlarged five times for easier viewing.
At each site, one of the two plots was chosen for mini-monolith excavation. Mini-monoliths were systematically distributed on the edge and diagonal of the plots (Fig. 1) with two exceptions: no mini-monolith was excavated at point O at Prémol or at point J at Bachat-Bouloud, as their locations were disturbed by an earlier excavation for rhizotron installation and root sampling in the summer of 2009 (Mao et al., 2013). A new point P at Prémol was selected randomly in the same plot. As a result, we obtained 25 mini-monoliths in all: 13 at Prémol and 12 at Bachat-Bouloud. Each mini-monolith had a dimension of 0·2 m (length) × 0·2 m (width) × 0·2–0·3 m (depth).
Tree measurement and eligibility of ‘visible trees’.
Within each plot, species name, diameter at breast height (DBH) and location of all the trees were registered during a forest inventory in September 2009 (Mao et al., 2012). In the spring of 2010, a second forest inventory was conducted. From the location of a mini-monolith, species name, DBH, azimuth and distance of each visible tree in any direction (0° to 360°), were registered within a radius of 10·0 m. Figure 1 shows the mapping of trees for both inventories in the two plots.
At each mini-monolith, two values of the maximum tree inclusion zone (MIZ) were tested: MIZ = 8·0 m and MIZ =10·0 m. Within the MIZ of each mini-monolith, a tree is considered visible if the centre of the trunk is not eclipsed by the trunk of any other visible trees. A visible tree can be either inside or outside the plot of 25 × 25 m2. For each monolith, only visible trees are assumed to be effective in influencing root density. A detailed protocol of visible tree selection and the outcomes of mapping at each sampling point are available in Supplementary Data S2.
Root data from mini-monoliths.
Root sampling in mini-monoliths (Fig. 2A) was carried out in the summer of 2010. For each mini-monolith, we gave a qualitative description of the location of the point with regard to tree canopies [three levels: outside, transitional (i.e. on the edge of canopies) and inside] and the absence of emerged obstacles (mainly rocks of diameter >0·5 m) between the point and each of the surrounding trees (two levels: 1 = yes, absence of obstacles; 0 = no, presence of obstacles). Root excavation was strictly limited within a zone of 0·2 m × 0·2 m. Soil was carefully removed by hand and sometimes using a long nail if rocks were present. Roots connected to the soil to remove and on the lateral walls were cut using either scissors (for thin and fibrous roots) or secateurs (for coarse and highly lignified roots) so as to avoid ripping roots from the lateral soil profiles. Finally, root tips were counted on the soil profiles, layer by layer, using a metal grid with a square unit of 0·1 m × 0·1 m. RID is always associated with the angle of the soil profile and hence can be measured on a vertical, horizontal or oblique soil profile. In this study, only RID on the lateral soil profiles, i.e. walls perpendicular to the ground surface, were shown and used for model fitting, as lateral soil profiles are one of the most conventional and representative cases of root sampling (Böhm, 1979). All roots (regardless of species) were counted and classed into seven different categories of diameter: ]0, 1], ]1, 2], ]2, 3], ]3, 5], ]5, 10], ]10, 20] and ]20, 50] mm. We assumed that the counted roots contained mostly living roots, as decomposed or dead roots usually dropped from the soil profile surface during excavation. Plant functional groups (trees and shrubby and herbaceous species; the latter two are considered understorey species) were distinguished for roots >1 mm in diameter. For root intercepts of ]0, 1] mm in diameter, the plant functional group was difficult to identify in situ due to the presence of a variety of understorey species at both sites. Therefore, we estimated the RLD of roots that were simultaneously collected from the mini-monoliths, then washed in the laboratory, sorted according to functional group, scanned and analysed using the software WINRHIZO® (Regent Inc., Canada). In the laboratory, the functional group to which a root belonged was identified by its colour, texture and smell. To separate the RID of trees from understorey species, we assumed:
| (12a) |
| (12b) |
Fig. 2.

Measurement of root interception density using (A) mini-monolith and (B) soil trenching techniques.
Pu is the percentage of total root density of understorey species. Pt is the percentage of total root density of tree species, with Pt = 100 – Pu. is the estimated RID based on the RLD data. RLD is the measured RLD from WINRHIZO® analysis. The subscripts (t,0–1) and (u,0–1) of the indicators denote roots of ]0, 1] mm in diameter from tree and understorey species (number of roots m–2), respectively.
Root data from trenches.
The RID data based on measurements using trenches (Fig. 2B) of 1·0 m (length) × 0·6 m (width) × 1·0 m (depth) in Mao et al. (2012) were determined in the summer of 2009. Four trenches were dug at each site. Within each trench, root distribution was measured along each soil profile. Therefore, there were 16 sections in total and eight sections per site (Mao et al., 2012). On each profile wall, root intercepts were counted using the same protocol as for mini-monoliths, except that the root diameter class ]2, 5] mm was used instead of the classes ]2, 3] and ]3, 5] mm used in the mini-monoliths. Plant functional groups were not distinguished. Since we measured neither the RID of tree species nor that of understorey species in any trenches, we used the average values of Pu and Pt of the mini-monoliths, which were classified as ‘inside the tree canopies’ and ‘outside the tree canopies’, towards trenches in tree islands and gaps, respectively:
| (13a) |
| (13b) |
where PTI and PG are the percentages of density of roots ]x, y] mm in diameter from species in islands and gaps, respectively. Ninside and Noutside are the total numbers of mini-monoliths situated inside and outside tree canopies. Subscript n is the sequence of mini-monolith, with n ∈ Ninside or Noutside; TI is tree islands; subscript G is gaps and subscripts x and y are the lower and upper limits of a class of root diameter ]x, y] mm.
Based on eqns (13a) and (13b), estimates of Pt for tree islands and gaps at two sites are available (Table 1). As no roots of ]5, 50] mm in diameter were identified as being from understorey species, we assumed Pt = 100 % and Pu = 0 % for these root diameter classes.
Table 1.
Mean and standard deviation (s.d.) of percentages of roots from tree species (Pt, %), estimated using root interception density data from mini-monoliths
| Site | Location with regard to tree canopies | Percentage of roots from tree species (Pt) |
|||||
|---|---|---|---|---|---|---|---|
| ]0, 1] mm |
]1, 2] mm |
]2, 5] mm |
|||||
| Mean | s.d. | Mean | s.d. | Mean | s.d. | ||
| Bachat-Bouloud | Outside | 24·5 | 9·2 | 72·7 | 19·8 | 85·4 | 22·6 |
| Transitional | 34·4 | 11·4 | 45·3 | 21·8 | 73·7 | 29·7 | |
| Inside | 60·0 | 17·4 | 95·2 | 9·5 | 98·4 | 3·2 | |
| Prémol | Outside | 13·6 | 13·9 | 76·9 | 22·1 | 86·7 | 18·9 |
| Transitional | 48·1 | 35·3 | 94·2 | 8·0 | 95·3 | 6·6 | |
| Inside | 78·5 | 19.7 | 86·0 | 19·4 | 96·6 | 4·9 | |
For root diameter ]0, 1] mm, Pt was estimated using root WINRHIZO®, which measured root length density of each type of functional group, as it was impossible to identify to which functional group a root tip belonged. See also Mao et al. (2015).
2.3 Statistical modelling
Data from mini-monoliths (Nf = 25, where Nf is the number of observations for model fit) were used to fit the sub-model of spatial heterogeneity and that of diameter spectrum for roots within a soil depth of ]0·0, 0·2] m. Beyond this depth, i.e. for the depth of ]0·2, 1·0] m, the data from root trenches were used to fit the sub-model of diameter spectrum (Nf = 16). Since the roots were measured to the maximum rooting depth at each site, these root data were also used to fit the sub-model of vertical profile (Nf = 16). To choose the optimal sub-models, we calculated (1) root mean square error:
| (14) |
where ı and Yi are the predicted and observed values; i ∈ [1, Nf], (2) the Akaike information criterion (AIC), (3) the Bayesian information criterion (BIC) and (4) the coefficient of determination (R2, dimensionless) as quantitative indicators (Burnham and Anderson, 2002).
All the sub-models were validated using root data that were not used for model fitting. The sub-model of spatial heterogeneity was validated using the database from root trenches within a soil layer of ]0·0, 0·2] m, in which RIDt,0–1 of four sections within one root trench were averaged (Nv = 8, where Nv is the number of observations for model validation). Regarding the sub-model of diameter spectrum and that of the vertical profile, only three sections out of four per root trench were chosen for fitting and the remaining one was used for model validation (Nv = 8). Statistical analyses were performed using R 2.13.0 (www.r-project.org).
RESULTS
Spatial heterogeneity
RIDt,1–5 significantly correlated with RIDt,0–1 at a soil depth of 0·2 m (Fig. 3). RIDt,1–5 was significantly higher at the Bachat-Bouloud site compared with Prémol for the same RIDt,0–1 (Fig. 3). Despite this significant site effect, occurring mainly on the intercept (b), we calibrated one slope (a) and one intercept (b) for both sites combined, to facilitate fits of eqns (10a) and (10b), instead of one pair of a and b per site, as the fit per site did not significantly improve R2 (0·34 for Prémol and 0·43 for Bachat-Bouloud) compared with the fit for both sites combined (0·42). A higher number of sites, as well as a higher number of points per site, would have been necessary to better explore this effect.
Fig. 3.
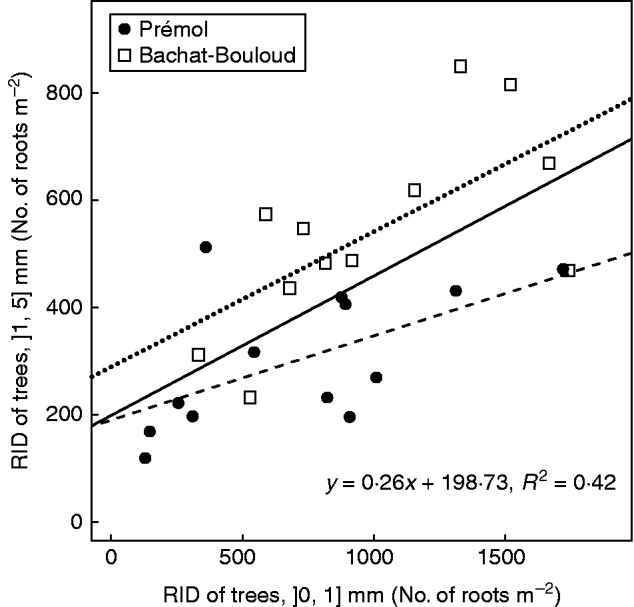
Correlation between root interception density (RID) of ]1, 5] mm and ]0, 1] mm. Round symbols represent the Prémol site and square symbols the Bachat-Bouloud site. Solid, dashed and dotted lines denote the linear regressions for both sites (to which the equation refers), Prémol and Bachat-Bouloud, respectively.
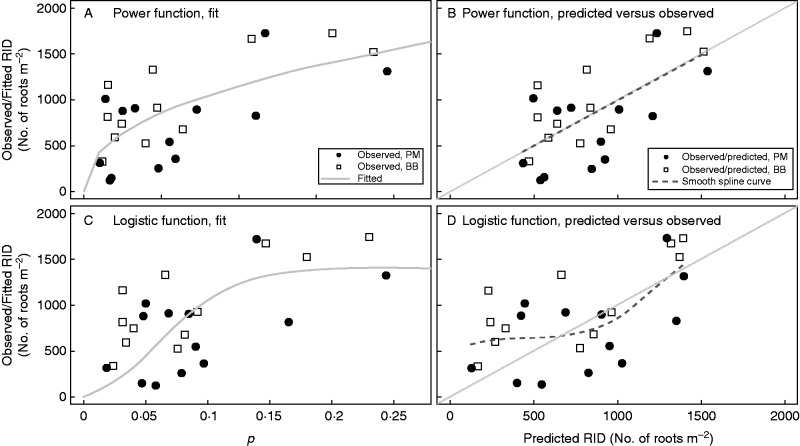
Neither the effect of obstacle nor the choice of MIZ (8·0 versus 10·0 m) improved the fit regardless of fitting index (Fig. 4). Hence, the final sub-models chosen omitted O, but included MIZ = 8·0 m. Power function-based sub-models possessed significantly higher R2 and lower RMSE, AIC and BIC than their homologous parameterization logistic function-based sub-models (Fig. 4). RIDt,0–1 within the soil layer ]0·0, 0·2] mm significantly increased as a function of p, regardless of the parameterization on α, β, λs in eqn (2) (Fig. 5 and Supplementary Data S3).
Fig. 4.
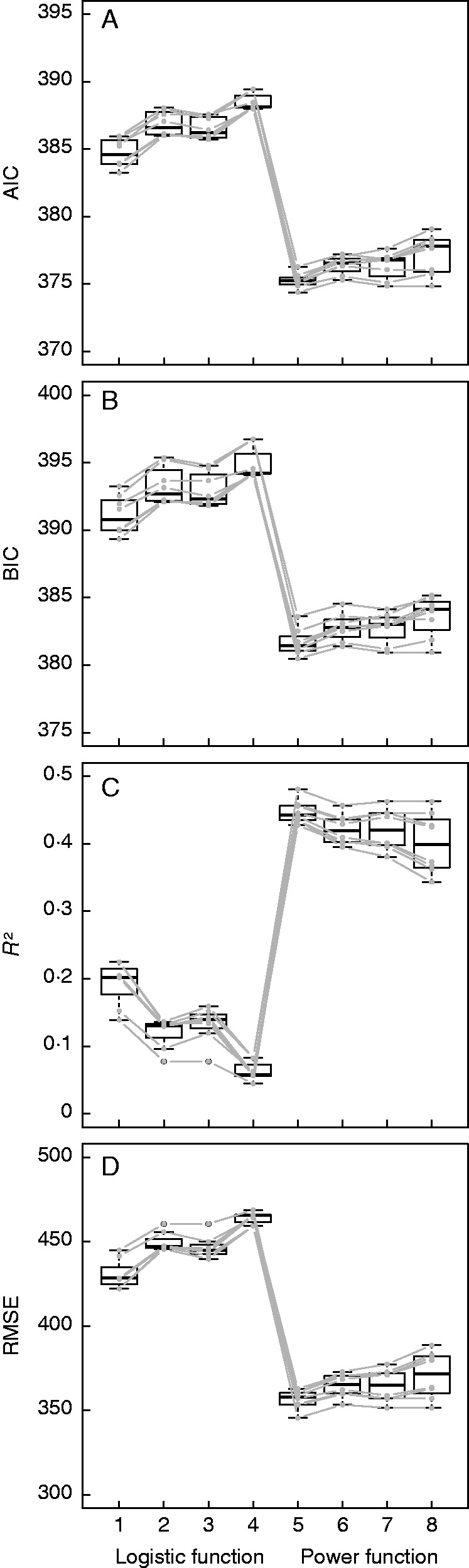
Fitting comparisons between the sub-models of spatial heterogeneity in terms of the choice of MIZ (radius = 8·0 versus 10·0 m), consideration of the effect of obstacles (included versus excluded) and type of function (logistic versus power function). In each plot, eight boxplots are numbered from 1 to 8. Plots 1–4 refer to the logistic function and 5–8 to the power function; within each group of four boxplots, from left to right: MIZ = 8·0 × exclusion of the effect of obstacles (1 and 5); MIZ = 8·0 × inclusion of the effect of obstacles (2 and 6); MIZ = 10·0 × exclusion of the effect of obstacles (3 and 7); MIZ = 10·0 × inclusion of the effect of obstacles (4 and 8). Each grey line shows the tendency of each pattern of parameterization (β; regrouping of broadleaves; λs) corresponding to eqn (2).
Fig. 5.
Fit of the two ultimately selected sub-models of spatial heterogeneity to the observed data. More details about the model comparison are available in Supplementary Data S3. p is the tree root potential. Note that the metric p differs according to the modelling approaches because of the parameter values of λs and α (Table 2).
We decided to select models having acceptable statistical index values and with all their parameters as significant. We selected one model per type of function (power versus logistic) because of the different ways that models were constructed. Both types of final sub-model selected, i.e. No. 2 for power function and No. 10 for logistic function, possessed exactly the same parameterisation of p (Supplementary Data S3). The most preferential structure for modelling p omitted the intercept β and kept the effect of species λs as effective at both nominator and denominator. The coefficient λs > 1·0 reflected the difference in RSA between the reference species P. abies and the other species. Despite the statistical significance, this effect remained less pronounced, with a value of λs close to 1·0 (Table 2). Regrouping broadleaves together with A. alba slightly improved the models (Supplementary Data S3; number 9 versus 10 and number 1 versus 2).
Table 2.
Coefficient estimate sub-model of spatial heterogeneity for the two ultimately selected sub-models of spatial heterogeneity
| No. of sub-model | Type of function | Coefficient | Estimate | Standard error | t-value |
|---|---|---|---|---|---|
| 2 | Power | λa | 1·176 | 0·239 | 4·933*** |
| α | 1·809 | 0·390 | 4·641*** | ||
| m | 3097·167 | 1064·776 | 2·909** | ||
| n | 0·429 | 0·179 | 2·394* | ||
| 10 | Logistic | λa | 1·005 | 0·105 | 9·565*** |
| α | 1·567 | 0·214 | 7·318*** | ||
| r | 24·608 | 9·978 | 2·466* | ||
| Kt | 1399·487 | 228·681 | 6·120*** |
The number of each sub-model corresponds to that in Supplementary Data S3.
Both sub-models were fitted for the case when MIZ = 8·0 m and the effect of obstacle was not considered.
***P < 0·001; **P < 0·01; *P < 0·05.
Residuals were generally well distributed, although high dispersion was detected at low values of p, especially for the logistic function-based sub-model (Fig. 5). Compared with Prémol, the measured RID for Bachat-Bouloud tended to have a higher baseline. Thus, global sub-models for both sites underestimated RIDt,0–1 for Bachat-Bouloud and overestimated RIDt,0–1 for Prémol (Fig. 5). This result was more pronounced for the logistic function.
Diameter spectrum
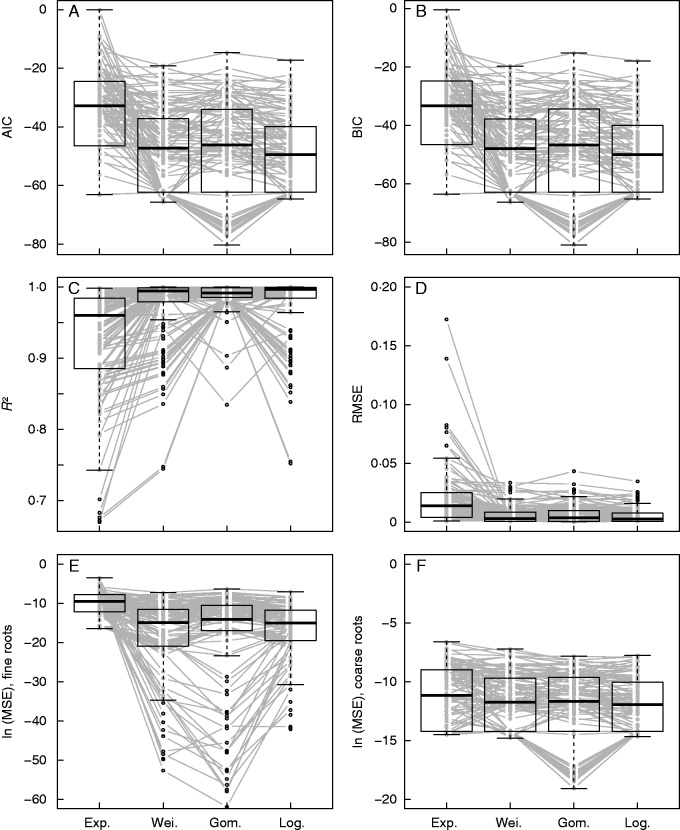
The two-parameter functions (Weibull, Gompertz and log-normal CDF) exhibited significantly better fits than the one-parameter exponential CDF (Fig. 6A–D; Table 3, Zone I). Decomposing the MSE (square of RMSE) into fine and coarse roots, we observe that the lower performance of the exponential CDF fits the fine root data (Fig. 6E). With regard to the coarse roots, no significant deterioration of fit was found with the exponential CDF compared with the other functions.
Fig. 6.
Comparison of fits between the sub-models of diameter spectrums in terms of the choice of function. Each grey line shows the tendency of the effect of the choice of functions on the same data set.
Table 3.
Distribution of the best fitted sub-models of root diameter spectrum with regard to the four functions
| Soil depth | Data for fitting | Total no. of equations | Zone I: lowest global MSE |
Zone II: lowest MSE of fine roots |
Zone III: lowest MSE of coarse roots |
|||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Exponential | Weibull | Gompertz | Log normal | Weibull | Gompertz | Log normal | Weibull | Gompertz | Log normal | |||
| ]0·0, 0·2] m | Mini-monolith | 25 | 0 | 2 | 2 | 21 | 4 | 4 | 17 | 1 | 8 | 16 |
| ]0·2, 0·4] m | Root trench | 24 | 0 | 2 | 7 | 15 | 6 | 12 | 6 | 3 | 6 | 15 |
| ]0·4, 0·6] m | Root trench | 24 | 0 | 5 | 3 | 16 | 10 | 11 | 3 | 4 | 5 | 15 |
| ]0·6, 0·8] m | Root trench | 24 | 0 | 6 | 7 | 11 | 13 | 8 | 3 | 4 | 8 | 12 |
| ]0·8, 1·0] m | Root trench | 24 | 0 | 3 | 18 | 3 | 20 | 2 | 2 | 2 | 18 | 4 |
Unit: number (No.) of equations.
Within each group (the three or four values in the same line and the same zone), the highest number of equations is underlined.
When the MSE is decomposed into fine roots (Zone II) and coarse roots (Zone III), only the three two-parameter functions (i.e. Weibull, Gompertz and log-normal CDFs) are compared.
Concerning the three two-parameter functions, the log-normal CDF usually performed better than the other functions when the soil depth was <0·8 m. It appeared that the log-normal CDF was most frequently the best function (Table 3, Zone I). This suitability was mainly due to a better fit of this function for coarse roots (Table 3, Zone III). For fine roots, the log-normal CDF was not better than the Weibull or Gompertz CDF (Table 3, Zone II). The log-normal CDF fitted a ‘round shoulder’ type of diameter spectrum, with a gradual saturation of Cd when ≥0·99 (Fig. 7A). The Gompertz CDF was the best function to fit the ‘angular shoulder’ type of diameter spectrum [i.e. Cd close to ≥0·99 up to the upper root diameter boundary (d) = 2 mm] or the ‘shoulderless’ type (i.e. Cd close to ≥0·99 until d = 1 mm) (Fig. 7B). Thus, the Gompertz and Weibull CDFs were more efficient in fitting the root diameter spectrum for deep depths, especially the layer ]0·8, 1·0] m, where the diameter spectrum was mainly of the angular shoulder or shoulderless type. As a consequence, we advise the use of the log-normal CDF for predicting diameter spectrum when Cd is <0·99 for d = 1 mm and the Gompertz CDF for predicting diameter spectrum when Cd is ≥0·99 for d = 1 mm.
Fig. 7.
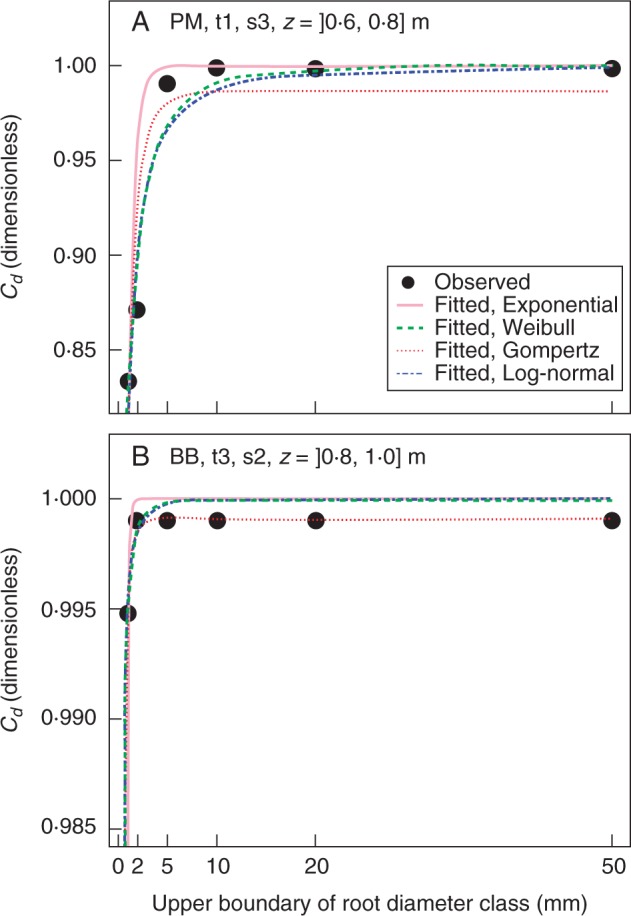
Two cases of fit of root diameter spectrum using four types of function. Note the different graduation of the y-axis in (A) and (B). In this study, the maximum cumulative relative RID was set to 0·999 instead of 1·000, as we were not certain whether the maximum sampled root diameter class ]20, 50] mm was the maximum in reality. The log-normal and the Gompertz CDF achieved the best fit in (A) and (B), respectively.
The two coefficients in both the log-normal and the Gompertz CDF exhibited significantly negative linear correlations and this result was more pronounced for the Gompertz CDF (Supplementary Data S3). Soil depth had a significant effect on the variation of the coefficients, but only σ showed a clear decreasing trend with soil depth (Supplementary Data S3).
Vertical profile
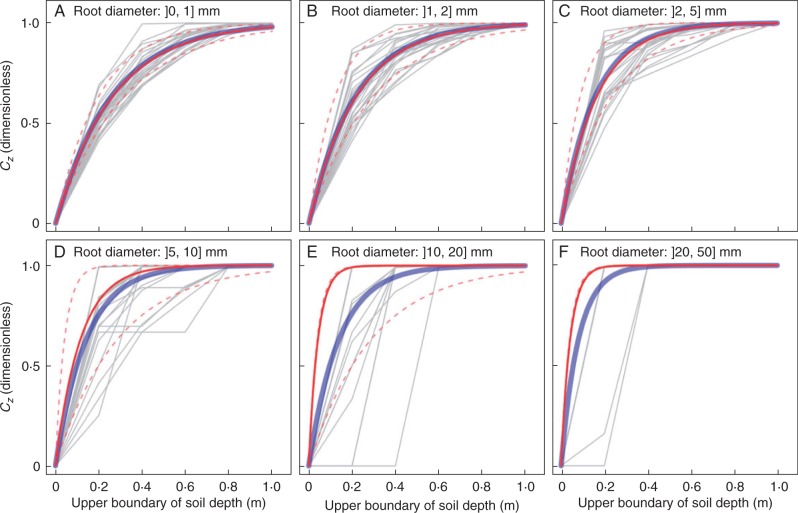
The increment in Cz decreased with increasing soil depth due to the lower root density at deeper soil layers. The quality of model fit deteriorated at higher root diameter classes, as R2 tended to be more dispersed and smaller with increasing root diameter (Fig. 8A). Root diameter significantly affected the value of ε (Fig. 8B) and the shape of the vertical profile (Fig. 9). Coarse roots were more concentrated in shallow soil layers (Fig. 9C–F), which explains why ε was higher for fine roots (Fig. 8B). Variation in the curve shape was high within each of the root diameter classes and cannot be explained by either the effect of site or that of p (data not shown). When root diameter was ≤5 mm, curves of global model per root diameter class almost overlapped with those using median ε (Fig. 9A–C). When root diameter was >5 mm, global-model curves performed better than median-ε curves, as the former better approached the observed data (Fig. 9D–F). Therefore, we selected the six global models for each root diameter class, with their ε plotted in Fig. 8B.
Fig. 8.
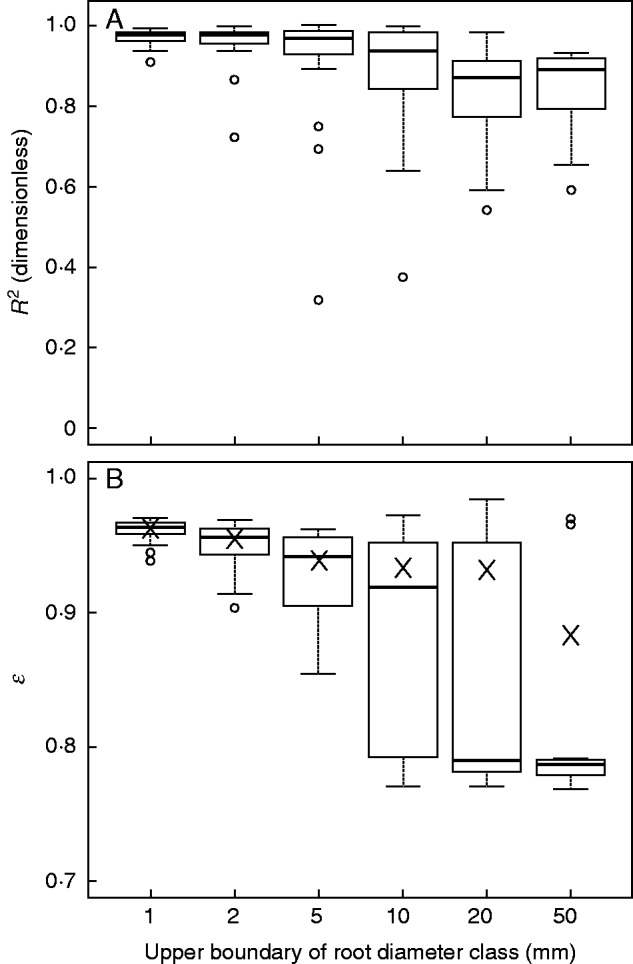
Fit comparisons of the sub-models of vertical profile between different classes of root diameter. Boxplots in (A) and (B) show the quantiles of R2 and ε of the one-curve-per-replicate fits, respectively (Nf = 24). In (B), crosses denote the value of ε for the global fits to all the root data within one diameter class; hollow points denote outliers. ε is the coefficient of the root profile shape. The closer ε approaches 1, the more the roots tend to be less concentrated at the soil surface.
Fig. 9.
Fitted (coloured curves) and observed (grey curves) values for the sub-model of vertical profile for different classes of root diameter. In each figure, there are four tracked fitted curves, including one global fit to all the root data within one diameter class (thick solid curve in blue) and three local one-curve-per-replicate fits (Nf = 24): the 10th quantile (upper thin dashed curve in red), median (medium solid curve in red) and 90th quantile (lower thin dashed curve in red) of ε.
Validation with non-fitted data
In general, the validation of each sub-model indicated that all sub-models of ChaMRoots had good fits (Supplementary Data S3). The sub-model of spatial heterogeneity had a more robust performance at higher p (Supplementary Data S3). For the sub-model of diameter spectrum, the preference for CDF (log-normal versus Gompertz) was well identified by soil depth. Despite a high level of data dispersion, diameter spectrum curves were quite evenly distributed at both sides of the predicted data when the log-normal CDF was used (Supplementary Data S3). The performance of the sub-model of vertical profile appeared ideal for roots in diameter classes ]0, 1] and ]1, 2] mm, but was less robust for the remaining root diameter classes (Supplementary Data S3).
DISCUSSION
Modelling algorithm for the first sub-model: spatial heterogeneity
The development of the parameter ‘tree root potential’, p, was highly relevant for the semi-mechanistic modelling of root distribution. RID increased with p in the top 20 cm of soil, thus demonstrating the validity of this approach. The use of p allowed us to adopt the classical approach used in previous ARB models, i.e. root density was based on both tree size and distance from the trunk. Additionally, p allowed us to take into account two sorts of biotic interaction between plants:
tree interception: roots at a given point are more influenced by immediate adjacent trees than by those at a distance. Despite the absence of hard data, ARB models focusing on an individual tree, support such a hypothesis, although they do not explicitly consider it at the forest scale.
root crossing: adjacent plants can extend and cross their roots in their shared soil environment (O’Brien et al., 2007; Gao et al., 2010).
Root crossing does not necessarily lead to a greater root density. In this study, we assumed that trees of the same species and size possess the same shape of p–distance curves. But trees close to each other might not have an increased root density at the mid-point between the trees, because of increased competition between roots for water and nutrients. For example, Ammer and Wagner (2002) found that root density of a single tree varies between closed and open canopies. In ChaMRoots, introducing the concept of production efficiency (E) avoids the over-estimation of root density for high values of p, because E declines with increasing p due to the presence of too many eligible individual trees. Therefore, the interaction between trees, although not explicitly considered in p, is implicitly involved in E. The conception of p and E in our study, especially the p and E based on the logistic function, is comparable with the metric G, i.e. plant individual fitness, in Gersani et al. (2001) and O’Brien et al. (2007). These authors hypothesized that tree root development is controlled by trade-offs between the cost of producing roots and benefits in nutrient uptake by roots. Here, root development is hypothesized to be a trade-off between root production and environmental limits.
When we compared the two types of sub-models of spatial heterogeneity, the power function-based sub-model generated a better fit than that based on the logistic function. Nevertheless, the latter is more ecologically meaningful and has the potential to be more easily applied to other situations. Once p increases, the two sub-models limit the growth of RID in different manners: the power function alone decreased the increment of root density at higher p, while the logistic function gave an asymptote of root density. We suggest using both sub-models for RID estimation, but preferentially choosing the power function for dense forest stands (more likely to have high p) and the logistic function for low-density stands (more likely to have low p). In certain cases, e.g. when calculating the contribution of root systems to hillslope stability (Pollen-Bankhead and Simon, 2009; Schwarz et al., 2010), it is safer to underestimate root density so that the evaluation of slope stability is more conservative. In such a case, preferring a logistic function, which tends to saturate much faster (at approximately p = 0·15), would be more suitable.
The polygon method we developed in the sub-model of spatial heterogeneity differs from the methods used to estimate root density developed by Roering et al. (2003) and Müller and Wagner (2003). In the method of Roering et al. (2003), root extension of a tree was considered to be a circle and the total root impact of surrounding trees on an oval-shaped landslide scarp (i.e. a surface instead of a point) was the sum of each tree’s impact, which varied as a function of tree size and distance. The method of Müller and Wagner (2003) consisted of sampling roots using cores from the centre of a tree gap to its edge (usually the first tree at the border of the gap), rendering a pattern resembling spokes around the gap centre. Our model is more refined because it introduces more precise tree selection criteria, as well as new factors, such as the effect of species, and the interactions between trees and understorey vegetation.
Spatial heterogeneity: abiotic and biotic factors
The effects of both obstacle and competition between trees and understorey species (θ) were considered in the sub-model of spatial heterogeneity, but neither increased the significance or improved the model’s fit. We speculate that the null effect of O may be dependent on our data, in which <30 % of mini-monoliths encountered obstacles (mainly at Bachat-Bouloud forest, occasionally at Prémol). Overall, although both θ and O had a null effect in our case studies, we suggest avoiding generalizations and testing these factors when using our model with data from other sites.
Comparisons between the different forms of the sub-model of spatial heterogeneity suggested retaining MIZ = 8·0 m. MIZ should be equal or slightly inferior to the maximum extension radius (MER) of the root system of trees. Schwarz et al. (2010) found that a P. abies with DBH 30 cm had an MER of ∼5·5 m. Ammer (2000, cited by Ammer and Wagner, 2005) proposed 10·0 m as the MER for a P. abies of 60 cm DBH. The MER of P. abies roots may even reach 12 m, as found by Laitakari (1929). A meta-analysis performed by Day et al. (2010) showed that the MER of P. abies reached an asymptote of around 6·0 m when DBH was 25–30 cm. As P. abies possesses a plate-like root system, it may have had a wider lateral root extension than a tree of similar size in the other species examined in this meta-analysis. The remaining species had either heart or taproot systems. At our sites, 75 % of trees had a DBH <30 cm and only two trees possessed a DBH >60 cm. Therefore, choosing MIZ = 8·0 m appears to be suitable when using data from the literature and was also appropriate for the specific characteristics of our field site. An alternative approach for selecting trees is angle count sampling, based on the use of a relascope (Schreuder, 1993). Such an approach, which is mostly used to estimate tree basal area in forest stands, requires choosing a limiting angle that defines the maximum distance within which a tree influences a point. Compared with MIZ, such a method may potentially include trees far away from the target point as well as excluding smaller but very close trees. The MIZ approach can, nevertheless, be used in conjunction with angle count sampling to explore the relationship between the surface area of visible trees and that of the stand.
We found that RSA depended significantly on species for the two selected forms of the sub-model of spatial heterogeneity, but fitted λs values were only slightly superior to 1·0. This result suggests that the effect of the plate-like root system of P. abies was only slightly greater than that of the other species. Therefore, in heterogeneous mountain forest stands, tree position and size influence root density more, compared with species and obstacles, especially when the distance between trees is great.
Our data points remained dispersed regardless of the type of function used, especially at lower p. This result might be attributed to the effect of site (Prémol versus Bachat-Bouloud), which is not an effect that could be fully investigated in the modelling process. The most distinct difference between the Prémol and Bachat-Bouloud sites concerns relative densities and proportions of species, i.e. there were more P. abies and almost no F. sylvatica at Bachat-Bouloud, and total stem density at Prémol was higher. In ChaMRoots, the effect of site was interpreted by the effect of species, root architecture and tree distance. Nevertheless, Bachat-Bouloud tended to have a higher baseline of RID compared with Prémol. This trend could be attributed to the soil fertility in shallow soil layers, as Bachat-Bouloud possessed a thicker humus layer than Prémol, potentially providing nutrients for maintaining root growth (Vanninen and Mäkelä 1999). Confirming such an effect would require the investigation of more sites along a forest productivity gradient in this region.
Diameter spectrum
Empirically, past studies have used non-linear and low-parameter distributions to model diameter spectrum, e.g. power, exponential, Rayleigh, normal, logistic, Weibull, log-normal and bimodal distributions (Anderson et al., 2007; Pollen-Bankhead and Simon, 2009; Scanlan and Hinz, 2010; Schwarz et al., 2010; Cohen et al., 2011). Results from these different models cannot be compared due to the disparity in species investigated and the use of different root diameter classes. For example, Anderson et al. (2007) proposed six-parameter bimodal functions instead of unimodal functions for the non-cumulative density of grass roots, because the interval of root diameter class was very small (0·064 mm). By using 0·2 mm as an interval of root diameter class, Scanlan and Hinz (2010) fitted a cumulative relative density for grass roots of ]0, 2] mm in diameter and found that log-normal and Weibull distributions resulted in better fits than exponential, Rayleigh, normal and logistic functions. Therefore, we adopted the following thresholds to split root diameter: 1, 2, (3), 5, 10 and 20 mm; these are frequently used for tree species (Hoffmann and Usoltsev, 2001). These heterogeneous root diameter classes can raise difficulties in modelling diameter spectrums because RID can be over-dispersed at large diameter values. This problem was not the case in our study as all the selected two-parameter CDFs provided satisfactory fits. Simultaneously, we found that the Gompertz and log-normal CDFs had complementary advantages in fitting data. The Gompertz CDF performed better in modelling angular shoulder and shoulderless diameter spectrums. This feature could be associated with its double exponential structure, which makes the curve increase rapidly to the maximum. The Gompertz model, which has been successfully applied in life sciences for modelling human mortality (Gompertz, 1825) and tumour growth (Laird, 1964), has thus also demonstrated strong potential for modelling root distributions.
Our results showed that the evolution of diameter spectrum was more vertical than horizontal, as soil depth significantly impacted diameter spectrum, but p did not. Soil depth also affected the choice of CDF by modifying the shape of the diameter spectrum, demonstrating its importance. No significant effect of p was found on the parameters in the diameter spectrum, suggesting that the spectrum varied independently of above-ground tree positions and size. Thus, a generic equation could be used for mountain forest sites in the future.
Vertical profile
The one-parameter exponential model of Gale and Grigal (1987) facilitates comparisons between sites and studies due to its unique coefficient. However, the model fit or prediction can be significantly biased if root excavation does not attain the maximum rooting depth. Our sub-model of vertical profile for modelling the cumulative root density is slightly different from the model of Gale and Grigal (1987) due to the term zmax. This term ensures that the value of the index varies between 0 and 100. We think that it is extremely important to estimate zmax when modelling cumulative root density, because otherwise it would not be possible to determine at which soil depth Cz attains 1·0.
Many studies have adopted the one-parameter exponential model for modelling cumulative root density at a continental scale (e.g. Jackson et al., 1996; Smart et al., 2006; Tao et al., 2009) and at local site scales (e.g. King et al., 2003; Moreno et al., 2005; Pollen-Bankhead and Simon, 2009; Meinen et al., 2009). Previous studies seldom investigated the effect of root diameter when characterizing or modelling vertical profiles, or they fitted a global curve for all roots. We found that root diameter significantly affected the vertical profile and that coarser roots were more concentrated in shallow soil layers. This result highlights the importance of taking into account root diameter in vertical profile modelling. Simultaneously, our results challenged the relevance of applying the model of Gale and Grigal (1987) at a local site scale, as our vertical profile showed drastically different shape variations at this local scale within and between root diameter classes. Moreover, the model fit tended to be poorer with increasing root diameter, suggesting the less appropriate use of one parameter models (Gale and Grigal, 1987) for very coarse roots (diameter >5 mm). This result was probably obtained because larger roots may have a more heterogeneous distribution due to their greater size and lower quantity in a population. Testing the relevance of using multiple-parameter functions for modelling a vertical profile is therefore of great interest for future studies.
Vertical profiles of plant roots can be significantly affected by functional groups (Jackson et al., 1996) or species (Kalliokoski, 2011). We showed that the effect of species on the vertical profile parameter ε could not be tested directly because the forest stands were mixed, but was included in tree potential p and the effect of site. The value of ε was only significantly different with regard to the site factor. However, this significant effect might be due to multiple reasons, e.g. species composition, tree density, and also soil properties either linked to sites themselves or a consequence of mixture of species (Rothe and Binkley, 2001). Therefore, more factors concerning species and soil characteristics should be considered in future studies in order to better explain the variation of ε.
Global structure of ChaMRoots
By combining the three sub-models of ChaMRoots, RID per class of diameter and per soil layer can be predicted. Theoretically, the algorithm used for the sub-model of spatial heterogeneity could have been applied to any class of diameter at any soil layer. The ‘three sub-models’ pattern is more adapted than the ‘one sub-model of spatial heterogeneity for all’ pattern for two reasons. Firstly, in our RID data, only the relationship between RIDt,0–1 of the upper soil layer and p was highly sensitive and thus feasible for root density prediction. This result was also found by Roberts (1976), who showed that the distance-dependent relationship was uniquely sensitive to the finest roots. Nevertheless, according to Vanninen and Mäkelä (1999), who investigated root density of Pinus sylvestris, it is more difficult to achieve a good allometric relationship with above-ground stand characteristics for very fine roots (]0, 2] mm) than for coarser roots (]2, 5] mm). This controversial point about the feasibility of modelling fine and coarse roots deserves further exploration. Besides, the ‘three sub-models’ pattern possessed significantly fewer parameters and thus was easier to calibrate. The ‘three sub-models’ approach connects and keeps each process (spatial heterogeneity, diameter spectrum and vertical profile) relatively independent, with potential future independent updates.
Limits and perspectives
Slope angle is an important factor affecting root distribution (Di Iorio et al., 2005; Chiatante and Scippa, 2006) and this might be particularly true for mountain forests with complex topography. Nevertheless, considering the effect of slope would make it necessary to take into account several factors associated with slope, including site exposition, location of the tree trunk (upslope/downslope), and position along a slope (crest, middle, toe, as this influences soil depth), thus rendering the modelling and root sampling work more complex. As this study was the first step towards modelling root distributions based on the concept of tree root potential, the effect of slope was not considered. Accordingly, our root sampling was conducted on gentle slopes (mostly <10°). With increasing interest in modelling root distribution along steeper slopes (≥20°), the impact of slope on root distribution will be explored on the basis of the existing model structure. For example, it could be feasible to weight the contribution of each tree to p by introducing parameters associated with slope angle and location of the tree trunk.
The growth of roots and their spatial distribution can also be affected by several edaphic factors [e.g. water and nutrient availability in soil, texture and compaction level (Coutts et al., 1999; Dexter, 2004)]. These factors may be spatially heterogeneous, thus resulting in patchiness. The current version of ChaMRoots can predict the gradient of root distribution in space, but cannot account for resource patchiness. Incorporating edaphic factors might thus be necessary for a more refined prediction at local scales. Nevertheless, extra soil parameters would also increase the number and cost of measurements as well as the complexity of the model. The choice of parameters for the model should be adapted according to the precision required.
Root grafting, defined as the functional union of two or several roots subsequent to their formation, occurs in many tree species, including P. abies (Külla and Lõhmus, 1999). Such a phenomenon is not considered by ChaMRoots, as we counted root tips without identifying whether a root was grafted or not. A better understanding of the mechanism and distribution of root grafting is primarily desired for heterogeneous mountain forests before it can be considered by models of root distribution.
ChaMRoots cannot predict the exact quantity of trees contributing to root density, but aims to include trees that significantly contribute to tree root potential (p). Determining the number of trees whose roots are present at a given point is therefore an important issue. Combining both in situ root excavation and molecular techniques to identify species would be highly useful to address this issue.
In our study, the data for model calibration and validation were obtained in the same plots. It would be useful to validate the model using ground truth data from other plots or even other types of forest. Unfortunately, data separating both tree and understorey species' roots and tree coordinates and dendrometric characteristics remain very scanty. Our mini-monolith techniques designed for this use should therefore be applied to other sites to improve model validation.
Conclusions
The majority of published root models have been developed at the scale of the plant individual. These models are in general not suitable for modelling the spatial distribution of root density for highly heterogeneous forests with regard to both species and environment. Alternatively, our semi-mechanistic model, ChaMRoots, focuses on the spatial distribution of root density at the tree cluster scale. Based on easy-to-measure characteristics, simple forest inventory protocols and three sub-models, we achieved a good compromise between the complexity of the case study area and that of the global model structure. Overall, ChaMRoots was a powerful tool for simulating root distribution at the scale of the forest ecosystem. In terms of model principles, structure and algorithms, ChaMRoots can be considered complementary to the state-of-art of modelling of root spatial distribution.
SUPPLEMENTARY DATA
Supplementary data are available online at www.aob.oxfordjournals.org and consist of the following. S1: derivation of the logistic function-based sub-model Spatial Heterogeneity in ChaMRoots. S2: protocol for selecting visible trees and outcomes of the application to the forest data collected from the French Alps. S3: supplementary table and figures giving details of model comparison, correlation between coefficients and model validation.
ACKNOWLEDGEMENTS
This study was financed by ARANGE project (FP7 Theme KBBE. 2011.1.2-07). The UR BEF is supported by the French National Research Agency through the Laboratory of Excellence ARBRE (ANR-11-LABX-0002-01) and the project QLSPIMS. We thank ONF and Chamrousse Mairie for their authorization of root sampling and support in site selection. We are grateful to many colleagues for their help with field and laboratory work and logistics: B. Courbaud (IRSTEA), Lu Feng (CIRAD), M. Foulonneau (USMB), C. Gadenne (AgroParisTech), M. Genet (INRA), H. Géraud (CIRAD), C. Jourdan (CIRAD), F.-X. Mine (ISARA), J. Nespoulous (INRA) and H. Rey (CIRAD). Finally, we thank H. Vogt-Schilb (WOAINI), Huaxiang Zhu (IRSTEA) and Wentao Chen (UGA) for their inspiring comments throughout the modelling study.
APPENDIX
Abbreviations and symbols
| Name | Meaning |
|---|---|
| Abbreviations used in the text | |
| AIC | Akaike information criterion |
| ARB | Allometric relationship-based (model) |
| BIC | Bayesian information criterion |
| CDF | Cumulative distribution function |
| DBH | Tree stem diameter at breast height (1·30 m) |
| MER | Maximum extension radius |
| MIZ | Maximum root inclusion zone |
| MSE | Mean square error |
| RID | Root interception density |
| RLD | Root length density |
| RSA | Root system architecture |
| RMSE | Root mean square error |
| Expressions used in equations | |
| a | Slope of the linear correlation between RIDt,1–5 and RIDt,0–1 |
| b | Intercept of the linear correlation between RIDt,1–5 and RIDt,0–1 |
| Cd | Cumulative frequency of root interception density from the finest roots to those of class of root diameter d mm (dimensionless) |
| Cz | Cumulative frequency of RID from ground surface to the soil depth z (dimensionless) |
| Di | Horizontal distance from the tree centre to the target point (m) |
| d | Upper boundary of root diameter class (mm) |
| E | Production efficiency (no. of roots / potential of trees to grow roots at a given point in the soil) |
| e | Subscript standing for a tree individual e |
| g | Basal area of tree i at height 1·3 m (m2) |
| K | Maximum RID0–1 of both tree and understorey species that the soil can support |
| Kt | Maximum RID0–1 of tree roots that the soil can support |
| k | Number of parameters in the model |
| L | Maximized value of the likelihood function for the estimated model |
| m | Coefficient of the power function, sub-model of spatial heterogeneity |
| Ne | Number of effective trees around the target point (number of trees) |
| Nf, Nv | Number of dataset used for model fitting and crossed validation and validation, respectively |
| Ninside, Noutside | Number of mini-monoliths situated inside and outside of tree canopies, respectively |
| No | Number of observations within each model fit |
| Ns | Number of tree species |
| n | Coefficient of the power function, sub-model of spatial heterogeneity; when it occurs as a subscript it stands for sequence of mini-monolith |
| Oi | Absence of emerged obstacles on the ground between the target point and tree i, either binary (1, 0) or unique (0) value (dimensionless) |
| Pt, Pu | Percentage of root density of tree and understorey species in total root density (%) |
| PTI, PG | Percentage of root density from tree species at tree islands and gaps (%) |
| p | Metric describing the potential of trees to grow roots at a given point in the soil. The term ‘tree root potential’ will be used below. |
| pi, pi,s | Tree root potential of tree i or tree i of species s |
| pp, pa, pb | Tree root potential of Picea abies, Abies alba and broadleaves (mainly composed of Fagus sylvatica) |
| ps | Generic symbol standing for pp, pa, pb (subscript s denotes species p, a or b) |
| R2 | Coefficient of determination (dimensionless) |
| RIDt,x–y | Measured root interception density of tree roots in the class of root diameter ]x, y] mm. |
| RIDt,0–1, | Measured and estimated root interception density of tree species of the diameter class ]0, 1] mm |
| RIDu,0–1, | Measured and estimated root interception density of understorey species of diameter class ]0, 1] mm |
| RLDt,0–1, RLDu,0–1 | Measured root length density of tree and understorey species of diameter class ]0, 1] mm |
| r | Average branching rate for the production of RID0–1 |
| s | Subscript standing for a species |
| t | Subscript standing for trees |
| U | Intermediary variable in the logistic function based sub-model of spatial heterogeneity |
| u | Subscript standing for understorey species |
| x, y | Lower and upper boundaries of diameter class (mm) |
| ı, Yi | Predicted and observed indicators |
| z | Upper boundary of depth of soil layer (m) |
| zmax | Maximum soil depth (m) |
| Symbols used in equations | |
| α | Coefficient toward Di to model tree root potential (index), sub-model of spatial heterogeneity |
| β | Coefficient toward Di, to model tree root potential (intercept), sub-model of spatial heterogeneity |
| γ | Coefficient of the Weibull cumulative distribution function (scale), sub-model of diameter spectrum |
| δ | Coefficient of the Gompertz cumulative distribution function (scale), sub-model of diameter spectrum |
| ε | Coefficient of the root profile shape, sub-model of vertical profile |
| ζ | Coefficient of the exponential cumulative distribution function, sub-model of diameter spectrum |
| η | Coefficient of the Gompertz cumulative distribution function (shape), sub-model of diameter spectrum |
| θ | Coefficient of competitiveness of understorey species' roots compared with tree roots, sub-model of spatial heterogeneity |
| κ | Coefficient of the Weibull cumulative distribution function (shape), sub-model of diameter spectrum |
| λp, λa, λb | Specific coefficients of root potential for Picea abies, Abies alba and broadleaves (mainly composed of Fagus sylvatica), sub-model of spatial heterogeneity |
| λs | Generic symbol standing for λp, λa, λb (the subscript s denotes species p, a or b), sub-model of spatial heterogeneity |
| μ | Coefficient of the log-normal cumulative distribution function (location), sub-model of diameter spectrum |
| σ | Coefficient of the log-normal cumulative distribution function (scale), sub-model of diameter spectrum |
| φs | Specific coefficients of root potential for Picea abies, Abies alba and broadleaves (mainly composed of Fagus sylvatica), and the subscript s that denotes species can be p, a or b, sub-model of spatial heterogeneity |
LITERATURE CITED
- Ammer C. 2000. Untersuchungen zum Einfluss von Fichtenaltbeständen auf die Entwicklung junger Buchen. Aachen: Shaker. [Google Scholar]
- Ammer C, Wagner S. 2002. Problems and options in modelling fine root biomass of single mature Norway spruce trees at given points from stand data. Canadian Journal of Forest Research 32: 581–590. [Google Scholar]
- Ammer C, Wagner S. 2005. An approach for modelling the mean fine-root biomass of Norway spruce stands. Trees: Structure and Function 19: 145–153. [Google Scholar]
- Anderson T, Starmer W, Thorne M. 2007. Bimodal root diameter distributions in Serengeti grasses exhibit plasticity in response to defoliation and soil texture: implications for nitrogen uptake. Functional Ecology 21: 50–60. [Google Scholar]
- Böhm W. 1979. Methods of studying root systems. Berlin: Springer. [Google Scholar]
- Burnham KP, Anderson DR. 2002. Model selection and multimodel inference: a practical information-theoretic approach, 2nd edn. New York: Springer. [Google Scholar]
- Cardinael R, Mao Z, Prieto I, et al. 2015. Competition with winter crops induces deeper rooting of walnut trees in a Mediterranean alley cropping agroforestry system. Plant and Soil 391: 219–235. [Google Scholar]
- Chiatante D, Scippa GS. 2006. Root architecture: influence of metameric organization and emission. Plant Biosystems 140: 307–320. [Google Scholar]
- Chopart JL, Rodrigues S, de Azevedo MC, Medina CD. 2008. Estimating sugarcane root length density through root mapping and orientation modelling. Plant and Soil 313: 101–112. [Google Scholar]
- Cohen D, Schwarz M, Or D. 2011. An analytical fiber bundle model for pullout mechanics of root bundles. Journal of Geophysical Research: Earth Surface 116 (F3) doi:10.1029/2010JF001886. [Google Scholar]
- Coleman M. 2007. Spatial and temporal patterns of root distribution in developing stands of four woody crop species grown with drip irrigation and fertilization. Plant and Soil 299: 195–213. [Google Scholar]
- Collet C, Löf M, Pagès L. 2006. Root system development of oak seedlings analysed using an architectural model. Effects of competition with grass. Plant and Soil 279: 367–383. [Google Scholar]
- Coutts MP. 1983. Root architecture and tree stability. Plant and Soil 71: 171−188. [Google Scholar]
- Coutts MP, Nielsen CNN, Nicoll BC. 1999. The development of symmetry, rigidity and anchorage in the structural root system of conifers. Plant and Soil 217: 1–15. [Google Scholar]
- Day SD, Wiseman PE, Dickinson SB, Harris JR. 2010. Contemporary concepts of root system architecture of urban trees. Arboriculture & Urban Forestry 36: 149–159. [Google Scholar]
- Dexter AR. 2004. Soil physical quality: part I. Theory, effects of soil texture, density, and organic matter, and effects on root growth. Geoderma 120: 201–214. [Google Scholar]
- Doussan C, Pagès L, Pierret A. 2003. Soil exploration and resource acquisition by plant roots: an architectural and modelling point of view. Agronomie 23: 419–431. [Google Scholar]
- Gale MR, Grigal DF. 1987. Vertical root distributions of northern tree species in relation to successional status. Canadian Journal of Forest Research 17: 829–834. [Google Scholar]
- Gao Y, Duan A, Qiu X, et al. 2010. Distribution of roots and root length density in a maize/soybean strip intercropping system. Agricultural Water Management 98: 199–212. [Google Scholar]
- Gersani M, O'Brien EE, Maina GM, Abramsky Z. 2001. Tragedy of the commons as a result of root competition. Journal of Ecology 89: 660–669. [Google Scholar]
- Gompertz B. 1825. On the nature of the function expressive of the law of human mortality, and on a new mode of determining the value of life contingencies. Philosophical Transactions of the Royal Society of London 115: 513–583. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hertel D, Schöling D. 2011. Below-ground response of Norway spruce to climate conditions at Mt. Brocken (Germany)—A re-assessment of Central Europe's northernmost treeline. Flora 206:127–135. [Google Scholar]
- Hoffmann CW, Usoltsev VA. 2001. Modelling root biomass distribution in Pinus sylvestris forests of the Turgai Depression of Kazakhstan. Forest Ecology and Management 149: 103–114. [Google Scholar]
- Di Iorio A., Lasserre B, Scippa GS, Chiatante D. 2005. Root system architecture of Quercus pubescens trees growing on different sloping conditions. Annals of Botany 95: 351–361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- IUSS Working Group WRB, 2007. World reference base for soil resources 2006, first update 2007. World Soil Resources Reports No. 103. Rome: FAO. [Google Scholar]
- Jackson RB, Canadell J, Ehleringer JR, Mooney HA, Sala OE, Schulze ED. 1996. A global analysis of root distributions for terrestrial biomes. Oecologia 108: 389–411. [DOI] [PubMed] [Google Scholar]
- Kalliokoski T. 2011. Root system traits of Norway spruce, Scots pine, and silver birch in mixed boreal forests: an analysis of root architecture, morphology, and anatomy. PhD Thesis, Department of Forest Sciences, Faculty of Agriculture and Forestry, University of Helsinki. [Google Scholar]
- King J, Gay A, Sylvester-Bradley R, et al. 2003. Modelling cereal root systems for water and nitrogen capture: towards an economic optimum. Annals of Botany 91: 383–390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Köstler JN, Brückner E, Bibelriether H. 1968. Die Wurzeln der Waldbäume. Untersuchungen zur Morphologie der Waldbaume in Mitteleuropa. Verlag Paul Parey: Hamburg & Berlin; 284: 3–4. [Google Scholar]
- Külla T, Lõhmus K. 1999. Influence of cultivation method on root grafting in Norway spruce (Picea abies (L.) Karst.). Plant and Soil 207: 91–100. [Google Scholar]
- Laird AK. 1964. Dynamics of tumor growth. British Journal of Cancer 18,:490–502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laitakari E. 1929. Männyn juuristo. Morfologinen tutkimus. Acta Forestalla Fennica 33: 1–380. [Google Scholar]
- Mao Z, Saint-André L, Genet M, et al. 2012. Engineering ecological protection against landslides in diverse mountain forests: choosing cohesion models. Ecological Engineering 45: 55–69. [Google Scholar]
- Mao Z, Jourdan C, Bonis ML, et al. 2013. Modelling root demography in heterogeneous mountain forests and applications for slope stability analysis. Plant and Soil 363: 357–382. [Google Scholar]
- Mao Z, Wang Y, Cécillon L, et al. 2015. Characterising above- and belowground carbon partitioning in forest trees along an altitudinal gradient using area-based indicators. Arctic, Antarctic, and Alpine Research 47: 59–69. [Google Scholar]
- Maurice J, Laclau JP, Re DS, et al. 2010. Fine root anisotropy in Eucalyptus grandis plantations. Towards the prediction of root length densities from root counts on trench walls. Plant and Soil 334: 261–275. [Google Scholar]
- Meinen C, Leuschner C, Ryan NT, Hertel D. 2009. No evidence of spatial root system segregation and elevated fine root biomass in multi-species temperate broad-leaved forests. Trees: Structure and Function 23: 941–950. [Google Scholar]
- Moreno G, Obrador JJ, Cubera E, Dupraz C. 2005. Fine root distribution in Dehesas of central-western Spain. Plant and Soil 277: 153–162. [Google Scholar]
- Mulia R, Dupraz C, van Noordwijk M. 2010. Reconciling root plasticity and architectural ground rules in tree root growth models with voxel automata. Plant and Soil 337: 77–92. [Google Scholar]
- Müller K, Wagner S. 2003. Fine-root dynamics in gaps of Norway spruce stands in the Germany Ore mountains. Forestry 76: 149–158. [Google Scholar]
- van Noordwijk M, Lawson G, Soumaré A, Groot JJR, Hairiah K. 1996. Root distribution of trees and crops: competition and/or complementary. In: Ong CK, Huxley P, eds. Tree-crop interactions. Wallingford: CAB International, 319–363. [Google Scholar]
- O'Brien EE, Brown JS, Moll JD. 2007. Roots in space: a spatially explicit model for below-ground competition in plants. Proceedings of the Royal Society of London B: Biological Sciences 274: 929–935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pagès L, Vercambre G, Drouet JL, Lecompte F, Collet C, Le Bot J. 2004. Root Typ: a generic model to depict and analyse the root system architecture. Plant and Soil 258: 103–119. [Google Scholar]
- Picard N, Saint-André L, Henry M. 2012. Manual for building tree volume and biomass allometric equations: from field measurement to prediction. Rome: Food and Agricultural Organization of the United Nations; Montpellier: Centre de Coopération Internationale en Recherche Agronomique pour le Développement. [Google Scholar]
- Pollen-Bankhead N, Simon A. 2009. Enhanced application of root-reinforcement algorithms for bank-stability modeling. Earth Surface Processes and Landforms 480: 471–480. [Google Scholar]
- Roberts J. 1976. A study of root distribution and growth in a Pinus sylvestris L. (Scots pine) plantation in East Anglia. Plant and Soil 44: 607–621. [Google Scholar]
- Roering JJ, Schmidt KM, Stock JD, Dietrich WE, Montgomery DR. 2003. Shallow landsliding, root reinforcement, and the spatial distribution of trees in the Oregon Coast Range. Canadian Geotechnical Journal 40: 237–253. [Google Scholar]
- Rothe A, Binkley D, 2001. Nutritional interactions in mixed species forests: a synthesis. Canadian Journal of Forest Research 31: 1855–1870. [Google Scholar]
- Scanlan CA, Hinz C. 2010. Using radius frequency distribution functions as a metric for quantifying root systems - root radius frequency distributions. Plant and Soil 332: 475–493. [Google Scholar]
- Schenk HJ, Jackson RB. 2002. Rooting depths, lateral root spreads and below-ground/above-ground allometries of plants in water-limited ecosystems. Journal of Ecology 90: 480–494. [Google Scholar]
- Schreuder HT. 1993. Sampling methods for multiresource forest inventory. New York: Wiley. [Google Scholar]
- Schwarz M, Lehmann P, Or D. 2010. Quantifying lateral root reinforcement in steep slopes – from a bundle of roots to tree stands. Earth Surface Processes and Landforms 35: 354–367. [Google Scholar]
- Smart DR, Schwass E, Lakso A, Morano L. 2006. Grapevine rooting patterns: a comprehensive analysis and a review. American Journal of Enology and Viticulture 57: 89–104. [Google Scholar]
- Soethe N, Lehmann J, Engels C. 2006. Root morphology and anchorage of six native tree species from a tropical montane forest and an elfin forest in Ecuador. Plant and Soil 279: 173–185. [Google Scholar]
- Stokes A, Atger C, Bengough AG, Fourcaud T, Sidle RC. 2009. Desirable plant root traits for protecting natural and engineered slopes against landslides. Plant and Soil 324: 1–30. [Google Scholar]
- Tao F, Yokozawa M, Zhang Z. 2009. Modelling the impacts of weather and climate variability on crop productivity over a large area: a new process-based model development, optimization, and uncertainties analysis. Agricultural and Forest Meteorology 149: 831–850. [Google Scholar]
- van Noordwijk M, Brouwer G, Meijboom F, do Rosario G, Oliveira M, Bengough AG. 2000. Trench profile techniques and core break methods. In: Smit AL, Bengough AG, Engels C, Van Noordwijk M, Pellerin S, Geijn Van der, eds. Root methods: a handbook. Berlin: Springer, 211–233. [Google Scholar]
- Vanninen P, Mäkelä A. 1999. Fine root biomass of Scots pine stands differing in age and soil fertility in southern Finland. Tree Physiology 19: 823–830. [DOI] [PubMed] [Google Scholar]
- Vogt KA, Vogt DJ, Palmiotto PA, Boon P, O’Hara J, Asbjornsen H. 1996. Review of root dynamics in forest ecosystems grouped by climate, climatic forest type and species. Plant and Soil 187: 159–219. [Google Scholar]
- Zianis D, Muukkonen P, Mäkipää R, Mencuccini M. 2005. Biomass and stem volume equations for tree species in Europe. Silva Fennica Monographs, Vol. 4. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.