Validation of an inexpensive and accurate mathematical method to measure long-term changes in free-living energy intake^,

Abstract

Background: Accurate measurement of free-living energy intake (EI) over long periods is imperative for understanding obesity and its treatment. Unfortunately, traditional methods rely on self-report and are notoriously inaccurate. Although EI can be indirectly estimated by the intake-balance method, this technique is prohibitively labor-intensive and expensive, requiring repeated measures of energy expenditure via doubly labeled water (DLW) along with multiple dual-energy X-ray absorptiometry (DXA) scans to measure changes in body energy stores.

Objective: Our objective was to validate a mathematical method to measure long-term changes in free-living energy intake.

Design: We measured body weight and EI changes (ΔEI) over 4 time intervals by using the intake-balance method in 140 individuals who underwent 2 y of caloric restriction as part of the Comprehensive Assessment of Long-term Effects of Reducing Intake of Energy study. We compared the ΔEI values calculated by using DLW/DXA with those obtained by using a mathematical model of human metabolism whose only inputs were the initial demographic information and repeated body weight data.

Results: The mean ΔEI values calculated by the model were within 40 kcal/d of the DLW/DXA method throughout the 2-y study. For individual subjects, the overall root mean square deviation between the model and DLW/DXA method was 215 kcal/d, and most of the model-calculated ΔEI values were within 132 kcal/d of the DLW/DXA method.

Conclusions: Accurate and inexpensive estimates of ΔEI that are comparable to the DLW/DXA method can be obtained by using a mathematical model and repeated body weight measurements. This trial was registered at clinicaltrials.gov as NCT00427193.

INTRODUCTION

The inability to accurately measure free-living energy intake (EI)⁵ has been called the “fundamental flaw in obesity research” (1). Traditional measurements of EI rely on self-reports that are notoriously inaccurate and may be insufficient for drawing scientific conclusions (2–4). Several technologies are under development for self-tracking food intake, including remote food photography (5, 6) as well as devices that count bites (7, 8) or measure chewing and swallowing (7). However, continuous tracking of diet by using such technologies over extended time periods is likely to be onerous and impractical and will still rely on self-report to some extent. Furthermore, such methods are likely to influence food intake behavior itself and therefore have limited ability to ascertain the independent effects of a weight loss intervention. Therefore, new methods that accurately measure EI noninvasively over extended time periods are greatly needed.

An indirect means of measuring EI is called the intake-balance method and involves using the energy balance equation to infer mean EI over a given time period by measuring the corresponding changes in energy expenditure (EE) and body energy stores (ES) (9, 10). In particular, measurements of EE changes can be obtained by using the doubly labeled water (DLW) method repeatedly over the period of interest, and changes in body ES can be measured by using multiple dual-energy X-ray absorptiometry (DXA) scans (9). Assuming that the individual measurements of EE and ES are unbiased, the intake-balance (DLW/DXA) method is theoretically sound and provides accurate calculations of mean EI over extended time periods. However, the DLW/DXA method is prohibitively labor-intensive, is expensive, and requires specialized training and equipment.

Based on the energy balance principle, mathematical models of human metabolism and body composition dynamics have been suggested as an inexpensive and simple alternative to the DLW/DXA approach, but such methods have been validated only in small numbers of subjects over relatively brief time periods (11–18). Here, we validated the EI changes calculated by a popular mathematical model of human body weight dynamics from the National Institute of Diabetes and Digestive and Kidney Diseases (NIDDK) (14, 16) by using repeated DLW/DXA measurements collected over 2 y of caloric restriction in 140 free-living subjects participating in the Comprehensive Assessment of Long-term Effects of Reducing Intake of Energy (CALERIE) study (19–21).

METHODS

Description of the data

We investigated EI changes in 140 free-living subjects who completed 2 y of a prescribed diet aiming to achieve 25% caloric restriction as part of the CALERIE study that began in May 2007 and ended in November 2012 (20, 21). Energy requirements were established from a pair of baseline DLW measurements of free-living EE in the month before the onset of caloric restriction. Subjects included men and women between 21 and 51 y of age with BMIs (in kg/m²) ranging from 21 to 29. Psychologists and nutritionists provided extensive counseling to promote diet adherence. In addition to baseline measurements, DLW was used to assess EE at months 6, 12, 18, and 24. DXA measurements were taken twice at baseline, twice at month 6, and once at months 12, 18, and 24. Body weight measurements were taken at months 1, 3, 6, 9, 12, 18, and 24. A sufficient number of body weight, EE, and body composition measurements were available to calculate ΔEI for 135 subjects over weeks 0–26, 125 subjects over weeks 26–52, 117 subjects over weeks 52–78, and 115 subjects over weeks 78–104.

Calculating ΔEI by using the intake-balance method

When body weight is not changing, EI is in balance with EE. However, during weight change, the mean EI can be approximated as the sum of the mean EE and the mean rate of change in body ES, ΔES, over the time interval Δt (10):

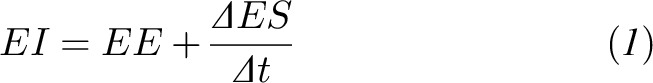The DLW procedure provides a measure of the mean rate of carbon dioxide production over some period of time, usually 1–2 wk, which can then be translated into the mean EE over this period by using assumptions about the respiratory quotient (22). To measure the mean EE over a more extended time period, repeated doses of DLW must be provided, and we assumed that the EE during the unmeasured intervening periods was equal to the mean of the measured EE immediately before and after the period. Changes in ES over each period were calculated by measuring fat mass (FM) and fat-free mass (FFM) changes and weighting these measurements by their respective energy densities (9):

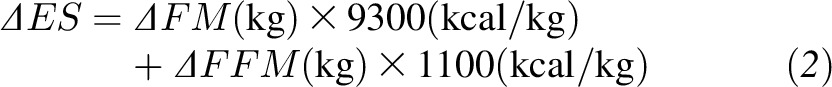We used the DXA data along with equation (2) to calculate the change in ES from baseline. The corresponding changes in EI from baseline, ΔEI, were calculated by subtracting the baseline energy requirement from the EI determined from equation (1).

The Supplemental Materials provide an estimate of the CI associated with the DLW/DXA method for individual subjects as determined by using standard methods for evaluating propagation of measurement uncertainties (23). To determine the uncertainty associated with the mean EE calculation, we assumed a CV of 5% for each DLW measurement (24). In determining the uncertainty of the ΔES calculation, we assumed a CV of 1% associated with each DXA measurement of fat mass (25–27).

Mathematical modeling to calculate ΔEI by using repeated body weight measurements

As previously described (14), all mathematical models of body weight dynamics can be linearized and solved for ΔEI as a function of body weight and its rate of change as follows:

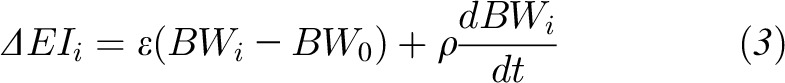The inputs to the model were the change in body weight from baseline over each interval, 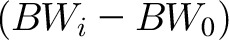, and the moving average of the measured body weight time course was used to calculate the rate of change in body weight over each interval, dBW_i/dt. The interval length was t = (N − 1)*T, where N was the number of body weight measurements per interval and T was the number of days between measurements. As described in the Supplemental Materials, we used the initial age, sex, and height, along with an assumed initial free-living physical activity level ∼1.6, to calculate the linearized model parameters for each subject (mean ± SD): ρ = 8840 ± 450 kcal/kg was the effective energy density associated with the change in body weight, and ε = 25.8 ± 1.0 kcal/kg/d was the change in EE per unit body weight change. All mathematical model parameters (Supplemental Table 1) were previously determined and were not adjusted to fit the ΔEI data. In other words, a favorable comparison of the model-predicted ΔEI values with those determined by using the DLW/DXA method constitutes a validation of the model. Details are described in the Supplemental Materials along with MATLAB code to run the model.

Statistical methods

For each individual subject, we evaluated the differences between the ΔEI values calculated by the model and the DLW/DXA method over 4 time intervals during the 2-y study. Agreement between the methods for individual subjects was quantified by the root mean square (RMS) deviation between the methods and the limits of agreement defined as the mean difference between the methods ± 1.96 × SD, where SD was the SD of the differences. Comparisons between mean ΔEI values obtained by using the model and DLW/DXA methods were performed by using paired, 2-sided t tests. Pearson correlation coefficients, r, were computed between pairs of calculated ΔEI values for individual subjects, and the significance of these correlations was computed by calculating the test statistic 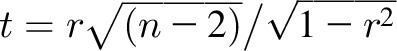, where n is the number of pairs of ΔEI values, and we assumed that this test statistic was t-distributed. It is well known that the Pearson correlation coefficient relating 2 variables is expected to underestimate the actual correlation when there is substantial measurement uncertainty in the variables. This phenomenon is called “attenuation of correlation,” and we used Spearman’s method (28) to obtain corrected correlation coefficients, r_s, between model and DLW/DXA calculations of ΔEI based on the estimated uncertainties of both methods (see the Supplemental Materials).

RESULTS

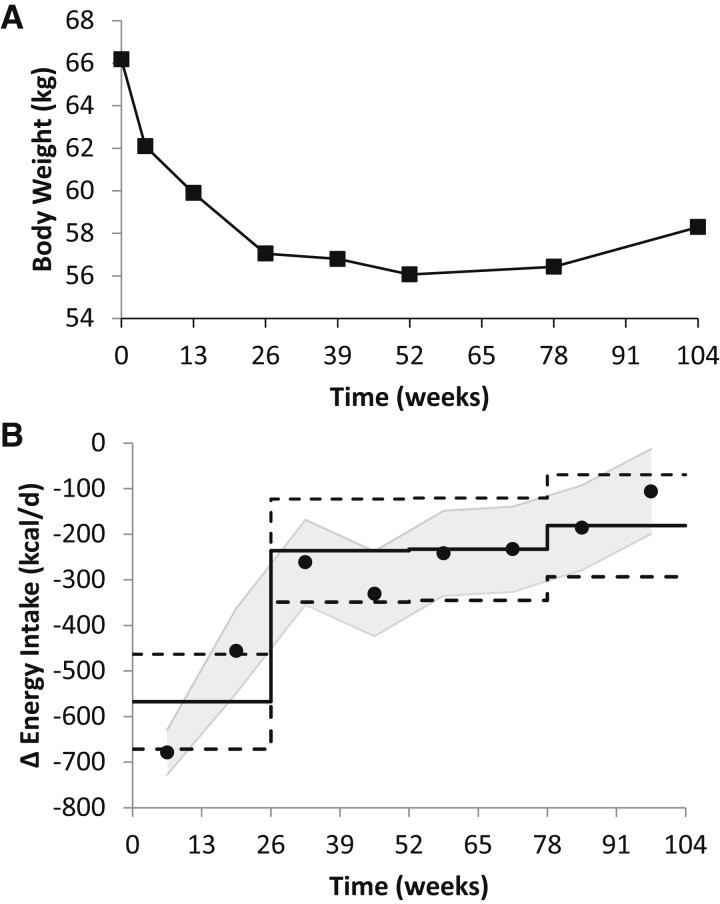
We applied the NIDDK mathematical model to estimate ΔEI over time for each CALERIE subject. An example from an individual who participated in the 2 y caloric restriction study is presented in Figure 1, with Figure 1A showing the body weight measurements that were used as model inputs and Figure 1B showing the ΔEI time course and the estimated 95% CIs of the model. The DLW/DXA-calculated ΔEI values and the estimated 95% confidence limits are also shown. In this example, the reduction in ΔEI calculated by the model and DLW/DXA method closely agreed with each other for each time segment. Note that the estimated 95% CIs for ΔEI overlap for both methods, and each spans several hundred kcal/d, indicating a modest level of precision when applied to an individual subject, even for the DLW/DXA method.

FIGURE 1.

Individual results for a 66-kg, 45-y-old woman on a 2-y calorie-restricted diet as part of the CALERIE study. (A) Body weight measurements (boxes) were used as inputs to the NIDDK mathematical model to calculate ΔEI. (B) Comparison of ΔEI and its estimated 95% CI as calculated by the NIDDK model (black dots with gray shading) and the ΔEI calculated by the DLW/DXA method (horizontal solid black line). The dashed horizontal lines indicate the estimated 95% CIs of the DLW/DXA method. CALERIE, Comprehensive Assessment of Long-term Effects of Reducing Intake of Energy; DLW, doubly labeled water; DXA, dual-energy X-ray absorptiometry; ΔEI, energy intake change from baseline; NIDDK, National Institute of Diabetes and Digestive and Kidney Diseases.

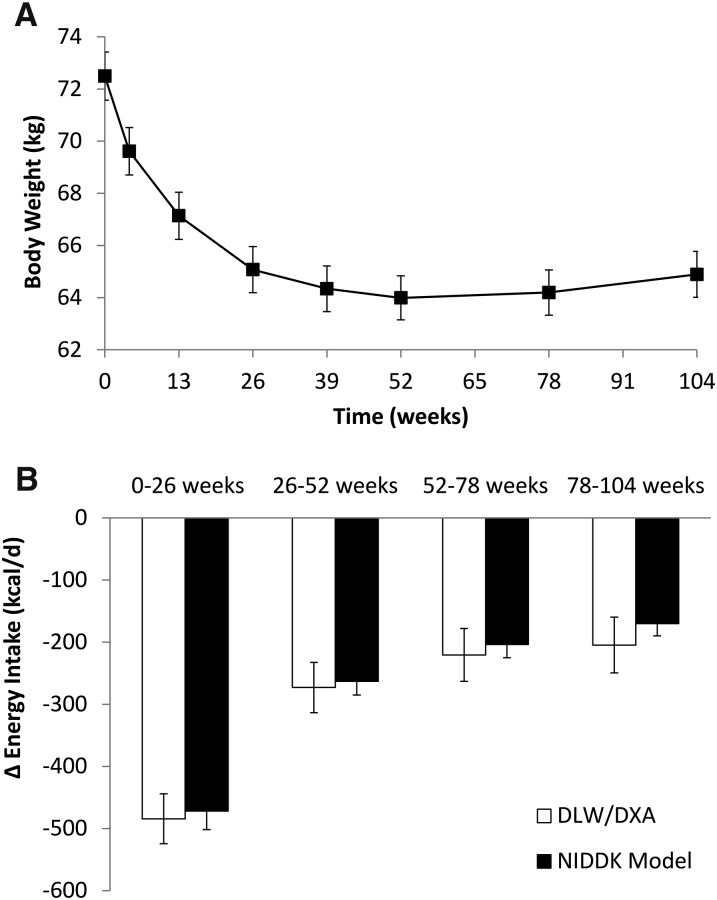
The mean body weight time course in the 112 subjects with complete data for the entire 2-y CALERIE study is illustrated in Figure 2A, and Figure 2B and Table 1 show the mean ΔEI calculated by the NIDDK model and the DLW/DXA method. The calculated mean ΔEI was not significantly different between the model and the DLW/DXA method for any of the time segments (weeks 0–26: P = 0.14; weeks 26–52: P = 0.34; weeks 52–78: P = 0.32; weeks 78–104: P = 0.11). Although the model consistently underestimated the mean reduction in EI as determined by the DLW/DXA method, the discrepancies were all <40 kcal/d.

FIGURE 2.

(A) Mean body weight time course (boxes, means ± SEMs) for the 112 subjects with complete data for the entire 2-y CALERIE study. (B) Comparison of the mean (95% CI) ΔEI calculated by the NIDDK model and the DLW/DXA method. Results from the 2 methods were not significantly different during any of the 4 time segments. CALERIE, Comprehensive Assessment of Long-term Effects of Reducing Intake of Energy; DLW, doubly labeled water; DXA, dual-energy X-ray absorptiometry; ΔEI, energy intake change from baseline; NIDDK, National Institute of Diabetes and Digestive and Kidney Diseases.

TABLE 1.

Comparison of mean ΔEI in the 2-y CALERIE study calculated by using the DLW/DXA method and NIDDK model¹

		NIDDK model
Time period	DLW/DXA method: ΔEI, kcal/d	ΔEI, kcal/d	P value2	RMS deviation, kcal/d	Limits of agreement, kcal/d	Pearson’s r (95% CI)	Spearman’s corrected rs (95% CI)
Weeks 0–26 (n = 135)	−480 ± 203	−455 ± 14	0.14	191	(−348, 397)	0.57* (0.45, 0.68)	0.69 (0.54, 0.82)
Weeks 26–52 (n = 125)	−274 ± 19	−257 ± 11	0.34	199	(−373, 407)	0.41* (0.25, 0.54)	0.59 (0.36, 0.78)
Weeks 52–78 (n = 117)	−224 ± 21	−203 ± 10	0.32	227	(−424, 466)	0.24** (0.06, 0.41)	0.36 (0.09, 0.60)
Weeks 78–104 (n = 115)	−208 ± 22	−171 ± 10	0.11	246	(−442, 514)	0.19*** (0, 0.36)	0.28 (0, 0.54)

¹The P values (*P < 0.0001, **P < 0.01, and ***P = 0.05) indicate the significance of the Pearson correlation coefficients between ΔEI values calculated via DLW/DXA and the NIDDK model. DLW, doubly labeled water; DXA, dual-energy X-ray absorptiometry; ΔEI, energy intake change from baseline; NIDDK, National Institute of Diabetes and Digestive and Kidney Diseases; RMS, root mean square.

²Paired, 2-sided t test comparing mean ΔEI values calculated via the DLW/DXA method and the NIDDK model.

³Mean ± SEM (all such values).

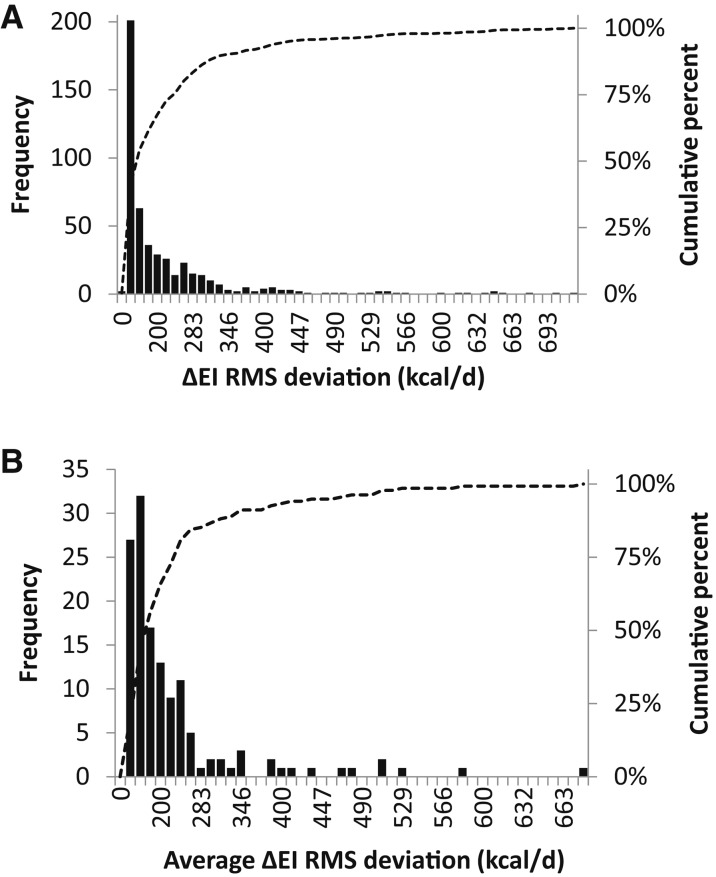
For individual subjects, the RMS deviation between the ΔEI values calculated by the model and DLW/DXA method was 215 kcal/d for all time intervals, and Table 1 presents the RMS deviation for each interval along with the limits of agreement. The distributions shown in Figure 3A indicate that most of the individual ΔEI values calculated by the model were within 132 kcal/d of the DLW/DXA method, and three-fourths were within 250 kcal/d. Averaged over all time intervals, Figure 3B illustrates that most of the individual subjects had model-calculated ΔEI values that were within 158 kcal/d of the DLW/DXA method, and three-fourths were within 230 kcal/d. The model and DLW/DXA ΔEI values were well correlated for the early measurements, but the magnitude of the correlation decreased with time while remaining statistically significant (Table 1).

FIGURE 3.

(A) Distributions of the frequency (black bars) and cumulative percentage (dotted curve) of RMS deviations between the model and DLW/DXA method for individual ΔEI values at all time intervals. (B) Distributions of the frequency (black bars) and cumulative percentage (dotted curve) of RMS deviations between the model and DLW/DXA method for ΔEI values averaged over all time intervals for each subject. DLW, doubly labeled water; DXA, dual-energy X-ray absorptiometry; ΔEI, energy intake change from baseline; RMS, root mean square.

DISCUSSION

Using only initial demographic information and repeated measurements of body weight, we assessed the validity of the NIDDK mathematical model in comparison to the DLW/DXA method for estimating free-living ΔEI during the CALERIE study. To our knowledge, the CALERIE study is unique in that it includes several repeated DLW/DXA measurements in >100 people undergoing a prolonged diet intervention resulting in weight loss (20, 21).

The mean ΔEI values calculated by the model were in close agreement with those calculated by the DLW/DXA method throughout the 2-y caloric restriction study. The mean results from both methods were within 40 kcal/d for all time intervals and were not significantly different. To put these results in the proper context, self-report estimates of EI often underestimate actual intake by several hundred kilocalories per day (2–4).

Despite the negligible bias of the model, it appeared to consistently underestimate the mean decrease in EI during caloric restriction over all time intervals as determined by the DLW/DXA method. We suspect that this was because the modeled decrease in physical activity expenditure during weight loss may have been slightly less than the mean physical activity expenditure decrease observed in these subjects. Because there appears to be a wide variation in how individuals alter their physical activity in response to diet changes, we decided not to include additional model assumptions about physical activity changes. Rather, we hypothesize that inexpensive direct measurements of physical activity in individuals (e.g., by using accelerometers and/or heart rate monitors) could be used to substantially improve model-calculated ΔEI values (see Supplemental Materials). Furthermore, more frequent body weight measurements over extended time periods will also improve the calculations.

Although the DLW/DXA method is currently the gold standard, its accuracy for calculating ΔEI may also be questioned because several assumptions of the method may introduce biases. For example, DXA may not provide accurate estimates of body fat changes during states of energy imbalance (29), which will result in a biased calculation of changes in ES. Furthermore, each DLW period estimates EE over 1–2 wk and provides no information about EE during the intervening periods between measurements. There is also the possibility that subjects’ behavior may be influenced by the DLW measurement process (especially if they know it is a measurement of their EE), and therefore the EE measurement during the DLW period may not be representative of the entire duration of the study. Future studies should aim to include more frequent EE data points that will also provide important information for further developing mathematical models.

We demonstrated that both the NIDDK model and DLW/DXA method for estimating ΔEI had a modest level of precision when applied to individual subjects in this study. The precision of the DLW/DXA method was estimated by propagation of measurement uncertainties associated with both DLW and DXA, which may be substantial for individual subjects (see Supplemental Materials). The limited precision of the DLW/DXA method does not appear to be widely appreciated, but it was comparable to the estimated precision of the model for individual subjects. The precision of the model-calculated ΔEI can be improved by use of more frequent body weight measurements as described in the Supplemental Materials (14).

Given the limited precision of both methods, their agreement at the level of individual subjects was also modest. The overall RMS deviation in ΔEI was 215 kcal/d, but most ΔEI values were within 132 kcal/d and, averaged over all time intervals, most subjects were within 158 kcal/d. Nevertheless, the limits of agreement spanned an interval of ∼800–1000 kcal/d, suggesting that any individual ΔEI value should be interpreted with caution and that model-based estimates of ΔEI cannot replace the DLW/DXA method for all purposes.

For example, baseline DLW data would be necessary for determining the absolute EI time course because the model was designed to estimate the intake changes from baseline, ΔEI, during periods of weight change. Otherwise, the substantial uncertainty of the baseline intake estimate must be added in quadrature to the ΔEI uncertainty, thereby greatly amplifying the uncertainty in the absolute EI time course. Furthermore, the model-based method is presently limited in its application to young and middle-aged adults whose EE and body composition dynamics are accurately represented by the model assumptions. Nevertheless, we suspect that the model-based method will become increasingly popular because it is several orders of magnitude less expensive than the DLW/DXA method and is also less expensive than traditional self-report measures that are known to be biased (2–4).

Over and above the obvious cost savings, there are additional advantages to using model-based calculations of ΔEI over the DLW/DXA method. Collection of DLW and DXA data can be burdensome and time-consuming for both subjects and researchers. In contrast, repeated body weight measurements are routinely performed, and the model can be used retrospectively to calculate ΔEI by using such data, as we did in the current study. Furthermore, DLW measurements are typically not available in real time because samples are often analyzed in a batch at the end of the study. In contrast, recent mobile health technologies allow for frequent, near real-time, remote measurements of changes in body weight and physical activity that can be used by our model to calculate ΔEI during the course of a diet intervention. Therefore, keeping in mind the limited precision of the method, model-calculated ΔEI values might be used to provide ongoing feedback to patients and weight management professionals regarding individual adherence to a diet prescription.

A significant limitation of the current study in its application to obesity research is that CALERIE subjects were not obese. To our knowledge, repeated DLW/DXA data taken at multiple intervals over a prolonged duration during an obesity intervention do not yet exist. Therefore, we cannot presently demonstrate the validity of the model for estimating ΔEI in people with obesity undergoing weight loss interventions. However, the model was originally built and validated to accurately represent changes in metabolism and body composition in people with obesity during controlled feeding experiments (i.e., where ΔEI was known) (16), so we are reasonably confident that the model will perform similarly well in obesity studies.