Viscosity of ring polymer melts

Abstract

We have measured the linear rheology of critically purified ring polyisoprenes, polystyrenes and polyethyleneoxides of different molar masses. The ratio of the zero-shear viscosities of linear polymer melts η_0,linear to their ring counterparts η_0,ring at isofrictional conditions is discussed as function of the number of entanglements Z. In the unentangled regime η_0,linear/η_0,ring is virtually constant, consistent with the earlier data, atomistic simulations, and the theoretical expectation η_0,linear/η_0,ring=2. In the entanglement regime, the Z-dependence of rings viscosity is much weaker than that of linear polymers, in qualitative agreement with predictions from scaling theory and simulations. The power-law extracted from the available experimental data in the rather limited range 1<Z<20, η_0,linear/η_0,ring~ Z^1.2±0.3, is weaker than the scaling prediction (η_0,linear/η_0,ring~ Z^1.6±0.3) and the simulations (η_0,linear/η_0,ring~ Z^2.0±0.3). Nevertheless, the present collection of state-of-the- art experimental data unambiguously demonstrates that rings exhibit a universal trend clearly departing from that of their linear counterparts, and hence it represents a major step toward resolving a 30-year old problem.

Ring polymers are fascinating macromolecules with significant implications to our understanding of polymer dynamics and biological functions^1,2. In particular, their lack of chain ends assures that their stress relaxation in the entanglement regime does not conform to the established mechanisms^3,4. Furthermore, melts of ring polymers are excellent models for de-swollen networks^2,5 and for several biophysical systems. DNA often comes in a cyclic form and melts of rings are relevant for understanding chromatin folding, enzymology, and protein structure stabilization^6–8.

In the 1980s there has been a significant experimental effort to study the properties of rings, starting from controlled anionic synthesis in dilute solution^9–13, focusing on melts of larger molar mass, and resulting in no consensus concerning their rheology. Whereas all agreed that ring melts had lower viscosity compared to their linear counterparts, several issues remained unsettled: how different were the viscosity and the plateau modulus of rings compared to the linear polymers, the role of trapped knots whose presence depended on the synthetic approach used (quality of the solvent)^10,13–16. Recently, it has been shown that the presence of unlinked polymer precursors (thereafter called contaminants) in the synthesis procedure had a huge impact on the rheological properties of the rings, and hence appropriate purification was necessary and accomplished with interaction chromatography at the critical condition¹⁷. Indeed, liquid chromatography at the critical condition (LCCC) represents the most reliable fractionation method to date¹⁷, yielding rings with a fraction of linear contaminants below 0.1%. Based on experiments with pure polystyrene rings, it was shown that entanglement plateau was absent and that stress relaxation was self-similar following a power-law with an exponent close to 0.4, a result consistent with predictions based on the lattice animal model of entangled rings conformation^3,8. Comparing ring rheology before and after LCCC has demonstrated the power of this technique and established it as an indispensable tool for obtaining pure experimental rings. This work left open the issue of knotting as the PS rings were synthesized in near-theta solvent conditions and the presence of some knots was unavoidable. Later however, Takano and coworkers confirmed the results of power-law relaxation of reference (3) with PS rings synthesized in good-solvent conditions ¹⁸. This suggests that knots may not affect the main rheological features, at least for moderately entangled rings. Moreover, considering the model of self-similar stress relaxation proceeding via motion of local double folds, self-knots may not affect the dynamics in a significant way³. We shall not discuss this thereafter in this work, but it remains a challenge for the future.

The extreme sensitivity of ring rheology to contamination was proven by deliberately mixing purified rings with linear chains. Experiments suggest that a contamination level of about 0.07% was sufficient to enhance the low-frequency moduli by over 50%. This result was rationalized by invoking the idea of linear chains percolation through the rings, which maximized the system’s entropy while at the same time forming a transient network. Recent simulations confirmed this extreme sensitivity, though with some quantitative disagreement ^19,20. In particular, molecular dynamics (MD) simulations involving perfectly pure unknotted rings suggested that the sensitivity is lower by about one decade. The limited experimental data due to the ultra-small amounts of samples do not allow a more accurate comparison. Nevertheless, it is evident that, despite the recent progress, there are still unsettled issues with respect to purity and dynamics of rings, as well as the dynamics of ring-linear polymer mixtures. Before tackling systematically the latter, it is clear that a consensus on the linear rheology of rings is much needed.

In this letter we address some of the challenges concerning ring polymers: (i) we test the universality of the power-law stress relaxation by using critically fractionated rings of different chemistries, which are as pure as currently possible; (ii) we study the dependence of the extracted zero-shear viscosity on molar mass; and (iii) we compare the experimental data of two polymers with two different chemistries (1,4-polyisoprene and polyethylene oxide) with published results for the third chemistry (polystyrene) as well as with predictions from modeling and molecular dynamics simulations.

Three 1,4-polyisoprene (PI) and two polyethylene oxide (PEO) linear and functionalized polymers were synthesized using anionic methods. The ring samples were synthesized in dilute solutions (hexane for PI and mixtures of THF and n-hexane for PEO). Their molecular characteristics are summarized in Table 1. Note that much lower molecular weights for PEO allow well entangled polymers due to the lower molar mass between entanglements for PEO in comparison to PI (for linear PEO is M_e=2000 g/mol while for linear PI 1,4-addition M_e=6190 g/mol)^4,21. The polydispersity index determined by SEC was always below 1.1. All rings were purified by LCCC.

Table 1.

Molecular characteristics of the ring samples

	Mw [kg/mol]	Tg, linear [°C]	Tg,ring [°C]	Z [−]	η0,linear [Pa.s]	η0,ring [Pa.s]
PI24	24	−64	−64	3.9	2255 (±11.8) at 0°C	1187 (±0.3) at 0°C
PI38	37.3	−44	−44	6.1	292000 (±2682) at 0°C	16028 (±433) at 0°C
PI81	81	−62	−62	12.9	21490 (±388.5) at 0°C	1266 (±82.5) at 0°C
PEO5	5.3	−0.5 (±0.3)	−46. 4 (±0.7)	2.6	0.072 (±0.003) at 115°C	0.018 (±0.002) at 70°C
PEO10	10.1	−14.6 (±3.1)	−53.5 (±1.1)	5	1.44 (±0.078) at 60°C	0.26 (±0.005) at 100°C
PS160	160	100	100	9.3	43240 (±236) at 170°C	2666 (±11.6) at 170°C
PS198	198	100	100	11.5	217200 (±1007) at 170°C	12750 (± 133) at 170°C
PS244	244	100	100	14.2	562553 (±3159) at 160°C	23022 (±425) at 160°C

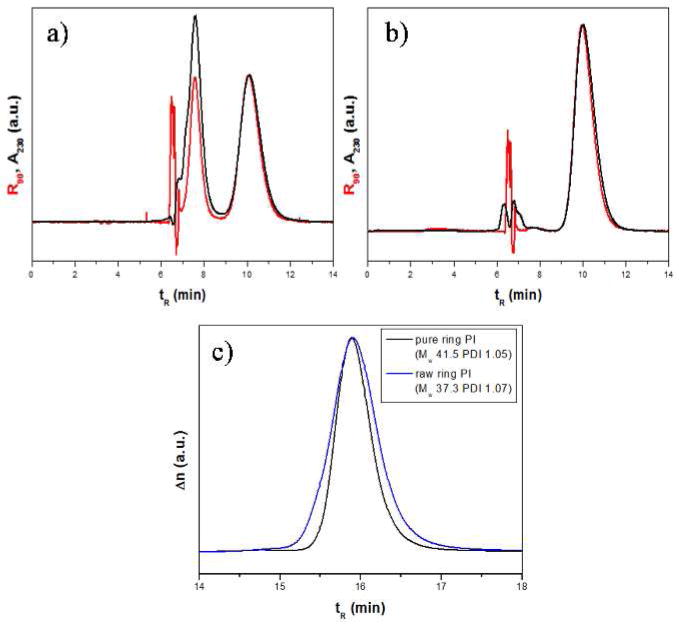
An example of this analysis is depicted in Figure 1 for PI 38000 g/mol, where the LCCC and SEC chromatograms are shown before and after the critical fractionation. In addition, we used for comparison two purified polystyrene (PS) rings synthesized in theta solvent cyclohexane, from Ref. 3, and one PS ring synthesized in good solvent tetrahydrofuran^22,23 (Me=17200 g/mol).

Figure 1.

LCCC chromatograms for ring PI 38 kg/mol before (a) and after (b) LCCC fractionation. (c) SEC chromatograms before (blue) and after (black) LCCC fractionation.

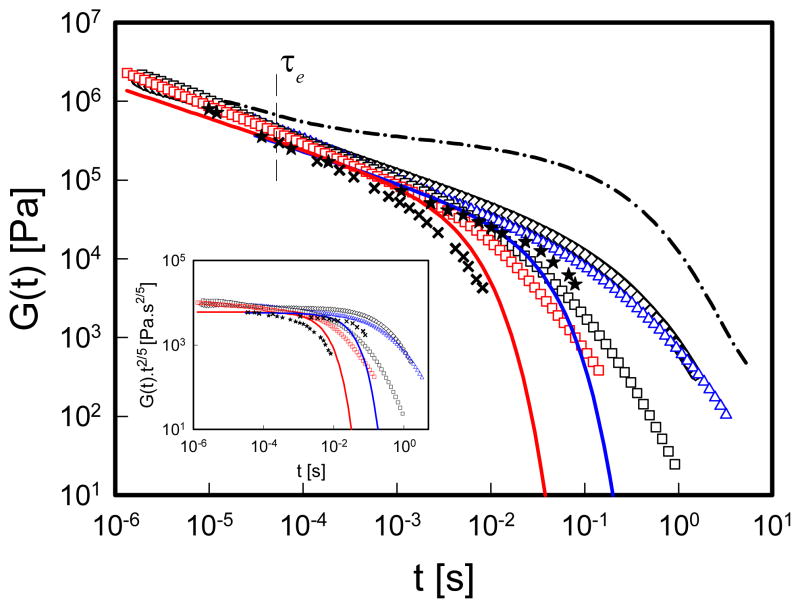
For the PI polymers it was possible to measure time-temperature superimposed (TTS) linear viscoelastic moduli as a function of shifted frequency, by using a strain-controlled ARES-2KFRTN1 rheometer (TA, USA) with homemade parallel plates of 4 mm diameter. From this data the stress relaxation modulus G(t) was extracted and is plotted in Figure 2. In the same figure we plot the PS ring data³, along with an entangled linear PI for comparison and molecular dynamic simulations data of coarse grained bead-spring ring melts²⁴. Due to the different glass transition temperatures T_g for PI and PS, the data are compared at isofrictional conditions, i.e., same distance from T_g (see also Table 1) ²⁵. In addition, a vertical shift of the PI data with respect to the PS data was performed, by the amount reflecting the ratio of the entanglement molar masses²⁶. For details in the shifting procedure of the relaxation moduli obtained by computer simulations, see Supplementary Information.

Figure 2.

Stress relaxation modulus for PI rings and PS rings at T-T_g=65°C. PI 81k ( ); PI 38k ( ); PS198k (◇); PS160k (□). The stars and the crosses are from molecular dynamic simulations on coarse grained bead-spring rings with Z≈3.6 and 14.4 from Ref. (24) (see Supplementary Information for details about the conversion of MD units into Pascal and seconds). The blue and the red lines are model prediction for PI 81k and 38k, respectively. The dash-dotted line is the relaxation modulus for PI 81k linear polymer, exhibiting an entanglement plateau. The Rouse time for entanglements τ_e, of the linear PI81k is also depicted for reference. Inset: Scaled version of the same plot, without the linear polymer data for clarity (see text for details).]

Figure 2 shows that all ring samples obey the same power law stress relaxation with a slope very close to 0.5 for over 3 decades of time, thereby confirming the universal dynamic response of moderately entangled ring polymer melts.

The predicted stress relaxation modulus³, G(t) = G_N(t/τ_e)^−2/5 exp(−t/τ_ring;) for t>τ_e, is in good agreement with data (see solid lines in Figure 2). The experimental data and MD simulations conform to the predicted power-law slope of logG(t) vs. logt within 20%, and in fact it is expected that this slope will slightly decrease as the molar mass of the ring increases (see Supplementary Information).

The inset in Figure 2 depicts the scaled relaxation modulus G(t)t^2/5 as a function of time, highlighting the extent of the power-law region for the ring polymers.

Despite the remarkable ability of the model to capture the power-law region, it does not properly describe the observed long-time relaxation. The single exponential decay expected in the terminal relaxation regime was not observed in most experiments. This could be related to traces of linear contaminants or to some degradation of the rings during measurements (the thermal treatment of the samples could result in some ring opening), which are not considered in the model and could delay the relaxation process. Of course, this influences the zero shear viscosity. For this reason we have determined the viscosities by fitting the complex viscosity curves with different methods to obtain reliable estimates and error bars (see Supplementary Information).

The semi-crystalline nature of the PEO samples prohibited measuring the entire frequency range via TTS. In this case the zero-shear viscosities at different temperatures were obtained from dynamic and steady shear measurements using a stress controlled rheometer Physica 501 (Anton Paar, Austria) as well as the ARES rheometer with parallel plates and a cone/plate geometry of 8 mm diameters and 0.166 rad. The ring viscosities were always lower than viscosities of the corresponding linear polymers. To compare at isofrictional conditions, the T_g was measured by differential scanning calorimetry and dielectric spectroscopy (Table 1). Note that for PI the difference in T_g was primarily due to microstructure²². NMR revealed 3,4-addition content of 15%, 32% and 17% for 24k, 38k and 81k, respectively. Hence, η_0,linear/η_0,ring for PI of the same molar mass does not depend on temperature. However, the difference in T_g for PEO (Table 1) was due to the different architectures. A detailed study of the dielectric and calorimetric properties of linear and ring PEOs will be presented in a future publication.

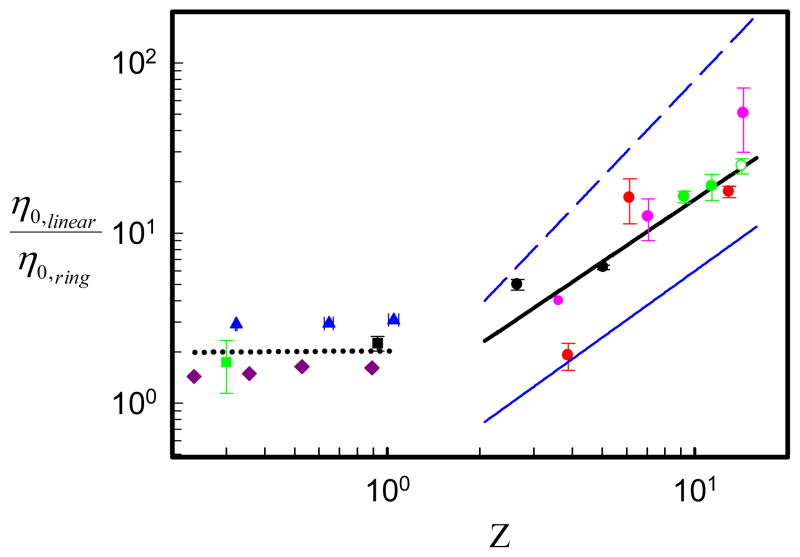
Figure 3 depicts the mean (symbols) and the standard deviation (error bars) of the ratio of isofrictional zero shear viscosities of the linear η_0,linear and ring η_0,ring polymers as a function of the number of entanglements Z. In our considerations, the entanglement molar mass is related to the plateau modulus of the linear polymer⁴.

Figure 3.

Ratio of the zero shear viscosities of linear and ring polymers as function of the number of entanglements. The black dotted horizontal line sets the theoretical value of 2 in the low-Z region. The black continuous line is the best fit of the experimental data (slope of 1.2±0.3). The continuous and dashed blue lines have slopes of 1.3 and 1.9, respectively (see text for details). ●: PEO experimental data set (Table 1); : PI experimental data set (Table 1); : PS experimental data point (Table 1)^22,23; : PS experimental data set from Ref. (3); ■: PEO experimental data point²⁷; : PS experimental data point (Table 1)²⁸; PEO experimental data set²⁹; : polyethylene (PE) atomistic simulations³⁰; : MD simulations on coarse-grained bead-spring chains²⁴.

Recent MD simulations results on coarse-grained bead-spring chains²⁴, atomistic simulations data on polyethylene (PE)³⁰, and experimental data on low-molar mass rings^27,29 are shown along with our experimental data on entangled PS, PI and PEO rings. The comparison between new and old viscosity data from literature^10,13–15 (see Supplementary information) is suggestive of the importance of LCCC in efficiently purifying rings^10,13–15. It is now clear that the new rings are characterized by much lower viscosity in the entangled regime (Supplementary Information). Moreover, within the unavoidable errors coming from the experiments, the extremely small amounts of samples and possible imperfections in ring purification (see also Supplementary material), the data are consistent and suggest universality of behavior in the examined Z range (see below). It has been shown elsewhere ^7,31 and also confirmed by our fractionation results that contamination by linear polymers increases with molecular weight. Hence, for very low molecular weight ring polymers, LCCC has the same level of success as multiple SEC. We also note that the available data from entangled PS rings synthesized in solvents of different quality^13,22 (hence with probably different number of knots per ring) are consistent within error.

At low molar masses, well below the entangled region, the viscosity of the linear polymer melt is about double the viscosity of the corresponding melt of ring, as well established ^32,33. In this region, noteworthy is the good agreement of PEO which were claimed to be very carefully fractionated ^27,29 and the atomistic simulations results on PE³⁰, although the latter are slightly above the 2 value. Moreover, PS rings fractionated via precipitational fractionation from benzene-methanol solution first³⁴ and subsequently by LCCC²⁸ show also a ratio η_0,linear/η_0,ring of 2. In the entangled regime there is a scatter of the data which is not unexpected given all issues discussed above. Nevertheless, the viscosity data of these as pure as currently possible ring polymers exhibit a universal trend marking a clear departure from the behavior of their linear counterparts, as demonstrated in Fig. 3, in contrast to the data of the 1980s (see Supplementary material). By fitting the experimental data in the entangled region we find that η_0,linear/η_0,ring ~ Z^1.2±0.3 (black continuous line in Figure 3). We note that the power-law exponent is smaller compared to that extracted from MD simulations, η_0,linear/η_0,ring ~ Z^2±0.3.²⁴

We compare our experimental data with two scaling theories: rings in the array of fixed obstacles (lattice animal model) ^3–5 and hyperscaling loopy globule for melt of rings³⁶. The main idea of the latter is that the conformation of a ring in a melt of other rings consists of self-similar loops on all length scales. Each of these loops is at entanglement threshold with loops of the same size from the same or neighboring rings. The corresponding overlap parameter is the same for loops of all length scales, according to the Kavassalis-Noolandi conjecture ³⁷. The lattice animal model predicts η_0,ring ~ N^3/2, while the hyperscaling loopy globule model predicts η_0,ring ~ N^5/3. The pure reptation model predicts η_0,linear ~ N³, while including the corrections such as tube length fluctuations yields higher effective exponent⁴ of 3.4. Therefore, there are four combinations of predictions for the ratio of viscosities of linear and ring melts ranging from 3.4−1.5=1.9 (for tube length fluctuations model of linear melts and lattice animal model for melts of rings) to 3−1.7=1.3 (for pure reptation model of linear and loopy globule model of rings). We represent this effective uncertainty of theoretical predictions by an average exponent 1.6±0.3, although its most likely value should be 3.4−1.7=1.7 (for tube length fluctuations model of linear melts and loopy globule model of rings). The blue lines in Figure 3 depict the variance of the predictions.

From the above we conclude that the available experimental data confirm the different Z-dependence of ring and linear polymer viscosity, but the extracted average scaling exponent is smaller by 0.4 (1.2±0.3 versus 1.6±0.3) compared to scaling predictions and by 0.8 compared to MD simulations (2.0±0.3)²⁴. However, more data would be required to make a truly unambiguous quantitative comparison with predictions, which means additional pure rings at many more molar masses (this is particularly important as up to Z=10 polymers are considered moderately entangled). Nevertheless, within the unavoidable uncertainty due to issues discussed (and more specifically to the likely presence of linear contaminants), the experimental results (new and recently published) represent in our opinion the current state of the art. A more rigorous study of the experimental scaling exponent will be the subject of future collaborative work.

We have presented experimental linear rheological data on as pure as currently possible ring polymers of different chemistries and molar masses. These samples exhibit a power-law stress relaxation^3,24. The predictions of G(t) based on the lattice animal model³ are in good agreement with the experimental data for about 3 decades in frequency. The deviation of the data from theoretical predictions in the terminal region may be due to minute linear contaminants, which are not accounted for in the model³, or additional ring-ring interactions, even if not seen in simulations²⁴. We have represented all experimental data in the form of η_0,linear/η_0,ring vs. Z. In the unentangled regime, linear and ring polymers follow the same scaling with molar mass. In the entangled regime, the experimental data confirm the universality of the behavior and the clearly weaker molecular weight dependence of ring viscosity as compared to linear polymers. In this respect, the issue of comparing linear and ring polymer viscosities in this range of molar masses is settled qualitatively. Given the available experimental data and related uncertainties, the experimental power law exponent of 1.2±0.3, is smaller compared to modeling predictions (1.6±0.3) and MD simulations (2.0±0.3). A reason for the slightly lower power-law exponent is the tiny amount of linear chain contaminants after the state-of-the-art LCCC purification. As already mentioned, the fraction of contaminants is expected to increase with molar mass^3,31. Even if this fraction will always be small (typically not exceeding 0.1%)³, it will result in a small increase of ring viscosity^3,20 (see also Supplementary material). This increase, which yields a decrease of the ratio η_0,linear/η_0,ring, becomes stronger with increasing molar mass and therefore increases the exponent of molar mass dependence of ring viscosity. We note in closing, that the presented data reflect the largest collection of as pure as currently possible rings. Nevertheless, despite the progress made in characterization, the role of the linear contaminants and possible stability of the formed rings, the availability of more and larger rings, as well as the presence of knots, remain formidable experimental challenges to be addressed in the future.