Abstract
We develop a Bayesian nonparametric model for a longitudinal response in the presence of nonignorable missing data. Our general approach is to first specify a working model that flexibly models the missingness and full outcome processes jointly. We specify a Dirichlet process mixture of missing at random (MAR) models as a prior on the joint distribution of the working model. This aspect of the model governs the fit of the observed data by modeling the observed data distribution as the marginalization over the missing data in the working model. We then separately specify the conditional distribution of the missing data given the observed data and dropout. This approach allows us to identify the distribution of the missing data using identifying restrictions as a starting point. We propose a framework for introducing sensitivity parameters, allowing us to vary the untestable assumptions about the missing data mechanism smoothly. Informative priors on the space of missing data assumptions can be specified to combine inferences under many different assumptions into a final inference and accurately characterize uncertainty. These methods are motivated by, and applied to, data from a clinical trial assessing the efficacy of a new treatment for acute Schizophrenia.
Keywords: Dirichlet process mixture, Identifiability, Identifying restrictions, Sensitivity analysis
1 Introduction
In longitudinal clinical trials it is often of interest to assess the efficacy of a treatment on one or more outcome processes of interest. Often the recorded outcome process is incomplete due to subject dropout; when dropout depends on the missing data, the dropout processes is nonignorable and must be modeled in order to draw valid inferences (Rubin, 1976). It is well known that the marginal distribution of a response is not, in general, identified in the presence of dropout (Little, 1993). Untestable assumptions about the process which generated the missingness are necessary to draw inferences in this setting, but often inferences are highly sensitive to the particular assumptions made (Molenberghs et al., 1997). It is desirable to assess the robustness of inferences by varying these assumptions in a principled fashion (Scharfstein et al., 1999; Vansteelandt et al., 2006; Daniels and Hogan, 2008; National Research Council, 2010). In this paper we present a Bayesian nonparametric model for conducting inference on (continuous-valued) longitudinal responses which accommodates a sensitivity analysis.
1.1 Schizophrenia Clinical Trial
Our work is motivated by a multi-center, randomized, double blind clinical trial which aimed to assess the safety and efficacy of a test drug (81 subjects) relative to placebo (78 subjects) and an active control drug (45 subjects) for individuals suffering from acute schizophrenia. The primary instrument used to assess the severity of symptoms was the Positive and Negative Syndrome Scale (PANSS) (Kay et al., 1987), a clinically validated measure of severity determined via a brief interview by a clinician. Measurements were scheduled to be collected at baseline, Day 4 after baseline, and Weeks 1,2,3, and 4 after baseline.
Let Yi = (Yi1, …, YiJ) denote the vector of PANSS scores that would have been collected had we continued to follow subject i after (potential) dropout, and let Ȳij = (Yi1, … Yij) be the history of responses through the first j visit times. J = 6 is the total number of observations scheduled to be collected. Dropout was monotone in the sense that if Yij was unobserved then Yi,j+1 was also unobserved, and we define Si = j if Yij was observed but Yi,j+1 was not (with Si = J if all data was collected). We write Vi = 1, 2, 3 if subject i was assigned to the test drug, active control, or placebo respectively. The observed data for subject i is (ȲiS, Si, Vi).
The targeted effects of interest in this study were the intention-to-treat effects
| (1.1) |
and in particular the contrasts η1−η3 and η2−η3 were of interest. Moderate dropout was observed with 33%, 19%, and 25% of subjects dropping out for V = 1, 2, 3 respectively.
Subjects dropped out for a variety of reasons including lack of efficacy and withdrawal of patient consent, and some unrelated to the trial such as pregnancy or protocol violation. The active control arm featured the smallest amount of dropout, and dropout on this arm was often for reasons that are not likely to be associated with missing response values (33% of dropout). Dropouts on the placebo and test drug arms were more often for reasons which are thought to be predictive of missing responses (100% and 82% of dropout, respectively). It is desirable to treat the different causes separately, particularly because the different treatments have different amounts of dropout and different proportions of dropout attributable to each cause.
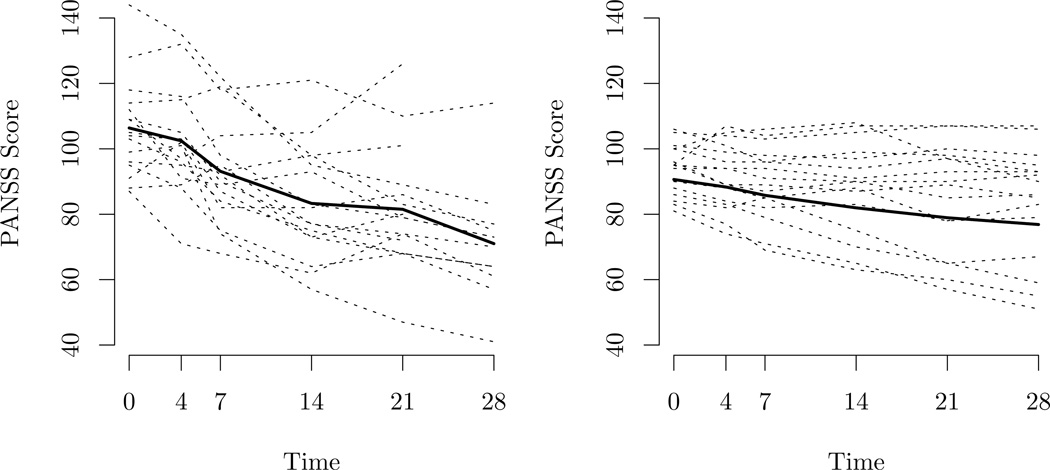
The primary analysis for this clinical trial was based on a longitudinal model assuming multivariate normality and MAR with the mean unconstrained across treatment and time and an unconstrained correlation structure shared across treatments. There is substantial evidence in the data that the multivariate normality assumption does not hold - there are obvious outliers and a formal test of normality gives a p-value less than 0.0001. Our experience is that this tends to be the rule rather than the exception. In addition to outliers there appears to be heterogeneity in the data that cannot be explained by a normal model. For example, Figure 1.1 shows two groups of observations in the placebo arm discovered from the latent class interpretation of the Dirichlet mixture we develop; subjects are grouped together if they have a high posterior probability of being the same mixture component. One group consists of 40 individuals who are relatively stable across time and the other consists of 16 individuals whose trajectories are more erratic but tend to improve more over the course of the study.
Figure 1.1.
Trajectories of two latent classes of individuals in the placebo arm of the trial, and mean response over time, measured in days from baseline, within class. Each figure contains 16 trajectories for the purpose of comparison.
These deviations from normality do not necessarily imply that analysis based on multivariate normality will fail as we might expect a degree of robustness, but it motivates us to assess the sensitivity of our analysis to the normality assumption and search for robust alternatives - particularly in the presence of nonignorable missingness where we are unaware of any methods with theoretical guarantees of robustness under model misspecification of the observed data distribution.
1.2 Missing Data in Longitudinal Studies
Identifying the effect (1.1) can be accomplished by specifying a joint distribution p(y, s | υ, ω) for the response and missingness, where ω denotes a (potentially infinite dimensional) parameter vector. In the presence of dropout, missingness is said to be missing at random (MAR) if the probability of an observed dropout depends only on outcomes which were observed; formally, p(s | y, υ, ω) = p(s | ȳs, υ, ω) for the realized ȳs. We call dropout missing not at random (MNAR) if this does not hold (Rubin, 1976).
Existing methods for addressing informative dropout can be broadly characterized as likelihood based (parametric) or likelihood-free (semiparametric). Likelihood-free methods based on estimating equations were developed in the seminal works of Rotnitzky et al. (1998) and Scharfstein et al. (1999) and characterize informative missingness with weakly identified selection model parameters which can be interpreted as deviations from MAR. Likelihood based approaches can be distinguished by how the joint distribution of the the outcome and dropout is factorized. These include selection models (Heckman, 1979; Diggle and Kenward, 1994), pattern mixture models (Little, 1993, 1994; Hogan and Laird, 1997), and shared-parameter models (Henderson et al., 2000; Wu and Carroll, 1988). Related to our method, in a cross-sectional setting Scharfstein et al. (2003) modeled the outcome of interest using a Dirichlet process and parameterized beliefs about the missing data mechanism in a weakly identified selection bias parameter, with an informative prior elicited from a field expert. A contribution similar to ours was made by Wang et al. (2010) who considered a longitudinal binary response with a densely parametrized joint model equipped with a shrinkage prior to flexibly model the observed data distribution.
1.3 Our General Approach
The extrapolation factorization, p(y, s | υ, ω) = p(ymis | yobs, s, υ, ω)p(yobs, s | υ, ω) factors the joint into two components, with the extrapolation distribution p(ymis | yobs, s, υ, ω) unidentified by the data in the absence of strong, uncheckable, distributional assumptions about the full data (Daniels and Hogan, 2008). To specify p(yobs, s | υ, ω) we propose the specification of a working model p⋆ and set p(yobs, s | υ, ω) = ∫ p⋆(y, s | υ, ω). As a result, any inference which depends only the observed data distribution may be obtained by conducting inference as though the working model were the true model. This allows for a high degree of flexibility on the observed data distribution while leaving the extrapolation distribution unidentified. We specify the working model so that sensitivity analysis is straightforward by taking it to be a Dirichlet process mixture (Escobar and West, 1995) of models in which the mixing distribution satisfies a missing at random (MAR) assumption. The restriction to mixtures of MAR models has computational properties which are exploited in Section 3.
We see the primary benefit of our approach as the meeting of two goals: robust modeling of the observed data distribution p(yobs, s | υ, ω) and ease of sensitivity analysis on the unidentified distribution p(ymis | yobs, s, υ, ω). Importantly we feel that, because the extrapolation distribution does not appear in the observed data likelihood, different assumptions about the extrapolation distribution should not result in different inferences about the observed data. While our approach assumes that dropout is monotone, we note that if missingness is not monotone we may still apply the methodology developed under the partial ignorability assumption p(r | y, s, υ, ω) = p(r | yobs, s, υ, ω) (Harel and Schafer, 2009) where rj = 1 if yj is observed.
We conduct a sensitivity analysis by applying different identifying restrictions (Little, 1993, 1994), introducing continuous sensitivity parameters representing deviations of the model from MAR (Daniels and Hogan, 2008; Scharfstein et al., 1999), and varying the sensitivity parameters continuously. There are at least two problems with this approach. First, it is inconvenient that this gives no final inferences, but rather a range of inferences, none of which the data prefer. When there are many sensitivity parameters, the range of inferences is also cumbersome to display. Second the individual interval estimates at each value of the sensitivity parameter do not account for our uncertainty in the sensitivity parameter and may be too narrow. A natural alternative is to place informative priors on the sensitivity parameters to average the separate inferences together in a principled fashion and differentially weight possible values of the sensitivity parameter based on subject matter knowledge specific to the data set.
1.4 Outline
In Section 2 we describe our approach to fitting flexible Bayesian models, and describe the Dirichlet process mixture model we implement as the working model. We then describe ways to complete the model specification by specifying the extrapolation distribution. In Section 3 we give an algorithmic framework for conducting inference using Markov chain Monte Carlo. In Section 4 we conduct a simulation study to assess the appropriateness of our model relative to parametric alternatives and show that it is capable of sufficient flexibility while giving up little in terms of performance if the true model is simpler. In Section 5 we implement our approach to draw inferences on the schizophrenia clinical trial. We close in Section 6 with a discussion.
2 Model Specification
2.1 The Working Model
We stratify the model by treatment, and the treatment variable υ is suppressed to simplify notation. We begin by specifying a working model for the joint distribution of the response and dropout processes.
Definition 1
For a model p(y, s | ω), a model p⋆(y, s | ω) is a working model if for all s,
| (2.1) |
A given specification of p⋆(y, s | ω) identifies p(y, s | ω) only up-to p(yobs, s | ω), leaving p(ymis | yobs, s, ω) unidentified. The parameter ω is the same for both p⋆ and p, but it will determine the joint distribution of (Y, S) in different ways for the two models. The following trivial proposition shows that, for the purposes of likelihood based inference, it suffices to fit p⋆(y, s | ω) to the data.
Proposition 2
A model p(y, s | ω) and corresponding working model p⋆(y, s | ω) have the same observed data likelihood.
Proof
The observed data likelihood is
This simple proposition has two significant implications.
We can focus on specifying p⋆ to fit the data well without affecting the extrapolation distribution. It may be easier conceptually to design p⋆ to induce desired sharing of information across dropout times without needing to take precautions in leaving the extrapolation distribution unidentified rather than specifying p directly.
For computational purposes, Ymis may be imputed via data augmentation using p⋆, which is substantially simpler than using p.
Here we will take p⋆ to be a mixture of models in which the missing data mechanism satisfies an MAR assumption. We note that mixtures of such MAR models are typically not themselves MAR models, an example being many shared parameter models. Let f(y | θ1) be a density for the full data response and g(s | y, θ2) a mass function for the dropout satisfying (abusing notation slightly)
That is, the probability under g that S ≥ j depends only on the observed data up-to time j − 1. Any choice of g satisfying this condition will admit an inference procedure as described in Section 3. We set
| (2.2) |
F is modeled as drawn from a Dirichlet process with base measure H and mass α > 0, written 𝒟(αH) (Escobar and West, 1995). The specification above is equivalent to the following “stick breaking” construction due to Sethuraman (1994), which shows that the Dirichlet process mixture is a prior on infinite latent class models,
| (2.3) |
where , and .
A typical choice for f(y | θ1) for continuous data is the normal kernel with θ1 = (μ, Σ). We specify a shrinkage prior as described in Daniels and Pourahmadi (2002) for Σ. For g(s | y, θ2) we model the discrete hazard of dropout at time j sequentially with a logistic regression (Diggle and Kenward, 1994),
with θ2 = (γ, ζ). Exact details on the shrinkage prior on θ and associated hyperprior may be found in the supplemental materials.
2.2 The Extrapolation Distribution
We now discuss specification of the extrapolation distribution p(ymis | yobs, s, ω). Identifying restrictions, which express the extrapolation distribution as a function of the observed data distribution, provide a natural starting point. The available case missing value (ACMV) restriction sets
| (2.4) |
for all k < j and 2 ≤ j < J, where subscripting by k and ≥ j denotes conditioning on the events S = k and S ≥ j respectively. This restriction was shown by Molenberghs et al. (1998) to be equivalent to the MAR restriction under monotone missingness. Other restrictions have been proposed in the literature (see for example Thijs et al., 2002).
A subclass of identifying restrictions is generated by the non-future dependence assumption (NFD) of Kenward et al. (2003). NFD results in missing data mechanisms with the attractive feature that the probability of dropout at time j depends only on ȳj+1,
| (2.5) |
In words, the probability that (j + 1) is the first time at which we fail to observe the outcome depends only on the observed data and the potentially missing data at time j + 1. In terms of identifying restrictions, NFD holds if and only if
for k < j − 1 and 2 < j ≤ J, but places no restrictions on the distributions pj−1(yj | ȳj−1, s, ω). A schematic representation of the NFD restriction is provided in Table 1.
Table 1.
Schematic representation of NFD when J = 4. Distributions above the dividing line are not identified by the observed data (dependence on (υ, ω) is suppressed).
| j = 1 | j = 2 | j = 3 | j = 4 | |
|---|---|---|---|---|
| S = 1 | p1(y1) | ? | p≥2(y3 | ȳ2) | p≥3(y4 | ȳ3) |
| S = 2 | p2(y1) | p2(y2 | y1) | ? | p≥3(y4 | ȳ3) |
| S = 3 | p3(y1) | p3(y2 | y1) | p3(y3 | ȳ2) | ? |
| S = 4 | p4(y1) | p4(y2 | y1) | p4(y3 | ȳ2) | p4(y4 | ȳ3) |
To identify the distribution pj−1(yj | ȳj−1, s, ω) we assume the existence of a transformation 𝒯j(yj | ȳj−1, ξj) such that
| (2.6) |
where denotes equality in distribution. Wang and Daniels (2011) implicitly take this approach, with 𝒯j(Yj | Ȳj−1, ξj) assumed to be an affine transformation. If 𝒯j is chosen so that 𝒯j(Yj | Ȳj−1, 0) = Yj then deviations of ξj from 0 represent deviations of the assumed model from MAR.
3 Computation and Inference
We work with an approximation of the Dirichlet process mixture based on truncating the stick-breaking construction at a fixed K by setting ,
| (3.1) |
This approach was studied in detail by Ishwaran and James (2001), who provide guidance for the choice of K. We break posterior computation into two steps.
Draw a sample (θ(1), β1, …, θ(K), βK) from the posterior distribution given the observed data using the working model p⋆(y, s | ω).
Calculate the posterior distribution of desired functionals of the true distribution p(y | ω).
We use a data-augmentation scheme similar to the one used by Ishwaran and James (2001), but which also includes augmenting the missing data, to complete step 1; see the supplementary material for details.
Once we have a sample from the posterior distribution of (θ(k), βk), interest lies in functionals of the form
This will typically not be available in closed form as it depends on p(s = j | ω) and E [t(Y) | S = j, ω]. The expectation E [t(Y) | S = j, ω] has a complicated form and depends on our assumption about the missing data. For example, under MAR,
We calculate E [t(Y) | ω] by Monte Carlo integration, sampling pseudo-data , and forming the average for some large N⋆. We note that this is essentially an application of G-computation (Robins, 1986; Scharfstein et al., 2013) within the Bayesian paradigm.
To sample a pseudo-data point Y⋆ under NFD we implement the following algorithm.
Draw S⋆ = s and from the working model p⋆ by choosing a class k with probability βk and simulating from , retaining the observed data.
Draw from ps(ys+1 | ȳs, ω).
For j > s + 1, sequentially draw from p≥j−1(yj | ȳj−1, ω).
MAR is attained as a special case when ps(ys+1 | ȳs, ω) = p≥s+1(ys+1 | ȳs, ω) and p≥j−1(yj | ȳj−1, ω) = p≥j(yj | ȳj−1, ω).
In both steps 2 and 3 we may need to sample from a distribution of the form
| (3.2) |
where
and g(≥ j | ȳj−1, θ2) is the probability under g(· | y, θ2) of observing S ≥ j. (3.2) is a mixture of the within-class conditional distributions with class probability ϖk,j and is easy to sample from given ȳj−1.
Sampling under NFD requires sampling from both pj−1(yj | ȳj−1, ω) (step 2) and p≥j−1(yj | ȳj−1, ω) (step 3). To sample from pj−1(yj | ȳj−1, ω) we draw from (3.2) and apply the transformation 𝒯j. A straight-forward calculation shows that we can draw from p≥j−1(yj | ȳj−1, ω) in the following steps:
Draw R ~ Bernoulli(r) where r = p(S ≥ j | ȳj−1, S ≥ j − 1, ω).
Draw ; if R = 0 apply 𝒯j, otherwise retain .
We now note the relevance of the restriction to mixtures of MAR models. Because the model satisfies MAR, the within-class probability of observing S ≥ j depends only on ȳj−1. This is relevant in computing the weights ϖk,j and in drawing R ~ Bernoulli(r) above.
4 Simulation Study
4.1 Performance for Mean Estimation Under MAR
We first assess the performance of our model to estimate the population mean at the end of a trial with J = 3 time points. Data was generated under (1) a normal model with AR-1 covariance matrix with Cov(Yj, Yj+1) = 0.7 and a lag-1 selection model and (2) a mixture of normal distributions and piecewise-constant hazard of dropout. Details on parameter specification can be found in the supplemental material.
We compare our Dirichlet mixture working model with ACMV imposed to (a) an assumed multivariate normal model with noninformative prior and (b) augmented inverse-probability weighting (AIPW) methods (Rotnitzky et al., 1998; Tsiatis, 2006; Tsiatis et al., 2011). The AIPW estimator used solves the estimating equation
where ∑i φ(Yi, θ) = 0 is a complete data least-squares estimating equation for the regression of Y1 on Y2 and (Y1, Y2) on Y3 and λj(Yi) is the dropout hazard at time j. This estimator is “doubly robust” in the sense that if either the dropout model or mean response model is correctly specified then the associated estimator is consistent and asymptotically normal. Our AIPW method used the correct dropout model and hence is consistent. A “sandwich estimator” of the covariance matrix of the parameter estimates was used to construct interval estimates.
One thousand datasets were generated with N = 100 observations per dataset. Results are given in Table 4.1. When the data is generated under normality all methods perform similarly. Under the mixture model, however, normal-based inference is now inefficient, although it does attain the nominal coverage rate. The AIPW estimator and Dirichlet process mixture give similar performance. These results suggest the Dirichlet mixture is a reasonable alternative to the normal model - even when the data are normally distributed we lose little by using the mixture while allowing robustness if the data is not normal. The AIPW method also performs well and is a reasonable semiparametric alternative but is not directly applicable to our desired approach to sensitivity analysis. The proposed modeling approach provides in this example the robustness of AIPW within a Bayesian framework and thus naturally allows for quantification of uncertainty about the missingness via priors and allows inference for any functional of the full data observed response model.
Table 2.
Comparison of methods for estimating the population mean at time J = 3. DP, Normal, and AIPW refer inferences based on the Dirichlet mixture model, the normal model, and AIPW methods respectively. Monte-Carlo standard errors are given in parentheses. Interval estimates were constructed at a 95% level.
| Bias | CI Width | CI Coverage | Mean Squared Error | |
|---|---|---|---|---|
| Normal Model | ||||
| DP | −0.001(0.004) | 0.493(0.001) | 0.963(0.006) | 0.01443(0.0006) |
| Normal | −0.005(0.004) | 0.494(0.002) | 0.944(0.007) | 0.01524(0.0007) |
| AIPW | −0.001(0.004) | 0.470(0.002) | 0.943(0.007) | 0.01530(0.0007) |
| Mixture of Normal Models | ||||
| DP | −0.010(0.004) | 0.542(0.001) | 0.542(0.001) | 0.0182(0.0008) |
| Normal | −0.039(0.005) | 0.586(0.001) | 0.586(0.001) | 0.0220(0.0010) |
| AIPW | 0.001(0.004) | 0.523(0.001) | 0.523(0.001) | 0.0185(0.0008) |
4.2 Performance for Effect Estimation Under MNAR
To determine the suitability of our approach for the Schizophrenia clinical trial we conducted a simulation study to assess the accuracy and robustness under several data generating mechanisms. We consider three different working models for data generation:
M1. A lag-2 selection model, Y ~ 𝒩(μ, Σ) and logitP(S = s | S ≥ s, Y) = ζs + γ1sYs + γ2sYs−1.
M2. A finite mixture of lag-1 selection models, C ~ Categorical(ξ), [Y | C] ~ 𝒩(μC, ΣC), and logitP(S = s | S ≥ s, Y, C) = ζsc + γscYs.
M3. A lag-2 selection model, Yj ~ Skew-𝒯ν(μj, σj, ωj) where ωj is a skewness parameter (see Azzalini, 2013) and logitP(S = s | S ≥ s, Y) = ζs + γ1sYs + γ2sYs−1. The marginals of Y are linked by a Gaussian copula.
We took α ~ log𝒩(−3, 22) to induce a strong preference for simpler models; recall α is the concentration parameter of the Dirichlet process prior. Parameters were generated by fitting the models to the active control arm of the Schizophrenia Clinical Trial and the sample sizes for the simulation was set to 200. A total of 300 datasets were generated under each assumption. Our approach was compared to a default analysis based on a the multivariate model in M1. Setting M1 was chosen to assess the loss of our approach from specifying the nonparametric mixture model when a simple parametric alternative holds. Setting M2 was chosen to determine the loss of accuracy of the inference based on a multivariate normal is used for analysis when a model similar to the Dirichlet mixture holds. At sample sizes of 200, datasets generated under M2 are not more obviously non-normal than the original data. M3 was chosen to assess the robustness of both the multivariate normal and the Dirichlet mixture to the presence of skewness, kurtosis, and a non-linear relationship between measurements. To generate data under M3 we generated data under M1 and transformed it to be more skewed, kurtotic, and nonlinear by applying a normal distribution function and skew-T quantile function; details and parameter values are given in the supplemental material, as well as sample datasets generated under M2 and M3.
To complete these models, the NFD completion was made, where σj was chosen to be the standard deviation of [Yj | Ȳj−1] under MAR. The parameter ξ represents the number of standard deviations larger Yj is, on average, for those who dropped out before time j compared to those who remained on study at time j.
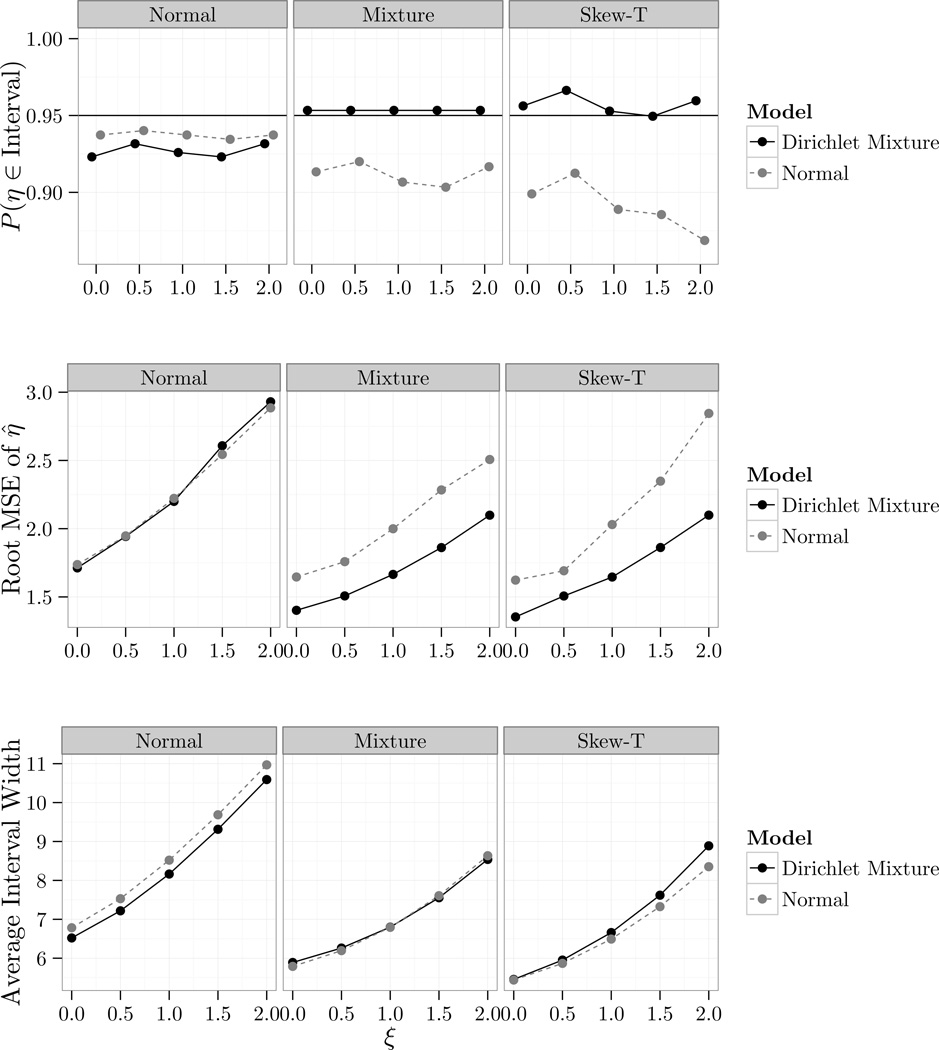
Figure 4.1 shows the frequentist coverage and average width of 95% credible intervals as well as the root mean squared error (RMSE) of the posterior mean η̂ of η = E[Y6] for each value of ξ along the grid {0, 0.5, …, 1.5, 2}; exact values and Monte-Carlo standard errors can be found in the supplementary material. We take ξ ≥ 0 to reflect the belief that those who dropped out had stochastically higher PANSS scores than those who stayed on study. This was done to assess whether the quality of inferences varies as the sensitivity parameter increases; intuitively this might happen for large values of ξ as the extrapolation distribution becomes increasingly concentrated on regions where we lack observed data.
Figure 4.1.
Results from the simulation study in 4.2. Normal refers to M1, Mixture to M2, and Skew-T to M3.
The Dirichlet mixture appears to perform at least as well as the normal model under M1 and uniformly better when either M2 or M3 hold; the Dirichlet mixture attains its nominal coverage under M2 and M3 while analysis based on the normal distribution does not and appears to degrade for larger values of ξ under M3. Given the negligible loss incurred using the Dirichlet mixture when the normal model generated the data and the larger drop in coverage and RMSE when the normal model did not generate the data we see little reason to use the normal distribution for analysis. Finally we note that under M3, while the average interval length is roughly the same for both models, the interval length varies twice as much for the Dirichlet mixture, so while on average the Dirichlet mixture produces intervals of similar length, intervals may be wider or smaller depending on the data.
These results again suggest that our approach may add a layer of robustness while giving up little when the corresponding parametric model holds, and we see no reason to prefer the parametric approach over the nonparametric approach.
5 Application to Schizophrenia Trial
We use our methodology to analyze the data from the Schizophrenia clinical trial. Recall that the effects of interest are ηυ = E(Yi6 − Yi1 | Vi = υ, ω) where υ = 1, 2, 3 denotes randomization to the test drug, active control, and placebo respectively, and in particular we are interested in the improvement of each treatment over placebo, ηυ − η3.
5.1 Comparison to Alternatives and Assessing Model Fit
We consider two parametric models for p⋆(y, s | ω) in addition to a Dirichlet process mixture of lag-2 selection models. We considered several variants of pattern mixture models and selection models and found that the following provided reasonable fits within each class.
A pattern mixture model. [S | ω] is modeled with a discrete distribution across time points and [Y | S, ω] ~ N(μS, ΣS). Due to sparsity in the observed patterns we must share information across S to get practical estimates of (μS, ΣS). Observations with S ∈ {1, 2, 3}, S ∈ {4, 5}, or S ∈ {6} were treated as having the same values of μS, while ΣS = Σ was shared across patterns. ACMV is imposed on top of this, with ACMV taking precedence over the sharing of μS.
A selection model. The outcome is modeled [Y | ω] ~ N(μ, Σ) and dropout is modeled with the a discrete hazard logistic model, which for j ≥ 3 was simplified further to expit(αj + β1jYj + β2jYj−1).
The Dirichlet mixture used is a mixture of the selection model above. Models were assessed by their posterior predictive ordinates,
where Yobs,−i and S−i denote the observed data with observation i removed (Geisser and Eddy, 1979). The PO’s can be easily calculated from the MCMC output and combined to give an omnibus model selection criteria , the log pseudo-marginal likelihood - see Lopes et al. (2003) and Hanson et al. (2008) for examples in a Bayesian nonparametric setting. See Table 5.1 for a comparison of model fit and a comparison of inferences. LPML selects the Dirichlet mixture over the selection model and pattern mixture model.
Table 3.
Comparison of results under MAR assumption. The posterior mean is given for ηυ − η3 and standard error is given in parenthesis.
| Model | η1 − η3 | η2 − η3 | LPML |
|---|---|---|---|
| Dirichlet Mixture | −1.7(−8.0, 4.8) | −5.4(−12.6, 2.3) | −3939 |
| Selection Model | −1.8(−8.8, 5.5) | −6.1(−14.2, 2.0) | −4080 |
| Pattern Mixture model | −2.2(−10.1,5.3) | −6.8(−15.6,2.3) | −4072 |
Improvement over the selection model is unsurprising in light of the established failure of multivariate normality. Like the Dirichlet mixture, the marginal response distribution for the pattern mixture model is a discrete normal mixture, so an improvement in LPML here is more informative. In addition to the improvement in LPML, the simulation results suggesting robustness argue for inference based on the Dirichlet mixture. We also note the Dirichlet mixture results in narrower interval estimates.
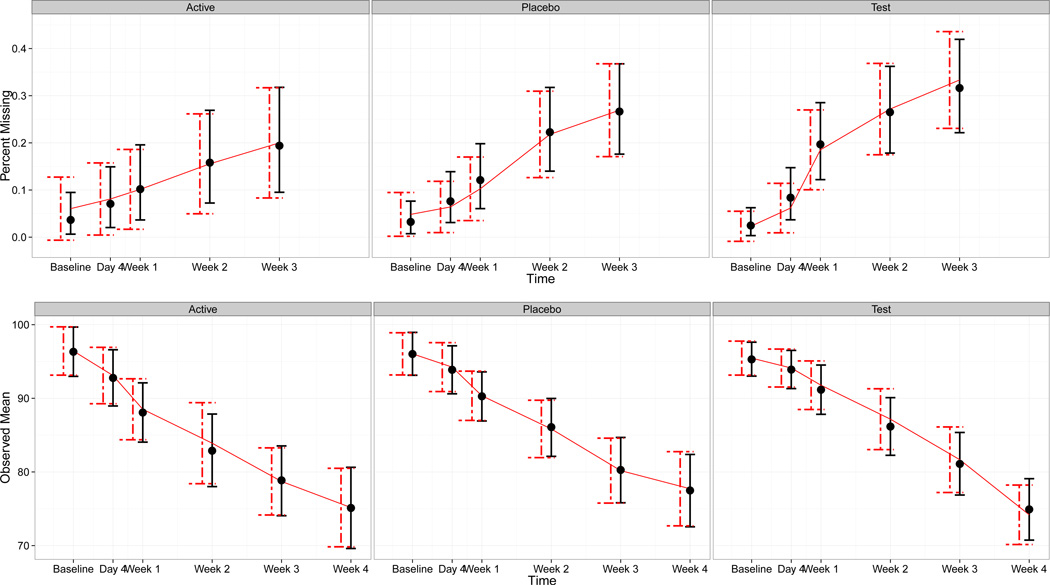
To confirm that the Dirichlet mixture reasonably models the observed data we compare model-free estimates and intervals of the dropout rates and observed-data means at each time point to those obtained by the model under each treatment. Results are displayed in Figure 5.1. There do not appear to be any problems with the model’s fit to results obtained from the empirical distribution of the data.
Figure 5.1.
Top: modeled dropout versus observed dropout over time. Bottom: modeled observed means versus empirical observed means. The solid line represents the empirical statistics, solid dots represent the modeled statistics. Dashed error bars represent frequentist 95% confidence intervals and solid error bars represent the models 95% credible intervals.
5.2 Inference and Sensitivity Analysis
Reasons for dropout were partitioned into those thought to be associated with MNAR missingness - withdrawal of patient consent, physician decision, lack of efficacy, and disease progression - and those which were thought to be associated with MAR missingness - pregnancy, adverse events such as occurrence of side effects, and protocol violation. We let Mij = 1 if a subject dropped out at time j for reasons consistent with MNAR missingness and Mij = 0 otherwise. Given that a subject is last observed at time S we model
| (5.1) |
λυ(ȳs) can be estimated from the data using information about dropout. To make use of this information in the G-computation we make the NFD completion given by the mixture distribution
| (5.2) |
This is a mixture of an ACMV completion and the transformation based NFD completion. This encodes the belief that, if a subject drops out for a reason associated with MAR missingness, we should impute the next missing value under ACMV. In selecting a model for λυ(ȳs), S and ȲS were found to have a negligible effect on the fit of (5.1) while the treatment V was found to be very important, so we take λυ(ȳs) = λυ to depend only on V. The coefficients λυ were given independent Uniform(0, 1) priors and were drawn from their posterior during the MCMC simulation.
To identify the effect of interest it still remains to specify the transformation 𝒯(y; ξ) and place an appropriate prior on ξ. We take 𝒯 (y; ξ) = y+ξ to be a location shift. This encodes the belief that the conditional distribution of Yj for an individual who dropped out at time j − 1 is the same as it is it would be for a hypothetical individual with the same history who is still on study but shifted by ξ. This can be explained to clinicians as an adjustment to the PANSS score of an individual who remained on study at time j that would need to be made to make this individual have the same average as an individual with the same history who dropped out for an informative reason, with the caveat that the same adjustment must be made regardless of their history and response value. In general if subject matter experts feel constrained by needing to specify a single adjustment this may be reflected by revising the transformation chosen.
Information regarding the scale of the data can be used as an anchor for prior specification. The residual standard deviation in the observed data pooled across time was roughly 8, and it is thought unlikely that deviations from MAR would exceed a standard deviation. The ξj were restricted to be positive to reflect the fact that subjects who dropped out were thought to be those whose PANSS scores were lower than predicted under MAR. From this we specified ξj ~ 𝒰 (0, 8) independently, and the ξj were shared across treatment. While it may seem as though sharing the ξj across treatment will cause the effect of MNAR to cancel out in comparisons, the differing amounts of dropout and differing proportions of dropout attributable to each cause will cause ξ to affect each treatment differently.
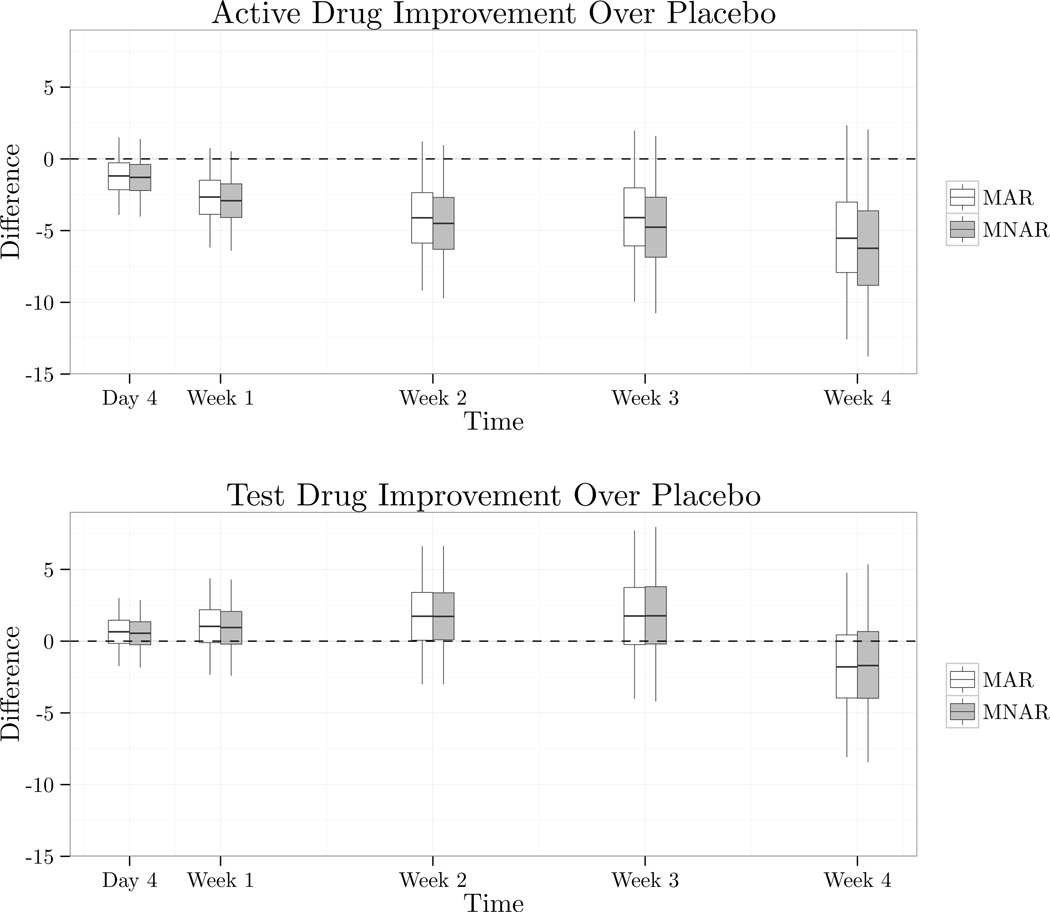
Results are summarized in Figure 5.2. The effect η1 − η3 had posterior mean −1.7 and 95% credible interval (−8.0, 4.8) under MAR and posterior mean −1.6 and credible interval (−8.4, 5.4) under MNAR. η2 − η3 had posterior mean −5.4 and credible interval (−12.6, 2.3) under MAR and posterior mean −6.2 and credible interval (−13.8, 2.0) under MNAR. There appears to be little evidence in the data that the test drug is superior to the placebo, and for much of the trial the placebo arm appears to have had better performance. The effect of the MNAR assumption on inferences is negligible here due the fact that the placebo and test drug arms had similar dropout profiles, and because the sensitivity parameters ξj had the same prior mean across treatments. The data does contain some evidence of an effect of the active control, and we see here that the MNAR assumption increases the gap between the active control and the placebo due to the fact the attrition on the active arm was less frequent and when it occurred was more frequently for noninformative reasons.
Figure 5.2.
Improvement of treatments, measured as the difference in change from baseline, over placebo over time. Smaller values indicate more improvement relative to placebo. Whiskers on the boxes extend to the 0.025 and 0.975 quantiles, the boundaries of the boxes represent the quartiles, and the dividing line within the boxes represents the posterior mean.
We varied this prior specification in two ways. First, we considered sensitivity to the dependence assumptions regarding the ξj by allowing the ξj to be dependent across j and allowing different values ξjυ across treatment, while keeping the marginal prior on each ξjυ the same. The ξjυ were linked together by a Gaussian copula parameterized by ρtime and ρtreatment determining the correlation between ξjυ with ρtime = 0 and ρtreatment = 1 corresponding to the original prior. The result of this analysis was that inferences were invariant to the choice ρtime and ρtreatment to within Monte-Carlo error, so detailed results are omitted.
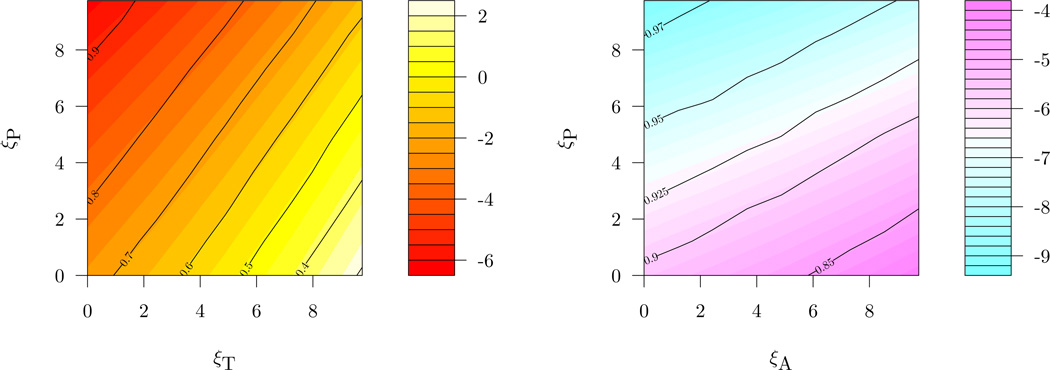
Second, we considered the effect of the mean and variability of the prior on inferences by giving each ξ a point-mass prior and varying the prior along a grid. This analysis is useful in its own right, as some may feel uncomfortable specifying a single prior on the sensitivity parameters. To ease the display of the inferences, we assume all ξj equal within treatment and we write ξP, ξT, and ξA for the sensitivity parameters corresponding to the placebo, test, and active control arms respectively. Figure 5.3 displays results of this analysis in a contour plot. To illustrate, if we chose as a cutoff a 0.95 probability of superiority as being significant evidence of an effect then we see that even for the most favorable values of ξT and ξP we do not reach a 0.95 posterior probability of η1 − η3 > 0. Conversely, a 0.95 posterior probability of η2 − η3 > 0 is attained, although it occurs in a region where ξA is substantially smaller than ξP. The additional uncertainty in the ηυ induced by using a prior itself appears for this data to have little effect on the posterior, as inference when ξP = ξT = ξA = 4 gives roughly the same inferences as the original prior.
Figure 5.3.
Contour plot giving inference for the effects ηυ − η3 for different choices of the sensitivity parameters. The color represents the posterior mean while dark lines give contours of the posterior probability of ηυ − η3 > 0.
6 Discussion
We have introduced a general methodology for conducting nonparametric Bayesian inference under nonignorable missingness which allows for a clear separation of the observed data distribution and extrapolation distribution as well as the ability to characterize uncertainty about untestable missing data assumptions. We attain both flexible modeling of the observed data and flexible specification of the extrapolation distribution. We note that there is nothing particular about the Dirichlet process to our specification; in principle our method could be applied to any joint distribution p⋆ for which the inference in Section 3 is tractable.
An alternative to the transformation based sensitivity analysis presented here is an exponential tilting assumption pj−1(yj | ȳj−1, s, ω) ∝ p≥j(yj | ȳj−1, s, ω) exp (qj(ȳj)). The function qj(ȳj) has a natural interpretation in terms of the log-odds of dropout at time j − 1 (Rotnitzky et al., 1998; Birmingham et al., 2003; Scharfstein et al., 2013). Our method is also amenable to this approach if the normal kernel is used and qj(ȳj) is piecewise-linear in yj. Since qj(ȳj) is unidentified and typically will be elicited from a subject-matter expert, the piecewise-linearity assumption may not be a substantial restriction.
In future work we hope to develop similar tools for continuous time dropout; when dropout time is continuous there is no longer a natural characterization of MAR in terms of identifying restrictions. Additionally, there is scope for incorporating baseline covariates. Often covariates are used to help imputation of missing values, or to make the MAR assumption more plausible, but are not of primary interest (i.e. auxiliary covariates). Another area for future work is extending our method to non-monotone missingness without needing to invoke a partial ignorability assumption. An R package is being developed to implement these methods.
Supplementary Material
Acknowledgments
This work was partially supported by NIH grant CA 85295 and CA 183854. The authors would like to thank the Bayes Missing Data Working Group for providing the data and important insights about the clinical trial, as well as Merck & Co., Inc. for allowing us the use of the data from their clinical trial.
References
- Azzalini A. The Skew-Normal and Related Families. Vol. 3. Cambridge University Press; 2013. [Google Scholar]
- Birmingham J, Rotnitzky A, Fitzmaurice G. Pattern-mixture and selection models for analysing longitudinal data with monotone missing patterns. Journal of the Royal Statistical Society, Series B. 2003;65:275–297. [Google Scholar]
- Daniels M, Hogan J. Missing Data In Longitudinal Studies. Chapman and Hall/CRC; 2008. [Google Scholar]
- Daniels M, Pourahmadi M. Bayesian analysis of covariance matrices and dynamic models for longitudinal data. Biometrika. 2002;89(3):553–566. [Google Scholar]
- Diggle P, Kenward M. Informative drop-out in longitudinal data analysis. Applied Statistics. 1994;43:49–73. [Google Scholar]
- Escobar D, West M. Bayesian density estimation and inference using mixtures. Journal of the American Statistical Association. 1995;90:577–588. [Google Scholar]
- Geisser S, Eddy WF. A predictive approach to model selection. Journal of the American Statistical Association. 1979;74(365):153–160. [Google Scholar]
- Hanson TE, Kottas A, Branscum AJ. Modelling stochastic order in the analysis of receiver operating characteristic data: Bayesian non-parametric approaches. Journal of the Royal Statistical Society: Series C (Applied Statistics) 2008;57(2):207–225. [Google Scholar]
- Harel O, Schafer J. Partial and latent ignorability in missing-data problems. Biometrika. 2009;96:37–50. [Google Scholar]
- Heckman J. Sample selection bias as a specification error. Econometrica. 1979;47:153– 161. [Google Scholar]
- Henderson R, Diggle P, Dobson A. Joint modelling of longitudinal measurements and event time data. Biostatistics (Oxford) 2000;1:465–480. doi: 10.1093/biostatistics/1.4.465. [DOI] [PubMed] [Google Scholar]
- Hogan J, Laird N. Mixture models for the joint distribution of repeated measures and event times. Statistics in Medicine. 1997;16:239–257. doi: 10.1002/(sici)1097-0258(19970215)16:3<239::aid-sim483>3.0.co;2-x. [DOI] [PubMed] [Google Scholar]
- Ishwaran H, James L. Gibbs sampling methods for stick-breaking priors. Journal of the American Statistical Association. 2001;96:161–173. [Google Scholar]
- Kay SR, Flszbein A, Opfer A. The positive and negative syndrome scale (panss) for schizophrenia. Schizophrenia Bulletin. 1987;13(2):261. doi: 10.1093/schbul/13.2.261. [DOI] [PubMed] [Google Scholar]
- Kenward M, Molenberghs G, Thijs H. Pattern-mixture models with proper time dependence. Biometrika. 2003;90:53–71. [Google Scholar]
- Little R. Pattern-mixture models for multivariate incomplete data. Journal of the American Statistical Association. 1993;88:125–134. [Google Scholar]
- Little R. A class of pattern-mixture models for normal incomplete data. Biometrika. 1994;81:471–483. [Google Scholar]
- Lopes HF, Müller P, Rosner GL. Bayesian meta-analysis for longitudinal data models using multivariate mixture priors. Biometrics. 2003;59(1):66–75. doi: 10.1111/1541-0420.00008. [DOI] [PubMed] [Google Scholar]
- Molenberghs G, Kenward M, Lesaffre E. The analysis of longitudinal ordinal data with non-random dropout. Biometrika. 1997;84:33–44. [Google Scholar]
- Molenberghs G, Michiels B, Kenward M, Diggle P. Monotone missing data and pattern-mixture models. Statistica Neerlandica. 1998;52:153–161. [Google Scholar]
- National Research Council. The Prevention and Treatment of Missing Data in Clinical Trials. The National Academies Press; 2010. [PubMed] [Google Scholar]
- Robins J. A new approach to causal inference in mortality studies with sustained exposure periods – application to control of the healthy worker survivor effect. Math Modeling. 1986;7:1393–1512. [Google Scholar]
- Rotnitzky A, Robins J, Scharfstein D. Semiparametric regression for repeated outcomes with non-ignorable non-response. Journal of the American Statistical Association. 1998;93:1321–1339. [Google Scholar]
- Rubin D. Inference and missing data. Biometrika. 1976;63:581–592. [Google Scholar]
- Scharfstein D, Daniels M, Robins J. Incorporating prior beliefs about selection bias ito the analysis of randomized trials with missing outcomes. Biostatistics. 2003;4:495. doi: 10.1093/biostatistics/4.4.495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scharfstein D, McDermott A, Olson W, Weigand F. Technical report. Johns Hopkins Bloomberg School of Public Health; 2013. Global sensitivity analysis for repeated measures studies with informative drop-out. [Google Scholar]
- Scharfstein D, Rotnitzky A, Robins J. Adjusting for nonignorable dropout using semiparametric nonresponse models. Journal of the American Statistical Association. 1999;94 [Google Scholar]
- Sethuraman J. A constructive definition of Dirichlet priors. Statistica Sinica. 1994;4:639–650. [Google Scholar]
- Thijs H, Molenberghs G, Michiels B, Verbeke G, Curran D. Strategies to fit pattern-mixture models. Biostatistics. 2002;3:245–265. doi: 10.1093/biostatistics/3.2.245. [DOI] [PubMed] [Google Scholar]
- Tsiatis A. Semiparametric Theory and Missing Data. New York: Springer-Verlag; 2006. [Google Scholar]
- Tsiatis A, Davidian M, Cao W. Improved doubly robust estimation when data are monotonely coarsened, with application to longitudinal studies with dropout. Biometrics. 2011;67:536–545. doi: 10.1111/j.1541-0420.2010.01476.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vansteelandt S, Goetghebeur E, Kenward M, Molenberghs G. Ignorance and uncertainty regions as inferential tools in a sensitivity analysis. Statistica Sinica. 2006;16:953–979. [Google Scholar]
- Wang C, Daniels M. A note on MAR, identifying restrictions, model comparison, and sensitivity analysis in pattern mixture models with and without covariates for incomplete date. Biometrics. 2011;67:810–818. doi: 10.1111/j.1541-0420.2011.01565.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang C, Danies M, Scharfstein D, Land S. A Bayesian shrinkage model for incomplete longitudinal binary data with application to the breast cancer prevention trial. Journal of the American Statistical Association. 2010;105:1333–1346. doi: 10.1198/jasa.2010.ap09321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu M, Carroll R. Estimation and comparison of changes in the presence of informative right censoring by modeling the censoring process. Biometrics. 1988;45 [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.