Abstract
Antisense transcription has been extensively recognized as a regulatory mechanism for gene expression across all kingdoms of life. Despite the broad importance and extensive experimental determination of cis-antisense transcription, relatively little is known about its role in controlling cellular switching responses. Growing evidence suggests the presence of non-coding cis-antisense RNAs that regulate gene expression via antisense interaction. Recent studies also indicate the role of transcriptional interference in regulating expression of neighboring genes due to traffic of RNA polymerases from adjacent promoter regions. Previous models investigate these mechanisms independently, however, little is understood about how cells utilize coupling of these mechanisms in advantageous ways that could also be used to design novel synthetic genetic devices. Here, we present a mathematical modeling framework for antisense transcription that combines the effects of both transcriptional interference and cis-antisense regulation. We demonstrate the tunability of transcriptional interference through various parameters, and that coupling of transcriptional interference with cis-antisense RNA interaction gives rise to hypersensitive switches in expression of both antisense genes. When implementing additional positive and negative feed-back loops from proteins encoded by these genes, the system response acquires a bistable behavior. Our model shows that combining these multiple-levels of regulation allows fine-tuning of system parameters to give rise to a highly tunable output, ranging from a simple-first order response to biologically complex higher-order response such as tunable bistable switch. We identify important parameters affecting the cellular switch response in order to provide the design principles for tunable gene expression using antisense transcription. This presents an important insight into functional role of antisense transcription and its importance towards design of synthetic biological switches.
Introduction
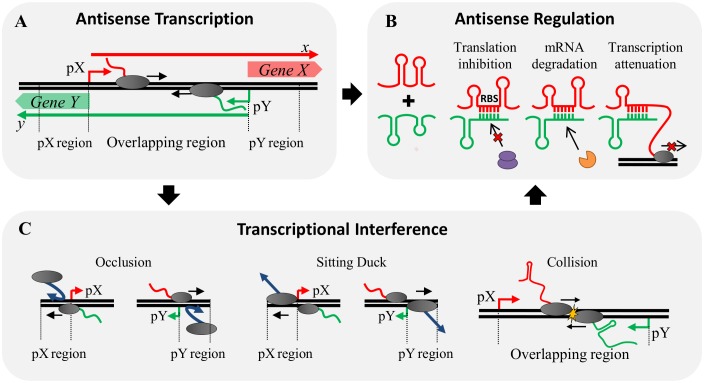
Tunable regulation of gene expression is essential to overcome multitude of adverse environmental conditions encountered by biological systems [1,2]. Non-coding genomic regions and closely spaced promoters observed in genome-wide studies have revealed the role of transcription in controlling gene expression [3–7]. Often, when both DNA strands are transcribed in the same genomic locus, convergent arrangements of promoters are observed, leading to antisense transcription (Fig 1A). This phenomenon plays an important role in cell differentiation [8], stress responses [9,10], pathogenic processes [11,12], virulence [13], and development of life-threatening diseases [14–17]. Regulatory mechanisms linked with antisense transcription include cis-antisense RNA regulation (AR) and transcriptional interference (TI).
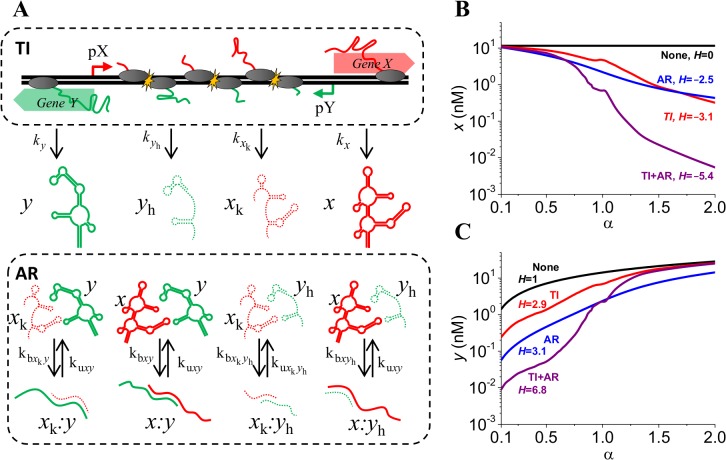
Fig 1. Antisense transcription mechanisms in a set of convergent genes.
(A) General set of convergent promoters driving expression of genes X and Y synthesizing transcripts x and y (bold arrows), respectively. Such a system is susceptible to TI and produces overlapping transcripts that may participate in AR. (B) AR can cause translational inhibition, mRNA degradation and transcriptional attenuation due to the interactions that may exist between full-length sense and antisense transcripts as well as truncated RNA produced as a result of RNAP collisions, one of the reported TI mechanisms. (C) Mechanisms of TI: Occlusion caused by passage of an opposing elongating RNAP on the antisense promoter which hinders binding of RNAP to the sense promoter; Sitting duck interference, dislodgement of an initiation complex due to collision with an opposing elongating RNAP; and Collision between opposing elongating RNAP molecules that produces truncated RNA of different sizes susceptible to participate in AR. Both TI and AR mechanisms are likely to be coupled during antisense transcription.
AR can arise between RNA transcripts encoded in opposite strands of the same DNA region, which are perfectly complementary, known as cis-antisense RNA interaction; or between transcripts encoded from different genome regions, which are only partially complementary, known as trans-antisense interaction. Antisense RNAs (asRNAs) are ubiquitous in all three domains of life and known to regulate gene expression in various ways [18–22]. asRNAs regulating sense mRNAs act via three predominant mechanisms (Fig 1B). Translation inhibition, whereby binding of the asRNA prevents translation of the mRNA by usually blocking its ribosomal binding site (RBS) [23] or, less commonly, other mRNA regions [24]. mRNA degradation, in which the resulting hybrid asRNA-mRNA double stranded RNA (dsRNA) is targeted for fast degradation by RNases (RNase III, E, etc.) [13,25–27]. Finally, transcriptional attenuation, where binding to the target mRNA disrupts its transcription [28–30]. Other less common mechanisms include degradation protection [11,31], inhibition of primer maturation and prevention of formation of an activator RNA pseudoknot [18,32].
During antisense transcription an additional mechanism affecting expression of neighboring genes is known as TI and is defined as the suppressive effect of transcription from one promoter on an adjacent promoter [33]. Presence of TI at various promoter arrangements has been shown to be ubiquitous [34–37]. For head to head, non-overlapping promoters, four TI mechanisms have been described (Fig 1C). Occlusion, whereby presence of a RNA polymerase (RNAP) originating from one promoter hinders the binding of a RNAP at the neighboring promoter [34,38]; sitting duck interference, in which an elongating RNAP collides with a promoter bound RNAP [36]; collision, in which two opposing elongating RNAPs collide while traversing the overlapping DNA, often producing truncated transcripts [39] and roadblock, where a DNA bound protein blocks movement of an elongating RNAP [40].
Despite the broad importance and extensive experimental determination of cis-antisense transcription, relatively little is known about its role in controlling cellular switching responses. Furthermore, majority of prior mathematical models have focused either on TI [41] or AR [42,43] mechanism alone, and little is understood about how cells utilize coupling of these mechanisms in advantageous ways that could also be used to design novel synthetic genetic devices. Here we present a discrete stochastic TI model that brings a new aspect to the previously existing TI model [41] as it calculates the rate of production of truncated RNA species produced as a result of RNAP collision during antisense transcription. The model predicts TI events occurring in a general set of convergent, non-overlapping promoters providing truncated and full-length RNA production rates, which are then used to solve a system of ordinary differential equations (ODEs) describing their presence. We show the tunability of TI through various parameters and that coupling of TI with AR gives rise to hypersensitive switches in expression of both antisense genes. In addition, we consider proteins encoded by the genes to regulate antisense transcription by implementing positive and negative feedback loops controlling the transcriptional process, and therefore affecting both TI and AR. Our approach reveals the regulatory potential that arises from coupling these three layers of gene regulation from convergent promoters. The model predicts multiple tunable responses, from first-order ramping switch to higher-order bistable switch by fine-tuning of the system parameters. Therefore, we identify the most important parameters affecting the cellular switch response in order to provide the design principles for tunable gene expression using antisense transcription. To the best of our knowledge, we present the first model for antisense transcription integrating three regulatory layers with the purpose of designing synthetic genetic devices taking advantage of antisense transcription.
Methods
Discrete TI model
RNAP binding, firing and elongation along the DNA
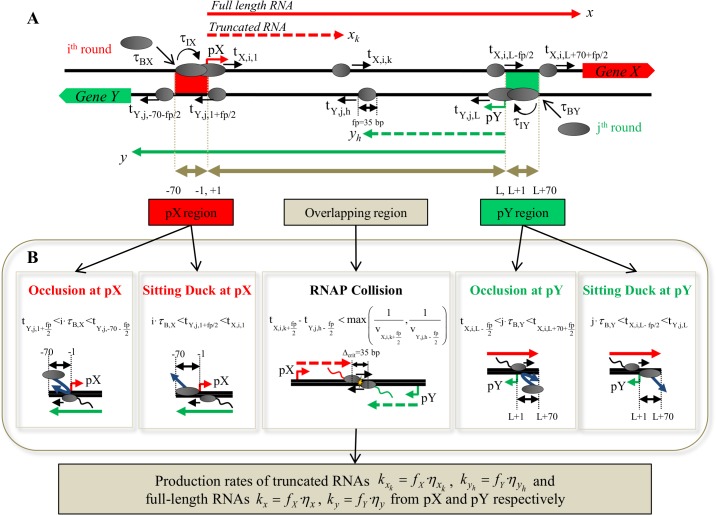
We developed a discrete model that simulates RNAP traffic originating from a general set of two convergent, non-overlapping promoters pX and pY present on sense and antisense strands of DNA, driving the expression of genes X and Y, respectively. The model calculates the outcome of every single round of transcription by tracking binding and movement of RNAP along three different regions along the DNA: the pX promoter region from position -70 to -1, the intermediate overlapping region of length L, which spans between positions +1 and L, and promoter pY region from position L+1 to L+70 (Fig 2).
Fig 2. Algorithm for discrete TI model.
(A) A pair of convergent promoters pX (present on sense/top DNA strand) and pY (present on antisense/bottom DNA strand) separated by overlapping DNA of length L is shown. Promoters pX and pY drive expression of genes X and Y respectively, which produce full-length transcripts x and y (denoted by bold arrows) respectively. For each ith and jth round of transcription from pX and pY promoters respectively, RNAP (denoted by large grey ovals) form DNA-bound RNAP complexes at the respective promoter region following a binding (τBX and τBY) and initiation (τIX and τIY) process. After firing, the center of RNAP moves to first position of the overlapping region to form an elongation complex (EC, denoted by smaller grey ovals). The time taken for each ith EC (fired from pX) to reach kth position on sense strand (tX,i,k) as well as the time taken for each jth EC (fired from pY) to reach hth position on the antisense (tY,j,h) strand along the overlapping DNA are tracked. The footprint of an EC is denoted by fp. (B) For each ith and jth rounds of transcription, the model calculates the outcome of TI depending on the region where opposing RNAPs meet. Occlusion and sitting duck interference occur at the promoters pX (left panels) or pY (right panels), and RNAP collisions between ECs occur along the overlapping DNA (middle panel) following the mathematical constraints shown. Upon RNAP collision, one or both ECs on the sense and antisense strand fall off the DNA and result in production of truncated transcripts x k and y h (denoted by dashed arrows) from pX and pY respectively. In absence of any kind of TI, transcription is successful, producing a full-length transcript (x, y). Once 30,000 rounds of transcription from the stronger promoter have been calculated the net rate of production of full-length (k x and k y) and truncated RNA ( and ) are obtained.
Transcriptional initiation follows the McClure model, which describes the multi-step transcription initiation process using two main steps [44–46]. Firstly, RNAP is considered to bind to promoters pX and pY at average binding times τBX and τBY respectively (Table 1) to form initiation complexes (IC). The IC then transitions into elongation complex (EC) after an average initiation time τIX and τIY at pX and pY promoters, respectively. During the initiation time the RNAP remains bound to the respective promoter while unwinding the double-stranded DNA (open complex). Promoter bound RNAP (IC) is assumed to occupy a footprint (fp) of 70 bp. Both RNAP binding (τBX±0.05τBX and τBY±0.05τBY) and initiation times (τIX±0.05τIX and τIY±0.05τIY) are assumed to follow a Gaussian distribution to account for inherent biological noise [47,48]. Average RNAP binding times lie in range of 5.5–55 s based on estimates for Pbla system in E. coli [49,50] and bacteriophage λ [51]. Average RNAP initiation time is assumed to be in a range of 5–16 s based on T7 RNAP [52]. We assume the time required for transition from IC to EC to be shorter than the binding time (τIX<τBX and τIY<τBY), thus self-occlusion at both promoters is neglected [53]. Since τIX<τBX and τIY<τBY, time between two consecutive RNAP firing events coincides with the time between two consecutive RNAP binding events at the promoter. Therefore, the RNAP firing rates or frequencies f X and f Y from promoters pX and pY respectively are solely given by the inverse of the corresponding RNAP binding time (f X = 1/τBX, f Y = 1/τBY). We define relative strength α of promoters pX-pY, as the ratio of RNAP firing rates (α = f Y/f X). α can vary between three states, α<1 when pX is more aggressive than pY promoter, α~1 when pX and pY have comparable strengths, and α>1 when pY is more aggressive than pX. RNAPs are assumed to be in excess, thus we consider no effect on transcription due to sequestering of transcriptional machinery [36]. The binding and firing events of RNAP at pX are assumed to be independent of binding and firing events at pY promoter and vice versa except for TI mechanisms.
Table 1. Parameters of discrete TI model.
| Parameter | Description |
|---|---|
| τBX | Average binding time at pX. |
| τBY | Average binding time at pY. |
| f X | Firing rate at pX, defined as inverse of pX average binding time, f X = 1/τBX |
| f Y | Firing rate at pY, defined as inverse of pY average binding time, f Y = 1/τBY |
| τIX | Average initiation time at pX |
| τIY | Average initiation time at pY |
| tX,i,k | Time at which center of RNAP corresponding to the ith round of transcription from pX reaches kth position |
| tY,j,h | Time at which center of RNAP corresponding to the jth round of transcription from pY reaches hth position |
| η x | Fraction of successful rounds of transcriptions relative to total rounds of transcription from pX |
| η y | Fraction of successful rounds of transcriptions relative to total rounds of transcription from pY |
| Fraction of rounds of transcription producing truncated RNA of size k relative to total rounds of transcription from pX | |
| Fraction of rounds of transcription producing truncated RNA of size h relative to total rounds of transcription from pY | |
| k x = f x η x | Transcription rate of full-length RNA x in presence of TI |
| k y = f y η y | Transcription rate of full-length RNA y in presence of TI |
| Transcription rate of truncated RNA x k (population of truncated RNAs longer than 60 bp) | |
| Transcription rate of truncated RNA y h (population of truncated RNAs longer than 60 bp) |
In case of successful RNAP firing, we assume elongation starts with the center of an EC RNAP discretely moving to the first position of overlapping DNA (+1 for pX, +L for pY). Footprint (fp) of an EC is considered to be 35 bp [54]. Movement of ECs is considered to occur in discrete steps [55] with an average velocity of 50 bp/s along the DNA following a Gaussian distribution (50±2.5 bp/s) based on experimental values [56]. The simulation calculates the time that RNAP center reaches each kth and hth position for every ith and jth round of transcription (tX,i,k, tY,j,h) (tpromoter,round,position) from pX and pY respectively. The time taken by the EC to cover this distance is given by the summation of product of RNAP velocity at a particular location along the DNA , where n is the number of nucleotides covered by the center of the EC, and v m is the local velocity of the EC at the mth position.
RNA production in absence of TI
In absence of TI, the RNAP molecules successfully transcribe and synthesize full-length RNAs x and y of length >L+70 (Table 2), i.e. length of the overlapping region plus length of the convergent promoter region (no further TI is considered beyond those positions). The rate of production of x and y is given by k x = f X and k y = f Y, respectively. Only full-length RNAs x and y are considered to be accessible for translation into proteins, excluding translation of any kind of truncated RNA.
Table 2. List of species and corresponding models.
| Species | Description | Models |
|---|---|---|
| x | Full-length RNA produced from promoter pX | TI, TI+AR, GN |
| y | Full-length RNA produced from promoter pY | TI, TI+AR, GN |
| x k | Truncated RNA produced from promoter pX | TI, TI+AR, GN |
| y h | Truncated RNA produced from promoter pY | TI, TI+AR GN |
| x:y | RNA hybrid between sense and antisense full-length RNA | TI+AR, GN |
| x k:y | RNA hybrid between sense truncated and antisense full-length RNA | TI+AR, GN |
| x:y h | RNA hybrid between full-length sense and antisense truncated RNA | TI+AR, GN |
| x k:y h | RNA hybrid between truncated sense and antisense truncated RNA | TI+AR, GN |
| X | Protein encoded by gene X | GN |
| Y | Protein encoded by gene Y | GN |
| Z | Activator protein | GN |
| W | Signaling molecule or upstream protein | GN |
| X:Z | Protein hybrid between X and Z proteins | GN |
| OY,T | Total concentration of operator sites at promoter pY | GN |
| OY | Unbound operator sites at promoter pY | GN |
TI via occlusion
For jth round of transcription, occlusion is considered to occur if EC of ith round of transcription fired from pX traverses pY region when jth RNAP tries to bind at pY (j·τBY). Time taken to traverse an antisense promoter starts when front end of the EC reaches position L (EC center reaches position L-fp/2 at time tX,i,L-fp/2) and the back end of the EC leaves position L+70 (EC center leaves position L+70+fp/2 at time tX,i,L+70+fp/2). Upon occlusion (tX,i,L-fp/2<j·τBY<tX,i,L+70+fp/2), jth round of transcription from pY does not occur. Similarly, for ith round of transcription at pX, occlusion is considered to occur if jth EC fired from pY is traversing pX region (from -70 to -1) when ith RNAP tries to bind at pX (tY,j,1+fp/2<i∙τBX<tY,j,-70-fp/2), (Fig 2B).
TI via sitting duck interference (SDI)
SDI at pY is considered to occur when ith EC fired from pX front end reaches the end of the overlapping region, i.e. position L, and encounters an IC stationed at pY (j∙τBY<tX,i,L-fp/2<tY,j,L), also known as sitting duck complex (SDC). SDI at pX occurs when jth EC fired from pY front end reaches the end of the overlapping region, i.e. +1, and encounters an IC stationed at pX (i·τBX<tY,j,1+fp/2<tX,i,1), (Fig 2B). SDI is considered to have two different outcomes that impact transcription. SDCs are usually removed from the DNA upon collision with an opposing EC, in which case while the SDC causes no RNA to be produced, the EC continues transcribing. However, some SDCs are tightly bound to the DNA and can act as roadblocks [33,41]. Therefore, we assume that 10% of SDCs survive the collision with an EC, in which case the converging EC falls off the DNA producing a truncated RNA of length equal to the overlapping length minus half the RNAP footprint (L-fp/2).
TI via RNAP collision
If neither occlusion nor SDI occur, RNAP starts transcribing. However, ECs may still interfere with other opposing ECs or SDCs on the antisense promoter. RNAP collisions are considered to occur along the overlapping DNA (positions +1 to L) when two opposing ECs are separated by critical distance, Δcritical or less. We consider the limiting case, where Δcritical = RNAP footprint of an EC (35 bp). Δcritical could be greater than the RNAP footprint when the torsional stress caused by simultaneous uncoiling of both DNA may cause the RNAPs to fall off the DNA [57]. Collision of two ECs is considered to result in one of two outcomes, either both ECs fall off the DNA strand, or only one EC falls off while the other continues to elongate (Fig 2B). We consider an RNAP survival probability of 80% in the case where one EC survives. We assume there is equal probability that it originated from pX or pY, resulting in an overall individual 40% probability to continue transcribing, as experimentally shown by Crampton et al. using Atomic Force Microscopy [57]. When one RNAP stops transcribing due to a collision event, it gives rise to a truncated RNA of length x k or y h depending on whether the EC originated from pX or pY respectively (Table 2).
Model for TI based regulation (TI model)
The discrete TI model simulates 30,000 rounds of transcription for the stronger promoter and calculates the extent of each TI mechanism and resulting RNA production from each promoter. In order to calculate cellular RNA levels, we then consider a model consisting of four ODEs describing RNA mass balance in the cell accounting for their production, k (calculated by the discrete TI simulation), their degradation rate, λ, and dilution due to growth rate, μ (Equations 1–4, Table 3). The value of these parameters are based on experimental values obtained for E. coli [58,59] (S1 Table). In presence of TI, the net rate of production of full length RNA x and y is given by k x = f X·η x, k y = f Y·η y, where η x and η y are the fraction of successful rounds of transcriptions relative to total rounds of transcription from the respective promoter. Similarly, the net rate of production of truncated RNA x k and y h is given by , , where and are the fraction of rounds of transcription producing a truncated RNA of a certain size relative to total rounds of transcription from the respective promoter (Table 1 and Fig 2B). It is important to note that in absence of TI all rounds of transcription produce full-length transcripts, and therefore η x = 1 and η y = 1 whereas no truncated RNAs are produced, i.e. and . The steady state levels of full-length x and y transcripts and truncated transcripts were calculated by numerically solving equations 1–4 (Table 3) considering the initial species concentrations equal to zero.
Table 3. List of equations in the TI model, TI+AR model and gene network model.
| Equation No. | Equation | Model |
|---|---|---|
| 1 | TI | |
| 2 | TI | |
| 3 | TI | |
| 4 | TI | |
| 5 | TI+AR GN | |
| 6 | TI+AR GN | |
| 7 | TI+AR GN | |
| 8 | TI+AR GN | |
| 9 | TI+AR GN | |
| 10 | TI+AR GN | |
| 11 | TI+AR GN | |
| 12 | TI+AR GN | |
| 13 | GN | |
| 14 | GN | |
| 15 | GN | |
| 16 | GN | |
| 17 | GN | |
| 18 | GN |
Model for TI and Antisense RNA interaction based regulation (TI+AR model)
In addition to regulation of full-length RNA production in presence of TI, the TI+AR model accounts for the interaction between fully and partially complementary RNA species produced from the pX-pY locus. Four kinds of RNA interactions are considered, species x:y refers to RNA hybrid complex between full-length sense and antisense transcripts, x k:y and x:y h represent truncated sense and full-length antisense RNA hybrid complexes and vice versa respectively; and x k:y h represents complex formed between truncated sense and truncated antisense RNA (Table 2). Based on lengths of naturally occurring cis-antisense RNAs known to participate in AR, we assume that the entire population of truncated RNAs longer than 60 bp would be able to fold into stem loops, hairpins and bulges required to catalyze interactions [60]. Mass balance analysis leads to a set of eight ODE equations (Equations 5–12 in Table 3) considering the rate of production of transcripts x, y, x k and y h provided by the discrete TI model, k, their mutual RNA interactions, k, degradation rates, λ, and dilution due to volume expansion caused by cell growth, μ. All RNA duplexes are assumed to be unavailable for translation and rapidly targeted for degradation [60]. Since all interacting RNAs are considered to have the requisite secondary structure to participate in RNA interactions, the binding of the four RNA complexes are assumed follow a second order kinetics with rate constants (kbxy, , , and ) within the range of 106−107 M-1 s-1, based on experimentally determined values in literature (Equations 9–12 Table 3, S1 Table) [61,62]. We assume species x:y, x k:y and x:y h to have a first order unbinding kinetics with the same unbinding rate constant, kuxy. Since truncated RNA hybrid complex x k:y h contain shorter regions of complementary, we consider a higher unbinding rate constant, (S1 Table). The steady state levels of full-length x and y transcripts and truncated transcripts were calculated by numerically solving equations 5–12 (Table 3). The initial concentrations for all species were considered to be zero.
Gene Network Model (GN model)
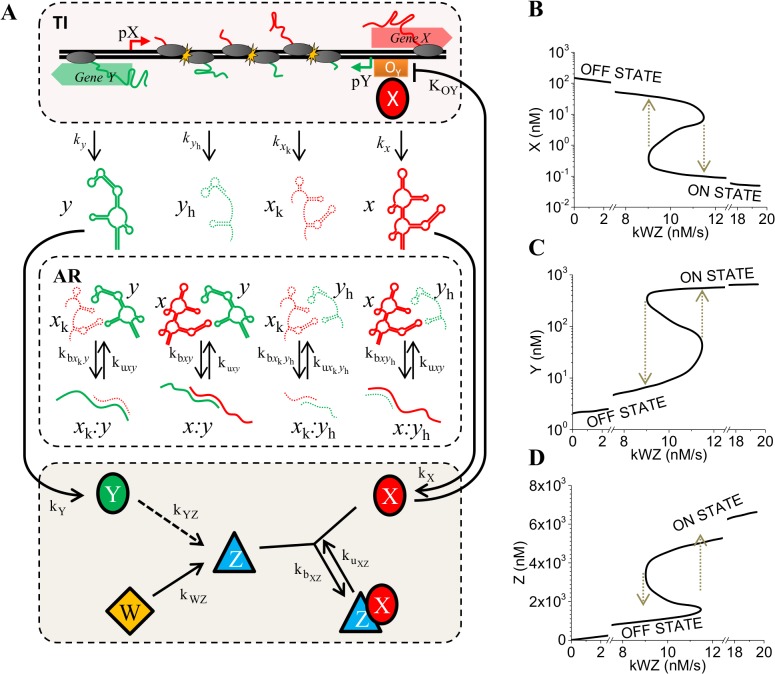
Based on the architecture of naturally occurring cis-antisense systems, we developed a representative cis-antisense transcription based gene regulatory network where one of the gene encodes for a transcriptional factor or an inducer molecule that regulates the expression of the antisense gene [39,63–66]. In order to describe the presence and effect of proteins, TI+AR model was extended to include six additional equations (Equations 13–18) to account for the production and interaction of protein species. We consider genes X and Y encode proteins X and Y respectively which are functionally related. Proteins X and Y are produced by translation of only full-length RNA x and y respectively following first order kinetics based on previously described naturally occurring systems [63,67,68] (Equations 13–14 and S1 Table). Protein X implements a negative feedback loop acting as a transcriptional repressor which binds to the operator site of pY promoter (OY) regulating its strength (Table 1). Upon binding of X, pY is repressed, increasing its RNAP binding time, therefore decreasing its firing rate (f Y). Assuming binding of repressor X to operator site OY reaches rapid equilibrium, the fraction of unbound operator sites is given by Equation 17. The RNAP binding rate at pY is considered to be proportional to the concentration of unbound operator sites at pY as described by Equation 18, where f Y,min and f Y,max are the RNAP firing rates at pY under repressed and de-repressed conditions, respectively. Protein Y implements a positive feedback by indirectly activating production of a transcriptional activator Z, which is considered to bind protein X and relieve repression at pY following a second order kinetics (Equations 15–16). Protein Z may also function as a signaling molecule produced independent of Y activation. We consider Z is also produced from an external source, W, which could be a host gene, a gene from an acquired plasmid, or an environmental signal (released by other cells), following a zero order kinetics, kWZ, (Equation 15). Dissociation of X:Z complex is considered to follow first order kinetics (Equation 16). Parameter nomenclature and their numerical values used are summarized in S1 Table.
For every value of kWZ, the steady state levels of cellular species in presence of TI, AR and protein feedback were calculated by numerically solving equations 5–18 (Table 2) in two steps. Since the RNAP firing rate of the inducible promoter pY depends on protein X levels, the first step involved calculating an initial guess for X (Equation 17–18). To achieve this, an initial guess for transcriptional rates for x RNA, and truncated RNA x k and y h was set at k x = 0.05 nM/s and = = 0.01 nM/s respectively. This initial guess was used to obtain steady state X levels by solving Equations 5–18. The updated protein X level was used to calculate the transcriptional rates for each RNA species using the discrete TI model. Finally, the system of equations (Equations 5–18) was solved a second time with the updated values of transcriptional rates to obtain steady state levels of all cellular species.
Software
Discrete TI model was developed in Matlab. Equations used in TI and TI+AR models were solved using the differential equation solver ode45 in Matlab. GN model equations were solved using Mathematica. Parameters values used were either obtained from the literature or estimated within the biological range and are summarized in S1 Table [49–52,58,59,61,62,67–69]. Only physiologically achievable solutions were considered.
Hill coefficient analysis
Response curves were fitted to the form where H is the Hill coefficient representing the sharpness of the switch response, k max represents the maximum value of the response, K denotes the value of α that results in half of the maximum value; α being the relative promoter strength. Fitting was performed using Method of Least Squares in Microsoft Excel. Adjusted R2 values were >0.95 for all fits. For fits of all x switches, k max = 10.3±0.3 (avg±SD) and K = 0.8±0.1. For fits of all y switches, k max = 39.0±7.8 and K = 1.7±0.2. Positive Hill coefficient values indicate increase in RNA production with increase in α whereas, negative values indicate decrease in RNA production with α increase.
Results
Tunable biological switch response using TI alone
Biological conditions can cause the relative strengths of pX and pY promoters, α, to change from α<1 to α>1, giving rise to a switch response in gene expression (see Methods). For the chosen system of convergent promoters with a given length of overlapping DNA between them (here L = 400 bp, S1 Table), we obtained the production of truncated and full-length transcripts over a range of α values between 0.1 and 2 (Fig 3A and 3B). We assume pX is a constitutive promoter with fixed average RNAP binding and initiation times (τBX = 20 s, τIX = 12 s), whereas pY is an inducible promoter with a variable RNAP binding time (τBY = ατBX), but a fixed RNAP initiation time (τIY = 9.5 s). These parameter values are used hereafter unless otherwise stated. The condition tested here assumes EC’s do not pause and move with an average velocity of 50 bp/s (⟨vx⟩ = ⟨vy⟩ = 50 bp/s) from pX and pY promoters.
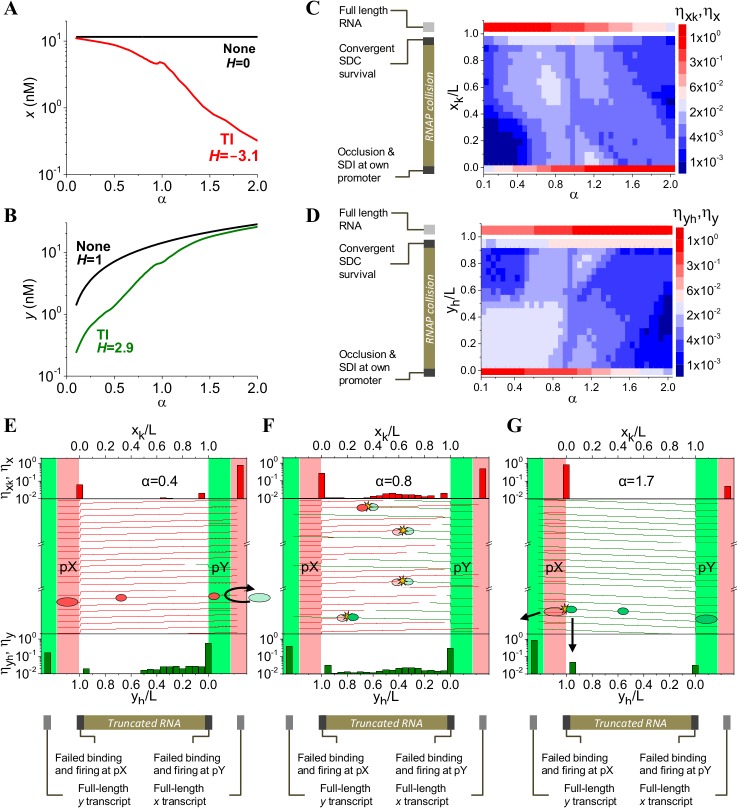
Fig 3. TI gives rise to a switch-like response.
(A, B) Reciprocal switch in expression of full-length x transcript level (A) and full-length y transcript level (B). x and y expression is inversely correlated, while x levels decrease as α increases, y levels increase. H denotes the value of Hill coefficient (see Methods) (C, D) Expression maps for full-length (η x, η y) and truncated () transcripts from pX (C) and pY (D) respectively. Fraction of rounds of transcription which failed to fire (due to occlusion or sitting duck interference, SDI) are depicted at positions x k/L = 0 and y h/L = 0. Production of truncated RNA transcripts due to survival of SDCs at pY and pX promoter is represented at positions x k/L = 0.95 and y h/L = 0.95, respectively. Fraction of successful full-length transcripts (η x, η y) appears at positions x k/L>1 and y h/L>1. (E) Mechanistic representation of occlusion at pY for α = 0.4. Middle panel shows representative trajectories of ECs along the DNA when occlusion at pY is the dominant mechanism. Horizontal green dashed lined at pY region (middle panel) indicate rounds of transcription that were occluded. Top and bottom panels show transcriptional fraction of full-length (η x, η y) and truncated RNA transcripts () originated at pX (top panel) and pY (bottom panel), respectively. Fraction of rounds of transcription which failed to fire (due to occlusion or sitting duck interference) are depicted at positions x k/L = 0 (top panel) and y h/L = 0 (bottom panel). (F, G) Analogous representations showing RNAP collision for α = 0.8 (F) and SDI at pX for α = 1.7 (G) as the dominant mechanism, respectively. For E, F, and G panels, opaque ellipses represent RNAPs that continued transcribing after TI occurred while translucent ellipses denote RNAPs that were not able to bind or remain bound to DNA. The simulations shown in panels A-G correspond to L = 400 bp, τBX = 20 s, τIX = 12 s and τIY = 9.5 s, and α values varied from 0.1 to 2 by varying τBY from 2 to 40 s. Initiation time always remained smaller than binding times in order to avoid self-occlusion.
The steady state levels of full-length x and y transcripts in presence of TI alone (Equations 1–4, Table 3) show that TI can give rise to a considerably sharper switching response compared to the no TI case (Fig 3A and 3B). In presence of TI, the constitutive pX promoter behaves as an inducible promoter with steady state full-length x levels decreasing nearly 2 orders of magnitude as α increases from 0.1 to 2. Conversely, full-length y RNA also increases nearly 2 orders of magnitude, thus demonstrating a reciprocal switch response. This is an outcome of a 41-fold decrease in η x and a 5-fold increase in η y (see Methods, Table 1) as α changes from 0.1 to 2 (Fig 3C and 3D). The sharpness of the switching response is characterized by higher Hill coefficient of -3.1 for x and 2.9 for y; compared to Hill coefficient of 0 for x and 1 for y in absence of TI. Similar switches in gene expression due to TI have been observed in naturally occurring systems such as the 30-fold decrease in expression of the gal promoter [70] and the 5.6-fold repression of bacteriophage 186 pL promoter in the convergent pR-pL system [36].
Changing α can also result in one or more TI mechanisms (occlusion, SDI and RNAP collision) to play a dominant role that can allow for tuning of full-length transcript expression as well as production of specific truncated RNA distributions. Carefully controlling TI may provide an opportunity to maximize production of specific sizes of truncated transcripts that may have the potential to interact with the antisense RNA [39,63,71]. For example, changing α from 0.1 to 0.75 can cause rate of production of truncated RNA of length 260 bp (at position xk/L = 0.65) to increase by 10.7-fold due to increased RNAP collisions (Fig 3C). As a general trend, collisions occur closer to the weaker promoter, i.e. close to pY for α<1 and move towards pX promoter as α increases. When pX is the aggressive promoter, such that α<1, most transcripts from pX end up as a full-length RNA (Fig 3C) whereas those from pY result in occlusion or short truncated RNAs (Fig 3D). The opposite happens when pY is the aggressive promoter, such that α>1 (Fig 3C and 3D).
When α is far from 1 (one promoter is much stronger than the neighboring promoter), occlusion is the dominant TI mechanism since high frequency of ECs severely hinders binding of RNAP at the weaker promoter. This is evident in the range of low α values from α = 0.1 to α = 0.4 (Fig 3C and 3D), where majority of the rounds transcription from the stronger pX promoter occlude RNAP binding at pY (Fig 3E). This is consistent with naturally occurring systems where occlusion has been proposed to be the dominant TI mechanism due to high values of relative promoter strength. For example, α = 0.03 has been previously reported for the Pgal promoter relative to the PL promoter [70]. Upon occlusion gene expression levels of full-length RNA (xk/L>1) are higher from the stronger pX promoter, whereas minimal from the weaker pY promoter (Fig 3E). Although stochasticity allows few binding events to occur at pY, majority of RNAPs that escape occlusion undergo RNAP collision shortly after elongation starts due to high density of opposing ECs originating from the stronger promoter (Fig 3E, bottom panel).
For α closer to 1, RNAP collision and SDI at both promoters gain importance (Fig 3C and 3D). For instance, at α = 0.8, RNAP collision becomes the dominant mechanism (Fig 3F). Since we assume RNAP binding and initiation times, and velocity profiles to follow Gaussian distributions in order to account for inherent biological noise, collisions occur at several loci along the overlapping DNA region ranging from 0 to L-fp/2. Such distributions are affected by the probability of RNAP survival (S1 Fig). As expected, an increase in L leads to increased collision caused due to higher RNAP residence time (S2 Fig). Changing α to 1.7 causes SDI at pX to become the dominant TI mechanism. Under this condition high levels of full-length y transcript are expressed in addition to a narrow truncated RNA size distribution, mainly corresponding to y h transcripts of length L-fp/2 due to SDC survival (Fig 3G). Thus, maximization of SDI can be used to increase production of truncated RNA with length similar to the length of the overlapping region that may further participate in AR. SDI at pY is maximum at α = 1, with an associated transcriptional fraction = 0.032 (at L-fp/2 or x k/L = 0.95) that then decreases by 18.5-fold at α = 2 (Fig 3C and 3D). As α increases, SDI is less important at pY while still being present at pX (Fig 3C and 3D). The frequency of SDI is also strongly influenced by RNAP initiation time at pX and pY. As τIX increases, SDI at pX gains importance and RNAP collision rate decreases, leading to slight sharpening of the switch response (S3A–S3C Fig). Analogous effect in y switch is seen when τIY is increased, while no effect is observed for x switch (S3D–S3F Fig).
RNAP pausing biases switching response
In addition to changing relative RNAP firing rates, RNA production can be affected by the presence of pause sites. The effect of RNAP collision can be enhanced by increasing the residence time of RNAP in the overlapping region; such as during a pausing event, the local speed of RNAP is reduced, resulting in an increased RNAP residence time at a certain base pair
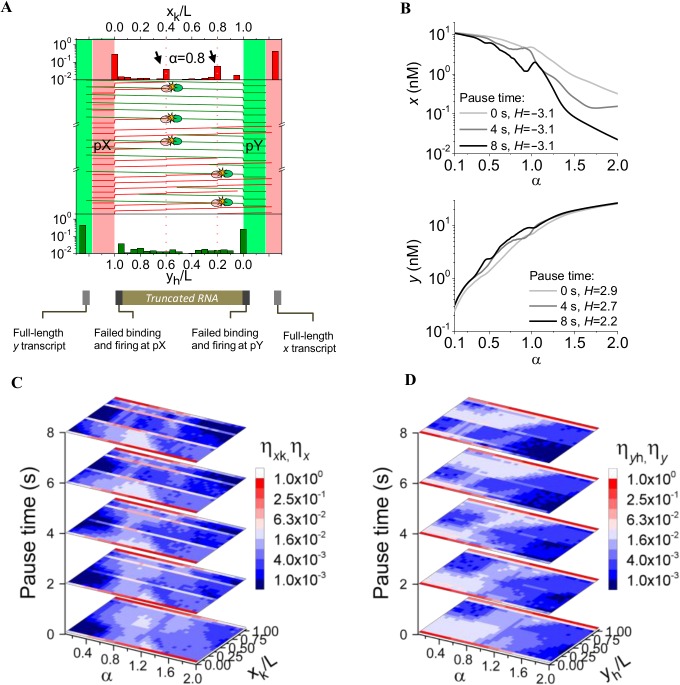
Previous experimental data indicate that transcriptional pausing is ubiquitous in natural systems and usually occurs at every 100–200 bp for durations of 1–6 s on an average [72]. To evaluate the contribution of RNAP pausing to TI we assume RNAP pausing along the sense strand of the DNA at positions 160 bp (xk/L = 0.4) and 320 bp (xk/L = 0.8). As a result the average velocity of ECs in the sense strand decrease ⟨vx⟩<50 bp/s, whereas ⟨vy⟩ = 50 bp/s. Paused RNAP are treated similar to SDCs initiating at the promoter region, i.e. in a collision event between an EC and a paused RNAP, we consider that the latter will fall off the DNA in 90% of the cases while in the remaining 10% of the cases the ECs will stop transcribing. Interestingly, the broad range of sizes of truncated RNA from pX in absence of RNAP pausing converges to narrower distributions in presence of 2 s long pauses [72] due to increased probability of head-on collision that arise from the longer residence time of RNAP at the pause site. The truncated RNA sizes expectedly correspond well with specific location of pause sites (Fig 4A). As an example, when 2 s pauses are considered, at α = 0.8 (where collision is the dominant mechanism in absence of pauses, Fig 3F), production of x k truncated RNA at pause site 160 bp (xk/L = 0.4) and 360 bp (xk/L = 0.8) increase 3.6- and 4.3-fold, respectively. Thus, pausing can be used as design tool to bias production of a truncated RNA predominantly along just one DNA strand. Importantly, such a strategy can be used to design synthetic constructs that express specific truncated RNA products including riboswitches or non-coding RNAs participating in RNA interaction.
Fig 4. TI in the presence of RNAP pause sites.
(A) Mechanistic representation of RNAP collision in presence of two pause sites in the sense strand at positions 160 bp (xk/L = 0.4) and 320 bp (xk/L = 0.8). Pause times are 2 s. Increased production of truncated RNA at the pause sites due to enhanced probability of collision is indicated by arrows. (B) Switch response in x levels maintains sharpness as pause time increases but the dynamic range of x is widened more than one order of magnitude. H denotes the value of Hill coefficient (see Methods). (C) Expression maps for truncated and full-length RNA from pX at different pause times. Truncated RNA production increases as pause time increases. (D) Expression maps for truncated and full-length RNA from pY at different pause times.
Pause sites not only increase the frequency of RNAP collision but also can decrease the transcription rate of full length RNA, and thus impact the switch response. Presence of longer pauses (4 and 8 s) at the same pause sites on sense strand did not significantly impact the sharpness of the x switch (H = -3.1), however, it caused an increase in the dynamic range of x (between α = 0.1 and 2) from 35-fold for no pause (0 s), to 70-fold for 4 s pause, and 475-fold for 8 s pause. Conversely, for y switch the dynamic range (y at α = 0.1/ y at α = 2) was slightly reduced from 106-fold for no pause (0 s), to 84-fold for both 4 s and 8 s pauses (Fig 4B). Pauses also cause shifts in the truncated RNA distribution originating from pY. Both effects become more important as the pause time increases (Fig 4C and 4D). In absence of pauses, short transcripts from pY are produced whereas at long pause times majority of truncated RNAs from pY are longer than 200 bp and therefore more susceptible to AR. Finally, it is important to note that experimental values of RNAP pause sites measured in vivo in E. coli show that pause durations can last more than 20 s, which would enormously increase the chances of RNAP collision [51]. The possibility of further engineering synthetic constructs by modifying the production of truncated RNA that are able to undergo AR expands the range of regulation during antisense transcription.
Coupled effect of TI and cis-antisense RNA interaction during convergent transcription gives rise to higher-order response
We postulate that both full-length RNA and a fraction of the truncated RNA may play a role in regulating expression of antisense gene through silencing of the antisense RNA. A model based on the proposed mechanism of TI and AR during antisense transcription is shown in Fig 5A. The underlying hypothesis is that RNA interaction between complementary sense and antisense truncated as well as full-length RNA species allows sharpening of the switch response compared to TI or AR mechanism alone. Using a two part mathematical model we first estimate the rate of generation of full-length RNA species (k x and k y) and truncated RNA species ( and ) using the discrete TI model, and then use these transcription rates to solve equations 5–12 (Fig 2, Methods section).
Fig 5. Effect of TI and AR on switch response.
(A) TI model predicts the rate of production of truncated (dashed) and full-length RNA (bold). Interactions between different species arise due to presence of secondary structures and complementary sequences. RNA duplexes are targeted for fast degradation. (B, C) Different switch responses of full-length x and y levels depending on presence or absence of TI and AR. Sharpest response is obtained when both mechanisms are coupled, H denotes value of Hill coefficient.
We analyzed the four potential combinations of mechanisms that occur during convergent transcription: presence of both TI and AR regulatory mechanisms (TI+AR), exclusively TI (TI), exclusively AR (AR), and none of the mechanisms of TI and AR (None). We eliminated TI by setting the transcription rate of full-length x and y RNA to the firing rate f X at pX and f Y at pY, respectively (Methods section). To eliminate AR, we set the rate constant for RNA interactions in corresponding equations to zero. Again we varied α from α<1 to α>1 by modifying τBY while keeping τIY, τBX and τIX constant. While the expression level of x stayed constant when varying α for the “None” case, x levels changed for AR, TI and TI+AR cases (Fig 5B and 5C), despite pX being a constitutive promoter. As α increases, strength of pY becomes greater than pX, and therefore gene expression of y increases. Interestingly, the sharpest hypersensitive response for both x and y (Hill coefficient, H = -5.4 for x and 6.8 for y, Methods section) was observed in the TI+AR case, followed by AR and TI cases, which had similar sharpness (TI: H = -3.1 for x and 2.9 for y; AR: -2.5 for x and 3.1 for y). If none of the mechanisms were considered the Hill coefficient was 0 for x as expected because constitutive pX strength is independent of α and 1 for y (No effect of α, y depends solely on f Y). It is important to note that hypersensitive switches confer the system with a higher-order response compared to a first-order response characterized by a linear or ramping behavior. As α increases from 0.1 to 2, TI+AR case allows three orders of magnitude change in x levels whereas no change is observed for “None” case. Similarly, y levels for TI+AR case vary three orders of magnitude compared to just one order for “None” case. The switch observed in x and y levels from α = 0.1 to α = 2 is approximately an order of magnitude wider in the TI+AR case when compared to TI only and AR only cases. For the chosen parameters, switch in gene expression is very similar for TI only and AR only cases. It is important to note that the switching response depends on RNA binding, unbinding and degradation rates of the interacting species.
Protein regulation creates bistable switch behavior
We next consider regulation of the transcriptional process when protein products X and Y, encoded by genes x and y respectively, exert negative and positive feedback to create a gene regulatory network based on cis-antisense transcription (see Methods). We consider that protein X implements a negative feed-back loop by controlling pY strength. Protein Y in turn acts as an antagonist of protein X, and through the indirect activation of protein Z production implements a positive feed-back loop by relieving pY repression via binding of Z to X (Fig 6A). In this and following section, α only varies from α = f Y,min/f X = 0.37 to α = f Y,max/f X = 1.74, corresponding to the repressed state and de-repressed state of pY, respectively (S1 Table). We numerically solved equations 5–18 to analyze the steady state behavior of the system in response to different rates of production (kWZ) of transcriptional activator/signaling molecule Z. Steady state solutions show that coupling TI and AR with feedback from regulatory proteins give rise to a characteristic bistable switch response. When bistability is present, cells can adopt two experimentally observable distinct states depending on the production rate of Z (Fig 6B) [73]. The bistable curve comprises the characteristic S-shaped section where multiple steady states reside. Two of these are stable steady states that correspond to ON (lower curve, Fig 6B) and OFF state of the switch (upper curve, Fig 6B), whereas the unstable steady state in the middle is not observed experimentally. At low rates of production of Z the systems exists in an OFF state which is characterized by low expression levels of Y and Z (Fig 6C and 6D), but high expression levels of repressor X (Fig 6B). As kWZ increases the system continues to be in the OFF state until it reaches a threshold rate of 11.5 nM/s, where the systems transitions to the ON state characterized by nearly two orders of magnitude increase in Z and Y levels and decrease in repressor X level. Conversely, once the switch is turned ON, the system continues to be in the ON state until the production rate kWZ drops below 8.8 nM/s. The system thus demonstrates a sophisticated hysteresis response to Z production rate, marked by well separated ON to OFF states occurring at different threshold rates. It is important to note that both hypersensitive and bistable switches are considered higher-order because their non-linearity indicates cooperation between different mechanisms integrating the system. In the model proposed here interactions arise between the three regulatory layers: TI, AR and protein regulation.
Fig 6. Antisense transcription coupled with protein feedback gives rise to bistability.
(A) Successful full-length x and y transcripts that do not undergo antisense interaction are free to be translated into proteins X and Y respectively. Production of inducer molecule, Z, is indirectly activated by protein Y. Protein X implements a negative feed-back loop by binding to operator site OY and repressing promoter pY. Z binds to X and relieves the repression of pY promoter. (B-D) These multiple regulatory layers enable cells to demonstrate a higher-order a bistable switch response to different rates of production of W (denoted by kWZ). ON state is characterized by production of proteins Y and Z while OFF state is characterized by production of protein X. Threshold kWZ value to switch between OFF to ON states is 11.5 nM/s whereas the threshold for the inverse switch between ON to OFF states occurs at kWZ = 8.8 nM/s.
Tunability of bistable switch behavior
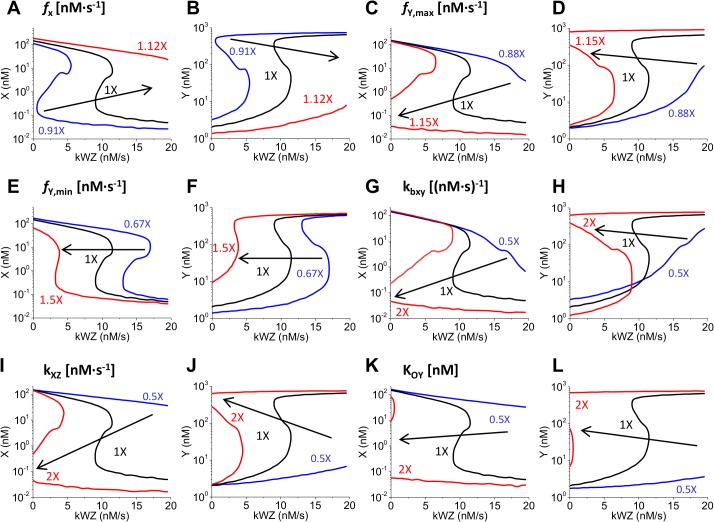
We next performed a sensitivity analysis to evaluate the impact of individual parameters on the steady state response in order to identify those that allow fine tuning of the dose-response curve. Parameters were divided into three groups: (i) transcriptional parameters, including the ones that affect the TI model and therefore influence the RNAP collision loci and truncated RNA distribution (from f X to L in S1 Table), (ii) RNA species parameters, including binding and unbinding constants between the different hybrids and their respective degradation rates (from kbxy to in S1 Table) and (iii) protein species parameters, including translational rates, binding and unbinding of protein molecules and their respective degradations (from kX to KOY in S1 Table). While keeping the values of the remaining parameters constant, each parameter of the second and third groups was decreased and increased 2-fold. However, each transcriptional parameter was modified in a smaller range so that it remained in the same range of values used in previous sections. Interestingly, parameter tuning led to different dose-response curves ranging from ramp-like behavior to a bistable switch. In this section, we describe some of the parameters that the bistable response curve was most sensitive to; parameters that did not significantly modify the response are only briefly mentioned. The former can be used to tune the cellular response of synthetic genetic constructs based on cis-antisense transcription.
In general, fine tuning of the parameters related with relative promoter strength α modified both the bistable range and type of switch behavior. Bistable region is highly sensitive to f X as a 12% increase (or 1.12 times the values shown in S1 Table, also denoted as 1.12X) caused the bistable switch to shift to higher values of kWZ, with eventual loss of bistability and transition into a ramping switch response (Fig 7A and 7B). Decreasing f X by 9% (or 0.91X) caused the bistable curve to shift to lower values of kWZ needed to observe the bistable region. Further decrease caused the bistable switch to become irreversible. It is also important to note that relative promoter strength at the de-repressed state of pY (α = f Y,max/f X) strongly influences the shape of the dose-response curve (Fig 7C and 7D). As f Y,max increases, the de-repressed pY becomes stronger and the bistable region shifts to lower values of kWZ because less full-length x transcripts are obtained, whereas more full-length y transcripts are synthesized due to TI, at the same rates of production of Z. This results in lower levels of protein X and therefore repression at OY operator site is more easily relieved. At f Y,max lower than 0.93X, which corresponds to weaker strength of de-repressed pY promoter compared to pX, we observe the bistable switch to transition into an ultrasensitive response. Further decrease in f Y,max yields to a Michaelian behavior (f Y,max = 0.88X). As pY at the repressed state gets stronger (f Y,min increases), bistable range shrinks, at the same time the curve is shifted to lower kWZ values. For f Y,min = 1.5X we observe bistability for a kWZ range ~0.6 nM/s (Fig 7E and 7F). On the other hand, higher initiation times at the antisense promoter increases the levels of full-length sense transcript whereas decreasing levels of truncated sense transcripts. However these changes did not modify the bistable range. Longer overlapping regions increased production of truncated RNA levels and resulted in higher hybrid RNA species, however changing L did not significantly modify the bistable range.
Fig 7. Parameters in GN model that impact bistable switch behavior.
Examples of some of the parameters that had a greater effect when fine-tuned. Protein X and Y levels are shown for each modified parameter. Arrows indicate the way the curve shifts as the following parameters are individually tuned relative to the values shown in S1 Table. (A, B) f X, firing rate at pX. (C, D) f Y,max, firing rate at pX at de-repressed state. (E, F) f Y,min, firing rate at pX at repressed state. (G, H) kbxy, binding rate of full-length transcripts x and y. (I, J) kXZ, binding rate of protein complex X:Z. (K, L) KOY, equilibrium binding constant of protein X at OY site.
Interestingly, x and y binding kinetics also had a significant effect on the system (Fig 7G and 7H). As kbxy increases, binding of full-length RNA transcripts increases full-length transcript sequestration. This caused widening of the bistable range, indicating that higher antisense interaction rates can serve as a noise filter due to increase in the separation between the thresholds to switch from ON to OFF. For low kbxy values (0.5X) a Michaelian response is observed, where X levels decrease over 2 orders of magnitude as kWZ increases from 0 to 20 nM/s. A 4-fold increase in kbxy (2X) transforms the response into a bistable switch, with X levels corresponding to OFF and ON states separated by 4 orders of magnitude, along with bistable region of nearly 10 kWZ units. Loss of bistability as kbxy decreases suggests that AR is a key regulatory player in order to obtain a bistable switch. This was confirmed by studying the previous None, TI, AR and TI+AR cases in presence of the protein regulation, and observing loss of bistability for None and TI cases (S4 Fig). and slightly shifted the bistable curve to higher and lower values of kWZ, respectively.
Degradation rate of full-length x transcript significantly impacted the system. As expected, both x and X levels at kWZ = 0 nM/s were decreased 6.6- and 7-fold, respectively when λ x increased 4-fold, which also led to a 61.5-fold narrower bistable region at lower kWZ values (S5A and S5B Fig). In the case of λ y, it also had a notorious effect on the bistable range (S5C and S5D Fig). A 26% increase in the value of λ y, caused loss of bistability. On the other hand, as λ y decreases, the higher accumulation of full-length y transcript causes a sharp increase in the levels of inducer, Z, that binds to repressor X and results in a wider range of kWZ values where pY can compete with pX, thereby expanding the bistable region. and slightly shifted the curve to the left and the right respectively; similar changes were caused by and . Degradation rates , and did not have a significant effect on the bistable curve although, as expected, these modified the levels of their respective hybrid RNA species.
Regarding the third group of parameters involving proteins, we observed that all of them significantly influenced the shape of the dose-response curve. Increased translational rate of protein X shifted the bistable region to higher values of kWZ, and as expected, also led to higher levels of protein X at the OFF state. Increasing translation rate of protein Y expanded the bistable region. Translational rate of protein Y, kY, greatly impacts both protein Y and Z levels, as Z is indirectly activated by Y. Change in degradation rates of proteins X and Y had an opposite effect to changes in translational rates. Another important parameter is the binding kinetics of repressor and inducer molecule, kXZ, which also affects the robustness of the switch-like behavior by expanding the bistable region when increased (Fig 7I and 7J). Increases in kXZ values greater than 72% led to an irreversible bistable switch, whereas bistability was lost turning to an ultrasensitive response when kXZ was decreased below 43% of its original value. Importantly, the system is also sensitive to KOY, the parameter controlling the binding of repressor to operator site OY, making it an important fine-tuning element (Fig 7K and 7L). Higher KOY values implies weaker repression of pY; in turn a stronger pY competes more effectively with pX, thus lower levels of transcripts x are produced, resulting in lower kWZ values required to turn on expression of protein Y.
Discussion
Convergent arrangements of promoters are widespread in archea, bacteria and eukaryotes [18,74,75]. Although prevalent in shorter compact genomes in prokaryotes, the presence of thousands of such antisense gene pairs in relatively larger eukaryotic genomes [3,76,77] indicates that antisense transcription is an important regulatory mechanism conserved over evolution [78]. Our mathematical model highlights the regulatory advantage offered by coupled effects of TI and AR based regulation during antisense transcription. Using TI alone cells can achieve a hypersensitive switching response (Fig 3A–3D). We show that TI exerted by an inducible promoter on a convergent constitutive promoter, can cause the latter to demonstrate inducible expression (Fig 3A and 3B). Depending on the relative strengths of the promoters, different mechanisms of TI may dominate. Our model shows that RNAP collision has greater effect when promoters have similar strength (α close to 1). This is evident from previous studies on PQ-PX convergent promoters of pCF10 plasmid in E. faecalis [39,71], under repressed conditions when both promoters have similar strengths the constitutive PX promoter exerts nearly 10 fold decrease in activity of the PQ promoter. Occlusion and SDI occur more frequently when one promoter is much more aggressive (α far from 1). This is exemplified by the pL-pR system of convergent promoters in coliphage 186, where, as a result of SDCs, a 5.6-fold reduction in activity of the weaker lysogenic (pL) promoter was observed, resulting in switching between the lysogenic and lytic states [36]. Experiments [36,39,51] also indicate that minor differences in strengths of convergent promoters can give rise to significant TI, such as during convergent transcription in the PR-PRE promoter pair of bacteriophage λ where TI from the weaker PRE promoter resulted in a 5.5 fold decrease in expression from the stronger PR promoter due to occlusion [51].
Previously, Sneppen et al. developed stochastic, numerical (mean field) and analytical approaches to fit TI in vivo data on sets of convergent promoters [41]; but concluded that the analytical model turns increasingly inaccurate as promoter strengths become similar or when the overlapping distance is large, in both cases overestimating interference at the weak promoter. Even though our approach is different, both models agree that: (1) SDI increases as the initiation time approaches the binding time; (2) occlusion becomes more important at the weaker promoter as the strength of the stronger promoter increases, i.e. α<<1 and α>>1, and (3) TI increases as the overlapping region becomes longer due to larger number of collisions. Therefore both models are in agreement, with the advantage of being able to calculate production of truncated RNAs in our model.
A less explored aspect of TI relates to the potential regulatory role of cis antisense RNA produced from both convergent promoters. In nature, both short [13,79] and long antisense RNAs [13,80–82] have been shown to participate in antisense interaction in various bacterial and mammalian systems. Similar to our model, previous antisense RNA models reported by Levine et al. [42] and Mehta et. al [43] also used a second order RNA binding kinetics to describe RNA interaction between sense and antisense RNA transcripts. These models only accounted for RNA interaction between transcripts expressed in trans, which is analogous to the AR only model shown in Fig 5. The cellular concentrations and the switching response of RNA predicted by our AR model corroborates with that reported by Levine et al and Mehta et al, thus highlighting the generality of our model. Our model further shows that adding cis-RNA interaction along with TI mechanism can considerably sharpen the switching response with as high as 3 orders of magnitude difference in of full-length RNA levels (Fig 5B and 5C). The relative stoichiometry of sense and antisense transcripts influences the final extent of suppression, which is in turn influenced by the generation rate and half-life of the transcripts. We also demonstrate situations where production of specific sizes of truncated RNA can be enhanced for AR, such as in the presence of pause sites (Fig 4).
Only few experimental systems have accounted for the role of truncated RNA including the prgQ/prgX operon of pCF10 plasmid in E. faecalis [39]. In this system truncated cis-antisense RNA transcripts with sizes ranging between 100–200 nt and 80–200 nt were expressed from convergent promoters PQ and PX respectively, and were more prominent when the promoters were of similar strengths, than when PQ activity was 10 times stronger than PX. Furthermore, these truncated transcripts were shown to inhibit expression of both full-length prgX and prgQ mRNA expression. Similarly, the ubiG/mccBA operon of Clostridium acetobutylicum has been shown to produce truncated RNA of various sizes ranging between 200–700 nt [83]. These truncated RNA lack Rho-dependent terminator structures at 3’ end, and their expression has been shown to be independent of RNase III and RNAse J1/J2 cleavage, potentially indicating that the termination mechanism could be based on RNAP collision.
Antisense transcription can result in complex cellular behavior especially in context of a biological gene network. Presence of a feedback loop, implemented in our generalized system by the control of promoter pY strength by protein X encoded from the convergent pX promoter enables the system to behave in a bistable fashion (Figs 6 and 7A–7L). Such gene networks with feedback loops have been observed in naturally occurring systems where sRNA plays an important role. OmrA and OmrB form a direct feedback regulation of OmpR, as well as RybB and σE transcription factor [84]. Indirect feedback regulation also exists as in the RyhB regulation of Fur [84]. We show that, in presence of a protein regulatory network, coupled effect of TI and AR is capable of demonstrating ramping, Michaelian (hyperbolic), ultrasensitive, as well as reversible and irreversible bistable behaviors (Fig 7A–7L). The bistable response is more sensitive to certain a set of parameters (such as f X, f Y,max, f Y,min, , , kbxy, KOY); which highlights the opportunity to tweak cellular responses when designing synthetic genetic devices based on cis-antisense transcription. Even for the parameters the system is more sensitive to, majority of them can be modified up to 4-fold without losing bistability. This confers the system with robustness as the noisy fluctuations are not expected to cause changes greater than 10% or 0.1-fold as previously shown in Elowitz et al. [85].
Reversible bistable switches are especially important for their robustness, allowing cells to make important decisions to adapt to new environments such production of antibiotics [63], plasmid conjugation [86], motility [87] or virulence status [88]. Some of these decisions involve the whole population and are usually require cellular communication via quorum sensing by means of a signaling molecule [89]. Bistability reduces the influence of signal noise that is inherent to biological systems due to stochasticity in cellular processes and environmental conditions. It does so by conferring the system with separation of threshold values in the production rate of signaling molecule to switch from one state to the other. The prgQ/prgX operon of E. faecalis [28,39] controlling conjugative transfer of drug resistance between cells has been shown to demonstrate bistable switch response using antisense transcription. On the other hand, the CopR system of B. subtilis controlling plasmid copy number has been speculated to be regulated by the three regulatory layers presented here: TI, AR and protein regulation of the transcriptional process, but no bistability has been observed [64]. In ubiG/mccBA operon of C. acetobutlyicum, both mechanisms of TI and RNA interaction confer a genetic switch regulating the expression of ubiG operon, which contains genes required for conversion of methionine to cysteine [83]. Similarly, antisense transcription has also been shown to facilitate two distinct bistable phenotypes in infectious pathogen Bordetella [90]. Finally, antisense transcription was recently shown to be important for functioning of circadian clocks [91].
Recent discovery of many new small RNAs, often with unknown function, indicate the presence of promoters opposite to protein-coding regions [92–94]. Most of these promoters in antisense orientation may express cis-antisense RNA not discovered yet that regulate the protein encoded by the antisense gene. Better understanding of TI and AR will provide important insights into biological functioning of microorganisms as well as higher organisms and development of improved biological systems. Given that promoter strength, overlapping DNA sequence and length is highly tunable, antisense transcription could be exploited to tweak naturally existing networks or create novel networks for synthetic biology applications. Moreover, genetic engineering taking advantage of these layers of regulation could allow us to develop engineered cells acting as biological sensors that perform different functions depending on the environmental conditions. Finally, although widespread presence of antisense transcription exists, further experimental characterization studies need to be done to understand whether antisense transcription is a fortuitous phenomenon in in nature or a well-designed set-up for gene regulation that could be controlled even at the genome scale.
Supporting Information
(DOCX)
(A, B) Expression maps of full-length (η x, η y) and truncated () transcripts originating from pX (A) and pY (B), respectively for a range of percentage of RNAP survival in event of RNAP collision. As RNAP survival increases less truncated RNA is produced (bluer central region). (C) Switch response in full-length x and y transcript levels becomes sharper for lower percentage of RNAP survival, at 80% the Hill coefficient is -3.1 for x and 2.9 for y, at 40% it is -4.0 for x and 4.4 for y, and at 0% it is -7.8 for x and 8.2 for y.
(TIFF)
(A, B) Effect of τIX. Maps of truncated and full-length transcripts originating from pX (A) and pY (B), respectively, at different initiation intervals at pX, τIX. Longer initiation times at pX increase probability of sitting duck interference at pX. Dislodgement of more sitting duck complexes at pX cause decreased RNAP collision and lowers expression of full-length x transcripts. (C) The switch response of x and y RNA at different τIX values. x transition becomes sharper at higher τIX values. (D, E) Effect of τIY. As the initiation time at pY increases, analogous effect is seen. Sitting duck interference at pY increases and less RNAP collisions occur. (F) Switch response in x and y levels at different τIY values. y levels are lowered at higher τIY.
(TIFF)
(A, B) Expression maps of truncated and full-length transcripts originating from pX (A) and pY (B), respectively, at different values of overlapping length, L. Longer overlapping regions yield to increased RNAP collisions. (C) Enhanced collisions lower the expression of full-length x and y transcripts. In this case, no clear trend was observed for the Hill coefficient.
(TIFF)
(A, B) Levels of full-length x (A) and y (B) transcripts, respectively, for None, TI, AR and TI+AR cases of antisense transcription in presence of the gene regulatory network implemented by proteins X, Y and Z. Bistability is only observed when AR is present (AR and TI+AR cases). When TI is coupled with AR (TI+AR case) the bistable range is expanded and the switch response is widened.
(TIFF)
Protein X and Y levels are shown for each modified parameter. Arrows indicate the way the curve shifts as the tuned parameter increases. (A, B) λ x, degradation rate of full-length x. (C, D) λ y, degradation rate of full-length y.
(TIFF)
Acknowledgments
This work has been funded by William M. Keck Foundation and University of Colorado start-up funds to AC. AEB was supported by Balsells Graduate fellowship from Balsells Foundation and University of Colorado. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
Data Availability
All relevant data are within the paper and its Supporting Information files.
Funding Statement
This work was supported by William M. Keck Foundation and University of Colorado start-up funds to AC. AEB was supported by Balsells Graduate fellowship from Balsells Foundation and University of Colorado. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Treviño-Quintanilla LG, Freyre-González JA, Martínez-Flores I. Anti-Sigma Factors in E. coli: Common Regulatory Mechanisms Controlling Sigma Factors Availability. Curr Genomics. 2013;14: 378–87. 10.2174/1389202911314060007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Peterson EJR, Reiss DJ, Turkarslan S, Minch KJ, Rustad T, Plaisier CL, et al. A high-resolution network model for global gene regulation in Mycobacterium tuberculosis. Nucleic Acids Res. 2014; 1–13. 10.1093/nar/gku777 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Katayama S, Tomaru Y, Kasukawa T, Waki K, Nakanishi M, Nakamura M, et al. Antisense transcription in the mammalian transcriptome. Science. 2005;309: 1564–6. 10.1126/science.1112009 [DOI] [PubMed] [Google Scholar]
- 4. Sittka A, Lucchini S, Papenfort K, Sharma CM, Rolle K, Binnewies TT, et al. Deep sequencing analysis of small noncoding RNA and mRNA targets of the global post-transcriptional regulator, Hfq. PLoS Genet. 2008;4: e1000163 10.1371/journal.pgen.1000163 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Mitschke J, Georg J, Scholz I, Sharma CM, Dienst D, Bantscheff J, et al. An experimentally anchored map of transcriptional start sites in the model cyanobacterium Synechocystis sp. PCC6803. Proc Natl Acad Sci U S A. 2011;108: 2124–2129. 10.1073/pnas.1015154108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Sharma CM, Hoffmann S, Darfeuille F, Reignier J, Findeiss S, Sittka A, et al. The primary transcriptome of the major human pathogen Helicobacter pylori. Nature. 2010;464: 250–255. 10.1038/nature08756 [DOI] [PubMed] [Google Scholar]
- 7. Neil H, Malabat C, D’Aubenton-Carafa Y, Xu Z, Steinmetz LM, Jacquier A. Widespread bidirectional promoters are the major source of cryptic transcripts in yeast. Nature. Nature Publishing Group; 2009;457: 1038–1042. 10.1038/nature07747 [DOI] [PubMed] [Google Scholar]
- 8. Grieshaber NA, Grieshaber SS, Fischer ER, Hackstadt T. A small RNA inhibits translation of the histone-like protein Hc1 in Chlamydia trachomatis. Mol Microbiol. 2006;59: 541–550. 10.1111/j.1365-2958.2005.04949.x [DOI] [PubMed] [Google Scholar]
- 9. Altuvia S, Weinstein-Fischer D, Zhang a, Postow L, Storz G. A small, stable RNA induced by oxidative stress: role as a pleiotropic regulator and antimutator. Cell. 1997;90: 43–53. [DOI] [PubMed] [Google Scholar]
- 10. Hoe CH, Raabe C a, Rozhdestvensky TS, Tang TH. Bacterial sRNAs: Regulation in stress. International Journal of Medical Microbiology. Elsevier GmbH.; 2013. pp. 217–229. 10.1016/j.ijmm.2013.04.002 [DOI] [PubMed] [Google Scholar]
- 11. Stazic D, Lindell D, Steglich C. Antisense RNA protects mRNA from RNase E degradation by RNA-RNA duplex formation during phage infection. Nucleic Acids Res. 2011;39: 4890–9. 10.1093/nar/gkr037 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Pichon C, Felden B. Small RNA genes expressed from Staphylococcus aureus genomic and pathogenicity islands with specific expression among pathogenic strains. Proc Natl Acad Sci U S A. 2005;102: 14249–14254. 10.1073/pnas.0503838102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Lee E-J, Groisman E a. An antisense RNA that governs the expression kinetics of a multifunctional virulence gene. Mol Microbiol. 2010;76: 1020–33. 10.1111/j.1365-2958.2010.07161.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Monti L, Cinquetti R, Guffanti A, Nicassio F, Cremona M, Lavorgna G, et al. In silico prediction and experimental validation of natural antisense transcripts in two cancer-associated regions of human chromosome 6. Int J Oncol. 2009;34: 1099–1108. 10.3892/ijo_00000237 [DOI] [PubMed] [Google Scholar]
- 15. Berteaux N, Aptel N, Cathala G, Genton C, Coll J, Daccache A, et al. A novel H19 antisense RNA overexpressed in breast cancer contributes to paternal IGF2 expression. Mol Cell Biol. 2008;28: 6731–45. 10.1128/MCB.02103-07 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Marshall L, White RJ. Non-coding RNA production by RNA polymerase III is implicated in cancer. Nat Rev Cancer. 2008;8: 911–914. 10.1038/nrc2539 [DOI] [PubMed] [Google Scholar]
- 17. Coiras M, López-Huertas MR, Pérez-Olmeda M, Alcamí J. Understanding HIV-1 latency provides clues for the eradication of long-term reservoirs. Nat Rev Microbiol. Nature Publishing Group; 2009;7: 798–812. 10.1038/nrmicro2223 [DOI] [PubMed] [Google Scholar]
- 18. Brantl S. Regulatory mechanisms employed by cis-encoded antisense RNAs. Current Opinion in Microbiology. 2007. pp. 102–109. 10.1016/j.mib.2007.03.012 [DOI] [PubMed] [Google Scholar]
- 19. Papenfort K, Vogel J. Multiple target regulation by small noncoding RNAs rewires gene expression at the post-transcriptional level. Res Microbiol. 2009;160: 278–287. 10.1016/j.resmic.2009.03.004 [DOI] [PubMed] [Google Scholar]
- 20. Waters LS, Storz G. Regulatory RNAs in Bacteria. Cell. Elsevier Inc.; 2009. pp. 615–628. 10.1016/j.cell.2009.01.043 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Georg J, Hess WR. cis-antisense RNA, another level of gene regulation in bacteria. Microbiol Mol Biol Rev. 2011;75: 286–300. 10.1128/MMBR.00032-10 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Shimoni Y, Friedlander G, Hetzroni G, Niv G, Altuvia S, Biham O, et al. Regulation of gene expression by small non-coding RNAs: a quantitative view. Mol Syst Biol. 2007;3: 138 10.1038/msb4100181 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Sayed N, Jousselin A, Felden B. A cis-antisense RNA acts in trans in Staphylococcus aureus to control translation of a human cytolytic peptide. Nature Structural & Molecular Biology. Nature Publishing Group; 2011. pp. 105–112. 10.1038/nsmb.2193 [DOI] [PubMed] [Google Scholar]
- 24. Bouvier M, Sharma CM, Mika F, Nierhaus KH, Vogel J. Small RNA Binding to 5′ mRNA Coding Region Inhibits Translational Initiation. Mol Cell. 2008;32: 827–837. 10.1016/j.molcel.2008.10.027 [DOI] [PubMed] [Google Scholar]
- 25. Arraiano CM, Andrade JM, Domingues S, Guinote IB, Malecki M, Matos RG, et al. The critical role of RNA processing and degradation in the control of gene expression. FEMS Microbiology Reviews. 2010. pp. 883–923. 10.1111/j.1574-6976.2010.00242.x [DOI] [PubMed] [Google Scholar]
- 26. Dühring U, Axmann IM, Hess WR, Wilde A. An internal antisense RNA regulates expression of the photosynthesis gene isiA. Proc Natl Acad Sci U S A. 2006;103: 7054–7058. 10.1073/pnas.0600927103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Kawano M, Aravind L, Storz G. An antisense RNA controls synthesis of an SOS-induced toxin evolved from an antitoxin. Mol Microbiol. 2007;64: 738–754. 10.1111/j.1365-2958.2007.05688.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Johnson CM, Manias D a, Haemig H a H, Shokeen S, Weaver KE, Henkin TM, et al. Direct evidence for control of the pheromone-inducible prgQ operon of Enterococcus faecalis plasmid pCF10 by a countertranscript-driven attenuation mechanism. J Bacteriol. 2010;192: 1634–1642. 10.1128/JB.01525-09 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Stork M, Di Lorenzo M, Welch TJ, Crosa JH. Transcription termination within the iron transport-biosynthesis operon of Vibrio anguillarum requires an antisense RNA. J Bacteriol. 2007;189: 3479–3488. 10.1128/JB.00619-06 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Giangrossi M, Prosseda G, Tran CN, Brandi A, Colonna B, Falconi M. A novel antisense RNA regulates at transcriptional level the virulence gene icsA of Shigella flexneri. Nucleic Acids Res. 2010;38: 3362–3375. 10.1093/nar/gkq025 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Opdyke JA, Kang J, Storz G. GadY, a Small-RNA Regulator of Acid Response Genes in Escherichia coli. J Bacteriol. 2004;186: 6698–6705. 10.1128/JB.186.20.6698 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Thomason MK, Storz G. Bacterial antisense RNAs: how many are there, and what are they doing? Annu Rev Genet. 2010;44: 167–188. 10.1146/annurev-genet-102209-163523 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Shearwin KE, Callen BP, Egan JB. Transcriptional interference—A crash course. Trends in Genetics. 2005. pp. 339–345. 10.1016/j.tig.2005.04.009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Martens J a, Laprade L, Winston F. Intergenic transcription is required to repress the Saccharomyces cerevisiae SER3 gene. Nature. 2004;429: 571–574. 10.1038/nature02538 [DOI] [PubMed] [Google Scholar]
- 35. Dodd IB, Egan JB. Action at a distance in CI repressor regulation of the bacteriophage 186 genetic switch. Mol Microbiol. 2002;45: 697–710. 10.1046/j.1365-2958.2002.03038.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Callen BP, Shearwin KE, Egan JB. Transcriptional interference between convergent promoters caused by elongation over the promoter. Mol Cell. 2004;14: 647–656. 10.1016/j.molcel.2004.05.010 [DOI] [PubMed] [Google Scholar]
- 37. Xu J, Koudelka GB. Mutually exclusive utilization of P(R) and P(RM) promoters in bacteriophage 434 O(R). J Bacteriol. 2000;182: 3165–3174. 10.1128/JB.182.11.3165-3174.2000 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Greger IH, Aranda A, Proudfoot N. Balancing transcriptional interference and initiation on the GAL7 promoter of Saccharomyces cerevisiae. Proc Natl Acad Sci U S A. 2000;97: 8415–8420. 10.1073/pnas.140217697 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Chatterjee A, Johnson CM, Shu C-C, Kaznessis YN, Ramkrishna D, Dunny GM, et al. Convergent transcription confers a bistable switch in Enterococcus faecalis conjugation. Proc Natl Acad Sci U S A. 2011;108: 9721–9726. 10.1073/pnas.1101569108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Epshtein V, Toulmé F, Rachid Rahmouni A, Borukhov S, Nudler E. Transcription through the roadblocks: The role of RNA polymerase cooperation. EMBO J. 2003;22: 4719–4727. 10.1093/emboj/cdg452 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Sneppen K, Dodd IB, Shearwin KE, Palmer AC, Schubert R a, Callen BP, et al. A mathematical model for transcriptional interference by RNA polymerase traffic in Escherichia coli. J Mol Biol. 2005;346: 399–409. 10.1016/j.jmb.2004.11.075 [DOI] [PubMed] [Google Scholar]
- 42. Levine E, Zhang Z, Kuhlman T, Hwa T. Quantitative characteristics of gene regulation by small RNA. PLoS Biol. 2007;5: e229 10.1371/journal.pbio.0050229 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Mehta P, Goyal S, Wingreen NS. A quantitative comparison of sRNA-based and protein-based gene regulation. Mol Syst Biol. 2008;4: 221 10.1038/msb.2008.58 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Record M, Reznikoff W. Escherichia coli RNA polymerase (Es70), promoters, and the kinetics of the steps of transcription initiation. 1996;
- 45. Hsu LM. Promoter clearance and escape in prokaryotes. Biochimica et Biophysica Acta—Gene Structure and Expression. 2002. pp. 191–207. 10.1016/S0167-4781(02)00452-9 [DOI] [PubMed] [Google Scholar]
- 46. Murakami KS, Darst S a. Bacterial RNA polymerases: The wholo story. Current Opinion in Structural Biology. 2003. pp. 31–39. 10.1016/S0959-440X(02)00005-2 [DOI] [PubMed] [Google Scholar]
- 47. Hasty J, Pradines J, Dolnik M, Collins JJ. Noise-based switches and amplifiers for gene expression. Proc Natl Acad Sci U S A. 2000;97: 2075–80. 10.1073/pnas.040411297 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Smits WK, Kuipers OP, Veening J-W. Phenotypic variation in bacteria: the role of feedback regulation. Nat Rev Microbiol. 2006;4: 259–271. 10.1038/nrmicro1381 [DOI] [PubMed] [Google Scholar]
- 49. Liang S, Bipatnath M, Xu Y, Chen S, Dennis P, Ehrenberg M, et al. Activities of constitutive promoters in Escherichia coli. J Mol Biol. 1999;292: 19–37. 10.1006/jmbi.1999.3056 [DOI] [PubMed] [Google Scholar]
- 50. Vo N V., Hsu LM, Kane CM, Chamberlin MJ. In vitro studies of transcript initiation by Escherichia coli RNA polymerase. 3. Influences of individual DNA elements within the promoter recognition region on abortive initiation and promoter escape. Biochemistry. 2003;42: 3798–3811. 10.1021/bi026962v [DOI] [PubMed] [Google Scholar]
- 51. Palmer AC, Ahlgren-Berg A, Egan JB, Dodd IB, Shearwin KE. Potent Transcriptional Interference by Pausing of RNA Polymerases over a Downstream Promoter. Mol Cell. Elsevier; 2009;34: 545–555. 10.1016/j.molcel.2009.04.018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52. Tang G-Q, Roy R, Bandwar RP, Ha T, Patel SS. Real-time observation of the transition from transcription initiation to elongation of the RNA polymerase. Proc Natl Acad Sci U S A. 2009;106: 22175–22180. 10.1073/pnas.0906979106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Lutz R, Lozinski T, Ellinger T, Bujard H. Dissecting the functional program of Escherichia coli promoters: the combined mode of action of Lac repressor and AraC activator. Nucleic Acids Res. 2001;29: 3873–3881. 10.1093/nar/29.18.3873 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54. Krummel B, Chamberlin MJ. Structural analysis of ternary complexes of Escherichia coli RNA polymerase. Deoxyribonuclease I footprinting of defined complexes. J Mol Biol. 1992;225: 239–50. [DOI] [PubMed] [Google Scholar]
- 55. Bai L, Shundrovsky A, Wang MD. Sequence-dependent kinetic model for transcription elongation by RNA polymerase. J Mol Biol. 2004;344: 335–349. 10.1016/j.jmb.2004.08.107 [DOI] [PubMed] [Google Scholar]
- 56. Neuman KC, Abbondanzieri E a, Landick R, Gelles J, Block SM. Ubiquitous Transcriptional Pausing Is Independent of RNA Polymerase Backtracking. Cell. 2003. pp. 437–447. 10.1016/S0092-8674(03)00845-6 [DOI] [PubMed] [Google Scholar]
- 57. Crampton N, Bonass W a, Kirkham J, Rivetti C, Thomson NH. Collision events between RNA polymerases in convergent transcription studied by atomic force microscopy. Nucleic Acids Res. 2006;34: 5416–5425. 10.1093/nar/gkl668 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58. Bernstein J a, Khodursky AB, Lin P-H, Lin-Chao S, Cohen SN. Global analysis of mRNA decay and abundance in Escherichia coli at single-gene resolution using two-color fluorescent DNA microarrays. Proc Natl Acad Sci U S A. 2002;99: 9697–9702. 10.1073/pnas.112318199 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59. Cox R a. Quantitative relationships for specific growth rates and macromolecular compositions of Mycobacterium tuberculosis, Streptomyces coelicolor A3(2) and Escherichia coli B/r: an integrative theoretical approach. Microbiology. 2004;150: 1413–1426. 10.1099/mic.0.26560-0 [DOI] [PubMed] [Google Scholar]
- 60. Brantl S. Antisense-RNA regulation and RNA interference. Biochim Biophys Acta. 2002;1575: 15–25. 10.1016/S0167-4781(02)00280-4 [DOI] [PubMed] [Google Scholar]
- 61. Shokeen S, Johnson CM, Greenfield TJ, Manias D a, Dunny GM, Weaver KE. Structural analysis of the Anti-Q-Qs interaction: RNA-mediated regulation of E. faecalis plasmid pCF10 conjugation. Plasmid. 2010;64: 26–35. 10.1016/j.plasmid.2010.03.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62. Eguchi Y, Itoh T, Tomizawa J. Antisense Rna. Annu Rev Biochem. 1991; 631–652. [DOI] [PubMed] [Google Scholar]
- 63. Chatterjee A, Drews L, Mehra S, Takano E, Kaznessis YN, Hu WS. Convergent transcription in the butyrolactone regulon in streptomyces coelicolor confers a bistable genetic switch for antibiotic biosynthesis. PLoS One. 2011;6: e21974 10.1371/journal.pone.0021974 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64. Licht A, Freede P, Brantl S. Transcriptional repressor CopR acts by inhibiting RNA polymerase binding. Microbiology. 2011;157: 1000–1008. 10.1099/mic.0.047209-0 [DOI] [PubMed] [Google Scholar]
- 65. Dodd IB, Shearwin KE, Sneppen K. Modelling transcriptional interference and DNA looping in gene regulation. J Mol Biol. 2007;369: 1200–13. 10.1016/j.jmb.2007.04.041 [DOI] [PubMed] [Google Scholar]
- 66. Murchland I, Ahlgren-Berg a., Priest DG, Dodd IB, Shearwin KE. Promoter Activation by CII, a Potent Transcriptional Activator from Bacteriophage 186. J Biol Chem. 2014;289: 32094–32108. 10.1074/jbc.M114.608026 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67. Voigt C a, Wolf DM, Arkin AP. The Bacillus subtilis sin operon: An evolvable network motif. Genetics. 2005;169: 1187–1202. 10.1534/genetics.104.031955 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68. Wong P, Gladney S, Keasling JD. Mathematical model of the lac operon: Inducer exclusion, catabolite repression, and diauxic growth on glucose and lactose. Biotechnol Prog. 1997;13: 132–143. 10.1021/bp970003o [DOI] [PubMed] [Google Scholar]
- 69. Santillan M, Mackey MC. Dynamic regulation of the tryptophan operon: a modeling study and comparison with experimental data. Proc Natl Acad Sci U S A. 2001;98: 1364–1369. 10.1073/pnas.98.4.1364 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70. Adhya S, Gottesman M. Promoter occlusion: transcription through a promoter may inhibit its activity. Cell. 1982;29: 939–944. 10.1016/0092-8674(82)90456-1 [DOI] [PubMed] [Google Scholar]
- 71. Shu CC, Chatterjee A, Dunny G, Hu WS, Ramkrishna D. Bistability versus bimodal distributions in gene regulatory processes from population balance. PLoS Comput Biol. 2011;7: e1002140 10.1371/journal.pcbi.1002140 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72. Landick R. The regulatory roles and mechanism of transcriptional pausing. Biochem Soc Trans. 2006;34: 1062–6. 10.1042/BST0341062 [DOI] [PubMed] [Google Scholar]
- 73. Chatterjee A, Kaznessis YN, Hu WS. Tweaking biological switches through a better understanding of bistability behavior. Curr Opin Biotechnol. 2008;19: 475–481. 10.1016/j.copbio.2008.08.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74. Sesto N, Wurtzel O, Archambaud C, Sorek R, Cossart P. The excludon: a new concept in bacterial antisense RNA-mediated gene regulation. Nat Rev Microbiol. Nature Publishing Group; 2013;11: 75–82. 10.1038/nrmicro2934 [DOI] [PubMed] [Google Scholar]
- 75. Yelin R, Dahary D, Sorek R, Levanon EY, Goldstein O, Shoshan A, et al. Widespread occurrence of antisense transcription in the human genome. Nat Biotechnol. 2003;21: 379–386. 10.1038/nbt808 [DOI] [PubMed] [Google Scholar]
- 76. Misra S, Crosby M a, Mungall CJ, Matthews BB, Campbell KS, Hradecky P, et al. Annotation of the Drosophila melanogaster euchromatic genome: a systematic review. Genome Biol. 2002;3: RESEARCH0083 10.1186/gb-2002-3-12-research0083 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77. Yamada K, Lim J, Dale JM, Chen H, Shinn P, Palm CJ, et al. Empirical analysis of transcriptional activity in the Arabidopsis genome. Science. 2003;302: 842–6. 10.1126/science.1088305 [DOI] [PubMed] [Google Scholar]
- 78. Chen J, Sun M, Hurst LD, Carmichael GG, Rowley JD. Genome-wide analysis of coordinate expression and evolution of human cis-encoded sense-antisense transcripts. Trends in Genetics. 2005. pp. 326–329. 10.1016/j.tig.2005.04.006 [DOI] [PubMed] [Google Scholar]
- 79. Thisted T, Gerdes K. Mechanism of post-segregational killing by the hok/sok system of plasmid R1: Sok antisense RNA regulates hok gene expression indirectly through the overlapping mok gene. J Mol Biol. 1992;223: 41–54. 10.1016/0022-2836(92)90714-U [DOI] [PubMed] [Google Scholar]
- 80. Toledo-Arana A, Dussurget O, Nikitas G, Sesto N, Guet-Revillet H, Balestrino D, et al. The Listeria transcriptional landscape from saprophytism to virulence. Nature. 2009;459: 950–6. 10.1038/nature08080 [DOI] [PubMed] [Google Scholar]
- 81. Hernández J a., Muro-Pastor AM, Flores E, Bes MT, Peleato ML, Fillat MF. Identification of a furA cis antisense RNA in the cyanobacterium Anabaena sp. PCC 7120. J Mol Biol. 2006;355: 325–334. 10.1016/j.jmb.2005.10.079 [DOI] [PubMed] [Google Scholar]
- 82. Cech TR, Steitz J a. The noncoding RNA revolution—Trashing old rules to forge new ones. Cell. Elsevier Inc.; 2014;157: 77–94. 10.1016/j.cell.2014.03.008 [DOI] [PubMed] [Google Scholar]
- 83. André G, Even S, Putzer H, Burguière P, Croux C, Danchin A, et al. S-box and T-box riboswitches and antisense RNA control a sulfur metabolic operon of Clostridium acetobutylicum. Nucleic Acids Res. 2008;36: 5955–5969. 10.1093/nar/gkn601 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84. Gottesman S, Storz G. Bacterial small RNA regulators: Versatile roles and rapidly evolving variations. Cold Spring Harb Perspect Biol. 2011;3: 1–16. 10.1101/cshperspect.a003798 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85. Elowitz MB, Levine AJ, Siggia ED, Swain PS. Stochastic gene expression in a single cell. Sci Signal. 2002;297: 1183 10.1126/science.1070919 [DOI] [PubMed] [Google Scholar]
- 86. Goryachev AB, Toh DJ, Wee KB, Lee T, Zhang HB, Zhang LH. Transition to quorum sensing in an Agrobacterium population: A stochastic model. PLoS Comput Biol. 2005;1: 0265–0275. 10.1371/journal.pcbi.0010037 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87. Guo Y, Quiroga C, Chen Q, McAnulty MJ, Benedik MJ, Wood TK, et al. RalR (a DNase) and RalA (a small RNA) form a type I toxin-antitoxin system in Escherichia coli. Nucleic Acids Res. 2014;42: 6448–6462. 10.1093/nar/gku279 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88. Parsek MR, Val DL, Hanzelka BL, Cronan JE, Greenberg EP. Acyl homoserine-lactone quorum-sensing signal generation. Proc Natl Acad Sci U S A. 1999;96: 4360–4365. 10.1073/pnas.96.8.4360 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89. Chatterjee A, Cook LCC, Shu C-C, Chen Y, Manias D a, Ramkrishna D, et al. Antagonistic self-sensing and mate-sensing signaling controls antibiotic-resistance transfer. Proc Natl Acad Sci U S A. 2013;110: 7086–90. 10.1073/pnas.1212256110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90. Mason E, Henderson MW, Scheller E V., Byrd MS, Cotter PA. Evidence for phenotypic bistability resulting from transcriptional interference of bvgAS in Bordetella bronchiseptica. Mol Microbiol. 2013;90: 716–733. 10.1111/mmi.12394 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91. Xue Z, Ye Q, Anson SR, Yang J, Xiao G, Kowbel D, et al. Transcriptional interference by antisense RNA is required for circadian clock function. Nature. Nature Publishing Group; 2014;001: 650–653. 10.1038/nature13671 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92. Tjaden B, Saxena RM, Stolyar S, Haynor DR, Kolker E, Rosenow C. Transcriptome analysis of Escherichia coli using high-density oligonucleotide probe arrays. Nucleic Acids Res. 2002;30: 3732–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93. Xu Z, Wei W, Gagneur J, Perocchi F, Clauder-Münster S, Camblong J, et al. Bidirectional promoters generate pervasive transcription in yeast. Nature. 2009;457: 1033–7. 10.1038/nature07728 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94. Kapranov P, Willingham AT, Gingeras TR. Genome-wide transcription and the implications for genomic organization. Nat Rev Genet. 2007;8: 413–423. 10.1038/nrg2083 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
(DOCX)
(A, B) Expression maps of full-length (η x, η y) and truncated () transcripts originating from pX (A) and pY (B), respectively for a range of percentage of RNAP survival in event of RNAP collision. As RNAP survival increases less truncated RNA is produced (bluer central region). (C) Switch response in full-length x and y transcript levels becomes sharper for lower percentage of RNAP survival, at 80% the Hill coefficient is -3.1 for x and 2.9 for y, at 40% it is -4.0 for x and 4.4 for y, and at 0% it is -7.8 for x and 8.2 for y.
(TIFF)
(A, B) Effect of τIX. Maps of truncated and full-length transcripts originating from pX (A) and pY (B), respectively, at different initiation intervals at pX, τIX. Longer initiation times at pX increase probability of sitting duck interference at pX. Dislodgement of more sitting duck complexes at pX cause decreased RNAP collision and lowers expression of full-length x transcripts. (C) The switch response of x and y RNA at different τIX values. x transition becomes sharper at higher τIX values. (D, E) Effect of τIY. As the initiation time at pY increases, analogous effect is seen. Sitting duck interference at pY increases and less RNAP collisions occur. (F) Switch response in x and y levels at different τIY values. y levels are lowered at higher τIY.
(TIFF)
(A, B) Expression maps of truncated and full-length transcripts originating from pX (A) and pY (B), respectively, at different values of overlapping length, L. Longer overlapping regions yield to increased RNAP collisions. (C) Enhanced collisions lower the expression of full-length x and y transcripts. In this case, no clear trend was observed for the Hill coefficient.
(TIFF)
(A, B) Levels of full-length x (A) and y (B) transcripts, respectively, for None, TI, AR and TI+AR cases of antisense transcription in presence of the gene regulatory network implemented by proteins X, Y and Z. Bistability is only observed when AR is present (AR and TI+AR cases). When TI is coupled with AR (TI+AR case) the bistable range is expanded and the switch response is widened.
(TIFF)
Protein X and Y levels are shown for each modified parameter. Arrows indicate the way the curve shifts as the tuned parameter increases. (A, B) λ x, degradation rate of full-length x. (C, D) λ y, degradation rate of full-length y.
(TIFF)
Data Availability Statement
All relevant data are within the paper and its Supporting Information files.