Commentary: Value Judgments in Health Inequality Measurement

Value judgments lurk beneath the surface in any study of health inequalities; analysts ought to understand them, make them explicit, and present results transparently to policymakers so that they, rather than analysts, decide which set of value judgments should be invoked. That is the key message of the paper “Lies, Damned Lies, and Health Inequality Measurements”¹ by Gustav Kjellsson, Ulf-G Gerdtham, and Dennis Petrie.

Kjellsson et al. remind us that all studies of health inequalities are implicitly or explicitly based on either an absolute or relative notion of equality, and that studies involving bounded variables also involve an implicit or explicit value judgment about whether it is inequalities in attainment (e.g., health) that matter or inequalities in shortfalls (e.g., ill health). The authors emphasize that the value judgment between attainment and shortfall gets intertwined in practice with the value judgment of whether it is absolute or relative inequality that matters.

Epidemiologists have often reported results for both absolute and relative inequalities, and shown that the choice of perspective can make a difference. For example, in an early study of socioeconomic inequalities in health, Pamuk² found that absolute inequality in mortality across social classes in England and Wales (measured using the slope index of inequality) was smaller in 1949–1953 than in 1930–1932, but relative inequality (measured using the relative index of inequality) was higher in 1949–1953. Although the tools were developed early on by economists to look at both types of health inequality,³ most economists have until recently analyzed relative inequalities in health much as their colleagues analyzing income inequality have focused largely on relative income inequality. An early article by Clarke et al.³ was an exception: it looked at absolute and relative inequalities, and explored the relationship between the two when the outcome variable could be expressed in terms of attainments or shortfalls (the so called mirror issue). This theme got picked up a few years later. An article of mine⁴ explored the bounds the concentration index (the economist’s analogue of the relative index of inequality) when the outcome variable is binary. This article led to a series of papers and exchanges^5–12 that simultaneously addressed the bounds issue and the mirror issue. In this debate, the question of absolute versus relative inequality resurfaced—initially only implicitly.

In this Commentary, I offer some thoughts on, and practical suggestions regarding, the two interrelated issues highlighted by Kjellsson et al. (absolute vs. relative inequality; and the mirror issue). In so doing, I use their valuable article as a springboard.

Absolute Versus Relative Inequality

The Kjellsson et al. paper is very much in the spirit of being transparent about value judgments and about presenting results so as to allow the policymaker (not the analyst) to decide which stance to adopt.

This is an approach I have argued for^9,11 so I applaud their article. However, I think we can say a little more about the difference between absolute and relative inequality than Kjellsson et al. do, and in so doing help policymakers in their decision. The fact is that the two types of inequality are not just related to one another, but are related in such a way that we can say which type of inequality is harder to reduce: reducing absolute inequality is a good deal harder than reducing relative inequality.

In the pills example in Kjellsson et al., moving from the original shortfall distribution to the blue distribution, which keeps relative inequality unchanged, involves giving both groups the same percentage increase in life expectancy. By contrast, moving from the original shortfall distribution to the red distribution, which keeps absolute inequality unchanged, involves giving both groups the same number of years of additional life expectancy. This second change involves giving a larger percentage increase to the group starting off with the lower level of life expectancy (125% vs. 83%); because of this, this second change is associated with a reduction in relative inequality. Table shows the values of the concentration index and the generalized concentration index for the various distributions in the Kjellsson et al. pills example; the generalized concentration index measures absolute inequality and is the analogue of the slope index of inequality.

TABLE.

Values of CI and GCI for the Kjellsson et al. Pills Example

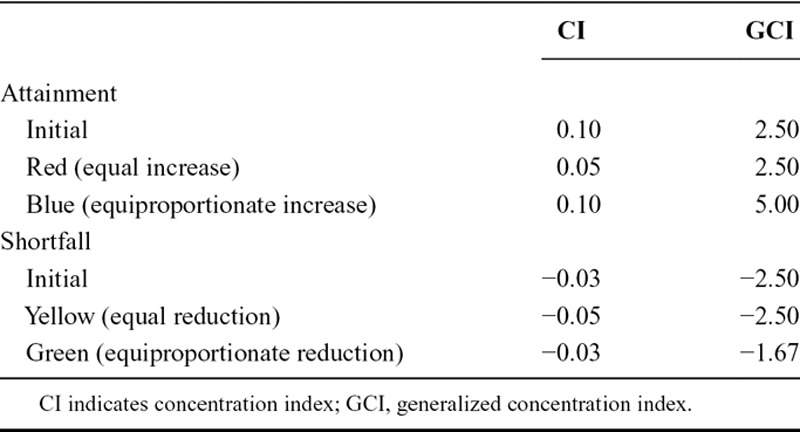
Reducing absolute inequality would require an even larger gap in the percentage change in favor of the initially disadvantaged group. In the pills example, the percentage increase for group A would have to be more than 125%, and the percentage increase for group B would have to be less than 83%. If such a change were to occur, relative inequality would fall by an even larger amount than it does in moving from the initial distribution to the blue distribution. I come back to this point in the Conclusion.

Attainment Versus Shortfalls (and Absolute vs. Relative Inequality)

For some time in the health economics literature, the importance of the choice between attainments and shortfalls was not widely appreciated. Clarke et al.² were the first to raise the issue in the health economics literature: they showed that while the choice does not matter in the measurement of absolute inequality, it (typically) does matter when measuring relative inequality.

The distinction between attainments and shortfalls has resurfaced recently in the health economics literature in the context of the debate over measuring inequalities in bounded variables. One important result⁵ is that the concentration index for the shortfall distribution is equal to the negative of the concentration index for the attainment distribution multiplied by the ratio of the means of the attainment and shortfall distributions. There is a corollary of this result, drawn out by Kjellsson et al.: if country A has more inequality in both attainments and shortfalls than country B, it follows that country A has a lower mean than country B in attainments and a higher mean in shortfalls, and therefore that country A has more absolute inequality (in both attainments and shortfalls) than country B. A nice feature of Kjellsson et al.’s ingenious diagrams is their ability to highlight cases where one country dominates another on both attainments and shortfalls, and hence—given the corollary above—also on absolute inequality. In Figure 5, France fares worse than Spain but better than Denmark on all criteria.

Typically, though, one’s results vis-à-vis levels of relative inequality will be sensitive to the choice between attainments and shortfalls. In the pills example, relative inequality measures say that (relative) inequality is larger before the switch to the shortfall distribution—cf. Table. In Figure 5, France does worse than Austria and Belgium on attainment inequality but better on shortfall inequality. The aforementioned result linking the concentration indices for attainments and shortfalls reminds us that in such cases, the ordering of countries vis-à-vis relative inequality can change as we move from the attainment to the shortfall distribution simply because the means of the attainment (and hence shortfall) distributions differ. This is rather unfortunate to say the least. I come back to this point as well in the Conclusion.

The pills example in Kjellsson et al. helped me stumble on what is, as far as I know, a new result, namely that although it does matter when it comes to analyzing (relative) inequality, the choice between attainment and shortfalls does not apparently matter when it comes to analyzing changes in inequality. Whether we use attainments or shortfalls, absolute and relative inequality measures both give us the right result (i.e., a zero change in inequality) when changes occur that leave inequality unaffected. Absolute inequality measures give the same results for inequality changes in attainment and shortfalls when the changes are equal in amount: in the Kjellsson et al. pills example, the generalized concentration index is unaffected by the move from the initial attainment distribution to the red distribution, just as it is by the move from the initial shortfall distribution to the yellow distribution—cf. Table. But exactly symmetrically, relative inequality measures give the same results for inequality changes in attainment and shortfalls when the changes are equiproportionate: in the pills example, the concentration index is unaffected in the move from the initial attainment distribution to the blue distribution, just as it is by the move from the initial shortfall distribution to the green distribution—cf. Table. Thus, while attainments may point one way and shortfalls the other when it comes to saying which country has more relative inequality in health to start with, attainments and shortfalls should point the same way when it comes to determining how far relative inequalities have changed.

CONCLUSIONS

On the distinction between absolute and relative inequality, there are two interrelated implications of the above. First, policymakers looking for reductions in absolute inequality are setting a higher bar than policymakers looking merely for reductions in relative inequality. We can think of the former kind of policymaker as a super-egalitarian. It would be helpful if analysts made this clear when presenting their results to policymakers. Second, the reasoning above suggests that reductions in absolute inequality will be less common in practice than reductions in relative inequality. Evidence from Wagstaff et al.¹³ is consistent with this: for each of 12 Millennium Development Goal indicators analyzed, the fraction of (developing) countries that have seen reductions in relative inequality is larger than the fraction of countries that have seen reductions in absolute inequality; in the case of health intervention indicators, the figures are 72% and 55%, respectively.

On the distinction between attainments and shortfalls, there are also implications of the above that are worth highlighting. First, when looking at relative inequality levels, it is helpful to use Kjellsson et al.’s ingenious diagrams to identify cases where the choice between attainment and shortfalls does not matter. When the choice does matter, however, it is worth keeping in mind why the results differ, namely that that the two approaches give different pictures of inequality (at least in part) because of differences in the means of the attainment and hence shortfall distributions. In other words, differences in means of the two distributions are confusing our inequality analysis. One escape route from this impasse would be to use the normalization of the concentration index, W, that I proposed in my bounds paper.³ Subsequent work⁵ generalized W to nonbinary-bounded variables, and showed that the normalization W solves not only the bounds problem (like the concentration index for an unbounded variable, W lies between −1 and +1) but also the mirror problem (in the Kjellsson et al. pills example, both the initial attainment and initial shortfall distributions give the same [absolute] value of W, namely 0.133). While some^5,8 have argued that W lacks specific desirable properties, others (including me)^6,9,11,12 have argued that the properties are only desirable if the aim is to measure absolute inequality; Kjellsson and Gerdtham¹² have argued that W is best seen as a measure of relative inequality that offers “a compromise between relative inequality in health and relative inequality in ill-health.” Second, I have argued above that while the distinction between “attainment-relative” and “shortfall-relative” matters if we are looking at the level of inequality, it does not matter if we are looking at changes in inequality. Whether we work in attainments or shortfalls, absolute inequality measures like the generalized concentration index will correctly record a zero change in inequality following equal increments, and relative inequality measures like the concentration index will correctly record a zero change in inequality following equiproportionate changes. This is reassuring for authors of studies of changes in inequality such as the aforementioned study of progress towards the Millennium Development Goals¹³; the implication is that the authors would have reached the same conclusions had they used shortfalls instead of attainments (e.g., in the cases of immunization and antenatal visits) and attainments instead of shortfalls (e.g., in the cases of mortality and malnutrition).

ABOUT THE AUTHOR

ADAM WAGSTAFF is a Research Manager in the Development Research Group of the World Bank where he has worked for 17 years. Before joining the World Bank, he was Professor of Economics at the University of Sussex. He was Associate Editor of the Journal of Health Economics for 20 years, and is President Elect of the International Health Economics Association. He has published extensively on distributional issues in health.