Conformational kinetics reveals affinities of protein conformational states

Significance

Despite 50 years of studies of coupled binding and conformational change reactions in proteins and nucleic acids, there has been no detailed analysis of the affinities of the multiple conformational states involved. The relationship between these affinities and the dynamics of conformational change has also been largely overlooked. We perform rigorous kinetic analysis of protein conformational change coupled to binding to concomitantly determine binding affinities of individual conformational states and rate constants for conformational changes. The results point to an inextricable link between affinities of the individual states and the change in conformational dynamics upon binding. The difference in affinities of conformational states is critical for driving conformational change and has implications in molecular recognition, allostery, and drug development.

Abstract

Most biological reactions rely on interplay between binding and changes in both macromolecular structure and dynamics. Practical understanding of this interplay requires detection of critical intermediates and determination of their binding and conformational characteristics. However, many of these species are only transiently present and they have often been overlooked in mechanistic studies of reactions that couple binding to conformational change. We monitored the kinetics of ligand-induced conformational changes in a small protein using six different ligands. We analyzed the kinetic data to simultaneously determine both binding affinities for the conformational states and the rate constants of conformational change. The approach we used is sufficiently robust to determine the affinities of three conformational states and detect even modest differences in the protein’s affinities for relatively similar ligands. Ligand binding favors higher-affinity conformational states by increasing forward conformational rate constants and/or decreasing reverse conformational rate constants. The amounts by which forward rate constants increase and reverse rate constants decrease are proportional to the ratio of affinities of the conformational states. We also show that both the affinity ratio and another parameter, which quantifies the changes in conformational rate constants upon ligand binding, are strong determinants of the mechanism (conformational selection and/or induced fit) of molecular recognition. Our results highlight the utility of analyzing the kinetics of conformational changes to determine affinities that cannot be determined from equilibrium experiments. Most importantly, they demonstrate an inextricable link between conformational dynamics and the binding affinities of conformational states.

The ensemble nature of proteins and nucleic acids, and their abilities to bind other molecules, are critical to their function (1). Often, the conformational ensembles of these macromolecules can be subdivided into kinetically distinguishable conformational subensembles or states in the thermodynamic sense. Thanks in part to the highly cooperative nature of biopolymer conformational changes (2–4), these conformational states are distinguishable by the kinetic barriers that separate them; conformers in separate states interconvert much more slowly than conformers within the same state. Thus, the reactions of such a system can be described as the interconversion of a small number of conformational states without ignoring the ensemble nature of each state (5, 6). To determine a mechanism that involves these conformational states, one must determine the timescale of their interconversion and their affinities for ligand. The practical definition of a conformational state is one whose delimiting kinetic barriers match the timescale of the experiment being used to measure its kinetics. In the case of the stopped-flow method used in this study, that timescale is 1–2 ms or slower. Numerous studies have focused on biophysical characterization of conformational transitions coupled to binding (7, 8). None of these studies has quantified the affinities of multiple exchanging states for native ligands, despite the fact that affinities must be key determinants of the mechanism by which binding is coupled to conformational change.

A wide range of proteins and nucleic acids undergo conformational changes coupled to the binding of other biological macromolecules and small molecules. This coupled conformational change and binding is key to many biological processes including signaling (9), catalysis (10, 11), and assembly of macromolecular complexes (12). Additionally, the design of small-molecule allosteric effectors that selectively bind, and thereby populate, a desired conformational state of a protein or nucleic acid represents an attractive therapeutic strategy (8, 13–15) and potentially powerful research tool. A robust understanding of coupling on a level that would allow us to both understand and exploit existing biological systems and design new allosteric effectors or molecular switches requires experimental determination of two types of quantifiable parameters: the binding affinities of each conformational state and the forward and reverse rate constants for interconversion between those states.

Numerous methods exist to determine the affinities of macromolecules for their binding partners. Most of these methods rely on equilibrium measurements and are unable to determine the intrinsic ligand binding affinity of individual conformational states when more than one state is present. Standard equilibrium binding measurements are unable to deconvolute the affinities of the distinct states and the free energy of the conformational changes. To determine the affinity of an individual conformational state using equilibrium techniques, the state must somehow be trapped or isolated. For many macromolecules, trapping of conformational states is prohibitively difficult or impossible. Lower-affinity states are often rapidly depopulated in the presence of ligand, which makes measuring their affinities by equilibrium methods nearly impossible. Measuring the affinities of individual states requires overcoming these difficulties.

Folding transitions are an important subclass of protein conformational changes and are often coupled to ligand binding (7). Recent folding studies suggest the utility of studying the kinetics of conformational changes that are coupled to binding as a way to determine the binding constants for the conformational states of proteins (16, 17). This approach contrasts with previous studies that used individually trapped states to estimate binding affinities of specific conformational states by equilibrium binding experiments (18–20). Unfortunately, neither of the recent kinetic studies explained why the affinities could be determined from kinetic experiments but not from equilibrium experiments. The authors also did not establish a conclusive link between the binding affinities of the conformational states and the effects of binding on conformational kinetics.

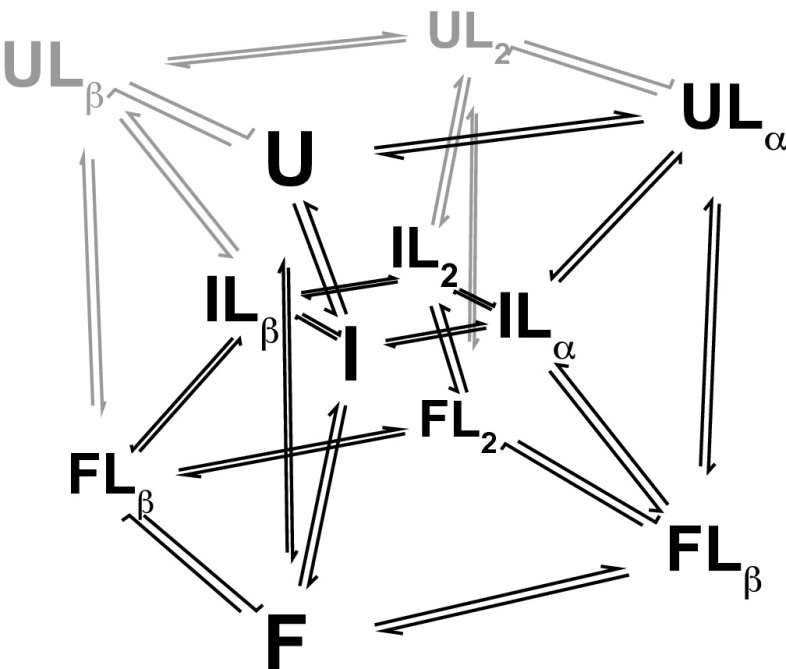
The protein subunit of bacterial RNase P has three conformational states: an unfolded state U, partially folded state I, and folded state F (21, 22). As shown in Fig. 1, folding of the protein is coupled to binding of anionic ligands at two high-affinity sites denoted α and β (23). Estimates of binding affinities for U and I cannot be obtained from equilibrium binding experiments because U and I rapidly fold to F upon binding ligand. Folding of P protein upon addition of sufficient ligand concentrations occurs within 1–2 s. Because ligand-bound U and I are not significantly populated at equilibrium, fits of equilibrium binding data (isothermal titration calorimetry, intrinsic tryptophan fluorescence, circular dichroism) give no insight into the affinities of U and I. Because we cannot readily isolate U, I, or F (Supporting Information) for binding studies or obtain sufficient information from equilibrium binding experiments, we turned to kinetics to determine the binding affinities and conformational equilibria between U, I, and F.

Fig. 1.

P^-Pro coupled folding and binding scheme. P^-Pro exhibits three-state folding with unfolded (U), partially folded intermediate (I), and folded (F) states. Folding is strongly coupled to the binding of two pyrophosphate ligands (L). Pyrophosphate may be bound at the α-site (Lα), β-site (Lβ), or both sites (L2) in any state. Unoccupied binding sites in U and I are reflected as undetectably weak affinities in the fits of the data. Species that remain unpopulated in stopped-flow kinetic experiments as revealed by fits of the data and their associated transitions are indicated in gray. Adapted from Daniels et al. (17).

In this study, we aimed to better understand the ligand-binding affinity and specificity in U, I, and F and the effects of binding on conformational kinetics in RNase P protein. To do so, we determined the kinetics of conformational change coupled to binding using six different phosphate derivatives. These were phosphate, pyrophosphate, and four nucleotide diphosphates: ADP, GDP, CDP, and UDP. Global analysis of the nucleotide-diphosphate kinetic data allowed simultaneous determination of the ligand-binding affinities and rate constants of conformational change. U, I, and F all have measurable affinities for the studied ligands. The results indicate that ligand-bound forms of U and I are undetectable at equilibrium. In striking contrast, the ligand-bound forms of U, I, and F are all populated and detectable over the time course of kinetic experiments. The ratio of affinities of two conformational states in exchange—which we refer to as κ—can be empirically related to the effect of ligand on conformational rate constants. The degree to which the change in dynamics is partitioned between changes in folding and unfolding rate constants—quantified in the parameter δ—depends on the conformational state and ligand type. As a consequence of the κ and δ values intrinsic to P protein, the dominant folding mechanism shifts from the indirect pathway (U–I–F) to the direct folding pathway (U–F) as ligand concentration rises. We also show that both κ and δ are strong determinants of the mechanism of molecular recognition—conformational selection versus induced fit—in coupled conformational change and binding.

Results and Discussion

Ligand-Bound U, I, and F Are Populated in Kinetic Experiments, but Not Equilibrium Experiments.

The kinetic experiments described here were conducted with the P39A/P90A/F107W (P^-Pro) variant of Bacillus subtilis ribonuclease P, a model system developed in previous studies (17, 21). To estimate the intrinsic affinities of U, I, and F, we used stopped-flow fluorescence to monitor folding of the protein upon mixing with varying concentrations of either P_i, ADP, GDP, UDP, or CDP. Stopped-flow kinetic data (Fig. 2 and Fig. S1) were fit to the coupled folding and binding model described previously (Fig. 1), to obtain estimates of the affinities, folding rate constants, and spectroscopic parameters (Tables S1–S7). The time dependence of ligand-induced folding is determined by the populations of the 12 conformational and liganding states depicted in Fig. 1 and their individual folding/unfolding kinetics. It follows that the rate of disappearance of U and I, and the formation of F upon the addition of ligand provides information about their conformational kinetics and affinities. The time-dependent populations of the 12 states in the coupled-folding and binding scheme are readily expressed as a system of differential equations that allow calculation of the observed fluorescence signal as a function ligand concentration, protein concentration, and time (Supporting Information).

Fig. 2.

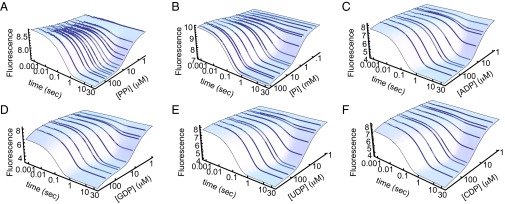
Kinetics of ligand-induced folding of P^-Pro monitored by stopped-flow fluorescence. P^-Pro was mixed with either PP_i (A), P_i (B), ADP (C), GDP (D), UDP (E), or CDP (F). Data points are the average of data points from three traces. The blue surfaces are the best fit of data to the coupled folding and binding models.

Fig. S1.

Kinetics of ligand-induced folding of P^-Pro monitored by stopped-flow fluorescence. P^-Pro was mixed with either PP_i (A), P_i (B), ADP (C), GDP (D), UDP (E), or CDP (F). Data points are the average of data points from three traces. The red lines are the best fit of data to the coupled folding and binding models.

Table S1.

Parameter values from global fit of PP_i and TMAO stopped-flow data

Parameter	Mean	SE	68% confidence interval	Units
SigU	8.759	0.001	(8.757, 8.760)	AFU
SigI	7.602	0.006	(7.596, 7.609)	AFU
SigF	7.5549	0.0008	(7.5542, 7.5558)	AFU
SigUBound	9.46	0.06	(9.40, 9.52)	AFU
SigIBound	8.45	0.02	(8.43, 8.47)	AFU
SigFBound	7.4743	0.0004	(7.4739, 7.4747)	AFU
Kαu	390	20	(370, 410)	M−1
Kαf	1.32 × 106	20,000	(1.29 × 106, 1.34 × 106)	M−1
Kαi	8,300	400	(7,900, 8,600)	M−1
Kβu	3	3	(0, 6)	M−1
Kβf	430,000	10,000	(420,000, 440,000)	M−1
Kβi	2,200	200	(2,000, 2,400)	M−1
kuiα	2.4	0.3	(2.1, 2.8)	s−1
kifα	7.3	0.8	(6.5, 8.1)	s−1
kifβ	13	7	(6, 20)	s−1
kifαβ	120	10	(110, 130)	s−1
kufα	9.1	0.5	(8.6, 9.7)	s−1

PP_i and TMAO stopped-flow data are from Daniels et al. (17).

Table S7.

Comparison of unliganded folding parameter values from global fits of PP_i and TMAO data and NDP data

Parameter	PPi and TMAO	NDP
ΔGui, cal⋅mol−1	859 ± 4	884 ± 5
ΔGif, cal⋅mol−1	372 ± 4	440 ± 10
kui, s−1	1.994 ± 0.006	2.5 ± 0.2
kif, s−1	1.06 ± 0.01	0.84 ± 06
kuf, s−1	0.036 ± 0.003	0.06 ± 0.01

PP_i and TMAO data are from Daniels et al. (17).

Table S2.

Parameter values from fit of P_i stopped-flow data

Parameter	Mean	SE	68% confidence interval	Units
SigU	10.26	0.02	(10.24, 10.28)	AFU
SigI	7.97	0.09	(7.89, 8.07)	AFU
SigF	7.8	0.1	(7.7, 7.9)	AFU
SigUBound	10.51	0.06	(10.46, 10.58)	AFU
SigIBound	10.3	0.1	(10.2, 10.5)	AFU
SigFBound	7.279	0.006	(7.273, 7.286)	AFU
Kαu	19	3	(17, 22)	s−1
Kαf	2,060	90	(1970, 2160)	s−1
Kαi	130	20	(110, 150)	s−1
Kβu	0.8	0.2	(0.5, 1.0)	s−1
Kβf	2,200	100	(2100, 2300)	s−1
Kβi	120	20	(100, 120)	s−1
kuiα	4.1	0.8	(3.3, 4.9)	s−1
kifα	2.5	0.9	(1.6, 3.5)	s−1
kifβ	2.3	0.6	(1.6, 2.9)	s−1
kifαβ	45	4	(42, 49)	s−1
kufα	4.7	0.6	(4.1, 5.2)	s−1

Table S3.

ADP parameter values from global fit of NDP stopped-flow data

Parameter	Mean	SE	68% confidence interval	Units
SigU	9.40	0.01	(9.39, 9.41)	AFU
SigI	4.66	0.05	(4.61, 4.71)	AFU
SigF	4.97	0.04	(4.93, 5.01)	AFU
SigUBound	6.4	0.6	(5.8, 6.9)	AFU
SigIBound	4.8	0.2	(4.5, 5.0)	AFU
SigFBound	4.23	0.01	(4.21, 4.24)	AFU
Kαu	430	40	(390, 470)	M−1
Kαf	960,000	30,000	(920,000, 990,000)	M−1
Kαi	5,900	800	(5,100, 6,700)	M−1
Kβu	7	4	(4, 11)	M−1
Kβf	540,000	30,000	(520,000, 570,000)	M−1
Kβi	3,000	400	(2,600, 3,400)	M−1
kuiα	18	4	(14, 22)	s−1
kifα	12	2	(9, 14)	s−1
kifβ	14	5	(9, 19)	s−1
kifαβ	130	30	(100, 160)	s−1
kufα	16	3	(13, 19)	s−1
ife	0.0003	0.0001	(0.0002, 0.0004)	AFU⋅μM−1

Table S4.

GDP parameter values from global fit of NDP stopped-flow data

Parameter	Mean	SE	68% confidence interval	Units
SigU	9.40	0.01	(9.39, 9.41)	AFU
SigI	4.66	0.05	(4.61, 4.71)	AFU
SigF	4.97	0.04	(4.93, 5.01)	AFU
SigUBound	4.9	0.4	(4.5, 5.2)	AFU
SigIBound	4.3	0.2	(4.1, 4.5)	AFU
SigFBound	4.01	0.01	(4.00, 4.03)	AFU
Kαu	560	40	(510, 600)	M−1
Kαf	1.06 × 106	50,000	(1.01 × 106, 1.11 × 106)	M−1
Kαi	8,200	800	(7,400, 9,000)	M−1
Kβu	7	4	(3, 11)	M−1
Kβf	570,000	40,000	(530,000, 610,000)	M−1
Kβi	3,400	500	(2,900, 3,900)	M−1
kuiα	13	3	(10, 16)	s−1
kifα	9	2	(7, 11)	s−1
kifβ	9	5	(4, 14)	s−1
kifαβ	140	20	(120, 160)	s−1
kufα	14	2	(11, 16)	s−1
ife	0.0016	0.0001	(0.0015, 0.0017)	AFU⋅μM−1

Table S5.

UDP parameter values from global fit of NDP stopped-flow data

Parameter	Mean	SE	68% confidence interval	Units
SigU	9.40	0.01	(9.39, 9.41)	AFU
SigI	4.66	0.05	(4.61, 4.71)	AFU
SigF	4.97	0.04	(4.93, 5.01)	AFU
SigUBound	6.1	0.7	(5.4, 6.8)	AFU
SigIBound	5.5	0.3	(5.1, 5.8)	AFU
SigFBound	4.14	0.02	(4.12, 4.16)	AFU
Kαu	360	40	(320, 390)	M−1
Kαf	320,000	20,000	(300,000, 340,000)	M−1
Kαi	4,900	600	(4,300, 5,500)	M−1
Kβu	7	3	(4, 10)	M−1
Kβf	240,000	13,000	(234,000, 260,000)	M−1
Kβi	1,600	300	(1,300, 1,900)	M−1
kuiα	18	5	(13, 23)	s−1
kifα	9	2	(7, 11)	s−1
kifβ	9	5	(5, 14)	s−1
kifαβ	140	30	(110, 170)	s−1
kufα	16	2	(14, 18)	s−1
ife	0.0002	0.0001	(0.00016, 0.0004)	AFU⋅μM−1

Table S6.

CDP parameter values from global fit of NDP stopped-flow data

Parameter	Mean	SE	68% confidence interval	Units
SigU	9.40	0.01	(9.39, 9.41)	AFU
SigI	4.66	0.05	(4.61, 4.71)	AFU
SigF	4.97	0.04	(4.93, 5.01)	AFU
SigUBound	5.4	0.6	(4.8, 5.9)	AFU
SigIBound	5.0	0.4	(4.6, 5.4)	AFU
SigFBound	4.07	0.02	(4.05, 4.09)	AFU
Kαu	430	40	(390, 470)	M−1
Kαf	227,000	9,000	(218,000, 236,000)	M−1
Kαi	2,800	400	(2,400, 3,200)	M−1
Kβu	8	4	(4, 12)	M−1
Kβf	179,000	8,000	(171,000, 187,000)	M−1
Kβi	1,100	200	(900, 1,300)	M−1
kuiα	27	5	(22, 32)	s−1
kifα	10	2	(8, 12)	s−1
kifβ	12	5	(7, 17)	s−1
kifαβ	110	20	(90, 130)	s−1
kufα	14	2	(12, 16)	s−1
ife	0.0009	0.0001	(0.0008, 0.0010)	AFU⋅μM−1

Because of the complexity of P^-Pro (three conformational states and two binding sites), ligand-induced folding data for any single ligand are insufficient to determine a coupled binding and folding mechanism. In a previous study, we addressed this problem by using the osmolyte trimethylamine N-oxide (TMAO) to induce folding in the absence of ligand and globally fit that data along with data obtained at various ligand (PP_i) concentrations. In the current work, the same problem was overcome by globally fitting all four of the NDP-induced folding datasets. The global fit of the TMAO and PP_i data and the global fit of the four NDP datasets yielded similar estimates of the conformational rate constants and equilibrium constants for unliganded P^-Pro (Table S7). This result suggests that, for other complex systems whose conformational changes cannot be easily induced with osmolyte or denaturant, global analysis of kinetic data for ligands of varying affinities would include kinetic and equilibrium information about the unliganded states. Notably, each NDP ligand binds P^-Pro with unique affinity and uniquely alters the conformational kinetics. Ligands with identical affinities or that induce identical changes in conformational kinetics would not allow determination of the coupled binding and conformational change mechanisms. In the case of macromolecules with only two conformational states and one ligand binding site, kinetic experiments with one ligand is usually sufficient to determine the full coupled binding and conformational change mechanism. These experiments must have appropriate concentration and time ranges. A Mathematica notebook for simulating and analyzing kinetic data for two-state one-site systems is included in File S1.

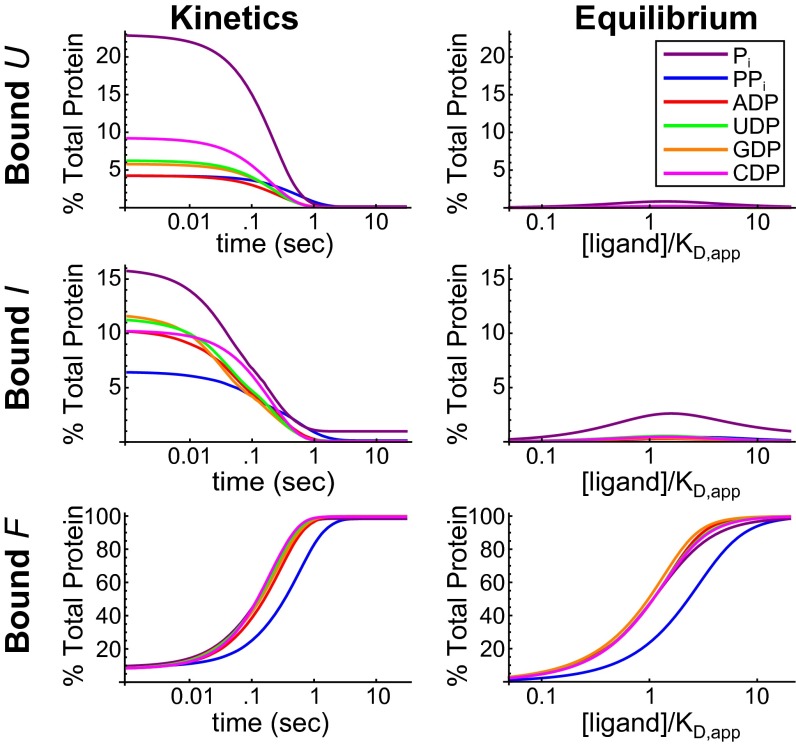
Kinetic and thermodynamic parameters from the fits of the stopped-flow data were used to calculate the populations of ligand-bound U, I, and F as a percentage of the total protein (Fig. 3). Populations at equilibrium are shown as a function of ligand concentration. The ligand concentration spans from well below the apparent K_D to well above, and therefore ranges from nonsaturating to saturating. Populations during a kinetic experiment (with ligand at 20 times the apparent K_D) are shown as a function of time. The population of liganded F in both equilibrium and kinetic experiments is substantial and well within the detection limit of intrinsic tryptophan fluorescence. The equilibrium populations of ligand-bound U and I are not significant at any concentration of ligand, including subsaturating ligand concentrations. Detection of ligand-bound U and I at equilibrium would require methods much more sensitive than standard optical or calorimetric binding assays. Ligand-bound U and I are only significantly populated during kinetic experiments. The populations of bound U and I in kinetic experiments are orders of magnitude greater than in equilibrium experiments, and in this case are well within the detection limit of tryptophan fluorescence experiments.

Fig. 3.

Populations of ligand-bound U, I, and F in kinetic and equilibrium experiments for six ligands. The populations of ligand bound P^-Pro states as a percentage of the total protein are shown as a function of time for stopped-flow experiments and as a function of ligand concentration for equilibrium experiments. Populations were calculated using parameters from the fits of the data using a protein concentration of 5 μM. Time-dependent populations were calculated using a ligand concentration of 20 × K_D,app.

The information in Fig. 3 suggests two reasons why kinetic experiments provide insights into affinities that equilibrium experiments do not. First, ligand-bound U and I are not significantly populated at equilibrium; they are populated in the mixture of protein and ligand before equilibrium is reached. Second, the change in fluorescence as a function of time reflects the transient populations of different species and their corresponding conformational rate constants. These populations are themselves dependent on the affinity of the corresponding state. Liganded species with unique conformational kinetics can only form if there is sufficient affinity, which is the property that makes them detectable in fits of the kinetic data.

Ligand Binding Affinity and Specificity Increase as P Protein Folds.

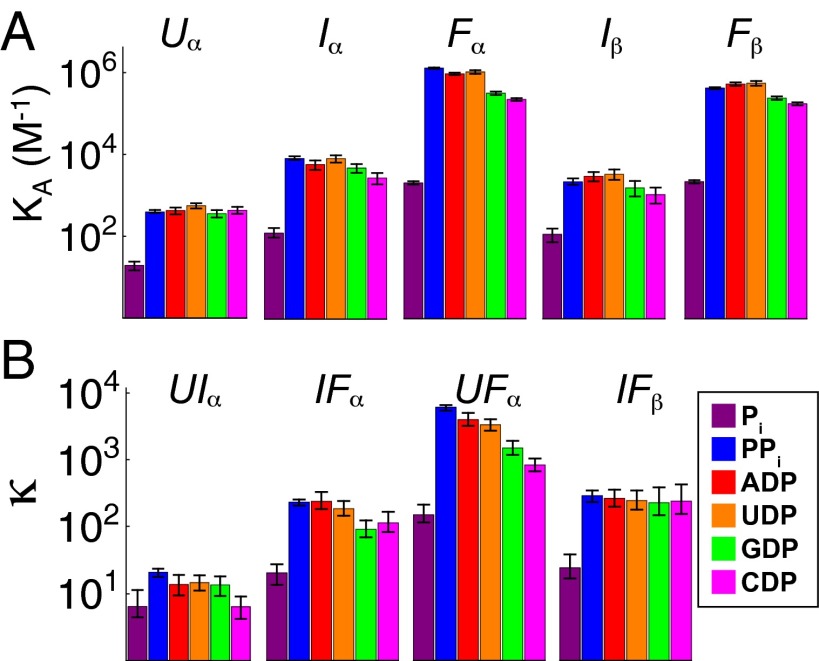
All three conformational states of P protein displayed significant affinity for P_i, PP_i, ADP, GDP, UDP, and CDP (Fig. 4A). The protein’s affinities for all six ligands increase monotonically as the protein folds; the protein does not experience any decreases in affinity along the folding trajectory. This monotonic increase in affinity as the protein becomes more folded enhances the rate of ligand-induced folding. If the binding affinity of I were lower than that of U, the ligand binding would not favor formation of I relative to U, and folding via the intermediate would be slowed. It is unknown whether this pattern holds for other proteins or whether low-affinity intermediates, with locally or globally disordered binding sites and thus lower affinity, may exist.

Fig. 4.

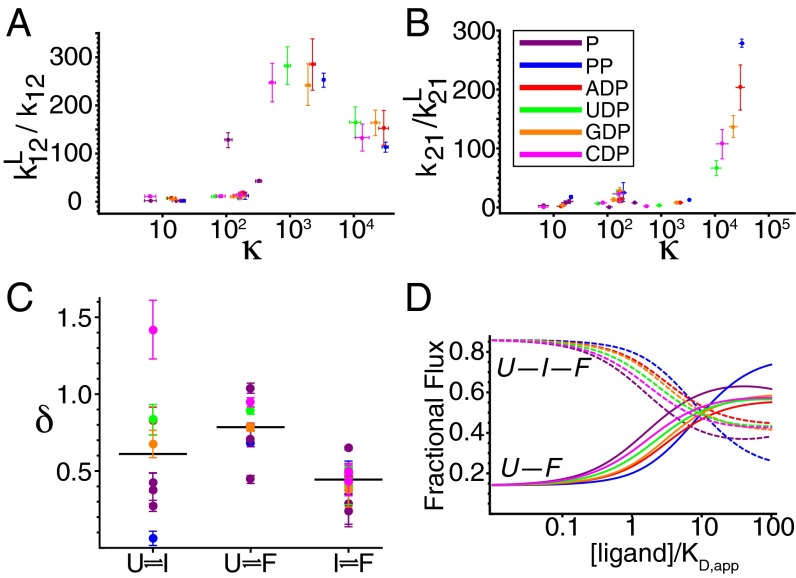
Affinities for U, I, and F for six ligands. (A) Binding affinities for the α-site of U, I, and F and β-site of I and F. (B) The affinity ratios (κ) for the binding sites U, I, and F. Error bars represent the 95% confidence interval.

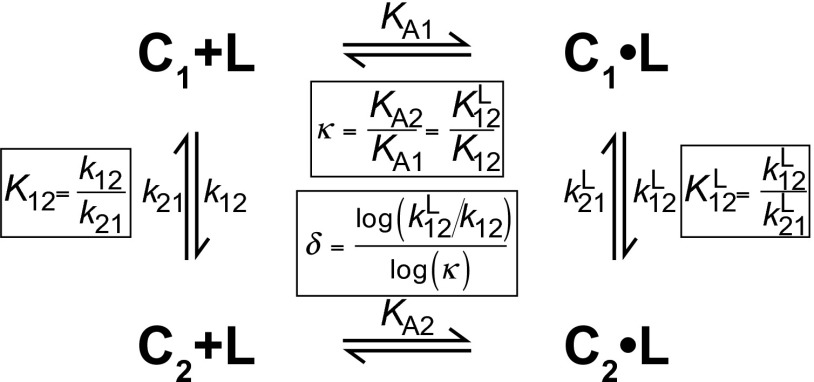
The relative affinities of two interconverting conformational states can be quantified by the ratio of their association constants, κ. κ is equal to K_A2/K_A1, where K_A2 and K_A1 are the ligand association constants of two conformational states in exchange. Because the binding and conformational change reactions are coupled (Fig. 5), κ is also the factor by which the conformational equilibrium constant changes as a result of ligand binding. More intuitively, κ is a measure of how selective a ligand is for one of two conformational states. The ability of a ligand to populate a macromolecule’s particular conformational state depends not only on the overall affinity of the ligand for the macromolecule, but also on κ. For two conformational states with a κ of 1, ligand binding would not be coupled to conformational change and would not shift the conformational equilibrium. Throughout this manuscript, we designate the affinity of the more folded state K_A2 and the affinity of the less folded state K_A1. Fig. 4B shows the κ values for the six ligands used to study the P^-Pro folding mechanism. For all six ligands, the U–F reaction has the largest κ values.

Fig. 5.

General scheme for coupled binding and conformational change for two conformations C1 and C2 that bind a ligand L. κ and δ are related to the equilibrium and rate constants as depicted. A Mathematica notebook to simulate and fit data for the scheme depicted is included in File S1.

As shown in Fig. 4, P_i binds to each state with the lowest affinities and κ values of the six ligands. Consequently, binding of P_i is not as strongly coupled to folding as binding of PP_i or the NDPs. Because of the lower κ values associated with P_i binding, the equilibrium and kinetic populations of ligand-bound U and I are higher for P_i than for any of the other five ligands (Fig. 3). Formation of these ligand-bound low-affinity states (such as UL_α) is a prerequisite for the induced-fit mechanism of coupled binding and conformational change. As discussed later, κ is an important determinant of how molecular recognition is partitioned between induced fit and conformational selection.

The extent of structure in a particular conformational state is the primary determinant of its binding specificity. For example, U contains only one moderate-affinity binding site—α—for the six ligands studied. This site can distinguish between P_i and the other ligands, but cannot distinguish between PP_i, and the NDPs. In U, the α-site is composed of highly basic, probably dynamic N-terminal residues (17) whose affinities for ligand appear to be determined primarily by the ligand’s charge. This lack of steric determinants due to poorly defined protein structure is presumably the origin of the low specificity in ligand recognition. Thus, the unfolded state α-site of P^-Pro lacks structure necessary to distinguish the uncharged moieties of ADP, GDP, CDP, and UDP.

In contrast, the I state exhibits enhanced specificity commensurate with its accretion of folded structure. The affinities of the α- and β-sites in I indicate that it can partially recognize the uncharged moieties in the NDPs. The α-site affinity of the NDPs are slightly decreased relative to PP_i, indicating that the additional structure at this site in I confers specificity that is lacking in U.

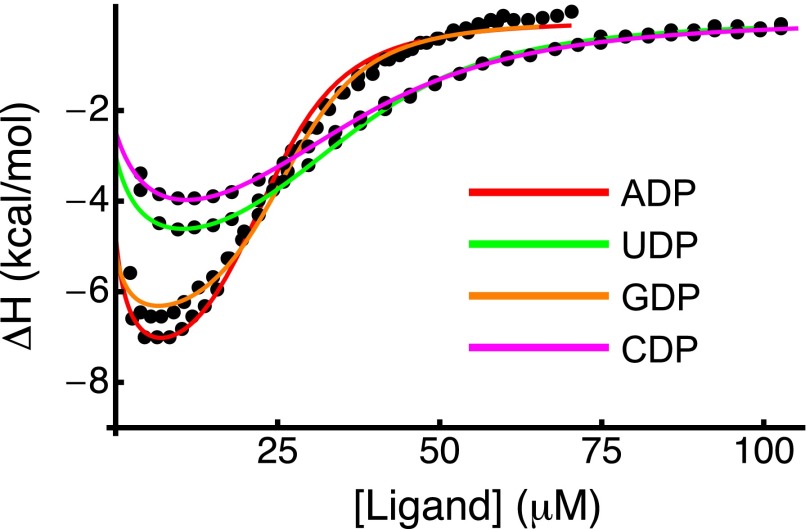
As depicted in Fig. 4, F has higher ligand binding specificity than U or I. The F α-site has similar affinities for PP_i, ADP, and GDP and approximately threefold to fivefold lower affinities for UDP and CDP. Isothermal titration calorimetry experiments confirmed that P protein binds ADP and GDP more tightly than UDP and CDP (Fig. S2 and Supporting Information). The threefold to fivefold reduction in affinity for UDP and CDP is modest compared with the ∼1,000-fold lower affinity for P_i. The increase in specificity as P protein folds strongly suggests structural elements that impart specificity are unformed in U, partially formed in I, and fully formed in F.

Fig. S2.

Isothermal titration calorimetry of P^-Pro with NDPs. Binding isotherms from ITC titrations with ADP (red), GDP (orange), UDP (green), or CDP (magenta) were fit to a three-state coupled binding and folding model to obtain estimates of ΔH of binding. Affinities and conformational equilibrium constants obtained from the corresponding stopped-flow dataset were fixed. Solid lines represent the best fit.

Based on a comparison with PP_i, the uncharged moieties of the NDPs decrease the affinity to binding sites in both I and F. This observation demonstrates that it is possible to parse the contributions of different ligand moieties to the affinity in the various conformational states. Although the selectivity for particular ligands here is modest (threefold to fivefold differences in affinities), other ligands and proteins could demonstrate much more selective binding. The kinetic strategy used here to measure affinities of conformational states may be of particular use in designing drugs that selectively bind and populate a particular state or pathway.

The Magnitude of Change in the Folding and Unfolding Rate Constants Depends on κ.

Thus far, our focus has been on thermodynamic characteristics of ligand recognition. However, a kinetic approach also allows interpretation of the rate constants for conformational changes. Ligand binding shifts the conformational equilibrium toward the more folded state by increasing folding rate constants and decreasing unfolding rate constants. In P^-Pro, the magnitude of the change in the folding and unfolding rate constants depends on which conformational reaction, ligand, and binding site are involved. The multiple pathways depicted in Fig. 1 allowed us to determine the rate constants for five unique ligand-bound folding reactions for each ligand, which amounts to 30 independent observations relating conformational kinetics to affinity ratios. Fig. 6 shows the ligand-induced increase (relative to the unbound reactions) in folding (forward) rate constants (A) and decrease in unfolding (reverse) rate constants (B) plotted versus κ. Although there is no single monotonic relationship between these parameters, the trend suggests that the greater the ratio of affinities (κ) of the two states, the more ligand binding increases the folding rate constant and decreases the unfolding rate constant.

Fig. 6.

Ligand-induced perturbations of conformational kinetics are enhanced in reactions with larger κ values. The increase in folding rate constant (A) and decrease in unfolding rate constant (B) for the conformational reactions of P^-Pro depicted in Fig. 1 upon binding to six ligands are plotted versus the affinity ratio κ of each reaction. Error bars represent the 95% confidence intervals in both parameters. The parameter δ (Fig. 5) quantifies the partitioning of the effect of ligand on conformational kinetics. When δ = 1, ligand only accelerates folding; when δ = 0, ligand only decelerates unfolding. Intermediate δ values correspond to perturbations of both rate constants. (C) δ values for folding reactions when bound to six ligands. Horizontal lines indicate average δs. (D) Fractional flux through the direct U-to-F folding pathway and the indirect U-to-I-to-F pathway as a function of the concentration of six ligands normalized to their apparent K_D,app.

The positive correlation between the magnitude of the change in the rate constants and the magnitude of κ underscores the fundamental link between κ and the binding-induced change in conformational kinetics. It can be shown that κ is equal to $k_{12}^L/k_{12}\times k_{21}/k_{21}^L,$ where $k_{12}$ and $k_{21}$ are the forward and reverse rate constants for conformational change without ligand bound, and $k_{12}^L$ and $k_{21}^L$ are the rate constants with ligand bound (Fig. 5). Conformational changes with larger κ values have larger changes in the conformational equilibrium constants upon ligand binding. Accordingly, the largest changes in rate constants upon ligand binding are seen in the reactions with the largest κ values. These constitute U–F reactions with ligand bound at the α-site and I–F reactions with ligand bound at both the α- and β-sites. The effects of ligand on conformational rate constants demonstrate that binding can alter the timescales for conformational changes by orders of magnitude. Because κ is equal to $k_{12}^L/k_{12}\times k_{21}/k_{21}^L,$ the magnitude of both $k_{12}^L/k_{12}$ and $k_{21}/k_{21}^L$ are strongly correlated with κ. However, the relative effects of ligand on folding and unfolding rate constants will depend on the interaction of ligand with the transition state, and this property can be very sensitive to conformation and ligand structure. A parameter that describes the partitioning of the ligand binding effect between forward and reverse conformational changes would provide useful mechanistic insights.

We investigated the degree to which changes in the conformational equilibrium constant upon binding were partitioned between changes in forward (folding) and reverse (unfolding) rate constants. This degree of partitioning, δ, was calculated as shown in Fig. 5. The calculation of δ is analogous to the calculation of φ (24), which quantifies the extent of native structure in the transition state at the site of an amino acid substitution. Unlike studies of φ values, we do not presume that δ indicates the extent of folding in the transition state because ligand binding may significantly perturb the reaction coordinate of the transition state. Rather, δ provides a measure of how ligand binding changes conformational equilibrium. A δ of 0 indicates that ligand decreases the unfolding (reverse) rate constant has no effect on the folding (forward) rate constant. Conversely, a δ of 1 corresponds to a reaction in which the forward rate constant increases and the reverse rate constant is unchanged. Intermediate δ values describe reactions in which forward rate constants increase and reverse rate constants decrease. Calculated δ values for the coupled folding and binding reactions in P^-Pro are shown in Fig. 6C.

Although the range of δ values for a given conformational transition is quite large, the average δ values for the U–F transition are higher than for the U–I and I–F transitions. In general, ligand binding shifts the increases in the folding rate constants of the U–F equilibrium more than it decreases unfolding rate constants. In contrast, ligand binding shifts the equilibrium for the U–I and I–F reactions by increasing folding rate constants and decreasing unfolding rate constants about equally. As a consequence of the κ and δ values inherent to this system, ligand binding shifts the dominant pathway of conformational change from the U–I–F pathway to the U–F pathway (Fig. 6D). For a more detailed discussion, see Supporting Information.

The Mechanism of Molecular Recognition Is Strongly Dependent on κ and δ.

The parameters κ and δ both describe changes in conformational kinetics upon ligand binding. As such, we hypothesized that together they might be determinants of molecular recognition mechanisms. The extreme limits of these mechanisms are as follows: (i) binding followed by conformational change (induced fit) and (ii) conformational change followed by binding (conformational selection). Fig. 7 shows the κ and δ dependence of fractional flux of the P^-Pro U + L → I•L, I + L → F•L, and U + L → F•L coupled transitions through the conformational selection and induced-fit mechanisms. Areas that are red favor conformational selection, whereas areas that are blue favor induced fit. Conformational selection is favored for high κ and low δ. Induced fit is favored at intermediate to high κ and high δ. There is significant flux through both mechanisms for low-to-intermediate κ and low-to-intermediate δ. Both κ and δ are important determinants of the mechanism of molecular recognition in coupled binding and conformational change. The exact influence of κ and δ on flux through conformational selection and induced-fit mechanisms depends on the intrinsic dynamics of the unbound conformational states and will therefore be unique to each conformational transition.

Fig. 7.

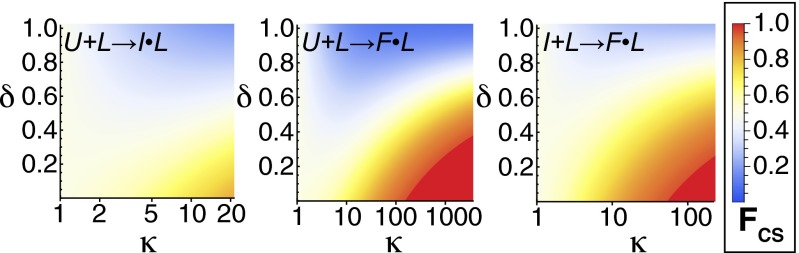
Partitioning of flux through conformational selection (red) and induced-fit (blue) pathways as a function of δ and κ for PP_i binding to P^-Pro. Conformational free energies and folding rate constants for the unliganded protein, as well as affinities for the low-affinity state were taken from fits of PP_i-induced folding monitored by stopped-flow fluorescence. Folding rate constants and affinities for the high-affinity state were calculated from δ, κ and the unliganded parameters. The fractional flux through conformational selection (F_CS) was calculated at the ligand concentration equal to K_D,app for the given parameters.

For systems under kinetic control, a macromolecule has a limited time to undergo a conformational change before being committed to a particular biological fate (e.g., aggregation, degradation, binding) determined by its conformation. The potentially different timescales of conformational selection and induced-fit mechanisms could lead to different biological outcomes. The timescale of conformational selection mechanism is limited by the rate of unliganded conformational change. Molecular recognition that proceeds primarily through induced fit is inherently more amenable to acceleration because the conformational change in the ligand-bound macromolecule can be orders of magnitude faster than in the unbound macromolecule. For this reason, a ligand that drives conformational change primarily through an induced-fit pathway is better suited to kinetically compete with biological processes that commit the macromolecule to a particular biological fate. κ and δ—and therefore the mechanism and timescale of molecular recognition—of a given macromolecule can be altered by changing the ligand or changing the binding site through mutation. Optimization of κ is sufficient for populating a desired conformational state for systems under thermodynamic control; however, optimization of both κ and δ are necessary for populating a desired conformation for systems under kinetic control, where the sequence of elementary steps determines the outcome of the overall reaction.

Conclusions

Literature discussion of conformational selection and induced-fit mechanisms in biomolecular binding has often overlooked the critical roles that conformational state affinities play in determining the mechanisms of coupled binding and conformational change (7, 8). We and others have previously shown that such mechanisms depend on ligand concentration (17, 25–27). We have shown here that the molecular origins of this ligand concentration dependence are in the intrinsic affinities of the conformational states and in the effects that ligand has on conformational kinetics. The importance of affinity in molecular recognition is demonstrated by the fact that relative flux between conformational selection and induced-fit mechanisms depends strongly on κ and δ. These two parameters quantify obvious features of molecular recognition: the propensity of each conformational state to bind ligand and the ability of the ligand to accelerate the conformational change to the high-affinity state. In general, induced fit is favored when ligand binds fairly weakly (intermediate κ) to the low-affinity state and greatly accelerates the conformational change (high δ). Conformational selection is favored when ligand binds extremely weakly (high κ) to the low-affinity state and does not accelerate conformational change (low δ). Conformational states of the same molecule can bind to a single ligand with affinities that vary by orders of magnitude. Interestingly, the kinetic studies with P^-Pro demonstrate that even relatively weak binding interactions in low-affinity states can be extremely important. These weak interactions are even more important when binding greatly accelerates conformational change and when ligand concentration approaches (<10%) the dissociation constant of the low-affinity state.

Kinetics of conformational changes coupled to binding can be used to determine affinities of conformational states. In fields such as mechanistic enzymology and protein folding, there is a rich history of using kinetic experiments to study poorly populated intermediates and determine thermodynamic parameters that cannot be determined from equilibrium experiments. We have demonstrated that such an approach can also be applied to gain a mechanistic understanding of coupled binding and conformational change. The findings of this work can be generalized to any conformational change in a protein or nucleic acid as long as the conformational states are separated by barriers and are detectable/distinguishable in a kinetic experiment. By estimating affinities of multiple ligands, one can estimate how much each chemical substituent of the ligand contributes to the affinity for the various conformational states. This information can be used to optimize the state/conformational selectivity of drugs that work by inducing conformational changes in the target protein, or to optimize synthetic molecular sensors that use coupled binding and conformational change. Recent advances in dynamic NMR techniques (28) that use chemical exchange to monitor conformational kinetics may provide the best estimates of affinities for conformational states.

Materials and Methods

Stopped-Flow Kinetics.

Stopped-flow fluorescence kinetic experiments were performed on an Applied Photophysics SX20 instrument at 25 °C. Samples were mixed in an observation cell with a 2-mm pathlength. Samples were excited at 285 nm for P_i and 295 nm for ADP, GDP, CDP, and UDP. Slit width was 1 mm. Emitted light was detected through a 320-nm high-pass filter. Experiments were performed by mixing protein with P_i, ADP, GDP, CDP, and UDP solutions at a volume ratio of 1:1. The initial protein concentration was 10 μM, and the final protein concentration was 5 μM. Final P_i concentrations ranged from 0.05 to 100 mM. Final ADP, GDP, CDP, and UDP concentrations ranged from 0 to 20 μM. Kinetic traces were collected over 30 s with logarithmic time sampling. Three traces were collected and averaged for each concentration of P_i, ADP, GDP, CDP, and UDP.

Analysis of Kinetic Data.

The model used to analyze stopped-flow data assumes that each of the three conformational states of P^-Pro contains up to two high-affinity binding sites (Fig. 1 for scheme) and that any conformational state can interconvert with any other state that has the same pattern of occupied ligand binding sites. The time-dependent concentrations of the 12 species in the scheme in Fig. 1 are represented as a system of differential equations. The fluorescence of the sample is expressed as the population-weighted fluorescence signals of free and bound U, I, and F. Rate constants for folding and unfolding are assumed to be dependent on the microscopic liganding state of the protein. Using mass balance constraints, we expressed many of the rate and equilibrium constants in terms of other rate and equilibrium constants to fit for as few parameters as possible and satisfy the principle of detailed balance. PP_i data were globally fit with TMAO-induced folding data as previously described. P_i data were fit using fixed values for unliganded conformational rate constants (obtained from the PP_i and TMAO fit) in the unliganded protein. The nucleotide diphosphate-induced folding data were fit globally with no fixed parameters. Parameter estimates were obtained by fitting the stopped-flow data to the model described above using a Bayesian approach as described in Supporting Information.

Complications with Isolation of U, I, and F

U can be isolated by addition of molar concentrations of urea or guanidinium chloride. However, use of these denaturants is not sufficient to study binding to U because even high concentrations of urea cannot prevent folding of P protein by tight-binding anions, and guanidinium chloride electrostatically interferes with binding. As of yet, no method of isolating the partially folded intermediate I has been discovered. The folded state, F, can be isolated in the absence of ligand using the osmolyte trimethylamine N-oxide (TMAO), but use of TMAO with polyanionic ligands such as pyrophosphate induces aggregation of P protein.

Isothermal Titration Calorimetry Confirms That P Protein Binds ADP and GDP More Tightly than UDP and CDP

Isothermal titration calorimetry was used to further investigate differences in the F state’s affinity for purines and pyrimidines. P protein was titrated with either ADP, GDP, UDP, or CDP (Fig. S2). Isotherms were fit to a coupled binding and folding model using the conformational equilibrium constants and binding affinities from the fit of stopped-flow data. The ITC isotherms provide no information about the affinities U or I because the liganded U and I are not significantly populated at equilibrium. The isotherms are consistent with the affinities obtained from fits of the stopped-flow data. ITC isotherms for ADP and GDP cannot be fit with the affinities for UDP and CDP. Likewise, isotherms for UDP and CDP cannot be fit using affinities for ADP and GDP. Both the kinetic and ITC data indicate that purines bind with higher affinity than pyrimidines to the folded state. The higher affinity of purines relative to pyrimidines is reflected in the observation that the binding isotherms for ADP and GDP saturate before the binding isotherms of UDP and CDP.

Either the ribose, base, or both have unfavorable steric interactions with the protein that decrease the affinity of UDP and CDP relative to PP_i. It is possible that ADP and GDP have fewer of these unfavorable interactions or more favorable interactions to compensate. The reduced affinity for pyrimidines, rather than an increased affinity for purines, may help P protein identify its specific binding site on P RNA. This site-dependent specificity may be an important determinant of holoenzyme assembly.

The Predominant P^-Pro Folding Mechanism Shifts from Indirect to Direct upon Ligand Binding

The P^-Pro folding reaction can follow one of two pathways; either through a partially folded intermediate (I) or directly from U to F. At low ligand concentration, the flux of the U–I–F pathway is sixfold higher than that of the U-to-F pathway. In this model system, these two conformational pathways represent the various routes by which macromolecular conformational changes can occur. The presence of bound ligand can have a profound effect on the route of conformational change. For the ligands studied, both κ and δ for the U–F transition are large relative to those of the U–I and I–F transitions. As a consequence, ligand binding shifts the dominant pathway of conformational change from the U–I–F pathway to the U–F pathway (Fig. 6D). As discussed before, a larger affinity ratio—κ—for two states corresponds to a larger increase in the conformational equilibrium constant upon ligand binding. The increase in the conformational equilibrium constant upon ligand binding is concomitant with a change in the conformational rate constants. Therefore, a larger κ naturally corresponds to larger changes in conformational kinetics. Of the three folding transitions, the U–F equilibrium constant is the most increased by ligand binding and, because of the high U–F d value, this change mostly manifests as an increase in the folding rate constant. This effect greatly enhances the relative flux through the U–F pathways. In other words, ligand binding lowers the activation energy of the U–F transition much more than that of the U–I and I–F transitions, leading to an increased flux through the U–F pathway.

In general, the ability of ligand binding to alter the pathway of conformational change in this way can allow biological systems to favor or disfavor sampling particular conformational states. Because conformational states can be functionally distinct, this can lead to an overall change in function. The strong link between κ and the conformational rate constants suggests that biological systems could achieve biologically necessary timescales and pathways for conformational changes by evolutionarily tuning the relative affinities of conformational states, thereby tuning κ.

Analysis of Kinetic Data

The kinetics of ligand association and dissociation are too fast to be observed by stopped flow. The tryptophan fluorescence increased within the mixing dead time (1.2 ms) in a ligand concentration-dependent manner when P^-Pro was mixed with either P_i or PP_i, and a similar magnitude decrease was observed when P^-Pro was mixed with ADP, GDP, CDP, or UDP. The burst phase amplitude increased with ligand concentration and provided a lower bound (10⁷ M⁻¹⋅s⁻¹) for the association rate constant k_on. We have assumed that the second-order association rate constant k_on is diffusion limited and set it to 10⁸ M⁻¹⋅s⁻¹. This assumption is consistent with our observation of a burst phase change in protein fluorescence upon ligand addition, which requires that k_on be at least 10⁸ M⁻¹⋅s⁻¹. The model is insensitive to changes in k_on between 10⁷ and 10¹⁰ M⁻¹⋅s⁻¹. The dissociation rate constant k_off for any individual binding reaction changes with k_on because it is the product of the fixed k_on and the fitted parameter for the association constant K_A. Spectroscopic parameters from the fit of the stopped-flow data indicated that the burst phase is primarily due to a spectroscopic change that occurs when ligand binds to the α-site of U.

Stopped-flow data for PP_i and TMAO-induced folding data were globally fit as previously described. The global fit of the PP_i and TMAO data yielded estimates for 30 parameters. The PP_i and TMAO-induced folding models share eight parameters: SigU, SigI, SigF, ΔGui, ΔGif, kui, kif, and kuf. Stopped-flow data for the NDP-induced folding (ADP, GDP, CDP, and UDP) were globally fit as described below. The global fit of the NDP data yielded estimates for 68 parameters. The ADP-, GDP-, CDP-, and UDP-induced folding models share eight parameters: SigU, SigI, SigF, ΔGui, ΔGif, kui, kif, and kuf. Stopped-flow data for the P_i-induced folding were fit as described below. For the fit of P_i data, the parameters ΔGui, ΔGif, kui, kif, and kuf were fixed to the values obtained from the fit of PP_i and TMAO data. With these parameters fixed, the fit of P_i data yielded estimates for 17 additional parameters. With the fitting strategies described above, the number of well-determined parameters unique determined to each ligand’s coupled binding and folding mechanism ranged from 14 to 17. For comparison, the folding mechanism for a three-state protein determined from osmolyte-induced folding or denaturant-induced unfolding consists of 14 (linear mechanism) to 16 (triangular mechanism) parameters that are readily determined by fitting both the amplitudes and time constants from stopped-flow data (17, 29).

Fits of stopped-flow data were initialized by specifying initial guesses for the values and uncertainties of each parameter. One thousand parameter sets were generated by using the initial guesses for the parameter values as means and the initial guess for the uncertainties as SDs to sample from a normal distribution. At each iteration, a parameter set (x) was chosen and a new was proposed using one of two methods: (i) the differences between two more parameter sets (y and z) were multiplied by a scaling factor a and added to parameter set x, or (ii) the parameter values in parameter set x were used as means to sample from normal distributions with SDs equal to the SD of the parameters in all 1,000 parameter sets multiplied by a scaling factor b. The proposed parameter set was either accepted as a replacement for parameter set x or rejected based on the Metropolis criterion. Scaling factors a an b were adjusted to achieve proposal acceptance rates of ∼20%. Fits were run for 1,000,000 iterations. Trajectories were examined to ensure that means and SDs for parameters had each converged. The final 1,000 parameter sets constituted the posterior. The 95% confidence intervals for each parameter were from the posterior distributions; after sorting, the 26th and 975th parameter value for each parameter were used as the upper and lower bounds of the 95% confidence interval. A Mathematica notebook implementing this code for analysis of the data are available upon request.

Isothermal Titration Calorimetry

The 5 μM P^-Pro was mixed with ADP, GDP, CDP, or UDP in a MicroCal VP-ITC instrument at 25 °C with a stir speed of 307 rpm. Binding isotherms were fit in Mathematica to a three-state coupled binding and folding mechanism to obtain estimates of the enthalpies of binding for the α- and β-sites of the folded state. Affinities and conformational equilibrium constants of the unliganded protein were fixed at the mean estimates obtained from the global fit of ADP, GDP, CDP, and UDP stopped-flow kinetic experiments.

Flux Plots (Fig. 7)

Fluxes were calculated using the binding affinity of PP_i to the α-site of the low-affinity state and the unliganded equilibrium constant and folding rate constant. The ligand-bound folding rate constant and the binding affinity for the higher-affinity state were calculated given κ and δ. Fluxes were calculated for the ligand concentration at which 50% of protein would be bound for the given thermodynamic parameters.

Mathematical Description of Coupled Binding and Folding Model

• Lt → total ligand concentration,

• Pt → total protein concentration,

• t → time,

• Lf → free ligand concentration,

• Kui → equilibrium constant for the U-to-I reaction,

• Kif → equilibrium constant for the I-to-F reaction,

• Kuf → equilibrium constant for the U-to-F reaction,

• kui → rate constant for the U-to-I transition,

• kif → rate constant for the I-to-F transition,

• kuf → rate constant for the U-to-F transition,

• kiu → rate constant for the I-to-U transition,

• kfi → rate constant for the F-to-I transition,

• kfu → rate constant for the F-to-U transition,

• kuiα → rate constant for the U-to-I transition with ligand bound at the α-site,

• kifα → rate constant for the I-to-F transition with ligand bound at the α-site,

• kufα → rate constant for the U-to-F transition with ligand bound at the α-site,

• kiuα → rate constant for the I-to-U transition with ligand bound at the α-site,

• kfiα → rate constant for the F-to-I transition with ligand bound at the α-site,

• kfuα → rate constant for the F-to-U transition with ligand bound at the α-site,

• kuiβ → rate constant for the U-to-I transition with ligand bound at the β-site,

• kifβ → rate constant for the I-to-F transition with ligand bound at the β-site,

• kufβ → rate constant for the U-to-F transition with ligand bound at the β-site,

• kiuβ → rate constant for the I-to-U transition with ligand bound at the β-site,

• kfiβ → rate constant for the F-to-I transition with ligand bound at the β-site,

• kfuβ → rate constant for the F-to-U transition with ligand bound at the β-site,

• kuiαβ → rate constant for the U-to-I transition with ligand bound at both the α- and β-sites,

• kifαβ → rate constant for the I-to-F transition with ligand bound at both the α- and β-sites,

• kufαβ → rate constant for the U-to-F transition with ligand bound at both the α- and β-sites,

• kiuαβ → rate constant for the I-to-U transition with ligand bound at both the α- and β-sites,

• kfiαβ → rate constant for the F-to-I transition with ligand bound at both the α- and β-sites,

• kfuαβ → rate constant for the F-to-U transition with ligand bound at both the α- and β-sites,

• Kαu → binding constant for the α-site in state U,

• Kαi → binding constant for the α-site in state I,

• Kαf → binding constant for the α-site in state F,

• Kβu → binding constant for the β-site in state U,

• Kβi → binding constant for the β-site in state I,

• Kβf → binding constant for the β-site in state F,

• kauα → association rate constant for ligand binding to the α-site in state U,

• kauβ → association rate constant for ligand binding to the β-site in state U,

• kaiα → association rate constant for ligand binding to the α-site in state I,

• kaiβ → association rate constant for ligand binding to the β-site in state I,

• kafα → association rate constant for ligand binding to the α-site in state F,

• kafβ → association rate constant for ligand binding to the β-site in state F,

• kduα → dissociation rate constant for the α-site in state U,

• kduβ → dissociation rate constant for the β-site in state U,

• kdiα → dissociation rate constant for the α-site in state I,

• kdiβ → dissociation rate constant for the β-site in state I,

• kdfα → dissociation rate constant for the α-site in state F,

• kdfβ → dissociation rate constant for the β-site in state F,

• U(t) → concentration of U as a function of time,

• Uα(t) → concentration of U with ligand bound at the α-site as a function of time,

• Uβ(t) → concentration of U with ligand bound at the β-site as a function of time,

• Uαβ(t) → concentration of U with ligand bound at the α- and β-sites as a function of time,

• I(t) → concentration of I as a function of time,

• Iα(t) → concentration of I with ligand bound at the α-site as a function of time,

• Iβ(t) → concentration of I with ligand bound at the β-site as a function of time,

• Iαβ(t) → concentration of I with ligand bound at the α- and β-sites as a function of time,

• F(t) → concentration of F as a function of time,

• Fα(t) → concentration of F with ligand bound at the α-site as a function of time,

• Fβ(t) → concentration of F with ligand bound at the β-site as a function of time,

• Fαβ(t) → concentration of F with ligand bound at the α- and β-sites as a function of time.

The Following Parameters Represent the First Derivatives of the Concentrations with Respect to Time.

• U′(t),

• Uα′(t),

• Uβ′(t),

• Uαβ′(t),

• I′(t),

• Iα′(t),

• Iβ′(t),

• Iαβ′(t),

• F′(t),

• Fα′(t),

• Fβ′(t),

• Fαβ′(t).

Signals and Fractions of U, I, and F.

• SigU → signal of U,

• SigI → signal of I,

• SigF → signal of F,

• SigUBound → signal of U with ligand bound,

• SigIBound → signal of I with ligand bound,

• SigFBound → signal of F with ligand bound,

• FuFree → fraction of protein as U,

• FuBound → fraction of protein as U with ligand bound,

• FiFree → fraction of protein as I,

• FiBound → fraction of protein as I with ligand bound,

• FfFree → fraction of protein as F,

• FfBound → fraction of protein as F with ligand bound.

Kinetic and Thermodynamic Relationships.

$$Kuf=Kui\hspace{0.17em}Kif.$$

On Rates.

$$kaf\alpha =kaf\beta =kai\alpha =kai\beta =kau\alpha =kau\beta =1\times {10}^8{\mathrm{M}}^{\mathrm{-1}}\times {\mathrm{s}}^{\mathrm{-1}}.$$

List of Off-Rate Constants kdxz Where x Is the Conformation and z Is the Site α or β.

$$kdu\alpha =kau\alpha /K\alpha u,$$

$$kdu\beta =kau\beta /K\beta u,$$

$$kdi\alpha =kai\alpha /K\alpha i,$$

$$kdi\beta =kai\beta /K\beta i,$$

$$kdf\alpha =kaf\alpha /K\alpha f,$$

$$kdf\beta =kaf\beta /K\beta f.$$

List of Unfolding Rate Constants in All Different Liganding States.

$$kfi=kif/Kif,$$

$$kfi\alpha =\left(kif\alpha \hspace{0.17em}K\alpha i\right)/\left(Kif\hspace{0.17em}K\alpha f\right),$$

$$kfi\beta =\left(kif\beta \hspace{0.17em}K\beta i\right)/\left(Kif\hspace{0.17em}K\beta f\right),$$

$$kfi\alpha \beta =\left(kif\alpha \beta \hspace{0.17em}K\alpha i\hspace{0.17em}K\beta i\right)/\left(Kif\hspace{0.17em}K\alpha f\hspace{0.17em}K\beta f\right),$$

$$kiu=kui/Kui,$$

$$kiu\alpha =\left(kui\alpha \hspace{0.17em}K\alpha u\right)/\left(Kui\hspace{0.17em}K\alpha i\right),$$

$$kiu\beta =\left(kui\beta \hspace{0.17em}K\beta u\right)/\left(Kui\hspace{0.17em}K\beta i\right),$$

$$kiu\alpha \beta =\left(kui\alpha \beta \hspace{0.17em}K\alpha u\hspace{0.17em}K\beta u\right)/\left(Kui\hspace{0.17em}K\alpha i\hspace{0.17em}K\beta i\right),$$

$$kfu=kuf/Kuf,$$

$$kfu\alpha =\left(kuf\alpha \hspace{0.17em}K\alpha u\right)/\left(Kuf\hspace{0.17em}K\alpha f\right),$$

$$kfu\beta =\left(kuf\beta \hspace{0.17em}K\beta u\right)/\left(Kuf\hspace{0.17em}K\beta f\right),$$

$$kfu\alpha \beta =\left(kuf\alpha \beta \hspace{0.17em}K\alpha u\hspace{0.17em}K\beta u\right)/\left(Kuf\hspace{0.17em}K\alpha f\hspace{0.17em}K\beta f\right).$$

Free Ligand Concentration in Terms of Concentrations of Total Ligand and Bound Protein.

$$\mathrm{Lf}=\left(\mathrm{Lt}-\left(U\alpha \left(t\right)+U\beta \left(t\right)+2\hspace{0.17em}U\alpha \beta \left(t\right)+I\alpha \left(t\right)+I\beta \left(t\right)+2\hspace{0.17em}I\alpha \beta \left(t\right)+F\alpha \left(t\right)+F\beta \left(t\right)+2\hspace{0.17em}F\alpha \beta \left(T\right)\right)\right).$$

Differential Equations for Rate Laws Describing P Protein Coupled Binding and Folding.

$$U\prime \left(t\right)=-kui\hspace{0.17em}U\left(t\right)+kiu\hspace{0.17em}I\left(t\right)-kau\alpha \hspace{0.17em}U\left(t\right)\mathrm{Lf}-kau\beta \hspace{0.17em}U\left(t\right)\mathrm{Lf}+kdu\alpha \hspace{0.17em}U\alpha \left(t\right)+kdu\beta \hspace{0.17em}U\beta \left(t\right)-kuf\hspace{0.17em}U\left(t\right)+kfu\hspace{0.17em}F\left(T\right),$$

$$U\alpha \prime \left(t\right)=-kdu\alpha \hspace{0.17em}U\alpha \left(t\right)+kau\alpha \hspace{0.17em}U\left(t\right)\mathrm{Lf}-kui\alpha \hspace{0.17em}U\alpha \left(t\right)+kiu\alpha \hspace{0.17em}I\alpha \left(t\right)-kau\beta \hspace{0.17em}U\alpha \left(t\right)\mathrm{Lf}+kdu\beta \hspace{0.17em}U\alpha \beta \left(t\right)-kuf\alpha \hspace{0.17em}U\alpha \left(t\right)+kfu\alpha \hspace{0.17em}F\alpha \left(T\right),$$

$$U\beta \prime \left(t\right)=-kdu\beta \hspace{0.17em}U\beta \left(t\right)+kau\beta \hspace{0.17em}U\left(t\right)\mathrm{Lf}-kui\beta \hspace{0.17em}U\beta \left(t\right)+kiu\beta \hspace{0.17em}I\beta \left(t\right)-kau\alpha \hspace{0.17em}U\beta \left(t\right)\mathrm{Lf}+kdu\alpha \hspace{0.17em}U\alpha \beta \left(t\right)-kuf\beta \hspace{0.17em}U\beta \left(t\right)+kfu\beta \hspace{0.17em}F\beta \left(T\right),$$

$$U\alpha \beta \prime \left(t\right)=-kdu\alpha \hspace{0.17em}U\alpha \beta \left(t\right)-kdu\beta \hspace{0.17em}U\alpha \beta \left(t\right)+kau\alpha \hspace{0.17em}U\beta \left(t\right)\mathrm{Lf}+kau\beta \hspace{0.17em}U\alpha \left(t\right)\mathrm{Lf}-kui\alpha \beta \hspace{0.17em}U\alpha \beta \left(t\right)+kiu\alpha \beta \hspace{0.17em}I\alpha \beta \left(t\right)-kuf\alpha \beta \hspace{0.17em}U\alpha \beta \left(t\right)+kfu\alpha \beta \hspace{0.17em}F\alpha \beta \left(T\right),$$

$$I\prime \left(t\right)=-kiu\hspace{0.17em}I\left(t\right)-kif\hspace{0.17em}I\left(t\right)+kui\hspace{0.17em}U\left(t\right)+kfi\hspace{0.17em}F\left(t\right)-kai\alpha \hspace{0.17em}I\left(t\right)\mathrm{Lf}-kai\beta \hspace{0.17em}I\left(t\right)\mathrm{Lf}+kdi\alpha \hspace{0.17em}I\alpha \left(t\right)+kdi\beta \hspace{0.17em}I\beta \left(t\right),$$

$$I\alpha \prime \left(t\right)=-kiu\alpha \hspace{0.17em}I\alpha \left(t\right)-kif\alpha \hspace{0.17em}I\alpha \left(t\right)+kui\alpha \hspace{0.17em}U\alpha \left(t\right)+kfi\alpha \hspace{0.17em}F\alpha \left(t\right)-kdi\alpha \hspace{0.17em}I\alpha \left(t\right)+kai\alpha \hspace{0.17em}I\left(t\right)\mathrm{Lf}-kai\beta \hspace{0.17em}I\alpha \left(t\right)\mathrm{Lf}+kdi\beta \hspace{0.17em}I\alpha \beta \left(t\right),$$

$$I\beta \prime \left(t\right)=-kiu\beta \hspace{0.17em}I\beta \left(t\right)-kif\beta \hspace{0.17em}I\beta \left(t\right)+kui\beta \hspace{0.17em}U\beta \left(t\right)+kfi\beta \hspace{0.17em}F\beta \left(t\right)-kdi\beta \hspace{0.17em}I\beta \left(t\right)+kai\beta \hspace{0.17em}I\left(t\right)\mathrm{Lf}-kai\alpha \hspace{0.17em}I\beta \left(t\right)\mathrm{Lf}+kdi\alpha \hspace{0.17em}I\alpha \beta \left(t\right),$$

$$I\alpha \beta \prime \left(t\right)=-kiu\alpha \beta \hspace{0.17em}I\alpha \beta \left(t\right)-kif\alpha \beta \hspace{0.17em}I\alpha \beta \left(t\right)+kui\alpha \beta \hspace{0.17em}U\alpha \beta \left(t\right)+kfi\alpha \beta \hspace{0.17em}F\alpha \beta \left(t\right)-kdi\alpha \hspace{0.17em}I\alpha \beta \left(t\right)-kdi\beta \hspace{0.17em}I\alpha \beta \left(t\right)+kai\alpha \hspace{0.17em}I\beta \left(t\right)\mathrm{Lf}+kai\beta \hspace{0.17em}I\alpha \left(t\right)\mathrm{Lf,}$$

$$F\prime \left(t\right)=-kfi\hspace{0.17em}F\left(t\right)+kif\hspace{0.17em}I\left(t\right)-kaf\alpha \hspace{0.17em}F\left(t\right)\mathrm{Lf}-kaf\beta \hspace{0.17em}F\left(t\right)\mathrm{Lf}+kdf\alpha \hspace{0.17em}F\alpha \left(t\right)+kdf\beta \hspace{0.17em}F\beta \left(t\right)+kuf\hspace{0.17em}U\left(t\right)-kfu\hspace{0.17em}F\left(T\right),$$

$$F\alpha \prime \left(t\right)=-kdf\alpha \hspace{0.17em}F\alpha \left(t\right)+kaf\alpha \hspace{0.17em}F\left(t\right)\mathrm{Lf}-kfi\alpha \hspace{0.17em}F\alpha \left(t\right)+kif\alpha \hspace{0.17em}I\alpha \left(t\right)-kaf\beta \hspace{0.17em}F\alpha \left(t\right)\mathrm{Lf}+kdf\beta \hspace{0.17em}F\alpha \beta \left(t\right)+kuf\alpha \hspace{0.17em}U\alpha \left(t\right)-kfu\alpha \hspace{0.17em}F\alpha \left(t\right),$$

$$F\beta \prime \left(t\right)=-kdf\beta \hspace{0.17em}F\beta \left(t\right)+kaf\beta \hspace{0.17em}F\left(t\right)\mathrm{Lf}-kfi\beta \hspace{0.17em}F\beta \left(t\right)+kif\beta \hspace{0.17em}I\beta \left(t\right)-kaf\alpha \hspace{0.17em}F\beta \left(t\right)\mathrm{Lf}+kdf\alpha \hspace{0.17em}F\alpha \beta \left(t\right)+kuf\beta \hspace{0.17em}U\beta \left(t\right)-kfu\beta \hspace{0.17em}F\beta \left(T\right),$$

$$F\alpha \beta \prime \left(t\right)=-kdf\alpha \hspace{0.17em}F\alpha \beta \left(t\right)-kdf\beta \hspace{0.17em}F\alpha \beta \left(t\right)+kaf\alpha \hspace{0.17em}F\beta \left(t\right)\mathrm{Lf}+kaf\beta \hspace{0.17em}F\alpha \left(t\right)\mathrm{Lf}-kfi\alpha \beta \hspace{0.17em}F\alpha \beta \left(t\right)+kif\alpha \beta \hspace{0.17em}I\alpha \beta \left(t\right)+kuf\alpha \beta \hspace{0.17em}U\alpha \beta \left(t\right)-kfu\alpha \beta \hspace{0.17em}F\alpha \beta \hspace{0.17em}\left(T\right).$$

Initial Conditions.

$$U\left(0\right)=\mathrm{Pt}/\left(1+KuI\left(1+Kif\right)\right),$$

$$U\left(0\right)+U\alpha \left(0\right)+U\beta \left(0\right)+U\alpha \beta \left(0\right)+I\left(0\right)+I\alpha \left(0\right)+I\beta \left(0\right)+I\alpha \beta \left(0\right)+F\left(0\right)+F\alpha \left(0\right)+F\beta \left(0\right)+F\alpha \beta \left(0\right)=\mathrm{Pt,}$$

$$U\beta \left(0\right)=0,$$

$$U\alpha \beta \left(0\right)=0,$$

$$I\left(0\right)=\left(Kui\hspace{0.17em}\mathrm{Pt}\right)/\left(1+KuI\left(1+Kif\right)\right),$$

$$I\alpha \left(0\right)=0,$$

$$I\beta \left(0\right)=0,$$

$$I\alpha \beta \left(0\right)=0,$$

$$F\left(0\right)=\left(Kui\hspace{0.17em}Kif\hspace{0.17em}\mathrm{Pt}\right)/\left(1+KuI\left(1+Kif\right)\right),$$

$$F\alpha \left(0\right)=0,$$

$$F\beta \left(0\right)=0,$$

$$F\alpha \beta \left(0\right)=0.$$

For PP_i and Pi.

$$\text{Signal}\hspace{0.17em}\text{Observed}=\left(\text{Sig}U\hspace{0.17em}\text{F}u\text{Free}+\text{Sig}U\text{Bound}\hspace{0.17em}\text{F}u\text{Bound}+\text{Sig}I\hspace{0.17em}\text{F}i\text{Free}+\text{Sig}I\hspace{0.17em}\text{F}i\text{Bound}+\text{Sig}F\hspace{0.17em}\text{F}f\text{Free}+\text{Sig}F\hspace{0.17em}\text{F}f\text{Bound}\right).$$

For ADP, GDP, UDP, and CDP.

$$\text{Signal}\hspace{0.17em}\text{Observed}=\left(\text{Sig}U\hspace{0.17em}\text{F}u\text{Free}+\text{Sig}U\text{Bound}\hspace{0.17em}\text{F}u\text{Bound}+\text{Sig}I\hspace{0.17em}\text{F}i\text{Free}+\text{Sig}I\hspace{0.17em}\text{F}i\text{Bound}+\text{Sig}F\hspace{0.17em}\text{F}f\text{Free}+\text{Sig}F\hspace{0.17em}\text{F}f\text{Bound}\right)-\left(ife\hspace{0.17em}\text{Lt}\right).$$

The ife parameter accounts for the inner filter effect caused by the nucleotide absorbance of excitation light.