Transition to chaos in random networks with cell-type-specific connectivity

Abstract

In neural circuits, statistical connectivity rules strongly depend on cell-type identity. We study dynamics of neural networks with cell-type specific connectivity by extending the dynamic mean field method, and find that these networks exhibit a phase transition between silent and chaotic activity. By analyzing the locus of this transition, we derive a new result in random matrix theory: the spectral radius of a random connectivity matrix with block-structured variances. We apply our results to show how a small group of hyper-excitable neurons within the network can significantly increase the network’s computational capacity by bringing it into the chaotic regime.

The theory of random matrices has diverse applications in nuclear [1] and solid-state [2, 3] physics, number theory and statistics [4] and models of neural networks [5–8]. The increasing use of boolean networks to model gene regulatory networks [9–11] suggests that random matrix theory may advance our understanding of those biological systems as well. Most existing theoretical results pertain to matrices with values drawn from a single distribution, corresponding to randomly connected networks with a single connectivity rule and cell-type. Recent experimental studies describe in increasing detail the heterogeneous structure of biological networks where connection probability depends strongly on cell-type [12–17]. As a step towards bridging this gap between theory and experiment, we extend here mean-field methods used to analyze conventional randomly connected networks to networks with multiple cell-types and allow for cell-type-dependent connectivity rules. We focus here on neural networks.

Randomly connected networks of one cell-type were shown to have two important properties. First, they undergo a phase transition from silent to chaotic activity as the variance of connection strength is increased [7, 8]. Second, such networks reach optimal computational capacity near the critical point [18, 19] in a weakly chaotic regime. We find both phenomena in networks with multiple cell-types. Importantly, the effective gain of multi-type networks deviates strongly from predictions obtained by averaging across the cell types, and in many cases these networks show greater computational capacity compared to networks with cell-type independent connectivity.

The starting point for our analysis of recurrent activity in neural networks is a firing-rate model where the activation x_i(t) of the ith neuron determines its firing-rate ϕ_i(t) through a nonlinear function ϕ_i(t) = tanh(x_i). The activation of the ith neuron depends on the firing-rate of all N neurons in the network:

$${ẋ}_i(t)=-x_i(t)+\sum _{j=1}^N{J}_{ij}{\varphi }_j(t),$$ (1)

where J_ij describes the connection weight from neuron j to i. Previous work [7] considered a recurrent random network where all connections are drawn from the same distribution. There, the matrix elements was drawn from a Gaussian distribution with mean zero and variance g²/N, where g defines the average synaptic gain in the network. According to Girko’s circular law, the spectral density of the random matrix J in this case is uniform on a disk with radius g [20, 21]. When the real part of some of the eigenvalues of J exceeds 1, the quiescent state x_i(t) = 0 becomes unstable and the network becomes chaotic [7]. Thus, for networks with one cell-type the transition to chaotic dynamics occurs when g = 1. The chaotic dynamics persist even in the presence of noise, but the critical point gcrit shifts to values > 1, with g_crit = 1 − σ² log σ² for small noise intensities σ² and $g_{\text{crit}}=\sqrt{\pi /2\sigma }$ for large noise [8].

We now consider networks with D cell-types, each with a fraction α_d of neurons in it. The mean connection weight is 〈J_ij〉 = 0. The variances $N\langle J_{ij}^2\rangle =g_{c_i{d}_j}^2$ depend on the cell-type of the input (c) and output (d) neurons; where c_i denotes the group neuron i belongs to. In what follows, indices i, j = 1, …, N and c, d = 1, …, D correspond to single neurons and neuron groups, respectively. Averages over realizations of J are denoted by 〈·〉. It is convenient to represent the connectivity structure using a synaptic gain matrix G. Its elements G_ij = g_cidj are arranged in D² blocks of sizes N α_c × N α_d (Fig. 1a–c, top insets). The mean synaptic gain, ḡ, is given by $N^{-1}{({\sum }_{i,j=1}^N{G}_{ij}^2)}^{\frac{1}{2}}={({\sum }_{c,d=1}^D{\alpha }_c{\alpha }_d{g}_{cd}^2)}^{\frac{1}{2}}$. Defining $J_{ij}^0~𝒩(0,N^{-1})$ (but see [22] for discussion of non-Gaussian entries) and $n_d=N{\sum }_{c=1}^d{\alpha }_c$ allows us to rewrite Eq. (1) in a form that emphasizes the separate contributions from each group to a neuron:

$${ẋ}_i=-x_i+\sum _{d=1}^D{g}_{c_{i}d}\sum _{j=n_{d-1}+1}^{n_d}{J}_{ij}^0{\varphi }_j(t).$$ (2)

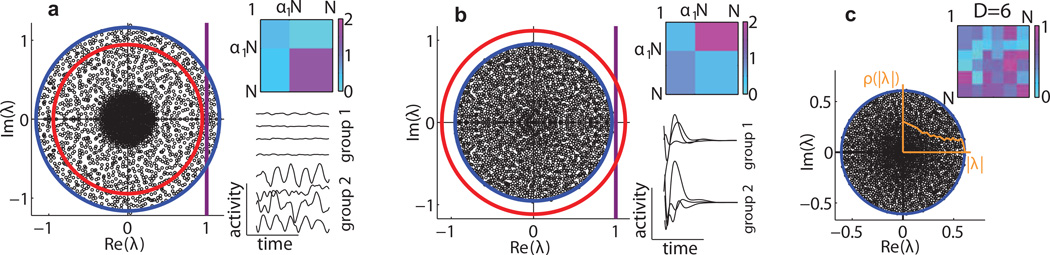
FIG. 1.

Spectra and dynamics of networks with cell-type dependent connectivity (N = 2500). The support of the spectrum of the connectivity matrix J is accurately described by $\sqrt{{\mathrm{\Lambda }}_1}$ (radius of blue circle) for different networks. Top insets - the synaptic gain matrix G summarizes the connectivity structure. Bottom insets - activity of representative neurons from each type. The line ℜ{λ} = 1 (purple) marks the transition from quiescent to chaotic activity. (a) An example chaotic network with two cell-types. The average synaptic gain ḡ (radius of red circle) incorrectly predicts this network to be quiescent. (b) An example silent network. Here ḡ incorrectly predicts this network to be chaotic. (c) An example network with six cell-types. In all examples the radial part of the eigenvalue distribution ρ(|λ|) (orange line) is not uniform [22].

We use the dynamic mean field approach [5, 7, 23] to study the network behavior in the N → ∞ limit. Averaging Eq. (2) over the ensemble from which J is drawn implies that only neurons that belong to the same group are statistically identical. Therefore, to represent the network behavior it is enough to look at the activities ξ_d(t) of D representative neurons and their inputs η_d (t).

The stochastic mean field variables ξ and η will approximate the activities and inputs in the full N dimensional network provided that they satisfy the dynamic equation

$${\dot{\xi }}_d(t)=-{\xi }_d(t)+{\eta }_d(t),$$ (3)

and provided that η_d (t) is drawn from a Gaussian distribution with moments satisfying the following conditions. First, the mean 〈η_d(t)〉 = 0 for all d. Second, the correlations of η should match the input correlations in the full network, averaged separately over each group. Using Eq. (3) and the property $N\langle J_{ij}^0{J}_{kl}^0\rangle ={\delta }_{ik}{\delta }_{jl}$ we get the self-consistency conditions:

$$\langle {\eta }_c(t){\eta }_d(t+\tau )\rangle =\sum _{a,b=1}^D\sum _{j=n_{a-1}+1}^{n_a}\sum _{l=n_{b-1}+1}^{n_b}{g}_{ca}{g}_{db}\langle J_{ij}^0{J}_{kl}^0\rangle \langle \varphi [x_j(t)]\varphi [x_l(t+\tau )]\rangle ={\delta }_{cd}\sum _{b=1}^D{\alpha }_b{g}_{cb}^2{C}_b(\tau ),$$ (4)

where 〈·〉 denotes averages over i = n_c−1 + 1, …, n_c and k = n_d−1 + 1, …, n_d in addition to average over realizations of J. The average firing rate correlation vector is denoted by C(τ). Its components (using the variables of the full network) are $C_d(\tau )=\frac{1}{N{\alpha }_d}{\sum }_{i=n_{d-1}+1}^{n_d}\langle \varphi [x_i(t)]\varphi [x_i(t+\tau )]\rangle$, translating to C_d(τ) = 〈ϕ[ξ_d(t)]ϕ[ξ_d(t + τ)]〉 using the mean field variables. Importantly, the covariance matrix ℋ(τ) with elements ℋ_cd (τ) = 〈η_c (t) η_d (t + τ)〉 is diagonal, justifying the definition of the vector H = diag (ℋ). With this in hand we rewrite Eq. (4) in matrix form

$$\mathbf{H}(\tau )=\mathbf{M}\mathbf{C}(\tau ),$$ (5)

where M is a constant matrix reflecting the network connectivity structure: $M_{cd}={\alpha }_d{g}_{cd}^2$.

A trivial solution to this equation is H(τ) = C(τ) = 0 which corresponds to the silent network state: x_i(t) = 0. Recall that in the network with a single cell-type, the matrix M = g² is a scalar and Eq. (5) reduces to H (τ) = g²C(τ). In this case the silent solution is stable only when g < 1. For g > 1 the autocorrelations of η are non-zero which leads to chaotic dynamics in the N dimensional system [7].

In the general case (D ≥ 1), Eq. (5) can be projected on the eigenvectors of M leading to D consistency conditions, each equivalent to the single group case. Each projection has an effective scalar given by the eigenvalue in place of g² in the D = 1 case. Hence, the trivial solution will be stable if all eigenvalues of M have real part < 1. This is guaranteed if Λ₁, the largest eigenvalue of M, is < 1 [24]. If Λ₁ > 1 the projection of Eq. (5) on the leading eigenvector of M gives a scalar self-consistency equation analogous to the D = 1 case for which the trivial solution is unstable. As we know from the analysis of the single cell-type network, this leads to chaotic dynamics in the full network. Therefore Λ₁ = 1 is the critical point of the multiple cell-type network.

Another approach to show explicitly that Λ₁ = 1 at the critical point is to consider first order deviations in the network activity from the quiescent state. Here C(τ) ≈ Δ(τ) where Δ(τ) is the autocorrelation vector of the activities with elements Δ_d(τ) = 〈ξ_d(t)ξ_d(t + τ)〉. By invoking Eq. (3) we have

$$\mathbf{H}(\tau )=(1-\frac{d^2}{d{\tau }^2})\mathbf{\Delta }(\tau ).$$ (6)

Substituting Eq. (6) into Eq. (5) leads to an equation of motion for a particle with coordinates Δ(τ):

$$\frac{d^2\mathbf{\Delta }(\tau )}{d{\tau }^2}=(𝕀-\mathbf{M})\mathbf{\Delta }(\tau ).$$ (7)

The particle’s trajectories depend on the eigenvalues of M. The first bifurcation (assuming the elements of M are scaled together) occurs when Λ₁ = 1, in the direction parallel to the leading eigenvector. Physical solutions should have ‖Δ(τ)‖ < ∞ as τ → ∞ because Δ(τ) is an autocorrelation function. When all eigenvalues of M are smaller than 1 the trivial solution Δ(τ) = 0 is the only solution (in the neighborhood of x_i(t) = 0 where our approximation is accurate). At the critical point (Λ₁ = 1) a non trivial solution appears, and above it finite autocorrelations lead to chaotic dynamics in the full system.

The eigenvalue spectrum of J is circularly symmetric in the absence of correlation between matrix entries as is evident from numerical simulations and direct calculations using random matrix theory techniques [25]. To derive the radius r of the support of its spectral density, one can use the following scaling relationship. If all elements of the matrix g_cd are multiplied by a constant κ, the radius r will scale linearly with κ. At the same time, $M_{cd}\propto g_{cd}^2$, so Λ₁ ∝ κ². Thus, $r\propto \sqrt{{\mathrm{\Lambda }}_1}$. The proportionality constant can be determined by noting that for both single and multiple cell-type networks this transition occurs when a finite mass of the spectral density of J has real part > 1, which can also be verified by direct computation of the largest Lyapunov exponent [22]. The transition occurs at Λ₁ = 1, meaning that for Λ₁ = 1 the eigenvalues of J are bounded in the unit circle r = 1, so in general:

$$r(\alpha ,\mathbf{g})=\sqrt{{\mathrm{\Lambda }}_1}=\sqrt{\text{max}[\lambda (\mathbf{M})]}.$$ (8)

Predictions for the radius according to Eq. (8) matched numerical simulations for a number of different matrix configurations (Fig. 1a,b). Eq. (8) also holds for networks with cell-type independent connectivity, in which case Λ₁ = g² and r = g. Importantly, r differs qualitatively from the mean synaptic gain ḡ. The inequality $\sqrt{{\mathrm{\Lambda }}_1}\ne ḡ$ is a signature of the block structured variances. It is not observed in the case where the variances have columnar structure [26] or when the J_ij ’s are randomly permuted.

Next we analyze the network dynamics above the critical point. In the chaotic regime the persistent population-level activity is determined by the structure matrix M. Consider the decomposition $\mathbf{M}={\sum }_{c=1}^D{\mathrm{\Lambda }}_c|u_c^R\rangle \langle u_c^L|$ where $|u_c^R\rangle ,\langle u_c^L|$ are the right and left eigenvectors ordered by the real part of their corresponding eigenvalues ℜ{Λ_c}, satisfying $\langle u_c^L|u_d^R\rangle ={\delta }_{cd}$. We find, with analogy to the analysis of the scalar self consistency equation in [7] that the trivial solution to Eq. (5) is unstable in the subspace ${𝒰}_{\mathbf{M}}=\text{span}\{|u_1^R\rangle ,\dots ,|u_{D^{*}}^R\rangle \}$, where D* is the number of eigenvalues of M with real part > 1. In that subspace the solution to Eq. (5) is a combination of D* different autocorrelation functions. In the D − D* dimensional orthogonal complement subspace ${𝒰}_{\mathbf{M}}^{\perp }$ the trivial solution is stable. Consequently, the vectors H(τ), Δ(τ) are significant in 𝒰_M with ≈ 0 projection on any vector in ${𝒰}_{\mathbf{M}}^{\perp }$ (Fig. 2). Note that for asymmetric M, $|u_c^R\rangle$ are not orthogonal and ${𝒰}_{\mathbf{M}}^{\perp }$ is spanned by the left rather than the right eigenvectors: ${𝒰}_{\mathbf{M}}^{\perp }=\text{span}\{\langle u_{D^{*}+1}^L|,\dots ,\langle u_D^L|\}$.

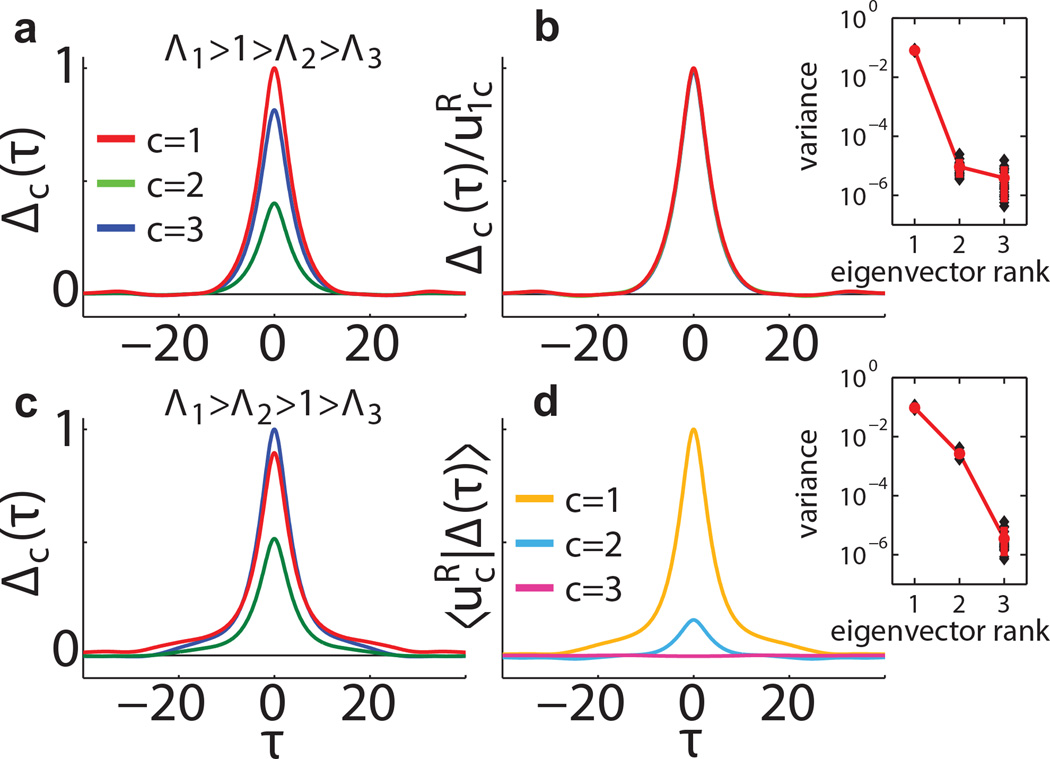
FIG. 2.

Autocorrelation modes. Example networks (N = 1200) have 3 equally sized groups with α, g such that M is symmetric. (a) When D* = 1 autocorrelations maintain a constant ratio independent of τ. (b) Rescaling by the components $u_{1c}^R$ collapses the autocorrelation functions (Here Λ₁ = 20, Λ₂ = 0.2, Λ₃ = 0.1). (c) When D* = 2, the autocorrelation functions are linear combinations of two autocorrelation “modes” that decay on different timescales. Projections of these functions $\langle u_c^R|\mathbf{\Delta }(\tau )\rangle$ are shown in (d). Only projections on $|u_1^R\rangle ,|u_2^R\rangle$ are significantly different from 0 (Here Λ₁ = 20, Λ₂ = 16, Λ₃ = 0.1). Insets show the variance of Δ (τ) projected on $|u_c^R\rangle$ averaged over 20 networks in each setting.

In the special case D* = 1 we can write ${\mathbf{u}}_1^R{q}_H(\tau )$ and $\mathbf{\Delta }(\tau )={\mathbf{u}}_1^R{q}_{\mathrm{\Delta }}(\tau )$ where q_H (τ), q_Δ (τ) are scalar functions of τ determined by the nonlinear self-consistency condition. Therefore, neurons in all groups have the same autocorrelation function with different amplitudes. The ratio of amplitudes is determined by the components $u_{1c}^R$ of the leading right eigenvector of M (see Fig. 2a,b) as ${\mathrm{\Delta }}_c(\tau )/{\mathrm{\Delta }}_d(\tau )=u_{1c}^R/u_{1d}^R$. This ratio is independent of τ and the firing rate nonlinearity. The latter affects only the overall amount of activity in the network but not the ratio of activity between the subgroups.

We illustrate how these results give insight into a perplexing question in computational neuroscience - how can a small number of neurons have a large effect on the representational capacity of the whole network? In adults, newborn neurons continuously migrate into the existing neural circuit in the hippocampus and olfactory bulb regions [27]. Impaired neurogenesis results in strong deficits in learning and memory. This is surprising since the young neurons, although hyperexcitable, constitute only a very small fraction (< 0.1) of the total network. To better understand the role young neurons may play, we analyzed a network with D = 2 groups of neurons: group 1 of young neurons that is significantly smaller than group 2 of mature neurons (α₁ ≪ α₂). The connectivity within the existing neural circuit is such that by itself that subnetwork would be in the quiescent state: g₂₂ = 1 − ε < 1. To model the increased excitability of the young neurons all connections of these neurons were set to: g₁₂ = g₂₁ = g₁₁ = γ > 1 − ε.

We analyzed the network’s capacity to reproduce a target output pattern f (t). The activity of the neurons serves as a “reservoir” of waveforms from which f (t) is composed. The learning algorithm in [28] allows us to find the vector w such that $z(t)={\sum }_{i=1}^N{w}_i{\varphi }_i(t)=f(t)$, where the modified dynamics have J_ij → J_ij + u_iw_j and u is a random vector with O(1) entries. For simplicity we choose periodic target functions f (t) = sin(Ωt), and define the learning index as the fraction of power that the output function z(t) has at the target frequency. The index varies from 0 to 1, and is computed by averaging over 50 cycles.

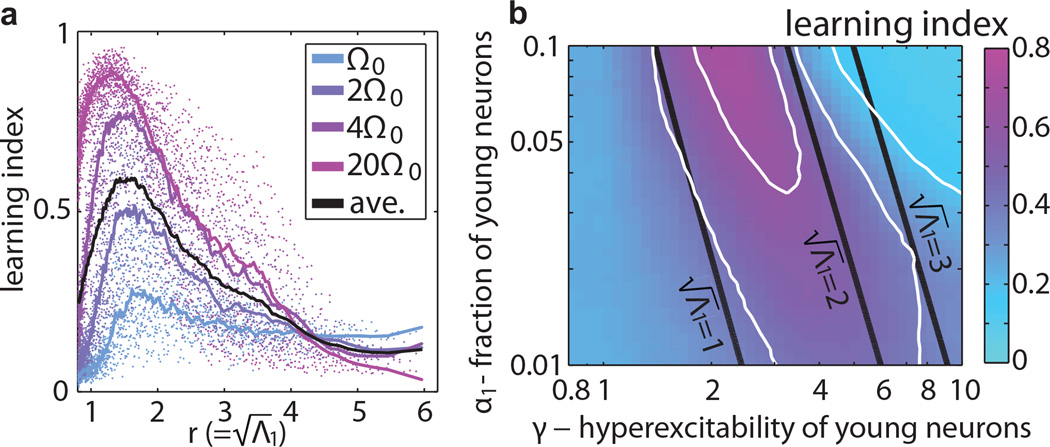
Performance depends primarily on Λ₁ and not on the network structure, peaking for $\sqrt{{\mathrm{\Lambda }}_1}\approx 1.5$ (Fig. 3). This is directly related to the maximal learning capacity observed at g ≈ 1.5 in networks with a single cell-type [28], further supporting the identification of $\sqrt{{\mathrm{\Lambda }}_1}$ as the effective gain. Importantly, because of the block structured connectivity, the effective gain is larger than the average gain ($\sqrt{{\mathrm{\Lambda }}_1}>ḡ$), for all values of γ and α₁ [22]. In other words, for the same average connection strength, networks with block-structured connectivity have a higher effective gain that can place them in a regime with larger learning capacity compared to networks with shuffled connections, demonstrating that a small group of neurons could place the entire network in a state conducive to learning. Moreover, since increases in average connection strength are generally associated with increased metabolic cost, networks with block-structured connectivity can provide a more metabolically efficient way to perform computation compared to statistically homogeneous networks.

FIG. 3.

Learning capacity is primarily determined by $\sqrt{{\mathrm{\Lambda }}_1}$, the effective gain of the network. (a) The learning index for four pure frequency target functions (Ω₀ = π/120) plotted as a function of the radius $r=\sqrt{{\mathrm{\Lambda }}_1}({\alpha }_1,\gamma )$. The training epoch lasted approximately 100 periods of the target signal. Each point is an average over 25 networks with N = 500, ε = 0.2 and different values of α₁ and γ. The line is a moving average of these points for each frequency. (b) The same data averaged over the target frequencies shown as a function of γ and α₁. Contour lines of l_Ω (white) and of $\sqrt{{\mathrm{\Lambda }}_1}$ (black) coincide approximately in the region where l_Ω peaks.

Outgoing connections from any given neuron are typically all positive or all negative, obeying Dale’s law [29]. Within random networks, this issue was addressed by Rajan and Abbott [26] and Tao [30] who computed the bulk spectrum and the outliers of a model where columns of J are separated to two groups, each with its offset and element variance. The dynamics of networks with cell-type-dependent connectivity that is offset to respect Dale’s law were addressed in [31] with some limitations, and remain an important problem for future research.

Ultimately, neural network dynamics need to be considered in relation to external inputs. The response properties of networks with D = 1 have been recently worked out [19, 32]. The analogy between the mean field equations suggests that our results can be used to understand the non-autonomous behavior of multiple cell-type networks.