Abstract
A detailed understanding of the genetic structure of populations and an accurate interpretation of processes driving contemporary patterns of gene flow are fundamental to successful spatial conservation management. The field of seascape genetics seeks to incorporate environmental variables and processes into analyses of population genetic data to improve our understanding of forces driving genetic divergence in the marine environment. Information about barriers to gene flow (such as ocean currents) is used to define a resistance surface to predict the spatial genetic structure of populations and explain deviations from the widely applied isolation-by-distance model. The majority of seascape approaches to date have been applied to linear coastal systems or at large spatial scales (more than 250 km), with very few applied to complex systems at regional spatial scales (less than 100 km). Here, we apply a seascape genetics approach to a peripheral population of the broadcast-spawning coral Acropora spicifera across the Houtman Abrolhos Islands, a high-latitude complex coral reef system off the central coast of Western Australia. We coupled population genetic data from a panel of microsatellite DNA markers with a biophysical dispersal model to test whether oceanographic processes could explain patterns of genetic divergence. We identified significant variation in allele frequencies over distances of less than 10 km, with significant differentiation occurring between adjacent sites but not between the most geographically distant ones. Recruitment probabilities between sites based on simulated larval dispersal were projected into a measure of resistance to connectivity that was significantly correlated with patterns of genetic divergence, demonstrating that patterns of spatial genetic structure are a function of restrictions to gene flow imposed by oceanographic currents. This study advances our understanding of the role of larval dispersal on the fine-scale genetic structure of coral populations across a complex island system and applies a methodological framework that can be tailored to suit a variety of marine organisms with a range of life-history characteristics.
Keywords: connectivity, dispersal, spatial conservation management, Acropora spicifera
1. Introduction
The resilience of marine systems to environmental perturbations is strongly linked to the degree of connectivity between populations through the dispersal and recruitment of larvae. Understanding both the genetic structure of populations and processes driving contemporary patterns of gene flow is pivotal for assessments of ecosystem resilience, and therefore spatial conservation management. Population genetic structure has traditionally been interpreted using a model of isolation by distance (IBD), a spatially explicit analysis that tests the fit of allele frequency variation with geographical distance between sampling locations [1–3]. Although patterns of IBD have proved to be widespread and common in nature [4], there is a frequent disconnect between genetic differentiation and geographical distance in the marine environment, particularly for highly fecund organisms with a pelagic larval stage [5–8]. In such cases, population genetic structure fails to reflect any clear spatial trend, and levels of differentiation can be greater between adjacent sites than between distant ones [9–13]. IBD does not account for the possible effects of the environment on gene flow and therefore can be too simplistic for interpretations of genetic structure for organisms with a high capacity for dispersal across oceanographically complex systems.
The field of seascape genetics incorporates environmental variables into the analysis of population genetic data in order to improve our understanding of processes driving gene flow in the marine environment [14,15]. As in landscape genetics, which incorporates physical features to explain patterns of restricted gene flow across terrestrial systems [16,17], similar information about barriers to gene flow in the marine environment is used to define a resistance surface to predict spatial genetic structure and explain deviations from the IBD model. This ‘isolation by resistance’ (IBR) pattern may be particularly evident when an organism's reproductive strategy involves a sedentary adult phase and a pelagic larval stage that is subject to prevailing currents. Complex ocean circulation can represent significant barriers to dispersal and can produce patterns of genetic structure that are often difficult to interpret; however, incorporating oceanographic mechanisms into the analyses of population genetic data has placed confounding patterns of genetic patchiness into more ecologically relevant contexts [18–22].
The majority of seascape approaches to date have been applied along essentially linear coastlines or at large spatial scales (more than 250 km) [23–30], with very few applied to complex systems (like island archipelagos) at smaller spatial scales (less than 100 km) [18,20,31]. These smaller spatial scales are generally more relevant to management, so linking gene flow with the physical environment at this spatial scale should be a priority, particularly for habitat-forming species such as reef-building corals, which are in decline globally [32]. Information from such studies can serve as a valuable resource for local management aimed at enhancing the resilience of a system through the use of protected area networks that accurately reflect contemporary source–sink dynamics.
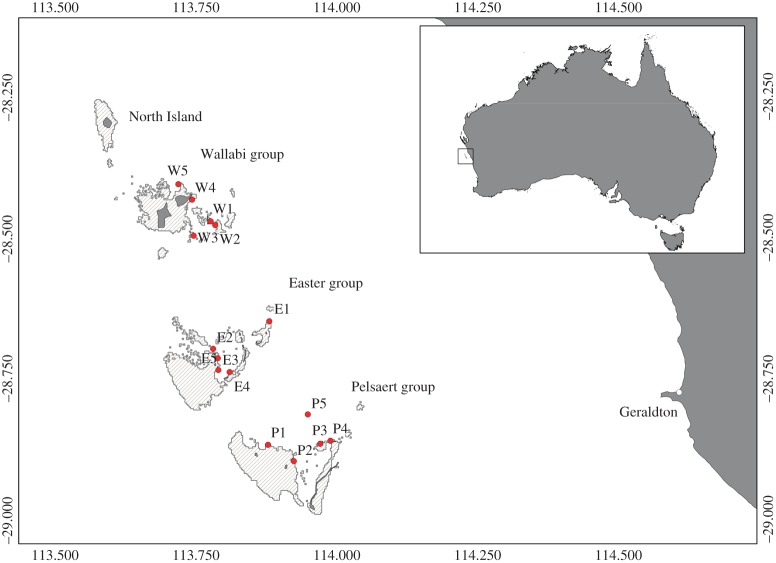
The Houtman Abrolhos Islands (HAI) represents an ideal opportunity to apply a seascape approach to a coral reef system with great complexity at a fine scale. The HAI is the southern-most coral reef system in the Indian Ocean, and is located at the edge of the continental shelf off the central coast of Western Australia (between 28°150′ and 29°00′ S) and in a region of convergence between temperate and tropical waters. The archipelago comprises a network of 122 low-lying islands that form three main groups (Wallabi, Easter and Pelsaert) that together span approximately 70 km north to south. The islands sit at the edge of the warm, poleward flowing Leeuwin Current [33], and while the exposed windward side of the islands is predominantly algal covered, the back reef lagoons and channels are dominated by diverse coral fauna (184 species representing 42 genera) [34]. Previous population genetic studies on intertidal gastropods [35–37] and finfish [38] have demonstrated that the complexities of currents within the system restrict gene flow and isolate populations, leading to significant and often complex patterns of spatial genetic structure that can be up to an order of magnitude greater than among adjacent mainland populations [39,40]. While existing studies highlight the effects of the islands on patterns of connectivity [37], they do not include independent estimates of larval advection.
The aim of this study was to test whether a seascape modelling approach could explain patterns of gene flow across a complex and isolated high-latitude coral reef system. Specifically, we coupled population genetic data from a panel of microsatellite DNA markers with a biophysical dispersal model to test the relationship between oceanographic currents and patterns of spatial genetic structure. We chose to focus our analysis on the broadcast-spawning coral species Acropora spicifera, which is considered rare throughout the Indo-Pacific and East Indian Ocean, but dominates coral assemblages of the HAI at the southern extent of its range [34]. We had three specific aims: (i) to test for significant population genetic structure in A. spicifera; (ii) to determine whether genetic divergences are a function of geographical distance between sample sites (i.e. IBD); and (iii) to determine whether genetic divergences are a function of resistance to connectivity imposed by ocean currents (i.e. IBR).
2. Material and methods
(a). Sample collection, DNA extraction and microsatellite genotyping
Samples of A. spicifera (n = 395) were collected in October 2013 and April 2014 from 15 sites across the HAI (figure 1; electronic supplementary material, table S1). Fragments (3–5 cm) of adult coral colonies were collected along a 200 m transect within each site from uniform habitats at a depth between 2.5 and 10 m. Genomic DNA was extracted from samples using a silica-based method [41]. Samples were amplified across a panel of 10 microsatellites originally developed for Acropora millepora [42,43] and optimized into four multiplexes using the Qiagen Multiplex PCR Kit (electronic supplementary material, table S2). PCR products were analysed on an ABI 3700 sequencer using a GeneScan-500 LIZ internal size standard and scored with manually prepared bins in GeneMarker v. 1.90 (SoftGenetics).
Figure 1.
Sample sites for A. spicifera collected across the HAI, Western Australia. Pale grey areas indicate shallow reef. (Online version in colour.)
(b). Microsatellite analysis
Allelic frequencies, observed and expected heterozygosities, and inbreeding coefficients were calculated in GeneAlex v. 6.5 [44] for each sample site and across all loci. Deviations from Hardy–Weinberg equilibrium (HWE) and tests for linkage disequilibrium (LD) were calculated using GenePop v. 4.0.1 [45], and tests for significance were based on 10 000 de-memorization, 10 000 batches and 10 000 iterations per batch. Tests for evidence of large allele dropout, stuttering and the presence of null alleles that could explain deviations from HWE were performed using MicroChecker v. 2.2.3 [46]. Significance levels were adjusted using sequential Bonferroni corrections in all statistical analyses that included multiple comparisons.
(c). Genetic connectivity
The statistical power of the panel of microsatellites to detect genetic structure was tested using a simulation approach in PowSim v. 4.0 [47]. The program uses Fisher's exact and χ2 tests to test the null hypothesis of genetic homogeneity using the number of loci, allele frequencies and sample sizes from the current dataset. Simulations were run using a range of combinations of Ne (effective population size) and t (time since divergence) for FST values ranging from 0.001 to 0.10. The power of the panel of microsatellites was determined by the proportion of significant tests (p < 0.05) across 1000 replicate runs.
Spatial genetic structure was estimated using several methods. A hierarchal analysis of variance (AMOVA) calculated in Arlequin v. 3.11 [48] was used to identify differences between island groups (ΦCT), among sample sites within island groups (ΦSC) and among sample sites irrespective of island group (ΦST). Tests for significance were based on 10 000 permutations. Pairwise levels of genetic differentiation between sample sites were estimated using the indices FST [49], Dest [50] and G′ST [51], as suggested by Verity & Nichols [52]. Bayesian clustering analyses were conducted in Geneland v. 3.2.4 [53] in R [54]. Geneland differs from the widely used clustering software Structure [55] in that geographical coordinates can be incorporated as a prior to produce more accurate inferences of population structure when genetic differentiation is subtle [56]. Analyses were performed under the spatial and null allele model with correlated alleles and with K (number of populations) ranging from 1 to 5. The maximum rate of Poisson process was set to 400 and the maximum number of nuclei to 1200 as suggested by Guillot et al. [53]. Analyses were based on 100 000 MCMC iterations and with a thinning of 100. Ten independent runs were used to determine the appropriate number of K, which was chosen based on the modal K with the highest posterior probability. An additional five independent runs were conducted with the K-value held constant (likely number of groups based on posterior probability of the previous run) to test for consistency of membership probabilities of each sample site across multiple runs. Although A. spicifera is the dominant coral species at the HAI, its relative abundance at each of the sample sites varied, resulting in considerable differences in numbers of samples collected per site. To account for biases associated with sample size variation on the observed patterns of genetic differentiation, we randomly subsampled each of the 15 sample sites (14 individuals per site reflecting the smallest sample size) for 100 sampling iterations, each time performing an AMOVA (1000 permutations) using the package ‘poppr’ [57] in R, with sample sites nested within island groups and within clusters identified by Geneland. We also used the subsampled datasets to generate 100 matrices of genetic ‘pseudo-distance’ using the package ‘mmod’ [58] in R, and calculated a coefficient of determination (R2) between the ‘pseudo-distance’ matrices and the actual genetic distances obtained from the entire dataset.
(d). Oceanographic connectivity
Levels of resistance to connectivity imposed by currents were determined by simulating the probability of larval dispersal among sample sites using a fully four-dimensional (three spatial dimensions + time), open-source object-oriented biophysical dispersal model developed by Kool & Nichol [59]. Coral spawning in Western Australia occurs predominantly in the Austral autumn [60], with a secondary smaller spawning event in the spring [61]. At the HAI, at least 60% of the scleractinian coral species, including A. spicifera, spawn within a one-week period in the main autumn event [62]. For the dispersal simulations, larvae were released following the third full moon of the year for five consecutive days and were considered eligible for recruitment following a three-day pre-competency period. Under controlled settings, 85% of A. spicifera larvae from the HAI settle on day 7 post-spawning [63], therefore a recruitment eligibility window of day 3 to day 9 was selected for simulated dispersal. Dispersal tracks were generated for 1000 simulated larvae per sample site with an exponential mortality rate. Details on model parameters are described in the electronic supplementary material, table S3. Larval density maps were generated using the ‘spatial analyst’ tool in ArcGIS v. 10.2 (Environmental Systems Research Institute) and were based on a circular area with a radius of 2 km around each raster cell.
A probability matrix describing the likelihood of individuals recruiting to a destination population (row) from a source population (column) was generated based on the proportion of simulated larvae that occurred within a 1 km zone around each sample site during the recruitment eligibility window. The matrix included data from four consecutive spawning events (2009–2012) to account for inter-annual variability. Values were then standardized across rows (destination populations) to generate a migration matrix (M), providing frequencies of recruitment contribution of each source population. The diagonal of this matrix is the proportion of simulated larvae that self-recruit. The migration matrix was then projected forward in time, as in the study of Kool et al. [64], to examine the probability of populations being connected over multiple generations. For details of this method, see electronic supplementary material S1. Finally, to generate a measure of distance that could be directly compared with the empirical genetic data, a similarity matrix was projected from each of the two migration matrices using the equation 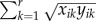 [65], where x and y are larval migration probabilities between pairs of populations over the r populations. This value was subtracted from 1 to generate a genetic distance matrix, hereafter referred to as derived oceanographic resistance (DOR).
[65], where x and y are larval migration probabilities between pairs of populations over the r populations. This value was subtracted from 1 to generate a genetic distance matrix, hereafter referred to as derived oceanographic resistance (DOR).
(e). Seascape effects on gene flow
We tested the correlations of genetic distance (linearized FST, Dest and G′ST) with geographical distance (IBD) and DOR (IBR) using one-tailed Mantel tests (null hypothesis: r ≤ 0) based on 10 000 permutations, using the package ‘ecodist’ [66] in R. To test the sensitivity of these correlations, we recalculated genetic distance by jack-knifing across all microsatellite loci and re-ran the tests. To test the influence of variation in sample size on this relationship, we used the ‘pseudo-distance’ matrices (see §2c) in the Mantel tests (as above) to determine the proportion of subsampled datasets (100 iterations) that returned a p-value less than the alpha level of 0.05. Finally, we carried out partial Mantel tests of genetic distance versus DOR while controlling for geographical distance to partition out the effects of geographical distance on our measures of DOR. Despite being a widely applied statistical method in evolutionary biology [67], there seems to be much debate about the validity of Mantel tests to test the independence of elements in two matrices [68–70]. An alternative approach involves fitting mixed-effects models to account for the correlated structure of regression on distance matrices (maximum-likelihood population effects or MLPE model) [71]; however, parameter optimization is achieved using the restricted/residual maximum-likelihood procedure, raising doubts about the use of traditional information criteria such as AIC for model selection [72]. Summaries of ‘variance explained’ such as the 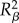 -value [73] have been proposed as suitable alternative statistics for model evaluation; however, several practical and theoretical issues remain, with an overall lack of consensus towards this approach [74]. The goal of our approach was to improve on the IBD model by including a measure of distance that reflected the physical seascape. As the IBD model has been traditionally interpreted using a Mantel test, which is generally more conservative than mixed-effects models [67], we chose to keep with this approach.
-value [73] have been proposed as suitable alternative statistics for model evaluation; however, several practical and theoretical issues remain, with an overall lack of consensus towards this approach [74]. The goal of our approach was to improve on the IBD model by including a measure of distance that reflected the physical seascape. As the IBD model has been traditionally interpreted using a Mantel test, which is generally more conservative than mixed-effects models [67], we chose to keep with this approach.
3. Results
(a). Microsatellite analysis
All microsatellite loci were polymorphic, with effective number of alleles per population ranging from 3.217 to 3.903 (electronic supplementary material, table S1). There was considerable variation in departures from HWE among loci (electronic supplementary material, table S4), with one locus (EST_254) showing significant deficits of heterozygosity across all populations, which suggested the presence of null alleles. The presence of null alleles was confirmed by MicroChecker, so this locus was removed from further analyses. Heterozygosity at each sample site ranged from 0.500 to 0.640, with six sites showing subtle but significant deviations from HWE (electronic supplementary material, table S1). Significant cases of LD were detected in only eight out of 540 comparisons. Replicate multi-locus genotypes (MLGs) were detected in 9% (n = 35) of the samples collected, and there was no instance where an MLG was shared between individuals from different sampling sites or between more than three individuals within a sampling site. Samples with matching MLGs were considered clones formed via fragmentation and were removed from the dataset.
(b). Genetic connectivity
Simulations in PowSim indicated a high statistical power (0.996) of the panel of microsatellites to resolve population structure at low levels (FST ≥ 0.005). AMOVA detected no significant heterogeneity among island groups (ΦCT = 0.002, p = 0.081), but there was significant structure among sites within island groups (ΦSC = 0.016, p = 0.001) and among sample sites irrespective of island group (ΦST = 0.019, p = 0.001). The three measures of genetic differentiation (FST, GST and Dest) were strongly correlated (0.946 < R < 0.998, p ≤ 0.001) and produced similar spatial genetic patterns (electronic supplementary material, figure S1). Pairwise comparisons ranged from 0.0069 to 0.0483 (FST) and from −0.019 to 0.128 (G′ST) (table 1). Dest-values can be found in electronic supplementary material, table S5. Twelve of the 105 pairwise FST comparisons were significant (adjusted p ≤ 0.0005), all of which involved a sampling site from the Pelsaert group. Bayesian clustering in Geneland identified K = 3 as the most likely number of clusters in the dataset (electronic supplementary material, figure S2). Maps of posterior probabilities showed that the first cluster comprised all Wallabi and Easter group samples sites, as well as P1 and P2 from the Pelsaert group (figure 2). The second cluster comprised P5, and the third cluster comprised P3 and P4. This pattern was consistent across the five additional independent runs. This pattern did not appear to be an artefact of differences in sample size, as AMOVAs based on the subsampled datasets returned a significant ΦCT (p < 0.05) 2% of the time when sample sites were clustered according to island group and 99% of the time under the Geneland nested arrangement. Furthermore, there was a strong relationship between the ‘pseudo-distances’ calculated from the subsampled datasets and the genetic distance matrix based on the entire dataset (R2 = 0.74; electronic supplementary material, figure S3).
Table 1.
Pairwise measures of genetic differentiation (FST below diagonal; G′ST above diagonal). Bold values indicate significance based on sequential Bonferroni adjusted p-value ≤ 0.0005.
| P1 | P2 | P3 | P4 | P5 | E1 | E2 | E3 | E4 | E5 | W1 | W2 | W3 | W4 | W5 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P1 | 0.003 | 0.056 | 0.114 | 0.002 | −0.005 | −0.015 | 0.032 | 0.020 | 0.001 | 0.016 | 0.008 | 0.018 | 0.010 | −0.007 | |
| P2 | 0.019 | 0.051 | 0.068 | 0.068 | 0.002 | −0.013 | −0.007 | −0.012 | −0.007 | −0.019 | 0.014 | 0.003 | 0.004 | 0.009 | |
| P3 | 0.028 | 0.029 | 0.000 | 0.111 | 0.046 | 0.054 | 0.089 | 0.077 | 0.073 | 0.048 | 0.057 | 0.052 | 0.125 | 0.062 | |
| P4 | 0.045 | 0.037 | 0.020 | 0.126 | 0.066 | 0.088 | 0.120 | 0.107 | 0.089 | 0.061 | 0.098 | 0.092 | 0.128 | 0.079 | |
| P5 | 0.018 | 0.033 | 0.039 | 0.048 | 0.060 | 0.026 | 0.087 | 0.079 | 0.068 | 0.069 | 0.053 | 0.097 | 0.073 | 0.012 | |
| E1 | 0.013 | 0.016 | 0.023 | 0.031 | 0.027 | −0.006 | 0.027 | 0.018 | −0.001 | −0.007 | 0.007 | 0.025 | 0.014 | 0.000 | |
| E2 | 0.011 | 0.012 | 0.025 | 0.036 | 0.020 | 0.010 | −0.004 | −0.014 | 0.004 | −0.014 | 0.002 | 0.013 | 0.005 | 0.001 | |
| E3 | 0.020 | 0.012 | 0.030 | 0.042 | 0.031 | 0.015 | 0.009 | −0.007 | 0.014 | −0.003 | 0.023 | 0.011 | 0.028 | 0.032 | |
| E4 | 0.018 | 0.012 | 0.029 | 0.040 | 0.031 | 0.014 | 0.008 | 0.008 | 0.022 | −0.007 | 0.016 | −0.007 | 0.024 | 0.022 | |
| E5 | 0.014 | 0.013 | 0.028 | 0.036 | 0.028 | 0.010 | 0.012 | 0.012 | 0.015 | 0.001 | 0.016 | 0.030 | 0.014 | 0.018 | |
| W1 | 0.016 | 0.010 | 0.022 | 0.028 | 0.027 | 0.008 | 0.007 | 0.008 | 0.008 | 0.009 | 0.025 | 0.004 | 0.017 | 0.005 | |
| W2 | 0.017 | 0.020 | 0.026 | 0.039 | 0.027 | 0.014 | 0.013 | 0.016 | 0.016 | 0.015 | 0.016 | 0.031 | 0.024 | 0.014 | |
| W3 | 0.016 | 0.014 | 0.022 | 0.034 | 0.032 | 0.014 | 0.012 | 0.010 | 0.008 | 0.014 | 0.008 | 0.016 | 0.041 | 0.037 | |
| W4 | 0.015 | 0.015 | 0.039 | 0.045 | 0.030 | 0.013 | 0.011 | 0.015 | 0.015 | 0.013 | 0.012 | 0.017 | 0.017 | 0.017 | |
| W5 | 0.012 | 0.016 | 0.024 | 0.032 | 0.016 | 0.010 | 0.011 | 0.015 | 0.014 | 0.013 | 0.010 | 0.014 | 0.015 | 0.013 |
Figure 2.
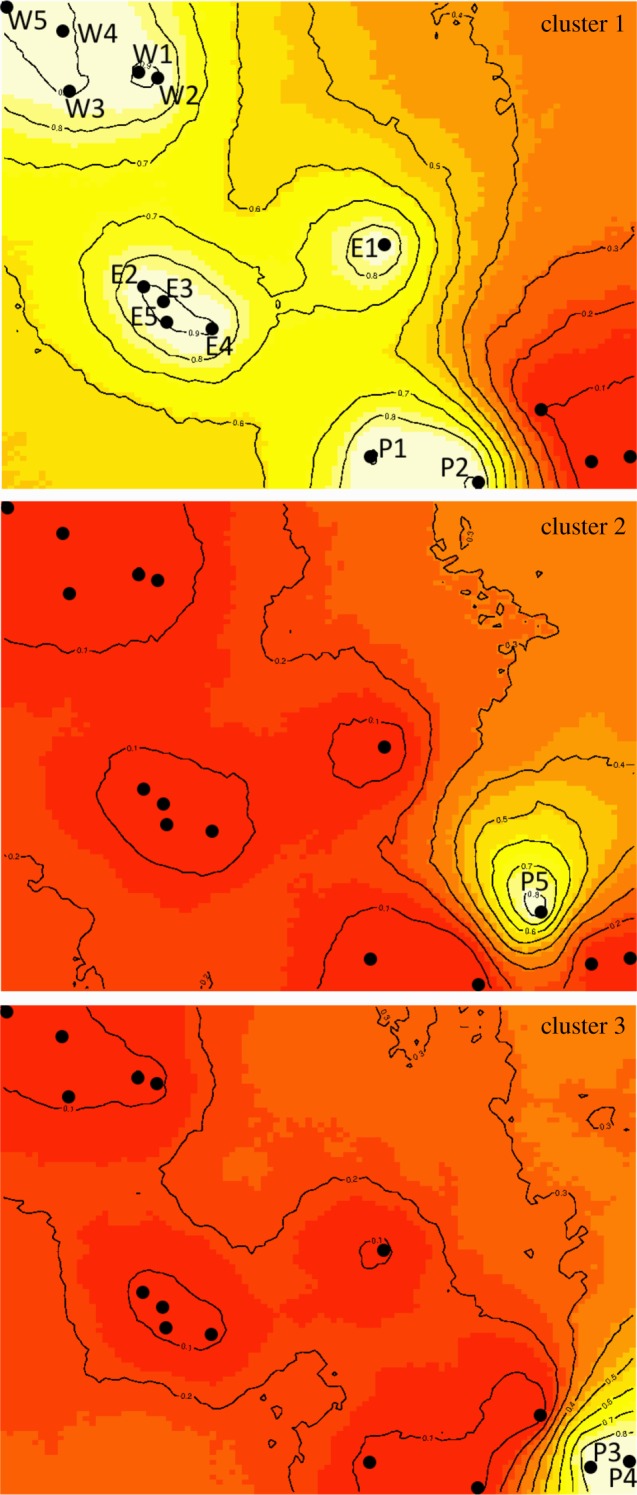
Distributions of genetic clusters (K = 3) in Geneland v. 3.2.4. Lighter colours indicate higher probabilities of membership to a cluster. (Online version in colour.)
(c). Oceanographic connectivity
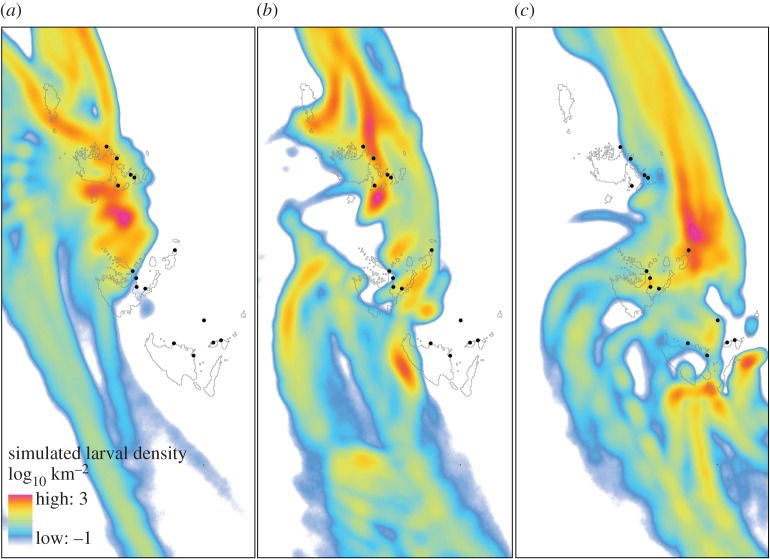
Larval density maps based on simulated particle trajectories illustrated that the distinct genetic clusters within the Pelsaert group lay outside the areas of high larval density (figure 3). In general, larvae that were released from the Wallabi or Easter groups tended to either track out through channels between the islands and then move in a southerly direction along the continental shelf, or track north in the lee of the islands before moving westward and being diverted south along the shelf. In both situations, very few simulated larvae came within recruiting distance of the eastern Pelsaert sample sites (identified as clusters two and three from the Geneland analysis). Probabilities of larval dispersal between sample sites, which were standardized to compare frequencies of contribution to recruitment at each site, supported a pattern of restricted larval recruitment to the Pelsaert group (electronic supplementary material, table S6). Both the Wallabi and Easter groups contributed very few recruits to the Pelsaert sample sites, with 92% of successful recruits to the Pelsaert sample sites originating from within this island group. The genetic similarity matrix, based on the standardized dispersal probabilities, identified a strong genetic break between the Wallabi and Pelsaert groups, particularly with the more eastern Pelsaert sample sites; however, this pattern became less pronounced when the migration matrix was projected forward 10 generations (electronic supplementary material, figure S4).
Figure 3.
Kernel density plots showing log-transformed densities per square kilometre of simulated larvae (75% confidence cut) released from all sample sites for years 2009–2012. Plots show simulated larval densities released from (a) Wallabi group, (b) Easter group and (c) Pelsaert group within the defined recruitment eligibility window. (Online version in colour.)
(d). Seascape effects on gene flow
Mantel tests revealed a non-significant relationship between observed genetic distance (linearized G′ST, Dest and FST) and log-transformed geographical distance (table 2). By contrast, there was a significant relationship between genetic distance and DOR. This relationship was significant for all measures of genetic differentiation at t = 0. Jack-knifing across loci showed that the results were significant in all cases and correlation coefficients remained relatively stable (electronic supplementary material, table S7). This relationship did not appear to be an artefact of differences in sample size, as the Mantel tests based on the subsampled ‘pseudo-distance’ matrices returned significant results 96% of the time (electronic supplementary material, figure S5). The correlations became marginally non-significant when projecting the matrix forward 10 generations, and partial Mantel tests controlling for the effects of geographical distance yielded similarly significant relationships between genetic distance and DOR (table 2).
Table 2.
Mantel randomization tests comparing IBD versus IBR across three measures of genetic differentiation (FST, G′ST and Dest). Bold values indicate significance (p ≤ 0.05). Partial Mantel tests of IBR, controlling for geographical distance, are also included.
|
FST |
G′ST |
Dest |
|||||
|---|---|---|---|---|---|---|---|
| predictor | description | p | Mantel r | p | Mantel r | p | Mantel r |
| D (log) | log-transformed geographical distance (IBD) | 0.072 | 0.120 | 0.070 | 0.132 | 0.062 | 0.133 |
| DOR | DOR based on transition probabilities (IBR) | 0.001 | 0.377 | 0.005 | 0.347 | 0.005 | 0.347 |
| DORFP | DOR based on forward-projected allele states (IBR) | 0.139 | 0.155 | 0.089 | 0.185 | 0.086 | 0.184 |
| DOR|D (log) | DOR, given geographic distance | 0.004 | 0.444 | 0.011 | 0.388 | 0.011 | 0.387 |
| DORFP|D (log) | forward-projected DOR, given geographical distance | 0.278 | 0.091 | 0.193 | 0.132 | 0.191 | 0.128 |
4. Discussion
The central finding of this study is one of localized genetic patchiness that can be explained by ocean currents. Gene flow over regional scales was not constrained by geographical distance, but by effective distance due to inter-island currents, which acted to restrict dispersal and isolate local populations. We linked patterns of genetic divergence to an oceanographic mechanism and identified an area of the archipelago that appeared to be isolated from the greater larval pool, and probably reliant on local sources of larvae to maintain healthy coral populations. Incorporating oceanographic data into interpretations of fine-scale genetic structure improved our understanding of processes driving regional connectivity across a complex seascape and corroborates the importance of integrating physical processes when studying gene flow in marine populations.
Acropora spicifera does not form a single panmictic population within the HAI. We identified significant variation in allele frequencies over distances of less than 10 km and showed that genetic heterogeneity was patchy, with significant variation occurring between adjacent sites in the Pelsaert group, but not between the most geographically distant ones. This pattern of genetic patchiness is a common finding for scleractinian corals, which regularly display fine-scale genetic structure within reefs (less than 10 km) but homogeneity across vast distances (more than 1000 km) [75–77]. As a result, geographical distance was a poor predictor of genetic divergence between sample sites, indicating that the population genetic structure of A. spicifera at the HAI is more complex than under a stepping-stone model of IBD. Significant patterns of IBD in coral species are generally indicative of restricted gene flow across large geographical areas [78,79], so the disconnect between genetic differentiation and geographical distance reported here was not surprising considering the small spatial scale of the study.
The population genetic structure of A. spicifera at the HAI appeared to be a function of restricted gene flow arising from differences in the source of larval recruits among sites. Currents have been well documented to be a major force influencing gene flow in the marine environment [20,24,30,80,81]. Variable ocean currents and bathymetric complexities can work synergistically to produce fine-scale source–sink dynamics that isolate local populations and produce high levels of genetic divergence, particularly across island archipelagos that are made up of a mosaic of reefs [37]. Populations may be sufficiently isolated for significant genetic subdivision to arise, but occasional long-distance dispersal (leptokurtic gene flow) can keep the broader set of populations connected. In this study, all of the significant between-site genetic divergences involved the Pelsaert group, and modelled larval transport from oceanographic data indicated that the distinct genetic clusters within the Pelsaert group lay outside the areas of high larval density in a region characterized by a heightened level of local recruitment. It may be the case that the Pelsaert group is shadowed from the strong and consistent north-to-south laminar flow of the Leeuwin Current by the northern island groups, with recruitment along the Pelsaert reefs instead more influenced by small-scale eddies that act to isolate local populations and enhance self-recruitment, but with the leptokurtic tail of dispersal maintaining genetic connectivity across groups over multiple generations. This interpretation would also explain why other species with a high capacity for dispersal, such as the pulmonate limpet, Siphonaria kurracheensis, also show significant genetic structure in the Pelsaert group but not elsewhere in the HAI [36].
Dispersal is a highly stochastic process, and patterns of genetic patchiness can arise from a number of pre-settlement processes that influence the spatial distribution of alleles. An alternative mechanism commonly invoked to explain patterns of local heterogeneity amid large-scale homogeneity, particularly for broadcast-spawning species, is the variable reproductive success of adults, where a small number of individuals contribute a substantial number of recruits to a given population due to a chance matching of reproduction and oceanography (sweepstake reproductive success) [82]. The resulting patterns of genetic patchiness are therefore ephemeral, and one generation's genetic patches will not predict the genetic patterns in the next generation. We were unable to test this hypothesis, as we did not collect recruits from multiple cohorts. While there is likely to be some sweepstake effects occurring, there is enough temporal stability in the genetic data that operates over enough generations to show a significant relationship with the oceanography when averaged over multiple years. Ultimately, more information on the intra-population dynamics at these sites is needed to fully test our interpretations; however, the combined evidence from genetic and oceanographic data strongly suggests that populations of A. spicifera in the more eastern reefs of the Pelsaert group are effectively isolated from larvae sourced from elsewhere within the HAI. Consequently, these areas of reef have a limited capacity to recover from disturbance in comparison with other regions of the HAI that maintain high levels of connectivity.
These findings have direct implications for management decisions and conservation planning. As the spatial arrangement and zoning of marine protected areas can have important effects on dispersal dynamics, the accurate identification and subsequent protection of key larval source populations is vital to help ensure that local populations are maintained. There are currently four habitat protection areas within the HAI aimed at conserving marine life, one of which is in the Pelsaert group and lies immediately adjacent to sample sites P3 and P4 [83]. Based on our analyses, this area probably protects a valuable larval source population for adjacent reefs in the Pelseart group. Considering that the HAI represents a stronghold for this otherwise uncommon coral species, conserving genetically distinct populations of A. spicifera within the HAI should be a priority for management.
These results are particularly relevant in light of the recent ‘marine heatwave’ that struck the coastline of Western Australia in 2011 and resulted in the first documented case of large-scale bleaching in the region [84]. The effects of the disturbance at the HAI were patchy, and bleaching varied widely within each island group and across the archipelago [85], making it difficult to draw any conclusions about the effects of this disturbance on the genetic structure of local coral populations, particularly because the small number of departures from HWE and LD suggests that populations are in mutation-drift equilibrium. In conclusion, there is an urgent need to better understand fine-scale processes driving larval dispersal and gene flow across coral reef archipelagos, so that spatial conservation management can be tailored to accurately reflect patterns of larval transport and contemporary source–sink dynamics. This study demonstrates the utility of combining genetic and oceanographic data at spatial scales relevant for management by applying a methodological framework that can be easily tailored for other marine organisms with complex life-history characteristics that include a pelagic larval or propagule stage. It also advances our understanding of the influence of physical processes on the fine-scale genetic structure of marine populations within complex island systems.
Supplementary Material
Acknowledgements
NERP Marine Biodiversity Hub partners include the Institute for Marine and Antarctic Studies, University of Tasmania; CSIRO, Geoscience Australia, Australian Institute of Marine Science, Museum Victoria, Charles Darwin University and the University of Western Australia. Comments from two anonymous reviewers, M. S. Johnson, E. A. Sinclair, J. Underwood and K. L. Travaille greatly improved this manuscript. This paper is published with the permission of the CEO, Geoscience Australia.
Ethics
All samples were collected under Fisheries Exemption no. 2294 issued by the Government of Western Australia, Department of Fisheries.
Data accessibility
Microsatellite data and R code have been deposited on Dryad: http://dx.doi.org/10.5061/dryad.m0420
Authors' contributions
L.T. and G.A.K. conceived of the study; L.T., W.J.K., M.S. and S.P.W. collected samples; L.T. carried out the molecular laboratory work; L.T., S.P.W. and W.J.K. carried out the statistical analyses; J.T.K. provided oceanographic data; all authors helped draft the manuscript; all authors gave final approval for publication.
Competing Interests
We declare we have no competing interests.
Funding
This work was undertaken for the Marine Biodiversity Hub, a collaborative partnership supported through funding from the Australian Government's National Environmental Research Program (NERP).
References
- 1.Wright S. 1943. Isolation by distance. Genetics 28, 114–138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Slatkin M. 1993. Isolation by distance in equilibrium and non-equilibrium populations. Evolution 47, 264–279. ( 10.2307/2410134) [DOI] [PubMed] [Google Scholar]
- 3.Rousset F. 1997. Genetic differentiation and estimation of gene flow from F-statistics under isolation by distance. Genetics 145, 1219–1228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Meirmans PG. 2012. The trouble with isolation by distance. Mol. Ecol. 21, 2839–2846. ( 10.1111/j.1365-294X.2012.05578.x) [DOI] [PubMed] [Google Scholar]
- 5.Doherty PJ, Planes S, Mather P. 1995. Gene flow and larval duration in seven species of fish from the great barrier reef. Ecology 76, 2373–2391. ( 10.2307/2265814) [DOI] [Google Scholar]
- 6.Magalon H, Adjeroud H, Veuille M. 2005. Patterns of genetic variation do not correlate with geographical distance in the reef-building coral Pocillopora meandrina in the South Pacific. Mol. Ecol. 14, 1861–1868. ( 10.1111/j.1365-294X.2005.02430.x) [DOI] [PubMed] [Google Scholar]
- 7.Purcell JFH, Cowen RK, Hughes CR, Williams DA. 2006. Weak genetic structure indicates strong dispersal limits: a tale of two coral reef fish. Proc. R. Soc. B 273, 1483–1490. ( 10.1098/rspb.2006.3470) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Bradbury IR, Bentzen P. 2007. Non-linear genetic isolation by distance, life history and dispersal estimation in aquatic organisms. Mar. Ecol. Prog. Ser. 340, 245–257. ( 10.3354/meps340245) [DOI] [Google Scholar]
- 9.Watts RJ, Johnson MS, Black R. 1990. Effects of recruitment on genetic patchiness in the urchin Echinometra mathaei in Western Australia. Mar. Biol. 151, 145–151. ( 10.1007/BF01344280) [DOI] [Google Scholar]
- 10.Ayre DJ, Hughes TP. 2000. Genotypic diversity and gene flow in brooding and spawning corals along the Great Barrier Reef, Australia. Evolution 54, 1590–1605. ( 10.1111/j.0014-3820.2000.tb00704.x) [DOI] [PubMed] [Google Scholar]
- 11.Hancock B. 2000. Genetic subdivision of Roe's abalone, Haliotis roei Greay (Mollusca: Gastropoda), in south-western Australia. Mar. Freshw. Res. 51, 679–687. ( 10.1071/MF99144) [DOI] [Google Scholar]
- 12.Arnaud-Haond S, Vonau V, Rouxel C, Bonhomme F, Prou J, Goyard E, Boudry P. 2008. Genetic structure at different spatial scales in the pearl oyster (Pinctada margaritifera cumingii) in French Polynesian lagoons: beware of sampling strategy and genetic patchiness. Mar. Biol. 155, 147–157. ( 10.1007/s00227-008-1013-0) [DOI] [Google Scholar]
- 13.Kennington W, Berry O, Groth D, Johnson MS, Melville-Smith R. 2013. Spatial scales of genetic patchiness in the western rock lobster Panulirus cygnus. Mar. Ecol. Prog. Ser. 486, 213–221. ( 10.3354/meps10360) [DOI] [Google Scholar]
- 14.Selkoe KA, Henzler CM, Gaines SD. 2008. Seascape genetics and the spatial ecology of marine populations. Fish Fish. 9, 363–377. ( 10.1111/j.1467-2979.2008.00300.x) [DOI] [Google Scholar]
- 15.Riginos C, Liggins L. 2013. Seascape genetics: populations, individuals, and genes marooned and adrift. Geogr. Compass 7, 197–216. ( 10.1111/gec3.12032) [DOI] [Google Scholar]
- 16.Manel S, Schwartz M, Luikart G, Taberlet P. 2003. Landscape genetics: combining landscape ecology and population genetics. Trends Ecol. Evol. 20, 136–142. ( 10.1016/j.tree.2004.12.004) [DOI] [Google Scholar]
- 17.Manel S, Holderegger R. 2013. Ten years of landscape genetics. Trends Ecol. Evol. 28, 614–621. ( 10.1016/j.tree.2013.05.012) [DOI] [PubMed] [Google Scholar]
- 18.Selkoe KA, Gaines SD, Caselle JE, Warner RR. 2006. Current shifts and kin aggregation explain genetic patchiness in fish recruits. Ecology 87, 3082–3094. ( 10.1890/0012-9658%282006%2987%5B3082%3ACSAKAE%5D2.0.CO%3B2) [DOI] [PubMed] [Google Scholar]
- 19.Selkoe KA, Watson JR, White C, Horin TB, Iacchei M, Mitarai S, Siegel DA, Gaines SD, Toonen RJ. 2010. Taking the chaos out of genetic patchiness: seascape genetics reveals ecological and oceanographic drivers of genetic patterns in three temperate reef species. Mol. Ecol. 19, 3708–3726. ( 10.1111/j.1365-294X.2010.04658.x) [DOI] [PubMed] [Google Scholar]
- 20.White C, Selkoe KA, Watson J, Siegel DA, Zacherl DC, Toonen RJ. 2010. Ocean currents help explain population genetic structure. Proc. R. Soc. B 277, 1685–1694. ( 10.1098/rspb.2009.2214) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Iacchei M, Ben-Horin T, Selkoe KA, Bird CE, García-Rodríguez FJ, Toonen RJ. 2013. Combined analyses of kinship and FST suggest potential drivers of chaotic genetic patchiness in high gene-flow populations. Mol. Ecol. 22, 3476–3494. ( 10.1111/mec.12341) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Wee AKS, et al. 2014. Oceanic currents, not landmasses, maintain the genetic structure of the mangrove Rhizophora mucronata Lam. (Rhizophoraceae) in Southeast Asia. J. Biogeogr. 41, 954–964. ( 10.1111/jbi.12263) [DOI] [Google Scholar]
- 23.Galindo HM, Olson DB, Palumbi SR. 2006. Seascape genetics: a coupled oceanographic-genetic model predicts population structure of Caribbean corals. Curr. Biol. 16, 1622–1626. ( 10.1016/j.cub.2006.06.052) [DOI] [PubMed] [Google Scholar]
- 24.Kenchington EL, Patwary MU, Zouros E, Bird CJ. 2006. Genetic differentiation in relation to marine landscape in a broadcast-spawning bivalve mollusc (Placopecten magellanicus). Mol. Ecol. 15, 1781–1796. ( 10.1111/j.1365-294X.2006.02915.x) [DOI] [PubMed] [Google Scholar]
- 25.Banks S, Piggott M, Williamson J, Bove U, Holbrook N, Beheregaray L. 2007. Oceanic variability and coastal topography shape genetic structure in a long-dispersing sea urchin. Ecology 88, 3055–3064. ( 10.1890/07-0091.1) [DOI] [PubMed] [Google Scholar]
- 26.Galindo HM, Pfeiffer-Herbert AS, McManus MA, Chao Y, Chai F, Palumbi SR. 2010. Seascape genetics along a steep cline: using genetic patterns to test predictions of marine larval dispersal. Mol. Ecol. 19, 3692–3707. ( 10.1111/j.1365-294X.2010.04694.x) [DOI] [PubMed] [Google Scholar]
- 27.Coscia I, Robins PE, Porter JS, Malham SK, Ironside JE. 2012. Modelled larval dispersal and measured gene flow: seascape genetics of the common cockle Cerastoderma edule in the southern Irish Sea. Conserv. Genet. 14, 451–466. ( 10.1007/s10592-012-0404-4) [DOI] [Google Scholar]
- 28.Godhe A, Egardt J, Kleinhans D, Sundqvist L, Hordoir R, Jonsson PR. 2013. Seascape analysis reveals regional gene flow patterns among populations of a marine planktonic diatom. Proc. R. Soc. B 280, 20131599 ( 10.1098/rspb.2013.1599) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Rouger R, Jump AS. 2014. A seascape genetic analysis reveals strong biogeographical structuring driven by contrasting processes in the polyploid saltmarsh species Puccinellia maritima and Triglochin maritima. Mol. Ecol. 23, 3158–3170. ( 10.1111/mec.12802) [DOI] [PubMed] [Google Scholar]
- 30.Schiavina M, Marino IAM, Zane L, Melià P. 2014. Matching oceanography and genetics at the basin scale: seascape connectivity of the Mediterranean shore crab in the Adriatic Sea. Mol. Ecol. 22, 5496–5497. ( 10.1111/mec.12956) [DOI] [PubMed] [Google Scholar]
- 31.Fievet V, Touzet P, Arnaud JF, Cuguen J. 2007. Spatial analysis of nuclear and cytoplasmic DNA diversity in wild sea beet (Beta vulgaris ssp. maritima) populations: do marine currents shape the genetic structure? Mol. Ecol. 16, 1847–1864. ( 10.1111/j.1365-294X.2006.03208.x) [DOI] [PubMed] [Google Scholar]
- 32.Hoegh-Guldberg O, et al. 2007. Coral reefs under rapid climate change and ocean acidification. Science 318, 1737–1742. ( 10.1126/science.1152509) [DOI] [PubMed] [Google Scholar]
- 33.Batteen ML, Miller HA. 2009. Process-oriented studies of the 5500 km long boundary flow off western and southern Australia. Cont. Shelf Res. 29, 702–718. ( 10.1016/j.csr.2008.11.011) [DOI] [Google Scholar]
- 34.Veron J, Marsh L. 1988. Hermatypic corals of Western Australia: records and annotated species lists. Perth, Australia: Western Australian Museum. [Google Scholar]
- 35.Johnson MS, Black R. 1991. Genetic subdivision of the intertidal snail. Heredity 67, 205–213. ( 10.1038/hdy.1991.81) [DOI] [Google Scholar]
- 36.Johnson MS, Bentley S, Ford SS, Ladyman M, Lambert G. 2001. Effects of a complex archipelago on genetic subdivision of the intertidal limpet Siphonaria kurracheensis. Mar. Biol. 139, 1087–1094. ( 10.1007/s002270100667) [DOI] [Google Scholar]
- 37.Johnson MS, Black R. 2006. Islands increase genetic subdivision and disrupt patterns of connectivity of intertidal snails in a complex archipelago. Evolution 60, 2498–2506. ( 10.1554/06-211.1) [DOI] [PubMed] [Google Scholar]
- 38.Johnson MS, Watts RJ, Black R. 1994. High levels of genetic subdivision in peripherally isolated populations of the atherinid fish Craterocephalus capreoli in the Houtman Abrolhos Islands, Western Australia. Mar. Biol. 119, 179–184. ( 10.1007/BF00349554) [DOI] [Google Scholar]
- 39.Parsons KE. 1996. The genetic effects of larval dispersal depend on spatial scale and habitat characteristics. Mar. Biol. 126, 403–414. ( 10.1007/BF00354622) [DOI] [Google Scholar]
- 40.Pudovskis MS, Johnson MS, Black R. 2001. Genetic divergence of peripherally disjunct populations of the gastropod Batillariella estuarina in the Houtman Abrolhos Islands, Western Australia. Mol. Ecol. 10, 2605–2616. ( 10.1046/j.0962-1083.2001.01398.x) [DOI] [PubMed] [Google Scholar]
- 41.Ivanova NV, deWaard JR, Hebert PDN. 2006. An inexpensive, automation-friendly protocol for recovering high-quality DNA. Mol. Ecol. Notes 6, 998–1002. ( 10.1111/j.1471-8286.2006.01428.x) [DOI] [Google Scholar]
- 42.van Oppen MJH, Underwood JN, Muirhead A, Peplow L. 2007. Ten microsatellite loci for the reef- building coral Acropora millepora (Cnidaria, Scleractinia) from the Great Barrier Reef, Australia. Mol. Ecol. 7, 436–438. ( 10.1111/j.1471-8286.2006.01610.x) [DOI] [Google Scholar]
- 43.Wang S, Zang L, Matz M. 2009. Microsatellite characterization and marker development from public EST and WGS databases in the reef-building coral Acropora millepora (Cnidaria, Anthozoa, Scleractinia). J. Hered. 100, 329–337. ( 10.1093/jhered/esn100) [DOI] [PubMed] [Google Scholar]
- 44.Peakall R, Smouse PE. 2006. GENALEX 6: genetic analysis in Excel: population genetic software for teaching and research. Mol. Ecol. Notes 6, 288–295. ( 10.1111/j.1471-8286.2005.01155.x) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Rousset F. 2008. Genepop'007: a complete re-implementation of the genepop software for Windows and Linux. Mol. Ecol. Res. 8, 103–106. ( 10.1111/j.1471-8286.2007.01931.x) [DOI] [PubMed] [Google Scholar]
- 46.van Oosterhout C, Hutchinson WF, Wills DPM, Shipley P. 2004. Micro-Checker: software for identifying and correcting genotyping errors in microsatellite data. Mol. Ecol. Notes 4, 535–538. ( 10.1111/j.1471-8286.2004.00684.x) [DOI] [Google Scholar]
- 47.Ryman N, Palm S. 2006. POWSIM: a computer program for assessing statistical power when testing for genetic differentiation. Mol. Ecol. Notes 6, 600–602. ( 10.1111/j.1471-8286.2006.01378.x) [DOI] [PubMed] [Google Scholar]
- 48.Excoffier L, Laval G, Schneider S. 2005. Arlequin ver. 3.0: an integrated software package for population genetics data analysis. Evol. Bioinform. 1, 47–50. [PMC free article] [PubMed] [Google Scholar]
- 49.Nei M. 1977. F-statistics and analysis of gene diversity in subdivided populations. Ann. Hum. Genet. 41, 225–233. ( 10.1111/j.1469-1809.1977.tb01918.x) [DOI] [PubMed] [Google Scholar]
- 50.Jost L. 2008. GST and its relatives do not measure differentiation. Mol. Ecol. 17, 4015–4026. ( 10.1111/j.1365-294X.2008.03887.x) [DOI] [PubMed] [Google Scholar]
- 51.Hedrick PW. 2005. A standardized genetic differentiation measure. Evolution 59, 1633–1638. ( 10.1111/j.0014-3820.2005.tb01814.x) [DOI] [PubMed] [Google Scholar]
- 52.Verity R, Nichols RA. 2014. What is genetic differentiation, and how should we measure it—GST, D, neither or both? Mol. Ecol. 23, 4216–4225. ( 10.1111/mec.12856) [DOI] [PubMed] [Google Scholar]
- 53.Guillot G, Mortier F, Estoup A. 2005. Geneland: a computer package for landscape genetics. Mol. Ecol. Notes 5, 712–715. ( 10.1111/j.1471-8286.2005.01031.x) [DOI] [Google Scholar]
- 54.R Development Core Team. 2014. R: a language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing. [Google Scholar]
- 55.Pritchard JK, Stephens M, Donnelly P. 2000. Inference of population structure using multilocus genotype data. Genetics 155, 945–959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Latch EK, Dharmarajan G, Glaubitz JC, Rhodes OEJ. 2006. Relative performance of Bayesian clustering software for inferring population substructure and individual assignment at low levels of population differentiation. Conserv. Gen. 7, 295–302. ( 10.1007/s10592-005-9098-1) [DOI] [Google Scholar]
- 57.Kamvar ZN, Tabima JF, Grünwald NJ. 2014. Poppr: an R package for genetic analysis of populations with clonal, partially clonal, and/or sexual reproduction. PeerJ. 2 e281 ( 10.7717/peerj.281) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Winter DJ. 2012. mmod: an R library for the calculation of population differentiation statistics. Mol. Ecol. Res. 2, 1158–1160. ( 10.1111/j.1755-0998.2012.03174.x) [DOI] [PubMed] [Google Scholar]
- 59.Kool JT, Nichol SL. 2015. Four-dimensional connectivity modelling with application to Australia's north and northwest marine environments. Environ. Model. Softw. 65, 67–78. ( 10.1016/j.envsoft.2014.11.022) [DOI] [Google Scholar]
- 60.Simpson CJ. 1991. Mass spawning of corals on Western Australian reefs and comparisons with the Great Barrier Reef. J. R. Soc. West. Aust. 74, 85–92. [Google Scholar]
- 61.Rosser NL, Gilmour JP. 2008. New insights into patterns of coral spawning on Western Australian reefs. Coral Reefs 27, 345–349. ( 10.1007/s00338-007-0335-6) [DOI] [Google Scholar]
- 62.Babcock RC, Willis BL, Simpson C. 1994. Mass spawning of corals on a high latitude coral reef. Coral Reefs 13, 161–169. ( 10.1007/BF00301193) [DOI] [Google Scholar]
- 63.Foster T, Gilmour JP, Chua CM, Falter JL, McCulloch MT. Submitted Effect of ocean warming and acidification on the early life stages of sub-tropical Acropora spicifera. Coral Reefs. [Google Scholar]
- 64.Kool JT, Paris CB, Andréfouët S, Cowen RK. 2010. Complex migration and the development of genetic structure in subdivided populations: an example from Caribbean coral reef ecosystems. Ecography 33, 597–606. [Google Scholar]
- 65.Nei M. 1987. Molecular evolutionary genetics. New York, NY: Columbia University Press. [Google Scholar]
- 66.Goslee SC, Urban DL. 2013. The ecodist package for dissimilarity-based analysis of ecological data. J. Stat. Softw. 22, 1–19. [Google Scholar]
- 67.Storfer A, Murphy MA, Spear SF, Holderegger R, Waits LP. 2010. Landscape genetics: where are we now? Mol. Ecol. 19, 3496–3514. ( 10.1111/j.1365-294X.2010.04691.x) [DOI] [PubMed] [Google Scholar]
- 68.Cushman SA, Landguth EL. 2010. Spurious correlations and inference in landscape genetics. Mol. Ecol. 19, 3592–3602. ( 10.1111/j.1365-294X.2010.04656.x) [DOI] [PubMed] [Google Scholar]
- 69.Legendre P, Fortin M. 2010. Comparison of the Mantel test and alternative approaches for detecting complex multivariate relationships in the spatial analysis of genetic data. Mol. Ecol. Res. 10, 831–844. ( 10.1111/j.1755-0998.2010.02866.x) [DOI] [PubMed] [Google Scholar]
- 70.Guillot G, Rousset F. 2013. Dismantling the Mantel tests. Methods Ecol. Evol. 4, 336–344. ( 10.1111/2041-210x.12018) [DOI] [Google Scholar]
- 71.Clarke RT, Rothery P, Raybould AF. 2002. Confidence limits for regression relationships between distance matrices: estimating gene flow with distance. JABES 7, 361–372. ( 10.1198/108571102320) [DOI] [Google Scholar]
- 72.Verbeke G, Molenberghs G. 2000. Linear mixed models for longitudinal data. New York, NY: Springer. [Google Scholar]
- 73.Edwards LJ, Muller KE, Wolfinger RD, Qaqish BF, Schabenberger O. 2008. An R2 statistic for fixed effects in the linear mixed model. Stat. Med. 27, 6137–6157. ( 10.1002/sim.3429) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Nakagawa S, Schielzeth H. 2013. A general and simple method for obtaining R2 from generalized linear mixed-effects models. Methods Ecol. Evol. 4, 133–142. ( 10.1111/j.2041-210x.2012.00261.x) [DOI] [Google Scholar]
- 75.Torda G, Lundgren P, Willis BL, van Oppen MJH. 2013. Revisiting the connectivity puzzle of the common coral Pocillopora damicornis. Mol. Ecol. 22, 5805–5820. ( 10.1111/mec.12540) [DOI] [PubMed] [Google Scholar]
- 76.Ayre DJ, Hughes TP. 2004. Climate change, genotypic diversity and gene flow in reef-building corals. Ecol. Lett. 7, 273–278. ( 10.1111/j.1461-0248.2004.00585.x) [DOI] [Google Scholar]
- 77.van Oppen MJH, Peplow L, Kininmonth S, Berkelmans R. 2011. Historical and contemporary factors shape the population genetic structure of the broadcast spawning coral, Acropora millepora, on the Great Barrier Reef. Mol. Ecol. 20, 4899–4914. ( 10.1111/j.1365-294X.2011.05328.x) [DOI] [PubMed] [Google Scholar]
- 78.Polato NR, Concepcion GT, Toonen RJ, Baums IB. 2010. Isolation by distance across the Hawaiian Archipelago in the reef-building coral Porites lobata. Mol. Ecol. 19, 4661–4677. ( 10.1111/j.1365-294X.2010.04836.x) [DOI] [PubMed] [Google Scholar]
- 79.Davies S, Treml E, Kenkel C, Matz M. 2015. Exploring the role of Micronesian islands in the maintenance of coral genetic diversity in the Pacific Ocean. Mol. Ecol. 24, 70–82. ( 10.1111/mec.13005) [DOI] [PubMed] [Google Scholar]
- 80.Schunter C, Carreras-Carbonell J, Macpherson E, Tintoré J, Vidal-Vijande E, Pascual A, Guidetti P, Pascual M. 2011. Matching genetics with oceanography: directional gene flow in a Mediterranean fish species. Mol. Ecol. 20, 5167–5181. ( 10.1111/j.1365-294X.2011.05355.x) [DOI] [PubMed] [Google Scholar]
- 81.Thomas L, Bell JJ. 2013. Testing the consistency of connectivity patterns for a widely dispersing marine species. Heredity 111, 345–354. ( 10.1038/hdy.2013.58) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Hedgecock D. 1994. Does variance in reproductive success limit effective population size of marine organisms? In Genetics and evolution of aquatic organisms (ed. Beaumont AR.), pp. 122–134. London, UK: Chapman and Hall. [Google Scholar]
- 83.Department of Fisheries. 2012. The Houtman Abrolhos Islands management plan. Fisheries Management Paper No. 260 Perth, Australia: Department of Fisheries. [Google Scholar]
- 84.Smale DA, Wernberg T. 2012. Ecological observation associated with an anomalous warming event at the Houtman Abrolhos Islands. Coral Reefs 31, 441 ( 10.1007/s00338-012-0873-4) [DOI] [Google Scholar]
- 85.Abdo DA, Bellchambers LM, Evans SN. 2012. Turning up the heat: increasing temperature and coral bleaching at the high latitude coral reefs of the Houtman Abrolhos Islands. PLoS ONE 7, e43878 ( 10.1371/journal.pone.0043878) [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Microsatellite data and R code have been deposited on Dryad: http://dx.doi.org/10.5061/dryad.m0420