Emergence of collective changes in travel direction of starling flocks from individual birds' fluctuations

Abstract

One of the most impressive features of moving animal groups is their ability to perform sudden coherent changes in travel direction. While this collective decision can be a response to an external alarm cue, directional switching can also emerge from the intrinsic fluctuations in individual behaviour. However, the cause and the mechanism by which such collective changes of direction occur are not fully understood yet. Here, we present an experimental study of spontaneous collective turns in natural flocks of starlings. We employ a recently developed tracking algorithm to reconstruct three-dimensional trajectories of each individual bird in the flock for the whole duration of a turning event. Our approach enables us to analyse changes in the individual behaviour of every group member and reveal the emergent dynamics of turning. We show that spontaneous turns start from individuals located at the elongated tips of the flocks, and then propagate through the group. We find that birds on the tips deviate from the mean direction of motion much more frequently than other individuals, indicating that persistent localized fluctuations are the crucial ingredient for triggering a collective directional change. Finally, we quantitatively verify that birds follow equal-radius paths during turning, the effects of which are a change of the flock's orientation and a redistribution of individual locations in the group.

1. Introduction

Moving animal groups are a paradigmatic example of collective behaviour in social species. The most striking features of such a collective motion are rapid, coherent changes in the direction of travel of the whole group. Each such collective change involves a decision to change state that starts with a few individuals, and its actual execution by propagation through the entire group. At any moment of this process, the stakes of decreasing the fitness of any individual of the group are high. Both slightest uncertainty and a slow and inefficient transfer of information are punished by decrease of cohesion, or even splitting of the group, leaving some individuals as easy prey for predators. Determining the factors that govern the collective change of direction and the mechanism ensuring efficient propagation of this directional change are thus key to understanding animal movement in groups.

Sudden collective changes of state in animal groups happen often [1–7]. Sometimes they may be a result of a global alarm cue, such as a shot heard by an entire flock of birds. In this case, the collective change of state is not necessarily a social response of the group. Sound propagates extremely quickly (the time needed for sound to cross an entire flock of intermediate size, e.g. 30 m, is comparable to an individual's startle reaction time [8]). Thus, there is no transfer of information between the group members when they hear the shot—all the birds react independently to the signal and at the same moment, apart from individual differences in response times. More fascinating are collective changes of state that have a localized spatial origin, starting from a few individuals that are close to each other. Once the decision to change direction is formed by the nearby group members, then the information to change state travels across the whole group and reaches all individuals.

In some cases, the cause of the localized spatial origin may be an external stimulus, such as a nearby predator that is seen by a small number of individuals in the group. Nevertheless, it has been shown that the collective directional switching can be also triggered spontaneously, without changes in the external environment [5]. Indeed, during aerial display, flocks of starlings often keep changing their direction of motion even in the absence of predators or obstacles. While responding to an external cue is a natural anti-predatory strategy, the occurrence of spontaneous collective manoeuvres poses questions as to why and how this kind of behaviour arises.

Here, we perform an experimental study in which we address these intriguing questions about collective turns in natural flocks of starlings. Using detailed data on individual trajectories of large groups, we reveal the mechanism responsible for the initiation of spontaneous turning in starling flocks. We find that such turns always start from the peripheral tips of the elongated flock. This result suggests that the turn occurs because individual birds which are positioned in specific locations—with higher risks for predatory attacks and lesser social feedback from neighbours—are more prone to rearrange their position. Indeed, we find that the birds that initiate the turn display unusual deviations from the mean flock's motion over longer periods compared with other birds. This persistent signal provokes a response of the neighbouring birds, which leads to a collective turn. Finally, we characterize the kinematics of turning and quantitatively verify that individuals follow equal-radius paths. As a consequence, birds change their position with respect to the global direction of motion: dangerous lateral tip locations can become front/back ones and individuals are able to acquire less risky locations.

2. Material and methods

2.1. Experiments

2.1.1. Location and materials

During winter, large flocks of European starlings (Sturnus vulgaris) are a common sight in Rome, where they populate several roosting sites. While returning to their roost shortly before sunset, starlings form sharp-bordered flocks which wheel and turn over the roosting place before setting down to the trees. They perform highly synchronized manoeuvres while maintaining strong coherence, either as a response to a predator attack, but most often with no visible external influence. We concentrate on the latter type of collective turns, where no changes in external environment are observed. Data were collected shortly before dusk at the site of Piazza dei Cinquecento, between November 2010 and December 2012. We acquired video sequences of turning flocks using three high-speed cameras IDT-M5 with monochromatic CMOS sensors with resolution 2288 × 1728 pixels, shooting at 170 fps. Lenses used were Schneider Xenoplan 28 mm f/2.0. Typical exposure parameters were aperture between f/2.8 and f/8; exposure time between 700 and 3500 μs.

2.1.2. Experimental technique

To obtain the three-dimensional coordinates of individual birds in a flock, we use stereophotography. Specifically, we use the trifocal technique with a system of three synchronized cameras positioned at three different points of view [9]. Flocks perform turns typically at a distance of 80–130 m from the cameras. The reconstruction error on the relative distance between two neighbouring birds is approximately 0.1 m. Time duration of the recorded events is between 1.8 and 12.9 s.

The full three-dimensional dynamical trajectories of individual birds in the flock are then reconstructed for the whole duration of the turn starting from the stereo video acquisitions. This was achieved by using a novel three-dimensional tracking algorithm that retrieves the three-dimensional spatial positions of the same individual through time using computer vision techniques (see [10] for details). The three-dimensional trajectories obtained by our method have very low time fragmentation: 90% of the reconstructed trajectories last more than 90% of the duration of the event. The dataset consists of 12 flocking events, each one including one distinct collective turn, as reported in the electronic supplementary material, table S1. A typical collective turn is shown in electronic supplementary material, video 1.

2.2. Statistical analysis

Having the reconstructed three-dimensional trajectories, at each time step t, bird i in a flock is determined by its position, r_i(t), velocity, v_i(t) and acceleration, a_i(t), where the latter two are calculated using a finite difference method. Therefore, we can study the individual dynamics of birds during a turn. When calculating accelerations, filtering is necessary for reducing experimental noise and eliminating wing flapping, whose frequency for starlings is ω_flap = 10 Hz and can be seen as the trajectories' zigzag in electronic supplementary material, video 1. By sampling at ω_sampl = 170 Hz, without filtering, the wing flapping motion would completely dominate acceleration, while instead we are interested in capturing a signal of changes in a travel direction. By applying a second-order low-pass digital Butterworth filter on the velocities, typically with a cut-off frequency ω_flap/30, obtained accelerations capture the low frequency corresponding to the turn (e.g. see the electronic supplementary material).

We now define several terms useful for the analysis of how a flock as a whole performs a global turn.

2.2.1. Turning plane

During a turn, the trajectories of birds lie approximately on a plane, as observed previously in [7], and as shown in figure 1a. We will use this fact in order to simplify visualization of the turning dynamics. We define the flock's ‘turning plane’ by using two flock's centre of mass velocities: at time t₁ when the turn started, and at time t₂ when the turn is finished. For a flock of N birds, its centre of mass velocity at time t is 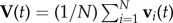. The turning plane is then determined by its normal unit vector 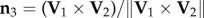which is perpendicular to the plane, and the flock's barycentre position at t₁, i.e. the flock's centre of mass defined as 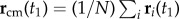. For data visualization, we use the orthogonal coordinate system (n ₁, n ₂, n ₃), where 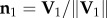is the direction of motion at the start of the turn, and n₂ = n₃ × n₁ (see the electronic supplementary material for more details and a quantitative check of turning on a plane for several events).

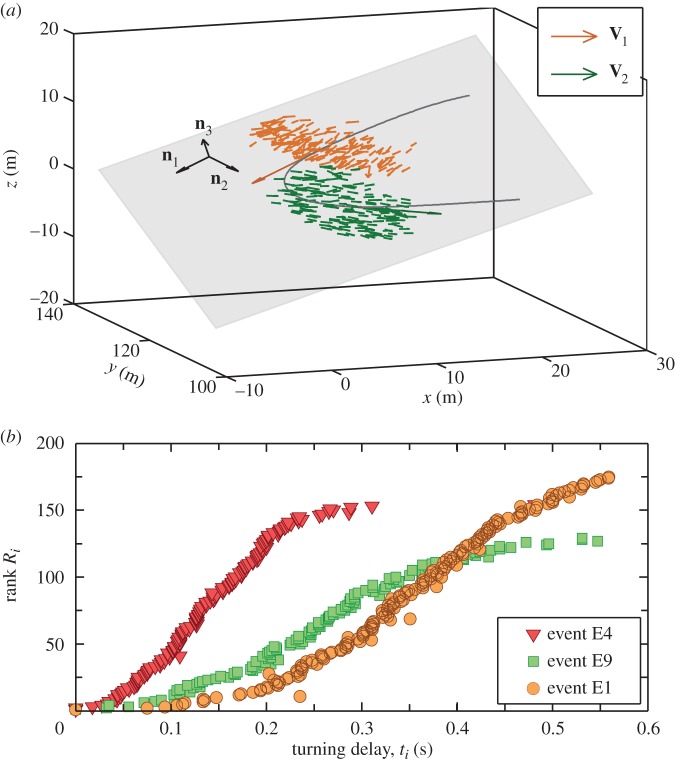
Figure 1.

Collective turn and ranking. (a) For a flock of 176 birds performing a collective turn (event E1 in electronic supplementary material, table S1), a trajectory of its barycentre is plotted (black curve). Individual birds and their velocity vectors are shown shortly before (orange velocity vectors) and after the turn (green velocity vectors). Average flock's velocities V₁ and V₂ are rescaled in order to emphasize the flock's direction of motion before and after the turn. The flock's ‘turning plane’ is shown in grey and determined by an orthogonal coordinate system (n ₁, n ₂, n ₃) defined in the Methods. Before and after the turn, the flock's trajectory is almost straight. (b) For three different events E1, E4 and E9, the rank R_i of each bird i, i.e. its order in the turning sequence, is plotted versus its turning time delay t_i with respect to the first bird to turn (ranking curves for all other turning events are given in [7]).

2.2.2. Elongation axes

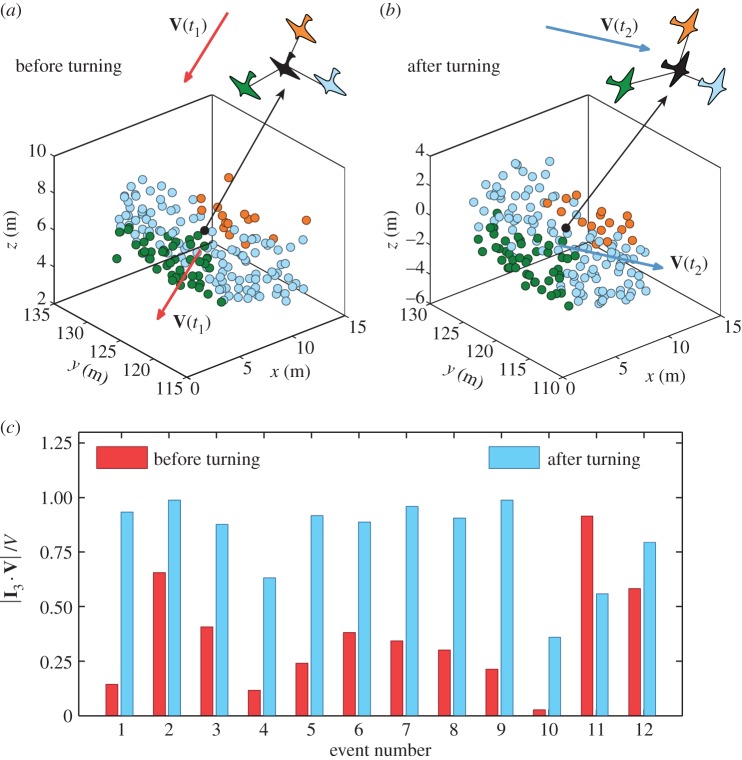
To understand how birds coordinate their movement during turns, we will study flocks' global orientation in space before, during and after turning. Similar to [11], we focus on starling flocks with sharp-bordered edges, performing a random walk above the roost, keeping the same global features for quite long timescales. These flocks have asymmetric flat shapes that are characterized by the three principal elongation axes with the unit vectors I₁, I₂ and I₃ [11]. The dimensions of the group along these axes are I₁ < I₂ < I₃. The reorientation of the flock during the turn can then be studied by looking at the angles between the three axes and the flock's velocity. As the turns we are analysing are almost planar (see the electronic supplementary material), a concise description of the turning is captured by the normalized scalar product between the longest elongation axis I₃ and the flock's velocity before and after the turn. For the full evolution of the flock's orientation during a turn, see electronic supplementary material.

2.2.3. Ranking

To determine the dynamics of turning, we rank all birds in the flock that turned according to their turning order. This ranking is established from the accelerations of single birds, since a turn can be detected by a strong peak in the acceleration curves a_i(t) (see the electronic supplementary material for an example and more details). Comparison of the acceleration curves gives us time delays in turning between each pair of birds in a flock, from which we can calculate the order and time of turning of each bird. We can therefore say who is the first to turn, who is the second, and so on. More details of the ranking procedure are given in [7]. In this ranking, each bird i is labelled by its rank R_i, and by its absolute turning time t_i, that is the turning delay with respect to the top-ranked bird—the initiator (whose delay is t₁ = 0). The ranking curve R(t) in figure 1b is obtained by plotting the rank R_i of each bird as a function of its turning delay t_i.

3. Results

Typical ranking curves for spontaneous turns have a shape shown in figure 1b, as discussed in [7]. This indicates that turns are initiated by a small number of birds, whose reaction times are relatively long as the turn starts. Moreover, in [7, fig. 2b], it was also found that the first birds to turn are physically close to each other. Hence, the decision to turn has a spatially localized origin and it then propagates across the flock through a social transfer of information from bird to bird. This information flow is illustrated in electronic supplementary material, video 2 in which each bird changes colour (from grey to red) once it starts turning, resulting in a turning wave that propagates through the whole flock.

The mechanism through which such propagation occurs is far from trivial, with directional information travelling undamped with a speed of propagation that is larger the more ordered the flock is. In [7], we quantified in detail the features of this propagation, which is not described by standard models of self-propelled motion, and introduced a new mathematical theory able to explain it [7,12]. There are, however, a few fundamental questions that remain to be addressed: why such a collective change of state started in the first place; who initiated the turn; and what are the consequences of turning in terms of global structure and individual rearrangements?

To investigate these questions, in figure 2, we first look at the spatial position of the top-ranked birds within the flock, and how from there the directional information propagates through the group. Birds are coloured according to their turning time delays, revealing a response chain from the first to the last bird. This figure shows a few very interesting facts. As noted above, the top-ranked birds (coloured in red) are physically close to each other. Moreover, they are located close to one of the lateral sides of the flock—outermost parts of the longest elongation axis—to which we will refer to as tips of a flock. Once the turn starts, the information propagates from the initiating birds in all directions, ending with the birds close to the opposite elongated tip of the flock (coloured in blue). As in electronic supplementary material, video 2, spatial modulation of the turning wave indicates a social nature of the response. Finally, the orientation of the flock with respect to the direction of motion changes upon turning, with the flock initially moving nearly perpendicularly to its longest axis and ending the turn with a direction of motion almost parallel to it.

Figure 2.

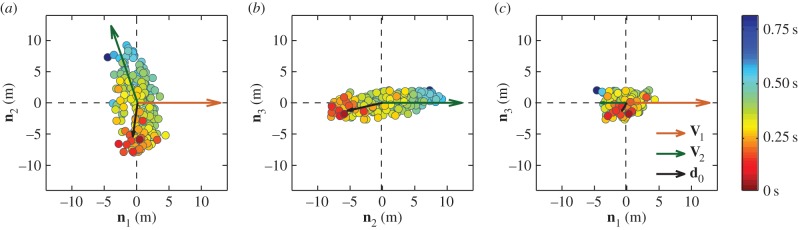
Propagation of the turn. Flock E1 is shown at the start of the turn t₁ by using its projections on the planes of the ‘turning plane’ orthogonal system (n ₁, n ₂, n ₃) centred at the flock's centre of mass. Different panels show a view on the flock (a) from the top, (b) from the front and (c) from a side. At time t₁, the flock is moving along the direction n ₁, with velocity V₁, which is to the right in (a,c), while in (b) it moves towards the viewer. At moment t₂ after the turn, the flock is moving with the velocity V₂. The velocity vectors are rescaled in order to emphasize the old and new direction of global flock's motion. A wave of turning information spreads through the flock during a turn. The birds are coloured according to their turning time delays t_i, as indicated by the colour bar on the right. The mean position of the first 10 birds to turn, with respect to the barycentre, is indicated by vector d ₀. Propagation of the directional information for several other turning flocks is shown in the electronic supplementary material.

All the features we have qualitatively described so far can be precisely quantified. As we shall discuss in the remainder of the paper, they hold systematically in almost all of the turning events we have analysed (for two turning events one of the features is not present and we speculate about the reason for this below), indicating that a majority of spontaneous turns occur with a generic mechanism.

3.1. Origin of the turn

We can quantitatively locate the origin of the turn by looking at the positions of the first birds that turn within the flock. The average position of the 10 top-ranked birds at the start of the turn t₁ with respect to the barycentre of the flock is

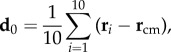3.1

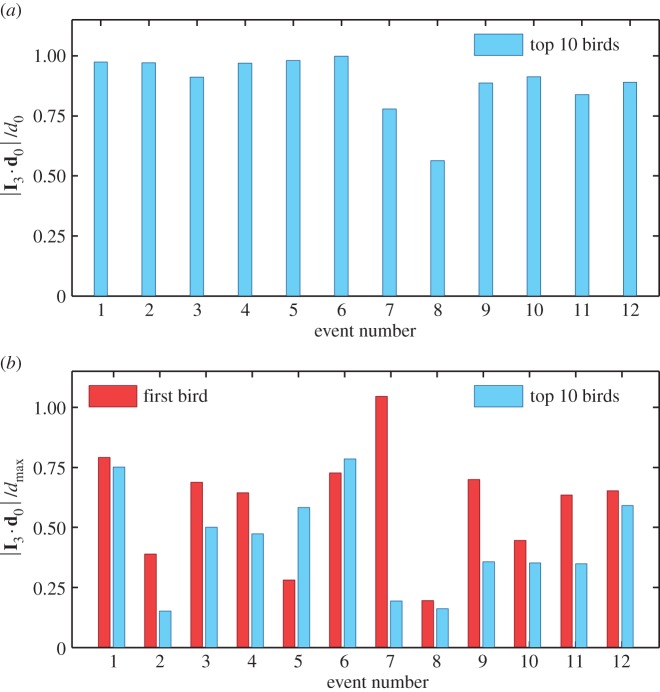
where r_i is the position of the bird with rank i at t₁, and 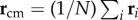is position of the centre of mass of the flock. In figure 2, we see that the first turning birds are positioned along the longest axis of the flock and close to its outermost lateral tip. To quantify this behaviour, we compute the absolute scalar product of the normalized vector d ₀/d₀ with the unitary vector I ₃ of the longest elongation axis at the start of the turn t₁ (see Material and methods and electronic supplementary material). This quantity gives a measure of the orientation of the initiating birds with respect to I ₃ and is displayed for all the turning events in figure 3a. Large values indicate that the first birds to turn are situated along the longest elongation axis I ₃ for all the analysed turns. To quantify how close these birds are to the lateral tips of the flock, we calculate 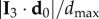, where is the maximal possible value of a bird's distance along I ₃ axis, with i going over all the birds on the side of the flock at which the turn started (as the two sides could be of different lengths, depending on the position of the flock's barycentre). In figure 3b, we show the values of this quantity both for the initiator itself and for the 10 top-ranked birds. The obtained values are quite high, confirming that the initiators are typically close to the lateral elongated tips.

Figure 3.

Position of the origin of the turn. (a) Absolute scalar product of the longest elongation axis unit vector I ₃ with the unitary vector of the mean position relative to the barycentre d ₀/d₀ of the 10 top-ranked birds (data are given in the electronic supplementary material, table S1). The result does not change qualitatively for another number of top-ranked birds, as long as this number is small compared with the total number of birds in the flock N. (b) Scalar product 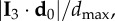where d_max is the maximal possible distance of the birds along the I ₃ axis at the tip where the turn started. We show the results for d ₀ calculated for the 10 top-ranked birds (blue bars), but also as a position of only the first bird that started the turn (red bars). For most events, the values are higher than 0.5, although not too close to 1 due to the sparseness of the flock at the very tips and particular orientations.

3.2. Individual deviations from the global direction

Let us now investigate the mechanism that triggers the start of the turn. As we have seen in the previous section, turns initiate spontaneously from the lateral elongated tips of the flock. There might be some important difference in the way birds located in these regions of the flock behave that can explain why this occurs. To elucidate this point, we look in more detail at the characteristics of individual motion, and its variability through the flock. In particular, since turns involve a permanent change in the direction of motion, we can quantify the individual tendency to deviate from the global flock's direction prior to the occurrence of the turn itself.

To this end, we define a directional correlation C_i(t) between the direction of motion of an individual bird i and the global direction of motion of the flock as

3.2

If at time t bird i is flying along the flock's global direction of motion, the value of the correlation is C_i(t) = 1 and bird i is completely aligned with the flock's direction. However, birds are almost never completely aligned with the flock's direction of motion, at the very least due to wing flapping (zigzag of the trajectories can be seen in electronic supplementary material, video 1). Therefore, values of C_i(t) fluctuate below, but very close to 1, while sometimes we observe a strong decline in this quantity, when a bird deviates strongly from the global direction of motion (figure 4a).

Figure 4.

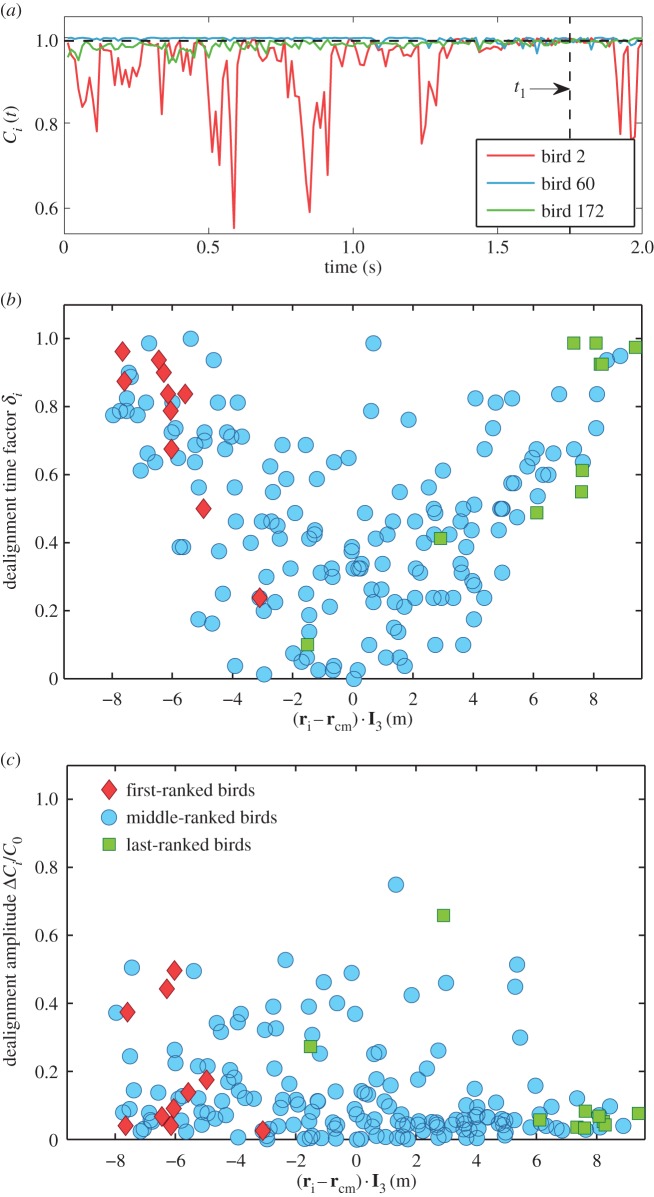
Deviations from the global direction of motion. (a) Directional correlation function C_i(t) is plotted for three individual birds ranked 2 (red), 60 (blue) and 172 (green), in a flock of 176 birds performing a collective turn (event E1 in the electronic supplementary material, table S1). Only times prior to the start of the turn t₁ = 1.75 s (vertical dashed line) are shown. A median value of all C_i(t) during time interval τ = 1 s is used as a threshold value C₀ = 0.9926 (horizontal dashed black line). (b) Dealignment time factor δ_i(τ), and (c) dealignment amplitude ΔC_i/C₀ are plotted as a function of position of bird i along the longest elongation axis I ₃, with respect to the flock's centre of mass. The top 10 ranked birds (red diamonds) are situated close to one lateral tip of the flock, while the last 10 birds to turn (green squares) are close to the opposite tip of the flock. On average, the farther away from the centre of the flock a bird is, the longer time its directional correlation is lower than C₀. No obvious dependence of ΔC_i/C₀ on the position is observed.

To understand which behaviour might trigger the collective decision to make the turn, we analyse a time interval τ shortly before the start of the turn at t₁. During this interval, for each bird i, we calculate its dealignment time factor, δ_i(τ), defined as the percentage of time during which bird i deviates significantly from the global direction of motion. Specifically, we check how frequently its directional correlation C_i(t) is lower than some threshold value C₀, i.e.

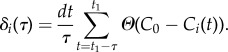3.3

Here, Θ(x) is a Heaviside step function, so that Θ(x) = 0 for x < 0, and Θ(x) = 1 for x > 0 and dt = 1/ω_sampl = 1/170 s is the sampling interval. For each event, for the threshold value C₀, we choose a median value of all C_i(t) during time interval τ = 1 s just before the start of the turn. The values for C₀ and τ are chosen in such a way to allow good statistics and most visible results for all analysed turning events. However, no qualitative difference was observed for other meaningful values of these parameters (see the electronic supplementary material for a more detailed discussion).

It might be thought that all birds are deviating from a median behaviour C₀ in a similar way, so that half the time they fly more aligned to the global direction of motion (with C_i(t) > C₀), while the rest of the time they deviate stronger from this direction (with C_i(t) < C₀). That would imply similar values of δ_i(τ) ∼ 0.5 for all the birds, independently of their position in the flock. This is not, however, what happens. As can be seen in figure 4b (for other flocks see the electronic supplementary material), there is a strong correlation between the location of an individual in the flock and the value of its dealignment factor: the farther away a bird is along the lateral elongation axis I ₃, the more frequently it exhibits consistent fluctuations from the global direction of motion. On the contrary, no correlation is observed for the other two elongation axes (see the electronic supplementary material).

The top-ranked birds, which are situated close to one lateral tip, are among the individuals with the highest dealignment time factor δ_i(τ). We also computed the dealignment amplitude ΔC_i/C₀, which measures how strongly bird i deviates from the median behaviour during the time interval τ. Here, ΔC_i is a maximal deviation from the global flock's direction of motion made by bird i during τ, i.e.

3.4

While top-ranked birds tend to have larger dealignment amplitude than average, they are not, in general, the individuals with strongest amplitude. There is no clear correlation of the amplitude with the position along the elongation axis (see figure 4c and electronic supplementary material). In fact, birds located centrally deviate as strongly or even more strongly than those closer to the edges. However, their deviations are not followed by a global change of direction. These results indicate that what really is distinctive in the behaviour of initiators is how persistently they deviate from the flock's direction. The turning event is triggered by the presence of such repeated deviations from average motion and is not due to a big, but momentary lapse of alignment.

Why do initiators, and edge individuals more generally, behave differently? Owing to the asymmetric elongated shape of flocks, individuals in different locations can experience rather different boundary conditions. Birds in the bulk of the group are surrounded by many neighbours and well protected from external perturbations. They can momentarily fluctuate from the mean motion, but persistent large fluctuations are rare since volume confinement and social adaptation produce a strong feedback to the average. The same is not true for individuals at the border of the flock, and particularly for the ones on the extremal lateral tips. These individuals are mostly surrounded by empty space. They can freely move towards the outside for a wide range of directions and experience an unbalanced social force by neighbours. According to the selfish herd model [13] and its modifications (e.g. [14]), they also are at larger predatory risk. For the individuals at the peripheral tips, this is especially true as their domains of danger (DOD), defined for each individual as an area that is closer to that individual than any other, are the largest [13,14]. This might enhance their alertness and wish to relocate. All these factors contribute to produce persistent individual fluctuations, as signalled by the values of the dealignment time factor. Statistically, this increases the probability of a coherent deviation of few individuals from the common flight direction, which might trigger spontaneous turns to occur.

3.3. Equal-radius paths and global reorientation during turns

During the process of turning, two things happen: each bird performs its own individual turn following a specific trajectory in space; and the flock as a whole performs a global collective turn. These two dynamics are strictly interconnected, and the way individuals coordinate turning with each other determines how the flock turns as a whole. Here, we show in detail how this occurs.

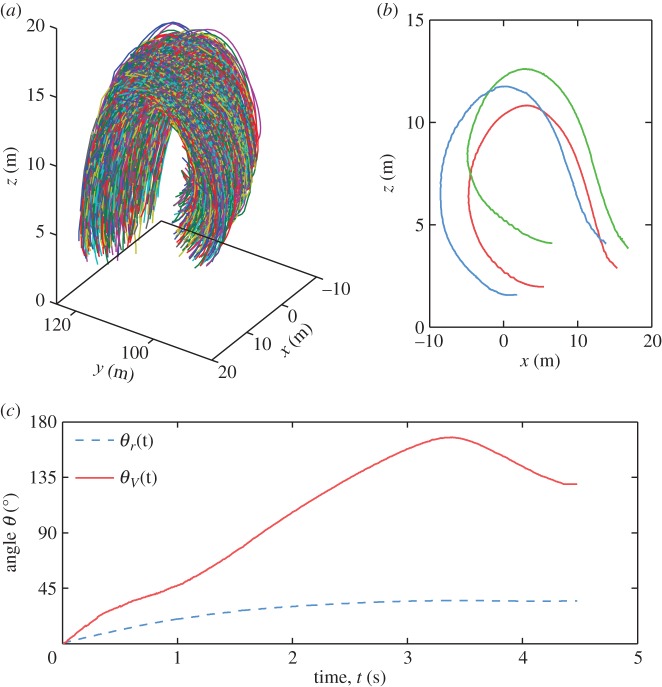
Seminal experimental work on flocks of rock doves indicated that, when turning, individual birds follow equal-radius paths [15]. Empirical observations of starling flocks in [11] indirectly supported this result, by showing that during a turn a flock changes its global velocity and orientation consistently with equal-radius dynamics. However, a more quantitative confirmation of this finding could not be made in that study due to the lack of individual birds' trajectories. Here, having the long three-dimensional trajectories of all individuals allows us for the first time to investigate this issue systematically. In figure 5, we report the individual trajectories during a turn, which clearly show very similar radii of curvature and trajectory crossing. Moreover, a detailed quantitative measurement of how the whole network changes during the turn confirms that birds indeed follow equal-radius paths. Let us look at the position of bird j relative to bird i, r_ij = r_j − r_i, and how its orientation in space changes over time with respect to the start of the turn. This is described by the angle θ_ij(t) between the two vectors r_ij(0) and r_ij(t) at initial time t = 0 and some later time t.

3.5

Figure 5.

Equal-radius turning. (a) Three-dimensional reconstruction of the full individual trajectories during the turning event E6 in the electronic supplementary material, table S1. (b) Three individual trajectories of nearby birds: the equal-radius paths are clearly visible, each bird turning around a different rotation centre but with the same radius of curvature of its neighbours. (c) Temporal evolution of the angles θ_r(t) measuring the angular variation of the structural network of birds (dashed blue line), and θ_V(t), the angle between the flock's velocity V(t) and V(t = 0) (solid red line), for turning event E6.

Averaging over all pairs of birds i and j, we obtain θ_r(t), measuring the angular variation of the whole structural network of birds over time. For equal-radius trajectories, the relative positions between individuals in an absolute reference frame do not change. Thus, the mutual orientations θ_ij, should remain approximately constant during a turn, while the global orientation of the group changes significantly. This is exactly what happens in real flocks as shown in figure 5c, where we compare the evolution in time of θ_r with the angle θ_V(t), measuring the change of the global direction of motion of the flock (see the electronic supplementary material for details and other turning events).

As compared to the observations in [15], the turns that we analyse are of a different species (starlings rather than doves) and of much larger flocks (hundreds rather than tens of individuals). This indicates that equal-radius turning might be a generic strategy of turning. Our analysis in [7,12] also shows that this kind of turning is intimately related to the fast and efficient way turns occur, where each bird starting to turn transfers to its neighbours information on its direction of motion and path curvature through a social interaction mechanism, giving rise to a propagating wave of turning individuals (for equal-radius turning in numerical models, see [12,16]).

Equal-radius turning is thus very non-trivial. It is also completely different from how a rigid assembly of particles (like a plane, or any solid body) would turn: in that case, all particles turn synchronously around the same rotation point, following parallel paths and having different speeds and radii of curvature (moreover, angles θ_r and θ_V must be highly correlated, contrary to figure 5c). Birds in a flock, on the contrary, turn following a social transfer of information, using different rotation points, but with the same radius of curvature and speed. This way of turning is advantageous in many respects. Firstly, individuals can keep approximately constant speed and produce amazingly quick collective turns. Secondly, as we shall discuss, the reciprocal positions of individuals and the orientation of the flock in space change, the by-product of which is that the distribution of the boundary locations and risk among the individuals alters.

To understand how this occurs, let us look at figure 6. In figure 6a, we show a reconstructed flock at the initial time t₁ of the turn. A random bird is plotted in black, and the other birds are coloured according to their angular position around this reference bird with respect to the barycentre velocity: green for the birds flying in front, light blue for the ones on the sides and orange for the birds flying behind. In figure 6b, we show the same flock at time t₂ after performing a turn of 120°, with the same colours previously assigned. The two figures reveal that the orientational topology changes with the change of the direction of motion, e.g. the birds that were in front of the reference bird (green) are now flying at the right of it. At the same time, the structural network of birds remains stable—their angular relative position does not change considerably (see figure 5c and electronic supplementary material).

Figure 6.

Reorientation of the flock during the turn. (a,b) Change of the orientational topology around a reference bird in the flock. (a) The flock at the start of the turn: the reference bird is pictured in black, birds flying in front with respect to the bird are green those on the sides are in light blue, the ones behind are in orange. (b) The flock at the end of the turn: birds are pictured with the same colours as in (a). (c) Global orientation of the flock before and after performing a turn. We report scalar products between unitary vector I ₃ of the flock's longest elongation axis with its direction of motion V(t)/V(t) at times t₁ (start of the turn) and t₂ (end of the turn). Data are given in the electronic supplementary material, table S1. The angle between the longest elongation axis and the direction of motion is large before the turn (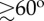 for almost all events) and it reduces during the turn. The exceptions are events E11 and E12 which correspond to two consecutive turns of the same flock, and occur after merging of two separate flocks into one (see the electronic supplementary material), which might be the reason why the reorientation is different.

When looking at the flock as a whole, this implies that the group retains the same orientation with respect to an absolute reference frame, but its overall orientation with respect to the direction of motion changes. For a turning event depicted in figure 2, just before the turn the flock has its longest elongation axis almost perpendicular to the direction of motion V₁. After the turn, however, the new direction of motion V₂ is no longer orthogonal to the longest elongation axis, but nearly parallel to it. This behaviour is characteristic for most of the analysed flocks (see the electronic supplementary material, figure S3 for more illustrative examples). To quantify it, we computed the normalized scalar product of the longest elongation axis I ₃ and the flock's velocity before and after the turn for all our turning events. The result displayed in figure 6c shows that, for majority of the analysed events, prior to a spontaneous turn flocks tend to have their longest elongation axis almost perpendicular to the direction of motion (small ). After the turn, the longest axis and the flock's velocity become much more aligned as the angle between them reduces (large ). A full analysis of the dynamical evolution of the three inertial axis during turns confirms this scenario (see the electronic supplementary material).

Interestingly, the flock's reorientation during the turn significantly changes the positional role of individuals in the group. Birds that were located at the largely populated front or back boundaries of the flock end up on the side, while birds on the lateral sparse tips, i.e. the same birds that initiated the turn in the first place, move much closer to the front or back, depending on how much the whole group turned. Collective turns therefore produce a global reorganization of the group—and of boundary birds, in particular—on very quick timescales (a few seconds). During straight flight, individuals relocate by diffusing through the flock, but this is in comparison a very slow process: persistence on the border is strong and in a few seconds boundary birds remain very close to their original location [17].

Finally, note that while for more central individuals a global reorganization of the group during a turn might result in losing privileged locations within the flock, their participation in a collective equal-radius turn is conditioned by safety and energetics: turns provide a quick reaction to a threat by fast social transfer of directional information [7,12]; and equal-radius paths ensure turning at approximately constant speed (no need to accelerate more than other flock members).

4. Discussion

Spontaneous turns exhibit interesting dynamics that mainly follow a general scenario outlined below.

During straight flight, flocks typically acquire asymmetric shapes, as they expand in the direction transverse to the flock's direction of motion, which can be clearly seen in some of our data (i.e. in all those acquisitions that are long enough to capture substantial time before the turn). This feature has a well-known theoretical explanation: in self-propelled systems, directional fluctuations perpendicular to the mean direction of motion V (and to gravity) are much larger than in other directions [17–19], owing to the breaking of the rotational symmetry in the polarized state. Indeed, as already argued in [17,18], if birds make small errors δθ in their direction of motion, then their random displacement perpendicular to V is proportional to 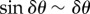, while along V it is 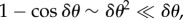the former being much larger than the latter. As a consequence, a coherent group gradually elongates in the transverse direction, with its main axis becoming more and more perpendicular to its velocity and to gravity (figure 6c). One of the main outcomes of this process is that birds situated in different regions of the flock experience rather different boundary conditions. In particular, the individuals in the elongated lateral parts of the group have much less spatial confinement, and a strongly anisotropic distribution of neighbours. These conditions cause a larger directional mobility, causing individuals at the tips to deviate more persistently from the global direction of motion, as shown in our data. For some of these birds, this effect can become so strong as to compensate the feedback to average motion, and initiate a turn. Once the turn starts—locally at the lateral tips—it propagates through the group thanks to the social interactions between individuals. Birds turn following equal-radius paths, the effect of which is the rearrangement of their positions with respect to the global flock's direction: at the end of the turn the very individuals that occupied lateral positions are much closer to the front/back of the group (depending on the turning angle), while the whole flock has its longest elongation axis more aligned to the direction of motion than before the turn (figure 6).

The fact that individuals on the border of a group behave differently has been already discussed in the literature on collective animal behaviour. Staying on the border is not usually a preferential location during collective motion, as these positions suffer higher risk under a predator attack or any other external perturbation [13,14]. Therefore, one might expect border individuals to be particularly risk alert and exhibit a strong pressure to exchange position for a more favourable one. Several studies have been performed on bird flocks while feeding on the ground, where it was shown that individuals on the edges display stronger vigilance, i.e. they scan the surrounding more frequently for predators and they feed more rapidly [20–24]. In the case of turns, we find that individuals at the lateral tips deviate from the mean motion more frequently than others. It might be that due to their location these birds increase their alertness so that each of them becomes more sensitive and prone to changes, much as border individuals in feeding groups have a larger scanning and feeding rate. However, this is not the only possible cause for their anomalous behaviour. When moving collectively, birds coordinate with one another using local adaptation rules (i.e. ‘align with your neighbours') [16,25–29]. In this respect, being close to the peripheral tips implies having an atypical neighbourhood, thereby experiencing a social force that is significantly different from inside the flock. This very fact can produce more persistent fluctuations at the border and trigger turns. While it is certainly very difficult to disentangle these effects in real data, the idea that social positional heterogeneities are important to explain the role of edge individuals is worth investigating in future studies.

Having understood that birds at the peripheral tips of the flock behave differently, we want to clarify which aspect of their behaviour is crucial for triggering a turn that then spreads through the whole flock. Our data show that what really matters to initiate a turn is that top-ranked birds deviate from the average motion much more persistently than others, while there is no correlation between the strength of such behavioural deviations and turning (figure 4). This could indicate that the response of the neighbours to the initiator of the turn might be related to a repeated signal—perceived as a persistent deviation from the average motion—exhibited by the initiator, and not to a sudden and strong fluctuation. Interestingly, similar results have been found in the works concerning vigilance behaviour in feeding birds where it has been shown that response to alarm cues occurs with repeated detection of an alarm signal [30,31]. It has been argued that this strategy is useful for avoiding false alarms which are common, as taking flight in the course of feeding is both costly in energy and time [32]. Nevertheless, what happens in a turning flock might be more complex: also the neighbours of the initiator are close to the lateral tips of the flock, thus their response to the initiator's signal is probably boosted by the fact that they are experiencing similar boundary conditions, and exhibit similar persistent directional deviations themselves.

One can wonder why spontaneous turns occur and to what extent such a collective behaviour can be advantageous to the individuals. On the one hand, spontaneous turns are a social response of the flock to the persistent deviations of some individuals. We can expect a similar mechanism to occur when an external repeated signal, like an approaching predator or an obstacle, is encountered. In this sense, spontaneous turns are a by-product of the very ability of the group to respond collectively to local perturbations. On the other hand, during a turn individuals change their positions with respect to the travel direction, with the important consequence that birds who suffered extremal conditions before the turn are able to acquire better locations after it. The idea that adaptive strategies to reduce the risk of predation might be based on positional relocation has long be debated in the literature on collective behaviour [13,15]. Interestingly, during a turn the reorganization of individuals is an emergent property of the highly coordinated equal-radius dynamics. Risk is redistributed between individuals at no expense of global order. In this respect, the whole process of turning is a remarkable example of how a self-organized system can sustain collective changes and reorganize, while retaining coherence.

Data accessibility

The data are available in electronic supplementary material, table S1, and data files Data_Fig3b and Data_Fig4bc.

Authors' contributions

A.C. and I.G. designed the study. A.C. coordinated the experiment. A.A., A.C., I.G., S.M., L.P., E.S. and M.V. set up and calibrated the three-dimensional system. L.D.C., S.M., O.P. and E.S. performed the experiment. A.A., A.C., L.P. and M.V. developed the tracking method. A.A., S.M., L.D.C., E.S. and M.V. tested the tracking method and produced the three-dimensional data. A.J. analysed the data. A.C., I.G. and A.J. interpreted the data. A.J. and I.G. wrote the paper.

Competing interests

We declare we have no competing interests.

Funding

This work was supported by grants IIT–Seed Artswarm, ERC–StG no. 257126 and US-AFOSR—FA95501010250 (through the University of Maryland).