Abstract
Although safety standards have reduced fatal head trauma due to single severe head impacts, mild trauma from repeated head exposures may carry risks of long-term chronic changes in the brain's function and structure. To study the physical sensitivities of the brain to mild head impacts, we developed the first dynamic model of the skull–brain based on in vivo MRI data. We showed that the motion of the brain can be described by a rigid-body with constrained kinematics. We further demonstrated that skull–brain dynamics can be approximated by an under-damped system with a low-frequency resonance at around 15 Hz. Furthermore, from our previous field measurements, we found that head motions in a variety of activities, including contact sports, show a primary frequency of less than 20 Hz. This implies that typical head exposures may drive the brain dangerously close to its mechanical resonance and lead to amplified brain–skull relative motions. Our results suggest a possible cause for mild brain trauma, which could occur due to repetitive low-acceleration head oscillations in a variety of recreational and occupational activities.
Keywords: mild traumatic brain injury, resonance frequency, rigid body motion, repetitive head exposure, tagged MRI, injury risk criterion
1. Introduction
Traumatic brain injury (TBI) is one of the most disabling health problems in the world. Every year an estimated 1.7 million people are diagnosed with TBI in the USA alone [1]. Of these cases, 80% are categorized as mild [2], with symptoms ranging from headache, dizziness and disorientation, to depression and loss of memory. The numbers for undiagnosed cases are much higher still [3,4]. Until recently, TBI research had focused on the acute consequences of single events involving moderate to severe head impacts. Similarly, mild traumatic brain injury (mTBI) was thought to result in only transient symptoms from single head exposure. However, several recent clinical studies have shown that even in the absence of diagnosed concussion, repeated ‘mild’ head exposures could lead to long-term progressive changes in white matter structure and abnormalities in functional magnetic resonance imaging (MRI) activation patterns [5–9]. It is known that the brain enters a state of metabolic depression after an injury [10]. If a repeated injury occurs prior to full recovery from initial trauma, there is a prolonged recovery period and higher probability of long-term effects [11]. In other words, the accumulation of head blows may lead to irreversible brain changes. Therefore, a study into the physics of repetitive ‘mild’ or low-acceleration head exposures is required in order to understand injury mechanisms and devise effective prevention.
Prevention of brain trauma has historically targeted skull deformation and its resulting focal injuries. This approach is most apparent in helmet design, where the basic principles have remained relatively unchanged over time: (i) a rigid shell spreads contact forces over a large area to avoid high focal stresses on the skull and (ii) an energy-absorbing medium decreases peak forces while increasing impact duration [12]. The current standards in helmet design ensure that levels of linear head acceleration remain below certain thresholds [13]. This approach has proven successful in reducing skull deformation and mitigating focal brain trauma and mortality in auto accidents and sports [14]. However, contrary to focal severe head injuries owing to skull fracture, the mechanisms of mTBI are diffuse in nature and are due to inertial forces on the brain [15,16]. This is evident in the prevalence of mTBI despite the ubiquity of helmet use in contact sports.
Although the magnitude of impacts has a significant influence in subsequent trauma, it is not the only deciding factor. Frequency content of the impact loading also plays an important role and, depending on the loading regime, it might in fact be more critical. From a structural engineering perspective, knowledge of system dynamics determines the safety bounds of loading conditions on a structure. In an under-damped system, oscillations may be amplified at certain frequencies depending on the system's dynamic properties—a phenomenon known as resonance. In engineering design, neglecting requirements to avoid resonance may cause violent motions and even failure. Ommaya et al. observed low-range natural frequencies (5–10 Hz) for rotational brain motion in primates and humans [17]. In contrast, skull resonance frequencies are found to be several orders of magnitude higher (around 1000 Hz) [18,19]. Thus, an important question is what occurs inside the head: does the skull–brain system exhibit an under-damped oscillation that could lead to resonance? Our objective is to investigate this question through reduced-order modelling of the brain–skull system.
Several reduced-order models exist in the literature, where brain tissue is modelled as a rigid mass and connective tissue linking skull and brain are modelled by discrete mechanical elements, i.e. springs and dampers. Alem [20] used a combination of linear and torsional springs to simulate the motion of the head and neck, which predicted very high relative brain motions (125°) in impact scenarios. Low and Stalnaker [21] developed a two-mass model of the brain with torsional springs, simulating the rotational motion of the brain. Willinger et al. [22] developed a lumped-model of the brain's translational motion and performed modal and temporal analysis. More recently, Zou et al. [23] developed a model of the brain–skull that includes, to some extent, the brain's coupled translational and rotational motion to investigate the sensitivity of the brain's relative motion to its size and mass. Compared with the ‘bottom-up’ approach taken by finite-element (FE) models with detailed component interactions, a reduced-order model allows for more direct and global observations of emergent system properties. It can also lead to hypotheses about the minimum number of essential components that govern behaviour. However, the majority of available reduced-order models are based on measurements from either phantom models of the head, or post-mortem human subjects (PMHS) rather than in vivo measurements. Moreover, these models have mostly focused on either only translational or rotational skull motions. They rely on a priori assumptions of kinematic constraints between the brain and skull and focus on fitting the dynamics of brain motion, whereas the kinematics, i.e. the motion of the brain isolated from that of the skull, are missing for the most part. This modelling feature is addressed in this study. Finally, with the exception of the study of Willinger et al. [22], which modelled only translational motion of brain, the above studies did not perform any frequency analysis of brain–skull dynamics. The frequency response of the brain is of particular interest to this study.
In this study, we develop the first reduced-order dynamical brain model based on previously published in vivo human measurements [24]. Using the acceleration of the skull as input and the brain's motion kinematics as output, we show that this system has an under-damped resonance frequency at around 15 Hz. We also examine the applicability of this model both in time and frequency domains to higher energy inputs that are more representative of typical on-field head impacts by comparing with previously published results from PMHS impact experiments [25]. Finally, we posit from our field measurements of athletic head motions that the brain's primary resonance frequency coincides with the primary frequency mode in head impacts experienced on the field.
2. Methods and results
2.1. Unconstrained kinematics
MRI provides a non-invasive method of measuring the displacement of brain tissue in vivo. We used tagged MRI measurements from a previously published study of brain displacements (three human male subjects aged 23–44) in 2 cm frontal head drops in the sagittal plane [24]. These impacts resulted in maximum linear and rotational accelerations of 1.5 g and 140 rad s−2, respectively. Feng et al. measured the displacement field of the entire brain pixels on a sagittal section of human brain for 168 ms with a spatial resolution of 1.3 × 1.3 mm2 and a temporal resolution of 5.6 ms.
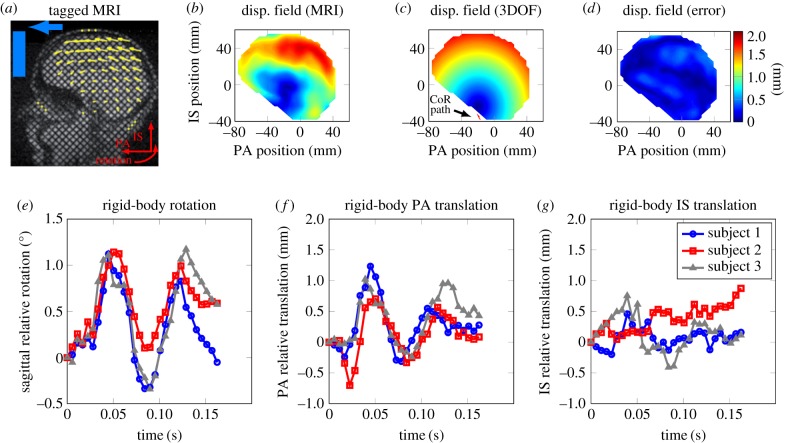
To investigate the motion of the brain relative to the skull, we first determined all the brain pixels that were available throughout the tagged MRI measurement for each subject (approx. 350, 560, 480 nodes for subjects 1 to 3, respectively; figure 1a). Taking the displacement of the tagged MRI brain pixels as various points on a body, we studied the contribution of rigid-body motion compared with deformation for the brain as a whole. The rigid-body motion consisted of three degrees of freedom (DOF): translation of the brain's centre of mass (CoM) in the posterior–anterior direction (PA), translation of the brain's CoM in the inferior–superior direction (IS) and sagittal rotation about a centre of rotation (CoR). We determined the rigid-body motion parameters at each time by minimizing the root mean square (RMS) distance error between each MRI pixel and rigid-body motion trajectories.
Figure 1.
Kinematic model of brain motion: (a) sagittal view of the tagged MRI with the displacement field superimposed (previously reported in [24]), (b) the experimental displacement field shown at the time of maximum rotation angle at t = 56 ms (reported in [24]), (c) displacement field from the unconstrained rigid-body model at t = 56 ms with the translation of brain CoR superimposed, (d) fringe plot of displacement error for the rigid-body model. (e–g) Time trace of unconstrained rigid-body sagittal rotation, PA translation and IS translation, respectively.
Analysing the displacement field from the MRI measurements resembled a rolling motion where the base of the brain was mostly stationary and the cortex had maximum relative displacement (figure 1b). This behaviour could be captured by the 3DOF kinematics model with relatively small errors (figure 1c,d). The distance error for the rigid-body model for all nodes through all time points has a median of about 10% when normalized by the maximum relative brain displacement (1.9–2.1 mm for all three subjects). This normalization was performed to eliminate large numerical errors pertaining to nodes with close to zero displacements. The low error levels suggest a possible coupling between rigid-body motion and maximum strain induced in the tissue, because the latter has been previously correlated with brain trauma [26,27]. Analysing the rigid-body motion from the 3DOF model showed similar trends in PA translation and sagittal rotation with only small translations in the IS direction, suggesting a possible coupling between the DOF (figure 1e,g). This agrees with previously published literature suggesting that the brain's rotation and translation are coupled [21,23].
2.2. Constrained kinematics
In order to investigate whether anatomical features of the skull and brain constrain brain motion, we performed principal component analysis (PCA) on the 3DOF kinematics for each of the three subjects. PCA is a statistical technique that reduces the dimensionality of a set of observations through orthogonal transformation into a set of eigendirections and their corresponding eigenvalues, where components with the largest eigenvalues have the most contribution [28]. PCA of the MRI measurements was achieved by combining the brain's translation in the PA direction (xb), translation in the IS direction (zb) and rotation in the sagittal plane (θb) as the three bases in the planar motion space. An array of displacement vectors A3m×n = [xb; zb; θb] was populated, where m is the number of MRI pixels and n is the number of MRI snapshots in time. The PCA on the 3DOF kinematic data showed the level of coupling between the translational and rotational DOF for the specific skull motions in the MRI study. The first principal component can explain more than 75% of the total variance in the different modes of rigid-body motion. This indicated that the brain's motion can be approximated by a single degree of freedom along the first eigendirection (figure 2a). The exponential decay in the magnitude of the eigenvalues of the 3DOF motion further justified this reduction (figure 2b). The kinematic relations between the three DOF (the first eigendirection) are given in table 1. The resulting 1DOF rotation showed that the brain lags behind in the initial motion of the skull but continues to oscillate even after the skull has settled (figure 2c). We use the 1DOF kinematic approximation for all further dynamic analyses of the brain–skull system.
Figure 2.
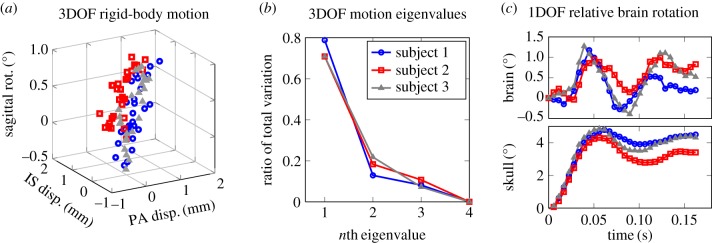
Principal component analysis of rigid-body motion based on tagged MRI data [24]: (a) 3DOF motion of brain in the sagittal plane is shown for the three subjects. There is a strong correlation between the 3DOF such that it can be approximated by a single DOF, (b) first few principal components for the rigid-body motion are shown as the ratio of total variance. The first principal component accounts for over 75% of total variance, (c) relative rigid-body rotation of brain determined by the model given the skull rotation as input. (Online version in colour.)
Table 1.
Results for PCA fits to the brain's relative rigid-body motion. Here, xb = αθb and zb = βθb, where θb, xb and zb represent sagittal rotation, PA displacement and IS displacement of the brain relative to the skull, respectively (electronic supplementary material; equation (A 8)).
| α (m rad−1) | β (m rad−1) | |
|---|---|---|
| subject 1 | 0.0024 | 0.0053 |
| subject 2 | 0.0021 | 0.0093 |
| subject 3 | 0.0010 | 0.0056 |
2.3. Constrained dynamics
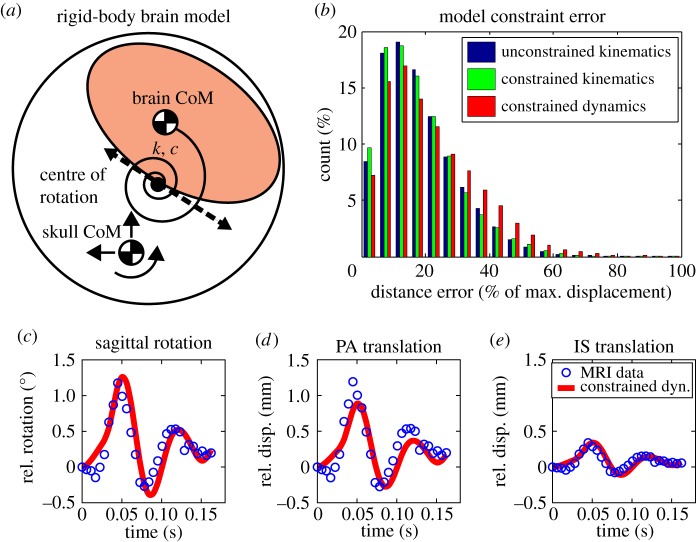
Given the clear periodic oscillatory behaviour of relative brain motion (figure 2c), we speculated that a linear second-order discrete system could explain the relative brain–skull motion. As seen in §2.2, we determined a CoR for the brain, which was defined as the point in the brain that translates minimally in the skull frame. The 3DOF motion of this CoR was shown to be coupled in a single DOF according to the PCA analysis, where the constraint constants were close to the effective radius of brain. In the small angle regime, this can be physically interpreted as the brain rolling along the inner surface of the skull. We chose to use the brain's relative angle as the independent degree of freedom because of the importance of brain rotation in diffuse axonal injury [15,16]. We subsequently used the constrained kinematics of relative brain motion (derived separately for each subject) to develop a coupled linear dynamic model with the skull's linear and rotational accelerations as the inputs. The model consists of a parallel torsional spring-damper element connecting the brain's CoR to the skull's CoM (figure 3a). Equations of motion for the 1DOF dynamic model are given in the electronic supplementary material, Dynamic modelling section.
Figure 3.
Dynamic model fit of experimental brain motion data. (a) Schematic of brain as a 1DOF dynamic model, where skull motion in the MRI experiments was used as input to the model. (b) Histogram of all errors for different model constraints: unconstrained kinematic (3DOF), constrained kinematics (1DOF) and unconstrained dynamic (1DOF) models. (c–e) Time traces of constrained dynamic fit to unconstrained kinematics for sagittal rotation, PA translation and IS translation, all relative to the skull.
The representative system could be described by rolling kinematics, where the translational motion is coupled to rotation through a kinematic constraint (CoR path in figure 1c). The model parameters include the stiffness (k) and damping (c) of the torsional spring-damper element, and the brain's mass (m) and moment of inertia (I), which were fitted separately for each subject. The average fitted values for the three subjects were determined as k = 160 Nm rad−1, c = 0.50 Nms rad−1, m = 1.34 kg and I = 0.0087 kg m2. The fitted parameters for each subject and their corresponding R2 values are reported in table 2. The fitted mass and moment of inertia values are close to the values reported in the literature for the brain, indicating the physical relevance of the model [19,23]. It should be noted that while this simple model is not anatomically detailed, it closely represents the coupled motion of the brain and skull observed in vivo, whereas physical parameters such as mass and inertia are preserved and the compliance of the brain–skull interface (subarachnoid space, bridging veins and trabeculae) is represented by the torsional spring-damper. An advantage of the model developed above is that while it captures the dynamic properties of the brain–skull system, it is based on the rolling kinematics of the brain, i.e. how the motion of the brain is coupled in various DOF.
Table 2.
Temporal dynamic model parameters fitted to MRI experimental data.
| k (Nm rad−1) | c (Nms rad−1) | m (kg) | I (kgm2) | R2 | |
|---|---|---|---|---|---|
| subject 1 | 157.06 | 0.17 | 1.39 | 0.0034 | 0.91 |
| subject 2 | 174.83 | 0.70 | 1.27 | 0.0071 | 0.73 |
| subject 3 | 148.92 | 0.62 | 1.37 | 0.0042 | 0.62 |
| average | 160.27 | 0.50 | 1.34 | 0.0049 |
To estimate the accuracy of the model's predictions, we calculated the error introduced at each stage of added modelling constraint: unconstrained kinematics (3DOF), constrained kinematics (1DOF) and constrained dynamics (1DOF). We calculated the distance errors between every experimental nodal value in MRI and the corresponding model prediction through all time steps for all three subjects. While the median error increases slightly for each stage of added constraint (from 10% to 12% median error values), the overall performance for all three stages is very good (figure 3b). Figure 3c–e shows a representative temporal fit for the constrained dynamic model to 1DOF brain motion kinematics for subject 1, where a primary frequency mode is apparent.
2.4. Frequency analysis
In order to study the frequency response of the brain–skull system, we reduced the 1DOF dynamic model to a linear single-input–single-output (SISO) system, by using PCA on the skull motion and assuming an equivalent stiffness, damping and torque in the constrained dynamic equations of motion (electronic supplementary material, Frequency modelling section). This step is feasible given the coupling between the DOF for both the brain and skull. We calculated the model's transmissibility function (the amplification of system response as a function of the input) by taking the skull rotational acceleration (θ¨s) as the input and relative brain rotation (θb) as the output (electronic supplementary material, equation (A 11)). The experimental measurements showed a distinct resonance (ωn) around 15 Hz with a 5- to 12-fold amplification in the relative brain–skull motion for non-dimensionalized output 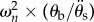 (figure 4).
(figure 4).
Figure 4.
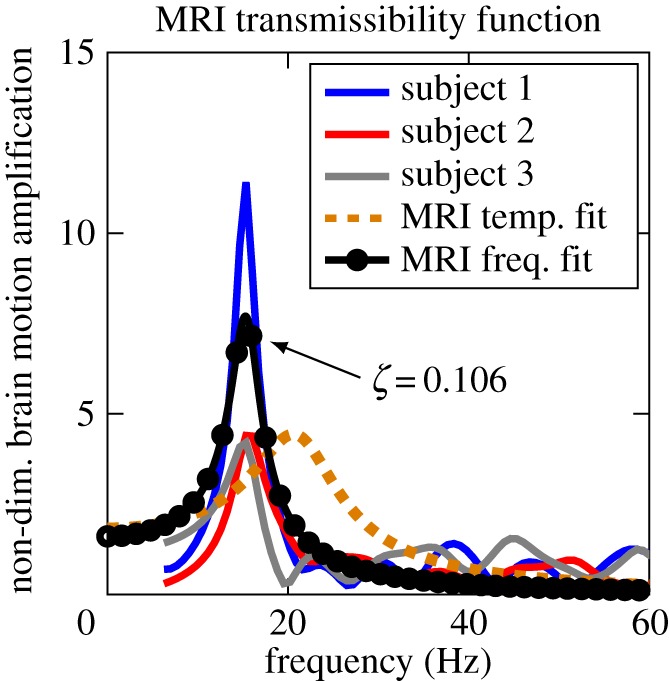
Resonance frequency: non-dimensionalized frequency domain fit of (electronic supplementary material, equation (A 11)) based on the empirical transmissibility amplitudes of MRI data for the three subjects. The low damping ratio (ζ) indicates under-damped oscillation and possible resonance in relative brain motion. As a reference, the temporal fit to the dynamic model is also shown. (Online version in colour.)
Although the dynamic parameters determined in the time domain above are expected to represent the system in the frequency domain as well, in order to study the system's frequency behaviour, it is customary to fit the parameters to the frequency response of the system. Therefore, we re-fitted the stiffness and damping parameters in the SISO model to match the experimental transmissibility functions based on MRI data, which resulted in k = 83.59 Nm rad−1 and c = 0.18 Nms rad−1. The frequency fit (marked as MRI frequency fit) closely replicates the experimental transmissibility function (figure 4). The transmissibility function calculated using the parameters from the time-domain fit (marked as MRI temporal fit) also shows a similar trend with a small difference in resonance frequency prediction, which might be due to the linearization of the transmissibility function as detailed in the electronic supplementary material, Frequency modelling section (figure 4). The 95% CI for the resonance frequency (ωn = 15 ± 2.9 Hz) is smaller than the uncertainties owing to the data acquisition time in the MRI study, indicating that the model is a good predictor of the brain's response.
2.5. Verification of one degree of freedom dynamic model with post-mortem human subjects measurements
In this section, we verify the 1DOF dynamic model both in frequency and time domains with brain displacement data derived from X-ray measurements during PMHS head impacts [25]. This step is crucial to examine the applicability of our model to loadings that are more representative of typical on-field head impacts. We used the neutral density target (NDT) displacement data from a test performed in the sagittal plane, which resulted in maximum linear and rotational accelerations of 20 g and 2000 rad s−2, respectively. Given the slightly higher density of the brain compared with the cerebrospinal fluid (CSF) and possible sinking in the inverted PMHS, we re-fitted the brain's kinematic path parameters for PMHS (figure 5a). Assuming symmetry of forces, we used the same dynamic parameters as determined from the in vivo data. Using the PMHS skull kinematics as input, we simulated the PMHS brain motion and observed similar resonating behaviour in the PMHS experimental data as was observed in the MRI data. Contrary to the MRI modelling predictions, the PMHS data in the frequency domain were better replicated by the MRI dynamic fit than the MRI frequency fit (figure 5b). Several factors might cause the discrepancy in the maximum amplification frequency in the brain response between the MRI and PMHS measurements, including variations in experimental protocols or changes in the material properties of the ex vivo tissue. Finally, as an additional step to verify the predictions of the constrained dynamic model, we compared its predictions with simulated injury monitor (SIMon) software, which is an FE model of the human head developed and used by the US National Highway Traffic and Safety Administration [29]. Despite the much fewer degrees of the freedom, the 1DOF model developed in this study fared well. The details of this verification are reported in electronic supplementary material, Model verification section (electronic supplementary material, figure S9).
Figure 5.
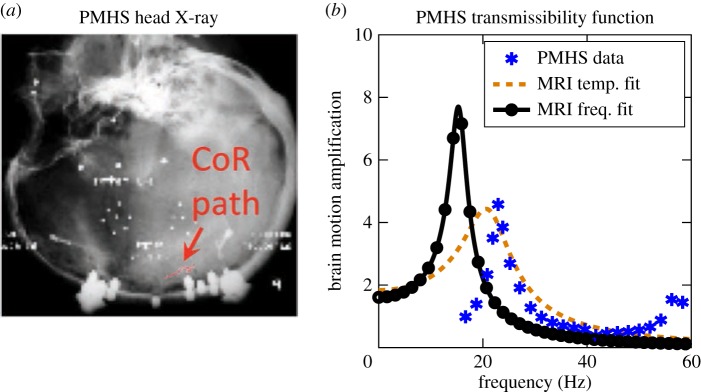
Model consistency verification with PMHS impact experiments: (a) X-ray of PMHS head with inserted NDTs (protocol C755-T2) in [25], (b) comparison of the frequency response of relative brain rotation using temporal and frequency domain fits to MRI data against PMHS measurements. Image in (a) is adopted from [25]. (Online version in colour.)
3. Discussion
We have developed the first reduced-order dynamical brain model based on in vivo human data. Owing to research ethics considerations, it is not yet possible to acquire in vivo brain data from concussive-level impacts. Thus, we developed our model based on mild impacts in an MRI study and subsequently investigated the applicability of the model in moderate impacts using PMHS brain displacement data. Our analysis of these datasets revealed that relative brain motion owing to head impacts can be described by an under-damped second-order system with linear dynamics that is driven to resonance at around 15 Hz. While modal behaviour of the brain was not the primary focus of most of previous lumped-parameter models, the reported or calculated values for natural frequency were either much smaller (less than 5 Hz) [20] or much greater than (more than 50 Hz) the values reported above [22,23].
In another study, we have collected head kinematic measurements from a number of contact sports using an instrumented mouthguard capable of recording 6DOF motion [30,31]. Our field data indicate that skull rotation is primarily in the sagittal plane for more than 60% of the head–head collisions. For these impacts, the median values for the distribution of peak linear and rotational acceleration vectors in on-field head exposures were 20 g and 1700 rad s−2. The MRI (1.5 g and 140 rad s−2) and PMHS (20 g and 2000 rad s−2) studies covered low to median range of on-field exposures (figure 6a). Of 445 field football head impacts, we selected 267 impacts where sagittal rotation was dominant (the sagittal component in rotational acceleration had the largest contribution to the peak magnitude of acceleration). With these impacts, we performed a fast Fourier transform (FFT) on the sagittal rotational acceleration time trace. The 100 ms time trace, sampled at 1000 Hz, was padded with 100 zeros to increase the resolution for the FFT. The frequency with the largest FFT amplitude was identified as the primary frequency of the impact. Analysing sagittal head rotations showed that the primary frequency mode (63% of all sagittal impacts) is 15–25 Hz (figure 6b). The striking uniformity of impacts oscillating around 20 Hz indicates that a substantial portion of sports head impacts are exciting a mechanical resonance of the skull–brain system and causing amplified skull–brain relative motions. In previous studies using our instrumented mouthguard, we showed that the natural frequency of the mouthguard is around 150 Hz and that head impacts had much higher energy levels at lower frequencies, suggesting that the measured frequency content has not been biased by the instrumentation [30,32]. The above information again prompts the long-ignored question: can mechanical resonance lead to mTBI?
Figure 6.
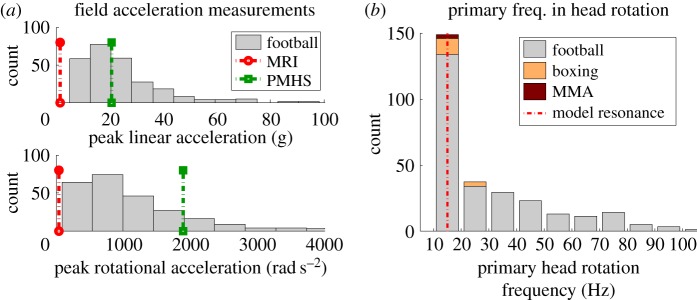
Field measurements of head impact kinematics: (a) comparison of translational (top) and rotational (bottom) input levels for MRI and PMHS studies against field measurements, (b) histogram of primary frequencies in rotational acceleration from field measurements. (Online version in colour.)
Although this simple model does not detail the tissue level stress and strains that are linked to trauma [33–35], there is evidence that relative brain motion can cause trauma. Several studies have employed Lucite and Lexan calvaria and high-speed cinematography to study relative brain–skull motion and resulting pathology [36–38]. Ommaya et al. [39] and Gosch et al. [40] observed minimal deformation associated with concussion, but large relative movement between the brain and skull correlated with contusions and contrecoup injuries. They suggested that damage occurred as a consequence of interference of structures moving at different rates. The brain is largely suspended in CSF and is connected to the skull only through a few nerves, vessels and the brain stem. As the skull rotates, these tethers allow the brain to lag behind and only when they are sufficiently stretched to overcome the brain's inertia, does the brain move to catch up to the skull. These tether forces spread throughout the brain, propagating from the outer grey matter to the inner white matter and into the deep structures of the brain. As explained by the centripetal theory [15], axonal injury by shear requires relative brain–skull motion and the transfer of forces from external vessels and nerves.
Despite good agreement with experimental data, there are several limitations associated with our proposed model. First, among the sagittal test protocols in the PMHS study [25], we compared our results against low-severity impacts (approx. 20 g), which is close to the median head acceleration range for soccer headers and football head impacts [41]. Although we compared our model's predictions against the medium-energy impacts, it is likely that the model might under-perform against the more severe impacts (more than 40 g) as more brain deformation is expected to occur [23,42]. Therefore, the current model is limited to mild and subconcussive head exposures. In addition, the derived transmissibility function is based on the linearization of the dynamical model assuming small relative rotations of the brain. To determine the complete spectrum of brain–skull frequency responses, it is necessary to evaluate the fully nonlinear dynamical model. Owing to the shorter data acquisition time in the PMHS studies (60 ms compared with 168 ms in MRI), resolution in the low-frequency domain is much lower than the MRI study, which emphasizes the importance of developing the model based on the in vivo MRI data. An additional limitation is that this model is developed based on measurements in the sagittal plane. A general model capable of simulating the response of the brain to an arbitrary load in an arbitrary direction would require a more sophisticated approach. For example, due to the presence of falx cerebri, it is expected that during head motions in coronal and transverse planes, the rigid-body approximation would perform less accurately [43]. However, we expect that a similar reduced-order modelling approach could be employed even in these anatomical planes [44].
We observed different kinematics between brain motions in MRI and PMHS. Previously, it was shown that gravity plays a major role in the displacement of the pons in different head orientations [45]. In accordance, our findings suggest that the brain might not be floating in CSF and instead might be sinking to the bottom owing to the different orientation in the two experiments and the difference, albeit minimal, in the density of brain tissue and CSF. Furthermore, the frequency response of MRI and PMHS studies were slightly different, which could be a result of the physiological and mechanical changes in ex vivo tissue properties [46]. The dehydration and re-hydration that occur post-mortem, which cause brain tissue to show slightly stiffer behaviour and thus higher frequencies. Also as mentioned by the authors, the biggest concern in terms of preparing the ex vivo specimens was the skull–brain coupling and evacuation of gases that occupy the intracranial space post-mortem, as air bubbles beneath the tentorium might affect this coupling [25].
For the available data from MRI and PMHS experiments, the skull's translation and rotation were not separately studied, which is difficult owing to existence of neck and high coupling between the two modes of motion. However, this might be important because it is not yet clear whether the kinematics of brain motion will remain constrained for different loading conditions, and therefore we cannot definitively say whether the skull's rotation or translation drives brain motion in general. Because on-field exposures may exhibit a range of translational and rotational head motion that are not identically coupled, more experimental measurements are required to separate the effect of each input on the motion of the brain.
Our finding that head impacts in sports may cause amplified brain–skull relative motion leads to a different perspective on the possible cause of repetitive brain trauma and as such, would require a different injury metric and criterion. Some traditional injury risk predictors such as head injury criterion (HIC) are focused primarily on focal injuries. Such metrics take both the magnitude and duration of impacts into account. However, because the timescale in these injury criteria is very small (e.g. 15 ms for HIC [47]), they typically predict injury risk to monotonically increase as magnitude and duration increase. In contrast, our findings suggest a dangerous frequency—close to typical on-field impact frequencies—around which relative brain motion is maximized. To explore this further, we simulated relative brain motion as a result of skull motion, using the sinc function with various amplitudes and frequencies. The results indicated that even for mild impacts, if the impact frequency is at or close to resonance, significant brain–skull relative motion could occur (figure 7). The median values of football impacts are superimposed on the contours for comparison. As can be seen, towards the lower end of the frequency spectrum (less than 20 Hz), which includes most football impacts, the contours are vertical. This indicates that relative brain motion is highly sensitive to skull motion frequency and less sensitive to the amplitude of skull acceleration. It should be noted that while here we describe a model of rigid body motion, it is probably local tissue deformation that is responsible for injury throughout the brain. An implicit hypothesis here is that this deformation is tightly coupled to the rigid body motion of the brain relative to the skull, which would require further investigation. Furthermore, bulk motion of the brain can cause stretching and tension in the bridging veins and cause dysfunction and pathology in blood–brain barrier, which have recently been linked to neurodegeneration [48].
Figure 7.
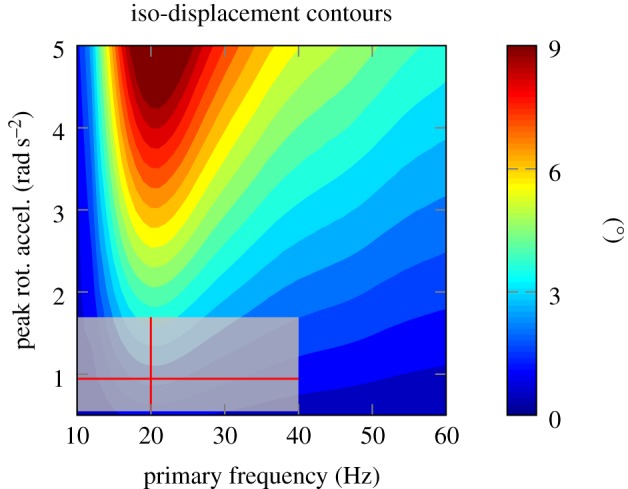
Implications of the results: contour plots of constant relative motion of brain as a function of skull's rotational acceleration amplitude and frequency based on simulated skull motion (sinc function with parameter sweep in frequency and amplitude). As we move towards lower frequencies on the left, relative brain motion shows more sensitivity to changes in frequency than peak rotational acceleration. The interquartile range of football head impacts is also shown as box plot in two dimensions for comparison.
In unpublished measurements of un-helmeted soccer headers, we have observed similar head motion frequency content of less than 20 Hz. This consistency between helmeted and un-helmeted head motions indicates that specific motions of the head may be primarily owing to head–neck anatomy rather than exposure amplitudes. Above results may not be limited to contact sports and could be applied to other activities involving cyclic head motions, e.g. off-road vehicles, machining operations, jackhammer, etc. As such, rigorous study of the body as a whole and its effect on head kinematics is required.
In summary, this study puts forth a reduced-order model of brain motion in low to moderate energy head impacts. Giving similar error levels compared to much more detailed FE models while significantly reducing computational cost (albeit for the macroscopic behaviour of brain), it allows real-time calculation and possibly automated screening on the field, as well as exhaustive equipment design optimizations. The dynamic model proposed here can be crucial for physical intuition regarding the underlying mechanics of brain motion as it can be used when performing sensitivity analysis and developing preventative and diagnostic technologies. The results of this study of the frequency response of the brain raise a fundamentally new possibility to devise better safety standards and design protective equipment to protect the brain from repeated head impacts.
Supplementary Material
Acknowledgements
We thank Dr Philip Bayly for sharing the MRI data.
Competing interests
We declare we have no competing interests.
Funding
The study was supported by the National Institutes of Health (NIH) National Institute of Biomedical Imaging and Bioengineering (NIBIB) 3R21EB01761101S1, David and Lucile Packard Foundation 38454, Child Health Research Institute-Transdisciplinary Initiatives Programme, and NIH UL1 TR000093 for biostatistics consultation.
References
- 1.Faul M., Xu L, Wald MM, Coronado VG. 2010. Traumatic brain injury in the United States. Atlanta, GA: Centers for Disease Control and Prevention, National Center for Injury Prevention and Control. [Google Scholar]
- 2.MacDonald CL, Johnson AM, Nelson EC, Werner NJ, Fang R, Flaherty SF, Brody DL. 2014. Functional status after blast-plus-impact complex concussive traumatic brain injury in evacuated United States military personnel. J. Neurotrauma 31, 889–898. ( 10.1089/neu.2013.3173) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Garrick JG. 2005. Unreported concussion in high school football players. Clin. J. Sport Med. 15, 385; author reply 385 ( 10.1097/01.jsm.0000181438.48892.1b) [DOI] [PubMed] [Google Scholar]
- 4.Williamson IJS, Goodman D. 2006. Converging evidence for the under-reporting of concussions in youth ice hockey. Brit. J. Sports Med. 40, 128–132; discussion 128–32 ( 10.1136/bjsm.2005.021832) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Bazarian JJ, Zhu T, Blyth B, Borrino A, Zhong J. 2012. Subject-specific changes in brain white matter on diffusion tensor imaging after sports-related concussion. Magn. Reson. Imaging 30, 171–180. ( 10.1016/j.mri.2011.10.001) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Breedlove E, Robinson M. 2012. Biomechanical correlates of symptomatic and asymptomatic neurophysiological impairment in high school football. J. Biomech. 45, 1265–1272. ( 10.1016/j.jbiomech.2012.01.034) [DOI] [PubMed] [Google Scholar]
- 7.Bazarian JJ, et al. 2014. Persistent, long-term cerebral white matter changes after sports-related repetitive head impacts. PLoS ONE 9, e94734 ( 10.1371/journal.pone.0094734) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Talavage TM, Nauman EA, Breedlove EL, Yoruk U, Dye AE, Morigaki KE, Feuer H, Leverenz LJ. 2014. Functionally-detected cognitive impairment in high school football players without clinically-diagnosed concussion. J. Neurotrauma 31, 327–338. ( 10.1089/neu.2010.1512) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Carman AJ, et al. 2015. Expert consensus document: mind the gaps—advancing research into short-term and long-term neuropsychological outcomes of youth sports-related concussions. Nat. Rev. Neurol. 11, 230–244. ( 10.1038/nrneurol.2015.30) [DOI] [PubMed] [Google Scholar]
- 10.Giza C, Hovda D. 2001. The neurometabolic cascade of concussion. J. Athl. Train. 36, 228. [PMC free article] [PubMed] [Google Scholar]
- 11.Prins ML, Alexander D, Giza CC, Hovda DA. 2013. Repeated mild traumatic brain injury: mechanisms of cerebral vulnerability. J. Neurotrauma 30, 30–38. ( 10.1089/neu.2012.2399) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Nahum AM, Melvin J. 2001. Accidental injury: biomechanics and prevention, 2nd edn, vol. 119 Springer Science & Business Media. [Google Scholar]
- 13.Gwin JT, Chu JJ, Diamond SG, Halstead PD, Crisco JJ, Greenwald RM. 2010. An investigation of the NOCSAE linear impactor test method based on in vivo measures of head impact acceleration in American football. J. Biomech. Eng. 132, 011006. [DOI] [PubMed] [Google Scholar]
- 14.Sosin D, Sniezek J, Waxweiler R. 1995. Trends in death associated with traumatic brain injury, 1979 through 1992, success and failure. JAMA 273, 9–11. ( 10.1001/jama.1995.03520460060036) [DOI] [PubMed] [Google Scholar]
- 15.Ommaya AK, Gennarelli TA. 1974. Cerebral concussion and traumatic unconsciousness. Brain 97, 633–654. ( 10.1093/brain/97.1.633) [DOI] [PubMed] [Google Scholar]
- 16.Gennarelli TA. 2014. Future directions in brain injury research. Prog. Neurol. Surg. 28, 243–250. ( 10.1159/000358788) [DOI] [PubMed] [Google Scholar]
- 17.Hirsch A, Ommaya A, Mahone R. 1968. Tolerance of subhuman primate brain to cerebral concussion. Tech. Report, 2876. Washington, DC: Department of the Navy Naval Ship Research and Development Center. [Google Scholar]
- 18.Hakansson B, Brandt A, Carlsson P. 1988. Resonance frequencies of the human skull in vivo. J. Acoust. Soc. Am. 95, 1474–1481. ( 10.1121/1.408535) [DOI] [PubMed] [Google Scholar]
- 19.Stalnaker RL, Fogle JL, McElhaney JH. 1971. Driving point impedance characteristics of the head. J. Biomech. 4, 127–139. ( 10.1016/0021-9290(71)90023-6) [DOI] [PubMed] [Google Scholar]
- 20.Alem NM. 1974. Simulation of head injury due to combined rotation and translation of the brain. SAE Technical Paper 741192 Warrendale, PA: SAE; ( 10.4271/741192) [DOI] [Google Scholar]
- 21.Low T, Stalnaker R. 1987. A lumped parameter approach to simulate the rotational head motion. Int. Res. Council on Biokinetics Impacts (IRCOBI) 15, 203–215. [Google Scholar]
- 22.Willinger R, Taleb L, Kopp C. 1995. Modal and temporal analysis of head mathematical models. J. Neurotrauma 12, 743–754. ( 10.1089/neu.1995.12.743) [DOI] [PubMed] [Google Scholar]
- 23.Zou H, Kleiven S, Schmiedeler JP. 2007. The effect of brain mass and moment of inertia on relative brain–skull displacement during low-severity impacts. Int. J. Crashworthiness 12, 341–353. ( 10.1080/13588260701433024) [DOI] [Google Scholar]
- 24.Feng Y, Abney TM, Okamoto RJ, Pless RB, Genin GM, Bayly PV. 2010. Relative brain displacement and deformation during constrained mild frontal head impact. J. R. Soc. Interface 7, 1677–1688. ( 10.1098/rsif.2010.0210) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Hardy WN, Foster CD, Mason MJ, Yang KH, King AI, Tashman S. 2011. Investigation of head injury mechanisms using neutral density technology and high-speed biplanar X-ray. Stapp Car Crash J. 45, 337–368. [DOI] [PubMed] [Google Scholar]
- 26.Kleiven S, Hardy WN. 2002. Correlation of an FE model of the human head with local brain motion—consequences for injury prediction. Stapp Car Crash J. 46, 123–124. [DOI] [PubMed] [Google Scholar]
- 27.Sullivan S, Eucker SA, Gabrieli D, Bradfield C, Coats B, Maltese MR, Lee J, Smith C, Margulies SS. 2014. White matter tract-oriented deformation predicts traumatic axonal brain injury and reveals rotational direction-specific vulnerabilities. Biomech. Model. Mechanobiol., pp. 1–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Abney TM, Feng Y, Pless R, Okamoto RJ, Genin GM, Bayly PV. 2011. Principal component analysis of dynamic relative displacement fields estimated from MR images. PLoS ONE 6, e22063 ( 10.1371/journal.pone.0022063) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Takhounts EG, Eppinger RH, Campbell JQ, Tannous RE, Power ED, Shook LS. 2003. On the development of the SIM on finite element head model. Stapp Car Crash J. 47, 107–133. [DOI] [PubMed] [Google Scholar]
- 30.Camarillo D, Shull P, Mattson J. 2012. An instrumented mouthguard for measuring linear and angular head impact kinematics in American football. Ann. Biomed. Eng. 41, 1939–1949. ( 10.1007/s10439-013-0801-y) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Hernandez F, Wu LC, Yip MC, Laksari K, Hoffman AR, Lopez J, Grant G, Kleiven S, Camarillo DB. 2014. Six degrees of freedom measurements of human mild traumatic brain injury. Ann. Biomed. Eng., pp. 1–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Wu L, Zarnescu L, Nangia V, Cam B, Camarillo D. 2014. A head impact detection system using SVM classification and proximity sensing in an instrumented mouthguard. IEEE Trans. Biomed. Eng. 9294, 1–11. [DOI] [PubMed] [Google Scholar]
- 33.Kleiven S. 2007. Predictors for traumatic brain injuries evaluated through accident reconstructions. Stapp Car Crash J. 51, 81–114. [DOI] [PubMed] [Google Scholar]
- 34.Takhounts EG, et al. 2008. Investigation of traumatic brain injuries using the next generation of simulated injury monitor (SIMon) finite element head model. Stapp Car Crash J. 52, 1–31. [DOI] [PubMed] [Google Scholar]
- 35.Weaver AA, Danelson KA, Stitzel JD. 2012. Modeling brain injury response for rotational velocities of varying directions and magnitudes. Ann. Biomed. Eng. 40, 2005–2018. ( 10.1007/s10439-012-0553-0) [DOI] [PubMed] [Google Scholar]
- 36.Pudenz R, Shelden C. 1946. The lucite calvarium—a method for direct observation of the brain. J. Neurosurg. 3, 487–505. ( 10.3171/jns.1946.3.6.0487) [DOI] [PubMed] [Google Scholar]
- 37.Shatsky SA, Evans DE, Miller F, Martins AN. 1974. High-speed angiography of experimental head injury. J. Neurosurg. 41, 523–530. ( 10.3171/jns.1974.41.5.0523) [DOI] [PubMed] [Google Scholar]
- 38.Stalnaker RL, Melvin JW, Nusholtz GS, Alem NM, Benson JB. 1997. Head impact response. SAE Technical Paper 770921 Warrendale, PA: SAE; ( 10.4271/770921) [DOI] [Google Scholar]
- 39.Ommaya A, Boretos J, Beile E. 1969. The Lexan calvarium: an improved method for direct observation of the brain. J. Neurosurg. 30, 25–29. [DOI] [PubMed] [Google Scholar]
- 40.Gosch H, Gooding E, Schneider R. 1060. Distortion and displacement of the brain in experimental head injuries. Surg. Forum 20, 425–426. [PubMed] [Google Scholar]
- 41.Naunheim RS, Bayly PV, Standeven J, Neubauer JS, Lewis LM, Genin GM. 2003. Linear and angular head accelerations during heading of a soccer ball. Med. Sci. Sports Exercise 35, 1406–1412. ( 10.1249/01.MSS.0000078933.84527.AE) [DOI] [PubMed] [Google Scholar]
- 42.Zou H, Schmiedeler JP, Hardy WN. 2007. Separating brain motion into rigid body displacement and deformation under low-severity impacts. J. Biomech. 40, 1183–1191. ( 10.1016/j.jbiomech.2006.06.018) [DOI] [PubMed] [Google Scholar]
- 43.Margulies SS, Thibault LE, Gennarelli TA. 1990. Physical model simulations of brain injury in the primate. J. Biomech. 23, 823–836. ( 10.1016/0021-9290(90)90029-3) [DOI] [PubMed] [Google Scholar]
- 44.Zou H, Schmiedeler J. 2008. Predicting brain injury under impact with a strain measure from analytical models. Int. J. Crashworthiness 13, 337–348. ( 10.1080/13588260801943047) [DOI] [Google Scholar]
- 45.Ji S, Margulies SS. 2007. In vivo pons motion within the skull. J. Biomech. 40, 92–99. ( 10.1016/j.jbiomech.2005.11.009) [DOI] [PubMed] [Google Scholar]
- 46.Gefen A, Margulies S. 2004. Are in vivo and in situ brain tissues mechanically similar? J. Biomech. 37, 1339–1352. ( 10.1016/j.jbiomech.2003.12.032) [DOI] [PubMed] [Google Scholar]
- 47.Versace J. 1971. A review of the severity index. SAE Technical Paper 710881 Warrendale, PA: SAE; ( 10.4271/710881) [DOI] [Google Scholar]
- 48.Weissberg I, Veksler R, Kamintsky L, Saar-Ashkenazy R, Milikovsky D, Shelef I, Friedman A. 2014. Imaging blood–brain barrier dysfunction in American football players. JAMA Neurol. 1453–1455. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.