Abstract
Every newly trained surgeon performs her first unsupervised operation. How do the health outcomes of her patients compare with the patients of experienced surgeons? Using data from 498 hospitals, we compare 1252 pairs comprised of a new surgeon and an experienced surgeon working at the same hospital. We introduce a new form of matching that matches patients of each new surgeon to patients of an otherwise similar experienced surgeon at the same hospital, perfectly balancing 176 surgical procedures and closely balancing a total of 2.9 million categories of patients; additionally, the individual patient pairs are as close as possible. A new goal for matching is introduced, called “refined covariate balance,” in which a sequence of nested, ever more refined, nominal covariates is balanced as closely as possible, emphasizing the first or coarsest covariate in that sequence. A new algorithm for matching is proposed and the main new results prove that the algorithm finds the closest match in terms of the total within-pair covariate distances among all matches that achieve refined covariate balance. Unlike previous approaches to forcing balance on covariates, the new algorithm creates multiple paths to a match in a network, where paths that introduce imbalances are penalized and hence avoided to the extent possible. The algorithm exploits a sparse network to quickly optimize a match that is about two orders of magnitude larger than is typical in statistical matching problems, thereby permitting much more extensive use of fine and near-fine balance constraints. The match was constructed in a few minutes using a network optimization algorithm implemented in R. An R package called rcbalance implementing the method is available from CRAN.
Keywords: Fine balance, network optimization, optimal matching, sparse networks
1 Introduction: Matching within natural blocks
1.1 What are natural blocks?
In observational studies of treatment effects, we often wish to compare treated and control subjects from the same natural block. Familiar examples of natural blocks are twins, siblings, surgical patients in the same hospital, or students in the same school. Important unmeasured covariates may be more similar within a natural block than between blocks: the genes of siblings; the nursing staff and intensive care unit in the same hospital; the teaching staff and socioeconomic conditions within the same school.
There can be a tension between the desire to compare treated and control individuals within natural blocks and the desire to compare treated and control groups with similar distributions of measured covariates. In our study in §3 comparing new and experienced surgeons, there are 1252 natural blocks of a new and experienced surgeon performing similar types of surgery working in the same hospital. Additionally there are many categories of measured covariates, including 176 surgical procedures, ultimately nearly 2.9 million categories defined by measured covariates. With many categories, it is difficult if not impossible to find similar patients inside the same natural block.
Attempts to balance many covariates by pairing individuals who are nearly identical almost invariably fail because nearly identical people do not exist. This is illustrated in Zubizarreta et al (2011, Table 6; 2014, §2.4) where close individual pairs are not available but covariate balance is attainable. Matching for a scalar propensity score can balance many covariates such as age or gender, but this approach can perform poorly with sparse nominal covariates having many categories, for instance the 176 surgical procedures and their interactions with comorbidities. Like randomization, matching on propensity scores balances covariates stochastically with the aid of the law of large numbers, whereas a nominal covariate with many categories may have small sample sizes in most categories.
Our algorithm pairs patients within a natural block, trying to pick individual pairs that are close on covariates. There is a limit to what can be achieved by finding individually close pairs on many variables, so a separate effort is made to balance distributions of covariates when individuals within a pair may differ. The approach comes as close as possible to balance for a sequence of nested nominal variables, starting with the 176 surgical procedures, gradually subdividing these 176 categories to finally reach nearly 2.9 million categories involving comorbidities and admission source, obtaining the best possible balance at each successive stage of the subdivision. This new objective, “refined covariate balance,” is defined in §4.4, where it is proved in Theorem 6 that our new network optimization algorithm yields a minimum distance match subject to the constraint of refined covariate balance. This new approach is made practical by exploiting network sparsity.
1.2 Natural blocks and network sparsity
Optimal matching in observational studies (Rosenbaum 1989; Hansen 2007) is often implemented using network optimization, a collection of mathematical and computational techniques originally developed to solve problems in operations research; see the review of network optimization in § 4.3. A network is a set of nodes together with a set of directed edges or ordered pairs of nodes. Think of the nodes as subjects and the edges as candidate pairings of two subjects. A network with N nodes might have N2 edges with loops or N (N − 1) edges if with no loops; that is, it might have O(N2) edges as N → ∞ and in this case the network is said to be dense. A network is said to be sparse if the number of edges is O (N) rather than O (N2). Matching within natural blocks, such as within hospital-surgeon-pairs, drastically restricts the number of permitted pairings of patients, resulting in a sparse network. The time and space required for optimization is much greater in dense than in sparse networks (e.g., Korte and Vygen 2008, Theorem 9.17).
Typical uses of optimal matching in observational studies do not exploit sparsity, in part because a network defined by measured covariates without natural blocks is likely to be dense. A program such as Hansen’s (2007) optmatch package in R can match thousands of individuals at once in a dense network. In current practice, if a problem has many more than thousands of individuals, then it is divided into smaller problems each consisting of thousands of individuals by matching exactly for several important covariates. This strategy often works well for measured covariates. However, with natural blocks, there may be relatively few choices within blocks, so more of the work needs to be done through balancing covariate distributions. By working with a network that is naturally sparse because of natural blocks, we are able to match hundreds of thousands of individuals at once, thereby making much more effective use of balancing techniques.
1.3 Outline: an example; a new objective; a new algorithm; the benefits of sparsity
The surgical example is discussed in §3 and §5. The general problem is described informally in §2 and developed precisely in §4. All new results and methods are contained in §4. Notation is introduced in §4.1, key concepts such as refined balance are defined in §4.2, and existing literature on network optimization is briefly reviewed in §4.3. The matching network for refined balance is defined in §4.4. The main theorem in §4.5 says that a minimum cost flow in the network defined in §4.4 is the closest possible match that exhibits refined balance while respecting the natural blocks. Sparsity is discussed in §4.7. The discussion in §6 considers how the proposed methods might be applied in other contexts.
For discussion of matching, see Baiocchi et al. (2012), Hansen et al. (2006, 2007), Heller et al. (2009), Lu et al. (2011), Rosenbaum (1989, 2010), Rosenbaum and Rubin (1985), Stuart (2010), Yang et al. (2012), and Zubizarreta et al. (2011, 2014). For recent applications of optimal matching, see Silber et al. (2013) and Neuman et al. (2014).
2 Abstract problem; intuition behind its solution; other applications
2.1 The abstract problem: refined balance in a sparse match
In a sparse matching problem, each treated subject has a short list of potential controls. When there are natural blocks, this short list consists of controls from the same block; however, sparse networks arise or can be produced in other ways; see §6.2. As the sample size increases, the length of the list of potential controls for each given treated subject does not increase. As you add more and more families or schools or hospitals or zip codes to the study, you have more and more subjects to match, but individual families or schools or hospitals or zip codes do not become larger. If the number of blocks increases in constant proportion to the increase in total sample size, then block effects are not consistently estimable without assumptions about their form (Kiefer and Wolfowitz 1956, p. 888); however, it is possible to match within blocks.
In addition to picking for each treated subject a control from the short list of candidates, the matching must balance many observed covariates. We would be satisfied if the balance on observed covariates after matching were similar to the balance on observed covariates in a completely randomized experiment, but this may not be possible in an observational study. Randomization also balances unmeasured covariates whereas matching for observed covariates cannot be expected to do this.
Because the list of candidate controls for a given treated subject is short, it is rarely possible to find a control on the short list who is identical to the treated subject with respect to many covariates. So the matching algorithm tolerates a mismatch in one pair providing it can counterbalance that mismatch in another pair. If it is necessary to match a treated male to a control female in one block, then a treated female will be matched to a control male in another block, so the final treated and control groups have exactly the same number of males and the same number of females. Exact counterbalancing is called “fine balance”; see Rosenbaum, Ross and Silber (2007). Fine balance means that the marginal distribution of a categorical covariate is exactly the same in treated and control groups, and in the surgical example the 176 surgical procedures are finely balanced. Counterbalancing is a familiar strategy in experimental design, for example in Latin square designs or crossover designs. Sometimes exact fine balance is not achievable: for instance, it is not possible in the surgical example to exactly balance all 2.9 million categories of patients. “Near fine balance” means that the marginal distributions of a categorical covariate in matched samples are “as close as possible” to fine balance given the data available; see Yang et al. (2012). In defining near fine balance, one may define “as close as possible” in various ways, but one natural and familiar measure is the total variation distance, the sum of the absolute treated-minus-control differences in category percents. See Arratia et al. (1990, §3) for several attractive equivalent definitions of the total variation distance. If the matched treated group is 51% male and the matched control group is 49% male, then the total variation distance in gender is |0.51 – 0.49|+|0.49 – 0.51| = 0.04 reflecting the 2% mismatch for males plus the corresponding 2% mismatch for females. One form of near fine matching minimizes the total variation distance in matched samples, and it achieves exact fine balance whenever this is achievable.
Refined balance is an extension of fine or near-fine balance. One defines a sequence of nested nominal variables, ν1, … , νK, so νk+1 subdivides νk. Refined balance comes as close as possible to fine balance for ν1, and among all matches that do that, it comes as close as possible to fine balance for ν2, and so on. In the surgical example, ν1 consists of the 176 surgical procedures and these are finely balanced, ν2 interacts the 176 surgical procedures with two types of hospital to make 352 categories for which the minimum total variation distance is 0.001 or one tenth of 1%, … , and νK for K = 6 has 2.9 million categories. Among all matched samples that exhibit refined covariate balance, the algorithm finds pairings from the short lists to minimize the total covariate distance within pairs.
2.2 Intuition behind the solution
In §4, the matching problem is represented by a network or directed graph. For each category of each of the nested nominal variables, νk, the network has two routes to a match. One route is free of charge, and a pair can take this route if it leaves this category balanced. The other route has a large toll or penalty, and a pair can take this route without balancing the category but must pay the penalty. The penalty for ν1 is much larger than for ν2, and so on. The objective function is the sum of all of these penalties plus the sum of the within-pair covariate distances. The penalization of certain paths is developed in detail in §4.4 and it involves a parameter ϒ. Network optimization minimizes this penalized objective function. If the penalties are both sufficiently large and sufficiently different for νk and νk+1, then they override all other considerations, producing refined balance. Among all matches that minimize the penalties, the optimal match minimizes the sum of the covariate distances. In the example, among matches that are equally good in terms of refined covariate balance, the algorithm tried to pair individuals with similar ages and estimated risks of death, two variables that were not explicitly balanced. Section 4 states the algorithm precisely and proves that it works.
Refined balance and sparsity are separate ideas that work well together. In a sparse network, it is difficult to find close individual pairs, and more of the work must be done by covariate balancing; hence, the attraction of refined balance for sparse problems. Conversely, balancing of rare categories is easier in very large problems, and computations for large problems require less computer time and storage if the problem is sparse; hence the attraction of sparsity for refined balance. Sparsity is discussed in §4.7.
3 Patient outcomes achieved by new and experienced surgeons
3.1 Background
Are the patient outcomes of newly trained surgeons comparable to the outcomes of experienced surgeons performing the same types of surgery at the same hospitals? If the typical patient of the typical new surgeon were instead treated by an experienced surgeon, would the patient’s outcomes be different? The data describe patients in Medicare in six states between 2004 and 2007 who had Medicare Part B, were not in a Medicare HMO, and had surgery performed at a hospital rather than on an out-patient basis at an ambulatory surgical center. Here, we look at 6260 patients of 1252 new surgeons and 6260 patients of 1252 experienced surgeons at the same hospitals, 5 patients per surgeon.
Surgical skill varies from surgeon to surgeon. Are the worst surgeons also the new surgeons? A typical hospital might have one new surgeon and a group of experienced surgeons. We expect that the performance of individual new surgeons will be more variable, more extreme, than the average performance of a group of experienced surgeons, simply because averages are more stable than individuals. Surgeons specialize, focusing on particular types of surgery, and the 30-day mortality rate following, say, elective orthopedic surgery is much lower than for some types of cancer surgery. These considerations, together with desire for a simple, transparent study design, led us to pair each new surgeon with an experienced surgeon performing similar types of surgery at the same hospital.
New surgeons gradually become experienced surgeons. As they become more experienced, they perform more surgery. Most of the population of patients of new surgeons are the patients of the most experienced of the new surgeons, but we are most interested in new surgeons when they are starting out, when most of their experience is from surgical training. For these reasons, we decided to give equal weight to each young surgeon, rather than weighting surgeons by the number of operations they performed. We considered only new and experienced surgeons who had performed at least five operations in our data. We sampled at random five surgical patients of each new surgeon as the treated group. For many newer new surgeons, five patients was a large part of the portion of the overlap of their surgical practice with our data. Our analysis describes the typical patient of the typical new surgeon, not the typical patient of new surgeons as a group, the latter being weighted towards the most experienced new surgeons.
3.2 Matching the patients of new and experienced surgeons within the same hospital
Surgical data are characterized by quite a bit of detail, much of it recorded in nominal variables. Using ICD-9 codes, we distinguish 176 surgical procedures (listed in Table 1 as Procedure). In addition, we distinguish among 498 hospitals, whose performance varies for reasons unrelated to surgical performance. Patients often have existing medical problems, called comorbidities, besides those treated by the current surgery, such as congestive heart failure (CHF) or chronic obstructive pulmonary disease (COPD), and these may increase the risk of death following surgery. We distinguish hospitals with many new surgeons or few new surgeons (Hospital Group). Patients are matched within surgeon pairs within the same hospital.
Table 1.
The K = 6 nominal variables νk that were balanced as closely as possible by the matching algorithm, where ν1 consists of L1 = 176 surgical procedures, and ν6 is the interaction of 176 surgical procedures with 14 binary covariates, making L6 = 176 × 211 categories, or about 2.9 million categories. An × indicates that the row variable contributes to nominal variable νk. The algorithm minimized the total imbalance for νk′ among all matches that minimized for νk for k < k′. The balance obtained by matching is much better than the best balance obtained in 10,000 simulated randomized experiments with the same marginal totals.
| Covariate | Levels | Nested nominal covariate,
νk k = 1, …, 6 |
|||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| Procedure | 176 | × | × | × | × | × | × |
| Hospital Group | 2 | × | × | × | × | × | |
| Male | 2 | × | × | × | × | ||
| ER-admit | 2 | × | × | × | × | ||
| Transfer | 2 | × | × | × | × | ||
| Paraplegia | 2 | × | × | × | |||
| Stroke | 2 | × | × | × | |||
| PPF | 2 | × | × | × | |||
| CC | 2 | × | × | ||||
| CHF | 2 | × | × | ||||
| Dementia | 2 | × | × | ||||
| Renal | 2 | × | × | ||||
| Liver | 2 | × | |||||
| Past A | 2 | × | |||||
| Past MI | 2 | × | |||||
|
| |||||||
| # Categories Lk | 176 = 176 | 176 × 2 = 352 | 176 × 24 = 2, 816 | 176 × 27= 22, 528 | 176 × 211= 360, 448 | 176 × 214 =2, 883, 584 | |
|
| |||||||
| Imbalance | 0 | 12 | 52 | 176 | 664 | 1242 | |
| % of maximum | 0.0% | 0.1% | 0.4% | 1.4% | 5.3% | 9.9% | |
| Independence χ2 | 0.0 | 4.9 | 43.3 | 142.3 | 588.9 | 1158.7 | |
|
| |||||||
| Balance in 10,000 simulated randomized experiments with the same margins | |||||||
|
| |||||||
| Simulated χ2 statistics for independence | |||||||
|
| |||||||
| Mean χ2 | 174.9 | 302.9 | 767.5 | 1062.0 | 1946.0 | 2814.0 | |
| Minimum χ2 | 117.0 | 226.5 | 645.7 | 933.6 | 1777.0 | 2645.0 | |
|
| |||||||
| Simulated Total Imbalance | |||||||
|
| |||||||
| Mean | 768 | 1051 | 1749 | 2086 | 3010 | 3812 | |
| Minimum | 540 | 814 | 1500 | 1826 | 2752 | 3578 | |
Table 1 lists covariates that structure the match, and additional covariates appear in Table 2. Table 1 includes notation that will be defined in §4. In the rows of Table 1, there are 15 nominal covariates, making 176 × 214 or about 2.9 million categories of patients. The columns of Table 1 define K = 6 nominal covariates, ν1, …, ν6, where ν1 is simply the L1 = 176 procedures, ν2 is the 176 procedures crossed with Hospital Group with L2 = 176 × 2 = 352 categories, ν3 is the 176 procedures crossed with Hospital Group, male, ER-admission, and Transfer-admission with L3 = 176 × 24 = 2816 categories, …, and ν6 crosses all 15 covariates with 176 × 214 ≐ 2.9 million categories.
Table 2.
Covariate imbalance before and after matching. The table compares new surgeons to experienced surgeons, before and after matching, in term of covariate means, standardized differences in means as a fraction of the standard deviation before matching, and two-sample P-values. New = new surgeon, Ex-B = experienced surgeon, before matching, Ex-A = experienced surgeon, after matching. Standardized differences above 1/10th of a standard deviation are in bold.
| Covariate Mean | Standardized Difference | 2-sample P-value | |||||
|---|---|---|---|---|---|---|---|
|
| |||||||
| Covariate | New | Ex-B | Ex-A | Before | After | Before | After |
| Sample size | 6,260 | 123,846 | 6,260 | ||||
|
| |||||||
| Age | 77.883 | 76.992 | 77.926 | 0.116 | −0.005 | 0.000 | 0.617 |
| Male | 0.345 | 0.358 | 0.346 | −0.027 | −0.003 | 0.038 | 0.880 |
| ER-admit | 0.538 | 0.323 | 0.537 | 0.444 | 0.003 | 0.000 | 0.886 |
| Transfer | 0.008 | 0.008 | 0.007 | 0.000 | 0.013 | 1.000 | 0.532 |
| Risk | 0.042 | 0.030 | 0.040 | 0.214 | 0.031 | 0.000 | 0.237 |
| CHF | 0.149 | 0.123 | 0.143 | 0.076 | 0.019 | 0.000 | 0.311 |
| Liver | 0.043 | 0.036 | 0.038 | 0.035 | 0.026 | 0.005 | 0.161 |
| Cancer | 0.164 | 0.175 | 0.164 | −0.029 | 0.001 | 0.030 | 0.981 |
| Past A | 0.170 | 0.171 | 0.161 | −0.002 | 0.024 | 0.880 | 0.178 |
| Diabetes | 0.189 | 0.197 | 0.199 | −0.019 | −0.024 | 0.145 | 0.198 |
| Renal | 0.069 | 0.058 | 0.064 | 0.046 | 0.020 | 0.000 | 0.282 |
| COPD | 0.167 | 0.147 | 0.160 | 0.055 | 0.019 | 0.000 | 0.298 |
| CC | 0.028 | 0.028 | 0.022 | −0.006 | 0.031 | 0.691 | 0.075 |
| Dementia | 0.101 | 0.065 | 0.093 | 0.131 | 0.032 | 0.000 | 0.103 |
| Paraplegia | 0.019 | 0.011 | 0.015 | 0.063 | 0.031 | 0.000 | 0.114 |
| Past MI | 0.058 | 0.054 | 0.051 | 0.015 | 0.031 | 0.265 | 0.083 |
| PPF | 0.023 | 0.020 | 0.021 | 0.023 | 0.015 | 0.069 | 0.429 |
| Stroke | 0.068 | 0.058 | 0.063 | 0.041 | 0.019 | 0.001 | 0.312 |
Ideally, the number of patients of new surgeons in each of 2.9 million categories would equal the number of patients of experienced surgeons. That was not quite possible while always also matching patients within the 498 hospitals. Subject to that requirement of matching within hospitals, the match minimized imbalance in a sense to be defined in a moment, and minimized the sum of a covariate distance over 6260 patient pairs.
A nominal covariate with Lk levels yields an Lk × 2 contingency table with two columns for the patients of new and experienced surgeons. In the matched sample, each column contains a total of 6260 patients distributed among Lk categories or rows. How different are the distributions in the two columns? Write βkℓ for the difference in counts of νk in row ℓ of the table; then and is proportional to a standard measure of the difference between two discrete probability distributions, namely the total variation distance. Now, could be as small as 0 if the distributions were identical or as large as 2 × 6260 = 12520 if they do not overlap. To equalize the two distributions, one would need to switch the categories for controls or the percentage (100/6260) .
The lower portion of Table 1 shows the total imbalance in the six nominal covariates, ν1, … , ν6. For procedures, ν1, the imbalance was 0, so the distribution of the 176 procedures is identical in the new and experienced groups. The imbalance for ν1 is as small as possible. For ν2, the imbalance was 6, meaning that there was a total excess of 3 in some of the rows of the 2 × 352 table and a total deficit of 3 in some other rows. The imbalance for ν2 is as small as possible among matches that minimize the imbalance in ν1. And so on. For ν6, the total absolute imbalance is 1242 for 2 × 6260 = 12520 patients in 2.9 million categories, or about 10% of the maximum imbalance. The imbalance for ν6 is as small as possible subject to minimizing the imbalance in ν1, … , ν5 and matching within surgeon pairs. In addition to producing a small imbalance in ν1, … , ν6, the matching algorithm certifies that the imbalance attained is the smallest possible imbalance when matching new and experienced surgeon patients within the same hospital; that is, there is no point in trying to achieve a smaller imbalance.
The balance described in the previous paragraph is much better than randomization would produce. We computed the usual χ2-statistic for independence in each of the six 2×Lk contingency tables. We created 10,000 simulated randomized experiments by simple random sampling without replacement of 6260 patients from the 12520 patients, so row and column margins of the 2 × Lk are unchanged, and computed 10,000 independence χ2-statistics and imbalances ; see the bottom of Table 1. For ν6 with 2.9 million categories, the actual matched sample had an imbalance of 1242 and χ2 of 1158.7, and that was much better balance than the best of 10,000 simulated randomized experiments with an imbalance of 3578 and χ2 of 2645.0.
Subject to the constraints of matching within hospital and minimizing imbalance in Table 1, the algorithm minimized the total over 6260 patient pairs of a covariate distance within pairs. Table 2 looks at the imbalance on the individual matching variables, including age and the risk score, neither of which is in Table 1.
Do new surgeons treat the easiest patients? Apparently not. In Table 2, before matching, the patients of new surgeons are much more likely to have entered through the emergency room, have higher estimated risks of death based on comorbidities, are more likely to have dementia, and tend to be older. These differences are largely absent after matching. New surgeons are treating a challenging and vulnerable group of patients. In §5, we ask: How do outcomes compare for new and experienced surgeons when experienced surgeons treat equally challenging patients?
4 A network algorithm for large, sparse optimal matching with refined balance
4.1 Notation: acceptable 1-to-m match; covariate imbalance βkℓ
There are T treated subjects,  = {τ1,
… , τT }, and C
≥ T potential controls,
= {τ1,
… , τT }, and C
≥ T potential controls, 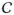 = {κ1,
… , κC}, with ∅ =
= {κ1,
… , κC}, with ∅ =
 ∩
∩ 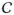 . In §3.2,
. In §3.2,  contains patients of new surgeons and
contains patients of new surgeons and 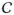 contains patients of experienced surgeons. Write |
contains patients of experienced surgeons. Write |
 | for the number of elements in a finite
set
| for the number of elements in a finite
set  , so that T = |
, so that T = |
 |. There were T =
6260 patients of new surgeons to be matched and C = 123846
candidate control patients of experienced surgeons. Treated subject
τt ∈
|. There were T =
6260 patients of new surgeons to be matched and C = 123846
candidate control patients of experienced surgeons. Treated subject
τt ∈  has observed covariate
xτt and potential control
κc ∈
has observed covariate
xτt and potential control
κc ∈  has covariate
xκc.
has covariate
xκc.
There is a subset of acceptable pairings,  ⊆
⊆  ×
×  , such that
(τt, κc) is an
acceptable pairing if and only if (τt,
κc) ∈
, such that
(τt, κc) is an
acceptable pairing if and only if (τt,
κc) ∈  . In §3.2, we had previously paired a new and an
experienced surgeon at the same hospital performing similar procedures, and the acceptable
pairings
. In §3.2, we had previously paired a new and an
experienced surgeon at the same hospital performing similar procedures, and the acceptable
pairings  are only of patients of these
paired new and experienced surgeons at the same hospital; that is,
(τt, κc)
∈
are only of patients of these
paired new and experienced surgeons at the same hospital; that is,
(τt, κc)
∈  if and only if
τt is a patient of a new surgeon and
κc is a patient of the experienced surgeon with
whom this new surgeon is paired. In §3.2, |
if and only if
τt is a patient of a new surgeon and
κc is a patient of the experienced surgeon with
whom this new surgeon is paired. In §3.2, |  | = 819230 < 7.75 × 108
= T × C = |
| = 819230 < 7.75 × 108
= T × C = |  ×
× 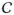 |.
|.
For each (τt,
κc) ∈  there is a distance
δtc between
xτt and
xκc,
δtc =
δ(xτt,
xκc), with 0 ≤
δtc < ∞. We would like to pair
individuals who are close on covariates. In §3.2,
δtc =
δ(xτt,
xκc) was a robust, rank-based
Mahalanobis distance (Rosenbaum 2010, §8)
based on age, sex, emergency admission, transfer admission, risk score and clusters of
procedures. There is competition for controls, so κc
may be the closest control to both τt and
τt′, and an optimal matching
will minimize the total distance for matched individuals subject to various constraints on
the balance of covariates.
there is a distance
δtc between
xτt and
xκc,
δtc =
δ(xτt,
xκc), with 0 ≤
δtc < ∞. We would like to pair
individuals who are close on covariates. In §3.2,
δtc =
δ(xτt,
xκc) was a robust, rank-based
Mahalanobis distance (Rosenbaum 2010, §8)
based on age, sex, emergency admission, transfer admission, risk score and clusters of
procedures. There is competition for controls, so κc
may be the closest control to both τt and
τt′, and an optimal matching
will minimize the total distance for matched individuals subject to various constraints on
the balance of covariates.
There are K nested nominal variables
νk (·), k = 1,
…, K; that is, νk (·)
is a function that assigns one of Lk values in 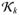 =
{λk1, … ,
λk,Lk}
to each subject in
=
{λk1, … ,
λk,Lk}
to each subject in  ∪
∪ 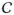 , or νk:
, or νk:
 ∪
∪ 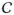 →
→ 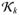 .
In §3.2 and Table 1, there were
K = 6 nominal variables. Importantly,
νk+1 refines or subdivides
νk. In other words, these K
variables are nested in the sense that all individuals who are the same on
νk+1 are the same on
νk; that is, formally, if
ι ∈
.
In §3.2 and Table 1, there were
K = 6 nominal variables. Importantly,
νk+1 refines or subdivides
νk. In other words, these K
variables are nested in the sense that all individuals who are the same on
νk+1 are the same on
νk; that is, formally, if
ι ∈  ∪
∪ 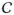 with
νk+1(ι)
= λk+1,ℓ and
ι′ ∈
with
νk+1(ι)
= λk+1,ℓ and
ι′ ∈  ∪
∪ 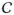 with
νk+1(ι′)
= λk+1,ℓ, then
νk (ι) =
νk (ι′). Variable
ν1 (·) is the coarsest and most important
variable and νK(·) is the finest and least
important variable. Expressed informally, the algorithm will do everything possible to
balance ν1(·) as closely as possible, whereas
it will merely do what it can to balance
νK·).
with
νk+1(ι′)
= λk+1,ℓ, then
νk (ι) =
νk (ι′). Variable
ν1 (·) is the coarsest and most important
variable and νK(·) is the finest and least
important variable. Expressed informally, the algorithm will do everything possible to
balance ν1(·) as closely as possible, whereas
it will merely do what it can to balance
νK·).
Definition 1
Acceptable 1-to-m match: An acceptable 1-to-m match is a
subset  ⊆
⊆  such that every τt
∈
such that every τt
∈  appears in exactly
m pairs (τt,
κc) ∈
appears in exactly
m pairs (τt,
κc) ∈  and every κc
∈
and every κc
∈ 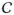 appears in at most one pair
(τt, κc)
∈
appears in at most one pair
(τt, κc)
∈  .
.
If  =
=  ×
× 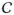 ,
then an acceptable 1-to-m match exists whenever C
≥ mT. If
,
then an acceptable 1-to-m match exists whenever C
≥ mT. If  ⊂
⊂  ×
× 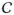 , then an 1-to-m acceptable match may
not exist even when C ≥ mT. The algorithm
finds an acceptable 1-to-m match if one exists; otherwise it reports
that no such match exists. The conditions required for the existence of an acceptable
match are stated in a famous theorem in graph theory, Hall’s theorem; see Diestel (2010, Theorem 2.1.2, p. 38); however, the
algorithm determines whether a match exists.
, then an 1-to-m acceptable match may
not exist even when C ≥ mT. The algorithm
finds an acceptable 1-to-m match if one exists; otherwise it reports
that no such match exists. The conditions required for the existence of an acceptable
match are stated in a famous theorem in graph theory, Hall’s theorem; see Diestel (2010, Theorem 2.1.2, p. 38); however, the
algorithm determines whether a match exists.
In addition to having an acceptable match with  ⊆
⊆  with a mall total distance
with a mall total distance 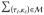 δtc, we also want to balance the K
nominal variables, emphasizing νk (·) over
νk+1 (·). Write
dkℓ for the number of treated
individuals τt falling in category ℓ of the
kth nominal variable
νk (·), so
dkℓ =
|{τt ∈
δtc, we also want to balance the K
nominal variables, emphasizing νk (·) over
νk+1 (·). Write
dkℓ for the number of treated
individuals τt falling in category ℓ of the
kth nominal variable
νk (·), so
dkℓ =
|{τt ∈  : νk
(τt) =
λkℓ}|. Ideally, an
acceptable 1-to-m match
: νk
(τt) =
λkℓ}|. Ideally, an
acceptable 1-to-m match  would have m×dkℓ
matched controls falling in category ℓ of the kth
nominal variable νk (·), so the
distributions of νk (·) would be identical
in matched treated and control groups; however, typically, this is not possible for
larger k. That is, ideally
|{(τt,
κc) ∈
would have m×dkℓ
matched controls falling in category ℓ of the kth
nominal variable νk (·), so the
distributions of νk (·) would be identical
in matched treated and control groups; however, typically, this is not possible for
larger k. That is, ideally
|{(τt,
κc) ∈  : νk
(κc) =
λkℓ}| would equal
m × dkℓ for
every k and ℓ. Because the K variables are
nested, an imbalance in νk (·) is
necessarily also an imbalance in
νk+1 (·).
: νk
(κc) =
λkℓ}| would equal
m × dkℓ for
every k and ℓ. Because the K variables are
nested, an imbalance in νk (·) is
necessarily also an imbalance in
νk+1 (·).
The imbalance βkℓ in
the ℓth category of the
kth nominal variable is a signed integer that is
m times the number of treated subjects
τt in  with level λkℓ of the
kth nominal variable minus the number of controls
κc in
with level λkℓ of the
kth nominal variable minus the number of controls
κc in  with level
λkℓ, that is,
with level
λkℓ, that is,
| (1) |
In (1),
βkℓ depends upon the match
 through
|{(τt,
κc) ∈
through
|{(τt,
κc) ∈  : νk
(κc) =
λkℓ}|, but the notation
does not indicate the dependence explicitly; that is, some matches
: νk
(κc) =
λkℓ}|, but the notation
does not indicate the dependence explicitly; that is, some matches  exhibit better covariate balance than do others. Here
βkℓ > 0 signifies that we
wanted more controls at level ℓ of nominal variable
νk (·), and
βkℓ < 0 signifies that we
wanted fewer. By the definition of an acceptable 1-to-m match, for each
k, the total of the signed imbalances is zero, (i.e., everyone has to go somewhere), but the total of
the absolute imbalances measures the degree to which matched treated and control
subjects have differing distributions of nominal variable
νk (·). In fact, is the total variation distance between the distribution
of νk (·) in matched treated and control
groups. In Table 1, . In some sense or other, we would like to pick an
acceptable 1-to-m match such that each of the is as small as possible and the within-pair distance
exhibit better covariate balance than do others. Here
βkℓ > 0 signifies that we
wanted more controls at level ℓ of nominal variable
νk (·), and
βkℓ < 0 signifies that we
wanted fewer. By the definition of an acceptable 1-to-m match, for each
k, the total of the signed imbalances is zero, (i.e., everyone has to go somewhere), but the total of
the absolute imbalances measures the degree to which matched treated and control
subjects have differing distributions of nominal variable
νk (·). In fact, is the total variation distance between the distribution
of νk (·) in matched treated and control
groups. In Table 1, . In some sense or other, we would like to pick an
acceptable 1-to-m match such that each of the is as small as possible and the within-pair distance
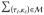 δtc is as small as possible.
δtc is as small as possible.
The kth nested nominal variable is said to satisfy “fine balance” if βkℓ = 0 for ℓ = 1, …, Lk, so νk (·) has the same distribution in matched treated and control groups; see Rosenbaum, Ross and Silber (2007). Because the K nominal variables are nested, nominal variable νk (·) is finely balanced whenever νk+1 (·) is finely balanced.
The kth nested nominal variable is said to satisfy
“near fine balance” if match  minimizes among all acceptable 1-to-m matches; see
Yang et al. (2012). Because the
K nominal variables are nested, for each k, as is seen in Table 1 where .
minimizes among all acceptable 1-to-m matches; see
Yang et al. (2012). Because the
K nominal variables are nested, for each k, as is seen in Table 1 where .
4.2 Two key definitions: What is an optimal refined acceptable
1-to-m match  ?
?
Where fine and near fine balance refer to a single nominal variable,
“refined balance” refers to a nested sequence of nominal variables, such
as νk (·), k = 1,
…, K, as in Table 1. Stated informally, each of the k levels is as balanced
as possible, but level k has priority over level k
+ 1. Write 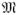 for the set of all
acceptable 1-to-m matches
for the set of all
acceptable 1-to-m matches  .
Each element
.
Each element  ∈
∈ 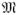 is one possible match. Each such match
is one possible match. Each such match  ∈
∈ 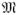 has values for βkℓ in (1) and a value for the total distance within
matched sets,
has values for βkℓ in (1) and a value for the total distance within
matched sets, 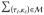 δtc. The two definitions that follow define a
“best” choice of
δtc. The two definitions that follow define a
“best” choice of  ∈
∈
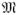 .
.
Definition 2 Refined balance
An acceptable 1-to-m match  ∈
∈ 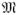 has refined balance if: (1) is minimized among all acceptable 1-to-m matches
has refined balance if: (1) is minimized among all acceptable 1-to-m matches
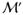 ∈
∈ 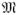 and (2) among acceptable 1-to-m matches that satisfy
(1),
and (2) among acceptable 1-to-m matches that satisfy
(1),  minimizes , …, (k)among acceptable 1-to-m matches that
satisfy (k−1),
minimizes , …, (k)among acceptable 1-to-m matches that
satisfy (k−1),  minimizes , …, (K) among acceptable 1-to-m matches that
satisfy (K−1),
minimizes , …, (K) among acceptable 1-to-m matches that
satisfy (K−1),  minimizes .
minimizes .
For example, in Table 1, 52 is the minimum possible value of among all acceptable 1-to-1 matches with and .
Definition 3 Optimal refined balance
An acceptable 1-to-m match  ∈
∈ 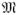 with refined balance is optimal
if it minimizes the total distance within pairs,
with refined balance is optimal
if it minimizes the total distance within pairs, 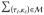 δtc, among all acceptable 1-to-m matches
δtc, among all acceptable 1-to-m matches
 ∈
∈ 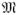 with refined balance.
with refined balance.
The goal is to find an optimal refined acceptable 1-to-m
match  if one exists and otherwise
determine that the problem is infeasible in that no such match exists.
if one exists and otherwise
determine that the problem is infeasible in that no such match exists.
4.3 Review of minimum cost flow in a network
The minimum cost flow problem is a standard combinatorial optimization problem with origins in operations research; see Bertsekas (1991), Cook et al. (1998), and Korte and Vygen (2008). This problem is a special type of integer program which, unlike most integer programs, can be solved with a worst-case time bound that is a polynomial in the size of the problem; that is, large problems can be solved quickly. A standard way to “solve” a combinatorial optimization problem is to show that it is equivalent to an appropriate minimum cost flow problem and to solve this equivalent problem. (In R, a good solver for minimum cost flow problems can be obtained as follows. Hansen’s optmatch package calls Fortran code RELAXIV created by Bertsekas and Tseng (see Bertsekas 1991) which solves minimum cost flow problems. Loading optmatch makes RELAXIV accessible in R and callable by imitating Hansen’s calls with different calling parameters. Documentation and code for RELAXIV are on Bertsekas’ web page at MIT.)
Metaphorically, objects are supplied and demanded at locations called nodes and
are shipped among nodes along edges connecting pairs of nodes, and the goal is to minimize
the total shipping cost while meeting demands subject to capacity constraints. Objects
cannot be cut in half (e.g., TVs cannot be cut in half for shipping) so the solution must
ship integer rather than fractional objects. Companies like FedEx solve minimum cost flow
problems in a literal rather than metaphorical sense. Optimal matching problems are
commonly reexpressed as minimum cost flow problems. We find an optimal refined acceptable
1-to-m match  by solving
an equivalent minimum cost flow problem.
by solving
an equivalent minimum cost flow problem.
A network is a set of nodes,  , a
set of edges
, a
set of edges  consisting of ordered pairs of
nodes,
consisting of ordered pairs of
nodes,  ⊆
⊆  ×
×  ,
so each e ∈
,
so each e ∈  is of
the form e = (n, n′)
where n, n′ ∈
is of
the form e = (n, n′)
where n, n′ ∈  . One draws a network with a point for each node
n ∈
. One draws a network with a point for each node
n ∈  and an arrow
connecting pairs of nodes for which there is an edge e =
(n, n′) ∈
and an arrow
connecting pairs of nodes for which there is an edge e =
(n, n′) ∈  , where the tail of the arrow is at n and
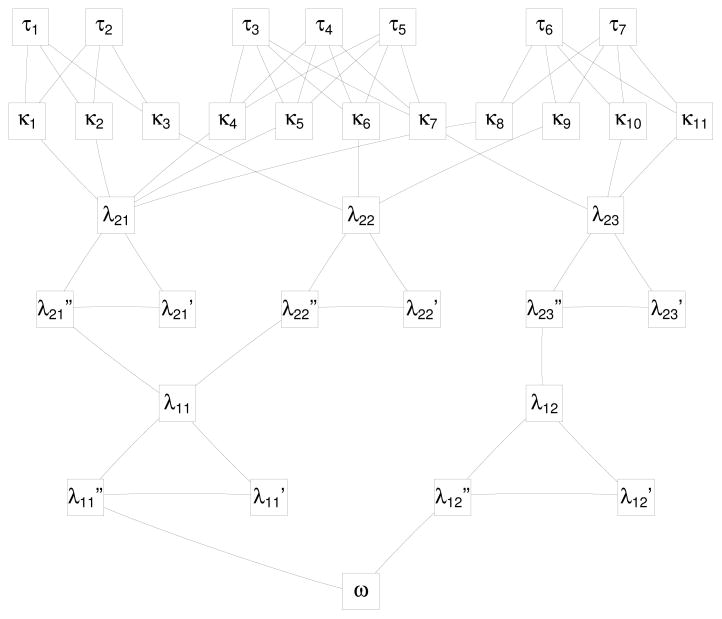
the point of the arrow is at n′. See Figure 1, where the arrowheads are omitted to limit clutter, but
edges that are not horizontal point down and horizontal edges point from right to left.
Our network is acyclic or without cycles, so we may speak of the early part of the network
— the upper part in Figure 1 — or the
late part of the network — the lower part in Figure
1.
, where the tail of the arrow is at n and
the point of the arrow is at n′. See Figure 1, where the arrowheads are omitted to limit clutter, but
edges that are not horizontal point down and horizontal edges point from right to left.
Our network is acyclic or without cycles, so we may speak of the early part of the network
— the upper part in Figure 1 — or the
late part of the network — the lower part in Figure
1.
Figure 1.
A small network for refined covariate balance with treated subject τ1, …, τ7, potential controls κ1, …, κ11, two balance layers λ1ℓ and λ2ℓ, and the sink ω.
Each edge e ∈  has a nonnegative, possibly infinite, integer capacity,
cap (e) with 0 ≤ cap (e) ≤ ∞,
and a nonnegative real cost, cost (e) with 0 ≤ cost
(e) < ∞. That is, e can carry up to cap
(e) units of flow and each unit costs cost (e) to
transport over e. Each node n ∈
has a nonnegative, possibly infinite, integer capacity,
cap (e) with 0 ≤ cap (e) ≤ ∞,
and a nonnegative real cost, cost (e) with 0 ≤ cost
(e) < ∞. That is, e can carry up to cap
(e) units of flow and each unit costs cost (e) to
transport over e. Each node n ∈  has a finite integer demand, demand (n)
with −∞ < demand (n) < ∞. Node
n absorbs demand (n) units of flow and passes the rest
on, and demand (n) < 0 means n creates an excess of
–demand (n) units of flow (e.g., manufactures –demand
(n) TVs). A feasible flow f is a function that assigns
a nonnegative integer f (e) to each edge
e = (n, n′) ∈
has a finite integer demand, demand (n)
with −∞ < demand (n) < ∞. Node
n absorbs demand (n) units of flow and passes the rest
on, and demand (n) < 0 means n creates an excess of
–demand (n) units of flow (e.g., manufactures –demand
(n) TVs). A feasible flow f is a function that assigns
a nonnegative integer f (e) to each edge
e = (n, n′) ∈
 , such that: (i) the flow is within the
capacity limits, 0 ≤ f (e) ≤ cap
(e) for each e ∈
, such that: (i) the flow is within the
capacity limits, 0 ≤ f (e) ≤ cap
(e) for each e ∈  , and the demand at each node n ∈
, and the demand at each node n ∈
 is met,
is met,
| (2) |
The first sum in (2) is the total
flow into n from neighboring nodes n′ with
(n′, n) ∈  , while the second sum is the total flow out from
n to neighboring nodes n″ with
(n, n″) ∈
, while the second sum is the total flow out from
n to neighboring nodes n″ with
(n, n″) ∈  , so the equation
(2) says that node n absorbs demand (n) units
of flow. A feasible flow may or may not exist. The total cost of a feasible flow is
, so the equation
(2) says that node n absorbs demand (n) units
of flow. A feasible flow may or may not exist. The total cost of a feasible flow is
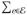 f (e) cost (e). An optimal feasible
flow is any feasible flow that minimizes the total cost. The problem of finding a minimum
cost flow in a network has several fast widely available solutions.
f (e) cost (e). An optimal feasible
flow is any feasible flow that minimizes the total cost. The problem of finding a minimum
cost flow in a network has several fast widely available solutions.
From a practical point of view, finding a minimum cost flow in a network may be
regarded by users as a standard mathematical computation, not unlike finding the inverse
of a matrix. The user specifies the network and is given a minimum cost flow, as the user
of matrix inversion software specifies a matrix and is given its inverse. Not all matrices
have inverses, and not all networks have feasible flows, and in both cases competent
software announces that the impossible has been requested. A network is dense if
O(|  |) = |
|) = |
 |2.
|2.
4.4 The network for optimal refined acceptable 1-to-m matching
The network involves a penalization parameter, ϒ > 1. Penalization will increase the cost of a flow when that flow is behaving in a way we wish to avoid. In §4.5, it will be shown that if ϒ is large enough, then the solution to a certain minimum cost flow problem yields an optimal refined acceptable 1-to-m matching.
The nodes,  , of the matching
network contain the treated subjects
, of the matching
network contain the treated subjects  = {τ1, …,
τT }, the potential controls,
= {τ1, …,
τT }, the potential controls,
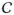 =
{κ1, …,
κC}, and an additional node
ω called a sink. Also the nodes contain all of the possible
values of the K nested nominal variables,
=
{κ1, …,
κC}, and an additional node
ω called a sink. Also the nodes contain all of the possible
values of the K nested nominal variables, 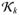 =
{λk1, …,
λk,Lk},
k = 1, …, K.
Additionally, the nodes contain a primed copy of values of the nested nominal variables, , k = 1,
…, K, and double primed copy of all of the
possible values of the nominal variables, , k = 1,
…, K. That is, the nodes are .
=
{λk1, …,
λk,Lk},
k = 1, …, K.
Additionally, the nodes contain a primed copy of values of the nested nominal variables, , k = 1,
…, K, and double primed copy of all of the
possible values of the nominal variables, , k = 1,
…, K. That is, the nodes are .
If (τt,
κc) ∈  ⊆
⊆  ×
× 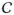 is an acceptable pairing in the
sense of §4.1, then (τt,
κc) is an edge of the network,
(τt, κc)
∈
is an acceptable pairing in the
sense of §4.1, then (τt,
κc) is an edge of the network,
(τt, κc)
∈  with capacity cap
{(τt,
κc)} = 1 and cost cost
{(τt,
κc)} =
δtc, where δtc
is the covariate distance between τt and
κc introduced in §4.1. There is an edge
(κc,
λKℓ) ∈
with capacity cap
{(τt,
κc)} = 1 and cost cost
{(τt,
κc)} =
δtc, where δtc
is the covariate distance between τt and
κc introduced in §4.1. There is an edge
(κc,
λKℓ) ∈  connecting each potential control
κc to the category
λKℓ of the last, most refined
nominal variable νK (·) that contains this
control; moreover, this edge has capacity 1 and zero cost, cap
{(κc,
λKℓ)} = 1 and
cost {(κc,
λKℓ)} = 0.
connecting each potential control
κc to the category
λKℓ of the last, most refined
nominal variable νK (·) that contains this
control; moreover, this edge has capacity 1 and zero cost, cap
{(κc,
λKℓ)} = 1 and
cost {(κc,
λKℓ)} = 0.
Every category kℓ of every nominal variable
νk (·) appears as a small triangle in
 involving
λkℓ, and . These triangles play an important role: each one makes an
effort to reduce a corresponding
|βkℓ| in (1), recognizing that it may not be possible to achieve
|βkℓ| = 0. Every node
λkℓ is connected to both and , so and , and is connected to so for all k, ℓ; that is,
λkℓ, and form a triangle. There is, therefore, a direct path from
λkℓ to and an indirect path from
λkℓ to that passes through . As discussed in §4.1, we would like to have
m × dkℓ controls
in category λkℓ as this would make
βkℓ = 0 in (1); however, this may not be possible. The
direct path has and cost , so that up to m ×
dkℓ units of flow can move directly
from λkℓ to for free, without cost. The indirect path is penalized as
we would prefer to use it as little as possible. The edge has infinite capacity, , and severely penalized cost of . The last leg of the triangle has infinite capacity and
zero cost, and . Notice that the penalty for
ν1 (·) is
ϒK but this gradually declines to penalty ϒ
for νK (·). Because the coarse, most important
ν1 (·) is after the fine, less important
νK (·), the penalties in triangles
increase from ϒ for νK (·) to
ϒK for ν1
(·) as we move from start to the end of the network. Informally, this says that a
one-patient imbalance in vk (·) is worse than a
one-patient imbalance in vk+1
(·).
involving
λkℓ, and . These triangles play an important role: each one makes an
effort to reduce a corresponding
|βkℓ| in (1), recognizing that it may not be possible to achieve
|βkℓ| = 0. Every node
λkℓ is connected to both and , so and , and is connected to so for all k, ℓ; that is,
λkℓ, and form a triangle. There is, therefore, a direct path from
λkℓ to and an indirect path from
λkℓ to that passes through . As discussed in §4.1, we would like to have
m × dkℓ controls
in category λkℓ as this would make
βkℓ = 0 in (1); however, this may not be possible. The
direct path has and cost , so that up to m ×
dkℓ units of flow can move directly
from λkℓ to for free, without cost. The indirect path is penalized as
we would prefer to use it as little as possible. The edge has infinite capacity, , and severely penalized cost of . The last leg of the triangle has infinite capacity and
zero cost, and . Notice that the penalty for
ν1 (·) is
ϒK but this gradually declines to penalty ϒ
for νK (·). Because the coarse, most important
ν1 (·) is after the fine, less important
νK (·), the penalties in triangles
increase from ϒ for νK (·) to
ϒK for ν1
(·) as we move from start to the end of the network. Informally, this says that a
one-patient imbalance in vk (·) is worse than a
one-patient imbalance in vk+1
(·).
The end of a triangle at level k is connected to the beginning λk−1,ℓ′ of the coarser category k −1, ℓ′ that contains category kℓ. This edge to a coarsened category has infinite capacity and zero cost, and . Finally, there is an edge from to the sink ω for each ℓ with infinite capacity and zero cost, and .
For each τt ∈  , demand (τt) =
−m. The sink has demand (ω) =
m|
, demand (τt) =
−m. The sink has demand (ω) =
m|  |. All other nodes have
demand (n) = 0. In words, each treated node issues
m units of flow, all nodes between the treated nodes and the sink pass
on all the flow they receive, and the sink ω collects all
mT units of flow issued by the T treated units.
|. All other nodes have
demand (n) = 0. In words, each treated node issues
m units of flow, all nodes between the treated nodes and the sink pass
on all the flow they receive, and the sink ω collects all
mT units of flow issued by the T treated units.
An important property of a feasible flow f in this network is
that control node κc ∈ 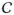 ⊂
⊂  may receive either zero or one unit of flow, because 0 ≤ f
(κc,
λKℓ) ≤ cap
{(κc,
λKℓ)} = 1, and if
f (κc,
λKℓ) = 1 then there is
only one possible sequence of ’s along which that unit of flow can pass to the
sink ω. For brevity, the network defined in this section will be
called “the network (
may receive either zero or one unit of flow, because 0 ≤ f
(κc,
λKℓ) ≤ cap
{(κc,
λKℓ)} = 1, and if
f (κc,
λKℓ) = 1 then there is
only one possible sequence of ’s along which that unit of flow can pass to the
sink ω. For brevity, the network defined in this section will be
called “the network (  ,
,
 ),” omitting explicit reference to
the capacities, costs and demands that are also part of its definition.
),” omitting explicit reference to
the capacities, costs and demands that are also part of its definition.
4.5 Main result: A minimum cost flow yields an optimal refined match
Lemma 4 says that the match we seek exists if and only if the minimum cost flow problem is feasible. Proofs are in the Appendix.
Lemma 4
There is a feasible flow f for the network (  ,
,  ) if and
only if there is an acceptable 1-to-m match
) if and
only if there is an acceptable 1-to-m match  . In particular,
. In particular,  =
{(τt,
κc) ∈
=
{(τt,
κc) ∈  : f
{(τt,
κc)} = 1}.
: f
{(τt,
κc)} = 1}.
Lemma 5 relates total cost to matching quantities, namely total covariate
distance within pairs, 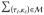 δtc, and the imbalance measures
βkℓ in (1).
δtc, and the imbalance measures
βkℓ in (1).
Lemma 5
Suppose there is a feasible flow f in (  ,
,  ), let
), let
 =
{(τt,
κc) ∈
=
{(τt,
κc) ∈  : f
{(τt,
κc)} = 1}, and let
βkℓ be the imbalance measure (1) for this match. Then the cost of this flow
satisfies
: f
{(τt,
κc)} = 1}, and let
βkℓ be the imbalance measure (1) for this match. Then the cost of this flow
satisfies
| (3) |
If f is a minimum cost feasible flow in (  ,
,  ), then
(3) holds as an equality.
), then
(3) holds as an equality.
Theorem 6 says we may find the match in Definition 3 by solving a standard combinatorial optimization problem. There is a finite value (see §4.6) of the penalty ϒ such that for that value and for all larger values, the resulting match satisfies the constraint of refined balance and minimizes the total covariate distance subject to that constraint.
Theorem 6
If there exists a feasible flow in (  ,
,  ), then
for sufficiently large ϒ, a minimum cost flow in (
), then
for sufficiently large ϒ, a minimum cost flow in (  ,
,  ) yields
an optimal refined acceptable 1-to-m match
) yields
an optimal refined acceptable 1-to-m match  given by
given by  =
{(τt,
κc) ∈
=
{(τt,
κc) ∈  : f
{(τt,
κc)} = 1}. If there exists
no feasible flow in (
: f
{(τt,
κc)} = 1}. If there exists
no feasible flow in (  ,
,  ), then there is no optimal refined acceptable 1-to-m
match.
), then there is no optimal refined acceptable 1-to-m
match.
4.6 Practical issues: deciding about ϒ and m
Theorem 6 speaks of “sufficiently large ϒ,” and in its
proof ϒ is very large, specifically ϒ > mTK +
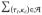 δtc. For stable computation, use a much smaller
ϒ, perhaps ϒ =
δtc. For stable computation, use a much smaller
ϒ, perhaps ϒ = 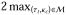 δtc or smaller. Theorem 6 says that as ϒ
increases, eventually the imbalances are the best possible imbalances and further increases in
ϒ do not change the imbalances, so it is reasonable to match a few times, starting
with a small ϒ and gradually increasing it until the imbalances stop changing.
δtc or smaller. Theorem 6 says that as ϒ
increases, eventually the imbalances are the best possible imbalances and further increases in
ϒ do not change the imbalances, so it is reasonable to match a few times, starting
with a small ϒ and gradually increasing it until the imbalances stop changing.
How many controls, m, should be matched to each treated unit? Match quality decreases as m increases, so one might match m = 1 to 1, examine the resulting average imbalances, , then match m = 2 to 1, and so on, stopping when the quality of the match is not acceptable.
4.7 Computation in sparse networks
Algorithms are standardly evaluated in terms of an upper bound on the rate of growth of the number of arithmetic steps required to solve them as the size of the problem increases (Cook et al. 1998, §1.2; Korte and Vygen 2008, §1.2). If steps =O (size3) then the number of arithmetic steps required to solve a problem grows by at most a constant multiple of the cube of the size of the problem. The point we want to make in the current section is that: (i) the new surgeons problem, and more generally the matching-within-natural-blocks problem, is sparse, with far fewer edges than typical matching problems, so (ii) vastly larger problems can be solved in these sparse networks than can be solved in dense networks commonly appearing in statistical matching problems, so (iii) we may balance covariates over an enormous number of natural blocks.
The network (  ,
,  ) is dense if |
) is dense if |  | = O(|
| = O(|  |2) and sparse if |
|2) and sparse if |  | = O(|
| = O(|  |). Our network is sparse; see §4.1. One can solve
the minimum cost flow problem in O(|
|). Our network is sparse; see §4.1. One can solve
the minimum cost flow problem in O(|  | log [|
| log [|  | {|
| {|  | + |
| + |  | log (|
| log (|  |)}]) steps; see Korte and Vygen (2008, Theorem 9.17, p. 214). If |
|)}]) steps; see Korte and Vygen (2008, Theorem 9.17, p. 214). If |
 | = |
| = |  |2, this is O{|
|2, this is O{|
 |2 log (|
|2 log (|  |)}, whereas if |
|)}, whereas if |  | = |
| = |  | it is O[|
| it is O[|  | log
{|
| log
{|  |}]. In
§4.4, |
|}]. In
§4.4, |  | > T
+ C = 130106 so |
| > T
+ C = 130106 so |  |2 log (|
|2 log (|  |) is much larger than |
|) is much larger than |  | log (|
| log (|  |).
|).
5 Do new and experienced surgeons differ?
5.1 Brief review of sensitivity analysis and attributable effects
There are I = 6260 pairs i =
1, …, I of two patients, j = 1, 2,
matched for covariates, xij, one treated with
Zij = 1, the other control with
Zij = 0, so
Zi1 +
Zi2 = 1. Write 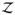 for the event that
Zi1+Zi2
= 1 for each i. Subject ij would exhibit binary
response rTij if treated with Zij
= 1 or binary response rCij if control with
Zij = 0, so the observed response from
ij is Rij = Zij
rTij+ (1 − Zij)
rCij and the effect of the treatment on
ij, namely θij =
rTij − rCij, is not
observed; see Neyman (1923) and Rubin (1974). Write θ
= (θ11,
θ12, …
θI2) for the
2I-dimensional parameter and write
for the event that
Zi1+Zi2
= 1 for each i. Subject ij would exhibit binary
response rTij if treated with Zij
= 1 or binary response rCij if control with
Zij = 0, so the observed response from
ij is Rij = Zij
rTij+ (1 − Zij)
rCij and the effect of the treatment on
ij, namely θij =
rTij − rCij, is not
observed; see Neyman (1923) and Rubin (1974). Write θ
= (θ11,
θ12, …
θI2) for the
2I-dimensional parameter and write 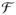 = {(rTij,
rCij, xij),
i = 1, …, I, j
= 1, 2}. In the current study, rTij =
1 if ij would die within 30 days of surgery performed by the young
surgeon in pair i, rTij = 0
otherwise, and rCij = 1 if ij would
die within 30 days of surgery performed by the experienced surgeon in pair
i, rCij = 0 otherwise. Then
(rTij, rCij) = (1, 0)
if patient ij would die if surgery were performed by the young surgeon in
pair i but not if performed by the experienced surgeon in pair
i. The notation refers to two specific surgeons in pair
i working at the same hospital.
= {(rTij,
rCij, xij),
i = 1, …, I, j
= 1, 2}. In the current study, rTij =
1 if ij would die within 30 days of surgery performed by the young
surgeon in pair i, rTij = 0
otherwise, and rCij = 1 if ij would
die within 30 days of surgery performed by the experienced surgeon in pair
i, rCij = 0 otherwise. Then
(rTij, rCij) = (1, 0)
if patient ij would die if surgery were performed by the young surgeon in
pair i but not if performed by the experienced surgeon in pair
i. The notation refers to two specific surgeons in pair
i working at the same hospital.
If treatments are randomly assigned, then Pr (Zij
= 1 | 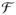 ,
, 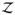 ) = 1/2 with independent assignments in distinct
pairs. The sensitivity analysis for nonrandom treatment assignment permits measured
deviations from random assignment, specifically (1 +
Γ)−1 ≤ Pr (Zij =
1 |
) = 1/2 with independent assignments in distinct
pairs. The sensitivity analysis for nonrandom treatment assignment permits measured
deviations from random assignment, specifically (1 +
Γ)−1 ≤ Pr (Zij =
1 | 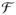 ,
,  ) ≤ Γ/(1 + Γ) for several
Γ ≥ 1; see Rosenbaum (2002). A
calculation in Rosenbaum and Silber (2009a) permits
Γ to be interpreted in terms of an unobserved covariate associated with treatment
and outcome. In the current paper, for a specified deviation from random assignment,
Γ ≥ 1, the sensitivity analysis will yield an upper bound on the
P-value testing some hypothesis about treatment effects, so that, if
that upper bound is at most α, then a bias of size Γ is
too small to lead to acceptance of the hypothesis at level α. A
sensitivity analysis asks: How much bias from non-random treatment assignment would need
to be present to alter the conclusions of a randomization test, that is, to accept a null
hypothesis that the randomization test has rejected?
) ≤ Γ/(1 + Γ) for several
Γ ≥ 1; see Rosenbaum (2002). A
calculation in Rosenbaum and Silber (2009a) permits
Γ to be interpreted in terms of an unobserved covariate associated with treatment
and outcome. In the current paper, for a specified deviation from random assignment,
Γ ≥ 1, the sensitivity analysis will yield an upper bound on the
P-value testing some hypothesis about treatment effects, so that, if
that upper bound is at most α, then a bias of size Γ is
too small to lead to acceptance of the hypothesis at level α. A
sensitivity analysis asks: How much bias from non-random treatment assignment would need
to be present to alter the conclusions of a randomization test, that is, to accept a null
hypothesis that the randomization test has rejected?
Fisher’s (1935) hypothesis of no treatment effect says H0 : rTij = rCij for all ij or equivalently H0 : θ = 0. If H0 were false, an interesting quantity is the attributable effect, ; it is the number of additional deaths among patients of young surgeons (Zij = 1) that would not have occurred had the experienced surgeon in the pair been picked to perform the surgery. If H0 were true, then A = 0. If H0 were false, then A would be an integer valued random variable. Of course, A is unobservable because θij = rTij − rCij is never observed; however, it is possible to draw inferences about A; see Rosenbaum (2002). This method uses a pivotal argument such that the observed number of deaths among patients of new surgeons, namely Σij ZijRij, minus the unknown true value of A, is a random variable that satisfies the null hypothesis of no effect, Σij ZijRij − A = Σij Zij rCij, so that, for example, in a randomized experiment Σij Zi j rCij is a constant plus a binomial random variable, as in McNemar’s test. A null hypothesis about A is rejected if the individual null hypotheses H0 : θ = θ0 compatible with this value of A are all rejected. The calculation involves a binomial tail probability computed from a table of adjusted counts; see Rosenbaum (2002, §6 and Table 5).
5.2 Sensitivity analyses for three-sided tests
Perhaps new surgeons are less capable and cause excess surgical deaths, so that A > 0. It is not inconceivable that new surgeons are more capable, having been more recently trained, so A < 0. Recent training might be relevant to laparoscopy and related techniques, in which a surgeon inserts a thin robotic surgical tool containing a camera, and manipulates the tool remotely. So it is of interest to test no effect H0 against a two-sided alternative.
Failure to reject H0 does not mean H0 is approximately true. Rather, we wish to be assured that A is tolerably close to zero. For this, some form of equivalence test is needed.
Building upon the work of Bauer and Kieser (1996), Goeman, Solari and Stijnen (2010) proposed a “three-sided test” for both difference and equivalence. It combines a two-sided test of no effect with the two-one-sided test procedure for testing inequivalence, all tests being done at the α-level, with no need of correction for multiple testing. Their underlying idea is both simple and clever. Three mutually incompatible hypotheses may be tested at level α without correction for multiple testing, because at most one hypothesis is true, so the α-risk of falsely rejecting a true null hypothesis is incurred at most once despite testing three null hypotheses. In brief, we may perform a two-sided test of no effect to establish both an effect and its direction, and perform a test of the null hypothesis of inequivalence to establish near equivalence, and do this without adjustment for multiple testing.
For sensitivity analyses, one attraction of the three-sided test is that we may use a standard method of sensitivity analysis three times, each time placing an upper bound on the relevant P-value in the presence of a bias in treatment assignment of at most Γ ≥ 1 for several values of Γ. The standard method says: if the null hypothesis is true and the bias in treatment assignment is at most Γ, then the chance that the upper bound on the P-value exceeds α is at most α. Logically, because at most one of the three null hypotheses is true, the standard method is either saying something trivial if all three null hypotheses are false, or it is referring to the one true null hypothesis despite our ignorance of the identity of that hypothesis. See Rosenbaum and Silber (2009b) for related discussion.
Fisher’s H0 : θ = 0 is tested against a two sided alternative. The null hypothesis of inequiva-lence in the direction of harm done by new surgeons is defined to be θ ≥ 0 (i.e., θij ≥ 0 for all ij) with A ≥ ι where ι > 0 is a standard of inequivalence. The null hypothesis of inequivalence in the direction of benefit from new surgeons is defined to be θ = 0 with A ≤ −ι where again ι > 0. At most one hypothesis is true.
In the US in 2008, the annual mortality rate between age 75 and 76 was 3.95%; see Arias (2012, Table 2). Most people aged 75 in 2008 did not undergo surgery. A risk associated with surgery in Medicare is small if it is small compared with the annual risk faced by the Medicare population. For illustration, we consider two definitions of inequivalence, ι, namely a quarter and a half of the annual mortality in the population at age 75, that is ι = 62 = 6260 × 0.039506/4 or ι = 124 = 6260 × 0.039506/2 extra deaths.
5.3 Mortality results
The overall 30-day mortality rate among the 2 × 6260 patients was 3.65%, made up of 3.59% for 6260 patients of experienced surgeons and 3.71% for 6260 patients of new surgeons. So the mortality rates for new and experienced surgeons look similar. The randomization test based on McNemar’s test has two-sided P-value 0.7689, so the null hypothesis of no effect is plausible even in the absence of unmeasured biases. From §3.2, this comparison refers to pairs of surgeons working at the same hospital, with identical distributions of operative procedures, and patients with similar comorbid conditions.
Table 4 gives the sensitivity analysis. For Γ = 1, this is a three-sided randomization test, and in the third column of Table 4, the hypothesis that experienced surgeons caused at least 62 extra deaths is rejected with P-value 0.0003, while in the fourth column the hypothesis that new surgeons caused at least an extra 62 deaths is rejected with P-value 0.0033. Biased assignment of patients to new or experienced surgeons might mask a substantial difference in mortality, making it appear to be no difference. In the fifth and sixth columns of Table 4, a bias of Γ = 1.7 is too small to mask a difference of ι = 124 extra deaths in either direction. Using the calculation in Rosenbaum and Silber (2009a), a bias of Γ = 1.7 could be produced by an unobserved covariate that more than tripled the odds of treatment by a young surgeon and more than tripled the odds of death.
Table 4.
Sensitivity analysis using the three-sided test of the null hypotheses of no effect and substantial inequivalence with two definitions of inequivalence, ι = 62 and ι = 124. The test of no effect is two-sided, but the equivalence tests are one-sided. The table gives the upper bounds on the P-value for various magnitudes of bias Γ in assignment of patients to surgeons.
| No effect | Definition of inequivalence | ||||
|---|---|---|---|---|---|
|
| |||||
| A = 0 | A ≥ ι = 62 | A ≥ ι = 124 | |||
|
| |||||
| Surgeon type that caused more deaths | |||||
|
| |||||
| Γ | Equal | Experienced | New | Experienced | New |
| 1.0 | 0.7689 | 0.0003 | 0.0033 | 0.0000 | 0.0000 |
| 1.1 | 1.0000 | 0.0065 | 0.0379 | 0.0000 | 0.0000 |
| 1.2 | 1.0000 | 0.0521 | 0.1804 | 0.0000 | 0.0000 |
| 1.3 | 1.0000 | 0.2017 | 0.4508 | 0.0000 | 0.0000 |
| 1.4 | 1.0000 | 0.4571 | 0.7276 | 0.0000 | 0.0003 |
| 1.5 | 1.0000 | 0.7147 | 0.9000 | 0.0002 | 0.0026 |
| 1.6 | 1.0000 | 0.8841 | 0.9721 | 0.0012 | 0.0131 |
| 1.7 | 1.0000 | 0.9628 | 0.9938 | 0.0061 | 0.0452 |
In short, in the example, there are three findings. There is no evidence that mortality rates for new and experienced surgeons differ. A difference of 62 extra deaths caused by either type of surgeon is rejected in a randomization test, but a small bias of Γ = 1.2 could mask this difference, making it appear to be no difference. A larger difference of 124 extra deaths is rejected unless the bias is larger than a moderate Γ = 1.7, that is, the bias that could result from failing to match for an unobserved covariate that tripled the odds of treatment by a young surgeon and tripled the odds of death.
6 Discussion of other applications of the methodology
6.1 Nested nominal covariates in other applications
The priorities in Table 1 were based on the judgment of the surgeon on the research team. Expert judgment is one good way to create and order ν1, …, vK. Are there other ways?
Important covariates predict both treatment assignment and outcomes. Covariates that predict treatment show up as important in propensity scores estimated from the current data (Rosenbaum and Rubin 1985), and covariates that predict outcomes show up as important in prognostic or risk scores estimated from external data (Hansen 2008). The scores suggest covariates deserving priority for balancing, with the distance δtc seeking close individual pairs on the scores. Traskin and Small (2011) approximate a propensity score using a regression tree, and such a tree creates a hierarchy of nominal variables to serve as ν1, …, vK. Alternatively, a lasso fit could prioritize the variables in either score.
A covariate that describes blocks or is constant for each block, such as hospital group in Table 1, has a marginal distribution that is balanced simply by matching within hospitals. However, including hospital group in Table 1 meant that its interactions with 14 other covariates were also balanced. A subgroup analysis that separately analyzed the two groups of pairs from the two types of hospitals would exhibit covariate balance within each subgroup separately, an important consideration for subgroup analyses.
6.2 Other sources of sparsity in optimal balanced matching
In the example, sparsity is created by the desire to match within natural blocks. Sparsity also arises in other ways. If there were one or two important continuous covariates, perhaps a propensity or risk score, then one might restrict the list of potential controls for a given treated subject to the short list comprised of the nearest c controls on those covariates. With fixed c, say c = 100, a sparse network is obtained. Refined covariate balance in such a network would obtain pairs that are close on the key covariates while balancing many nominal categories. As discussed by Zubizarreta et al. (2014), a match that reduces the heterogeneity of matched pair differences in outcomes, perhaps by matching closely for predictors of those outcomes, will both increase the power of a randomization test of no effect and increase its insensitivity to unmeasured biases.
With many nominal covariates, one might require exact matches for the most important nominal covariates, merely balancing the rest; then the short list of potential controls is comprised of the exact matches for those most important nominal covariates. If the treatment is applied to everyone in a state or province, then one might wish to match treated subjects near the state boundary to nearby controls just across that boundary, and again this creates sparsity; see Keele et al. (2014) for one such study.
Table 3.
Mortality in 6260 pairs of matched pairs of patients, one treated by a new surgeon, the other by an exerienced surgeon. The table counts pairs, not patients.
| Experienced Surgeon | New Surgeon | Total | Percent | |
|---|---|---|---|---|
| Dead | Alive | |||
| Dead | 20 | 205 | 225 | 3.59% |
| Alive | 212 | 5823 | 6035 | 96.41% |
|
| ||||
| Total | 232 | 6028 | 6260 | |
| Percent | 3.70% | 96.30% | 100.00% | |
Acknowledgments
Supported by Grant SBS 1260782 from the MMS Program of the US National Science Foundation, Grant AG032963 from the US National Institute of Aging, and by Fellowship FA9550-11-C-0028 from the Department of Defense, Army Research Office, National Defense Science and Engineering Graduate (NDSEG) Fellowship Program, 32 CFR 168a4. 6 December 2014
Appendix: Proofs of main results
Proof of Lemma 4
Suppose there is a feasible flow f for the network (
 ,
,  ) and define
) and define  = {(τt,
κc) ∈
= {(τt,
κc) ∈  : f
{(τt,
κc)} = 1}. By the
definition of
: f
{(τt,
κc)} = 1}. By the
definition of  in §4.4, if
(τt, κc)
∈
in §4.4, if
(τt, κc)
∈  then
(τt, κc)
∈
then
(τt, κc)
∈  . There is only one edge exiting
from control κc ∈
. There is only one edge exiting
from control κc ∈  ⊂
⊂  , namely (κc,
λKℓ) for the category
Kℓ to which κc belongs,
and because f is feasible we have 0 ≤ f
(κc,
λKℓ) ≤ cap
{(κc,
λKℓ)} = 1, so
either f (κc,
λKℓ) = 0 or
f (κc,
λKℓ) = 1. If
f (κc,
λKℓ) = 1 then
κc received its one unit of flow from a unique
treated node τt ∈
, namely (κc,
λKℓ) for the category
Kℓ to which κc belongs,
and because f is feasible we have 0 ≤ f
(κc,
λKℓ) ≤ cap
{(κc,
λKℓ)} = 1, so
either f (κc,
λKℓ) = 0 or
f (κc,
λKℓ) = 1. If
f (κc,
λKℓ) = 1 then
κc received its one unit of flow from a unique
treated node τt ∈  ⊂
⊂  . Moreover, because f is feasible and demand
(τt) = −m, it
follows that m =
. Moreover, because f is feasible and demand
(τt) = −m, it
follows that m =  f (τt,
κc) for each
τt ∈
f (τt,
κc) for each
τt ∈  , so
, so  is
indeed an acceptable 1-to-m match
is
indeed an acceptable 1-to-m match  such that (τt,
κc) ∈
such that (τt,
κc) ∈  implies (τt,
κc) ∈
implies (τt,
κc) ∈  . Conversely, suppose there is an acceptable
1-to-m match
. Conversely, suppose there is an acceptable
1-to-m match  . Then, by
the definition in §4.1 of an acceptable 1-to-m match,
(τt, κc)
∈
. Then, by
the definition in §4.1 of an acceptable 1-to-m match,
(τt, κc)
∈  implies
(τt, κc)
∈
implies
(τt, κc)
∈  . For
τt ∈
. For
τt ∈  and κc ∈
and κc ∈
 define f
(τt, κc)
= 1 if (τt,
κc) ∈
define f
(τt, κc)
= 1 if (τt,
κc) ∈  and f
(τt, κc)
= 0 otherwise. By the definition of an acceptable 1-to-m match,
each treated unit τt ∈
and f
(τt, κc)
= 0 otherwise. By the definition of an acceptable 1-to-m match,
each treated unit τt ∈  issues m units of flow,
m =
issues m units of flow,
m = 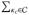 f (τt,
κc), so (2) is satisfied for n =
τt. By the definition of an acceptable
1-to-m match, each control κc is
matched to at most one treated unit τt, so 1
≥
f (τt,
κc), so (2) is satisfied for n =
τt. By the definition of an acceptable
1-to-m match, each control κc is
matched to at most one treated unit τt, so 1
≥ 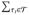 f (τt,
κc) for each
κc ∈
f (τt,
κc) for each
κc ∈ 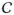 , and the zero or one unit of flow leaving
κc may be passed through
(κc,
λKℓ) ∈
, and the zero or one unit of flow leaving
κc may be passed through
(κc,
λKℓ) ∈  with its capacity of cap
{(κc,
λKℓ)} = 1. The
indirect paths in triangles, and , have infinite capacity, so all of the flow reaching
λkℓ may feasibly be passed on
to the corresponding
λk−1,ℓ′
and on to the sink ω, so a feasible flow f may
be completed by passing flow along indirect paths.
with its capacity of cap
{(κc,
λKℓ)} = 1. The
indirect paths in triangles, and , have infinite capacity, so all of the flow reaching
λkℓ may feasibly be passed on
to the corresponding
λk−1,ℓ′
and on to the sink ω, so a feasible flow f may
be completed by passing flow along indirect paths.
Proof of Lemma 5
Compute βkℓ in (1) for match  recalling that for k = 1, …,
K. Write and so that and or equivalently . The total cost of f is the sum of the
costs in two disjoint subsets of edges of (
recalling that for k = 1, …,
K. Write and so that and or equivalently . The total cost of f is the sum of the
costs in two disjoint subsets of edges of (  ,
,  ), namely
), namely 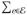 f (e) cost (e) =
f (e) cost (e) =
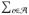 f (e) cost (e) +
f (e) cost (e) +
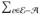 f (e) cost (e). The total cost of
f over
f (e) cost (e). The total cost of
f over  ⊂
⊂
 , namely
, namely 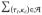 f {(τt,
κc)} cost
{(τt,
κc)}, is precisely
f {(τt,
κc)} cost
{(τt,
κc)}, is precisely 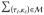 δtc by the definition of f. The
remaining cost of the flow f is
δtc by the definition of f. The
remaining cost of the flow f is 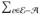 f (e) cost (e), and in
f (e) cost (e), and in
 −
−  there is nonzero cost only from edges of the form in the indirect paths in triangles because . The triangle defined by
λkℓ, , and receives
|{(τt,
κc) ∈
there is nonzero cost only from edges of the form in the indirect paths in triangles because . The triangle defined by
λkℓ, , and receives
|{(τt,
κc) ∈  : νk
(κc) =
λkℓ}| units of flow
entering λkℓ, and , so from (1), at least units of flow pass through with total . This yields the inequality (3). In a minimum cost feasible flow, as pointlessly increases the cost. This proves the case of
equality in (1) for a minimum cost
flow.
: νk
(κc) =
λkℓ}| units of flow
entering λkℓ, and , so from (1), at least units of flow pass through with total . This yields the inequality (3). In a minimum cost feasible flow, as pointlessly increases the cost. This proves the case of
equality in (1) for a minimum cost
flow.
Proof of Theorem 6
Because the specific value of ϒ > 1 is not relevant for
feasibility, the parts of the proposition that discuss existence merely restate Lemma 4.
Fix ϒ > mTK + 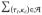 δtc. With this ϒ, let f be
a minimum cost feasible flow in (
δtc. With this ϒ, let f be
a minimum cost feasible flow in (  ,
,
 ), and let
), and let  =
{(τt,
κc) ∈
=
{(τt,
κc) ∈  : f
{(τt,
κc)} = 1} be the
corresponding acceptable 1-to-m match. Let
βkℓ be the imbalances (1) for the match
: f
{(τt,
κc)} = 1} be the
corresponding acceptable 1-to-m match. Let
βkℓ be the imbalances (1) for the match  . The triangle defined by
λkℓ, , and receives
|{(τt,
κc) ∈
. The triangle defined by
λkℓ, , and receives
|{(τt,
κc) ∈  : νk
(κc) =
λkℓ}| units of flow
entering λkℓ, and so from the
proof of Lemma 5, with a cost of .
: νk
(κc) =
λkℓ}| units of flow
entering λkℓ, and so from the
proof of Lemma 5, with a cost of .
The cost of f is by Lemma 5. Because the total flow is only
mT, for each k we have . Because  ⊂
⊂  , we have
, we have 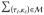 δtc ≤
δtc ≤ 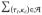 δtc. We now use these to bound the total cost of
f strictly before all of the triangles defined by
λkℓ, , and , that is,
δtc. We now use these to bound the total cost of
f strictly before all of the triangles defined by
λkℓ, , and , that is,
| (4) |
| (5) |
where (4)
uses the two upper bounds, the first inequality in (5) simply uses
ϒK−k
≥ 1, and the second inequality in (5) uses ϒ > mTK +  δtc. The cost of each single unit of flow passing
through any edge is
ϒK−k+1,
and from (5) it exceeds the total cost of
everything before in (
δtc. The cost of each single unit of flow passing
through any edge is
ϒK−k+1,
and from (5) it exceeds the total cost of
everything before in (  ,
,
 ). Using (4)–(5) with k = 1 shows that it is not possible to
further reduce , because if any feasible flow f′
had a lower value of then f′ would have a lower total
cost than f, and this is not possible because f is a
minimum cost flow. Similarly, it is not possible to further reduce for the same reason: even a 1 unit reduction in any of
these quantities would reduce the cost by at least
ϒK−k+1,
and this is greater than the total cost of all flow routing decisions made before the
λkℓ ∈
). Using (4)–(5) with k = 1 shows that it is not possible to
further reduce , because if any feasible flow f′
had a lower value of then f′ would have a lower total
cost than f, and this is not possible because f is a
minimum cost flow. Similarly, it is not possible to further reduce for the same reason: even a 1 unit reduction in any of
these quantities would reduce the cost by at least
ϒK−k+1,
and this is greater than the total cost of all flow routing decisions made before the
λkℓ ∈  , so this would (impossibly) reduce the cost of a
minimum cost flow. In short, the match
, so this would (impossibly) reduce the cost of a
minimum cost flow. In short, the match  from a feasible minimum cost flow f exhibits refined balance in the
sense of Definition 2. A match achieving refined balance in Definition 2 must, by virtue
of this definition, have achieved the smallest possible value of , and in particular
from a feasible minimum cost flow f exhibits refined balance in the
sense of Definition 2. A match achieving refined balance in Definition 2 must, by virtue
of this definition, have achieved the smallest possible value of , and in particular  has done this; moreover,
has done this; moreover,  has minimized , so it has minimized
has minimized , so it has minimized  δtc among all 1-to-m acceptable
matches with refined balance.
δtc among all 1-to-m acceptable
matches with refined balance.
References
- Arias E. US Life Tables, 2008. National Vital Statistics Reports. 2012;61:3. 9/24. Poisson Approximation and the Chen-Stein Method. [PubMed] [Google Scholar]
- Arratia R, Goldstein L, Gordon L. Poisson approximation and the Chen-Stein method (with Discussion) Statistical Science. 1990;5:403–434. [Google Scholar]
- Baiocchi M, Small DS, Yang L, Polsky D, Groeneveld PW. Near/far matching. Health Services and Outcomes Research Methodology. 2012;12:237–253. doi: 10.1007/s10742-012-0091-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bauer P, Kieser M. A unifying approach for confidence intervals and testing of equivalence and difference. Biometrika. 1996;83:934–937. [Google Scholar]
- Bertsekas DP. Linear Network Optimization. Cambridge, MA: MIT Press; 1991. [Google Scholar]
- Cook WJ, Cunnigham WH, Pulleyblank WR, Schrijver A. Combinatorial Optimization. New York: Wiley; 1998. [Google Scholar]
- Diestel R. Graph Theory. 4. New York: Springer; 2010. [Google Scholar]
- Fisher RA. Design of Experiments. Edinburgh: Oliver & Boyd; 1935. [Google Scholar]
- Goeman JJ, Solari A, Stijnen T. Three-sided hypothesis testing. Statistics in Medicine. 2010;29:2117–2125. doi: 10.1002/sim.4002. [DOI] [PubMed] [Google Scholar]
- Hansen BB, Klopfer SO. Optimal full matching and related designs via network flows. Journal of Computational and Graphical Statistics. 2006;15:609–627. [Google Scholar]
- Hansen BB. Optmatch. R News. 2007;7:18–24. (Package optmatch in R) [Google Scholar]
- Hansen BB. Prognostic analogue of the propensity score. Biometrika. 2008;95:481–8. [Google Scholar]
- Heller R, Manduchi E, Small DS. Matching methods for observational microarray studies. Bioinformatics. 2009;25:904–909. doi: 10.1093/bioinformatics/btn650. [DOI] [PubMed] [Google Scholar]
- Keele L, Titiunik R, Zubizarreta JR. Enhancing a geographic regression discontinuity design through matching to estimate the effect of ballot initiatives on voter turnout. Journal of the Royal Statistical Society. 2014 A, to appear. [Google Scholar]
- Kiefer J, Wolfowitz J. Consistency of the maximum likelihood estimator in the presence of infinitely many incidental parameters. Annals of Mathematical Statistics. 1956;27:887–906. [Google Scholar]
- Korte B, Vygen J. Combinatorial Optimization. NY: Springer; 2008. [Google Scholar]
- Lu B, Greevy R, Xu X, Beck C. Optimal nonbipartite matching and its statistical applications. American Statistician. 2011;65:21–30. doi: 10.1198/tast.2011.08294. (R package nbpmatching) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neuman MD, Rosenbaum PR, Ludwig JM, Zubizarreta JR, Silber JH. Anesthesia technique, mortality, and length of stay after hip fracture surgery. Journal of the American Medical Association. 2014;311:2508–2517. doi: 10.1001/jama.2014.6499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neyman J. On the application of probability theory to agricultural experiments. Statistical Science. 1923, 1990;5:463–480. [Google Scholar]
- Rosenbaum PR, Rubin DB. Constructing a control group using multivariate matched sampling methods that incorporate the propensity score. American Statistician. 1985;39:33–38. [Google Scholar]
- Rosenbaum PR. Optimal matching for observational studies. Journal of the American Statistical Association. 1989;84:1024–1032. [Google Scholar]
- Rosenbaum PR. Attributing effects to treatment in matched observational studies. Journal of the American Statistical Association. 2002;97:183–192. doi: 10.1198/jasa.2009.tm08470. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenbaum PR, Ross RN, Silber JH. Minimum distance matched sampling with fine balance in an observational study of treatment for ovarian cancer. Journal of the American Statistical Association. 2007;102:75–83. [Google Scholar]
- Rosenbaum PR, Silber JH. Amplification of sensitivity analysis in observational studies. Journal of the American Statistical Association. 2009a;104:1398–1405. doi: 10.1198/jasa.2009.tm08470. (amplify function in R package sensitivitymv) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenbaum PR, Silber JH. Sensitivity analysis for equivalence and difference in an observational study of neonatal intensive care units. Journal of the American Statistical Association. 2009b;104:501–511. doi: 10.1198/jasa.2009.tm08470. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenbaum PR. Design of Observational Studies. New York: Springer; 2010. [Google Scholar]
- Rubin DB. Estimating causal effects of treatments in randomized and nonrandomized studies. Journal of Educational Psychology. 1974;66:688–701. [Google Scholar]
- Silber JH, Rosenbaum PR, Clark AS, et al. Characteristics associated with differences in survival among black and white women with breast cancer. Journal of the American Medical Association. 2013;310:389–397. doi: 10.1001/jama.2013.8272. [DOI] [PubMed] [Google Scholar]
- Stuart EA. Matching methods for causal inference. Statistical Science. 2010;25:1–21. doi: 10.1214/09-STS313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Traskin M, Small DS. Defining the study population for an observational study to ensure sufficient overlap: a tree approach. Statistics in Biosciences. 2011;3:94–118. [Google Scholar]
- Yang D, Small DS, Silber JH, Rosenbaum PR. Optimal matching with minimal deviation from fine balance in a study of obesity and surgical outcomes. Biometrics. 2012;68:628–636. doi: 10.1111/j.1541-0420.2011.01691.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zubizarreta JR, Reinke CE, Kelz RR, Silber JH, Rosenbaum PR. Matching for several sparse nominal variables in a case-control study of readmission following surgery. American Statistician. 2011;65:229–238. doi: 10.1198/tas.2011.11072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zubizarreta JR, Paredes RD, Rosenbaum PR. Matching for balance, pairing for heterogeneity in an observational study of the effectiveness of for-profit and not-for-profit high schools in Chile. Annals of Applied Statistics. 2014;8:204–231. [Google Scholar]