Skip to main content
PMC home page
Nature Portfolio logoLink to Nature Portfolio
. 2015 Aug 4;6:7820. doi: 10.1038/ncomms8820

Universal self-field critical current for thin-film superconductors

E F Talantsev 1,a, J L Tallon 1,2,b
PMCID: PMC4532791  PMID: 26240014

Abstract

For any practical superconductor the magnitude of the critical current density, Jc, is crucially important. It sets the upper limit for current in the conductor. Usually Jc falls rapidly with increasing external magnetic field, but even in zero external field the current flowing in the conductor generates a self-field that limits Jc. Here we show for thin films of thickness less than the London penetration depth, λ, this limiting Jc adopts a universal value for all superconductors—metals, oxides, cuprates, pnictides, borocarbides and heavy Fermions. For type-I superconductors, it is Hc/λ where Hc is the thermodynamic critical field. But surprisingly for type-II superconductors, we find the self-field Jc is Hc1/λ where Hc1 is the lower critical field. Jc is thus fundamentally determined and this provides a simple means to extract absolute values of λ(T) and, from its temperature dependence, the symmetry and magnitude of the superconducting gap.

Inline graphicIn type-I superconductors the London penetration depth relates the self-field critical current density to the critical field. Here, the authors show that this relation extends to thin films of type-II superconductors, providing the chance to compute the penetration depth from critical current measurements.

Superconductors are characterized by two microscopic length scales: the London penetration depth, λ, and the coherence length, ξ. These strongly influence both their fundamental and applied behaviour, especially the critical current density Jc—above which the current becomes dissipative. In practical superconductors, which are all type II, Jc is arguably its most important property and for example, in the high-Tc superconductors, a huge effort has been expended in attempting to maximize Jc as a function of temperature, T, and magnetic field, H1. Jc falls rapidly with increasing external field, but even in zero external field the current flowing in the conductor generates a self-field that itself limits Jc. We refer to this limiting value as Jc(sf).

In a type-II superconductor, Jc is widely thought to be governed by pinning of flux vortices as well as by geometrical factors arising from the detailed pinning microstructure. As a consequence, much of the above-noted effort has been applied to modifying and tuning this microstructure. On the other hand, nearly a century ago Silsbee2 proposed that, for a type-I superconductor, the critical current ‘is that at which the magnetic field due to the current itself is equal to the critical magnetic field'. In other words, the self-field Jc is just that which is sufficient to generate a surface field equal to the critical field. By this was meant what we now understand to be the thermodynamic critical field, Hc, given by3

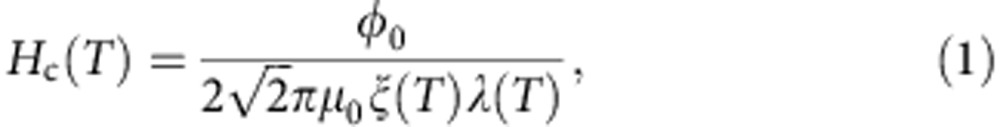graphic file with name ncomms8820-m1.jpg

where φ0 is the flux quantum and μ0 is the permeability of free space. Of course for a type-I superconductor, where flux vortices are absent, pinning is irrelevant and Silsbee's hypothesis is credible. Jc may depend on geometry but not on microstructure. But for a type-II superconductor, the general consensus that pinning governs Jc would insist that both geometry and microstructure are key players, and any kind of universal Silsbee criterion is untenable.

Here, by examining a wide range of experimental data, we ask whether this criterion does have any relevance to type-II superconductors. Surprisingly, the answer for conductors of thickness comparable to λ is yes, and here the relevant critical field is the lower critical field Hc1, given by3

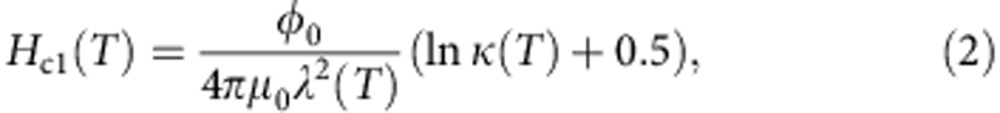graphic file with name ncomms8820-m2.jpg

where κ(T)=λ(T)/ξ(T) is the Ginsburg–Landau parameter, which is effectively constant under the logarithm. With this thickness constraint, we find for type-I superconductors:

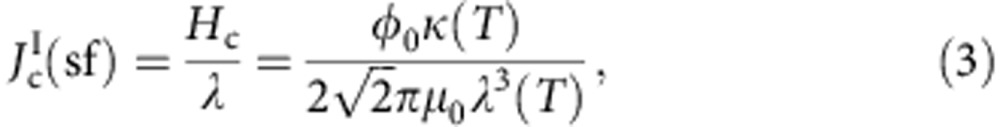graphic file with name ncomms8820-m3.jpg

and for type-II superconductors:

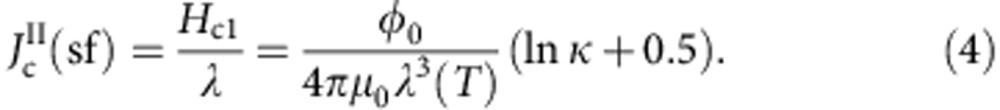graphic file with name ncomms8820-m4.jpg

As a consequence, Jc(sf) is fundamentally determined just by λ and ξ and independent of both geometry and microstructure. Because of the near constancy of ln(κ), for type-II superconductors Jc(sf) is dependent only on λ and this then provides a simple means to extract absolute values of λ(T) and, from its temperature dependence, the symmetry and magnitude of the superconducting gap. We present an indicative theoretical justification for this remarkably general and unexpected result, but we recognize that some questions remain to be resolved. We predict the doping and temperature dependence of Jc(sf) for YBa2Cu3O7–δ (YBCO) as a test of our hypothesis. Hereafter, we consider only self-field Jc values and therefore drop the identifier ‘sf', except where we feel it is still needed.

Results

Basic model

We consider a thin film of the type-II superconductor in the form of a long thin tape of rectangular cross-section in the x–y plane and of thickness 2b and width 2a, such that b<<a. Our conductor is of quasi-infinite length along the z axis in which a current of magnitude I is flowing along its axis. The tape interior is defined by −a≤x≤+a and −b≤y≤+b. According to London, in the Meissner state for small currents the self-field and transport current penetrate to a depth ∼λ, and the amplitude of the local surface current density, J, is4

graphic file with name ncomms8820-m5.jpg

where, in the usual notation, B is the magnetic flux density and H the field intensity, within the conductor surface. We use equation (5) to make an estimate of Jc when b≈λ. In this case (i) the current penetrates the entire cross-section, so that J is no longer a surface current density but is approximately global across the film thickness, and (ii) when the x-component of H reaches Hc1, vortices of opposite sign will tend to nucleate at the opposing surfaces and self-annihilate at the centre. They will do so both because of the Lorentz force driving them inwards and because of the attraction of overlapping vortices of opposite sign on opposite faces, which diverges logarithmically when b<λ. The consequent onset of dissipation defines J=Jc where, from equation (5), Jc≥Hc1/λ and equality only applies if this force exceeds surface and bulk pinning forces. In the following, we observe that equality is indeed found for a wide range of superconducting materials and this leads immediately to equation (4).

This very approximate analysis leaves many open questions. For example, for b>λ it is usual to discuss Jc in terms of flux entry from the edges. This is discussed later. Our approach is simply to examine the available data from self-field Jc studies on a wide variety of thin-film superconductors. If equation (4) does prove to be valid, then we have a simple means to determine absolute values of λ (and the superfluid density ρs≡λ−2) from measurements of Jc(T). The test of success is how well inferred values of λ concur with reported values. Moreover, the magnitude of the superconducting gap may then be determined from fitting the low-T behaviour of ρs as follows5. For s-wave symmetry:

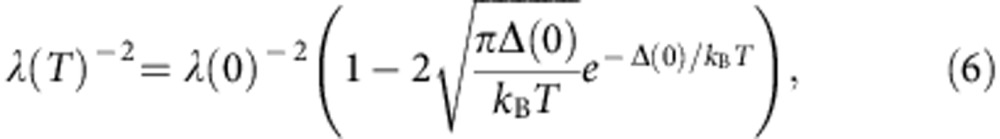graphic file with name ncomms8820-m6.jpg

while for d-wave symmetry:

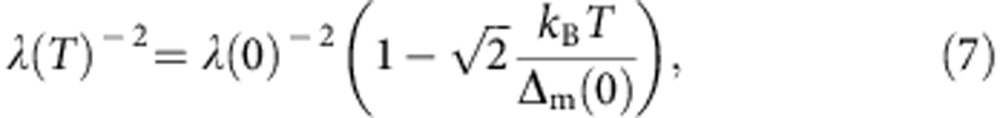graphic file with name ncomms8820-m7.jpg

where Δm is the maximum amplitude of the k-dependent d-wave gap, Δ=Δmcos(2θ).

London penetration depth

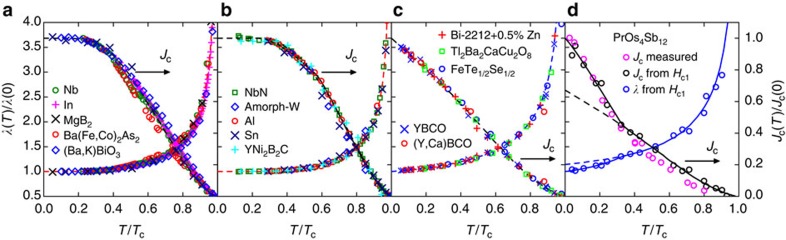
Figure 1 shows normalized plots of reported self-field Jc(T) values (right-hand scale, arrowed) for a wide range of superconductors including type I, type II, s-wave and d-wave. Also plotted are the inferred values of λ(T) (left-hand scale) calculated from the Jc(T) values by inverting equations (3) or (4), . Individual plots are presented and discussed in Supplementary Note 1. Panels (a) and (b) in Fig. 1 are s-wave, while (c) and (d) are d-wave superconductors. For both s- and d-wave cases, the T-dependence of κ, calculated from λ × Δ (ref. 6), is weak and, in view of the logarithm and the cube root, we conveniently take κ to be constant. The residual effect of a T-dependent κ is discussed in Supplementary Note 2. Values of κ are sourced from the literature and are listed in Supplementary Table 1.

Figure 1. Summary of reported Jc and calculated λ.

Figure 1

Open in a new tab

The temperature dependence of the normalized penetration depth, λ(T)/λ(0) (left-hand scale) calculated from the normalized values of self-field critical current density, Jc(T)/Jc(0) (right-hand scale, as indicated by arrows) for many different type-I and type-II superconductors. Values of λ(T) are calculated using equations (3) and (4). (a,b) s-wave superconductors. (c,d) d-wave superconductors, as also seen by their very different low-T behaviour. The dashed red curves are the fitted s-wave weak-coupling T-dependence of λ(T) and the dashed blue curves are the d-wave counterparts. The dashed black curves are Jc back-calculated from these λ(T) curves using equations (3) and (4). The deduced normalization parameters, Tc, Jc0 and λ0=λ(0) are listed in Supplementary Table 1. (d) A slightly different analysis for PrOs4Sb12. Both Jc and λ are calculated from measurements of Hc1 using equation (4), and the calculated Jc is compared with values measured from remnant magnetization (magenta data points). They are in excellent agreement. The two curves (dashed and solid) are obtained by adding two separate d-wave superfluid densities below 0.6 K.

Our approach is as follows. From Jc(T) data we calculate the λ data points as plotted. Using λ0 as the only fitting parameter, we then fit theoretical s-wave (dashed red) or d-wave (dashed blue) curves6. From these curves, we back-calculate Jc(T) to give the dashed black curves, from which Jc0 is found. These deduced values of λ0 and Jc0 are listed in Supplementary Table 1. The calculated λ(T) data points are then fitted at low-T using equations (6) or (7), to determine Δ0. This is done using the nonlinear curve fit routine in the plot package ‘Origin'. All data sources, film thicknesses and results are also summarized in Supplementary Table 1 along with reported values of λ0 and Δ0 for comparison with our inferred values.

In Fig. 1, the radical difference between s-wave and d-wave symmetry at low T is immediately apparent. In the former case Jc(T) exhibits an exponential plateau due to the isotropic gap, while in the latter Jc(T) remains linearly increasing due to the nodal d-wave gap, in either case consistent with equations (6) or (7), . Figure 1a shows examples of s-wave superconductors: Nb, In, MgB2, Ba(Fe,Co)2As2 and (Ba,K)BiO3. The fit with the weak-coupling s-wave model is excellent though MgB2 and Ba(Fe,Co)2As2 show small deviations, possibly due to multiple gaps on distinct bands7.

Figure 1b shows the same analysis for five samples where the fit is better using the dirty s-wave model. YNi2B2C will be discussed later. For the type-I elements Al, Sn and In in Fig. 1, we have used equation (3). This is the so-called London depairing current density. We discuss this in relation to the Ginzburg–Landau depairing current density in Supplementary Note 5. For weak-coupling, s-wave superconductors κ1/3 changes by <5% between 0≤T≤Tc so by assuming constancy of κ we again infer that 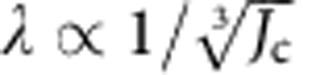Inline graphic, but here with a different prefactor. The data for Al, Sn and In in Fig. 1a,b strongly support this analysis, and the deduced values of λ0 shown in Supplementary Table 1 are in excellent agreement with directly measured values.

Next, Fig. 1c shows five d-wave examples: FeTe0.5Se0.5, YBa2Cu3O7, 1% Ca-doped YBa2Cu3O7, 0.5% Zn-doped Bi2Sr2CaCu2O8 and Tl2Ba2CaCu2O8. For each of these samples, the fit to the weak-coupling d-wave model is excellent across the entire temperature range. This is surprising because other techniques such as muon spin relaxation8 suggest that the T-dependence of ρs does not always follow the canonical d-wave form.

Finally, for Fig. 1d PrOs4Sb12, we used a different approach. From reported data for Hc1 (ref. 9), we calculated both Jc(T) and λ(T) from equation (4) using κ=29.7 (refs 10, 11). Both parameters reveal a transition to a second phase below 0.6 K (ref. 9), which results in an additional reduction of λ(T). The two distinct curves (dashed and solid) are obtained by adding two separate d-wave superfluid densities below 0.6 K. Cichorek et al.9 also determined Jc(T) from remanent magnetization measurements. This is shown by the magenta symbols and, significantly, Jc(T) shows an enhancement below 0.65 K that almost exactly mirrors our Jc(T) values calculated from Hc1. This represents a quite exacting test of our central thesis.

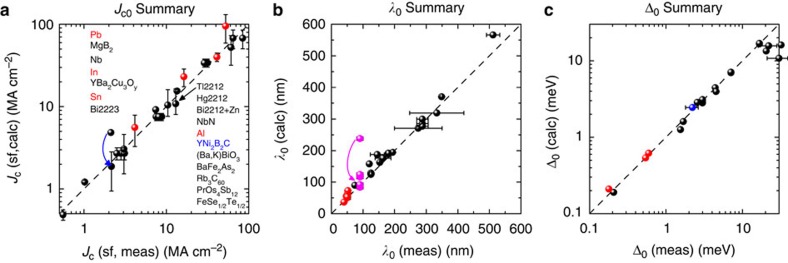
All our results for calculated absolute values of Jc0, λ0 and Δ0 are plotted versus measured values in Fig. 2. The error bars reflect the 2σ-uncertainties in measured values of λ0 or Δ0 summarized in Supplementary Table 1. In each case the correlation is excellent and it is this that validates our primary conclusion. Supplementary Note 3 shows how these results validate Silsbee's hypothesis. Figure 2a shows that, using equations (3) and (4), Jc scales with λ−3 over nearly three orders of magnitude. The only significant outlier is YNi2B2C (ref. 12), but this is our only example for which b>λ. Applying the thickness-correction factor (λ/b)tanh(b/λ), as introduced below, the calculated Jc0 now falls close to the dashed line as indicated by the curved blue arrow.

Figure 2. Summary comparison of calculated and measured values.

Figure 2

Open in a new tab

(a) Comparison of calculated thin-film self-field Jc0 values with measured Jc0 values. Jc0 is calculated from reported λ values using equations (3) and (4). Red data points are type-I superconductors, black data points are type II. The blue arrow for YNi2B2C shows the effect of the correction factor (λ/b)tanh(b/λ), discussed in the text, when b>λ. Error bars reflect the range of reported λ0 values—see Supplementary Table 1. The sample annotation follows the vertical order of the data points. (b) λ0 values calculated from reported Jc(T) data and plotted versus independently measured λ0 values. The magenta arrow and symbols show the effect of improvement over time in self-field Jc for six films of MgB2. The data terminates on the dashed line where Jc is now fundamentally limited by the superfluid density. Comparative data for YBCO over time is shown in Supplementary Figure 4. (c) Summary of values of Δ0 calculated from the low-T behaviour of λ(T) using equations (6) and (7), plotted versus measured values of Δ0.

Figure 2b shows values of λ0 calculated from Jc. As hypothesized, the best Jc values give values of λ0 that match the measured values. In other films, where Jc is low due to impurities, weak links or misalignment, λ0 always exceeds the measured values. This is especially notable where a system has been improved over time, as for example, with the six films shown for MgB2 (magenta data points). Here the inferred values of λ descend towards the dashed line, as shown by the magenta arrow, as films were progressively improved. They do not fall below the line. A similar data progression over time for YBCO is discussed in Supplementary Note 6. Jc(T) is thus fundamentally limited by λ and not, for example, by the pinning, as we discuss further below. It is also important to recognize that the close correlation seen in Fig. 2b does not artificially arise simply from error reduction by taking the cube root to extract λ. This correlation is also seen without the cube root in Fig. 2a over now a much wider range, and also notably, where the relative order of type-I and type-II materials is significantly altered, but without loss of correlation.

Energy gaps and symmetry

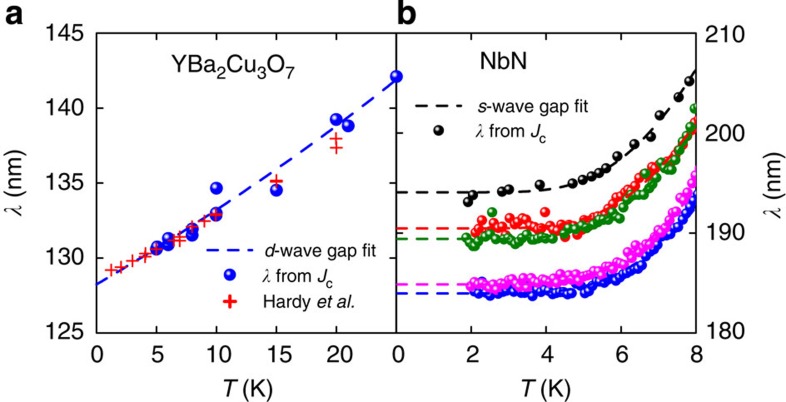
We select two examples to illustrate the calculation of Δ0. Figure 3a,b shows the contrasting low-T data for λ(T) calculated from Jc(T, sf) for (a) YBa2Cu3O7 (this work) representing the d-wave case, and (b) five films of NbN (refs 13, 14, 15), representing the s-wave case. The dashed black curves are the data fits to equations (7) and (6), respectively. For YBa2Cu3O7, the inferred gap value, Δ0=16.6 meV, compares well with the tunnelling measurements of Dagan et al.16 (16.7 meV) and gives the ratio 2Δ0/kBTc=4.26 close to the d-wave weak-coupling ratio 4.28. It also compares well with the estimate of 17.7 meV from the condensation free energy17, but infrared ellipsometry measurements give a higher value of 25 meV (ref. 18). And generally, our calculated values of Δ0 for the cuprate superconductors tend to be lower than reported values. Partly, this is due to the lack of very low-T data for Jc, but in fact experimental values of gap magnitudes in the cuprates remain contentious. Tunnelling and ARPES data tend to show the presence of the (generally) larger pseudogap, and in our view the most reliable means of distinguishing the two is Raman scattering where B2g symmetry exposes the superconducting gap around the nodes, while B1g exposes the pseudogap around the antinodes19. In the present case, any sample that is optimally doped will have the pseudogap present and this will steepen the slope in λ(T), thus reducing the inferred gap magnitude. The red crosses show the low-T penetration depth measurements of Hardy et al.20 and the agreement with ours, determined from Jc, is excellent.

Figure 3. Low-temperature fits: gap symmetry.

Figure 3

Open in a new tab

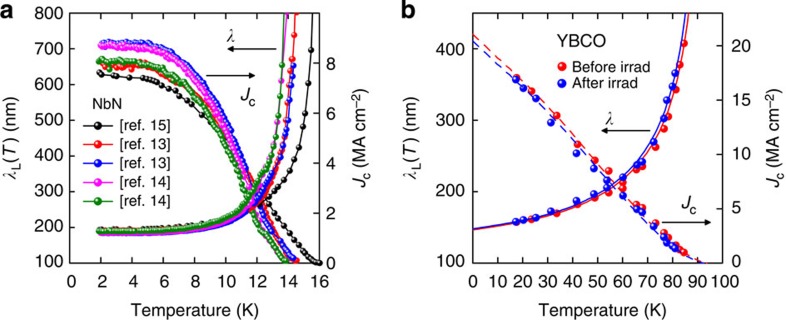
(a) The low-T fit to λ(T) data determined from our measurements of Jc(sf) for YBa2Cu3O7 using equation (7). The fit yields λ=128.3 nm and Δ0=16.6 meV. The red crosses show the low-T penetration depth measurements of Hardy et al.20 for comparison. (b) The low-T fit to λ(T) for NbN using equation (6) to determine Δ0. The characteristic flat T-dependence of s-wave superconductors at low T is evident. The fits yield λ=189 nm and Δ0=2.95 meV.

For NbN, we show in Fig. 3b fits to five data sets13,14,15. Here <λ0> is found to be 189 nm with <3% variation. The s-wave fits yield <Δ0>=2.95 meV with <5% variation and we find 2Δ0/kBTc=4.13, somewhat more than the weak-coupling s-wave limit of 3.53. Independent measurements21 give 2Δ0/kBTc=4.24, which is rather close to our value.

Figure 2c shows inferred Δ0 values calculated for all 17 superconductors plotted against measured values as listed in Supplementary Table 1. There is generally good agreement over two orders of magnitude and across all systems. We note that equations (6) and (7) are restricted to the weak-coupling limit and this does not apply to all the samples investigated. In the case of Bi2Sr2Ca2Cu3O10, the estimated value of Δ0 is particularly low and this is due to the presence of two-layer intergrowths as is evident in the original paper. This causes λ(T)−2 to rise more rapidly below 90 K and thus yield a low value for Δ0. As noted, for the cuprates in general Δ0 values do tend to be low. This could be an indication of strong coupling but, if the samples are optimally doped then already the competing pseudogap is present22 and this will diminish the inferred Δ0 values. This can only be clarified via the doping dependence of the low-T behaviour of Jc(T) where, in the sufficiently overdoped region, the pseudogap is no longer present.

Doping dependence of J c in YBa2Cu3O7–δ

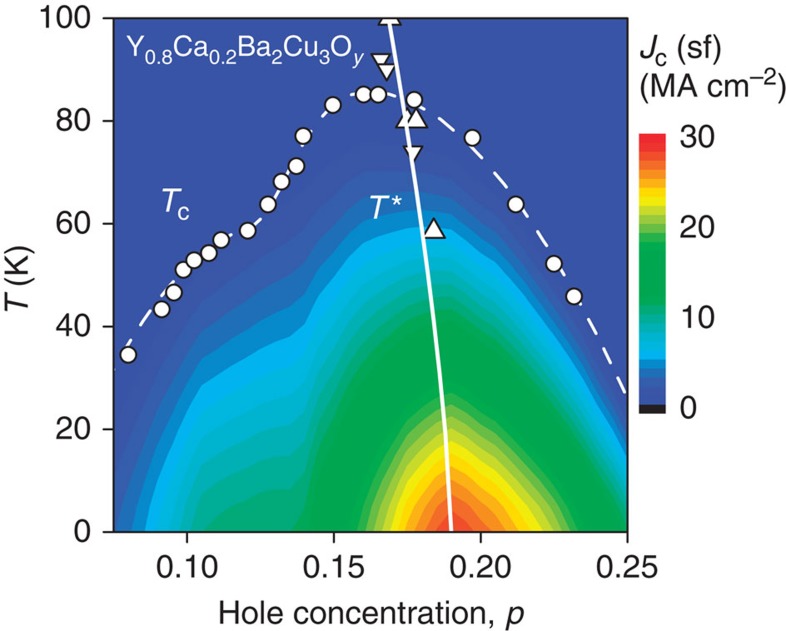
We conclude that the self-field Jc(T) for high-quality, weak-link-free thin films with b≤λ appears to be a fundamental quantity, governed only by the absolute value of the superfluid density. If so we may use the superfluid density to predict the evolution of Jc(T, p) with doping, p, for high-Tc cuprates. Figure 4 shows the self-field Jc calculated in this way from the ground-state doping-dependent superfluid density, ρs(0), reported previously for Y0.8Ca0.2Ba2Cu3O7–δ (refs 23, 24). Using 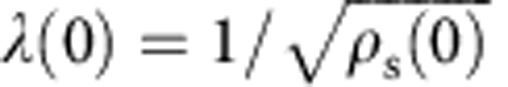Inline graphic and the theoretical d-wave T-dependence of ρs(T)/ρs(0) (ref. 6), we generate the full p- and T-dependence of Jc, which is shown as a false-colour map in the p–T plane in Fig. 4.

Figure 4. Predicted Jc across the YBCO phase diagram.

Figure 4

Open in a new tab

Map of Jc(sf) across the phase diagram for Y0.8Ca0.2Ba2Cu3Oy calculated from the superfluid density23,24 using equation (4). A sharp peak is centred on the critical doping where the pseudogap T* line falls to zero (solid white curve). The triangles show the low-T data points for T* reported from field-dependent resistivity29. A second smaller peak is predicted just below P≈0.12 where charge ordering has been reported33. The circles are Tc data points.

Predicted values are seen to rise to a sharp maximum of about 30 MA cm−2 centred at p=0.19 holes per Cu in the slightly overdoped region, beyond optimal doping (P≈0.16) where Tc reaches its maximum. (Doping with Ca introduces some impurity scattering that lowers the superfluid density. As a consequence, the maximum Jc is less than that predicted from the superfluid density for Ca-free YBa2Cu3O7: 37 MA cm−2 for nearly fully oxygenated chains, and ∼42 MA cm−2 for fully ordered chains25.)

It is important to understand the significance of this skewed behaviour of Jc(p) relative to optimal doping shown in Fig. 4. High-Tc cuprates are characterized by the opening of a gap in the normal-state excitation spectrum, which is probably associated with reconstruction of the Fermi surface due to short-range magnetic order26,27,28. This phenomenon is associated with the so-called pseudogap that dominates the properties of optimally doped and under-doped cuprates, resulting in ‘weak superconductivity' as indicated by a reduction in condensation energy, superfluid density and their associated critical fields22.

The link between Jc and the pseudogap is made by plotting in Fig. 4 the previously determined T* line where the pseudogap closes, as determined from field-dependent resistivity studies on epitaxial thin films29,30. The T* data extend to much higher temperatures, but some of the lower-T data points are visible in the plot. The key result here is that Jc maximizes just at the point where the pseudogap closes and T*→0. Note, also, how the ridge in Jc(T, p) follows the T* line, inclining towards lower doping at higher T notwithstanding the fact that these two quantities are determined by quite different techniques. Clearly the rapid decline in Jc below T* is due to the opening of the pseudogap and the consequent crossover to weak superconductivity. One is also impressed by the resemblance between this phenomenology and that associated with the presence of a quantum critical point31, where a ‘bubble' of high Jc is centred on the point where T*→0.

This sharp peak in Jc(p) at p=pcrit is recently confirmed by our wider group32, but Fig. 4 also predicts a second smaller peak at p≈0.12. This second peak is also apparent in the upper critical field Hc2 of YBa2Cu3O7–δ (ref. 33), and the search for a second peak in Jc provides a strong test for the present ideas. A similar double peak in ρs(p) is found in La2–xSrxCuO4 (ref. 34), suggesting that a double peak in Jc(p) will be a common, perhaps universal, cuprate behaviour. Another test is that if Jc(T) varies as 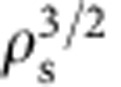Inline graphic, then Jc(0)2/3 should be diminished by impurity scattering in the same canonical way that the superfluid density is reduced35. This is distinguished by a much more rapid reduction in ρs than in Tc. These ideas can be tested in Zn-substituted YBa2Cu3O7–δ and have recently been confirmed by us.

Refined model

We return now to better justify the theoretical basis for our observations. The usual approaches to field distribution and critical currents are those of Brojeny and Clem36 and Brandt and Indenbom37, where for a very thin film the y-component of this field, By(x=±a), diverges at the film edges36. As a consequence, Abrikosov vortices must enter from the edges and there then exists a domain extending in from the edges where the local current density J(x) is constant (=Jc) and in which these vortices are pinned. At the inner edge of this domain, By falls to zero with infinite slope37. The onset of dissipation, defining the overall film Jc, occurs when this domain extends to the centre of the film at x=0 and Jc is now the global value not just the local value.

But, as we have suggested, an alternative approach is to consider the entry of vortices, not from the edges but from the large flat surfaces. For a very thin conductor the x-component of this self-field at the surface, Bx(x, y=±b), is uniform across the width and of magnitude μ0bJ (ref. 36). Consequently, if the current I is increased until this field reaches B=Bc1, then vortices will nucleate at the flat surface in the form of closed loops around the conductor surface normal to the transport current38. These loops will tend to collapse inwards under the self-imposed Lorentz force (J × B) on each vortex. It is only surface and bulk pinning that will prevent them from migrating to the conductor centre and self-annihilating there. Thus, inverting the above relation

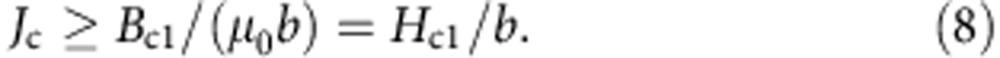graphic file with name ncomms8820-m11.jpg

where the inequality arises from the, as yet, indeterminate role of pinning.

Now consider the interesting case when b≈λ. These vortex loops now experience the additional attractive force of adjacent vortices of opposite sense located just λ apart. This force becomes unbounded and thus inevitably overcomes pinning. The vortices mutually annihilate at the centre and the process continues indefinitely causing dissipation. This vortex entry from the faces defines a first critical current density given by the equality sign in equation (8), which is alternative to a second, which is associated with vortex entry from the edges. Which of these has the smaller Jc and therefore is the operative mechanism?

To answer this, let us suppose that J=Hc1/b over the full conductor cross-section and we calculate the degree of flux entry at the edges. Rearranging equation (13) of Brojeny and Clem36 (or indeed equation (8) for a non-vanishingly-thin film) the y-component of the field near the edges for a uniform current distribution becomes

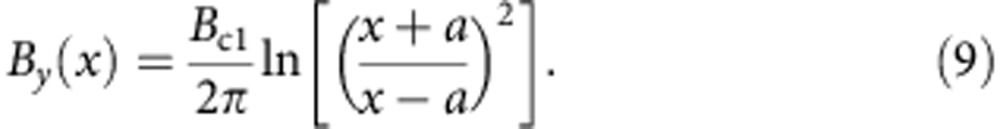graphic file with name ncomms8820-m12.jpg

From this we find that By falls to the value of Bc1 when x=±0.917a, that is, perpendicular vortices can enter at either edge to only 4.2% of the film width. Thus the dominant mechanism for Jc when b≈λ is flux entry from the large flat surfaces and Jc is given by:

graphic file with name ncomms8820-m13.jpg

We note that, when b=λ, equation (10) becomes equivalent to equation (4), but there is yet one final ingredient to add. The energy of formation of a vortex/anti-vortex pair on opposite faces of the film is reduced by an interaction term 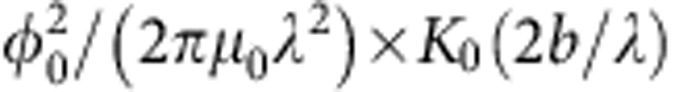Inline graphic (ref. 38). Here K0(x) is the zeroth-order Bessel function of the second kind, and 2b is the vortex separation. This diverges logarithmically at small b so that Bc1 is reduced as 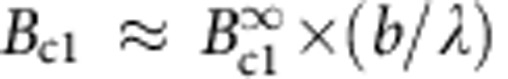Inline graphic, where 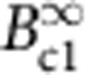Inline graphic is the bulk value at large b. We adopt a heuristic crossover between the two limits in the form 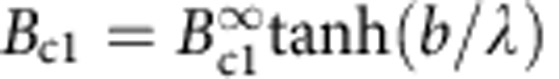Inline graphic. Combining with equation (10) and dropping the ∞ sign, we obtain our final result:

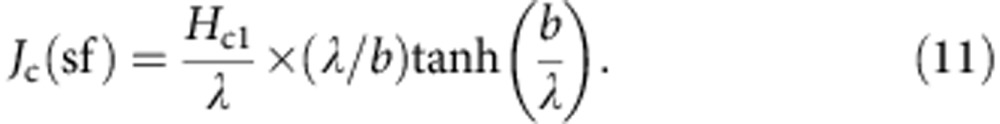graphic file with name ncomms8820-m18.jpg

where Hc1 is the bulk value. This concurs with equation (4) but with the additional correction factor (λ/b)tanh(b/λ). This accounts for all isotropic superconductors in Figs 1 and 2 with b<λ. In the case of anisotropic superconductors with λx<λy (as in the case of high-Tc cuprates), we simply rescale the problem b→b × (λx/λy) and Jc in equation (11) becomes:

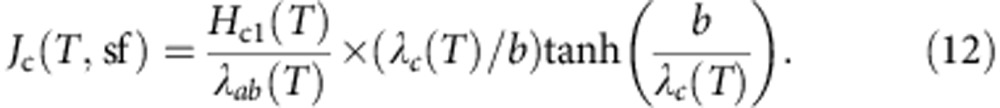graphic file with name ncomms8820-m19.jpg

Here we have replaced λy by λc and λx by λab, as is the usual convention for the cuprates, where λc>λab. Equation (12) is the full generalization of equation (4). For b<λc, we recover equation (4), while for b>λc we recover the 1/b falloff in Jc. A consequence of this is that if b≤λc(0), then equation (4) remains applicable to the highest temperatures because λc(T) diverges as T→Tc and the small-b limit is preserved. Let us now compare this functional dependence on b with experimental data.

Figure 5a shows our analysis using equation (4) of five sets of Jc(T) data for NbN. Four13,14 have b=4 nm and one15 has b=11 nm, all much less than λ=194 nm. Despite these different thicknesses, all five data sets yield values of λ close to this measured value (see Supplementary Table 1). The implication is that equation (4) is accurate for all b≤λ. In contrast, for the alternative case b>λ, Stejic et al.39 report for Nb-Ti films an inverse thickness dependence of Jc(T), where Jc∝1/b. This is precisely what we argue above.

Figure 5. Thickness and irradiation dependence of Jc.

Figure 5

Open in a new tab

The T-dependence of Jc(sf) and λ calculated from equation (4) for thin films of (a) NbN with different thicknesses, b=4 nm (refs 13, 14) and 11 nm (ref. 15) and different bridge widths. (b) YBCO before and after ‘nano-dot' irradiation45. The solid red and blue curves are weak-coupling d-wave fits to the calculated λ(T) data, before and after irradiation, respectively. The red and blue dashed curves are the respective back-calculated Jc(T) curves from these d-wave fits. Note in a the small variation in λ0 despite the quite large variation in Jc, and λ0 is evidently independent of b when b<λ. Values of Δ0=2.95±0.02 meV obtained from fitting the low-T behavior of λ(T) also reveal little variation. In b, Jc(sf) and λ are independent of irradiation despite the large increase in pinning evidenced by a 60% increase in Jc(T, H) above 1 Tesla.

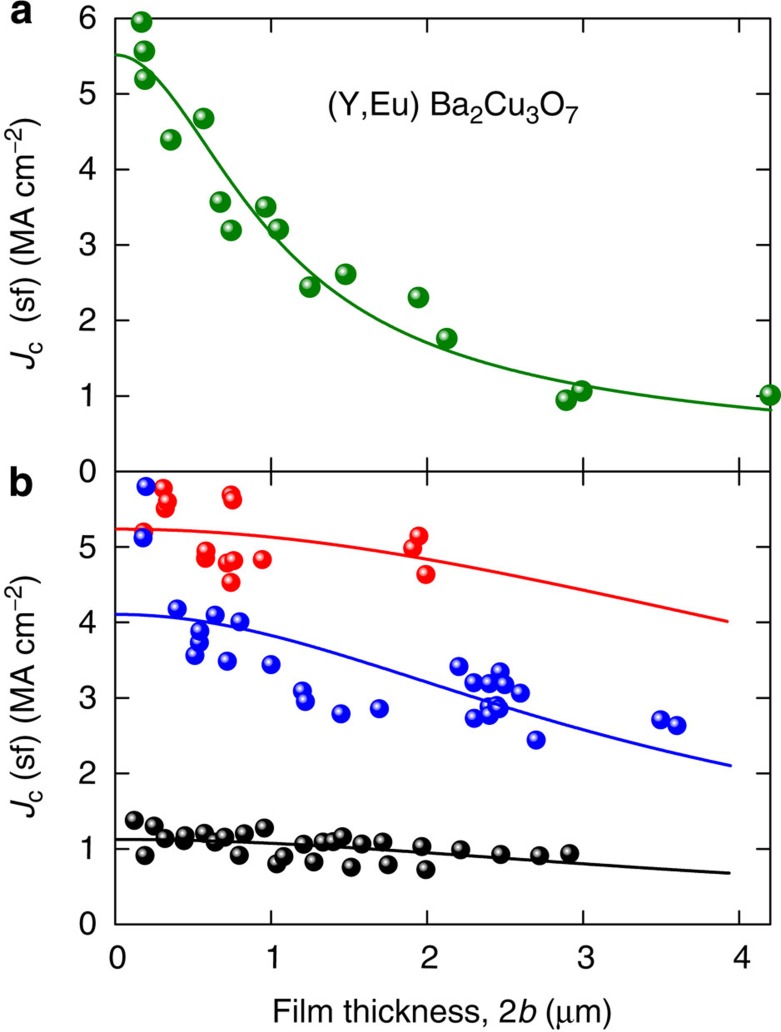
Pursuing this further, Zhou et al.40 report self-field Jc measurements on many epitaxial thin films of YBa2Cu3O7–δ and (Y0.67Eu0.33)Ba2Cu3O7–δ of varying thickness deposited on SrTiO3 by pulsed laser deposition. Figure 6a shows the Jc data measured at 75.5 K as a function of film thickness (data points). Also plotted is equation (12) fitted to this data—solid curve. The excellent agreement is misleading. The value of λc=620 nm is too low and reflects a non-uniform composition and microstructure, which grows with increasing film thickness. Fits to other available data including Foltyn et al.1 and Arendt et al.41 give similar λc values, 634 and 654 nm, respectively. Again these are smaller than the expected ≥1,100 nm. In contrast, Fig. 6b shows data for films with an intentionally highly uniform through-thickness microstructure42,43,44. In the case of Feldmann42, this uniformity was confirmed by progressive ion milling of a single film. Here the λc values shown in the figure are now indeed realistic.

Figure 6. Thickness dependence of Jc for YBCO.

Figure 6

Open in a new tab

Jc(sf) for epitaxial YBCO films versus film thickness. (a) (Y0.67Eu0.33)Ba2Cu3O7–δ at T=75.5 K, from Zhou et al.40 The solid curve is equation (12) with λc=620 nm. This value is too low and reflects increasingly non-uniform composition and microstructure across the thickness. (b) YBCO systems with a highly uniform through-thickness microstructure: Feldmann et al.42 (black data points and curve), with λab(77)=339±5 nm and λc(77)=1,153±238 nm progressively thinned by ion milling; Zhou et al.43 (blue data points and curve) gives λab(75.6)=253±4 nm and λc(75.6)=1,063±28 nm; Feldmann et al.44 (red data points and curve) gives λab(75.6)=233±2 nm and λc(75.6)=1,980±790 nm.

We conclude that equations (11) and (12) provide a good description of Jc for uniform films in the general case when b≠λ. Of course, as b is increased, the alternative Jc mechanism involving flux entry from the edges must eventually become dominant.

Pinning

Our claim is that self-field Jc is independent of pinning when b≤λ unless, perhaps, very strong pinning is introduced. We illustrate this with one of the few examples available. Lin et al.45 scribed an array of nanocolumns into a YBCO microbridge using a focused electron beam. The array had a lattice constant of 90 nm (corresponding to a matching field of 0.25 Tesla) and diameters about double the coherence length at 77 K, while the film thicknesses were 50 and 90 nm, thus satisfying our condition b≤λ. We show our analysis of the H=0 self-field Jc in Fig. 5b. These authors report a 60% increase in the in-field Jc(T) above 1 Tesla but, we note, there is essentially no change in Jc(T, sf), indeed a small decrease consistent with a small loss of effective cross-sectional area. There is no change in the inferred λ0. Thus the evident increase in bulk pinning and inevitable changes in surface roughness and surface pinning have no apparent effect on Jc(T, sf), consistent with our hypothesis. Similarly, with 25 MeV 16O ion irradiation of YBCO films Roas et al.46 report an 80% increase in Jc above 1 Tesla, but a significant reduction in Jc(sf). On the other hand, a later study by this group47 showed fast neutron irradiation lifted Jc(sf) at 4.2 K from 19.4 to 32 MA cm−2. While this is no more than the Jc(0, sf) values we quote above for our pristine films, it suggests that strong pinning could, in the extreme, overtake the Silsbee mechanism we advance here. But here they use an extremely high electric field criterion of 50 μV cm−1, and the apparent enhancement could simply be caused by a reduction in n-value due to irradiation. Later neutron irradiation studies48,49,50 on epitaxial YBCO films, reported only a detrimental effect on Jc(sf) while lifting in-field performance. On the basis of this, we feel it still remains to be confirmed that pinning centres created by irradiation can improve Jc(sf). Further literature examples supporting the pinning independence of Jc(sf) are given in Supplementary Note 4.

Discussion

We have shown that for thin films of thickness b<λ, the self-field Jc is given by Hc/λ for type-I superconductors and Hc1/λ for type-II superconductors. This provides a simple, direct means to determine the absolute magnitude of the penetration depth and means that, contrary to widespread thinking, Jc(T, sf) is a fundamental property independent of pinning landscape and microstructural architecture. We have thus confirmed Silsbee's hypothesis for all the superconductors we have examined. In the case of the cuprates, our prediction of a sharp peak in Jc(p, sf) at the critical doping, where T*→0, is borne out in separate studies32.

To conclude, we suggest the following possible tests of the ideas we have presented. We predict a second peak in Jc(p, sf) near p≈0.12, near which charge ordering occurs33, and we suggest that, for Zn-substituted YBa2Cu3Oy, Jc(sf)2/3 will be suppressed by impurity scattering in the same canonical manner as the superfluid density. Along with this the T-dependence of Jc(sf) should cross over from a linear-in-T behaviour to T2 consistent with the superfluid density6. A further key test would be to measure and correlate both superfluid density and self-field Jc in a single film as a function of progressive disorder via irradiation. Inspection of equation (11) shows that, with increasing film thickness, Jc(sf) should cross over from a λ−3 dependence when b<λ to a λ−2 dependence when b>λ. It should be relatively straightforward to test this. The approach reported here should readily translate to superconducting nanowires and could be used to measure the transport mass anisotropy in layered superconductors by comparing Jc(sf) measurements in a-axis- and c-axis-aligned films. A key challenge will be to treat the crossover from a Silsbee-dominated mechanism in self-field to a more conventional pinning-dominated mechanism with flux entry from the edges as external field is increased. The implications for a.c. loss should be explored and, finally, the model we present here lends itself to an error-function onset to resistance (rather than the conventional power law) due to the local distribution of superfluid density51.

Methods

Data sources—self-field critical current density

Of the vast literature for Jc, surprisingly few data sets are available that meet the collective requirements for the present analysis. These are as follow: we require transport (not magnetization) Jc data; data reported under self-field conditions; Jc data for weak-link-free thin films; in which b≤λ; and that extend down to temperatures, T≤0.2Tc. The analyses reported here more or less exhaust the available data.

Data sources—penetration depth

We have chosen to test equations (3) and (4) using literature data for λ0 and not for Hc and Hc1 for which even recent literature shows quite divergent values. An illustrative example reports a breakdown of the Uemura relation between Tc and ρs by a factor of eight, based on Hc1 data for Ba0.6K0.4Fe2As2 (ref. 52). Subsequent measurements of superfluid density using muon spin relaxation showed that this system was in fact in full agreement with the Uemura relation53,54,55. Early penetration depth data are variable in quality, and microwave measurements often do not yield absolute values, probing as they do values of Δλ=λ(T)—λ(0), only. Where possible we have relied on muon spin relaxation or polarized neutron reflectometry for λ values, because these directly probe the field profile and tend to be rather reproducible from one group to another. Where possible we also give multiple sources, and the ranges from these sources are reflected in Supplementary Table 1 and the error bars in Fig. 2 and Supplementary Fig. 2.

Additional information

How to cite this article: Talantsev, E. F. & Tallon, J. L. Universal self-field critical current for thin-film superconductors. Nat. Commun. 6:7820 doi: 10.1038/ncomms8820 (2015).

Supplementary Material

Supplementary Information

Supplementary Figures 1-4, Supplementary Tables 1, Supplementary Notes 1-6 and Supplementary References

ncomms8820-s1.pdf (406.7KB, pdf)

Acknowledgments

J.L.T. thanks the Marsden Fund of New Zealand and the MacDiarmid Institute for Advanced Materials and Nanotechnology for financial support. We also thank N.M. Strickland, S.C. Wimbush and J.G. Storey for developing the HTS-based Jc measuring rig, and Professor A.M. Campbell, S.C. Wimbush, A. Malozemoff and the referees for helpful comments on this manuscript.

Footnotes

Author contributions Both authors contributed equally to all aspects of this work.

References

  1. Foltyn S. R. et al. Materials science challenges for high-temperature superconducting wire. Nat. Mater. 6, 631–642 (2007). [DOI] [PubMed] [Google Scholar]
  2. Silsbee F. B. Note on electrical conduction in metals at low temperatures. J. Franklin Inst. 184, 111 (1917). [Google Scholar]
  3. Poole C. P., Farach H. A., Creswick R. J. & Prozorov R. Superconductivity Chaps 2, 11, 12, 14, Academic Press (2007). [Google Scholar]
  4. London H. Phase-equilibrium of supraconductors in a magnetic field. Proc. R. Soc. Lond. A 152, 650 (1935). [Google Scholar]
  5. Prozorov R. & Kogan V. G. London penetration depth in iron-based superconductors. Rep. Prog. Phys. 74, 124505 (2011). [Google Scholar]
  6. Won H. & Maki K. d-wave superconductor as a model of high-Tc superconductors. Phys. Rev. B 49, 1397–1402 (1994). [DOI] [PubMed] [Google Scholar]
  7. Kogan V. G., Martin C. & Prozorov R. Superfluid density and specific heat within a self-consistent scheme for a two-band superconductor. Phys. Rev. B 80, 014507 (2009). [Google Scholar]
  8. Sonier J. E. et al. Hole-doping dependence of the magnetic penetration depth and vortex core size in YBa2Cu3Oy: evidence for stripe correlations near 1/8 hole doping. Phys. Rev. B 76, 134518 (2007). [Google Scholar]
  9. Cichorek T. et al. Pronounced enhancement of the lower critical field and critical current deep in the superconducting state of PrOs4Sb12. Phys. Rev. Lett. 94, 107002 (2005). [DOI] [PubMed] [Google Scholar]
  10. MacLaughlin D. E. et al. Muon spin relaxation and isotropic pairing in superconducting PrOs4Sb12. Phys. Rev. Lett. 89, 157001 (2002). [DOI] [PubMed] [Google Scholar]
  11. Bauer E. D., Frederick N. A., Ho P.-C., Zapf V. S. & Maple M. B. Superconductivity and heavy fermion behavior in PrOs4Sb12. Phys. Rev. B 65, 100506(R) (2002). [Google Scholar]
  12. Wimbush S. C., Schultz L. & Holzapfel B. Critical current in YNi2B2C and HoNi2B2C thin films. Physica C 388-389, 191–192 (2003). [Google Scholar]
  13. Bartolf H., Engel A., Schilling A., Ilin K. & Siegel M. Fabrication of metallic structures with lateral dimensions less than 15 nm and Jc(T)-measurements in NbN micro- and nanobridges. Physica C 468, 793–796 (2008). [Google Scholar]
  14. Engel A. et al. Temperature- and field-dependence of critical currents in NbN microbridges. J. Phys. Conf. Ser. 97, 012152 (2008). [Google Scholar]
  15. Clem J. R., Bumble B., Raider S. I., Gallagher W. J. & Shih Y. C. Ambegaokar-Baratoff-Ginzburg-Landau crossover effects on the critical current density of granular superconductors. Phys. Rev. B 35, 6637–6642 (1987). [DOI] [PubMed] [Google Scholar]
  16. Dagan Y., Krupke R. & Deutscher G. Determination of the superconducting gap in YBa2Cu3O7–δ by tunneling experiments under magnetic fields. Phys. Rev. B 62, 146–149 (2000). [Google Scholar]
  17. Tallon J. L., Barber F., Storey J. G. & Loram J. W. Coexistence of the superconducting energy gap and pseudogap above and below the transition temperature of cuprate superconductors. Phys. Rev. 87, 140508(R) (2013). [Google Scholar]
  18. Yu L. et al. Evidence for two separate energy gaps in underdoped high-temperature cuprate superconductors from broadband infrared ellipsometry. Phys. Rev. Lett. 100, 177004 (2008). [DOI] [PubMed] [Google Scholar]
  19. Sacuto A. et al. Electronic Raman scattering in copper oxide superconductors: Understanding the phase diagram. C. R. Physique 12, 480–501 (2011). [Google Scholar]
  20. Hardy W. N., Bonn D. A., Morgan D. C., Liang R. & Zhang K. Precision measurements of the temperature dependence of λ in YBa2Cu306.95: strong evidence for nodes in the gap function. Phys. Rev. Lett. 70, 3999–4002 (1993). [DOI] [PubMed] [Google Scholar]
  21. Kihlstrom K. E., Simon R. W. & Wolf S. A. Tunneling α2F(ω) from sputtered thin-film NbN. Phys. Rev. B 32, 1843–1845 (1985). [DOI] [PubMed] [Google Scholar]
  22. Loram J. W., Luo J., Cooper J. R., Liang W. Y. & Tallon J. L. Evidence on the pseudogap and condensate from the electronic specific heat. J. Phys. Chem. Solids 62, 59–64 (2001). [Google Scholar]
  23. Tallon J. L., Loram J. W. & Cooper J. R. The superfluid density in cuprate high-Tc superconductors—a new paradigm. Phys. Rev. B 68, 180501(R) (2003). [Google Scholar]
  24. Tallon J. L., Cooper J. R., Naqib S. H. & Loram J. W. Scaling relation for the superfluid density in cuprate superconductors. Phys. Rev. B 73, 180504(R) (2006). [Google Scholar]
  25. Tallon J. L. et al. In-plane anisotropy of the penetration depth due to superconductivity on the CuO chains in YBa2Cu3O7–δ, Y2Ba4Cu7O15–δ and YBa2Cu4O8. Phys. Rev. Lett. 74, 1008–1011 (1995). [DOI] [PubMed] [Google Scholar]
  26. Storey J. G. & Tallon J. L. Two-component electron fluid in underdoped high-Tc cuprate superconductors. Europhys. Lett. 98, 17011 (2012). [Google Scholar]
  27. Yang K.-Y., Rice T. M. & Zhang F.-C. Phenomenological theory of the pseudogap state. Phys. Rev. B 73, 174501 (2006). [Google Scholar]
  28. Fujita K. et al. Simultaneous transitions in cuprate momentum-space topology and electronic symmetry breaking. Science 344, 612–616 (2014). [DOI] [PubMed] [Google Scholar]
  29. Naqib S. H., Cooper J. R., Tallon J. L., Islam R. S. & Chakalov R. A. Doping phase diagram of Y1–xCaxBa2(Cu1–yZny)3O7–δ from transport measurements: tracking the pseudogap below Tc. Phys. Rev. B 71, 054502 (2005). [Google Scholar]
  30. Tallon J. L., Barber F., Storey J. G. & Loram J. W. Coexistence of the superconducting gap and pseudogap above and below the transition temperature in cuprate superconductors. Phys. Rev. B. 87, 140508(R) (2013). [Google Scholar]
  31. Tallon J. L. et al. Critical doping in overdoped high-Tc superconductors: a quantum critical point? Phys. Stat. Sol. (b) 215, 531–540 (1999). [Google Scholar]
  32. Talantsev E. F. et al. Hole doping dependence of critical currents in YBCO conductors. Appl. Phys. Lett. 104, 242601 (2014). [Google Scholar]
  33. Grissonnanche G. et al. Direct measurement of the upper critical field in a cuprate superconductor. Nat. Commun. 5, 3280 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Panagopoulos C. et al. Evidence for a generic quantum glass transition in high-Tc cuprates. Phys. Rev. B 66, 064501 (2002). [Google Scholar]
  35. Bernhard C. et al. Suppression of the superconducting condensate in the high-Tc cuprates by Zn substitution and overdoping: evidence for an unconventional pairing state. Phys. Rev. Lett. 77, 2304–2307 (1996). [DOI] [PubMed] [Google Scholar]
  36. Brojeny A. B. & Clem J. R. Self-field effects upon critical current density of flat superconducting strips. Supercond. Sci. Technol. 18, 888–895 (2005). [Google Scholar]
  37. Brandt E. H. & Indenbom M. Type-II-superconductor strip with current in a perpendicular magnetic field. Phys. Rev. B 48, 12893–12906 (1993). [DOI] [PubMed] [Google Scholar]
  38. Tinkham M. Introduction to Superconductivity Ch. 5, (McGraw-Hill (1996). [Google Scholar]
  39. Stejic G. et al. Effect of geometry on the critical currents of thin films. Phys. Rev. B 49, 1274–1288 (1994). [DOI] [PubMed] [Google Scholar]
  40. Zhou H. et al. Improved microstructure and enhanced low-field Jc in (Y0.67Eu0.33)Ba2Cu3O7–δ films. Supercond. Sci. Technol. 21, 025001 (2008). [Google Scholar]
  41. Arendt P. N. et al. High critical current YBCO coated conductors based on IBAD MgO. Physica C 412-414, 795–800 (2004). [Google Scholar]
  42. Feldmann D. M. et al. Through-thickness superconducting and normal-state transport properties revealed by thinning of thick film ex situ YBa2Cu3O7–x coated conductors. Appl. Phys. Lett. 83, 3951–3953 (2003). [Google Scholar]
  43. Zhou H. et al. Thickness dependence of critical current density in YBa2Cu3O7–d films with BaZrO3 and Y2O3 addition. Supercond. Sci. Technol. 22, 85013 (2009). [Google Scholar]
  44. Feldmann D. M. et al. 1000 A cm−1 in a 2μm thick YBa2Cu3O7–x film with BaZrO3 and Y2O3 additions. Supercond. Sci. Technol. 23, 115016 (2010). [Google Scholar]
  45. Lin J.-Y. et al. Flux pinning in YBa2Cu3O7–δ thin films with ordered arrays of columnar defects. Phys. Rev. B 54, R12717–R12720 (1996). [DOI] [PubMed] [Google Scholar]
  46. Roas B., Hensel B., Saemann-Ischenko G. & Schultz L. Irradiation-induced enhancement of the critical current density of epitaxial YBa2Cu3O7–x thin films. Appl. Phys. Lett. 54, 1051–1053 (1989). [Google Scholar]
  47. Schindler W., Roas B., Saemann-Ischenko G., Schultz L. & Gerstenberg H. Anisotropic enhancement of the critical current density of epitaxial YBa2Cu3O7–x films by fast neutron irradiation. Physica C 169, 117–122 (1990). [Google Scholar]
  48. Vostner A. et al. Neutron irradiation studies on Y-123 thick films deposited by liquid phase epitaxy on single crystalline substrates. Physica C 399, 120–128 (2003). [Google Scholar]
  49. Withnell T. D., Schöppl K. R., Durrell J. H. & Weber H. W. Effects of irradiation on vicinal YBCO thin films. IEEE Trans. Appl. Supercon. 19, 2925–2928 (2009). [Google Scholar]
  50. Eisterer M., Fuger R., Chudy M., Hengstberger F. & Weber H. W. Neutron irradiation of coated conductors. Supercond. Sci. Technol. 23, 014009 (2010). [Google Scholar]
  51. Luan L. et al. Local measurement of the superfluid density in the pnictide superconductor Ba(Fe1–xCox)2As2 across the superconducting dome. Phys. Rev. Lett. 106, 067001 (2011). [DOI] [PubMed] [Google Scholar]
  52. Ren C. et al. Evidence for two energy gaps in superconducting Ba0.6K0.4Fe2As2 single crystals and the breakdown of the Uemura plot. Phys. Rev. Lett. 101, 257006 (2008). [DOI] [PubMed] [Google Scholar]
  53. Khasanov R. et al. Two-gap superconductivity in Ba1–xKxFe2As2: a complementary study of the magnetic penetration depth by muon-spin rotation and angle-resolved photoemission. Phys. Rev. Lett. 102, 187005 (2009). [DOI] [PubMed] [Google Scholar]
  54. Goko T. et al. Superconducting state coexisting with a phase-separated static magnetic order in (Ba,K)Fe2As2, (Sr,Na)Fe2As2, and CaFe2As2. Phys. Rev. B 80, 024508 (2009). [Google Scholar]
  55. Guguchia Z. et al. Muon-spin rotation measurements of the magnetic penetration depth in the iron-based superconductor Ba1–xRbxFe2As2. Phys. Rev. B 84, 094513 (2011). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Figures 1-4, Supplementary Tables 1, Supplementary Notes 1-6 and Supplementary References

ncomms8820-s1.pdf (406.7KB, pdf)

Articles from Nature Communications are provided here courtesy of Nature Publishing Group

RESOURCES