Robust network oscillations during mammalian respiratory rhythm generation driven by synaptic dynamics

Significance

The mechanism underlying mammalian respiratory rhythm generation in the preBötzinger complex is still under debate. Here, we developed a simulation model to show that a synaptic depression/facilitation mechanism sufficient for neurons to generate network rhythms, without the need for intrinsically rhythmic neurons. Simulations of the model under several normal or pathological conditions the living system experiences, together with critical electrophysiological experiments, converge to show that randomly connected neuronal networks with synaptic dynamics underlie rhythmic activity. This study provides a generally applicable mechanism for other central pattern generator systems that are less well understood.

Abstract

How might synaptic dynamics generate synchronous oscillations in neuronal networks? We address this question in the preBötzinger complex (preBötC), a brainstem neural network that paces robust, yet labile, inspiration in mammals. The preBötC is composed of a few hundred neurons that alternate bursting activity with silent periods, but the mechanism underlying this vital rhythm remains elusive. Using a computational approach to model a randomly connected neuronal network that relies on short-term synaptic facilitation (SF) and depression (SD), we show that synaptic fluctuations can initiate population activities through recurrent excitation. We also show that a two-step SD process allows activity in the network to synchronize (bursts) and generate a population refractory period (silence). The model was validated against an array of experimental conditions, which recapitulate several processes the preBötC may experience. Consistent with the modeling assumptions, we reveal, by electrophysiological recordings, that SF/SD can occur at preBötC synapses on timescales that influence rhythmic population activity. We conclude that nondeterministic neuronal spiking and dynamic synaptic strengths in a randomly connected network are sufficient to give rise to regular respiratory-like rhythmic network activity and lability, which may play an important role in generating the rhythm for breathing and other coordinated motor activities in mammals.

Central pattern generators (CPGs) are neuronal circuits that generate coordinated activity in the absence of sensory input (1). One such mammalian CPG, the preBötzinger complex (preBötC), gives rise to the eupneic respiratory rhythm (2, 3). Located in the medulla, the preBötC preserves a spontaneous respiratory-like rhythm when isolated in transverse slices, but the precise nature of the cellular and synaptic mechanisms underlying rhythmogenesis remains elusive (3–7). An early hypothesis was that the neuronal activity is driven by intrinsically bursting pacemaker neurons synchronized via excitatory synaptic connections (2, 6, 8, 9). However, electrophysiological and modeling studies (7, 10–12) now suggest the rhythm emerges through stochastic activation of intrinsic currents conveyed by recurrent synaptic connections, without the need for pacemaker neurons (3, 4, 11, 13, 14). In either case, excitatory synapses are required for rhythm generation; the possibility that synaptic properties also underlie periodic burst initiation and termination is yet to be demonstrated.

Synaptic transmission relies on the release of vesicles, which can be modulated at the presynaptic terminal. Synaptic depression (SD), based on vesicular release, consists of decaying release probability after sustained activity, which subsequently decreases excitability within the underlying connected network. Conversely, synaptic facilitation (SF) enhances vesicular release probability and promotes neuronal synchronization. These synaptic dynamics are critical for short-term synaptic plasticity, and here they are explored in the context of preBötC rhythm generation.

We first consider a randomly connected network where each neuron is modeled using a generalized Hodgkin–Huxley system of equations and exhibits spontaneous spiking activity based on a random process, but the neurons do not have intrinsic bursting mechanisms. These neurons are sparsely connected within a realistically sized network by excitatory synapses. The distinction of this model, from previous preBötC models, is that synapses express SF and SD that is implemented using two separate pools of vesicles and creates dynamic synapses. The first pool is the readily releasable pool (RRP) and the other is the recycling pool (RP) (15), modeled with mass-action kinetics. Synaptic dynamics has been repeatedly used to describe changes in spike rates in neural network populations (16) and emergence of gamma oscillations (17). Furthermore network connectivity can also participate to define bursting or the oscillation frequency in neural networks (18, 19).

We show here that random networks connected with these synaptic properties, with random spiking, are sufficient for periodic bursting and examine a variety of experimental scenarios testing this model. The present model shows that an ensemble of excitatory neurons driven by synaptic dynamics can generate population-wide rhythmic activity and behaves in a manner similar to the preBötC under different conditions observed in vitro. Finally, we show experimentally that excitatory inputs to preBötC neurons often exhibit dynamically changing excitatory postsynaptic currents (EPSCs), supporting the modeled concept that SF/SD occurs on a timescale relevant to influence respiratory periods.

Results

Robust Rhythmic Activity Generated in the Model Network.

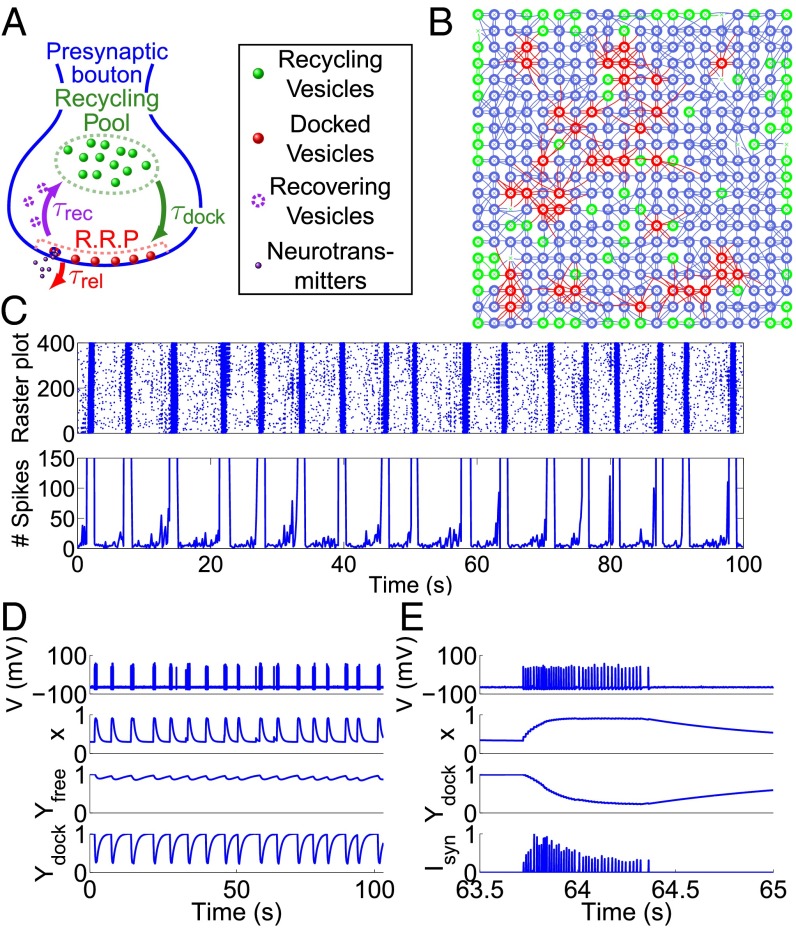
To investigate whether rhythmic activity can emerge from randomly connected neurons with dynamic synapses, we simulated the membrane potential (V) in 400 neurons (Materials and Methods), comparable to the number of preBötC rhythm-generating neurons (20). For each neuron, the key active properties are the RP and RRP for synaptic vesicles (Fig. 1A), whereas neuronal spikes are governed by Hodgkin–Huxley equations and driven by random membrane noise. The network has a structure where the neurons were laid on a 2D grid with a Gaussian distance-based connection probability with respect to each neurons neighbors (21) and is within the bounds of previous experimental observations (10, 13, 22). The average number of output connections per neuron was 3.7, and the mean total number of connections was 7.5 (Fig. 1B and SI Appendix, Fig. S1A; $s=0.9$; Eq. 2), which represents a neuron-to-neuron connection probability of about 2%. The connection probability required to obtain rhythmicity, with these cellular parameters, is in the range 1.2–2.5% (Discussion and SI Appendix, Fig. S2).

Fig. 1.

The preBötzinger complex model and resulting network activity. (A) Schematic representation of the presynaptic bouton: vesicles are divided into two pools: diffusing (green) and docked at the active zone (AZ, red) with recovering ones (purple). After fusion, vesicles recover and enter the recycling pool. (B) Example of a neuronal network (400 neurons) where neurons are located on a square lattice. The connections can be higher than 10 (red), between 5 and 10 (blue), or less than 5 (green). Neurons with no input or output are marked by green crosses, with no circles around. (C) (Upper) Raster plot for spiking neurons generated in Fig. 1B. During 100 s, the synchronous rhythmic patterns alternate between active and silent periods. (Lower) Time-dependent plot of the number of spikes in the network, computed in time windows of 100 ms. The y axis is zoomed to observe the preburst increase in the number of spikes. (D) Time-dependent plot of the voltage V, the facilitation variable x, and the scaled variables $Y_{\text{free}}=y_{\text{free}}/y_{\text{free}}^{\text{max}}$, $Y_{\text{dock}}=y_{\text{dock}}/y_{\text{dock}}^{\text{max}}$ for a single neuron chosen randomly from the network (the mean bursting duration is 777 $\pm$ 98 ms, and the mean interburst interval is 5.2 $\pm$ 1.0 s). (E) Magnification of V, x, $Y_{\text{dock}}$, and $I_{\text{syn}}$ for the neuron in D, during 1.5 s (same simulation as C and D).

In the absence of any external input, we found that local spontaneous spiking can generate rhythmic activity among the population (Fig. 1C and SI Appendix, Fig. S1B), and like in experimental studies (13), the model reproduced the cycle-to-cycle variability both in the identity of the neurons leading successive population bursts (Movie S1) and the timing jitter of individual neuronal spike patterns across cycles. The bursts lasted on average 708 $\pm$ 140 ms and were followed by silent periods lasting on average 5.1 $\pm$ 1.2 s (SI Appendix, Fig. S1 C and D), which is in the range observed for inspiratory cycles in vitro (3) (SI Appendix, Fig. S3).

To further characterize bursting in this model, we illustrate the four principal state variables of a neuron with respect to time (Fig. 1 D and E): its voltage V, its facilitation variable x, and the normalized depression-related variables $Y_{\text{free}}$ and $Y_{\text{dock}}$. The fraction of vesicles in the RP ($Y_{\text{free}}$) is quite stable, oscillating between 80% and 98% of its maximum value, whereas the fraction of docked vesicles in the RRP ($Y_{\text{dock}}$) fluctuates between 20% and 100% of its filled state. Thus, the RRP alternates between an empty and full state, where the mean maximum number of vesicles is 4.5. When the percentage of vesicles in the RRP ($Y_{\text{dock}}$) reaches its minimal value, the bursting period ends, leading to a decrease in the facilitation variable (x) that relaxes back to equilibrium (Fig. 1E). On the contrary, x increases exponentially when each population burst begins (Movie S2), which, associated with the decrease in $Y_{\text{dock}}$, is reflected by a transient increase and subsequent decrease in the amplitude of synaptic currents during the bursts ($I_{\text{syn}}$; Fig. 1E). Each neuron within the network that reaches its minimum $y_{\text{dock}}^{\text{min}}$ enters a refractory state that shuts down its synaptic transmission (SI Appendix, Fig. S1 E and F). This minimum value leads to burst termination across the population because recurrent excitation ceases. As synapses recover, a subsequent burst can begin when several connected neurons spike in a short time interval to facilitate postsynaptic neuronal activation. This nonlinearly promotes spiking activity to spread through neighboring neurons and invade the entire network (Movies S2 and S3). These features were characteristic of additional networks with similar topologies and each network resulted in similar cycle periods (CPs), burst durations (BDs), and interburst intervals (IBIs) of 5.5 $\pm$ 1 s, 694 $\pm$ 138 ms, and 4.8 $\pm$ 1 s, respectively (n = 10 networks), which is in the range observed in vitro. Additionally, the CP and BD can be altered by changing synaptic parameters (SI Appendix, Figs. S4 and S5), and the spiking frequency during a burst (normally up to 60 Hz) can be modified by changing the HH-model parameters (SI Appendix, Fig. S6). Altogether, this suggests that a large range of in vitro and in vivo data can be accounted for by this model.

Rhythmic Activity Depends on the Number and Strength of Connected Neurons.

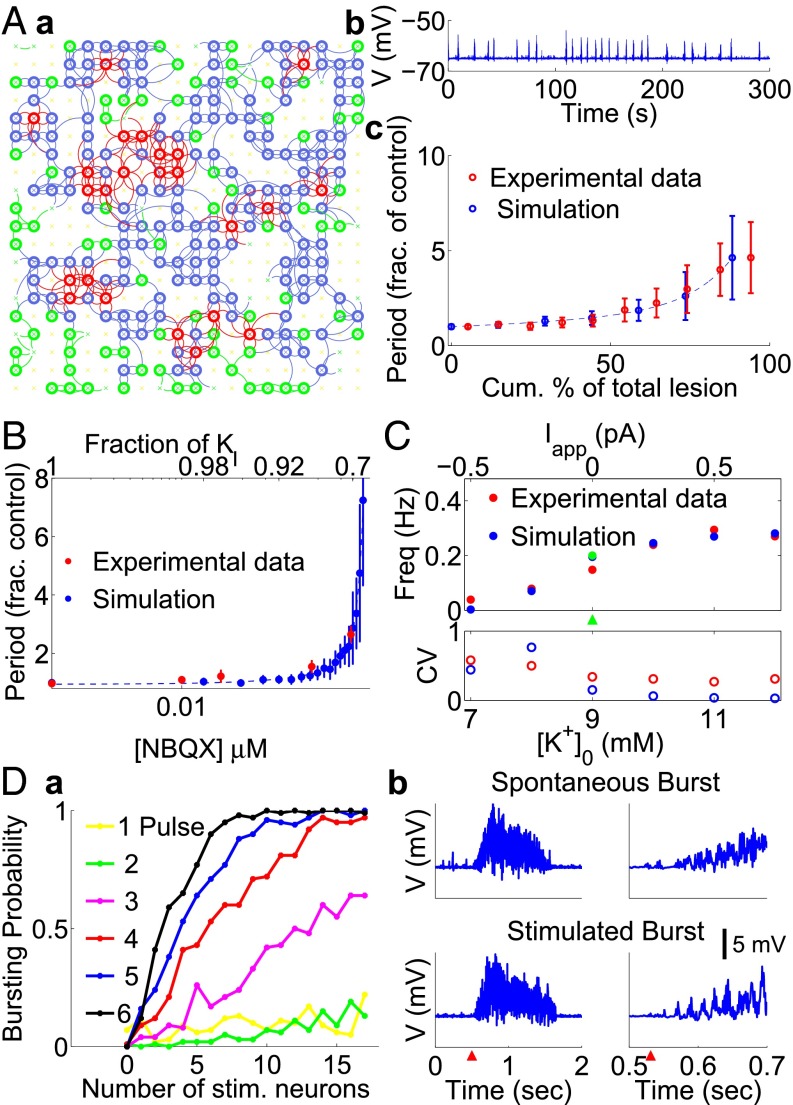
With some neurodegenerative diseases, brainstem neurons die and are not replenished (23). Similar conditions in rats cause sleep apneas that could lead to death without intervention (24). To investigate the role of network size in our model, we randomly removed neurons as shown in Fig. 2A. When 12.5% of the network neurons were removed (50 neurons; SI Appendix, Fig. S7), the network activity was not perturbed. When 25% (100 neurons) of the network was removed, the rhythm started to be affected, whereas bursts became erratic when this fraction reached 31% (125 neurons; Fig. 2 Aa and Ab), and disappeared when more than 44% of neurons were removed ($\ge$ 175 neurons; SI Appendix, Fig. S7). Lesioning 175 neurons resulted in a CV of ∼1, indicating a very unstable rhythm, and lesions beyond that eliminated all spontaneous bursts. Normalizing the number of lesioned neurons to the total required for complete rhythm cessation resulted in exponential increases in the CPs and variability (Fig. 2Ac), comparable to those obtained in previous physiological in vitro experiments (20, 25). The proportion of lesioned neurons required to stop bursting is nevertheless higher than observed experimentally in vitro (Discussion and SI Appendix, Fig. S7E). The BD (about 670 ms) was not statistically changed by reduction of the network size by 50, 100, and 125 neurons, whereas the CP increased from 5.5 $\pm$ 1.1 to 7.1 $\pm$ 2.2 to 10.2 $\pm$ 5.3, and to 15.5 $\pm$ 13.3 s, respectively. If CP depends on the number of neurons within the population, it could be because each lesioned cell creates holes in the network that put at risk the spread of activity within the population (Movies S4 and S5). In addition, these lesions also effectively decrease the number of inputs to each remaining neuron and thus the strength of inputs to each of them.

Fig. 2.

Modeled characteristics of burst induction comply with physiology. (A) Effect of deleting random neurons on the network rhythm. (a) 125 neurons (31% of the network) have been removed. (b) Corresponding mean membrane potential over the whole lesioned network. (c) Comparison between simulated (blue) and experimental lesions (red, extracted from ref. 20) of increasing numbers of preBötC neurons (see also SI Appendix, Fig. S7). (B) Consequences of gradually decreasing synaptic strength. Comparison between simulations (blue) and experimental results (red, extracted from ref. 26). The initial synaptic strength, controlled via $K_I$ in the model and via [NBQX] in the experimental protocol, is gradually decreased (see also SI Appendix, Fig. S8). (C) Hyperpolarizing and depolarizing the network from its resting state (green arrowhead) leads, respectively, to slower more variable and accelerated more regular rhythms in simulated (blue) and experimental conditions (red, extracted from ref. 28); see also SI Appendix, Fig. S9. (D) Response of the network to increasing stimulations. (a) Probability of stimulus evoked population bursts as a function of the number of randomly stimulated neurons (n = 1–17) and the number of stimuli per train (n = 1–6 pulses). (b) (Left) Mean V over the whole network for spontaneous and stimulated bursts (n = 9 neurons, six pulses at 60 Hz, starting at t = 550 ms, red arrowhead). (Right) Magnification of the burst induction. The vertical calibration bar applies to all burst, each having a baseline potential of −65 mV.

To test the role of unitary synaptic strength, in contrast to the spread of excitatory transmission through the network, we simulated a decrease in the maximum synaptic transmission from 100% to 65% to mimic pharmacological blockade of AMPA receptors, until population burst cessation with the full 400 neuron network (Fig. 2B and SI Appendix, Fig. S8). The results were similar to experimental conditions (26) and were notably similar to Fig. 2Ac with respect to the exponential divergence of cycle period as well. The latter point further suggests that the net strength of connections between neurons is of principal importance for burst induction, and thereby, rhythm generation.

Depolarizing Neurons Increase the Rhythm Frequency.

The preBötC is the target of many neuromodulators, the balance of which can affect the tonic excitability of the network (27). To investigate how tonic changes in V affect bursting, we modulated the neuronal excitability by adding an applied current ($I_{\text{app}}$) to the current balance equation of the entire network. Positive $I_{\text{app}}$ is equivalent to increasing extracellular $\left[K^{+}\right]$. After hyperpolarization ($I_{\text{app}}$ = −0.5 pA), the IBI and variability in rhythm increases drastically (Fig. 2C and SI Appendix, Fig. S9), whereas depolarizing the network ($I_{\text{app}}$ = 0.75 pA) decreased the CP and variability in rhythm. At higher depolarization, the frequency of bursting reaches a plateau principally constrained by the refractoriness in the model (${\text{CP}}_{\text{plateau}}$ = 3.5 $\pm$ 0.1 s and ${\text{BD}}_{\text{plateau}}$ = 560 $\pm$ 227 ms compared with control values $I_{\text{app}}$ = 0 pA: CP = 5.1 $\pm$ 0.8 s and BD = 660 $\pm$ 161 ms). These values are comparable to the ones reported in physiological experiments (28) for CP = 5.7 $\pm$ 0.5 s and ${\text{CP}}_{\text{plateau}}$ = 3.5 $\pm$ 0.2 s, with no notable decreases in BD and spike frequency. In the case of hyperpolarization, we detected very few bursts after 1,500 s, corresponding to CP = 240.6 $\pm$ 185.7 s, which is comparable to the long CP (143.2 $\pm$ 3.9 s) reported in ref. 28. We conclude that changing the tonic excitability in our model has drastic consequences on CP owing to changes in IBI but not BD, in agreement with previous experimental data.

At hyperpolarized potentials we also observed, during the IBI or immediately preceding bursts, patterns of activity reminiscent of burstlets, described in the preBötC as rhythmic bouts of low-rate spiking (SI Appendix, Fig. S10) (29). These patterns did not involve SF/SD like in full-network bursts (SI Appendix, Fig. S11). They rested on tens of spiking neurons but cannot properly be considered burstlets, as the latter involve $\sim$ 90% of preBötC neurons. Rather, these simulated patterns constitute low amplitude events that may seed burstlets and preinspiratory activity (29).

Few Active Neurons Are Sufficient to Trigger Population Bursts.

Another important feature of the preBötC network is its rapid responsiveness to phasic inputs from central or peripheral (reflex) origins (30–32). Therefore, we sought to evaluate the minimal number of concurrently active neurons necessary for initiating a preBötC network response. To do so, we depolarized a variable number of randomly chosen neurons with graded trains of stimulation (one to six stimulations per train, 50 μs, 60 Hz). We quantified the probability of evoked bursts for the respective conditions (Fig. 2D and SI Appendix). When 17 neurons (4.25% of the network) were stimulated with a single stimulus, or with a two-stimulus train, it was possible to induce a burst with a low probability $\le$ 15%. However, using trains of five to six stimuli, the probability was higher than 80%, and in these cases, decreasing the number of stimulated neurons revealed that 5–10 neurons were sufficient to induce network bursts. The early phase of the evoked burst, manifesting the propagation of excitatory synaptic inputs in the network (Movie S3), was similar to that of spontaneously occurring bursts (Fig. 2Db), in agreement with the group-pacemaker hypothesis (11, 12, 33) and burstlet-dependent generation of bursts (29). Finally, these results are in keeping with the recent physiological demonstration in slice preparations that targeting four to nine preBötC neurons with glutamate uncaging was sufficient to induce ectopic endogenous-like bursts (34).

Short-Term Synaptic Plasticity in the preBötC Inspiratory Rhythm Generator.

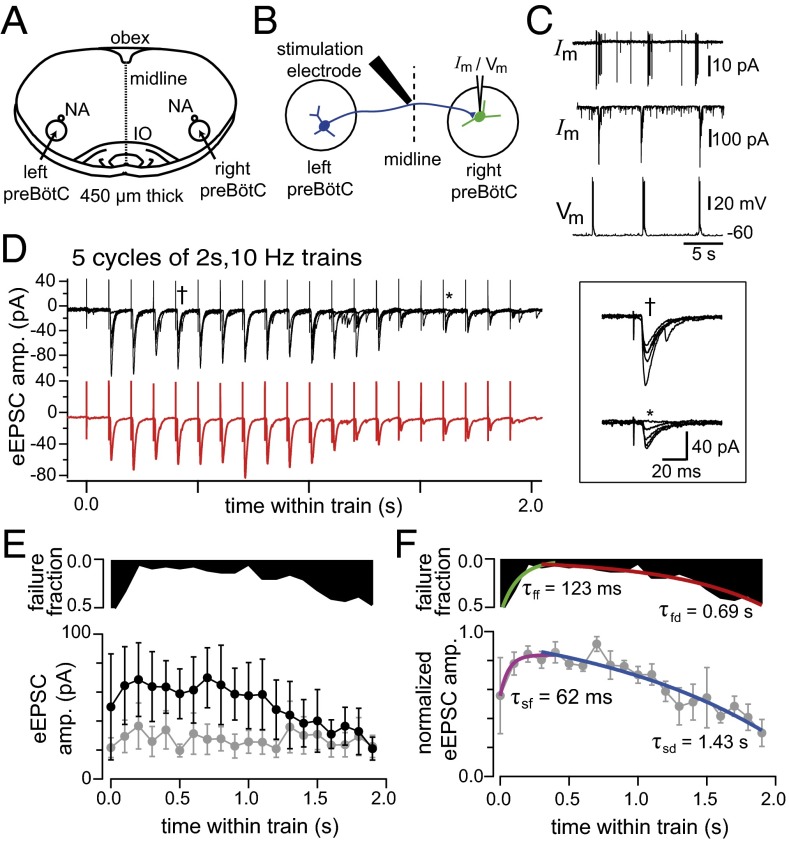
To support the possibility that SD, and also SF, may be occurring in vitro on timescales that could impact normal respiratory rhythms, we recorded synaptic responses in inspiratory preBötC neurons in slice preparations (Fig. 3A) evoked by electrical stimulation of preBötC commissural axons (35) (Fig. 3B). The experiments were performed in the presence of picrotoxin and strychnine (5 μM) suppressing GABAergic and glycinergic synaptic currents known to be dispensable for rhythm generation (10, 36, 37) to best reproduce the predominant glutamatergic synaptic transmission of the model. We concurrently reduced the extracellular $\left[K^{+}\right]$ from 8 to 3 mM to minimize spontaneous population activity after identifying recorded inspiratory neurons (Fig. 3C), and these recordings did not exhibit unclamped spikes (SI Appendix, Fig. S12). For electrical stimulation we used trains (2- to 5-s duration) of repetitive (10–30 Hz) stimuli. The intensity of stimulation was set so that at low frequency (1/9 s) the stimulus resulted in about 50% EPSC failures.

Fig. 3.

Experimental support for rapid accommodation of synaptic strength. (A) A transverse preBötC slice depicting key features of the in vitro preparation (IO, inferior olive; NA, subcompact nucleus ambiguus; obex, caudal termination of the IVth ventricle). (B) The experimental strategy (see text for details). (C) (Top) On-cell voltage-clamp recording, (Middle) whole-cell voltage-clamp recording, and (Bottom) current-clamp recording. (D) (Upper) Five cycles of train stimuli from the cell recorded in C and (Lower) the mean of the five cycles. (Inset) Details showing the eEPSCs overlayed at the indicated places within the trains. (E) (Solid-black histogram) Fraction of trials that failed to produce eEPSCs. (Lower) eEPSC amplitudes (black: n = 3 neurons, n = 5–16 trials; gray: n = 4 neurons, n = 4–10 trials). (F) Same data as E normalized to the peak within each neuron’s mean train (gray) with exponential fit overlays to the rising components (green/magenta) and the falling components (red/blue) of the normalized data. The command potential for all voltage-clamp recordings was −60 mV.

At 20 and 30 Hz, stimulation frequently resulted in population recruitment even in our suppressed excitability. In three of seven preBötC neurons stimulated at 10 Hz, the amplitude of evoked EPSCs (eEPSCs) varied according to their timing during the stimulus trains. Typically in these cells, the amplitude of successive eEPSCs in the train showed a rapid waxing phase followed by a slow waning phase so that eEPSCs increased amplitude over the first few stimuli of the train and declined thereafter during the train, resulting in the reoccurrence of transmission failures at the end of subsequent trains (Fig. 3D). We quantified failures of transmission during the trains of stimuli and observed that failures mirrored changes in EPSC amplitudes (black histograms in Fig. 3 E and F), suggesting that the two phenomena might be tied through a similar mechanism like the availability of vesicles at the synapse as modeled here. The other four cells did not show any discernible modulation in eEPSC amplitude during the train (Fig. 3E, gray). In these four cells, the slope of the time-dependent change of eEPSC amplitude during the train was significantly different from that of the aforementioned ones (−1.2$\pm$ 0.9 pA/s, n = 4 vs. −20.1$\pm$ 8.3 pA/s, n = 3, t test: P = 0.043). These stationary cells may belong to the $\sim$ 50% fraction of nonrhythmogenic inhibitory neurons within the preBötC (38) and were not considered further.

For the recordings that exhibited dynamic synapses (Fig. 3E, black), normalizing their eEPSC amplitudes with respect to the maximal eEPSC of each neuron’s mean train revealed a more consistent trend among the data than the raw data may have initially suggested (Fig. 3F, gray; n = 3, n = 5–16 trials), with exponential fits to their rising and falling components. The rising exponential suggests the presence of short-term SF, (as illustrated by x in Fig. 1E) and the falling exponential consistent with short-term SD (an amalgamation of x and $Y_{\text{dock}}$; Fig. 1E). These electrophysiological data match the predicted model dynamics of $I_{\text{syn}}$ in Fig. 1E and would suggest that, together with the rest of the favorable modeling tests performed here recapitulating experimental results (20, 26, 28, 34), the modeling approach we exercised is applicable to the respiratory rhythm-generating network in vitro.

Discussion

Can Bursting Oscillations Be Generated in Neuronal Networks Without Any Intrinsically Rhythmic Neurons?

We found that a neuronal network based on Gaussian-distributed sparse synaptic connections can generate an endogenous rhythm initiated by neuronal noise. A key feature of the network is the SF and SD dynamics. Here, SD was based on a two-pool model where vesicles of one pool interact with the RRP and is a refinement of the classical SD model (39).

Pacemaker neurons can generate an intrinsic oscillation based on their biophysical properties such as persistent sodium current ($I_{NaP}$). For $I_{NaP}$, this current slowly inactivates to hyperpolarize and terminate bursts, whereas subsequent deinactivation causes the next depolarization and burst (8, 40, 41), which sustains rhythmic activity under certain parameter regimes. A calcium-activated nonspecific cation current ($I_{CAN}$), ubiquitous in preBötC neurons (11, 42), can also give rise to intrinsic bursting activity (41, 43) and may contribute to SF in preBötC neurons by enhancing excitatory postsynaptic potentials (EPSPs) (42). However, electrophysiological recordings (4, 11, 44, 45) revealed that endogenous rhythmic activity was not driven by pacemaker neurons, as inhibiting them does not suppress population bursting or change the frequency. This result led to the conclusion that bursting oscillations could be generated by other mechanisms, such as the group-pacemaker hypothesis (5, 7, 11, 33), where respiratory rhythm is thought to emerge from the dynamics of synaptic input impinging on inspiratory neurons and those interactions with intrinsic cellular properties.

Modeling approaches (12, 46) have shown that the cooperation of $I_{CAN}$, activated by synaptic activity, coupled with activity-dependent outward currents, can generate periods of bursting separated by quiescent phases. These quiescent periods can also be achieved by transient inactivation of an $I_{NaP}$ similar to the one observed in pacemaker neurons, which is equivalent to activating an outward current. However, that model requires intrinsic regular spiking to activate $I_{CAN}$ and initiate the bursts even when the system is driven by synaptic noise, and $I_{CAN}$-mediated SF and depolarization-block dependent SD alone are not sufficient for regular bursting.

Here, we modeled a neuronal network that contains sparse connections and is based on SF with a two-pool state for SD. Burst initiation relies on spontaneous spiking of a small number of neurons that recruit the entire network by recurrent excitation among neurons. The increase in SF in our model promotes the recurrent excitation, similar to the $I_{CAN}$ evoked by intrinsic activity in ref. 12, and observed in electrophysiological recordings in vitro (45, 47). To propagate to the entire network, nearly synchronous firing must first occur in several neurons. This synchronization may be caused by synaptic inputs coincidently converging onto small groups of preBötC neurons or, in recurrently connected neurons, in a stochastic manner, from the relief of the refractory period during the interburst interval. After a few hundred milliseconds, the first part of SD takes over and stops each neuron from transmitting synaptic activity. Population spiking subsequently terminates. Finally, the second part of the SD, characterized by the entry of neurons in a refractory period to let synapses recover to equilibrium, prevents neurons from firing back immediately. This behavior is in agreement with previous studies (34, 48). The next cycle starts after the neuronal refractory periods end and when noise-driven spontaneous spiking occurs at several neurons. The end of the refractory period and the beginning of the next burst (SI Appendix, Fig. S1E) principally depend on four factors: the rate of SF ${\tau }_{\text{f}}$ (see x in Fig. 1E), the effective degree of network connectivity (Fig. 2A and SI Appendix, Fig. S2–S7), the maximal synaptic strength $K_I$ (Fig. 2B and SI Appendix, Fig. S8), and the amount of spontaneous spiking (Fig. 2 C and D and SI Appendix, Fig. S9). Changing any one of these factors affects the bursting frequency and regularity.

To conclude, our modeling confirms the group pacemaker hypothesis (11), where eupneic respiratory rhythm is attributed to the cooperative interactions between inspiratory neurons. The present results show that periodic inspiratory bursts can emerge from recurrent neuronal connections and synaptic dynamics, without the need of any underlying neuronal rhythm driven by pacemaker neurons or a subpopulation of oscillatory firing neurons. Synaptic dynamics are thus a plausible mechanism of preBötC rhythmogenesis, even if other nonsynaptic mechanisms might be involved to fully reproduce the range of respiratory behaviors.

Local Network Structure and Dynamics.

Network connectivity within the preBötC could influence the dynamics of population activity (49). Other preBötC–related studies have used all-to-all coupling (9) or various degrees of sparse networks (13, 25) including small-world topology (7). In this study, we modeled a realistic-sized preBötC network using random connections between neurons with a distribution law that decays exponentially with the distance between neurons (Fig. 1B and SI Appendix, Fig. S2B). This decay has been used in several models such as the visual cortex (figure 5 from ref. 50) or the auditory cortex (51). Connectivity between preBötC neurons could be as high as 13% when recorded in local proximity ($<\sim$60 μm) (10), whereas it could be as low as 1% as determined from multielectrode array experiments (13). Additionally, experiments with organotypic slices suggest that a preBötC–like network could be organized into loosely connected clusters, i.e., a small-world network (22).

Our choice of connectivity is broadly consistent with the three previous experimental results (10, 13, 22) when the pair-to-pair coupling decays fast at large distances. The decay of neuronal connectivity with the distance between neurons prevents the emergence of nonhomogeneous connectivity in the network. Indeed, in the classical Erdős-Rényi preBötC network model, increasing the coupling probability leads to the occurrence of higher connected neurons, as studied in ref. 49. The connectivity map used in ref. 13 for a low coupling probability is nevertheless very similar to the one used in our model. Varying the Gaussian distribution (parameter s in Eq. 2; SI Appendix, Fig. S2) shows that the rhythm is preserved only for s in the range 0.8–1. With $s\le$ 0.8, the IBI has large variability, and when $s\ge$ 1, waves of APs at low frequency can emerge in the network (SI Appendix, Fig. S2F and Movies S6 and S7).

Role of Synaptic Depression in Burst Termination.

Synaptic depression is described classically as the depletion of vesicles following activation (52). Here we had to account for the depletion of both the RRP and the RP so that vesicles can arrive with the proper dynamics, which is not contained in the classical coarse-grained depression model where the rate of synaptic depression depends on the resource’s availability (39). In the classical depression model, presynaptic stimulation through a spike train produces a regime of stationary EPSPs postsynaptically after a few spikes, which does not result in burst termination due to full depletion of available vesicles. The two-pool model where vesicles can either be in the RRP or RP compartments resolves this difficulty: the arrival of a presynaptic AP triggers fusion of vesicles from the RRP, and the postsynaptic current is proportional to the amount of fused vesicles. Bursting termination in the preBötC is still unknown and might be due to several different processes such as synaptic depression, voltage-dependent/ion-activated outward currents (48), or, as postulated in previous models, due to the deactivation of inward currents (8), or a combination. In our model, burst termination is based on short-term SD, where the ready-to-fuse vesicles are lacking. Indeed, they are released in the high firing rate bursting that lasts several hundreds of milliseconds and take up to seconds to recover, consistent with respiratory refractory periods observed experimentally in vitro (34). Our approach shows that bursting oscillations can be generated in an ensemble of neurons connected by synapses, driven by depression/facilitation dynamics, without the need for any underlying endogenously rhythmic pacemaker neurons. In addition, the IBI is controlled by recurrent excitations arising from the network’s spontaneous activity. This phenomenon may be quite generic and could explain oscillations in other neuronal networks, where the mechanism remains unclear, such as the circuits for chewing, swallowing, whisking, locomotion, or, indeed, any coordinated ensembles of repetitively synchronous neuronal activities.

Materials and Methods

Electrophysiology.

All animal studies were done in accordance with the guidelines issued by the European Community and have been approved by the research ethics committee in charge (Comité d’éthique pour l’expérimentation animale) and the French Ministry of Research.

Swiss mice (P0–P4) were anesthetized and dissected in artificial cerebrospinal fluid (ACSF) containing (in mM) 132.5 NaCl, 8 KCl, 0.58 ${\text{Na}}_2{\text{HPO}}_4$, 8.5 ${\text{NaHCO}}_3$, 30 d-glucose, 1.26 ${\text{CaCl}}_2$, and 1.15 ${\text{MgCl}}_2$. Hindbrains were quickly removed and embedded within a 4% (wt/vol) agarose block and glued to the pedestal of a Leica microtome. Transverse slices were cut from the medulla (450 μm thick) where the rostral surface was 400–500 μm caudal to the caudal end of the facial nucleus in line with the calibrated atlas of ref. 53. Slices were then placed into a recording chamber and held down by a platinum grid with nylon fibers. The slices were perfused with 30–31 °C extracellular ACSF for at least 30 min before patch recording commenced. Picrotoxin (5 μM) and strychnine (5 μM) were bath-applied to block GABA_A and glycinergic synaptic currents. Evoked EPSCs (eEPSCs) were identified by patch-recording preBötC respiratory neurons and electrically stimulating the midline of the slice just dorsal to the midline aspect of the inferior olive (Fig. 3 A and B) using an ISO-Flex stimulation isolation unit (A.M.P.I.). The 8 mM $\left[K^{+}\right]$ was exchanged with 3 mM $\left[K^{+}\right]$ ACSF to suppress spontaneous population activity once a recorded neuron was identified. For voltage-clamp recordings, we used a command potential of −60 mV, and recordings with unclamped spikes were discarded. Further details are given in SI Appendix, Materials and Methods.

Mathematical Modeling.

Neuronal network modeling.

We model a neuronal network consisting of 20 × 20 (i.e., 400) connected neurons organized on a square lattice and account for synaptic dynamic and voltage properties. To model the membrane potential of each neuron, we use a simplified Hodgkin–Huxley model, where we consider the changes in ${\text{Na}}^{+}$, ${\text{K}}^{+}$, and leak channels. The associated currents are $I_{Na}$, $I_K$, and $I_L$. The resting potential of each neuron is at a mean of −65.1 mV, distributed randomly according to a Gaussian distribution with a variance of 0.2. To account for spontaneous fluctuations of the membrane potential, we add a Gaussian noise source term $\dot{W}$ to the potential with a variance σ. The general equation for one neuron is

$$C\dot{V}=-I_{Na}-I_K-I_L+{\displaystyle \sum _j{I}_{syn,j}}+\sigma \dot{W}.$$ [1]

The synaptic current for each neuron is ${\displaystyle {\sum }_j{I}_{syn,j}}$, which is the sum of the postsynaptic currents over all connected neurons (SI Appendix). These currents are computed for each synapse from the short-term facilitation and depression properties, modeled by two pools of vesicles (SI Appendix). These two pools generate two different time scales for the synaptic depression. The model we adopted for the facilitation dynamics is, however, classical, as developed in ref. 54. Synaptic depression results from the depletion of the RRP, where synaptic vesicles are gathered at the membrane before fusion. We also account for the other pool of recycling vesicles (RP) that are diffusing.

Computing the synaptic current.

To compute the synaptic current between two connected neurons, we use the synaptic model described above (SI Appendix). The postsynaptic current $i\left(t\right)$, due to an action potential generated in the presynaptic neuron, is proportional to the amount of released vesicles.

Construction of the network connectivity.

The connectivity map for the network is implemented between every neuron. They are distributed on a square lattice (Fig. 1B) and connected randomly according to the probability distribution

$$\mathbf{P}\left(i\to j\right)=\text{exp}\left[-d{\left(i,j\right)}^2/\left(2s^2\right)\right],$$ [2]

for neuron i and j, where $d\left(i,j\right)$ is the Euclidian distance between neurons i and j normalized by the minimal distance between two neurons.