Abstract
The identification of the genetic structure of populations from multilocus genotype data has become a central component of modern population-genetic data analysis. Application of model-based clustering programs often entails a number of steps, in which the user considers different modeling assumptions, compares results across different pre-determined values of the number of assumed clusters (a parameter typically denoted K), examines multiple independent runs for each fixed value of K, and distinguishes among runs belonging to substantially distinct clustering solutions. Here, we present Clumpak (Cluster Markov Packager Across K), a method that automates the post-processing of results of model-based population structure analyses. For analyzing multiple independent runs at a single K value, Clumpak identifies sets of highly similar runs, separating distinct groups of runs that represent distinct modes in the space of possible solutions. This procedure, which generates a consensus solution for each distinct mode, is performed by the use of a Markov clustering algorithm that relies on a similarity matrix between replicate runs, as computed by the software Clumpp. Next, Clumpak identifies an optimal alignment of inferred clusters across different values of K, extending a similar approach implemented for a fixed K in Clumpp, and simplifying the comparison of clustering results across different K values. Clumpak incorporates additional features, such as implementations of methods for choosing K and comparing solutions obtained by different programs, models, or data subsets. Clumpak, available at http://clumpak.tau.ac.il, simplifies the use of model-based analyses of population structure in population genetics and molecular ecology.
Keywords: Admixture, ancestry, clustering, population structure
INTRODUCTION
Model-based identification of population structure from individual multilocus genotypes is of great importance for the study of genetic relationships among individuals and populations. In diverse organisms, population structure inference provides a basis for interpreting patterns of extant genetic variation, serving as a foundation for the study of evolutionary history (Rosenberg et al. 2002; Parker et al. 2004; Whitfield et al. 2006; Driscoll et al. 2007; Zhao et al. 2013). In association mapping of complex traits, inference of population structure can assist in avoiding the false-positive genotype–phenotype associations that structure can generate (Pritchard and Donnelly 2001; Thornsberry et al. 2001; Hoggart et al. 2003; Breseghello and Sorrells 2006). In conservation genetics and molecular ecology, population structure inferences are regularly used to investigate such topics as population boundaries, population connectivity, and gene flow, aiding the understanding and management of natural populations (Manel et al. 2005; Gompert and Buerkle 2013).
A particularly important family of methods for investigating population structure examines multi-locus genotypes of individuals using model-based cluster analysis (Pritchard et al. 2000; Dawson and Belkhir 2001; Corander et al. 2003; Falush et al. 2003; Corander et al. 2004; Guillot et al. 2005; Tang et al. 2005; François et al. 2006; Pella and Masuda 2006; Chen et al. 2007; Falush et al. 2007; Gao et al. 2007; Huelsenbeck and Andolfatto 2007; Corander et al. 2008a; Corander et al. 2008b; Guillot 2008; Alexander et al. 2009; Durand et al. 2009; Hubisz et al. 2009; Shringarpure and Xing 2009; Alexander and Lange 2011; Huelsenbeck et al. 2011; Frichot et al. 2014). These methods, the most widely-used of which is Structure (Pritchard et al. 2000; Falush et al. 2003; Falush et al. 2007; Hubisz et al. 2009), classify individuals into a prespecified number of populations, disregarding predefined labels for the sampled individuals and therefore performing “unsupervised” clustering. In typical uses, Structure, like many other clustering programs, views each individual as a distinctive mixture of a set of inferred statistical populations or clusters, each characterized by distinct allele frequencies. Coefficients of membership of each individual in the various clusters, summing to 1 across clusters, are estimated in an iterative procedure. The various “Structure-like” (Weiss and Long 2009) programs, which consider both mixed-membership models that view individuals as mixtures of the clusters, and assignment models in which membership coefficients represent probabilities of membership in the clusters, approach the same conceptual problem with a variety of choices of modeling assumptions and various alternative computational strategies. They enable rich and complex data analyses, allowing the user to modify a wide variety of parameters and to examine different models—for instance, supervised models, in which the predefined population labels are used to assist the inference process. For most programs, users have considerable choice in model assumptions, and they are advised to test different assumptions as well as a range of predefined values of the number of clusters, K.
Structure-like algorithms typically involve stochastic simulations, and therefore can produce different outcomes in replicate analyses. For this reason, it is important to perform several independent assessments of the same data set using the same modeling assumptions and free parameters (Rosenberg et al. 2001a; Gilbert et al. 2012). Differences among solutions tend to arise from two phenomena (Jakobsson and Rosenberg 2007). The first is “label-switching,” caused by the arbitrary way in which inferred clusters are labeled, resulting in unmatched labels between replicate runs even when the same membership coefficients are produced. The second type of difference is “genuine multimodality,” in which data analyses result in two or more truly distinct solutions, or modes. To distinguish label-switching from genuine multimodality, Jakobsson & Rosenberg (2007) developed Clumpp (Cluster Matching and Permutation Program), which computes a pairwise similarity score between pairs of runs with the same K, identifying an optimal alignment of the replicate runs that eliminates label-switching so that genuine multimodality can be detected. A matrix of similarity scores produced by Clumpp for pairs of aligned runs can be used to identify groups of runs that produce nearly identical solutions and can be said to fall into the same mode. For example, Wang et al. (2007) and Jakobsson et al. (2008) identified as modes all sets of replicates for which the pairwise similarity score for each pair of runs exceeded a specific threshold. This approach amounts to identifying fully connected subgraphs of a graph, or cliques, where vertices represent runs and edges indicate occurrences of pairwise similarity scores above the threshold. Once distinct modes are identified, users can choose a single run from each inferred mode, or they can alternatively average runs in each mode by a second application of Clumpp only on those runs within the mode. A drawback of this approach is that determination of modes is often highly dependent on the exact threshold chosen. Moreover, cliques found by this approach can have a high percentage of overlap, and therefore might not necessarily represent truly distinct solutions.
In addition to eliminating label-switching and identifying distinct modes for a single K, users often compare clustering modes for a range of K values. As Clumpp aligns only those runs with a fixed value of K, however, automated alignment of runs across multiple K values has not been possible. This challenge is particularly noticeable in cases in which simultaneous examination of multiple modes at multiple K values is of interest, such as when the clustering pattern in the most frequently occurring mode for a given K does not provide a refinement of the corresponding solution for a smaller choice of K (Wang et al. 2007). Additional tasks, including comparisons of results obtained for multiple model choices, subsets of data, or different programs altogether, have also required that computations be performed external to Clumpp and other cluster post-processing software such as Distruct (Rosenberg 2004) and Structure Harvester (Earl and Vonholdt 2012). From the end-user perspective, performing a thorough Structure-like analysis can be a tedious task.
To overcome these difficulties in identification of modes, alignment of runs across K values, and automation of additional post-processing steps, we have developed Clumpak, the Cluster Markov Packager Across K. Clumpak clusters replicate runs for the same K via a Markov clustering algorithm that improves upon the commonly used fixed threshold approach. Clumpak summarizes the modes identified, eliminating the additional step of “re-Clumpping” runs within modes to obtain consensus results for each mode. A newly developed extension further enables cluster matching across different values of K, and simplifies the examination and presentation of results across a range of K values. Clumpak additionally allows users to easily compare results obtained under different models, programs, or subsets of the data. Here, we describe the methods underlying Clumpak, and we use simulations to demonstrate the ability of Clumpak to accurately cluster individual runs. We further illustrate the use of Clumpak on an example human population-genetic dataset.
MATERIALS AND METHODS
Generating clusters of runs at a single value of K
Clumpak aids users in summarizing the entire set of runs produced for their data set using one or more clustering programs. Users normally run their analysis using a range of K values, performing multiple replicates for each K. Clumpak obtains similarity matrices for pairs of replicate runs using the SSC’ similarity score of Jakobsson and Rosenberg (2007) as implemented in Clumpp, employing as a default the LargeKGreedy algorithm of Clumpp with 2,000 random input sequences (both of these choices can be changed by the user). From among the replicates, Clumpak then identifies different modes within a single value of K—that is, genuinely different solutions if they are present.
First, Clumpak treats the similarity matrix as a fully-connected, undirected, weighted graph, G=(V,E), where vertices in set V represent independent runs, and the edge weight connecting vertices u and v is the similarity score SSC’(u, v). Second, given the weighted graph, Clumpak uses the Markov Clustering (MCL) algorithm (Van Dongen 2000; Van Dongen 2008) to partition the graph into distinct modes. This algorithm is a general method for identifying clusters, and it has previously been adapted for diverse biological problems, including orthology assignments (Enright et al. 2002), detection of operational taxonomic units (Ratnasingham and Hebert 2013), and identification of co-occurring associations among microbes (Faust et al. 2012). The similarity matrix obtained for a single K, as represented by the graph G, is transformed into a column-stochastic matrix or Markov matrix, where entry (i, j) represents a probability of “transition” from vertex j to vertex i. The MCL algorithm involves alternating between matrix “expansion” and matrix “inflation,” where expansion refers to taking the power of a stochastic matrix (i.e. normal matrix squaring), and inflation refers to taking the Hadamard power (Horn and Johnson 1991) of the matrix (taking powers entrywise) with coefficient r, and rescaling the matrix so that columns sum to 1. These alternating steps of matrix expansion and matrix inflation are aimed at simulating random walks on a graph: expansion steps correspond to computing probabilities associated with higher-length paths, and inflation boosts the probabilities of intra-cluster walks, accentuating the similarity of related runs and the dissimilarity of divergent runs. The single parameter r, which determines the “granularity” of the clusters obtained, controls the outcome of the algorithm, producing finer granularity, and more clusters, with larger r. Figure 1 illustrates the steps involved in the clustering process.
Figure 1. Schematic of the Markov clustering algorithm for a similarity matrix of 7 independent Structure runs.
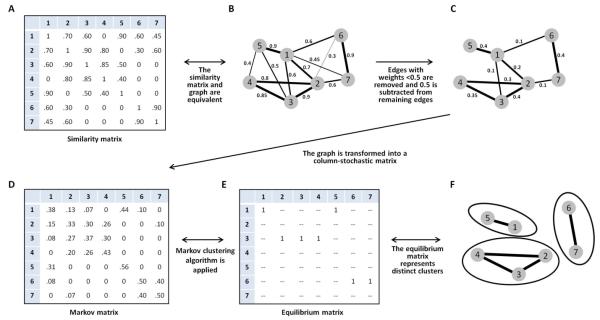
(A) Similarity matrix, with the entry in a cell representing the similarity of the runs represented in the associated row and column. (B) A graph equivalent to the similarity matrix, with nodes representing runs and edges representing similarity scores for distinct pairs of runs (loops connecting nodes to themselves are not shown). (C) A graph following the removal of edges whose weights are smaller than a fixed threshold, 0.5. The weights of the remaining edges have been shifted by −0.5. (D) A column-stochastic matrix for the 7 runs. (E) The equilibrium matrix obtained by iterating expansion and inflation steps in the Markov clustering algorithm. (F) Clusters of runs identified by the Markov clustering algorithm.
To obtain a suitable level of granularity with the MCL algorithm, a useful pre-processing step is to use a threshold for the inclusion of edges in the graph (S. van Dongen, personal communication). This threshold can be set by the user or determined dynamically given the properties of the graph analyzed (the default setting in Clumpak). Specifically, for a given data set and for each value in the range of thresholds explored, the mean node degree, as well as the fraction of singleton nodes, representing runs that are not connected to any other runs, are examined (accomplished using the vary-threshold option of MCL). The dynamic threshold that is used by Clumpak is the largest threshold for which the fraction of singletons is smaller than 0.1 and the mean node degree across all nodes in the graph is at least 50% of the total number of vertices. Once a threshold has been set, edges whose weights are smaller than the threshold are removed, and the weights of the remaining edges are shifted downward by the value of the threshold (accomplished using the tf option of MCL). Other than using a threshold, the default parameters of MCL are used by Clumpak (equivalent to setting the parameter r to 2 without using pre-inflation). Notably, MCL can cluster two vertices together even if the input graph does not contain an edge connecting them; thus, the choice of the threshold is less influential than in the clique approach.
Once clusters are identified within replicate runs with the same K value, Clumpak utilizes Clumpp (Jakobsson and Rosenberg 2007) for obtaining an average run representing each cluster, and Distruct (Rosenberg 2004) for graphical display of the results. Clumpak reports to the user the number of replicate runs clustered in each mode detected, the mean posterior probability of runs clustered in each mode, and the mean Clumpp scores between all pairs of runs within a mode. Notably, the largest mode (the one containing the largest number of replicate runs) might not have the highest mean posterior probability; users are advised to consider both attributes when interpreting their results.
Aligning clustering results across different K values
Clumpak aligns cluster labels across replicate runs, clusters of runs, and different K values. Clumpak relies on a previously developed algorithm for alignments at fixed K values (Jakobsson and Rosenberg 2007), whereas the label-matching algorithm for different K values is a novel extension and proceeds as follows. We refer to the matrix of membership coefficients [Q]C×K as the Q-matrix, with C rows corresponding to individuals and K columns corresponding to clusters, and the value in the cth row and kth column representing the membership coefficient for individual c in cluster k as inferred in a single run (or the mean of a set of runs). Each matrix consists of non-negative entries, and the sum of the entries in any row is 1. Following Jakobsson and Rosenberg (2007), the similarity score between replicate runs i and j (i.e. two Q-matrices of the same dimension), is defined as
| (1) |
where ||.||F denotes the Frobenius matrix norm. The normalization constant constrains G’ to lie between 0 to 1 (see Eq. 6 in Jakobsson and Rosenberg 2007).
Consider now a pair of Q-matrices produced for two consecutive K values, [Qi ]C×K and [Qj ]C×(K+1) . To account for the different sizes of Qi and Qj , a column of zeros is added to Qi , as a final (K+1) column, representing a cluster that does not exist for K clusters but does exist for K+1. This addition produces a C×(K+1) matrix . We then compute the similarity score
| (2) |
Using G” to measure similarity, the optimal alignment of matrices Qi and Qj is defined as the permutation of columns of Qj that maximizes G’’ over all (K+1)! possible permutations. We sequentially align clustering solutions starting from an initial value K0 , aligning a solution with K0+1 clusters to the K0 solution, the K0+2 solution to the K0+1 solution, and so on. This process examines alignments of the various modes at K0+1 clusters to the corresponding modes at K0 clusters.
Comparing results across different models
Clumpak enables a comparison of clustering solutions across different programs (e.g. comparing output from Structure and Admixture), different model choice (e.g. comparing output for a no-admixture model and an admixture model), or different subsets of genetic markers across the same data set (e.g. comparing output for half of the markers to the other half), each with its own sets of runs. Hereafter all three of these scenarios are termed “different models.” Clumpak first analyzes and summarizes the results of each model separately, but it aligns cluster labels across the two models, thus enabling easy visual inspection of the results. Additionally, Clumpak provides users with Clumpp similarity scores between the modes identified for the two models, and for comparison, Clumpp similarity scores within each mode.
Simulation study
We used simulations to assess the accuracy of Clumpak in differentiating runs into distinct clustering solutions. We simulated Structure-like outputs directly, for three a priori distinct populations, each with a sample of 25 individuals. Q-matrices were generated for three predefined clusters (K=3). A single simulation contained 40 Q-matrices, corresponding to 40 individual Structure-like runs.
We explored two aspects of variation across runs. First, we allowed mean membership coefficients for each a priori population to vary across replicate runs, representing stochastic variation across individual Structure-like runs. Second, within each run and each population, we varied individual membership coefficients around the population mean for that run. The standard deviation (SD) parameters for these two sources of variation are termed SDRUNS and SDINDIVS , respectively (described in more detail below). By increasing these standard deviations, we obtained Q-matrices that are increasingly more challenging for accurate clustering (see Supplementary Note 1 for the relation of the similarity scores between runs to SDRUNS and SDINDIVS ).
The simulations assumed that each a priori population is characterized by its own “seed” membership coefficients, denoting the mean genomic proportion within a priori population i originating from cluster k (k=1, 2, 3). Thus, for example, , corresponds to a scenario in which the mean membership coefficients for individuals belonging to population 1 are 0.5, 0.4, and 0.1 for clusters 1, 2, and 3, respectively. We chose the seed vectors on the basis of empirical examples, as described in Appendix 1 (Supporting Information).
We simulated data in a two-step manner as follows. First, for each run (m=1, 2, …, 40), a set of mean membership coefficients for each a priori population was sampled around the predefined population seed vector. For a priori population i, we sampled around the seed vector using a Dirichlet distribution , where α(i) is a concentration parameter adjusted so that the standard deviation of the first component of the Dirichlet distribution was equal to a predefined value of SDRUNS (see Appendix 2, Supporting Information). Let denote the mean membership coefficients for population i that were sampled for a certain run (for clarity, we omit the notation of the run index). This vector is the output of the first simulation step.
In the second step, we sampled individual membership coefficients around the run-specific vector of population-mean membership coefficients for each of the 25 individuals belonging to a priori population i. To this end, we sampled around using , where β(i) is a concentration parameter adjusted so that the standard deviation of the Dirichlet distribution was equal to a predefined value of SDINDIVS (Appendix 2, Supporting Information). In summary, obtaining a single Q-matrix requires sampling once around for each a priori population i = 1, 2, 3, and then for each i, sampling 25 sets of membership coefficients around . A single simulation iterates this process 40 times, obtaining a simulated set of 40 Structure-like runs on 75 individuals. These runs were then provided as input to Clumpak.
The procedure outlined above represents a scenario in which all 40 Structure runs are drawn from a single set of seed vectors, and we thus expect these runs to be clustered together, obtaining a single mode. We are also interested, however, in examining the performance of Clumpak under genuine bimodality, that is, when Structure-like runs can be divided into two truly distinct solutions. The procedures for generating simulated data under bimodality were similar to the unimodal case, with two exceptions. First, instead of having a single seed membership vector per population we now have two: one representing a major mode and the other a minor mode. Second, among the 40 simulated runs, we choose a fraction of runs, f, to represent the minor mode, placing fraction 1-f into the major mode. We used several values of f, simulating data for f=0, 0.125, 0.25, 0.375. The fraction 0.125, for example, corresponds to the case in which the minor mode has 5 runs and the major mode has 35 runs. The f=0 case represents a unimodal simulation.
Simulations were performed for a range of values of SDRUNS and SDINDIVS , 0.01 to 0.15, for both parameters. Values exceeding 0.15 represent very high variation, as evident from the similarity scores between simulated runs, compared to the similarities observed in the empirical datasets that we considered (Supplementary Note 1, Supporting Information). For each combination of SDRUNS , SDINDIVS , and f, we performed 30 simulations. The seed membership coefficients were taken from empirical examples for which bimodality was evident (Appendix 1, Supporting Information). The seed vectors for the simulations in Figures 2 and 3 are based on mean membership coefficients in major and minor modes for the Mozabite, Bedouin, and Druze populations at K=3, for the same set of runs presented in the Results section (Figures 4 and 5). Simulation sets based on other empirical examples (Supporting Information) yielded similar results.
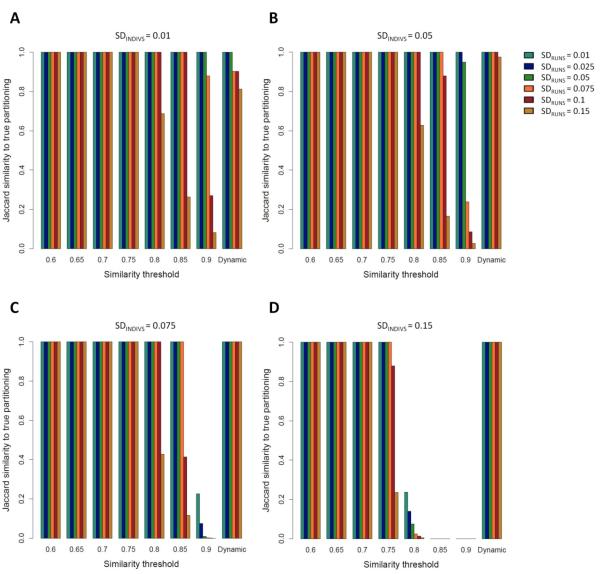
Figure 2. Jaccard similarity scores between the clustering solutions obtained by Clumpak and the “true” (simulated) partitioning in a unimodal case, as a function of SDRUNS , SDINDIVS , and either a fixed threshold value or a dynamic threshold.
Simulations were carried out with one underlying mode. Different colors represent different values of SDRUNS as given by the color palette on the right side of panel B. (A) SDINDIVS =0.01. (B) SDINDIVS =0.05. (C) SDINDIVS =0.075. (D) SDINDIVS =0.15.
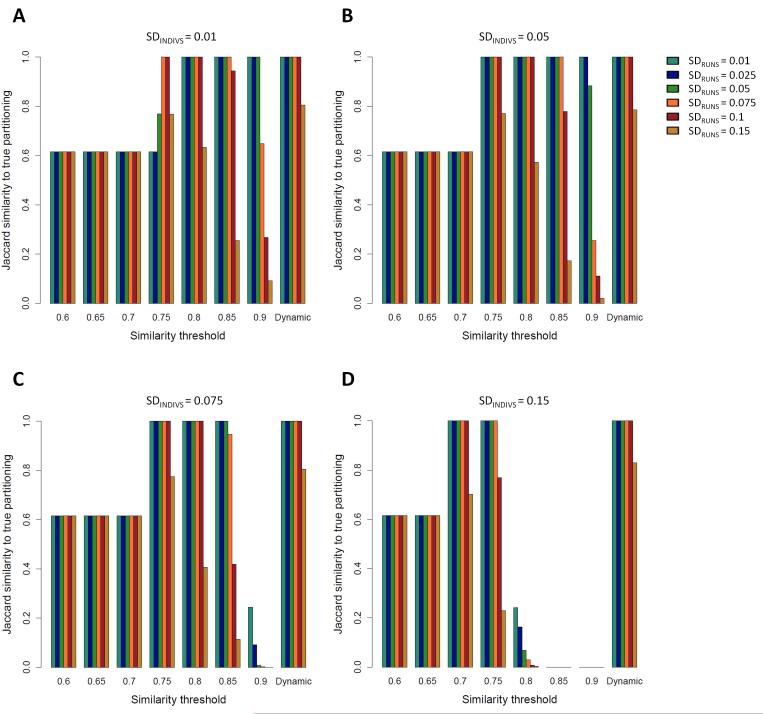
Figure 3. Jaccard similarity scores between the clustering solution obtained by Clumpak and the “true” (simulated) partitioning in a bimodal case, as a function of SDRUNS , SDINDIVS , and either a fixed threshold value or a dynamic threshold.
Simulations were carried out with a fraction f=0.25 of the runs assigned to the minor mode. Different colors represent different values of SDRUNS as given by the color palette on the right side of panel B. (A) SDINDIVS =0.01. (B) SDINDIVS =0.05. (C) SDINDIVS =0.075. (D) SDINDIVS =0.15.
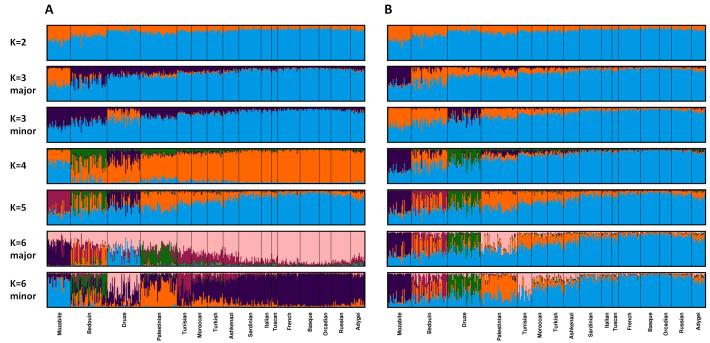
Figure 4. Major and minor modes identified for 399 individuals from 16 populations, illustrating Clumpak’s label-matching across K values.
For each K value, Structure was run 40 times. (A) Membership coefficients produced by Clumpak when label-matching across K values was disabled (for illustration only). (B) Membership coefficients produced by Clumpak for the same set of runs as in (A), matching labels across K values. Clusters have been permuted to sequentially match the configuration for the lowest K in the range (K=2).
Figure 5. Membership coefficients compared using two different Structure models with K=6.
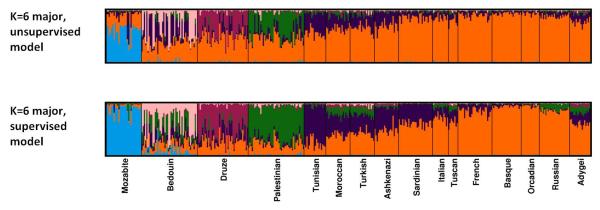
The same set of 399 individuals from 16 populations was used for both panels. For each model, Structure was run 40 times, and Clumpak was used to identify distinct solutions among runs of the same model as well as to compare the different modes across the two models. For the runs without the locprior model (unsupervised), the runs are the same as in Figure 4. Top: The major mode for the unsupervised admixture model without the locprior model. Bottom: The major mode for the locprior (supervised) admixture model.
We used the simulations both to assess accuracy of mode identification and to validate choices of settings in Clumpak. Each simulation was given to Clumpak as input under different program settings. First, we modified the similarity threshold, using either a fixed similarity threshold in the range of 0.6 to 0.9, reasonable in light of past choices (Wang et al. 2007; Jakobsson et al. 2008), or by the default approach in which the threshold was determined dynamically. We also examined values of the inflation parameter that differed from the Clumpak default of r=2.
We used the Jaccard index (Jain and Dubes 1988; Kaufman and Rousseeuw 1990) to measure the accuracy of the clustering solution obtained by Clumpak in comparison to the “real” (simulated) modes. This index varies from 0 to 1, with 1 being a perfect match between the inferred and simulated clustering of runs. Specifically, each simulation contains 40 runs; thus, each has (40×39)/2=780 pairs of runs. Each pair was tabulated in one of four categories: (1) N11 , the runs truly belong in the same mode, and were placed in the same mode by Clumpak, (2) N10 , the runs belong in the same mode, but were placed in different modes by Clumpak, (3) N01 , the runs belong in different modes, but were placed in the same mode, (4) N00 , the runs belong in different modes, and were placed in different modes. The Jaccard index is calculated according to the following formula:
| (3) |
Availability and requirements
Clumpak is available through a web-server, at http://clumpak.tau.ac.il, or can be downloaded and used on Linux, Unix, and Mac operating systems. With either approach, Clumpak includes calls to Clumpp, Distruct, and MCL (all of which the user needs to install if running Clumpak locally). In the downloaded version, users can explore a range of values of optional parameters—especially those concerned with running Clumpp—that are more restricted in the web server in order to limit exhaustive running times.
By using the Distruct program (Rosenberg 2004), and by allowing users to specify graphical parameters used by Distruct, Clumpak provides users with high-quality images produced for each K (and within each K for each mode of convergence); the modes are graphically aligned across K. For its main pipeline, Clumpak requires that users submit the results of clustering programs in Structure or Admixture format, allowing any range of K values and single or multiple runs for each K. Clumpak also implements the methods of Evanno et al. (2005) and Pritchard et al. (2000) for selecting a preferred value of K.
RESULTS
Simulations
We used simulations to examine the accuracy of Clumpak in assigning independent Structure-like runs into separate modes. We first compared the default setting of Clumpak, under which a threshold for the inclusion of edges in the similarity graph (Figure 1) is chosen dynamically, to a range of fixed values for the threshold.
Figure 2 presents the Jaccard similarity score between the partition obtained by Clumpak and the true partition for unimodal simulations, in which all replicate runs were sampled from the same mode. Under this setting, as the value of the fixed threshold increases, the accuracy of the clustering obtained using the MCL algorithm decreases. This pattern is expected, because higher thresholds lead to sparser graphs, resulting in the separation of replicate runs into distinct clusters, whereas in the correct configuration, all runs are clustered together to form a single mode. Comparing the four panels in Figure 2, representing different values of SDINDIVS , and comparing different values of SDRUNS for fixed values of SDINDIVS , the decline in accuracy with an increasing threshold is more noticeable for simulations at higher SD values. This pattern is also expected, as higher SD values indicate more variation between the runs, and hence sparser graphs at a fixed threshold.
Figure 3 presents the Jaccard score for the bimodal case, when two distinct modes were simulated, with 25% of the runs belonging to the minor mode (other fractions are examined in Supporting Information, Figures S1 and S2). Here, the accuracy of the fixed threshold exhibits a peaked pattern, with the most accurate clustering achieved at intermediate values of the threshold. Whereas low thresholds lead to erroneous clustering of all replicate runs into a single mode, thresholds that are too high break the similarity graph into too many components, identifying too many distinct modes. As the SD values increase, the peak moves to the left, and thus, the optimal fixed threshold is lower.
The differing performance of the graph clustering procedure in the unimodal and bimodal cases in Figures 2 and 3 suggests that a single fixed threshold does not yield an optimal solution applicable in all scenarios, as the optimal threshold is influenced both by the number of modes among the replicate runs and by the level of variation across runs and individuals. These tradeoffs are accommodated using the dynamic procedure implemented in Clumpak, which sets the threshold according to the characteristics of the input data. Indeed, as the level of variation increases in either of two ways (SDRUNS and SDINDIVS ), the dynamic threshold is set to lower values, thus allowing more variability within modes inferred to be distinct (Supplementary Note 1, Supporting Information). In both the unimodal and bimodal cases, the performance of the dynamic threshold is optimal or near the optimum for all simulation scenarios (rightmost bars in each panel of Figures 2 and 3). For example, in the unimodal simulations, the mean Jaccard similarity score calculated across 30 simulations for each set of parameters is 1.0 or close to 1.0 in most settings, including the challenging setting of low SDINDIVS values coupled with high values of SDRUNS . The somewhat lower accuracy in such cases arises from the separation of the runs into multiple modes; the clustering is still adequate, as in nearly all simulations, there is a major cluster containing most replicate runs (>35 of 40). In the bimodal simulations, the accuracy of the inferred clusters obtained using the dynamic threshold is high for both low and high SDINDIVS and SDRUNS values, and exceeds that of any single fixed value (Figure 3).
In addition to the manner of choosing the threshold for inclusion in the similarity graph, the inflation parameter, r, of the MCL algorithm, potentially also influences the clustering of runs. We found that for the range of values examined (ranging from 1.1 to 12, representing the range of reasonable values for that parameter; S. van Dongen, personal communication), however, this parameter has little influence on the clustering results for low values of SDINDIVS and SDRUNS , whereas for higher values the optimal performance is obtained for r=2, the Clumpak default (Figure S3, Supporting Information). Taken together, for the clustering task of distinguishing between modes, we found that the threshold choice is more influential than the inflation parameter r, and that the dynamic threshold implemented in Clumpak produces high accuracy that is optimal or close to optimal.
Empirical example
To illustrate a data application of Clumpak, we have reexamined a data set of 678 autosomal microsatellites in 399 individuals from 16 European and Middle Eastern human populations, including 78 individuals of Jewish descent (Ashkenazi, Moroccan, Tunisian, and Turkish Jews). Using Structure, Kopelman et al. (2009) previously studied the membership coefficients of the 399 individuals for a range of K values. For each value of K, 40 individual Structure runs were conducted and then assessed using Clumpp (Jakobsson and Rosenberg 2007). The clique clustering approach was then used to detect distinct solutions.
To reanalyze this data set through Clumpak, we first generated new Structure replicates, running Structure 40 times for each value of K from 2 to 6, using the mixed-membership admixture model with a burn-in period of 10,000 iterations followed by 20,000 additional iterations for each run. The resulting runs were provided to Clumpak.
Figure 4 presents the output obtained from Clumpak for this collection of runs before and after label-matching across different values of K. The main distinct solutions—the major modes for each K as identified by the Markov clustering algorithm—are similar to those presented by Kopelman et al. (2009) on the basis of the clique approach. In addition to the major modes, Clumpak further identifies minor modes for K=3 (13 runs), K=4 (7 runs), K=5 (4 runs), and K=6 (10 runs). Figure 4 includes the minor modes for K=3 and K=6. Interestingly, the minor mode for K=6 distinguishes the Tunisian Jewish population from other Jewish populations. This distinction, which was not present in the major modes reported by Kopelman et al. (2009), was in fact observed by Kopelman et al. when the population structure of Jewish individuals was examined separately. We might argue, however, that by simplifying the user experience of examining minor modes, Clumpak can uncover biologically interesting minor clustering solutions that might otherwise go unnoticed.
To demonstrate the comparison of models using Clumpak, we ran Structure a second time on the same data set of 399 individuals using the admixture model along with the locprior model (i.e. supervised clustering), which takes into consideration sampling locations of individuals, treating separate population identifiers as separate locations in prior information to assist clustering. This option is recommended for cases in which the inferred population structure is weak, or the populations examined are very closely related (Hubisz et al. 2009). We ran the locprior model with K=6, comparing the results to those obtained without the use of the locprior model.
Figure 5 illustrates the comparison of 40 runs obtained for K=6 without the locprior model to 40 runs with the locprior model. Visual comparison of the results obtained under the two models is simplified using the Clumpak alignment across the two models (as well as across multiple modes obtained under the same model). This comparison demonstrates the tendency of the supervised approach to intensify weak population structure within the a priori populations, leading to somewhat different inferences. The “Compare models” option of Clumpak further provides users with Clumpp similarity scores between the modes that were identified by the two models. Indeed, the similarity score between the major modes obtained under the two models (0.79) is lower than the similarity score for the major and minor modes of the unsupervised runs (0.85), giving further indication that the results obtained under the two models are not identical.
DISCUSSION
Analysis of population structure using model-based clustering methods is a complex task that requires careful handling (Pritchard et al. 2000; Rosenberg et al. 2001b; Evanno et al. 2005; Weiss and Long 2009). Due to the inherent stochasticity of Structure and other genetic clustering programs, independent runs of these programs often arrive at distinct solutions, and thus, understanding the replicability of the results and distinguishing distinct solutions are not always trivial tasks. We have developed Clumpak to simplify and enhance the user experience in evaluating, comparing, and displaying the results produced by these programs. Clumpak treats the problem of grouping Structure-like runs as a graph-based clustering problem, providing a useful method for separating distinct solutions within K values, averaging runs belonging to the same mode, and comparing runs across K values. It additionally supports the possibility of comparing different programs, models, and subsets of the data, and identifying a preferred K value via the methods of Evanno et al. (2005) and Pritchard et al. (2000). Using simulations and an example data set of Kopelman et al. (2009), we found that Clumpak can identify major and minor solutions observed in replicate runs, potentially facilitating the assessment of biologically interesting clustering behavior that is only visible in minor modes. We have also validated the dynamic procedure by which Clumpak identifies the optimal similarity threshold for each value of K , finding that this approach, set as the Clumpak default, is preferable to a fixed-threshold approach.
Three other tools are currently available to assist users with post-processing and presentation of the results from Structure-like programs—the aforementioned Clumpp (Jakobsson and Rosenberg 2007), Distruct (Rosenberg 2004), and Structure Harvester (Earl and Vonholdt 2012). As noted earlier, a typical post-processing effort has involved use of two or all three of these programs. Clumpak combines many of the features of these existing tools, incorporating calls to Clumpp and Distruct, and providing users with a single program to accomplish primary aspects of post-processing (Table 1). Most of the options provided by Distruct and Clumpp also appear in Clumpak, including the choice of algorithm in Clumpp, and color options, labeling, and order of populations in Distruct. Structure Harvester is used for preparing Clumpp input files and for determining the most suitable K according to the method of Evanno et al. (2005); the former functionality is subsumed in Clumpak, and the latter appears in Clumpak via the “Best K” feature. Beyond its incorporation of features of these programs in a single convenient form, Clumpak is the first to automate the process of distinguishing between distinct solutions for a single K value, and to perform cluster matching across different K values. Finally, Clumpak offers a natural visualization for comparing results obtained using different models, programs, or subsets of the data.
Table 1. Programs that aid in the post-processing of results obtained from Structure-like methods.
| Software | Platform | Input type/ format |
Description | Refs |
|---|---|---|---|---|
|
Structure
Harvester |
Online & downloadable Python script |
Zipped Structure result files |
Determines a choice of K. Produces input files for Clumpp. |
(Earl and Vonholdt 2012) |
| Clumpp | Unix, Linux, Dos, Mac |
Clumpp formata |
Deals with label switching within a single K value. Evaluates the similarity of replicate runs. |
(Jakobsson and Rosenberg 2007) |
| Distruct | Unix, Linux, Dos, Mac |
Distruct formata,b |
Produces graphical display for a single replicate run. |
(Rosenberg 2004) |
| Clumpak | Online & Unix, Linux, Mac |
Multiple formats, enabling direct input from Structure and other Structure- like programs |
Deals with label switching within a single K value. Deals with label switching across multiple K values. Clusters replicate runs into distinct modes. Produces graphical displays for each mode within each K. Determines a choice of K. |
This paper |
Input files can be obtained from the output of Structure-like programs.
One of the input files can be obtained from the output of Clumpp.
One view of “genuine multimodality” in clustering studies, as opposed to label-switching, is that it represents a failure of clustering programs to identify a single optimal mode, and that multimodality is simply an algorithmic artifact. From this idealistic standpoint, widely used algorithms such as Structure are problematic, and rather than facilitating the analysis of multimodality as a feature of clustering results, it would be preferable to improve algorithms to eliminate it. However, a pragmatic approach to available methods regards genuine Structure multimodality as a regular feature of the analysis that can be used to assist with biological interpretations (e.g. Rosenberg et al. 2001a; Wang et al. 2007; Kopelman et al. 2009). Especially for complex data sets, different modes for a given data set can reflect the existence of population groupings that are comparably supported (Pritchard et al. 2000), so that exploration of multiple modes contributes information to an analysis. For example, in examining how distinct solutions—both major and minor modes—change across a range of K values, Wang et al. (2007) observed multimodality at certain values of K, but found that solutions for larger K could be viewed as refinements of several of the modes observed at lower K. The distinct modes at smaller K each possessed some of the biological structure made apparent at larger K—structure portended in full by the collection of modes at small K—and they thus contributed to the understanding of major subdivisions in Native American population structure.
Finally, we note that although we have implemented Clumpak primarily for use specifically with Structure and Admixture, it is suitable for use with any program that generates cluster membership coefficients, provided the results produced by these programs are appropriately formatted for Clumpak. Notably, each of the model-based clustering programs requires that users make appropriate choices regarding the underlying model and optional running parameters (for example, running Structure long enough). Though Clumpak does not guide the users regarding these clustering choices, making sense of the results of such programs is rendered easier by the use of Clumpak. If the number of distinct clusters of runs inferred by Clumpak is too large, however, or if the similarity scores between replicate runs are low, then the Structure-like program might be uninformative or might have employed inappropriate settings; in these circumstances, we advise the user to inspect the original outputs and parameter choices for the program used to obtain the membership matrices.
Supplementary Material
ACKNOWLEDGMENTS
We are grateful to Stijn van Dongen for helpful suggestions. We thank Ofer Chay for help with establishing the web server, and Sohini Ramachandran and Aaron Behr for early testing and feedback. This work was supported by the Edmond J. Safra postdoctoral fellowship at Tel Aviv University (NMK) and by NIH grant R01 HG005855 (NAR).
Footnotes
DATA ACCESIBILITY
Clumpak is freely available for online use and for download at http://clumpak.tau.ac.il. The microsatellite data of Kopelman et al. (2009) used in the empirical example are available at https://rosenberglab.stanford.edu/datasets.html.
AUTHOR CONTRIBUTIONS
N.M.K. and I.M conceived and supervised the study, with advice from M.J. and N.A.R.; J.M. and N.M.K. coded and tested the software; N.M.K., I.M., and N.A.R. wrote the manuscript.
REFERENCES
- Alexander DH, Novembre J, Lange K. Fast model-based estimation of ancestry in unrelated individuals. Genome Research. 2009;19:1655–1664. doi: 10.1101/gr.094052.109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alexander DH, Lange K. Enhancements to the ADMIXTURE algorithm for individual ancestry estimation. BMC Bioinformatics. 2011;12:246. doi: 10.1186/1471-2105-12-246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Breseghello F, Sorrells ME. Association mapping of kernel size and milling quality in Wheat (Triticum aestivum L.) cultivars. Genetics. 2006;172:1165–1177. doi: 10.1534/genetics.105.044586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen C, Durand E, Forbes F, François O. Bayesian clustering algorithms ascertaining spatial population structure: a new computer program and a comparison study. Molecular Ecology Notes. 2007;7:747–756. [Google Scholar]
- Corander J, Waldmann P, Sillanpaa MJ. Bayesian analysis of genetic differentiation between populations. Genetics. 2003;163:367–374. doi: 10.1093/genetics/163.1.367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corander J, Waldmann P, Marttinen P, Sillanpaa MJ. BAPS 2: enhanced possibilities for the analysis of genetic population structure. Bioinformatics. 2004;20:2363–2369. doi: 10.1093/bioinformatics/bth250. [DOI] [PubMed] [Google Scholar]
- Corander J, Marttinen P, Siren J, Tang J. Enhanced Bayesian modelling in BAPS software for learning genetic structures of populations. BMC Bioinformatics. 2008a;9:539. doi: 10.1186/1471-2105-9-539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corander J, Siren J, Arjas E. Bayesian spatial modeling of genetic population structure. Computational Statistics. 2008b;23:111–129. [Google Scholar]
- Dawson KJ, Belkhir K. A Bayesian approach to the identification of panmictic populations and the assignment of individuals. Genetical Research. 2001;78:59–77. doi: 10.1017/s001667230100502x. [DOI] [PubMed] [Google Scholar]
- Driscoll CA, Menotti-Raymond M, Roca AL, et al. The Near Eastern origin of cat domestication. Science. 2007;317:519–523. doi: 10.1126/science.1139518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Durand E, Jay F, Gaggiotti OE, François O. Spatial inference of admixture proportions and secondary contact zones. Molecular Biology and Evolution. 2009;26:1963–1973. doi: 10.1093/molbev/msp106. [DOI] [PubMed] [Google Scholar]
- Earl DA, Vonholdt BM. Structure Harvester: a website and program for visualizing Structure output and implementing the Evanno method. Conservation Genetics Resources. 2012;4:359–361. [Google Scholar]
- Enright AJ, Van Dongen S, Ouzounis CA. An efficient algorithm for large-scale detection of protein families. Nucleic Acids Research. 2002;30:1575–1584. doi: 10.1093/nar/30.7.1575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evanno G, Regnaut S, Gould J. Detecting the number of clusters of individuals using the software STRUCTURE: a simulation study. Molecular Ecology. 2005;14:2611–2620. doi: 10.1111/j.1365-294X.2005.02553.x. [DOI] [PubMed] [Google Scholar]
- Falush D, Stephens M, Pritchard JK. Inference of population structure using multilocus genotype data: linked loci and correlated allele frequencies. Genetics. 2003;164:1567–1587. doi: 10.1093/genetics/164.4.1567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Falush D, Stephens M, Pritchard JK. Inference of population structure using multilocus genotype data: dominant markers and null alleles. Molecular Ecology Notes. 2007;7:574–578. doi: 10.1111/j.1471-8286.2007.01758.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Faust K, Sathirapongsasuti JF, Izard J, et al. Microbial co-occurrence relationships in the human microbiome. PLoS Computational Biology. 2012;8:e1002606. doi: 10.1371/journal.pcbi.1002606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- François O, Ancelet S, Guillot G. Bayesian clustering using hidden Markov random fields in spatial population genetics. Genetics. 2006;174:805–816. doi: 10.1534/genetics.106.059923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frichot E, Mathieu F, Trouillon T, Bouchard G, François O. Fast and efficient estimation of individual ancestry coefficients. Genetics. 2014;196:973–983. doi: 10.1534/genetics.113.160572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gao H, Williamson S, Bustamante CD. A Markov chain Monte Carlo approach for joint inference of population structure and inbreeding rates from multilocus genotype data. Genetics. 2007;176:1635–1651. doi: 10.1534/genetics.107.072371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilbert KJ, Andrew RL, Bock DG, et al. Recommendations for utilizing and reporting population genetic analyses: the reproducibility of genetic clustering using the program STRUCTURE. Molecular Ecology. 2012;21:4925–4930. doi: 10.1111/j.1365-294X.2012.05754.x. [DOI] [PubMed] [Google Scholar]
- Gompert Z, Buerkle CA. Analyses of genetic ancestry enable key insights for molecular ecology. Molecular Ecology. 2013;22:5278–5294. doi: 10.1111/mec.12488. [DOI] [PubMed] [Google Scholar]
- Guillot G, Estoup A, Mortier F, Cosson JF. A spatial statistical model for landscape genetics. Genetics. 2005;170:1261–1280. doi: 10.1534/genetics.104.033803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guillot G. Inference of structure in subdivided populations at low levels of genetic differentiation—the correlated allele frequencies model revisited. Bioinformatics. 2008;24:2222–2228. doi: 10.1093/bioinformatics/btn419. [DOI] [PubMed] [Google Scholar]
- Hoggart CJ, Parra EJ, Shriver MD, et al. Control of confounding of genetic associations in stratified populations. American Journal of Human Genetics. 2003;72:1492–1504. doi: 10.1086/375613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horn RA, Johnson CR. Topics in matrix analysis. Cambridge University Press; Cambridge: 1991. [Google Scholar]
- Hubisz MJ, Falush D, Stephens M, Pritchard JK. Inferring weak population structure with the assistance of sample group information. Molecular Ecology Resources. 2009;9:1322–1332. doi: 10.1111/j.1755-0998.2009.02591.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huelsenbeck JP, Andolfatto P. Inference of population structure under a Dirichlet process model. Genetics. 2007;175:1787–1802. doi: 10.1534/genetics.106.061317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huelsenbeck JP, Andolfatto P, Huelsenbeck ET. Structurama: Bayesian inference of population structure. Evolutionary Bioinformatics. 2011;7:55–59. doi: 10.4137/EBO.S6761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jain AK, Dubes RC. Algorithms for clustering data. Prentice-Hall; Upper Saddle River, NJ, USA: 1988. [Google Scholar]
- Jakobsson M, Rosenberg NA. CLUMPP: a cluster matching and permutation program for dealing with label switching and multimodality in analysis of population structure. Bioinformatics. 2007;23:1801–1806. doi: 10.1093/bioinformatics/btm233. [DOI] [PubMed] [Google Scholar]
- Kaufman L, Rousseeuw PJ. Finding groups in data: an introduction to cluster analysis. Wiley; New York, NY, USA: 1990. [Google Scholar]
- Kopelman NM, Stone L, Wang C, et al. Genomic microsatellites identify shared Jewish ancestry intermediate between Middle Eastern and European populations. BMC Genetics. 2009;10:80. doi: 10.1186/1471-2156-10-80. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manel S, Gaggiotti OE, Waples RS. Assignment methods: matching biological questions with appropriate techniques. Trends in Ecology & Evolution. 2005;20:136–142. doi: 10.1016/j.tree.2004.12.004. [DOI] [PubMed] [Google Scholar]
- Parker HG, Kim LV, Sutter NB, et al. Genetic structure of the purebred domestic dog. Science. 2004;304:1160–1164. doi: 10.1126/science.1097406. [DOI] [PubMed] [Google Scholar]
- Pella J, Masuda M. The gibbs and split-merge sampler for population mixture analysis from genetic data with incomplete baselines. Canadian Journal of Fisheries and Aquatic Sciences. 2006;63:576–596. [Google Scholar]
- Pritchard JK, Stephens M, Donnelly P. Inference of population structure using multilocus genotype data. Genetics. 2000;155:945–959. doi: 10.1093/genetics/155.2.945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pritchard JK, Donnelly P. Case-control studies of association in structured or admixed populations. Theoretical Population Biology. 2001;60:227–237. doi: 10.1006/tpbi.2001.1543. [DOI] [PubMed] [Google Scholar]
- Ratnasingham S, Hebert PD. A DNA-based registry for all animal species: the Barcode index number (BIN) system. PLoS ONE. 2013;8:e66213. doi: 10.1371/journal.pone.0066213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenberg NA, Burke T, Elo K, et al. Empirical evaluation of genetic clustering methods using multilocus genotypes from 20 chicken breeds. Genetics. 2001a;159:699–713. doi: 10.1093/genetics/159.2.699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenberg NA, Woolf E, Pritchard JK, et al. Distinctive genetic signatures in the Libyan Jews. Proceedings of the National Academy of Sciences of the United States of America. 2001b;98:858–863. doi: 10.1073/pnas.98.3.858. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenberg NA, Pritchard JK, Weber JL, et al. Genetic structure of human populations. Science. 2002;298:2381–2385. doi: 10.1126/science.1078311. [DOI] [PubMed] [Google Scholar]
- Rosenberg NA. DISTRUCT: a program for the graphical display of population structure. Molecular Ecology Notes. 2004;4:137–138. [Google Scholar]
- Shringarpure S, Xing EP. mStruct: inference of population structure in light of both genetic admixing and allele mutations. Genetics. 2009;182:575–593. doi: 10.1534/genetics.108.100222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang H, Peng J, Wang P, Risch NJ. Estimation of individual admixture: analytical and study design considerations. Genetic Epidemiology. 2005;28:289–301. doi: 10.1002/gepi.20064. [DOI] [PubMed] [Google Scholar]
- Thornsberry JM, Goodman MM, Doebley J, et al. Dwarf8 polymorphisms associate with variation in flowering time. Nature Genetics. 2001;28:286–289. doi: 10.1038/90135. [DOI] [PubMed] [Google Scholar]
- Van Dongen S. Graph clustering by flow simulation. University of Utrecht; Utrecht: 2000. PhD thesis. [Google Scholar]
- Van Dongen S. Graph clustering via a discrete uncoupling process. SIAM Journal on Matrix Analysis and Applications. 2008;30:121–141. [Google Scholar]
- Wang S, Lewis CM, Jakobsson M, et al. Genetic variation and population structure in Native Americans. PLoS Genetics. 2007;3:e185. doi: 10.1371/journal.pgen.0030185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weiss KM, Long JC. Non-Darwinian estimation: my ancestors, my genes’ ancestors. Genome Research. 2009;19:703–710. doi: 10.1101/gr.076539.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whitfield CW, Behura SK, Berlocher SH, et al. Thrice out of Africa: ancient and recent expansions of the honey bee, Apis mellifera. Science. 2006;314:642–645. doi: 10.1126/science.1132772. [DOI] [PubMed] [Google Scholar]
- Zhao S, Zheng P, Dong S, et al. Whole-genome sequencing of giant pandas provides insights into demographic history and local adaptation. Nature Genetics. 2013;45:67–71. doi: 10.1038/ng.2494. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.