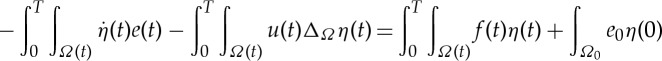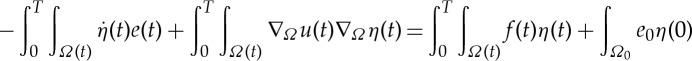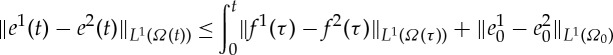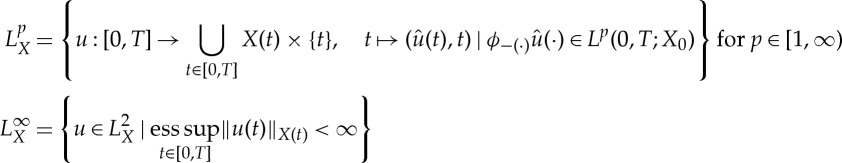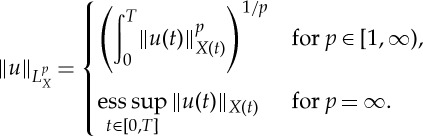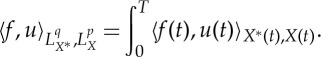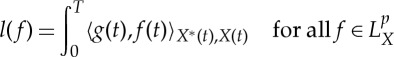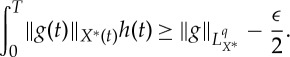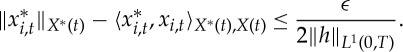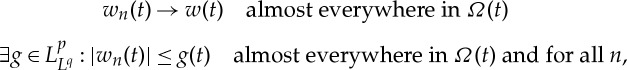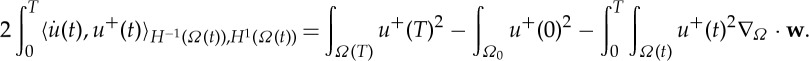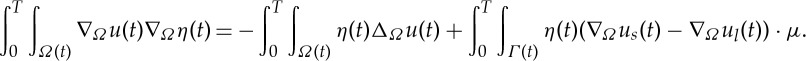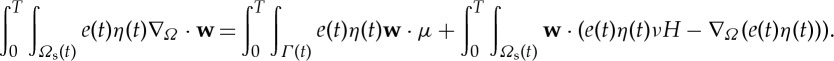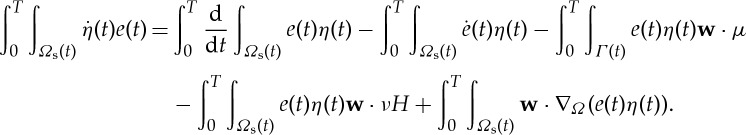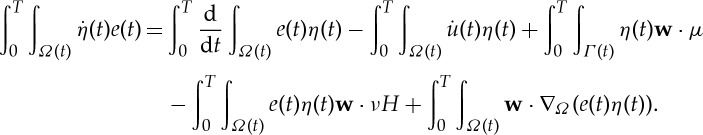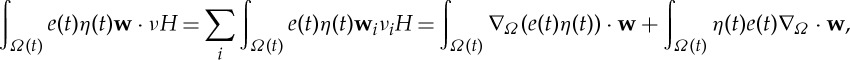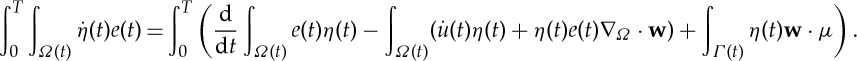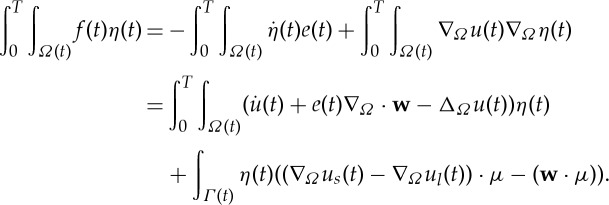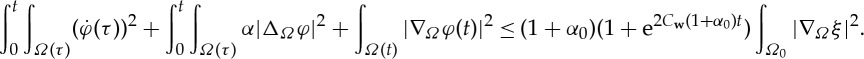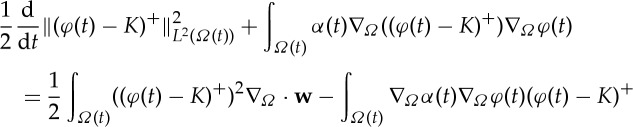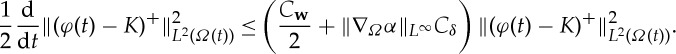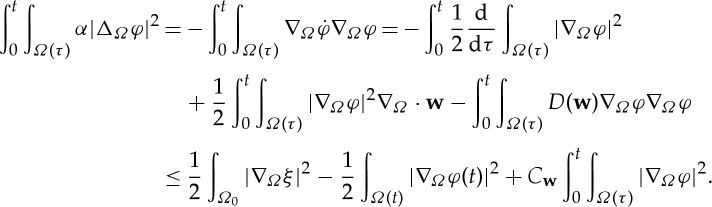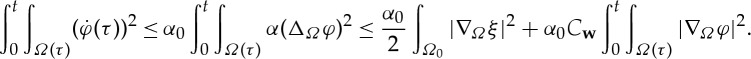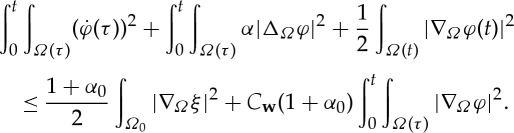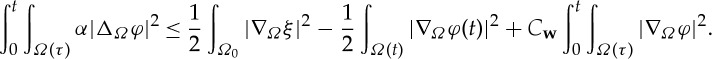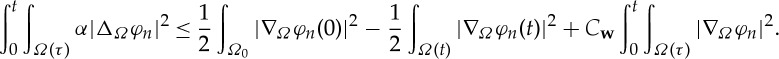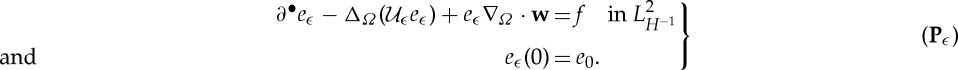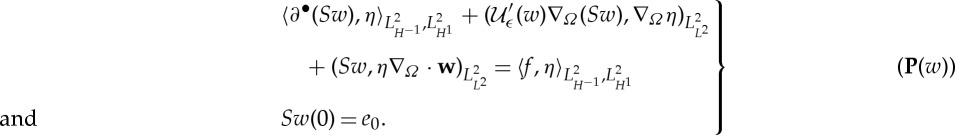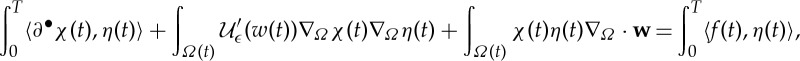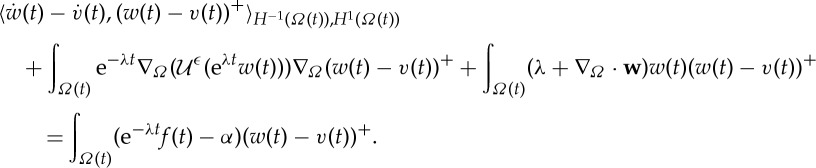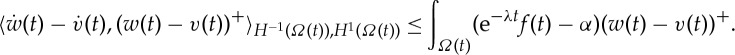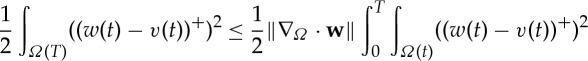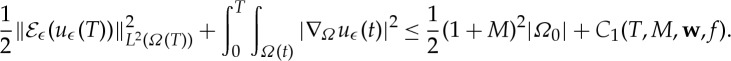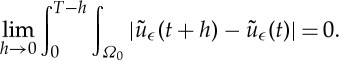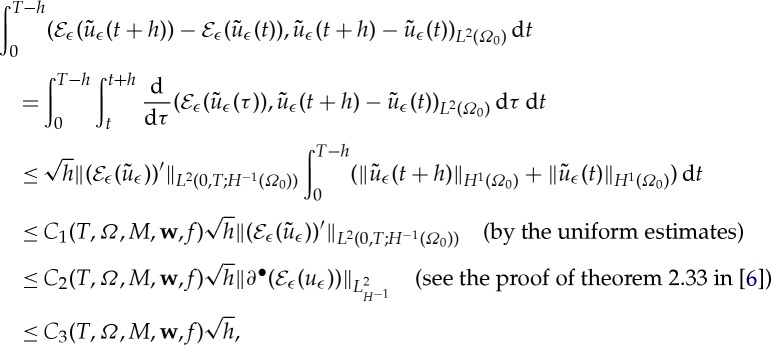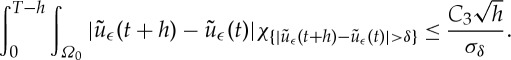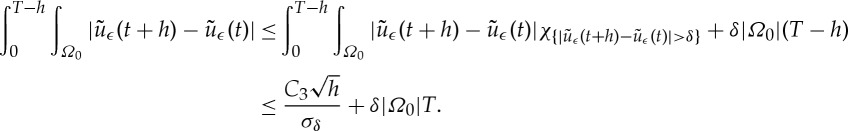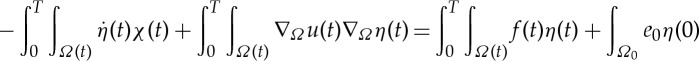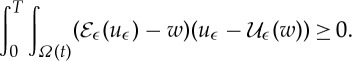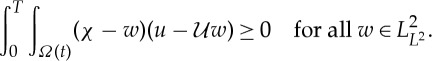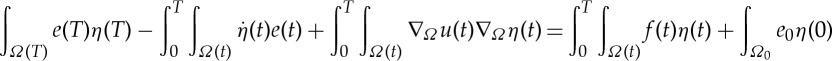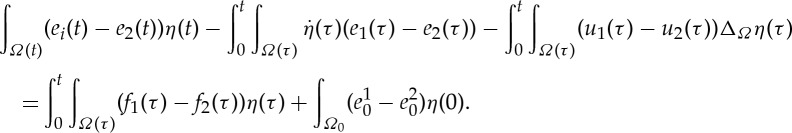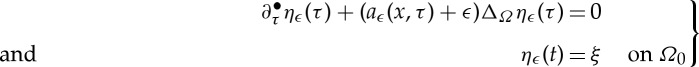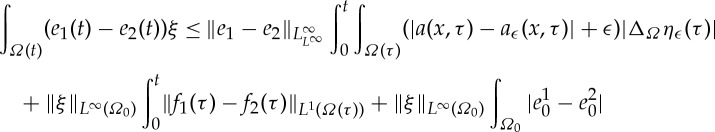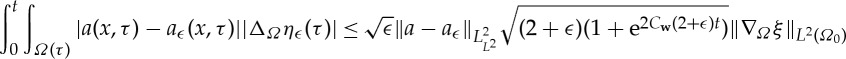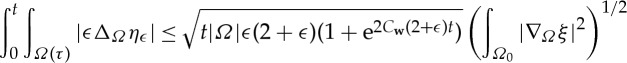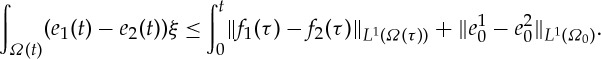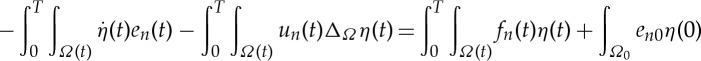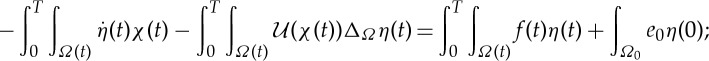A Stefan problem on an evolving surface

Abstract

We formulate a Stefan problem on an evolving hypersurface and study the well posedness of weak solutions given L¹ data. To do this, we first develop function spaces and results to handle equations on evolving surfaces in order to give a natural treatment of the problem. Then, we consider the existence of solutions for 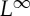data; this is done by regularization of the nonlinearity. The regularized problem is solved by a fixed point theorem and then uniform estimates are obtained in order to pass to the limit. By using a duality method, we show continuous dependence, which allows us to extend the results to L¹ data.

1. Introduction

The Stefan problem is the prototypical time-dependent free boundary problem. It arises in various forms in many models in the physical and biological sciences [1–4]. In this paper, we present the theory of weak solutions associated with the so-called enthalpy approach [1] to the Stefan problem on an evolving curved hypersurface.

Our interest is in the existence, uniqueness and continuous dependence of weak solutions to the Stefan problem

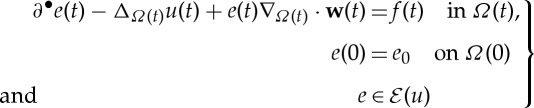1.1

posed on a moving compact hypersurface 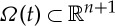evolving with (given) velocity field w, where the energy 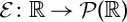is defined by

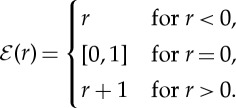Note that 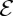is a maximal monotone graph in the sense of Brézis [5].

In (1.1), ∂^•e means the material derivative of e (which we shall also write as 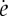), and ∇_Ω(t) and Δ_Ω(t) are, respectively, the surface gradient and Laplace–Beltrami operators on Ω(t). The novelty of this work is that the Stefan problem itself is formulated on a moving hypersurface and our chosen method to treat this problem, which we believe is naturally suited to equations on moving domains, requires the use of some new function spaces and results that we shall introduce, building upon the spaces and concepts presented in [6,7]. There is, as alluded to above, a rich literature associated to Stefan-type problems [8–13]. We will show that arguments similar to those used in the standard setting are also amenable to our problem on a moving hypersurface, thanks in part to the function spaces we decide to use. Let us remark that the techniques and functional analysis we develop here can be directly applied to study many other nonlinear PDE problems posed on moving domains.

Let us work out a possible pointwise formulation of (1.1). Start by supposing Ω(t)=Ω_l(t)∪Ω_s(t)∪Γ(t), where Ω_l(t) and Ω_s(t) divide Ω(t) into a liquid and a solid phase (respectively) with an a priori unknown interface Γ(t). The quantity of interest is the temperature 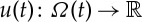, which we suppose satisfies

and thus u=0 is the critical temperature where the change of phase occurs. Define

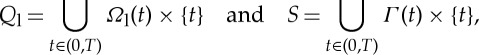and Q_s similarly. Given f and u₀, we formally elucidate in remark 2.12 the relationship between (1.1) and the following model describing the temperature u:

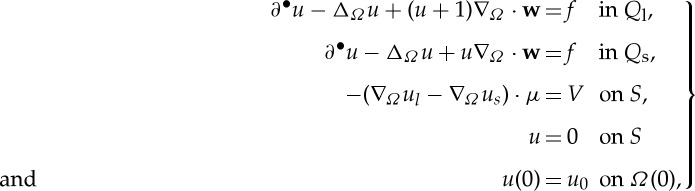1.2

where u_s denotes the trace of the restriction u|_Ωs to the interface Γ (likewise with u_l), V (t) is the conormal velocity of Γ(t) and μ(t) is the unit conormal vector pointing into Ω_l(t) (this vector is tangential to Ω(t) and normal to ∂Ω_l(t)).

We now introduce some notions of a weak solution, similar to [10]. The function spaces 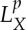below will be made precise in §2 but for now can be thought of as generalizations of Bochner spaces L^p(0,T;X₀), where now 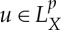implies u(t)∈X(t) for almost all t (for a suitable family {X(t)}_t∈[0,T]).

Definition 1.1 (Weak solution) —

Given and e₀∈L¹(Ω₀), a weak solution of (1.1) is a pair such that and there holds

for all with and η(T)=0.

Definition 1.2 (Bounded weak solution) —

Given and , a bounded weak solution of (1.1) is a pair such that (u,e) is a weak solution of (1.1) satisfying

1.3

for all η∈W(H¹,L²) with η(T)=0.

We prove the following results.

Theorem 1.3 (Existence of bounded weak solutions) —

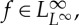
If and then there exists a bounded weak solution to (1.1).

Theorem 1.4 (Uniqueness and continuous dependence of bounded weak solutions) —

If for i=1,2, (uⁱ,eⁱ) are two bounded weak solutions of (1.1) with data then

for almost all t.

Theorem 1.5 (Well posedness of weak solutions) —

If e₀∈L¹(Ω₀) and then there exists a unique weak solution to (1.1). Furthermore, if for i=1,2, are two weak solutions of (1.1) with data then

Below, we shall use the notation ↪ and 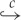to denote (respectively) a continuous embedding and a compact embedding. We will at times refer to the electronic supplementary material where more explanation can be found for the interested reader.

2. Preliminaries

(a). Abstract evolving function spaces

In [6], we generalized some concepts from [14] and defined the Hilbert space 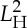given a sufficiently smooth parametrized family of Hilbert spaces {H(t)}_t∈[0,T]. We need a generalization of this theory to Banach spaces.

For each t∈[0,T], let X(t) be a real Banach space with X₀:=X(0). We informally identify the family {X(t)}_t∈[0,T] with the symbol X. Let there be a linear homeomorphism ϕ_t: X₀→X(t) for each t∈[0,T] (with the inverse ϕ_−t: X(t)→X₀) such that ϕ₀ is the identity. We assume that there exists a constant C_X independent of t∈[0,T] such that

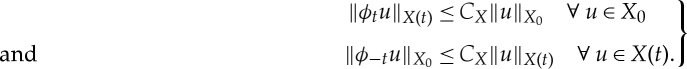2.1

We assume for all u∈X₀ that the map 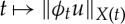is measurable.

Definition 2.1 —

Define the Banach spaces

endowed with the norm

2.2

Note that we made an abuse of notation after the definition of the first space and identified 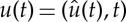with 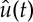. That (2.2) defines a norm is easy to see once one checks that the integrals are well defined (the case 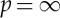is easy), which can be shown by a straightforward adaptation of the proof of theorem 2.8 in [6] for the case when each X(t) is separable (see also electronic supplementary material, S1) and the proof of lemma 3.5 in [14] for the non-separable case. The fact that 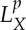is a Banach space follows from lemma 2.3 below.

Important Notation 2.2 —

Given a function , the notation will be used to mean the pullback , and vice versa.

Lemma 2.3 —

The spaces L^p(0,T;X₀) and are isomorphic via ϕ_(⋅) with an equivalence of norms:

Proof. —

We show the case here; an adaptation of the p=2 case done in [6] easily proves the lemma for (see also electronic supplementary material, S2). Let . Measurability of follows as . Now, by definition, we have that for all t∈[0,T]∖N, , where N is a null set and This means that for all t∈[0,T]∖N, by the assumption (2.1), i.e.

so . Similarly, we conclude that if then . ▪

Remark 2.4 —

The dual operator is also a linear homeomorphism with and [15, theorem 4.5-2 and §4.5], and if X₀ is separable, is measurable for ; thus, in the separable setting, the dual operator also satisfies the same boundedness properties as ϕ_t. This means that the spaces are also well-defined Banach spaces given separable {X(t)}_t∈[0,T] (the map plays the same role as ϕ_(⋅) did for the spaces ).

The following subspaces will be of use later:

and

(i). Dual spaces

In this subsection, we assume that {X(t)}_t∈[0,T] is reflexive. In order to retrieve weakly convergent subsequences from sequences that are bounded in 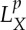, we need 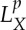to be reflexive. This leads us to consider a characterization of the dual spaces. We let 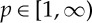and (p,q) be a conjugate pair in this section.

Theorem 2.5 —

The space is isometrically isomorphic to and hence we may identify and the duality pairing of with is given by

To prove this theorem, although we can exploit the fact that the pullback is in a Bochner space, showing that the natural duality map is isometric is not so straightforward because ϕ_(⋅) is not assumed to be an isometry. In fact, we have to go back to the foundations and emulate the proof for the dual space identification for Bochner spaces [16], §IV.

Lemma 2.6 —

For every the expression

2.3

defines a functional such that .

Proof. —

Let and define by (2.3); the integral is well defined by similar reasoning as before (see lemma 2.13 in [6] and the electronic supplementary material, S3). By Hölder’s inequality, we have so and We now show the reverse inequality. First suppose g has the form where the and the E_i are measurable, pairwise disjoint and partition [0,T]. It is clear that Let which satisfies and hence for any ϵ>0 we have

2.4

Now choose x_i,t∈X(t), (see electronic supplementary material, S4) such that

2.5

Define by and note that We obtain using (2.5) and (2.4) that This proves that whenever is of the stated form. Now suppose is arbitrary. Then there exist with such that in and so the sequence satisfies g_n→g in . Because the , we know by our efforts above that defined by has norm . We also have

which implies and also  ▪

We have shown that 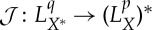defined by 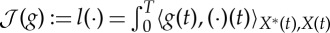is isometric: 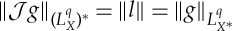. We now show that 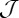is onto. Given 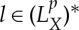, define 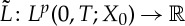by 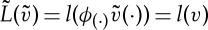for all 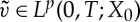. It is obvious that 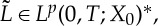and by the dual space identification for Bochner spaces, there exists an 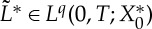such that

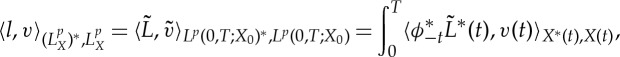so 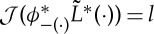, wher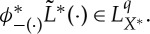e Hence 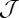is onto, and we have proved theorem 2.5.

(b). Function spaces on evolving surfaces

We now make precise the assumptions on the evolving surface Ω(t) our Stefan problem is posed on and we discuss function spaces in the context of the previous subsections. For each t∈[0,T], let 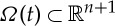be an orientable compact (i.e. no boundary) n-dimensional hypersurface of class C³, and assume the existence of a flow 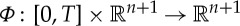such that for all t∈[0,T], with Ω₀:=Ω(0), the map 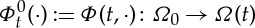is a C³-diffeomorphism that satisfies 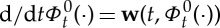and 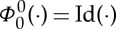for a given C² velocity field 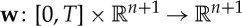, which we assume satisfies the uniform bound |∇_Ω(t)⋅w(t)|≤C for all t∈[0,T]. A C² normal vector field on the hypersurfaces is denoted by 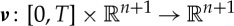. It follows that the Jacobian 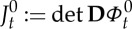is C² and is uniformly bounded away from zero and infinity.

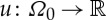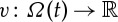For and , define the pushforward 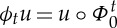and pullback 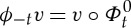, where 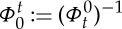. We showed in [7] that ϕ_t: L²(Ω₀)→L²(Ω(t)) and ϕ_t: H¹(Ω₀)→H¹(Ω(t)) are linear homeomorphisms (with uniform bounds) and (thus) with L²≡{L²(Ω(t))}_t∈[0,T], H¹≡{H¹(Ω(t))}_t∈[0,T] and 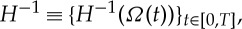the spaces 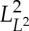, 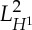and 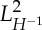are well defined (see [7,17] for an overview of Lebesgue and Sobolev spaces on hypersurfaces) and we let 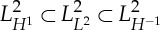be a Gelfand triple.

A function 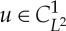has a strong material derivative defined by 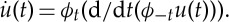Given a function 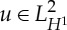, we say that it has a weak material derivative 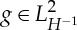if

holds, and we write 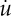or ∂^•u instead of g. Define the Hilbert spaces (see [6,7] for more details)

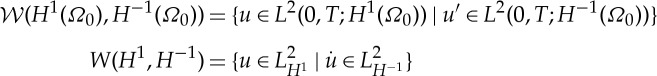endowed with the natural inner products. For subspaces X↪H¹ and Y ↪H⁻¹, we also define the subset W(X,Y)⊂W(H¹,H⁻¹) in the natural manner.

Lemma 2.7 (See [6,7]) —

Let either X=W(H¹,H⁻¹) and or X=W(H¹,L²) and . For such pairs, the space X is isomorphic to X₀ via ϕ_−(⋅) with an equivalence of norms:

We showed in [6,7] that, for u, v∈W(H¹,H⁻¹), the map t↦(u(t),v(t))_L²(Ω(t)) is absolutely continuous, and

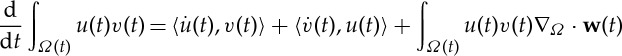holds for almost all t, where the duality pairing is between H⁻¹(Ω(t)) and H¹(Ω(t)).

(i). Some useful results

In this subsection, p and q are not necessarily conjugate. The first part of the following lemma is a particular realization of lemma 2.3. Consult the electronic supplementary material, S5–S7, for more details of the next three results.

Lemma 2.8 —

For p, the spaces and L^p(0,T;L^q(Ω₀)) are isomorphic via the map ϕ_(⋅) with an equivalence of norms. If , the spaces are isometrically isomorphic. The embedding is continuous.

Lemma 2.9 —

The space W(H¹,H⁻¹) is compactly embedded in .

Theorem 2.10 (Dominated convergence theorem for ) —

Let p, . Let {w_n} and w be functions such that and are measurable (e.g. membership of will suffice). If for almost all t∈[0,T],

then w_n→w in .

Lemma 2.11 —

If u∈W(H¹,H⁻¹), then

2.6

Proof. —

By density, we can find {u_n}⊂W(H¹,L²) with u_n→u in W(H¹,H⁻¹). It follows that (this is sensible because w∈H¹(Ω) implies w⁺∈H¹(Ω)) and therefore (2.6) holds for u_n (see electronic supplementary material, S8). As , it follows that in L²(Ω(t)) (for example see [18], lemma 2.88 or [19], lemma 1.22). So we can pass to the limit in the first two terms on the right-hand side.

Now we just need to show that in . It is easy to show the convergence in , so we need only to check the convergence of the gradient. Let g(r)=χ_{r>0}. Then, using g≤1,

For the second term, let us note that as u_n→u in , for almost all t, u_n(t,x)→u(t,x) almost everywhere in Ω(t) for a subsequence (which we have not relabelled). Let us fix t. Then for almost every x∈Ω(t), it follows that g(u_n(t,x))∇_Ωu(t,x)→g(u(t,x))∇_Ωu(t,x) pointwise (see electronic supplementary material, S9). Because g≤1, the dominated convergence theorem gives overall in . ▪

(c). Preliminary results

Remark 2.12 —

It is well known in the standard setting that a mushy region (the interior of the set where the temperature is zero) can arise in the presence of heat sources [1,20]; with no heat sources, the initial data may give rise to mushy regions. We will content ourselves with the following heuristic calculations under the assumption that there is no mushy region.

Let the bounded weak solution of (1.1) (in the sense of definition 1.2) have the additional regularity u∈W(H¹,L²) and and suppose that the sets Ω_l(t)={u>0} and Ω_s(t)={u<0} divide Ω(t) with a common interface Γ(t), which we assume is a sufficiently smooth n-dimensional hypersurface (of measure zero with respect to the surface measure on Ω(t)). Then the bounded weak solution is also a classical solution in the sense of (1.2). To see this, suppose that (u,e) is a weak solution satisfying the equality in (1.3). The integration by parts formula on each subdomain of Ω implies

2.7

With e(t)η(t)∇_Ω⋅w=∇_Ω⋅(e(t)η(t)w)−w⋅∇_Ω(e(t)η(t)) and the divergence theorem [17], §2.2,

We use this result in the formula for integration by parts over time over Ω_s:

A similar expression over Ω_l can also be derived this way, the difference being that the term with μ has the opposite sign. Then, using e_s(t)|_Γ(t)=0, and e_l(t)|_Γ(t)=1, we get

2.8

Since by the partial integration formula , we have (with g=w_ie(t)η(t)) that the fourth term in the right-hand side of (2.8) is

so the calculation (2.8) becomes

2.9

Now, taking the weak formulation (1.3) and substituting (2.9) together with the expression for the spatial term (2.7), we get for η with η(T)=η(0)=0

Taking η to be compactly supported in Q_s, and afterwards taking η compactly supported in Q_l, we recover exactly the first two equations in (1.2). So we may drop the first integral on the left- and the right-hand side. Then with a careful choice of η, we will obtain precisely the interface condition in (1.2).

Lemma 2.13 —

Given ξ∈C¹(Ω₀) and satisfying 0<ϵ≤α≤α₀ a.e., there exists a unique solution φ∈W(H¹,L²) with to

2.10

satisfying and (cf. [21, ch. V, §9])

2.11

Proof. —

Define the bilinear form which is clearly bounded and coercive on H¹(Ω(t)). Split a(t;⋅,⋅) into the forms and One sees that a_s(t;η,η)≥0 and that both and are bounded. Also, letting , where are the normalized eigenfunctions of −Δ_Ω0, we have for , , α_j∈AC([0,T]) and α_j′∈L²(0,T)}

where r is such that (see [17], lemma 2.1; note that and thus ). Hence by [6, theorem 3.13], we have the unique existence of φ∈W(H¹,L²). Rearranging equation (2.10) shows that . As α is uniformly bounded by positive constants, it follows that .

The bound. Let . Test the equation with (φ−K)⁺:

which becomes, through the use of Young’s inequality with δ,

An application of Gronwall’s inequality and noticing yields . Repeating this process with (−φ(t)−K)⁺ allows us to conclude.

The inequality (2.11). Multiply equation (2.10) by Δ_Ωφ and integrate: formally,

2.12

See [17], lemma 2.1 or [7] for the definition of the matrix D(w). This calculation is merely formal because we have not shown that ; however, the end result of the calculation is still valid by lemma 2.14. We also have by squaring (2.10), integrating and using (2.12):

Adding the last two inequalities then we obtain

Gronwall’s inequality can be used to deal with the last term on the right-hand side. ▪

Lemma 2.14 —

With φ∈W(H¹,L²) from the previous lemma, the following inequality holds:

2.13

Proof. —

Let . We start with a few preliminary results. Let us show Take so that . By smoothness of , it follows that , and because . So η∈W(H²,H¹).

Let us also prove that is dense. Let w∈W(H²,L²); then since by smoothness of and since (because ). By [22], lemma II.5.10, there exists with in . Then, (by definition) and

where we used the smoothness of and the reasoning behind assumption 2.37 of [6] (see also [6, theorem 2.33]).

Given φ∈W(H²,L²), by the density result, there exists such that φ_n→φ in W(H²,L²) with φ_n satisfying (2.13):

2.14

We know that in (this is just how we construct the sequence φ_n; see above), and [22], lemma II.5.14 implies φ_n(t)→φ(t) in H¹(Ω(t)). Now we can pass to the limit in every term in (2.14). ▪

3. Well posedness

We can approximate 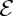by 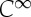bi-Lipschitz functions 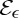such that (e.g. [12,13])

(where 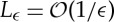is the Lipschitz constant of the approximation to the Heaviside function). We write 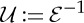and 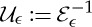. In order to prove theorem 1.3, that of the well posedness of 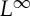weak solutions given bounded data, we consider the following approximation of (1.1).

Definition 3.1 —

Find for each ϵ>0 a function e_ϵ∈W(H¹,H⁻¹) such that

Theorem 3.2 —

Given and e₀∈L²(Ω₀), the problem (P_ϵ) has a weak solution e_ϵ∈W(H¹,H⁻¹).

Proof. —

Using the chain rule on the nonlinear term leads us to consider for fixed w∈W(H¹,H⁻¹)

If S denotes the solution map of (P(w)) that takes w↦Sw, then we seek a fixed point of S. First, note that, since the bilinear form involving the surface gradients is bounded and coercive, the solution Sw∈W(H¹,H⁻¹) of (P(w)) does indeed exist by [6, theorem 3.6], and, moreover, it satisfies the estimate

3.1

where the constant C does not depend on w because is uniformly bounded from below (in w). Then the set which is a closed, convex and bounded subset of X:=W(H¹,H⁻¹), is such that S(E)⊂E by (3.3). We now show that S is weakly continuous. Let in W(H¹,H⁻¹) with w_n∈E. From the estimate (3.3), we know that Sw_n is bounded in W(H¹,H⁻¹), so for a subsequence

and

by the compact embedding of lemma 2.9. Now we show that χ=Sw. Due to , in . This implies in L²(Ω₀) (to see this consider for arbitrary f∈L²(Ω₀) the functional defined by ). As Sw_nj(0)=e₀, it follows that

3.2

On the other hand, as w_n are weakly convergent in W¹(H¹,H⁻¹), they are bounded in the same space. Now, , hence w_n→w in . It follows that the subsequence w_nj→w in too, and so there is a subsequence such that, for almost every t∈[0,T], w_njk(t)→w(t) a.e. in Ω(t). By continuity, for a.a. t, a.e., and also we have with the right-hand side in . Thus, we can use the dominated convergence theorem (theorem 2.10), which tells us that in . Now we pass to the limit in the equation (P(w)) with w replaced by w_njk to get

which, along with (3.4), shows that χ=S(w), so . However, we have to show that the whole sequence converges, not just a subsequence. Let x_n=S(w_n) and equip the space X=W(H¹,H⁻¹) with the weak topology. Let x_nm=S(w_nm) be a subsequence. By the bound of S, it follows that x_nm is bounded, hence it has a subsequence such that

By similar reasoning as before, we identify x*=S(w), and theorem 3.3 tells us that indeed . Then by the Schauder–Tikhonov fixed point theorem [23, theorem 1.4, p. 118], S has a fixed point. ▪

Theorem 3.3 —

Let x_n be a sequence in a topological space X such that every subsequence x_nj has a subsequence x_njk converging to x∈X. Then the full sequence x_n converges to x.

(a). Uniform estimates

We set . Below we denote by M a constant such that .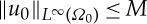

Lemma 3.4 —

The following bound holds independent of ϵ:

Proof. —

We substitute w(t)=e^−λte_ϵ(t) in (P_ϵ) and use to get

Let and and define v(t)=αt+β. Note that and v(0)=β. Subtracting from the above and testing with (w(t)−v(t))⁺, we get

3.3

Note that because ∇_Ωv(t)=0. Set , then the last term on the left-hand side of (3.5) is non-negative because, if w>v, w>0 since v≥0. So we can throw away that and the gradient term to find

Integrating this and using lemma 2.11, we find

as and . The use of Gronwall’s inequality gives almost everywhere on Ω(t). So we have shown that for all t∈[0,T]∖N₁, w(t,x)≤C for all , where A similar argument yields for all t∈[0,T]∖N₂, w(t,x)≥−C for all , where Taking these statements together tells us that for all t∈[0,T]∖N, |w(t,x)|≤C on Ω(t)∖M^t, where N=N₁∪N₂ and have measure zero. This gives . From this and , we obtain the bound on u_ϵ. The bound on follows from . ▪

Lemma 3.5 —

The following bound holds independent of ϵ:

3.4

Proof. —

Testing with in (P_ϵ), using , integrating over time and using the previous estimate, we find

The bound on the time derivative follows by taking supremums. See the electronic supplementary material, S10, for more details. ▪

Lemma 3.6 —

Define . The following limit holds uniformly in ϵ:

Proof. —

We follow the proof of theorem A.1 in [8] here. Fix h∈(0,T) and consider

3.5

with the last inequality by (3.6). Now, as the are uniformly bounded above, they are uniformly equicontinuous. Therefore, for fixed δ, there is a σ_δ (depending solely on δ) such that

3.6

So in the set we must have (this is the contrapositive of (3.8)). This implies from (3.7) that

Writing , note that

Taking the limit as h→0, using the arbitrariness of δ>0 and the fact that the right-hand side of the above does not depend on ϵ gives us the result. ▪

(b). Existence of bounded weak solutions

With all the uniform estimates acquired, we can extract (weakly) convergent subsequences. In fact, we find (we have not relabelled subsequences)

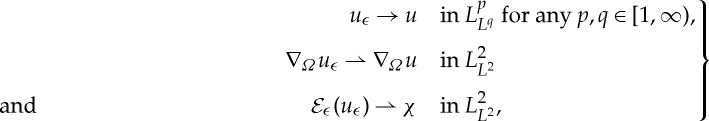3.7

where only the first strong convergence listed requires an explanation. Indeed, the point is to apply [24, theorem 5] with H¹(Ω₀) c ’−→L¹(Ω₀)⊂L¹(Ω₀), which gives us a subsequence 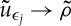strongly in L¹(0,T;L¹(Ω₀)). It follows that u_ϵj→ρ in 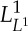, whence, for a.a. t, u_ϵjk(t)→ρ(t) a.e. in Ω(t). We also know that, for a.a. t, |u_ϵjk(t)|≤C a.e. in Ω(t) by lemma 3.4, and so, for a.a. t, the limit satisfies |ρ(t)|≤C a.e. in Ω(t) too. By theorem 2.10, u_ϵjk→ρ in 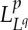for all p, 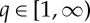. As 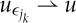(subsequences have the same weak limit), it must be the case that ρ=u.

Proof of theorem 1.3 —

In (P_ϵ), we can test with a function η∈W(H¹,L²) with η(T)=0, integrate by parts and then pass to the limit to obtain

and it remains to be seen that or equivalently By monotonicity of , we have for any

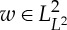
Because uniformly, for a.a. t, a.e. in Ω(t), and , and the dominated convergence theorem shows that in . Using this and (3.9), we can easily pass to the limit in this inequality and obtain

By Minty’s trick we find ; see the electronic supplementary material, S11, for more details. To see why , we have from the estimate in lemma 3.4 that, for a.a. t∈[0,T], giving in and (by weak-* lower semi-continuity) for a.a. t, and we just need to identify . It follows from (3.9) that in by Lions–Aubin, and so, for a.e. t and for a subsequence (not relabelled), in H⁻¹(Ω(t)). This allows us to conclude that χ=ζ (the weak-* convergence of to also gives weak convergence in any L^p(Ω(t)) to the same limit). ▪

(c). Continuous dependence and uniqueness of bounded weak solutions

The next lemma, which has an extended proof in the electronic supplementary material, S12, allows us to drop the requirement for our test functions to vanish at time T.

Lemma 3.7 —

If (u,e) is a bounded weak solution (satisfying (1.3)), then (u,e) also satisfies

for all η∈W(H¹,L²).

Proof. —

To see this, for s∈(0,T], consider the function which has a weak derivative χ_ϵ,s′(t)=−ϵ⁻¹χ_(s−ϵ,s)(t). Take the test function in (1.3) to be χ_ϵ,Tη, where η∈W(H¹,L²), send ϵ→0 and use the Lebesgue differentiation theorem. ▪

We can finally prove theorem 1.4. See the electronic supplementary material, S13–S16, for additional comments on the proof.

Proof of theorem 1.4 —

We can prove the continuous dependence as in [21], ch. V, §9. As explained in lemma 3.7, we drop the requirement η(T)=0 in our test functions and we now suppose that . Suppose for i=1,2 that (u_i,e_i) is the solution to the Stefan problem with data , so

3.8

Define a=(u₁−u₂)/(e₁−e₂) when e₁≠e₂ and a=0 otherwise, and note that 0≤a(x,t)≤1. Let η_ϵ solve in the equation

3.9

with ξ∈C¹(Ω₀) and where a_ϵ satisfies ϕ_−(⋅)a_ϵ∈C²([0,T]×Ω₀) and 0≤a_ϵ≤1 a.e. and . This is well posed by lemma 2.13. Equation (3.10) can be written in terms of a_ϵ, and if we choose η=η_ϵ and use (3.11), we find

3.10

using the bound from lemma 2.13. We can estimate the first integral on the right-hand side:

and

by the results in lemma 2.13. Sending ϵ→0 in (3.12) gives us (recalling ξ≤1)

Now pick ξ=ξ_n, where ξ_n(x)→sign(e₁(t,x)−e₂(t,x))∈L²(Ω(t)) a.e. in Ω(t). ▪

(d). Well posedness of weak solutions

Proof of theorem 1.5 —

Suppose are data and consider functions and satisfying

The existence of f_n holds because, by density, there exist such that in L¹((0,T)×Ω₀)≡L¹(0,T;L¹(Ω₀)). Denote by (u_n,e_n) the respective (bounded weak) solutions to the Stefan problem with the data (e_0n,f_n). By virtue of these solutions satisfying the continuous dependence result, it follows that {e_n}_n is a Cauchy sequence in and thus e_n→χ in for some χ. Recall that , so, by consideration of an appropriate Nemytskii map, we find . Now we can pass to the limit in

and doing so gives

overall this shows that there exists a pair which is a weak solution of the Stefan problem. For these integrals to make sense, we need with .

Now suppose that (u¹,e¹) and (u²,e²) are two weak solutions of class L¹ to the Stefan problem with data and in respectively. We know that there exist approximations , of the data satisfying

These approximate data give rise to the approximate solutions and , both of which are elements of . It follows from above that and in . Now consider the continuous dependence result that and satisfy:

3.11

Regarding the right-hand side, by writing (and similarly for the ) and using triangle inequality, along with the fact that in , we can take the limit in (3.13) as and we are left with what we desired. ▪

Funding

A.A. was supported by the Engineering and Physical Sciences Research Council (EPSRC) grant no. EP/H023364/1 within the MASDOC Centre for Doctoral Training.