Abstract
Many drug candidates fail in clinical trials due to a lack of efficacy from limited target engagement or an insufficient therapeutic index. Minimizing off-target effects while retaining the desired pharmacodynamic (PD) response can be achieved by reduced exposure for drugs that display kinetic selectivity in which the drug:target complex has a longer half-life than off-target:drug complexes. However, while slow-binding inhibition kinetics are a key feature of many marketed drugs1,2, prospective tools that integrate drug-target residence time into predictions of drug efficacy are lacking, hindering the integration of drug-target kinetics into the drug discovery cascade. Here we describe a mechanistic PD model that includes drug-target kinetic parameters including the on- and off-rates for the formation and breakdown of the drug-target complex. We demonstrate the utility of this model by using it to predict dose response curves for inhibitors of the LpxC enzyme from Pseudomonas aeruginosa in an animal model of infection.
Introduction
The majority of drug candidates fail in human clinical trials due to lack of efficacy or insufficient therapeutic index, often as a result of limited target engagement or concomitant drug binding to off-target receptors3,4. Currently, these critical drug parameters are not routinely fully evaluated until late stages of drug discovery. Developing a fundamental understanding of the pharmacokinetic (PK) and pharmacodynamic (PD) principles that govern drug action throughout the drug discovery process has been proposed as a mechanism for improving the success rate of new drug approvals4,5. Recently, approaches that utilize prolonged occupancy of the drug on the designated target, while minimizing binding to off-target proteins (kinetic selectivity), have been identified as particularly promising strategies for improving a drug candidate therapeutic index. Indeed, many marketed drugs dissociate slowly from their targets, emphasizing the potential importance of drug-target complex life-time (residence time, tR) for in vivo drug activity1,2,6–8. The therapeutic index will be maximized in these circumstances if the long on-target residence time leads to kinetic selectivity, with the drug having a short lifetime on off-target proteins (and no or minimal on-target toxicity). As a result, there is a growing interest in assessing kinetic selectivity and developing structure-kinetic relationships to drive compound optimization.
While compelling arguments can be made for the tuning of drug-target kinetics in a drug discovery campaign, major barriers still exist for the implementation of this approach including the lack of prospective tools that integrate drug-target residence time parameters with PK models to yield predictions of drug efficacy. Current PD models typically assume “rapid equilibrium” between the bacterial target and the fraction of drug in human plasma that is not protein bound (serum free fraction)9,10. Moreover, during drug discovery and optimization, it is common to characterize compound activity with steady-state in vitro measurements that disregard effects that may be time-dependent, such as IC50 values for inhibition of a purified target or the minimum inhibitory concentration (MIC) required to prevent cell growth. Although this “thermodynamic approach” is fully appropriate for predictions of efficacy when drug concentrations at the target site change slowly relative to target engagement, there are many examples of drugs that dissociate slowly from their targets on the time scale of in vivo PK1. In such situations free drug and drug-engaged target will not be in rapid equilibrium and hence predictions of drug efficacy cannot be accounted for accurately based exclusively on thermodynamic measurements. Early insight into such an outcome could be highly valuable, particularly for agents which require high exposures for efficacy leading to narrow therapeutic margins11.
To address this, we have developed a PK/PD model that incorporates drug-target kinetic parameters including the on- and off-rates for the formation and breakdown of the drug-target complex. We demonstrate the utility of this model by using it to predict dose response curves for inhibitors of the LpxC enzyme from Pseudomonas aeruginosa (paLpxC) in an animal model of infection. The enzyme LpxC, UDP-3-O-acyl-N-acetylglucosamine deacetylase (EC 3.5.1.108), is a zinc metalloenzyme involved in the biosynthesis of cell wall lipopolysaccharide (Supplementary Results, Supplementary Fig. 1) and is a promising target for the development of antibacterial agents against problematic Gram-negative pathogens12. We first demonstrated that the model could predict time dependent antibacterial activity at the whole cell level by measuring the postantibiotic effect (PAE)13 for the compound series. We found that the PAE correlated with the off-rate for dissociation of inhibitors from paLpxC but, importantly, not with the thermodynamic affinity of the compounds for the target. We then extended the model to include time-dependent antibacterial activity in a mouse thigh model of Pseudomonas infection and were able to accurately predict efficacy at three drug doses. Given the strong predictive power of pre-clinical infection models to clinical outcomes, and the fact that doses of novel antibiotics tend to be high resulting in narrow therapeutic margins, the argument for including drug-target kinetics in the discovery of new antibiotics is compelling. Further, the approach used to develop this model is generally applicable across all therapeutic areas where drug-target binding kinetics impact drug activity. The generation of time-dependent PD models, tailored to the specific drug physiological effects, can be used to improve both drug candidate selection and development.
Results
Profiling Slow-binding of LpxC Inhibitors
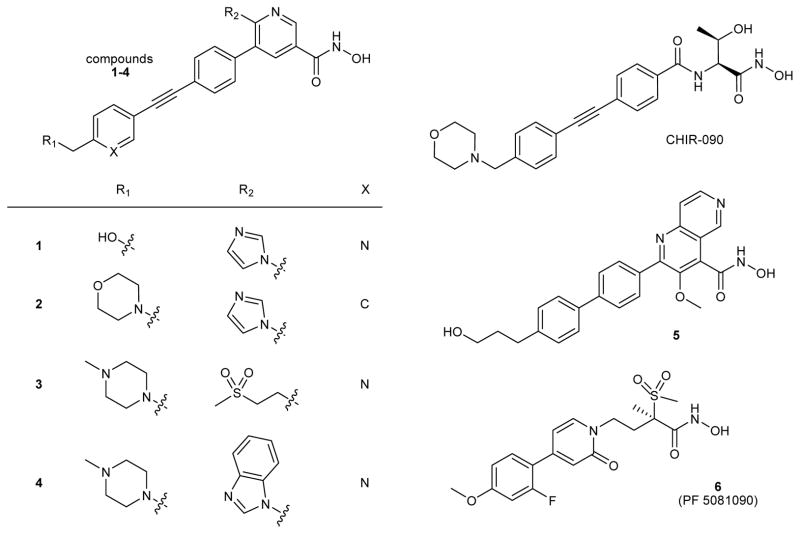
Compounds 1–6 used in this study (Fig. 1) represent a series of chemical tools for interrogating the relationship between in vitro parameters, such as equilibrium binding and residence time profiles, and cellular and in vivo pharmacological effects. These closely related structural analogs are competitive inhibitors of LpxC and contain a hydroxamic acid group that binds the catalytic zinc ion in the active site, as well as a lipophilic group that binds within an occluded hydrophobic passage that is normally occupied by the hydroxyl-alkyl substituent of the native substrate14,15. The well-known LpxC inhibitor CHIR-09012 (Fig. 1), inhibits LpxC through a 2-step binding mechanism (Supplementary Note)16, in which formation of an initial EI encounter complex, defined by Ki, is followed by a slow step (conformational change) resulting in a more stable non-covalent complex (EI*, defined by Ki*). Compounds 1–6 exhibit a similar mechanism of inhibition as exemplified by Compound 2 in which forward progress curves in the presence of inhibitor values are indicative of time-dependent slow-onset inhibition (Supplementary Fig. 2)16. A global analysis approach was used to interpret these data17, and a good fit was obtained for the two-step inhibition model for competitive inhibition. This yielded a value for Ki* of 11 ± 4 pM, which compares favorably to the same constant determined from extended preincubation time IC50 measurements (Ki* = 10 ± 7 pM). Good fits were also obtained for a one-step kinetic binding mechanism; however, this mechanism was discounted due to the fact that the encounter complex (Ki) is substantially larger than the highest compound concentration tested and the precedent of a two-step binding mechanism with CHIR-090.
Figure 1.
Structures of P. aeruginosa LpxC Inhibitors (CHIR-090, compounds 1–6)
The dissociation rates of respective inhibitors bound to LpxC were determined using a rapid dilution assay at 37 °C (Fig. 2) and 23°C (Supplementary Fig. 3)18, in which LpxC was incubated with a stoichiometric equivalent of inhibitor at concentrations above Ki* for 3 hours to allow formation of EI*, followed by rapid 1000-fold dilution into buffer containing excess LpxC substrate (present at 5x Km), to minimize the effects of rebinding on the off-rate determinations19. Accumulation of the deacylated LpxC reaction product yielded the recovery rate constant, kobs, which was used to estimate the target:inhibitor residence time (tR, Table 1) and assumed to be the off-rate constant k6. Note that the values of k6 are lower limit approximations since the kinetics of initial binding are assumed to be in rapid equilibrium. However these processes may contribute to the slow-binding kinetic profile and therefore require inclusion of the rate constants for these steps in the overall dissociation rate equation20. At 37°C, full activity was restored under the experimental assay timeframe (<3 h, Fig. 2) except for Compound 4, which has the lowest Ki* in the series, suggesting that rebinding effects were contributing to prolonged enzyme inhibition19. In this case, the dissociation rate was obtained by fitting the data to the expected fractional final velocity calculated from the amount of free enzyme expected under the final experimental conditions21.
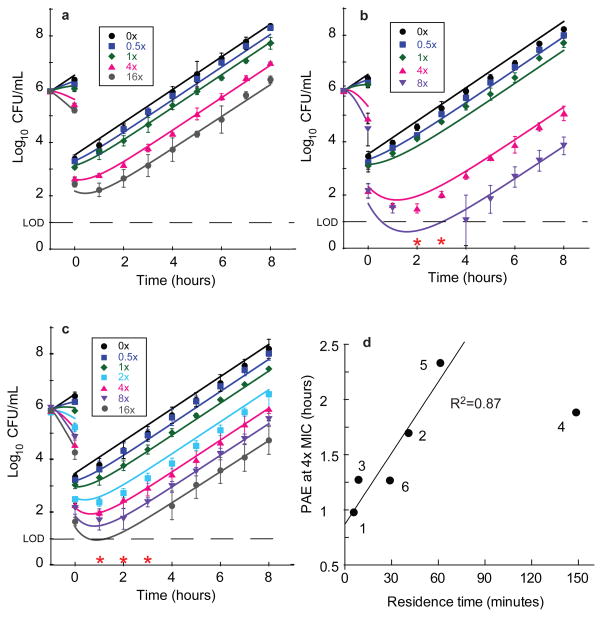
Figure 2. Rapid-dilution progress curves for P. aeruginosa LpxC inhibitors establish residence time.
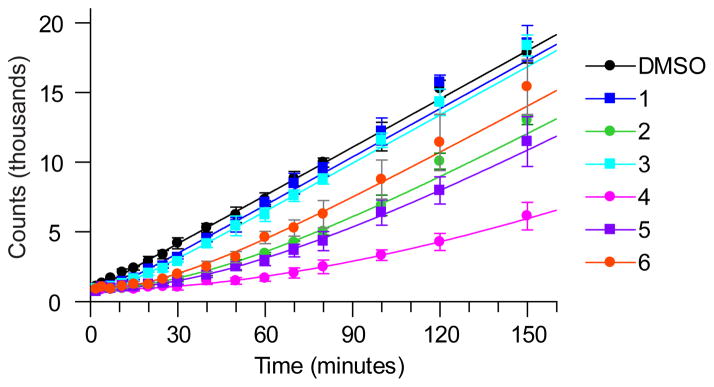
Progress curve data for P. aeruginosa LpxC inhibitors at 37 °C. Legend indicates compound 1–6. Reactions were conducted under conditions where compound rebinding after disassociation is minimized and the observed time constant for reactivation is indicative of the residence time.
Table 1.
Biochemical and microbiological measurements for inhibitors of P. aeruginosa LpxC at 37°Ca
| Compound | Ki, (nM)b | Ki*, (nM)c | k6 (min−1) d | k5 (min−1) e | residence time, tR (min)f | P.ae MIC PAO1 MexABCDXY− (μg/ml; μM) | P.ae MIC PAO1 (μg/ml; μM) | maximum killing rate (log10 CFU/hr) | PAE at 16x MIC (hr)g | PAE at 8x MIC (hr)g | PAE at 4x MIC, (hr)g |
|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 0.80 ± 0.60 | 0.51 ± 0.03 | 0.16 ± 0.08 | 0.09 ± 0.09 | 6.1 ± 3.2 | 0.016; 0.039 | 1.75; 4.3 | 2.4 | 1.68 | ND | 0.97 |
| B | 0.83 ± 0.48 | 0.020 ± 0.003 | 0.024 ± 0.012 | 1.0 ± 0.8 | 41 ± 21 | 0.04; 0.083 | 1; 2.1 | 1.8 | 3.90 | 2.6 | 1.69 |
| C | 1.9 ± 0.45 | 0.50 ± 0.15 | 0.11 ± 0.06 | 0.3 ± 0.2 | 9.1 ± 4.6 | 0.13; 0.24 | 12.5; 23 | 1.9 | 1.84 | ND | 1.27 |
| D | 1.3 ± 0.8 | 0.003 ± 0.001 | 0.007 ± 0.001 | 2.7 ± 1.9 | 150 ± 13 | 0.06; 0.11 | 4; 7.4 | 2.5 | NDh | 3.22 | 1.88 |
| E | 0.57 ± 0.14 | 0.014 ± 0.005 | 0.016 ± 0.008 | 0.63 ± 0.42 | 62 ± 31 | 0.016; 0.037 | 0.5; 1.2 | 4.4 | 3.90 | 2.07 | 2.33 |
| F | 0.48 ± 0.61 | 0.020 ± 0.010 | 0.034 ± 0.018 | 0.8 ± 1.2 | 29 ± 16 | 0.0075; 0.018 | 0.25; 0.61 | 2.8 | 1.93 | 1.67 | 1.26 |
|
| |||||||||||
| Correlation coefficients to PAE values | |||||||||||
|
| |||||||||||
| 4x MIC | −0.19 | −0.70 | −0.78 | 0.45 | 0.63 | −0.14 | 0.27 | 0.75 | |||
| 16x MIC | −0.35 | −0.66 | −0.76 | 0.66 | 0.89 | −0.24 | −0.42 | 0.66 | |||
Listed errors represent 1 standard deviation,
measured in triplicate with no EI preincubation and the Ki calculated as Ki = IC50(1+S/Km),
measured in a minimum of triplicate using 16 hour preincubation of EI,
k6 is assumed to be equal to the activity recovery rate constant (kobs) from jump-dilution assays measured in triplicate with propagated error; these values represent lower limit estimates since the actual values may be larger if the kinetics of formation and depletion of the initial encounter complex, governed by Ki, do not operate under rapid equilibrium20,
calculated as k6 × (Ki/Ki* - 1); error is propagated from the contributing parameters,
calculated as the reciprocal of the rate constant (kobs) in activity recovery assays measured in triplicate with propagated error;
measured in three independent experiments vs. P. aeruginosa PAO1,
not determined, insoluble at 16× MIC.
Values for Ki and Ki* were obtained at 37°C. For Ki* determinations, compound was preincubated with enzyme overnight (16–18 hours) prior to reaction initiation with substrate. Alternately, Ki determinations avoided preincubation, and reaction time was minimized (2.5 min). Despite the high sensitivity of the LS/MS/MS detection system, assay conditions for Compounds 4–6 were within the range of tight-binding behavior (5 pM LpxC), and thus estimates of Ki* values were determined using the Morrison equation22,23 followed by application of the Cheng-Prusoff correction24 for substrate-competitive inhibitors (Supplementary Table 1).
In sum, the kinetic profiling confirmed that all of the compounds studied exhibit slow-binding kinetics similar to CHIR-090. Additionally, whereas small variations were observed among the Ki values, a correlation was observed between Ki* and the measured residence times, indicating that the slow off-rates are governed by ground-state stabilization of EI*8,25. This range of kinetic and thermodynamic properties across the compound set provided an excellent foundation for evaluating the physiological effects of both residence time and rebinding on cellular activity and regrowth.
Microbiological Activity and Post-Antibiotic Effects
Antimicrobial activities were determined as minimum inhibitory concentrations (MICs) against a reference P.aeruginosa strain, PAO1, and an isogenic derivative lacking the major efflux-pumps MexABCDXY, N15026. MIC values against P. aeruginosa PAO1 ranged from 0.2 to 12.5 μg/mL (Table 1) whereas those against the efflux-deficient strain were 1–2 orders of magnitude lower, suggesting that in wild-type P. aeruginosa the intracellular compound concentrations are significantly lowered due to bacterial efflux pump action. A clear correlation was noted between the MIC values for both strains and the Ki values determined for each compound (Supplementary Fig. 4), which strongly suggests that the cellular mode of action of these compounds is driven through the inhibition of LpxC. This correlation is not maintained with Ki* values (Supplementary Fig. 4) suggesting that formation of the initial LpxC:inhibitor encounter complex (described by Ki) is sufficient for inhibition of bacterial growth as reported by the endpoint MIC determinations, and that the formation of a time-dependent complex of enhanced potency, driven by Ki*, does not influence the MIC determination. Finally, all of the compounds exhibited rapid bactericidal activity, with ≥3 log10 decrease in CFU/mL within 3 hours and maximal killing rates >1.8 log CFU/hr (Table 1, Supplementary Fig. 5). Although there was some variation of maximum kill rate within this compound set (Table 1), these differences were considered minor as this range of variation has been observed in other antibiotic compound sets27.
Target overexpression studies were conducted to further demonstrate that these compounds maintained a mechanism of action consistent with LpxC inhibition over the concentrations required to complete kinetic evaluations on cellular activity. In all cases, elevated MIC values were observed with lpxC overexpression28 and the fold shifts were similar across the compound set (Supplementary Table 2). These results indicate that the effects on growth are driven by LpxC inhibition, even at elevated compound concentrations.
The determination of the PAEs for LpxC inhibitors in the wild-type PAO1 strain followed a dilution-based protocol13,29. Cells were first incubated for one hour with varied concentrations of inhibitor normalized to the MIC followed by a 1000-fold dilution. Subsequently, the PAE value was calculated as the time required for compound-treated cells to successfully grow ten-fold (1 log10CFU) compared to untreated cells13. All of the calculated PAEs demonstrated a concentration-dependent growth delay (Fig. 3, Supplementary Fig. 6), that varied across the compound set from ~1 to ~4 h (Table 1). A statistical analysis was performed to better understand the linkage of the measured biochemical and microbiological data with the observed PAEs at 4× and 16×MIC (Table 1), and the strongest correlations were observed between tR, Ki* and the maximum killing rate for both PAE datasets, with the relative strengths of the correlations for these parameters being concentration-dependent. A clear dependence of PAE on residence time was observed (Fig. 3). The effect of Ki* and residence time on PAE results from sustained target engagement following compound washout. In contrast, linkage of maximum killing rate to PAE reflects the sensitivity of the PAE experiment to scalar effects on growth inhibition. In other words, high kill rates increase the dynamic range of effect and therefore enable clearly observable effects (the PAE) after compound washout.
Figure 3. P. aeruginosa PAO1 post antibiotic effect data for representative LpxC inhibitors.
Legends on plots indicate the fold-excess of compound above MIC for the first hour of incubation. Post antibiotic effect data and mechanistic pharmacodynamic model fit for a, Compound 1, b, Compound 4 and c, Compound 6. Data points (symbols) represent mean values from triplicate, independent test occasions. Error bars represent 1 standard deviation of the log10CFU mean. Lines represent model fits to the data using parameters as described in Supplemental Tables 3, 6 and 8. Red asterisks indicate data that were below the limit of detection and omitted from fits (2 and 3 hours 8× MIC panel b and 1–3 hours 16× MIC panel c). d, Correlation of calculated PAE determined at 4×MIC with measured residence time (Table 1). Fitting these data to a linear regression model resulted in a correlation coefficient of 0.87; Compound 4 was excluded from this analysis since the residence time measurements may have been confounded by target rebinding and/or additional slow-binding kinetic effects for this analog (Table 1).
Developing a Mechanistic Time-dependent PD Model
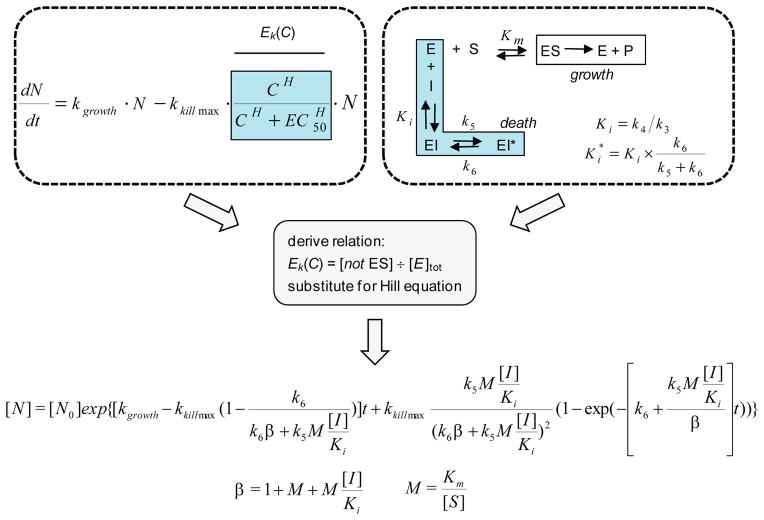
To further study the correlations observed between the biochemical parameters and pharmacological outcomes such as the PAE, a mechanistic PD model was derived. As shown in Figure 4, general PD models typically invoke a concentration-dependent bacterial “enhancement of kill” function, Ek(C), implementing the Hill equation logistic30,31 which assumes a rapid equilibrium mass-action binding manifold. In order to incorporate the impacts of time-dependent inhibitor:target binding, it was assumed that the bacterial growth was dependent on the metabolic flux of substrate through the target enzyme, and that depletion of the enzyme:substrate species through the distribution to target:inhibitor complexes results in growth inhibition. This assertion is supported by the observation that growth inhibition (MIC) is most closely correlated with Ki and not Ki* (Supplementary Fig. 4). Applying this reasoning, the replacement of the Hill equation logistic with the mathematical solution representing the collection of inactive enzyme species led to a fully integrated, closed solution model that links the effects of target inhibition and bacterial cell count (Supplementary Note). The resulting equation includes a total of six mathematically-independent parameters (k5, k6, Ki, Km/[S], kgrowth and kkill), four of which (k5, k6, Ki, Km/[S]) describe the typical two-step binding and kinetic profile of competitive slow-binding enzyme inhibitors. Inspection of the model indicates that the encounter complex dissociation constant (Ki) and the free, intracellular inhibitor concentration ([I]) are always present in the model as a ratio and therefore these variables are treated as a single composite parameter in all modeling exercises. The parameter term M, which is equivalent to Km/[S], accounts for the impact of enzyme substrate concentration changes on competitive inhibitor binding efficiency. This mechanistic model was derived assuming competitive inhibition, but recent assessments of time dependent behavior for non-competitive inhibitors in cellular systems suggest that these effects may not be sensitive to specific inhibition modalities25.
Figure 4. Derivation of a pharmacodynamic model incorporating time-dependent target inhibition parameters.
A two-step, competitive binding kinetic mechanism was used to describe the time-dependent inhibition parameters, where the enzyme states E, ES and EI are in rapid equilibrium governed by the catalytic and dissociation constants Km and Ki with substrate (S) and free inhibitor (I) respectively. The time-dependent conversion of EI to EI* is described by the (on) rate constant k5, and the slower (off)-rate constant, k6. The general antibacterial PD model for drug effects on logarithmically growing cells (N), is a mass balance relationship of the intrinsic growth rate, kgrowth, and intrinsic maximal drug-induced kill rate (kkill_max) as function of the drug concentration (C) governed by the Hill equation logistic. To link these two models, growth was modeled as being dependent on the amount of ES, and that all other enzyme species contribute to cellular growth inhibition. Solving for the mathematical relationship corresponding to all enzyme states except ES, substitution of this manifold for the Hill logistic, and integration led to a closed, analytical solution. For this new PD model, definitions of the terms M and β are also shown. We added an additional parameter, pm, to all instances of the ratio [I]/Ki to account for permeation effects that reduce the level of free I at the target site from that in bulk media.
Validation of the PD Model with in vitro PAE data
With this model in hand, simulation and fitting tools were developed to enable the analysis of complex datasets with dynamic concentration functions that include both step-function changes as seen in PAE studies and as well as different in vivo dosing administration options (IV and PO). Specifically, a data-fitting tool was developed that utilizes non-linear regressions to perform global fits to the physiological response data. The first application was to test the performance of this tool and the mechanistic PD model to the set of concentration response data collected for each compound in the PAE studies. To initiate the fitting process, the experimentally determined values for Ki, k6, k5, and kkill_max were used as seed values for the model parameters (Table 1), and estimates of kgrowth were obtained from control cultures grown without LpxC inhibitors. Since the LpxC substrate concentration has not been determined, parameter M was seeded as 0.15 based on the ranges of this parameter reported for metabolic enzymes in cellular systems32. This parameter was allowed to vary by 3-fold, but was assumed to be time-invariant, since it was assumed that substrate accumulation would not occur in this case due to the high maximum killing rates observed for the LpxC inhibitors. The [I]/Ki term presented the greatest challenge for initial seed value estimation. Since the model was derived in terms of drug concentration at the target site and LpxC is a cytoplasmic target, estimates of the intracellular concentration were needed for simulations and data analysis. Obtaining accurate measurements of intracellular drug concentrations are challenging, particularly for Gram-negative bacteria, due to complications attributed in part to non-specific binding to the outer and inner membrane fractions33. As a result, an empirical approach was taken to estimate the intracellular concentration using a correction factor based on the bulk media concentration. It was assumed that the cellular penetration mechanism of these inhibitors is similar to the majority of antibacterial agents and governed by mass action, rather than through an active transport and subsequent accumulation against a concentration gradient34. Further, based on the observation that isogenic efflux-deficient strains exhibit significant improvements in MIC potency relative to wild-type cells, it was therefore reasoned that the upper limit for intracellular concentration could be estimated from the ratios of the MIC values for the efflux-deficient and wild-type strains (pm) and the bulk media concentration. The pm factor was used during the fitting process to scale the [I]/Ki parameter in all cases. With these seed input values in hand, data fitting was performed using non-linear regressions where the parameters were allowed to float within pre-defined constraints to identify an optimal global fit solution for the full concentration range of PAE data for each compound. Narrow constraint windows were employed for the cellular parameters of kgrowth and kkill_max (4-fold), due to the high confidence that these parameters reflected the cellular growth conditions. In contrast, the biochemical parameters (Ki, k5, k6) were effectively free-floating since large windows were employed for these variables (100-fold deviation tolerated).
The model produced good fits to the PAE data for each compound using these conditions. In all cases, high correlation coefficients were observed (R2 > 0.98) and the performance was high across the full spectrum of cellular response, including for datasets where the experimental CFU counts were near or below the limit of quantitation for early post-dilution time points (Fig. 3, Supplementary Fig. 6). As a further assessment of the model performance, the deviations of the final output parameters from the initial seed values were analyzed (Supplementary Tables 3–8). For each dataset the model fits converged with parameters that were very close to the initial seed values. In particular, there was very little deviation for the microbiological parameters kgrowth and kkill_max. Similarly, a trend was observed between the level of convergence on the seed values for k6 and increasing residence time, and the most variation in this parameter was observed for compounds with shorter residence time values and small PAEs (Compounds 1, 3). These results are consistent with the empirical correlation observed between residence time and PAEs, and indicates that the predictive power of the biochemically measured k6 on PAE effects is proportional to the residence time value. More variation was observed for k5, which may be rationalized by the fact that this biochemical parameter is computed as a function of Ki, Ki* and k6. The composite parameter of pm/Ki exhibited large variance for both Compounds 1 and 6 relative to the other compounds. The reason for this variance is unclear, but may reflect different levels of bacterial permeation across the series. Lastly, the set of parameter values for the substrate metabolic flux (M parameter) from the fitting process across all of the datasets was tightly clustered around a mean value of 0.19 ± 0.05. While the concentration of LpxC substrate has not been determined in P. aeruginosa, this value is in good agreement with the majority of metabolic enzymes using global metabolomic methods in E. coli under logarithmic growth condition32.
To further investigate the impact of the parameter M, for which we had the least corroborating data, we performed a second fitting analysis. As exemplified for compounds with short, medium, and long residence times, compounds 1, 4, and 6 were fit initializing parameter M reflective of a greater competition against substrate (M=0.0015) and allowing that value to change at most 10-fold. Good fits were again obtained, with R2 > 0.97 (Supplementary Fig. 7 and Supplementary Table 9). Importantly, the output M values in this case rose to the upper constraint for two compounds (Compounds 1, 6). In all three cases, output values for k6 were very close to those obtained previously, demonstrating the importance of this critical factor within the fit. The values returned for the kgrowth and kkill_max parameters, as in the prior analysis for these compounds, changed at most 20% from the seed values and showed an average of 1.6-fold shift. The value of k5, exhibited even more dramatic deviations (as great as 88-fold for compound 1) from the seed values in this latter analysis; this outcome is expected for a system requiring more efficient formation of the EI* enzyme form during the compound incubation phase due to the greater competition against substrate encoded in the low M value.
To further confirm the integrated mechanistic model fitting, simulations of the Compound 6 PAE were performed using numerical integration over a system of differential equations for the two-step slow-binding enzyme inhibition mechanism and the general PD model (Supplementary Note). As with the integrated mechanistic model, the experimentally derived values were used as seed values for parameters in these simulations. Minimal perturbation of these input parameters was required to produce simulations that demonstrated excellent agreement with the experimental data (Supplementary Fig. 8, Supplementary Table 10), with the exception of the permeability factor, pm. In these simulations, the pm value was significantly lower than that predicted by the integrated mechanistic model (50–100-fold lower). This difference can be attributed to the fundamental assumptions regarding the formation of the inhibitor:LpxC encounter complex and substrate binding between the two modeling approaches. Unlike the integrated mechanistic model, which assumed a rapid equilibrium between the free enzyme, substrate and inhibitor, the differential equations embody a steady-state formalism, where the rates of enzyme:substrate complex and enzyme:inhibitor complex are explicitly defined. It was noted that the optimal differential equation-based simulations also required significantly larger rate constants for EI complex formation relative to substrate binding to the free enzyme form (100-fold faster). Taken together, the differential equation model predicts that the initial encounter inhibitor complex formation is significantly more kinetically efficient than substrate binding, and therefore lower intracellular drug concentrations are required to demonstrate a physiological effect. As noted above, experimental measurements of intracellular drug concentrations in Gram-negative bacteria are technically demanding, and therefore comparison of the differential output from the differential equations and integrated mechanistic model provides a bounded range of estimates for inhibitor permeability and, by extension, the intracellular concentration governing physiological response for extremely potent inhibitors such as Compound 6.
PD Model Simulations of in vivo Pharmacodynamic Responses
Having established the ability of our model to provide realistic fits that link PAE data to separately determined inhibitor-target potency measures and kinetic factors, we sought to predict bacterial growth under conditions of continuously changing inhibitor concentrations, such as encountered in in vivo efficacy testing. There are several factors that were considered in the transition from cellular studies to the in vivo environment. First, unlike the cellular PAE experiment which utilizes a step function concentration profile, the PK profiles in advanced PD models feature varying concentration profiles due to distribution and clearance mechanisms. To maintain the linkage between the PD response and continuously changing compound concentrations, it was necessary to perform successive stepwise calculations in small iterative steps to satisfy the assumption that compound concentrations do not significantly change over an evaluation interval of the enzyme:inhibitor states (Supplementary Note). This approach is particularly important in cases where the concentration profile results in a change from net formation or loss of the slow-dissociating species, since a mathematical boundary condition exists between these states.
Compound 6 was selected for in vivo efficacy studies based on the reported high serum protein binding free fraction and overall PK profile of this compound35, coupled with the fact that acute tolerability issues were observed in the series represented by compounds 1–5 that restricted further in vivo work. Since the free serum fraction is assumed to drive in vivo efficacy, the high free fraction (fu) was confirmed for Compound 6 in mouse and human plasma (mouse fu = 0.41, human fu = 0.28). These data were used to define the PK profiles for simulating the PD response with the mechanistic model. Of the six parameters invoked in the model, the growth and maximal killing rates were anticipated to exhibit the largest change upon translation to the in vivo conditions. From previous experience with the mouse thigh infection model, the organism growth rate can be ~3-fold lower than that seen under in vitro conditions, which likely reflects nutrient limitation in vivo36. Using this observation as an anchor, the compound-induced maximal killing rates were expected to be attenuated, but the relative ratio of killing rate to growth rates was assumed to remain constant. Based on this logic, the growth rate was estimated as ~0.4 log CFU/hr and the maximum killing rate ~1.3 log CFU/hr. The output values from the PAE modelling were used for the remaining parameters, with the exception of pm which was arbritrarily set to unity, since it is not possible to quantitatively assess the overlapping factors such as the potential for drug accumlation at the site of infection, and altered permeation potentials or changes in Ki under in vivo growth conditions. Simulations with this parameter set identified three doses that were expected to span the dynamic range of the in vivo model upon single dose administration (10, 50, 250 mg/kg, Supplementary Fig. 9).
PD model Validation with in vivo efficacy data
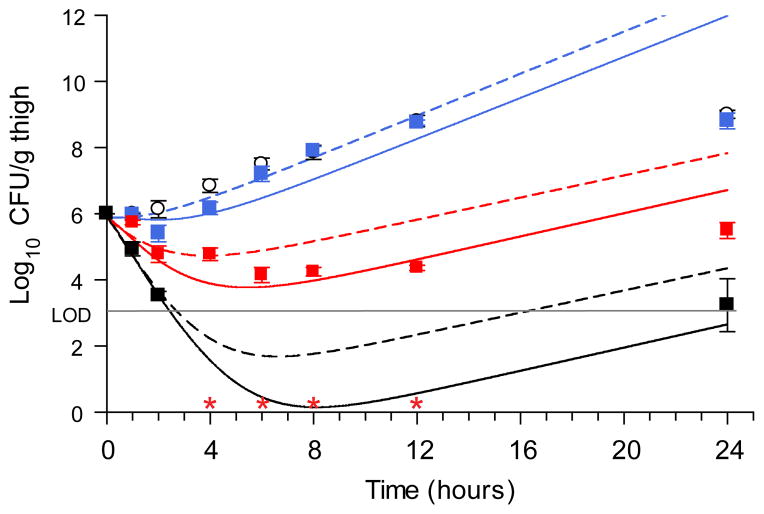
A three-dose efficacy study was performed using the doses predicted from our simulations in a neutropenic mouse thigh infection model (P. aeruginosa strain PAO1). Single dose PK studies in a satellite group of infected animals revealed a rapid clearance profile with a non-linear dose:exposure relationship (Supplementary Fig. 10). Also, we measured the in vivo growth and maximal killing rates in a second experiment using both control (vehicle) and a high dose (250 mg/kg) regimen incorporating an early data sampling protocol to directly inform our predictive model.(Supplementary Fig. 11). Importantly, the PD effects closely matched the simulated profiles (Fig. 5). Moreover, recovered colonies were found to be completely susceptible, as no CFU were obtained by plating samples from 24 h timepoints on selective media (4× MIC). The most dramatic effects were observed at the top dose, where the level of bacterial burden was below the limit of detection (LOD > 3 log10CFU/g thigh tissue) for the majority of the experimental timeframe (2–12 h). With the improved knowledge of maximal in vivo growth and kill rates, the simulations were repeated using the experimentally derived PK exposures at each dose and good agreement between the PD simulations and the experimental results was obtained (Fig. 5). Importantly, the model demonstrated robust performance across the doses and highlighted that the small variance in observed growth rate (kgrowth = 0.45–0.60 log10CFU/h) accounted for the model deviation from the in vivo experimental response (Supplementary Fig. 11). A further feature of this model is that the ramifications of slow-binding can be directly shown. Simulations where the thermodynamic potency was retained, but the slow-binding step was minimized were performed by increasing the values of k5 and k6 by 2000-fold (thereby allowing EI and EI* equilibration within seconds, Fig. 6, dashed lines). The impact of these changes is most evident in the compromised predictions of the top doses, wherein the greatest partitioning of target to the EI* form is expected. This result, combined with the fact that the value of k6 was one of the best described parameters in fitting PAE data suggests the importance of incorporating slow-binding inhibition in the model. In order to provide additional support for these observations, simulations using numerical integration over a system of differential equations were performed using the parameters from the integrated mechanistic model. These simulations were in excellent agreement with the in vivo experimental data (Supplementary Fig. 8, Supplementary Table 12), with the caveat that a much lower permeability factor was required for this approach, as was observed in the in vitro PAE simulations. Thus, these results provide an independent confirmation of the integrated mechanistic PD model approach for predicting the effects of time-dependent inhibitors on in vivo physiological response.
Figure 5. In vivo efficacy curves for Compound 6 with mechanistic pharmacodynamic model fit.
In vivo single dose bacterial P. aeruginosa PAO1 CFU thigh tissue burden after administration of Compound 6 at 10 mg/kg (blue square), 50 mg/kg (red square) and 250 mg/kg (black square). Error bars represent the S.E.M. (n=6 mice/timepoint). Open circles represent the vehicle, untreated control group. Lines represent mechanistic PD model simulations. Solid lines utilized PK parameters from Supplementary Table 11 and biochemical parameters from Supplementary Table 8, but with kgrowth = 0.45 (10 mg/kg dose) or 0.60 (50 and 250mg/kg doses) log10CFU/h and kkill_max = 1.9 log10CFU/h. Dashed lines represent the identical simulation but with k5 and k6 each increased 2000-fold to 120 and 40 min−1 respectively to simulate fast reversible target binding behavior while maintaining the full potency ascribed to the Ki* state.
Discussion
Long residence time drugs often exhibit pharmacological effects that are prolonged beyond that predicted by rapid equilibrium models of systemic exposure6. While numerous marketed drugs have this property1,8, prospective translation of slow-binding kinetics into desired PD remains a major challenge in the drug discovery process. This shortcoming is particularly acute for the discovery of novel antibacterial agents which often require high and sustained target engagement levels to ensure effective therapy and to avoid resistant subpopulation emergence. As a consequence, predicted efficacious exposures for antibacterial candidate drugs are among the highest of any therapeutic area11, leading to high attrition rates in early development due to inadequate safety margins37. Where extended drug-target residence times are observed, consideration of kinetic selectivity has the potential to reveal and explain lower dosing requirements than would otherwise be predicted, thus leading to improved safety while maintaining the desired PD2.
In this report we have characterized a series of slow-binding inhibitors of paLpxC that demonstrate extended cellular and in vivo physiological responses and have developed a mechanistic PD model that links the key parameters of slow-binding inhibition to cellular and in vivo bacterial growth dynamics. Unlike PD models that incorporate target:binding kinetics using a single-step kinetic mechanism38, our model provides a comprehensive framework for target:inhibitor binding kinetics and is based on the two-step, induced fit kinetic mechanism which has been most commonly observed for slow-binding inhibitors7,22. As a result, it is possible to differentiate the effects of rapid equilibrium encounter complex formation from the slower, time-dependent formation of the more potent target:inhibitor complex. Currently, differentiating these effects requires a selection process between independent PD models for each of these cases39. In practice, transitions between these target:inhibitor states will be both time- and dose-dependent and therefore, the PD model developed here provides a more general solution. Further, our PD model includes terms for physiological changes to substrate upon target inhibition. For metabolic pathway targets, elevation of substrate concentration would be expected following target inhibition, which can reduce the physiological effect of competitive inhibitors. Surprisingly, these effects were not influential in the analyses of paLpxC inhibitor cellular and in vivo effects, since excellent concordance with the model was observed when this term was modeled as being time-invariant. Additionally, our modeling of PAE studies with low Km/[S] ratios further suggest that LpxC is a vulnerable target in that the downstream physiological impacts following inhibition are rapid and not readily reversed. However, we note that the fully parameterized PD model requires detailed knowledge of the target:inhibitor binding kinetics, which may appear to be a major barrier to implementation of our approach. Importantly, these challenges were considered when collecting data for the paLpxC inhibitors. For example, estimates of the equilibrium constants were obtained from standard dose-response, high-throughput IC50 measurements and residence time values were obtained using a medium throughput jump-dilution assay format. As a result, the overall data collection burden for this project was not significantly higher than other drug discovery programs in the portfolio and represented a typical workstream for generating structure:kinetic relationships.
Emergence of resistant or antibiotic-tolerant populations can also affect PD modeling, particularly when extended periods of delayed re-growth is observed. The analysis of the PAE experiments assumed that intrinsic resistance rates were very low and that regrowth was dominated by inhibitor-susceptible organisms. This assumption was based on the fact that the frequency of spontaneous resistance emergence for LpxC inhibitors in P. aeruginosa is low (< 10−7)40. Further, cultures sampled during the outgrowth phase of the PAE experiments were found to be fully susceptible, as were organisms harvested from 24 h timepoints in animal efficacy experiments, when tested on drug containing media. These results indicate that PD effects are not dominated by resistance emergence in this case. However, in cases where the selection of resistance is likely to be encountered, there are a number of methods that incorporate resistant sub-population compartments that could be amended to the mechanistic time-dependent PD model31,41.
The successful prediction of in vivo response described by our PD model represents a major step towards the prospective modeling of dosing requirements for compounds with residence time effects. This advancement required the integration of two interrelated factors that are each time-dependent: changing concentrations of drug and the binding kinetics of the inhibitor with paLpxC. The single dose efficacy experiments in Figure 6 are standard components of drug discovery programs and are used to ensure that analogs being optimized exhibit an acceptable efficacy profile. Clinical dose predictions require a deeper understanding of the dose requirements and utilize multiple dosing algorithms. In this work, however, we have focused on developing an analytical solution for a PD model incorporating residence time effects as a first step towards this goal, with an emphasis on demonstrating its utility with experimentally-accessable parameters. This advance has applications to the drug discovery efforts across the therapeutic spectrum. For example, potent, slow-dissociating inhibitors of P38 kinase were recently reported as potential therapies for chronic obstructive pulmonary disease42. Due to the range of target-mediated side effects of systemic P38 inhibition43, selecting a drug candidate with optimal target:drug kinetic properties and low systemic exposure will be critical for therapeutic success. In oncology, the dual EGFR/HER2 inhibitor Lapatinib, approved for the treatment of breast cancer, demonstrated superior activity to reversible inihibitors44 due to extended residence times for both targets and recently, the slow-dissociating histone methyl transferase DOT1L inhibitor EPZ-5676, demonstrated potent activity in a mouse xenograph model despite low systemic exposure45. Finally, covalent inhibition mechanisms can be considered as an extreme sub-case of the residence time model, and there is growing interest in pursuing irreversible inhibitors in the field of oncology46, as exemplified by the recent approval of the covalent Bruton’s tyrosine kinase inhibitor Ibrutinib47 for the treatment of chronic lymphocytic leukemia and mantle cell lymphoma. In these cases, the physiological effects are driven by the onset of inhibition and our PD model could be adapted to simulate the effects of compounds with very low off-rates.
It is anticipated that the tools we have described will aid in the understanding and selection of compounds during preclinical stages of drug discovery to balance the complex ensemble of PK, target binding kinetic profiles and physiological dynamics desired in advance of costly clinical development campaigns. Ultimately this, or specialized models tailored to reflect more complex phyisology, may have utility in predicting the most effective dose regimen that maintains efficacy through extended target engagement and maximizes the therapeutic window by avoiding exposure-related, off-target side effects.
Online Methods
Chemistry
Compounds 1–3 were prepared as described in the Supplementary Note. Compound 448 and Compound 5 (example 3749) were prepared as described previously and Compound 6 (PF-5081090) was acquired from Sigma-Aldrich (Cat. number PZ0194).
Biochemistry
Materials
HPLC grade water, HPLC acetonitrile, ammonium acetate, sucrose, NaH2PO4, anhydrous DMSO were of reagent grade quality or higher.
Ki, Ki* determinations
P. aeruginosa LpxC (paLpxC) enzyme was prepared and the protocol for measuring inhibition of activity was followed as described previously50. Linearity of mass spectral response was confirmed on each occasion, with correlation coefficients (R2) of > 0.99 up to an instrument response of 60–100k (minimally 1 μM product). For representative traces see Supplementary Fig. 11. Data fitting was performed with GraFit 5.0.13 (Erithracus Software, Ltd, Surrey, UK) or XLfit (ID Business Solutions, Ltd). To estimate dissociation binding constants Ki and Ki*, serial dilutions of compound (2-fold dilutions) were prepared. For Ki measurements (no enzyme:inhibitor preincubation), 15 μL of assay buffer containing 10 μM substrate was added to compound dilutions, mixed, and allowed to stand 30 min, then reactions were initiated by addition of 15 μL assay buffer containing 0.2 nM paLpxC was added, mixed, and allowed to react for 2.5 min before quenching. For Ki* measurements, 15 μL assay buffer containing enzyme (23 °C, [LpxC] = 30 pM, 37 °C, [LpxC] = 10 pM) was added to compound dilutions, shaken, and allowed to stand covered overnight (16 hours) at the desired temperature. Reactions were then initiated by addition of 15 μL of 10 μM substrate buffer and allowed to proceed for 60 min. Both IC50 assay formats were performed in triplicate from separate dilutions and dispenses of compounds and reagents. Data from experiments without preincubation were fitted using standard 4-parameter logistic models to determine IC50s, and the extended preincubation experimental datasets were fit using the Morrison equation22. Dissociation constants were computed from the IC50 values using the Cheng-Prusoff equation24 with the following parameters: [S], Km = 5 μM.
Jump dilution recovery assay
Enzyme was incubated with inhibitor for 16 hours at room (23°C) or physiological (37 °C) temperature in the absence of substrate. The mixture was then diluted 1000-fold, in order to establish the final inhibitor concentration well below the Ki*, into an assay mixture containing 25 μM substrate (5-fold the Km) and product formation was monitored for ~180 min by LC/MS/MS as described 50. Data was fit to Equation (1) using the uninhibited enzyme velocity as vs, and incorporating the term C to account for a weak background signal detected in the MS spectra. Since no additional background product accumulation occurs in the absence of enzyme, v0 was set to zero. Data were acquired in triplicate from separate experiments. The residence time was calculated as the reciprocal of the observed activity recovery rate constant, kobs, as described in Equation (2).
| (1) |
| (2) |
In cases where the progress curve final velocity (vs) did not approach the DMSO control (e.g. tight-binding inhibitors) over the reaction timeframe, the data were fit using the calculated fractional final velocity back-calculated from the Ki* value and the Morrison equation. It was noted that under these conditions, the observed slow dissociation rates are likely influenced by many factors including target rebinding and slow binding kinetics for the initial encounter complex. As a result, k6 ≥ kobs and these measurements therefore provide a lower limit estimate of k6.
Onset of inhibition studies
Solutions containing 30 μM substrate with varying concentrations of Compound 2 (0 – 14 nM) were combined with an equal volume of reaction mixture containing 0.1 nM LpxC. After mixing, reactions were allowed to progress and aliquots were collected and quenched to measure product accumulation by LC/MS/MS. Progress curve data were analyzed using a global fitting approach and a system of equations (equations 3–6)17 using Prism 6.0 (GraphPad Software, Inc.), where v0 is the uninhibited (control) reaction velocity, vi is the initial reaction velocity, vs is the final velocity and kobs is the rate constant describing the onset of inhibition at each inhibitor concentration. These analyses were performed using values of 5 μM and 3.5 nM/min for Km and Vmax for LpxC under the assay conditions used here. The formation of the inhibitor encounter complex was assumed to be governed by rapid equilibrium kinetics and the apparent binding constant was fixed to the estimated value from IC50 measurements (Table 1, Ki = 6.4 nM).
| (3) |
| (4) |
| (5) |
| (6) |
Microbiology
Microrganisms
P.aeruginosa strain PAO1 and an efflux-pump deficient P.aeruginosa strain (ΔMexABCDXY), N150, derived from PAO126.
Culture medium
P. aeruginosa was cultured in Mueller Hinton II broth, (Difco no. 275730), cation adjusted to final 20–25 mg/L of calcium and 10–12.5 mg/L of magnesium (CAMHII). Inoculants were incubated at 35°C on Mueller Hinton II agar plates (Becton Dickinson BBL no. 211438) for PAE & killing kinetics measurements.
MIC determinations
Minimum inhibitory concentrations were determined in duplicate by broth microdilution according to the Clinical and Laboratory Standards Institute guidelines51. Compounds were dissolved in DMSO and diluted in culture medium to prepare 11 doubling dilutions at 2% final DMSO (v/v) covering 64 to 0.06 μg/mL compound. Bacteria in the logarithmic phase of growth were diluted to approximately 5×105 CFU/mL and incubated at 37 °C. Visible growth was recorded after 24 h.
Mode of Action Studies
Mode of action via LpxC was confirmed by an increase in MIC upon over-expression of P. aeruginosa LpxC. To that end, derivatives of P.aeruginosa PAO1 and its efflux mutant were created that either contained an LpxC expression plasmid, pLH1783 or an empty control plasmid pUCP1852,53. Plasmid pLH1783 was constructed by amplification of lpxC from P. aeruginosa PAO1 genomic DNA using oligonucleotides ACGTGAATTCATGATCAAACAACGCACCTTG and ACGTAAGCTTCTACACTGCCGCCGCCGGGCGC. The PCR product was purified and digested with EcoRI and HindIII, ligated into similarly digested pUCP1852, and transformed into E. coli DH5α-T1R chemically competent cells (Life Technologies). Transformants were selected on LB agar plates with 25 μg/mL ampicillin, and the plasmid was verified by sequencing. Plasmids were transformed into P. aeruginosa strains53 and selected on LB agar plates containing 250 μg/ml carbenicillin. Strains were pregrown on MHBII agar plates containing 250 μg/mL carbenicillin to ensure the presence of the plasmids; when determining MIC values, however, carbenicillin was absent from the medium.
Killing kinetics
P. aeruginosa cells (106 CFU/mL) in logarithmic phase of growth were exposed to drug at 37°C in a shaking incubator. The inoculum was confirmed at time 0; subsequent viable counts were determined at 0.5, 1, 1.5, 1, 2, 3, 4, 5 and 6 h. Sampling for colony counts was done by removing 0.1 mL samples of broth at the specified times. Each sample was serially diluted 10-fold with broth. The antibiotic carryover was minimized by dilution in CAMHII + 5 mM bovine serum albumin. Colonies were counted after incubation at 35°C for 24 h. The rate and extent of killing were determined by plotting log10 viable counts (CFU/mL) against time. The maximal killing rate was determined from the linear regressions on the data following the observed lag taken as 1 hr.
In vitro PAE
P. aeruginosa cells (106 CFU/mL) in logarithmic phase of growth were exposed to varying compound concentrations at 37°C in a shaking incubator for 1 h. A tube containing no antimicrobial agent was included as a growth control. Drug removal was effectively accomplished by 1:1000 dilution into fresh, pre-warmed CAMHII media. Bacterial regrowth at 37 °C was determined by removal of aliquots immediately after dilution and every hour for 8 h and assayed by viable counting. The lower limit of detection was 1 log10 CFU/mL. The combined effect of the dilution step and the rapid bactericidal nature of the LpxC inhibitors resulted in several cases where the number of viable bacteria to fall below the limit of detection (LOD) post-dilution. This was especially true for compounds with >20 min residence times (2, 3, 5 and 6). Although other methods of drug removal - such as repeated washing with fresh media - were attempted to improve the LOD, but pelleting the bacteria was found to cause an increase in non-specific cell killing, possibly due to the fragility of the cell wall upon LpxC inhibition54,55 The PAE was calculated by the formula13 PAE = T – C where T is the time for the drug exposed culture to increase 1 log10 following drug removal and C is the corresponding time for the nonexposed control to increase 1 log10CFU following drug removal. Pearson correlation coefficients between PAE values and the biological parameters were computed in MATLab using the CORECOEF function.
Mechanistic Pharmacodynamic Modeling
Details on the mechanistic model derivation are provided in the Supplementary Note. A set of tools were developed in MATLab 7.5 (MathWorks, Natick MA) for simulations and data fitting as follows (Matlab program files outlined below are included in Supplementary Data Sets 1–3):
IncubFit.txt
Fits “incubation data” for in vitro PAE studies. Data is input with cell count in log10 CFU/mL units, time-spaced (hours) with the same interval for three replicates, and with initial estimates of the parameters Ki, Ki*, k5, k6, M, pm kgrowth and kkill_max. The program retruns fitted values for the above listed parameters, as well as an r2 value. The program additionally takes as input compound concentration, which is assumed to remain constant until the dilution step of the PAE study.
PAEFit.txt
Fits pharmacokinetic dose response data, such as is generated from animal model data, to incorporate the parameters corresponding to residence time effects. Note that this program handles more complicated compound PK profiles than for IncubFit. Requirements for input parameters and output data are the same as for IncubFit. Program internal functions enable compound concentration profiles to be specified to match known PK.
EITool.txt
This program generates an interactive graphical interface to simulate and visualize the impact on cell growth by compounds using a variety of PK profiles. It also enables output of the simulations containing both parameter values and also simulated data curves for replotting.
Modeling using differential equations
The effect of Compound 6 on bacterial growth in culture (in vitro) and in the mouse thigh efficacy model (in vivo) was simulated in Mathematica (Wolfram, Champaign, Il) using a series of differential equations to calculate the concentration of each enzyme species (E, ES, EI and EI*) in (i) the drug exposure phase and (ii) in the post-antibiotic (PAE) phase following compound washout. Details on the system of system of equations used can be found in the Supplementary Note. Experimental values were used for input values for the parameters k5, k6, Ki, Km, kcat, ρm, kgrowth and kkill (Table 1). The values for these parameters were not altered in the simulation apart from the value for ρm which had to be changed to get a satisfactory fit to the data (see below). The rate constant parameters k1, k2, k3 and k4 were defined based on the following relationships: k2 = Km × k1−kcat, where experimental values of Km and kcat were obtained from the biochemical measurements (see Onset of inhibition methods) and assuming Km/[S] = 0.15 (M-value obtained from analytical model fitting). Further, k4 = Ki × k3.
Initial estimates for the parameters k1 and k3 were set within the range of typical second-order association rate constants (105–108 μM−1.min−1). The parameters k3, k1, and ρm were then manually adjusted to obtain the best simulation of the full set of experimental data for Compound 6 (Supplementary Fig. 13). Supplementary Tables 11 and 12 contain the input and output values resulting from these simulations. In addition, these simulations identified the minimum and maximum achieved target-occupancy are 0.42 and 0.7 respectively, resulting in a slope-factor equal to: .
Pharmacokinetics and Pharmacology
All animal studies were approved by the Institutional Animal Care and Use Committee of AstraZeneca and were conducted in accordance with the guidelines of the American Association for Accreditation of Laboratory Animal Care.
in vitro
Physical properties including mouse and human plasma protein binding, logD, and aqueous solubility were determined as described previously56,57.
In vivo time course studies
CD-1 mice (Charles River Wilmington US) were rendered neutropenic with two intraperitoneal doses of cyclophosphamide (150 mg/kg −4 days and 100 mg/kg −1 day prior to infection58. Animals were infected via an intramuscular challenge of ~1 × 106 CFU administered within 70 μL of 0.9% saline to each thigh. The inoculum was prepared from agar plate scrapings of P. aeruginosa PAO1 cultured overnight in tryptic soy broth media (~25mL). Following an OD600 determination, the inoculum was diluted in 0.9% saline to a concentration of ~1.5 × 107 CFU/mL prior to inoculation. Therapy with Compound 6 was initiated 2 hours post-bacterial challenge at 10, 50 and 250 mg/kg. Doses were solubilized in 40% Captisol and administered subcutaneously at a dose volume of 10 mL/kg. For determination of pharmacokinetics, blood samples were obtained from n=3 animals/timepoint/dose group via submandibular (~20 μL) and cardiac puncture (for terminal samples) following anesthesia with 5% isoflurane at 0.5, 1, 2, 4, 6, 8, 12, and 24 h post initiation of therapy. Blood samples were collected in EDTA microfuge tubes (Beckton Dickenson) and processed for plasma (centrifuge @ 13,200 rpm for 5 minutes). Plasma samples were stored at −20 °C prior to bioanalysis. For terminal endpoints at 1, 2, 4, 6, 8, 12 and 24 hr, thighs were asceptically removed, weighed and homogenized in 1 mL of saline. Bacterial burden enumeration of tissue homogenate was performed by serial dilution on TSA plates which were incubated overnight at 37 °C prior to colony (CFU) counting. When testing for resistance emergence, a similar protocol was followed, substituting TSA plates supplemented with compound at 4× MIC.
Drug concentration in plasma was quantified by LC/MS/MS. Plasma samples and fortified plasma standards (25 μL) were precipitated with 200 μL of mobile phase B (acetonitrile/0.1% formic acid) containing 250 ng/mL of carbutamide as an internal standard. The samples were vortexed and centrifuged at 4000 rpm for 15 min. The supernatant (120 μL) was combined with 120 μL of mobile phase A (water containing 0.1% formic acid) prior to injection (5 μL) on the LC/MS/MS system. Separation was achieved with a Varian Polaris 3 C18 30×3 mm column using a flow rate of 0.8 mL/min and a ballistic gradient with the following schedule: 0–0.3 min, 5% mobile phase B; 0.30–1.20 min, 5–95% mobile phase B; 1.20–1.70 min, 95% mobile phase B; 1.70–1.71 min, 95–5% mobile phase B; 1.71–2.0 min, 5% mobile phase B.
Compound 6 and the internal standard were detected from the HPLC effluent using a Sciex API 4000 triple quadropole mass spectrometer utilizing electrospray ionization operated in the positive ion mode. Ion spray voltage was set at 4500V and the collision energy (25 eV) was optimized for multiple reaction monitoring (MRM) transitions of 413.2 to 380.0 and 272.4 to 156.0 for Compound 6 and carbutamide, respectively. Linear regression of the peak area ratio of Compound 6/carbutamide associated with fortified standards was used to quantify Compound 6 concentrations in plasma samples. The assay had a dynamic range of 1 – 10,000 ng/mL. Plasma protein binding was determined at a concentration of 50 μM and completed using 96-well format equilibrium dialysis57.
Pharmacokinetic parameters summarized in Supplementary Table 9 were estimated by fitting time vs. concentration data for each dose level to a one-compartment model with first-order input and elimination (Phoenix for WinNonlin 6.2, Certara, St. Louis MO). Since it is assumed that only free drug concentrations can drive pharmacological effect, PK input into the model was adjusted by the unbound fraction determined from plasma protein binding experiments. Time course of bacterial burden (log10 CFU/g of tissue) were plotted as the difference in colony counts vs. the initial burden determined at initiation of therapy. The lower limit of detection was 3 log10 CFU/g of tissue.
Supplementary Material
Acknowledgments
P.J.T. acknowledges this research was partially funded by the National Institutes of Health (GM102864) and through a sponsored research agreement with AstraZeneca. We thank Joanne Kotz and Robert A. Copeland for advice in preparation of the manuscript. We also acknowledge contributions from Pamela Hill, Amanda Li, Tyler Grebe, and Camil Joubran as well as Senthilkumar Kuppusamy and the chemists at Syngene chemical synthesis and analytical support, Boudewijn de Jonge for guidance on microbiological assessments, and Kanishk Kapilashrami and Andrew Chang for helpful discussions. Finally, we thank the anonymous reviewers for their careful and insightful evaluation of this work.
Footnotes
Infection Innovative Medicines Unit, AstraZeneca Research & Development, Waltham, Massachusetts, USA.
Grant K. Walkup, Zhiping You, Philip L. Ross, Michael R. Hale, John O’Donnell, David E. Ehmann, Virna J. A. Schuck, Ed T. Buurman, Allison L. Choy, Laurel Hajec, Kerry Murphy-Benenato, Valerie Marone, Sara A. Patey, Lena A. Grosser, Michele Johnstone, and Stewart L. Fisher
Institute for Chemical Biology & Drug Discovery, Department of Chemistry, Stony Brook University, Stony Brook, New York, USA.
Eleanor K. H. Allen, Fereidoon Daryaee & Peter J. Tonge
Department of Oral Biology and Pathology, Stony Brook University, Stony Brook, New York, USA.
Stephen G. Walker
Author Contributions
E.K.H.A. designed experiments and performed post-antibiotic effect (PAE) experiments. P.L.R. measured compound residence time and inhibition onset. Z.Y, S.L.F., V.J.A.S., & G.K.W. derived the integrated pharmacodynamic model. V.M, A.L.C, and K.M.-B. designed and synthesized compounds. S.A.P., E.T.B, L.H., & M.J. collected PAE data, determined resistance frequencies, or MICs. L.H., prepared lpxC overexpression strains. J.O’D., and L.A.G. designed and performed animal experiments. Z.Y. and D.E.E. performed data analysis of integrated equation models. S.G.W. oversaw PAE experiments. F.D. performed data analysis of differential equation models. M.J.H., G.K.W., Z.Y., P.L.R., E.K.H.A, M.R.H., J.O’D., D.E.E. P.J.T., & S.L.F. analyzed PAE and animal efficacy data and designed experiments. G.K.W., P.J.T, and S.L.F. wrote the manuscript.
Competing financial interests
All authors except E.K.H.A, F.D., S.G.W., and P.J.T. were employees of AstraZeneca during the conduct of this research.
References
- 1.Swinney DC. Biochemical Mechanisms of New Molecular Entities (NMEs) Approved by United States FDA During 2001–2004: Mechanisms Leading to Optimal Efficacy and Safety. Curr Top Med Chem. 2006;6:461–478. doi: 10.2174/156802606776743093. [DOI] [PubMed] [Google Scholar]
- 2.Swinney DC. The role of binding kinetics in therapeutically useful drug action. Curr Opin Drug Discov Devel. 2009;12:31–39. [PubMed] [Google Scholar]
- 3.Arrowsmith J. Trial watch: Phase II failures: 2008–2010. Nat Rev Drug Discov. 2011;10:328. doi: 10.1038/nrd3439. [DOI] [PubMed] [Google Scholar]
- 4.Cook D, et al. Lessons learned from the fate of AstraZeneca’s drug pipeline: a five-dimensional framework. Nat Rev Drug Discov. 2014;13:419–431. doi: 10.1038/nrd4309. [DOI] [PubMed] [Google Scholar]
- 5.Morgan P, et al. Can the flow of medicines be improved? Fundamental pharmacokinetic and pharmacological principles toward improving Phase II survival. Drug Discov Today. 2012;17:419–24. doi: 10.1016/j.drudis.2011.12.020. [DOI] [PubMed] [Google Scholar]
- 6.Copeland RA, Pompliano DL, Meek TD. Drug-target residence time and its implications for lead optimization. Nat Rev Drug Discov. 2006;5:730–9. doi: 10.1038/nrd2082. [DOI] [PubMed] [Google Scholar]
- 7.Copeland RA. The dynamics of drug-target interactions: drug-target residence time and its impact on efficacy and safety. Expert Opin Drug Discov. 2010;5:305–10. doi: 10.1517/17460441003677725. [DOI] [PubMed] [Google Scholar]
- 8.Lu H, Tonge PJ. Drug-target residence time: critical information for lead optimization. Curr Opin Chem Biol. 2010;14:467–74. doi: 10.1016/j.cbpa.2010.06.176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Drusano GL. Antimicrobial pharmacodynamics: critical interactions of ‘bug and drug’. Nat Rev Microbiol. 2004;2:289–300. doi: 10.1038/nrmicro862. [DOI] [PubMed] [Google Scholar]
- 10.Hickey E. Tools to define the relevance of PK/PD parameters to the efficacy, toxicity and emergence of resistance of antimicrobials. Curr Opin Drug Discov Devel. 2007;10:49–52. [PubMed] [Google Scholar]
- 11.McKenzie C. Antibiotic dosing in critical illness. J Antimicrob Chemother. 2011;66(Suppl 2):ii25–31. doi: 10.1093/jac/dkq516. [DOI] [PubMed] [Google Scholar]
- 12.Barb AW, Zhou P. Mechanism and inhibition of LpxC: an essential zinc-dependent deacetylase of bacterial lipid A synthesis. Curr Pharm Biotechnol. 2008;9:9–15. doi: 10.2174/138920108783497668. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Bundtzen RW, Gerber AU, Cohn DL, Craig WA. Postantibiotic suppression of bacterial growth. Rev Infect Dis. 1981;3:28–37. doi: 10.1093/clinids/3.1.28. [DOI] [PubMed] [Google Scholar]
- 14.Gennadios HA, Christianson DW. Binding of uridine 5′-diphosphate in the ‘basic patch’ of the zinc deacetylase LpxC and implications for substrate binding. Biochemistry. 2006;45:15216–23. doi: 10.1021/bi0619021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Gennadios HA, Whittington DA, Li X, Fierke CA, Christianson DW. Mechanistic Inferences from the Binding of Ligands to LpxC, a Metal-Dependent Deacetylase. Biochemistry. 2006;45:7940–7948. doi: 10.1021/bi060823m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Morrison JF, Walsh CT. The behavior and significance of slow-binding enzyme inhibitors. Adv Enzymol Relat Areas Mol Biol. 1988;61:201–301. doi: 10.1002/9780470123072.ch5. [DOI] [PubMed] [Google Scholar]
- 17.Zhang R, Windsor WT. in vitro kinetic profiling of Hepatitus C virus NS3 protease inhibitors by progress curve analysis. In: Gong EY, editor. Antivir Methods Protoc Methods Mol Biol. Vol. 1030. Humana Press; 2013. pp. 59–79. [DOI] [PubMed] [Google Scholar]
- 18.Copeland RA. Evaluation of Enzyme Inhibitors in Drug Discovery: A Guide for Medicinal Chemists and Pharmacologists. John Wiley and Sons, Inc; 2013. p. 538. [PubMed] [Google Scholar]
- 19.Vauquelin G. Rebinding: or why drugs may act longer in vivo than expected from their in vitro target residence time. Expert Opin Drug Discov. 2010;5:927–941. doi: 10.1517/17460441.2010.512037. [DOI] [PubMed] [Google Scholar]
- 20.Tummino PJ, Copeland RA. Residence time of receptor-ligand complexes and its effect on biological function. Biochemistry. 2008;47:5481–5492. doi: 10.1021/bi8002023. [DOI] [PubMed] [Google Scholar]
- 21.Copeland RA, Basavapathruni A, Moyer M, Scott MP. Impact of enzyme concentration and residence time on apparent activity recovery in jump dilution analysis. Anal Biochem. 2011;416:206–10. doi: 10.1016/j.ab.2011.05.029. [DOI] [PubMed] [Google Scholar]
- 22.Williams JW, Morrison JF. The kinetics of reversible tight-binding inhibition. Methods Enzymol. 1979;63:437–67. doi: 10.1016/0076-6879(79)63019-7. [DOI] [PubMed] [Google Scholar]
- 23.Morrison JF. Kinetics of the reversible inhibition of enzyme-catalysed reactions by tight-binding inhibitors. Biochim Biophys Acta. 1969;185:269–86. doi: 10.1016/0005-2744(69)90420-3. [DOI] [PubMed] [Google Scholar]
- 24.Cheng Y, Prusoff WH. Relationship between the inhibition constant (KI) and the concentration of inhibitor which causes 50 per cent inhibition (I50) of an enzymatic reaction. Biochem Pharmacol. 1973;22:3099–108. doi: 10.1016/0006-2952(73)90196-2. [DOI] [PubMed] [Google Scholar]
- 25.Chang A, et al. Rational optimization of drug-target residence time: insights from inhibitor binding to the Staphylococcus aureus FabI enzyme-product complex. Biochemistry. 2013;52:4217–28. doi: 10.1021/bi400413c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Masuda N, et al. Substrate Specificities of MexAB-OprM, Pumps in Pseudomonas aeruginosa Substrate Specificities of MexAB-OprM, MexCD-OprJ, and MexXY-OprM Efflux Pumps in Pseudomonas aeruginosa. Antimicrob Agents Chemother. 2000;44:3322–3327. doi: 10.1128/aac.44.12.3322-3327.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Fung-Tomc JC, Gradelski E, Valera L, Kolek B, Bonner DP. Comparative Killing Rates of Fluoroquinolones and Cell Wall-Active Agents Comparative Killing Rates of Fluoroquinolones and Cell Wall-Active Agents. Antimicrob Agents Chemother. 2000;44:1377–1380. doi: 10.1128/aac.44.5.1377-1380.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Mdluli KE, et al. Molecular validation of LpxC as an antibacterial drug target in Pseudomonas aeruginosa. Antimicrob Agents Chemother. 2006;50:2178–2184. doi: 10.1128/AAC.00140-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Spangler SK, Bajaksouzian S, Jacobs MR, Appelbaum PC. Postantibiotic Effects of Grepafloxacin Compared to Those of Five Other Agents against 12 Gram-Positive and -Negative Bacteria. Antimicrob Agents Chemother. 2000;44:186–189. doi: 10.1128/aac.44.1.186-189.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Mager DE, Wyska E, Jusko WJ. Diversity of mechanism-based pharmacodynamic models. Drug Metab Dispos. 2003;31:510–8. doi: 10.1124/dmd.31.5.510. [DOI] [PubMed] [Google Scholar]
- 31.Czock D, Keller F. Mechanism-based pharmacokinetic-pharmacodynamic modeling of antimicrobial drug effects. J Pharmacokinet Pharmacodyn. 2007;34:727–51. doi: 10.1007/s10928-007-9069-x. [DOI] [PubMed] [Google Scholar]
- 32.Bennett BD, et al. Absolute metabolite concentrations and implied enzyme active site occupancy in Escherichia coli. Nat Chem Biol. 2009;5:593–9. doi: 10.1038/nchembio.186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Taber HW, Mueller JP, Miller PF, Arrow AS. Bacterial Uptake of Aminoglycoside Antibiotics. Microbiol Rev. 1987;51:439–457. doi: 10.1128/mr.51.4.439-457.1987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Nikaido H, Thanassi DG. Penetration of Lipophilic Agents with Multiple Protonation Sites into Bacterial Cells: Tetracyclines and Fluoroquinolones as Examples. Antimicrob Agents Chemother. 1993;37:1393–1399. doi: 10.1128/aac.37.7.1393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Montgomery JI, et al. Pyridone methylsulfone hydroxamate LpxC inhibitors for the treatment of serious Gram-negative infections. J Med Chem. 2012;55:1662–70. doi: 10.1021/jm2014875. [DOI] [PubMed] [Google Scholar]
- 36.Smith H. Pathogenicity and the microbe in vivo. J Gen Microbiol. 1990;136:377–383. doi: 10.1099/00221287-136-3-377. [DOI] [PubMed] [Google Scholar]
- 37.DiMasi JA, Feldman L, Seckler A, Wilson A. Trends in risks associated with new drug development: success rates for investigational drugs. Clin Pharmacol Ther. 2010;87:272–7. doi: 10.1038/clpt.2009.295. [DOI] [PubMed] [Google Scholar]
- 38.Mager DE. Target-mediated drug disposition and dynamics. Biochem Pharmacol. 2006;72:1–10. doi: 10.1016/j.bcp.2005.12.041. [DOI] [PubMed] [Google Scholar]
- 39.Yan X, Mager DE, Krzyzanski W. Selection between Michaelis–Menten and target-mediated drug disposition pharmacokinetic models. J Pharmacokinet Pharmacodyn. 2011;37:25–47. doi: 10.1007/s10928-009-9142-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Caughlan RE, et al. Mechanisms decreasing in vitro susceptibility to the LpxC inhibitor CHIR-090 in the Gram-negative pathogen Pseudomonas aeruginosa. Antimicrob Agents Chemother. 2012;56:17–27. doi: 10.1128/AAC.05417-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Nikolaou M, Schilling AN, Vo G, Chang KT, Tam VH. Modeling of microbial population responses to time-periodic concentrations of antimicrobial agents. Ann Biomed Eng. 2007;35:1458–1470. doi: 10.1007/s10439-007-9306-x. [DOI] [PubMed] [Google Scholar]
- 42.Millan DS, et al. Design and synthesis of inhaled p38 inhibitors for the treatment of chronic obstructive pulmonary disease. J Med Chem. 2011;54:7797–814. doi: 10.1021/jm200677b. [DOI] [PubMed] [Google Scholar]
- 43.Cohen SB, et al. Evaluation of the efficacy and safety of Pamapimod, a p38 MAP kinase inhibitor, in a double-blind, methotrexate-controlled study of patients with active rheumatoid arthritis. Arthritis Rheum. 2009;60:335–44. doi: 10.1002/art.24266. [DOI] [PubMed] [Google Scholar]
- 44.Wood ER, et al. A Unique Structure for Epidermal Growth Factor Receptor Bound to GW572016 (Lapatinib): Relationships among Protein Conformation, Inhibitor Off-Rate, and Receptor Activity in Tumor Cells. Cancer Res. 2004;64:6652–6659. doi: 10.1158/0008-5472.CAN-04-1168. [DOI] [PubMed] [Google Scholar]
- 45.Daigle SR, et al. Potent inhibition of DOT1L as treatment of MLL-fusion leukemia. Blood. 2013;122:1017–25. doi: 10.1182/blood-2013-04-497644. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Liu Q, et al. Developing irreversible inhibitors of the protein kinase cysteinome. Chem Biol. 2013;20:146–59. doi: 10.1016/j.chembiol.2012.12.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Schwarzbich M-A, Witzens-Harig M. Ibrutinib. In: Martens UM, editor. Small Mol Oncol Recent Results Cancer Res. Vol. 201. Springer; Berlin Heidelberg: 2014. pp. 259–267. [DOI] [PubMed] [Google Scholar]
- 48.Gao N, et al. Overexpression of Pseudomonas aeruginosa LpxC with its inhibitors in an acrB-deficient Escherichia coli strain. Protein Expr Purif. 2014;104:57–64. doi: 10.1016/j.pep.2014.09.006. [DOI] [PubMed] [Google Scholar]
- 49.Takashima H, et al. Preparation of quinoline-4-carbohydroxamic acid and naphthyridine-4-carbohydroxamic acid derivatives as antibacterial agents. WO2008105515A1. PCT Int Appl. 2008
- 50.Hale MR, et al. Exploring the UDP pocket of LpxC through amino acid analogs. Bioorg Med Chem Lett. 2013;23:2362–7. doi: 10.1016/j.bmcl.2013.02.055. [DOI] [PubMed] [Google Scholar]
- 51.CLSI. Methods for Dilution Antimicrobial Susceptibility Tests for Bacteria That Grow Aerobically; Approved Standard. 9. Clinical Laboratory Standards Institute; Wayne, PA: 2012. CLSI Doc. M07-A9. [Google Scholar]
- 52.West SEH, Schweizer HP, Dall C, Sample AK, Runyen-Janecky LJ. Construction of improved Escherichia-Pseudomonas shuttle vectors derived from pUC18/19 and sequence of the region required for their replication in Pseudomonas aeruginosa. Gene. 1994;148:81–86. doi: 10.1016/0378-1119(94)90237-2. [DOI] [PubMed] [Google Scholar]
- 53.Choi KH, Kumar A, Schweizer HP. A 10-min method for preparation of highly electrocompetent Pseudomonas aeruginosa cells: application for DNA fragment transfer between chromosomes and plasmid transformation. J Microbiol Methods. 2006;64:391–7. doi: 10.1016/j.mimet.2005.06.001. [DOI] [PubMed] [Google Scholar]
- 54.Gudmundsson S, Vogelman B, Craig WA. The in vivo postantibiotic effect of imipenem and other new antimicrobials. J Antimicrob Chemother. 1986;18(Suppl E):67–73. doi: 10.1093/jac/18.supplement_e.67. [DOI] [PubMed] [Google Scholar]
- 55.Parker RF, Marsh HC. The action of penicillin on Staphylococcus. J Bacteriol. 1946;51:181–6. doi: 10.1128/JB.51.2.181-186.1946. [DOI] [PubMed] [Google Scholar]
- 56.De Jonge BLM, et al. Discovery of inhibitors of 4’-phosphopantetheine adenylyltransferase (PPAT) to validate PPAT as a target for antibacterial therapy. Antimicrob Agents Chemother. 2013;57:6005–15. doi: 10.1128/AAC.01661-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Kariv I, Cao H, Oldenburg KR. Development of a high throughput equilibrium dialysis method. J Pharm Sci. 2001;90:580–87. doi: 10.1002/1520-6017(200105)90:5<580::aid-jps1014>3.0.co;2-4. [DOI] [PubMed] [Google Scholar]
- 58.Gerber AU, et al. Impact of dosing intervals on activity of gentamicin and ticarcillin against Pseudomonas aeruginosa in granulocytopenic mice. J Infect Dis. 1983;147:910–917. doi: 10.1093/infdis/147.5.910. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.