DNA loops generate intracentromere tension in mitosis

The geometry and arrangement of DNA loops in the pericentric region of the budding yeast centromere create a DNA-based molecular shock absorber that serves as the basis for how tension is generated between sister centromeres in mitosis.

Abstract

The centromere is the DNA locus that dictates kinetochore formation and is visibly apparent as heterochromatin that bridges sister kinetochores in metaphase. Sister centromeres are compacted and held together by cohesin, condensin, and topoisomerase-mediated entanglements until all sister chromosomes bi-orient along the spindle apparatus. The establishment of tension between sister chromatids is essential for quenching a checkpoint kinase signal generated from kinetochores lacking microtubule attachment or tension. How the centromere chromatin spring is organized and functions as a tensiometer is largely unexplored. We have discovered that centromere chromatin loops generate an extensional/poleward force sufficient to release nucleosomes proximal to the spindle axis. This study describes how the physical consequences of DNA looping directly underlie the biological mechanism for sister centromere separation and the spring-like properties of the centromere in mitosis.

Introduction

DNA looping was first observed in preparations of salamander eggs under a light microscope in the early 1900s (Hertwig, 1906). Later, Paulson and Laemmli (1977) found DNA loops that emanate from a protein-rich chromosome scaffold when examining chromosome spreads in mammalian cells. Loops are particularly prominent in meiotic chromosomes (Zickler and Kleckner, 1999; Kleckner, 2006). Most recently, methods such as Hi-C were used to generate genome-wide contacts and provide a statistical, population-averaged view of the loop organization of the chromosome (Maeshima and Laemmli, 2003; Kleckner et al., 2013; Naumova et al., 2013). Sister chromatids are organized as stacks of radial arrays, with each loop in the array linked at its base. The base of these loops comprises the chromosome scaffold that defines a primary axis spanning the length of the chromosome. These loops have garnered much attention in regard to their role in chromosome packaging and gene expression (Rao et al., 2014).

The radial loops exhibit thermal entropic fluctuations, as well as nonthermal ATP-dependent random motion inside cells (Weber et al., 2012; Vasquez and Bloom, 2014). A significant feature of these loops is their influence on the primary axis or chromosome scaffold. Polymer physics shows that a linear polymer will collapse into a random coil in a thermal bath, whereas a linear polymer with side chains will adopt an entropically favored state that is more extended than a random coil (de Gennes, 1979). Recent work has demonstrated that a particular type of branched polymer, a bottle brush, with a high number of sidechains (i.e., crowded), can generate extensional forces (outward/poleward) that under certain conditions are strong enough to break covalent bonds (Panyukov et al., 2009a,b; Lebedeva et al., 2012). Given that chromosomes contain side loops off a main axis, we wanted to investigate if the centromere region of a chromosome would have fluctuations and enhanced tension along its axis similar to those in a bottle brush polymer.

The centromere is a unique structure built to mediate chromosome segregation via spindle microtubules in mitosis and to hold sister chromatids together in meiosis I. It is highly condensed relative to the remainder of the genome, and is sufficiently compacted that tension at one sister kinetochore can be transmitted to the other sister, ∼1 µm away, through kilo-to-megabase pairs of DNA. Tension is monitored by surveillance pathways (known as checkpoints) at the kinetochore, but mechanical integrity between sister chromatids is critical for the fidelity of segregation and checkpoint signaling. Like the axis of mitotic mammalian chromosomes, the budding yeast pericentromere is comprised of radial loops emanating from a central scaffold that runs between sister kinetochores. This scaffold is proximal to the spindle axis in budding yeast and is enriched in condensin and cohesion, which function in tethering and confining the loops (Stephens et al., 2011, 2013). Based on the increased concentration of cohesin and condensin, the radial loops are three times more compacted in the centromere relative to the chromosome arms. Through motion analysis and visualization of conformational states, we demonstrate that the spatial arrangement of radial loops in the centromere can generate tension along the spindle axis. These studies reveal the physical basis for tension between sister chromatids, a conserved mechanism throughout eukaryotes.

Results

Pericentric chromatin motion is dominated by thermal and nondirected ATP-dependent motion, rather than microtubule-based events

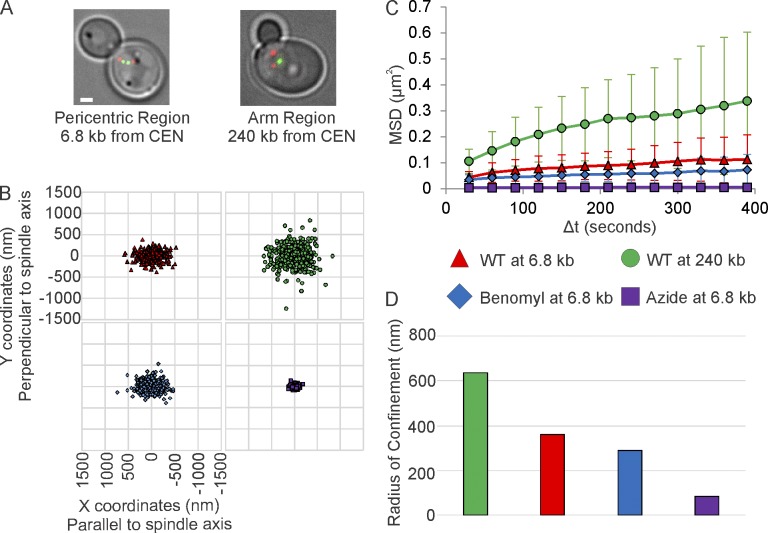
We tracked the motion of a 10-kb GFP-labeled chromatin array (lacO/LacI-GFP) relative to a Spc29-RFP–labeled spindle pole body (SPB) at two chromosomal loci during metaphase (Fig. 1 A). The array was placed at either the pericentric region (6.8 kb from CEN15, Cen-linked) or the arm region (240 kb from CEN2). Both of the arrays appear as nearly diffraction-limited spots. To quantify chromatin motion, we measured the DNA locus position over time. From these data, a radius of confinement (R_c) was estimated from the plateau value of mean square displacement (MSD) or mean positional variance (Verdaasdonk et al., 2013). The Cen-linked array was more confined than the arm region (Fig. 1 and Table 1; Verdaasdonk et al., 2013) and exhibited similar R_c values whether tethered to the spindle pole in G1 (before DNA replication and spindle formation) or after DNA replication and spindle formation in G2–M (R_c Cen-linked = 396 nm G1, 363 nm G2–M; R_c Arm = 705 nm G1, 609 nm G2–M; Table 1; Verdaasdonk et al., 2013). The variance in the X and Y position of LacI-GFP were similar for all arrays measured; however, when coordinates were rotated in relation to the spindle axis, physical constraints on the pericentric locus were evident in the scatter plots of position of LacI-GFP parallel or perpendicular to the spindle axis (Fig. 1 B). The variance, and thus the R_c, in pericentric position was greater parallel to the spindle axis (x-axis) than perpendicular to the axis (y-axis; Fig. 1 B and Table S1). The R_c in arm motion (240 kb) exhibited no directional constraint (Fig. 1 B and Table S1). The reduction in fluctuations of pericentric chromatin relative to arm loci is predicted from polymer models of dual-tethered bead springs (Verdaasdonk et al., 2013). The anisotropy in Cen-linked motion is indicative of radial compression relative to the mitotic spindle axis.

Figure 1.

Single-particle tracking of pericentric chromatin reveals fluctuations predicted from models of polymer chains tethered at both ends. (A) Representative images of metaphase yeast with a 10-kb lacO/LacI-GFP array at the pericentromere (6.8 kb) or chromosome arm (240 kb; green). Red, SPBs (pc29-RFP). Bar, 1 µm. (B) Scatter plots of 2D-position relative to the proximal SPB in untreated cells, cells treated with low-doses of benomyl, or with sodium azide + deoxy-glucose. The x-axis is set to the spindle axis. (C) MSD of arrays in untreated and drug-treated cells. Error bars are standard deviation. (D) Radii of confinement of untreated and drug-treated cells. Values were calculated from the entire population of data (B) from multiple experiments (WT at 6.8 kb, n = 41; WT at 240 kb, n = 40; Benomyl at 6.8 kb, n = 41; and Azide at 6.8 kb, n = 37). See Table 1 for alternative calculation methods for values with standard deviations. All values are significantly different (Levene’s Test, P < 0.05).

Table 1. Radii of confinement calculated for untreated and treated cells.

Metric	Equation	Calculation	LacO array distance from centromere
			240 kb untreated	240 kb azide	6.8 kb untreated	6.8 kb benomyl	6.8 kb azide
			Sample size (foci)
			40	41	41	41	37
Rc (nm)	$=\frac{5}{4}\mathrm{ }\times \sqrt{MS{D}_{plateau}}$	Plateau (individual cell)	664 ± 243	187 ± 68.3	388 ± 152	306 ± 118	89.6 ± 25.6
	$=\frac{5}{4}\mathrm{ }\times \sqrt{\mathrm{ }(2{\sigma }^2\mathrm{ }+\mathrm{ }\Delta r_0^2)}$	σ (individual cell)	593 ± 170	165 ± 56.7	350 ± 112	280 ± 84	84.0 ± 22.9
		σ (entire data set)	609	172	363	289	86
Effective spring constant (pN/nm)	$=\mathrm{ }\frac{2k_{b}T}{MS{D}_{plateau}-\mathrm{ }\Delta r_0^2}$	Plateau (individual cell)	9.4 × 10−5 ± 1.0 × 10−4	1.22 × 10−3 ± 1.7 × 10−3	2.4 × 10−4 ± 2.2 × 10−4	4.4 × 10−4 ± 3.9 × 10−4	4.0 × 10−3 ± 4.0 × 10−3
	$=\mathrm{ }\frac{k_{B}T}{{\sigma }^2}$	σ (individual cell)	9.1 × 10−5 ± 5.7 × 10−5	1.54 × 10−3 ± 1.8 × 10−3	2.9 × 10−4 ± 2.2 × 10−4	4.4 × 10−4 ± 3.4 × 10−4	4.7 × 10−3 ± 3.4 × 10−3
		σ (entire data set)	6.9 × 10−5	8.6 × 10−4	1.9 × 10−4	3.1 × 10−4	4.7 × 10−3

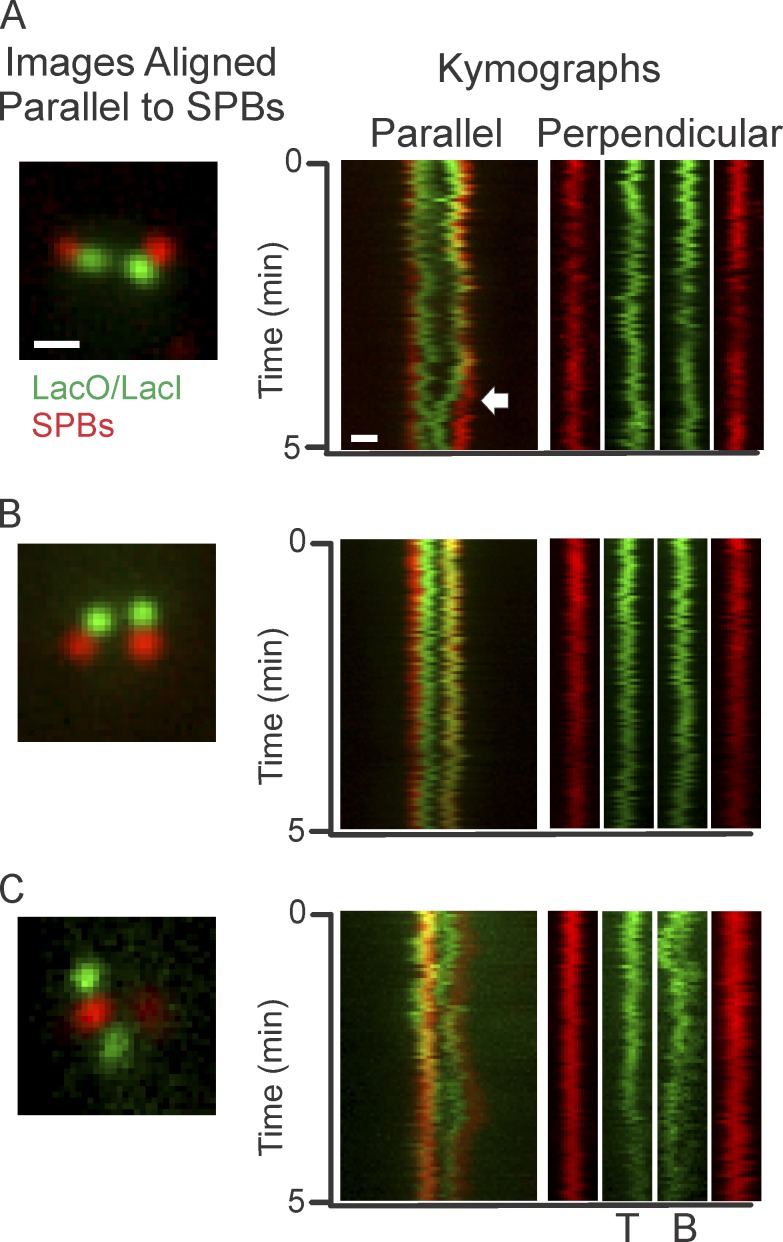
Microtubule dynamics could contribute to pericentric chromatin motion in two ways. One is through the random jostling of kinetochores that is propagated through the pericentric chromatin. The other is through persistent kinetochore microtubule (kMT) growth or shortening that would appear as directed motion. Suppression of microtubule dynamics with the drug benomyl (t_1/2 of tubulin turnover = 59 s [WT] vs. 259 s; Pearson et al., 2003) had little if any influence on Cen-linked motion (Fig. 1, benomyl). The spot motion remained anisotropic and R_c values were reduced from 363 nm (WT) to 289 nm (benomyl; Fig. 1, Table 1, and Table S1). The step size of benomyl-treated pericentric spots was reduced compared with untreated pericentric spots (156 ± 104 vs. 177 ± 110 nm, respectively), with the displacement parallel to the spindle axis more reduced than the displacement perpendicular to the spindle axis (Table S2). To illustrate directed DNA motion, kymographs were generated from time-lapse images of cells containing labeled pericentric chromatin (6.8 kb from CEN15) and SPBs. DNA foci undergo infrequent poleward or antipoleward excursions along the spindle axis (Fig. 2 A, middle). If these excursions are caused by kMTs, they should travel at rates similar to kMT dynamics, 17–25 nm/s (Gardner et al., 2005). To track chromatin motion, GFP foci and SPBs were tracked using Gaussian fitting (see Materials and methods). Defining an excursion as any event that persisted for 300, 350, or 400 nm at a rate of >10 nm/s, we found that directed events comprise 19–11% of pericentric chromatin motion parallel to the axis, and 4–1% of motion perpendicular to the axis (Table 2). Upon benomyl treatment, directed excursions were completely suppressed (Fig. 1 B and Table 2). Because benomyl results in Bub1-dependent phosphorylation of histone H2A (S121; Kawashima et al., 2010; Haase et al., 2012), we treated bub1Δ cells with benomyl. Directed motion was decreased, but not to the degree observed in benomyl-treated WT cells (Table S3). Alternatively, we suppressed microtubule dynamics by depleting protein levels of Stu2 via copper-inducible degradation of Stu2 (Stu2^CU; t_1/2 of tubulin turnover = 40 s WT vs. 233 s; Kosco et al., 2001; Pearson et al., 2003). Reducing Stu2p levels decreases directed motion but not to the extent of benomyl (see Materials and methods; Table S4). Thus, only a fraction of the directed events can be attributed to microtubule dynamics. These findings lend further support to the conclusion that the drivers of centromere chromatin fluctuations are not dominated by microtubule dynamics.

Figure 2.

Microtubule-dependent events contribute fractionally to off-axis fluctuations. (A, left) Image of metaphase yeast with pericentric chromatin (6.8 kb from CEN15) labeled in green and SPBs (Spc29-RFP) labeled in red. (middle) Corresponding kymographs of single-plane time-lapses of motion parallel to the spindle axis. (right) Kymograph of motion perpendicular to the spindle axis. Arrows indicate an excursion event. Left SPB is fixed in position. Bar, 0.5 µm. (B, left) Image of metaphase cells treated with low-concentrations of benomyl. (middle) Corresponding kymographs of single-plane time-lapses of motion parallel to the spindle axis. (right) Kymograph showing motion perpendicular to the spindle axis. Left SPB is fixed in position. (C, left) Image of cfb5-AUU mutant cells with a LacO/LacI-GFP array 12.5-kb from CEN11 and labeled SPBs (red). (middle) Kymographs of single-plane time-lapses of motion parallel to the spindle axis. (right) Kymograph of motion perpendicular to the spindle axis. T is the top GFP foci, B is the bottom GFP foci. The bottom GFP foci stretches, giving it an elongated appearance in the kymograph.

Table 2. Percent of directed motion of pericentric chromatin.

Minimum displacement	Untreated (n = 22 foci)			Benomyl (n = 16 foci)		kMT dynamics from mitotic simulationa
	Parallel	Perpendicular		Parallel	Perpendicular
nm
300	19%	4%		0%	0%	20%
350	16%	1%		0%	0%	14%
400	11%	0%		0%	0%	9%

^aSimulated kMT dynamics were generated using the default settings of a MATLAB Mitotic Spindle Simulation that incorporates kMT dynamics with a chromatin spring to recapitulate lacO fluctuation and stretching in WT and mutant cells (Stephens et al., 2013).

In addition to directed motion analysis, we measured the speed correlation index (SCI) to quantify the percent of directed motion (Fig. S1). SCI measures the trajectory of particle motion over time, the more constant the direction, the higher the SCI value. A particle traveling in one direction has an SCI value of 1. A particle traveling in the exact, opposite direction has an SCI value of −1 (Bouzigues and Dahan, 2007). Defining a directed event with an SCI score >0.5 that persisted for two to five consecutive windows (each window is the mean of four frames), we found that directed motion comprised 4–8% of pericentric chromatin motion. The directed events defined by both analyses are suppressed upon benomyl treatment (≤1% Table 2 benomyl; Fig. S1). Thus, 80–90% of pericentric chromatin motion in untreated cells is nondirected and exhibits a random trajectory.

Separated sister lacO arrays can lie perpendicular to the spindle axis (Snider et al., 2014; Fig. 2 C), indicative of nonmicrotubule-based force for centromere separation. Kymographs from these orientations reveal fluctuations similar to those observed in benomyl-treated samples (Fig. 1 C). Disruption of the kinetochore using a temperature-sensitive ndc10-2 mutation also leads to off-axis separated pericentric sister foci (LacO/LacI-GFP 1.7 kb from CEN11; Fig. S1 D). Thus, pericentric sister separation is not dependent on directed microtubule-based spindle force. The random motion is a consequence of Brownian motion (thermal fluctuations), nonthermal ATP-dependent events (WT vs. azide treatment, Fig. 1), and jostling caused by the stochastic dynamics of the microtubule plus-ends (benomyl; Fig. 1 and Fig. S1).

Pericentric chromatin is subject to higher tension proximal to the spindle axis

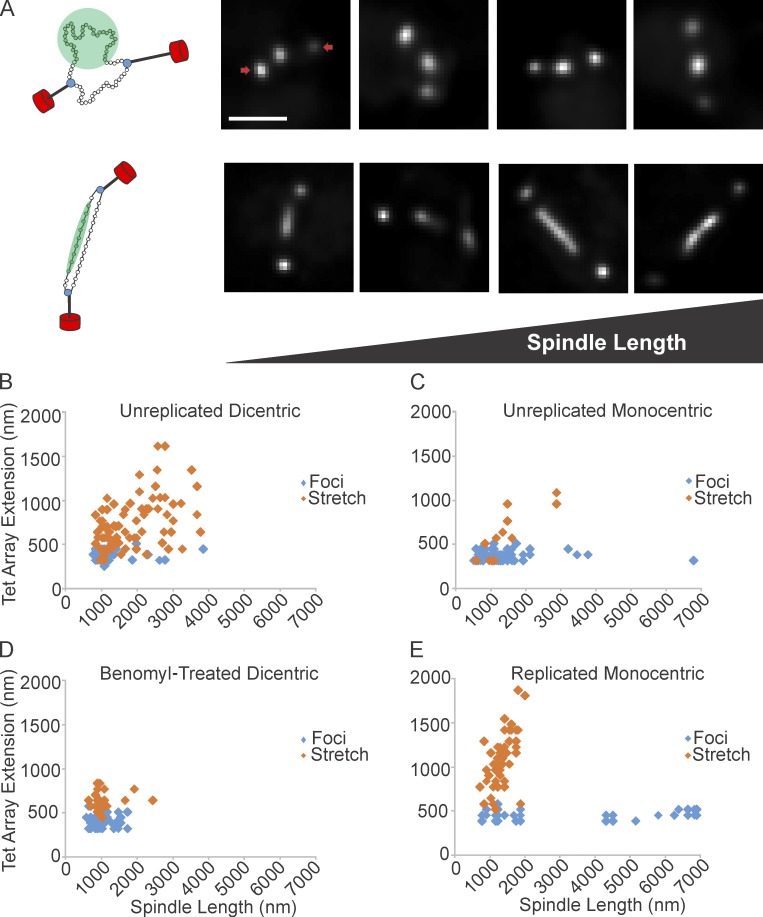
During metaphase LacO signals in pericentric chromatin occupy two distinct areas throughout the spindle. The majority of LacO signals (90%) appear as near-diffraction spots and are radially displaced from the spindle axis, whereas the elongated filaments reside closer to the axis. Foci that are stretching will move closer to the spindle axis, and a filament compacting into a focus will move away from the spindle axis (Stephens et al., 2011, 2013). To characterize the force along the axis, we used a conditionally functional dicentric plasmid with an excisable origin of replication (Dewar et al., 2004). Growth in the appropriate media prevents DNA replication and activates the conditional centromere. Each centromere independently attaches to kMTs and the unreplicated plasmid bi-orients on the mitotic spindle. The DNA is visualized via TetR-GFP bound to a tandem tetO operator DNA array (5.5 kb tetO/7 kb total, 1.8 µm B-form length, 260-nm nucleosome fiber) between the two centromeres. Elongation was defined as an increase in the ratio of the axes of a distribution of the TetR-GFP signal (parallel 1.2× > perpendicular). The short span of DNA between the two centromeres reduces the potential for DNA looping, predisposing the DNA toward the spindle axis. Images of foci and stretching events are shown in Fig. 3 A. As with endogenous chromosomes, TetR-GFP signals from dicentric plasmids that are elongated lie closer to the spindle axis than signals that appear as foci (Fig. S2). The dicentric plasmid was elongated in ∼45% of cells (1.0–1.5 µm spindle length; Table 3) versus 10% for chromosomal spots (Stephens et al., 2011). As the spindles elongate, more frequent and greater extensions of plasmid DNA are observed (Fig. 3 B; ∼86%, >2 µm spindles). The mean dicentric chromatin extension in metaphase (1.0–2.0 µm spindle length) was ∼630 nm. This corresponds to the release/unwrapping of ∼6 nucleosomes (for loss of 6 nucleosomes, 320 nm of 11-nm fiber + 320 nm of 2-nm fiber = 640 nm).

Figure 3.

Tension along the spindle axis is sufficient to release nucleosomes. (A, left) Schematic of dicentric plasmid. The plasmid is attached to kMTs (black) via the kinetochore (blue). Nucleosomes are green, SPBs are red. The DNA appears as a near-diffraction spot (green circle, top) or a filament (green bar, below). Right four panels show deconvolved images of near-diffraction foci (top) and filaments (bottom) of dicentric plasmids. SPBs are indicated by arrows. (B) TetO/TetR-GFP extension vs. spindle length for unreplicated dicentric (n = 129 arrays). (C) Unreplicated monocentric plasmids (n = 102 arrays). (D) Benomyl-treated dicentric plasmids (n = 92 arrays). (E) Replicated monocentric plasmids (n = 94 arrays). Scatter plots display population data from multiple experiments. Bar, 1 µm.

Table 3. Frequency and magnitude of elongated TetR-GFP signals.

Spindle length	Unreplicated dicentric plasmid (n = 129)				Unreplicated monocentric plasmid (n = 102)				Unreplicated benomyl, dicentric plasmid (n = 92)				Replicated monocentric plasmid (n = 94)
	n	Stretch frequency	Stretch length		n	Stretch frequency	Stretch length		n	Stretch frequency	Stretch length		n	Stretch frequency	Stretch length
µm		%	nm			%	nm			%	nm			%	nm
0.5–1.0	20	35	587 ± 165		27	11	384 ± 91		47	28	645 ± 105		11	55	892 ± 215
1.0–1.5	60	45	634 ± 171		49	10	653 ± 212		38	16	597 ± 95		46	72	1,000 ± 237
1.5–2.0	14	65	648 ± 185		18	6	576		7	29	704 ± 64		20	75	1,342 ± 292
>2.0	35	86	1,252 ± 378		8	25	1,024 ± 64		NA	NA	NA		17	0	NA

The force for generating tension between sister centromeres has been attributed to the shortening of kMTs. An alternative hypothesis is that thermal fluctuations of the pericentric loops observed as radially displaced foci (Fig. 1), anchored by condensin along the central spindle can generate an outward/poleward force (Panyukov et al., 2009a). This tension force would be generated via fluctuations of chromatin loops that repel one another as a consequence of their crowding (Panyukov et al., 2009a,b). The repulsion of the loops is balanced by the inward/antipoleward entropic spring force of the chromatin along the primary axis. The extension of the chromatin along the primary axis is an entropically disfavored state, resulting in a net inward force seeking to collapse the chromatin into a random coil. In vivo, the balance of the loop’s outward repulsive force and the primary axis’s inward spring force generates the tension between sister centromeres. To distinguish microtubule shortening from crowding-based extension, microtubule dynamics were suppressed with benomyl and the length of the TetR-GFP signal of the dicentric plasmid along the primary axis was quantitated. The fraction of stretched (parallel 1.2× > perpendicular) chromatin is largely insensitive to benomyl treatment in cells with short spindles (percent stretched ± benomyl; Fig. 3, B and D; 35 vs. 28% stretched in spindles, 0.5–1.0 µm; Table 3). Likewise, chromatin stretch length is insensitive to spindle length up to 2.0 µm (chromatin stretch length: WT, 630 nm; benomyl, 637 nm; binning, 0.5–2.0-µm spindles; Table 3). Thus, dynamic microtubules are not required for chromatin extension. Repulsion between pericentric loops can generate sufficient force to release or unwrap several nucleosomes.

Spindle length is dependent on microtubule dynamics and growth, and lengths much beyond 2 µm in metaphase are not observed in benomyl-treated cells. Likewise, the fraction of stretched dicentric chromatin fibers is reduced upon benomyl treatment, 45–16% in spindles 1–1.5 µm in length, and 65–29% in 1.5–2.0-µm-long spindles (Fig. 3 E and Table 3). The fraction and magnitude of chromatin stretching is microtubule-independent on length scales <1 µm, but microtubule-dependent in spindles >1 µm. The limited length scale of repulsive forces is consistent with the short length scales of polymer crowding models for generating extensional forces (Bloom, 2014).

Extended chromatin promotes tension-based kMT rescue

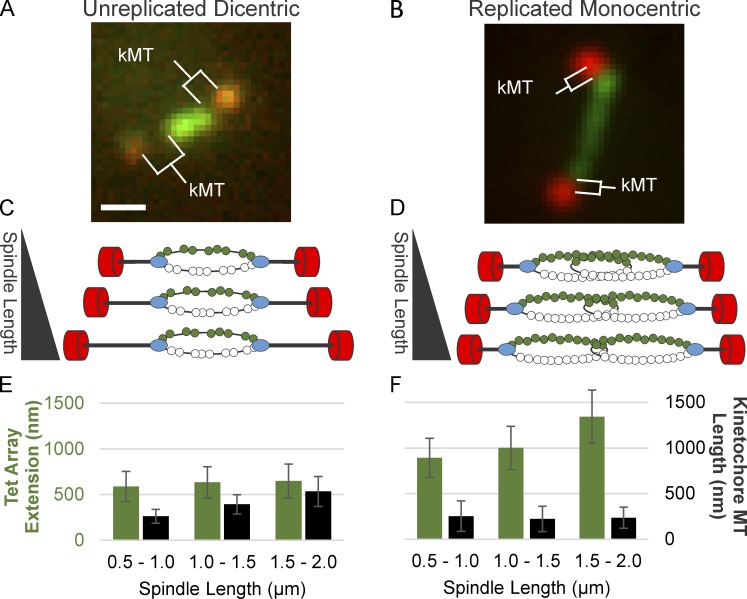
Chromatin forces along the spindle axis will be transmitted through the kinetochore to the attached microtubule. The dicentric plasmid provides a unique opportunity to correlate chromatin extension with kMT length. 80% of DNA between the two centromeres (5.5 and 7 kb) is labeled with TetR. When the plasmid is extended along the spindle axis, the distance between the Tet array and the SPB provides an estimate of kMT length (Fig. 4, A–D). In cells containing the unreplicated dicentric plasmid, chromatin extension is constant, whereas kMTs lengthen as a function of spindle length (Fig. 4, A, C, and E). In cells where a monocentric plasmid (pT323), the parent plasmid of the dicentric (pT431; Dewar et al., 2004), has replicated, chromatin extension increases, whereas kMT length is constant as a function of spindle length (Fig. 4, B, D, and F). Thus, the more compact the DNA (e.g., looped), the more tension is exerted at the microtubule plus-end, promoting the growth state. In contrast, if there is sufficient DNA extension (two times the DNA length in a replicated plasmid), less tension is exerted at the microtubule plus-end, and the microtubules shorten. These results highlight the interplay between chromatin length and kMT state. Kinetochore dynamics are not the sole drivers of tension; rather, the chromatin and its length regulation can dictate microtubule dynamics. Limiting DNA length in the unreplicated plasmid keeps tension constant and at a level sufficient to drive kMT growth (Fig. 4).

Figure 4.

Tension along the spindle axis promotes microtubule growth. TetO array extension and kMT length in unreplicated, dicentric plasmids versus replicated, monocentric plasmids. Image of metaphase yeast containing an unreplicated, dicentric plasmid (A) and a replicated, monocentric plasmid (B). Schematic of a spindle containing an unreplicated, dicentric plasmid (C) and a replicated, monocentric plasmid (D). SPBs are shown in red, kinetochores are shown in blue, and DNA is shown in green. Tet array extension and kMT length versus spindle length for unreplicated, dicentric plasmids (E) and for replicated, monocentric plasmids (F). Bar, 0.5 µm. Error bars are standard deviation. The data shown are from multiple experiments (dicentric, n = 43 arrays; replicated monocentric, n = 54).

Increased tension on chromatin proximal to versus displaced from the spindle axis

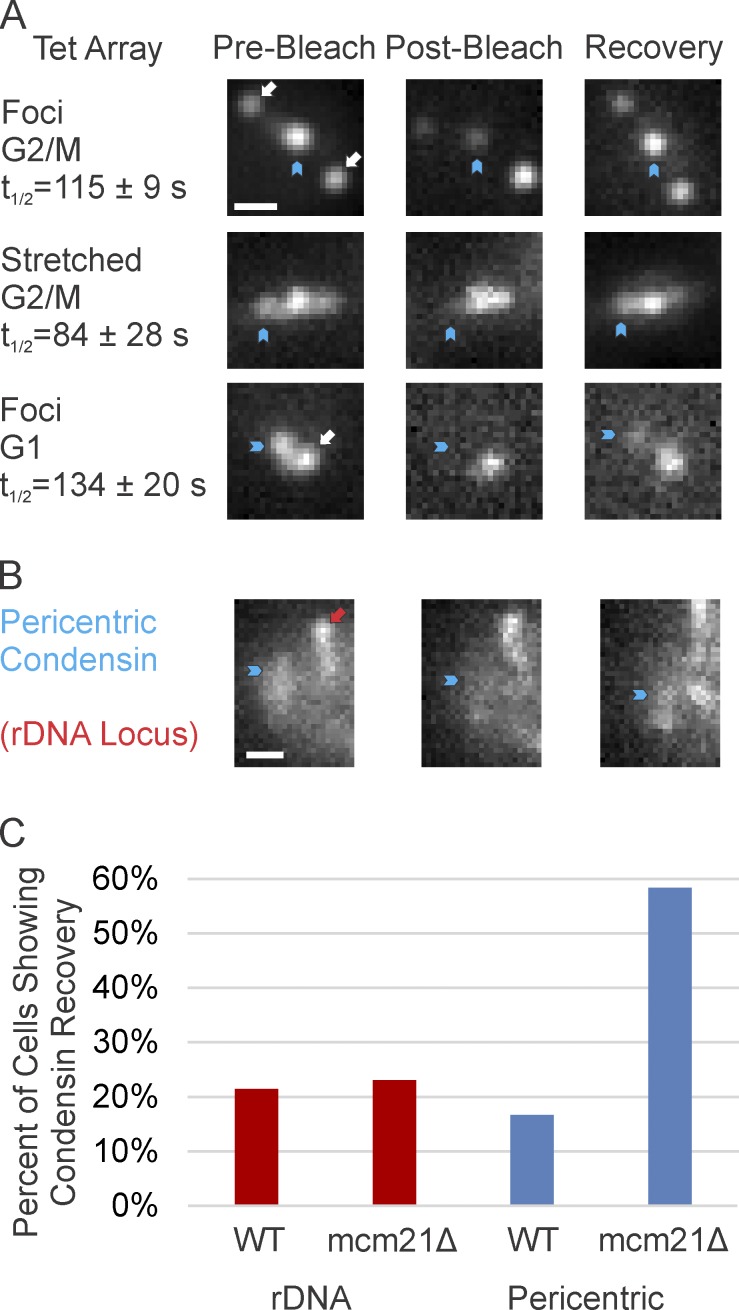
An alternative approach to demonstrate multiple tension regimes in the pericentric chromatin is the ability to measure turnover of the DNA-binding proteins. Mechanical tension can reduce t_1/2 of DNA factor binding (Blumberg et al., 2005), and disrupt nucleosomes in vitro (Brower-Toland et al., 2002) and in vivo (Fig. 3; Thrower and Bloom, 2001). We determined the t_1/2 of TetR-GFP bound to tetO using FRAP (Fig. 5 A). The t_1/2 of TetR-GFP bound to the tetO array in the compact loop configuration was 115 ± 9 s in G2–M cells. TetR-GFP binding to stretched dicentric plasmids was more rapidly exchanged, with a t_1/2 of 84 ± 28 s (P = 0.01, compared with G2–M foci). The t_1/2 was 134 ± 20 s for cells in G1 in cases where the dicentric chromosome is attached but under no tension (Fig. 5 A).

Figure 5.

Higher DNA binding protein turnover proximal to the spindle axis. FRAP analysis of TetR-GFP and condensin. (A) Representative images of dicentric plasmids pre, post, and 2–4 min after photobleaching. Blue arrowhead marks the bleached TetR-GFP spot. SPBs are indicated by white arrows. Bar, 0.5 µm. (B) Images of condensin pre, post, and 5 min after photobleaching. Blue arrowhead indicates the bleached condensin bound to pericentric DNA. Red arrow indicates condensin bound to the rDNA locus. Only pericentric condensin was bleached in the cell shown. Bar, 0.5 µm. (C) The percentage of cells showing recovery of condensin bound to the pericentric and rDNA loci in WT and mcm21Δ cells 10 min after bleaching. Recovery threshold is 30% of the original corrected signal. Each dataset summarizes multiple experiments (WT rDNA, n = 14; mcm21Δ, n = 13; WT pericentric, n = 12; mcm21Δ pericentric, n = 12 cells).

During metaphase, pericentric condensin is enriched along the spindle axis, whereas pericentric cohesin is radially displaced from the spindle axis (Yeh et al., 2008; Stephens et al., 2011). Pericentric cohesin shows little recovery after photobleaching (Yeh et al., 2008). Condensin showed ≥30% recovery after photobleaching in ∼20% WT cells at the pericentric and rDNA loci (Fig. 5, B and C). Yeast lacking Mcm21 have decreased levels of pericentric cohesin, which results in increased extension of pericentric chromatin (Stephens et al., 2011). In mcm21Δ mutants, condensin showed ≥30% recovery in ∼60% of cells at the pericentric locus and ∼20% at the rDNA locus. Thus, chromatin extension results in an increased turnover rate of DNA-binding proteins, which is indicative of an increase in tension proximal to the spindle axis.

Discussion

The dynamics and configurational state of pericentric chromatin leads to a fundamental new model for the function of a eukaryotic centromere. Centromere-proximal DNA loops ∼10 kb in length are bound by condensin at their base (Snider et al., 2014) and extend radially from the spindle axis in metaphase (Fig. 6 A; Stephens et al., 2011, 2013). Visualization of pericentric DNA loops via TetR-GFP bound to TetO array reveals random fluctuations that explore an area larger than expected from thermal force, but consistent with energy from randomly directed, nonthermal, ATP-dependent sources. Using benomyl treatment and Stu2 depletion to dampen microtubule dynamics, we show that only a fraction of motion (<20%) can be attributed to microtubule-based directional force. The DNA loops fluctuate into random coils and are constantly being jostled by neighboring loops. In three dimensions, this means that sister chromatids are not constrained to a linear position between sister kinetochores. The appearance of sister chromatids perpendicular to the spindle axis have been reported in the literature and constitute 30% of the configurational states upon depletion of condensin (Figs. 2 C and 6 C; Snider et al., 2014). The motion analysis of the loops reveals two important features. The perpendicular foci exhibit virtually no directed motion, which is expected if they remain constrained at their bases and extended from the axis. Second, the foci move independently, each loop moving around the axis. Protein turnover is slower on these off-axis loci, consistent with a more relaxed configurational state (Fig. 5).

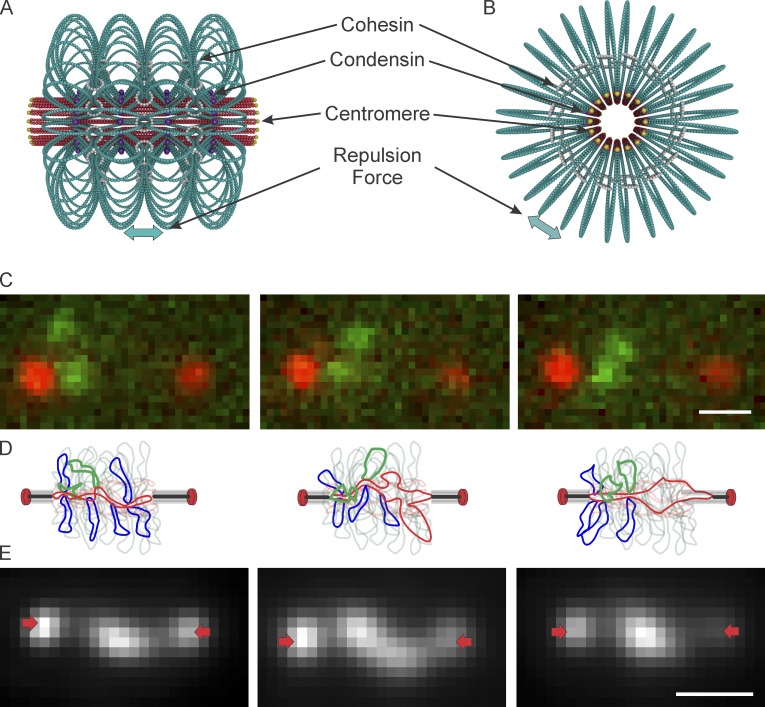
Figure 6.

Mechanistic basis for extensional forces from packed centromere DNA loops. (A) Model of pericentric chromatin in budding yeast. The pericentric chromatin from all 16 chromosomes is shown. 50 kb of DNA (red and teal) surround the centromeres, shown at the apex of a DNA loop (centromere DNA in yellow, DNA primary axis in red) and form a cylinder around the spindle microtubules (not depicted). Sister centromeres are at opposite ends of the cylinder. DNA loops (teal) are formed via the action of condensin (purple) binding to the base of loops. The number of loops and their geometric arrangement are based on experimental evidence from the spatial segregation of condensin, cohesin, and LacO DNA arrays. The loops repel each other, resulting in a net outward/poleward force. Cohesin rings are depicted in white. (B) End-on view of the model. (C) Time-lapse of pericentric LacO arrays in cbf5-AUU mutant yeast during metaphase. (D) Schematic of sister chromatid loop fluctuations (in green) over time. SPBs (red ovals), lines are kMTs. Chromatin proximal to the spindle axis is indicated as the red line, loops extending off axis are indicated in blue. The green loops depict the labeled chromatin in C. Microtubule shortening will release condensin bound at the base of a loop as the DNA transits from a radial to an axial position (panels should be read left to right). The release of a loop results in a precipitous drop in tension as a result of increased DNA length along the axis. As the microtubule shortens, DNA (red) elongates along the spindle axis, until it reaches equilibrium and greater force is required to further stretch the fiber. This leads to tension-dependent microtubule rescue, allowing the DNA to recoil and adopt a random coil. DNA fluctuation off the spindle axis allows condensin binding and loop formation (panels should be read right to left). (E) Time-lapse of TetO/TetR-GFP labeled, dicentric plasmid. These plasmids lie along the primary axis, where tension force is sufficient to extend the chromatin beyond its nucleosomal length. SPBs are indicated with arrows (red). Bar, 0.5 µm.

In WT cells, the loops undergo a configurational state change from a larger than diffraction spot to an extended filament that is aligned with the spindle axis (Fig. 3 and Fig. S2; Stephens et al., 2011). Chromatin extension provides a quantitative measure of nucleosome occupancy where the two ends of DNA are accounted for in vitro. For the in vivo measurement, two centromeres on the same dicentric molecule are attached to microtubules and the intervening DNA visualized by TetR-GFP bound to the intervening tetO array. Unlike the radial displaced spots, chromatin on the spindle axis appeared to be highly extended, well beyond nucleosome packing. On average, six nucleosomes were released (out of 35 total, 5.5 kb/160 bp) on chromatin proximal to the spindle axis during metaphase (spindle length 1.0–2.0 µm). The estimates of the force threshold for nucleosome release range from 3–5 pN in the presence of cell extract to 20 pN in the absence of cell extract (Brower-Toland et al., 2002; Yan et al., 2007). Nucleosomes for biophysical studies are often assembled on DNA that has been selected for strong nucleosome positioning. The advantage for the in vitro experiment is in knowing the number of nucleosomes with some certainty. Nucleosomes are assembled on lacO arrays introduced into yeast (Thrower and Bloom, 2001), but they are not positioned with respect to sequence, and are not likely bound with the same affinity relative to the 601-bp sequence used in in vitro experiments (Lowary and Widom, 1998). However, the conformational state and the release of nucleosomes are indicative of higher tension relative to adjacent off-axis chromatin. The increased turnover of DNA-binding proteins is an independent indicator that the extended chromatin is subject to higher tension (Fig. 5). These strands along the axis are not rigid, as indicated by the change in angular distribution relative to the spindle axis (Fig. S3). Thus, extended fibers are still subject the random jostling and pushing from the close packing of neighboring strands.

A unique feature of the dicentric plasmid is that almost all of the DNA between sister centromeres is bound by TetR-GFP (Fig. 4). Consequently, we are able to track the growth and shortening of a single kMT in a living cell. As the spindle elongates, the kMT grows without further extension of chromatin (Fig. 4 A). Microtubules are dynamically unstable, and tension at the plus-end rescues them from the shortening state and promotes polymer growth. The extended chromatin spring of the single dicentric plasmid is stiff enough to promote microtubule growth. It is noteworthy that the chromatin does not continue to extend upon spindle growth during metaphase. In late anaphase, we have demonstrated that the DNA can extend to its B-form length (1 µm/3.3 kb; Thrower and Bloom, 2001). Thus, there is no physical constraint to extension beyond the loss of 6–8 nucleosomes out of 35 upon anaphase onset. The loop organization is dynamic, and chromatin can flow toward the spindle as evidenced in the replicated plasmid situation (Fig. 4 B). In this case, the two centromeres are on individual molecules, and as the spindle elongates, the amount of DNA proximal to the spindle increases based on length of the tet array (Fig. 4 B). The constraint on extension of the dicentric plasmid most likely reflects the force balance between the chromatin spring and microtubule-based extensional forces. The unfolding of chromatin beyond the nucleosome length reaches an equilibrium state where ∼50% of the length is nucleosomal (29 nucleosomes × 11 nm = ∼320 nm) and ∼50% is B-form length DNA (release of 6 nucleosomes [160 bp] × 6 × 0.33 = 320 nm).

The chromatin spring is not completely dependent on microtubules, based on the properties of the extension observed in the presence of benomyl (Fig. 3 and Table 3) and the separation of pericentric chromatin in a kinetochore-disrupted, ndc10-2 mutant at restrictive temperature (Fig. S1 D). Rather, it is interactive with the microtubules as a result of the physical effects of the chromatin loops attached to the primary axis. The remarkable feature of the centromere is that it resembles a particular type of branched polymer called a bottle brush (Fig. 6 A) based on the heterogeneity of stress distribution within the centromere. Tension is generated along the primary brush axis (known as tension amplification) created by the collective effect of steric repulsion of the side chains resisting the inward/antipoleward spring force of the primary axis seeking to collapse into a random coil. The individual side chains themselves are shielded from this tension and fluctuate thermally (Panyukov et al., 2009a). The extensional force of radial loops on the primary axis explains how sister chromatids could be held apart in the absence of spindle-based force in the ndc10-2 mutants where the kinetochores have been compromised (Fig. S1 D). Unlike a simple bottle brush polymer, the centromere can alter the density of side-loops of chromatin through loop popping and reforming, consistent with the presence of chromatin remodeling factors such as RSC and SWI/SNF at the centromere (Xue et al., 2000; Hsu et al., 2003; Fig. 6 D). The dynamic nature of the chromatin loops allows the centromere to act as a molecular shock-absorber. A stationary bottle brush polymer will have an equilibrium configuration when all forces are balanced. However, the centromere is nonstationary with active, stochastic forces acting along the primary axis from microtubule dynamics. This creates a variation in force balance in which the primary axis of pericentric chromatin is occasionally under an enhanced tensional load because of microtubule shortening. The tensile load is initially relieved when a loop pops, effectively lengthening the primary axis while decreasing the side loop density. The newfound slack in the primary allows microtubule shrinkage to occur. Once the microtubule grows again, the slack can be taken up by a chromatin loop reforming. This coupling of structure and force conspires to maintain a dynamic tensile balance within the chromatin during mitosis. The centromere is thus a molecular shock absorber that can modulate its length and stiffness to buffer the stochastic effects of microtubule dynamics.

Materials and methods

Strain and construct information

The detailed genotypes and mutations of each strain are listed in Table 4. For KS406 and KBY8065, the lac operon arrays (Straight et al., 1996) were targeted adjacent to the Rad16 promoter (467,248, Chromosome 2; Lobachev et al., 2004) and ∼1 kb to the left of CEN15 (325,382–326,687; Goshima and Yanagida, 2000), respectively. For KBY2157 and Y589 (Stu2^CU), the lac operon array was targeted to the MET14 locus (438,816–439,365) using PCR fragments from pLKL60Y, which contains a 32mer (1.2-kb in length) of the lac operator with a G418 resistance marker (Pearson et al., 2001). For KBY9533.1, the pLKL60Y-derived lac operon array was targeted to 12.7 kb from CENXI (440,246–440,129; Pearson et al., 2001). The LacI-GFP used to visualize the lac operators is a fusion protein of GFP, a truncation of the LacI gene lacking the final 11 C-terminal amino acids to prevent tetramerization, and a nuclear localization signal (NLS; Straight et al., 1996).

Table 4. Strain number and genotypes of yeast strains.

Strain number	Genotype
KS406	MATα CEN2(240kb)-GFP[10kb] ade5-1, trp1-289, ura3Δ, leu2-3, 112, lys2::insI-Sce1, lacO array next to RAD16 promoter, tetO array next to LYS2 promoter, arg4::hisG Gal1/10 I-Sce1, thr1::HISpLacI-GFP:Nat, ade1::URAptetR-CFP:Hyg, Spc29-RFP:Bsd
KBY8065	MATa CEN15(1.8)-GFP[10kb] ade2-1, his3-11, trp1-1, ura3-1, leu2-3,112, can1-100, LacINLSGFP:HIS3, lacO::URA3, Spc29-RFP:Hyg
T3000	W303 MATa; (T2726 carrying pT431-URA3 (2xCEN, 2xRS)) trp1::MET-Recombinase::TRP leu2::TetR-GFP::LEU2 spc42::Spc42-YFP:HIS3
T2755	W303 MATa, (T2726 carrying pT323-URA3 (1xCEN, 2XRS)) trp1::MET-Recombinase::TRP leu2::LEU2::tetR-GFP spc42::Spc42-YFP::HIS3
JLY1018.1	W303 MATa, (T2726 carrying pT323-URA3 (1xCEN, 2XRS)) trp1::MET-Recombinase::TRP leu2::LEU2::tetR-GFP spc42::Spc42-RFP:kan
KBY9533.1	MATa ade1 met14 ura3-52 leu2-3,112 lys2Δ::lacI-GFP-NLS-NATr his3-11,15 12.5 kb XI::lacO-KANMX NatΔ::His3MX6, Spc29-RFP-Hb, cbf5-AUU-Nat
KBY2157	MATa his3-delta200, leu2-3,112 ura3-52 Gal+, ndc10-2, met14::lacO:KAN, lys2::lacI:GFP:NAT, Spc29-CFP::Hb
MAY8602	MATa LacINLSGFP:HIS3 lacO::URA3(1.8kb from CEN15) Spc29RFP:Hb uraΔ:TRP bub1Δ:URA
Y589 (Stu2CU)	MATa Ace1-UBR1 Ace1-ROX trp1-D1 ade2-101 ura3-52 lys2-801 stu2-D::URA3::pAnb1UB-R-STU2 lacO32::KANr::met14 LacI-GFP-NAT
KBY9035.1	(YEF 473a) Smc4-GFP-Kan, Spc29-RFP-Hb
KBY9097.1	(YEF 473a) Smc4-GFP-Kan, Spc29-RFP-Hb, mcm21D-Nat

T2755, JLY1018.1, and T3000 were derived from yeast strain T2726, a derivative of the W303 yeast strain containing a Zygosaccharomyces rouxii R recombinase gene under the control of the MET3 promoter, a TetR-GFP-NLS under the URA3 promoter (Michaelis et al., 1997), and SPC42-YFP C-terminal fusion protein (He et al., 2000). JLY1018.1 was derived from T2755 by swapping the SPC42-YFP for a SPC42-RFP:KAN using chimeric PCR primers with homology to SPC42 and pKS390 (pFA6a-mCherry-kanMX6; Wach et al., 1997). The monocentric plasmid pT323 was made by inserting two recombination sites, from pHM401 (Araki et al., 1992), using XhoI and HindIII cut sites, and a tet operon array (112 repeats) into a BamHI cut site of YCp50 (available from GenBank under accession no. X70276; Tanaka et al., 2002). The dicentric plasmid pT431 was made by cloning a fragment of CEN4 (730-bp DNA containing CDEI-II-III) under control of the GAL1-10 promoter into pT323 (Dewar et al., 2004).

Y589 (Stu2^CU) was derived from a strain that, upon the addition of copper (CuS0₄), undergoes simultaneous repression of STU2 mRNA synthesis and degradation of Stu2 (Kosco et al., 2001). KBY2157 was derived from a strain containing an ndc10-2 mutation (Kopski and Huffaker, 1997). For cbf5-AUU, the AUG start codon was mutated to AUU (Kendall et al., 2000; Snider et al., 2014). SMC3-GFP and SPC29-RFP are C-terminal fusions of Smc4 to GFP and Spc29 to RFP, respectively (Stephens et al., 2011). The mcm21, ura3, and nat gene deletions were performed using chimeric PCR primers with homology upstream and downstream of the gene to be deleted and the pFA6a plasmid series (Wach et al., 1997). Bub1 was deleted by transforming with the pTR92 plasmid (Roberts et al., 1994).

Cell preparations and drug treatments

Cell strains KBY2157, KBY8065, KS406, KBY9035.1, KBY9097.1, KBY9533.1, MAY8602, and Y589 (Stu2^CU) were grown to logarithmic phase at 24°C in rich YPD media with 0.5 mg additional adenine per ml of media. Strain KBY2157 (ndc10-2 temperature-sensitive mutation) was shifted to 37°C in SD^-–HIS media at least 4 h before imaging. Cells containing the dicentric (T3000) or monocentric (T2755) plasmids were grown to logarithmic phase at 24°C in YCAT-galactose media, with 0.5 mg of additional adenine and methionine per ml of media. 4 h before imaging, cells were washed with ddH₂O and resuspended in SG (synthetic-containing galactose) media lacking methionine to induce loss of the origin of replication, as previously described by Dewar et al. (2004). 20 min before imaging, cells were resuspended in YPD at 24°C to repress transcription from the GAL1 promoter and activate the conditional centromere (Dewar et al., 2004). Before imaging, the replicated monocentric plasmid, strain JLY1018.1 was grown to logarithmic phase at 24°C in YCAT-glucose media with 0.5 mg additional adenine per ml of media. For benomyl treatment, a 10 mg/ml stock of benomyl was added directly to growth media so that the final concentration was 55 or 85 µM. For strains KBY8065, KS406, and Y589 (Stu2^CU), cells were incubated with benomyl for 1 h before imaging. For strains T3000 and T2755, cells were incubated with benomyl for at least 30 min during their YPD incubation. For ATP depletion, sodium azide and deoxy-glucose were added to YC-complete lacking sugar, with 0.5 mg additional adenine per ml of media to a final concentration of 0.02% and 1 µM, respectively. Cells were washed and resuspended in YC-complete, sodium azide, deoxy-glucose media and incubated at 24°C for 20 min before imaging. To deplete Stu2p in Y589 (Stu2^CU) cells, cupric sulfate (CuS0₄) was added to growth media to a final concentration of 500 µM for 4 h before imaging, as previously described in Kosco et al. (2001). All cells were imaged in media with the final concentration of drug added.

Microscopy

Population images of JLY1018.1- and 10-min time-lapse images for MSD and variance analysis for strains KBY8065 and KS406 were acquired every 30 s at room temperature (25°C) using an Eclipse Ti wide-field inverted microscope (Nikon) with a 100× Apo TIRF 1.49 NA objective (Nikon) and Clara charge-coupled device camera (Andor) using Nikon NIS Elements imaging software (Nikon). Time-lapse stacks contained 7 z-plane sections with 400 nm step-sizes. 5-min time-lapse images for kymographs, directed motion analysis, and SCI analysis were acquired every 3–4 s using the same imaging setup as described in the previous section for KBY8065, KBY9533.1, Y589 (Stu2^CU), and MAY8602. Images of T3000, T2755, KBY9533.1, and KBY2157 were acquired at room temperature (25°C) using an Eclipse E600FN microscope (Nikon) with a 100× Plan Apo TIRF 1.45 NA objective (Nikon) and ImagEM EM-CCD digital camera (Hamamatsu) with a custom Lumencor LED illumination system (Lumencor Inc.) using MetaMorph 7.7 imaging software (Molecular Devices). Single stacks contained 7 Z-planes sections with 300 nm step-size. Population images of KBY9533.1 images were taken on an inverted, widefield microscope (Eclipse TE2000-U; Nikon) with a 100× Plan Apo 1.4 NA digital interference contrast oil emersion lens with an Orca ER camera (Hamamatsu) using MetaMorph 6.1 software at room temperature (25°C). All strains were imaged in YC complete media with 2% filter sterile glucose added, except for condensin containing strains (KBY9035.1 and KBY9097.1), which were imaged with YC complete media lacking glucose.

Radii of confinement

All LacO/LacI-GFP and SPB foci were tracked using the Speckle Tracker program in MATLAB (The Mathworks; Wan et al., 2009, 2012). Speckle Tracker is a graphical user interface that detects GFP and RFP foci in a digital image file, tracks the foci through the time-lapse images, determines the centroids of the signals by fitting a 2D Gaussian function to a 5 × 5 pixel region using MATLAB’s nonlinear curve-fitting methods (lsqcurvfit), and exports the subpixel x and y coordinates to an Excel (Microsoft) spreadsheet. Radii of confinement and effective spring constants in Fig. 1 and Table I were calculated as described in Verdaasdonk et al. (2013) before coordinate rotation. A custom PERL script was used to parse the coordinates generated by Speckle Tracker, convert the coordinates from pixels to nanometers, subtract the coordinates of the proximal pole from the lacO/LacI-GFP coordinates, subtract the mean position of the resulting lacO/LacI-GFP coordinates, calculate the MSD of each time-lapse, and export the MSDs and coordinates to Excel spreadsheets. Radii of confinement using MSD curve plateau values were calculated using$R_c=\frac{5}{4} \times \sqrt{MS{D}_{plateau}}$, where MSD_plateau is the mean plateau value (calculated manually in Excelby averaging the MSD values at time steps 330, 360, and 390 s) of the MSD curves generated by the PERL program. Effect spring constants using MSD curve plateau values were calculated automatically using a custom MATLAB program using the equation$k_s= \frac{2k_{b}T}{MS{D}_{plateau}- \Delta r_0^2}$, where k_b is the Boltzmann constant, T is temperature (Kelvin), and MSD_plateau is the mean plateau value. Radii of confinement using positional variance σ² were calculated using$R_c=\frac{5}{4} \times \sqrt{ (2{\sigma }^2 + \Delta r_0^2)}$, where σ² is the variance of the distribution of foci positions calculated by${\sigma }^2=mean({\sigma }_x^2, {\sigma }_y^2)$. The variance in x and y are calculated by fitting the pole and mean subtracted coordinates generated by the PERL script to a normal distribution using MATLAB’s normfit function. The mean squared deviation from the mean position, $\langle \Delta r_0^2\rangle$, is calculated by $\Delta r_0^2=\Delta x_0^2+\Delta y_0^2$. Effective spring constants were calculated using$k_s= \frac{k_{B}T}{{\sigma }^2}$, where k is the Boltzmann constant, T is temperature (Kelvin), and σ² is the variance of the distribution of foci positions. For variance-based (σ²) equations, both the population distribution and the mean individual cell distributions were calculated for comparison. Population variance based equations were calculated manually in MATLAB, whereas individual R_c and K_s values were calculated by a custom MATLAB script. Radii of confinement and spring constants calculated by population variance were compared using Levene’s Test in MATLAB. The coordinates of LacI-GFP were rotated to set the spindle axis to the x-axis using a custom MATLAB program. One-dimensional R_c values were calculated from rotated coordinates using $R_c=\frac{5}{2}\times \sqrt{{\sigma }^2+ \Delta r_0^2}$, where ${\sigma }^2$ is the variance of the distribution of positions in one dimension and $\langle \Delta r_0^2\rangle$ is the mean squared deviation from the mean position.

Kymograph, direction motion, and SCI analysis

Kymographs were generating using MetaMorph 7.7 software without background subtraction using the maximum intensity setting from single-plane time-lapses. Kymograph showing parallel motion captured both GFP/RFP foci in a single kymograph. Kymographs showing perpendicular motion contain only a single foci. Image rotation to align spindle axis with the x-axis was performed using a custom MATLAB program. Directed motion analysis using minimum displacement and minimum rate criteria was performed by tracking the GFP and RFP foci in the images using the MATLAB program Speckle Tracker (Wan et al., 2009, 2012), and then analyzing the resulting coordinates using a custom MATLAB program. SCI analysis was performed on the coordinates using a custom Python script. Directed motion analysis for the Stu2^CU strain was performed using the distance between the GFP foci with a minimum rate of 20 nm/s and a minimum displacement of 300, 350, or 400 nm. To test the GFP separation–based method, the same dataset shown in Table I was analyzed with this method and showed a reduction of directed motion events upon benomyl treatment in WT cells (Table S4).

Dicentric and monocentric minichromosome analysis

Images of unreplicated dicentric and monocentric minichromosomes were deconvolved using Huygens Essential compute engine 4.3.1p3 64b (Scientific Volume Imaging). The CMLE deconvolution algorithm and automatic background subtraction were used. The maximum iterations setting was set to 50, signal to noise was set to 40, quality threshold was set to 0.01, iteration mode was set to “optimized,” bleaching correction was set to “if possible,” and brick layout was set to “auto.” Spindle lengths were measured using MetaMorph 7.7 software by measuring the distance between brightest pixels of the two SPB foci. Dicentric and monocentric chromosome lengths were measured parallel and perpendicular to the spindle axis by generating linescans using MetaMorph 7.7 software and calculating the full-with-half-max of the linescan as previously described (Stephens et al., 2011). The angle of TetR/tetO-GFP array was determined by taking the angle between a line along the longest axis of the TetR/tetO-GFP array and a line connecting the two brightest pixels of the SPB foci. The kMT length was measured as the distance between the end of the TetR-GFP signal, as determined by full-width-half-max analysis, to the brightest pixel of the proximal SPB signal on compiled image stacks that were not deconvolved. Replicated monocentric extension length was measured using the full-width-half-max analysis on compiled image stacks that were not deconvolved. For Fig. 4, only extended signals (aspect ratio > 1.2) were included. Heatmaps of the TetR-GFP arrays of dicentric plasmids were constructed using a custom MATLAB program as described in Stephens et al. (2011).

FRAP

Cell strain T3000 was prepared as described in Cell preparations and drug treatment and imaged on the same microscope system as above. GFP signal from a dicentric chromosome were photobleached with a Sapphire 488–50 CDRH laser (Coherent). To compensate for photobleaching during acquisition, 3 z-series were taken to estimate the bleaching rate during z-series acquisition. A z-series was obtained immediately before, immediately after, and then at 1-min intervals after photobleaching. Integrated intensity values were measured using MetaMorph 7.7 imaging software (Molecular Devices) for a 5 × 5 region over the photobleached spot for the in-focus plan of each z-series at each time point. The half-life of photobleaching was calculated as (ln 2)/k, where k is the rate constant, calculated as: [F_inf − F(t)]/[F_inf − F(0)] = e^−kt, where F_inf is the mean fluorescence intensity after maximum recovery, F(t) is the fluorescence intensity at each time point, F(0) is the fluorescence intensity immediately after photobleaching, and t is time.

Cells containing labeled condensin (Smc4-GFP) were photobleached and analyzed as described for the T3000 strain, except images were taken on an inverted, widefield microscope (Eclipse TE2000-U; Nikon) with a 100× Plan Apo 1.4 NA digital interference contrast oil emersion lens with a camera (Orca ER; Hamamatsu) with MetaMorph 6.1 software. After photobleaching, images were taken every 5 min for a 10-min duration.

Online supplemental material

Fig. S1 shows the speed correlation index of the 6.8-kb lacO/LacI-GFP foci in untreated and benomyl-treated cells and the distribution of the 1.7 kb LacO/LacI-GFP foci orientations in an ndc10-2 mutant. Fig. S2 shows the radial and axial displacement and heat maps of the dicentric plasmid arrays when stretched versus when appearing as a foci. Fig. S3 shows the fluctuations and trajectories of the dicentric plasmid arrays in untreated and benomyl treated cells. The supplemental material also contains a PERL script to calculate spindle pole subtracted and mean subtracted coordinates and to calculated MSD curves from particle tracking data, a MATLAB script to calculate individual radii of confinement and effective spring constants, a MATLAB script to rotate the coordinates generated by the PERL script, a MATLAB script to summarize all rotated coordinates into a single file, a set of MATLAB scripts to perform directed motion analysis based on displacement and rate, a set of Python scripts to perform SCI, and a MATLAB script to perform image rotation. All of the scripts can be downloaded as a ZIP file. Online supplemental material is available at http://www.jcb.org/cgi/content/full/jcb.201502046/DC1.