Highly Permeable Silicon Membranes for Shear Free Chemotaxis and Rapid Cell Labeling

Abstract

Microfluidic systems are powerful tools for cell biology studies because they enable the precise addition and removal of solutes in small volumes. However, the fluid forces inherent in the use of microfluidics for cell cultures are sometimes undesirable. An important example is chemotaxis systems where fluid flow creates well-defined and steady chemotactic gradients but also pushes cells downstream. Here we demonstrate a chemotaxis system in which two chambers are separated by a molecularly thin (15 nm), transparent, and nanoporous silicon membrane. One chamber is a microfluidic channel that carries a flow-generated gradient while the other chamber is a shear-free environment for cell observation. The molecularly thin membranes provide effectively no resistance to molecular diffusion between the two chambers, making them ideal elements for creating flow-free chambers in microfluidic systems. Analytical and computational flow models that account for membrane and chamber geometry, predict shear reduction of more than five orders of magnitude. This prediction is confirmed by observing the pure diffusion of nanoparticles in the cell-hosting chamber despite high input flow (Q = 10 µL min⁻¹; v_avg ~45 mm min⁻¹) in the flow chamber only 15 nm away. Using total internal reflection fluorescence (TIRF) microscopy, we show that a flow-generated molecular gradient will pass through the membrane into the quiescent cell chamber. Finally we demonstrate that our device allows us to expose migrating neutrophils to a chemotactic gradient or fluorescent label without any influence from flow.

Introduction

Cells exhibit many responses to fluid shear stress, including gene regulation [1–3], protein production and trafficking [2, 3], surface receptor presentation [4], morphology changes [1, 5], growth [5, 6], and migration [7–9]. Devices that control the magnitude of fluid shear stress in cell cultures date back three decades [10] and have been instrumental in elucidating physiological responses to shear. Fluid forces can also be unwanted in cell studies when they confound the interpretation of responses to other cellular activators or because they simply push loosely bound cells out of a region of observation. An example where shear stress confounds measurement of cell behaviour is in chemotaxis systems that use fluid flow to establish steady gradients of chemoattractants. In these systems, cells experience both the lateral push of fluid flow and the orthogonal influence of a chemical gradient, and consequently crawl diagonally in the field of observation [11, 12]. We correct this problem with a microfluidic system that employs a transparent and highly permeable silicon nanomembrane that allows solutes to be rapidly delivered to cells while reducing shear forces by five orders of magnitude.

Classical chemotaxis systems include the under-agarose migration assay [13] and the Boyden [14], Zigmond [15], and Dunn [16] chambers. These devices rely on the passive diffusion of molecules from a source and so controlling and reproducing the gradient is a challenge. The delicate nature of the gradient also makes the assays sensitive to any inadvertent convection, such as from evaporation or during the addition of reagents and cells. The introduction of flow-based gradient generators by Jeon et al. and Kamholz et al. enabled chemotaxis with steady, linear chemotactic gradients for the first time [11, 17], but introduced new complications from fluid flow. Because the cells in these devices are placed directly into the fluid channel downstream of the gradient generator, they are pushed downstream at the same time as they crawl across the channel in response to the gradient.

In recent years a number of “shear-free” chemotaxis systems have been developed that maintain steady, well-defined gradients while isolating the cell chamber from the flow in microfluidic channels [18–20]. The general strategy is to incorporate flow resistive elements between flow channel and cell chamber that still permit the exchange of chemotactic factors via diffusion. For example, three chamber designs in which the cell chamber is flanked by channels that serve as a chemical source and a sink, establish steady and linear gradients in the cell chamber after ~ 30 minutes of operation [18–20]. A long set-up time for establishing the desired gradient is not simply an inconvenience; cells such as neutrophils are only active for ~30 minutes in migration assays and so the use of these systems to study the migration of short-lived cells is problematic. Furthermore, transient responses to soluble factors, such as turning and repolarization, cannot be efficiently examined. The microjet system of Keenan et al., which also consists of three chambers, can establish a gradient in the middle cell chamber within 4 minutes through fast mixing of jets emitted from the source and the sink channel [21]. However, in this system cells near the jet output are temporarily exposed to shear stress as higher as 0.7 dyn cm⁻². Other design strategies that have cell chamber as a depression in floor of the flow channel have only a modest shear reduction because of direct fluid coupling [22].

Recent systems by Kim et al. [23], and VanDersarl et al. [24] use porous membranes to directly separate the flow generated-gradient from the cell chamber. The porous membranes are used to buffer fluid shear forces while permitting the diffusive exchange of soluble factors between chambers. These designs allow for a vertical alignment of the flow and cell chambers, which is convenient for both cell culture and for imaging with inverted microscopes [23]. The membrane interfaces can also be placed downstream of [24] or directly on top of [23] rapid gradient mixers. The time to establish chemical equilibrium between the cell and flow chamber is a function of the chamber geometry and membrane permeability [24].

Here we describe the use of a membrane-based microfluidic system for shear-free chemotaxis studies. The elimination of shear forces is particularly important for the study of neutrophil chemotaxis because prior studies have shown that microfluidic flow can bias cell migration. We show that this artifact is completely eliminated by placing a nanoporous membrane between the cell migration chamber and a gradient carrying flow channel. In addition to improving the chemotaxis chamber for the study of shear sensitive cells, our paper makes several general contributions to microfluidics. First is the development of analytical and computational flow models that predict the fluid coupling between chambers separated by thin membrane. Given the input flow, membrane properties, and channel geometries, the flow distribution throughout the cell chamber can be predicted. Second is a direct demonstration of shear elimination using highly sensitive particle tracking to reveal that nanoparticles are diffusive in the cell chamber despite input flow speed exceeding 10 µL min⁻¹ (average fluid velocity (v_avg) ~45 mm min⁻¹). Finally is the use of ultrathin (15 nm) silicon-based nanomembranes for separating the flow and the cell chamber. These membranes are so highly permeable that they offer effectively no resistance to the diffusion of molecules significantly smaller than their pore sizes (~30 nm) [25, 26]. The combination of dramatic shear reduction with no diffusive resistance makes the membranes ideal for rapid but shear-free delivery of solutes to cells. The membranes also have excellent optical properties for phase and fluorescence microscopy [27] and the silicon ‘chip’ platform makes for straightforward integration into microfluidic devices.

Materials and methods

Silicon Nanomembranes

The fabrication of ultrathin porous nano-crystalline silicon membranes (pnc-Si) has been described previously [28–30]. For the current work, membranes were manufactured on 300 µm thick silicon wafers, in a 13 mm by 31 mm chip format. The membranes were freestanding over a rectangular area of 450 µm by 4 mm, with a thickness of 15 nm, average pore diameter of 30 nm, and a porosity of 10%. A 120 nm thick silicon nitride (SiN) scaffold was overlaid onto the pnc-Si membrane to enhance its mechanical strength, as previously described [31]. The scaffold openings were either tessellated hexagons or circles arranged in hexagonal close packing. For hexagonal openings, each of the six sides measured 62.5 µm and the encasing SiN frame measured 8.5 µm wide. For the circular openings, both the diameter and the edge-to-edge distance between pores measured 3 µm.

Device assembly

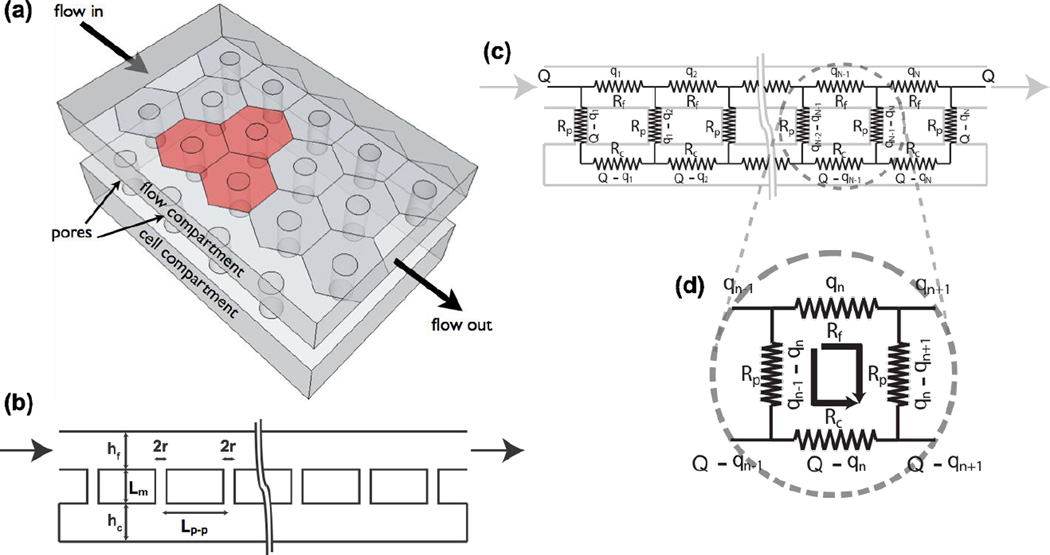
The chemotaxis chamber consisted of three main components: 1. the flow chamber, 2. a pnc-Si/SiN hybrid membrane, and 3. the cell chamber (Fig. 1). The flow chamber (Fig. 1a) is covalently bonded to the membrane (Fig. 1b) using ultraviolet-ozone treatment, while the attachment of the flow chamber/hybrid membrane complex to the cell chamber (Fig. 1c) is reversible through a simple conformal contact. The flow chamber, which is also the gradient generator in our system [11], is made with Sylgard 184 PDMS (Dow Corning, Midland, MI) patterned and cured on a custom-ordered SU-8 mold with a feature height of 50 µm (Stanford Microfluidics Foundry, Stanford, CA). Holes for the inlets and outlets were punched into the cured PDMS using a blunt 20- gauge needle (Small Parts Inc., Logansport, IN). The cell chamber is made from a 100 µm thick silicone gasket custom-cut using the Silhouette CAMEO cutter (Silhouette America, Oren, UT). The gasket, which forms the walls of the cell chamber, is covalently bonded via ultraviolet-ozone treatment to either a glass slide or a coverslip, which forms the floor of the cell chamber. Two additional openings were patterned into the chip and aligned with glass microcapillaries (ID/OD 500 µm /900 µm; Friedrich & Dimmock, Inc., Millville, NJ) that serve as adaptors for tubing to bring fluid into and out of the cell chamber (Fig. 1). Tygon tubing with ID/OD of 1/32”(~0.8 mm)/ 3/32”(~2.4 mm) (Saint-Gobain Performance Plastics Corporation) was used to connect the microcapillaries to syringe pump (NE-1800; New Era Pump Systems, Inc., Farmingdale, NY].

Fig. 1. Shear-free Chemotaxis Chamber.

(a) The flow chamber, which is also a gradient generator. The length, width and height of the main channel are 1 cm, 450 µm, and 50 µm, respectfully). (b) The hybrid membrane chip, which hosts a 500 µm by 4 mm pnc-Si/SiN membrane. (c) The silicone gasket that forms the cell chamber. (d) The assembled system. The width × height of (a) through (d) are ~ 1.3 cm × 3.1 cm. The red dashed arrow passing through (a), (b), and (c) indicates the flow path for cell seeding. (e) Magnified view of the gradient generator, featuring the 5 microchannels that converge the flow to form a gradient. (f) Magnified views featuring the pnc-Si membrane (left) and the SiN scaffold (right). The SiN scaffold in this case is a honeycomb. The white objects in the pnc-Si are the nanopores and the black objects are silicon nanocrystals. (g) Magnified view featuring migrating human neutrophils in the cell chamber, with cell edges enhanced for cell tracking.

Nanoparticle tracking

We used particle tracking [32] of green fluorescent polystyrene particles (210 nm; Bangs Laboratories, Inc., Fisher, IN) to measure cross-flow between the cell and flow chambers. To obtain reference motions, we first forced fluid through the cell chamber at fixed rates of 0.1 or 0.5 µL min⁻¹ (v_avg ~720 or ~3600 µm min⁻¹, respectively). The flow was then stopped completely with all access fluid ports closed, and the thermal motions of the particles were tracked. Flow rates of 10, 50, and 100 µL min⁻¹ were then applied to the flow chamber (v_avg of ~45, 225, and 450 mm min⁻¹, respectively) and the motions of the nanoparticles were again tracked. The nanoparticle motion was recorded at 10 frames per min (10 fpm) in an epifluorescence microscope at a total magnification of 200X. The average speed of each nanoparticle was obtained by dividing the total path length travelled by the respective duration of tracking. We defined the system to be shear-free if the average speed of the nanoparticles is not statistically different from zero under the two-tailed student’s T-test at the alpha level of 0.05. We also performed an analysis where we assume the nanoparticle motion to be a combination of both convection and diffusion. For each nanoparticle, we performed a linear regression on the×and the y coordinates with respect to time to obtain the underlying convection. We then subtracted the convection component in each direction from the particle positions and calculated the mean squared displacements (MSDs). The MSDs were then used to calculate the diffusion coefficients of each particle [32]. By this method, we defined the system to be shear-free when the average speed of the nanoparticles was not statistically significantly different from zero under the two-tailed student’s T-test at an alpha level of 0.05.

Analytical model

We developed a 2D analytical model to predict the amount of convective cross-talk between the flow and cell chambers. The model considers an idealized membrane with pores in a hexagonally close packed arrangement and with rows of pores aligned with the long axis of the channel (Fig. 2a). The pore-to-pore distance L_p-p for the membrane is calculated with:

$$L_{p-p}=\sqrt{\frac{\pi r^2}{\text{sin}(60)·p}}$$ (1)

where p is the membrane porosity and r is the pore radius.

Fig. 2. Analytical model of fluid coupling.

(a) Model Geometry. Pores are assumed to be in a hexagonal close packed arrangement with rows that align with the flow direction. (b) A 2-D cross section with key dimensions labeled: r is the pore radius (15 nm); L_m is the membrane thickness (15 nm), L_p-p is the pore-to-pore spacing (108 nm), and h is the chamber height (350 µm and 100 µm for the flow and the cell chamber, respectively). (c) A circuit representation of (b). The subscript indexed each repeating segment of the circuit loop. Q represents the input flow rate, and the q_n’s represent the flow rate through each segment of the flow chamber. R_p, R_f, and R_c represent the pore resistance, flow chamber resistance, and cell chamber resistance, respectively. (d) Unit of the resistance circuit that forms the basis of a recurrence relation that is solved to find the flow rate through any channel in the flow network.

The pores in membranes are modeled as a series of small cylindrical channels connecting the top and bottom channel (Fig. 2b). We solved the flow in the channels and pores using an electrical circuit analogy (Fig. 2c). By indexing the flow in the pores within a unit segment (Fig. 2d) of length L_p-p, we obtained a generalized recurrence relation that allows us to solve for the flow through the network. A brief outline of this derivation follows below with the more detailed derivation given in the electronic supplemental information (ESI†).

The flow rate in the n^th segment of the cell chamber is given by:

$$q_c=Q\left(\frac{R_f}{R_f+R_c}\right)(1-\omega )$$ (2)

$$\text{where\hspace{1em}}\omega =\frac{e^{\beta ·n}}{e^{\beta }+e^{\beta ·N}}+\frac{e^{-\beta ·n}}{e^{-\beta }+e^{-\beta ·N}}\text{\hspace{1em}and\hspace{1em}}\beta ={\text{cosh}}^{-1}\left(\frac{2R_p+R_f+R_c}{2R_p}\right)$$ (3&4)

N is the total number of segments, Q is the input flow rate, and R_p, R_f, and R_c, are the resistance of the pore, the flow chamber, and the cell chamber within each loop, respectively.

Taking the derivative of equation (2) with respect to n reveals that q_c is maximum at n = 0.5N (see ESI†). Using the fact that the number of segments (i.e. pores) will be large so that β ≪ β·N, we can construct a Taylor expansion of equation (2) to yield the following asymptotic approximation for the maximum flow rate in the cell chamber:

$$q_{c,\text{max}}=Q\frac{R_f}{R_f+R_c}\left[\frac{1}{8}{(\beta ·N)}^2\right]$$ (5)

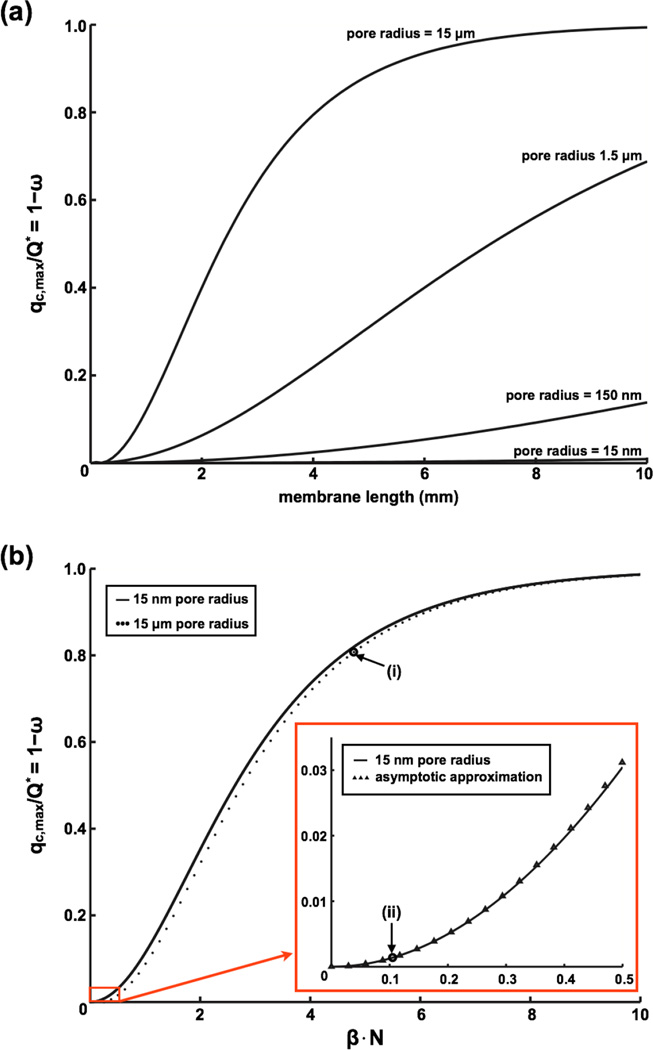
We found this approximation agrees well with the analytical solution (< 3% error) in equation (2) for β < 1×10⁻⁵ and β·N < 0.5. For the membranes used in this paper we are ~ 3 fold below these thresholds.

The chamber and pore resistances can be estimated using the Hagen-Poiseuille equation of flow in rectangular and cylindrical channels resepctively [33]:

$$R_{\mathit{\text{rec}}}=\frac{12\mu L}{w{h}^3}\text{ and }{R}_{\mathit{\text{cyl}}}=\frac{8\mu L}{\pi r^4}$$ (6&7)

where µ is the fluid viscosity, L is the channel length, w and h are the channel width and height, respectively, and r is the cylinder radius.

Since the membrane is thin, it is more accurate to use Daegan’s equation to account for entrance/exit effects for flow through a short through pore [34]. The associated resistance is:

$$R_{\mathit{\text{pore}}}=\frac{\mu }{r^3}[3+\frac{8}{\pi }(\frac{L}{r}\left)\right]$$ (8)

Note that the pore resistance calculated in equation (8) is for a single pore. To obtain the total pore resistance for a sheet of membrane, we multiplied the resistance of a single pore by the total number of pores across the width of the membrane. Essentially, we treated the pores across the membrane width as resistors connected in parallel. The number of pores across the membrane width is calculated with:

$$\frac{W}{L_{p-p}·\text{sin}(60)}$$ (9)

where W is the membrane width.

Finite Element Model

We also calculated the flow rate expected in the cell chamber using a commercial finite element analysis package (COMSOL, Stockholm, Sweden). Here the membrane is treated as a porous media and the flow through the membrane is solved using Brinkman’s equation. We calculated the constant of hydraulic permeability K required in Brinkman’s equation with the following relationship:

$$K=\frac{\mu Lp}{\pi r^2{R}_{\mathit{\text{pore}}}}$$ (10)

A derivation of equation (10) is given in the ESI†. The hybrid membrane has a porosity of ~ 6.9%, a product of a 69% porosity for the SiN scaffold and 10% porosity from pnc-Si. The flow field before and after the flow through the membrane is determined with the steady-state Navier-Stokes equation. Due to the computational difficulty in modeling both nanoscale membrane domains and microscale channel domains with a single continuous mesh, we assumed a microscale membrane thickness, found trends as a function of thickess (ESI† Fig. 1), and extrapolated results to the nanoscale. We created a baseline case in which the membrane is 2 mm long by 450 µm wide and 30 µm thick. We then simulated different membrane lengths, thicknesses, and porosities/pore sizes to determine trends in the amount of fluid cross talk between chambers. We then extrapolated results to the actual membrane length (4 mm), thickness (15 nm), pore radius (15 nm), and porosity of 6.9%.

Total internal reflection (TIRF) microscopy

We used TIRF microscopy [35], a technique that specifically excites fluorescent molecules within ~140 nm of a substrate surface, to confirm that the molecular gradient generated in the flow chamber propagates through the membrane and preserves its linear profile near the floor of the cell chamber. The fluorescent gradient was generated by flowing 2 µM of fluorescein isothiocyanate (FITC) against pure PBS in the gradient mixing segment of the flow chamber. Each solution was pushed at a flow rate of 0.25 µL min⁻¹ (v_avg of ~2 mm min⁻¹). TIRF was performed under a Nikon TE2000 microscope with an argon-ion illumination laser and a 100X oil objective (NA 1.45).

Demonstration of shear-free chemotaxis and cell labeling

Primary human neutrophils were isolated from whole blood by density separation over a solution of 1-Step™ Polymorph (Accurate Chemical & Scientific Co., Westbury, NY), then washed and stored in pH 7.4 HBSS–– buffer, made with calcium- and magnesium-free Hank’s balanced salt solution (Gibco, Grand Island, NY) supplemented with 10 mM HEPES (Sigma-Aldrich, St. Louis, MO) for extra pH buffering and 4% volume ratio of heat-inactivated fetal calf serum (FCS) to prevent non-specific adhesion of neutrophils to container walls. Thereafter, and throughout migration experiments, neutrophils were suspended in pH 7.4 HBSS++ (HBSS buffer supplemented with the calcium (1.26 mM) and the magnesium (0.9 mM) needed for facilitating activation and integrin-mediated adhesion). The channel walls of the entire microfluidic system were pre-coated with 2 mg/mL bovine serum albumin (BSA) (CalBiochem, La Jolla, CA), a known adhesion molecule that allows integrin binding during cell migration. After washing the BSA off with HBSS++, cells were introduced into the cell chamber at a flow rate of 50 µL min⁻¹. Once a significant number of neutrophils were observed under the hybrid membrane, the flow was stopped and the neutrophils were allowed to adhere to the BSA-coated substrate. To create the chemoattractant gradient to direct neutrophil migration, the bacterial peptide N-formylmethionine-leucyl-phenylalanine (fMLP) and pure HBSS++ buffer were each injected with a syringe into the flow chamber at a flow rate of 0.25 µL min⁻¹ (v_avg ~2 mm min⁻¹). Prior to the injection, the hydrophobic fMLP was solubilized with DMSO (dimethyl sulfoxide) into phosphate buffered saline (PBS) in the volume ratio of 0.01%, then further diluted to 40 nM in HBSS++. After the chemotaxis experiment, we labeled cells with a fluorescent gradient by perfusing 1 mM of rhodamine 6 G (R6G) through the flow chamber instead of fMLP.

Measurement and analysis of cell migration

Cell migration was recorded at 4 frames per minutes (4 fpm) under a phase contrast microscope at a total magnification of 200X. Most cells were tracked automatically but occasionally with a custom-written MATLAB program (MathWorks, Inc., Natick, MA). All cells that travelled for less than 12 frames (3 min) and less than 30 µm in displacement (~3 cell body lengths) were considered inactive and excluded from the analysis. Inactive cells accounted for less than 5% of the total population. Each data set consisted of all the cells tracked in a microscopic field of view (~150–400 cells depending on the seeding). The starting and the ending positions of a cell trajectory were used to define the migration direction vector. The polar plane (see Fig. 7) was divided into 12 sectors, with spans of 30°. The migration direction vectors falling within each sector were counted to determine the general directionality of the whole population. To illustrate how the presence of flow can influence cell migration, control experiments were performed with cells in the flow chamber, with or without the 0.5 µL min⁻¹ input flow (v_avg of ~22 mm min⁻¹), with the cells exposed to either 10 nM of uniformly distributed fMLP or a linear gradient that ramped from 0 to 40 nM over a 450 µm span. In these control experiments, the flow-based chemotaxis chamber that generates the gradient was bonded to glass instead of the hybrid membrane chip. The inner walls of the entire system were also coated with BSA as in the case of the shear-free chemotaxis system. The 0.5 µL min⁻¹ input flow was chosen to generate a corresponding wall shear stress of 0.4 dyn cm⁻², a value at the low end of the physiological range and used by other investigators in their chemotaxis studies with neutrophils [9, 11, 12, 36–40].

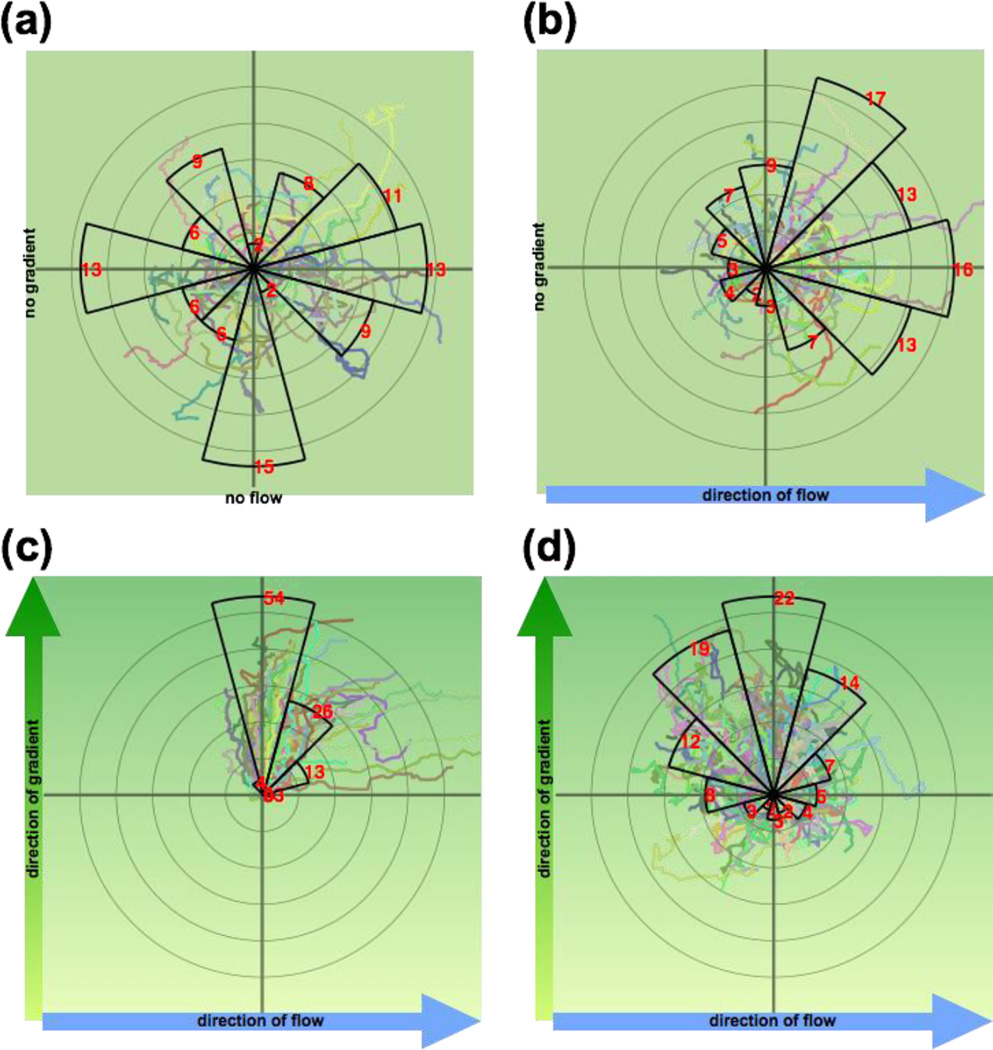
Fig. 7. Radial histograms of neutrophil migration.

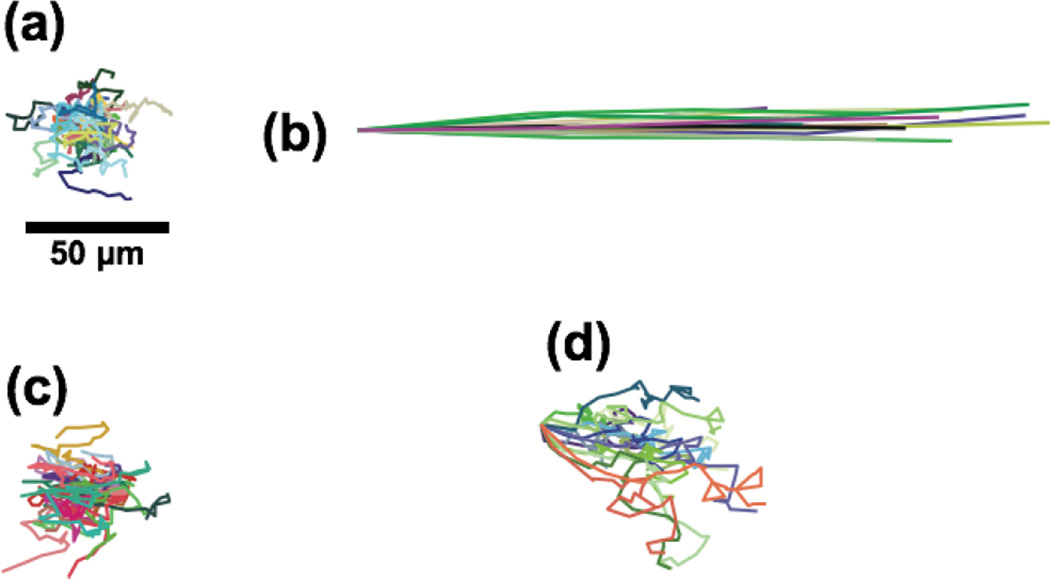
Each sector spans 30°, and the distance between each pair of successive concentric rings is 50 µm. The red number and the radius of each sector represent the percentage of cells (n > 150) that migrated into each sector. Superimposed on the radial histogram are the actual trajectories of the migrating neutrophils, each with the starting position centered at the origin of the radial histogram. (a) Uniform fMLP (10 nM) stimulation and no flow; (b) Uniform fMLP (10 nM) stimulation with left-to-right flow; (c) System without membrane, bottom-to-top fMLP gradient (0 nM – 40 nM over 500 µm), and left-to-right flow. Downstream bias of cell migration is evident. (d) System with membrane, bottom-to-top fMLP gradient (0 nM – 40 nM over 500 µm), and left-to-right flow. In (b), (c), and (d), an input flow rate of 0.50 µL min⁻¹ was used.

Results and Discussion

Analytical and computational models of flow reduction

The analytical model provides insight into the conditions that produce flow reduction in the cell chamber. By equation (2), the maximum possible flow rate in the cell chamber occurs when ω = 0. Under this condition, the membrane is of no consequence and the flow simply splits between the two chambers according to their relative resistances so that the maximum cell chamber flow becomes Q · Rf (Rf + Rc)⁻¹. Because the pore resistance will generally be much higher than the chamber resistances, cosh(β) ~ 1 and β ≪ 1 a condition which tends to keep ω ~ 1. Thus flow is significant in the cell chamber only when the number of pores along the length of the channel, N, becomes large enough that the product β·N is sizable. We visualize these results in Fig. 3 for a 6.9% porosity membrane of different lengths and pore sizes. With the porosity fixed, the length of the membrane determines how many pores are encountered by the flow before exiting the device. The figure clearly shows the benefit of using a nanoporous (pore size < 100 nm) membrane for flow reduction as it allows much longer membranes to be used under shear-free conditions. The strong influence of the β·N term on ω allows us to construct the non-dimensional curves shown in Fig. 3b to describe the partitioning of flow between chambers. Because pore sizes lower than 15 nm have only a small influence on ω, the curves nearly all collapse to a ‘universal’ curve.

Fig. 3. Impact of membrane parameters on cell chamber flow rate.

(a) Impact of membrane pore size on flow rate. The term 1 – ω in equation (2) describes the membrane’s contribution to flow reduction. It is also equal to the ratio of the maximum flow rate in the cell chamber q_c,max to the membrane independent flow rate Q*. The figure demonstrates the advantages of using a nanoporous membrane over a microporous one to reduce fluidic coupling between chambers (membrane thickness = 15 nm and porosity = 6.9%). (b) Plotting 1 – ω vs β·N for the case of small β results in near universal curve for flow reduction. While the pore size has a minimal impact on the curve, it does impact the value of β· N. Examples: (i) average pore radius = 15 µm, 4 mm long membrane, β· N = ~4.6, flow reduction = ~0.8; (ii) average pore radius = 15 nm, 4 mm long membrane, β· N is ~0.11, flow reduction = ~0.0015.

A finite element (COMSOL) simulation was used to validate the analytical solution and provide 2D flow visualization. Due to the three orders-of-magnitude differences between the thickness of the membrane and the channel heights, it was not practical to conduct COMSOL simulations with the actual membrane geometry. Instead, we compared the two models assuming micron-thick membranes. We found good agreement between the models over a range of membrane thicknesses, permeabilities, lengths, and porosities (ESI† Fig. 1). The small discrepancies between the analytical and computational models at the microscale get smaller when extrapolating to the actual nanoscale membrane dimensions.

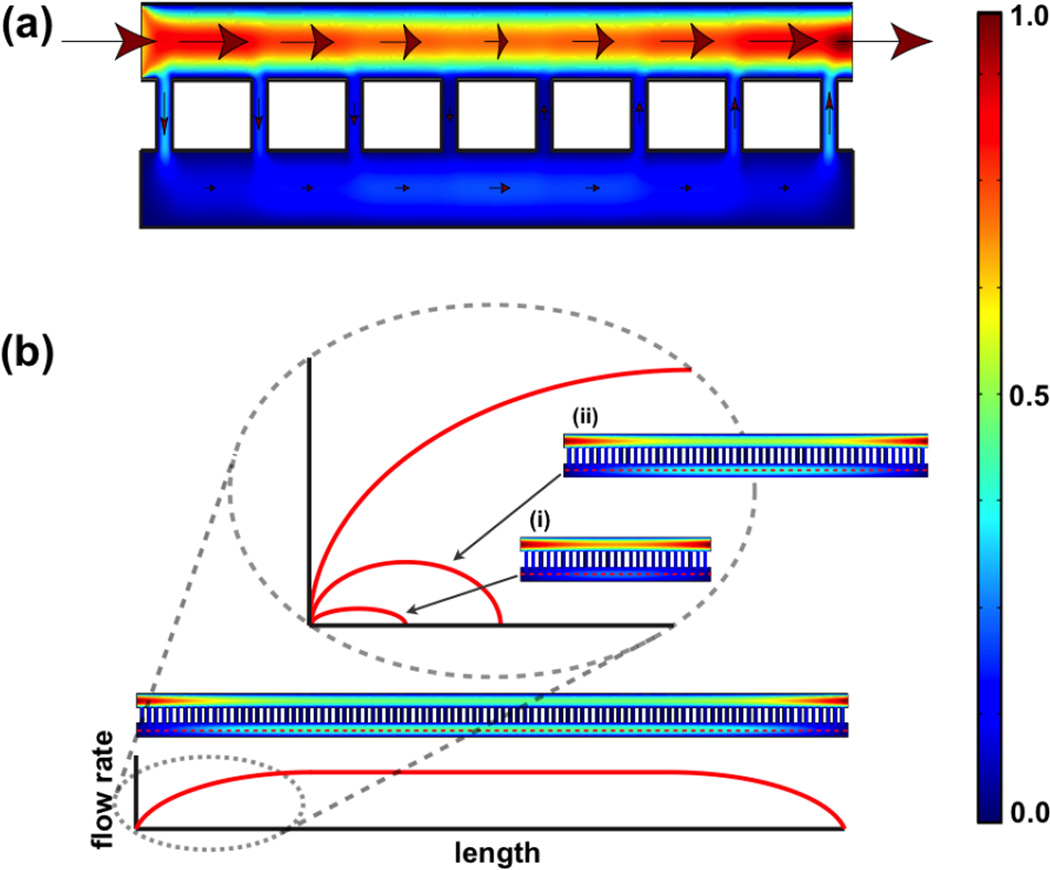
A COMSOL simulation for an artificially short system with only a few very large pores illustrates the symmetric nature of the flow about the midpoint of the system (Fig. 4a). Upstream of the midpoint, fluid transfers from the flow chamber to the cell chamber, until it reaches a maximum at the midpoint. Downstream of the midpoint, the flow through the pores reverses and the volumetric flow in the cell chamber begins to diminish. The existence of peak volumetric flow at the midpoint of the cell chamber can also be appreciated by the analytical model by taking the derivative of ω from equation (3) with respect to n to locate the maximum at n = N 2⁻¹ (see ESI†). The symmetric nature of flow serves as a check on mass conservation.

Fig. 4. Flow rate distribution predicted from COMSOL simulation.

(a) Simulation of a system with short membrane span. The arrows indicate the directions of flow and the size of the arrows represents the magnitude of flow rate (not drawn to scale). The heat map reference to the far right indicates the magnitude of flow rate, with the red and blue representing the normalized maximum and minimum. (b) Given a system with sufficiently long span of membrane, the flow rate in the cell chamber reaches a plateau value that is independent of the membrane. The key to achieving a shear-free condition is to use membranes that are much smaller than the length required to reach this plateau value.

Given a sufficiently long membrane span, the flow in the cell chamber will reach a plateau value before the midpoint (Fig. 4b). This plateau value corresponds to the membrane-independent flow rate (ω =0) discussed for the analytical model. Thus the key to achieving low shear is to create a system that operates in the ‘entrance length’ of this limiting case. Our membrane (thickness = 15 nm, pore radius = 15 nm, and porosity of 6.9%) would reach ω ~ 37% (or e⁻¹) at 124 mm. Thus our 4 mm long system achieves dramatic shear reduction by operating in the first 4% of the entrance length of this extreme profile. Clearly, the more resistive a membrane is to convective flow, the longer the device can be made and still operate shear-free.

Given an input flow rate of 1 µL min⁻¹ (v_avg of ~4 mm min⁻¹) in our system, the analytical model predicted the peak cell chamber flow rate to be 33 pL min⁻¹, corresponding to ~30,000 fold reduction in volumetric flow. The corresponding maximum fluid velocities in the flow and the cell chamber are 8.6 mm min⁻¹ and 1 µm min⁻¹ respectively, for a 8500-fold reduction in maximum fluid velocity. The shear reduction provided by the membrane can be calculated with

$${\tau }_{\mathit{\text{wall}}}=\frac{6\mu Q}{w{h}^2}$$ (11)

where µ is the fluid viscosity, Q is the volumetric flow rate, and w and h are the channel width and height, respectively [41]. At 1 µL min⁻¹ input flow, the maximum shear stress at the flow chamber side of the membrane is 16.3 ×10⁻³ dyn cm⁻² (16.3 ×10⁻⁴ Pa), while the maximum shear at the cell chamber floor is 6.7 ×10⁻⁸ dyn cm⁻², yielding a 240,000 fold reduction.

Our flow models are complementary to the model in VanDersarl et al. [24] that describes molecular diffusion between a membrane-separated fluid channel and a cell chamber. Together, the fluid and diffusive transport models allow for a rather complete assessment of mass distribution in our system. The results should be useful for more than the design of shear-free cell culture chambers; they can inform the design of other microsystems where semi-permeable membranes are used to separate fluidic compartments such as dialysis [31] and flat membrane bioreactors [42, 43].

Nanoparticle tracking in the cell chamber

To test the membrane’s ability to create a shear-free microenvironment, we tracked the motion of nanoparticles (210 nm) in the cell chamber over 3 minutes with different flow rates in the flow and the cell chamber (Fig. 5). As reference conditions, we examined the motion of nanoparticles with no flow in the system and with 0.1 µL min⁻¹ (v_avg of ~720 µm min⁻¹) applied directly to the cell chamber. The first reference condition resulted in purely diffusive motion (Fig. 5a). The second reference condition produced ballistic particle trajectories and an average particle velocity of 588 µm min⁻¹ (Fig. 5b). When a flow rate of 10 µl min⁻¹ is applied to the flow chamber (v_avg of ~45 mm min⁻¹), nanoparticle motions in the cell chamber are purely diffusive (Fig. 5c). At 50 µL min⁻¹ (v_avg of 225 mm min⁻¹), a slow drift of the nanoparticles in the cell chamber could be detected (~13 µm min⁻¹). Increasing the flow rate in the flow chamber to 100 µL min⁻¹ (v_avg of 450 mm min⁻¹) resulted in more obvious convection (Fig. 5d) and a measured particle velocity of 19 µm min⁻¹. Note that the particle velocity under these conditions was more than 30-fold lower than the convection reference case, despite the fact that the input flow rate was 1000-fold higher.

Fig. 5. Nanoparticle tracking demonstrating shear-free conditions.

Particles with diameter of 210 nm were tracked at the mid-height of the cell chamber at the mid-span of the membrane where the flow velocity is the highest. (a) Particles tracked in the absence of any system flow. (b) Particles tracked with a flow rate of 0.10 µL min⁻¹ (v_avg ~720 µm min⁻¹) applied directly to the cell chamber as a reference for convection. (c) Particles tracked with 10 µL min⁻¹ in the flow chamber (v_avg ~45 mm min⁻¹). (d) With the flow input increased to 100 µL min⁻¹ (v_avg of ~450 mm min⁻¹), particle drift was observed. Particles were tracked for 3 min except for case (b), where the particles were tracked for 2.5 sec.

The particle tracking experiments suggest that an input flow rate of 50 µL min⁻¹ is a upper threshold for the maintenance of shear-free conditions. This result is supported by a simple analysis of the excursion expected for diffusive vs. convective nanoparticles in our system. The Stokes-Einstein equation gives a theoretical diffusion coefficient D = 124 µm min⁻¹ for a 210 nm particle in water. Experimentally, we determined a similar value for D (107 µm² min⁻¹) using a mean-square-displacement analysis of nanoparticle trajectories in the 10 µL min⁻¹ flow case. Employing the theoretical value of 124 µm² min⁻¹, the excursion expected for a purely diffusive particle in T = 3 minutes of observation is

$$L_d=\sqrt{4DT}=36\mu m$$

Thus a particle requires a drift velocity exceeding L_d T⁻¹ = 14.4 µm min⁻¹ for convective motion to be comparable to simple Brownian motion during the tracking experiment. Since this value aligns with the 13 µm min⁻¹ drift detected in the 50 µL min⁻¹, we conclude that input flows less than 50 µL min⁻¹ give ‘shear-free’ conditions in the cell chamber.

Although there have been several prior attempts to create microfluidic systems with ‘shear-free’ chambers [18–24], none have defined ‘shear-free’ conditions, nor have they measured the degree of fluidic coupling with the flow chamber to show that they meet the definition. Here we define a ‘shear-free’ environment to be one where the Brownian motion of a 210 nm particle in the cell chamber is equal or greater than any measurable convection during 3 minutes of observation. It is necessary to create such a particular definition because there will always be some fluidic coupling between the chambers. The practical questions are what is measurable and what is tolerable. In our case, with longer observation times or larger particles, convective motion could likely be detected at 50 µl min⁻¹ over three minutes of observation. For the purpose of delivering solutes to crawling neutrophils however, the criterion we put forth is highly conservative. Even if these experiments were conducted with an input flow rate of 50 µL min⁻¹, the shear stress experience by neutrophils in the cell chamber would be less than 4 × 10⁻⁵ dynes cm⁻² (4 × 10⁻⁶ Pa). The levels of wall shear stress that are known to bias neutrophil migration in conventional microfluidic assays [9, 11, 12, 36–40] are 5 orders higher than this value (0.4 dynes cm⁻²).

While a high flow rate is desirable for the rapid delivery of solutes, the rate of solute arrival to the cell compartment also depends on the diffusion time across the membrane. Therefore the ideal membrane for creating shear-free chambers is one that offers a high resistance to transmembrane fluid flow, but a low resistance to transmembrane diffusion. The ultrathin membranes used here have a negligible transmembrane resistance to the diffusion of molecules smaller than ~30% of the pore size [25, 26]. The high fluid resistance for these membranes derives primarily from the low average pore size of the pnc-Si membrane (~30 nm) and takes advantage of the 4^th order dependence of fluid resistance on pore radius, as indicated in equation (7). By contrast, the polymer membranes used by others have 10× larger pore sizes, 100× larger thicknesses, and a 10× lower porosity [23, 24]. Increasing thickness and lowering porosity increase fluid and diffusive resistances to the same degree. Only by employing an ultrathin membrane can the fluidic resistance be increased through smaller pore sizes without simultaneously increasing the diffusive resistance. To illustrate, the diffusion times for a ~ 1 nm molecule to transit the membrane will be less than < 10 µs for our ultrathin membranes compared to ~ 60s for the membranes used by VanderSarl et al. (thickness = 24 µm; porosity = 0.44%; pore diameter = 750 nm), while the hydraulic resistance of these membranes are of the same order.

TIRF visualization of gradient in the cell chamber

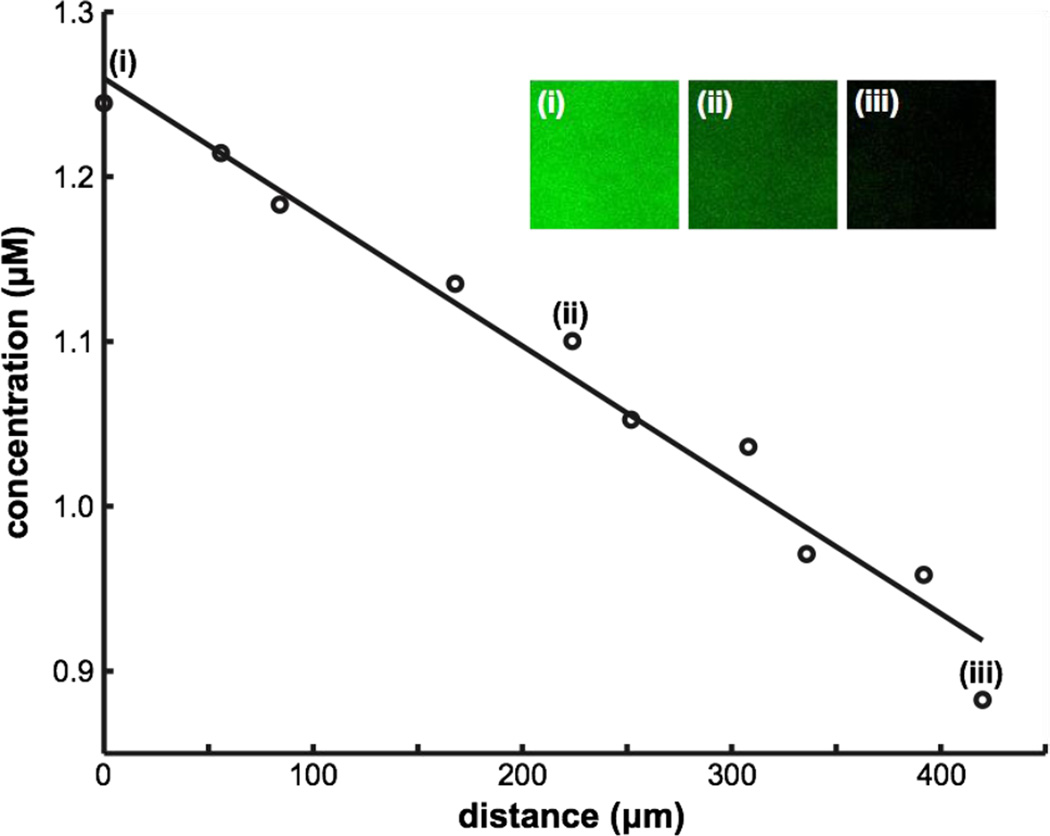
We used TIRF microscopy to demonstrate that a chemical gradient can be transferred from the flow chamber to the cell chamber (Fig. 6). Running FITC dye against PBS buffer in the gradient generator (Fig. 1a), we created a steady linear gradient over the membrane in the flow chamber. Using TIRF microscopy, we imaged the bottom ~ 0.2 µm of the cell chamber and confirmed the presence of a linear gradient with a 27% slope across the 450 µm membrane width and a peak concentration ~ 60% of the input FITC concentration, consistent with a previous literature report [24]. The decrease in both the steepness and the peak concentration of the linear gradient is consistent with Monte Carlo simulation of pure diffusion and indicates that lateral diffusion in the flow chamber and cell chamber tends to homogenize the sample before it reaches the bottom of the cell chamber. A shorter chamber and placement closer to the exit of the gradient generator would both increase the steepness of the gradient.

Fig. 6. Total internal reflection fluorescence (TIRF) microscopy of a gradient at the cell chamber surface.

A gradient of FITC dye (0 µM – 2 µM) was visualized via TIRF to ensure that the gradient reaches the bottom of the cell chamber. At the high magnification required by TIRF microscopy, it is necessary to take sequential TIRF images at regular spacings to evaluate the gradient. The insets show images taken at ~50 µm (i), ~225 µm (ii), and, ~425 µm (iii) away from the edge of the membrane with the higher concentration of FITC.

Shear-free chemotaxis and labeling of cells

To demonstrate the utility of the membrane-integrated system, we tracked the movement of neutrophils in response to a chemotactic gradient of fMLP. This experiment was selected because the flow required to generate the chemotactic gradient in the Whitesides chamber has been seen to bias neutrophil migration in the direction of flow (at wall shear stress as low as 0.23, 0.6, and 1.2 dyn cm⁻²) [11, 12, 40]. In control experiments with uniform fMLP and no flow, a similar percentage of cells migrated into each sector of a radial plot indicating random migration (Fig. 7a). With the addition of flow but a uniform distribution of fMLP (0.50 µL min⁻¹, wall shear stress ~ 0.4 dyn cm⁻²), cell trajectories were clearly biased toward the flow direction (Fig. 7b). Consistent with prior work, flow and chemotaxis both influenced cell migration in a system without a membrane to buffer shear (Fig. 7c). The same conditions in the membrane-based system however, resulted in ~80% of ~400 tracked cells migrating directionally toward the higher fMLP concentration without any detectable bias in the flow direction (Fig. 7d). Despite being biased downstream, cells appear more persistent in the presence of shear (Fig. 7c) than in the shear free system (Fig. 7d). We suspect that this is because of lateral diffusion of molecules in the cell chamber results in a shallower chemotactic gradient than in the flow channel.

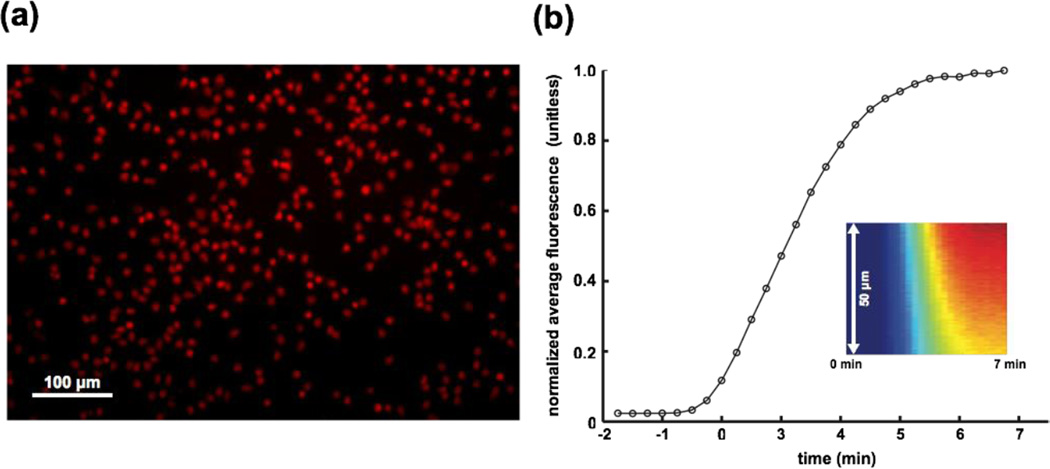
To illustrate the use of our shear-free device for fluorescent labeling, we replaced the fMLP gradient with the fluorescent molecule rhodamine 6G (R6G) at the conclusion of a migration study. R6G is a general stain of cell membranes. After maintaining a gradient of R6G for several minutes, we flushed the system with HBSS++ to reveal the labeled cells. As a result of prolonged exposure, the majority of cells were saturated with R6G labeling (Fig. 8a). Most importantly, the cell positions appeared undisturbed by the labeling and washing flows of 20 µL min⁻¹ (see movies in the ESI†).

Fig. 8. Rapid labeling of cells in the absence of flow.

(a) Image of cells labeled after exposure to rhodamine gradient. The majority of cells were saturated with labeling after prolonged exposure to rhodamine. (b) Response time of gradient establishment. Line-scans of fluorescence intensity over a 50 µm span were monitored over a duration of 7 min, starting from the onset of the flow to establish the gradient (kymograph inset). The average intensity of each line-scan was calculated and normalized by that of the 7 min time point and plotted against time. As expected, a steep increase was seen within 2 min, corresponding to the transit time of a 20 µL min⁻¹ flow through the inlet tubing with inner volume of ~50 µL. The subsequent plateau in fluorescence suggests a system response time of ~3 min for the establishment of a steady state gradient. Note the negative times denote the delay required for the fluid to pass through the inlet tubing.

Measuring the fluorescence at the midspan of the cell chamber during this experiment established the time scale for establishing a steady concentration at the membrane is less than 5 minutes at 20 µL min⁻¹ (Fig. 8b), a time scale on par with the 4–6 min response times by Keenan et al., Wang et al., and Vandersarl et al. in their gradient generators [21, 22, 24]. While compared to traditional chemotaxis systems, 5 minutes is a short time to establish a steady gradient, much faster times are needed to understand the fastest temporal response of cells to activating solutes. To improve on the temporal response of these systems it is important to recognize that the majority of the 5 minute response was attributed to fluid transport time through the inlet tubing, the mixer, and the upstream sections of the flow channel. Additional device miniaturization and control from on-chip chemical reservoirs [22], in-line micropumps [44], pneumatic valves [45], and voltage gated membranes [46] would allow chemical microenvironments to be changed in seconds rather than minutes and would take better advantage of the rapid diffusion enabled by ultrathin silicon nanomembranes. The time required for fMLP (D ~ 5 × 10⁻¹⁰ cm² s⁻¹) to pass through the membrane (< 1 s) and the 100 µm tall cell chamber (20 s) is much smaller than the time for gradient stabilization. With improvements to the fluid delivery mechanisms, it is possible the diffusive transport time through the cell chamber becomes limiting. In this case, a thinner chamber or the placement of cells on the membrane surface, would further improve the time resolution. Note that the diffusion time through an ultrathin silicon membrane is highly unlikely to be rate limiting under any conditions.

Summary and Conclusions

While microfluidics devices are powerful tools for the culture and study of cells, fluid forces can cause unwanted cellular responses or simply wash cells out of regions of observation or culture. Shear-free microfluidic systems allow efficient handling of cells while eliminating these complications of fluid flow. The fastest responding shear-free systems use a porous membrane to protect cells from high shear forces in an adjacent flow chamber. Here we contribute to the design of these systems by introducing porous nanocrystalline silicon (pnc-Si) as an ideal membrane for shear-free microfluidics and by presenting an analytical framework to assess the degree of fluidic coupling between two chambers separated by a porous membrane. Ultrathin (15 nm) pnc-Si membranes are ideal because of their transparency and their extraordinary permeability to the diffusion of small molecules despite attenuating fluid forces by 5 orders-of-magnitude. We are the first to quantify shear reduction in a shear-free microfluidic system. Using highly sensitive nanoparticle tracking, we show that nanoparticles remain purely diffusive in the cell chamber with flow rates as high as 50 µL min⁻¹ in the flow chamber (v_avg of 225 mm min⁻¹).

We employ our shear reduction system in combination with a rapid gradient mixer to create an improved chemotaxis chamber for use with shear-sensitive cells. We demonstrate the successful passage of a chemical gradient from the flow chamber to the floor of the cell chamber where neutrophils are seeded. We use neutrophils because their migration is known to be biased by flow in microfluidic systems that do not employ shear reduction. We demonstrate that this bias is completely eliminated in our device so that neutrophils migration is determined only by a chemoatractant gradient. While ultrathin membranes should enable excellent temporal resolution for studying transient cell responses such as cell activation or re-polarization to suddenly introduced soluble factors, a highly permeable membrane is only one component needed for a fast-responding shear-free system. Currenty the large fluidic paths and resevoirs in our microfluidic system are rate limiting. Advanced systems that use on-chip pumps, resevoirs, and valves in conjuction with ultrathin membranes for shear reduction should be able to alter the microchemical environment of a cell in seconds instead of minutes.