Abstract
We show that many salient hemodynamic flow properties, which have been difficult or impossible to assess in microvessels in vivo, can be estimated by using microviscometry and fluorescent microparticle image velocimetry in microvessels >20 μm in diameter. Radial distributions in blood viscosity, shear stress, and shear rate are obtained and used to predict axial pressure gradient, apparent viscosity, and endothelial-cell surface-layer thickness in vivo. Based solely on microparticle image velocimetry data, which are readily obtainable during the course of most intravital microscopy protocols from systemically injected particle tracers, we show that the microviscometric method consistently predicted a reduction in local and apparent blood viscosity after isovolemic hemodilution. Among its clinical applications, hemodilution is a procedure that is used to treat various pathologies that require reduction in peripheral vascular-flow resistance. Our results are directly relevant in this context because they suggest that the fractional decrease in systemic hematocrit is ≈25–35% greater than the accompanying fractional decrease in microvascular-flow resistance in vivo. In terms of its fundamental usefulness, the microviscometric method provides a comprehensive quantitative analysis of microvascular hemodynamics that has applications in broad areas of medicine and physiology and is particularly relevant to quantitative studies of angiogenesis, tumor growth, leukocyte adhesion, vascular-flow resistance, tissue perfusion, and endothelial-cell mechanotransduction.
Dating back to the work of Fåhræus over 70 years ago, studies related to blood flow in the microcirculation (1–4) have been featured prominently in scientific investigations across various fields, including endothelial-cell mechanotransduction, inflammation, vascular permeability, angiogenesis, and tissue engineering. Nevertheless, no method has been developed for either quantitatively predicting or measuring the salient dynamic, kinematic, and rheological properties of microvascular blood flow in vivo other than in the single-file flow regime within capillaries of 5–8 μm in diameter (4–7). All attempts at analyzing microvascular blood-flow properties in microvessels above the capillary range have depended on knowledge of quantities, such as the axial pressure gradient within the vessel and the red-cell concentration of blood discharged by the vessel, which are essentially unknown in these vessels (2, 3, 8, 9). In the absence of any satisfactory way of estimating these hemodynamic quantities, researchers have had to resort to indirect methods, which often contain errors of nearly an order of magnitude.
In 1830, the physiologist J. L. M. Poiseuille arrived at his celebrated law relating the volumetric flow rate of a Newtonian fluid in a cylindrical tube to the difference in pressure acting across the length of the tube (10). A century later, Fåhræus and Lindqvist showed that, because of the phase separation between red cells and plasma that occurs in microvessels and glass capillary tubes (11), an increasing departure from Poiseuille's law is observed with decreasing diameter (12). However, although they were able to establish this fact, which has come to be known as the Fåhræus–Lindqvist effect, the means for predicting blood-flow parameters on theoretical grounds in either glass capillary tubes or microvessels beyond the single-file flow regime eluded scientists working in this area for the remainder of the century.
Because red blood cells are less concentrated near the wall than near the center of microvessels, mean red-cell velocity exceeds mean plasma velocity. This disparity in mean velocities gives rise to the so-called Fåhræus effect, which is associated with a decrease in the instantaneous volume fraction of red cells in the vessel or tube hematocrit, HT, relative to the red-cell concentration discharged from the vessel, or discharge hematocrit, HD. In general, neither HT nor HD are equal to the systemic hematocrit, Hsys, which is obtained from a large artery or vein, because red cells and plasma distribute unevenly at microvascular bifurcations (13). Measurements of HT in microvessels in vivo have been attempted either by using microphotometric methods (8, 14) or by counting labeled red cells (15), neither of which are reliable in microvessels more than ≈20 μm in diameter. Measurements of HD have been attempted in microvessels in vivo either by micropipette aspiration and centrifugation (16), which is extremely cumbersome and feasible only in some tissues, or by a microphotometric method (13), which assumes the same Fåhræus effect in glass tubes and microvessels of the same size. The accuracy of this assumption, however, is dubious in light of recent evidence of the influence of the endothelial surface layer (ESL) on plasma flow near the wall of microvessels in vivo (17, 18). In addition to the difficulties associated with determining HT and HD in vivo, attempts (8, 19) at measuring or estimating either axial pressure gradient or flow resistance accurately in microvessels have been unsuccessful in vivo.
The central tenet of our approach (20), which we hereafter shall refer to as the microviscometric method, is that distributions in the local viscosity, μ(r), as a function of the radial position, r, over the cross section of glass capillary tubes and microvessels, can be determined analytically from the cross-sectional axial velocity distribution, vz(r), where vz(r) can be extracted from particle tracers in the flow by using intravital fluorescent microparticle image velocimetry (μ-PIV) (17, 21, 22). In addition to the viscosity distribution, μ(r), we can use the microviscometric method to predict quantitatively various flow parameters in microvessels in vivo, including axial pressure gradient, dp/dz; volume flow rate, Q; and the relative apparent blood viscosity, ηrel, defined as the ratio of steady volume–flow rates per unit pressure drop of blood plasma relative to whole blood. The velocity distribution, vz(r), is related kinematically to the shear rate distribution, 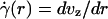 , where
, where 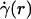 is assumed to be related constitutively to the shear stress distribution, τ(r) = μ(r)
is assumed to be related constitutively to the shear stress distribution, τ(r) = μ(r) 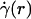 , for a linearly viscous fluid. By means of rigorous analysis of glass-tube experiments in vitro, where pressure gradient and feed hematocrit can be measured directly, and isovolemic hemodilution experiments in vivo, where the change in systemic hematocrit is known, we provide quantitative validation of the microviscometric method and show a decrease in local and apparent blood viscosity in individual microvessels as a direct result of reducing systemic hematocrit.
, for a linearly viscous fluid. By means of rigorous analysis of glass-tube experiments in vitro, where pressure gradient and feed hematocrit can be measured directly, and isovolemic hemodilution experiments in vivo, where the change in systemic hematocrit is known, we provide quantitative validation of the microviscometric method and show a decrease in local and apparent blood viscosity in individual microvessels as a direct result of reducing systemic hematocrit.
Materials and Methods
Analytical Methods. The analysis (20) on which the microviscometric method is based invokes the continuum approximation and regards the heterogeneous red-cell suspension as a homogeneous, continuously varying, and linearly viscous incompressible fluid that has a spatially nonuniform viscosity distribution (23) over the vessel cross section. Cokelet (2) found support for the continuum approximation in his studies by using physiological concentrations of red blood cells suspended in plasma flowing at physiological shear rates in glass tubes as small as 20 μm in diameter. As for our constitutive assumption, our results are consistent with the linearly viscous approximation because, as we will show, over most of the tube or vessel cross section, shear rates are more than ≈50 s-1 under physiologically typical flow rates. Blood viscosity at a given hematocrit is nearly constant at such shear rates (24). Thus, we assume that at shear rates of more than ≈50 s-1, blood is Newtonian in the sense that local viscosity depends only on local thermodynamic state and local hematocrit and is independent of shear rate.
It is further assumed that, in postcapillary venules, the flow is steady and the velocity profile is axisymmetric and fully developed. A brief summary of the analysis of an axisymmetric, fully developed, and steady incompressible flow of a linearly viscous fluid having a spatially varying viscosity distribution over the cross section of both cylindrical glass tubes and ESL-lined microvessels is provided in Supporting Text, which is published as supporting information on the PNAS web site. Full details are given in ref. 20.
Glass-Tube Experiments. Fluorescent μ-PIV (21, 22) was performed by using a method described in ref. 17. Fluoresbrite yellow–green microspheres (0.47 ± 0.01 μm, 1.05 g/cm3; Polysciences) were visualized by using stroboscopic double-flash (5- to 16.67-ms apart; Strobex 11360, Chadwick–Helmuth, El Monte, CA) epi-illumination, and recordings were made by using a VE-1000CD charge-coupled device camera (Dage–MTI, Michigan City, IN) on an S-VHS recorder (Panasonic, Secaucus, NJ).
The in vitro perfusion system consisted of a 3-ml feed reservoir and a horizontally mounted glass capillary tube (length, 27.5, 26.2, and 20 mm; i.d., 54.2, 50.7, and 81.0 μm, respectively), which were connected by a microhematocrit tube (i.d., 1.2 mm) and silastic tubing (Dow-Corning), to a 10-ml downstream reservoir that could be manipulated vertically with a Vernier caliper (Nolan Supply, Syracuse, NY) (17, 25). To account for the unavoidable mismatch of refractive indices between the perfusate and the inner tube wall, the radial position of every microsphere was corrected by using Snell's law (17). Human blood samples were obtained from healthy volunteers by means of venipuncture, anticoagulated with heparin (final concentration, 10 units/ml), and used within 2–4 h after withdrawal. The buffy coat was discarded after centrifugation, and erythrocytes were resuspended in plasma. The hematocrit of each sample, which was adjusted to one of five nominal values between 0% and 60%, was determined by using a Hemavet 850 cell counter (CDC Technologies, Oxford, CT).
Intravital Experiments. Male mice (C57BL/6) obtained from The Jackson Laboratory were prepared for intravital microscopy by following the methods described in ref. 17. All animal experiments were conducted under a protocol approved by the University of Virginia Institutional Animal Care and Use Committee (protocol no. 2474). All mice appeared to be healthy and were 8–14 weeks of age. Microscopic observations of microspheres in vivo were made in venules of the exteriorized cremaster muscle and followed the in vitro protocols described above and in Supporting Text. No optical correction of the radial positions of microspheres measured in vivo was necessary because the difference in the refractive indices of blood plasma and the surrounding tissue is negligibly small (17).
Hemodilution. Mice were given a 1.0-ml i.p. injection of physiological saline to help prevent fluid imbalance before cremaster exteriorization. During hemodilution, the carotid artery cannula was allowed to bleed into an inverted syringe tube for accurate volume measurements. Saline was infused through the jugular vein cannula at a volume flow rate matched to the carotid bleed rate until 0.75 ml was exchanged. Blood samples (30 μl) were drawn from the carotid artery at least 25 min before and after hemodilution for systemic hematocrit measurements. Up to two vessels per animal were recorded before and after hemodilution and analyzed offline by using the microviscometric method, as described above and in Supporting Text. Exact vessel locations were noted by using muscle striations as markers.
Data Analysis. Video recordings were digitized with premiere software (Adobe Systems, Mountain View, CA; final resolution 5.43 pixels per μm) and then analyzed with the public domain National Institutes of Health image program (available at http://rsb.info.nih.gov/nih-image), as described in refs. 17 and 26. The flash-time interval for μ-PIV recordings was chosen such that the two images for a given microsphere were 3- to 30-μm apart. The center-to-center distance between these two images and the shortest distance between the microsphere center and the vessel or tube wall were measured for ≈75 microspheres in each glass capillary tube and ≈50 microspheres in each microvessel. Measurements were restricted to a section of capillary tube or microvessel <180 μm or 15 μm in axial length, respectively. Each μ-PIV data set was used to extract an axisymmetric velocity profile, vz(r), by following the methods described in Supporting Text.
Results
To test the validity of the microviscometric method in a model system, we obtained fluorescent μ-PIV data over the cross section of glass capillary tubes (i.d., ≈50–80 μm) that were perfused steadily with saline, plasma, and red-cell suspensions in plasma, as described above. Distributions predicted in glass capillary tubes by using the microviscometric method were qualitatively similar to those shown in Fig. 1 (see Figs. 5–14, which are published as supporting information on the PNAS web site). For red-cell suspensions, results consistently revealed a concentrated red-cell core and a cell-poor region near the vessel wall (see Figs. 5–12). Furthermore, the shear-rate distributions consistently showed a nearly linear variation over ≈50–70% of the tube cross section around the center of the tube and a highly nonlinear variation near the tube wall (see Figs. 1 and 5–12). The nearly parabolic velocity distributions and linear shear rate distributions predicted in saline-perfused glass tubes (see Figs. 1 A and C, 13, and 14) after optically correcting the measured radial position of each microsphere provide confidence in the optical correction procedure that we used for all of our glass-tube μ-PIV data. Further validation is provided in ref. 17.
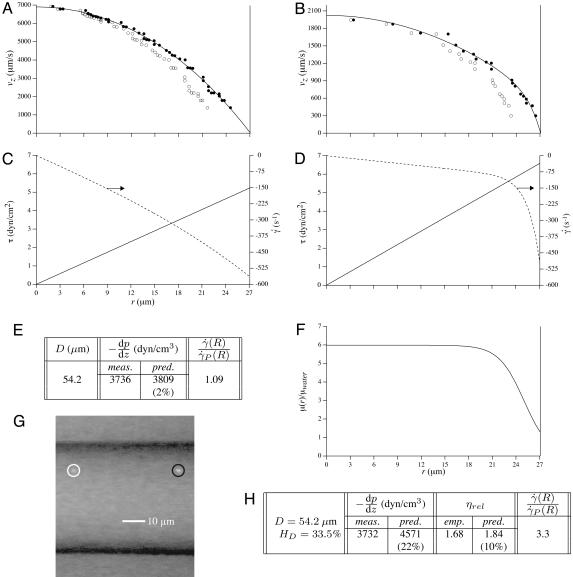
Fig. 1.
Optically corrected fluorescent (•) and raw (○) μ-PIV data obtained from a 54.2-μm-diameter glass tube steadily perfused with saline (A) and washed red cells suspended in plasma (B) (human blood, HD = 33.5%). Superimposed on the μ-PIV data in A and B are axisymmetric velocity distributions, vz(r), extracted from the data by following the methods described in ref. 20. (C and D) Distributions in shear rate (dashed curves, right axes) and shear stress (solid curves, left axes) over the tube cross section, corresponding to the velocity distributions shown in A and B.(F) Predicted distribution in the normalized viscosity, μ(r)/μwater, derived by using the analytical expression for μ(r) (see Supporting Text). (E and H) Geometric and rheological quantities associated with A and B, respectively, including the measured tube diameter, D, and discharge hematocrit, HD; the measured and predicted values of the axial pressure gradient, dp/dz; and the ratio of the predicted wall shear rate, 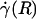 , to the wall shear rate,
, to the wall shear rate, 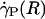 , of a Poiseuille flow, having the centerline velocities shown in A and B. Also tabulated in H are the empirically estimated (3) and predicted values of the relative apparent viscosity, ηrel. Percentages given in parentheses under each of the predicted values listed in the tables correspond to the percentage of difference between measured (or empirically estimated) and predicted values. (G) Bright-field image of the saline-perfused glass tube referenced in A showing dual images of one microsphere (upstream, white circle; downstream, black circle) separated in time by the double-flash interval.
, of a Poiseuille flow, having the centerline velocities shown in A and B. Also tabulated in H are the empirically estimated (3) and predicted values of the relative apparent viscosity, ηrel. Percentages given in parentheses under each of the predicted values listed in the tables correspond to the percentage of difference between measured (or empirically estimated) and predicted values. (G) Bright-field image of the saline-perfused glass tube referenced in A showing dual images of one microsphere (upstream, white circle; downstream, black circle) separated in time by the double-flash interval.
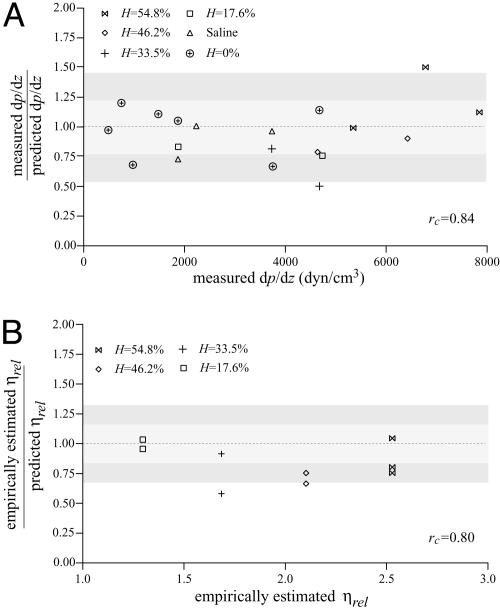
Evidence to support the validity of the microviscometric method in vitro is shown in Fig. 2, in which directly measured values of dp/dz and empirically estimated (3) values of ηrel agree closely with their corresponding values predicted by using the microviscometric method for each μ-PIV data set. Furthermore, these results provide support for the validity of using the continuum approximation of blood to obtain estimates of dp/dz and ηrel in glass capillary tubes ≈50 μm in diameter.
Fig. 2.
Predictability of dp/dz and ηrel by using microviscometric analysis of μ-PIV data obtained from glass capillary tubes in vitro. Ratio of the measured to predicted value of dp/dz versus the corresponding measured value (A) and ratio of the empirically estimated (3) to predicted value of ηrel versus the corresponding empirically estimated value (B). Predicted values were determined by applying the microviscometric method to the μ-PIV data obtained from the glass-tube experiments. The light and dark shaded regions span, respectively, one and two standard deviations in the distributions around unity. The standard deviation corresponds to 23% for dp/dz and 16% for ηrel. The correlation coefficient, rc, is shown for its corresponding predicted quantity.
To apply the microviscometric method to blood flow in microvessels in vivo, a generalization is introduced (20) to account for the hemodynamic influence of the ESL (17, 18, 27, 28). Expressions for μ(r) and dp/dz apply in microvessels (see Supporting Text) if the tube radius, R, is replaced by a, where a is the radial location of the effective hydrodynamic interface between the blood in the lumen and the ESL (17, 20). It is assumed that red cells and particle tracers do not invade the ESL (7, 17, 28–30) and that plasma flow through the ESL can be well approximated with the Brinkman equation (17, 20, 29, 31, 32), where the hydraulic resistivity, K, of the ESL is taken to be more than ≈109 dyn·s/cm4 (1 dyn = 10 μN) (7, 17, 29, 30). The thickness, R - a, of the ESL is estimated by following the methods described in ref. 20, in which the value of a is determined by minimizing the least-squares error in the fit to the μ-PIV data. The minimum least-squares error for the 12 microvessels that we analyzed (i.d., 34.2 ± 1.7 μm) occurred over ESL thicknesses ranging 0.29–0.71 μm, with an average thickness of ≈0.51 ± 0.04 μm for K = 109 dyn·s/cm4 (see Table 1 and Figs. 15–26, which are published as supporting information on the PNAS web site). By contrast, the least-squares error associated with in vitro μ-PIV data increased monotonically with increasing R - a > 0 (see Figs. 5–12), which is consistent with the fact that no ESL is present in glass tubes. In each of the microvessels that we analyzed, ESL thickness estimates showed little sensitivity to values of K > 109 dyn·s/cm4 (see D in Figs. 15–26).
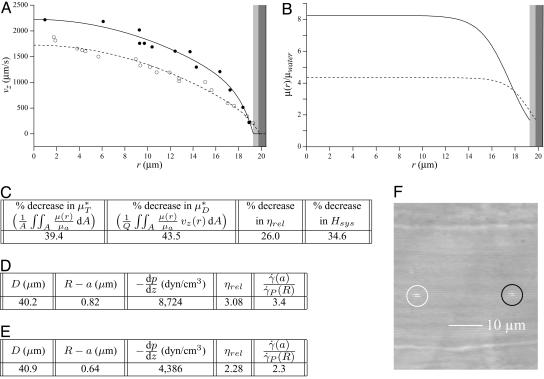
As an example, Fig. 3 shows the results of one in vivo hemodilution experiment in a mouse cremaster-muscle venule (diameter, ≈40 μm). Results for other hemodilution experiments are shown in Figs. 27–31 and Table 2, which are published as supporting information on the PNAS web site. To facilitate a quantitative comparison between the results of our hemodilution experiments and quantities that can be predicted by the microviscometric method, we define 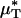 , which is analogous to tube hematocrit, HT, and
, which is analogous to tube hematocrit, HT, and 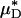 , which is analogous to discharge hematocrit, HD, where
, which is analogous to discharge hematocrit, HD, where
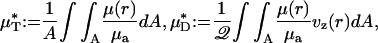 |
[1] |
A is the cross-sectional area of the vessel lumen, Q is the volume flow rate in the vessel, and μa = μ(a). The analogous quantities, HT and HD, correspond to the mean instantaneous red-cell concentration in the vessel and the mean red-cell flux fraction through the vessel, respectively (see Supporting Text). It is evident from Eq. 1 that 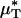 corresponds to the mean instantaneous normalized viscosity over the vessel cross section, whereas for a unit volume flow rate,
corresponds to the mean instantaneous normalized viscosity over the vessel cross section, whereas for a unit volume flow rate, 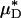 is simply the product of the local viscosity (which depends on the local red-cell concentration) and the local volume flow rate integrated over the vessel cross section. If both vz(r) and μ(r) are positive functions over the vessel cross section and decrease monotonically with increasing radial position, it will always be the case that
is simply the product of the local viscosity (which depends on the local red-cell concentration) and the local volume flow rate integrated over the vessel cross section. If both vz(r) and μ(r) are positive functions over the vessel cross section and decrease monotonically with increasing radial position, it will always be the case that 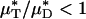 , just as the Fåhræus effect implies that HT/HD < 1. The relative apparent viscosity, ηrel, however, is a measure of flow resistance of whole blood relative to blood plasma.
, just as the Fåhræus effect implies that HT/HD < 1. The relative apparent viscosity, ηrel, however, is a measure of flow resistance of whole blood relative to blood plasma.
Fig. 3.
Results of a microviscometric analysis of μ-PIV data obtained from a mouse cremaster venule during one hemodilution experiment. Intravital fluorescent μ-PIV data with predicted velocity profiles (A) and normalized viscosity profiles (B) in a venule (diameter, ≈40 μm) of the mouse cremaster muscle before (•, solid curves) and after (○, dotted curves) systemic hemodilution. Curves shown have the same interpretation as those shown in Fig. 1. The shaded regions near the vessel wall represent the ESL before (light gray) and after (dark gray) systemic hemodilution, where the ESL is modeled as a Brinkman medium (20, 31, 32) having a hydraulic resistivity, K = 109 dyn·s/cm4. The thickness of the ESL is estimated by minimizing the normalized least-squares error associated with the fit to the μ-PIV data (see Figs. 5–12), as described in ref. 20. Tabulated in C for this vessel is the percentage of decrease after systemic hemodilution in 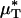 ,
, 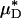 , ηrel, and the systemic hematocrit, Hsys. Parameters tabulated for before (D) and after (E) hemodilution include the measured vessel diameter, D; the estimated ESL thickness, R - a, corresponding to K = 109 dyn·s/cm4; the predicted axial pressure gradient, dp/dz; the predicted relative apparent viscosity, ηrel; and the ratio of the predicted interfacial shear rate,
, ηrel, and the systemic hematocrit, Hsys. Parameters tabulated for before (D) and after (E) hemodilution include the measured vessel diameter, D; the estimated ESL thickness, R - a, corresponding to K = 109 dyn·s/cm4; the predicted axial pressure gradient, dp/dz; the predicted relative apparent viscosity, ηrel; and the ratio of the predicted interfacial shear rate, 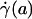 , to the wall shear rate,
, to the wall shear rate, 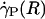 , of a Poiseuille flow having the centerline velocity associated with the profiles shown in A. (F) Bright-field image of a venule showing dual images of one microsphere (upstream, white circle; downstream, black circle) separated in time by the double-flash interval.
, of a Poiseuille flow having the centerline velocity associated with the profiles shown in A. (F) Bright-field image of a venule showing dual images of one microsphere (upstream, white circle; downstream, black circle) separated in time by the double-flash interval.
If the species-specific transport relationship, H(μ), were available for mouse blood, the distribution μ(r)/μa could be replaced by H[μ(r)] in Eq. 1 to provide expressions for HT and HD (see Supporting Text). In the absence of such data, we cannot estimate HT or HD directly; however, we can nevertheless use Eq. 1 to quantitatively evaluate the accuracy of the microviscometric method in vivo by noting that the percentage of decrease in 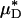 would likely be very similar to the percentage of decrease in its counterpart, H (and likewise for
would likely be very similar to the percentage of decrease in its counterpart, H (and likewise for 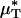 and its counterpart, HT), because the transport relationship enters into the integrand of each term in the numerator of the percentage of decrease in HD in the same way as it does in the denominator. That is, we assume that
and its counterpart, HT), because the transport relationship enters into the integrand of each term in the numerator of the percentage of decrease in HD in the same way as it does in the denominator. That is, we assume that 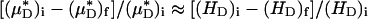 , where i and f refer a particular quantity to its value in the same vessel before and after systemic hemodilution, respectively.
, where i and f refer a particular quantity to its value in the same vessel before and after systemic hemodilution, respectively.
To test the validity of this assumption quantitatively, we again turn to the results of our glass-tube experiments in which HD is known. We can regard any pair of glass-tube experiments having different measured values of HD as an “in vitro hemodilution experiment,” in which the higher and lower values of HD in the pair can be thought of as corresponding to before and after hemodilution, respectively. Substituting the distribution μ(r) predicted from the microviscometric method into Eq. 1, we have determined 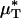 and
and 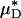 for each of our glass-tube experiments involving red-cell suspensions in plasma. For any two glass-tube experiments having different measured values of HD, the accuracy with which we can predict the percentage of difference in the directly measured values of HD from the percentage of difference in our predicted values of
for each of our glass-tube experiments involving red-cell suspensions in plasma. For any two glass-tube experiments having different measured values of HD, the accuracy with which we can predict the percentage of difference in the directly measured values of HD from the percentage of difference in our predicted values of 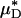 is shown in Fig. 4. It is evident from these results that, even without knowledge of the specific transport relationship, H(μ), we can indirectly infer the percentage of difference in HD from our predictions of the percentage of difference in
is shown in Fig. 4. It is evident from these results that, even without knowledge of the specific transport relationship, H(μ), we can indirectly infer the percentage of difference in HD from our predictions of the percentage of difference in 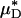 with an accuracy that is similar to that which was achieved in our direct predictions of the rheological quantities shown in Fig. 2.
with an accuracy that is similar to that which was achieved in our direct predictions of the rheological quantities shown in Fig. 2.
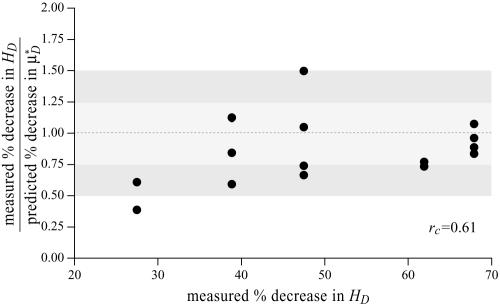
Fig. 4.
Ratio of the measured percentage of decrease in HD to the predicted percentage of decrease in 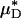 versus the corresponding measured percentage of decrease in HD. Predicted values were determined by applying Eq. 1 and the microviscometric method to the μ-PIV data obtained from the glass-tube experiments. The light and dark shaded regions span, respectively, one and two standard deviations in the distributions around unity, where the standard deviation corresponds to 25%. The correlation coefficient, rc, is 0.61.
versus the corresponding measured percentage of decrease in HD. Predicted values were determined by applying Eq. 1 and the microviscometric method to the μ-PIV data obtained from the glass-tube experiments. The light and dark shaded regions span, respectively, one and two standard deviations in the distributions around unity, where the standard deviation corresponds to 25%. The correlation coefficient, rc, is 0.61.
Having established, in glass tubes, the accuracy with which the percentage of change in 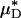 can be used to infer the percentage of change in HD, provides some measure of confidence for using this metric in vivo. Further support, however, can be found directly from our in vivo hemodilution experiments (see Figs. 3 and 27–31) by comparing the average percentage of decrease in
can be used to infer the percentage of change in HD, provides some measure of confidence for using this metric in vivo. Further support, however, can be found directly from our in vivo hemodilution experiments (see Figs. 3 and 27–31) by comparing the average percentage of decrease in 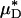 with the average percentage of decrease in Hsys after isovolemic hemodilution (see Table 2). In all five vessels analyzed in vivo,
with the average percentage of decrease in Hsys after isovolemic hemodilution (see Table 2). In all five vessels analyzed in vivo, 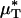 and
and 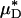 decreased after systemic hemodilution. For an average decrease in Hsys of 33.5 ± 1.0%, the average percentage of decrease in
decreased after systemic hemodilution. For an average decrease in Hsys of 33.5 ± 1.0%, the average percentage of decrease in 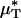 and
and 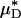 (and, by inference, HT and HD) across all five vessels was predicted to be 33.5 ± 5.2 and 36.3 ± 4.8%, respectively. Because red-cell screening and plasma skimming at vessel branch points gives rise to network heterogeneity in the discharge hematocrits of individual microvessels, the percentage of decrease in HD for any individual microvessel is not, in general, equal to the percentage of decrease in the systemic hematocrit of the animal. Although it was impractical to measure the percentage of decrease in HD directly after hemodilution in each of the vessels that we analyzed, there is evidence that in microvessels more than ≈20 μm in diameter, the average discharge hematocrit across N microvessels in a network does indeed approach the systemic hematocrit with increasing N (13). Hence, the mean fractional decrease in
(and, by inference, HT and HD) across all five vessels was predicted to be 33.5 ± 5.2 and 36.3 ± 4.8%, respectively. Because red-cell screening and plasma skimming at vessel branch points gives rise to network heterogeneity in the discharge hematocrits of individual microvessels, the percentage of decrease in HD for any individual microvessel is not, in general, equal to the percentage of decrease in the systemic hematocrit of the animal. Although it was impractical to measure the percentage of decrease in HD directly after hemodilution in each of the vessels that we analyzed, there is evidence that in microvessels more than ≈20 μm in diameter, the average discharge hematocrit across N microvessels in a network does indeed approach the systemic hematocrit with increasing N (13). Hence, the mean fractional decrease in 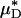 should approach the mean fractional decrease in Hsys as the number of analyzed vessels increases. This trend is observed in the in vivo results presented here.
should approach the mean fractional decrease in Hsys as the number of analyzed vessels increases. This trend is observed in the in vivo results presented here.
As with 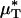 and
and 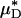 , our microviscometric analysis predicted that in every vessel that we analyzed, flow resistance, as measured by the relative apparent viscosity, ηrel, was also seen to decrease (25.1 ± 6.1%, on average) after systemic hemodilution. Collectively, these results provide the first direct and quantitative estimate of the accompanying fractional decrease in local and apparent blood viscosity in individual microvessels that is associated with the clinically relevant procedure of isovolemic hemodilution.
, our microviscometric analysis predicted that in every vessel that we analyzed, flow resistance, as measured by the relative apparent viscosity, ηrel, was also seen to decrease (25.1 ± 6.1%, on average) after systemic hemodilution. Collectively, these results provide the first direct and quantitative estimate of the accompanying fractional decrease in local and apparent blood viscosity in individual microvessels that is associated with the clinically relevant procedure of isovolemic hemodilution.
A noteworthy trend observed in these results is that the average percentage of decrease in measured Hsys and predicted 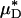 were, respectively, 33% and 45% greater than the average percentage of decrease in predicted ηrel in vivo. This trend was observed also in our glass-tube studies, in which the average percentage of decrease in measured HD and predicted
were, respectively, 33% and 45% greater than the average percentage of decrease in predicted ηrel in vivo. This trend was observed also in our glass-tube studies, in which the average percentage of decrease in measured HD and predicted 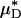 were, respectively, 26% and 48% greater than the average percentage of decrease in predicted ηrel. This trend has potentially important clinical implications in the context of hemodilution procedures because it is the decrease in ηrel, and not the decrease in HD or Hsys, that quantitatively determines the decrease in microvascular-flow resistance. Thus, these results suggest that the fractional decrease in systemic hematocrit is ≈25–35% greater than the accompanying fractional decrease in microvascular-flow resistance.
were, respectively, 26% and 48% greater than the average percentage of decrease in predicted ηrel. This trend has potentially important clinical implications in the context of hemodilution procedures because it is the decrease in ηrel, and not the decrease in HD or Hsys, that quantitatively determines the decrease in microvascular-flow resistance. Thus, these results suggest that the fractional decrease in systemic hematocrit is ≈25–35% greater than the accompanying fractional decrease in microvascular-flow resistance.
Discussion
By using fluorescently labeled platelets as endogenous particle tracers, previous work has revealed blunted velocity profiles in microvessels in vivo and showed that the Poiseuille flow approximation underestimates wall shear rate in these microvessels (21, 23). However, those results were not analyzed rigorously to yield all of the distributions and rheological parameters estimated here, nor could they have been, because the particle tracers that were used were too large to provide the necessary spatial resolution. Furthermore, these earlier studies did not account for the ESL, which was not well documented at the time. In fact, the near complete retardation of plasma by the ESL adjacent to the vessel wall causes fluid shear stress and fluid shear rate at the luminal endothelial-cell surface [i.e., wall shear rate, 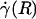 , and wall shear stress, τ(R)] to be very nearly zero for values of hydraulic resistivity more than ≈109 dyn·s/cm4 (17). Consequently, these results show that the appropriate quantitative metrics characterizing near-wall microfluidics in microvessels are the interfacial shear rate,
, and wall shear stress, τ(R)] to be very nearly zero for values of hydraulic resistivity more than ≈109 dyn·s/cm4 (17). Consequently, these results show that the appropriate quantitative metrics characterizing near-wall microfluidics in microvessels are the interfacial shear rate, 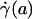 , and interfacial shear stress,
, and interfacial shear stress, 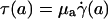 , which can now be predicted by using the microviscometric method.
, which can now be predicted by using the microviscometric method.
The most popular and widespread method for estimating microvascular blood-flow parameters in vivo is the dual-slit technique, which uses mean blood-flow velocity, derived from centerline velocity measured by cross correlation (8, 33), to estimate wall shear rate. Most studies make this estimate by assuming a Poiseuille flow in the microvessel and imposing the no-slip condition at the vessel wall. However, as these results show, under physiologically typical discharge hematocrits and flow rates, the interfacial shear rate, 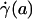 , corresponding to the shear rate at the effective interface between the ESL and the free lumen, is, on average, about five times greater than estimates of wall shear rate based on the dual-slit technique assuming Poiseuille flow (see Table 1).
, corresponding to the shear rate at the effective interface between the ESL and the free lumen, is, on average, about five times greater than estimates of wall shear rate based on the dual-slit technique assuming Poiseuille flow (see Table 1).
Microrheological phenomena in terminal vascular beds impact broad areas of medicine and physiology. We have demonstrated that the microviscometric method allows estimation of the axial pressure gradient and relative apparent viscosity of steady flows in microvessels 20–50 μm in diameter, without the need to impale these vessels with micropipettes and without any prior assumptions about the Fåhræus or Fåhræus–Lindqvist effects in vivo. Because the experimental methods used to obtain μ-PIV data are compatible with most intravital microscopy protocols, the microviscometric method can provide a systematic, standardized approach by which microvascular-flow parameters can be estimated in vivo. The radial distributions in viscosity, shear stress, and shear rate predicted here, as well as the means for determining them, will allow detailed quantitative modeling of the hemodynamics of microvascular networks in vivo. Furthermore, the ability of the microviscometric method to detect the presence of the ESL and estimate its hydrodynamically relevant thickness in microvessels >20 μm in diameter is essential to the quantitative aspects of a broad range of fields in microvascular physiology. In particular, by using the microviscometric method before and after various treatments to degrade the ESL (17, 18, 20, 28, 34), we are now poised to gain insight into the role of the ESL in inflammation, endothelial-cell mechanotransduction, microvascular hemodynamics, and flow-mediated mechanisms in angiogenesis (27). Finally, by using the microviscometric method before and after isovolemic hemodilution, we have directly demonstrated the impact of this procedure on hemodynamics in individual microvessels. These results have direct clinical relevance because systemic hemodilution has been used to save blood during surgery and to reduce peripheral resistance, and it is sometimes used in the treatments of Ménières disease, polycythemia vera, sickle-cell anemia, and new-borns with a systemic hematocrit in excess of ≈70%. Because data similar to the data underlying the present analysis can be obtained in many organs and tissues, including those that are not transparent and require fluorescent epi-illumination, it is likely that data sets with broad applicability to physiology and pathophysiology will now become available.
Supplementary Material
Acknowledgments
We thank A. L. Butterworth for assistance in data acquisition from video tape. This work was supported by Whitaker Foundation Grant TF-02-0024, National Science Foundation Grant BES-0093985 (to E.R.D.), and National Institutes of Health Grants HL64381 and T32GM 08715-01A1 (to K.L.).
Abbreviations: μ-PIV, microparticle image velocimetry; ESL, endothelial surface layer.
References
- 1.Goldsmith, H. L. (1986) Microvasc. Res. 31, 121-142. [DOI] [PubMed] [Google Scholar]
- 2.Cokelet, G. R. (1999) Biorheology 36, 343-358. [PubMed] [Google Scholar]
- 3.Pries, A. R., Neuhaus, D. & Gaehtgens, P. (1992) Am. J. Physiol. 263, H1770-H1778. [DOI] [PubMed] [Google Scholar]
- 4.Secomb, T. W., Skalak, R., Özkaya, N. & Gross, J. F. (1986) J. Fluid. Mech. 163, 405-423. [Google Scholar]
- 5.Damiano, E. R. (1998) Microvasc. Res. 55, 77-91. [DOI] [PubMed] [Google Scholar]
- 6.Secomb, T. W., Hsu, R. & Pries, A. R. (1998) Am. J. Physiol. 274, H1016-H1022. [DOI] [PubMed] [Google Scholar]
- 7.Secomb, T. W., Hsu, R. & Pries, A. R. (2001) Am. J. Physiol. 281, H629-H636. [DOI] [PubMed] [Google Scholar]
- 8.Lipowsky, H. H., Kovalcheck, S., Zweifach, B. W. (1978) Circ. Res. 43, 738-749. [DOI] [PubMed] [Google Scholar]
- 9.Sharan, M., Popel, A. S. (2001) Biorheology 38, 415-428. [PubMed] [Google Scholar]
- 10.Poiseuille, J. L. M. (1830) J. Physiol. Exp. Pathol. 10, 277-295. [Google Scholar]
- 11.Fåhræus, R. (1928) Klin. Wochenschr. 7, 100-106. [Google Scholar]
- 12.Fåhræus, R. & Lindqvist, T. (1931) Am. J. Physiol. 96, 562-568. [Google Scholar]
- 13.Pries, A. R., Ley, K. & Gaehtgens, P. (1986) Am. J. Physiol. 251, H1324-H1332. [DOI] [PubMed] [Google Scholar]
- 14.Jendrucko, R. J. & Lee, J. S. (1973) Microvasc. Res. 6, 316-331. [DOI] [PubMed] [Google Scholar]
- 15.Sarelius, I. H. & Duling, B. R. (1982) Am. J. Physiol. 243, H1018-H1026. [DOI] [PubMed] [Google Scholar]
- 16.Desjardins, C. & Duling, B. R. (1987) Am. J. Physiol. 252, H494-H503. [DOI] [PubMed] [Google Scholar]
- 17.Smith, M. L., Long, D. S., Damiano, E. R. & Ley, K. (2003) Biophys. J. 85, 637-645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Pries, A. R., Secomb, T. W., Jacobs, H., Sperandio, M. B., Osterloh, K. & Gaehtgens, P. (1997) Am. J. Physiol. 273, H2272-H2279. [DOI] [PubMed] [Google Scholar]
- 19.Pries, A. R., Secomb, T. W., Gessner, T., Sperandio, M. B., Gross, J. F. & Gaehtgens, P. (1994) Circ. Res. 75, 904-915. [DOI] [PubMed] [Google Scholar]
- 20.Damiano, E. R., Long, D. S. & Smith, M. L. (2004) J. Fluid Mech. 512, 1-19. [Google Scholar]
- 21.Tangelder, G. J., Slaaf, D. W., Muijtjens, A. M., Arts, T., oude Egbrink, M. G. & Reneman, R. S. (1986) Circ. Res. 59, 505-514. [DOI] [PubMed] [Google Scholar]
- 22.Santiago, J. G., Wereley, S. T., Meinhart, C. D., Beebe, D. J. & Adrian, R. J. (1998) Exp. Fluids 25, 316-319. [Google Scholar]
- 23.Bugliarello, G. & Hayden, J. W. (1963) Trans. Soc. Rheol. 7, 209-230. [Google Scholar]
- 24.Chien, S., Usami, S., Taylor, H. M., Lundberg, J. L. & Gregersen, M. I. (1966) J. Appl. Physiol. 21, 81-87. [DOI] [PubMed] [Google Scholar]
- 25.Alonso, C., Pries, A. R., Kiesslich, O., Lerche, D. & Gaehtgens, P. (1995) Am. J. Physiol. 268, H25-H32. [DOI] [PubMed] [Google Scholar]
- 26.Norman, K. E. (2001) Microcirculation 8, 243-249. [DOI] [PubMed] [Google Scholar]
- 27.Pries, A. R., Secomb, T. W., Gaehtgens, P. (2000) Pflügers Arch. 440, 653-666. [DOI] [PubMed] [Google Scholar]
- 28.Vink, H. & Duling, B. R. (1996) Circ. Res. 79, 581-589. [DOI] [PubMed] [Google Scholar]
- 29.Feng, J. & Weinbaum, S. (2000) J. Fluid Mech. 422, 281-317. [Google Scholar]
- 30.Damiano, E. R. & Stace, T. M. (2002) Biophys. J. 82, 1153-1175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Damiano, E. R., Duling, B. R., Ley, K. & Skalak, T. C. (1996) J. Fluid Mech. 314, 163-189. [Google Scholar]
- 32.Damiano, E. R., Long, D. S., El-Khatib, F. H. & Stace, T. M. (2004) J. Fluid Mech. 500, 75-101. [Google Scholar]
- 33.Baker, M. & Wayland, H. (1974) Microvasc. Res. 7, 131-143. [DOI] [PubMed] [Google Scholar]
- 34.Desjardins, C. & Duling, B. R. (1990) Am. J. Physiol. 258, H647-H654. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.