Skip to main content
PMC home page
Bioinformatics logoLink to Bioinformatics
. 2015 Jun 10;31(12):i53–i61. doi: 10.1093/bioinformatics/btv238

IgRepertoireConstructor: a novel algorithm for antibody repertoire construction and immunoproteogenomics analysis

Yana Safonova 1,2,†, Stefano Bonissone 3,†, Eugene Kurpilyansky 2, Ekaterina Starostina 1,2, Alla Lapidus 1,2, Jeremy Stinson 4, Laura DePalatis 4, Wendy Sandoval 4, Jennie Lill 4, Pavel A Pevzner 1,4,5,*
PMCID: PMC4542777  PMID: 26072509

Abstract

The analysis of concentrations of circulating antibodies in serum (antibody repertoire) is a fundamental, yet poorly studied, problem in immunoinformatics. The two current approaches to the analysis of antibody repertoires [next generation sequencing (NGS) and mass spectrometry (MS)] present difficult computational challenges since antibodies are not directly encoded in the germline but are extensively diversified by somatic recombination and hypermutations. Therefore, the protein database required for the interpretation of spectra from circulating antibodies is custom for each individual. Although such a database can be constructed via NGS, the reads generated by NGS are error-prone and even a single nucleotide error precludes identification of a peptide by the standard proteomics tools. Here, we present the IgRepertoireConstructor algorithm that performs error-correction of immunosequencing reads and uses mass spectra to validate the constructed antibody repertoires.

Availability and implementation: IgRepertoireConstructor is open source and freely available as a C++ and Python program running on all Unix-compatible platforms. The source code is available from http://bioinf.spbau.ru/igtools.

Contact: ppevzner@ucsd.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

Until 2009, the computational analysis of antibodies had been performed via proteomics techniques (Bandeira et al.., 2008) and had not utilized DNA sequencing technologies. Weinstein et al. (2009) were the first to demonstrate the power of DNA sequencing for analyzing antibody repertoires and to open a ‘next generation sequencing (NGS) era’ in antibody analysis (Fig. 1a). Although this study was quickly followed by many other immunosequencing (Ig-seq) studies (Arnaout et al., 2011; Jiang et al., 2011, 2013; Laserson et al. 2014; Vollmers et al.., 2013); until 2012, there were no attempts to integrate NGS and mass spectrometry (MS) approaches for antibody analysis. Such integration (immunoproteogenomics) is important since it represents a bottleneck for an emerging approach that promises to transform the antibody industry from focusing on single (monoclonal) antibodies, toward analyzing polyclonal antibodies.

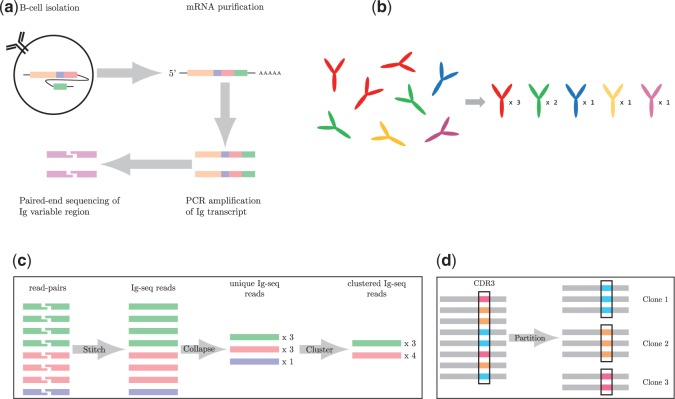
Fig. 1.

Fig. 1.

Open in a new tab

(a) An overview of immunoglobulin (Ig-seq) sequencing. Briefly, B-cells are isolated; transcripts are purified; antibody chains are amplified by PCR; and finally, paired-end sequencing of the Ig variable region is performed on the amplified Ig transcript molecules. (b) An antibody repertoire containing five different antibodies (shown on the left) is characterized by a set of pairs <sequence, abundance > (shown on the right). For example, the abundance of the ‘red’ antibody is 3. (c) The varying levels of sequence information. First, the paired reads are stitched together to form contiguous reads. These reads are then compressed to unique reads with count information, and finally clustered reads. E.g. the red and blue unique reads (with counts 3 and 1) are clustered into a single cluster with count 4 because they represent reads (with errors) derived from the same antibody. (d) Reads are partitioned according to identical CDR3 sequences (shown in the black rectangles). Each resulting cluster of antibodies is referred to as a clone

Cheung et al. (2012) pioneered a new immunoproteogenomics approach for identification of circulating monoclonal antibodies from serum that enables high-throughput antibody development. Although sequencing purified monoclonal antibodies has now become routine (Bandeira et al.., 2008; Castellana et al.., 2011; Liu et al., 2009), sequencing multiple antibodies from a complex sample represents a breakthrough with great biomedical potential. The important conclusion in Cheung et al. (2012) is that antibody analysis should combine NGS and MS to infer antibodies interacting with a specific antigen (see also Georgiou et al.., 2014; Lavinder et al.., 2014; Sato et al., 2012; Wine et al., 2013; Yadav et al.., 2014). In particular, Cheung et al. (2012) showed that the most well represented transcripts in the antibody repertoire (revealed by NGS alone) may not be the most biomedically relevant. Thus, immunoproteogenomics is the key ingredient of the emerging new technology for antibody analysis. However, no publicly available immunoproteogenomics software is currently available.

An antibody repertoire (rather than a set of all DNA reads as in previous immunoproteogenomics studies) represents a sensible choice of a database for the follow up MS/MS searches. However, construction of an antibody repertoire is a difficult problem since antibody genes in antigen stimulated B-lymphocytes are not directly encoded in the germline but are diversified by somatic recombination and mutations (Wine et al. 2013). Therefore, the protein database required for the interpretation of mass spectra from circulating antibodies differs between individuals. Moreover, even a single error in an error-prone NGS read precludes identification of a peptide (spanning the erroneous position) by the standard proteomics tools.

We emphasize that construction of antibody repertoires is a different problem than the well studied VDJ classification (Brochet et al.., 2008; Gaëta et al., 2007; Volpe et al.., 2006) and CDR3 classification (Freeman et al., 2009; Robins et al., 2009, 2010; Warren et al.., 2011) problems. In fact, VDJ classification, CDR3 classification and repertoire construction are three different clustering problems with increasing granularity of partitions into clusters and different biological applications:

  • VDJ classification refers to classifying reads into 225×30×13 clusters (since human genome has 225 V, 30 D and 13 J functional and complete antibody gene-segments). There is currently a multitude of VDJ classification tools, e.g. Bonissone and Pevzner (2015) report 94.5, 99.1 and 99.4% accuracy for V, D and J gene segments, respectively.

  • CDR3 classification is a more granular clustering that refers to classifying reads according to their CDR3 region, the most biologically important segment of an antibody.

  • Full length antibody repertoire classification is the most granular clustering of antibodies that extends the above two clustering approaches by accounting for somatic hypermutations (SHMs). It is arguably the most biologically relevant clustering and a prerequisite for the future studies of antibody evolution.

The antibody repertoire can potentially subpartition each VDJ class/CDR3 class into thousands of subclusters based on the identity of CDR regions and hypermutations. Because various antibodies often share similar segments, the computational challenge of antibody clustering is not unlike the computational challenge of classifying repeats in a genome. From this perspective, the VDJ classification corresponds to distinguishing between different families of repeats (e.g. between Alu and MIR repeats in the human genome), while constructing antibody repertoires corresponds to a very different algorithmic problem of classifying different subfamilies within the same repeat family, e.g. distinguishing between AluJ and AluY repeat subfamilies (Price et al.., 2004) on the challenge of the repeat subfamily classification).

Until recently, there were no attempts to cluster full length antibodies since it was nearly impossible to derive an accurate antibody repertoire with previous experimental approaches based on error-prone and low coverage 454 sequencing technology. MiGEC (Shugay et al.., 2014) is the only tool for the full length repertoire analysis that, however, is not applicable to standard Ig-seq protocols since it requires a special barcode-based sample preparation.

Below we summarize the new contributions of this work to immunoproteogenomics:

  • The crucial distinction between the previous Ig-seq studies (Cheung et al.., 2012; Sato et al.., 2012; Wine et al.., 2013) and the one presented [with a notable exception of Greiff et al. (2014)], is the number of reads. Our Ig-seq runs capture ≈3.8 million reads, compared with the thousands of reads obtained with 454 sequencing technology that dominated Ig-seq prior to 2014. This allows for greater depth in characterizing the repertoire and immunoproteogenomics analysis, but comes with its own set of computational challenges.

  • Although Ig-seq studies have been rapidly developing in the last 5 years, the error-correction techniques from genome sequencing (Pevzner et al.., 2001) have not been applied to Ig-seq yet and the previous immunoproteogenomics studies have not attempted to construct antibody repertoires for the follow up MS/MS searches. Some other studies did perform a simple variant of error correction in the context of VDJ labeling (Jiang et al.., 2011; Reddy et al.., 2010; Weinstein et al., 2009). However, since these studies addressed a relatively simple task of VDJ classification rather than repertoire construction, they have limited ability to correct errors in the most important CDR regions that do not contribute to VDJ classification. IgRepertoireConstructor is the first tool for generating antibody repertoires from standard Ig-seq protocols.

  • In addition to the problem of constructing an antibody repertoire, there is also a challenge of validating this repertoire. Indeed, since there is no gold standard that represents a curated and verified antibody repertoire, it is not clear how to validate the accuracy of the constructed repertoires (on real rather than simulated data). We show that immunoproteogenomics allows one to resolve this Catch-22 and to evaluate the accuracy of the antibody repertoire (due to the complementary nature of errors in DNA reads and in peptides identified by MS).

  • Immunoproteogenomics analysis of circulating antibodies requires searches of all spectra against a highly repetitive database derived from millions of Ig-seq reads. Cheung et al. (2012) found surprisingly few Peptide-Spectrum Matches (PSMs) from spectra they analyzed suggesting that many spectra evaded the identification either due to errors in NGS reads or due to statistical artifacts of searches in a highly repetitive database. Recently, Boutz et al. (2014) discussed the challenge of peptide identification in large highly repetitive database of antibodies that is further amplified by the limitations of the target-decoy approach (Gupta et al.., 2011). We argue that construction of the antibody repertoire enables a new multi-layer approach to immunoproteogenomics searches (each layer corresponds to antibodies with abundances falling into specific intervals) that significantly boosts the number of identified PSMs [≈22% of spectra are identified at 1% false discovery rate (FDR) as compared with ≈6% at 2% FDR identified in Cheung et al. (2012)].

  • Cheung et al. (2012) raised a concern about the lack of correlation between genomics-based and proteomics-based quantification of antibodies (that far exceeds the commonly observed limited correlation in traditional proteogenomics studies (Nesvizhskii, 2014). However, since previous immunoproteogenomics studies were based on low-coverage 454 technology, it was not clear whether this lack of correlation represents sampling artifacts or reflects the fact that previous immunoproteogenomics studies did not correct sequencing errors. Our analysis of Illumina datasets (orders of magnitude increase in coverage as compared with previous immunoproteogenomics studies) revealed an even more alarming lack of correlation between two approaches to quantification: more than half of identified peptides come from antibodies that are represented by a single read in the antibody repertoire! However, we show that switching from quantification of individual antibodies, to quantification of antibody clones, partially restores correlation between genomics-based and proteomics-based quantification.

2 Methods

2.1 Antibody repertoires

If we view an antibody as a center of a cluster formed by reads derived from this antibody, then construction of a repertoire corresponds to a difficult clustering problem with many closely located centers so that the radius of a cluster may exceed the distance from one cluster to another one. Because the standard clustering techniques (like k-means clustering) are not applicable to such problems (Price et al.., 2004), we have designed IgRepertoireConstructor, a novel algorithm for constructing antibody repertoires.

Each antibody in an antibody repertoire is characterized by its sequence and abundance; estimated by the number of reads derived from this antibody (Fig. 1b). The complexity of the antibody repertoire mirrors the complexity of the immune system, e.g. clonal selection leads to a highly uneven distribution of abundances of antibodies (Burnet, 1976). Abundant antibodies mutate and yield new antibodies that share the same VDJ recombination pattern, but differ only by SHMs. As a result, the antibody repertoire contains a mixture of closely related antibodies with differing abundances. The abundances of ≈2.3 million antibodies in our dataset vary from 1 to ≈33,000 with the most abundant antibody representing ≈1% of all reads (all examples below refer to the heavy chain Ig-seq dataset described in the ‘Section 3.1’).

The major challenge in constructing antibody repertoires is the identification of all reads that are derived from a single antibody. If reads were error-free, we would simply group together reads that are identical (up to small shifts) into unique reads to generate an antibody repertoire. In reality, reads are error-prone necessitating error-correction of reads prior to any analysis. IgRepertoireConstructor error-corrects reads; partitions them into clusters; and computes the consensus sequence and abundance of each antibody. Figure 1c depicts the different levels of clustering performed by IgRepertoireConstructor. First, we computationally stitch paired-end reads of Ig molecules to derive the contiguous Ig-seq reads. Subsequently, the Ig-seq reads are grouped together to provide unique Ig-seq reads. Finally, the unique reads are clustered to obtain clustered Ig-seq reads (antibodies). In addition, we can represent antibodies according to the somatically recombined B-cell from which they originate, i.e. their clonality. We define an antibody clone as the set of all antibodies in the repertoire with the same CDR3 sequence [as determined by IgBlast (Ye et al.., 2013)]. Figure 1d diagrams this clone identification process. A clone is trivial if it consists of a single cluster and non-trivial otherwise. The sharp distribution of clone sizes (Supplementary Fig. A1) can be attributed to B-cell response to an antigen, i.e. clonal selection (Weinstein et al.., 2009).

2.2 Limitations of existing error correction tools

At first glance, it appears that the problem of error-correction in Ig-seq is not unlike the problem of error-correction in genome assembly (Pevzner et al.., 2001). However, popular error-correction tools, e.g. Quake (Kelley et al.., 2010) or BayesHammer (Nikolenko et al.., 2013), that were optimized for genome assembly, are not suited for Ig-seq data. Indeed, Ig-seq data contain a large number of sequences differing by very few mismatches or indels, and feature the extremely uneven coverage of various antibodies by reads (since abundances of antibodies differ by orders of magnitudes). Both Quake and BayesHammer start by identifying solid k-mers in reads (that are likely to be present in the genome) and use them to correct reads. However, to find solid k-mers, Quake uses the read coverage, an approach that is not applicable in the case of Ig-seq with highly variable abundances. In contrast, BayesHammer (part of the SPAdes assembler, Bankevich et al.., 2012) was designed to assemble single cell sequencing data with uneven coverage. However, it is also not applicable to Ig-seq since an antibody repertoire yields numerous similar, correct, k-mers from different antibodies (Supplementary Fig. A2). BayesHammer is unable to distinguish these correct k-mers from similar incorrect k-mers derived from the same antibody.

2.3 Hamming graph for analyzing Ig-seq data

IgRepertoireConstructor uses the idea of the Hamming graph for error correction (Medvedev et al.., 2011; Nikolenko et al. 2013) to correct Illumina reads. With the emergence of longer (250 nt) Illumina reads in 2013 (until 2013, Illumina technology generated shorter reads that did not fully cover the variable region of antibodies), it is now possible to interrogate repertoires using accurate high-throughput Illumina technology. The Hamming distance d(s1,s2) between sequences s1 and s2 of equal length is defined as the number of positions where the symbol in s1 differs from a symbol in s2 (Supplementary Fig. A3a). We extend the concept of Hamming distance to any two sequences (including sequences with different lengths) by considering all sufficiently long overlaps between sequences s1 and s2 (longer than the default value δ), and computing the Hamming distance between the overlapping parts. We define d˜(s1,s2) as the minimum of such distances (Supplementary Fig. A3b). We define the Hamming Graph HG(Strings) as the complete weighted graph whose vertices correspond to a collection of sequences Strings and the weight of the edge (s1, s2) is equal to d˜(s1,s2). The Bounded Hamming Graph, denoted HG(Strings,τ), is a subgraph of the Hamming Graph where edge (s1, s2) exists iff d˜(s1,s2)≤τ. The time- and space-efficient construction of large Hamming Graphs is a challenging problem that was addressed in Nikolenko et al. (2013) and adapted in IgRepertoireConstructor. Note that compared with Hammer (Medvedev et al.., 2011) and BayesHammer (Nikolenko et al.., 2013), we construct the Bounded Hamming Graph on the entire reads (rather than on k-mers) and use the generalized Hamming distance.

2.4 Repertoire construction and search for dense subgraphs

We construct an antibody repertoire by partitioning reads into clusters that correspond to the same antibody. Our goal is to place reads differing by sequencing errors into the same cluster, while placing reads corresponding to different antibodies into different clusters. This becomes difficult since the number of errors in a read from a given cluster may be larger than the number of differences between antibodies from different clusters. We define the antibody sequence as the consensus of reads in a cluster, and its abundance as the number of reads in a cluster.

Because Illumina reads have a small indel rate, the generalized Hamming distance between reads from the same cluster should be low. We thus construct the Bounded Hamming Graph HG(Reads,τ) from all reads. Our analysis revealed that the generalized Hamming distance for most Ig-seq reads, originating from the same antibody, does not exceed 3 and that many antibodies form complete, or nearly complete, subgraphs of the Bounded Hamming Graph with τ = 3 (Appendix A). Ideally, we would like to choose τ in such a way that HG(Reads,τ) is a clique graph, i.e. a graph where each connected component is a complete subgraph (clique).

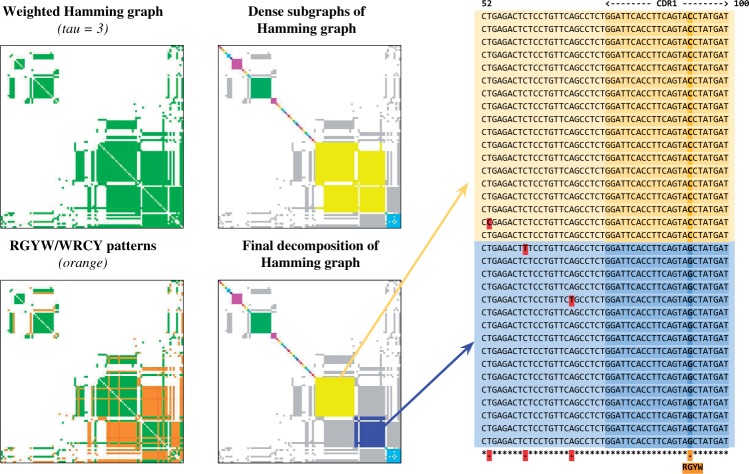
In reality, the large connected components of the Bounded Hamming Graph often have a more complex structure. Given a connected component with m edges and n vertices, we define its edge fill-in as the ratio of the number its edges (m) to the maximal possible number of edges in the graph on n vertices [n·(n−1)/2]. Figure 2a presents a connected component of the Bounded Hamming graph with edge fill-in 0.25 (τ = 3). The lion’s share of large connected components in the Bounded Hamming Graph (i.e. components with more than 100 vertices) have similar structures characterized by small edge fill-ins; the average edge fill-in for large components is 0.32 (Supplementary Fig. A4). Additional analysis of the connected components reveals that the nearly all of them (98.6%) consist of dense (complete or nearly complete) subgraphs connected by very few edges. Most vertices in these dense subgraphs correspond to error-prone reads derived from a single antibody or from highly similar antibodies differing from each other by a small number of SHMs.

Fig. 2.

Fig. 2.

Open in a new tab

(a) A connected component with 107 vertices and 1426 edges in the Bounded Hamming graph with τ = 3 (fill-in is 0.25). The sizes of vertices are proportional to their degrees. (b) Clusters constructed as result of vertex decomposition of the Bounded Hamming Graph. Vertices of the same colors define the dense subgraphs in the decomposition [the colors are coordinated with Fig. 3 (bottom right)]. IgRepertoireConstructor constructs 42 clusters but 35 of them are trivial, i.e. are induced by a single read. Sizes and edge fill-ins (in brackets) of the remaining seven non-trivial clusters are: 2 (1.0), 3 (1.0), 6 (1.0), 8 (1.0), 12 (1.0), 18 (0.9) and 23 (0.9)

Thus, the first step in constructing an antibody repertoire is solving a very large instance of the Corrupted Cliques Problem: finding the smallest number of additions and removals of edges that transform the Bounded Hamming Graph into a clique graph. Although there exist a number of algorithms for solving the Corrupted Cliques Problem (such as CAST; Ben-Dor et al.., 1999), they are too slow for the Bounded Hamming Graphs with many vertices. We thus developed a different approach for analyzing the Bounded Hamming Graph that is based on transforming it into a triangulated graph (i.e. a graph where every cycle of length longer than three has a chord) rather than a clique graph using the Minimum Fill-in Problem (Garey and Johnson, 1979).

2.5 Repertoire construction and minimum fill-in problem

The minimum fill-in edge-set for a graph is the edge-set of minimal size whose addition turns this graph into a triangulated graph. We are interested in triangulated graphs because maximal cliques in these graphs can be generated in polynomial time (Galinier et al.., 1995) and because maximal cliques in the triangulated Bounded Hamming Graph help to reveal dense subgraphs of the original Bounded Hamming Graph (Appendix B for details).

Although the Minimum Fill-in Problem is NP-complete (Yannakakis, 1981), there exist efficient approximation algorithms for solving it, e.g. METIS algorithm (Karypis and Kumar, 1999). The METIS algorithm is based on the equivalence between triangulated graphs and perfect elimination orderings. A perfect elimination ordering in a graph is such an ordering of its vertices that, for each vertex v, v and the vertices following it in the order, form a clique (Supplementary Fig. A11d). A graph is triangulated if and only if it has a perfect elimination ordering (Rose et al.., 1976). METIS finds an ordering that generates an approximation of a minimum fill-in edge-set and this ordering can be used for finding cliques in the triangulated graph (Galinier et al.., 1995). As we mentioned earlier, these cliques correspond to dense subgraphs in the original graph. To construct maximal dense subgraphs, we additionally merge subgraph connected by many edges.

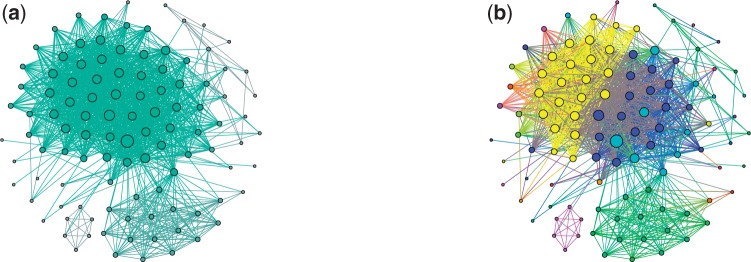
IgRepertoireConstructor solves the Minimum Fill-in Problem in the Bounded Hamming Graph using METIS and converts its solution into a list of dense subgraphs in the original Bounded Hamming Graph. Note that some of the resulting dense subgraphs may share vertices forcing us to assign these shared vertices to one of the dense subgraphs. To assign a vertex v to a single dense subgraph, we select a subgraph with maximum number of vertices adjacent to v. Thus, dense subgraphs generated by METIS provide us with a vertex decomposition of the Bounded Hamming Graph. A vertex decomposition of the graph in Figure 2a is shown in Figure 3 (top right).

Fig. 3.

Fig. 3.

Open in a new tab

Construction of the antibody repertoire based on the decomposition of the Bounded Hamming Graph into dense subgraphs. (Top left) The adjacency matrix of the Bounded Hamming Graph shown in Figure 2a. Each element in the matrix corresponds to a pair of vertices x and y and is colored green if the edge (x, y) is presented in the graph. (Top right) Decomposition of the Bounded Hamming Graph into dense subgraphs (highlighted by different colors). Edges connecting vertices from different dense subgraph are colored in grey. (Bottom left) The adjacency matrix with edges corresponding to SHM-triggering patterns RGYW/WRCY highlighted in orange. (Bottom right) The final decomposition of the Bounded Hamming Graph takes into account the multiple alignment of reads corresponding to the same subgraph in the decomposition and breaks the large yellow subgraph (top right subfigure) into two smaller subgraphs highlighted in yellow and blue. The multiple alignment of ‘yellow’ and ‘blue’ reads from these smaller subgraphs is shown on the right (limited to positions 52–100). Note that all ‘yellow’ reads are similar to each other and all ‘blue’ reads are similar to each other (the differences are highlighted in red and likely represent sequencing errors). However, there exists a systematic difference (C/G mismatch within RGYW pattern in CDR1 region) between ‘yellow’ and ‘blue’ reads that allows IgRepertoireConstructor to split the large yellow subgraph in top right subfigure

Analysis of all found subgraphs in the decomposition of the Bounded Hamming Graph reveals that the lion’s share of them have high edge fill-ins (the average edge fill-in is 0.94), thus confirming that IgRepertoireConstructor indeed finds dense subgraphs of the Bounded Hamming Graph. The histogram of edge fill-in for all subgraphs in this decomposition is shown in Supplementary Figure A5.

Dense subgraphs correspond to clusters of Ig-seq reads representing either identical or very similar antibodies (i.e. antibodies differing by very few substitutions). However, to construct the antibody repertoire, we need to further partition some of the dense subgraphs (that correspond to multiple antibodies) into subgraphs corresponding to single antibodies. To illustrate this challenge, consider the SHM-triggering patterns RGYW/WRCY (Rogozin and Kolchanov, 1992) and define an edge in the Bounded Hamming Graph as an SHM-edge if at least one mismatch on this edge conforms to the RGYW/WRCY motif. Figure 3 (bottom left) shows the Bounded Hamming Graph where the SHM-edges are highlighted in orange. This coloring reveals that the yellow dense subgraph in Figure 3 (upper right) corresponds to two similar antibodies rather than to a single one [Fig. 3 (bottom right)]. Indeed, the multiple alignment of reads corresponding to the yellow subgraph shows a mismatch in the CDR1 region which separates reads into two groups (right panel of Fig. 3). Thus, we need to split the constructed dense subgraphs using detected SHMs. The final solution is shown in Figure 3 (bottom right) and illustrated in Figure 2b. See Appendix C for more details on splitting dense subgraphs, and Appendices D and E on benchmarking of IgRepertoireConstructor on real and simulated antibody Ig-seq datasets.

2.6 Immunoproteogenomics search

The previous immunoproteogenomics studies (Boutz et al., 2014; Cheung et al.., 2012; Sato et al.., 2012) conducted searches on a database of unique Ig-seq reads that we refer to as unique reads database. We argue that a better option is the antibody repertoire database (formed by centers of clusters constructed by IgRepertoireConstructor) as it eliminates many sequencing errors. Furthermore, to assess the divergence from reference gene-segments, a dataset of canonical V, D and J gene-segments was searched; this database is termed the canonical VDJ database. In order to obtain peptide identifications from the constant region, we also included all 41 intact variants of the constant region, obtained from the IMGT repository (Lefranc et al.., 2009). These sequences are concatenated to the VDJ database.

Proteomic searches were conducted using MS-GF+ (Kim et al.., 2008; Kim and Pevzner, 2014) on partially digested peptides (e.g. for trypsin, semi-tryptic peptides were considered). The FDR was controlled by selecting a MS-GF+ threshold of spectral probabilities such that we maintained a 1% FDR. Supplementary Figure A6 shows the distribution of spectral probabilities for the target and decoy datasets.

Blind modification searches were performed using MODa (Na et al.., 2012), allowing for a single modification with mass between −200 and 200Da. Peptides with at least one enzymatic end were considered and a 1% FDR was enforced.

As discussed in Boutz et al. (2014), immunoproteogenomics searches require new algorithmic and statistical approaches since the standard peptide identification algorithms were not designed for searches in large and highly repetitive immunoproteogenomics databases. We argue that yet another key difference between the standard and immunoproteogenomics searches is that, in the latter case, after constructing the antibody repertoire, we have information about antibody abundances. Because higher-abundance antibodies are more promising candidates for spectral searches than lower-abundance antibodies (despite limited correlation between genomics- and proteomics-derived abundances), we partition all antibodies into layers according to their abundances. The rationale for such partitioning is that higher-abundance antibodies form much smaller protein databases than lower-abundance antibodies. For example, there are 1564, 10 782 and 48 564 antibodies with abundances in the intervals from 100 to 30 000, from 10 to 99 and from 2 to 9, respectively. This contrasts with 2 267 863 singleton antibodies with abundance 1. Thus, since E-values of PSMs rapidly deteriorate with the increase in the database size (Gupta et al.., 2011), we partition all antibodies into four layers (according the abundance intervals specified earlier) and employ a separate 1% FDR control, for each layer, based on selecting a spectral probability threshold in MS-GF+. Note that our multi-layer approach is very different from the two-stage MS/MS search approach with logical dependencies between two stages. Because there are no such dependencies in the multi-layer approach, the controversy about the statistical foundations of the two-stage approach (Gupta et al.., 2011) does not extend to our multi-layer approach.

3 Discussion

3.1 Datasets

We have benchmarked IgRepertoireConstructor on multiple Mi-Seq and Orbitrap datasets. Below we only describe the results for a single heavy chain dataset. Similarly to BayesHammer, the running time of IgRepertoireConstructor is dominated by the construction of the Bounded Hamming graph (≈5 h for the heavy chain dataset). All further steps (finding and splitting dense subgraphs, etc.) took > 30 min on a single thread. MS searches and subsequent cluster/clone peptide assignments took ≈8 h.

3.1.1 Ig-seq dataset

The Ig-seq library contains overlapping paired-end reads that cover the variable region of heavy chain (3.83 million 250-nt long reads with average insert size 366 nucleotides). We pre-process the Ig-seq library by merging overlapping paired-end reads, and removing contaminants as described in Appendix F. After pre-processing, IgRepertoireConstructor generated 2 925 095 unique reads, 2 406 121 clustered reads and 586 341 clones. See Appendix G for the analysis of contaminants.

3.1.2 Spectral dataset

We analyzed CID tandem mass-spectra generated using the following digestive enzymes; AspN (21 385 spectra), chymotrypsin (24 956 spectra), trypsin (26 740 spectra) and elastase (20 604 spectra). Enzymes with differing cleavage specificity improve coverage over the length of the antibody sequence. We searched spectral datasets against the protein databases derived from the antibody repertoire. Three-frame translations were created for each antibody in the repertoire, and any frames containing a stop codon were discarded; 165 675 antibodies (≈7%) had a stop codon in all frames.

3.4 Analysis of antibody repertoires

Below we compare the repertoires formed by unique reads and by IgRepertoireConstructor. To compare the repertoires, we used various metrics measuring cluster sizes [# clusters, # singletons (single-element clusters), max cluster size, # clusters of size exceeding X (where X is a parameter)] as well as metrics based on CDR3 analysis (see Appendix H for more details). Table 1 illustrates that IgRepertoireConstructor generates a rather different (more compact) representation of antibodies than the set of unique reads used in previous immunoproteogenomics studies.

Table 1.

Comparison of the antibody repertoire generated by IgRepertoireConstructor with the set of unique reads (heavy chain Ig-seq data)

Unique reads IgRepertoireConstructor
# clusters 3 099 967 2 328 773
# singletons 3 027 123 2 267 863
Max cluster size 2 203 33 021
# clusters (>10) 5 532 12 346
# clusters (>50) 377 3 571
# clusters (>500) 7 206
# clones 602 536 538 928
# non-trivial clones 151 612 132 431
Avg. non-trivial clone size 15.64 12.90
Max clone size 30 571 15 977
Avg. non-trivial clone divergence 0.21 0.23
Open in a new tab

The avg. clone divergence metric is computed as the fraction of the number of columns in the multiple alignment of all antibodies in a clone that have mutations or indels. The avg. non-trivial clone divergence shows the average clone divergence computed over all non-trivial clones.

3.5 Peptide identifications

Table 2 shows the number of identified peptides and PSMs. Modified peptides are considered identical to those without modifications should their sequences be the same; and hence are not counted when considering unique peptides. Note the large number of peptides identified only with modifications (i.e. unmodified versions of these peptides were not identified) suggesting that future immunoproteogenomics searches should include search for post-translational modification (PTMs). Overall, we identify nearly 13% of all spectra when performing restrictive PTM searches at 1% FDR. The number of identified peptides is further boosted when employing a multi-layer strategy, noted by the ‘layer’ column in the table. Blind modification search was performed on the trypsin dataset only (since MODa is not designed for spectral datasets generated with other digestive enzymes). MODa identified 3334 PSMs with modifications, corresponding to 970 peptide IDs; 815 of which were identified only by the blind modification search. It brings the total percentage of identified spectra to ≈22.6% at 1% FDR [Cheung et al.., (2012) identified 6% of spectra at 2% FDR]. See Appendix I on specific modifications found by our blind search. Figure 4c shows the breakdown of the origin of each identified peptide.

Table 2.

Peptides and PSMs identified by MS-GF+

Peptides PSMs
Database Layer PTM AspN Chymo Trypsin Elastase Total AspN Chymo Trypsin Elastase Total Total (%)
Repertoire m X 814 1 706 2 505 776 5 801 2 665 4 989 10 021 1 786 19 461 20.77
Repertoire s X 832 1 441 2 291 628 5 192 1 881 2 365 6 675 878 11 799 12.59
Repertoire s 61 636 1 756 357 2 810 89 896 3 753 377 5 115 5.46
Constant region s 279 205 109 107 700 865 583 933 286 2 667 2.85
Canonical VDJ s 25 122 122 69 338 115 441 618 173 1 347 1.44
Open in a new tab

The number of peptide identifications at an 1% FDR cutoff for each spectral dataset. For example, a 1% FDR cutoff corresponds to a spectral probability cutoff of 1.4e-08 for AspN, 2.3e-10 for chymotrypsin, 7.5e-10 for trypsin and 3.8e-10 for elastase datasets, when searching antibodies with the constant region appended, and restrictive PTM search. The total column shows the number of total peptides, or PSMs, across the four different MS datasets. The total % column shows the percentage of identified spectra, among all spectra. The ‘layer’ column denotes the type of search; single layer (s), or multi-layer (m). The restrictive MS-GF+ searches for PTMs were conducted by searching for carbamidomethyl (C + 57) as a fixed modification, oxidation of methionine, oxidation (single and double) of tryptophan, and N-terminal pyroglutamate (Q-17, E-18) as optional modifications.

Fig. 4.

Fig. 4.

Open in a new tab

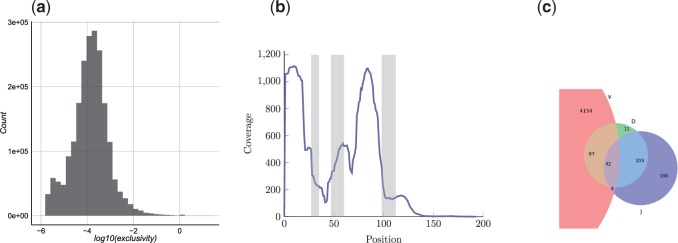
(a) Distribution of exclusivity scores of antibodies. (b) PSM coverage along positions of each cluster. Positions of CDR1, CDR2 and CDR3 shown in gray as determined for a single cluster. Coverage is normalized for shared peptides using their exclusivity scores. (c) Origin of identified peptides. For each identified peptide, a representative cluster sequence was used to determine from which reference segment it originated; V, D or J. Each peptide is classified as V-, D- or J-peptide depending on whether it overlaps with segments marked as V, D or J regions for the heavy chain sequence (peptides spanning more than one region, e.g. V and J, are classified as both V-peptides and J-peptides)

3.6 Assigning peptides to multiple antibodies

Interestingly, only 67 124 antibodies (2.6% of all antibodies) did not encode any identified peptide. Moreover, as expected, these are mainly antibodies with minimal abundance 1 (total abundance of these 67 124 antibodies is 73 764 and maximal abundance is 300). This (surprisingly) low number of antibodies with no peptide evidence is due to the fact that many identified peptides map to multiple antibodies. As a result, the number of antibodies A in a repertoire R encoding a peptide P is often large. We define exclusivity score of a peptide as exclusivity (P,R)=1/number of antibodies in R encoding P and exclusivity score of an antibody as exclusivity (A,R)=∑all peptides P mapping to Aexclusivity(P,R). The exclusivity score distribution of the antibodies, seen in Figure 4a, shows few antibodies having peptides exclusive to them alone [only 1472 antibodies with exclusivity (A,R)>1.0]. Figure 4b shows the peptide coverage over the position of each clone. Supplementary Figure A7 illustrates the peptide coverage of a single clone.

3.7 Correlation between Ig-seq and MS/MS abundances

To compare the relation between peptides and their Ig-seq counterparts, we introduce the notions of total Ig-abundance and maximal Ig-abundance of a peptide. Total (maximal) Ig-abundance of a peptide is the total (maximal) abundance of antibodies that encode this peptide. Supplementary Figure A8a shows the relation of the total Ig-abundance for each peptide to its spectral count (number of PSMs). Supplementary Figure A8b shows a histogram of spectral peptide counts binned over maximal Ig-abundance for each peptide. A strikingly large number of peptides, 2702, can be attributed to singleton antibodies. The remarkable lack of correlations between genomics-based and proteomics-based abundances further amplifies the concern first expressed in Cheung et al. (2012). Supplementary Figure A8c shows the correlations between clone abundances measured by MS/MS and Ig-seq (compare with Supplementary Fig. A9 that measures antibody, rather than clone, abundance). These plots show the difference when considering the unit of a repertoire (antibody), and the unit of antibody evolution (the clone) raising the concern that Ig-seq data do not adequately represent antibody abundances. When considering only the antibodies, there is no correlation with the MS evidence, as previously reported by Cheung et al. (2012). However, when considering the amalgam of antibodies forming each clone, a moderate correlation emerges (ρ=0.5687614). One possible explanation is that certain antibodies, within highly expressed clones, are not captured by MS.

4 Conclusion

Our study is the first to validate the constructed antibody repertoires (by using complementary proteomics data) that confirmed that IgRepertoireConstructor generates accurate repertoires. With an accurate tool for constructing antibody repertoires, we can move to studies of evolution of antibody repertoires, the analysis that has not been possible in the past. Because analysis of antibody repertoires is not unlike analysis of repeat subfamilies, the existing algorithms for analyzing repeat evolution (Cordaux and Batzer, 2009; Price et al., 2004) can be applied to study evolution of antibodies. We also addressed the problem of peptide identification in large and highly repetitive databases by designing multi-layer immunoproteogenomics search algorithm. Finally, we revealed an alarming lack of correlation between NGS-based and MS-based quantitation of antibodies [consistent with Cheung et al. (2012)] and proposed a way to partially restore this correlation by considering clone abundances rather than individual antibody abundances.

Supplementary Material

Supplementary Data
supp_31_12_i53__index.html (786B, html)

Acknowledgement

We are grateful to Marina Granovskaya, the Head of Research Collaboration at F. Hoffmann-La Roche in Moscow, Russia, for initiating this project as an international academia-industry collaboration and supporting it with a grant to Saint-Petersburg Academic University, Russia. We thank Wenwu Zhai for designing the antibody-specific primer library and Gerry Nakamura for isolating the B-memory cells and extracting RNA. We are grateful to Nuno Bandeira for insightful comments on identification of modified peptides.

Funding

Y.S., E.S. and A.L. are supported by Russian Science Foundation (grant No 14-50-00069). S.B. and P.A.P. are supported by National Institute of Health (grant 5P41GM103484). P.A.P. has an equity interest in Digital Proteomics, LLC, a company that may potentially benefit from the research results. The terms of this arrangement have been reviewed and approved by the University of California, San Diego in accordance with its conflict of interest policies.

Conflict of Interest: none declared.

References

  1. Arnaout R., et al. (2011) High-resolution description of antibody heavy-chain repertoires in humans. PloS One, 6, e22365. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Bandeira N., et al. (2008) Automated de novo protein sequencing of monoclonal antibodies. Nat. Biotechnol., 26, 1336–1338. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Bankevich A., et al. (2012) SPAdes: a new genome assembly algorithm and its applications to single-cell sequencing. J. Comput. Biol., 19, 455–477. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Ben-Dor A., et al. (1999) Clustering gene expression patterns. J. Comp. Biol., 6, 281–297. [DOI] [PubMed] [Google Scholar]
  5. Bonissone S., Pevzner P.A. (2015) Immunoglobulin Classification Using the Colored Antibody Graph. Lecture Notes in Computer Science, RECOMB 2015, Springer International Publishing, pp. 44–59. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Boutz D.R., et al. (2014) Proteomic identification of monoclonal antibodies from serum. Anal. Chem., 86, 4758–4766. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Brochet X., et al. (2008) IMGT/V-QUEST: the highly customized and integrated system for IG and TR standardized VJ and VDJ sequence analysis. Nucleic Acids Res., 36(Suppl. 2), W503–W508. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Burnet F.M. (1976) A modification of Jerne’s theory of antibody production using the concept of clonal selection. CA Cancer J. Clin., 26, 119–121. [DOI] [PubMed] [Google Scholar]
  9. Castellana N., et al. (2011) Resurrection of a clinical antibody: template proteogenomic de novo proteomic sequencing and reverse engineering of an anti-lymphotoxin-α antibody. Proteomics, 11, 395–405. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Cheung W.C., et al. (2012) A proteomics approach for the identification and cloning of monoclonal antibodies from serum. Nat. Biotechnol., 30, 447–452. [DOI] [PubMed] [Google Scholar]
  11. Cordaux R., Batzer M.A. (2009) The impact of retrotransposons on human genome evolution. Nat. Rev. Genet., 10, 691–703. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Freeman J., et al. (2009) Profiling the T-cell receptor beta-chain repertoire by massively parallel sequencing. Genome Res., 19, 1817–1824. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Gaëta B.A., et al. (2007) iHMMune-align: hidden Markov model-based alignment and identification of germline genes in rearranged immunoglobulin gene sequences. Bioinformatics, 23, 1580–1587. [DOI] [PubMed] [Google Scholar]
  14. Galinier P., et al. (1995) Chordal graphs and their clique graphs. Graph-Theoretic Concepts in Computer Science, Lecture Notes in Computer Science, Vol. 1017, Springer Berlin Heidelberg, pp. 358–371. [Google Scholar]
  15. Garey M.R., Johnson D.S. (1979) Computers and Intractability, A Guide to the Theory of NP-Completeness . W.H. Freeman and Company, New York. [Google Scholar]
  16. Georgiou G., et al. (2014) The promise and challenge of high-throughput sequencing of the antibody repertoire. Nat. Biotechnol., 32, 158–168. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Greiff V., et al. (2014) Quantitative assessment of the robustness of next-generation sequencing of antibody variable gene repertoires from immunized mice. BMC Immunol., 15, 40. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Gupta N., et al. (2011) Target-decoy approach and false discovery rate: when things may go wrong. J. Am. Soc. Mass. Spectr., 22, 1111–1120. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Jiang N., et al. (2011) Determinism and stochasticity during maturation of the zebra fish antibody repertoire. Proc. Natl. Acad. Sci. U.S.A., 108, 5348–5353. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Jiang N., et al. (2013) Lineage structure of the human antibody repertoire in response to influenza vaccination. Sci. Transl. Med., 5, 171ra19. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Karypis G., Kumar V. (1999) A fast and high quality multilevel scheme for partitioning irregular graphs. SIAM J. Sci. Comput., 20, 35992. [Google Scholar]
  22. Kelley D., et al. (2010) Quake: quality-aware detection and correction of sequencing errors. Genome Biol., 11, R116. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Kim S., Pevzner P.A. (2014) MS-GF+ makes progress towards a universal database search tool for proteomics. Nat. Commun., 5, 5277. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Kim S., et al. (2008) Spectral probabilities and generating functions of tandem mass spectra: a strike against decoy databases. J. Proteome Res., 7, 3354–3363. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Laserson U., et al. (2014) High-resolution antibody dynamics of vaccine-induced immune responses. Proc. Natl. Acad. Sci. U.S.A., 111, 492833. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Lavinder J.J., et al. (2014) Identification and characterization of the constituent human serum antibodies elicited by vaccination. Proc. Natl. Acad. Sci. U.S.A., 111, 2259–2264. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Lefranc M.-P., et al. (2009) IMGT®, the international ImMunoGeneTics information system®. Nucleic Acids Res. , 37(Suppl. 1), D1006–D1012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Liu X., et al. (2009) Automated protein (re) sequencing with MS/MS and a homologous database yields almost full coverage and accuracy. Bioinformatics, 25, 2174–2180. [DOI] [PubMed] [Google Scholar]
  29. Medvedev P., et al. (2011) Error correction of high-throughput sequencing datasets with non-uniform coverage. Bioinformatics, 27, i137–i141. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Na S., et al. (2012) Fast multi-blind modification search through tandem mass spectrometry. Mol. Cell. Proteomics, 11, M111.010199. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Nesvizhskii A.I. (2014) Proteogenomics: concepts, applications and computational strategies. Nat. Methods., 11, 1114–1125. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Nikolenko S., et al. (2013) BayesHammer: bayesian clustering for error correction in single-cell sequencing. BMC Genomics, 14, S7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Pevzner P., et al. (2001) An Eulerian path approach to DNA fragment assembly. Proc. Natl. Acad. Sci. U.S.A., 98, 9748–9753. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Price A.L., et al. (2004) Whole-genome analysis of Alu repeat elements reveals complex evolutionary history. Genome Res., 14, 2245–2252. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Reddy S., et al. (2010) Monoclonal antibodies isolated without screening by analyzing the variable-gene repertoire of plasma cells. Nat. Biotechnol., 28, 965–969. [DOI] [PubMed] [Google Scholar]
  36. Robins H., et al. (2009) Comprehensive assessment of T-cell receptor beta-chain diversity in alphabeta T cells. Blood, 114, 4099–4107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Robins H., et al. (2010) Overlap and effective size of the human CD8+ T cell receptor repertoire. Sci. Transl. Med., 2, 47–64. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Rogozin I., Kolchanov N. (1992) Somatic hypermutagenesis in immunoglobulin genes. ii. influence of neighbouring base sequences on mutagenesis. Biochim. Biophys. Acta., 1171, 11–18. [DOI] [PubMed] [Google Scholar]
  39. Rose D.J., et al. (1976) Algorithmic aspects of vertex elimination on graphs. SIAM J. Comput., 2, 26683. [Google Scholar]
  40. Sato S., et al. (2012) Proteomics-directed cloning of circulating antiviral human monoclonal antibodies. Nat. Biotechnol., 30, 1039–1043. [DOI] [PubMed] [Google Scholar]
  41. Shugay M., et al. (2014) Towards error-free profiling of immune repertoires. Nat. Methods, 11, 653–655. [DOI] [PubMed] [Google Scholar]
  42. Vollmers C., et al. (2013) Genetic measurement of memory B-cell recall using antibody repertoire sequencing. Proc. Natl. Acad. Sci. U.S.A., 110, 13463–13468. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Volpe J.M., et al. (2006) SoDA: implementation of a 3D alignment algorithm for inference of antigen receptor recombinations. Bioinformatics, 22, 438–444. [DOI] [PubMed] [Google Scholar]
  44. Warren R., et al. (2011) Exhaustive T-cell repertoire sequencing of human peripheral blood samples reveals signatures of antigen selection and a directly measured repertoire size of at least 1 million clonotypes. Genome Res., 21, 790–797. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Weinstein J., et al. (2009) High-throughput sequencing of the zebrafish antibody repertoire. Science, 324, 807–810. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Wine Y., et al. (2013) Molecular deconvolution of the monoclonal antibodies that comprise the polyclonal serum response. Proc. Natl. Acad. Sci. U.S.A., 110, 2993–2998. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Yadav M., et al. (2014) Predicting immunogenic tumour mutations by combining mass spectrometry and exome sequencing. Nature, 515, 572–576. [DOI] [PubMed] [Google Scholar]
  48. Yannakakis M. (1981) Computing the minimum fill-in is NP-complete. SIAM J. Alg. Disc. Meth., 2, 77–79. [Google Scholar]
  49. Ye J., et al. (2013) IgBlast: an immunoglobulin variable domain sequence analysis tool. Nucleic Acids Res., 41, W34–W40. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Data
supp_31_12_i53__index.html (786B, html)
supp_btv238_Pevzner_70_sup_1.pdf (518.6KB, pdf)
supp_btv238_Pevzner_70_sup_2.pdf (1.2MB, pdf)

Articles from Bioinformatics are provided here courtesy of Oxford University Press

RESOURCES