Abstract
Motivation: Systematically predicting gene (or protein) function based on molecular interaction networks has become an important tool in refining and enhancing the existing annotation catalogs, such as the Gene Ontology (GO) database. However, functional labels with only a few (<10) annotated genes, which constitute about half of the GO terms in yeast, mouse and human, pose a unique challenge in that any prediction algorithm that independently considers each label faces a paucity of information and thus is prone to capture non-generalizable patterns in the data, resulting in poor predictive performance. There exist a variety of algorithms for function prediction, but none properly address this ‘overfitting’ issue of sparsely annotated functions, or do so in a manner scalable to tens of thousands of functions in the human catalog.
Results: We propose a novel function prediction algorithm, clusDCA, which transfers information between similar functional labels to alleviate the overfitting problem for sparsely annotated functions. Our method is scalable to datasets with a large number of annotations. In a cross-validation experiment in yeast, mouse and human, our method greatly outperformed previous state-of-the-art function prediction algorithms in predicting sparsely annotated functions, without sacrificing the performance on labels with sufficient information. Furthermore, we show that our method can accurately predict genes that will be assigned a functional label that has no known annotations, based only on the ontology graph structure and genes associated with other labels, which further suggests that our method effectively utilizes the similarity between gene functions.
Availability and implementation: https://github.com/wangshenguiuc/clusDCA.
Contact: jianpeng@illinois.edu
Supplementary information: Supplementary data are available at Bioinformatics online.
1 Introduction
Automated annotation of gene (or protein) function has become a critical task in the post-genomic era (Radivojac et al., 2013). Fortunately, an increasing compendium of genomic, proteomic and interactomic data allows us to extract patterns from functionally well-characterized genes (or proteins) to accurately infer functional properties of lesser-known ones. In particular, recently developed high-throughput experimental techniques, such as yeast two-hybrid screens and genetic interaction assays, have helped to build molecular interaction networks in bulk. Topological structures of these networks can be exploited for function prediction using the ‘guilt-by-association’ principle, which states that genes (or proteins) that share similar neighbors or other topological properties in interaction networks are more likely to be functionally related.
To this end, a variety of graph-theoretic and machine learning algorithms (Karaoz et al., 2004; Letovsky and Kasif, 2003; Murali et al., 2006; Sefer and Kingsford, 2011) have been developed to provide a way of refining and enhancing existing functional annotations [e.g. Gene Ontology (GO) database (Ashburner et al., 2000)] based on network data. A popular class of graph-theoretic algorithms uses a diffusion process to examine the local topology of nodes, exploiting both direct and indirect linkages (Cao et al., 2014, 2013; Cho et al., 2015; Kohler et al., 2008; Nabieva et al., 2005). Alternatively, the number of occurrences of different elementary subgraphs (known as graphlets) in the neighborhood can be used to characterize each node and to establish pairwise affinity scores (Gligorijevic et al., 2014; Milenkovic et al., 2010; Milenkovic and Przulj, 2008). More sophisticated machine learning algorithms, such as GeneMANIA (Mostafavi and Morris, 2010; Mostafavi et al., 2008), have also been proposed. GeneMANIA uses label propagation on an integrated network specifically constructed for each functional label, and is currently available as the state-of-the-art web interface for gene function prediction in multiple organisms.
Despite the success of existing algorithms, a major difficulty that has not been sufficiently addressed is that of predicting rare labels. Because many molecular functions (MFs) are inherently specific in their scope, a large number of functional labels have only a few annotated genes (or positive annotations); for instance, in the human GO annotation database (Ashburner et al., 2000), there are currently 8626 GO labels with at least 3 annotations, 4178 of which have <10 annotated genes and 7905 labels have <100 genes. The distributions of GO labels with different numbers of annotations in yeast and human are shown in Figure 1. Nearly half of the GO labels have <10 annotations in both species.
Fig. 1.
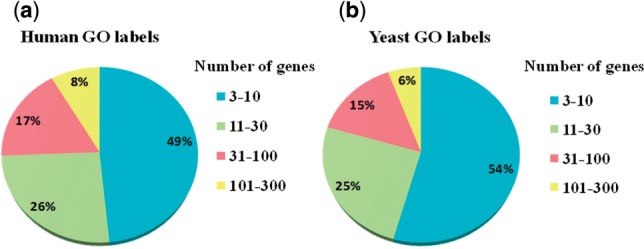
A breakdown of GO labels by the number of annotated genes in (a) human and (b) yeast
Predicting new associations for these sparsely annotated labels is substantially more challenging than those for labels with a lot of annotations, because patterns extracted from the few known genes are more likely to be statistical artifacts that cannot be generalized, which is commonly known as the ‘overfitting’ problem in machine learning and statistics.
One way to mitigate overfitting is to take similarities between labels into account. For instance, if we have a priori knowledge that two labels reflect similar MFs (e.g. they are both children of the same parent in the ontology graph), we would also expect the two corresponding sets of genes (or proteins) to be similar. If one of the gene sets contains only a few genes, then the other may provide valuable information about missing associations. Thus, by propagating information along the edges in the ontology graph, one can pool available data together for increased robustness to overfitting.
Notably, previous efforts to incorporate label similarity into function prediction algorithms have largely been unsuccessful. They formulated the problem as a single structured-output hierarchical classification (HC) instead of binary classification, but its predictive performance for sparsely annotated functional labels is far from satisfactory (Clark and Radivojac, 2013; Eisner et al., 2005; Guan et al., 2008; Jiang et al., 2014; Kim et al., 2008; Obozinski et al., 2008; Sokolov and Ben-Hur, 2010). Another related work (Wang et al., 2013) exploited the similarity between 17 Munich Information Center for Protein Sequences (MIPS) functional categories via a regularization scheme. However, this approach does not scale to tens of thousands of sparse GO annotations in human, as it employs a computationally expensive optimization.
Our approach to this problem is based on diffusion component analysis (DCA) (Cho et al., 2015), a recently developed algorithm that combines network diffusion, such as random walk with restart (RWR) (Kohler et al., 2008), with dimensionality reduction to obtain low-dimensional vector representations of nodes in a graph that capture topological properties. Topological features extracted from interaction networks in this manner can be used in conjunction with k-nearest neighbors (kNNs) or support vector machines (SVMs) to outperform the corresponding state-of-the-art for predicting hundreds of MIPS labels in yeast (Cho et al., 2015). However, DCA also suffers from overfitting for sparsely annotated labels when predicting GO labels for a larger human interactome, if we want to train label-wise classifiers for all labels.
In this work, we introduce clusDCA, an improved function prediction algorithm based on DCA (we attached a two-page abstract of DCA in the Supplementary Data), which (i) incorporates the similarity between functional labels and (ii) scales to a large number of annotations. The key idea of clusDCA is to perform DCA also on the ontology graph to obtain compact vector representations of labels. The gene vectors from the original method are then projected onto the space of label vectors so that the projections of positively annotated genes are geometrically close to their assigned labels. Because labels that are similar to each other in the ontology graph are co-localized in the label vector space, classifiers for sparsely annotated labels will now favor genes associated with other similar labels in the neighborhood. This is how information is transferred between labels to avoid overfitting in our approach.
When compared with state-of-the-art methods that do not incorporate label similarity, our experiments on yeast, mouse and human datasets demonstrate that our method substantially improves the predictive accuracy of sparsely annotated labels while achieving comparable performance for GO labels with sufficiently many genes. We also demonstrate the performance improvement of clusDCA over an alternative approach to utilizing the ontology graphs based on HC. Furthermore, our method can be used to predict new genes for a given GO label, even in the extreme case where there are no existing gene annotations and the only information available is the label’s position in the ontology graph and the genes associated with other labels. In addition to improving function prediction on its own, this demonstrates the potential for our method to be used in conjunction with recent methods that extract new ontology terms from data (Dutkowski et al., 2013; Kramer et al., 2014) to provide an improved way of refining and extending our knowledge of gene or protein function.
2 Methods
As an overview, clusDCA first computes the ‘diffusion state’ of each node by performing a RWR on each input network, and subsequently finds a low-dimensional vector representation for each gene via an efficient matrix factorization of the diffusion states. A key contribution is that clusDCA then follows an analogous procedure to obtain a low-dimensional vector representation of each functional label based on the ontology graph. Intuitively, the gene vectors encode the topology of the interactome, which in turn reflects gene function, while the label vectors encode the topology of the ontology graph, which reflects the semantic and relational properties of the labels. Given both the gene and the label vectors, clusDCA novelly finds the best projection of the gene vectors onto the label vector space, thus keeping the projected gene vectors geometrically close to their known labels. In the final step, clusDCA computes its predictions for an uncharacterized gene by sorting the candidate functions by their proximity to the projected gene vector, based on the optimal projection. An illustration of this pipeline is given in Figure 2. We give a more detailed description of this pipeline below.
Fig. 2.
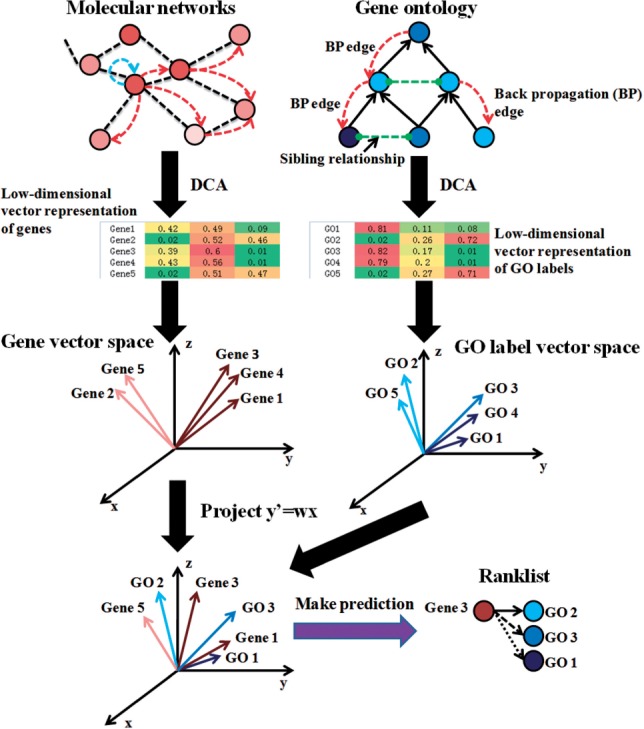
Overview of clusDCA
2.1 Low-dimensional vector representations of genes
2.1.1 Review of DCA
The first step of clusDCA is to use DCA to compute low-dimensional vector representations of genes in molecular networks. To achieve this goal, DCA first runs RWR on each node in each molecular network (e.g. protein–protein interaction or co-expression network) to compute the ‘diffusion state’ of each node, which summarizes local topology. RWR is different from conventional random walks in that it introduces a pre-defined probability of restarting at the initial node after every iteration.
Formally, let A denote the weighted adjacency matrix of a molecular interaction network with n genes (or proteins). Each entry in the transition matrix represents the probability of a transition from node to node and is defined as:
| (1) |
Next, letting be an -dimensional distribution vector in which each entry stores the probability of a node being visited from node after steps, RWR from node with restart probability is defined as:
| (2) |
where is an -dimensional distribution vector with and , . Note that the restart probability controls the relative influence of global and local topological information in the diffusion, where a larger value places greater emphasis on the local structure. We can obtain the stationary distribution of RWR at the fixed point of this iteration, and we refer to this as the ‘diffusion state’ of node (i.e. , using the same definition as previous work (Cao et al., 2014). Intuitively, the jth entry Sij stores the probability that RWR starts at node i and ends up at node j in equilibrium. The fact that two nodes having similar diffusion states implies they are in similar positions with respect to other nodes in the graph, which may reflect functional similarity. However, the diffusion states are not entirely accurate, partially due to the noisy and incomplete nature of interactomes. Moreover, high dimensionality imposes additional computational constraints on directly using the diffusion states as features for classification or regression tasks.
To address this issue, DCA employs the following dimensionality reduction scheme. The probability assigned to node j in the diffusion state of node i is modeled as
| (3) |
where for . DCA refers to as the context feature and as the node feature of node i, both capturing the topological properties of the network. If and are close in direction and have large inner product, then it is likely that node j is frequently visited in the random walk starting from node i. DCA takes a set of observed diffusion states as input and optimizes over w and x for all nodes, using KL-divergence as the objective function:
| (4) |
The original framework uses a standard quasi-Newton method L-BFGS (Zhu et al., 1997) to solve this optimization problem. Although the learnt low-dimensional vector representation can effectively capture the network structure, we found that optimizing in this way is time consuming.
2.1.2 New contributions
To make DCA more scalable to large molecular networks, we developed a fast, matrix factorization-based approach to decompose the diffusion states. Based on the definition of , we have:
| (5) |
The first term in the above equation corresponds to the low-dimensional approximation of , while the second term is the normalization factor that enforces , where is the -dimensional probability simplex. In our new formulation, we relax the constraint that the entries in sum to one by dropping the second term; while the resulting low-dimensional approximations of diffusion states are no longer strictly valid probability distributions, we find that the approximations are close enough to the true distribution that the relaxation has a negligible impact. As a result, can be simplified as:
| (6) |
In addition, instead of optimizing the relative entropy between the true and the approximated diffusion states, we use the sum of squared errors as the new objective function
| (7) |
Now, the resulting optimization problem can be easily solved by the classic singular value decomposition (SVD) (Golub and Reinsch, 1970). To avoid taking a logarithm of zeros, we added a small positive constant to and computed the logarithm diffusion state matrix L as:
| (8) |
where with , and is the concatenation of . With SVD, we decompose into three matrices , and :
| (9) |
where , and is the diagonal singular value matrix. To obtain the low-dimensional vectors and with dimensions, we simply choose the first singular vectors , and the first singular values . More precisely, let denote the low-dimensional vector representation matrix, and denote the context feature matrix. and can be computed as:
| (10) |
| (11) |
2.1.3 Runtime improvements
The key benefit of this new optimization procedure is significantly reduced computational time. For example, decomposing the STRING yeast network into 500-dimensional vectors takes <5 min on a standard server (with six 3.07 GHz Intel Xeon CPUs and 32GB RAM) for SVD, while the original approach with L-BFGS takes >2 h. We noticed that the prediction accuracies for both methods are almost identical in predicting yeast gene function.
To integrate heterogeneous network data, we extend the above single-network DCA to multiple networks. Let denote the set of logarithm diffusion state matrices based on the diffusion states from the k input networks. Here, we optimize the following objective function:
| (12) |
where for each node i in network r, we assign a network-specific context feature , which encodes the intrinsic topological properties of node i in network r. The node features x are shared across all k networks to be able to capture more global patterns. This objective function can be also optimized by SVD. It is worth noting that it is possible to weight each network differently when concatenating the networks, but we give equal importance to each network in this work for simplicity.
In the following sections, we use as the low-dimensional vector representations of genes. Note that one can also use , but we observed that the performances of these two representations are quite similar.
2.2 Low-dimensional vector representations of functional labels
The GO graph is a directed acyclic graph (DAG) over functional labels where the edges represent various semantic relationships. In this work, we only consider the ‘is a’ and ‘part of’ edges, which results in a hierarchy of labels with edges going from the more specific to the more generic terms. As a consequence of this hierarchical structure, which is generally not present in molecular networks, a naive application of RWR on the ontology graph where the edges are treated as undirected unfairly favors high-level nodes, which tend to have higher centrality. On the other hand, allowing a random walk to only move from high- to low-level nodes would greatly restrict the portion of the graph a random walk can explore.
To address these issues, we allow both edge directions but with different weights, whose ratio is controlled by the ‘back propagation’ parameter . With denoting the transition matrix of the original graph with unidirectional edges, our modified RWR for the ontology graph is defined as
| (13) |
We chose a value for that generally shrinks the diffusion scores of high-level nodes, and confirmed that the final prediction performance is stable for different values of α between 0.5 and 0.8.
Based on the diffusion states from this modified random walk, we learned a low-dimensional vector representation of the ontology graph using the same procedure as the one for molecular networks. Importantly, our representation captures not only single-hop parent–child relationships, but also more global patterns such as long-range sibling relationships in the network.
In the following sections, we use to denote the low-dimensional vector representation matrix of functional labels. is the vector for function j.
2.3 Projecting gene vectors into ontology label space
After obtaining the low-dimensional vector representations of both genes and functional labels, we use these vectors to predict gene function. Because the vectors reflect the topological structure of nodes in the network, genes that are close in their vector directions are more likely to be similar in their functions. Analogously, functional labels that are close in their vector directions may be more semantically similar. Based on this intuition, we use a transformation matrix to project genes from the gene vector space to the function vector space, which allows us to match genes to functions based on geometric proximity. Let be the projection of the gene vector :
| (14) |
Then we define the pairwise affinity score between gene i and function j to be used for function prediction as:
| (15) |
A larger zij indicates that gene i is more likely to be annotated with function j
We want to optimize W so that positively annotated genes are geometrically similar to their assigned GO labels. In this work, we use the inner product as the similarity function. We also explored the L2 distance, but it performed generally worse than the inner product, possibly due to the fact that the inner product explicitly models both positive and negative annotations. Next, we define (as the set of genes that are positively (negatively) annotated with function j. Note that whenever a gene is positively annotated with a particular function we also positively annotated all of its ancestors with the gene. Our constrained optimization problem for finding the best projection that incorporates both positive and negative annotations is given by
| (16) |
where the weights and correct for the imbalance in the training data. Instead of simply maximizing the affinity scores of positive annotations, this formulation aims at maximizing the margin between the affinity scores of positive and negative annotations. This problem can be solved analytically by a closed-form solution:
| (17) |
where is a weight matrix with and .
Because modeling the complex relationship between genes and functional labels with a single transformation matrix may be overly restrictive, we group functions into different clusters and learn a separate projection model for each cluster. For the main results, we divide the GO labels into the following four groups based on the number of annotated genes in the training data: [3–10], [11–30], [31–100] and [101–300]. We also tested using the partition given by the clustering of our learned label vectors and obtained comparable prediction performance (see Supplementary Data).
3 Results
3.1 Networks and annotations
We obtained a collection of six molecular networks each for human, yeast and mouse from the STRING database v9.1 (Franceschini et al., 2013). These networks are built from heterogeneous data sources, including high-throughput interaction assays, curated protein-protein interaction databases, and conserved co-expression. We excluded text mining-based networks to avoid confounding by links based on functional similarity. There were 16 662 nodes in human, 6311 in yeast and 18 248 in mouse. The number of edges in these networks varied from 1183 to 673 410 in human, from 1059 to 293 921 in yeast and from 3917 to 1 638 107 in mouse. Note that each edge is associated with a weight between 0 and 1 representing the confidence of interaction. Next, we obtained gene-function associations and the ontology of functional labels from the GO Consortium (Ashburner et al., 2000). We built a DAG of GO labels from all three categories [biological process (BP), MF, cellular component] based only on the ‘is a’ and ‘part of’ relationships for each species. Labels without any associated genes were removed, resulting in three species-specific ontology graphs for yeast, human and mouse. The human ontology graph had 13 708 functions and 19 206 edges, the yeast ontology graph had 4240 functions and 4804 edges and the mouse ontology graph had 13 807 functions and 19 704 edges.
3.2 Experimental setting
Following previous work (Mostafavi et al., 2008), we used 3-fold cross-validation to evaluate our method, where a randomly chosen subset of one-third of the genes are held out as the test set. After computing the optimal projection of gene vectors into the functional label space based only on the training data, we calculated the affinity scores (see Equation 15) to get a ranked list of test genes for each function. Then we measured the extent to which true annotations are concentrated near the top of the list by calculating the area under the receiver operating characteristic curve (AUROC) and the area under the precision recall curve (AUPRC), which are standard performance metrics in this field (Mostafavi et al., 2008). To summarize results across different labels, we used both micro- and macro-averages. The micro-average directly combines the entries in the confusion matrix constructed from different labels prior to calculating the predictive performance, and the macro-average calculates the areas under the curves for each label independently and then takes the average.
We compared clusDCA to two state-of-the-art network-based function prediction algorithms, GeneMANIA (Mostafavi et al., 2008) and DCA (Cho et al., 2015), and another algorithm based on HC (Sokolov and Ben-Hur, 2010), which exploits the hierarchical structure of functional labels. For consistency, we used the same dataset (i.e. annotations, genes, networks) and the same evaluation scheme for every method we tested.
We obtained the original MATLAB implementation of GeneMANIA from http://morrislab.med.utoronto.ca/Data/GB08/. For DCA, we tested only the kNN version, because the SVM version seriously suffers from overfitting for sparsely annotated labels and also does not scale to the human dataset. Importantly, neither GeneMANIA nor DCA leverages topological information from the GO graph. Noting that the original formulation of HC does not scale to large datasets, we instead implemented an efficient version that utilizes the clusDCA framework. In particular, we associate each gene with a ‘macro-label’ , where is a ‘micro-label’ which is set to 1 when the gene is positively annotated with label i and 0 otherwise. Following HC, we impose a constraint that if then for every ancestor j of i. We then find the optimal projection from DCA gene vectors to the space of macro-labels using the same optimization problem we introduced in Equation 16. After solving the optimization problem, we use the optimized transformation matrix to compute the pairwise affinity score zij between gene i and function j.
For clusDCA, we set the back propagation parameter to 0.8 and the restart probability to 0.8 for the GO graph. We observed that our performance is stable for different values of between 0.5 and 0.8. For the molecular networks, we used a restart probability of 0.5, adopted from our previous work (Cho et al., 2015). We set a larger restart probability for the GO graphs because they are generally much sparser. We used d = 2500 as the dimensionality of the learned vectors for the main results. The effect of varying this parameter is analyzed in Section 3.7.
We followed the same procedure as the one in GeneMANIA to group the GO labels into two major gene ontologies: ‘BP’ and ‘MF’. For both ontologies, we further binned GO labels into four sparsity levels, each consisting of GO labels with [3–10], [11–30], [31–100] and [101–300] annotated genes (see Table 1). Although we used all of the GO terms in human and yeast, for mouse, we used only the GO terms with evidence codes that are also used in the evaluation of GeneMANIA (Mostafavi et al., 2008): TAS, RCA, ND, NAS, ISS, IPI, IMP, IGI, IEP, IEA, IDA and IC (Peņa-Castillo et al., 2008).
Table 1.
Number of GO terms in different sparsity levels
| 3–10 | 11–30 | 31–100 | 101–300 | |
|---|---|---|---|---|
| Human MF | 886 | 390 | 222 | 99 |
| Human BP | 2940 | 1677 | 1122 | 553 |
| Yeast MF | 351 | 156 | 92 | 29 |
| Yeast BP | 815 | 408 | 235 | 87 |
| Mouse MF | 188 | 215 | 165 | 84 |
| Mouse BP | 337 | 568 | 678 | 329 |
3.3 GO label vectors capture semantic similarity
Unlike some of the previous work (Mostafavi et al., 2008; Wang et al., 2014) that did not explicitly incorporate the GO graph, our approach exploits the ontology structure to learn a low-dimensional vector representation of each GO label. If these vectors can be clustered into semantically meaningful clusters, it would validate our attempt to enforce gene assignments to be similar between labels that are geometrically close in the label vector space as being well founded. To test this hypothesis, we used K-means to cluster the GO labels based on the cosine similarity of our low-dimensional vector representations of labels. We determined the number of clusters by restricting the largest cluster to have at most 80% of the total number of labels. In Supplementary Figure S1 (Supplementary Data), two of the 41 clusters we identified are visualized with Cytoscape (Smoot et al., 2011). The complete list of clusters can be found in Supplementary Data. In the visualization, the node size reflects the number of genes that the corresponding function is annotated with, and the edge width reflects the cosine similarity between the vector representations of the two nodes. The first cluster represents functions related to molecular binding, such as cation binding, metal ion binding, nucleotide binding and NAD binding, whereas the second cluster represents functions related to different transmembrane transporter activity. The fact that the set of GO labels in each of these clusters is highly consistent in function provides evidence that the learned vectors faithfully reflect the semantic relationships among the labels.
3.4 clusDCA substantially improves prediction of sparsely annotated GO labels
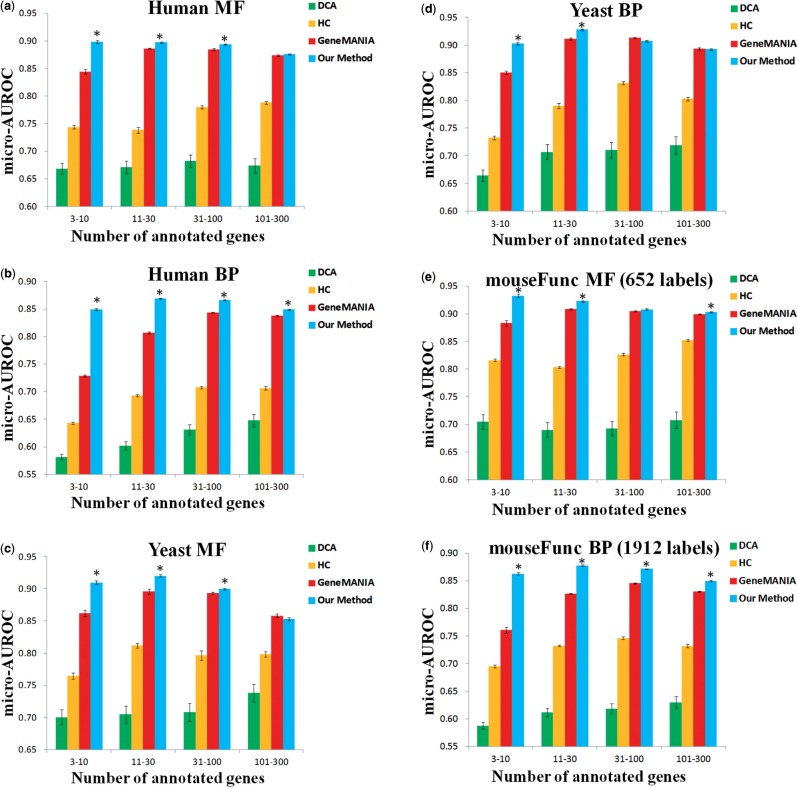
To evaluate clusDCA, we performed large-scale function prediction for human, yeast and mouse. The results are summarized in Figure 3 and Supplementary Figure S2 (Supplementary Data). It is clear that our approach significantly outperforms other methods on sparsely annotated labels in all three datasets. For example, in human, our method achieved 0.8491 micro-AUROC and 0.8648 macro-AUROC on BP labels with 3–10 annotations, which is much higher than 0.5815 (micro), 0.5857 (macro) for DCA and 0.7288 (micro), 0.8002 (macro) for GeneMANIA. It is worth noting that DCA performs consistently worse than GeneMANIA at this task, possibly due to the fact that GeneMANIA adaptively integrates the input networks for each functional label to optimize performance on training data. In yeast, clusDCA achieved 0.9025 micro-AUROC on BP labels with 3–10 annotations, which is again substantially higher than 0.6645 for DCA and 0.8504 for GeneMANIA. In mouse, clusDCA achieved 0.8627 micro-AUROC and 0.8802 macro-AUROC on BP labels with 3–10 annotations, which is again substantially higher than 0.5873 (micro), 0.5937 (macro) for DCA and 0.7609 (micro), 0.8245 (macro) for GeneMANIA. A similar improvement was observed for functional labels with 11–30 annotations and also for the MF labels in human, yeast and mouse (Fig. 3 and Supplementary Fig. S2). We found most of the improvements to be statistically significant (P < 0.05; paired Wilcoxon signed-rank test). The improvement was most pronounced in human overall, presumably because the human dataset is much sparser than the other two.
Fig. 3.
Comparison of our approach with other methods in terms of micro-AUROC. Asterisk indicates that our approach is statistically significant in comparison with GeneMANIA. Performance is evaluated for different subsets of GO labels with varying sparsity levels as shown on the x-axis
The above results suggest that the topological information in ontology graphs can be exploited to greatly improve function prediction performance for sparse labels. It remains to be shown whether clusDCA is better than other approaches to incorporating the ontology. To this end, we found that clusDCA substantially outperforms HC. For instance, in human, our method achieved 0.8984 micro-AUROC and 0.9135 macro-AUROC on MF labels with 3–10 annotations, which is much higher than 0.7435 (micro), 0.7580 (macro) for HC. The improvement was more pronounced where the number of GO labels was large (e.g. human BP). This is likely because the number of candidate predictions for HC grows exponentially with the number of GO labels. As a result, HC is highly prone to overfitting in a dataset with a large number of labels. Notably, HC also invariably performed worse than GeneMANIA in most of our experiments.
In addition, we observed consistent improvements over GeneMANIA with respect to the AUPRC. In human, our method achieved 0.0429 macro-AUPRC on BP labels with 3–10 annotations, which is higher (better) than 0.0368 AUPRC for GeneMANIA. In yeast, clusDCA achieved 0.1360 AUPRC on MF labels with 3–10 annotations, which is substantially higher than 0.1075 macro-AUPRC for GeneMANIA. Similarly, in mouse, clusDCA achieved 0.0516 macro-AUPRC on BP labels with 3–10 annotations, which is substantially higher than 0.0389 macro-AUPRC for GeneMANIA
Interestingly, we note that the improvement of our method is negatively correlated with the number of annotations of the GO labels. In other words, we observed a greater improvement of clusDCA over previous methods for sparser labels. This observation suggests that clusDCA indeed addresses the overfitting issue, which has more significant impact on the sparsely annotated labels.
3.5 clusDCA achieves comparable performance for labels with a large number of annotations
In addition to sparsely annotated labels, our approach also achieved a performance comparable to GeneMANIA and greatly outperformed HC and DCA on labels with a large number of annotations (i.e. 31–100 and 101–300) with respect to both AUROC and AUPRC. The difference between clusDCA and GeneMANIA is not statistically significant in this case, but clusDCA is still marginally better than GeneMANIA on most categories.
3.6 clusDCA accurately predicts genes for new GO labels
Given that the current GO database is likely incomplete, in the event that a new GO label is created, we hope to automatically find genes that this label may be associated with. Remarkably, our framework can be directly used to tag genes with a newly created GO label using only the topological information from the ontology graph and other annotated labels. When the new GO labels are added to the ontology graph, we first obtain the low-dimensional vectors of these labels with DCA. Then, given the low-dimensional vectors for both genes and functions, we can inversely project function vectors onto the gene vector space and predict associated genes for the new GO labels. This approach can also potentially help to refine and enhance the current GO annotation database, thus serving as a verification platform.
As a proof-of-concept, we repeatedly held out one-third of the GO labels as the validation set of ‘uncharacterized’ labels. We then used the remaining two-third GO labels to learn the projection model and to predict genes that are associated with the held out labels. Figure 4 shows the result of this experiment in yeast. We observed that our framework achieves a promising performance on all categories with micro-AUROC ranging from 0.81 to 0.87. It is worth noting that, to our best knowledge, no other existing method is able to predict associated genes for new GO labels without any existing annotations. Disease gene prioritization is a closely related task where the goal is to predict genes associated with a particular disease, but most algorithms proposed for this problem also require an initial set of associated genes to be able to make predictions.
Fig. 4.
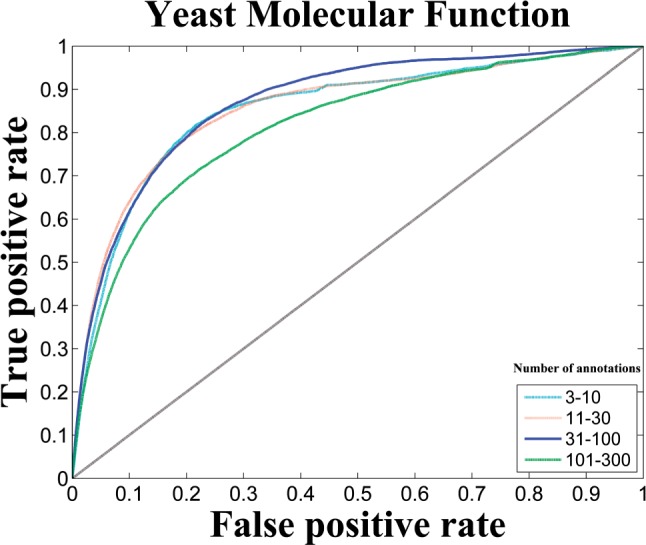
Micro ROC curve of predicting genes for new GO labels on MF in yeast
3.7 Choice of the dimensionality of low-dimensional representations
Here, we examined the impact of the number of dimensions used for clusDCA on the prediction performance. To this end, we calculated the micro-AUROC of BP label prediction in yeast with different number of dimensions (Supplementary Fig. S3 in Supplementary Data). We observed that our method is quite robust over a wide range of dimensions. A good performance is achieved from 1000 dimensions and above, with a notable exception of the [3–10] label group, which seems to improve further at 2000 dimensions. Interestingly, we found that labels with more annotations are less affected by this parameter. In our previous work (Cho et al., 2015), DCA achieved a good performance with only 500 dimensions. We think this is due to the fact that the GO graph is sparser than the yeast interactome and thus shows less clustering properties locally; random walks are therefore more localized on the GO graph, which requires more dimensions to be accurately modeled.
4 Conclusion
We introduced a novel algorithm, clusDCA, for gene function prediction. The major idea of clusDCA is to leverage similarity between functional labels in addition to similarity between genes to prevent overfitting of sparsely annotated GO labels. We achieve this goal by learning low-dimensional vector representations of genes and functions and matching gene vectors to function vectors via a projection that best preserves known gene-function associations. Similar labels are co-localized in the vector space, which allows the transfer of information between neighboring functions when genes are assigned to them. Since learning the projection solves the prediction of all labels simultaneously, our method has the added benefit of being scalable to datasets with a large number of annotations.
Although based on DCA, clusDCA is a substantial advance, as evidenced by its superior performance over DCA, as well as GeneMANIA and HC, on sparsely annotated GO labels, while maintaining a comparable performance on labels with many genes. Moreover, we demonstrated clusDCA’s ability to identify putatively associated genes for newly created GO labels without any annotations, which suggests that our method can be used to improve poorly annotated labels and thus takes a significant step towards more comprehensive understanding of gene or protein function in various organisms.
Funding
This research was partially supported by grant 1U54GM114838 awarded by NIGMS through funds provided by the trans-NIH Big Data to Knowledge (BD2K) initiative (www.bd2k.nih.gov). The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
Conflict of Interest: none declared.
Supplementary Material
References
- Ashburner M., et al. (2000) Gene ontology: tool for the unification of biology. The Gene Ontology Consortium. Nat. Genet. 25, 25–29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cao M., et al. (2014) New directions for diffusion-based network prediction of protein function: incorporating pathways with confidence. Bioinformatics , 30, i219–i227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cao M., et al. (2013) Going the distance for protein function prediction: a new distance metric for protein interaction networks. PloS One, 8, e76339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cho H., et al. (2015) Diffusion component analysis: unraveling functional topology in biological networks. In: Research in Computational Molecular Biology. Lecture Notes in Computer Science, Springer International Publishing, Switzerland, Vol. 9029, pp. 62–64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clark W.T., Radivojac P. (2013) Information-theoretic evaluation of predicted ontological annotations. Bioinformatics, 29, i53–i61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dutkowski J., et al. (2013) A gene ontology inferred from molecular networks. Nat. Biotechnol., 31, 38–45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eisner R., et al. (2005) Improving protein function prediction using the hierarchical structure of the gene ontology. In: Computational Intelligence in Bioinformatics and Computational Biology, 2005. CIBCB'05. Proceedings of the 2005 IEEE Symposium on. IEEE , pp. 1–10. [Google Scholar]
- Franceschini A., et al. (2013) STRING v9.1: protein-protein interaction networks, with increased coverage and integration. Nucleic Acids Res., 41 (Database issue), D808–D815. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gligorijevic V., et al. (2014) Integration of molecular network data reconstructs Gene Ontology. Bioinformatics, 30, i594–i600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golub G.H., Reinsch C. (1970) Singular value decomposition and least squares solutions. Numer. Math., 14, 403–420.. [Google Scholar]
- Guan Y., et al. (2008) Predicting gene function in a hierarchical context with an ensemble of classifiers. Genome Biol., 9 (Suppl 1), S3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang Y., et al. (2014) The impact of incomplete knowledge on the evaluation of protein function prediction: a structured-output learning perspective. Bioinformatics, 30, i609–i616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karaoz U., et al. (2004) Whole-genome annotation by using evidence integration in functional-linkage networks. Proc. Natl. Acad. Sci. USA, 101, 2888–2893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim W.K., et al. (2008) Inferring mouse gene functions from genomic-scale data using a combined functional network/classification strategy. Genome Biol. , 9 (Suppl 1), S5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kohler S., et al. (2008) Walking the interactome for prioritization of candidate disease genes. Am. J. Hum. Genet., 82, 949–958. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kramer M., et al. (2014) Inferring gene ontologies from pairwise similarity data. Bioinformatics, 30, i34–i42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Letovsky S., Kasif S. (2003) Predicting protein function from protein/protein interaction data: a probabilistic approach. Bioinformatics, 19 (Suppl 1), i197–i204. [DOI] [PubMed] [Google Scholar]
- Milenkovic T., et al. (2010) Systems-level cancer gene identification from protein interaction network topology applied to melanogenesis-related functional genomics data. J.R. Soc. Interface, 7, 423–437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Milenkovic T., Przulj N. (2008) Uncovering biological network function via graphlet degree signatures. Cancer Inform., 6, 257–273. [PMC free article] [PubMed] [Google Scholar]
- Mostafavi S., Morris Q. (2010) Fast integration of heterogeneous data sources for predicting gene function with limited annotation. Bioinformatics, 26, 1759–1765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mostafavi S., et al. (2008) GeneMANIA: a real-time multiple association network integration algorithm for predicting gene function. Genome Biol., 9 (Suppl. 1), S4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murali T.M., et al. (2006) The art of gene function prediction. Nat. Biotechnol., 24, 1474–1475; author reply 1475–1476. [DOI] [PubMed] [Google Scholar]
- Nabieva E., et al. (2005) Whole-proteome prediction of protein function via graph-theoretic analysis of interaction maps. Bioinformatics, 21 (Suppl 1), i302–i310. [DOI] [PubMed] [Google Scholar]
- Obozinski G., et al. (2008) Consistent probabilistic outputs for protein function prediction. Genome Biol., 9 (Suppl 1), S6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peņa-Castillo L., et al. (2008) A critical assessment of Mus musculus gene function prediction using integrated genomic evidence. Genome Biol., 9, S2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Radivojac P., et al. (2013) A large-scale evaluation of computational protein function prediction. Nat. Methods, 10, 221–227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sefer E., Kingsford C. (2011) Metric labeling and semi-metric embedding for protein annotation prediction. In: Research in Computational Molecular Biology. Springer, London, pp. 392–407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smoot M.E., et al. (2011) Cytoscape 2.8: new features for data integration and network visualization. Bioinformatics, 27, 431–432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sokolov A., Ben-Hur A. (2010) Hierarchical classification of Gene Ontology terms using the GOstruct method. J. Bioinform. Comput. Biol., 8, 357–376. [DOI] [PubMed] [Google Scholar]
- Wang H., et al. (2013) Function–function correlated multi-label protein function prediction over interaction networks. J. Comput. Biol., 20, 322–343. [DOI] [PubMed] [Google Scholar]
- Wang H., et al. (2014) Correlated protein function prediction via maximization of data-knowledge consistency. In: Research in Computational Molecular Biology. Springer, London, pp. 311–325. [DOI] [PubMed] [Google Scholar]
- Zhu C., et al. (1997) Algorithm 778: L-BFGS-B: Fortran subroutines for large-scale bound-constrained optimization. ACM Trans. Math. Softw., 23, 550–560. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.