Mechanistic Investigation of the Arrhythmogenic Role of Oxidized CaMKII in the Heart

Abstract

Oxidative stress and calcium (Ca²⁺)/calmodulin (CaM)-dependent protein kinase II (CaMKII) both play important roles in the pathogenesis of cardiac disease. Although the pathophysiological relevance of reactive oxygen species (ROS) and CaMKII has been appreciated for some time, recent work has shown that ROS can directly oxidize CaMKII, leading to its persistent activity and an increase of the likelihood of cellular arrhythmias such as early afterdepolarizations (EADs). Because CaMKII modulates the function of many proteins involved in excitation-contraction coupling, elucidation of its role in cardiac function, in both healthy and oxidative stress conditions, is challenging. To investigate this role, we have developed a model of CaMKII activation that includes both the phosphorylation-dependent and the newly identified oxidation-dependent activation pathways. This model is incorporated into our previous local-control model of the cardiac myocyte that describes excitation-contraction coupling via stochastic simulation of individual Ca²⁺ release units and CaMKII-mediated phosphorylation of L-type Ca²⁺ channels (LCCs), ryanodine receptors and sodium (Na⁺) channels. The model predicts the experimentally measured slow-rate dependence of H₂O₂-induced EADs. Upon increased H₂O₂, simulations suggest that selective activation of late Na⁺ current (I_NaL), although it prolongs action potential duration, is not by itself sufficient to produce EADs. Similar results are obtained if CaMKII effects on LCCs and ryanodine receptors are considered separately. However, EADs emerge upon simultaneous activation of both LCCs and Na⁺ channels. Further modeling results implicate activation of the Na⁺-Ca²⁺ exchanger (NCX) as an important player in the generation of EADs. During bradycardia, the emergence of H₂O₂-induced EADs was correlated with a shift in the timing of NCX current reversal toward the plateau phase earlier in the action potential. Using the timing of NCX current reversal as an indicator event for EADs, the model identified counterintuitive ionic changes—difficult to experimentally dissect—that have the greatest influence on ROS-related arrhythmia propensity.

Introduction

Oxidative stress, defined as a pathologically high level of reactive oxygen species (ROS) in cells, is known to play a central role in the development of cardiac disease (1). ROS accumulation impairs cardiac function by directly modulating a broad variety of protein targets, including ion channels, membrane transporters, and signaling kinases (2). However, the exact mechanisms by which increased oxidative stress is converted to sustained alteration of heart function remains largely unknown. One molecule that has recently been suggested as a sensor of oxidative stress in the heart is calcium (Ca²⁺)/calmodulin (CaM)-dependent protein kinase II (CaMKII) (3). Excessive CaMKII activation, as occurs under pathological conditions such as heart failure, has been linked to altered excitation-contraction coupling (ECC) and proarrhythmic electrical remodeling (4).

The CaMKII holoenzyme exists as a macromolecular complex consisting of two stacked ring-shaped hexamers (5). Each of its 12 subunits can be activated through binding of Ca²⁺-bound CaM (Ca²⁺/CaM) to the CaMKII regulatory domain in response to beat-to-beat transient increases of intracellular Ca²⁺ concentration ([Ca²⁺]_i). Activated CaMKII molecules can be autophosphorylated by neighboring subunits at threonine amino acid residues in the regulatory domain. This results in the kinase retaining activity even upon dissociation of Ca²⁺/CaM (6). We refer to this sequence of events as the phosphorylation activation pathway. Recently, a novel mechanism for oxidative CaMKII activation was discovered that involves the oxidation of CaMKII at specific methionine residues (7). This newly identified oxidation activation pathway produces persistent kinase activity and increases the likelihood of cellular arrhythmias known as early and delayed afterdepolarizations (EADs and DADs, respectively) (8,9).

These new findings implicate oxidative CaMKII activation as a putative mechanistic link between ROS accumulation and life-threatening cardiac arrhythmias (3). CaMKII phosphorylates several proteins involved in ECC, including L-type Ca²⁺ channels (LCCs) (10), ryanodine receptors (RyRs) (11), and phospholamban (PLB) (12). CaMKII also phosphorylates sodium (Na⁺) and potassium (K⁺) channels to regulate their function (12–14). Because CaMKII acts on multiple targets, its effects on integrative myocyte behavior are best interpreted through development and application of quantitative models. Here, we use a computational model that links cellular ROS and CaMKII activation to understand their effects on whole-cell electrophysiology.

In one recent study, Christensen et al. (15) developed a model of oxidative CaMKII activation and used this model to study the role of CaMKII in the border zone of cardiac infarcts. Simulation results demonstrated that enhanced oxidative CaMKII activation is associated with reduced conduction velocity, increased refractory periods, and a greater likelihood of conduction block. These results were attributed primarily to CaMKII-mediated regulation of Na⁺ channel kinetics and availability. Although Christensen et al. noted that CaMKII activation also has an impact on major ECC proteins in ways that may promote arrhythmias, these mechanisms were not explored in their study. Accordingly, the purpose of this study is to develop a cardiac myocyte model of CaMKII-mediated regulation of ECC targets arising from both the phosphorylation and oxidative activation pathways, and to analyze their functional significance in the genesis of ROS-induced arrhythmias.

We develop, to our knowledge, a novel stochastic model of CaMKII activation using recent experimental data for CaM affinity and autophosphorylation/oxidation rates measured specifically for CaMKII_δ, the cardiac isoform of CaMKII (7,16). This modeling effort builds upon our previous work (17), incorporating the functional effects of CaMKII-mediated phosphorylation of LCCs, RyRs, PLB, and Na⁺ channels into an integrative myocyte model (18). Our simulations recapitulate previous experimental data indicating that the arrhythmogenic pattern of EADs observed during oxidative stress is dependent on oxidative CaMKII activation and pacing-cycle length. The model further establishes that occurrence of these EADs results from nonintuitive synergistic interactions between individual CaMKII substrates and other ECC proteins, which would be difficult to dissect from experiments alone.

Materials and Methods

Stochastic model of cardiac CaMKII activation

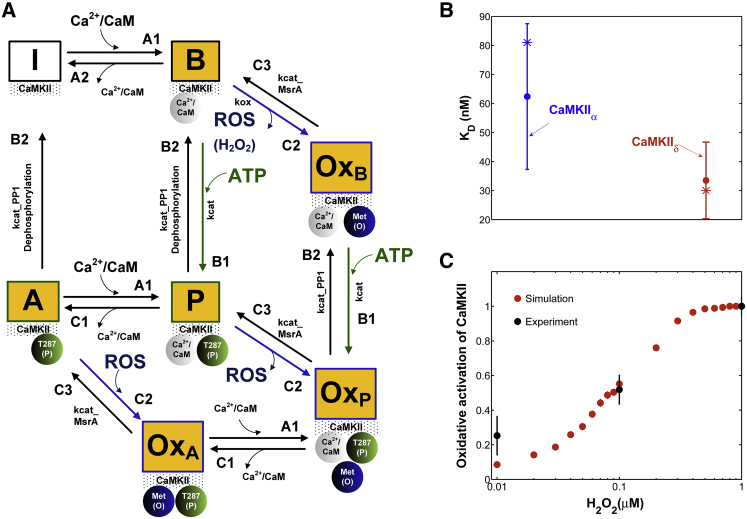
The stochastic model of CaMKII activation (Fig. 1) reflects the functional properties of the cardiac isoform including both the phosphorylation activation pathway and the newly identified oxidation activation pathway. Before the introduction of Ca²⁺/CaM, each CaMKII subunit is inactive (state I in Fig. 1 A). Activation occurs upon binding of Ca²⁺/CaM followed by autophosphorylation and/or oxidation. Autonomous active states (Ca²⁺/CaM-unbound) can be either autophosphorylated or oxidized. The model also includes an active state that is both oxidized and phosphorylated (state Ox_P in Fig. 1 A). This model builds upon the work of Hashambhoy et al. (17,19) with the incorporation of recent experimental data for CaM affinity (Fig. 1 B, circles) and autophosphorylation/oxidation rates measured specifically for CaMKII_δ (7,16). Predicated upon this, we have implemented the four-state deterministic activation model of Chiba et al. (20) within a stochastic framework that is constrained by the geometry of the CaMKII holoenzyme. This was accomplished by restricting CaMKII autophoshorylation events to occur only between adjacent CaMKII subunits, as previously described by Hashambhoy et al. (21) (see the Supporting Material for model details). Under this constraint, the model reproduces the relevant experimental data of CaMKII-Ca²⁺/CaM interaction, as well as the autophosphorylation rate and frequency dependence of CaMKII activation (see Figs. S1 and S2). The stochastic activation model was further modified by including oxidized active states in addition to a Ca²⁺/CaM-bound active state, an autophosphorylated Ca²⁺/CaM-bound state, and an autophosphorylated Ca²⁺/CaM-dissociated state (i.e., an autonomous active state). Consistent with experimental observations (7), Ca²⁺/CaM must bind to a CaMKII subunit before phosphorylation or oxidation can occur. Phosphorylated or oxidized CaMKII molecules retain activity even upon dissociation of Ca²⁺/CaM (states A and OxA in Fig. 1 A). Kinetic rate constants for state transitions were obtained either from the literature or by fitting to recent experimental data obtained under a variety of experimental protocols (e.g., Fig. 1, B and C). For instance, the oxidation-dependent rate (Fig. 1 A, k_ox (mM⁻¹ ms⁻¹)) is estimated using the dose-response activation of CaMKII by H₂O₂ as measured by Erickson et al. (7) (Fig. 1 C, black symbols). All model parameter values are given in Tables S1 and S2.

Figure 1.

(A) State diagram of the stochastic CaMKII activation model. Before the introduction of Ca²⁺/CaM, all CaMKII subunits are in the inactive form (state I). Activation occurs upon binding of Ca²⁺/CaM (state B), followed by autophosphorylation (state P) or oxidation (state Ox_B). Autonomous active states (Ca²⁺/CaM-unbound) can be either autophosphorylated (state A) or oxidized (state Ox_A). The model also includes an active state that is both oxidized and phosphorylated (state Ox_P). (B) Simulated (asterisks) binding affinity for CaM (K_D) for the brain-specific α isoform (blue) and the cardiac-specific δ isoform (red) compared to experimental data (solid circles) of Gaertner et al. (16). (C) Simulated dose-response of CaMKII activation by H₂O₂ (red) compared to experimental data (black) of Erickson et al. (7). Simulations correspond to the experimental condition where [Ca²⁺] = 200 μM and [CaM] = 1 μM in the absence of ATP (to prevent autophosphorylation). To see this figure in color, go online.

Whole-cell model

To investigate the mechanisms by which oxidative CaMKII activation triggers cellular arrhythmias, we incorporated the CaMKII activation model into what is referred to here as the stochastic local-control ventricular myocyte model (17). This model incorporates the functional effects of CaMKII-mediated phosphorylation of LCCs, RyRs, PLB, and Na⁺ channels into an integrative model of the canine ventricular myocyte, with stochastic simulation of LCC and RyR channel gating within a local population of Ca²⁺ release sites known as Ca²⁺ release units based on the theory of local control of ECC (18). Under physiological conditions, our model predicts negligible cytosolic CaMKII activation and thereby negligible PLB phoshorylation (∼0.1%) due to low enrichment of [Ca²⁺] and [CaM] within this compartment (Fig. S6). Huke and Bers (22) showed that the fraction of PLB phosphorylated by CaMKII is minimal (<5%) under normal conditions (2 Hz action potential (AP) pacing). Furthermore, these results are broadly consistent with other experimentally validated computational models of Ca²⁺/CaM (23,24) indicating that cytosolic CaMKII is not appreciably activated due to the relatively low affinity of CaM’s Ca²⁺ binding sites (high apparent K_D of 10 μM). The model predicts negligible cytosolic CaMKII activation, even under oxidative stress. This is not surprising given that CaMKII oxidation occurs upon binding of Ca²⁺/CaM (7). Since CaMKII-mediated phosphorylation of PLB is negligible, the analysis here is focused on the impact of CaMKII-dependent alterations of LCCs, RyRs, and Na⁺ channels on APs during conditions of elevated oxidant stress. The dynamic interactions between CaMKII, LCCs, and RyRs are described as a function of dyadic Ca²⁺ concentration ([Ca²⁺]_dyad) and CaM levels, assuming that there is one 12-subunit CaMKII holoenzyme tethered to each LCC (25). Each CaMKII monomer can transition among a variety of conformational states, and CaMKII monomers can catalyze phosphorylation of individual LCCs and RyRs. In this model, CaMKII phosphorylation of LCCs promotes transitions from mode 1 gating (normal activity) to mode 2 gating (high activity with long openings), as described previously by Hashambhoy et al. (21). Further, CaMKII phosphorylation of RyRs is assumed to increase the RyR sensitivity to [Ca²⁺]_dyad (19). With regard to CaMKII-dependent regulation of Na⁺ current (I_Na), Hashambhoy et al. (17) used a modified version of the Na⁺ channel model of Grandi et al. (26) to simulate the acute effects of CaMKII on cardiac I_Na as reported by Aiba et al. (27). A detailed description of all parameter changes made to the cardiac myocyte model of Hashambhoy et al. (17) is provided in the Supporting Material.

Design of in silico experiments

To assess the performance of the proposed model of CaMKII signaling within the context of cardiac ECC, we 1) verified whether the model captures the experimentally measured rate dependence of EAD occurrence in the presence of 200 μM H₂O₂ (28); 2) evaluated whether the model predicts the differential effects of the Na⁺-Ca²⁺ exchanger (NCX) and RyR inhibition on H₂O₂-induced EADs; and finally 3) performed a comparative analysis to identify H₂O₂-sensitive CaMKII targets that have the greatest influence on the genesis of H₂O₂-induced EADs. All of these simulations represent model predictions in the presence of 200 μM H₂O₂. H₂O₂ level in human blood may reach as high as ∼35 μM in normal conditions (29). Under oxidative stress conditions (e.g., ischemia-reperfusion injury, heart failure), ROS levels can increase as much as 100; hence, a level of 200 μM H₂O₂ lies reasonably within its pathophysiological range. Paced APs were stimulated by a current pulse train of −100 pA/pF in magnitude and 0.5 ms in duration at pacing-cycle lengths (PCLs) of 6.0, 4.0, 2.0, and 1.0 s. A typical simulation involves the generation of 60 consecutive APs with an ensemble of 12,500 Ca²⁺ release units within a single myocyte. For stable APs, the average AP duration at 90% repolarization (APD₉₀) is taken as the mean measured over the final 50 APs of the pacing protocol. In the case of EADs, the median value of APD₉₀ (taken over the final 50 APs) is considered. For the sake of simplicity, APD₉₀ is referred to simply as APD. The distribution of these data is also summarized in the form of a box plot, which displays five values: the minimum, the first quartile, the median, the third quartile, and the maximum. In a typical box plot, the central rectangle spans from the first to the third quartile, and a horizontal line segment inside the rectangle (in this study, a shorter red line) represents the median. The whiskers above and below the box show the locations of the maximum and minimum, respectively, and outliers (points beyond the whiskers) are displayed using symbols (in this study, + symbols). Statistical significance is determined by estimating a p-value using the Kruskal-Wallis one-way-analysis-of-variance method.

Results

Rate dependence of H₂O₂-induced EADs

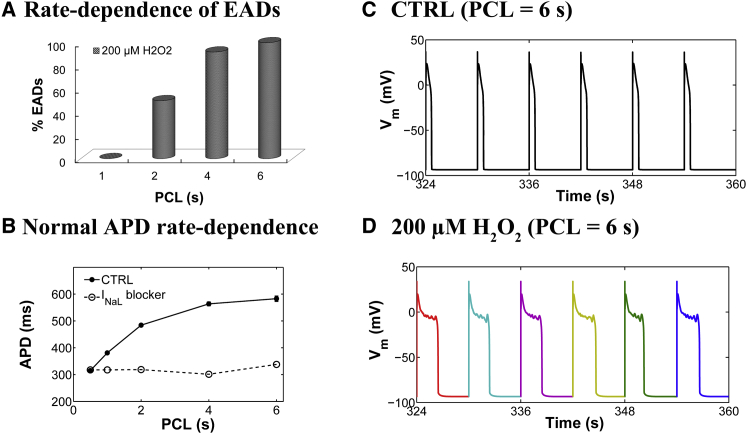
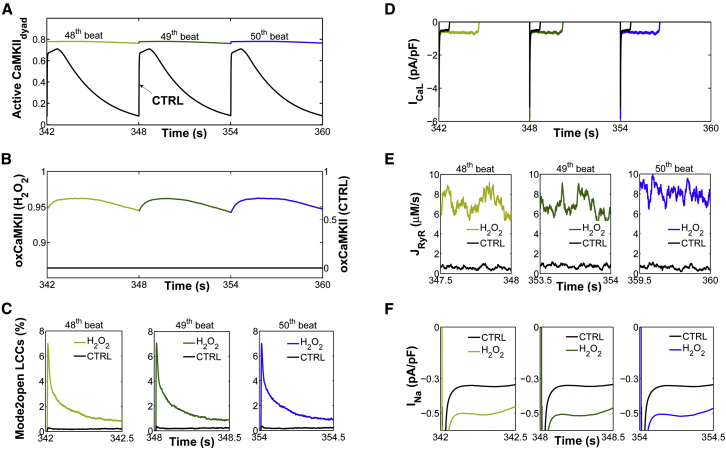
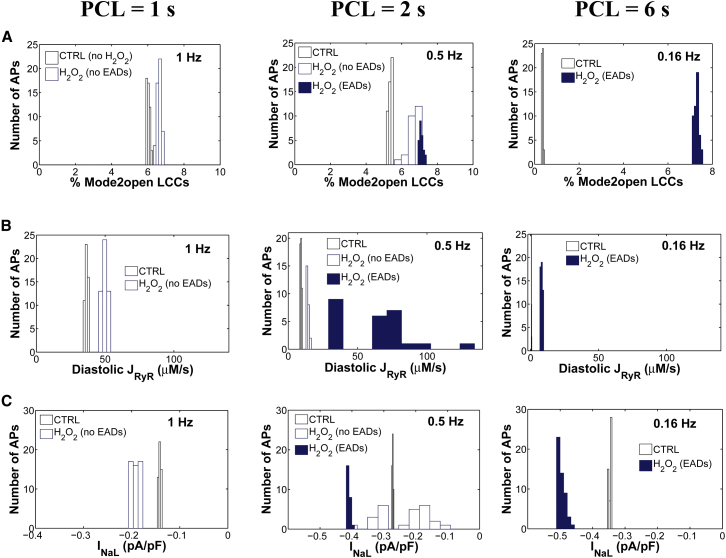
Experiments have shown that oxidative stress caused by exposure to 200 μM H₂O₂ for 5–15 min predisposes cardiac myocytes to EADs (8,9,12), and that the occurrence of EADs is highly dependent on the PCL (28). With slow pacing (PCL = 6 s), EADs usually occur on every AP, whereas with faster pacing (PCL = 1 s), EADs are typically not present. In the intermediate range, the occurrence of EADs is irregular from beat to beat. As shown in Fig. 2 A, the experimentally measured rate dependence of H₂O₂-induced EADs is accurately predicted as an emergent behavior of the model. Simulations showed no EADs in the presence of 200 μM H₂O₂ at a PCL of 1 s, whereas at a PCL of 6 s, EADs appeared consistently in every AP. Under normal conditions (absence of H₂O₂), the model also predicts a physiologically relevant rate adaptation of AP duration (APD), as reported by Guo et al. (30) (Fig. 2 B). Specifically, this control rate dependence of ventricular repolarization has been experimentally shown to be driven by rate-dependent changes in basal late Na⁺ current (I_NaL). Consistent with these experimental findings, the model predicts no rate adaptation of APD in the absence of I_NaL. In the presence of H₂O₂, the APD histograms for different PCLs including both fast (i.e., PCL = 1 s) and slow pacing rates (PCL ≥ 2 s) are shown in Fig. S7. Results for the last six consecutive APs from a 6 s PCL protocol in the absence and presence of H₂O₂ are shown in Fig. 2, C and D, respectively. Under this protocol and upon increased oxidative stress, the model predicts increased oxidative CaMKII activation (Fig. 3, A and B), an increased maximum fraction of open LCCs gating in mode 2 (Fig. 3 C, Mode2open) and thereby increased I_CaL (Fig. 3 D), as well as enhanced Ca²⁺ leak from the sarcoplasmic reticulum (SR) (Fig. 3 E, J_RyR) and I_NaL (Fig. 3 F). The increase in I_CaL at a PCL of 6 s via oxidized CaMKII corroborates the experimental findings of Song et al. (31), who demonstrated that oxidative CaMKII activation is involved in the facilitation of LCCs, observed as an increase of the peak amplitude of I_CaL and apparent slowing of inactivation (they refer to this as oxidation-dependent facilitation). In particular, the in silico model presented here predicts that the maximum fraction of open LCCs gating in mode 2 shifts from ∼0.35% in control (absence of H₂O₂) to ∼7% with increased H₂O₂ (Fig. 4 A). Similarly, diastolic J_RyR is predicted to increase from 0.6 μM/s in control conditions to 8 μM/s upon this increase in H₂O₂ (Fig. 4 B). As expected, our control model at slow pacing predicts a negligible CaMKII-mediated shift in LCC gating and insignificant diastolic SR Ca²⁺ leak. These effects are not surprising given that CaMKII activity increases in response to fast pacing (Fig. S8). On the other hand, at slow pacing, where there is little reduction of Na⁺ channel availability at steady state, the model predicts the presence of a significant amplitude of I_NaL in control (Fig. 4 C). As already shown (Fig. 2 B), it is this basal rate-dependent enhancement of I_NaL that prolongs the APD at slow heart rates. Upon H₂O₂ treatment, the model predicts further augmentation of I_NaL at long PCLs (e.g., 0.45% of peak I_Na at a PCL of 6 s), and this increase contributes to the appearance of EADs via a synergism that is discussed in greater detail in the next section.

Figure 2.

(A) Simulated rate dependence of H₂O₂-induced EADs. The EAD incidence rate is predicted to be higher at low pacing rates (long PCLs) in the presence of 200 μM H₂O₂. (B) PCL dependence of APD under control (CTRL) conditions (solid circles) and in the absence of baseline I_NaL (open circles). Under control conditions, the APD increases with PCL and this rate-dependent increase is abolished in the absence of I_NaL. (C) Simulated APs from a 6 s PCL protocol in the absence of oxidative stress (CTRL, 0 μM H₂O₂) (12,500 Ca²⁺ release units). Results for the last six consecutive APs are shown. (D) Simulated APs, all of which exhibit EADs, under conditions of elevated oxidative stress (200 μM H₂O₂). To see this figure in color, go online.

Figure 3.

Simulations for the last three consecutive APs from a 6 s PCL protocol under both control (CTRL, black lines) and oxidative stress conditions (colored lines). (A) Simulated sustained dyadic CaMKII activity before (CTRL) and after H₂O₂ treatment. (B) Simulated fraction of oxidized CaMKII subunits under the same conditions. (C) Simulated traces for the percentage of open LCCs gating in mode 2 (Mode2open). (D) Simulated I_CaL current before (CTRL) and after H₂O₂ treatment. (E) Simulated diastolic SR Ca²⁺ leak (J_RyR) under the same conditions. (F) Simulated I_NaL current before (CTRL) and after H₂O₂ treatment. For clarity, the results for the last three beats are shown separately during either the first 500 ms from the AP upstroke (e.g., Mode2open and I_NaL) or the last 500 ms (e.g., diastolic RyR flux). To see this figure in color, go online.

Figure 4.

Simulated rate dependence of CaMKII-mediated effects on I_CaL, J_RyR, and I_NaL in the absence (CTRL, black) or presence (blue) of H₂O₂. EADs are indicated with solid blue bars. Simulated PCL dependence of (A) the maximum fraction of open LCCs gating in mode 2, (B) the diastolic RyR flux (J_RyR), and (C) I_NaL (average value calculated from 100 to 300 ms) in the absence (CTRL) or presence of oxidative stress. To see this figure in color, go online.

Synergy between I_NaL, I_CaL, and I_NCX on EAD genesis by H₂O₂

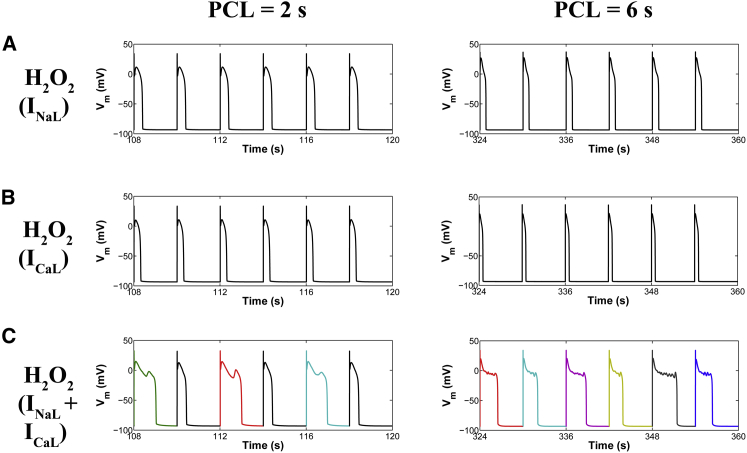
With regard to ionic mechanisms underlying H₂O₂-induced EADs, recent experimental studies (9,32) implicate activation of I_NaL as playing a key role. Song et al. (12) showed that ranolazine, a selective blocker of I_NaL, attenuates H₂O₂-induced arrhythmic activity and contractile dysfunction. This finding was further supported by Xie et al. (9), who reported elimination of H₂O₂-induced EADs with ranolazine block. However, activation of I_NaL may not by itself be sufficient to produce these EADs. For example, the application of ATX, an agent that selectively delays the late-phase inactivation of I_Na, prolongs the APD but fails to induce EADs, implying that other changes are also required (9). Although there is a consensus on the role of I_CaL modification in EAD generation (33–36), the relative contributions of each of these changes under elevated H₂O₂ are difficult to establish experimentally. Since significant uncertainties exist regarding the key mechanisms of these EADs, we used the model to further examine the functional impact of each individual CaMKII substrate (e.g., I_Na, I_CaL, and J_RyR) on AP response. Individual substrate contributions were isolated by allowing CaMKII-dependent phosphorylation of only a single target. Our simulations indicate that selective activation of I_NaL in the presence of 200 μM H₂O₂ is not, by itself, sufficient to produce EADs (Fig. 5 A), even though I_NaL is increased (Fig. 4 C). Similar results with no EADs are predicted if CaMKII, activated via oxidation, phosphorylates only LCCs (Fig. 5 B). However, upon the simultaneous targeting of both I_CaL and I_NaL by active CaMKII, the model predicts the rate-dependent emergence of EADs. Therefore, synergy between these two mechanisms, rather than either one alone, appears necessary for EAD generation (Fig. 5 C). With regard to the role of CaMKII phosphorylation of RyRs, model results indicate that RyR phosphorylation either alone or in combination with CaMKII-mediated LCC phosphorylation does not result in EAD generation in response to increased H₂O₂ (Fig. S9). Similar results with no EADs are obtained if instead of LCCs, CaMKII targets both RyRs and Na⁺ channels.

Figure 5.

Comparative analysis of CaMKII target effects in the presence of oxidative stress (200 μM H₂O₂) under a 2 s and a 6 s PCL protocol. Simulated APs are shown from both PCL protocols in the presence of 200 μM H₂O₂ and under the assumptions that CaMKII targets only Na⁺ channels (A), only LCCs (B), or both Na⁺ channels and LCCs (C). In the case of PCL = 6 s, all APs exhibit EADs. To see this figure in color, go online.

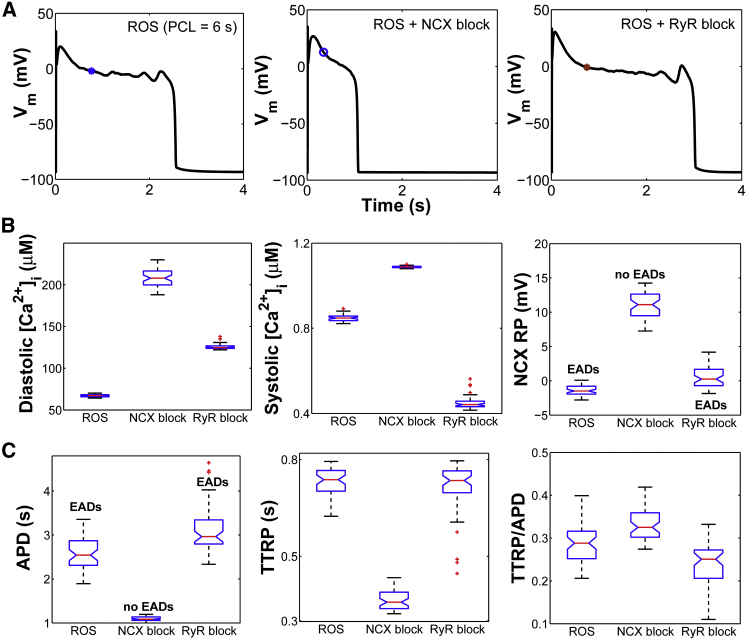
Since H₂O₂-induced EADs are related to changes in both the I_NaL and I_CaL, we evaluated the possible role of the NCX current (I_NCX) in the occurrence of EADs. To examine its depolarizing contribution to H₂O₂-induced EADs, we performed simulations at long PCL with H₂O₂ (Fig. 6 A) and in the presence of I_NCX inhibition (Fig. 6 A, ROS + NCX block). Blocking the I_NCX ablates the formation of EADs, confirming the experimental findings of Zhao et al. (28). Because NCX is the primary pathway for Ca²⁺ efflux from the cardiac cell, inhibition of I_NCX (Fig. S10 A) increases diastolic [Ca²⁺]_i significantly (from 67 nM to 208 nM) and systolic [Ca²⁺]_i to a lesser extent (from 0.85 μM to 1.08 μM) (Fig. 6 B). The time course of [Ca²⁺]_i before and after NCX block is shown in Fig. S10 B. NCX block also leads to an ∼2 mM reduction in intracellular Na⁺ concentration ([Na⁺]_i). As a consequence of both a higher [Ca²⁺]_i and a lower [Na⁺]_i, the reversal potential (RP) of NCX—defined as the membrane potential at which the NCX driving force, and thereby I_NCX, equals zero—is shifted toward more depolarized potentials (Fig. 6 B, NCX RP). To determine the phase of the AP in which NCX RP occurs, the time (from AP upstroke) to NCX RP (time to RP (TTRP)) is computed and normalized to APD (Fig. 6 C, TTRP/APD). Thus, TTRP/APD represents the fraction of the APD in which the NCX was in reverse mode versus forward mode (37). In the comparison of the ROS and ROS + NCX block conditions, APD is significantly reduced (approximately twofold) after NCX block (Fig. 6 C, APD), whereas the absolute TTRP decreases as much as twofold (Fig. 6 C, TTRP). As a result of this symmetric variation, the normalized TTRP (TTRP/APD) remains nearly the same before and after NCX block. Similar results are obtained even when simulations are performed at an intermediate pacing rate (PCL = 2 s (Fig. S11)).

Figure 6.

Effects of NCX and RyR inhibition on H₂O₂-induced EADs. (A) Simulated APs from a 6 s PCL protocol in the presence of oxidative stress (ROS) including the presence of either NCX inhibitor (ROS + NCX block) or RyR inhibitor (ROS + RyR block). Note that no EADs occur in the ROS + NCX block condition, whereas they are present in the ROS + RyR block condition. Whole-cell NCX current (I_NCX), as well as RyR flux (J_RyR), before and after block are shown in Figs. S10 A and S13 A. (B) Box plots of diastolic [Ca²⁺]_i, systolic [Ca²⁺]_i, and NCX RP under ROS, ROS + NCX block, and ROS + RyR block conditions. (C) Box plots of APD, absolute TTRP, and TTRP/APD (i.e., normalized TTRP) under the same conditions. To see this figure in color, go online.

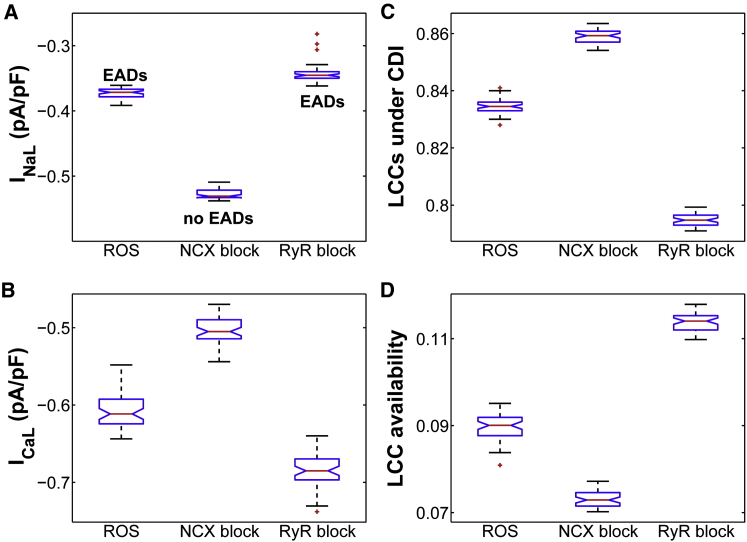
In the case of EADs that arise with ROS, the NCX RP (Fig. 6 A, blue asterisk) appears to occur early in the AP plateau (long before the EAD upstroke). Using the moment of NCX reversal as a critical event of the AP, we next compared major plateau currents (e.g., I_NaL and I_CaL) at this time before and after NCX block. Interestingly, I_NaL increases significantly (p < 0.001) from a median value of −0.37 pA/pF in ROS (with EADs) to −0.53 pA/pF in ROS + NCX block (no EADs) (Fig. 7 A). On the other hand, I_CaL (Fig. 7 B) decreases after NCX block due to a shift in LCC gating toward stronger inactivation that occurs via Ca²⁺-dependent inactivation (CDI) (Fig. 7 C) and voltage-dependent inactivation (VDI) mechanisms (Fig. S10 C). As a result, more LCCs become inactive, reducing the likelihood of their recovery from both CDI and VDI and thereby their reopening during the AP plateau. Complementary to this, upon NCX inhibition, the fraction of available (i.e., noninactivated) LCCs significantly decreases (Fig. 10 D). Since [Ca²⁺]_dyad affects the intrinsic rates of CDI, we further plotted [Ca²⁺]_dyad before and after NCX block and found that, as expected, it is further elevated during the AP plateau as a result of NCX block (Fig. S10 D). With regard to the total membrane current (Fig. S10 E, I_tot), model simulations show that it changes from 0.017 pA/pF in ROS to 0.056 pA/pF in the ROS + NCX block condition. This is likely due to the preceding decrease in I_CaL. Based on our analysis of the timing of NCX RP, we further repeated the NCX block simulations (PCL = 6 s) following a different intervention strategy. Rather than block NCX at the beginning of the simulation, we blocked it at the moment NCX reverses to forward mode (i.e., at TTRP) in the presence of ROS (Fig. S12, asterisk) and maintained the NCX block for only 200 ms. As a result of this acute intervention, EADs were still abolished (Fig. S12, dashed line), which suggests that the inward (forward-mode) I_NCX is a key player in the formation of these EADs.

Figure 7.

(A and B) Box plots of I_NaL (A) and I_CaL (B) in the presence of ROS and after NCX inhibition (ROS + NCX block) or RyR block (ROS + RyR block), as simulated at the time of NCX reversal from a 6 s PCL protocol. (C) Box plot of the total fraction of LCCs undergoing CDI under the same conditions. (D) Box plot of the total fraction of available LCCs as simulated at the time of NCX reversal under the same conditions (ROS, NCX block, and RyR block). To see this figure in color, go online.

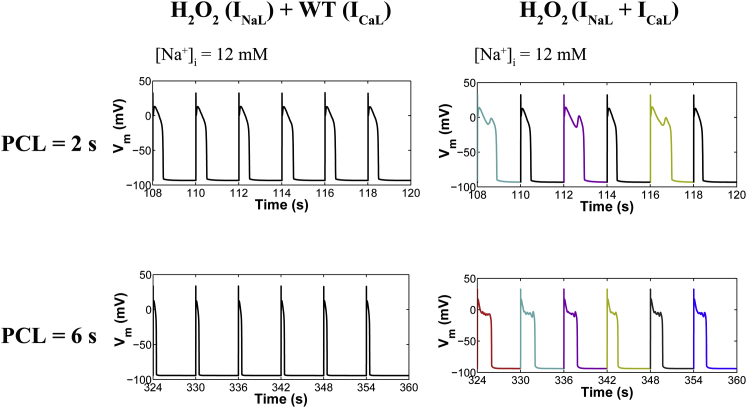
Figure 10.

(Left) CaMKII-I_NaL positive feedback during oxidative stress at an intermediate (PCL = 2 s) and a slow pacing rate (PCL = 6 s) with [Na⁺]_i = 12 mM. Simulated APs from a 2 s and 6 s PCL protocol in the presence of 200 μM H₂O₂ and under the assumption that oxidized CaMKII increases I_NaL, but not I_CaL. Note that we assume that basal (or wild-type) CaMKII-mediated phosphorylation of LCCs is intact. This condition is referred to as H₂O₂ (I_NaL) + WT (I_CaL). For simplicity, the effect of CaMKII on RyRs is not considered, because it is not necessary for the genesis of EADs. (Right) Simulated APs from both PCLs in the presence of ROS, with [Na⁺]_i = 12 mM, and assuming that oxidized CaMKII increases both I_NaL and I_CaL, referred to as H₂O₂ (I_NaL + I_CaL). To see this figure in color, go online.

Since [Ca²⁺]_dyad is heavily influenced by RyR function, we further assessed its effect on CDI of LCCs, and thereby I_CaL, by repeating the H₂O₂-dependent simulations in the presence of RyR inhibition. In this particular case (referred to as ROS + RyR block (Figs. 6 and 7)), EADs still appear on every AP but are prolonged, consistent with the experimental findings by Zhao et al. (28). Simulated APDs before and after RyR block are shown in Fig. 6 C. Similar to the above analysis, the time of NCX reversal (Fig. 6 A, brown asterisk) also occurs long before the onset of the EAD. Comparison of the ROS and ROS + RyR block conditions shows that diastolic [Ca²⁺]_i increases significantly, from 67 nM in ROS to 125 nM after RyR block, whereas systolic [Ca²⁺]_i decreases from 0.85 μM to 0.44 μM after RyR block. The latter is expected due to reduced RyR activity and, thereby, SR Ca²⁺ release flux (Fig. S13 A, J_RyR). As a result of this decrease, fewer LCCs enter CDI (Fig. 7 C) and the fraction of LCCs that are not in VDI also increases (Fig. S13 B). As a consequence, more LCCs are likely to be available—not in CDI or VDI—for reactivation after RyR block (Fig. 7 D). This in turn increases the likelihood of LCC opening, and thereby I_CaL, from −0.6 pA/pF in ROS to −0.7 pA/pF after RyR block (p < 10⁻¹⁶). Despite this increase, I_NaL significantly decreases from −0.4 pA/pF in the ROS condition to −0.3 pA/pF after RyR block (longer APDs with EADs). Despite this nonintuitive decrease, I_tot is not significantly altered after RyR block (median value ∼0.017 pA/pF (Fig. S13 C)). Based on the analysis of the model, however, the longer EAD-containing APDs occurring with RyR block can be explained via subsequent shifts of LCC gating toward reduced inactivation that occur early in the AP plateau (at the time of NCX reversal) and thereby allow for maintaining the plateau phase.

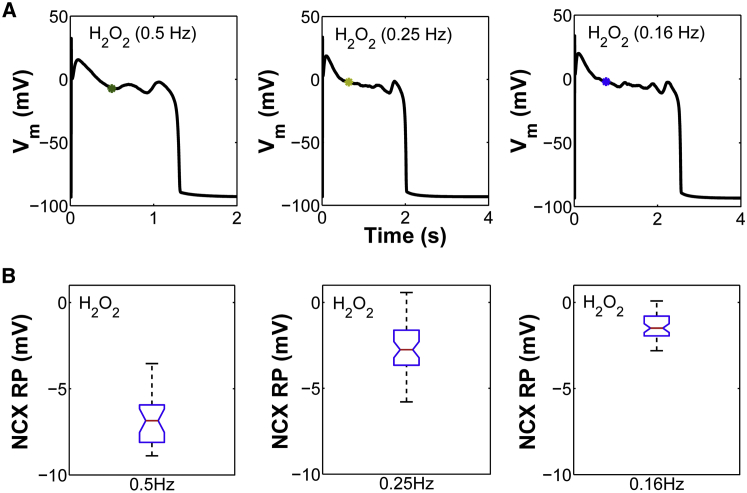
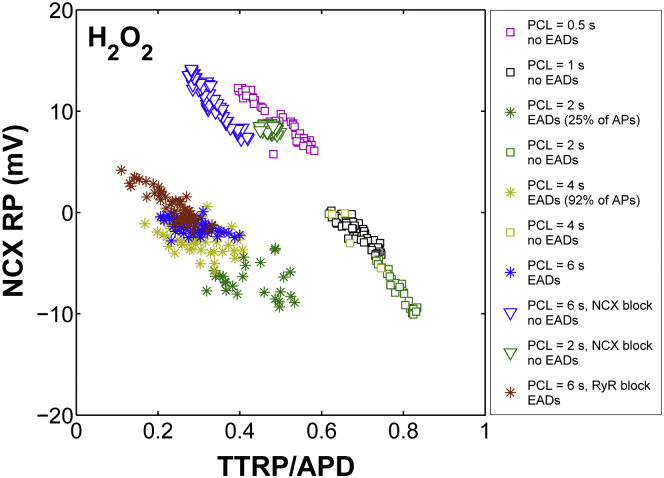
We next used the model to predict the NCX RP for all slow-rate-dependent EADs generated by ROS (Fig. 8). Consistent with the above simulations, the NCX TTRP (Fig. 8 A, asterisks) also occurs before the EAD upstroke, and the NCX RP lies within a narrow voltage range (from 0 to −10 mV) (Fig. 8 B). Similar results are obtained if these rate-dependent simulations are repeated with the same [Na⁺]_i as that seen experimentally under ROS at a PCL of 2 s (12 mM (Fig. S14)). To extend these results, the NCX RP is plotted as a function of TTRP/APD for all H₂O₂-induced EADs including stable APs simulated either at faster pacing rates (e.g., PCL ≤ 1 s) or under interventions such as ROS + NCX block. In the latter case, NCX-block simulations are performed not only at slow pacing rates (e.g., PCL = 6 s), as seen experimentally, but also at intermediate pacing rates (e.g., PCL = 2 s). As shown in Fig. 9, the development of EADs generated by either ROS or ROS + RyR block (colored asterisks) is correlated with a shift in the NCX TTRP from the repolarization phase toward the AP plateau (median TTRP/APD ∼0.3). This shift was further accompanied by a change in the NCX RP that placed it within a voltage range from −10 mV to +5 mV, referred to here as the EAD voltage range. Based on this voltage range, the median NCX RP value is ∼−2 ± 2 mV and thus hyperpolarized. Previous studies have shown that the EAD take-off potentials—defined as membrane voltages at which EADs occurred in the H₂O₂ model—were within a wide range (from +20 mV to −30 mV), which was consistent with that corresponding to the window current of I_CaL (28). Although it should be clarified that NCX RP does not represent the EAD take-off potential (NCX TTRP consistently occurs well before the EAD upstroke), here, the time of NCX reversal serves as a critical phase of the AP that clearly distinguishes the occurrence of EADs from stable APs. In the case of stable APs arising from NCX block (Fig. 9, triangles), the NCX RP shifts toward a range of more depolarized potentials with a median value of ∼+9 ± 2 mV. As such, NCX block shifts the NCX RP toward potentials that are more depolarized than the EAD voltage range (median ∼−2 mV). Note that NCX RP increases with increased [Ca²⁺]_i and/or decreased [Na⁺]_i (Fig. S15, A and B). Similar depolarizing shifts in NCX RP are also obtained in the case of stable APs simulated in the presence of ROS but at faster pacing rates (e.g., PCL = 0.5 s). In this case, the NCX RP is significantly depolarized (Fig. 9, magenta squares) due to the frequency-dependent increase in [Ca²⁺]_i (Fig. S15 C). Interestingly, in the case of a 1 s PCL protocol, stable APs (Fig. 9, black squares) are correlated with significant delays in TTRP. In this particular case, NCX transitions from reverse to forward mode during the repolarization phase of the AP (Fig. S16) and thereby compromises the development of EADs by preventing I_CaL reactivation. Taken together, we consider that if the timing of NCX reversal occurs during the AP plateau, inward I_NCX may facilitate EADs by maintaining the AP plateau phase in a range of voltages that allow for I_CaL reactivation.

Figure 8.

(A) Simulated EADs in the presence of oxidative stress (H₂O₂) at low pacing rates (PCL ≥ 2 s). The NCX RP is marked with colored asterisks. (B) Box plot of the NCX RP for all H₂O₂-induced EADs. To see this figure in color, go online.

Figure 9.

Emergence of H₂O₂-induced EADs is related to a shift in the time of NCX current reversal. The NCX RP for all EADs (asterisks) generated in the presence of ROS (PCL ≥ 2 s), including those with interventions such as RyR inhibition, lies within a narrow voltage range. Squares represent stable APs simulated in the presence of ROS either at a fast pacing rate (e.g., PCL ≤ 1 s) or at a slower pacing rate (e.g., PCL = 2 s). Note that at PCL = 2 s, both stable APs (green squares) and EADs (green asterisks) occur in the model output. For a PCL of 4 s, only four stable APs out of 50 simulated APs are predicted. Stable APs as a result of NCX inhibition at PCL = 2 s and PCL = 6 s are shown by green and blue triangles, respectively. To see this figure in color, go online.

CaMKII-I_NaL positive feedback loop in the presence of H₂O₂

Accumulating evidence shows that the activities of CaMKII and I_NaL are interrelated. It is well known that overexpression of CaMKII in ventricular cardiomyocytes enhances I_NaL (12,32,38). Further studies have shown that such an increase in I_NaL is sufficient to activate CaMKII (and enhance target phosphorylation) via elevation of [Ca²⁺]_i mediated by reverse-mode NCX activity (39). These findings suggested the presence of a positive feedback loop in which CaMKII-dependent increases of I_NaL, and the resulting increase of [Na⁺]_i, alters Ca²⁺ homeostasis and leads to further CaMKII activation. Along these lines, the positive feedback loop from Na⁺ to Ca²⁺ to CaMKII was tested in the modeling study of Morotti et al. (40), who investigated the arrhythmogenic role of an increase in [Na⁺]_i at fast pacing rates similar to those reported in failing mouse ventricular myocytes. Upon this increase in [Na⁺]_i, the model of Morotti et al. (40) predicts Ca²⁺ overload and enhancement of CaMKII activity, which in turn increases RyR phosphorylation and spontaneous Ca²⁺ release events, leading to electrophysiological instability. Using our model, we focus on analyzing the function of the CaMKII-I_NaL positive feedback pathway at slow pacing rates, i.e., examining whether an increase in I_NaL similar to that reported in oxidative stress (200 μM H₂O₂) in the presence of a basal level of I_CaL facilitation can shift the NCX RP toward the EAD voltage range and thereby sufficiently promote EADs. To rule out the possibility that perturbed Na⁺ fluxes underlie changes in the NCX RP, simulations are performed with [Na⁺]_i clamped to 12 mM, similar to the level observed experimentally under ROS (8). Notably, under this condition, where only oxidation-dependent I_CaL facilitation is blocked but I_NaL is allowed to increase during H₂O₂ (referred to as [H₂O₂ (I_NaL) + WT (I_CaL)]), the model predicted no EADs at both intermediate (PCL = 2 s) and long pacing rates (PCL = 6 s) (Fig. 10, left). However, if both I_CaL and I_NaL are allowed to increase as a result of ROS-mediated CaMKII activation, EADs do occur (Fig. 10, right). Thus, these results indicate that ROS-mediated enhancement of both I_CaL and I_NaL is required for the genesis of these EADs. The increase in these inward currents is likely to prolong the APD and form a conditioning phase that facilitates the synergy between I_NCX and I_CaL. Our simulations demonstrate that the occurrence of H₂O₂-induced EADs can be related to the NCX RP (Fig. 9). It is therefore likely that NCX plays a key role in this synergism by maintaining the AP plateau phase in a range of voltages that allow for I_CaL reactivation.

Discussion

To clarify the role of oxidative CaMKII activation in the genesis of H₂O₂-induced EADs at different PCLs, a stochastic CaMKII model was developed that includes both the phosphorylation-dependent and the newly identified oxidation-dependent activation pathways. This model reproduces a wide range of experimental data describing the CaMKII-Ca²⁺/CaM interaction, measured autophosphorylation and oxidation rates, and the frequency dependence of CaMKII activation. After incorporation into our local-control cardiac myocyte model (17), the experimentally measured rate dependence of H₂O₂-induced EADs was reproduced as an emergent behavior of the model. We then used the model to study the impact of CaMKII-dependent modulation of LCCs, RyRs, and Na⁺ channels on rate dependence of EADs caused by H₂O₂. Our simulation results show that the underlying mechanism involves oxidative CaMKII activation of both I_CaL and I_NaL, since activation of either current in isolation is insufficient to generate H₂O₂-induced EADs. The increase in these currents alters membrane potential as well as Ca²⁺/Na⁺ homeostasis, and consequently, NCX RP and I_NCX are altered as well. Further modeling results implicate this indirect activation of NCX as another key player in EAD generation. Of more importance, the emergence of slow-rate dependence of H₂O₂-induced EADs was correlated with a shift in the NCX TTRP from the repolarization phase toward the AP plateau. TTRP consistently occurred well before the EAD upstroke, and its shift to an earlier time within the AP clearly distinguished the occurrence of EADs from stable APs. The shift in TTRP was accompanied by a change in NCX RP that placed it within a narrow voltage range from −10 mV to 0 mV; referred to here as the EAD voltage range. Interestingly, at faster pacing rates (e.g., PCL = 1 s), stable APs were correlated with significant delays in TTRP. In this particular case, NCX transitioned from reverse to forward mode during the repolarization phase of the AP. On the other hand, in the case where APs were stable as a result of NCX inhibition, the normalized timing (TTRP/APD) of the NCX RP did not significantly vary; rather, it was the RP itself that was shifted beyond the EAD voltage range toward more depolarized potentials. Based on these findings, we conclude that once NCX reverses during the AP plateau, inward I_NCX may facilitate EADs by maintaining the AP plateau phase in a range of voltages that allows for I_CaL reactivation.

The model reveals that oxidative activation of both I_CaL and I_NaL lengthens the APD and forms a conditioning phase that facilitates the synergy between I_NCX and I_CaL reactivation. Upon I_NCX inhibition, APs became stable and the model predicted an increase in I_NaL, as measured at the time of NCX reversal. Despite this counterintuitive increase, I_CaL significantly decreased due to shifts of LCC gating toward more inactivation via CDI and/or VDI. As a result, more LCCs became inactive during the plateau phase of the AP, and this in turn prevented LCC reactivation and reduced arrhythmia propensity. Further analysis was also performed for another intervention, that of RyR inhibition. The model predicted that upon RyR inhibition, EADs would occur within every AP, yielding longer APDs, as seen experimentally. Surprisingly, in this condition where APD is prolonged, I_NaL amplitude was significantly decreased. Despite this decrease, I_tot estimated at the time of NCX reversal did not vary significantly. It was, however, I_CaL that increased during the plateau after RyR block. This particular increase was attributed to a higher fraction of available LCCs at the time of NCX reversal (early in the AP plateau) due to reduced inactivation. In this context, the appearance of EADs reflects integrative effects of many underlying changes whose functional consequences are difficult to deduce using intuition alone. Using the time at which the membrane potential crosses the NCX RP as a critical event in the AP and an early predictor of EADs, this study provides quantitative insights into these synergistic effects that would otherwise be difficult to experimentally dissect.

Limitations

Although our in silico H₂O₂ model predicts an increase in SR Ca²⁺ leak (Fig. 4 B, J_RyR) from 9.2 μM/s (control) to 64.3 μM/s (200 μM H₂O₂), this is ∼15-fold less than that measured experimentally at a PCL of 2 s (8). Wagner et al. (8), however, provide additional evidence indicating that their observed increase in Ca²⁺ leak does not require the presence of CaMKII, suggesting an important role for CaMKII-independent mechanisms of ROS-mediated alteration of cardiac ECC as well. For instance, ROS can directly oxidize RyRs, leading to increased Ca²⁺ spark frequency (41). In addition to this, the model is unable to replicate H₂O₂-induced Na⁺ and Ca²⁺ overload and the subsequent occurrence of DADs. Wagner et al. (8) proposed that the increase in [Na⁺]_i accompanying oxidative stress precedes the major rise in [Ca²⁺]_i based on their observation that a reduction of [Na⁺]_i slowed the rise in [Ca²⁺]_i. This elevation of [Na⁺]_i was further shown to mediate shifts in NCX activity (reverse mode) and cause substantial Ca²⁺ entry, which may be sufficient to increase I_NCX (forward mode) and may thereby underlie membrane depolarization generating a DAD. Although DADs are more commonly seen at fast heart rates, H₂O₂-induced DADs have been observed in experiments only occasionally after prolonged treatment with H₂O₂ (28). Typically, DADs occur after repolarization of the membrane and are triggered by synchronized large-scale events of Ca²⁺ release from the SR propagated as a wave (24,42–44). The model presented here, however, lacks the necessary mechanisms (e.g., no subsarcolemmal or other spatial tracking of [Ca²⁺] gradients) essential for the genesis of these waves and, hence, DADs. This limitation of the model should have little to no impact on the results of this study, because the model was developed to understand the underlying mechanism of H₂O₂-induced EADs as seen in experiments during acute exposure to H₂O₂, a condition where DADs are not typically observed. Although H₂O₂-induced [Na⁺]_i overload was experimentally shown by Wagner et al. (8) to be facilitated by a CaMKII-dependent increase in I_NaL, this was not completely abolished upon CaMKII inhibition. Thus, other mechanisms (e.g., ROS-mediated impairment of Na⁺/K⁺ ATPase (NKA) function (45)) may also be involved in H₂O₂-induced [Na⁺]_i overload. To test this hypothesis, we repeated the simulations of increased H₂O₂ at slow pacing in the presence and absence of NKA inhibition. From the modeling standpoint, the gain of [Na⁺]_i is modestly increased (by ∼2 mM) in the absence of NKA inhibition. However, upon inhibition of NKA (∼50% reduction), the model accounts for an overall 6 mM gain in [Na⁺]_i (Fig. S17) demonstrated by the experiments of Wagner et al. (8). Taken together, the arrhythmogenic effects of ROS are clearly multifactorial. These additional ROS-mediated effects require further examination in future studies.

A simplifying feature of the cardiac Na⁺ channel model is that it does not include dynamic CaMKII-mediated phosphorylation of Na⁺ channels. Modeling such phosphorylation would require data on the underlying phoshorylation dynamics (e.g., phosphorylation and dephosphorylation rates), which are not yet available. To simulate the CaMKII-dependent effect of H₂O₂ on I_NaL, the value of the transition rate between background and bursting modes of I_Na (referred to as a₈ in the model of Grandi et al. (26)) was increased so that the model reproduced experimental data for the amplitude of I_NaL (8). Since these data accounted only for the amplitude of I_NaL, a₈ was the only parameter modified within the I_Na model. Other previously observed CaMKII effects on I_Na (e.g., shifted steady-state inactivation, recovery from inactivation) were not measured in this H₂O₂ experimental protocol. Hence, the kinetic parameters of the I_Na model that underlie these processes were not modified in the presence of H₂O₂. To assess the impact of this assumption on H₂O₂-induced EADs, we modified the H₂O₂ exposure model to incorporate a shift in steady-state inactivation and a slowing of recovery from inactivation, as seen with CaMKII overexpression. Relevant I_Na model parameters were increased to the values reported previously by Grandi et al. (26) for CaMKII overexpression. At a PCL of 6 s, H₂O₂ simulations were repeated with this model (Fig. S18) and the results were essentially the same as those from our original model, in which CaMKII-mediated effects on I_Na are limited to a functional change only in the I_NaL (Fig. 2 D). Based on this finding, in the simulations performed in this study, we limited the impact of H₂O₂-induced CaMKII activity on I_Na to a change only in I_NaL, not in other kinetic properties of the current.

Moreover, the model does not incorporate CaMKII-dependent alterations of the transient outward K⁺ current (I_to), which tends to increase I_to and shorten APD in rabbit ventricular myocytes (46). Since APD of rabbit cardiac myocytes is prolonged during oxidative stress (8,9), these CaMKII effects would play a less important role in H₂O₂-induced EADs. On the other hand, ROS can directly decrease outward currents such as I_to (47) and hence may be responsible for the observed H₂O₂-induced APD prolongation. We have previously shown (48) that the relationship between APD and I_to density is complex, suggesting strong coupling between I_CaL and I_to. Future work will investigate how this coupling is modulated at low pacing rates, with emphasis on its potential influence on APD prolongation caused by H₂O₂.

Author Contributions

P.T.F. designed and performed the research and wrote the article. All authors discussed and interpreted the results. J.L.G. and R.L.W. critically revised and edited the manuscript.

Editor: Andrew McCulloch.