Large-scale evidence of dependency length minimization in 37 languages

Significance

We provide the first large-scale, quantitative, cross-linguistic evidence for a universal syntactic property of languages: that dependency lengths are shorter than chance. Our work supports long-standing ideas that speakers prefer word orders with short dependency lengths and that languages do not enforce word orders with long dependency lengths. Dependency length minimization is well motivated because it allows for more efficient parsing and generation of natural language. Over the last 20 y, the hypothesis of a pressure to minimize dependency length has been invoked to explain many of the most striking recurring properties of languages. Our broad-coverage findings support those explanations.

Abstract

Explaining the variation between human languages and the constraints on that variation is a core goal of linguistics. In the last 20 y, it has been claimed that many striking universals of cross-linguistic variation follow from a hypothetical principle that dependency length—the distance between syntactically related words in a sentence—is minimized. Various models of human sentence production and comprehension predict that long dependencies are difficult or inefficient to process; minimizing dependency length thus enables effective communication without incurring processing difficulty. However, despite widespread application of this idea in theoretical, empirical, and practical work, there is not yet large-scale evidence that dependency length is actually minimized in real utterances across many languages; previous work has focused either on a small number of languages or on limited kinds of data about each language. Here, using parsed corpora of 37 diverse languages, we show that overall dependency lengths for all languages are shorter than conservative random baselines. The results strongly suggest that dependency length minimization is a universal quantitative property of human languages and support explanations of linguistic variation in terms of general properties of human information processing.

Finding explanations for the observed variation in human languages is the primary goal of linguistics and promises to shed light on the nature of human cognition. One particularly attractive set of explanations is functional in nature, holding that language universals are grounded in the known properties of human information processing. The idea is that grammars of languages have evolved so that language users can communicate using sentences that are relatively easy to produce and comprehend. Within the space of functional explanations, a promising hypothesis is dependency length minimization (DLM).

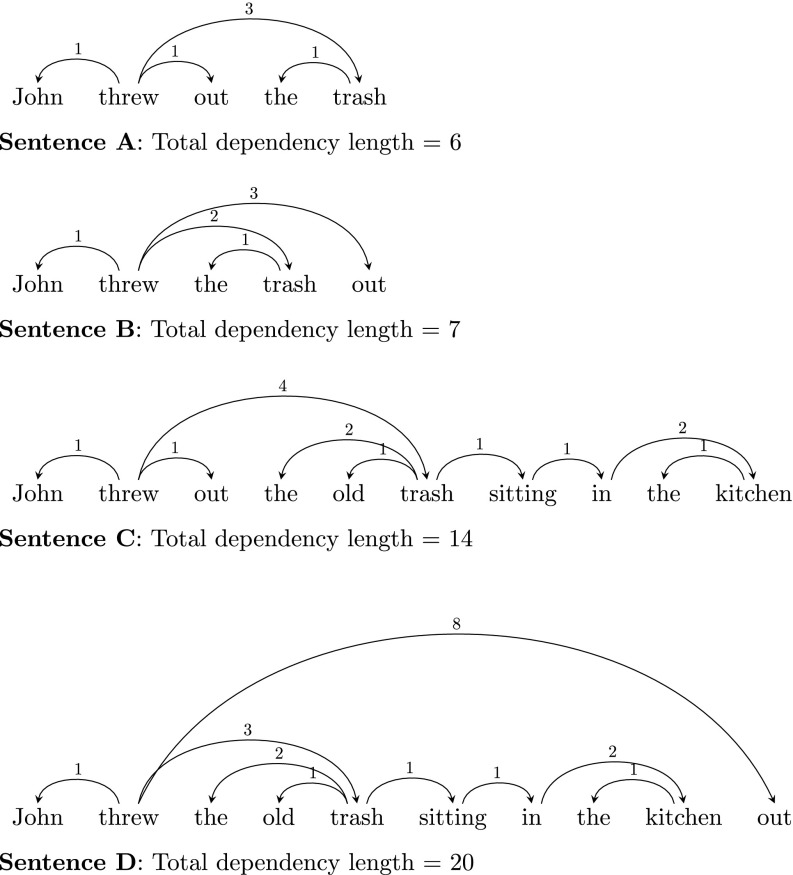
Dependency lengths are the distances between linguistic heads and dependents. In natural language syntax, roughly speaking, heads are words that license the presence of other words (dependents) modifying them (1). For example, the verb “throw” in sentence C in Fig. 1 licenses the presence of two nouns, “John”—its subject—and “trash”—its object. Subject and object relations are kinds of dependency relations where the head is a verb and the dependent is a noun. Another way to think about dependency is to note that heads and dependents are words that must be linked together to understand a sentence. For example, to correctly understand sentence C in Fig. 1, a comprehender must determine that a relationship of adjectival modification exists between the words “old” and “trash”, and not between, say, the words “old” and “kitchen”. In typical dependency analyses, objects of prepositions (“him” in “for him”) depend on their prepositions, articles depend on the nouns they modify, and so on. Most aspects of dependency analysis are generally agreed on, although the analysis of certain relations is not settled, primarily those relations involving function words such as prepositions, determiners, and conjunctions. Fig. 1 shows the dependencies involved in some example sentences according to the analysis we adopt.

Fig. 1.

Four sentences along with their dependency representations. The number over each arc represents the length of the dependency in words. The total dependency length is given below each sentence. Sentences A and B have the same semantics, and either word order is acceptable in English; English speakers typically do not find one more natural than the other. Sentences C and D also both have the same semantics, but English speakers typically find C more natural than D.

The DLM hypothesis is that language users prefer word orders that minimize dependency length. The hypothesis makes two broad predictions. First, when the grammar of a language provides multiple ways to express an idea, language users will prefer the expression with the shortest dependency length (2). Indeed, speakers of a few languages have been found to prefer word orders with short dependencies when multiple options are available (3, 4) (Fig. 1 provides English examples). Second, grammars should facilitate the production of short dependencies by not enforcing word orders with long dependencies (5, 6).

Explanations for why language users would prefer short dependencies are various, but they all involve the idea that short dependencies are easier or more efficient to produce and comprehend than long dependencies (7, 8). The difficulty of long dependencies emerges naturally in many models of human language processing. For example, in a left-corner parser or generator, dependency length corresponds to a timespan over which a head or dependent must be held in a memory store (9–11); because storing items in memory may be difficult or error prone, short dependencies would be easier and more efficient to produce and parse according to this model. In support of this idea, comprehension and production difficulty have been observed at the sites of long dependencies (8, 12).

If language users are motivated by avoiding difficulty, then they should avoid long dependencies. Furthermore, if languages have evolved to support easy communication, then they should not enforce word orders that create long dependencies. The DLM hypothesis thus provides a link between language structure and efficiency through the idea that speakers and languages find ways to express meaning while avoiding structures that are difficult to produce and comprehend.

Over the last 20 y, researchers have proposed DLM-based explanations of some of the most pervasive properties of word order in languages. We can see the word order in a sentence as a particular linearization of a dependency graph, where a linearization is an arrangement of the words of the dependency graph in a certain linear order. For instance, sentences A and B in Fig. 1 are two linearizations of the same graph. Below we give examples of applications of the DLM idea.

Languages constrain what linearizations are possible; for example, some languages require that a noun depending on a preposition come after the preposition, and some require that it come before. Greenberg (13) found striking correlations between different ordering constraints in languages, such that languages tend to be consistent in whether heads come before dependents or vice versa (14, 15). Both this generalization and exceptions to it have been explained as linearizations that minimize dependency length (7, 16). Hawkins (17) documents that the basic grammatical word orders for many constructions in many languages minimize dependency length over alternatives.

Another pervasive property of languages is projectivity, the property that, in linearizations of dependency graphs, the lines connecting heads and dependents do not cross (18). Ferrer i Cancho (19) has argued that this ubiquitous property of languages arises from dependency length minimization, because orders that minimize dependency length have a small number of crossing dependencies on average.

Minimal dependency length has also been widely assumed as a reliable generalization in the field of natural language processing. For example, most state-of-the-art models for natural language grammar induction incorporate a bias toward positing short dependencies, and their performance is greatly improved by this assumption (20, 21). Influential practical parsing algorithms also incorporate this assumption (22).

The studies mentioned above, for the most part, use categorical descriptions of the most common word orders in languages or examine small numbers of languages. Therefore, a crucial question remains open: is dependency length actually minimized overall in real utterances, considering the full range of possible syntactic constructions and word orders as they are used, or is the effect confined to the constructions and languages that have been studied? If indeed there is a universal preference to minimize dependency lengths, then utterances in all natural languages should have shorter dependency lengths than would be expected by chance. On the other hand, if observed dependency lengths are consistent with those that would be produced by chance, then this would pose a major challenge to DLM as an explanatory principle for human languages.

Here, we answer that question using recently available dependency-parsed corpora of many languages (23–25). We obtained hand-parsed or hand-corrected corpora of 37 languages, comprising 10 language families. Thirty-six of the corpora follow widely recognized standards for dependency analysis (25, 26); the remaining corpus (Mandarin Chinese) uses its own system that is nonetheless similar to the standards [see Table S1 for details on each corpus]. The texts in the corpora are for the most part written prose from newspapers, novels, and blogs. Exceptions are the corpora of Latin and Ancient Greek, which include a great deal of poetry, and the corpus of Japanese, which consists of spoken dialogue. Previous comprehensive corpus-based studies of DLM cover seven languages in total, showing that overall dependency length in those languages is shorter than various baselines (16, 27–30). However, these studies find only weak evidence of DLM in German, raising the possibility that DLM is not a universal phenomenon. Noji and Miyao (31) use dependency corpora to show that memory use in a specific parsing model is minimized in 18 languages, but they do not directly address the question of dependency length minimization in general.

We compare real language word orders to counterfactual baseline orders that experience no pressure for short dependencies. These baselines serve as our null hypotheses. Our baselines represent language users who choose utterances without regard to dependency length, speaking languages whose grammars are not affected by DLM. We do not distinguish between DLM as manifested in grammars and DLM as manifested in language users’ choice of utterances; the task of distinguishing grammar and use in a corpus study is a major outstanding problem in linguistics, which we do not attempt to solve here. In addition to the random baselines, we present an optimal baseline for the minimum possible dependency length in a projective linearization for each sentence. This approach allows us to evaluate the extent to which different languages minimize their dependency lengths compared with what is possible. We do not expect observed dependency lengths to be completely minimized, because there are other factors influencing grammars and language use that might come into conflict with DLM.

Results

Free Word Order Baseline.

Our first baseline is fully random projective linearizations of dependency trees. Random projective linearizations are generated according to the following procedure, from Gildea and Temperley (28), a method similar to one developed by Hawkins (32). Starting at the root node of a dependency tree, collect the head word and its dependents and order them randomly. Then repeat the process for each dependent. For each sentence in our corpora, we compare real dependency lengths to dependency lengths from 100 random linearizations produced using this algorithm. Note that the 100 random linearization all have the same underlying dependency structure as the original sentence, just with a potentially different linear order. Under this procedure, the random linearizations do not obey any particular word order rules: there is no consistency in whether subjects precede or follow verbs, for example. In that sense, these baselines may most closely resemble a free word order language as opposed to a language like English, in which the order of words in sentences are relatively fixed.

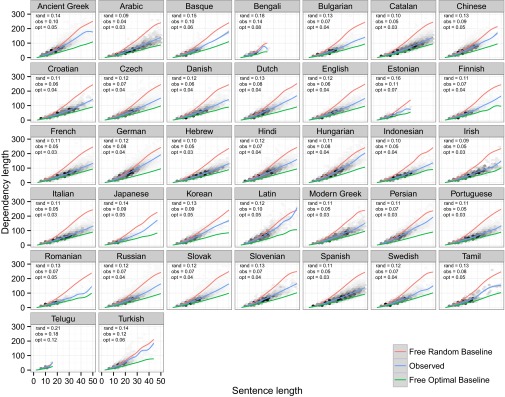
Fig. 2 shows observed and random dependency lengths for sentences of length 1–50. As the figure shows, all languages have average dependency lengths shorter than the random baseline, especially for longer sentences. To test the significance of the effect, for each language, we fit regression models predicting dependency length as a function of sentence length. The models show a significant effect where the dependency length of real sentences grows more slowly than the dependency length of baseline sentences (P < 0.0001 for each language).

Fig. 2.

Random Free Word Order baseline dependency lengths, observed dependency lengths, and optimal dependency lengths for sentences of length 1–50. The blue line shows observed dependency length, the red line shows average dependency length for the random Free Word Order baseline, and the green line shows average dependency length for the optimal baseline. The density of observed dependency lengths is shown in black. The lines in this figure are fit using a generalized additive model. We also give the slopes of dependency length as a function of squared sentence length, as estimated from a mixed-effects regression model. rand is the slope of the random baseline. obs is the slope of the observed dependency lengths. opt is the slope of the optimal baseline. Due to varying sizes of the corpora, some languages (such as Telugu) do not have attested sentences at all sentence lengths.

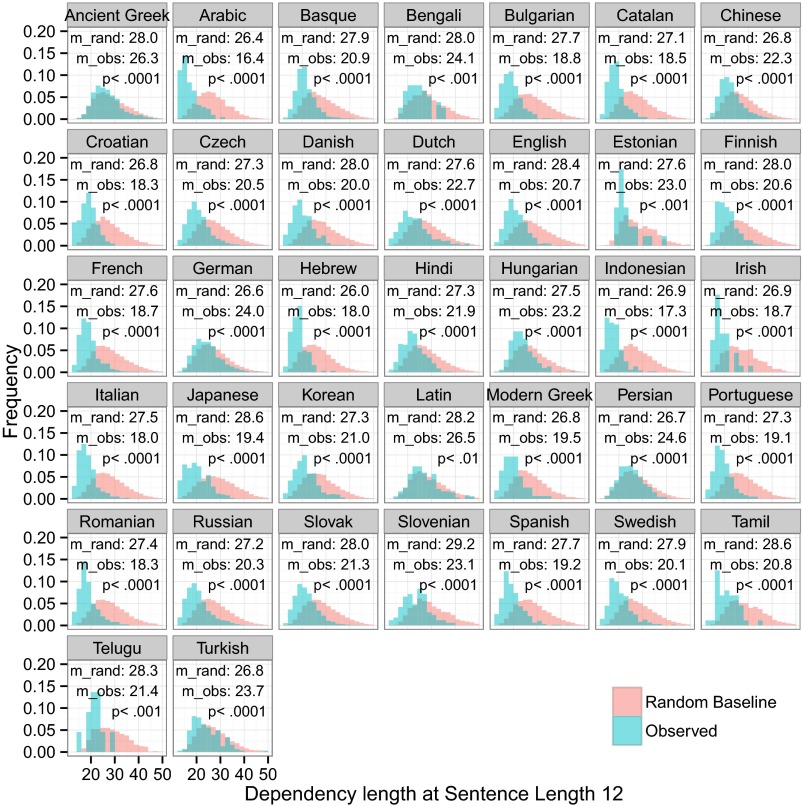
Fig. 3 shows histograms of observed and random dependency lengths for sentences of length 12, the shortest sentence length to show a significant effect in all languages (P < 0.01 for Latin, P < 0.001 for Telugu, and P < 0.0001 for all others, by Stouffer’s method). In languages for which we have sufficient data, there is a significant DLM effect for all longer dependency lengths.

Fig. 3.

Histograms of observed dependency lengths and Free Word Order random baseline dependency lengths for sentences of length 12. m_rand is the mean of the free word order random baseline dependency lengths; m_obs is the mean of observed dependency lengths. We show P values from Stouffer’s Z-transform test comparing observed dependency lengths to the dependency lengths of the corresponding random linearizations.

Fixed Word Order Baseline.

The first baseline ignores a major common property of languages: that word order is often fixed for certain dependency types. For example, in English, the order of certain dependents of the verb is mostly fixed: the subject of the verb almost always comes before it, and the object of a verb almost always comes after. We capture this aspect of language by introducing a new baseline. In this baseline, the relative ordering of the dependents of a head is fixed given the relation types of the dependencies (subject, object, prepositional object, etc.). For each sentence, we choose a random ordering of dependency types and linearize the sentence consistently according to that order. We perform this procedure 100 times to generate 100 random linearizations per sentence.

Fig. 4 shows observed dependency lengths compared with the random fixed-order baselines. The results are similar to the comparison with the free word order baselines in that all languages have dependencies shorter than chance, especially for longer sentences. We find that this random baseline is more conservative than the free word order baseline in that the average dependency lengths of the fixed word order random baselines are shorter than those of the free word order random baselines (with significance P < 0.0001 by a t test in each language). For this baseline, the DLM effect as measured in the regression model is significant at P < 0.0001 in all languages except Telugu, a small corpus lacking long sentences, where P = 0.15. For further baselines and analysis, see Further Baselines and Figs. S1 and S2.

Fig. 4.

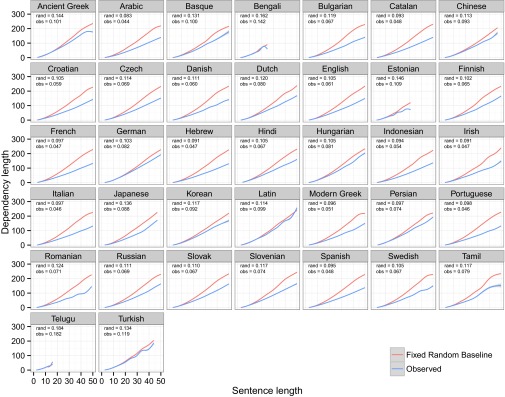
Real dependency lengths as a function of sentence length (blue) compared with the Fixed Word Order Random baseline (red). GAM fits are shown. rand and obs are the slopes for random baseline and observed dependency length as a function of squared sentence length, as in Fig. 2.

Fig. S1.

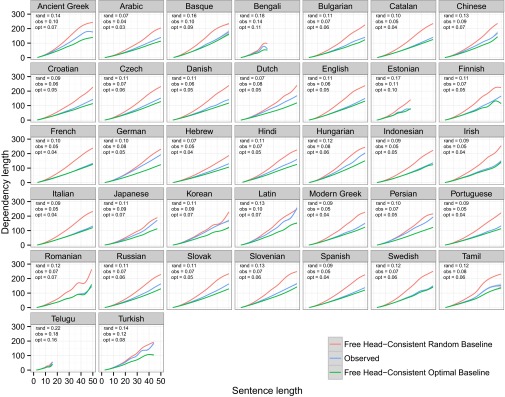
Real dependency lengths as a function of sentence length (blue) compared with the Consistent Head Direction Free Word Order Random baseline (red) and the Consistent Head Direction Free Word Order Optimal baseline (green). GAM fits are shown. rand, obs, and opt are the slopes for random, observed, and optimal dependency length as a function of squared sentence length, as in Fig. 3.

Fig. S2.

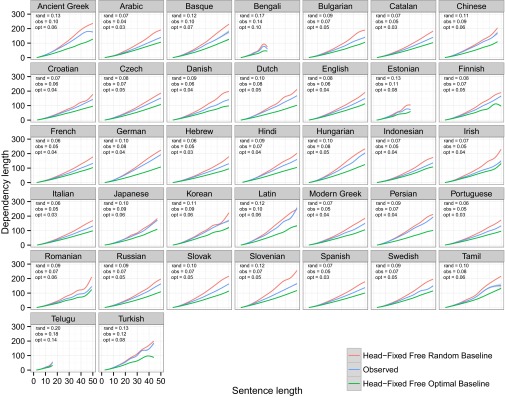
Real dependency lengths as a function of sentence length (blue) compared with the Head-Fixed Free Word Order Random baseline (red) and the Head-Fixed Free Word Order Optimal baseline (green). GAM fits are shown. rand, obs, and opt are the slopes for random, observed, and optimal dependency length as a function of squared sentence length, as in Fig. 3.

Further Baselines

Consistent Head Direction Baseline.

DLM has been advanced as an explanation for the consistency of head direction in languages: the fact that whether heads come before dependents or vice versa is typically consistent across dependency types within a language. The argument is that consistent head direction leads to lower dependency lengths, given that a language is not head medial, i.e., that heads do not appear between their dependents. However, there are plausible alternative explanations for consistency in head direction. Most compelling is the argument that the grammar of a language with consistent head direction is less complex than the grammar of a language with inconsistent head direction, because describing head direction in such a language requires only a single parameter. If there is a simplicity bias in grammars, then we would expect consistent head order independent of DLM. There is the possibility that our findings actually reflect independently motivated consistency in head order rather than DLM per se.

Here we test this idea by comparing languages to random and optimal baselines where head direction is fixed for all relation types. In this case, the only way that dependency length can be minimized is by choosing an optimal ordering of the dependents of a single head; this is accomplished by ordering constituents from short to long in the case of a head initial language or from long to short in the case of a head final language.

Fig. S1 shows real dependency lengths compared with the consistent head direction baselines. We find that all languages have shorter dependencies than we would expect by chance given consistent head direction. The difference between real and random slopes is significant at P < 0.001 for all languages. The baseline is especially interesting in the case of the overwhelmingly head final languages in our sample, such as Japanese, Korean, Turkish, Telugu, Tamil, and Hindi. For these languages, which are similar to the baselines in the consistency of their head direction, the fact that they have dependency lengths shorter than the random baseline indicates that they accomplish dependency length minimization through long before short order.

Fixed Head Position Baseline.

To what extent is DLM accomplished by choosing an optimal position of the head relative to its dependents and to what extent is it accomplished by choosing an optimal ordering of the dependents? To address this question, we compare real dependency lengths to random and optimal baselines where the position of the head and the direction of each dependent with respect to the head is fixed at the observed values. For example, given an observed head H with left dependents A, B, and C, and right dependents D, E, and F, we consider random orderings such as $\left[C,A,B,H,E,F,D\right]$, $\left[A,C,B,H,D,F,E\right]$, etc., where A, B, and C and D, E, and F are shuffled but maintain their direction with respect to the head.

Fig. S2 shows real dependency lengths compared with the random and optimal fixed head position baselines. We find that all languages have dependency lengths shorter than this baseline. The difference between real and random slopes is significant at P < 0.001 for all languages. The finding suggests that given a fixed head position, the ordering of dependents of the head is optimized across all languages, i.e., there is long before short order before heads and short before long order after heads.

Discussion

Although there has previously been convincing behavioral and computational evidence for the avoidance of long dependencies, the evidence presented here is the strongest large-scale cross-linguistic support for the dependency length minimization as a universal phenomenon, across languages and language families.

Fig. 2 also reveals that, whereas observed dependency lengths are always shorter than the random baselines, they are also longer than the minimal baselines (although some languages such as Indonesian come quite close). In part, this is due to the unrealistic nature of the optimal baseline. In particular, that baseline does not have any consistency in word order [see ref. 16 for attempts to develop approximately optimal baselines which address this issue].

In general, we believe dependency length should not be fully minimized because of other factors and desiderata influencing languages that may conflict with DLM. For example, linearizations should allow the underlying dependency structure to be recovered incrementally, to allow incremental understanding of utterances. In a sequence of two words A and B, when the comprehender receives B, it would be desirable to be able to determine immediately and correctly whether A is the head of B, B is the head of A, or A and B are both dependents of some as-yet-unheard word. If the order of dependents around a head is determined only by minimizing dependency length, then there is no guarantee that word orders will facilitate correct incremental inference. More generally, it has been argued that linearizations should allow the comprehender to quickly identify the syntactic and semantic properties of each word [see Hawkins (17) for detailed discussion of the interaction of this principle with DLM]. The interactions of DLM with these and other desiderata for languages are the subject of ongoing research.

The results presented here also show great variance in the effect size of DLM across languages. In particular, the head-final languages such as Japanese, Korean, and Turkish show much less minimization than more head initial languages such as Italian, Indonesian, and Irish, which are apparently highly optimized. This apparent relationship between head finality and dependency length is a new and unexpected discovery. Head final languages typically have highly informative word morphology such as case marking on dependents (33), and morphology might give languages more freedom in their dependency lengths because it makes long dependencies easier to identify. In line with this idea, long dependencies in German (a language with case marking) have been found to cause less processing difficulty than in English (34). In general, explaining in general why dependency lengths in some languages are shorter than in others is an interesting challenge for the DLM hypothesis.

This work has shown that the preference for short dependencies is a widespread phenomenon that not confined to the limited languages and constructions previously studied. Therefore, it lends support to DLM-based explanations for language universals. Inasmuch as DLM can be attributed to minimizing the effort involved in language production and comprehension, this work joins previous work showing how aspects of natural language can be explained by considerations of efficiency (17, 35–39).

Materials and Methods

Data.

We use the dependency trees of the HamleDT 2.0, Google Universal Treebank 2.0, and Universal Dependencies 1.0 corpora (23–25); these are projects that have aimed to harmonize details of dependency analysis between dependency corpora. In addition, we include a corpus of Mandarin, the Chinese Dependency Treebank (40). See the Table S1 for details on the source and annotation standard of each corpus. We normalize the corpora so that prepositional objects depend on their prepositions (where the original corpus has a case relation) and verbs depend on their complementizers (where the original corpus has a mark relation). For conjunctions, we use Stanford style. We also experimented with corpora in the original content-head format of HamleDT and Universal Dependencies; the pattern of results and their significance was the same.

Measuring Dependency Length.

We calculate the length of a single dependency arc as the number of words between a head and a dependent, including the dependent, as in Fig. 1. For sentences, we calculate the overall dependency length by summing the lengths of all dependency arcs. We do not count any nodes representing punctuation or root nodes, nor arcs between them; sentences that are not singly rooted are excluded.

Fixed Word Order Random Baseline.

Fixed word order random linearizations are generated according to the following procedure per sentence. Assign each relation type a random weight in $\left[-\mathrm{1,1}\right]$. Starting at the root node, collect the head word and its dependents and order them by their weight, with the head receiving weight 0. Then repeat the process for each dependent, keeping the same weights. This procedure creates consistency in word order with respect to relation types.

This linearization scheme can capture many aspects of fixed order in languages, but cannot capture all of them; for example, linearization order in German depends on whether a verb is in a subordinate clause or not. The fixed linearization scheme is also inaccurate in that it produces entirely deterministic orders. In contrast, many languages permit the speaker a great deal of freedom in choosing word order. However, creating a linearization model that can handle all possible syntactic phenomena is beyond the scope of this paper.

Generalized Additive Models.

For the figures, we present fits from generalized additive models predicting dependency length from sentence length using cubic splines as a basis function. This model provides a line that is relatively close to the data for visualization.

Regression Models.

For hypothesis testing and comparison of effect sizes, we use regression models fit to data from each language independently. For these regressions, we only consider sentences with length <100 words. For each sentence s in a corpus, we have $N+1$ data points: 1 for the observed dependency length of the sentence and $N=100$ for the dependency lengths of the random linearizations of the sentence’s dependency tree. We fit a mixed-effects regression model (41) with the following equation, with coefficients β representing fixed effects and coefficients S representing random effects by sentence:

$${\widehat{y}}_i={\beta }_0+S_0+{\beta }_1{l}_s^2+\left({\beta }_2+S_2\right)r_i+{\beta }_3{r}_i{l}_s^2+{\mathit{ϵ}}_i,$$ [1]

where ${\widehat{y}}_i$ is the estimated total dependency length of data point i, ${\beta }_0$ is the intercept, $l_s^2$ is the squared length of sentence s in words, $r_i$ is an indicator variable with value 1 if data point i is a random linearization and 0 if it is an observed linearization, and $m_i$ is an indicator variable with value 1 if data point i is a minimal linearization and 0 if it is an observer linearization. We use $l_s^2$ rather than $l_s$ because we found that a model using squared sentence length provides a better fit to the data for 33 of 37 languages, as measured by the Akaike information criterion and Bayesian information criterion; the pattern and significance of the results are the same for a model using plain sentence length rather than squared sentence length. The coefficient ${\beta }_3$ determines the extent to which dependency length of observed sentences grows more slowly with sentence length than dependency length of randomly linearized sentences. This growth rate is the variable of interest for DLM; summary measures that are not a function of length fall prey to inaccuracy due to mixing dependencies of different lengths (30). For significance testing comparing the real dependencies and random baselines, we performed a likelihood ratio test comparing models with and without ${\beta }_3$. We fit the model using the lme4 package in R (42).