High Precision and High Yield Fabrication of Dense Nanoparticle Arrays onto DNA Origami at Statistically Independent Binding Sites

Abstract

High precision, high yield, and high density self-assembly of nanoparticles into arrays is essential for nanophotonics. Spatial deviations as small as a few nanometers can alter the properties of near-field coupled optical nanostructures. Several studies have reported assemblies of few nanoparticle structures with controlled spacing using DNA nanostructures with variable yield. Here, we report multi-tether design strategies and attachment yields for homo- and hetero-nanoparticle arrays templated by DNA origami nanotubes. Nanoparticle attachment yield via DNA hybridization is comparable with streptavidin-biotin binding. Independent of the number of binding sites, >97% site-occupation was achieved with four tethers and 99.2% site-occupation is theoretically possible with five tethers. The interparticle distance was within 2 nm of all design specifications and the nanoparticle spatial deviations decreased with interparticle spacing. Modified geometric, binomial, and trinomial distributions indicate that site-bridging, steric hindrance, and electrostatic repulsion were not dominant barriers to self-assembly and both tethers and binding sites were statistically independent at high particle densities.

Introduction

High precision, high yield, and high density self-assembly of nanoparticles into arrays is essential for understanding and exploiting function-property relationships in organic and inorganic materials. For example, macromolecular docking of protein-protein, protein-nucleic acid, and antibody-antigen complexes are proximally defined.^1,2 In addition, plasmonic and coherent energy transport between nanoparticles is proximally confined.^3-8 Independent of the material system being investigated, deviations from the optimal position have detrimental effects on function and performance. For example, near-field coupling between metal nanoparticles is distance dependent.^9,10 In addition, when metal nanoparticles are organized into optical beam-splitters, a change of interparticle spacing affects the power splitting ratio.¹¹ To realize near-field, sub-diffraction, optoelectronics, self-assembly of metallic arrays and heterostructures containing gold nanoparticles (AuNPs) and quantum dots (QDs) is required. DNA nanotechnology also necessitates both high precision and high yield to become practical for scalable nano-manufacturing. Towards this goal, the probability of site-occupation by nano-particles, and the spatial deviation of attached nanoparticles are extensively studied on DNA templates using modified geometric, binomial, and trinomial distributions at elevated packing densities.

DNA Nanotechnology

Assembly of nanomaterials into discrete arrays is made possible by structural DNA nanotechnology. By implementing simple design rules,^12-14 DNA can be programmed into complex nanostructures using tiled motifs,^15,16 origami,¹⁷ bricks,^18,19 or a combination thereof. Here, we present a viable directed self-assembly fabrication route using DNA nanostructures to extend beyond the fabrication limits of lithography.

Functionalization

Nucleic acid functionalization is an active sub-field in DNA nanotechnology. Within this subfield, two methods coexist: intrinsic chemical modification of oliogonucleotides via covalent bonds and extrinsic physical attachment of synthetic components to oliogonucleotides via secondary bonds. Intrinsic modifications to oligonucleotides may include dye-labeled nucleic acids,²⁰ glycol nucleic acids (GNA),²¹ locked nucleic acids (LNA),^{22, 23} peptide nucleic acids (PNA),^{24, 25} and zipped nucleic acids (ZNA).²⁶ In comparison, extrinsic components hybridized onto oligonucleotides may include proteins,^27,28 virus capsides,²⁹ carbon nanotubes,³⁰ chromophores,³¹ quantum dots,^32-34 metallic nanoclusters,^35-38 and metallic nanoparticles.^39-43 Extrinsic components are often attached to DNA using streptavidin-biotin binding³² or Watson Crick base-pairing.⁴⁴

Binding Sites

While streptavidin-biotin binding and Watson Crick base-pairing encode the location of the binding sites, base-pairing also distinguishes between the binding sites. Site-specificity is implemented by incorporating sequence-specific tethers at select sites and conjugating components, such as metallic nanoparticles, with complementary tethers. Site-specificity minimizes site-bridging by increasing the distance between binding sites with identical tether sequences, while also enabling the reduction of the overall binding site periodicity between components.^39,45 Site-bridging is further reduced by restricting the length⁴⁶ and/or number of single-stranded DNA conjugates on the nanoparticles.^47,48

Challenges

A common challenge in DNA nanotechnology is that the nanoparticle attachment probability decreases with increasing component density.^32,33 Attachment barriers include: (A) site-bridging – individual components bridging multiple binding sites, (B) steric hindrance – physical crowding via neighboring components,^32,33 (C) electrostatic repulsion – Coulombic interaction between neighboring components, and (D) binding energy – the energy required to disassemble the component-template complex.

Prior Solutions

To increase component attachment probabilities, Sharma et al. utilized di-thiol modified single-stranded DNA strands to strengthen the bond between AuNPs and the conjugating oligonucleotides.⁴⁷ In comparison, Ko et al. demonstrated an increased attachment probability of QDs onto DNA origami using trivalent biotin binding sites.³² Within their study, the yield of streptavidin-functionalized QDs binding to biotinylated DNA origami was controlled by the: biotin linker length, valency (i.e. # of tethers) of the binding location, organization of the binding locations, and spacing of the binding locations. The designed (and experimental) spacings between QDs were 50 nm (52.7 ± 4.3 nm), 35 nm (40.8 ± 6 nm), and 22 nm (42.1 ± 5 nm) – indicating that steric hindrance and/or electrostatic repulsion significantly contributed to interparticle obstruction. Although heterostructures were also fabricated,⁴⁵ the component density was well below the geometric threshold where site-bridging, steric hindrance, and electrostatic repulsion were expected.^45,49,50 Here, we present fourteen successful binding site designs for extending the geometric threshold and maximizing component densities of AuNPs and QDs onto DNA nanostructures with high precision and high yield. For all designs, site-bridging, steric hindrance, and electrostatic repulsion were not dominant self-assembly barriers – even at elevated packing densities. In addition, both tethers and binding sites were statistically independent at high particle densities.

Binding Site Design

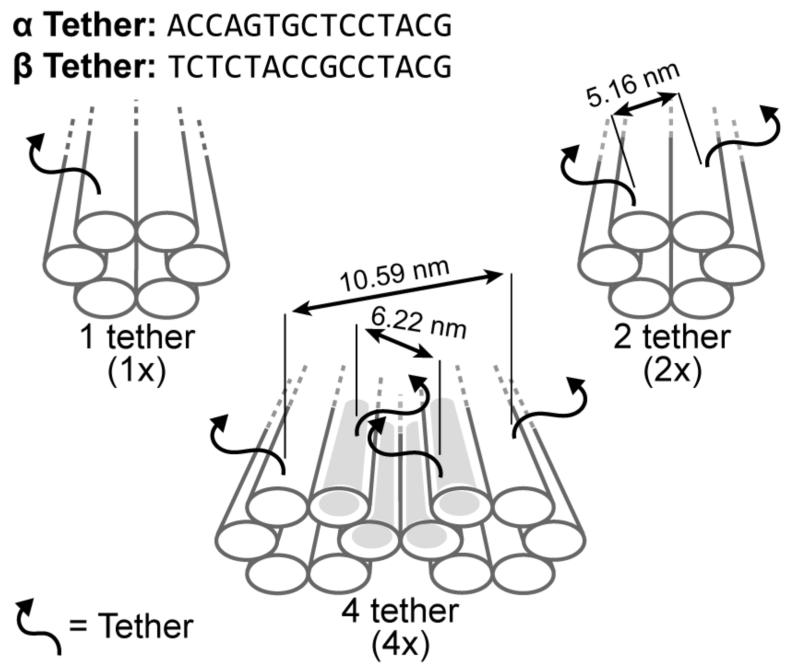
To explore binding energy versus the probability of AuNP attachment in the absence of site-bridging, steric hindrance, and electrostatic repulsion, three nanoparticle arrays with 43 nm periodicities were designed. Sequence-level designs for the DNA nanostructures are provided in Support Information S1. For each design, sequence dependent binding probabilities were evaluated using α (5’-ACCAGTGCTCCTACG-3’) or β (5’-TCTCTACCGCCTACG-3’) tethers generated by in-house software for creating random sequences with minimal secondary structures.⁵¹ As illustrated in Figure 1, designs included: (I) one tether per binding site for nine binding sites – 1×9_α or 1×9_β, (II) two tethers per binding site for nine binding sites – 2×9_α or 2×9_β, and (III) four tethers per binding site for nine binding sites – 4×9_α or 4×9_β. In all cases, the tether sequence at a multi-tether site is the same for each tether (i.e., all α or β). The 1×9 and 2×9 designs used DNA nanotubes³³ and the 4×9 design cross-linked two DNA nanotubes together into a nanorail;⁷ creating a nested trench with four tethers per binding site. For convenience, all designs are referred to as nanostructures.

Figure 1.

Binding site strategies for attaching DNA conjugated AuNPs onto DNA nanostructures. Nanostructures with one tether (1×), two tethers (2×), and four tethers (4×) per binding site correlate the probability of site-occupation to the number of tethers per binding site. A binding site is a cluster of tethers with either a α or β sequence. The grey nested trench axially aligns nanoparticles between two cross-linked nanotubes to form a nanorail.⁷

To explore site-bridging, steric hindrance, and electrostatic repulsion at elevated nanoparticle densities, three additional designs were created: (IV) one tether per binding site for 14 binding sites – 1×14_α, (V) two tethers per binding site for 14 binding sites – 2×14_α, and (VI) four tethers per binding site for 14 binding sites – 4×14_α. To minimize site-bridging, two additional designs were created in which adjacent binding sites alternated between α and β tethers – doubling the distance between equivalent binding sites. Alternating tether designs included: (VII) two tethers per binding site for 18 binding sites – 2×18_α/β and (VIII) four tethers per binding site for 18 binding sites – 4×18_α/β. For comparison, the 14 and 18 binding site designs had a 29 nm and a 14 nm binding site periodicity, respectively.

Heterostructure Design

Three heterostructures were designed to compare the average probability of site-occupation between AuNPs and QDs measured in a prior study.³³ The heterostructures contained at least one QD-AuNP bundle – a 2× QD binding site flanked by two pairs of 4× AuNP binding sites. The AuNP binding site pairs alternated between α and β tethers to prevent site-bridging. As illustrated in Figure 2, the three designs included a: (Ix) single QD-AuNP bundle in H1, (X) single QD-AuNP bundle with seven 4× AuNP binding site pairs in H2, and (XI) four QD-AuNP bundles with a 4× AuNP binding site pair in H3. Site-bridging between QD binding sites, which were 45 nm apart, was not expected.³³

Figure 2.

Three heterostructures with one or more QD-AuNP bundles – a 2× QD binding site flanked by two pairs of 4× AuNP binding sites. The heterostructures include a QD-AuNP bundle (H1), a QD-AuNP bundle with seven AuNP binding site pairs (H2), and four QD-AuNP bundles with one AuNP binding site pair (H3). The nearest-neighbor binding site distance was 14 nm.

Results and Discussion

Experimental Probability of Site-Occupation

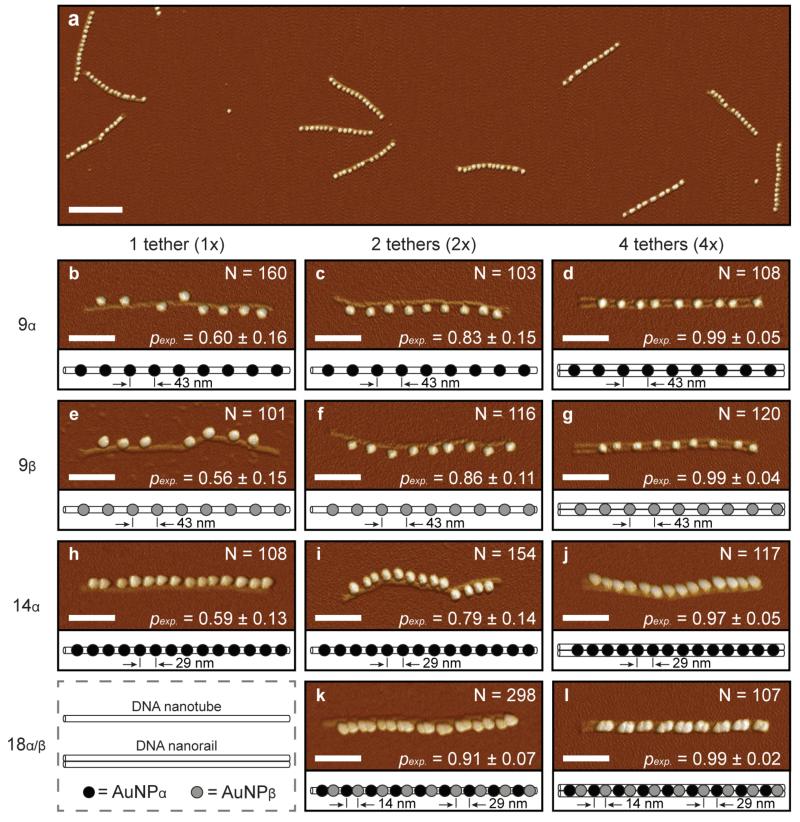
The probability of site occupation for 10 nm diameter AuNPs onto DNA nanostructures was evaluated from hundreds of atomic force microscope (AFM) images. Representative data used in this study are shown in Figure 3. To distinguish individual nanoparticles, the height and peak force error channels were superimposed. For reference, the corresponding height images are provided in Support Information S2. For all images, the average probability of AuNP site-occupation, p_exp in Equation 1, was determined by counting arrays containing a number of nanoparticles equal to or less than the number of binding sites. This practice was statistically validated and hence adopted because of the experimental uncertainty when determining occupancy of individual binding sites. As expected, p_exp increased and the standard deviation decreased as the number of tethers per binding site increased. For example, the average probability of site-occupation ranged between 0.56 ± 0.15 for 1×9_β nanostructures and 0.99 ± 0.02 for 4×18_α/β nanostructures. Comparatively, all 4× nanostructure designs achieved >97% average probability of site occupation – equivalent to or better than previous studies with lower nanoparticle densities.^34,52 In addition, the binding performance of the α and β binding sites were statistically equivalent, and thus the binding energy was sequence independent.

Figure 3.

AFM images of DNA nanostructures functionalized with gold nanoparticles (AuNPs). To distinguish individual nanoparticles, the height and peak force error channels were superimposed. For reference, the corresponding height images are provided in Support Information S2. The scale bars are 300 nm for (a) and 100 nm for (b - l). (a) Low-resolution AFM image of 4×14_α nanostructures. (b-l) High-resolution AFM images of DNA nanostructures with corresponding nanoparticle schematics. DNA nanostructure designs included: (b) 1×9_α, (c) 2×9_α, (d) 4×9_α, (e) 1×9_β, (f) 2×9_β, (g) 4×9_β, (h) 1×14_α, (i) 2×14_α, (j) 4×14_α, (k) 2×18_α/β, and (l) 4×18_α/β. The columns from left to right represent increasing numbers of tethers per binding site including one tether (1×), two tethers (2×), and four tethers (4×). The rows from top to bottom represent increasing numbers of binding sites including 9 sites, 14 sites, and 18 sites for α (5’-ACCAGTGCTCCTACG-3’) and/or β (5’-TCTCTACCGCCTACG-3’) tethers. N is the total number of nanostructures counted to determine the average probability of AuNP site-occupation, p_exp. The designed diameter and length of the 1× and 2× nanostructures was 6 nm and 412 nm, respectively. The designed width, height, and length of the cross-linked, 4× nanostructure were 12 nm, 6 nm, and 412 nm, respectively.

When alternating between α and β binding sites, the probability of AuNP site occupation for the 2×18_α/β nanostructure was 12% greater than the 2×14_α nanostructure, even though the theoretical nearest-neighbor binding site distance was 15 nm less for the 18-site structure. A binding performance of 0.99 ± 0.02 was obtained using the 4×18_α/β nanostructures because each binding site was equipped with 4 tethers, and the binding sites alternated between α and β tethers to prevent bridging between neighboring sites.

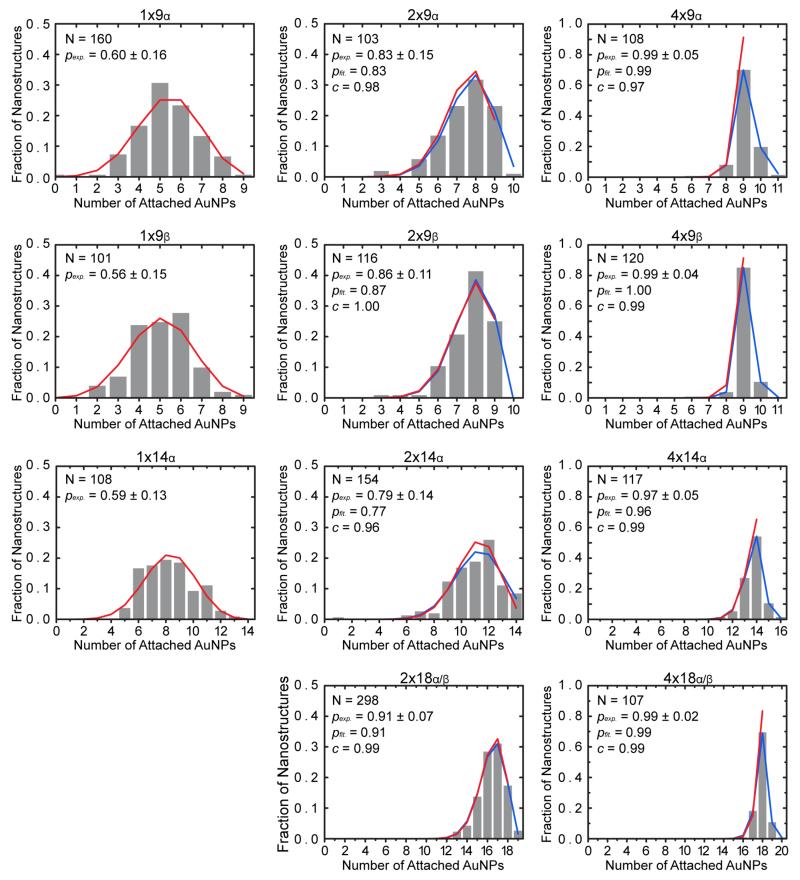
Binomial & Trinomial Distributions

Binomial distributions were initially computed using Equation 2 for each nanostructure based on the experimentally measured average probability of AuNP site-occupation, p_exp. Trinomial distributions were then computed using Equation 3 to account for excess nanoparticle occupancy and used to fit two parameters to the data. The first parameter was p_fit, the calculated estimate of the average probability of site-occupation. The second parameter was c, the conditional probability of a binding site having only one AuNP assuming the site is occupied (Figure 4). For all 2× and 4× nanostructures – where multiple occupancy was observed – the close fit to a trinomial distribution with c nearly equal to 1 confirms that site-bridging, steric hindrance, and electrostatic repulsion were not dominant effects. The binomial distribution, with no free parameters fit to the data, further supports the conclusion that binding sites within a nanostructure were statistically independent.

Figure 4.

Fraction of nanostructures versus the number of attached AuNPs to the nanostructures. Experimental, binomial and trinominal distributions are shown by gray histograms, red solid lines, and blue solid lines, respectively. Histogram values are listed in the Support Information S9, Table S3. In the absence of site-bridging, steric hindrance, and electrostatic repulsion, histograms should be well-described by binomial and trinomial distributions. Binominal distributions were computed using Equation 2 based on the experimentally determined average probability of AuNP site-occupation, p_exp, and the histograms were fitted to trinomial distributions with Equation 3 to determine c, the conditional probability of a binding site having exactly one bound AuNP among occupied binding sites, and p_fit, the calculated average probability of site-occupation. N is the total number of nanostructures counted for each design to determine p_exp.

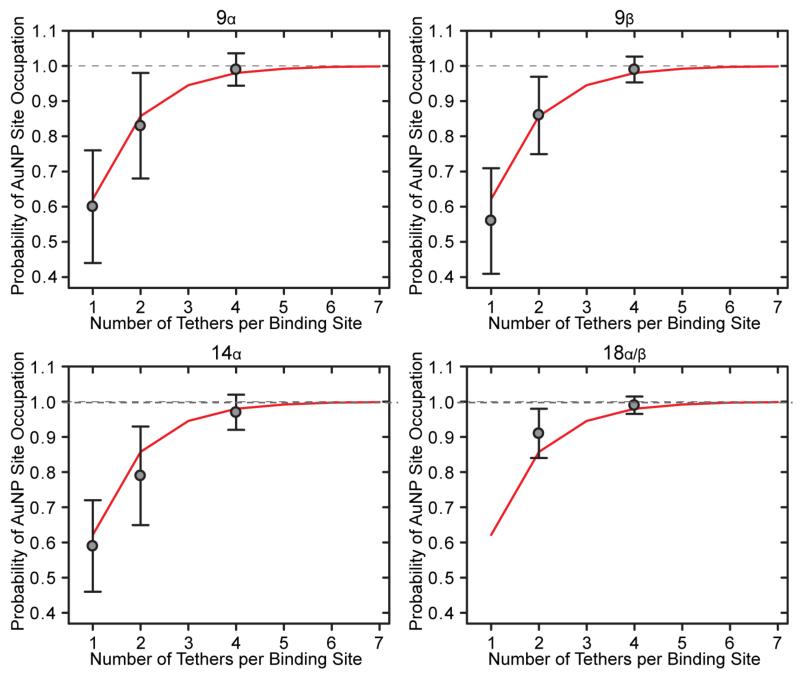
Theoretical Probability of Site-Occupation

To determine the number of tethers per binding site that achieved satisfactory attachment of a AuNP, the theoretical probability of site-occupation, p_th, for 9_α, 9_β, 14_α, and 18_α/β nanostructures was compared to the average probability of AuNP site-occupation, p_exp. Predictions were calculated using Equations 4 and 5, which assumed that hybridization of one tether to a AuNP is independent of neighboring tethers on the same binding site. As the number of tethers increases, p_th asymptotically approaches 100% site-occupation. For example, 4, 5, 6, and 7 tethers correspond to 97.9%, 99.2%, 99.7%, and 99.9% site-occupation, respectively. As shown in Figure 5, the theoretical and experimental values agree well for all designed nanostructures – statistically confirming: (a) site-occupation is independent of the number of binding sites, (b) α and β binding sites are equivalent, (c) tethers and binding sites are independent, and (d) an engineering point of diminishing returns occurs as the number of tethers increase.

Figure 5.

Probability of AuNP site-occupation versus the number of tethers per binding site. The theoretical probability of site-occupation (p_th = red lines) and the experimentally measured average probability of AuNP site-occupation (p_exp = gray dots) for 9_α, 9_β, 14_α, and 18_α/β nanostructures. The theoretical probability of site-occupation, p_th, was calculated from Equations 4 and 5. The correlation statistically confirms that: (a) site-occupation is independent of the number of binding sites, (b) α and β binding sites are equivalent, (c) tethers and binding sites are independent, and (d) an engineering point of diminishing returns occurs as the number of tethers increases in this study.

Modified Geometric Distribution

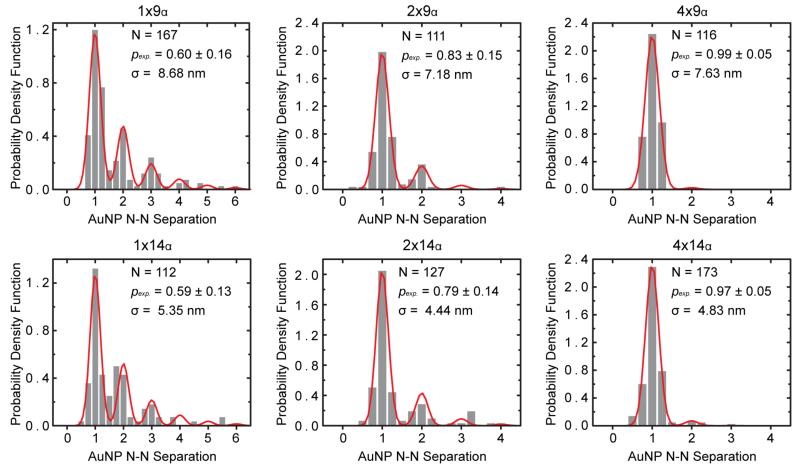
The experimental periodicities of each nanostructure were determined by multiplying the theoretical periodicity by the ratio between the measured nanostructure length and the calculated theoretical length. Calculated experimental periodicities were slightly smaller than the theoretical values (Table 1). Experimental periodicities for the 9_α and 14_α nanostructures were used to calculate the modified geometric distribution in Equation 6 by fitting the nearest-neighbor AuNP separation histograms (Figure 6). The nearest-neighbor AuNP separation is defined as the distance between the center of a AuNP to the center of an adjacent nanoparticle, whereas the interparticle distance is the gap between two nanoparticles. In comparison, the AuNP spatial deviation, σ, is the standard deviation of the nearest-neighbor AuNP separation – which ranged between 4.4 nm to 8.68 nm and did not correlate to the number of tethers per binding site even though it decreased as the interparticle distance decreased. Neglecting capillary effects during drying, the degree of freedom of AuNPs is largely influenced by the nanostructure periodicity and not the binding site design.

Table 1.

Experimental Periodicity of DNA Nanostructures

Nanostructure Design	1×	2×	4×
9α (Theoretical: 43 nm)	41.2 nm	40.8 nm	42.0 nm
14α (Theoretical: 29 nm)	28.2 nm	27.9 nm	27.3 nm

Figure 6.

Probability density function versus AuNP nearest-neighbor separation periodicity. Nearest-neighbor AuNP separation histograms (gray bars) and modified geometric distribution fits (red lines). The modified geometric distributions were computed from the experimentally measured average probability of AuNP site-occupation, p_exp, using Equation 6. Experimental periodicities for nanostructures were computed by multiplying the theoretical periodicity by the ratio between the measured nanostructure length and the calculated theoretical length. The spatial deviation of the nearest-neighbor AuNP separation, σ, was determined by the fitting. N is the total number of nearest-neighbor AuNP separations measured to generate the histogram and N-N is nearest neighbor.

Heterostructures

Three heterostructures were also synthesized by combining four tethers per binding site for AuNPs and two tethers per binding site for QDs (Figure 2). The nanostructures were evaluated using AFM and transmission electron microscopy (TEM) to correlate the physical structure to the chemical difference between each nanoparticle (Figure 7). To distinguish individual nanoparticles, the AFM height and peak force error channels were superimposed. For reference, the corresponding height images are provided in Support Information S2. In the TEM images, the AuNPs appear dark and the QDs appear light due to differences in their atomic numbers. Energy dispersive spectroscopy (EDS) line-scans were performed on individual QDs and AuNPs on the H1 nanostructure (Support Information S3) – confirming that the lighter and darker nanoparticles were indeed QDs and AuNPs, respectively. Additional micrographs of the H2 nanostructure are available in Support Information S4. As experimental controls, AuNPs and QDs were independently functionalized onto select heterostructures. The average probability of AuNP site-occupation was 0.99 ± 0.06 for H1, 0.98 ± 0.03 for H2, 0.98 ± 0.04 for H3 – which are comparable with the 4× AuNP arrays shown in Figure 3. In comparison, the average probability of QD site-occupation was 0.79 ± 0.41 for H1, 0.84 ± 0.37 for H2, 0.79 ± 0.26 for H3 – which agree with previous studies,^32,33 and suggests that the 2× biotin binding sites for QDs are equivalent to the 2× DNA binding sites for AuNPs.

Figure 7.

TEM (a, c, e) and AFM (b, d, f) images of H1, H2, and H3 heterostructures, including schematics for each design. The images show successful site-specific attachment of AuNPs and QDs. To distinguish individual nanoparticles in AFM, the height and peak force error channels were superimposed. For reference, the corresponding height images are provided in Support Information S2. The number of samples evaluated, N, and the experimentally measured average probability of overall site-occupation, p_exp, are shown in the upper and lower right-hand corners for the TEM images, respectively. The EDS analysis of the QD and the AuNP for H1, shown in Support Information S3, confirmed that the nanoparticle attached in the middle of H1 is a QD and the two nanoparticles on either side of the QD are AuNPs. Based on the QD and AuNP mass contrast difference in TEM, successful synthesis of H2 and H3 is also implied. The scale bars are 100 nm.

Experimental

Gold Nanoparticles

For all experiments, the AuNPs were 10 nm in diameter and were conjugated with 5’ thiolated DNA strands with a 5-thymine spacer. The hydrodynamic diameter of the DNA conjugated AuNPs was estimated to be 27 nm in buffer.⁵³ In comparison, the hydrodynamic diameter of the streptavidin conjugated quantum dots was ~20 nm according to the manufacturer specification; which was validated in a prior study.³³

DNA Nanostructures

Individual DNA nanotubes with one (1×) or two tethers (2×) per binding site were synthesized by combining single-stranded M13mp18 viral DNA (New England Biolabs) with ~170 unique staple strands (Integrated DNA Technologies) in a molar ratio of 1:10 in a 1× TAE, 14 mM MgCl₂ buffer. The samples were annealed at 90 °C for 20 min and then cooled to 20 °C at 0.6 °C/min. Well-formed nanotubes were purified by agarose gel electrophoresis using a 0.5× TBE, 12 mM MgCl₂ buffer. DNA nanostructures with four tethers (4×) per binding site were synthesized by combining two nanotubes with two tethers (2×) per binding site each. While both nanotubes were structurally equivalent, select staple strands were modified between the nanotubes to promote cross-linking. To overcome electrostatic repulsion between the monomers, they were combined stoichiometrically in a 0.5× TBE, 40 mM MgCl₂ buffer and then annealed at 45 °C for 2 hours and cooled to 25 °C at 0.6 °C/min. For synthesis details, see Support Information S5.

Functionalization

For all designs, AuNPs were site-specifically attached to DNA nanostructures using established methods.⁷ Briefly described, 10 nm AuNPs were functionalized with the complementary sequence to the α or β tethers. Functionalized AuNPs were mixed in a 1:5 binding site to AuNP ratio in a 0.5× TBE, 12 mM MgCl₂ buffer. Because AuNPs are known to aggregate at high Mg²⁺ concentrations, the amount of MgCl₂ was normalized to 12 mM. A typical DNA nanostructure concentration before mixing the 1× and 2× designs was ~10 nM and before mixing the 4× designs was ~1 nM. Once mixed, samples were annealed at 45 °C for 41 min and then cooled to 25 °C at 0.6 °C/min. Functionalized DNA nanostructures were separated from excess AuNPs using agarose gel electrophoresis (Support Information S6).

Heterostructures

Heterostructures were synthesized by mixing DNA nanostructures, functionalized AuNPs, and the QDs in 1:5:5 binding site to AuNP to QD ratio, respectively. The mixture was heated to 45 °C for 41 minutes and then cooled to 25 °C at 0.6 °C/min. The mixtures were purified by agarose gel electrophoresis and the recovered heterostructures were stained with 2% uranyl acetate solution and imaged via TEM (Support Information S7 and S8). Once synthesized, all samples were prepared for (Support Information S8) and characterized by atomic force microscopy (AFM) and transmission electron microscopy (TEM).

Statistical Analysis

The number of nanoparticles that site-specifically attached to the DNA nanostructures was measured from over 100 structures per design modification via AFM and TEM. In total, 2,578 nanostructures were analyzed from 14 unique designs. The guidelines for analyzing nanostructures are provided in Support Information S9. Once compiled, statistical models of site-occupation were applied and compared using binomial and trinomial distributions, both of which consider binding sites to be independent. Binomial distributions are included for simple comparison with the literature as a model to validate the independence of the binding sites without free parameters in the equation.^32,33 Trinomial distributions are included to analyze more complex cases where the number of bound AuNPs exceeded the number of binding sites.

In the binomial analysis, the average probability of AuNP site-occupation, p_exp, between a AuNP and its binding site was approximated by:

$$p_{\mathit{exp}}=\frac{\Sigma \text{Attached Nanoparticles}}{\Sigma \text{Available Sites}}$$ (1)

This sum was restricted to cases where the number of nanoparticles attached did not exceed the number of binding sites because AFM and TEM cannot resolve the occupancy of a particular site. This restriction provides an estimate of the average probability of AuNP site-occupation given a very low probability of having two or more particles bound to one site – an assumption that was validated by fitting parameters to the data using the trinomial distribution in Equation 3, as discussed in the next paragraph. In the absence of site-bridging, steric hinderance, electrostatic repulsion, and multiple occupancy, the average probability of AuNP site-occupation is expected to follow a binominal distribution, P_bi(m), given by:

$$P_{\mathit{bi}}\left(m\right)=\frac{n!}{m!(n-m)!}{p}_{\mathit{exp}}^m{(1-p_{\mathit{exp}})}^{(n-m)}$$ (2)

where n is the number of available binding sites, m is the number of AuNPs attached per nanostructure, and p_exp is the average probability of AuNP site-occupation. In order to calculate the AuNP spatial deviation, over 100 center-to-center nearest-neighbor AuNP distances were measured via AFM, processed using WSxM^{™ 54} and analyzed using Origin^™ (Support Information S10).

Analogous to the binomial distribution, the trinomial distribution, Equation 3, calculates the probability that m nanoparticles bind to an array with n binding sites. However, when written in terms of the site-binding probabilities for zero, one, or two nanoparticles the trinomial distribution can account for cases where the number of bound nanoparticles exceeds the number of binding sites. All possible ways to attach m particles to n sites are summed over the possible numbers of double-occupancy sites (up to a max of $\lfloor \frac{m}{2}\rfloor$), indexed by j (Support Information S11). Briefly, the trinomial distribution in formulated in terms of p_fit, the fitted probability of AuNP site-occupation, and c, the conditional probability that only one nanoparticle is bound to a site given that it is occupied, yielding the following trinomial distribution, P_tri(m):

$$\begin{array}{cc}\hfill P_{\mathit{tri}}\left(m\right)=& {\Sigma }_{j=\max (0,m-n)}^{{\lfloor }^m{∕}_2\rfloor }\frac{n!}{(n-m+j)!(m-2j)!j!}.\hfill \\ \hfill & {(1-p_{\text{fit}})}^{(n-m+j)}{\left({\mathit{cp}}_{\text{fit}}\right)}^{(m-2j)}{\left\{\right(1-c\left)p_{\text{fit}}\right\}}^j\hfill \end{array}$$ (3)

This equation was fit to the occupancy data shown in Figure 4 with p_fit and c as free parameters determined by the best fit to the data. The experimentally derived, p_exp, and the fit parameter, p_fit, are in close agreement. As further validation of the values obtained for p_fit and c, the expected average site-occupancy was in close agreement to the observed average site-occupancy (Support Information S11).

The probability of site-occupation for an individual tether per binding site, p₁, was then calculated from the average probability of AuNP site occupation p_exp, for binding site designs with t tethers, and was given by:

$$p_1=1-\sqrt[t]{1-p_{\mathit{exp}}}$$ (4)

Independent of the number of binding sites (i.e. 9_α and 14_α), the number of tethers per binding site (i.e. 1×9_α and 4×9_α), or the sequence of binding sites (i.e. 9_α and 9_β), p₁ was assumed to be identical for all design strategies, which was validated in Figure 5. The theoretical probability of site-occupancy, p_th, was then calculated from the average p₁ from all AuNP designsp_ave, given by:

$$p_{\mathit{th}}=1-{(1-p_{\mathit{ave}})}^t$$ (5)

Nearest-neighbor AuNP separations were then normalized by the experimental periodicity of DNA nanostructures with α-tethers to account for the change in periodicity due to the change in structure length. Experimental periodicities were calculated by multiplying the theoretical periodicity by the ratio between the experimental and theoretical nanostructure lengths (Support Information S12). Distributions were then fit to a modified geometric distribution for nanostructures with α-tethers, given by:

$$P_{\mathit{geo}}\left(x\right)={\Sigma }_{k=1}^{\infty }\frac{1}{\sigma \sqrt{2\pi }}\exp \left[-\frac{{(x-k)}^2}{2{\sigma }^2}\right]p_{\mathit{exp}}{(1-p_{\mathit{exp}})}^{(k-1)}$$ (6)

where k is the integer number of periods between nearest neighbors, x is the distance along the axis of a nanostructure divided by the experimental periodicity, σ is the spatial deviation, and p_exp is the average probability of AuNP site-occupation (Support Information S13). By fitting the distribution with the modified geometric equation, the spatial deviation for the nearest-neighbor AuNP separation was calculated. The analysis for the 18_α/β nanostructures was not performed because the modified geometric distribution does not account for aperiodicity.

Conclusion

High precision, high yield, and high density self-assembly of nano-particles into arrays on DNA nanostructures have been successfully synthesized and characterized – providing a bottom-up route towards optoelectronics. Eleven AuNP arrays with variable periodicity were shown. Modified geometric, binomial, and trinomial distributions indicate that site-bridging, steric hindrance, and electrostatic repulsion were not dominant barriers to self-assembly and both tethers and binding sites are statistically independent of one another at high particle densities.

Experimentally, nanostructures with 4 tethers per binding site achieved greater than 97% average probability of site-occupation – equivalent to or better than previous studies with lower nanoparticle densities. Theoretical and experimental values agreed well for all nanostructures – statistically confirming that: (a) site-occupation is independent of the number of binding sites, (b) α and β binding sites are equivalent, (c) tethers and binding sites are independent, and (d) an engineering point of diminishing returns occurs as the number of tethers increases. In addition, the nanostructure periodicity rather than the number of tethers per binding site-dominated the spatial deviation for the nearest-neighbor AuNP separation distances.

Three heterostructures functionalized with AuNPs and QDs were also synthesized with average probabilities of overall site-occupation greater than 85%. The nanoparticles were effectively touching, even though the binding site-separation between the QD and the AuNP was 14 nm – because the hydrodynamic diameters of the QDs and the AuNPs were 20 nm and 27 nm, respectively. The results suggest that increasing the number of biotin tethers for QD binding sites would also increase their binding probability.