Modeling Image Patches with a Generic Dictionary of Mini-Epitomes

Abstract

The goal of this paper is to question the necessity of features like SIFT in categorical visual recognition tasks. As an alternative, we develop a generative model for the raw intensity of image patches and show that it can support image classification performance on par with optimized SIFT-based techniques in a bag-of-visual-words setting. Key ingredient of the proposed model is a compact dictionary of mini-epitomes, learned in an unsupervised fashion on a large collection of images. The use of epitomes allows us to explicitly account for photometric and position variability in image appearance. We show that this flexibility considerably increases the capacity of the dictionary to accurately approximate the appearance of image patches and support recognition tasks. For image classification, we develop histogram-based image encoding methods tailored to the epitomic representation, as well as an “epitomic footprint” encoding which is easy to visualize and highlights the generative nature of our model. We discuss in detail computational aspects and develop efficient algorithms to make the model scalable to large tasks. The proposed techniques are evaluated with experiments on the challenging PASCAL VOC 2007 image classification benchmark.

1. Introduction

Our goal in this work is to investigate to which extent generative image models can also be competitive for visual recognition tasks. We use the raw image patch intensity as the fundamental representation in our model. Appearance patches have been successfully applied so far mostly in image generation tasks such as texture synthesis, image denoising, and image super-resolution [2, 10, 12].

Using raw appearance patches maximally preserves information in the original image. The main challenge with this modeling approach in image classification tasks is that the associated image description can be too sensitive to nuisance parameters such as illumination conditions or object position. Therefore, most computer vision systems for image categorization and recognition rely on features built on top of discriminative patch descriptors like SIFT [19]. SIFT has been explicitly designed for invariance to these nuisance parameters, which allows it to work reliably in conjunction with simple classification rules in a bag of visual words framework [17, 30]. However, the SIFT and other similar descriptors are not suitable for image generation tasks and are very difficult to visualize [28].

Instead of designing an image descriptor to be maximally invariant from the ground up, we attempt to explicitly model photometric and position nuisance parameters as attributes of a generative patch-based representation. Specifically, we develop a probabilistic epitomic model which can faithfully reconstruct the raw appearance of an image patch using just a single patch selected from a compact dictionary of mini-epitomes. Our first main contribution is to show that explicitly matching the image patches to their best position in the mini-epitomes greatly improves reconstruction accuracy compared to a non-epitomic baseline which does not cater for position alignment. This allows us to accurately capture the appearance of image patches by a generic, i.e., universal rather than image specific, visual dictionary learned from a large set of images.

We design image descriptors for image classification tasks based on the proposed mini-epitomic dictionary. Our second main contribution is to show that bag-of-words type classifiers built on top of our epitomic representation not only improve over ones built on non-epitomic patch dictionaries, but also yield classification results competitive to those based on the SIFT representation. Beyond histogram-type encodings, we also investigate an “epitomic footprint” encoding which captures how the appearance of a specific image deviates from the appearance of the generic dictionary. This epitomic footprint descriptor can be visualized or stored as a small image and at the same time be used directly as feature vector in a linear SVM image classifier.

Employing the proposed model requires finding the best match in the epitomic dictionary for each patch in an image. We have experimented with both a fast GPU implementation of exact search as well as approximate nearest neighbor search techniques. Both allow efficient epitomic patch matching and image encoding in about 1 sec for 400 × 500 images and typical settings for the model parameter values, making the model scalable to large datasets. In the main part of the paper we report image classification results on the challenging PASCAL VOC 2007 image classification benchmark [11] and compare the performance of our model both with a non-epitomic baseline and the tuned implementations of SIFT-based classification techniques reviewed by [6]. The supplementary material elaborates on aspects of the proposed model and includes further experimental results on the Caltech-101 dataset. Accompanying software can be found at our web sites.

2. Related work

Key element of the proposed method is the explicit modeling of patch position using mini-epitomes. The epitomic image representation and the related idea of transformation invariant clustering were developed in [13, 15] and also used in [31] for texture modeling, but have not been applied before for learning generic visual dictionaries on large datasets and in the context of visual recognition tasks.

The idea to use a patch-based representation for image classification first appeared in [23] and was further developed by [26], who applied it to homogeneous texture classification and compared it to the filterbank-based texton representation of [18]. Recently, [7] demonstrated competitive image classification results on the CIFAR-10 dataset of small images with patch dictionaries trained by K-means. Neither of these works explicitly handles patch position or demonstrates performance comparable to modern SIFT encodings [6] on challenging large-scale classification tasks.

More generally, unsupervised learning of image features has received considerable attention recently. Most related to our work is [29], which also attempts to explicitly model the position of visual patterns in a deconvolutional model. However, their model requires iteratively solving a large-scale sparse coding problem both during train and test time. The image classification performance they report significantly lags modern SIFT-based models such as those described in [6], despite the fact that they learn a multi-layered feature representation. The power of learned patch-level features has also been demonstrated recently in [5, 9, 24]. Using mini-epitomes instead of image patches could also prove beneficial in their setting.

Sparsity provides a compelling framework for learning image patch dictionaries [22]. Sparsity coupled with epitomes has been explored in [1, 4] but these works focus on learning dictionaries on a single or a few images. While each image patch is represented as a linear combination of a few dictionary elements in sparse models, it is approximated by just one dictionary element in our model. One can thus think of the proposed model as an extremely sparse representation, or alternatively as an epitomic form of K-means or vector quantization.

3. Image Modeling with Mini-Epitomes

3.1. Model description

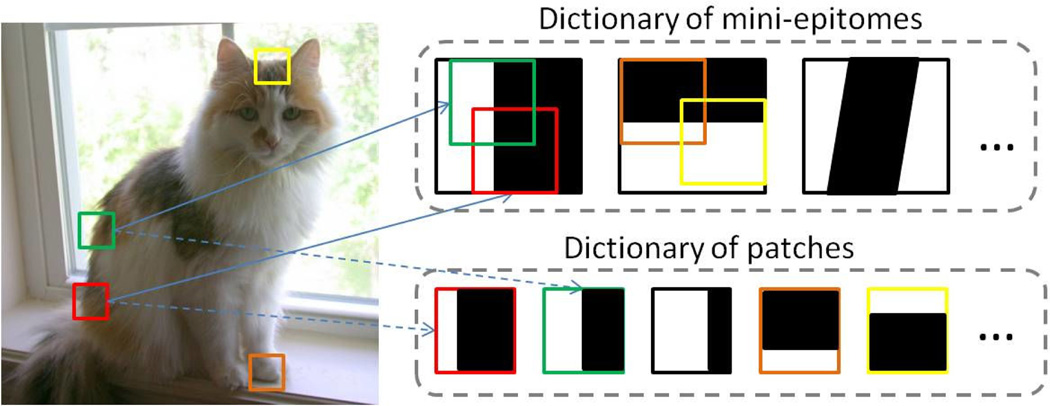
With reference to Fig. 1, let ${\{{\mathbf{x}}_i\}}_{i=1}^N$ be a set of possibly overlapping image patches of size h × w pixels. Our dictionary comprises K mini-epitomes ${\{{\mathit{\mu }}_k\}}_{k=1}^K$ of size H × W, with H ≥ h and W ≥ w. The length of the vectorized patches and epitomes is then d = h · w and D = H · W, respectively. We approximate each image patch x_i with its best match in the dictionary by searching over the N_p = h_p × w_p (with h_p = H−h+1, w_p = W −w+1) distinct sub-patches of size h × w fully contained in each mini-epitome. Typical sizes we employ are 8 × 8 for patches and 16 × 16 for mini-epitomes, implying that each mini-epitome can generate N_p = 9 · 9 = 81 patches of size 8 × 8. Our focus is on representing every image with a common vocabulary of visual words, so we use a single universal epitomic dictionary for analyzing image patches from any image. We have been working with datasets consisting of overlapping patches extracted from thousands of images and with dictionaries containing from K = 32 up to 2048 mini-epitomes.

Figure 1.

In the epitomic representation each image patch moves to find its best match within a mini-epitome. Search is over epitome positions instead of image positions (standard max-pooling).

We model the appearance of image patches using a Gaussian mixture model (GMM).We employ a generative model in which we activate one of the image epitomes μ_k with probability P(l_i = k) = π_k, then crop an h × w sub-patch from it by selecting the position p_i = (x_i, y_i) of its top-left corner uniformly at random from any of the N_p valid positions. We assume that an image patch x_i is then conditionally generated from a multivariate Gaussian distribution

$$P({\mathbf{x}}_i|{\mathbf{z}}_i,\mathit{\theta })=𝒩({\mathbf{x}}_i;{\alpha }_i{\mathbf{T}}_{p_i}{\mathit{\mu }}_{l_i}+{\beta }_i\mathbf{1},c_i^2{\mathbf{\Sigma }}_0).$$ (1)

The label/position latent variable vector z_i = (l_i, x_i, y_i) controls the Gaussian mean via ν_zi = T_piμ_li. Here T_pi is a d × D projection matrix of zeros and ones which crops the sub-patch at position p_i = (x_i, y_i) of a mini-epitome. The scalars α_i and β_i determine an affine mapping on the appearance vector and account for some photometric variability, 1 is the all-ones d × 1 vector, and x̄ is the patch mean value. In the experiments reported in this paper we choose π_k = 1/K and fix the d × d covariance matrix ${\mathbf{\Sigma }}_0^{-1}={\mathbf{D}}^T\mathbf{D}+\epsilon \mathbf{I}$, where D is the gradient operator computing the x− and y− derivatives of the h × w patch and ε is a small constant. This implies that we compute distances between patches by a Mahalanobis metric which corresponds to whitening the vectorized image patches by left-multiplying them with D. Importantly, we assume that Σ₀ is modulated by the patch gradient contrast $c_i^2\triangleq {\Vert \mathbf{D}({\mathbf{x}}_i-{\overline{x}}_i\mathbf{1})\Vert }_2^2+\lambda$ but is shared across all dictionary elements and thus does not depend on the latent variable vector; λ is a small regularization constant (we use λ = d for image values between 0 and 255). We present algorithms for learning the epitomic means ${\{{\mathit{\mu }}_k\}}_{k=1}^K$ in Sec. 3.4.

3.2. Epitomic patch matching

To match a patch x_i to the dictionary, we seek the mini-epitome label and position z_i = (l_i, x_i, y_i), as well as the photometric correction parameters (α_i, β_i) that maximize the probability in Eq. (1), or equivalently minimize the squared reconstruction error (note that D1 = 0)

$$R^2({\mathbf{x}}_i;k,p)=\frac{1}{c_i^2}({\Vert \mathbf{D}({\mathbf{x}}_i-{\alpha }_i{\mathbf{T}}_p{\mathit{\mu }}_k)\Vert }^2+\lambda {(|{\alpha }_i|-1)}^2),$$ (2)

where the last regularization term discourages matches between patches and mini-epitomes whose contrast widely differs. We can compute in closed form for each candidate match ν_zi = T_piμ_li in the dictionary the optimal β̂_i = x̄_i − α̂_iν̄_zi and ${\hat{\alpha }}_i=\frac{{\tilde{\mathbf{x}}}_i^T{\tilde{\mathit{\nu }}}_{{\mathbf{z}}_i}\pm \lambda }{{\tilde{\mathit{\nu }}}_{{\mathbf{z}}_i}^T{\tilde{\mathit{\nu }}}_{{\mathbf{z}}_i}+\lambda }$, where x̃_i = Dx_i and ν̃_zi = Dν_zi are the whitened patches. The sign in the nominator is positive if ${\tilde{\mathbf{x}}}_i^T{\tilde{\mathit{\nu }}}_{{\mathbf{z}}_i}\ge 0$ and negative otherwise. Having computed the best photometric correction parameters, we can substitute back in Eq. (2) and evaluate the reconstruction error R²(x_i; k, p).

Epitomic matching versus max-pooling

Searching for the best match in the epitome resembles the max-pooling process in convolutional neural networks [14]. However in these two models the roles of dictionary elements and image patches are reversed: In epitomic matching, each image patch is assigned to one dictionary element. On the other hand, in max-pooling each dictionary element (filter in the terminology of [14]) looks for its best matching patch within a search window. Max-pooling thus typically assigns some image patches to multiple filters while other patches may remain orphan. This subtle but crucial difference makes it difficult for max-pooling to be used as a basis for building whole image probabilistic models, as the probability of orphan image areas is not well defined. Contrary to that, mini-epitomes naturally lend themselves as building blocks for probabilistic image models able to explain and generate the whole image area.

3.3. Efficient epitomic search algorithms

We search over all mini-epitomes and positions in them to select the mini-epitome label and position pair (k, p) which achieves the least reconstruction error. The most expensive part of this matching process is computing the inner product of every patch in an image with all h × w sub-patches in every mini-epitome in the dictionary.

Exact search

The complexity of the straightforward algorithm for matching N image patches to a dictionary with K mini-epitomes is 𝒪 (N · K·h_p · w_p · h·w). For the patch and epitome sizes we explore in our experiments, it takes more than 10 sec to exactly match a 400 × 500 grayscale image with an optimized Matlab CPU implementation. Our optimized GPU software has drastically reduced this computation time: for a dictionary with K=256 mini-epitomes, epitomic matching takes 0.7 sec on a laptop’s NVIDIA GTX 650M graphics unit and 0.1 sec on a workstation’s NVIDIA Tesla K20. The starting point of our implementation has been the fast CUDA convolution library cuda-convnet [16] but we are able to achieve epitome-specific improvements by exploiting the fact that patches within a mini-epitome share filter values, which allows us to make better use of the GPU’s fast shared memory. As a result, matching with a 16 × 16/8 × 8 epitomic dictionary is only about 5 times more expensive than matching with a non-epitomic 8 × 8 dictionary, although the epitomic dictionary contains 81 times more patches. We have also tested the recursive algorithm of [21] and FFT techniques [13], but they have proven less efficient than our GPU code for the range of epitome and patch sizes we have experimented with.

Approximate search

We have also investigated the use of approximate nearest neighbor (ANN) methods for epitomic patch matching. Contrary to exact search methods, ANN search time typically grows sub-linearly with the dictionary size, and is thus better scalable to extremely large dictionary sizes. The approach we have followed is to extract all patches from each mini-epitome along with their negated pairs, whiten, and then normalize them to be unit-norm vectors, resulting in an inflated epitomic dictionary with K · N_p · 2 elements. After similarly whitening and normalizing the input image patches, we search for their best match with standard off-the-shelf kd-tree and hierarchical k-means algorithms as implemented in the FLANN library [20]. When using kd-trees, we have found it crucial to apply a rotation transformation based on the fast 2-D discrete cosine transform (DCT), instead of searching directly for the best match in the image gradient domain. We provide more details about this important technical point in the supplementary material. We also present experiments there which show that the performance loss due to ANN is negligible, for moderate search times comparable to those of SIFT-based VQ encoding algorithms.

3.4. Epitomic dictionary learning

Parameter refinement by Expectation-Maximization

Given a large training set of unlabeled image patches ${\{{\mathbf{x}}_i\}}_{i=1}^N$, our goal is to learn the maximum likelihood model parameters $\mathit{\theta }={\{{\mathit{\mu }}_k\}}_{k=1}^K$) for the epitomic GMM model in Eq. (1). We employ the EM algorithm [8] and maximize the expected complete log-likelihood

$$L(\mathit{\theta })=\sum _{i=1}^N\sum _{k=1}^K\sum _{p\in \wp }{\gamma }_i(k,p)·\text{log}({\pi }_k𝒩({\mathbf{x}}_i;{\alpha }_i{\mathbf{T}}_p{\mathit{\mu }}_k+{\beta }_i\mathbf{1},c_i^2{\mathbf{\Sigma }}_0)),$$ (3)

where ℘ is the set of valid positions in the epitome. In the E-step, we compute the assignment of each patch to the dictionary, given the current model parameter values. We use the hard assignment version of EM and set γ_i(k, p) = 1 if the i-th patch best matches in the p-th position in the k-th mini-epitome and 0 otherwise. In the M-step, we update each of the K mini-epitomes μ_k by

$$(\sum _{i,p}{\gamma }_i(k,p)\frac{{\alpha }_i^2}{c_i^2}{\mathbf{T}}_p^T{\mathbf{\Sigma }}_0^{-1}{\mathbf{T}}_p){\mathit{\mu }}_k=\sum _{i,p}{\gamma }_i(k,p)\frac{{\alpha }_i}{c_i^2}{\mathbf{T}}_p^T{\mathbf{\Sigma }}_0^{-1}({\mathbf{x}}_i-{\beta }_i\mathbf{1}).$$ (4)

In all reported experiments we run EM for 10 iterations.

In all reported experiments we run EM for 10 iterations. Diverse dictionary initialization with epitomic K-means++

Careful parameter initialization helps EM converge faster and reach a good local optimum solution. The K-means++ algorithm [3] selects a diverse subset of training data instances as initialization to dictionary learning. It randomly picks the first one and then incrementally grows the dictionary by selecting subsequent elements with probability proportional to their squared distance to the elements already in the dictionary. We adapt the standard K-means++ algorithm to our epitomic setup and select a H × W training image patch as a new mini-epitome with probability proportional to the sum of R²(x_i; k, p) in a neighborhood of size h_p × w_p around the i-th patch. This corresponds to spatially smoothing the squared reconstruction error R²(x_i; k, p) by a h_p × w_p box filter.

Learned epitomic dictionary

We show in Fig. 2 the epitomic dictionary with K = 256 mini-epitomes we learned with the proposed algorithm on the full VOC 2007 training set. We juxtapose it with the corresponding non-epitomic dictionary with K = 1024 members we learned with the same algorithm, simply setting H = W = h = w = 8. We have chosen the non-epitomic dictionary to have 4 times as many members so as both dictionaries occupy the same area (note that 16²/8² = 4) and thus be commensurate in the sense that they have equal number of parameters.

Figure 2.

Patch dictionaries learned on the full VOC 2007 training set, ordered column-wise from top-left by their relative frequency.

As expected, the non-epitomic dictionary looks very similar to the K-means patch dictionaries reported in [7]. Our epitomic dictionary looks qualitatively different: It is more diverse and contains a rich set of visual patterns, including sharp edges, lines, corners, junctions, and sinewaves. It has less spatial redundancy than its non-epitomic counterpart, which needs to encode shifted versions of the same pattern as distinct codewords.

3.5. Reconstructing patches and images

Beyond qualitative comparisons, we have tried to systematically evaluate the generative expressive power of our epitomic dictionary compared to the non-epitomic baseline.

For this purpose, having trained the two dictionaries on the PASCAL VOC 2007 train set, we have quantified how accurately they perform in reconstructing the images in the full VOC 2007 test set. From each test image, we extract its 8 × 8 overlapping patches (with stride 2 pixels in each direction) that form the set of ground truth patches ${\{{\mathbf{x}}_i\}}_{i=1}^N$. For each patch x_i we compute its closest match x̂_i = (α_iT_pμ_k + β_i1) in each of the two dictionaries by finding the parameters (α_i, β_i) and (k, p) that minimize the squared reconstruction R²(x_i; k, p) in Eq. (2) – note that p = (0, 0) in the non-epitomic case.

We quantify how close x_i and x̂_i are in terms of normalized cross-correlation in both the raw intensity and gradient domains, $\mathrm{N}\mathrm{C}\mathrm{C}(i)=\frac{{({\mathbf{x}}_i-{\overline{x}}_i)}^T({\hat{\mathbf{x}}}_i-{\overline{x}}_i)+\lambda }{\Vert {\mathbf{x}}_i-{\overline{x}}_i\Vert \lambda \Vert {\hat{\mathbf{x}}}_i-{\overline{x}}_i\Vert \lambda }$ and $\mathrm{N}\mathrm{C}{\mathrm{C}}_D(i)=\frac{{({\mathbf{x}}_i-{\overline{x}}_i)}^T{\mathbf{D}}^T\mathbf{D}({\hat{\mathbf{x}}}_i-{\overline{x}}_i)+\lambda }{{\Vert \mathbf{D}({\mathbf{x}}_i-{\overline{x}}_i)\Vert }_{\lambda }{\Vert \mathbf{D}({\hat{\mathbf{x}}}_i-{\overline{x}}_i)\Vert }_{\lambda }}$ respectively, where ‖x‖_λ ≜ (x^T x + λ)^1/2. Note that NCC takes values between 0 (poor match) and 1 (perfect match).

We can also reconstruct the original full-sized images by placing the reconstructed patches x̂_i in their corresponding image positions and averaging at each pixel the values of all overlapping patches that contain it. We quantify the full image reconstruction quality in terms of PSNR. We show an example of such an image reconstruction in Fig. 3(a,b). Note that reconstructing an image from its SIFT descriptor [28] is far less accurate and less straightforward than using a generative image model such as the proposed one.

Figure 3.

(a,b) Image reconstruction example with the K = 512 epitomic dictionary. (c) Image reconstruction on VOC 2007 test set: K = 512 epitomic vs. K = 2048 non-epitomic dictionaries.

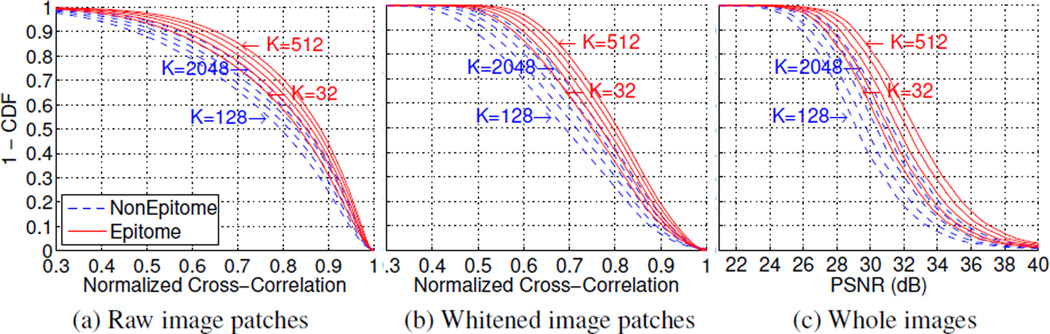
To evaluate the reconstruction ability of each dictionary, we plot in Fig. 4 the empirical complementary cumulative distribution function (CCDF=1-CDF, where CDF is the cumulative distribution function) for the selected metrics. If p = CCDF (υ), then p × 100% of the samples in the dataset have values at least equal to υ (higher CCDF curves are better). The plots summarize VOC 2007 test set statistics of: (a/b) the NCC/ NCC_D for all N ≈ 5 × 10⁷ patches and (c) the PSNR for all 4952 images.

Figure 4.

Image reconstruction evaluation on the full VOC 2007 test set with our epitomic patch dictionary vs. a non-epitomic dictionary for various dictionary sizes K (powers of 2). (a,b): Normalized cross-correlation of raw (NCC) and whitened (NCC_D) image patches. (c): PSNR of reconstructed whole images. Plots depict 1-CDF (higher is better).

There are several observations we can make by inspecting Fig. 4. First, for either dictionary type, whenever we double the dictionary size K, the CCDF curves shift to the right/up by a rouphly constant step. For example, we can read from Fig. 4(a) that the K = 32 epitomic dictionary already suffices to explain 58% of the image patches with NCC ≥ 0.8. Each time we double K we explain 3% more image patches at this level, with the K = 512 epitomic dictionary being able to reconstruct 70% of the image patches at NCC ≥ 0.8. In comparison, the K = 2048 non-epitomic baseline can only reconstruct 62% of the image patches at the same accuracy level.

Second, comparing the performance of the two dictionary types, we observe that our epitomic model significantly improves over the non-epitomic baseline in terms of reconstruction accuracy. For example, we can see that the K = 64 epitomic dictionary is roughly as accurate as the K = 2048 non-epitomic dictionary which has 32 times more elements (the same holds for the K = 32/1024 dictionaries). Accounting for the fact that each 16 × 16 mini-epitome occupies 4 times larger area than each cluster center of the 8 × 8 non-epitomic dictionary, implies that the epitomic dictionary is 32/4 = 8 times more compact (in terms of number of model parameters) than the non-epitomic baseline. We further show in Fig. 3(c) that the epitomic dictionary consistently performs better (except for 1 out of the 4952 test images) in terms of image reconstruction PSNR (1.34 dB on average).

4. Image Classification with Mini-Epitomes

4.1. Image classification tasks

Here we show how the proposed dictionary of mini-epitomes can be used in image classification tasks. We focus our evaluation on the challenging PASCAL VOC 2007 image classification benchmark [11].

We extract histogram-type features from both epitomic and non-epitomic patch representations which we feed to 1-vs-all SVM classifiers. We use χ² kernels approximated by explicit feature maps [27] and also employ spatial pyramid matching [17]. Our implementation closely follows the publicly available setup of [6], which presents a systematic evaluation and tuned implementation of SIFT features coupled with state-of-the-art encoding techniques.

4.2. Image description with mini-epitomes

Here we focus on extracting histogram type descriptors treating our epitomic dictionary as a bag of visual words. From each image, we densely extract h × w overlapping patches ${\{{\mathbf{x}}_i\}}_{i=1}^N$ (with stride 2 pixels in each direction). Matching each patch x_i to the epitomic dictionary yields its closest h × w patch in the epitomic dictionary, encoded by the epitomic label l_i ∈ 1 : K and the position p_i = (x_i, y_i), with x_i = 0 : w_p − 1 and y_i = 0 : h_p − 1. We use hard assignments (VQ) in all reported results.

In this setting, the most straightforward way to summarize the content of an image is to build a histogram with K bins, each counting how many times the specific epitome has been activated. This “Epitome-Pos-1×1” descriptor is very compact but completely discards the exact position of the match within the epitome.

Our epitomic dictionary allows us to also encode the position information p_i into the descriptor. While some of the H × W mini-epitomes in our learned dictionary (see Fig. 2) are homogeneous, others contain h × w patches with visually diverse appearance. We can encode the exact position p_i of the match in the epitome by a product histogram with K · N_p bins, where N_p = h_p × w_p. However this yields a rather large descriptor (note that N_p = 81 in our setting) which is very sensitive to the exact position. We opt instead to encode the epitome position p_i more coarsely. Specifically, we summarize the match positions in a t × t spatial grid of bins yielding an “Epitome-Pos-t × t” descriptor with total length K · t · t. For example, in the Epitome-16/8-Pos-4×4 descriptor the epitomic position bins have size 3 × 3 pixels and stride 2 pixels in each direction. The (b_x, b_y) bin (b_x, b_y = 0 : 3) gets a vote for each matched patch whose position p_i = (x_i, y_i) satisfies 2b_x ≤ x_i < 2b_x + 3 and 2b_y ≤ y_i < 2b_y + 3.

In all experiments we also encode the sign of the match, putting matches with positive and negative α_i’s in different bins, which we have found to considerably improve performance at the cost of doubling the descriptor size.

4.3. Classification results

For all the results involving the epitomic as well as the non-epitomic patch models, we have learned dictionaries of various sizes on the full VOC 2007 train set. We summarize our results in Table 1 and illustrate them with plots in Fig. 5.

Table 1.

Image classification results (mAP) of our epitomic dictionary on the Pascal VOC 2007 dataset.

Epitome /Patch	Position Encod.	Dictionary Size K
		32	64	128	256	512	1024	2048
16/8	1×1	40.66	45.22	48.07	49.00	51.98	53.54	54.37
	2×2	47.11	49.89	51.59	52.89	54.50	56.12	56.16
	4×4	49.59	51.98	53.10	54.75	55.62	56.45	56.18
	9×9	52.03	53.53	54.03	54.07	-	-	-
12/8	1×1	41.01	44.94	47.24	49.56	51.76	53.48	55.33
	2×2	46.20	47.89	50.19	51.91	53.64	55.17	56.47
10/8	1×1	41.12	44.07	46.85	49.33	51.28	53.01	54.87
	2×2	44.10	46.32	48.71	50.98	52.85	54.52	55.71
	2×2/4	44.46	46.73	48.37	51.03	52.31	54.33	55.08
12/6	1×1	40.69	43.83	46.55	49.73	51.05	52.37	54.24
	2×2	46.80	48.72	50.96	52.70	53.91	54.80	55.40
	3×3	48.43	50.40	52.17	53.45	55.16	55.11	55.47
8/8	1×1	38.02	40.92	44.54	46.75	48.84	51.13	52.73
6/6	1×1	38.17	41.89	45.01	47.35	48.88	51.15	52.85

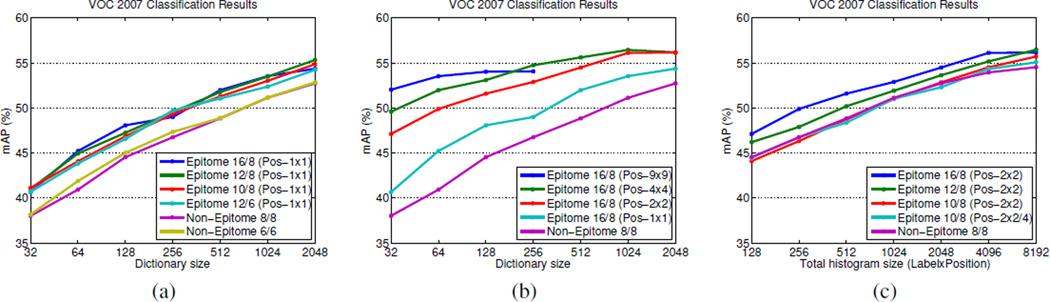
Figure 5.

(a) Performance of the epitomic dictionary model (without epitome position encoding) and the non-epitomic baseline for different epitome/patch sizes, as a function of dictionary size K. (b) Effect of encoding the epitome position at different detail levels. (c) Comparison of the epitomic model (with or without position encoding) and the non-epitomic baseline, for the same total histogram length.

We first explore in Fig. 5(a) how epitome and patch sizes as well as dictionary sizes affect the performance of the epitomic model. We find that the performance of the epitomic model is not too sensitive to the exact setting of the epitome/patch size. Similarly to the findings of [7], we observe that the performance of all descriptors increases when we use dictionaries with more elements.

In Fig. 5(b) we show that position encoding considerably improves the recognition performance of the epitomic dictionary, with the coarse 2 × 2 scheme exhibiting an excellent trade-off between performance and descriptor size.

We can evaluate the proposed epitomic model relative to the non-epitomic baseline along multiple axes. First, as we can see in Figs. 5(a,b), the epitomic dictionary performs much better than the non-epitomic baseline for fixed dictionary size K. Second, we can see in Fig. 5(c) that epitomes have an edge over non-epitomes for fixed histogram descriptor length K · t · t. Note that descriptor length directly affects the classifier training and evaluation time, as well as the number of labeled data required for training. Third, epitomes perform better than non-epitomes when the two models have the same number of parameters, e.g., the K = 512 Epitome-16/8-Pos-2×2 dictionary achieves 54.50 mAP vs. 52.73 mAP of the comparable K = 2048 Non-Epitome-8/8. Fourth, we compare epitomes and non-epitomes that require the same number of reconstruction error computations for matching with the exact search algorithm (note however that Sec. 3.3 presents more efficient matching algorithms for epitomes). For this purpose, we run an experiment with the K element Epitome-10/8-Pos-2×2 dictionary and only searching at 4 candidate positions (x_i, y_i) ∈ {0, 2}² in each mini-epitome (2×2/4 entry in Table 1 and Fig. 5(c)). This performs very similarly to the comparable 4 · K element Non-Epitome-8/8 dictionary.

Overall, classification performance of both models is strongly correlated with the total number of patches contained in the dictionary, yet the epitomic representation offers distinct advantages over the non-epitomic baseline: It generates a given number of patches with much fewer model parameters, it controls the descriptor length by adjusting the coarseness of epitome position encoding, and is amenable to fast search.

Comparing with the performance of VQ descriptors based on SIFT, see Table 2, the most impressive finding is that epitomic descriptors built on dictionaries with as few as K = 256 or 512 mini-epitomes yield performance around 55% mAP, which takes SIFT dictionaries of size 10K to achieve. Our best result at 56.47% mAP with 2048 mini-epitomes even slightly outperforms the best SIFT VQ result reported in [6], attained with a dictionary of 25K visual words. This result is also comparable to KCB and LLC-based methods for encoding SIFT but still lags behind the state-of-the-art Fisher Vector descriptor whose performance is about 61% mAP [6, 25].

Table 2.

Image classification results (mAP) of top-performing SIFT-based methods on the Pascal VOC 2007 dataset [6].

Method	mAP	Method	mAP	Method	mAP
VQ-4K	53.42	KCB-4K	54.60	LLC-4K	53.79
VQ-10K	54.98	KCB-25K	56.26	LLC-10K	56.01
VQ-25K	56.07	FV-256	61.69	LLC-25K	57.60

Epitomic footprint encoding

We have also explored an epitomic footprint encoding, which is related to the mean-vector Fisher Vector encoding in [25]. The main idea is to encode the difference between the appearance content of a specific image compared to the generic epitome, which captures how much the epitome needs to adapt to best approximate a novel image. An appealling property of the epitomic footprint descriptor is that it can be visualized or stored as a small image and at the same time be used directly as feature vector in a linear SVM image classifier, yielding performance around 52% mAP in our experiments. Please see Fig.6 for a visualization and the supplementary material for further details and examples.

Figure 6.

Epitomic footprint descriptor.

5. Discussion and Future Work

We have shown that explicitly accounting for illumination and position variability can significantly improve both reconstruction and classification performance of a patch-based image dictionary. Moreover, we have demonstrated that the proposed epitomic model can perform similarly to SIFT in image classification, implying that generative patch image models can be competitive with discriminative descriptors when properly accounting for nuisance factors.

In future work, we plan to extend the current system towards capturing visual attributes such as depth or color and modeling a richer set of spatial transformations, including scale and rotation. We also plan to build deep variants of our model, employing epitomes in hierarchical models.