Abstract
Semi-empirical quantum mechanical methods traditionally expand the electron density in a minimal, valence-only electron basis set. The minimal-basis approximation causes molecular polarization to be underestimated, and hence intermolecular interaction energies are also underestimated, especially for intermolecular interactions involving charged species. In this work, the third-order self-consistent charge density functional tight-binding method (DFTB3) is augmented with an auxiliary response density using the chemical-potential equalization (CPE) method and an empirical dispersion correction (D3). The parameters in the CPE and D3 models are fitted to high-level CCSD(T) reference interaction energies for a broad range of chemical species, as well as dipole moments calculated at the DFT level; the impact of including polarizabilities of molecules in the parameterization is also considered. Parameters for the elements H, C, N, O, and S are presented. The Root Mean Square Deviation (RMSD) interaction energy is improved from 6.07 kcal/mol to 1.49 kcal/mol for interactions with one charged species, whereas the RMSD is improved from 5.60 kcal/mol to 1.73 for a set of 9 salt bridges, compared to uncorrected DFTB3. For large water clusters and complexes that are dominated by dispersion interactions, the already satisfactory performance of the DFTB3-D3 model is retained; polarizabilities of neutral molecules are also notably improved. Overall, the CPE extension of DFTB3-D3 provides a more balanced description of different types of non-covalent interactions than Neglect of Diatomic Differential Overlap type of semi-empirical methods (e.g., PM6-D3H4) and PBE-D3 with modest basis sets.
INTRODUCTION
Semi-empirical (SE) quantum mechanical (QM) methods have enabled QM to be used where ab initio methods are too computationally expensive. Conceptually, the SE methods are approximations to ab initio QM methods, but introduce parameters that must be fitted empirically based on either ab initio or experimental data. SE methods have been discussed and benchmarked thoroughly, as most recently reviewed in Refs. 1–5.
In the Neglect of Diatomic Differential Overlap/Modified Neglect of Diatomic Overlap (NDDO/MNDO)-based methods, the formalism is derived from Hartree-Fock theory, but with several approximations in both the matrix algebra and integral calculation.6,7 In the density functional tight-binding (DFTB) methods,8,9 the formalism is derived from a Taylor expansion of the DFT energy in terms of density fluctuation with respect to a reference, and the matrix elements are calculated from first-principles density functional theory (DFT).10,11 The basic DFTB method has recently been expanded to second- and third-order monopole charge expansions of the density fluctuation, leading to DFTB2 (referred to also as SCC-DFTB), and DFTB3, respectively.12,13
Both the NDDO/MNDO and DFTB methods discard three- and four-center electron-repulsion integrals, and hence the computational bottleneck of these methods lies in solving a set of secular equations. Traditionally the methods employ minimal, valence electron-only basis sets to keep the computational cost at a minimum. One downside to the use of a minimal basis set is that intermolecular polarization is underestimated by about 25%, which leads to poor accuracy for the description of intermolecular forces, especially for polar interactions, such as hydrogen bonds and interactions to ionic groups.14 Furthermore, the minimal basis also limits the accuracy of computed Pauli-repulsion within the current DFTB framework.13
This well-known problem has recently led to a plethora of hydrogen-bond corrections to be added as post-SCF terms to the electronic energy calculated by the SE methods. Within the last decade, the H, H2, H2X, H+ H4, and H4X hydrogen bond corrections have been published.1,15–20 While such mechanical post-SCF corrections greatly increase the accuracy of SE methods, they do not directly address the fundamental problem at the QM level, as they do not alter the electron density at all. Therefore, the transferability of these corrections is likely limited (see discussions below).
Several improvements for the DFTB3 method are currently under development. In the context of non-covalent interactions, these involve extending the monopole expansion to include dipoles and quadrupoles in the density fluctuation,21 as well as improvements of the description of Pauli repulsion. This work addresses the low accuracy of DFTB3 for intermolecular interactions that implicate highly polarizable moieties, while keeping the increase in computational cost at a minimum. Such effort is important for the enhancement of not only the accuracy of DFTB3 but also its transferability to the analysis of chemical events in different environments.22,23
It has previously been proposed to lift the rudimentary restriction of minimal, valence-only basis sets in several NDDO/MNDO-based SE methods. For instance, the minimal-basis SINDO1 method24 was augmented with p-function on hydrogen atoms, which greatly improved the accuracy of dimerization energies and hydrogen bonding geometries.25 Likewise, the MNDO/d and PM6 methods26,27 add d-functions to several main-group and transition metals, for more accurate descriptions of these elements. More recently, the Polarized Molecular Orbital (PMO) and PMO2 methods28–30 were developed with a focus on molecular polarizabilities. As observed for the SINDO1 method, the PMO polarization functions on hydrogen atoms increase the accuracy of predicted hydrogen bonding geometries,29 and additionally reduce the PMO2 error in predicted molecular polarizabilities by about 80%.30 Similar to the NDDO/MNDO based SE methods, the tight-binding based DFTB2 method has also been previously augmented with p-orbitals on hydrogen with similar improvements in energetics and geometries.31,32
For biological molecules, the addition of polarization functions to hydrogen atoms would increase the size of the DFTB Hamiltonian and overlap matrices by about a factor of two. Since the diagonalization step formally scales as , the valence polarized method would be eight times slower, which is not desirable for simulation studies.
An alternative approach to increasing the size of the basis set was explored in the self-consistent polarizing (SCP)-NDDO, where an NDDO density matrix is augmented by an additional, SCP multipole density matrix.33,34 A related approach is the chemical-potential equalization (CPE) method, in which the density is augmented by an additional, polarizable response density.35–37 The CPE approach has previously been combined with the MNDO/d method37,38 and, more recently, the DFTB239 and DFTB3 methods.40 In both cases, the addition of the CPE response density increased the accuracy of molecular dipoles and polarizabilities, but the effect on intermolecular binding has not been addressed.
In the present work, we discuss the implementation of the CPE method in the framework of DFTB3, leading to a combined model we refer to as DFTB3/CPE. The new, additional parameters are obtained by fitting DFTB3/CPE calculated data to reference values obtained from high-level QM data. We note that DFTB is in itself unable to describe dispersion due to the use of Perdew-Burke-Ernzerhof (PBE) as the functional. Thus, we also derive the relevant parameters for DFTB3/CPE using the empirical two- and three-body dispersion interaction corrections due to Grimme.41
THEORY
Third-order SCC-DFTB (DFTB3)
The third-order SCC-DFTB (DFTB3) method is thoroughly discussed elsewhere, here we introduce the necessary equations to help present the combined implementation of DFTB3 and CPE (DFTB3/CPE) and its variants. In DFTB3, the total energy is given as13
| (1) |
The matrix elements are calculated numerically using the PBE functional and tabulated in the Slater-Koster files. Expressions for the second-order kernel, γab, and its charge derivative, Γab, are derived in previous work,12,13 and the pair-wise repulsive potentials are fitted empirically and tabulated in the form of splines.42,43
The LCAO-MO orbital coefficients, Cμi and Cνi, and the partial Mulliken charges, Δqa and Δqb, are obtained by solving the secular Kohn-Sham equations
| (2) |
where Sμν is the overlap matrix.
The Mulliken charges in turn enter the Hamiltonian matrix elements,
| (3) |
and Eq. (2) must be iteratively solved until self-consistency is reached.
Chemical-potential equalization
In the chemical-potential equalization method,36 the electron density is augmented with a (additional) polarization response density, δρcpe, described by a set of atom-centered basis functions
| (4) |
The response basis functions are taken to be p-type Gaussian functions of the following form:
| (5) |
where the atom is centered at Ri, and k, and Ki are the x-, y-, or z-components of r and Ri, respectively; ζi is a basis-set exponent. As suggested by Giese and York,37 the ζ-exponent takes into account fluctuations in the partial charge, via an exponential factor, i.e.,
| (6) |
The parameters Zi and Bi are element-specific parameters, the value of which must be calculated or fitted from empirical or ab initio data.
In this work, the CPE basis functions interact by means of a simple kernel36 in the form of a Coulomb integral
| (7) |
The interaction between the DFTB3 basis and the CPE basis is likewise described by an approximate Coulomb integral
| (8) |
where is a function in the DFTB3 atomic-orbital Slater monopole auxiliary basis set, and screening function f(Rij) is applied to the DFTB3-CPE interaction term as an empirical term to account for the missing kinetic energy component and also dampens the short-range interaction with the DFTB3 density which seems well-described already,37,40
| (9) |
where
| (10) |
and Ru = Ri,u + Rj,u and Rl = Ri,l + Rj,l. The parameters Ri,u and Ri,l are empirical parameters that relate to atom i. These parameters are fitted element-wise. This approach has previously been used successfully to improve the description of molecular dipole moments and polarizabilities in DFTB2+CPE39 and DFTB3+CPE frameworks.40
The correction to the total energy in the combined DFTB3 and CPE model (DFTB3/CPE) is then
| (11) |
where
| (12) |
The variational implicit dependence of the response density coefficients, c, which must be added to the DFTB3 Hamiltonian matrix (Eq. (3)) is (derived in the supplementary material68):
| (13) |
where
| (14) |
The set of coefficients of the CPE response density basis that variationally minimizes the total DFTB3/CPE energy in Eq. (11) is given by
| (15) |
These are re-calculated in each SCF cycle. In practice, 2-3 cycles are sufficient to converge the response density coefficients, whereas the DFTB3 method typically requires around 10-20 SCF cycles to converge the Mulliken charges. If the CPE basis set exponents depend on the Mulliken charges, the inversion of N must be performed each cycle. If the CPE model is assumed to be independent of the Mulliken charges, i.e., by setting B = 0 in Eq. (6), the inversion is only performed once. This inversion is fortunately much cheaper than solving the Kohn-Sham equations, and the resulting overhead is about 5% for a charge-independent CPE model and up to 30% for the charge-dependent model.40
The DFTB3/CPE gradient contribution is derived in the supplementary material,68 and the relevant equations necessary to calculate molecular dipole moments and polarizabilities in DFTB3 and DFTB3/CPE are also derived in the supplementary material.68
D3 dispersion correction
To avoid fitting the parameters of the CPE model such that the response density is implicitly compensating for the missing dispersion in the DFTB3 Hamiltonian, we augment DFTB3 energy with the two-body D3 dispersion due to Grimme41,44 and three-body Axilrod-Teller-Muto dispersion correction also due to Grimme.41 The two-body D3 term is given by
| (16) |
where rab is the interatomic distance and f(rab) is the Becke-Johnson damping function,44
| (17) |
In this scheme, all parameters besides s8, a1, and a2 are determined from first principles. A value of s6 = 1.0 is used as suggested by Grimme.41
Furthermore, we include the Axilrod-Teller-Muto three-body dispersion term given by
| (18) |
where θa, θb, and θc are the angles formed by the triangle formed by the atoms a, b, and c, and rab, rbc, and rca are the corresponding interatomic distances, and finally C9,abc is a constant calculated from first principles. fd,3(rabc) is a damping function described in Ref. 41.
The total energy of the dispersion corrected DFTB3/CPE-D3 model is then
| (19) |
Optimization of parameters
We employ an optimization approach based on Bayesian inference to find the most likely set of parameters given the data available in our training set. Since the chemical nature of the data sets is diverse and the reference interaction energies span two orders of magnitude, we also apply different weights to the restraints in our optimization. Rather than hand-picking these weights, we optimize them on-the-fly during the parameterization by including these in our probability function.
Cost function
The probability of a set of unknown parameters {Pj} and the unknown relative weights {σi} of the reference data sets, given the set of input reference data sets {Di} is given from Bayes’ theorem by the following relation:
| (20) |
Here, j is the index of each parameter in the model and i is the index of each data set available. The probability of observing a particular set of reference data given a set of parameters and a set of weights is given as
| (21) |
where χ2 is the chi-squared agreement between the reference data and the corresponding data, calculated using a particular set of parameters. This assumes that the error in the reference and model data follows a Gaussian distribution. According to the principle of maximum entropy, this is the least biasing choice.45 Since all that is known about the parameters and weights is that they are positive numbers, these are described using Jeffery’s prior as the least biasing uninformative prior, in this case,46
| (22) |
Maximizing the probability in Eq. (20) is in practice carried out by minimizing the following equivalent cost function:
| (23) |
| (24) |
where β is an artificial simulation temperature factor.
Likely parameter sets are generated by running a Monte Carlo Metropolis-Hastings47 simulation at β = 0.25 for 10 000 to 25 000 steps. From this simulation, a number of parameter sets with high likelihood are picked and a greedy optimization is performed on these, until the cost function has converged into a minimum.
Akaike information criterion (AIC)
The CPE model introduces a considerable number of free parameters (see Table I) that are fitted to a relatively limited set of data. The validity of adding each parameter is evaluated using the Akaike information criterion48 which is a measure of the relative Kullback-Leibler distance between a collection of models and a possible “true” model.
TABLE I.
Parameters with the highest likelihood for the DFTB3/CPE-D3 models parameterized from interaction energies. Models marked with (pol) are parametrized using additional polarization data for a set of 87 neutral molecules.
| Method (au) | DFTB3 | DFTB3i-D3a | DFTB3/CPE(U)-D3*b,c | DFTB3/CPE(U)-D3c | DFTB3/CPE(ζ)-D3 | DFTB3/CPE(q)-D3 | DFTB3/CPE(ζ)-D3 (pol) | DFTB3/CPE(q)-D3 (pol) |
|---|---|---|---|---|---|---|---|---|
| a1 | 0.5719 | 0.5719 | 0.1227 | 0.3772 | 0.3942 | 0.3863 | 0.3045 | |
| a2 | 3.6017 | 3.6017 | 5.2156 | 4.3174 | 3.7047 | 3.5912 | 0.0000 | |
| s8 | 0.5883 | 0.5883 | 0.0166 | 0.0179 | 0.0139 | 0.0128 | 4.1738 | |
| H Z | 1.8557 | 2.1040 | 1.3356 | 2.2551 | 2.3933 | 2.8005 | ||
| H B | 0.0000 | 0.0000 | 0.0000 | 0.8566 | 0.0000 | 0.4084 | ||
| H rl | 0.0624 | 0.1398 | 0.1315 | 0.3796 | 0.1449 | 0.4029 | ||
| H ru | 5.1978 | 4.5281 | 5.3714 | 0.3796 | 2.2003 | 0.4030 | ||
| C Z | 1.6133 | 1.8292 | 1.2331 | 1.4783 | 2.4025 | 1.9271 | ||
| C B | 0.0000 | 0.0000 | 0.0000 | 0.0048 | 0.0000 | 0.0111 | ||
| C rl | 2.2399 | 3.0349 | 2.1469 | 1.0862 | 0.4482 | 1.5431 | ||
| C ru | 6.9382 | 5.8196 | 6.5002 | 2.3530 | 1.6382 | 1.9163 | ||
| N Z | 2.1914 | 2.4847 | 5.3497 | 2.0292 | 28.867 | 2.1352 | ||
| N B | 0.0000 | 0.0000 | 0.0000 | 0.3238 | 0.0000 | 0.2542 | ||
| N rl | 6.2019 | 6.3024 | 5.8490 | 1.6511 | 6.0026 | 2.0131 | ||
| N ru | 6.2023 | 6.3027 | 5.8496 | 2.2921 | 6.0028 | 2.0321 | ||
| O Z | 1.9061 | 2.1612 | 53.419 | 4.3227 | 58.602 | 9.7552 | ||
| O B | 0.0000 | 0.0000 | 0.0000 | 0.0451 | 0.0000 | 0.0965 | ||
| O rl | 3.0359 | 3.0606 | 3.5507 | 3.4832 | 3.4609 | 3.4807 | ||
| O ru | 3.7043 | 3.6479 | 3.6175 | 3.6050 | 4.3822 | 3.5745 | ||
| S Z | 1.4545 | 1.6491 | 1.4068 | 3.2853 | 1.4895 | 2.9192 | ||
| S B | 0.0000 | 0.0000 | 0.0000 | 1.8661 | 0.0000 | 1.7258 | ||
| S rl | 3.0731 | 3.2127 | 3.1834 | 17.555 | 2.4655 | 16.577 | ||
| S ru | 3.0731 | 3.2127 | 3.1836 | 1884.98 | 2.4659 | 2752.47 | ||
| No. of parameters | 0 | 3 | 11 | 14 | 18 | 23 | 18 | 23 |
D3 parameters from Gerit et al.
The D3 parameters are not fitted for this model.
The values of Z for each element is set to the value of the Hubbard U times the globally fitted constant.
For the data presented in this paper, the AIC can be calculated as
| (25) |
where k is the number of parameters in the model, i is the index of each data set, Ni is the number of data points for the ith data set, and RMSDi is the Root Mean Square Deviation (RMSD) between the model calculated and reference data for the ith data set. See the supplementary material68 for a detailed derivation of this expression for the AIC.
In cases where k2 ≪ N () is not true—when the data are somewhat sparse compared to the number of fitting parameters—the AIC is slightly biased towards more parameters.49 In these cases, the corrected AIC (AICc) can be used to correct for finite-size effects, by adding a slightly heavier penalty on more parameters.50 The AIC and AICc are asymptotically equivalent for N → ∞, and also for k → 0. The AICc can be derived as an added correction to the AIC,
| (26) |
The Akaike weight (wi) is a measure of the relative likelihood for each model amongst a collection of candidate models.49 In the following, we use the AICc values to calculate the Akaike weights as
| (27) |
where ΔAICci = AICci − AICcmin, i.e., the difference between the AICc for a particular model minus the lowest AICc observed across all models.
COMPUTATIONAL METHODOLOGY
The dispersion correction models and the CPE model are added to the SCCDFTB module of CHARMM version 40a1.51 All DFTB3 and DFTB3/CPE calculations are carried out in CHARMM using the 3OB parameter set and the X-H correction.42,43 DFT calculations are carried out in Gaussian 09.52 CCSD(T) and MP2 calculations are carried out in MOLPRO 2012.1.17.53,54
Reference data sets
The data sets used to parameterize and test the DFTB3/CPE method are described here; among them, S22 is not used in the parameterization and serves as a test set for the final models, while all other datasets are included in the training set. We note that there is some overlap between S22 and S66 (5 complexes are found in both sets). All interaction energies are calculated at the CCSD(T) level of theory. If the counter poise approximation is used to compensate for basis set-superposition error, this is noted as (cp) in the following.
We note that an auxiliary basis of purely p-functions will likely only contribute very little to the anisotropic (i.e., out-of-plane) polarizability,40 as this would necessitate the use of higher order polarizing functions, such as d-functions, or a polarizing sp-basis. Therefore, only isotropic polarizabilities are included in the training data.
S22
The S22 data set consists of 22 small organic molecules with a mix of polarization and dispersion dominated interactions.55 We use the updated energies for the S22 data set given by Takatani et al. in Ref. 56. Energies are calculated at the CCSD(T)/CBS(cp)//MP2/cc-pVTZ level of theory.
S66
The S66 data set consists of 66 small organic molecules with a mix of polarization and dispersion dominated interactions.57 Energies are calculated at the CCSD(T)/CBS(cp)//MP2/cc-pVTZ level of theory.
Charged interactions (“C15”)
This dataset1 consists of 15 dimer complexes where one species is charged, and is thus dominated by strong polarization interactions. This dataset is referred to as the C15 dataset in this paper. Energies are calculated at the CCSD(T)/CBS(cp)//MP2/cc-pVTZ level of theory.
During parameter optimization, it was discovered that one complex in the C15 dataset, namely, the imidazolium-methylamine complex, had a discrepancy of 12 kcal/mol between the CCSD(T)/CBS and DFTB3 interaction energy. This complex is excluded from the fitting data and also from the statistics presented in the Results section, as the large error reflects an intrinsic limitation of the DFTB3 model for treating (nitrogen) lone-pairs rather than issues related to the limited polarizability (see additional discussions below).
Sulfur (“S14”)
This data set consists of 14 dimer complexes where one species contains a sulfur atom, and is very similar in nature to the S22, S66, and C15 datasets.58 This dataset is referred to as the S14 dataset in this work. Energies are calculated at the CCSD(T)/CBS(cp)//MP2/cc-pVTZ level of theory.
Ionic bonds (“I9”)
This dataset is created similar to the S22, S66, and C15 datasets, and consists of 9 salt-bridge dimer complexes, using combinations of guanidinium, imidazolium, and methyl ammonium as cations and methyl acetate, thiomethoxide, and methoxide as anions. Details about this dataset, including coordinates and interaction energies, are described in the supplementary material.68 This dataset is referred to as the I9 dataset in this paper. Energies are calculated at the CCSD(T)/CBS(cp)//MP2/cc-pVTZ level of theory.
Charged water clusters
This dataset consists of 9 water clusters, where each complex contains one hydronium and one to three water molecules. Details about this dataset, including coordinates and interaction energies, are described in the supplementary material.68 Energies are calculated at the CCSD(T)/CBS(cp)//MP2/cc-pVTZ level of theory.
Charged water dimers (“W2”)
This dataset consists of two dimer complexes: the hydronium-water complex and the hydroxide-water complex. Details about this dataset, including coordinates and interaction energies, are described in the supplementary material.68 This dataset is referred to as the W2 dataset in this paper. Energies are calculated at the CCSD(T)/CBS(cp)//MP2/cc-pVTZ level of theory.
Large water
This dataset consists of 15 water clusters, ranging from 6 to 17 water molecules.59 Interaction energies are calculated at the CCSD(T)/aug-cc-pVTZ//MP2/aug-cc-pVTZ level of theory.
L7
This dataset consists of 7 large organic complexes that are dominated by large dispersion forces.60 Interaction energies are calculated at the DLPNO-CCSD(T)/CBS(cp)//TPSS/TZVP level of theory, and are given in the supplementary material.68
Polarizabilities
The geometries for 133 molecules are taken from the QCRNA database,61 and dipole moments and isotropic molecular polarizabilities are re-calculated at the B3LYP/aug-cc-pVTZ level of theory.62 This data set is divided into 87 neutral molecules, 27 anions and 19 cations.
RESULTS
The optimization process outlined above results in four different models discussed below. They differ in the number of parameters.
-
•
DFTB3/CPE(U)-D3*: In this model, the values of the parameters in the D3 dispersion model are fixed to those found in Ref. 3. Additionally, the charge dependence of the CPE basis functions is set to B = 0 in Eq. (6). Furthermore, the value of Z is set to the Hubbard U,12 but scaled for all elements by single adjustable parameters.
-
•
DFTB3/CPE(U)-D3: This model additionally relaxes the parameters of the D3 dispersion model.
-
•
DFTB3/CPE(ζ)-D3: This model relaxes all parameters, except that the charge dependence of the CPE basis functions is ignored by setting B = 0 in Eq. (6). Two versions of this model are parametrized: one based on only interaction energies, and one additionally using isotropic polarizabilities for neutral molecules.
-
•
DFTB3/CPE(q)-D3: In this model, all parameters are optimized. Two versions of this model are parametrized: one based on only interaction energies, and one additionally using isotropic polarizabilities for neutral molecules.
The final parameters of the four models are summarized in Table I, and the final RMSD values of the fitting datasets and the S22 test set are presented in Table II, which also includes comparison to several other semi-empirical methods as well as PBE calculations. A graphic overview for the performance of several methods is presented on Fig. 1. We note that these parameters are rather different from those optimized in Ref. 40 based on polarizabilities. Indeed, parameters from Ref. 40 would lead to very poor intermolecular interaction energies for some systems (see Table II and discussion below).
TABLE II.
RMSD and mean error for 10 data sets using various methods. Reference energies are calculated at the CCSD(T)/CBS(cp)//MP2/cc-pVTZ(cp) level of theory, and polarizabilities using B3LYP/aug-cc-pVTZ. Values are given in kcal/mol for energies and bohrs3 for polarizabilities. Models marked with (pol) are parametrized using additional polarizability data for neutral molecules. The model marked (orig) uses the CPE parameter set of Kaminski et al.40 and the D3 parameters of Ref. 3.
| S22 | S66 | C15 | I9 | S14 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Method | RMSD | Mean | RMSD | Mean | RMSD | Mean | RMSD | Mean | RMSD | Mean |
| DFTB3 | 4.12 | 3.38 | 2.99 | 2.74 | 6.07 | 4.82 | 5.60 | 4.74 | 2.04 | 1.60 |
| DFTB3-D3 | 1.45 | 0.68 | 1.07 | 0.36 | 4.99 | 3.59 | 3.91 | 2.56 | 1.08 | 0.46 |
| DFTB3-D3H4 | 1.24 | 0.48 | 0.89 | 0.29 | 4.10 | 2.22 | 4.66 | 2.69 | 1.48 | 0.81 |
| DFTB3/CPE(U)-D3*a | 1.18 | 0.30 | 0.85 | 0.04 | 2.27 | 1.27 | 3.02 | 1.44 | 1.00 | 0.17 |
| DFTB3/CPE(U)-D3 | 1.19 | 0.44 | 0.84 | 0.19 | 2.37 | 1.40 | 3.09 | 1.71 | 0.98 | 0.29 |
| DFTB3/CPE(ζ)-D3 | 1.21 | 0.48 | 0.80 | 0.16 | 1.78 | 0.41 | 2.58 | 0.20 | 1.01 | 0.14 |
| DFTB3/CPE(q)-D3 | 1.13 | 0.51 | 0.63 | −0.02 | 1.49 | 0.62 | 1.73 | 0.51 | 0.85 | 0.07 |
| DFTB3/CPE(ζ)-D3 (pol) | 1.17 | 0.24 | 0.92 | 0.04 | 2.22 | 1.40 | 2.36 | 0.24 | 0.68 | −0.06 |
| DFTB3/CPE(q)-D3 (pol) | 1.15 | 0.52 | 0.60 | −0.09 | 2.17 | 1.08 | 2.41 | 1.80 | 0.93 | 0.22 |
| DFTB3/CPE(q)-D3 (orig) | 1.23 | 0.23 | 0.00 | 0.16 | 3.12 | 1.96 | 3.49 | 1.51 | 0.98 | 0.32 |
| PM6 | 4.18 | 3.38 | 2.99 | 2.65 | 4.57 | 4.27 | 9.13 | 8.50 | 1.74 | 1.35 |
| PM6-D3H4 | 0.83 | 0.38 | 0.64 | 0.17 | 1.48 | 0.80 | 6.05 | 5.61 | 1.19 | 0.56 |
| PBE/6-31G(d) | 3.07 | 0.51 | 2.14 | 0.30 | 4.57 | −4.30 | 12.96 | −12.13 | 1.38 | −0.55 |
| PBE-D3/6-31G(d) | 2.82 | −2.18 | 2.34 | −2.04 | 5.71 | −5.46 | 14.90 | −14.22 | 1.90 | −1.72 |
| PBE/def2-QZVP | 3.71 | 2.55 | 2.65 | 2.05 | 0.67 | 0.05 | 2.39 | −1.88 | 1.08 | 0.63 |
| PBE-D3/def2-QZVP | 0.79 | −0.14 | 0.52 | −0.29 | 1.25 | −1.11 | 4.31 | −3.97 | 0.61 | −0.54 |
| Large water | Charged water | L7 | W2 | Polarizability | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Method | RMSD | Mean | RMSD | Mean | RMSD | Mean | RMSD | Mean | RMSD | Mean |
| DFTB3 | 14.16 | 11.05 | 5.75 | 5.61 | 15.92 | 14.10 | 6.04 | −0.81 | 19.08 | −18.30 |
| DFTB3-D3 | 2.04 | −1.43 | 3.77 | 3.72 | 2.31 | −1.36 | 6.04 | −1.39 | ||
| DFTB3-D3H4 | 23.88 | −20.31 | 2.51 | 2.46 | 2.61 | 0.75 | 6.03 | −0.69 | ||
| DFTB3/CPE(U)-D3*a | 3.59 | −3.14 | 2.04 | 2.01 | 4.23 | −2.90 | 5.78 | −1.88 | ||
| DFTB3/CPE(U)-D3 | 3.44 | −2.95 | 2.01 | 1.97 | 3.72 | −1.89 | 5.75 | −1.87 | ||
| DFTB3/CPE(ζ)-D3 | 2.51 | −1.57 | 1.21 | 1.14 | 4.03 | −1.79 | 5.49 | −2.23 | 92.37 | 82.29 |
| DFTB3/CPE(q)-D3 | 3.04 | −1.89 | 2.97 | 2.94 | 2.11 | −0.55 | 5.63 | −1.79 | 23.27 | 21.29 |
| DFTB3/CPE(ζ)-D3 (pol) | 2.46 | −0.78 | 2.50 | 2.41 | 2.40 | −1.51 | 5.48 | −1.78 | 3.64 | 1.53 |
| DFTB3/CPE(q)-D3 (pol) | 2.75 | 0.92 | 4.04 | 3.97 | 2.08 | −0.81 | 5.75 | −1.40 | 4.75 | 3.41 |
| DFTB3/CPE(q)-D3 (orig) | 223.69 | −156.88 | 3.32 | −2.06 | 2.18 | −0.93 | 6.37 | −2.35 | 3.67 | −3.00 |
| PM6 | 34.81 | 27.89 | 14.01 | 12.24 | 12.83 | 10.92 | 11.50 | 6.63 | ||
| PM6-D3H4 | 11.04 | 8.85 | 9.34 | 8.22 | 3.42 | −1.06 | 11.73 | 6.92 | ||
| PBE/6-31G(d) | 69.57 | −58.30 | 15.86 | −13.76 | 14.53 | 11.49 | 14.58 | −13.02 | 9.88 | −9.46 |
| PBE-D3/6-31G(d) | 82.69 | −68.79 | 17.42 | −15.09 | 5.02 | −4.35 | 14.98 | −13.51 | ||
| PBE/def2-QZVP | 4.11 | −3.69 | 3.90 | −3.45 | 17.88 | 15.56 | 4.41 | −3.85 | ||
| PBE-D3/def2-QZVP | 16.05 | −14.17 | 5.43 | −4.78 | 1.79 | −0.29 | 4.81 | −4.35 | ||
“*” denotes that the D3 parameters are not fitted for this model.
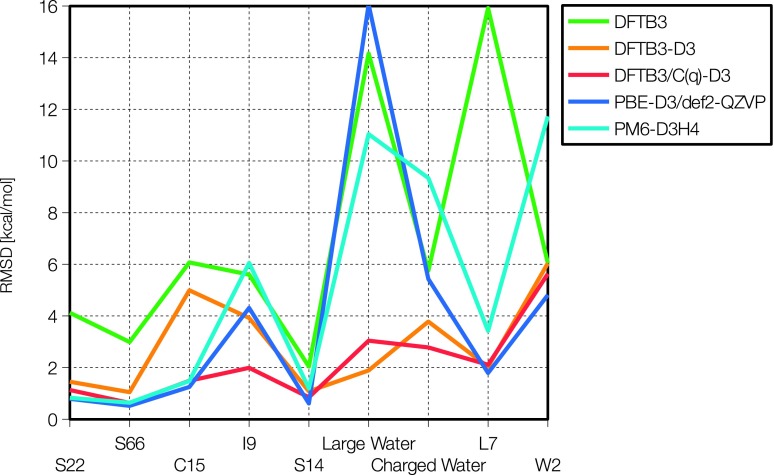
FIG. 1.
The RMSD interaction energy relative to CCSD(T) for 9 data sets (see text) using five different methods.
We start by examining the results of DFTB3, DFTB3-D3, and DFTB3-D3H4 models1,3,42,43 as a reference to gauge the performance of the DFTB3/CPE models. As shown in Table II, DFTB3-D3 and DFTB3-D3H4 are major improvements over the original DFTB3/3OB for dispersion dominated datasets; for datasets where no charged molecules are present, the RMSD is typically around 1 kcal/mol for smaller complexes and 2.31 kcal/mol and 2.61 kcal/mol, respectively, for the L7 dataset, as opposed to the value of 15.92 kcal/mol for DFTB3. However, for the charged C15 and I9 data sets, the degree of improvement is notably smaller. The RMSD values are 4.99 kcal/mol and 3.91 kcal/mol for the DFTB3-D3 model, and 4.10 kcal/mol and 4.66 kcal/mol for the DFTB3-D3H4 model; the corresponding values are 6.07 and 5.60 kcal/mol for DFTB3. We also note that for the large water dataset of Truhlar et al.,59 the average binding energy is greatly underestimated by DFTB3, which gives a large RMSD of 14.16 kcal/mol. With the inclusion of D3 dispersion, the RMSD drops significantly to a remarkable value of 2.04 kcal/mol, supporting discussions in the literature regarding the importance of dispersion to bulk water properties.34,59,63–65 Interestingly, the binding energies of large water clusters are severely overestimated by DFTB3-D3H4, with a RMSD of 23.88 kcal/mol. This is likely caused by the lack of cooperative hydrogen-bonding effects in the D3H4 model, which is molecular mechanical in nature.
Regarding the DFTB3/CPE models, it is seen from Table II that both adjusting the D3 dispersion and improving the response properties of DFTB3 are required to achieve a satisfactory description for intermolecular interactions of different nature. Without adjusting the D3 model, for example, large errors are seen for dispersion dominated cases such as L7. On the other hand, including the CPE component is essential to bringing down errors for polar cases such as C15, I9, and charged water clusters. For C15 and I9, for example, the RMSD values for DFTB3/D3 and DFTB3/D3H4 are in the range of 4-5 kcal/mol, while DFTB3/CPE-D3 models have RMSD errors on the order of 2 kcal/mol. Among the four DFTB3/CPE-D3 models introduced here, as the number of parameters in the fitting procedure is increased, the RMSD for the fitting datasets is lowered. Therefore, which model to choose requires a statistical analysis as we present in the section titled Model selection . Finally, we note that the impact of geometry optimization on the performance of the DFTB3/CPE models is rather modest (see supplementary material).68
As a comparison to representative NDDO models, we focus on PM6 and its recent extension, PM6-D3H4. As shown in Table II, PM6 has lower RMSD interaction energies than DFTB3 for the smaller complexes, but somewhat higher RMSD interaction energies for the C15 and I9 datasets. The addition of the -D3H4 correction makes the PM6-D3H4 model rather accurate for the S22, S66, and C14 datasets, but only improves I9 from 9.13 kcal/mol to 6.05 kcal/mol. Additionally, the RMSD values for the water clusters are rather large for the PM6 models: for the “Large water” dataset of Truhlar et al.,59 for example, the RMSD is 34.81 kcal/mol for PM6 and 11.04 kcal/mol for PM6-D3H4. The latter can be compared to DFTB-D3 (i.e., without any hydrogen bond correction), for which the same RMSD value is only 2.04 kcal/mol. Again, we attribute this to the lack of cooperativity in the D3H4 model, which results in a loss of accuracy when the molecular cluster size is scaled towards the condensed phase.
As emphasized in our recent discussions,42,2 it is worthwhile comparing DFTB3 models to “first principles” DFT methods, especially when modest basis sets are used, because typical DFT based molecular dynamics simulations require the use of modest basis sets. Accordingly, we show in Table II also RMSD values for PBE and PBE-D3 DFT models with a small basis set, 6-31G(d), and a large basis set, def2-QZVP. The PBE functional with the 6-31G(d) basis set gives very large RMSD error across all the test sets, presumably due to basis set superposition errors, while using the large def2-QZVP yields very accurate interaction energies for all the smaller complexes. For various water clusters, even the PBE-D3/def2-QZVP method gives large errors in some cases (see Fig. 1); for the “Large water” dataset, for example, the RMSD is 16.05 kcal/mol.
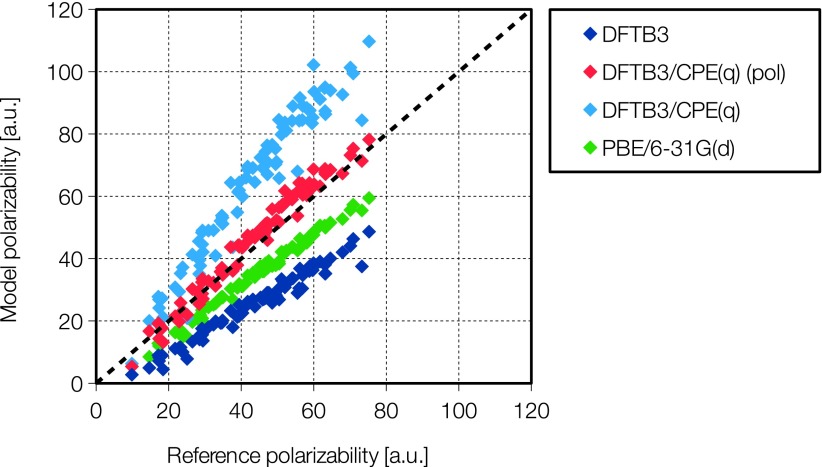
We note from Table II (also see Fig. 2) that DFTB3 with no CPE correction gives an underpolarization for neutral molecules in the gas phase of ∼18 bohrs3 on average. If the DFTB3/CPE models are parametrized using only interaction energies, the combined model actually overpolarizes greatly by 82 bohrs3 on average for the charge-independent CPE model and by ∼21 bohrs3 for the charge dependent model. These numbers can be improved by including polarization data in the parametrization to 1.5 and 3.4 bohrs3, respectively. This, however, increases the RMSD interaction energy error by between 0.1 and 3.4 kcal/mol, except for the charged water data set, which improves by about 1 kcal/mol. For comparison, PBE with the modest sized 6-31G(d) basis set underpolarizes by 10 bohrs3 on average.
FIG. 2.
Gas-phase polarizability for 87 neutral molecules calculated with four different methods, compared to a B3LYP/aug-cc-pVTZ reference. DFTB3/CPE(q) is parameterized without polarizabilities in the training data, while for DFTB3/CPE(q) (pol) polarizabilities are included in the training data.
Using DFTB3/CPE(q) with the original parameters from Kaminski et al.40 and the standard D3 parameters, predicted interaction energies are generally improved compared to DFTB3-D3. However, for the large water clusters there is a catastrophic overpolarization, and the binding energy is greatly overestimated by up to around 200 kcal/mol. As the CPE from Kaminski et al. parameters were fitted using the MIO parameter set, we re-did the same calculation with the MIO parameters set with the same observations. The fact that a single set of CPE parameters is not optimal for simultaneously describing intermolecular interactions and polarizabilities to high accuracy reflects the semi-empirical nature of the current DFTB3 model; i.e., some of the errors are compensated empirically during the fitting process, which emphasizes on energetics. On the other hand, the fact that a reparameterization of essentially the same DFTB3/CPE model has alleviated the over polarization problem in large water clusters highlights the importance of considering larger clusters than dimer models for the calibration and parameterization of intermolecular interactions for condensed phase applications.
In the supplementary material,68 we present the performance of the models on anions and cations. Generally, all the new DFTB3/CPE models as well as PBE/6-31G(d) fail to reproduce the gas-phase polarizability of anions accurately; this is hardly surprising because for anions much more diffuse functions are needed in the gas phase. However, we note that anions in solution are generally much more electronically restricted and, hence, much less polarizable. For example, in the supplementary material68 we show for one of the worst outliers (thiomethoxide), that when embedded in a droplet of water, the predicted DFTB3/CPE polarizability is close to that of a higher level DFT calculation. These results further underline the great importance and difficulty of extrapolating from properties of gas-phase model systems to an accurate description of solution-phase behavior.
Before concluding this section, we note that in the C15 dataset, the imidazolium-methylamine complex has an discrepancy of 12 kcal/mol between the CCSD(T)/CBS and DFTB3 interaction energies. Hence, we chose to leave this complex out of the optimization procedure, as otherwise the cost function was dominated by this single outlier. Also, the methylammonium-methylamine complex differs by almost 10 kcal/mol between CCSD(T)/CBS and DFTB3 results. In fact, we note a general trend in S66: complexes that include a nitrogen atom with a lone pair have a larger deviation between CCSD(T)/CBS and DFTB3 compared to other cases (see supplementary material68). These observations suggest a limitation of the current DFTB3/3OB model,42 which likely reflects the inadequacy of a monopole charge model for treating strong interactions involve a lone-pair, as also discussed in Ref. 66. We do not expect the CPE model to solve this problem, apart from fact that the CPE parameters will be fitted such that they may implicitly compensate for this issue. A more physical improvement requires including multipoles in the charge fluctuations21 and is being pursued independently. Similarly, although the performance of DFTB3 for water clusters is rather encouraging once dispersion is included, the coupled DFTB3/CPE approach remains to have sizable errors for charged water clusters, especially for water-hydroxide interactions (W2 set); along this line, we note that a recent study that included an “on-site” integral correction67 seemed to reduce the error for charged water cluster considerably.
Model selection
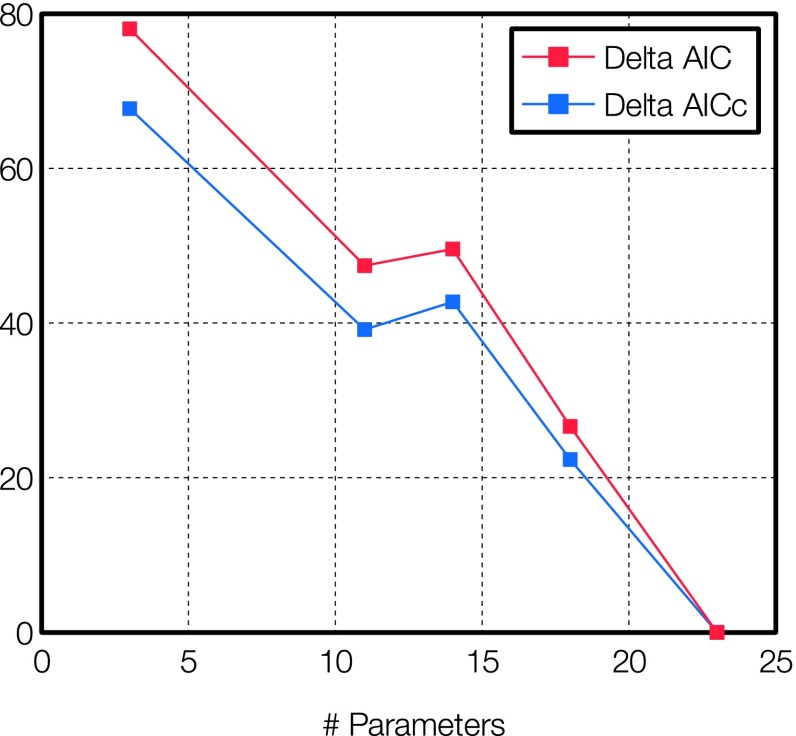
Since the CPE model introduces a number of new parameters, we estimate the effect of the increasing number of parameters in the models against the relative likelihood of each DFTB3/CPE model using the AICc.
The baseline model is the introduction of 0 parameters, i.e., the DFTB3/3OB model with no further corrections. The AICc for this model is 359.0. As expected from the higher accuracy of the DFTB3-D3 model, the three parameters introduced in this model vastly decrease the AICc to 131.5. A graphical overview of the ΔAICc values vs. number of parameters is displayed in Fig. 3. AIC values for the DFTB3/CPE models are presented in Table III. The lowest scoring (i.e., favorable) models are the DFTB3/CPE(ζ)-D3 and DFTB3/CPE(q)-D3 models. The AIC weight clearly favors a DFTB3/CPE model over DFTB3 (wi = 0.0%) and DFTB3-D3 (wi = 0.0%). Additionally, it also seems very beneficial to optimize the parameters in the dispersion model along with the parameters in the CPE model. The lowest AICc is found for the model with the most parameters, namely, the DFTB3/CPE(q)-D3 model (wi = 99.999%).
FIG. 3.
AIC values for the DFTB-D3 model and four DFTB3/CPE models with an increasing number of parameters (see also Table III).
TABLE III.
Akaike information criterion.
| Method | k | AIC | AICc | ΔAICc | wi (%) | S22 RMSD (kcal/mol) |
|---|---|---|---|---|---|---|
| DFTB3 | 0 | 359.0 | 359.0 | 295.29 | 0.000 | 4.12 |
| DFTB3-D3 | 3 | 131.3 | 131.5 | 67.72 | 0.000 | 1.45 |
| DFTB3/CPE(U)-D3*a | 11 | 100.7 | 102.9 | 39.16 | 0.000 | 1.18 |
| DFTB3/CPE(U)-D3 | 14 | 102.8 | 106.5 | 42.73 | 0.000 | 1.18 |
| DFTB3/CPE(ζ)-D3 | 18 | 79.9 | 86.1 | 22.34 | 0.001 | 1.21 |
| DFTB3/CPE(q)-D3 | 23 | 53.2 | 63.8 | 0.00 | 99.999 | 1.13 |
“*” denotes that the D3 parameters are not fitted for this model.
The RMSD for the S22 test set, which is not included in the training data, is improved both by addition of the D3 model and the CPE model. Among the DFTB3/CPE models, the RMSD varies by a few percent, although such small variations may also reflect the fact that the S22 test set does not include charged molecules.
Additional insights can also be gained from the values of the parameters presented in Table I. In DFTB, the second order integrals are evaluated using Slater functions: in this case, the parameter (corresponding to Zi) is proportional to the chemical hardness. For CPE, Gaussian functions are used, i.e., the squared value of Zi would correspond to the chemical hardness. The chemical hardness suggested by the value of the calculated DFTB3 Hubbard parameters13 suggests that reasonable values for Zi are on the order of 2-4 a.u. for a Gaussian function. This trend is indeed observed for the CPE(U) models. However, for the CPE(ζ) models with no constraints on Zi, we find values of Zi for oxygen and nitrogen that seem unreasonably high. When charge dependence is introduced in the CPE(q) models, however, the values of Zi seem to relax to values in the expected range. These observations are also consistent with the AICc values reported in Table III: removing the constraints on the Zi-values in the CPE(ζ) model lowers the AICc considerably compared to the CPE(U) models, but the cost seems to be unreasonable values of the exponents. Introducing the charge dependence in the CPE(q) models leads the exponents to a very reasonable range, and at the same time, lowers the AICc considerably, suggesting that the CPE(q) models better capture the underlying physics.
Effects of geometry optimization with the DFTB3/CPE
Here we investigate the effects of geometry optimization with the DFTB3/CPE(q)-D3 model. We re-optimize the S22, S66, C15, S14, large water, charged water, and L7 data sets, and calculate the interaction energies using the re-optimized geometries. The structures were optimized using the adopted basis Newton-Raphson in CHARMM, with a tolerance of 5.0 × 10−4 Hartree/bohrs. A summary of the effects of optimization is in Table IV. For the data sets used in the training set, the RMSD of the interaction energy is increased from 0.63–3.04 kcal/mol to 1.14–4.87 kcal/mol. An increase in this RMSD value is expected, since the parameters were specifically optimized to the reference geometries. For the S22 data set which we use as validation, the RMSD is practically unchanged; in fact, it is lowered by 0.09 kcal/mol, which suggests that the model is indeed transferable.
TABLE IV.
The RMSD of the calculated interaction energy (RMSD ΔE) in kcal/mol for the various data sets using either reference geometries or DFTB3/CPE(q)-D3 optimized geometries is listed. All RMSD values are in kcal/mol. Energies are evaluated using the DFTB3/CPE(q)-D3 model. The root mean squared structural RMSDs (i.e., the RMS RMSD) between the reference and the re-optimized complexes are listed for each data set.
| Data set | RMSD ΔE (Ref)a | RMSD ΔE (Opt)a | RMS RMSD (Å) |
|---|---|---|---|
| S22 | 1.13 | 1.02 | 0.09 |
| S66 | 0.63 | 1.14 | 0.08 |
| C15 | 1.49 | 2.09 | 0.09 |
| S14 | 0.85 | 1.20 | 0.11 |
| Large water | 3.04 | 4.87 | 0.12 |
| Charged water | 2.97 | 3.11 | 0.10 |
| L7 | 2.11 | 3.77 | 0.11 |
(Ref) denotes that the high-level optimized, while (Opt) denotes that the DFTB3/CPE(q)-D3 re-optimized complexes are used.
In terms of changes in the structures of the complexes, we observe no case where the optimized geometry differs by more than 0.4 Å from the reference. The few largest changes are illustrated in Figs. S2-S4 of the supplementary material.68 Over all, the root mean squared structural RMSDs between the reference and the re-optimized complexes are found to be in the range of 0.09–0.12 Å, as shown in Table IV.
CONCLUDING REMARKS
We have augmented the DFTB3 method with a CPE response density and the D3 dispersion correction in a combined methodology termed DFTB3/CPE-D3. Depending on the number of free parameters, four different DFTB3/CPE-D3 models are parametrized using a broad range of molecular complexes of biological interest. Compared to DFTB3-D3, the accuracy is largely unchanged for small, neutral complexes, whereas the accuracy is clearly improved for charged complexes. Compared to the D3H4 corrected DFTB3 and PM6 models, the accuracy of DFTB3/CPE-D3 models is comparable for small, neutral complexes, but the scaling to larger clusters and larger complexes is notably improved. Compared to PBE and PBE-D3 models with modest (double-zeta quality) or large (def2-QZVP) basis sets, the DFTB3/CPE-D3 models are also competitive, especially for large water clusters. The statistical analysis using the AICc favors the DFTB3/CPE-D3 models over the DFTB3-D3 and DFTB3 models.
Despite these encouraging observations, we emphasize that the DFTB3 methodology requires further development for a generally robust and accurate treatment of non-covalent interactions in different environments.23 As discussed in our and related studies, including multipoles and improved description of Pauli repulsion are of the highest priority; this is also underlined by the large errors for several cases involving nitrogen lone-pairs noted in this study. What we hope to illustrate in this work is that improving the response properties of DFTB3 is a viable approach to improve intermolecular interactions involving charged and highly polarizable molecules. Ultimately, these developments need to be integrated together to form an efficient and robust computational framework for condensed phase properties, especially reactive events in polar liquids and biomolecules. Along this line, developing test cases beyond the relatively small clusters used here and most benchmark studies is also crucial, as illustrated by the different performances of the previous40 and current DFTB3/CPE models for large water clusters. Nevertheless, to echo the point of the recent work of Grimme et al.,3 the future of describing non-covalent interactions using the DFTB3 methodology seems bright.
Acknowledgments
This work is supported by NIH Grant No. R01-GM106443 to Q.C. The authors thank Professor Dr. Stefan Grimme for the reference energies for the DPLNO-CCSD(T)/CBS interaction energies for the L7 data set, and for providing the FORTRAN routines to calculate the dispersion correction. Discussions with Dr. T. Giese and Dr. K. Welke are also acknowledged. Computational resources from the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by NSF Grant No. OCI-1053575, are greatly appreciated; computations are also supported in part by NSF through a major instrumentation grant (Grant No. CHE-0840494) to the chemistry department.
REFERENCES
- 1.Řezáč J. and Hobza P., J. Chem. Theory Comput. 8, 141–151 (2012). 10.1021/ct200751e [DOI] [PubMed] [Google Scholar]
- 2.Cui Q. and Elstner M., Phys. Chem. Chem. Phys. 16, 14368–14377 (2014). 10.1039/c4cp00908h [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Brandenburg J., Hochheim M., Bredow T., and Grimme S., J. Phys. Chem. Lett. 5, 4275–4284 (2014). 10.1021/jz5021313 [DOI] [PubMed] [Google Scholar]
- 4.Yilmazer N. D. and Korth M., Comput. Struct. Biotechnol. J. 13, 169–175 (2015). 10.1016/j.csbj.2015.02.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Korth M. and Thiel W., J. Chem. Theory Comput. 7, 2929–2936 (2011). 10.1021/ct200434a [DOI] [PubMed] [Google Scholar]
- 6.Pople J. A., Santry D. P., and Segal G. A., J. Chem. Phys. 43, S129–S135 (1965). 10.1063/1.1701475 [DOI] [Google Scholar]
- 7.Dewar M. J. S. and Thiel W., J. Am. Chem. Soc. 99, 4899–4907 (1977). 10.1021/ja00457a004 [DOI] [Google Scholar]
- 8.Seifert G. and Joswig J. O., Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2, 456–465 (2012). 10.1002/wcms.1094 [DOI] [Google Scholar]
- 9.Gaus M., Cui Q., and Elstner M., Wiley Interdiscip. Rev.: Comput. Mol. Sci. 4, 49–61 (2014). 10.1002/wcms.1156 [DOI] [Google Scholar]
- 10.Seifert G., Porezag D., and Frauenheim T., Int. J. Quantum Chem. 58, 185–192 (1996). [DOI] [Google Scholar]
- 11.Porezag D., Frauenheim T., Köhler T., Seifert G., and Kaschner R., Phys. Rev. B 51, 12947–12957 (1995). 10.1103/PhysRevB.51.12947 [DOI] [PubMed] [Google Scholar]
- 12.Elstner M., Porezag D., Jungnickel G., Elsner J., Haugk M., Frauenheim T., Suhai S., and Seifert G., Phys. Rev. B 58, 7260–7268 (1998). 10.1103/PhysRevB.58.7260 [DOI] [Google Scholar]
- 13.Gaus M., Cui Q., and Elstner M., J. Chem. Theory Comput. 7, 931–948 (2011). 10.1021/ct100684s [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Matsuzawa N. and Dixon D. A., J. Phys. Chem. 96, 6872–6875 (1992). 10.1021/j100196a007 [DOI] [Google Scholar]
- 15.Řezáč J., Fanfrlík J., Salahub D., and Hobza P., J. Chem. Theory Comput. 5, 1749–1760 (2009). 10.1021/ct9000922 [DOI] [PubMed] [Google Scholar]
- 16.Korth M., Pitoňák M., Řezáč J., and Hobza P., J. Chem. Theory Comput. 6, 344–352 (2010). 10.1021/ct900541n [DOI] [PubMed] [Google Scholar]
- 17.Řezáč J. and Hobza P., Chem. Phys. Lett. 506, 286–289 (2011). 10.1016/j.cplett.2011.03.009 [DOI] [Google Scholar]
- 18.Korth M., J. Chem. Theory Comput. 6, 3808–3816 (2010). 10.1021/ct100408b [DOI] [PubMed] [Google Scholar]
- 19.Kromann J. C., Christensen A. S., Steinmann C., Korth M., and Jensen J. H., PeerJ 2, e449 (2014). 10.7717/peerj.449 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Řezáč J., Riley K. E., and Hobza P., J. Chem. Theory Comput. 8, 4285–4292 (2012). 10.1021/ct300647k [DOI] [PubMed] [Google Scholar]
- 21.Bodrog Z. and Aradi B., Phys. Status Solidi B 249, 259–269 (2012). 10.1002/pssb.201100524 [DOI] [Google Scholar]
- 22.Huang J., Lopes P. E. M., Roux B., and A. D. MacKerell, Jr., J. Phys. Chem. Lett. 5, 3144–3150 (2014). 10.1021/jz501315h [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Goyal P., Qian H.-J., Irle S., Lu X., Roston D., Mori T., Elstner M., and Cui Q., J. Phys. Chem. B 118, 11007–11027 (2014). 10.1021/jp503372v [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Nanda D. and Jug K., Theor. Chim. Acta (Berl.) 57, 95–106 (1980). 10.1007/BF00574898 [DOI] [Google Scholar]
- 25.Jug K. and Geudtner G., J. Comput. Chem. 14, 639–646 (1993). 10.1002/jcc.540140603 [DOI] [PubMed] [Google Scholar]
- 26.Thiel W. and Voityuk A. A., J. Phys. Chem. 100, 616–626 (1996). 10.1021/jp952148o [DOI] [Google Scholar]
- 27.Stewart J., J. Mol. Model. 13, 1173–1213 (2007). 10.1007/s00894-007-0233-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Fiedler L., Gao J., and Truhlar D. G., J. Chem. Theory Comput. 7, 852–856 (2011). 10.1021/ct1006373 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Zhang P., Fiedler L., Leverentz H. R., Truhlar D. G., and Gao J., J. Chem. Theory Comput. 7, 857–867 (2011). 10.1021/ct100638g [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Isegawa M., Fiedler L., Leverentz H. R., Wang Y., Nachimuthu S., Gao J., and Truhlar D. G., J. Chem. Theory Comput. 9, 33–45 (2013). 10.1021/ct300509d [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Elstner M., Frauenheim T., Kaxiras E., Seifert G., and Suhai S., Phys. Status Solidi B 217, 357–376 (2000). [DOI] [Google Scholar]
- 32.Srinivasan S. G., Goldman N., Tamblyn I., Hamel S., and Gaus M., J. Phys. Chem. A 118, 5520–5528 (2014). 10.1021/jp5036713 [DOI] [PubMed] [Google Scholar]
- 33.Chang D. T., Schenter G. K., and Garrett B. C., J. Chem. Phys. 128, 164111 (2008). 10.1063/1.2905230 [DOI] [PubMed] [Google Scholar]
- 34.Murdachaew G., Mundy C. J., Schenter G. K., Laino T., and Hutter J., J. Phys. Chem. A 115, 6046–6053 (2011). 10.1021/jp110481m [DOI] [PubMed] [Google Scholar]
- 35.Chelli R. and Procacci P., J. Chem. Phys. 117, 9175–9189 (2002). 10.1063/1.1515773 [DOI] [Google Scholar]
- 36.York D. M. and Yang W., J. Chem. Phys. 104, 159–172 (1996). 10.1063/1.470886 [DOI] [Google Scholar]
- 37.Giese T. J. and York D. M., J. Chem. Phys. 123, 164108 (2005). 10.1063/1.2080007 [DOI] [PubMed] [Google Scholar]
- 38.Giese T. J. and York D. M., J. Chem. Phys. 127, 194101 (2007). 10.1063/1.2778428 [DOI] [PubMed] [Google Scholar]
- 39.Giese T. J. and York D. M., Theor. Chem. Acc. 131, 1145 (2012). 10.1007/s00214-012-1145-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Kaminski S., Giese T. J., Gaus M., York D. M., and Elstner M., J. Phys. Chem. A 116, 9131–9141 (2012). 10.1021/jp306239c [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Grimme S., Antony J., Ehrlich S., and Krieg H., J. Chem. Phys. 132, 154104 (2010). 10.1063/1.3382344 [DOI] [PubMed] [Google Scholar]
- 42.Gaus M., Goez A., and Elstner M., J. Chem. Theory Comput. 9, 338–354 (2013). 10.1021/ct300849w [DOI] [PubMed] [Google Scholar]
- 43.Gaus M., Lu X., Elstner M., and Cui Q., J. Chem. Theory Comput. 10, 1518–1537 (2014). 10.1021/ct401002w [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Grimme S., Ehrlich S., and Goerigk L., J. Comput. Chem. 32, 1456–1465 (2011). 10.1002/jcc.21759 [DOI] [PubMed] [Google Scholar]
- 45.Jaynes E. T., Phys. Rev. 106, 620–630 (1957). 10.1103/PhysRev.106.620 [DOI] [Google Scholar]
- 46.Jeffreys H., Proc. R. Soc. London, Ser. A 186, 453–461 (1946). 10.1098/rspa.1946.0056 [DOI] [PubMed] [Google Scholar]
- 47.Metropolis N., Rosenbluth A. W., Rosenbluth M. N., Teller A. H., and Teller E., J. Chem. Phys. 21, 1087–1092 (1953). 10.1063/1.1699114 [DOI] [Google Scholar]
- 48.Sugiura N., Commun. Stat.–Theory Methods 7, 13–26 (1978). 10.1080/03610927808827599 [DOI] [Google Scholar]
- 49.Burnham K. P. and Anderson D. R., Model Selection and Multimodel Inference (Springer-Verlag, New York, Inc., 2002). [Google Scholar]
- 50.Cavanaugh J. E., Stat. Probab. Lett. 33, 201–208 (1997). 10.1016/S0167-7152(96)00128-9 [DOI] [Google Scholar]
- 51.Brooks B. R., Bruccoleri R. E., Olafson B. D., States D. J., Swaminathan S., and Karplus M., J. Comput. Chem. 4, 187–217 (1983). 10.1002/jcc.540040211 [DOI] [Google Scholar]
- 52.Frisch M. J. et al. , gaussian 09, Revision D.01, Gaussian, Inc., Wallingford, CT, 2009.
- 53.Werner H.-J., Knowles P. J., Knizia G., Manby F. R., and Schütz M., Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2, 242–253 (2012). 10.1002/wcms.82 [DOI] [Google Scholar]
- 54.Werner H.-J. et al. , molpro, version 2012.1, a package of ab initio programs, 2012, see http://www.molpro.net.
- 55.Gráfová L., Pitoňák M., Řezáč J., and Hobza P., J. Chem. Theory Comput. 6, 2365–2376 (2010). 10.1021/ct1002253 [DOI] [PubMed] [Google Scholar]
- 56.Takatani T., Hohenstein E. G., Malagoli M., Marshall M. S., and Sherrill C. D., J. Chem. Phys. 132, 144104 (2010). 10.1063/1.3378024 [DOI] [PubMed] [Google Scholar]
- 57.Řezáč J., Riley K. E., and Hobza P., J. Chem. Theory Comput. 7, 2427–2438 (2011). 10.1021/ct2002946 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Mintz B. J. and Parks J. M., J. Phys. Chem. A 116, 1086–1092 (2012). 10.1021/jp209536e [DOI] [PubMed] [Google Scholar]
- 59.Leverentz H. R., Qi H. W., and Truhlar D. G., J. Chem. Theory Comput. 9, 995–1006 (2013). 10.1021/ct300848z [DOI] [PubMed] [Google Scholar]
- 60.Sedlak R., Janowski T., Pitoňák M., Řezáč J., Pulay P., and Hobza P., J. Chem. Theory Comput. 9, 3364–3374 (2013). 10.1021/ct400036b [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Giese T. J., Gregersen B. A., Liu Y., Nam K., Mayaan E., Moser A., Range K., Faza O. N., Lopez C. S., de Lera A. R., Schaftenaar G., Lopez X., Lee T.-S., Karypis G., and York D. M., J. Mol. Graphics Modell. 25, 423–433 (2006). 10.1016/j.jmgm.2006.02.011 [DOI] [PubMed] [Google Scholar]
- 62.Hickey A. L. and Rowley C. N., J. Phys. Chem. A 118, 3678–3687 (2014). 10.1021/jp502475e [DOI] [PubMed] [Google Scholar]
- 63.Yoo S. and Xantheas S. S., J. Chem. Phys. 134, 121105 (2011). 10.1063/1.3573375 [DOI] [PubMed] [Google Scholar]
- 64.Ma Z., Zhang Y., and Tuckerman M. E., J. Chem. Phys. 137, 044506 (2012). 10.1063/1.4736712 [DOI] [PubMed] [Google Scholar]
- 65.Medders G. R., Babin V., and Paesani F., J. Chem. Theory Comput. 9, 1103–1114 (2013). 10.1021/ct300913g [DOI] [PubMed] [Google Scholar]
- 66.Giese T. J., Panteva M. T., Chen H., and York D. M., J. Chem. Theory Comput. 11, 451–461 (2015). 10.1021/ct500799g [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Domínguez A., Niehaus T. A., and Frauenheim T., J. Phys. Chem. A 119, 3535–3544 (2015). 10.1021/acs.jpca.5b01732 [DOI] [PubMed] [Google Scholar]
- 68.See supplementary material at http://dx.doi.org/10.1063/1.4929335 E-JCPSA6-143-059532 for a more detailed discussion of the Akaike Information Criterion (AIC), calculation procedure for the new data sets (I9, CHW9, and W2), the corresponding interaction energies, and Cartesian coordinates are included. Also included are the detailed RMSD values for all the methods discussed here for the collection of benchmark and test sets. Figures displaying the impact of geometry optimization on the DFTB3/CPE-D3 results are also shown. Detailed derivations for DFTB3/CPE, especially for gradient and polarizability calculations, are included.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Citations
- See supplementary material at http://dx.doi.org/10.1063/1.4929335 E-JCPSA6-143-059532 for a more detailed discussion of the Akaike Information Criterion (AIC), calculation procedure for the new data sets (I9, CHW9, and W2), the corresponding interaction energies, and Cartesian coordinates are included. Also included are the detailed RMSD values for all the methods discussed here for the collection of benchmark and test sets. Figures displaying the impact of geometry optimization on the DFTB3/CPE-D3 results are also shown. Detailed derivations for DFTB3/CPE, especially for gradient and polarizability calculations, are included.