Random bursts determine dynamics of active filaments

Significance

Biological active systems like swimming bacteria or molecular motors in the cell cytoskeleton consume energy locally to create movements or stresses. Although the surrounding fluid gives rise to thermal fluctuations of the system’s dynamic variables, the corresponding statistics can deviate significantly from a thermal Boltzmann distribution. To quantify these differences, we compare the statistics and dynamics of actin filaments driven by molecular motors with Brownian filaments. In both cases, energy injection is local and random; however, for active filaments, motors can generate sudden jump-like changes in the system’s dynamic variables, leading to nonequilibrium energy dissipation. Motor activity results in a nonthermal distribution of filament curvatures and a faster relaxation of filament bends than in the thermal case.

Abstract

Constituents of living or synthetic active matter have access to a local energy supply that serves to keep the system out of thermal equilibrium. The statistical properties of such fluctuating active systems differ from those of their equilibrium counterparts. Using the actin filament gliding assay as a model, we studied how nonthermal distributions emerge in active matter. We found that the basic mechanism involves the interplay between local and random injection of energy, acting as an analog of a thermal heat bath, and nonequilibrium energy dissipation processes associated with sudden jump-like changes in the system’s dynamic variables. We show here how such a mechanism leads to a nonthermal distribution of filament curvatures with a non-Gaussian shape. The experimental curvature statistics and filament relaxation dynamics are reproduced quantitatively by stochastic computer simulations and a simple kinetic model.

In active systems, perpetual local energy input prevents relaxation into a thermal equilibrium state (1–3). Examples are living matter (4–10) or appropriately reconstituted or synthetic model systems (11–17). It is widely accepted that nonthermal fluctuations play a crucial role for the dynamics of active systems (8, 9, 18–24) and may even cause an apparent violation of the fluctuation-dissipation theorem (11). The physical origin of the violation can be attributed to local tensile stresses generated by myosin minifilaments, as shown by rheological measurements of 3D actin networks consisting of myosin II, actin filaments, and cross-linkers (11). Although this study focused on how the macroscopic properties of the active filament network are altered with respect to its equilibrium counterpart, we consider how local stresses generated by motors mesoscopically affect the dynamics and the conformational statistics of individual filaments. To this end, we use the actin gliding assay (25, 26), which has become a paradigm of active systems. In this assay, actin filaments are moved by individual nonprocessive myosin motors, which are bound to a substrate. We find that motile filaments in this assay display a nonthermal distribution of curvatures with an exponential shape, which is essentially different from its equilibrium counterpart. Based on our observations, we were able to elucidate the origin of the nonthermal fluctuations in the gliding assay and introduce a mechanism that explains how nonthermal distributions may emerge in active matter systems. The mechanism relies on the interplay between local and random input of energy, acting as an analog of a thermal heat bath, and nonequilibrium energy dissipation processes due to sudden jump-like changes in the system’s dynamic variables. We perform stochastic simulations of the filament’s dynamics and provide a rationale drawn from kinetic theory. Both approaches quantitatively reproduce the experimental curvature distribution and correctly predict the relaxation dynamics of the active filament.

Results

Experimental Findings.

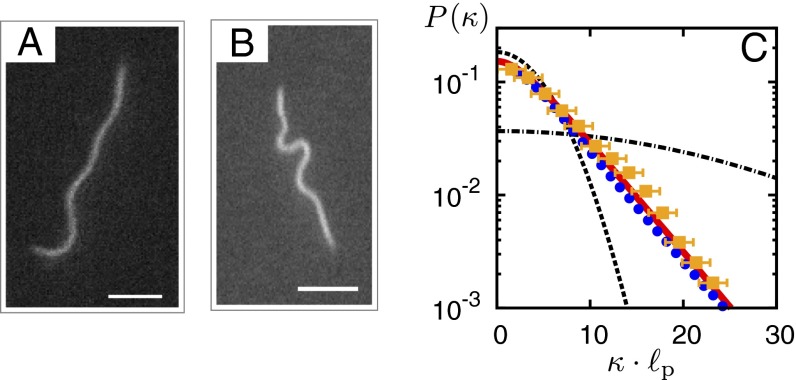
In the gliding assay (25, 26), labeled actin bind to molecular motors, which are immobilized on a glass substrate, and are transported along the surface in a “gliding” movement (details are provided in Materials and Methods). During their chemo-mechanical cycle, motors may act both as static cross-linkers, holding filaments in place, and as force-generating elements, propelling filaments in the direction of their local tangents. As a result, individual filaments move mainly along their own contour at some average speed v, but their path is tortuous and displays no long-term directionality. It was recognized recently that gliding assays are crucial for understanding the emergence of collective motion in active systems (12, 15). Here, we performed gliding assay experiments at highly dilute filament densities and imaged the contours of individual filaments. The observed filament configurations ranged from smoothly bent shapes to contours of more pronounced kinks (Fig. 1 A and B). To quantify the curvature statistics, we discretized the polymer contour into segments of fixed length and extracted the local curvature values κ; for details, refer to Materials and Methods. Surprisingly, we found that the curvature distribution $P\left(\kappa \right)$ exhibits an exponential tail (Fig. 1C), which is fundamentally different from the Gaussian curvature statistics for semiflexible filaments in thermal equilibrium (27). The exponential tail precludes an explanation of the curvature statistics in terms of a Gaussian distribution with an elevated effective temperature (28, 29).

Fig. 1.

Curvature statistics of active actin filaments. (A and B) Snapshots of two distinct filament configurations observed in a filament gliding assay experiment. (Scale bar, 2 μm.) (C) Quantitative agreement between the curvature distributions $P\left(\kappa \right)$ as obtained from gliding assay experiments (squares), a simplified computational model (circles), and a kinetic theory (red solid line) (Eq. 2). In particular, all exhibit an exponential tail. For comparison, the thermal curvature probability distribution for a semiflexible polymer, $P_{thermal}\left(\kappa \right)\propto \exp \left(-{\kappa }^2{\ell }_p\mathrm{\Delta }s/2\right)$ (27), is shown, where ${\ell }_p=16\hspace{0.17em}\mu \text{m}$ denotes the thermal persistence length (33) and $\mathrm{\Delta }s=0.8\hspace{0.17em}\mu \text{m}$ (dashed) and $\mathrm{\Delta }s=0.032\hspace{0.17em}\mu \text{m}$ (dash-dotted). The latter value of the segment length was chosen in the gliding assay experiments. Experiments were performed at a motor density of $c=1.5\cdot {10}^3{\mu \text{m}}^{-2}$, and filament length L in the range of 2–12 μm. For the computational model, the average number of bound motors was $m_b=20$, and $L={\ell }_p/3$ (for additional details, see SI Materials and Methods, Figs. S1–S4, and Movies S1–S3).

Stochastic Simulation.

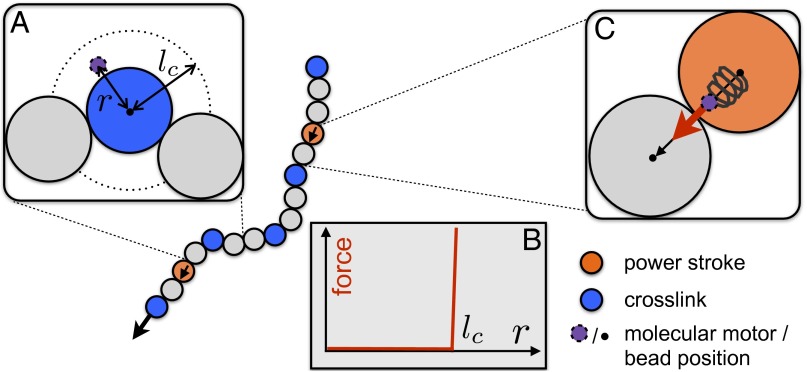
To understand how the local forces generated by molecular motors give rise to such nonthermal curvature statistics, we studied a computational model for a propelled actin polymer as illustrated in Fig. 2 (for details, see SI Materials and Methods). We considered filaments with a bending elasticity described by the worm-like chain model (27). Here, motors can bind to the filament anywhere along its contour at a rate ${\tau }_{off}^{-1}$. For simplicity, we assumed that the total number of motors attached to a filament, $m_b$, stays constant. Once bound, the motor passes through the following states: A stroke phase of duration ${\tau }_s$ during which the motor exerts a pushing force on the filament, acting along its local tangent, is followed by a period ${\tau }_{\times }$, in which the motor acts as a cross-link with a nonlinear force-extension relation. Subsequently, the motor detaches from the filament and the chemo-mechanical cycle starts anew.

Fig. 2.

Computational model for actin filaments propelled by molecular motors. We consider a bead-spring model in which each bead is bound to a molecular motor that either forms a cross-link (blue beads) or is engaged in executing a power stroke (orange beads). In addition, the filament is subject to thermal forces. (A) During some fraction ${\tau }_{\times }$ of its chemo-mechanical cycle, the molecular motor acts as a cross-link. We assume a highly nonlinear force-extension relation for the linker domain as illustrated in B. The linker domain acts as a rigid link if the distance r between the bead position and the motor anchoring point exceeds a certain value $l_c$ (referred to as capturing length); otherwise, the force exerted on the bead is zero. (C) During the power stroke phase, the linker domain of the motor acts like a spring, releasing stored elastic energy as it snaps forward parallel to the local tangent of the filament’s contour. For simplicity, we assume that the total number of motors attached to a filament, $m_b$, stays constant. For a typical experiment of motor density, $c=1.5\cdot {10}^3{\mu \text{m}}^{-2}$, we estimate $m_b\approx 20$ (SI Materials and Methods).

We performed stochastic simulations based on this model, using the same parameters as in the experiment, and consistently found that the curvature statistics also showed an exponential tail (Fig. 1C). To check for robustness of these results against changes in the motor-filament interaction, we also simulated the filament dynamics in the extreme case where cross-links were absent. As shown in Figs. S5 and S6, this also results in an exponential tail. Interestingly, in the simulation model, the probability distribution of motors performing a power stroke, which are in the direct neighborhood along the filament, also decays exponentially (see SI Materials and Methods and Figs. S7 and S8). There might be a connection to the exponential shape of the curvature distribution; however, its understanding requires a microscopic relation between the simulation model and the filament’s distribution of curvatures, which goes beyond the scope of this work.

To further assess how the curvature statistics depends on the motor-filament interaction, we studied the impact of filament length and motor density in the experiment, as well as in the computational model (Fig. 3 A–C). We consistently found that filament length L has no significant effect on the curvature distribution $P\left(\kappa \right)$. In contrast, increasing the motor density c in the experiment, or equivalently the average number of bound motors $m_b$ in the computational model, strongly shifts the distribution toward larger curvatures (Fig. 3 A–C). Taken together, these results reveal that motor-filament interactions play an important role and suggest that nonthermal active fluctuations determine the actin filament’s contour. Changes in the filament’s local curvature and the exponential curvature distribution emerge due to local injection and dissipation of energy by the actions of the molecular motors.

Fig. 3.

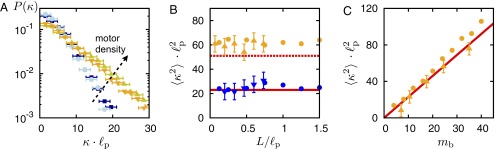
Dependence of the curvature statistics on motor density and filament length. (A) Experimental curvature distribution $P\left(\kappa \right)$ for two different motor densities [shades of blue (circles/squares): $c=1.5\cdot {10}^3{\mu \text{m}}^{-2}$; shades of red (triangles): $c=5\cdot {10}^3{\mu \text{m}}^{-2}$], and two different filament length intervals (upright triangles/squares: 1–4 μm; reversed triangles/circles: 4–8 μm). Segment length $\mathrm{\Delta }s=0.032\hspace{0.5em}\mu \text{m}$ (SI Materials and Methods). (B and C) Dependence of the second moment $\langle {\kappa }^2\rangle$ (in units of ${\ell }_p^{-2}$) of the curvature distribution function on filament length and motor density. At two fixed motor densities (blue: $m_b=10$; orange: $m_b=22$), the width $\langle {\kappa }^2\rangle$ remains essentially unchanged on varying filament length L. In contrast, raising the number of bound motors $m_b$ at fixed filament length ($L={\ell }_p/3$) leads to a linear increase in the variance of the distribution ($\langle {\kappa }^2\rangle$). The results of gliding assay experiments (triangles) and the one from the computer simulations (dots), as well as the prediction by Eq. 3 (red lines), agree quantitatively. Surface density of molecular motors, c, and average number of attached motors to a single filament, $m_b$, are related by $m_b\approx \delta \hspace{0.17em}c\left(d+2l_c\right)L$, where $\delta :=\left({\tau }_s+{\tau }_{\times }\right)/{\tau }_{off}$ is the motor’s duty ratio, d is the filament diameter, and $l_c$ is the capture length (SI Materials and Methods).

Kinetic Model.

What causes these nonthermal features of the curvature statistics and thereby invalidates an effective temperature description? Recall that for thermal systems, the stationary distribution results from an antagonism between agitating thermal noise and restoring forces due to the filament’s bending stiffness; the thermal diffusion constant $D_{th}$ is related to temperature and filament friction coefficient ζ by the Stokes–Einstein relation: $D_{th}=k_{B}T/\zeta$. For active filaments, stochastic contour fluctuations are caused by motors locally pushing the filament. Therefore, the amplitude of the curvature diffusion constant $D_{\kappa }$ is not determined by the energy scale $k_{B}T$ but by the number of bound motors engaged in a power stroke $m_b\hspace{0.17em}{\tau }_s/\left({\tau }_{\times }+{\tau }_s\right)$; note that the action of a molecular motor is characterized by stroke length and duration rather than by the force exerted during a stroke (30). Then, a dimensional analysis dictates that

$$D_{\kappa }\left(m_b\right)=a_D\cdot \frac{{\tau }_s^{-1}}{{\ell }_p^2}\cdot \frac{{\tau }_s}{{\tau }_{\times }+{\tau }_s}{m}_b,$$ [1]

where the typical time and curvature scales are given by the stroke time ${\tau }_s$ and the inverse thermal persistence length ${\ell }_p^{-1}$, respectively. The dimensionless parameter $a_D$ is material specific and may depend on the particular type of molecular motor and molecular features of the motor-filament interaction. In the present context, it may be considered as a fixed numerical prefactor as we do not vary any of these molecular properties. Up to this point, the active system would still be qualitatively similar to the thermal system, with an effective active temperature $T_{active}\sim m_b$, which cannot explain the exponential distribution in Figs. 1C and 3A. The key difference between the thermal and the active system lies in the nature of the restoring forces. In the active system, dissipative curvature relaxation is not driven by a bending potential as in the thermal case. In fact, as we observe in both experiment and computer simulations, the contour of the actin filament is almost never flat but undulated either due to Brownian fluctuations or the impact of the molecular motors and that relaxation of curvature appears as abrupt contour flattening events. Thus, we propose the following minimal principle of how activity affects the system that goes beyond a description based on effective temperature: We assume that the power strokes executed by motors that are attached along the filament pull it taut [this refers to pulling the filament straight; compressions are rather unlikely and not included in our models because the corresponding force exceeds the one for bending (31, 32)], $\kappa \to \eta \hspace{0.17em}\kappa$, with a stretching parameter $\eta <1$. The rate λ of these discrete jump-like processes is primarily determined by the time required for the rearrangement of bound motors on the filament: $\lambda =a_{\lambda }\cdot {\tau }_{\times }^{-1}$, with $a_{\lambda }$ being a numerical prefactor similar to $a_D$. Taken together, the curvature distribution is given by the stationary solution of the following kinetic equation:

$${\partial }_{t}P\left(\kappa \right)=D_{\kappa }\left(m_b\right){\partial }_{\kappa }^{2}P\left(\kappa \right)+\frac{\lambda }{\eta }\hspace{0.17em}P\left(\kappa /\eta \right)-\lambda \hspace{0.17em}P\left(\kappa \right).$$ [2]

This equation is mathematically equivalent to that obtained for the velocity statistics in an electrostatically driven granular gas suspension (21) or sheared hard spheres suspended in a fluid (22). In both cases, dissipation is of viscous origin, whereas the electrostatic driving or shearing in the steady state is successfully modeled as random injection of energy. In contrast, for the motility assay, both generation and relaxation of curvature are caused by the actions of molecular motors, and thereby the diffusion constant $D_{\kappa }$, as well as the time scale λ, are of active origin.

The stretching parameter η of the kinetic theory can be determined from the experimental and computational data by measuring the kurtosis of the curvature distribution ${\kappa }_4:=\langle {\kappa }^4\rangle /{\langle {\kappa }^2\rangle }^2$. With ${\kappa }_4=6/\left(1+{\eta }^2\right)$ (22), we find ${\kappa }_4=5.35$, or equivalently $\eta \approx 0.35$, for the data shown in Fig. 1C, reaffirming that the distribution is non-Gaussian. More importantly, our experiments and computer simulations consistently show that the kurtosis is to a good approximation independent of motor density and the filament length. This observation indicates that the stretching parameter η, and with it the shape of the curvature distribution, is system specific and only depends on particular molecular features of the motor-filament interaction. Moreover, it implies that the variance

$$\langle {\kappa }^2\rangle =\frac{2}{1-{\eta }^2}\hspace{0.17em}\frac{m_b}{{\ell }_p^2}\hspace{0.17em},$$ [3]

depends only on the filament stiffness and motor density but not on filament length; for the numerical prefactors, we have taken $a_D/a_{\lambda }=1$. These results of the kinetic theory agree very well with both the experimental and numerical data (cf solid lines in Fig. 3 B and C). Over a wide range of parameters, the variance of the curvature is independent of filament length and scales linearly with the motor density. This variance dependence strongly affirms the validity of the above kinetic equation and suggests that the exponential curvature distribution generically emerges in active systems with local and random injection and dissipation of energy where there is a time-scale separation between these two processes. Thus, as a general consequence of our analysis, we expect similar behavior in all active systems exhibiting those two features.

Relaxation Dynamics.

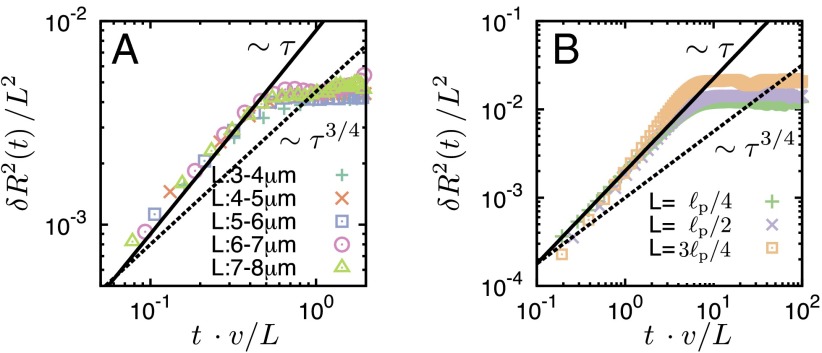
In addition to the curvature statistics, the action of the molecular motors also leads to qualitative changes in the filament’s dynamics compared with the thermal case (33). We measured the mean square displacement (MSD) of the end-to-end distance of a filament, $R\left(t\right)$. For thermally fluctuating filaments, it has been shown that the MSD for polymers of different length can be collapsed to a single curve if time is rescaled by the characteristic relaxation time of the first bending mode, $\tau \propto \left(\zeta /{\ell }_p\right)L^4$, and the amplitude by $\delta R_{eq}^2\propto L^4/{\ell }_p^2$ (33). In stark contrast, for active filaments, we obtained a scaling plot for the MSD by rescaling time in terms of the characteristic time for a filament to traverse a distance equivalent to its own length, $L/v$ (v, mean velocity) and the amplitude by $L^2$ (Fig. 4A). Moreover, the initial increase of the MSD exhibits power law behavior $\delta R^2\propto t^{\alpha }$ with an exponent $\alpha =1$ that is distinct from the thermal exponent $\alpha =3/4$ (30). The behavior of the MSD shows that the relaxation of bending modes is not driven by dissipative relaxation of bending modes but, again, is due to mechanisms linked to the motor activity. All of these qualitative features of the dynamics are also reproduced by the computational model (Fig. 4B and Fig. S6). Please note that exponents larger than the thermal exponent have been recently reported in analytic studies of active polymers of zero mean active force (34) and of driven active filaments (35).

Fig. 4.

MSD of the end-to-end distance of a filament, $\delta R^2\left(t\right)=\langle {\left[R\left(t\right)-R\left(0\right)\right]}^2\rangle$ (rescaled by $1/L^2$) vs. time t (rescaled by $v/L$). (A) Experiments were performed for filaments with the length range 3–8 μm. To achieve sufficient statistical power, we averaged over a large number of filaments and, in addition, performed a moving time average (Materials and Methods). The typical relaxation time is 0.5 s, which implies for a filament speed of 6 μm/s that the filament must move approximately half its length before bending modes are relaxed. (B) Results obtained from the computational model for different values of $L/{\ell }_p$ as indicated in the graph. Experiment and computer simulations both show that relaxation of bending modes for active filaments is independent of filament length L, and that $\delta R^2\left(t\right)\propto t^{\alpha }$ with an exponent $\alpha =1$, which significantly deviates from Brownian scaling with $\alpha =3/4$. There are differences in the absolute scale, which we attributed to the simplification of the motor dynamics and the motor-filament interaction. Parameters: $c=1.5\cdot {10}^3{\mu \text{m}}^{-2}$ corresponding to a linear motor density of $60/{\ell }_p$.

Conclusion

Active actin filaments in the motility system exhibit nonthermal curvature statistics and a faster relaxation of filament bends than in the thermal case. Non-Gaussian curvature distributions have already been found in reptating equilibrium polymer networks (36); however, this behavior is rationalized in terms of entropic trapping effects. Here we showed that nonthermal curvature statistics and relaxation of filament bends arise due to nonequilibrium energy input of molecular motors dominating over thermal fluctuations. Specifically, the exponential curvature distribution originates from the random and local injection and dissipation of energy due to the actions of the molecular motors. Although molecular motors acting as cross-links are crucial to reproduce the saturation of velocity at large motor densities, the cross-link property has only a little impact on the curvature distribution and the filament’s relaxation dynamics of bending modes. Our findings suggest that anomalous curvatures of actin filaments in the motility assay originate from motors along the filament, which locally and independently increase and decrease the filament’s elastic energy.

Although our results are derived from a specific in vitro assay, they may have implications for a broader class of active matter systems, e.g., swimmer suspensions, fluctuating active membranes and gels, tissues, or flocks, where the constituents gain and dissipate energy locally. For example, shape fluctuations of the phospholipid bilayer in human red blood cells have been shown to exhibit nonequilibrium signatures arising from the presence of ATP (24). Although the physical mechanisms of anomalous fluctuations are certainly system specific, active events like power strokes of molecular motors or collisions between swimmers result in nonthermal statistics and overpopulated tails of the distribution functions.

In general, nonthermal statistics are manifested in quantities such as time correlation and scaling of a polymer’s end-to-end distance, which lead to physical bulk properties of active matter (e.g., rheological or mechanical) (11, 13, 17, 23) that differ distinctively from those found in equilibrium systems. A general understanding of nonthermal statistics in active matter should therefore provide insights into the role of fluctuations in biological systems (18).

Materials and Methods

Assay Preparation.

We used standard protocols to prepare the actin filaments and heavy meromyosin (HMM) motor proteins. Fluorescently labeled filaments stabilized with Alexa Fluor 488 phalloidin were used to visualize filaments with a fluorescence microscopy. Flow chambers built from nitrocellulose-coated coverslips were incubated with HMM (15–250 μg/mL). BSA was used to passivate the surfaces inside the chamber after the incubation with HMM, and then a dilute solution of actin filaments (25 nM) was introduced. We added 2 mM ATP to enable the HMM to drive the filaments, and a standard antioxidant buffer supplement was used to prevent oxidation of the fluorophore.

Imaging.

A Leica DMI 6000B inverted microscope with a 100$\times$ oil objective (NA: 1.4) was used to acquire data. Images of resolution 1,344 $\times$ 1,024 pixels were captured with a CCD camera (C4742-95; Hamamatsu) attached to a 1.0 camera mount. Acquisition and storage of the images were performed by the image processing software OpenBox.

Data Analysis.

To obtain the filament contour from the images, we used a spline fit; for further detail, see SI Materials and Methods. The contour was discretized into equal segments of length $\mathrm{\Delta }s=0.032\hspace{0.5em}\mu \text{m}$ leading to $\mathcal{O}\left(100\right)$ coordinates ${\overrightarrow{x}}_i$, where i denotes the segment. Note that before the spline fit, the raw images have a resolution of $\approx 0.06\hspace{0.5em}\mu \text{m}$. We then calculated the local curvature ${\kappa }_{\left(i\right)}=\text{arccos}\left({\overrightarrow{T}}_i{\overrightarrow{T}}_{i+1}\right)/\mathrm{\Delta }s$, where ${\overrightarrow{T}}_i=\left({\overrightarrow{x}}_{i+1}-{\overrightarrow{x}}_i\right)/\mathrm{\Delta }s$ signifies the local tangent vector. Here, note that curvature for both experimental data and the simulation model is not continuous and defined between discrete points along the filament tangent. For each filament, ∼50–300 curvature values (depending on filament length) were obtained. For each motor density investigated, $P\left(\kappa \right)$ is based on ${10}^6$–${10}^7$ sample points. Due to the resolution of the images and the curvature analysis algorithm, curvatures lower than $0.1\hspace{0.5em}{\mu \text{m}}^{-1}$ are indefinite and thereby neglected in the statistical analysis. To ensure sufficient statistical power, the MSD was estimated by averaging over a large number of filaments and using a time average (33). The latter was obtained by scanning over different initial times $t_0$, i.e., $\delta R^2\left(\tau \right)=\langle {\langle {\left[R\left(\tau +t_0\right)-R\left(t_0\right)\right]}^2\rangle }_{t_0}\rangle$. Trajectories longer than 5 s were used; however, longer time tracking was not possible as active filaments soon moved out of the field of view.