Log-gamma linear-mixed effects models for multiple outcomes with application to a longitudinal glaucoma study

Abstract

Glaucoma is a progressive disease due to damage in the optic nerve with associated functional losses. Although the relationship between structural and functional progression in glaucoma is well established, there is disagreement on how this association evolves over time. In addressing this issue, we propose a new class of non-Gaussian linear-mixed models to estimate the correlations among subject-specific effects in multivariate longitudinal studies with a skewed distribution of random effects, to be used in a study of glaucoma. This class provides an efficient estimation of subject-specific effects by modeling the skewed random effects through the log-gamma distribution. It also provides more reliable estimates of the correlations between the random effects. To validate the log-gamma assumption against the usual normality assumption of the random effects, we propose a lack-of-fit test using the profile likelihood function of the shape parameter. We apply this method to data from a prospective observation study, the Diagnostic Innovations in Glaucoma Study, to present a statistically significant association between structural and functional change rates that leads to a better understanding of the progression of glaucoma over time.

1 Introduction

Glaucoma is an eye disease characterized by progressive neuroretinal rim thinning, excavation, and loss of the retinal nerve fiber layer. These structural changes are usually accompanied by functional losses. Although there is a relationship between structural and functional damage in glaucoma, the precise association and the evolution of this association over time are still unclear. For example, it is not yet known whether the glaucomatous structure and function develop at about the same rate, and how rates of change in structure are related to those of function at different stages of the disease. The evolution of association in rates of change is essential to enhance the understanding of the glaucomatous process and to determine the relative utility of tests for structure and function in monitoring different stages of glaucoma. Many studies have investigated the structural and functional relationship in glaucoma (Harwerth et al., 2010; Malik et al., 2012; Medeiros et al., 2012). These studies have shown different degrees of association between quantitative structural measures derived from imaging technologies and psychophysical tests such as standard automated perimetry (SAP). Similarly, large disagreements have been reported in longitudinal studies evaluating glaucoma progression (Keltner et al., 2006; Strouthidis et al., 2006).

The association between the functional and structural changes in glaucoma can be modeled by studying the relationships among the subject-specific effects in mixed effects models for the longitudinal data. Statistically, we study the correlation of the random intercepts between the two change responses, and the correlation of the random slopes of time effects. Multivariate models are used when responses for two or more response variables are observed over time for each individual in a longitudinal study; such data are commonly collected in the health sciences and epidemiological studies. There is much literature on multivariate longitudinal data. For example, Reinsel (1984) considered the random effects model for multiple outcomes with a complete and balanced design. Shah et al. (1997) extended linear-mixed models to allow for multiple longitudinal outcomes in the case where the number and timing of observations may differ from individual to individual. Roy and Lin (2000) extended latent variable models to multivariate longitudinal data. There are two sources of within-subject correlation that should be reflected in the multiple-outcomes model: (i) among different outcomes; (ii) among repeated measures of the same outcome over time. Although one can perform separate analyses of the two outcomes, this does not address the main question of interest: how overall treatment practices have changed over time. Moreover, the analysis will have increased power if information from all of the outcomes is used (Pocock et al., 1987).

Our research is motivated by analyzing data obtained from a prospective observational study, the Diagnostic Innovations in Glaucoma Study (DIGS). The DIGS started in Sep. 2005 and finished recruitment in Aug. 2011. It was carried out at the Hamilton Glaucoma Center of the Department of Ophthalmology, University of California, San Diego. The DIGS was designed to investigate the longitudinal structure and function relationship in glaucoma. Two responses, the visual field index (VFI) and the global average thickness of the retinal nerve fiber layer (RNFL), were collected for 203 patients at 6-month intervals. The first response characterizes the functional loss, while the second characterizes the structural changes. Section 5 gives more information about the study and the responses.

In a preliminary analysis (see Supporting Information Fig. S1), we observed that the intercepts from a within-subject linear regression analysis fitting the logit-transformed VFI to time had a left-skewed distribution, while the within-subject distributions of the slopes for VFI and those of the intercepts and slopes for RNFL were roughly symmetric. To accommodate the skewness of one of the random effects and the associations among the multivariate responses, we propose extending the mixed effects model for longitudinal data of Zhang et al. (2008) to a bivariate linear-mixed effects model where the random effects are assumed to follow the log-gamma distribution. For the multivariate response model, the usual distributional assumption for the random effects is multivariate normal. However, there are only a few results on the consequences for statistical inference of misspecifying the random-effects distribution. This may impact the bias and variance of the parameter estimation and the power of hypothesis-testing procedures. Ghosh et al. (2007) developed a Bayesian approach to the bivariate-mixed effects model via a multivariate skew-normal distribution. However, there is no closed form of the marginal distribution of the responses when the random effects are assumed to be nonnormal. In this paper, we present a nonnormal linear-mixed effects model for multiple outcomes, which is feasible mathematically and computationally less complex. It is applied to the bivariate longitudinal study of glaucoma to investigate the association between the structural and functional progressions in the patients’ eyes.

The remainder of this article is organized as follows. Section 2 presents a nonnormal multivariate linear-mixed effects model. Section 3 discusses the inferences of the fixed effects, variance components, and random effects. We use a Gauss–Newton algorithm to calculate the maximum likelihood estimates (MLEs) of the parameters and the Markov chain Monte Carlo (MCMC) method for the inference of the random effects. Section 4 presents a lack-of-fit test, based on the fact that the limiting distribution of the log-gamma distribution is normal, to test the adequacy of the log-gamma assumption. Section 5 presents the tests and the results, and Section 6 provides a discussion. Two figures and a brief introduction to the log-gamma distribution are given in the Supplementary Material.

2 Model and assumptions

In this section, we define a general multivariate linear-mixed effects model assuming that the skewed random effect follows a log-gamma distribution. Consider a multivariate longitudinal study with p responses and N subjects. For i = 1,…, N and k = 1,…, p, let ${\mathbf{Y}}_{\mathit{ik}}=(Y_{i1k},\dots ,Y_{{\mathit{in}}_{i_k}k})\prime$ denote the collection of $n_{i_k}$ observations for the k-th outcome of the i-th subject. We assume a linear-mixed effects model for Y_ik of the form

$${\mathbf{Y}}_{\mathit{ik}}={\mathrm{X}}_{\mathit{ik}}{\mathit{\beta }}_k+{\mathrm{Z}}_{\mathit{ik}}{\mathbf{b}}_{\mathit{ik}}+{\mathit{\epsilon }}_{\mathit{ik}},i=1,\dots ,N;k=1,\dots ,p.$$ (1)

Here β_k is a vector of fixed effects for the k-th response, X_ik is the design matrix of fixed effects β_k, b_ik is a vector of random effects for the k-th response, and Z_ik is the design matrix of random effects b_ik.

Further, let ${\mathbf{Y}}_i=({\mathbf{Y}}_{i1}^{\prime },\dots ,{\mathbf{Y}}_{ip}^{\prime })\prime$ be a stacked vector of p responses for the i-th subject, $\mathit{\beta }=({\mathit{\beta }}_1^{\mathbf{\prime }},\dots ,{\mathit{\beta }}_p^{\mathbf{\prime }})\prime$ be a stacked vector of all fixed effects, ${\mathbf{b}}_i={({{\mathbf{b}}^{\mathbf{\prime }}}_{i1},\dots ,{{\mathbf{b}}^{\mathbf{\prime }}}_{ip})}^{\prime }$ be a stacked vector of all random effects, X_i = diag (X_i1,…, X_ip) be a block diagonal design matrix for all fixed effects, Z_i = diag (Z_i1,…, Z_ip) be a block diagonal design matrix for all random effects, and ${\mathit{\epsilon }}_i=({\mathit{\epsilon }}_{i1}^{\mathbf{\prime }},\dots ,{\mathit{\epsilon }}_{\mathit{ip}}^{\mathbf{\prime }})\prime$ be a stacked vector of error terms. Then the linear-mixed effects model in (1) can be written

$${\mathrm{Y}}_i={\mathrm{X}}_i\mathit{\beta }+{\mathrm{Z}}_i{\mathbf{b}}_i+{\mathit{\epsilon }}_i,i=1,\dots ,N.$$ (2)

We assume that Y_i is independent of Y_j for i ≠ j. That is, the stacked response vectors of two different subjects are independent. We also assume that Y_ik and Y_il, k≠l are conditionally independent given the random effects b_i. That is, for the same subject, the k-th and l-th response vectors are conditionally independent, given the random effects for that subject. Further, we assume that E (b_i) = 0 and E(ε_i) = 0.

To model the skewness of the random effects, we rearrange the components in b_i and divide them into two parts. Denote the reordered vector ${\mathbf{b}}_i^{\ast }=(b_{i1}^{\ast },\dots ,b_{\mathit{iq}}^{\ast })\prime$. The first q₀ components have skewed distributions, and the remaining q – q₀ components are symmetric. The reordering also results in the interchange of the columns in the design matrix Z_i according to the subscripts of ${\mathbf{b}}_i^{\ast }$. To allow correlated random intercepts and random slopes, we define ${\mathbf{b}}_i^{\ast }=\mathrm{R}{\mathbf{s}}_i^{\ast },$, where ${\mathbf{s}}_i^{\ast }=(s_{i1}^{\ast },\dots ,s_{\mathit{iq}}^{\ast })\prime$, and the linear transformation matrix R is an upper triangular matrix with unknown entries r_ij, 1 ≤ i < j ≤ q, and 1’s on the diagonal. The components of the vector ${\mathbf{s}}_i^{\ast }$ are independent of each other. Expressing the transformation in matrix notation gives

$$\left(\begin{array}{c}\hfill b_{i1}^{\ast }\hfill \\ \hfill ⋮\hfill \\ \hfill b_{{\mathit{iq}}_0}^{\ast }\hfill \\ \hfill ⋮\hfill \\ \hfill b_{\mathit{iq}}^{\ast }\hfill \end{array}\right)=\left(\begin{array}{ccccc}\hfill 1\hfill & \hfill \dots \hfill & \hfill r_{1q_0}\hfill & \hfill \dots \hfill & \hfill r_{1q}\hfill \\ \hfill \dots \hfill & \hfill \dots \hfill & \hfill \dots \hfill & \hfill \dots \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill \dots \hfill & \hfill 1\hfill & \hfill \dots \hfill & \hfill r_{q_{0}q}\hfill \\ \hfill \dots \hfill & \hfill \dots \hfill & \hfill \dots \hfill & \hfill \dots \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 1\hfill \end{array}\right)\left(\begin{array}{c}\hfill s_{i1}^{\ast }\hfill \\ \hfill ⋮\hfill \\ \hfill s_{i{q}_0}^{\ast }\hfill \\ \hfill ⋮\hfill \\ \hfill s_{iq}^{\ast }\hfill \end{array}\right).$$ (3)

In (3), we specify that just one random effect in ${\mathbf{s}}_i^{\ast }$, $s_{{\mathit{iq}}_0}^{\ast }$, is from the log-gamma distribution. See Section 2 of the Supplementary Material for a brief introduction to the log-gamma distribution. From (3), we observe that $b_{i1}^{\ast },\dots ,b_{{\mathit{iq}}_0}^{\ast }$ are linear combinations of $s_{{\mathit{iq}}_0}^{\ast }$ and other random effects in ${\mathbf{s}}_i^{\ast }$. By specifying the distribution of $s_{{\mathit{iq}}_0}^{\ast }$ to be skewed, we can model $b_{i1}^{\ast },\dots ,b_{i{q}_0}^{\ast }$ as skewed random effects. Allowing multiple random effects in ${\mathbf{s}}_i^{\ast }$ to be from the log-gamma distribution would complicate the calculation of the MLEs of the unknown parameters. Moreover, in our real-data analysis, there is only one skewed random effect, that is the random intercept for the logit-transformed VFI. In (3), we just need to set q₀ = 1. More details can be found in Section 5.

The mean of the log-gamma random variable $s_{{\mathit{iq}}_0}^{\ast }$ is set to zero, and the remaining components of ${\mathbf{s}}_i^{\ast }$ are assumed to have a multivariate normal distribution with mean 0 and diagonal covariance matrix G. Thus, from (3), $E({\mathbf{b}}_i^{\ast })=0$ and so E(b_i) = 0. If the distribution of the random effect $b_{{\mathit{iq}}_0}^{\ast }$ is positively skewed, then a minus log-gamma distribution should be selected for $s_{{\mathit{iq}}_0}^{\ast }$ because the log-gamma distribution is negatively skewed (see Supporting Information Fig. S3). For the other skewed components, the sign of the coefficient of $s_{\mathit{ij}}^{\ast },1\le j<q_0$, determines the direction of skewness. The advantage of introducing the linear transformation matrix R rather than specifying the correlated random effects directly is that this gives a relatively simple model and also makes it easy to implement the log-gamma mixed-effects model.

3 Inference

In this section, we discuss how to calculate the estimates of the unknown parameters and the random effects. We denote the unknown parameters as θ = (β′,G,R,κ, Σ_i)′, where β contains the regression coefficients, G contains the covariance components, R contains the parameters of the linear transformation matrix in (3), κ is the log-gamma shape parameter, and Σi = Cov(ε_i) = diag $({\sigma }_1^2{I}_{n_{i_1}},{\sigma }_2^2{I}_{n_{i_2}},\dots ,{\sigma }_p^2{I}_{n_{i_p}})$ contains the conditional covariance parameters. The estimation and inference of θ are based on the marginal likelihood function, which is given by

$$L(\mathit{\theta })={\displaystyle \prod _{i=1}^N{\displaystyle \int \{{\displaystyle \int \cdots {\displaystyle \int \varphi ({\mathbf{y}}_i|{\mathbf{s}}_i^{\ast })\cdot \varphi (s_{i1}^{\ast },\dots ,s_{i{q}_0-1}^{\ast },s_{i{q}_0+1}^{\ast },\dots ,s_{\mathit{iq}}^{\ast })}}}}d{s}_{i1}^{\ast }\cdots d{s}_{i{q}_0-1}^{\ast }d{s}_{i{q}_0+1}^{\ast }\cdots d{s}_{\mathit{iq}}^{\ast }\}\cdot f(s_{{\mathit{iq}}_0}^{\ast })d{s}_{{\mathit{iq}}_0}^{\ast },$$ (4)

where $f(s_{{\mathit{iq}}_0}^{\ast })$ represents the density function of the standard log-gamma distribution (see Eq. (1) of the Supplementary Material). The MLE of θ is defined to be $\widehat{\mathit{\theta }}=\text{arg}{\text{sup}}_{\mathit{\theta }}L(\mathit{\theta })$. By verifying the regularity conditions in Weiss (1973) and Jiang (2001), we can show that the MLE $\widehat{\mathit{\theta }}$ is consistent and asymptotically normal, with the asymptotic covariance matrix equal to the inverse of the Fisher information matrix. Because there is no closed-form expression for the integration (4), we need numerical integration techniques to maximize the likelihood function.

To find $\widehat{\mathit{\theta }}$ numerically, we use a Gauss–Newton algorithm (Ruppert, 2005), in which the Fisher information matrix is approximated by $\text{B(}\mathit{\theta })={\displaystyle {\sum }_{i=1}^N{i}_i}({\mathbf{y}}_i;\mathit{\theta })i_i({\mathbf{y}}_i;\mathit{\theta })\prime$, where l_i(y_i; θ) is the log-likelihood contributed by the i-th subject and l_i(y_i; θ) is the first derivative of l_i(y_i; θ) with respect to θ. Thus, only the first-order derivatives of the log likelihood are involved. The key step of this algorithm is to halve the value of δ, which guarantees a steady increase in the likelihood between iterations. To be more precise, the (k + 1)-th iteration calculates

$${\mathit{\theta }}^{k+1}={\mathit{\theta }}^k+\delta {\{\text{B(}{\mathit{\theta }}^k\text{)}\}}^{-1}i({\mathit{\theta }}^k),$$

where δ is the step-halving term and $i(\mathit{\theta })={\displaystyle {\sum }_{i=1}^N{i}_i}({\mathbf{y}}_i;\mathit{\theta })$. The algorithm starts with δ = 1 and halves δ until the log-likelihood function l(θ) = log L (θ) satisfies l(θ^k+1) > l(θ^k). It stops when an increase in the likelihood is no longer possible, or the difference between two consecutive updates is smaller than a prespecified precision. The starting values are obtained by fitting a bivariate linear-mixed model assuming normal random effects using the SAS procedure MIXED, as discussed by Thiébaut et al. (2002).

Once $\widehat{\mathit{\theta }}$ has been obtained, we use it to estimate the random effects. The posterior distribution of ${\mathbf{b}}_i^{\ast }$ is given by

$$f({\mathbf{b}}_i^{\ast }|{\mathbf{y}}_i)=\frac{\varphi ({\mathbf{y}}_i|{\mathbf{b}}_i^{\ast })f({\mathbf{b}}_i^{\ast })}{{\displaystyle \int \varphi ({\mathbf{y}}_i|{\mathbf{b}}_i^{\ast })f({\mathbf{b}}_i^{\ast })d{\mathbf{b}}_i^{\ast }}}.$$ (5)

The posterior mean is used to predict the random effects ${\mathbf{b}}_i^{\ast }$, and the unknown parameters θ are replaced by their MLEs $\widehat{\mathit{\theta }}$. We may use the MCMC to simulate direct draws from the posterior distribution in (5) to obtain the posterior mean.

4 Lack-of-fit test

In this section, we consider the lack-of-fit test. That is, we would like to test if the log-gamma distribution is as good as or better than the normal distribution. Note that the mean and variance of the standard log-gamma distribution W are E(W)=ψ(κ) and Var(W)=ψ′(κ), which behave like log κ and κ⁻¹ respectively for large κ. Here ψ and ψ′ are the digamma and trigamma functions. It has been shown that the transformed log-gamma variate Z = κ^1/2 (W – logκ) converges to the standard normal distribution as κ → ∞ (Bartlett and Kendall, 1946; Prentice, 1974). Therefore, for the lack-of-fit test, we test if κ₀ = ∞, where κ₀ is the true value of κ.

Let the profile log-likelihood function be l_p (κ) for κ. The statistic of the likelihood ratio test Λ(κ₀) for the hypothesis H₀: κ = κ₀ versus H_a : κ ≠ κ₀ is

$$\mathrm{\Lambda }({\kappa }_0)=2l_p(\widehat{\kappa })-2l_p({\kappa }_0),$$

where $\widehat{\kappa }$ is the MLE that maximizes l_p(κ). For finite κ₀ the distribution of Λ(κ₀) is asymptotically ${\mathrm{\chi }}_1^2$ under H₀. A slight technical difficulty arises in testing the normal model, since κ₀ = ∞ is on the boundary of the parameter space. However, the other parameters in θ with true values are not on the boundary. Therefore. when κ₀ = ∞, the asymptotic distribution of Λ(κ₀) is a 50:50 mixture of ${\mathrm{\chi }}_0^2$ and ${\mathrm{\chi }}_1^2$; then for $a\le 0,\mathit{Pr}(\mathrm{\Lambda }(\text{∞})\le a)=0.5+0.5\mathit{Pr}({\chi }_1^2\le a)$ (Self and Liang, 1987).

5 Data analysis

In DIGS, subjects were included if they had a diagnosis of glaucoma or were suspected of having the disease at the baseline. At each visit during the follow-up, the subjects underwent a comprehensive ophthalmologic examination and additional tests designed to evaluate glaucoma structure and function. They were tested at 6-month intervals. The functional assessment was performed with visual field testing by SAP (the SITA 24-2 test, Humphrey perimeter, Carl-Zeiss Meditec, Dublin, CA). The evaluation of the rates of visual field change during the follow-up was performed using the VFI. The VFI represents the percentage of normal age-corrected visual function, and it is used to calculate rates of progression and the staging of glaucomatous functional damage. The VFI can range from 100% (normal visual field) to 0% (perimetrically blind field). The structural assessment was performed by measuring the thickness of the RNFL using optical coherence tomography (OCT). The RNFL thickness measurements were obtained in a 3.2-mm diameter circle around the optic nerve head. The global average RNFL thickness (calculated as the average of all the RNFL measurements obtained in the circle around the optic nerve) was used in this study.

A total of 1939 repeated measures were collected from each of the 203 patients included in DIGS. The mean (± standard deviation) age of the participants was 64.1 ± 12.1 years; 54.5% of the subjects were female and 32.9% were of African ancestry. There was a wide range of disease severities at the baseline, with the SAP mean deviation (MD) values ranging from −19.6 to 2.3 dB and the RNFL thickness values ranging from 40 to 123 μm.

Because we investigate two types of outcomes simultaneously in this study, we have p = 2 in the general model (2). The VFI scores are proportional data, so we apply a logit transformation. The measures of RNFL are regular continuous values. We assume that the disease progression is a linear function of time and that the slope depends on the individual patient. For the i-th patient, the baseline measures of the k-th (k = 1, 2) outcome recorded can be expressed as β_k0 + b_ik0, where β_k0 is an unknown parameter and b_ik0 is the random intercept. Several measures are collected at time t_ijk, for $j=1,\dots ,n_{i_k}$. The coefficient β_k1 is an unknown parameter, b_ik1 is the random slope for the i-th patient, and the subject-specific progression rate can be expressed as β_k1 + b_ik1t_ijk. Hence, b_i1 = (b_i10, b_i11)′, b_i2 = (b_i20, b_i21)′, and b_i = (b_i10, b_i11, b_i20, b_i21)′. Therefore, we have q = 4 in model (3). Furthermore, a random error is associated with each time measurement. Using the vector and matrix notation, the linear-mixed effects model can be written

$$\left(\begin{array}{c}\hfill {\mathbf{Y}}_{i1}\hfill \\ \hfill {\mathbf{Y}}_{i2}\hfill \end{array}\right)=\left(\begin{array}{cc}\hfill {\mathrm{X}}_{i1}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\mathrm{X}}_{i2}\hfill \end{array}\right)\left(\begin{array}{c}\hfill {\mathit{\beta }}_1\hfill \\ \hfill {\mathit{\beta }}_2\hfill \end{array}\right)+\left(\begin{array}{cc}\hfill {\mathrm{Z}}_{i1}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\mathrm{Z}}_{i2}\hfill \end{array}\right)\left(\begin{array}{c}\hfill {\mathbf{b}}_{i1}\hfill \\ \hfill {\mathbf{b}}_{i2}\hfill \end{array}\right)+\left(\begin{array}{c}\hfill {\mathit{\epsilon }}_{i1}\hfill \\ \hfill {\mathit{\epsilon }}_{i2}\hfill \end{array}\right)$$

where

$${\mathbf{X}}_{\mathit{ik}}={\mathbf{Z}}_{\mathit{ik}}=\left(\begin{array}{cc}\hfill 1\hfill & \hfill t_{i1k}\hfill \\ \hfill 1\hfill & \hfill t_{i2k}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill 1\hfill & \hfill t_{i{n}_{i_k}k}\hfill \end{array}\right),k=1,2.$$

A preliminary analysis indicated that the intercepts of the VFI scores, the first outcome, show a negatively skewed pattern when only the linear-mixed model for the Y_i1’s is fitted. Histograms of the regression coefficients for the within-subject regressions of the two outcomes on time are shown in Supporting Information Fig. S1. They not only verify that the distribution of the subject-specific intercepts for VFI is negatively skewed but also clearly indicate the relationship between the two random intercepts and that of the two slopes.

The random intercept of the first outcome b_i10 in b_i is the only skewed element. It is in the first position, so there is no need to reorder b_i to obtain the desired form. That is, q₀ = 1 in (3). Then, we define the linear transformation b_i = Rs_i with

$$\mathrm{R}=\left(\begin{array}{cccc}\hfill 1\hfill & \hfill r_1\hfill & \hfill r_2\hfill & \hfill r_3\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill r_4\hfill & \hfill r_5\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill r_6\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right),$$

where s_i = (s_i10, s_i11, s_i20, s_i21)′, with independent components. We model s_i10 through the log-gamma distribution, and the remaining components in s_i are multivariate normal. Since the log-gamma distribution is negatively skewed, b_i10 is negatively skewed also. Conditioning on the random effects, we assume the responses for a particular individual to be independent and conditionally normal:

$${\mathbf{Y}}_i|{\mathbf{s}}_i~N({\mathrm{X}}_i\mathit{\beta }+{\mathrm{Z}}_i\mathrm{R}{\mathbf{s}}_i,{\sum }_i),i=1,\dots ,N.$$

Table 1 gives the estimates of the parameters in the log-gamma and normal random effects models. The estimates of the parameters in the log-gamma model are close to those of the normal model. In univariate longitudinal data analysis, deviations from the normality assumption have little impact on the estimation of the fixed effects and the variance components. Based on the parameter estimates in Table 1, the same appears to be true for the multivariate case. We use the multivariate delta method and the asymptotic properties of the MLEs $\widehat{\mathit{\theta }}$ to calculate the standard errors of the variance components of b_i. The introduction of the linear transformation matrix R does not lead to any difficulties in the computation of the standard errors of the variance component estimates. The computational complexity is similar to that for the setting of the random effects in the normal case; they are usually specified with a nondiagonal covariance matrix. The estimated average regression coefficients for VFI and RNFL are −0.0327 and −0.5310, respectively. For both outcomes, larger values of the regression coefficients of time indicate a slower deterioration. Therefore, negative slopes indicate disease progression over time.

Table 1.

Estimates of the fixed effects and the variance components of the log-gamma and normal random effects models.

Para.	Log-gamma			Normal
	Estimate	SE	p-value	Estimate	SE	p-value
β10	4.0425	0.0623	<0.0001	3.9671	0.0919	<0.0001
β11	−0.0327	0.0153	0.0326	−0.0290	0.0148	0.050
β20	47.7384	0.2876	<0.0001	47.4261	0.4630	<0.0001
β21	−0.5310	0.0297	<0.0001	−0.5746	0.0713	<0.0001
${\sigma }_{b_{i10}}^2$	0.9117	0.0360	<0.0001	1.5998	0.1705	<0.0001
${\sigma }_{b_{i11}}^2$	0.0031	0.0006	<0.0001	0.0104	0.0040	<0.0001
${\sigma }_{b_{i20}}^2$	35.4466	3.2269	<0.0001	41.6805	4.3238	<0.0001
${\sigma }_{b_{i21}}^2$	0.3243	0.0807	<0.0001	0.3948	0.1034	<0.0001
${\sigma }_1^2$	0.2116	0.0083	<0.0001	0.2396	0.0119	<0.0001
${\sigma }_2^2$	2.1999	0.1229	<0.0001	2.4707	0.1778	<0.0001

The profile likelihood functions l_p(κ) are derived by maximizing log L(θ) with κ fixed. The likelihood-ratio statistic Λ (∞) is 2402.4, and the p-value is extremely small: < 0.0001. There is strong evidence to reject the null hypothesis that the normal random effects model is equivalent to the log-gamma model, suggesting that the log-gamma model has a better fit to the data.

Table 2 lists the means and standard errors of the N = 203 predicted random effects under the log-gamma and normal models, the means of the posterior distributions of b_i given Y_i. In the log-gamma model, given estimates of the fixed effects, variance components, and R, the random effects b_i were predicted from 18,000 sample points of three chains generated from the posterior distributions f(b_i|y_i), with the first 4000 sample points discarded for burn-in. In the normal model, the random effects b_i were predicted from Empirical Bayes estimates. The distributions of the estimates of the random effects b_i from the N = 203 posterior means under the log-gamma model are shown in Supporting Information Fig. S2. We found that the distribution of the predicted random effects (b_i10’s) is negatively skewed, which confirms the observed skewness from the preliminary study. The estimate of the skewness parameter κ = 2.5762 shows that the estimated distribution of the random slopes is not close to a normal distribution.

Table 2.

Results for the posterior distribution outcomes of random effects under the log-gamma and normal random effects models.

Random effect	Log-gamma		Normal
	Mean	SE	Mean	SE
bi10	−0.0676	1.2142	−0.0000	1.2444
bi11	0.0006	0.0672	0.0000	0.0538
bi20	−0.3418	6.5187	−0.0002	6.3864
bi21	−0.0186	0.7049	0.0001	0.3978

The correlations between the two random intercepts, ρ₀, and between the two random slopes, ρ₁, of the two outcomes are of most interest. We obtained the correlations of the pairs of random effects and their standard errors from the log-gamma and normal-mixed effects models; they are presented in Table 3. Under the log-gamma model, for the null hypothesis H₀: ρ₀ = 0, the Wald test statistic has z = 21.7790 with p-value < 0.0001, which shows that there is a significant positive relationship between the two random intercepts of the regressions of the two test results on time. The positive relationship between the intercepts of the two outcomes is clearly seen in the scatterplot of the intercepts from the single-patient regression analysis, which is shown in the upper-left panel of Fig. 1. The Wald test for the hypothesis regarding the correlation of slopes, H₀ : ρ₁= 0, gives z = 3.1588 with p-value 0.0016. The intercepts represent the level of disease at the start of the study. The positive correlation coefficient of the two random intercepts indicates that the structural and functional outcomes are consistent with each other. A high baseline in one test will be associated with a high level in the other. Most importantly, the rates of progressive RNFL loss are significantly associated with the rates of functional change in glaucoma, as indicated by the small p-value of the correlation between the two random slopes. Under the normal model, the test for H₀ : ρ₀ = 0 gives z = 8.8771 with p-value < .0001, and the test for slopes, H₀: ρ₁= 0, has z = 1.4845 with p-value 0.1378. Clearly the model with misspecified distributions of the random effects gives less reliable conclusions on the correlations of the random effects. The normal model underestimates the correlation of the random slopes of the two outcomes, which results in a small value in the test statistic and a large p-value. The log-gamma mixed-effects model gives a better fit to the data, so the results on the correlations of the random effects are more reliable. Hence, the progression rates of function in glaucoma, measured with the VFIs, and the progression rates of structures, measured with the RNFLs, are shown to be positively correlated in glaucoma patients.

Table 3.

Correlations of random effects under the log-gamma and normal random effects models.

corr	Log-gamma			Normal
	Estimate	SE	p-value	Estimate	SE	p-value
ρ0	0.7688	0.0353	<0.0001	0.5044	0.0568	<0.0001
ρ1	0.8794	0.2784	0.0016	0.3280	0.2210	0.1378

Figure 1.

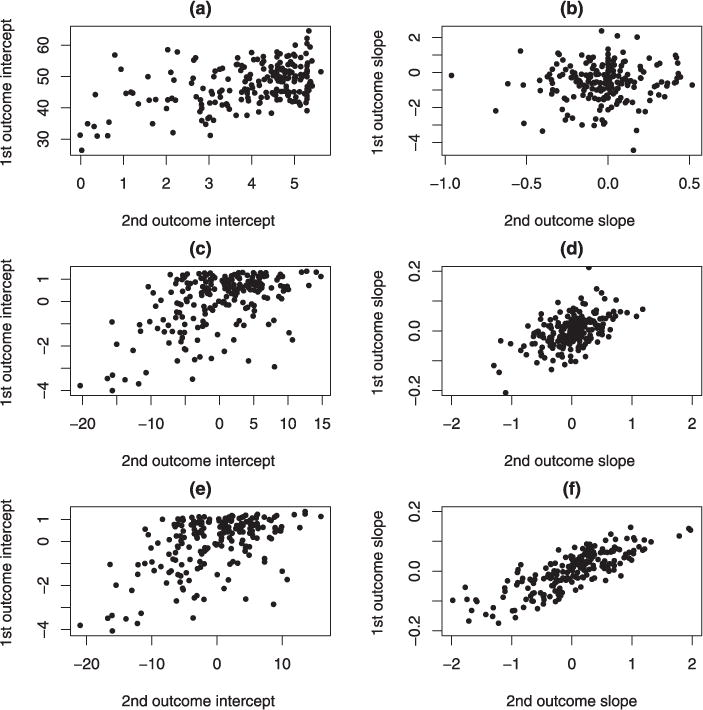
Panels (A) and (B) are scatterplots of the intercepts and slopes for the within-subject regressions of two outcomes on time. Panels (C) and (D) are scatterplots of the empirical estimates of the intercepts and slopes from the posterior distributions of the random effects of the normal random effects model. Panels (E) and (F) are scatterplots of the estimates from the log-gamma random effects model.

6 Discussion

We have proposed a class of log-gamma linear-mixed models for modeling longitudinal data with multiple outcomes and applied it to a longitudinal glaucoma study. To address the main scientific questions of whether the structural and functional measurements are associated and how the progressions of the two outcomes are related, we performed hypothesis tests based on the proposed model. We concluded that the progressions of the structural and functional outcomes are positively correlated, and the rates of change in the two outcomes are highly correlated.

Besides reflecting the covariance structure of the multivariate responses, the main advantage of the class of log-gamma mixed-effects models lies in its simplicity in accounting for the skewness of the random effects, which results in a more efficient estimation of the parameters. We considered the density functions in the location family of the standard log-gamma distributions with mean zero for the modeling of the skewed random effects. This subfamily of the location-scale family of the log-gamma distributions is sufficient to model the skewness, and it reduces the computational complexity of the search for the MLEs of the marginal log-likelihood function, especially when the dimension of the vector of parameters is high. The expression of the reordered random effects by the product of the linear transformation matrix and the random vector of independent components avoids high-dimensional integration in the marginal log-likelihood function and makes the implementation feasible. The introduction of the linear transformation matrix not only accounts for the correlated random effects, but also ensures that the dimension of the numerical integration of the marginal likelihood is one, since the convolution of two normal distributions is still normal. This new class provides a generalized method for estimating the correlation between two or more slopes. In the case of a single response, the model reduces to that of Zhang et al. (2008). The family of log-gamma distributions possesses the nice property that the limiting distribution is normal, and a lack-of-fit test on the adequacy of the log-gamma distributional assumption of the random effects can be derived. It would be of interest to extend the model to the case of mixed multivariate responses in which the continuous outcome response shows a skewed pattern.

In this bivariate longitudinal data analysis, we observed that the random slopes of time effects from one of the outcomes had a skewed distribution. Modeling this feature using the log-gamma distribution not only led to a better fit than that for the regular multivariate normal-mixed effects models but also led to a different conclusion on the correlation between the two random effects from the two outcomes. This is because the log-gamma model gives more accurate estimates of the random effects by assuming more realistic distributions for the random effects than normal models do. Better accuracy in the estimation of subject-specific effects using the log-gamma model rather than normal models has been observed in univariate longitudinal data analysis (Zhang et al. 2008). Future work will include a theoretical investigation into how misspecifications of the random effects distributions affect the estimation and inference of the correlations of the random effects of multivariate longitudinal data.