A Fast Algorithm for Denoising Magnitude Diffusion-Weighted Images with Rank and Edge Constraints

Abstract

Purpose

To accelerate denoising of magnitude diffusion-weighted images subject to joint rank and edge constraints.

Methods

We extend a previously proposed majorize-minimize (MM) method for statistical estimation that involves noncentral χ distributions and joint rank and edge constraints. A new algorithm is derived which decomposes the constrained noncentral χ denoising problem into a series of constrained Gaussian denoising problems each of which is then solved using an efficient alternating minimization scheme.

Results

The performance of the proposed algorithm has been evaluated using both simulated and experimental data. Results from simulations based on ex vivo data show that the new algorithm achieves about a factor of 10 speed up over the original Quasi-Newton based algorithm. This improvement in computational efficiency enabled denoising of large data sets containing many diffusion-encoding directions. The denoising performance of the new efficient algorithm is found to be comparable to or even better than that of the original slow algorithm. For an in vivo high-resolution Q-ball acquisition, comparison of fiber tracking results around hippocampus region before and after denoising will also be shown to demonstrate the denoising effects of the new algorithm.

Conclusion

The optimization problem associated with denoising noncentral χ distributed diffusion-weighted images subject to joint rank and edge constraints can be solved efficiently using an MM-based algorithm.

INTRODUCTION

Low signal-to-noise ratio (SNR) is a major concern for high-resolution quantitative diffusion imaging (1). Many denoising methods have been proposed to enhance the SNR for diffusion imaging, either working with the complex data (e.g., (2, 3)) or with the magnitude data (e.g., (4–11)). Although denoising complex data can generally be advantageous (e.g., less computational challenge and easier characterization), it is desirable to effectively denoise magnitude data for a number of practical reasons (such as less storage usage, easier data management and free of phase artifacts (12)).

In a recent paper (13), we presented a new magnitude image denoising method for diffusion MRI that integrates noncentral χ noisy data model (14–16) with a low-rank image sequence model (17–21) and a joint edge constraint (2). The method uses a Quasi-Newton (i.e., L-BFGS) (22) based algorithm to solve the underlying nonlinear optimization problem and its long computational time is a limiting factor for processing large data sets (e.g., 3D high-resolution diffusion-weighted image volumes).

This note presents a new fast algorithm for solving the nonlinear optimization problem associated with magnitude image denoising in the presence of rank and edge constraints. The algorithm is based on a recently proposed efficient quadratic majorize-minimize (MM) method (23). It decomposes the original denoising problem into a series of constrained “Gaussian denoising” problems, each of which can be solved very efficiently using an alternating minimization scheme, significantly reducing the computation time (around 10-fold acceleration overall). We demonstrate here the improved performance of the new algorithm using both simulations based on ex vivo data and in vivo experimental data. The new algorithm will enhance the practical utility of joint rank and edge constrained magnitude image denoising.

THEORY

Problem Formulation

We represent a series of noisy magnitude diffusion-weighted images (DWI) by a matrix Y ∈ ℝ^{M × Q}, in which each column is an image frame, M is the number of voxels in each frame, and Q is the number of images, and the corresponding noise-free images by X ∈ ℝ^{M × Q}. It is well established that magnitude images obtained from sum-of-squares reconstruction follow a noncentral χ distribution, of which Rician distribution is a special case for single coil reconstructions (24). With the data distribution, the magnitude image denoising problem can be formulated as the following penalized maximum likelihood estimation problem

$$\widehat{\mathbf{X}}=arg\underset{\mathbf{X}}{min}L(\mathbf{X},\mathbf{Y},n,\sigma )+\lambda R(\mathbf{X}),$$ [1]

where X̂ ∈ ℝ^{M × Q} contains the denoised images, L(·) denotes the negative log-likelihood function, and R(·) is a regularization functional used to incorporate prior information, n is the number of coils and σ is the noise standard deviation. As proposed in (13), when an explicit rank constraint is imposed on X, the joint rank and edge constrained noncentral χ denoising problem can be formulated as

$$\widehat{\mathbf{U}},\widehat{\mathbf{V}}=arg\underset{\mathbf{U},\mathbf{V}}{min}L(\mathbf{U},\mathbf{V},\mathbf{Y},n,\sigma )+\lambda R(\mathbf{U},\mathbf{V}),$$ [2]

where U ∈ ℝ^{M × r} and V ∈ ℝ^{r × Q} are two rank r matrices (r < Q, r ≪ M) such that X = UV, and R(·) absorbs the joint edge constraint (2,13). Specifically, we have

$$\widehat{\mathbf{U}},\widehat{\mathbf{V}}=arg\underset{\mathbf{U},\mathbf{V}}{min}\sum _{m,q}\left[\frac{{[\mathbf{UV}]}_{mq}^2}{2{\sigma }^2}+(n-1)log\left({[\mathbf{UV}]}_{mq}\right)-log{I}_{n-1}\left(\frac{{\mathbf{Y}}_{mq}{(\mathbf{UV})}_{mq}}{{\sigma }^2}\right)\right]+\lambda \sum _m\sum _{p\in {\mathrm{\Omega }}_m}H\left(\sqrt{\sum _q{w}_q^2{\left|{(\mathbf{UV})}_{mq}-{(\mathbf{UV})}_{pq}\right|}^2}\right),$$ [3]

where I_n(·) is the nth-order modified Bessel function of the first kind, H(·) is an edge-preserving penalty function, Ω_m is the neighborhood of the mth voxel (defined as the adjacent voxels along all spatial dimensions) and {w_q} are coefficients weighing the contributions from different image frames to the joint edge penalty (2). In addition, the first summation term in this equation corresponds to the negative log-likelihood L(·) while the second summation corresponds to the regularization term R(·). Eq. [3] is a challenging computational problem due to nonconvexity and the repeated evalution of complicated functions such as the modified Bessel functions. We next describe a new efficient algorithm to solve this problem.

An MM-Based Algorithm

According to the MM theory (25, 26), if an upper bound (also referred to as the majorizer) can be obtained for an objective function, the original minimization problem can be transferred into a series of subproblems (usually in a simpler form) in which the majorizer is updated and minimized iteratively. Based on the derivations in (23), it can be shown that L(·) in Eq. [3] can be upper bounded/majorized as

$$L(\mathbf{U},\mathbf{V},\mathbf{Y},n,\sigma )\le \sum _{m,q}\left[\frac{{[\mathbf{UV}]}_{mq}^2}{2{\sigma }^2}+\left(\frac{n-1}{{\mathbf{X}}_{mq}^{(i)}}-\frac{\left(I_{n-2}\left(\frac{{\mathbf{X}}_{mq}^{(i)}{\mathbf{Y}}_{mq}}{{\sigma }^2}\right)+I_n\left(\frac{{\mathbf{X}}_{mq}^{(i)}{\mathbf{Y}}_{mq}}{{\sigma }^2}\right)\right)}{I_{n-1}\left(\frac{{\mathbf{X}}_{mq}^{(i)}{\mathbf{Y}}_{mq}}{{\sigma }^2}\right)}\frac{{\mathbf{Y}}_{mq}}{2{\sigma }^2}\right){[\mathbf{UV}]}_{mq}\right]+C^{(i)}$$ [4]

where ${\mathbf{X}}_{mq}^{(i)}$ contains the voxel intensities at the current iteration. C⁽ⁱ⁾ is a constant that depends on X⁽ⁱ⁾ and Y but is independent of U and V (detailed derivation of C⁽ⁱ⁾ can be found in the Appendix). Therefore, we can transfer the original optimization problem into a series of problems defined as

$$\widehat{\mathbf{U}},\widehat{\mathbf{V}}=arg\underset{\mathbf{U},\mathbf{V}}{min}\frac{1}{2{\sigma }^2}{\Vert \mathbf{UV}-\stackrel{\sim }{\mathbf{Y}}\Vert }_F^2+\lambda R(\mathbf{U},\mathbf{V})$$ [5]

where

$${\stackrel{\sim }{\mathbf{Y}}}_{mq}=\left(\frac{{\mathbf{Y}}_{mq}}{2}\frac{\left(I_{n-2}\left(\frac{{\mathbf{X}}_{mq}^{(i)}{\mathbf{Y}}_{mq}}{{\sigma }^2}\right)+I_n\left(\frac{{\mathbf{X}}_{mq}^{(i)}{\mathbf{Y}}_{mq}}{{\sigma }^2}\right)\right)}{I_{n-1}\left(\frac{{\mathbf{X}}_{mq}^{(i)}{\mathbf{Y}}_{mq}}{{\sigma }^2}\right)}-\left(\frac{n-1}{{\mathbf{X}}_{mq}^{(i)}}\right){\sigma }^2\right).$$ [6]

This is essentially a Gaussian denoising (least-squares) problem subject to the original rank and edge constraints, but with the modified noisy data. This problem can then be solved using the following alternating minimization scheme:

1. Compute the weighting coefficients {l_mp} as described in (13) for the edge constraint;

2. With a fixed V̂^(k), solve the following U-subproblem:

   $${\widehat{\mathbf{U}}}^{(k)}=arg\underset{\mathbf{U}}{min}\frac{1}{2{\sigma }^2}{\Vert \mathbf{U}{\widehat{\mathbf{V}}}^{(k)}-\stackrel{\sim }{\mathbf{Y}}\Vert }_F^2+\lambda \sum _{q=1}^Q{w}_q^2{\Vert \mathbf{WDU}{\widehat{\mathbf{V}}}_q^{(k)}\Vert }_2^2,$$
   where D is a finite difference operator, W a diagonal matrix with {l_mp} on its diagonal and ${\widehat{\mathbf{V}}}_q^{(k)}$ the qth column of V̂^(k). More specifically, this is a quadratic problem and thus equivalent to solving

   $$\mathbf{U}{\widehat{\mathbf{V}}}^{(k)}{({\widehat{\mathbf{V}}}^{(k)})}^T+2{\sigma }^2\lambda {\mathbf{D}}^T{\mathbf{W}}^T\mathbf{WDU}{\widehat{\mathbf{V}}}^{(k)}\mathbf{\Omega }{\mathbf{\Omega }}^T{({\widehat{\mathbf{V}}}^{(k)})}^T=\stackrel{\sim }{\mathbf{Y}}{({\widehat{\mathbf{V}}}^{(k)})}^T$$

   with Ω being a diagonal matrix with {w_q} on its diagonal. This system of linear equations can then be solved by efficient iterative algorithms such as linear conjugate gradient (CG);

3. With a fixed Û^(k), solve the following V-subproblem:

   $${\widehat{\mathbf{V}}}^{(k+1)}=arg\underset{\mathbf{V}}{min}\frac{1}{2{\sigma }^2}{\Vert {\widehat{\mathbf{U}}}^{(k)}\mathbf{V}-\stackrel{\sim }{\mathbf{Y}}\Vert }_F^2+\lambda \sum _{q=1}^Q{w}_q^2{\Vert \mathbf{WD}{\widehat{\mathbf{U}}}^{(k)}{\mathbf{V}}_q\Vert }_2^2$$
   which is again equivalent to solving

   $${({\widehat{\mathbf{U}}}^{(k)})}^T{\widehat{\mathbf{U}}}^{(k)}\mathbf{V}+2{\sigma }^2\lambda {({\widehat{\mathbf{U}}}^{(k)})}^T{\mathbf{D}}^T{\mathbf{W}}^T\mathbf{WD}{\widehat{\mathbf{U}}}^{(k)}\mathbf{V}\mathbf{\Omega }{\mathbf{\Omega }}^T={({\widehat{\mathbf{U}}}^{(k)})}^T\stackrel{\sim }{\mathbf{Y}};$$

4. Repeat 1 – 3 until a certain convergence criterion is met or a given number of iterations is reached.

Once the problem in Eq. [5] is solved, Eq. [6] can be used to update the majorizer again and these two steps can be iterated until a certain convergence criterion is met. In our implementation, we terminated the Gaussian denoising iterations when the relative ℓ₂-norm of the successive change in Û is less than 10⁻⁵ and repeat the majorizer computation and the Gaussian denoising step 10 times. We found that after 10 iterations the changes in the majorizer were negligible. A detailed derivation of the majorizer in Eq. [4] is given in the Appendix.

METHODS

Experiments Based on Ex Vivo Data

The performance of the proposed algorithm has been evaluated using simulations based on ex vivo experimental data. Specifically, simulated noisy Rician distributed data (n = 1) were generated from a high SNR and high-resolution ex vivo whole pig brain DWI data set available online (27). The original DWI series has 64 3D volumes, including 61 diffusion directions at b = 4009 mm²/s and three volumes at b = 0. Each 3D volume has a size of 128 × 128 × 70 (see (27) for other detailed information on the data). The constrained denoising as described by Eq. [3] was applied to process the entire 3D noisy series simultaneously with n =1 and r = 12, using the original L-BFGS-based algorithm (13) and the new MM-based algorithm, respectively. Diffusion tensor parameters were then estimated from the original high SNR images, the noisy images and the denoised images using the standard least-squares method (28). The results from the original high SNR images were treated as a gold standard for performance comparison.

In addition to comparing the denoised DWI images and the estimated diffusion parameter maps qualitatively, two error metrics were also calculated. One is the relative ℓ₂ error (denoted as RE) calculated for a representative image frame as

$$\text{RE}=\frac{{\Vert I_0-\widehat{I}\Vert }_2}{{\Vert I_0\Vert }_2}$$

where I₀ is the gold-standard and Î is the noisy or denoised images. The other metric is the root-mean-squared-error for the estimated fractional anisotropy (FA) values (denoted as FA-RMSE) calculated as

$$\text{FA}-\text{RMSE}=\sqrt{\frac{{\sum }_{m=1}^{M_1}{\left(F{A}_m-{\widehat{FA}}_m\right)}^2}{M_1}}$$

where FA and $\widehat{FA}$ are FA maps from the noise-free images and noisy/denoised images, respectively, and M₁ is the number of voxels extracted from the brain region for computing the RMSE. The first metric is a good indicator for image quality and the latter is a good indicator for diffusion parameter estimation accuracy. The regularization parameter (λ) was chosen such that the FA-RMSE was minimized compared to the gold standard. Both algorithms were implemented in Matlab (R2012b; The Mathworks, Natick, MA) on a workstation with a 3.47 GHz dual-hex-core Intel Xeon processor X5690, 96 GB RAM and Linux operation system.

In Vivo Experiments

In vivo human brain diffusion MRI data were acquired at the Center for Imaging of Neurodegenerative Diseases at the University of California, San Francisco. The participants were recruited with written consent prior to the study. The data were acquired on a Siemens Skyra 3T scanner (Siemens Medical Solutions, Erlangen, Germany) with a 16-channel receiver head coil. The diffusion-weighted imaging sequence was single refocused spin-echo EPI with 128 diffusion encoding directions at b = 1500 s/mm² in addition to 15 b = 0 s/mm² images evenly interleaved with the DWI volumes. The rest of the imaging parameters were: TR/TE = 3500/86 ms, field-of-view (FOV) = 192 × 192 mm², matrix size = 128 × 128, 26 axial slices covering the medial temporal lobe with no gap (resulting in 1.5 mm isotropic resolution). A factor of two parallel acceleration and a factor of 6/8 phase partial Fourier acquisition were used and GRAPPA reconstruction with sum-of-squares coil combination was applied. The total acquisition time was eight and a half minutes. Note that although theoretically the reconstructed noisy magnitude images do not exactly follow a noncentral χ distribution, it has been shown that the noncentral χ likelihood is still an accurate model for magnitude data obtained by GRAPPA reconstruction (24), which justifies the usage of the proposed denoising formulation. For this large data set with so many diffusion directions, the original algorithm would take about 10 to 20 hours to finish denoising if applied to the entire data set. Therefore, to simplify the comparison, we randomly selected one b = 0 image and 40 diffusion directions from the original data and applied the constrained denoising to this smaller data set with n = 16 and r = 12, using the L-BFGS-based algorithm and the proposed MM-based algorithm, respectively. The regularization parameter was selected based on visual inspection of both the denoised DWIs and FA maps to avoid oversmoothing.

The improved processing efficiency offered by the new algorithm allows us to apply the constrained denoising to larger data sets with many more diffusion directions. We have processed the entire data sets with all the 128 diffusion-encoding directions using the new algorithm and compared the fiber tracking results before and after denoising. The orientation distribution function (ODF) reconstruction and the fiber tracking were done using the MRtrix software package (29).

RESULTS

Simulations Based on Ex Vivo Data

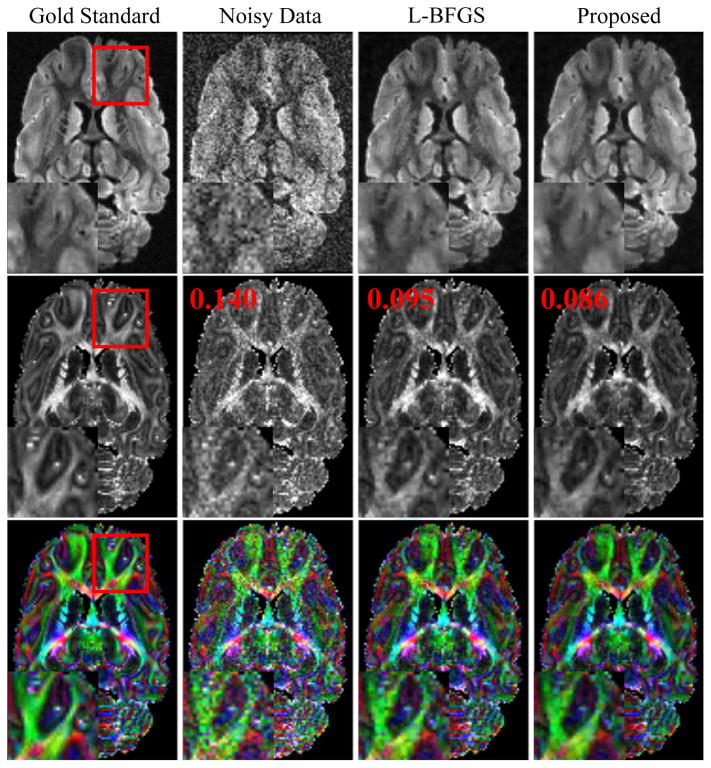
Figure 1 shows some representative results from the simulation study based on ex vivo data. As expected, denoising significantly improves the quality of the DWIs and the estimated FA maps. In this study, the new algorithm produced denoised DWIs and FA maps comparable to those from the original algorithm. However, the new algorithm took significantly less time (2760 sec) than the old algorithm (46491 sec), and obtained even slightly lower RE and FA-RMSE (also shown in Fig. 1). This improvement is consistent with the plots shown in Fig. 2, which compare the RE and FA-RMSE for the two algorithms at different noise levels.

Figure 1.

Representative DWIs (top row), FA maps (middle row) and color-coded FA maps (bottom row) for one slice from an ex vivo data set. The color encodes the orientations of the primary eigenvectors of the estimated diffusion tensors: red for left-right, green for anterior-posterior and blue for superior-inferior. Different columns correspond to results from the gold standard, noisy data, denoised data generated by the L-BFGS-based algorithm and the proposed algorithm, respectively. The numbers in red letters are the FA-RMSEs for different results.

Figure 2.

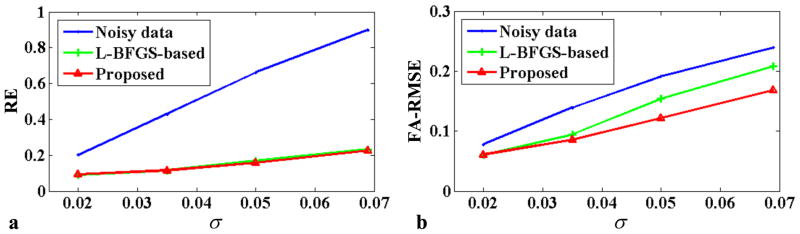
Relative errors for a representative DWI image (a) and the FA-RMSEs for one slice (b) at different noise levels, for the noisy data, denoised data generated by the L-BFGS-based algorithm and denoised data generated by the proposed algorithm. The x-axis denotes the noise standard deviation (σ).

To further illustrate the significant gain achieved by the proposed algorithm in terms of tradeoff between computational efficiency and performance, we compare the RE changes over time and iteration for the two algorithms. As shown in Fig. 3, although the proposed algorithm has a slightly lower empirical convergence rate (Fig. 3a) than the original L-BFGS-based algorithm, it requires much simpler computations per iteration. Thus overall, the proposed algorithm is able to achieve a lower RE in much less time compared to the original algorithm (Fig. 3b).

Figure 3.

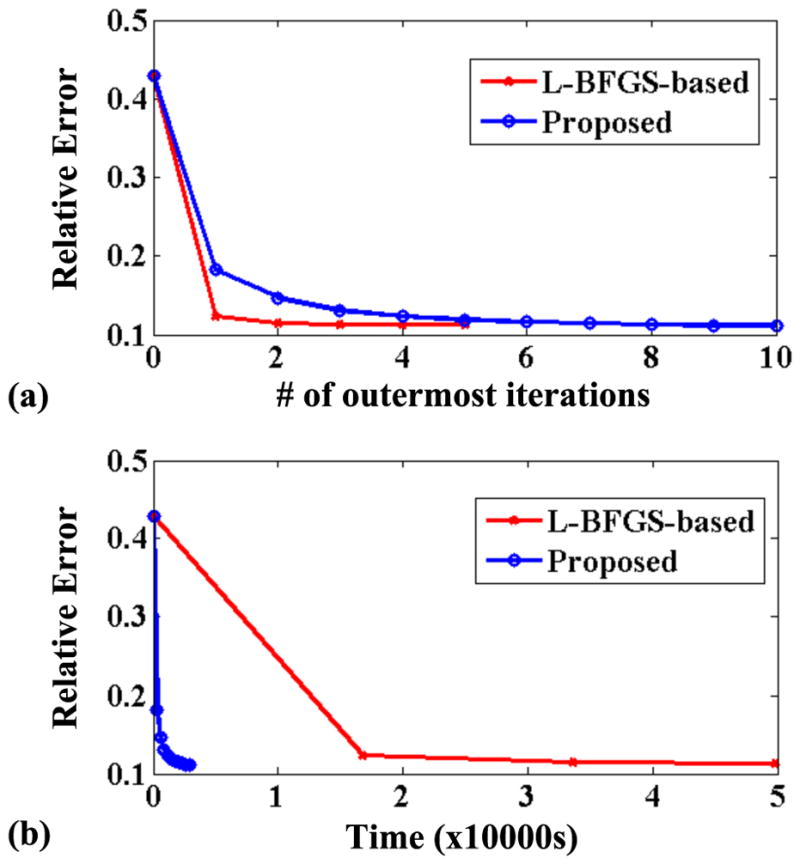
Empirical convergence curves for the original L-BFGS-based algorithm and the proposed algorithm. The curves show the relative error changes with respect to the number of outermost iterations (a) and time (b). Note that each iteration for the proposed algorithm includes a majorization and a minimization (solving the regularized least-squares problem) steps, while each iteration for the original algorithm includes an alternation between updating U and V (13). Note also that due to the processing time consideration only five outermost iterations were run for the L-BFGS-based algorithm which already suffices for the demonstration purpose.

In Vivo Experiments

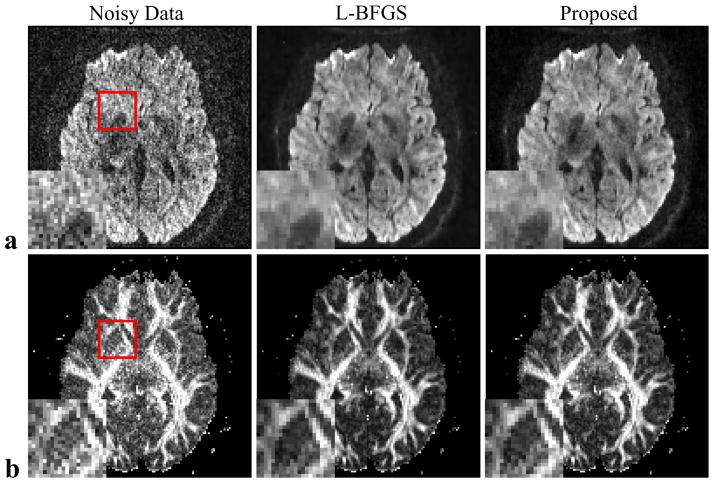
Figure 4 shows a set of results from in vivo data. Representative DWIs and diffusion parameter (FA) maps from the original noisy data and denoised data from the L-BFGS-based algorithm and the proposed MM-based algorithm are shown. As can bee seen, both algorithms offer similar reduction in noise and improvement in image quality. However, the new algorithm took approximately only 15 minutes of processing time while the old algorithm took around 4 hours.

Figure 4.

Representative DWIs (a) and estimated FA maps (b) from an in vivo data set. The images correspond to results from the noisy data (left column), denoised data generated by the L-BFGS-based algorithm (middle column) and denoised data generated by the proposed MM-based algorithm (right column).

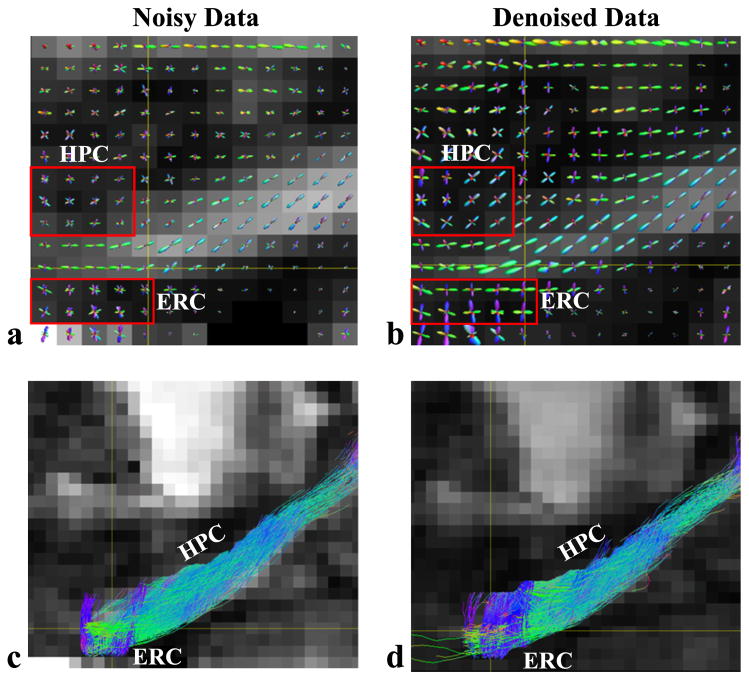
Figure 5 compares the reconstructed ODFs and fiber tracking results around the hippocampus region from the 128-direction diffusion MRI data, before and after denoising. The denoising process was finished in slightly over an hour using the new algorithm. As can be seen, the effect of denoising is very noticeable. For example, the maxima of the ODFs around the hippocampus are better defined and the tracking results from the denoised data seem to reveal more perforant path fibers that were tracked from entorhinal cortex to hippocampus. Histological tract tracing would be desirable to confirm this observation.

Figure 5.

Reconstructed ODFs (a,b) and fiber tracking results (c,d) around the hippocampus region from a data set with 128 diffusion-encoding directions. The results from the noisy data (left) and the denoised data (right) are compared. Two regions near the hippocampus (HPC) and the entorhinal cortex (ERC) are identified by red boxes in (a) and (b) to highlight the denoising effects.

DISCUSSION

The effectiveness of integrating noncentral χ likelihood model, rank and edge constraints for de-noising magnitude diffusion-weighted image series was demonstrated in (13). However, its long computational time for large data sets is a major practical limitation. The proposed MM-based algorithm effectively addresses this problem. The improved computational efficiency (i.e., better tradeoff between convergence rate and computation time per iteration as illustrated in Fig. 3) offered by the new algorithm can provide several additional benefits. First, it provides more flexibility for parameter tuning (e.g., selection of rank and regularization parameter); Second, it enables the use of more complex regularization functionals if needed. Furthermore, as shown in the derivation of the algorithm in the Appendix, the decomposition of the original problem into a series of regularized least-squares problems opens up opportunities to adopt advanced Gaussian denoising methods for magnitude data denoising or to develop methods for direct estimation of diffusion parameters from noisy magnitude data (30).

A key factor to improving computational efficiency in the proposed algorithm is the reduction in calculations involving the modified Bessel functions. In the original algorithm, one has to deal with intensive computations associated with the modified Bessel functions in each iteration updating U and V (and for solving the large-scale nonlinear programming problems repeatedly (13)), while in the proposed algorithm, only the majorizer computation is related to those functions. After majorization, the alternating between U and V only involves solving regularized linear least-squares problems which are computationally much simpler. Moreover, we have also observed that the computation time for solving the least-squares problems is much shorter than that for the line search step during solving the nonlinear programming problems (to update U and V) which again involves intensive computations for the modified Bessel functions. We believe that this significantly improved efficiency offered by the MM algorithm leads to better convergence to the optimal solution of the original problem in Eq. [3] than the L-BFGS-based algorithm within a same period of time, which can be one main reason for the quantitative improvement observed. In addition, the MM-based algorithm also provided better numerical stability (by avoiding the nonlinear functions such as log(·) and I_n(·) when updating U and V) which also contributes to the better performance observed.

It is also worth noting that due to the nonconvexity of the original problem in Eq. [3], choosing a proper initial point to start the iterative algorithm is important. In this work, we initialized the entire algorithm as follows: (1) compute the first majorizer from the noisy data and obtain the modified data Ỹ; (2) apply SVD to Ỹ and choose the first r singular vectors to initialize U and V in Eq. [5]. After solving the problem in Eq. [5], we saved the current solutions Û and V̂ as a warm start for the next iteration. We have also experimented with alternative initialization schemes such as computing the first majorizer from filtered magnitude data or initializing the problem in Eq. [5] using the SVD Ỹ of each time, and found that they had negligible effects on the final results.

This paper has considered only spatially invariant noise variance, but the formulation in Eq. [3] and the proposed algorithm can readily be extended to incorporate spatially varying noise variances (13), with slight changes in computing the majorizer (σ → σ_m) and modification of the least-squares term in Eq. [5] (to a weighted least-squares form). Note that in this case, accurate estimation of the spatially varying variance is necessary to ensure the denoising performance (10, 11,31). Extension to spatially correlated noncentral χ distributions is however nontrivial and would require more careful examinations (23).

CONCLUSION

An MM-based algorithm is proposed for efficient denoising of magnitude images subject to rank and edge constraints. The algorithm will enhance the practical utility of constrained denoising, especially in high-resolution diffusion imaging with a large number of diffusion encoding directions.

APPENDIX

Derivation of the majorizer for L(·) in Eq. [2]

Given the noncentral χ likelihood function

$$p(y\mid x)=\frac{1}{{\sigma }^2}\frac{y^n}{x^{n-1}}exp\left(-\frac{x^2+y^2}{2{\sigma }^2}\right)I_{n-1}\left(\frac{xy}{{\sigma }^2}\right),$$

and

$$I_{n-1}(ax)=\frac{{(a/2)}^{n-1}{x}^{n-1}}{\mathrm{\Gamma }(n)}{t}_n(ax),$$

where t_n(·) denotes the hypergeometric function, Γ(·) denotes the Gamma function and a = y/σ², it is shown in (32) that t_n(x) is strictly log-convex in x. Accordingly, I_n−1 (ax)/xⁿ⁻¹ = (a/2)ⁿ⁻¹t_n(ax)/Γ(n) is strictly log-convex in x. Therefore

$$v(x)=(n-1)log(x)-log{I}_{n-1}(\frac{xy}{{\sigma }^2})=-log\left(\frac{1}{x^{n-1}}{I}_{n-1}\left(\frac{xy}{{\sigma }^2}\right)\right)$$

is strictly concave in x. Furthermore, since v(x) is differentiable, it can be upper-bounded as follows (23):

$$v(x)\le g(x\mid x_i)=v(x_i)+v^{\prime }(x_i)(x-x_i),$$

where

$$v^{\prime }(x_i)=\frac{n-1}{x_i}-\frac{1}{2}\frac{\left(I_{n-2}\left(\frac{x_{i}y}{{\sigma }^2}\right)+I_n\left(\frac{x_{i}y}{{\sigma }^2}\right)\right)}{I_{n-1}\left(\frac{x_{i}y}{{\sigma }^2}\right)}·\frac{y}{{\sigma }^2}$$

and x_i corresponds to a specific intensity at the current iteration. Accordingly, the negative log-likelihood, −logp(y|x) = −log(yⁿ/σ²) + (x² + y²)/2σ² + v(x), can be majorized as

$$-logp(y\mid x)\le \frac{x^2}{2{\sigma }^2}+\left(\frac{n-1}{x_i}-\frac{\left(I_{n-2}\left(\frac{x_{i}y}{{\sigma }^2}\right)+I_n\left(\frac{x_{i}y}{{\sigma }^2}\right)\right)}{I_{n-1}\left(\frac{x_{i}y}{{\sigma }^2}\right)}·\frac{y}{2{\sigma }^2}\right)x+c^{(i)}$$

where c⁽ⁱ⁾ = −log(yⁿ/σ²) + y²/2σ² + v(x_i) − v′(x_i) x_i is a constant independent of x which is to be optimized. As a summation of −logp(y|x), L(·) can then be majorized as

$$L(\mathbf{U},\mathbf{V},\mathbf{Y},n,\sigma )\le \sum _{m,q}\left[\frac{{[\mathbf{UV}]}_{mq}^2}{2{\sigma }^2}+\left(\frac{n-1}{{\mathbf{X}}_{mq}^{(i)}}-\frac{\left(I_{n-2}\left(\frac{{\mathbf{X}}_{mq}^{(i)}{\mathbf{Y}}_{mq}}{{\sigma }^2}\right)+I_n\left(\frac{{\mathbf{X}}_{mq}^{(i)}{\mathbf{Y}}_{mq}}{{\sigma }^2}\right)\right)}{I_{n-1}\left(\frac{{\mathbf{X}}_{mq}^{(i)}{\mathbf{Y}}_{mq}}{{\sigma }^2}\right)}·\frac{{\mathbf{Y}}_{mq}}{2{\sigma }^2}\right){[\mathbf{UV}]}_{mq}\right]+C^{(i)}.$$

The constant C⁽ⁱ⁾ results from a summation of c⁽ⁱ⁾ (over the indices m and q). As shown in the derivations above, C⁽ⁱ⁾ is independent of U and V. Therefore, it can be ignored for solving the regularized least-squares problem (Eq. [5]) once the majorizer has been computed.