Saturation analysis of ChIP-seq data for reproducible identification of binding peaks

Abstract

Chromatin immunoprecipitation coupled with next-generation sequencing (ChIP-seq) is a powerful technology to identify the genome-wide locations of transcription factors and other DNA binding proteins. Computational ChIP-seq peak calling infers the location of protein–DNA interactions based on various measures of enrichment of sequence reads. In this work, we introduce an algorithm, Q, that uses an assessment of the quadratic enrichment of reads to center candidate peaks followed by statistical analysis of saturation of candidate peaks by 5′ ends of reads. We show that our method not only is substantially faster than several competing methods but also demonstrates statistically significant advantages with respect to reproducibility of results and in its ability to identify peaks with reproducible binding site motifs. We show that Q has superior performance in the delineation of double RNAPII and H3K4me3 peaks surrounding transcription start sites related to a better ability to resolve individual peaks. The method is implemented in C+l+ and is freely available under an open source license.

Chromatin immunoprecipitation (ChIP) followed by massively parallel sequencing (ChIP-seq) is designed to detect genome-wide protein–DNA interaction. ChIP-seq can identify both sharp peaks typically associated with sequence-specific transcription factors, as well as broad histone-modification signals (Park 2009; Peng and Zhao 2011), and has become a central technology for the investigation of gene regulation. The ChIP-seq procedure involves formaldehyde-mediated crosslinking of chromatin followed by fragmentation of protein–DNA complexes into short fragments, which are then subjected to immunoprecipitation using an antibody directed against a protein of interest (e.g., a transcription factor or a modified histone), thereby enriching genomic segments that are bound by the protein of interest prior to sequencing (Laajala et al. 2009).

A crucial challenge in the computational analysis of ChIP-seq data pertains to finding peaks in ChIP-seq data that correspond to protein–DNA binding sites. Numerous peak calling algorithms have been presented, most of which address the same basic analytical tasks with methods to estimate the mean DNA fragment length from the data, to shift or extend the reads toward the center of the binding peak, to identify candidate peak regions, and to evaluate the statistical significance of the read depth of the candidate peaks. The sequence reads represent only the 5′ ends of the coprecipitated DNA fragments, which are generally 100- to 500-bp in length. Around true binding sites of the target protein, this results in a characteristic bimodal distribution of reads on the forward and reverse strands, which depends on the distribution of fragment lengths in the library and can be exploited for signal detection and evaluation. Therefore, an initial step in many algorithms is the estimation of the actual fragment-length distribution. Following fragment-length estimation, in order to better represent the original DNA fragment rather than just the 5′ sequence read, most peak calling algorithms either shift the read in the 3′ direction toward the peak center or computationally extend tags to the estimated length of the original fragments. Regions for hypothesis testing are chosen with a sliding window, or alternatively, some programs generate a continuous coverage and specify a minimum height criterion in order to report peaks. Finally, a variety of statistical tests are applied to identify peaks as regions with significantly increased read density. Most commonly, read distribution is modeled by a Poisson or negative binomial distribution (Pepke et al. 2009).

Numerous peak calling algorithms have been systematically compared in many studies (Laajala et al. 2009; Pepke et al. 2009; Wilbanks and Facciotti 2010; Kim et al. 2011; Rye et al. 2011). However, only a small number of data sets were used in these studies. Nevertheless, one recurrent conclusion is that the performance of different peak callers depends on the particular data set examined (Laajala et al. 2009; Wilbanks and Facciotti 2010), as well as on manual “fine-tuning” of the parameters required by the various algorithms (Wilbanks and Facciotti 2010; Szalkowski and Schmid 2011). In this work, we present an approach to ChIP-seq peak calling that is based on saturation analysis of positions within candidate peaks. Our method estimates the fragment length from the data and does not require fine-tuning of parameters for typical runs. If a control data set is used, the statistical model we use does not require down-sampling of the control reads. We present efficient and accurate algorithms for each of the major steps of computational ChIP-seq analysis and show, using ENCODE data for 38 experiments, that they outperform previous methodologies based on irreproducible discovery rate (IDR) analysis (Li et al. 2011; Landt et al. 2012), motif identification, resolution, and running time.

Results

In this work, we present a ChIP-seq peak caller called Q, which exploits a quadratic measure of coverage to identify candidates followed by a statistical saturation analysis to call significant peaks. The Q workflow can be divided into four main phases: (1) estimation of fragment length (Fig. 1), (2) preprocessing of reads (transformation to “qfrags”) (Fig. 2A), (3) analysis of qfrag depth to identify summits at the center of candidate peaks (Fig. 2B), and (4) statistical hypothesis testing of candidate peaks with respect to saturation (Fig. 2C).

Figure 1.

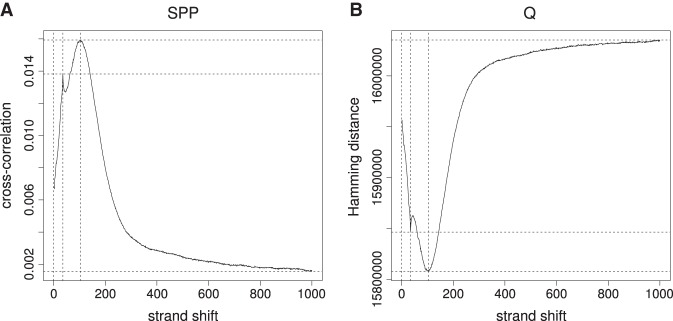
Fragment-length estimation. (A) Cross-correlation plot produced by SPP (Kharchenko et al. 2008) for GM12878-BATF-REP1. (B) Hamming distance plot produced by Q for the same data set.

Figure 2.

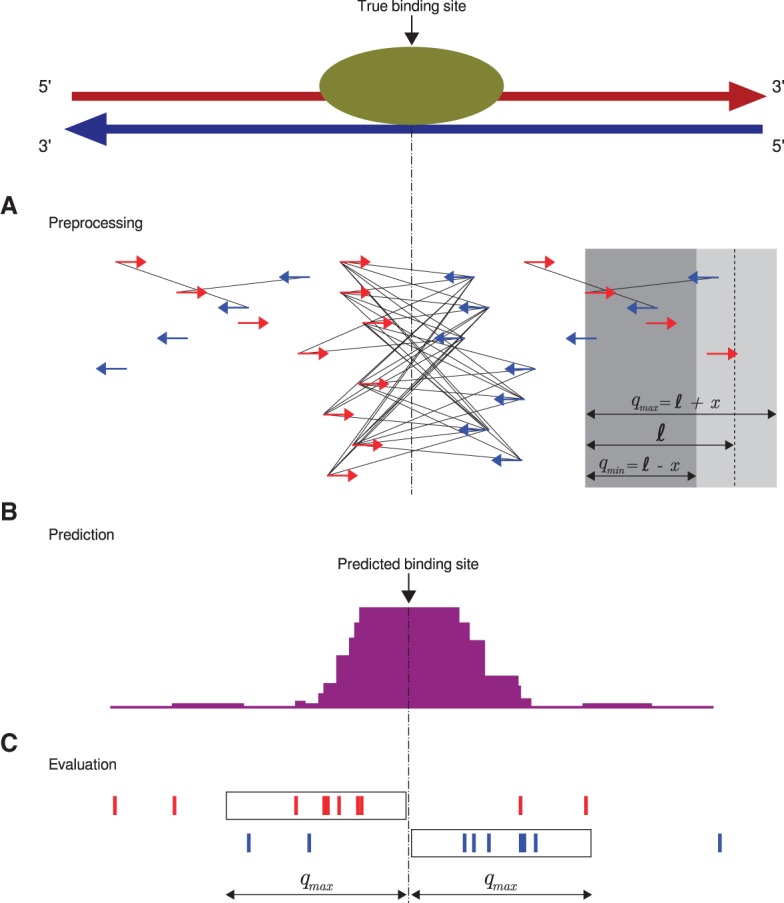
Q workflow. (A) A preprocessing step identifies “qfrags” as pairs of reads on opposite strands located within ℓ±x nucleotides from one another. In regions of true signal, this has the effect of approximately quadratically amplifying the signal, whence the name of the algorithm. The qfrags are shown as black lines connecting the 5′ ends of compatible reads. For instance, the red (forward strand) read at the left edge of the gray box can form a qfrag with any blue (reverse strand) read that is located in the light gray portion of the box (≥q_min and ≤q_max nucleotides). qfrags are symbolized by black lines between 5′ ends of red and blue reads. (B) The qfrag depth is calculated for each position along the genome. Candidate regions for hypothesis testing are identified as local qfrag height maxima (summits, or predicted binding sites). (C) Candidate regions are defined as the regions comprising the q_max nucleotides upstream of and downstream from the predicted binding site, and statistical testing is performed on each candidate peak based on the saturation analysis in a window defined by 2 · q_max.

Estimation of fragment length by Hamming distance

The estimated fragment length is an essential parameter for nearly all published peak callers. A commonly used method involves the calculation of cross-correlation between reads mapped to the forward and reverse strands, thereby taking advantage of the bimodal peak distribution characteristic of ChIP-seq peaks. The implementation of this procedure in SPP (Kharchenko et al. 2008) calculates the shift at which the highest Pearson correlation between the forward and reverse strand is noted. If this procedure is performed after removal of duplicates, the comparison is based on values of zero (no read starting at some position) and one (at least one read). We reasoned that a comparable operation could be performed using bit operations to calculate the Hamming distance. The position with the smallest distance corresponds to the position with the maximum Pearson correlation (Fig. 1; Supplemental Fig. S1). Therefore, an equivalent result is obtained, but the computation can be performed three to four times faster on average, based on an evaluation of the 38 data sets examined in this work (Supplemental Tables S1, S2).

qfrags: identification of candidate ChIP-seq peaks

Our method replaces the read shifting or extension step of most other ChIP-seq peak callers with an approach that is intended to better capture signal from true peaks and to center the called peak at the middle of bimodal accumulations of reads. We reasoned that if a read is located within a true peak, then it is likely that there will be multiple reads on the opposite strand located within a window centered at one mean fragment length away from the read. To capture this intuition, we define q_min = ℓ−x and q_max = ℓ + x, where ℓ denotes the estimated mean fragment length, and x, which reflects deviations from the mean fragment length, determines the size of the window.

We define a qfrag to be the segment of genomic positions between any pair of 5′ end positions on the forward and reverse strand with a distance of at least q_min and at most q_max (Fig. 2A). The qfrag depth at any one position is the total number of qfrags that cover the position. The center of the local maximum of qfrag depth is then defined to be a predicted binding site or “summit” (Fig. 2B). The region comprising the q_max nucleotides upstream of and downstream from the summit then represents a candidate peak that will be statistically tested as described below (Fig. 2C).

We note that a critical point of ChIP-seq peak calling algorithms is the identification and centering of candidate peaks for statistical testing. Intuitively, our method will tend to yield a “quadratic” signal around true peaks but only a linear one elsewhere in the genome. Consider the situation where there are n reads on the forward strand and n reads on the reverse strand that are located at a distance of ℓ±x nucleotides to one another. Our method would then define n² qfrags, whereas methods that involve read extension or shifting would identify 2n reads. Approximately speaking, our method would characterize a “quadratic” number of qfrags surrounding a true peak while identifying only a linear number of qfrags for nonpeak regions (Fig. 2A). The qfrag method therefore leads to a different depth distribution than that of the raw reads, the shifted reads, or the extended reads (Supplemental Fig. S2).

Statistical analysis of peak saturation

To model the signal for a single true binding site, we made the following two assumptions: First, each fragment end is sequenced with equal probability from the forward or reverse strand. Second, there is no preference for fragment positions to which the target protein is bound; i.e., given a fragment of certain length, the target protein is bound to each fragment position with equal probability. The first assumption implies that the 5′ ends of fragments should accumulate before a true binding site on the forward strand and on the reverse strand behind it. The second assumption implies that the 5′ ends of fragments should be evenly distributed in a radius of q_min nucleotides around true binding sites, and at a distance of more than q_max nucleotides from the true binding site, the signal should resemble that of the background level. We validated our model empirically and found a distribution largely consistent with our model (Supplemental Fig. S3).

With this distribution in mind, we reasoned that a saturation score might be a good measurement for enrichment. By “saturation” we mean that many individual positions surrounding the true peak center tend to be occupied by the 5′ end of one or more mapped reads that belong to qfrags. Our procedure for identifying qfrags assigns candidate peaks with high saturation better scores than peaks with the same number of overall reads, which are distributed to a lower number of positions. The qfrag methodology thus intends to identify well-saturated candidate peaks.

We therefore defined saturation as the number of positions within the tested peak region that are covered by at least one 5′ end position of a qfrag (Fig. 2C). We implemented a statistical test that is formulated as a binomial test for the number of saturated positions and derived the binomial parameter p (probability for any given position to be covered) based on the classical occupancy problem (Feller 1968).

Although it is possible to call ChIP-seq peaks based only on the expected number of reads, assuming a uniform background distribution (Robertson et al. 2007), a number of factors such as GC content, read mappability, DNA repeats, copy number variations, and local chromatin structure can influence read depth (Feng et al. 2012). For this reason, ChIP-seq experiments are often accompanied by a control experiment in which generic (nonspecific) IgG is used in place of the specific antibody. A comparison of the treatment and control experiments can then be performed to reduce background biases in order to be able to reliably identify read-enriched regions obtained from ChIP-seq. In general, a similar number of reads are derived for the control sample as for the treatment sample, although the exact number may be higher or lower. We therefore developed an implementation of this test for ChIP-seq experiments performed with a control experiment. In this case, we test the difference of saturation between ChIP and the control experiment for statistical significance. Our method does not require down-sampling of reads from the control experiment (Supplemental Fig. S4).

Reproducibility analysis

To evaluate our method, we developed a test framework based on the IDR procedure (Li et al. 2011; Landt et al. 2012), which provides a measure of the reproducibility of the ChIP-seq experiments and is described in detail in the Supplemental Methods. We compared the performance of Q to that of the three widely used peak callers MACS2 (Zhang et al. 2008; Feng et al. 2012), SPP (Kharchenko et al. 2008), and PeakSeq (Rozowsky et al. 2009) using 38 published ChIP-seq data sets from the ENCODE Project Consortium (Supplemental Table S1). We measured reproducibility of the methods using pseudoreplicates generated from these data sets.

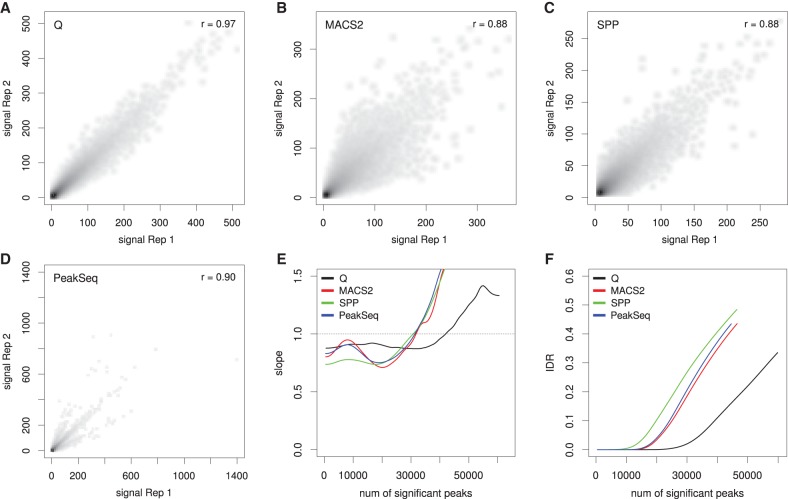
Figure 3 shows an example of our analysis for RNA polymerase II (RNAPII). Q identifies a larger overall number of overlaps between the top 100,000 peaks of each pseudoreplicate (60,450 compared with 45,022–46,976 for the other three peak callers) with a higher correlation coefficient between pseudoreplicates (Fig. 3A–D). We then applied the change of correspondence method (Supplemental Methods) to the data, which estimates the rate of change of reproducibility for the top n peaks as n ranges from zero to the total number of overlapping peaks (which was 60,450 for Q). High reproducibility is reflected in a late transition (i.e., at large n) to a segment with a positive slope (Li et al. 2011). In this example, the transition occurs at around 15,000 peaks for SPP, 20,000 for MACS2 and PeakSeq, and over 35,000 for Q (Fig. 3E). We also assessed the overall reproducibility of the replicates using the IDR. For all numbers of selected peaks, Q identifies fewer irreproducible peaks (Fig. 3F; Supplemental Methods).

Figure 3.

Reproducibility analysis for RNA polymerase II (RNAPII). The ENCODE data set HeLa-S3-POL2-REP1 is shown as an example. The alignment data were split randomly into two pseudoreplicates, and peaks were called using Q, MACS2, SPP, and PeakSeq. (A–D) The scatterplots show the negative decadic logarithm of P-values of Q (A), MACS2 (B), and PeakSeq (D), and signal values of SPP (C) for overlapping signals of the two pseudo replicates. Compared with the overlaps for MACS2 (46,976), SPP (45,759), and PeakSeq (45,022), Q shows a considerably larger overlap (60,450). In addition, Q shows the highest Pearson correlation coefficient (0.97) compared with three other methods. (E) Change of correspondence curve (Ψ′ plot) (Li et al. 2011). The peak set derived from Q remains consistent for about 15,000 peaks more than those of the other peak callers. (F) The plot shows the IDR at different numbers of selected peaks. For all peak counts, Q displays a considerably smaller proportion of irreproducible signals.

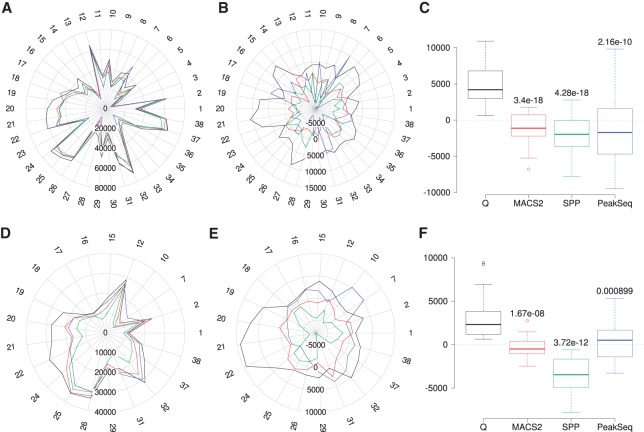
We performed the same analysis for all 38 data sets. The mean number of peaks identified by the four peak callers for any specific experiment ranged from 5991 to 70,663 (Supplemental Table S3). In 31 cases, Q displayed the highest number of overlapping peaks among the top 100,000 peaks (Fig. 4A–C) and, in 33 cases, the highest Pearson correlation coefficient (Fig. 3A–D; Supplemental Table S4). To highlight the differences between the four peak callers, we visualized the results by subtracting the mean number of overlapped peaks for each experiment from the count of peaks called by each individual peak caller. Overall, the mean normalized peak overlaps for Q are significantly larger than for MACS2, SPP, and PeakSeq (Fig. 4A–C).

Figure 4.

Reproducibility analysis for the 38 data sets. (A) Overlapping peak counts for the four peak callers (Q, black; MACS2, red; SPP, green; PeakSeq, blue). The numbers around the radar plots indicate the individual samples (Supplemental Table S1). (B) Mean normalized numbers for the data shown in A; the row mean (data from all four peak callers) was subtracted from each value. (C) Distribution of the mean normalized numbers for the overlapping peaks. P-values relative to Q were calculated using two-sample, two-sided Wilcoxon tests. (D–F) Panels are analogous to panels A through C except that the analysis is restricted to peaks with IDR ≤ 0.01. Data sets for which incompatibility with the IDR procedure was observed were excluded from the analysis (Supplemental Methods, Supplemental Figs. S5–S7; Supplemental Table S5).

For some data sets, we observed a proportion of overlapping peaks with very weak signal scores for both replicates that are classified as reproducible, given a threshold of IDR ≤ 0.01. This observation contradicts the basic concept of the IDR procedure whereby strong signals are more reproducible than weak signals. We systematically investigated this phenomenon. In our analysis, Q demonstrated the best overall compatibility with the IDR procedure (Supplemental Methods; Supplemental Fig. S5; Supplemental Table S5).

We then repeated the analysis shown in Figure 4A–C for data sets that exhibited good overall compatibility with the IDR procedure. For these 21 data sets, we restricted the analysis on reproducible peaks with IDR ≤ 0.01. As with the previous analysis, we found that for Q the number of mean-normalized, reproducible peak overlaps is significantly higher than for the other methods (Fig. 4D–F; Supplemental Table S6).

Motif content analysis

One of the major applications of ChIP-seq analysis is to characterize transcription factor binding sites (TFBSs) for ab initio motif discovery or motif enrichment analysis (Zhang et al. 2008; Machanick and Bailey 2011; Newkirk et al. 2011; Xing et al. 2012; Bardet et al. 2013). We reasoned that true binding sites are more likely to contain a sequence-binding motif of the corresponding transcription factor than other sequences. We called initial peak sets using Q, MACS2, SPP, and PeakSeq and took the four-way intersection of the top 50,000 peaks of each caller as a reference peak set. We conducted de novo motif analysis on these peak sets using the motif finder DREME (Bailey 2011) and defined the 10 most significant DREME motifs as the reference motifs. We then asked what proportion of the 50,000 peaks of the individual peak callers contained at least one of the reference motifs. This approach relies on two assumptions. First, the four-way intersection of the original peak calls is enriched in true peaks, and second, the overall proportion of peaks that contain at least one of the reference motifs is a reflection of the accuracy of the individual peak callers.

We extracted genomic sequences of one estimated fragment length around the center of the peaks called by each caller, and masked repetitive regions. All high-scoring occurrences of the reference motifs (P ≤ 0.0001) were determined using FIMO (Grant et al. 2011). Subsequently, the number of peaks that contain at least one high-scoring motif occurrence was determined for the top 50,000 peaks of the individual peak callers.

We applied the motif content analysis to the 38 data sets. In 33 of 38 cases, the top 50,000 peaks of Q include the highest number of peaks with at least one reference motif (Supplemental Table S7). On average, the top 50,000 peaks of Q include 4.1% (2063) more peaks containing at least one reference motif compared with MACS2, 2.6% (1323) compared with SPP, and 5.7% (2840) compared with PeakSeq. The mean difference was statistically significant (Fig. 5).

Figure 5.

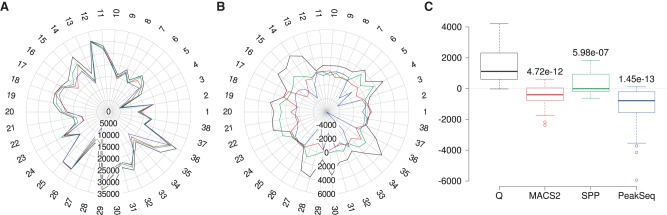
Motif content analysis for 38 ENCODE data sets. We counted the number of peaks among the top 50,000 called peaks that contained at least one occurrence of the corresponding transcription factor binding motifs. (A) Radar plot of the raw peak counts (Supplemental Table S7). Q called the most peaks containing at least one reference motif in 33 of the 38 experiments. The colors of the lines in the radar plot are the same as those shown in the legend of Figure 4. (B) Radar plot of the mean-normalized peak counts. (C) P-values relative to Q were calculated using two-sample, two-sided, Wilcoxon tests comparing mean-normalized peak counts.

Q identifies TSS flanking double summits for RNAPII and H3K4me3

We next focused on the four RNAPII data sets, for which our method had shown the greatest advantage (Figs. 3–5). Pausing RNAPII is characterized by two separate ChIP-seq peaks located directly upstream of and downstream from the transcription start site (TSS) (Stadelmayer et al. 2014). Visual inspection revealed that Q often identified TSS flanking double summits (TFDSs) at promoters where the other peak callers identified a single summit. We therefore tested the ability of Q to identify this biologically relevant signature of pausing RNAPII. Q did indeed detect TFDSs at 39.5%–48.4% of all RNAPII bound promoters, while other methods, mainly reporting single summits, identified a substantially smaller number of TFDSs (10.4%–23.5%) (Supplemental Table S8). Plotting of the distribution of TFDSs identified by Q showed two clearly defined peaks with one sharp peak 50–100 nt downstream from and a second, less pronounced peak 150–250 nt upstream of the TSS separated by a median distance of 375–426 nt. Plotting of the results of the other peak callers failed to produce similar results (Fig. 6A; Supplemental Figs. S8, S9).

Figure 6.

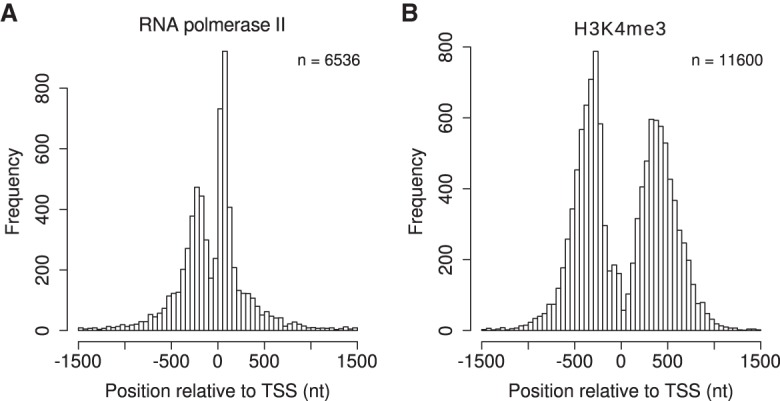
Distribution of TSS flanking double summits (TFDSs). Each TFDS consists of two summits directly upstream of and downstream from the TSS. The TFDSs of Q for HCT-116 RNAPII (A) and HCT-116 H3K4me3 (B) were integrated over all non-overlapping promoters (TSS ± 1500 nt).

Nucleosome-depleted regions (NDRs) at TSS are often flanked by histones marked by H3K4me3 (Cairns 2009; Arya et al. 2010). We therefore applied the same analysis to the H3K4me3 data sets for the same two cell types as for RNAPII (Supplemental Table S1). Q identified TFDSs at 59.2%–70.6% of H3K4me3 bound promoters, compared with only 12.5%–36.5% for the other peak callers (Supplemental Table S9). The distribution of H3K4me3 again showed two clearly defined peaks upstream of and downstream from the TSS (Fig. 6B; Supplemental Fig. S10). For Q, the upstream peak at 250–300 nt is slightly sharper than the downstream peak at 300–400 nt. Peaks are separated by at least 400 nt and by a median distance between summits from 710–778 nt (Supplemental Fig. S11).

The overlap of promoters with TFDS ranges for biological replicates from 78.1%–90.6%, which suggests that TFDSs are reproducibly identified by Q (Supplemental Table S10). Promoters that have a TFDS for RNAPII overlap by 77.1%–87.0% with promoters that have also a TFDS for H3K4me3. For 63.5%–68.7% of those overlapping promoters, we observed a pattern in which the region between the TFDS of RNAPII is completely contained in the region between the TFDS for H3K4me3, which is significantly more than expected by chance. For our simulation study (Methods) (Supplemental Table S11), we observed this pattern in 51.3%–58.7% of promoters (empirical P-value <10⁻⁴). The results of these downstream analyses of TFDSs identified by Q are in perfect agreement with the architecture of paused open promoters that are characterized by a large NDR flanked by H3K4me3 modified histones with interspersed RNAPII (Cairns 2009).

Runtime analysis

Q is implemented in C++ using functionality of SeqAn, a library of efficient data types and algorithms for sequence analysis (Doring et al. 2008). As mentioned above, the fragment length estimation implemented in Q was at least threefold faster than the method as implemented by SPP (Supplemental Table S2). We also compared the runtime of all four algorithms for all steps following fragment length estimation by examining the average runtime across all 38 data sets. Q displayed a threefold to 19-fold improvement in runtime (Supplemental Table S12).

Discussion

Although ChIP-seq is being used in an ever-increasing range of genomics experiments, the computational analysis of the data is not trivial. The called peak regions form the basis of downstream analysis of transcription factor binding motifs, correlation with gene expression, transcriptional regulation, histone modifications, and the correlation of binding profiles of transcription factors with their biological effects (Pepke et al. 2009; Ibrahim et al. 2013). The accuracy and reproducibility of peak calling are thus key issues in the computational analysis of ChIP-seq data and have a major influence on downstream biological analysis.

In this work, we compared Q against three of the most highly used general purpose peak callers—MACS2 (Feng et al. 2012), PeakSeq (Rozowsky et al. 2009), and SPP (Kharchenko et al. 2008)—because these programs have been extensively tested in the ENCODE Project Consortium (The ENCODE Project Consortium 2012). We demonstrated that Q shows advantages over previous methods with respect to reproducibility of the called peaks, consistency of motifs inferred from peak sequences, and runtime.

The Q algorithm leads to a depth distribution distinct from that of the other peak callers (Supplemental Fig. S2); this in turn can have a substantial effect on downstream biological analysis. For example, we analyzed in detail the distribution of RNAPII and H3K4me3 TFDSs in HCT-116 and HeLa-S3 cells. We found substantially more RNAPII TFDSs using Q, which show an overlap of 77.1%–87.0% with the H3K4me3 TFDSs. Thus, Q demonstrates a superior resolution that consistently identifies TFDSs in promoters. This pattern has previously been associated with RNAPII stalling and nucleosome depletion. Q opens up the possibility of investigating this data with higher reproducibility and higher resolution.

Our method is based on an algorithm that shifts the focus from an analysis of peak height on the basis of a Poisson or negative binomial distribution to the identification and assessment of peaks that are highly saturated with respect to the start positions of mapped reads. The concentration on saturation also allows us to perform an estimation of the fragment length using fast Boolean operations, resulting in a runtime that is over three times faster than previous methods that use Pearson correlation. Furthermore, the runtime for peak calling with Q was 3.5 to 18.5 times faster than MACS2, PeakSeq, and SPP. We have additionally shown that our statistical analysis does not require down-sampling of reads from the control experiment, which is commonly used in other tools to enable testing of candidate peaks for enrichment in the test data set. Q is intended to be used without any parameter tuning, although if desired the estimated fragment length can be set as an argument. Therefore, Q is easy to use and fast. Q is available under a BSD2 license together with a detailed tutorial at https://github.com/charite/Q.

Methods

Mapping and ChIP-seq

Our procedure starts with aligned reads from a ChIP-seq experiment performed with a specific antibody and optionally with a control experiment in which the specific antibody is replaced by generic immunoglobulins. The reads are aligned against the forward or reverse strand of a target sequence with l positions. BAM files were downloaded from ENCODE, and duplicate reads were removed by rmdup from the SAMtools package (Li et al. 2009).

Fragment-length estimation

The Hamming distance d_H(x,y) between the bit strings x = x₁x₂…x_n and y = y₁y₂…y_n is defined as the number of positions in which the strings differ; i.e., x_i ≠ y_i. The Hamming distance between two strings can be efficiently calculated in C/C++ using the bitwise XOR operator and summing the number of ones in the result.

$$H(\delta )=\sum _{c\in C}{d}_H[n_c^f(x+\delta ),n_c^r(x)].$$

The value of δ is varied from one to 1000, and the shift corresponding to the minimum value of H(δ) is taken as the estimated fragment length ℓ.

$$\ell =\mathrm{argmi}{\mathrm{n}}_{\delta }H\left(\delta \right).$$

Summit detection

We define a hit h to refer to the 5′ end of each mapped read that is assigned to a specific position (pos) and strand of the target sequence with l positions, i.e., h = (pos, strand). The outcome of a ChIP-seq experiment is modeled as a set of hits:

$$T=\{h=(\mathrm{pos},\mathrm{strand})|\mathrm{pos}\in \{1,\dots ,l\}\wedge \mathrm{strand}\in \{f,r\}\}.$$

If a control experiment (C) is included in the analysis, the hits for C are defined analogously. Each set of hits is subdivided into hits on the forward and reverse strand (T_f and T_r for treatment; C_f and C_r for the control data set). Due to the experimental design of ChIP-seq experiments, we expect that the number of hits on each strand is approximately equal; i.e., $|T_f|\approx |T_r|$ and $|C_f|\approx |C_r|$. According to our null model, the hits of T and C are evenly distributed across the positions 1,…,l of the target sequence, and the hits for the two strands are independently distributed.

In order to form qfrags, we first estimate the mean fragment length ℓ as described above. We define q_min = ℓ−x and q_max = ℓ + x. We have chosen x = 50 nt for the experiments described here. A qfrag is then defined as an ordered pair of hits (h_i,h_j), such that h_i is on the forward strand, h_j is on the reverse strand, and the distance between the two hits is at least q_min but not more than q_max nucleotides, q_min ≤ h_j.pos − h_i.pos ≤ q_max.

Once the qfrags have been identified, our method searches for local maxima of the qfrag depth profile that exceeds a given threshold and is greater than at all other positions within a distance of q_max nucleotides (Fig. 2B). Each local maximum at position i represents a candidate summit; the region i ± q_max, the candidate peak that is subjected to statistical evaluation (Fig. 2C), as described in the following section.

Saturation score

For each candidate peak centered at position i (i.e., a qfrag depth profile local maximum at position i), we consider the nucleotide positions i − q_max,…,i + q_max. For didactic purposes, we will first describe the saturation score for ChIP-seq experiments that are performed without a control and then describe the full algorithm.

Saturation score: without control experiment

We define the random variable Q_t on the sample space Ω = {0,…,2 · q_max}, where each possible outcome corresponds to the number of positions that are covered by the 5′ end of at least one qfrag within a window of length 2 · q_max centered at position i.

Note that a qfrag is constructed for a given hit h at position i of the forward strand for each reverse strand hit at positions i + q_min,…,i + q_max. Position i is covered if there is at least one such qfrag. Given that there are |T_r| reverse strand hits and that the target region has a length of l, we expect |T_r|/l hits at any given position of the target sequence. Because of linearity of expectation, we can estimate the number of reverse strand hits at positions i + q_min,…,i + q_max as

$${\lambda }_t=(q_{\max }-q_{\min })\cdot \frac{|T_r|}{l}.$$

The subscript t stands for treatment. We can now calculate the probability for a given hit on the forward strand to be part of a qfrag using the Poisson distribution Pois(k,λ_t) in order to calculate the probability of finding at least one reverse strand hit at positions i + q_min,…,i + q_max (which is the same as saying that the forward strand hit at position i forms part of a qfrag):

$$P(h_i\mathrm{is}\mathrm{part}\mathrm{of}\mathrm{qfrag}|h_i.\mathrm{strand}=f)=1-\mathrm{Pois}(0,{\lambda }_t).$$

Since we expect to find |T_f|/l hits on the forward strand at position i, the expected rate of qfrag starting positions at any given position i is

$$\frac{|T_f|}{l}\cdot (1-\text{Pois}(0,{\lambda }_t)).$$

For hits on the reverse strand, the rate is approximately equal, because we expect the number of hits on each strand is nearly the same. If we do not distinguish between strands, we calculate the expected rate r_t of qfrag start and end positions as

$$r_t=2\cdot \frac{|T_f|}{l}\cdot (1-\text{Pois}(0,{\lambda }_t)).$$

Our method models the saturation of positions in the framework of the occupancy problem (Feller 1968). That is, if we place m balls randomly into n bins, how many bins remain empty? The probability that one particular ball lands in a certain bin is 1/n. Then the probability that the ball does not land in the bin is (1 − 1/n), and the probability that the bin is missed by all m balls is

$$P(\text{bin remains empty})={\left(1-\frac{1}{n}\right)}^m\cong e^{-m/n}.$$

In our model, we can thus estimate the probability that a given position i is not covered by the start or end position of a qfrag as $e^{-r_t}$. Then the probability that a given position is covered by at least one qfrag start or end position is

$$p_t=1-e^{-r_t}.$$

In the null model, we assume that each of the 2 · q_max positions can be represented as an independent and identically distributed Bernoulli trial. Therefore, Q_t has the following binomial distribution:

$$Q_t\sim \text{Bin}(n=2\cdot q_{\max },p=p_t).$$

The probability that exactly k positions in a window of length 2 · q_max are covered by at least one qfrag start or end position is then

$$P(Q_t=k)=\left(\begin{array}{c}2\cdot q_{max}\\ k\end{array}\right)\cdot p_t^k\cdot (1-p_t{)}^{2\cdot q_{\max }-k}.$$

Similarly, the probability that at least k positions in a window of length 2 · q_max are covered by at least one qfrag start or end position is

$$P(k\le Q_t\le q_{\max })=\sum _{i=k}^{2\cdot q_{\max }}\left(\begin{array}{c}2\cdot q_{\max }\\ i\end{array}\right)\cdot p_t^i\cdot (1-p_t{)}^{2\cdot q_{\max }-i}.$$

We take P(k ≤ Q_t ≤ q_max) as the nominal probability of there being a ChIP-seq peak surrounding the local maximum at position i.

Saturation score: with control experiment

We define the random variable Q_c on the sample space Ω = {0,…,2 · q_max}, which is analogous to Q_t. Then we define a third random variable Q_d = Q_t − Q_c, which describes the difference between the treatment and control samples. Q_d can take on values in the sample space Ω = {−2 · q_max,…,0,…,2 · q_max}. Thus, if more positions are covered by at least one qfrag start or end position in the control set than in the treatment set, Q_d < 0, and if more positions are covered in the treatment set than in the control set, Q_d > 0. The distribution of Q_c is completely analogous to that of Q_t:

$${\lambda }_c=(q_{\max }-q_{\min })\cdot \frac{|C_r|}{l},$$

$$r_c=2\cdot \frac{|C_r|}{l}\cdot (1-\text{Pois}(0,{\lambda }_c)),$$

$$p_c=1-e^{-r_c}.$$

According our null model, we note that Q_t and Q_c are independent according to the null model. Calculating the distribution of Q_d then involves the analysis of the convolution of two independent binomial distributions. To gain intuition, imagine we draw two random numbers, one from Q_t and one from Q_c. What is the probability to observe a difference of d? Let us assume for a moment that d ≥ 0. There are 2 · q_max − d + 1 different ways to observe a difference of d. For instance, there can be zero saturated positions in the control experiments (Q_c = 0) and d saturated positions in the treatment experiments (Q_t = d), or one saturated position in the control experiments (Q_c = 1) and d + 1 saturated positions in the treatment experiments (Q_t = d + 1), and so on up to a maximum of 2 · q_max − d saturated positions in the control experiments (Q_c = 2 · q_max − d) and 2 · q_max such positions in the treatment experiments (Q_t = 2 · q_max). To calculate the probability of observing Q_d = d, we have to sum up the 2 · q_max − d + 1 products for each possible combination.

$$P(Q_d=d)=\sum _{i=0}^{2\cdot q_{\max }-d}P(Q_t=i+d)\cdot P(Q_c=i).$$

In general, however, if Q_c > Q_t, there will be terms where i + d < 0 and terms where i + d > 2 · q_max. Furthermore, there are terms where i becomes larger than 2 · q_max. Therefore, we use the preceding equation for d ≥ 0 and the following equation for d < 0:

$$P(Q_d=d)=\sum _{i=0}^{2\cdot q_{\max }-|d|}P(Q_t=i)\cdot P(Q_c=i+|d|).$$

It is useful to allow for negative differences, which may be observed if the sequencing depth for the control sample is much higher than that for the treatment sample. This definition therefore allows us to use control sample data without necessarily having to down-sample the reads to a level comparable to that of the test samples (Supplemental Fig. S4). Finally, the probability that a candidate region represents a ChIP-seq peak with a difference in saturated positions of Q_d = d between treatment and control is

$$P(d\le i\le 2\cdot q_{\max })=\sum _{i=d}^{2\cdot q_{\max }}P(Q_d=i).$$

Multiple testing correction

All regions covered by at least one qfrag are tested. P-values are corrected for multiple testing using the Benjamini–Hochberg procedure (Benjamini and Hochberg 1995).

Data preparation

We evaluated the performance of our method based on the analysis of 38 ChIP-seq experiments of the ENCODE Project Consortium. These experiments correspond to 19 biological replicates, seven cell types, and 17 target proteins (Supplemental Table S1). Data sets were downloaded from UCSC (Rosenbloom et al. 2013) in BAM format. Unmapped reads, duplicates, and reads mapping to chromosomes other than Chromosomes 1–22, X and Y were removed.

Peak calling

We compared our method to the peak callers MACS2 (version 2.0.10.20120913), SPP (version 1.11), and PeakSeq (version 1.1). We determined an average fragment length ℓ and a window half size whs using the cross-correlation analysis of SPP. To ensure a standardized comparison, we used ℓ as input for all peak callers; whs was also used as an input parameter for SPP. For the experiments described here, we performed down-sampling for the treatment or control data sets to an equal number of mapped reads as for the treatment data sets. We performed low stringency analyses for all peak callers by setting the thresholds appropriately. Peak lists were sorted by significance and truncated at 100,000 for reproducibility analysis and at 50,000 for motif content analysis. The parameters used for peak calling are shown in the Supplemental Methods.

Reproducibility analysis

The IDR procedure is intended to assess the reproducibility of peaks called in ChIP-seq experiments (Li et al. 2011). We performed IDR analysis as detailed in Supplemental Methods. Two pseudoreplicates (Li et al. 2011; Landt et al. 2012) were created for each data set by dividing the treatment and control data randomly into two halves. For each of the four peak callers, we set up a workflow for IDR analysis using the recommended parameters. For Q, MACS2, and PeakSeq, the peaks were sorted by P-value and for SPP by signal value. The top 100,000 peaks were used as input for the IDR analysis and for the calculation of the counts of overlapping peaks.

Motif content analysis

For the peak callers Q, MACS2, SPP, and PeakSeq peaks were called using the prepared data sets (Supplemental Table S1) and parameters as described above. Peak lists were sorted as for reproducibility analysis. Summits were extended upstream and downstream by one estimated fragment length ℓ.

To get the reference peak set, the top 50,000 peaks were iteratively and pairwise intersected using intersectBed of BEDTools (Quinlan and Hall 2010), requiring an overlap of at least 50%. At first, the top 50,000 peaks for Q and MACS2 were intersected, the resulting peak list was then intersected with the top 50,000 peaks of SPP, and the resulting peak list was finally intersected with the top 50,000 peaks of PeakSeq. In this way, two summits in a combined peak are separated by a distance of at most 3·ℓ, and there is no peak broader than 5·ℓ.

The genomic sequences of reference peaks were cut out, and repeats were masked by replacing lowercase letters with Ns. These sequences were used as input for DREME (Bailey 2011) to derive the top 10 most significant motifs. For the summits of the top 50,000 peaks, the genomic sequences ℓ/2 upstream and downstream were extracted. These sequences were scanned for occurrences of the 10 reference motifs using FIMO (Grant et al. 2011) with a P-value cutoff of 0.0001. For each of the initial top 50,000 peaks of the different peak callers, the number of peaks that contain at least one motif occurrence was determined.

TSS flanking double summits

We analyzed the H3K4me3 data sets (Supplemental Table 1) in the same way as we did for the reproducibility analysis of other data sets. We took the overlap of the top 100,000 peaks as input for the TFDS analysis. We used the transcript annotation from NCBI (build 37.2; NCBI Homo sapiens annotation release 104). Promoters were defined as TSS ± 1500 nt. The total of 29,692 promoters were filtered for 19,722 non-overlapping promoters.

In order to assess whether the observed number of cases in which for a given promoter the TFDS for RNAPII is completely contained between the TFDS for H3K4me3 occurs by chance, we generated data simulations as follows: For each promoter that had been assigned a TFDS for both RNAPII and H3K4me3, we obtained the distances of the upstream and downstream summit for H3K4me3 and for RNAPII. We shuffled the observed intervals for the H3K4me3 TFDSs among these promoters and then examined the number that show the pattern where the RNAPII TFDS is completely contained in the H3K4me3 TFDS. In 10,000 simulations, we did not observe even a single case in which the number of promoters showing this pattern was as high as in the observed data (empirical P-value <10⁻⁴) (Supplemental Table S11).

Software availability

The Q algorithm was implemented in C++, and the source code is available in the Supplemental Material and under an open-source BSD2 license at https://github.com/charite/Q. The GitHub site has a link to a detailed tutorial.