Abstract
Polyglutamine (polyQ) peptides are a useful model system for biophysical studies of protein folding and aggregation, both for their intriguing aggregation properties and their own relevance to human disease. The genetic expansion of a polyQ tract triggers the formation of amyloid aggregates associated with nine neurodegenerative diseases. Several clearly identifiable and separable factors, notably the length of the polyQ tract, influence the mechanism of aggregation, its associated kinetics, and the ensemble of structures formed. Atomistic simulations are well positioned to answer open questions regarding the thermodynamics and kinetics of polyQ folding and aggregation. The additional, explicit representation of water permits deeper investigation of the role of solvent dynamics, and it permits a direct comparison of simulation results with infrared spectroscopy experiments. The generation of meaningful simulation results hinges on satisfying two essential criteria: achieving sufficient conformational sampling to draw statistically valid conclusions, and accurately reproducing the intermolecular forces that govern system structure and dynamics. In this work, we examine the ability of 12 biomolecular force fields to reproduce the properties of a simple, 30-residue polyQ peptide (Q30) in explicit water. In addition to secondary and tertiary structure, we consider generic structural properties of polymers that provide additional dimensions for analysis of the highly degenerate disordered states of the molecule. We find that the 12 force fields produce a wide range of predictions. We identify AMBER ff99SB, AMBER ff99SB∗, and OPLS-AA/L to be most suitable for studies of polyQ folding and aggregation.
Introduction
Molecular simulations have become an increasingly useful tool for studying the dynamics and thermodynamics of protein folding and self-assembly. The generation of meaningful results from simulation relies on two principal elements, both of which are areas of active research. First, the simulation must sample the relevant regions of phase space in a manner sufficient to reach statistically valid conclusions—the sampling problem (1–19). Second, the potential energy functions used to represent interactions in the simulated system must provide a reasonable approximation to the behavior of the real system—the force field problem (20–24).
Several recent studies, empowered by the ability to simulate over long timescales and thoroughly sample configurational space, have revealed inaccuracies in atomistic force fields designed to simulate biomolecules in explicit water (25–30). Such inaccuracies include incorrect secondary and tertiary structures, folding mechanisms, and NMR chemical shifts and couplings. The functional form and parametrization of the backbone torsional potential have attracted special interest because of their central, cooperative role in the formation of secondary structure. Benchmark molecules for the aforementioned studies included small oligopeptides and proteins with a well-defined native fold, such as ubiquitin, the villin headpiece, and the FiP35 WW domain (26–29). Relatively few studies, however, have investigated whether atomistic force fields with explicit water models can reproduce the structural properties of proteins that lack a unique native conformation, known as intrinsically disordered proteins or intrinsically disordered polypeptides (IDPs) (31). As a result, it remains difficult to determine a priori which force field, if any, is best suited for modeling IDPs.
In this work, we evaluate the ability of 12 atomistic force fields to reproduce the structural properties of a 30-residue polyglutamine (polyQ) peptide in dilute solution. The appearance of aggregates rich in polyQ-containing peptides is associated with the onset of symptoms in nine neurodegenerative diseases, notably Huntington’s disease (32–34). Some of the relevant aggregation behavior has been reproduced in vitro using synthetic peptides containing only the polyQ tract and solubilizing or labeling residues, known as simple polyQ peptides (35–45). Identifying a force field that faithfully models simple polyQ peptides in solution is directly relevant to ongoing efforts by multiple research groups to model the dynamics and thermodynamics of its folding and aggregation.
More generally, simple polyQ peptides are an archetypal IDP for which there is sufficient experimental data in the literature to validate candidate force fields. In vitro studies have repeatedly shown that polyQ repeats of lengths 5 to 44 natively populate a heterogeneous ensemble of collapsed, disordered conformations (35,40–48). Circular dichroism experiments on simple polyQ peptides, and NMR experiments on a polyQ tract fused to a larger protein, indicate a lack of regular, stable secondary structure in the polyQ tract. It is important to note that neither circular dichroism nor NMR is capable of resolving individual conformations that interconvert on the microsecond timescale or faster; the signals measured represent only an average over the conformational ensemble. To the best of our knowledge, experimental studies have not reported the precise proportions of various secondary structure elements in simple polyQ chains; the consensus, however, is that any regular secondary structure is metastable (35,40,42,46,48). Because polyQ does not exhibit a marked preference for any particular secondary structure, we believe that the simulated peptide might be particularly sensitive to biases in the torsional potentials that overstabilize particular combinations of the Ramachandran angles.
Simple polyQ peptides exhibit a particular type of disorder that is quantified by the scaling of polymer size with length. Fluorescence correlation spectroscopy experiments (49) indicate that water is a poor solvent for simple polyQ peptides of lengths 15 to 53—a surprising finding, given that the glutamine monomer is highly soluble in water. The driving force for collapse is favorable self-solvation by intramolecular hydrogen bonding and the concomitant tendency to minimize the high-tension peptide-water interface. Given the lack of sequence specificity and the similarity between backbone and side chain functional groups, there is no unique fold that minimizes the solvent-accessible surface. In other words, a large number of collapsed structures contribute to thermodynamic stability, and the formation of an extended conformation is thermodynamically unfavorable. The poorness of water as a solvent for polyQ also suggests a generic driving force for aggregation. Therefore, the accurate computational modeling of polyQ requires a realistic representation of collapse and extension in dilute solution.
PolyQ has been the subject of numerous in silico studies at the atomistic/explicit-solvent (50–55), atomistic/implicit-solvent (56–58), and coarse-grained (59–61) levels of description. The most extensive data on aggregation processes has emerged from simulations using a coarse-grained protein model and/or an implicit solvent, because those simulations can more easily access the long timescales characteristic of aggregation. Still, there are important problems for which simulations in explicit solvent are appropriate and necessary. One is to better understand the dynamics of solvent reorganization, which have been suggested as a rate-limiting phenomenon for amyloid aggregation in general (62) and for polyQ aggregation in particular (63). Another is to facilitate the interpretation of two-dimensional infrared spectroscopy (2D IR) experiments, which provide structural and dynamic information with single-residue specificity and on subnanosecond timescales (64). The accurate theoretical modeling of 2D IR spectra from classical molecular dynamics (MD) simulations requires that both protein and solvent be represented in atomistic detail. Moreover, the classical force field and water model determine the parametrization of so-called frequency maps, which bridge simulation and theory and enable the direct comparison of simulations and IR experiments (65,66).
To date, it is unclear which atomistic force field and companion water model are most appropriate for MD simulations of polyQ and other IDPs. OPLS-AA/L (67) and TIP3P (68) predicted an ensemble of disordered, collapsed conformations for the Q20 peptide (50). The polymer physics approach described therein inspired parts of our analysis in this work. The combination of OPLS-AA/L and TIP4P also predicted results consistent with experiment for the Q5 and Q15 peptides (52). For other systems, OPLS-AA/L has been variously reported to overstabilize disordered conformations (69) or overstabilize β-sheets (70). Given those findings, it is worthwhile to verify OPLS-AA/L for a longer polyQ peptide, which ought to form β-hairpins and β-sheets more easily because there are more locations for potential turn element(s). Our previous work on Q54 used AMBER ff99 (71) and TIP3P, which performed poorly in a recent survey of force fields (28). The AMBER ff03w force field (31), which was optimized for the TIP4P/2005 water model (72), is also of special interest here, because TIP4P/2005 represents water dynamics more accurately than its predecessors. Such a model is promising for simulations of IDPs, and our study investigates whether the successes of an earlier study (31) transfer to polyQ.
In the following section, we describe the model system and the simulation techniques employed in this study. We then present measures of secondary and tertiary structure, and polymer size, shape, stiffness, and scaling in aqueous solution, as predicted by the 12 force fields we considered. Three force fields predict structural properties for polyQ in qualitative agreement with experiments: AMBER ff99SB, AMBER ff99SB∗, and OPLS-AA/L.
Materials and Methods
Simulated system and force fields
The model system considered in this study consists of a single 30-residue polyglutamine oligopeptide (hereafter denoted Q30) surrounded by 8,192 water molecules, which are represented explicitly. To match conditions at physiological pH, the amino and carboxy termini of the peptide are assigned charges of +1 and –1, respectively. Glutamine has zero net charge at physiological pH; therefore, the zwitterionic peptide has zero net charge, and the system contains no additional counterions or salts. The system was placed in a cubic simulation box measuring 6.3 nm on each side. Periodic boundary conditions were enforced in all three dimensions.
The simulations described in the next subsection were performed in 12 independent runs. In each run, the protein was modeled using one of 12 force fields. For each force field, the companion water model was the same used in the original publication that introduced the force field. The 12 force fields are listed in Table 1.
Table 1.
Force fields and companion water models
| Force Field | Water Model | References |
|---|---|---|
| AMBER ff99 | TIP3P | (68,71) |
| AMBER ff99SB | TIP3P | (73) |
| AMBER ff99SB∗ | TIP3P | (74) |
| AMBER ff03 | TIP3P | (75) |
| AMBER ff03∗ | TIP3P | (74) |
| AMBER ff03w | TIP4P/2005 | (31,72) |
| CHARMM27 | TIP3P for CHARMM | (76,77) |
| CHARMM22∗ | TIP3P for CHARMM | (27) |
| CHARMM36 | TIP3P | (78) |
| GROMOS96 53a6 | SPC | (79,80) |
| GROMOS96 54a7 | SPC | (81) |
| OPLS-AA/L | TIP4P | (67,68) |
In every force field except GROMOS96 53a6 and GROMOS96 54a7, all atoms were represented. GROMOS96 53a6 and GROMOS96 54a7 are united-atom force fields, meaning that each nonpolar methylene group was coarse-grained into a single interaction site.
Coulombic forces were calculated using the particle mesh Ewald algorithm (82,83). During equilibration, annealing, and replica exchange molecular dynamics (REMD) simulations, temperature and pressure coupling were achieved using the Nosé-Hoover thermostat algorithm (84) and the Parrinello-Rahman barostat algorithm (85,86), respectively. To generate an initial structure, we extracted a disordered peptide conformation from our previous REMD simulations of Q54 and shortened it to Q30 (53). Steric clashes were relaxed via a conjugate gradients energy minimization scheme. Water molecules were then added to fill the remainder of the box, and the energy was minimized a second time. All subsequent simulations were performed with a time step of 2 fs. Equilibration of velocities, of temperature to reference 298 K, and of pressure to reference 1 bar was achieved in a series of short MD simulations of order 10 ps in length. During production simulations, all bond lengths were constrained to their equilibrium values by the linear constraint solver algorithm (87). To generate initial configurations for REMD simulations, the equilibrated peptide-water system was annealed from 298 K to 478 K at a rate of 4 K/ns, at a constant pressure of 1 bar.
Replica exchange molecular dynamics
REMD, also known as parallel tempering molecular dynamics, is a method for accelerating the sampling of configurational space in an MD simulation (2,88). In a REMD simulation, multiple physical realizations, or replicas, of the system are simulated in parallel, each at a different, constant temperature. Periodically, a Monte Carlo move is attempted. The move consists of exchanging the coordinates of replicas that are adjacent in temperature space. The attempted moves are accepted with a probability defined by the following modified Metropolis criterion (89):
| (1) |
where the indices of the lower- and higher-temperature replicas are i and j, respectively; the inverse temperatures of replicas i and j are β(i) and β(j), respectively; the pressures of replicas i and j are P(i) and P(j), respectively; the volumes of replicas i and j are V(i) and V(j), respectively; the potential energy as a function of atomic coordinates is U; and the atomic coordinate vectors of replicas i and j are X(i) and X(j), respectively. The exchange criterion satisfies detailed balance. Consequently, at each temperature a correct Boltzmann energy distribution is generated, but with a discontinuity in the dynamics at the instant of each accepted exchange move. Put another way, each spatially continuous trajectory performs a stochastic walk in the temperature space spanned by the replicas. Potential energy barriers are more easily surmounted at high temperatures, providing for a more efficient sampling of configurational space than is possible in a brute-force MD simulation. REMD is an especially valuable tool for the study of systems whose ergodicity is inhibited by the roughness of the underlying free energy hypersurface. Biomolecules, and instrinsically disordered peptides such as polyQ in particular, constitute one such class of systems. Unlike umbrella sampling and density-of-states-based methods that also accelerate configurational sampling, REMD does not require a priori knowledge of the collective variables or reaction coordinates that describe conformational changes.
In our simulations, temperatures were chosen in an exponential distribution (90) to achieve an exchange acceptance rate of 0.2 to 0.3, which is believed to optimize the efficiency of the method (91). For AMBER ff99, 60 replicas spanned 298–459 K, for GROMOS96 53a6 and GROMOS96 54a7, 72 replicas spanned 298–459 K, and for all other force fields, 72 replicas spanned 298–478 K. The temperatures are listed in Table S1 in the Supporting Material. For each temperature, a corresponding configuration was extracted from the temperature annealing simulation described in the previous subsection. All 72 replicas were then run in parallel for 150 ns each, at a constant pressure of 1 bar and each at a different, constant temperature in the distribution. The equations of motion were integrated using the leap-frog algorithm. Coordinate exchanges were attempted every 2 ps. Configurational snapshots containing particle positions and velocities were saved every 20 ps. Production statistics were gathered from the last 100 ns of simulation of each replica. For each force field, the total simulated time was 10.8 μs, and the total simulated production time was 7.2 μs. REMD simulations were carried out using the GROMACS 4.5.3 simulation package (10,92,93) built on PBS clusters at the University of Wisconsin–Madison and the University of Chicago, and on a Cray cluster at the University of Chicago and Argonne National Laboratory. We assessed the convergence of our simulations by unmixing the REMD trajectories and calculating the conformational relaxation time (see Table S4).
Results
Secondary and tertiary structure
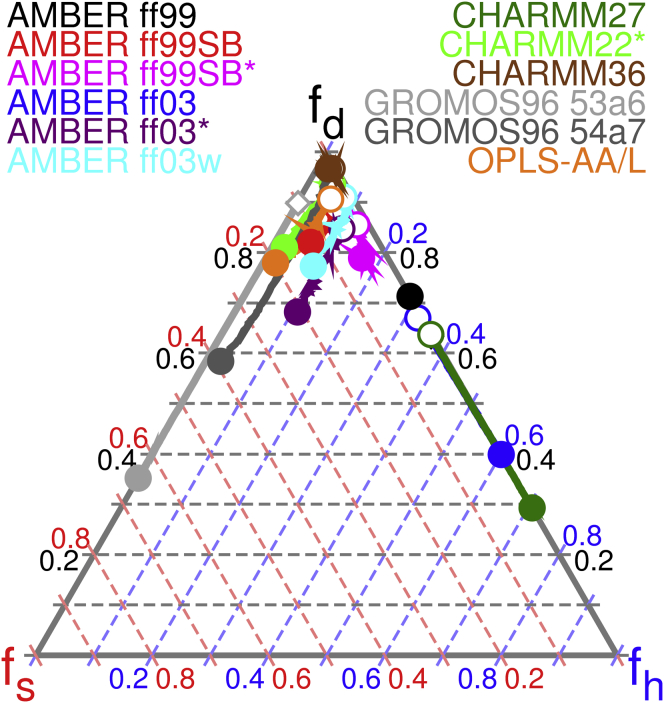
As discussed earlier, polyQ is an attractive model system for force field evaluations because it possesses no unique, native conformation, nor does it exhibit regular secondary structure. We hypothesized that inaccuracies in the force fields, particularly in the torsional potentials, might be more readily apparent for polyQ than for other polypeptides previously studied. The fractional secondary structure for all 12 force fields, calculated from REMD simulations, is shown in Fig. 1.
Figure 1.
Average fractional secondary structure of Q30 in water, computed for 12 biomolecular force fields. The disordered (fd), strand-like (fs), and helix-like (fh) fractions are plotted for 298 K (solid circles), for the highest-temperature replicas in each simulation, 478 K (open circles) or 459 K (open diamonds), and for the intervening temperatures (lines). For every snapshot saved during the production REMD simulations, each residue was assigned one of the eight secondary structure states defined by the DSSP criteria, which are based on hydrogen bond energy and curvature of the backbone chain (94). We grouped the DSSP assignments into broader categories: disordered (coil, bend, and turn), strand-like (β-sheet and β-bridge), and helix-like (α-helix, 310-helix, and π-helix). At each temperature, the corresponding secondary structure fractions were averaged over all 5000 production snapshots. The 459 K symbol of AMBER ff99 is hidden beneath the 478 K symbol of CHARMM27, and the 459 K symbol of GROMOS96 54a7 is hidden beneath the 298 K and 478 K symbols of CHARMM36. By construction, fd + fs + fh = 1. Estimates of the sampling errors are provided in Tables S2 and S3 and in Fig. S1.
Our REMD simulations reveal significant discrepancies among the predictions of the chosen force fields. Nine of 12 force fields predict a mostly disordered conformational ensemble for Q30 in water at 298 K: AMBER ff99, AMBER ff99SB, AMBER ff99SB∗, AMBER ff03∗, AMBER ff03w, CHARMM22∗, CHARMM36, GROMOS96 54a7, and OPLS-AA/L. Those nine predict average disordered fractions ranging from 0.584 ± 0.007 (GROMOS96 54a7) to 0.965 ± 0.007 (CHARMM36), although there is significant variance in the proportions of helical and strand content in the remainder (for instance, compare AMBER ff99 with GROMOS96 54a7). In contrast, the AMBER ff03 and CHARMM27 force fields predict average helix fractions of 0.601 ± 0.053 and 0.707 ± 0.015, respectively, at 298 K. GROMOS96 53a6 predicts an average strand fraction of 0.648 ± 0.008 at 298 K.
The temperature dependence of secondary structure content is also plotted in Fig. 1. All models, with the exception of AMBER ff99, predict increasing structural disorder as temperature increases. The β-sheet structures that dominate the conformational ensemble predicted by GROMOS96 53a6 (and that comprise a significant fraction of the ensemble predicted by GROMOS96 54a7) at 298 K are largely unfolded at 459 K. AMBER ff03 and CHARMM27 also predict smaller fractions of helix at 478 K than at 298 K, but the difference is less pronounced than it is for GROMOS96 53a6. AMBER ff99 predicts a small increase in helical content with increasing temperature, but at no temperature does that model predict any significant β-sheet content.
We note that our simulation protocol quenches the liquid-vapor phase transition at 373 K—i.e., the water is superheated—because the formation of a liquid-vapor interface in a microscopic system incurs a significant thermodynamic penalty. In Figs. S6 and S7 we plot the density and pressure, respectively, of the replicas as functions of temperature. The Metropolis exchange criterion (Eq. 1) satisfies detailed balance at each temperature and thus guarantees a Boltzmann distribution of states—including at 298 K, which is of prime interest in this study. We do not attempt to establish any physical relevance of results at high temperatures because 1) to our knowledge, there is no experimental data with which to compare, and 2) in general, the models were parameterized to reproduce the correct physics under standard laboratory conditions, and are not necessarily reliable at higher temperatures. Still, the results provide some insight into the stability of the conformations identified in simulations.
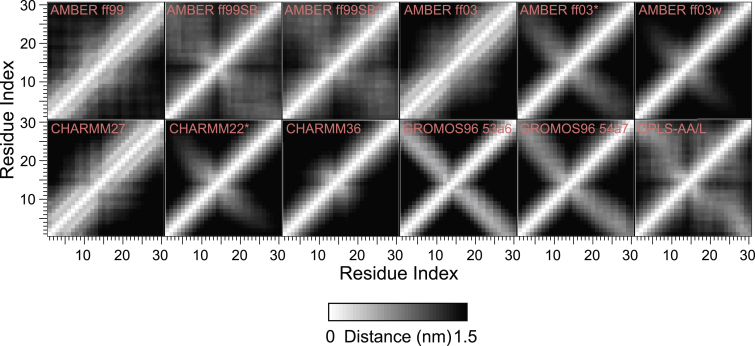
Residue contact maps are plotted in Fig. 2. Persistent contacts between pairs of residues are indicated by gray. Gray lines offset from the main diagonal by three to five residues represent helices, gray lines parallel to the antidiagonal represent antiparallel β-sheets, and gray lines parallel to the diagonal represent parallel β-sheets. Based on the absence of persistent contacts other than those corresponding to the secondary structure preferences illustrated in Fig. 1, the Q30 peptide appears to have little, if any, regular tertiary structure. Note, however, that nonspecific contacts between distant residues are prevalent in some force fields (e.g., AMBER ff99SB, ff99SB∗, OPLS-AA/L) and virtually nonexistent in others (e.g., AMBER ff03w, CHARMM36). Such an observation suggests that different force fields predict varying degrees of polymer swelling or collapse in solution. This idea is treated more rigorously in the following section.
Figure 2.
Residue contact maps for Q30 in water at 298 K. The shade measures the average smallest distance between the indicated residues over 5000 production snapshots from REMD simulations. All distances greater than or equal to 1.5 nm are shaded black. By construction, the maps are symmetric across the diagonal. Estimates of the sampling error are provided in Fig. S2.
Polymeric properties
The force fields can be further differentiated according to generic measures of polymer size, shape, and stiffness. These measures act as additional dimensions for analysis of the highly degenerate disordered states that dominate the conformational ensembles predicted by 9 of 12 force fields. Our approach is in the spirit of a previous in silico study of polyQ that characterized the collapse of the molecule in aqueous solution (50). The radius of gyration, Rg, is defined by the following:
| (2) |
where the number of atoms is N, the mass of atom i is mi, the position of atom i is xi, and the position of the center of mass is xCM. The radius of gyration may also be calculated from the gyration tensor T, according to the following equations:
| (3) |
| (4) |
where the eigenvalues of T are λ1, λ2, and λ3. The asphericity, δ, which ranges from δ = 0 for a perfectly spherical object to δ = 1 for an infinitely long rod, is defined by the following:
| (5) |
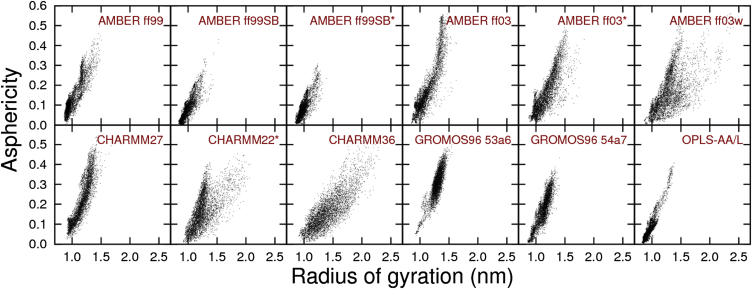
In Fig. 3 we plot the values of Rg and δ for all production snapshots at 298 K. Owing to the high secondary structure content, AMBER ff03, CHARMM27, and GROMOS96 53a6 predict significant populations of elongated structures. More surprisingly, the nine force fields that predict a predominantly disordered conformational ensemble give varying distributions of size and shape. AMBER ff99SB, AMBER ff99SB∗, and OPLS-AA/L exhibit a tight cluster of nearly spherical conformations with Rg ≈ 1.0. AMBER ff03∗, AMBER ff03w, CHARMM22∗, and CHARMM36 exhibit more diffuse distributions and sample many more elongated conformations. The distributions predicted by AMBER ff99 and GROMOS96 54a7 are intermediate between these two classes. Among those force fields that predict mostly disordered conformations for Q30 in water, some (but not all) of the variance in the radius of gyration and asphericity is attributable to the following differences in the persistence length lp:
| (6) |
where the bond length is l, the first bond vector is , and the end-to-end vector is . The persistence length and end-to-end distance are shown in Table 2. Both measures vary significantly across the 12 force fields. Note that because the backbone changes direction constantly within an α-helix and comparatively little within a β-strand, secondary structure propensities are embedded in the value of the persistence length. It is not trivial to separate the two. Therefore, the value of the persistence length is most informative for force fields in which the proportions of regular secondary structure are low.
Figure 3.
Histograms of radius of gyration and asphericity for Q30 in water at 298 K. Each point corresponds to one production snapshot. Block histograms, which are an indicator of convergence, are provided in Figs. S3 and S4.
Table 2.
Polymeric measures of Q30 in water and estimates of the sampling error
| Force Field | Radius of Gyration (nm) | Asphericity | Persistence Length (nm) | End-to-End Distance (nm) |
|---|---|---|---|---|
| AMBER ff99 | 1.025 ± 0.017 | 0.135 ± 0.013 | 0.244 ± 0.001 | 1.815 ± 0.119 |
| AMBER ff99SB | 0.982 ± 0.003 | 0.073 ± 0.002 | 0.448 ± 0.011 | 1.334 ± 0.052 |
| AMBER ff99SB∗ | 0.986 ± 0.005 | 0.081 ± 0.003 | 0.344 ± 0.010 | 1.537 ± 0.111 |
| AMBER ff03 | 1.127 ± 0.017 | 0.185 ± 0.028 | 0.223 ± 0.005 | 2.698 ± 0.078 |
| AMBER ff03∗ | 1.179 ± 0.025 | 0.162 ± 0.012 | 0.718 ± 0.021 | 1.854 ± 0.085 |
| AMBER ff03w | 1.299 ± 0.014 | 0.167 ± 0.005 | 0.761 ± 0.043 | 2.353 ± 0.091 |
| CHARMM27 | 1.170 ± 0.014 | 0.218 ± 0.043 | 0.197 ± 0.005 | 3.019 ± 0.120 |
| CHARMM22∗ | 1.255 ± 0.018 | 0.165 ± 0.005 | 0.670 ± 0.017 | 2.247 ± 0.198 |
| CHARMM36 | 1.397 ± 0.022 | 0.160 ± 0.004 | 0.496 ± 0.014 | 3.311 ± 0.073 |
| GROMOS96 53a6 | 1.294 ± 0.006 | 0.301 ± 0.003 | 1.124 ± 0.009 | 1.043 ± 0.031 |
| GROMOS96 54a7 | 1.125 ± 0.006 | 0.172 ± 0.005 | 0.595 ± 0.011 | 1.109 ± 0.030 |
| OPLS-AA/L | 0.951 ± 0.030 | 0.072 ± 0.019 | 0.511 ± 0.076 | 0.975 ± 0.033 |
The balance of peptide-peptide and peptide-solvent interactions influences whether a polymer adopts predominantly collapsed or expanded structures in solution. The scaling of a polymer’s three-dimensional size as a function of length is an indicator of solvent quality that can be quantitatively compared with experimental data. If the radius of gyration follows the scaling law , where the number of monomers is Nr, then the value of the exponent ν depends on the solvent quality. In a poor solvent, ν = 1/3; in a neutral (theta) solvent, ν = 1/2; in a good solvent, ν ≈ 0.588. The value of ν for simple polyQ peptides in dilute solution was determined from experiments to be 0.32 ± 0.02 (49).
The single chain form factor P(q), defined to be the ratio of the scattering intensity of the polymer solution Is to the Rayleigh scattering intensity Is0 as a function of scattering wavelength q, captures polymer scaling behavior across all relevant length scales. In the limit of infinite molecular weight, the value of ν may be extracted from the single chain form factor. The Q30 peptide, which contains fewer than 100 bonds along the backbone, falls well short of that limit and, as shown below, the value of ν cannot be determined. Still, this analysis provides a useful summary of polymer structure across multiple length scales. Given an ensemble of conformations, the single chain form factor is modeled by the following equation:
| (7) |
| (8) |
The sums run over all Cα atoms in the peptide. The scattering wavevector is q, the number of residues is Nr, the vector distance between atoms k and l is rkl, and the scalar distance between atoms k and l is rkl.
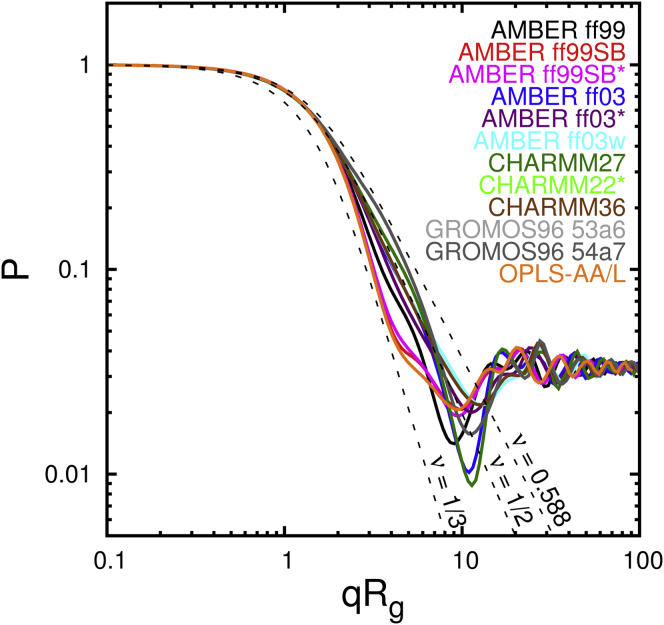
For each force field, the single chain form factor was calculated by evaluating Eq. 8 on the interval and averaging over 5000 production snapshots from the REMD simulations. The results are plotted in Fig. 4, with each curve scaled horizontally by the average value of Rg in the corresponding force field.
Figure 4.
Single chain form factor of Q30 in water at 298 K. Solid lines indicate REMD data. Dashed lines indicate analytical predictions (Eq. 9) for collapsed globule (ν = 1/3), theta coil (ν = 1/2), and swollen coil (ν = 0.588) of infinite molecular weight. Estimates of the sampling error are provided in Fig. S5.
The plot includes analytical curves (i.e., infinite molecular weight) for selected values of ν, according to the following equation:
| (9) |
where Γ(a,z1,z2) is the generalized incomplete gamma function with exponent a and lower and upper limits of integration z1 and z2, respectively (95–97).
The force fields exhibit a variety of scaling behaviors. For qRg < 2, all curves from simulation follow the analytical prediction for ν = 1/2. On longer length scales, the curves diverge, reflecting the varied degrees of collapse described earlier. As qRg continues to increase, the scattering wavelength approaches the length of covalent bonds, and no useful information about macromolecular structure is available. As mentioned earlier, the curves calculated from simulation cannot be fit well by the analytical curves for any single value of ν. The difficulty appears to be related to the fact that in all of the models, the radius of gyration is within an order of magnitude of the persistence length. Our data are insufficient to determine a value for the polymer scaling coefficient. Nevertheless, the marked differences in the degree of collapse aid our ability to discriminate among force fields.
Discussion
The simulated structural and thermodynamic properties of a simple polyQ peptide in solution have been examined for 12 atomistic force fields for biomolecules and their companion water models. We carried out extensive REMD simulations to thoroughly sample the equilibrium phase space of the Q30 peptide. The models chosen for evaluation included at least one from each of the four major families of atomistic force fields for biomolecules. They included recent versions as well as older ones that have been used extensively in the literature. Our simulations revealed substantial differences in the predicted equilibrium properties of Q30 in water, including the secondary and tertiary structure, radius of gyration, asphericity, persistence length, and single chain form factor. In several cases, significant discrepancies were observed between the predictions of a particular force field and experiment.
Three force fields—AMBER ff99SB, AMBER ff99SB∗, and OPLS-AA/L—yield predicted conformational ensembles for polyQ in qualitative agreement with experimental findings regarding secondary structure and collapse in solution (35,41,42,46). All three predict predominantly disordered, collapsed conformations in water. Four others—AMBER ff03∗, AMBER ff03w, CHARMM22∗, and CHARMM36—exhibit no obvious biases in secondary structure but do exhibit larger persistence lengths, leading to more extended, aspherical, and diffuse conformations in water. AMBER ff99 appears to understabilize β-sheets but does not severely overstabilize helical structures, and predicts a distribution of collapsed and extended conformations that is intermediate between the two aforementioned classes. In analogy to AMBER ff99, GROMOS96 54a7 appears to understabilize α-helices and overstabilize β-sheets. Of the remaining three force fields, AMBER ff03 and CHARMM27 predict a large fraction of helical secondary structure in Q30 and GROMOS96 53a6 predicts a large fraction of β-strand content. It is especially difficult to reconcile the results produced by the latter three models with the available experimental data on simple polyQ peptides.
Our results confirm some of the biases reported in the literature, shed light on others that have not been discussed (to our knowledge), and put in perspective their importance with regard to the simulation of polyQ and IDPs in general. AMBER ff99, AMBER ff03, and CHARMM27 have been repeatedly observed to overstabilize α-helices and understabilize β-sheets (25–30,69,70,74,98–100). AMBER ff99 also performed poorly in simulations of the native state of ubiquitin in comparison with NMR data (28). In our simulations, the bias toward the α-helix is more pronounced in AMBER ff03 and CHARMM27. It has been suggested that AMBER ff99SB understabilizes β-sheets (74). Based on our data, AMBER ff99SB is appropriate for simulations of the natively disordered state of simple polyQ peptides, but if the reported bias is significant, this force field may perform suboptimally in calculations of the stability of candidate nuclei that are rich in β-sheet. GROMOS96 53a6 was reported to understabilize α-helices (69). In the case of polyQ, the apparent bias in favor of β-sheets is more damaging, because calculations of the stability of candidate nuclei are meaningless if the β-sheet is purported to be the dominant native conformation. OPLS-AA/L has been reported to understabilize both α-helices and β-sheets and overstabilize disordered conformations (30,69,100). A different study suggested that OPLS-AA/L overstabilizes the β-sheet conformation (70). In our simulations, however, OPLS-AA/L performs favorably—especially so in light of its age and relative simplicity.
AMBER ff03∗, AMBER ff03w, and CHARMM22∗ are more recent models and have not been evaluated as thoroughly in the literature, but some existing benchmarks do exist. AMBER ff03∗ and AMBER ff03w performed reasonably well in matching the NMR structures of ubiquitin and various oligopeptides (28). In another study that incorporated simulations of the native states of ubiquitin and GB3, temperature-dependent conformational properties of the (AAQAA)3 and CLN025 peptides, and folding simulations of villin and the WW domain, CHARMM22∗ exhibited good agreement with experiment and outperformed all other force fields tested except AMBER ff99SB∗-ILDN, according to a scoring system designed by the authors (29). All three appear to have repaired the biases that plagued their predecessors, AMBER ff03 and CHARMM27; these three also retain the stiff backbones that hinder polyQ collapse in dilute solution.
AMBER ff99SB, AMBER ff99SB∗, and OPLS-AA/L replicate the essential properties of polyQ observed in experiments, namely, a lack of regular secondary structure and highly collapsed structures in water. The former property is necessary for studying folding energetics, and the latter is necessary for studying collapse, extension, and aggregation. In the absence of additional experimental data, we conclude that any of these three models is appropriate for folding and aggregation studies of simple polyQ peptides.
The nature of polyQ’s conformational preferences (or lack thereof, depending on one’s perspective) dictates that the experimental data available for validating candidate force fields are coarse and generic. They simply lack the precision offered by RMSD structural variation or NMR chemical shifts, to name two metrics frequently employed in this type of study. This is not a failure of the experiments, but a consequence of polyQ’s enigmatic, heterogeneous structural ensemble. Yet, a majority of the force fields in this study fail even to qualitatively reproduce experimental findings. We hope that the results we present will serve as a guide—and a caution—to researchers interested in studying IDPs by way of MD simulations.
Author Contributions
A.M.F. and J.J.d.P. designed research. A.M.F. performed research and analyzed data. A.M.F. and J.J.d.P. wrote the article.
Acknowledgments
We thank Dr. Jian Qin and Dr. Kyle Hoffmann for helpful discussions.
This work was supported by NSF CBET-1264021. Some of the results presented in this work were obtained using the computational resources of the Research Computing Center at the University of Chicago. Simulations were also performed on the Beagle supercomputer, which is supported by NIH through resources provided by the Computation Institute and the Biological Sciences Division of the University of Chicago and Argonne National Laboratory under grant 1S10OD018495-01. We specifically acknowledge the assistance of Dr. Lorenzo Pesce and Ana Marija Sokovic. A.M.F. acknowledges the support of NSF DGE-0718123.
Editor: Amedeo Caflisch
Footnotes
Seven figures and five tables are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(15)00724-9.
Supporting Material
References
- 1.Berne B.J., Straub J.E. Novel methods of sampling phase space in the simulation of biological systems. Curr. Opin. Struct. Biol. 1997;7:181–189. doi: 10.1016/s0959-440x(97)80023-1. [DOI] [PubMed] [Google Scholar]
- 2.Sugita Y., Okamoto Y. Replica-exchange molecular dynamics method for protein folding. Chem. Phys. Lett. 1999;314:141–151. [Google Scholar]
- 3.Okamoto Y. Generalized-ensemble algorithms: enhanced sampling techniques for Monte Carlo and molecular dynamics simulations. J. Mol. Graph. Model. 2004;22:425–439. doi: 10.1016/j.jmgm.2003.12.009. [DOI] [PubMed] [Google Scholar]
- 4.Shea J.-E., Brooks C.L., 3rd From folding theories to folding proteins: a review and assessment of simulation studies of protein folding and unfolding. Annu. Rev. Phys. Chem. 2001;52:499–535. doi: 10.1146/annurev.physchem.52.1.499. [DOI] [PubMed] [Google Scholar]
- 5.Lei H., Duan Y. Improved sampling methods for molecular simulation. Curr. Opin. Struct. Biol. 2007;17:187–191. doi: 10.1016/j.sbi.2007.03.003. [DOI] [PubMed] [Google Scholar]
- 6.Singh S., Chopra M., de Pablo J.J. Density of states-based molecular simulations. Annu. Rev. Chem. Biomol. Eng. 2012;3:369–394. doi: 10.1146/annurev-chembioeng-062011-081032. [DOI] [PubMed] [Google Scholar]
- 7.Scheraga H.A., Khalili M., Liwo A. Protein-folding dynamics: overview of molecular simulation techniques. Annu. Rev. Phys. Chem. 2007;58:57–83. doi: 10.1146/annurev.physchem.58.032806.104614. [DOI] [PubMed] [Google Scholar]
- 8.Prinz J.-H., Wu H., Noé F. Markov models of molecular kinetics: generation and validation. J. Chem. Phys. 2011;134:174105. doi: 10.1063/1.3565032. [DOI] [PubMed] [Google Scholar]
- 9.Bowers K.J., Dror R.O., Shaw D.E. Zonal methods for the parallel execution of range-limited N-body simulations. J. Comput. Phys. 2007;221:303–329. [Google Scholar]
- 10.Hess B., Kutzner C., Lindahl E. GROMACS 4: algorithms for highly efficient, load-balanced, and scalable molecular simulation. J. Chem. Theory Comput. 2008;4:435–447. doi: 10.1021/ct700301q. [DOI] [PubMed] [Google Scholar]
- 11.Eastman P., Pande V.S. OpenMM: a hardware independent framework for molecular simulations. Comput. Sci. Eng. 2015;12:34–39. doi: 10.1109/MCSE.2010.27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Vendruscolo M., Dobson C.M. Protein dynamics: Moore’s law in molecular biology. Curr. Biol. 2011;21:R68–R70. doi: 10.1016/j.cub.2010.11.062. [DOI] [PubMed] [Google Scholar]
- 13.Shaw D.E., Deneroff M.M., Wang S.C. Anton, a special-purpose machine for molecular dynamics simulation. Commun. ACM. 2008;51:91–97. [Google Scholar]
- 14.Shirts M., Pande V.S. COMPUTING: screen savers of the world unite! Science. 2000;290:1903–1904. doi: 10.1126/science.290.5498.1903. [DOI] [PubMed] [Google Scholar]
- 15.Stone J.E., Hardy D.J., Schulten K. GPU-accelerated molecular modeling coming of age. J. Mol. Graph. Model. 2010;29:116–125. doi: 10.1016/j.jmgm.2010.06.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Laio A., Parrinello M. Escaping free-energy minima. Proc. Natl. Acad. Sci. USA. 2002;99:12562–12566. doi: 10.1073/pnas.202427399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Micheletti C., Laio A., Parrinello M. Reconstructing the density of states by history-dependent metadynamics. Phys. Rev. Lett. 2004;92:170601. doi: 10.1103/PhysRevLett.92.170601. [DOI] [PubMed] [Google Scholar]
- 18.Singh S., Chiu C.-c., de Pablo J.J. Efficient free energy calculation of biomolecules from diffusion-biased molecular dynamics. J. Chem. Theory Comput. 2012;8:4657–4662. doi: 10.1021/ct3003755. [DOI] [PubMed] [Google Scholar]
- 19.Sutto L., Marsili S., Gervasio F.L. New advances in metadynamics. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012;2:771–779. [Google Scholar]
- 20.MacKerell A.D., Jr. Empirical force fields for biological macromolecules: overview and issues. J. Comput. Chem. 2004;25:1584–1604. doi: 10.1002/jcc.20082. [DOI] [PubMed] [Google Scholar]
- 21.Maple J.R., Dinur U., Hagler A.T. Derivation of force fields for molecular mechanics and dynamics from ab initio energy surfaces. Proc. Natl. Acad. Sci. USA. 1988;85:5350–5354. doi: 10.1073/pnas.85.15.5350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Beachy M.D., Chasman D., Friesner R.A. Accurate ab initio quantum chemical determination of the relative energetics of peptide conformations and assessment of empirical force fields. J. Am. Chem. Soc. 1997;119:5908–5920. [Google Scholar]
- 23.Cieplak P., Dupradeau F.-Y., Wang J. Polarization effects in molecular mechanical force fields. J. Phys. Condens. Matter. 2009;21:333102. doi: 10.1088/0953-8984/21/33/333102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Antila H.S., Salonen E. Polarizable force fields. Methods Mol. Biol. 2013;924:215–241. doi: 10.1007/978-1-62703-017-5_9. [DOI] [PubMed] [Google Scholar]
- 25.Best R.B., Buchete N.-V., Hummer G. Are current molecular dynamics force fields too helical? Biophys. J. 2008;95:L07–L09. doi: 10.1529/biophysj.108.132696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Freddolino P.L., Park S., Schulten K. Force field bias in protein folding simulations. Biophys. J. 2009;96:3772–3780. doi: 10.1016/j.bpj.2009.02.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Piana S., Lindorff-Larsen K., Shaw D.E. How robust are protein folding simulations with respect to force field parameterization? Biophys. J. 2011;100:L47–L49. doi: 10.1016/j.bpj.2011.03.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Beauchamp K.A., Lin Y.-S., Pande V.S. Are protein force fields getting better? A systematic benchmark on 524 diverse NMR measurements. J. Chem. Theory Comput. 2012;8:1409–1414. doi: 10.1021/ct2007814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Lindorff-Larsen K., Maragakis P., Shaw D.E. Systematic validation of protein force fields against experimental data. PLoS One. 2012;7:e32131. doi: 10.1371/journal.pone.0032131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Cino E.A., Choy W.-Y., Karttunen M. Comparison of secondary structure formation using 10 different force fields in microsecond molecular dynamics simulations. J. Chem. Theory Comput. 2012;8:2725–2740. doi: 10.1021/ct300323g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Best R.B., Mittal J. Protein simulations with an optimized water model: cooperative helix formation and temperature-induced unfolded state collapse. J. Phys. Chem. B. 2010;114:14916–14923. doi: 10.1021/jp108618d. [DOI] [PubMed] [Google Scholar]
- 32.Perutz M.F., Johnson T., Finch J.T. Glutamine repeats as polar zippers: their possible role in inherited neurodegenerative diseases. Proc. Natl. Acad. Sci. USA. 1994;91:5355–5358. doi: 10.1073/pnas.91.12.5355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.MacDonald M.E., Gusella J.F. Huntington’s disease: translating a CAG repeat into a pathogenic mechanism. Curr. Opin. Neurobiol. 1996;6:638–643. doi: 10.1016/s0959-4388(96)80097-3. [DOI] [PubMed] [Google Scholar]
- 34.Mangiarini L., Sathasivam K., Bates G.P. Exon 1 of the HD gene with an expanded CAG repeat is sufficient to cause a progressive neurological phenotype in transgenic mice. Cell. 1996;87:493–506. doi: 10.1016/s0092-8674(00)81369-0. [DOI] [PubMed] [Google Scholar]
- 35.Chen S., Berthelier V., Wetzel R. Polyglutamine aggregation behavior in vitro supports a recruitment mechanism of cytotoxicity. J. Mol. Biol. 2001;311:173–182. doi: 10.1006/jmbi.2001.4850. [DOI] [PubMed] [Google Scholar]
- 36.Chen S., Berthelier V., Wetzel R. Amyloid-like features of polyglutamine aggregates and their assembly kinetics. Biochemistry. 2002;41:7391–7399. doi: 10.1021/bi011772q. [DOI] [PubMed] [Google Scholar]
- 37.Chen S., Ferrone F.A., Wetzel R. Huntington’s disease age-of-onset linked to polyglutamine aggregation nucleation. Proc. Natl. Acad. Sci. USA. 2002;99:11884–11889. doi: 10.1073/pnas.182276099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Bhattacharyya A.M., Thakur A.K., Wetzel R. Polyglutamine aggregation nucleation: thermodynamics of a highly unfavorable protein folding reaction. Proc. Natl. Acad. Sci. USA. 2005;102:15400–15405. doi: 10.1073/pnas.0501651102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Slepko N., Bhattacharyya A.M., Wetzel R. Normal-repeat-length polyglutamine peptides accelerate aggregation nucleation and cytotoxicity of expanded polyglutamine proteins. Proc. Natl. Acad. Sci. USA. 2006;103:14367–14372. doi: 10.1073/pnas.0602348103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Klein F.A., Pastore A., Trottier Y. Pathogenic and non-pathogenic polyglutamine tracts have similar structural properties: towards a length-dependent toxicity gradient. J. Mol. Biol. 2007;371:235–244. doi: 10.1016/j.jmb.2007.05.028. [DOI] [PubMed] [Google Scholar]
- 41.Lee C.C., Walters R.H., Murphy R.M. Reconsidering the mechanism of polyglutamine peptide aggregation. Biochemistry. 2007;46:12810–12820. doi: 10.1021/bi700806c. [DOI] [PubMed] [Google Scholar]
- 42.Walters R.H., Murphy R.M. Examining polyglutamine peptide length: a connection between collapsed conformations and increased aggregation. J. Mol. Biol. 2009;393:978–992. doi: 10.1016/j.jmb.2009.08.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Kar K., Jayaraman M., Wetzel R. Critical nucleus size for disease-related polyglutamine aggregation is repeat-length dependent. Nat. Struct. Mol. Biol. 2011;18:328–336. doi: 10.1038/nsmb.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Wetzel R. Physical chemistry of polyglutamine: intriguing tales of a monotonous sequence. J. Mol. Biol. 2012;421:466–490. doi: 10.1016/j.jmb.2012.01.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Kar K., Hoop C.L., Wetzel R. β-hairpin-mediated nucleation of polyglutamine amyloid formation. J. Mol. Biol. 2013;425:1183–1197. doi: 10.1016/j.jmb.2013.01.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Altschuler E.L., Hud N.V., Rupp B. Random coil conformation for extended polyglutamine stretches in aqueous soluble monomeric peptides. J. Pept. Res. 1997;50:73–75. doi: 10.1111/j.1399-3011.1997.tb00622.x. [DOI] [PubMed] [Google Scholar]
- 47.Scherzinger E., Sittler A., Wanker E.E. Self-assembly of polyglutamine-containing huntingtin fragments into amyloid-like fibrils: implications for Huntington’s disease pathology. Proc. Natl. Acad. Sci. USA. 1999;96:4604–4609. doi: 10.1073/pnas.96.8.4604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Masino L., Kelly G., Pastore A. Solution structure of polyglutamine tracts in GST-polyglutamine fusion proteins. FEBS Lett. 2002;513:267–272. doi: 10.1016/s0014-5793(02)02335-9. [DOI] [PubMed] [Google Scholar]
- 49.Crick S.L., Jayaraman M., Pappu R.V. Fluorescence correlation spectroscopy shows that monomeric polyglutamine molecules form collapsed structures in aqueous solutions. Proc. Natl. Acad. Sci. USA. 2006;103:16764–16769. doi: 10.1073/pnas.0608175103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Vitalis A., Wang X., Pappu R.V. Quantitative characterization of intrinsic disorder in polyglutamine: insights from analysis based on polymer theories. Biophys. J. 2007;93:1923–1937. doi: 10.1529/biophysj.107.110080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Armen R.S., Bernard B.M., Daggett V. Characterization of a possible amyloidogenic precursor in glutamine-repeat neurodegenerative diseases. Proc. Natl. Acad. Sci. USA. 2005;102:13433–13438. doi: 10.1073/pnas.0502068102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Wang X., Vitalis A., Pappu R.V. Characterizing the conformational ensemble of monomeric polyglutamine. Proteins. 2006;63:297–311. doi: 10.1002/prot.20761. [DOI] [PubMed] [Google Scholar]
- 53.Chopra M., Reddy A.S., de Pablo J.J. Folding of polyglutamine chains. J. Chem. Phys. 2008;129:135102. doi: 10.1063/1.2980043. [DOI] [PubMed] [Google Scholar]
- 54.Côté S., Wei G., Mousseau N. All-atom stability and oligomerization simulations of polyglutamine nanotubes with and without the 17-amino-acid N-terminal fragment of the Huntingtin protein. J. Phys. Chem. B. 2012;116:12168–12179. doi: 10.1021/jp306661c. [DOI] [PubMed] [Google Scholar]
- 55.Buchanan L.E., Carr J.K., Zanni M.T. Structural motif of polyglutamine amyloid fibrils discerned with mixed-isotope infrared spectroscopy. Proc. Natl. Acad. Sci. USA. 2014;111:5796–5801. doi: 10.1073/pnas.1401587111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Vitalis A., Wang X., Pappu R.V. Atomistic simulations of the effects of polyglutamine chain length and solvent quality on conformational equilibria and spontaneous homodimerization. J. Mol. Biol. 2008;384:279–297. doi: 10.1016/j.jmb.2008.09.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Vitalis A., Lyle N., Pappu R.V. Thermodynamics of beta-sheet formation in polyglutamine. Biophys. J. 2009;97:303–311. doi: 10.1016/j.bpj.2009.05.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Williamson T.E., Vitalis A., Pappu R.V. Modulation of polyglutamine conformations and dimer formation by the N-terminus of huntingtin. J. Mol. Biol. 2010;396:1295–1309. doi: 10.1016/j.jmb.2009.12.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Wang Y., Voth G.A. Molecular dynamics simulations of polyglutamine aggregation using solvent-free multiscale coarse-grained models. J. Phys. Chem. B. 2010;114:8735–8743. doi: 10.1021/jp1007768. [DOI] [PubMed] [Google Scholar]
- 60.Deng L., Wang Y., Ou-yang Z.-C. Concentration and temperature dependences of polyglutamine aggregation by multiscale coarse-graining molecular dynamics simulations. J. Phys. Chem. B. 2012;116:10135–10144. doi: 10.1021/jp210683n. [DOI] [PubMed] [Google Scholar]
- 61.Ruff K.M., Khan S.J., Pappu R.V. A coarse-grained model for polyglutamine aggregation modulated by amphipathic flanking sequences. Biophys. J. 2014;107:1226–1235. doi: 10.1016/j.bpj.2014.07.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Thirumalai D., Reddy G., Straub J.E. Role of water in protein aggregation and amyloid polymorphism. Acc. Chem. Res. 2012;45:83–92. doi: 10.1021/ar2000869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Walters R.H., Jacobson K.H., Murphy R.M. Elongation kinetics of polyglutamine peptide fibrils: a quartz crystal microbalance with dissipation study. J. Mol. Biol. 2012;421:329–347. doi: 10.1016/j.jmb.2012.03.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Ganim Z., Chung H.S., Tokmakoff A. Amide I two-dimensional infrared spectroscopy of proteins. Acc. Chem. Res. 2008;41:432–441. doi: 10.1021/ar700188n. [DOI] [PubMed] [Google Scholar]
- 65.Lin Y.-S., Shorb J.M., Skinner J.L. Empirical amide I vibrational frequency map: application to 2D-IR line shapes for isotope-edited membrane peptide bundles. J. Phys. Chem. B. 2009;113:592–602. doi: 10.1021/jp807528q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Wang L., Middleton C.T., Skinner J.L. Development and validation of transferable amide I vibrational frequency maps for peptides. J. Phys. Chem. B. 2011;115:3713–3724. doi: 10.1021/jp200745r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Kaminski G.A., Friesner R.A., Jorgensen W.L. Evaluation and reparametrization of the OPLS-AA force field for proteins via comparison with accurate quantum chemical calculations on peptides. J. Phys. Chem. B. 2001;105:6474–6487. [Google Scholar]
- 68.Jorgensen W.L., Chandrasekhar J., Klein M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983;79:926. [Google Scholar]
- 69.Todorova N., Marinelli F., Yarovsky I. Exploring the folding free energy landscape of insulin using bias exchange metadynamics. J. Phys. Chem. B. 2009;113:3556–3564. doi: 10.1021/jp809776v. [DOI] [PubMed] [Google Scholar]
- 70.Patapati K.K., Glykos N.M. Three force fields’ views of the 3(10) helix. Biophys. J. 2011;101:1766–1771. doi: 10.1016/j.bpj.2011.08.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Wang J., Cieplak P., Kollman P.A. How well does a restrained electrostatic potential (RESP) model perform in calculating conformational energies of organic and biological molecules? J. Comput. Chem. 2000;21:1049–1074. [Google Scholar]
- 72.Abascal J.L., Vega C. A general purpose model for the condensed phases of water: TIP4P/2005. J. Chem. Phys. 2005;123:234505. doi: 10.1063/1.2121687. [DOI] [PubMed] [Google Scholar]
- 73.Hornak V., Abel R., Simmerling C. Comparison of multiple Amber force fields and development of improved protein backbone parameters. Proteins. 2006;65:712–725. doi: 10.1002/prot.21123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Best R.B., Hummer G. Optimized molecular dynamics force fields applied to the helix-coil transition of polypeptides. J. Phys. Chem. B. 2009;113:9004–9015. doi: 10.1021/jp901540t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Duan Y., Wu C., Kollman P. A point-charge force field for molecular mechanics simulations of proteins based on condensed-phase quantum mechanical calculations. J. Comput. Chem. 2003;24:1999–2012. doi: 10.1002/jcc.10349. [DOI] [PubMed] [Google Scholar]
- 76.MacKerell A.D., Jr., Feig M., Brooks C.L., 3rd Extending the treatment of backbone energetics in protein force fields: limitations of gas-phase quantum mechanics in reproducing protein conformational distributions in molecular dynamics simulations. J. Comput. Chem. 2004;25:1400–1415. doi: 10.1002/jcc.20065. [DOI] [PubMed] [Google Scholar]
- 77.MacKerell A.D., Jr., Bashford D., Karplus M. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B. 1998;102:3586–3616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- 78.Best R.B., Zhu X., MacKerell A.D., Jr. Optimization of the additive CHARMM all-atom protein force field targeting improved sampling of the backbone φ, ψ and side-chain χ(1) and χ(2) dihedral angles. J. Chem. Theory Comput. 2012;8:3257–3273. doi: 10.1021/ct300400x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Oostenbrink C., Villa A., van Gunsteren W.F. A biomolecular force field based on the free enthalpy of hydration and solvation: the GROMOS force-field parameter sets 53A5 and 53A6. J. Comput. Chem. 2004;25:1656–1676. doi: 10.1002/jcc.20090. [DOI] [PubMed] [Google Scholar]
- 80.Berendsen H., Grigera J., Straatsma T.P. The missing term in effective pair potentials. J. Phys. Chem. 1987;91:6269–6271. [Google Scholar]
- 81.Schmid N., Eichenberger A.P., van Gunsteren W.F. Definition and testing of the GROMOS force-field versions 54A7 and 54B7. Eur. Biophys. J. 2011;40:843–856. doi: 10.1007/s00249-011-0700-9. [DOI] [PubMed] [Google Scholar]
- 82.Darden T., York D., Pedersen L. Particle mesh Ewald: an N log N method for Ewald sums in large systems. J. Chem. Phys. 1993;98:10089. [Google Scholar]
- 83.Essmann U., Perera L., Pedersen L.G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995;103:8577. [Google Scholar]
- 84.Nose S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984;81:511. [Google Scholar]
- 85.Parrinello M., Rahman A. Polymorphic transitions in single crystals: a new molecular dynamics method. J. Appl. Phys. 1981;52:7182. [Google Scholar]
- 86.Nose S., Klein M. Constant pressure molecular dynamics for molecular systems. Mol. Phys. 1983;50:1055–1076. [Google Scholar]
- 87.Hess B., Bekker H., Fraaije J.G. LINCS: a linear constraint solver for molecular simulations. J. Comput. Chem. 1997;18:1463–1472. doi: 10.1021/ct700200b. [DOI] [PubMed] [Google Scholar]
- 88.Earl D.J., Deem M.W. Parallel tempering: theory, applications, and new perspectives. Phys. Chem. Chem. Phys. 2005;7:3910–3916. doi: 10.1039/b509983h. [DOI] [PubMed] [Google Scholar]
- 89.Okabe T., Kawata M., Mikami M. Replica-exchange Monte Carlo method for the isobaric-isothermal ensemble. Chem. Phys. Lett. 2001;335:435–439. [Google Scholar]
- 90.Patriksson A., van der Spoel D. A temperature predictor for parallel tempering simulations. Phys. Chem. Chem. Phys. 2008;10:2073–2077. doi: 10.1039/b716554d. [DOI] [PubMed] [Google Scholar]
- 91.Rathore N., Chopra M., de Pablo J.J. Optimal allocation of replicas in parallel tempering simulations. J. Chem. Phys. 2005;122:024111. doi: 10.1063/1.1831273. [DOI] [PubMed] [Google Scholar]
- 92.Berendsen H.J., van der Spoel D., van Drunen R. GROMACS: a message-passing parallel molecular dynamics implementation. Comput. Phys. Commun. 1995;91:43–56. [Google Scholar]
- 93.Van Der Spoel D., Lindahl E., Berendsen H.J. GROMACS: fast, flexible, and free. J. Comput. Chem. 2005;26:1701–1718. doi: 10.1002/jcc.20291. [DOI] [PubMed] [Google Scholar]
- 94.Kabsch W., Sander C. Dictionary of protein secondary structure: pattern recognition of hydrogen-bonded and geometrical features. Biopolymers. 1983;22:2577–2637. doi: 10.1002/bip.360221211. [DOI] [PubMed] [Google Scholar]
- 95.Peterlin A. Excluded volume effect on light scattering of the coiled linear macromolecule. J. Chem. Phys. 1955;23:2464–2465. [Google Scholar]
- 96.Akcasu A.Z., Benmouna M. Concentration effects on the dynamic structure factor in polymer solutions. Macromolecules. 1978;11:1193–1198. [Google Scholar]
- 97.Hammouda B., Akcasu A., Benmouna M. Concentration dependence of the first cumulant for partially labeled chains in dilute solutions. J. Polym. Sci., Polym. Phys. Ed. 1984;22:853–862. [Google Scholar]
- 98.García A.E., Sanbonmatsu K.Y. Alpha-helical stabilization by side chain shielding of backbone hydrogen bonds. Proc. Natl. Acad. Sci. USA. 2002;99:2782–2787. doi: 10.1073/pnas.042496899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Okur A., Strockbine B., Simmerling C. Using PC clusters to evaluate the transferability of molecular mechanics force fields for proteins. J. Comput. Chem. 2003;24:21–31. doi: 10.1002/jcc.10184. [DOI] [PubMed] [Google Scholar]
- 100.Yoda T., Sugita Y., Okamoto Y. Comparisons of force fields for proteins by generalized-ensemble simulations. Chem. Phys. Lett. 2004;386:460–467. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.