Modeling the hypothalamus-pituitary-adrenal axis: A review and extension

Abstract

Multiple models of the hypothalamus-pituitary-adrenal (HPA) axis have been developed to characterize the oscillations seen in the hormone concentrations and to examine HPA axis dysfunction. We reviewed the existing models, then replicated and compared five of them by finding their correspondence to a dataset consisting of ACTH and cortisol concentrations of 17 healthy individuals. We found that existing models use different feedback mechanisms, vary in the level of details and complexities, and offer inconsistent conclusions. None of the models fit the validation dataset well. Therefore, we re-calibrated the best performing model using partial calibration and extended the model by adding individual fixed effects and an exogenous circadian function. Our estimated parameters reduced the mean absolute percent error significantly and offer a validated reference model that can be used in diverse applications. Our analysis suggests that the circadian and ultradian cycles are not created endogenously by the HPA axis feedbacks, which is consistent with the recent literature on the circadian clock and HPA axis.

1. Background

The hypothalamus-pituitary-adrenal (HPA) axis is a central neuroendocrine system, which involves the hypothalamus, pituitary, and adrenal glands. The paraventricular nucleus of the hypothalamus secrets corticotropin releasing hormone (CRH), which is transferred to the pituitary and stimulates the synthesis and release of adrenocorticotropic hormone (ACTH). ACTH moves through the bloodstream and reaches the adrenal gland in which it stimulates the secretion of glucocorticoids (i.e., cortisol in human and corticosterone in rodents). In response to stress, the concentrations of the HPA axis hormones are increased. Elevated cortisol levels direct the distribution of energy to different organs that underlie the stress response (1). Circulating cortisol levels also induce three feedback loops to inhibit the secretion of CRH in the hypothalamus and hippocampus and to restrain the release of ACTH in the pituitary in order to return the system to basal levels (2, 3).

The feedback mechanisms are mediated through the binding of cortisol to glucocorticoid receptors (GR) and mineralocorticoid receptors (MR). GRs regulate the secretion of CRH differently depending on their location in the brain (2). When cortisol binds to GRs in the hypothalamus, a negative feedback loop is induced and secretion of CRH is inhibited while a positive loop is activated and CRH is synthesized when cortisol binds to the GRs in the hippocampus (4–6). The positive feedback loop of cortisol on CRH is life-sustaining because it keeps the system responsive to acute stressors during a chronic stress (7). There are two other negative feedback loops that are mediated through the binding of cortisol to GRs in the pituitary, and to MRs in the hippocampus which inhibit the secretion of ACTH and CRH respectively (2, 6).

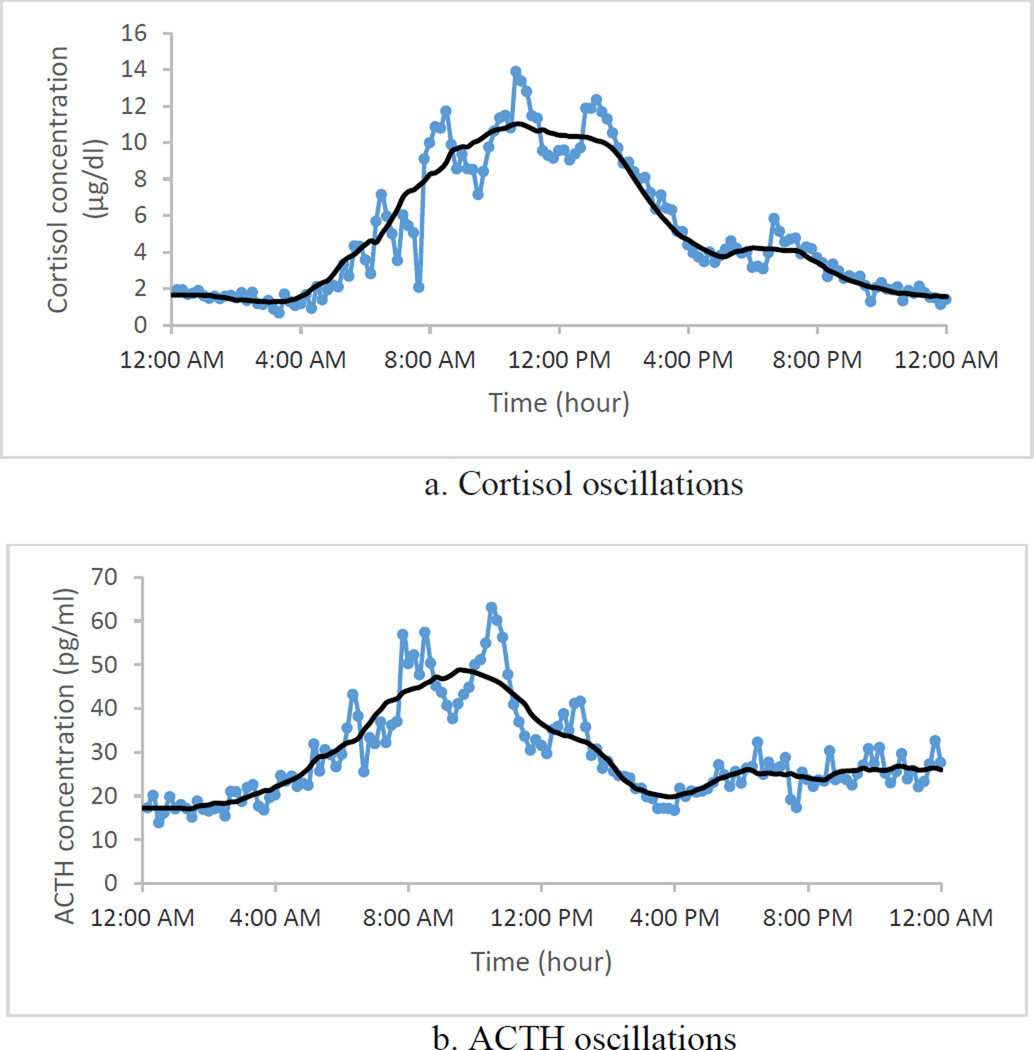
Besides the response to external stressors, ACTH and cortisol concentrations display two types of oscillations: ultradian and circadian. Ultradian rhythm refers to the one to three secretory episodes per hour shown in Figure 1-a. The circadian oscillation, captured in the solid line in Figure 1-a, has a 24-hour rhythm, with low concentrations of plasma cortisol between 8 p.m. and 4 a.m., which increases to a maximum level between 4 a.m. and 12 p.m., and eventually goes through a decline back to lower levels between 12 p.m. and 8 p.m. (8). Similar rhythms are seen in plasma ACTH concentrations (Figure 1-b).

Figure 1.

Ultradian and circadian oscillations in plasma cortisol and ACTH of one healthy subject. The dotted line is the raw data. To show the circadian behavior, we sketched the solid line, which is the smoothed version of the data. The smoothed line was found by calculating the average of 6 points before and 6 points after a particular point. Blood sampling started at midnight (00:00) with frequency of 10 minutes and continued for 24 hours. Data provided by Carroll and colleagues (8).

It is speculated that the circadian rhythm was developed in many species to equip them for times when encountering a stressor was more likely and for times when the body needed more energy to search for food. Elevated cortisol levels prepare organisms for such challenges (9). The ultradian oscillation and its frequency appear to be important for proper response to stress. In rats, the response to noise stress is limited during the non-secretory phase of the ultradian cycle while the response to stress increases when it coincides with the secretory phase (10). In addition, the frequency of ultradian oscillation increases and the response to acute stress declines during chronic stress (11).

Maintaining cortisol levels within a given range is critical for health. Chronically elevated cortisol levels are associated with depression, cardiovascular disease, type 2 diabetes mellitus (12, 13), and hippocampal dysfunction (14) while low levels of cortisol may impair memory formation or lead to adrenal crises (15, 16). Elevated cortisol levels are potentially related to reduced feedback inhibition of the HPA axis while low levels of cortisol are associated with increased feedback inhibition of the HPA system (7, 17, 18). Besides the changes in the level of cortisol, alteration in the frequency of the ultradian oscillation have been reported in a subset of patients with depression, post-traumatic stress disorder (PTSD), post infection fatigue, and chronic fatigue syndrome (19–22). These alterations highlight the importance of quantifying and modeling HPA axis dynamics, which could provide a tool to understand how these malfunctions can occur. Experimental studies of the HPA axis are limited to the administration of hormones, which offer limited information about this system. Also, there are validity issues with generalizing animal studies to humans (23). As a result, multiple mathematical models of the HPA axis have been developed to study how dysfunction of the HPA axis occurs and to explain the consequences of such malfunction.

There is no commonly used model of the HPA axis in the field. Previous models have included different structures, rest on a variety of assumptions, and offer conflicting results on the possibility of getting ultradian and/or circadian oscillations from the structure of the HPA axis itself (24–27). In addition, none of the models provide statistical measures of validity to indicate the extent to which they can replicate actual data on which they were not calibrated. Also, there is limited understanding of their relative validity, making it difficult to select a model for a new application. As a result, there is a need for comparing and contrasting existing models with the goal of providing more reliable models to be used in diverse applications, as well as guidance for selecting a valid model.

To fill this need, we reviewed recent mathematical models of the HPA axis and replicated five of them. We then compared the replicable models by calculating different measures of fit to a dataset not used for model calibration. We used partial prediction method and observations over 24 hours from 17 healthy human subjects (8) to determine the average error between the model output and the actual data. We then selected the best performing model and calibrated it against the aforementioned dataset to provide better fitting model parameters. We extended the model by adding an exogenous circadian function which varies across individuals. A description of our review and analysis and a discussion of the implications of the best fitting model parameters in relation to the endogenous creation of natural oscillations in the HPA hormones follows.

2. Method

2.1. Literature Review and Model Selection Procedure

We searched PubMed for "HPA axis modeling" and, as a result, identified 56 articles. Given the fast evolution of the field, we selected those that were published after 2000. Then, we read the abstracts of the remaining papers and narrowed the articles to those that had a simulation model of the HPA axis. Finally, we tracked additional articles based on citations in the sample. Our final sample included 14 articles (24–37). These 14 reports developed mathematical models of the HPA axis to show how an HPA axis might become impaired (25, 31, 37), to offer treatment for normalizing HPA axis (29), to show the role of ultradian oscillation in response to stress and in homeostasis (34, 35), and to replicate the ultradian and/or circadian oscillations observed in the cortisol and ACTH concentrations (24–28, 30, 32, 33, 36).

A major distinction we found across these models is related to their treatment of the circadian and ultradian oscillations. Specifically, we categorized the studies based on their assumption of the origin of the oscillations (Table 1). This categorization led to the assignment of each study to one of four potential groups: 1) those that assumed that both oscillations can be generated inside the HPA axis system by interaction of its elements (i.e., endogenous circadian and endogenous ultradian) (25, 28, 33), 2) models that assumed both rhythms are external inputs (i.e., exogenous circadian and exogenous ultradian), 3) those that took circadian rhythm as endogenous while considering the ultradian as exogenous (i.e., endogenous circadian and exogenous ultradian), and 4) models with endogenous ultradian and exogenous circadian (24, 26, 27, 29, 31, 32, 34–37). Only one model made no explicit assumption about the origin of the oscillations and was developed to replicate the HPA axis response to CRH injection (30). Table 1 summarizes the existing models based on their assumptions of the endogeneity of circadian and ultradian cycles.

Table 1.

Categorization of HPA models based on their assumptions of the oscillations’ sources. Numbers in the parentheses are reference numbers.

	Endogenous Ultradian	Exogenous Ultradian
Endogenous Circadian	Sriram et al. 2012 (25) Lenbury and Pornsawad, 2005 (33) Bairagi et al. 2008 (28)	-
Exogenous Circadian	Zarzer et al. 2013 (37) Vinther et al. 2011 (24) Jelic et al. 2005 (26) Markovic et al. 2011 (34) Andersen et al. 2013 (27) Scheff et al. 2012 (35) Walker et al. 2010 (36) Gupta et al. 2007 (31) Kyrylov et al. 2005 (32) Ben-Zvi et al. 2009 (29)	-

The majority of the models reviewed assumed that at least one cycle was endogenously generated by the HPA axis. The model presented in (28) captured ultradian oscillation endogenously. In (25), it was claimed that the model can generate both types of oscillation depending on the values of parameters. Among models that were developed to create ultradian oscillation, two models demonstrated that the interaction of three hormones cannot generate ultradian oscillation unless unrealistic parameters are used (24, 27). To our knowledge, no study has treated the two types of oscillations as externally triggered. However, if these oscillations are indeed externally driven, trying to fit them to the HPA axis models will result in biased parameter estimates for these models which may reduce the usefulness of the models for other applications. In the next section, we explain why calibration of a feedback model with a potential exogenous process noise may lead to biased parameters.

2.2. Model Replication and Validation

Next, we replicated and compared the models to enhance our understanding of the relative precision of the existing models. We had two criteria for selecting models to replicate. First, the models needed to provide enough information to allow for replication. Second, they needed to model human as opposed to animal HPA axis given the validity concerns of animal models and so that they could be compared against each other. Five models from the literature fit these criteria (24–27, 30). They were all deterministic ordinary differential equation models that captured the interactions in the HPA axis and their evolution through time. These five models were replicated in Vensim™, a simulation software program used for developing and analyzing dynamic feedback models.¹ All replicated simulation models are available as part of the online appendix accompanying this paper.

To validate the models, we used a dataset by Carroll and colleagues which included plasma ACTH and cortisol concentrations of 17 healthy subjects (8). The datasets reported the concentrations every 10 minutes for a 24 hour period, thus offering 17 individual data series to validate the models against.

Comparing model predictions from fully endogenous models (i.e., standalone models not driven by time series data; the existing models all fall into this category) against individual time series data is not straightforward. The model produces a single trajectory for simulated hormone levels while environmental and individual variations have created multiple different time series data at the individual level. Direct comparison of these individual trajectories with the single simulation outcome ignores those individual and environmental variations, which may trigger various endogenous dynamics inside the model, and thus could be misleading. To address this challenge we investigated the extent to which each model replicated the data by using the partial prediction method (38). In this method, the behavior of different pieces of a model in response to input data is examined. The partial model testing is critical in this context, because much noise and internal oscillation may combine to show significant variations between data and deterministic simulations, regardless of the actual accuracy of the models’ core mechanisms. Specifically, we used data on two hormones, ACTH and cortisol. Therefore, for each model we fed ACTH data for each individual and computed the simulated cortisol levels for that individual, thus removing the need to endogenously track the feedback of cortisol on ACTH. The simulated cortisol outcomes could then be reliably compared against cortisol data and the fit provided a measure of the model quality for the mechanisms capturing the causal pathways from ACTH to cortisol. As measures of fit, we reported the root mean square error (RMSE), mean absolute percent error (MAPE), r-squared and Theil statistics which inform the type of errors. In the other partial test, we followed the same procedure for measuring the goodness of fit for ACTH predictions: we fed cortisol data to the model, found simulated CRH and ACTH, and used simulated ACTH and actual ACTH to determine the fit statistics.

MAPE is most useful when data and simulations vary in their range (e.g., oscillations) and in the absence of the formal likelihood function. In addition, the unit of hormone concentrations varies across the models that we have selected to validate and compare (i.e., mol/dm³ versus ng/ml). Therefore, MAPE is the most relevant fit measure for this analysis. Nevertheless, MAPE suffers from asymmetry in errors: if the simulation predictions are smaller than the data, MAPE is capped at 100%, whereas larger values for simulations can lead to very large MAPE outcomes. A direct comparison of MAPE numbers is in this asymmetry. Theil statistics help to reveal the source of errors by breaking the mean squared error into three components: bias (U_m), unequal variation (U_s), and unequal covariation (U_c). A large U_m indicates that the model output and data have different means. Finding a sizable U_s shows that two series have different variance and getting a large U_c indicates that the output of the model and actual data are imperfectly correlated (39).

2.3. Extending the Models by New Parameter Estimates

After validating and comparing the five models, we used partial prediction method to re-estimate the parameters of the best fitting model. Only one of the previous studies used multiple observations to calibrate the model. Thus, we assumed that feeding more observations may improve the existing model. In addition, estimating feedback systems that include process noise, random processes outside of model boundary that impact model behavior significantly, requires special care (38). Specifically, process noise could propagate through the system’s dynamics and lead to behavior patterns not due to the structure captured in the model. For example, we may observe oscillations in the HPA axis dynamics that are due to factors exogenous to the model boundary. If the full model is then estimated by matching the historical trajectories, the calibration processes varies the model parameters to match the observed patterns, even if those patterns have resulted from external noise that we cannot replicate within the model. As a result, the model parameters would be mis-specified even if the overall behavior appears to fit the empirical trends (40). Partial prediction method remedies this challenge by cutting the feedback loops in the model and estimating the model pieces separately. When feasible, this method stops the propagation of the process noise and thus provides more accurate parameter estimates. This method has been widely used for calibration of complex models in different applications, such as business, health, and medicine (41–44). Moreover, partial model calibration, as opposed to calibrating the whole model in one step, shows which part of the model works better and gives more reliable estimates (38). In section 3.3.1, we show how we use the partial prediction method to improve the structure of the model.

The resulting model can be compared with the existing models and provides a more reliable choice for future applications. In addition to MAPE and Theil statistics, we report approximate values for Akaike Information Criterion (AIC). AIC helps to select the best model by rewarding goodness of fit while penalizing extra parameters.

3. Results

In this section, we first discuss the characteristics and key findings of the five models that met our inclusion criteria. Then, we compare these models in terms of their goodness of fit to our validation dataset. Finally, we re-estimate one of these models using the partial model calibration protocol.

3.1. Review of Previous Models

Table 2 summarizes the previous models that were included in our analysis according to the inclusion criteria. In (24), three hormones (i.e., CRH, ACTH, and cortisol) and two negative feedback loops from cortisol on CRH and ACTH were included. The authors showed that with realistic parameter values a unique fixed point exists which is globally stable. Thus, the model is unable to generate ultradian oscillation. Then, a specific realization of the general model was developed by using the Hill function and receptor dynamics to determine the rates of change for CRH, ACTH, and cortisol. The model could generate the ultradian oscillation if physiologically unrealistic parameters (i.e., 19 minutes delay for cortisol to impact the release of hormones from hypothalamus and pituitary and the same delay for ACTH to stimulate adrenal release of cortisol) were used.

Table 2.

Summary of replicated models.

Author	Stocks	Behavior	Problems
Vinther et al. 2011 (24)	CRH, ACTH, and Cortisol	No oscillation (oscillation with 19 min delay)
Andersen et al. 2013 (27)	CRH, ACTH, and Cortisol	No oscillation
Sriram et al. 2012 (25)	CRH, ACTH, Cortisol, and GR	Circadian oscillation (model can generate both types of oscillations depending on the value of parameters)	ACTH is off by a factor of 10,000
Jelic et al. 2005 (26)	ACTH and cortisol	Ultradian oscillation	ACTH is off by a factor of 10,000
Conrad et al. 2009 (30)	ACTH and cortisol	No oscillation

Numbers in the parentheses are reference numbers.

(27) extended the model presented in (24) by adding the regulatory impact of the hippocampus on CRH. This effect was captured by including the negative feedback of cortisol on CRH through the hippocampal MR and the positive feedback of cortisol on CRH through the hippocampal GR (27). The model had a unique fixed point and it could not generate any oscillation if physiologically reasonable parameters are used. It can achieve two stable fixed points by perturbing the parameters. Solutions converged to one of the two fixed points depending on the initial values. The authors concluded that having two fixed points was consistent with the fact that the HPA axis of people with mental health problems are usually hyperactive or hypoactive, however it is not clear if the parameter settings required for observing two stable equilibria are biologically realistic. Circadian oscillations were treated as external input in both (27) and (24).

In (26), it was assumed that changes in CRH are negligible and only two variables (i.e., ACTH and cortisol) were included. The model included the positive feedback of cortisol through the hippocampal GR and the negative feedback of cortisol through the hippocampal MR, and hypothalamic and pituitary GR. The major difference between this model and others is that the differential equations are based on “approximated stoichiometric relations between species” (24). The model generates the ultradian oscillation. The circadian oscillation was treated as an external input.

Four stock variables², CRH, ACTH, cortisol, and GR were included in (25). Besides two negative feedbacks from GR to CRH and ACTH, a positive feedback that captured the GR homodimerzation was incorporated. In the pituitary, cortisol binds to GR and the cortisol-GR complex translocates to the nucleus in which the GR synthesis is increased and the ACTH production declines (31). In contrast to the other models, the authors included two terms for the hormone eliminations; a linear term and a nonlinear one. The authors claimed that including the elimination of the hormones in their respective region of the brain as a nonlinear term would introduce delays in the system and produce the circadian oscillation. However, dropping those terms in the model did not eliminate the oscillation. The data of (45) was used to estimate the parameters of the model and generate the circadian oscillation. The authors also argued that the model was capable of producing ultradian oscillation, depending on the choice of parameters.

(30) proposed a differential equation model with two stock variables, one that represented CRH and ACTH and one for Cortisol. Unlike other models, it assumed that cortisol exerts its positive feedback on ACTH through MR and its negative feedback through GR. The mathematical part of the study showed that the model had a stable equilibrium. The parameters of the model were estimated by using clinical data from an experiment in which 1 µg CRH per kilogram body weight was administered to 20 healthy subjects and ACTH and cortisol were measured.

3.2. Validation Results

First, we fed the cortisol data to each model for each individual and found the simulated level of ACTH. Then, we compared ACTH data and simulated ACTH concentrations to determine MAPE, R-Squared, RMSE, and Theil statistics. These measures were then averaged over the 17 individuals in the validation dataset. MAPE is often a more reliable metric for comparison in this setting because it accounts for differences in the scale of different variables. Nevertheless, by also reporting R-Squared we provide a more nuanced picture of the variations across models. Table 3 shows the results.

Table 3.

Validation Results for ACTH.

Studies	MAPE	R-Squared	RMSE (pg/ml)	Theil_Um	Theil_Us	Theil_Uc
Vinther et al. 2011 (24)	92.8%	0.35	16.24	15.9%	3.1%	81.0%
Andersen et al. 2013 (27)	44.5%	0.25	9.0	35.7%	35.4%	29.0%
Sriram et al. 2012 (25)	1,338,600 %3	0.15	334,100	77.4%	22.6%	0.0%
Jelic et al. 2005 (26)	26,534%	0.05	4,920	68.5%	31.4%	0.3%
Conrad et al. 2009 (30)	58.0%	0.30	16.65	45.6%	4.5%	49.9%

Numbers in the parentheses are reference numbers.

The model presented in (24) was extended in (27) by including the effect of the hippocampus on the HPA axis. (27) did not examine how much this addition improved the model. Based on our calculations, adding the effect of the hippocampus on the HPA axis improved the MAPE of ACTH by 48.3 percentage points (from 92.8% to 44.5%). Other models have large MAPE. The high U_m values in the models of (25) and (26) indicate that the error is mostly due to bias. The ACTH level is off by a factor of 10,000 and the ACTH and cortisol are in antiphase in (26) which is unrealistic.

A similar procedure was repeated next, this time by inputting ACTH and comparing the simulated cortisol against empirical patterns. These results are reported in Table 4. Again, all models showed significant deviation from empirical results. In this case, the models by (24), (27), and (25) underestimated cortisol significantly, thus leading to MAPE results close to 90% which represent an order of magnitude difference between simulations and data.

Table 4.

Validation Results for Cortisol

Studies	MAPE	R-Squared	RMSE (ng/ml)4	Theil_Um	Theil_Us	Theil_Uc
Vinther et al. 2011 (24)	94.5%	0.64	1.90	33.1%	43.0%	23.9%
Andersen et al. 2013 (27)	94.6%	0.64	1.90	33.1%	43.0%	23.9%
Sriram et al. 2012 (25)	91.0%	0.08	3.68	65.8%	24.4%	9.8%
Jelic et al. 2005 (26)	72.8%	0.03	3.18	57.1%	34.4%	8.8%
Conrad et al. 2009 (30)	206.0%	0.76	3.26	75.2%	9.5%	15.3%

Numbers in the parentheses are reference numbers.

3.3. New Calibration of an Existing Model

Previous models do not replicate the actual data well. The model presented in (27) by Andersen and colleagues provides the best overall fit (i.e., lowest MAPE) among the reviewed models. Still, the MAPE value for cortisol is above 90% in their model. Their model was developed to investigate the existence of oscillations and they did not resolve the inverse problem to estimate the parameters. Some of the parameters come from the literature and others are chosen to be mathematically and physiologically relevant. Thus, estimating the parameters by 17 observations may improve their model and its fit to empirical outcomes.

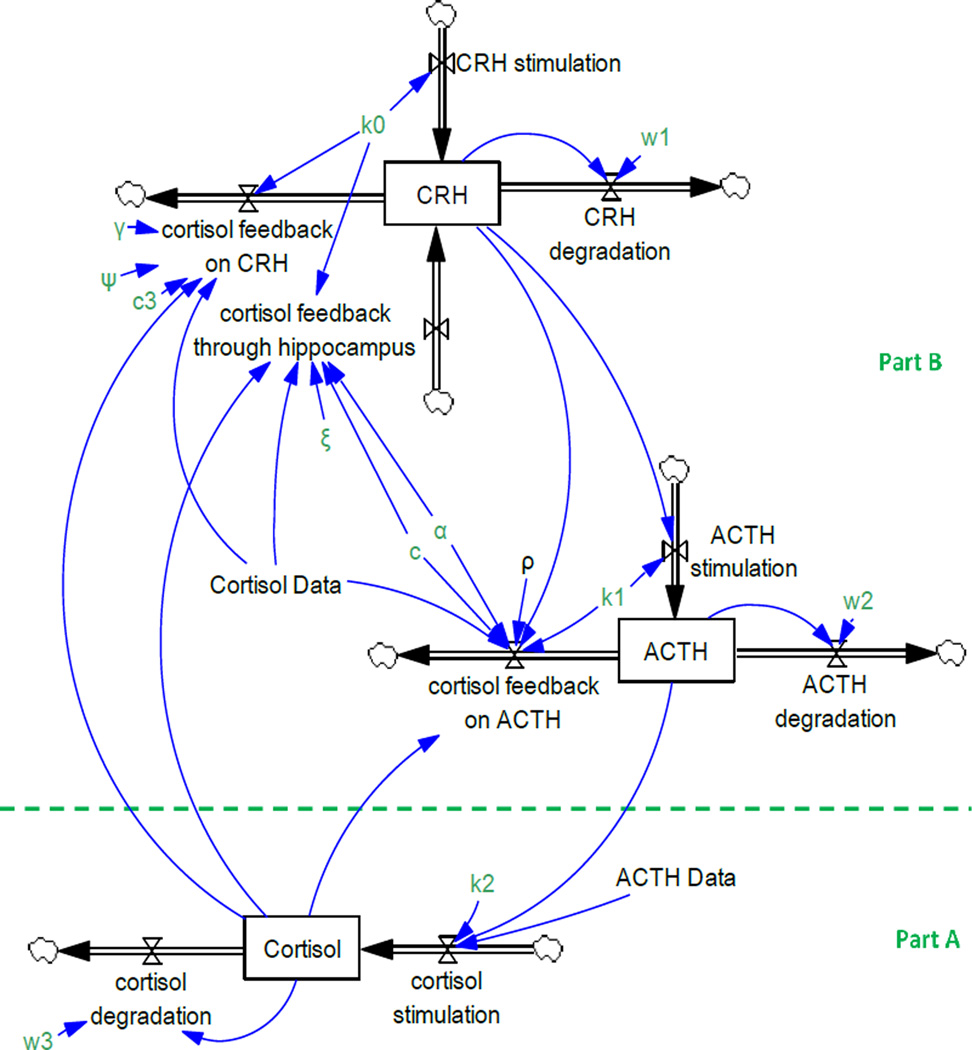
There are three stocks (i.e., CRH, ACTH, and Cortisol hormones) and three feedbacks from cortisol on CRH and ACTH in (27) (Figure 2). CRH stimulates ACTH secretion in the pituitary and ACTH causes the adrenal glands to release cortisol. The differential equations of their model are reported in appendix 1 according to Rahmandad and Sterman (46)’s guidelines.

Figure 2.

Andersen and colleagues’ model of the HPA axis. Arrows with valves represent flows, single-line arrows indicate causal relationships among variables, and boxes depicts stock variables. A stock variable is the accumulation of the difference between its inflows and outflows. Formally, Cortisol(t) = ∫_t [Cortisol Stimulation(s) − Cortisol degradation(s)]ds + Cortisol(t₀)

Since we have data on ACTH and cortisol, the model can be divided into two parts, below the dashed line (part A) and above the dashed line (part B), and each one can be calibrated separately using partial model calibration (Figure 2).

3.3.1. Calibrating Cortisol Parameters (part A)

If we assume that the degradation rate of cortisol reported in the literature is correct, only one parameter, k₂, is needed to be estimated in part A. The differential equation of the cortisol stock is as follows,

$$\frac{\mathit{\text{dCortisol}}}{\mathit{\text{dt}}}=k_2*\mathit{\text{ACTH}}-w_3*\mathit{\text{Cortisol}}$$ (1)

Assuming that the measurements are frequent in comparison with the delays involved in the balancing feedback loops, the equation can be converted to a difference equation:

$$\frac{\Delta \mathit{\text{Cortisol}}}{\Delta t}+w_3*{\mathit{\text{Cortisol}}}_{t-1}=k_2*{\mathit{\text{ACTH}}}_{t-1}$$ (2)

The cortisol concentration was measured every ten minutes. As a result, Δt is equal to ten minutes. The degradation rate, w₃, is 0.009 [1/min] and it is found by using the half-life of the cortisol concentration reported in the literature (8). The left side of equation (2) was regressed against the right side and k₂ was found to be 0.00166 [ng/pg.min] (The Confidence Interval is reported in table 6). The second row in Table 5 shows the validation results (specification 1).

Table 6.

Estimated parameters by partial calibration

Specification	Models	k2	w3
-	Original Model (27)	0.00132 ng/pg.min	0.00907 1/min
1	Population-fit* k2	0.00166 ng/pg.min [0.0014, 0.0019] **	0.009 1/min
2	Population-fit k2 and w3	0.00158 ng/pg.min [0.0013, 0.0019] **	0.0083 1/min [0.0069, 0.0096] **
3	Individual-fit** k2 and w3	0.00521 ng/pg.min [0.0041, 0.0063] **	0.0221 1/min [0.0173, 0.0270] **
4	Population-fit k2 and w3 with individualized circadian function	0.00564 ng/pg.min [0.00516, 0.00612] **	0.0352 1/min [0.0326, 0.0377] **
5	Population-fit k2, w3 and circadian function	0.00136 ng/pg.min [0.00107, 0.00166] **	0.0109 1/min [0.0093, 0.0125] **

^**Significantly different from zero at 0.05 confidence level.

95% confidence interval are presented in brackets.

K2 and w3, reported in the 3rd specification, are the averages of individualized K2 and w3. For estimating k2 and w3 for each individual, we regressed ($\frac{\Delta \mathit{\text{Cortisol}}}{\Delta t}$) against 17 variables for ACTH and 17 variables for cortisol. The estimated k2s and w3s are listed in Table 3 of the online appendix. The program that we wrote to estimate these parameters are included in the online appendix.

Table 5.

Validation results for cortisol in the original and revised models of Andersen et al. (21)

Specification	Models	MAPE	Theil_Um	Theil_Us	Theil_Uc	AIC
-	Original Model (27)	94.6%	33.1%	43.0%	23.9%	-
1	Population-fit* k2	94.1%	38.5%	33.7%	27.8%	−6528.91
2	Population-fit k2 and w3	93.4%	38.6%	32.4%	29.0%	−6528.16
3	Individual-fit**k2 and w3	45.9%	3.7%	31.8%	64.4%	−6863.44
4	Population-fit k2 and w3 with individualized circadian function	27.0%	0.1%	10.3%	89.6%	−7027.83
5	Population-fit k2 w3, and circadian function	66.1%	38.8 %	10.6%	50.6%	−6572.94

^*A population-fit parameter is a parameter with the same value across all individuals.

^**An individual-fit parameter is a parameter that has different value for each individual.

Calibration with 17 observations did not improve the MAPE. All previous models have used a similar structure and similar degradation rates. Because this part of the model is small and it has only two parameters, we hypothesized that the degradation rate used in the previous models might not be precise. So, we estimated both k₂ and w₃ by running the regression captured in equation (2). However, new k₂ and w₃ (0.001578 [ng/pg.min] and 0.0083 [1/min]) did not improve MAPE (Table 5, specification 2). There could be two reasons for the poor fit of the model. First, there might be some individual differences that we have not considered. Second, some important structures could be absent in the current model of the cortisol secretion and degradation.

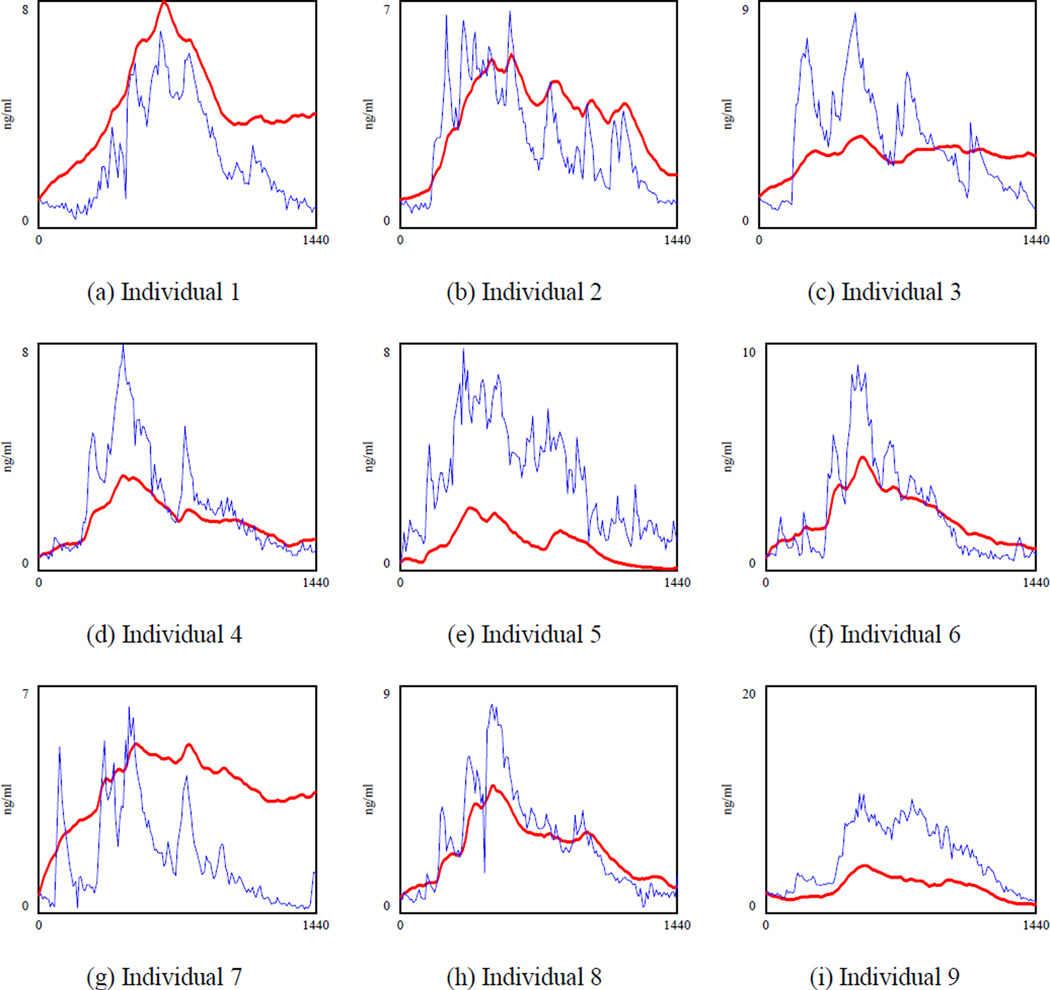
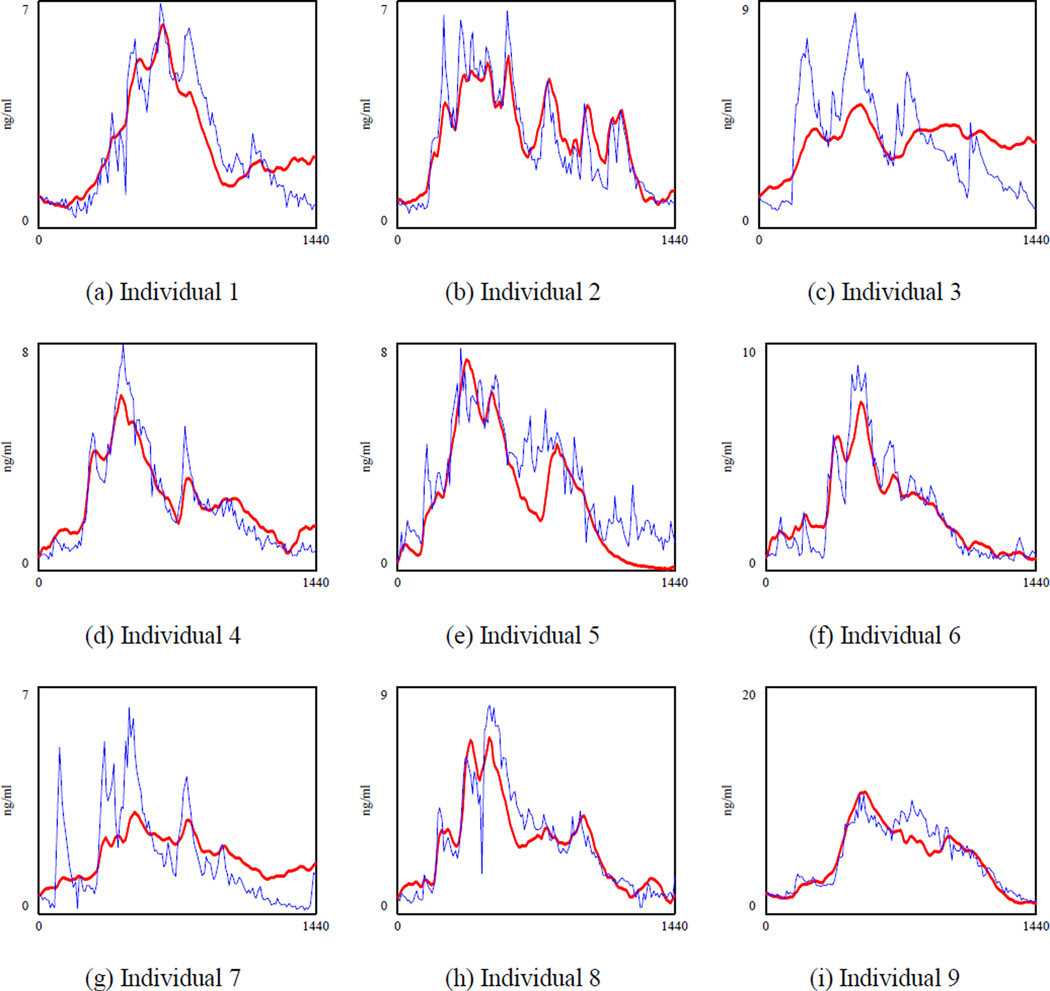
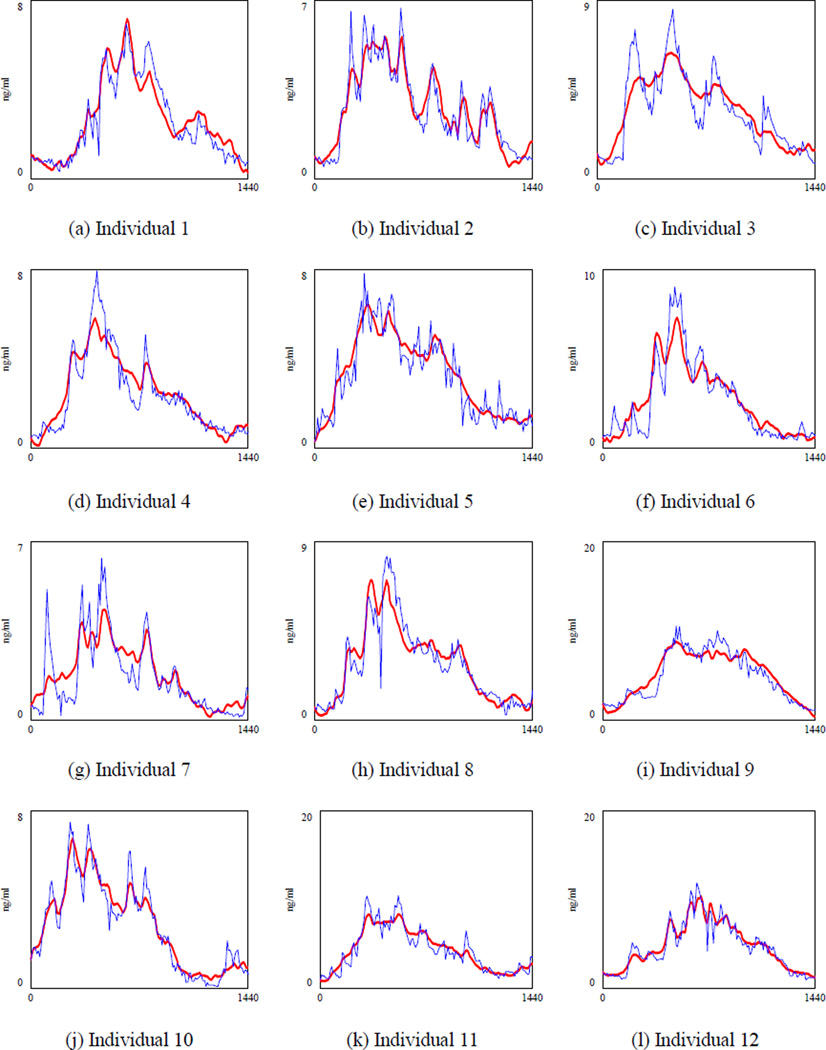
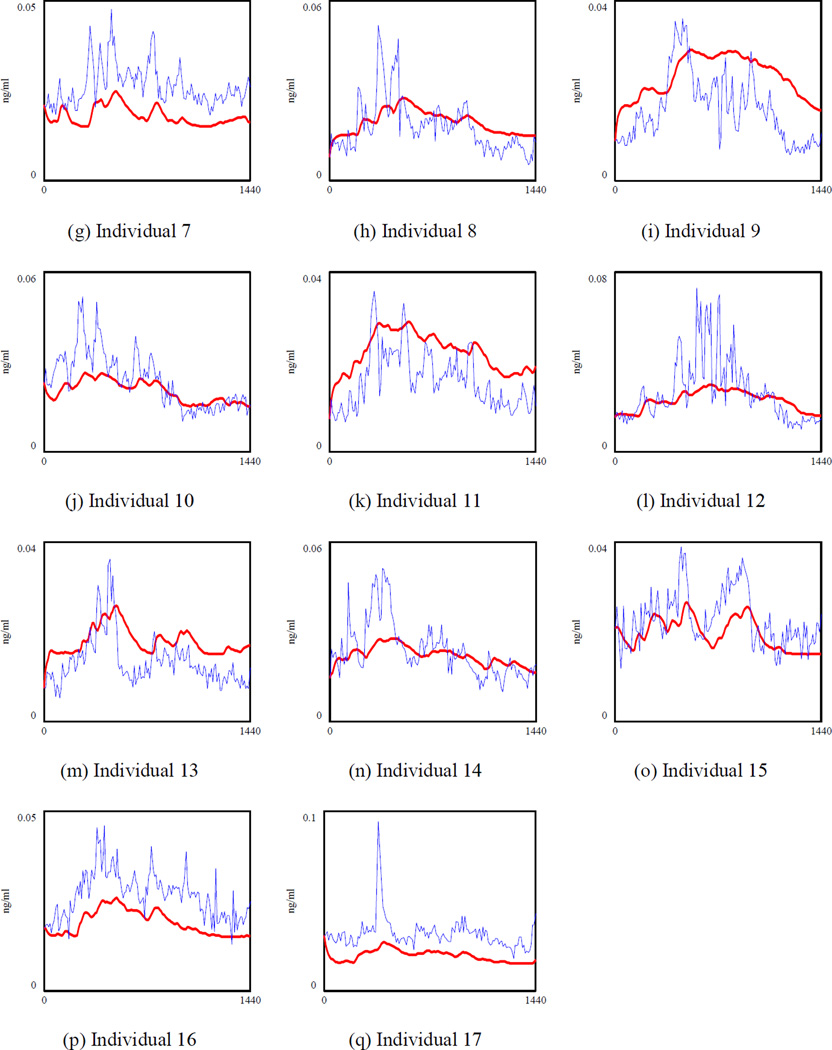
Figure 3 shows the cortisol concentration when both k₂ and w₃ are calibrated (specification 2 in which $\frac{\Delta \mathit{\text{Cortisol}}}{\Delta t}$ is regressed against ACTH_t−1 and Cortisol_t−1). To save space, we draw the graphs for the first nine individuals, but parameters were optimized using data of 17 subjects. We observed significant variations in the model fit across different individuals. For example, the model had larger errors in the cortisol level for person 1, 3, 7 and 9 depicted in Figure 3.a., 3.c., 3.g., and 3.i. respectively. Thus, there are some individual differences that can be taken into account by adding a fixed effect. To understand how important the individual differences are, we calibrated both k₂ and w₃ for each individual and MAPE was reduced to 45.9% (Table 5, specification 3), which showed that individual differences drove some of the errors of the previous models. However, the relatively large MAPE indicated that some important structures were still missing in the current model. Moreover, k₂ and w₃ values were averaged at 0.00521 (stdev 0.002) and 0.0221 (stdev 0.01) respectively across different subjects. Yet these two are biological parameters which should not be very different across individuals (For instance, the half-life of ACTH for healthy individuals reported in (8) is 19.9 minutes with a relatively tight standard deviation of 4 minutes). Fitted graphs of the first nine observations in Figure 4 showed that the model underestimated the cortisol level during the peak time and overestimated it in the afternoon when cortisol was reaching the minimum level (see Figure 4.c and 4.g). Although we were feeding the ACTH data, which had the circadian behavior, the model could not capture the circadian rhythm of the hormone completely. Based on the literature, the suprachiasmatic nucleus (SCN) projects the circadian rhythm through both the paraventricular nucleus (PVN) of the hypothalamus and adrenal gland (9). Thus, it is reasonable to expect that circadian rhythm is partly induced through the cortisol inflow. Therefore, in our fourth specification we changed the “cortisol stimulation” rate and included an individualized oscillatory input for circadian rhythm exogenously at this part of the model.

Figure 3.

Simulated cortisol (bold line) and actual cortisol for nine observations when k2 and w3 are calibrated (specification 2). The optimization was performed for all 17 individuals together. To save space, we showed the results for the first 9 healthy subjects. A single value for k2 and w3 are estimated and shared across the 17 subjects.

Figure 4.

The simulated cortisol (bold line) and the actual cortisol for nine individuals when k₂ and w₃ are calibrated for each individual (specification 3). The optimization was performed for 17 individuals. To save space we showed the results for the first 9 healthy subjects.

To determine a function for the circadian behavior of the hormone, we modified equation (2) by adding a 3^rd order function of time to it. The individual differences were taken into account by defining b1 through b4 for each individual while we switched back to using population-fit k₂ and w₃.

$$\frac{\Delta \mathit{\text{Cortisol}}}{\Delta t}=k_2*{\mathit{\text{ACTH}}}_{t-1}-w_3*{\mathit{\text{Cortisol}}}_{t-1}+b_{1i}+b_{2i}t+b_{3i}{t}^2+b_{4i}{t}^3$$ (3)

Adding the individual-level circadian rhythm (Figure 5) reduced the MAPE to 27.0% (Table 5, specification 4) and provided a better fit (Figure 6). In addition, this specification had the lowest AIC which meant that adding parameters for each individual was worth the additional costs. The parameters of the circadian function captures the individual differences that are not observable, such as daily routines, age, race, and sex. To show the relevance of adding a third degree polynomial, we have sketched the average of the individual-level circadian rhythm in Figure 5 (dashed line). In typical circadian oscillations, the hormone is at the minimum level between 8 p.m. and 4 a.m. It increases to a maximum level between 4 a.m. and 12 p.m. then it declines to a minimum level from 12 p.m. to 8 p.m. (8). The average of the included circadian rhythm also shows the same behavior. It adds negative values between 0 a.m. to 4 a.m. (reduces the cortisol concentration) while it adds to the hormone concentration between 4 a.m. and 2 p.m. Then it reduces the hormone after 2 p.m.

Figure 5.

The circadian function over 24 hours for 17 individuals. These graphs are sketched by using calibrated b1 to b4 and they only capture the circadian rhythm that SCN projects to the adrenal gland and they do not include the circadian rhythm projected through the PVN. The dashed line is the average of those 17 individualized circadian rhythms.

Figure 6.

The simulated cortisol (bold line) and the actual cortisol for 17 subjects when k₂ and w₃ are calibrated and the individualized circadian function is added (specification 4). A single k2 and one w3 are estimated for all 17 individuals.

Inspection of fit statistics in this specification suggests that the majority of the error is due to differences in variance and covariance between data and simulations. These could potentially be explained by additional drivers of cortisol not captured in our model, e.g., a cortisol specific stimulus within the ultradian cycle mechanisms. Given the quick and irregular nature of the ultradian cycle capturing such a term would not be possible within our current model. The estimated parameters are listed in Table 6 (parameters of the circadian function are in the appendix). The k₂ parameter from our estimation (0.00564 [ng/pg.min]) is significantly different from the estimated parameter in (27) (0.001321). The reason is that the formula of cortisol stimulation in our final specification (specification 4) includes the individualized circadian function and it is different from the formula in (27). Still their estimated k₂ falls in the confidence interval of our second specification which does not have the circadian function (Table 6, row 3).

Finally, to assess whether a general circadian function would have sufficed, we conducted a fifth estimation exercise in which population-fit k₂ and w₃ are combined with a single circadian function for every individual removing index i from equation (3). The results (Table 5, specification 5) show significant deterioration suggesting that individual variations in exogenous (to HPA) circadian stimulation of cortisol are a critical part of understanding cortisol variations across individuals.

3.3.2. Calibrating ACTH Parameters (Part B)

In the second partial calibration exercise we cut the link from cortisol to CRH and ACTH, fed cortisol data from each individual to each model, found the simulated ACTH, and minimized the difference between the simulated ACTH and actual ACTH to estimate the related parameters. The causal links from cortisol to CRH and ACTH are more complex and include multiple parallel mechanisms. These formulations are captured in equation (4) and equation (5). Ordinary regressions could not be specified to capture this relationship. We used Vensim’s internal optimization engine that utilizes a modified Powell gradient search method for finding the parameters that minimized mean squared error. In addition, parameter values that make CRH out of range are penalized in the objective function by adding a relatively large number (1000) when CRH is more than 2.5 times the average level (0.00766). Moreover, to ensure convergence to good solutions for this nonlinear optimization we conducted 601,326 independent searches from random points on the parameter space.

$$\frac{\mathit{\text{dCRH}}}{\mathit{\text{dt}}}=k_0(1+\xi \frac{{\mathit{\text{Cortisol}}}^{\alpha }}{{\mathit{\text{Cortisol}}}^{\alpha }+c^{\alpha }}-\psi \frac{{\mathit{\text{Cortisol}}}^{\gamma }}{{\mathit{\text{Cortisol}}}^{\gamma }+c{3}^{\gamma }})-w_1\mathit{\text{CRH}}$$ (4)

$$\frac{\mathit{\text{dACTH}}}{\mathit{\text{dt}}}=k_1(1-\mathrm{\rho }\frac{{\mathit{\text{Cortisol}}}^{\alpha }}{{\mathit{\text{Cortisol}}}^{\alpha }+c^{\alpha }})\mathit{\text{CRH}}-w_2\mathit{\text{ACTH}}$$ (5)

The calibrated parameters reduced the MAPE of ACTH by only 0.8 percentage points from 44.5% to 43.7% (Table 7). However, the R-square was improved by 52% from 0.25 to 0.38. Estimated parameters are listed in Table 8 and compared with the original parameters. ρ comes from the literature (27). Overall the original model by Anderson and colleagues provides a good match to the causal mechanisms from cortisol to CRH and ACTH and the new calibrations offer limited improvements. Inclusion of individual level circadian terms, as we did in the previous part, might improve the fit, but introduce many new free parameters which would risk significant overfit and failure of the optimization algorithm to find a reliable global fit for the more biologically relevant parameters.

Table 7.

Validation results for ACTH in the original and revised models of Andersen et al. (21)

Studies	MAPE	R-Squared	RMSE	Theil_Um	Theil_Us	Theil_Uc
Andersen et al. 2013	44.5%	0.25	9.0	35.7%	35.4%	29.0%
Population-fit parameters	43.7%	0.38	9.0	39.9%	25.8%	34.3%

Table 8.

Estimated parameters by partial calibration

Parameters	Estimated values	Andersen et al. (2013)’s estimate
k1	0.12 1/min	0.127 1/min
ρ	0.5	0.5
γ	2	3
α	1	3
k0	1.5 pg/ml.min	0.859 pg/ml.min
ξ	3.32	2
ψ	0.50	0.5
c	10 ng/ml	3.06 ng/ml
c3	0.42 ng/ml	1.42 ng/ml
w1	0.231 1/min	0.173/min
w2	0.043 1/min	0.0348 1/min

3.3.3. Fixed Point and Stability of Calibrated Reclosed Model

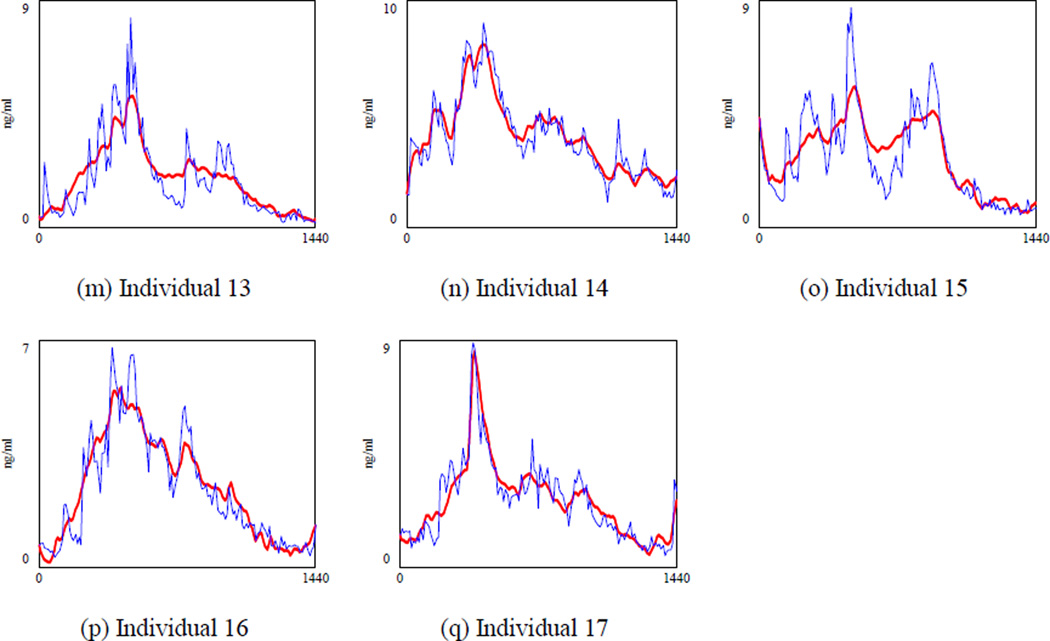
In this section, we show the behavior of the model when we reclose the model and use the calibrated parameters found in section 3.3.1. (sprecification 3) and 3.3.2 without any data input. For the cortisol part of the model, we used the individualized k₂ and w₃ reported in the online appendix and we did not include the exogenous circadian rhythm that was added to the cortisol stimulation. As it is depicted in Figure 8, the HPA axis cannot generate either of the oscillation cycles endoglogenously, rather they are largely the result of oscillatory inputs outside of HPA models’ boundaries. Thus, if we omit the data input and run the fully calibrated model (without the exogenous circadian rhythm), we would not get any oscillation as it is shown in the following figures.

Figure 8.

ACTH and Cortisol concentrations without circadian input exogenous to the HPA-axis for 17 healthy individuals when the model was run with individualized k₂ and w₃ for part A (specification 3 in Table 6) and calibrated parameters of part B reported in Table 8.

3.3.4. Fixed Point and Stability

Anderson and colleagues (27) provided an analytical and numerical investigation of the stability conditions and fixed points for their model. Using the new optimized parameters estimated above, we solved for the fixed points of the system. The system of equations that defined the fixed points included a single fixed point in the real domain at a cortisol concentration of 3.43 ng/ml, ACTH of 21.41 pg/ml, and CRH of 8.79 pg/ml. These values are in the correct range when compared to averages of healthy individual data from (8, 47) as reported in (27) which found 3.06 ng/ml for cortisol, 21 pg/ml for ACTH, and 7.66 pg/ml for CRH providing further confidence in the overall plausibility of the results. The single fixed point found through this analysis is stable. The system included no inherent oscillatory modes and these observations were confirmed in multiple simulation experiments.

4. Sources of Ultradian and Circadian Oscillations

In the absence of an inherent oscillatory mode, it is difficult to attribute a role to HPA axis endogenous dynamics in the creation or amplification of circadian or ultradian cycles. In fact, an exogenous circadian input is required for close replication of cortisol trends. Other models that hypothesize a central role for the HPA axis in the generation of either cycle fail to replicate those oscillations using biologically relevant parameter values. We therefore conclude that the sources of these cycles should be sought elsewhere. In fact, the current literature provides additional evidence about those alternative sources (9).

Although circadian rhythms of hormones are synchronized by environmental cues such as light, they are generated by an endogenous system called the circadian clock. Many species have evolved this system over ages to be prepared for the changes in the environment. The current understanding of the system is that the suprachiasmatic nucleus (SCN) of the hypothalamus controls the circadian system, but it is not limited to SCN (9). It has been shown that the circadian rhythm exists even at the organ level in the culture and the cellular level (48, 49). In sum, the circadian clock includes the SCN and cellular clocks in almost all tissues of the body which regulate the system in a hierarchical manner. SCN coordinates the regulation of cellular clocks by sending hormonal and electrical signals (50).

The sources of ultradian oscillation is less clear. It was initially believed that the pulsatile release of CRH from the hypothalamus creates ultradian oscillations. However, blocking the effect of CRH on the pituitary did not eliminate the pulsatile release of ACTH (51). Thus, it was speculated that the pituitary might be enough for generating the ultradian rhythm. However, in the experiment presented in (51), the pituitary was only isolated from the CRH impact and it could interact with the rest of the body. In addition, sometimes ACTH and glucocorticoids dissociate substantially from each other (9, 52). Thus, it has been speculated that multiple and redundant mechanisms regulate the ultradian oscillation (9, 53).

5. Modeling Implications

Our analysis showed that Andersen and colleagues’ model is the best available HPA axis model and our extension and procedure for calibration of their model improves the fit. In this section, we elaborate on how modelers can use Andersen and colleagues’ model for their own research. If one is mainly interested in replicating the circadian behavior of the hormones while having appropriate mean values for all three of them, the reclosed model can be adopted without adding any other components. The reported parameters in Table 8 can be used as good approximations because they are each fitted to a population of subjects. However, the parameters related to individualized trends in cortisol would need to be re-calibrated to each subject because the parameters of the circadian function are individual-level and they would need to be estimated for each particular patient. The procedure, mentioned in section 3.3.1, can be easily adapted to such applications and we provided the program for calibrating these parameters in the online appendix.

If one needs to replicate both ultradian and circadian oscillations, then it would be necessary to add other components including an auto-correlated random noise that captures the ultradian cycle (and other factors outside of model boundary) for the three rate functions (i.e., inflow of the three stocks). In such cases, new parameters should be introduced to capture those additional components and the model should be re-calibrated by breaking the model into two parts and following the procedures explained in section 3.3.1 and 3.3.2. Nevertheless we would expect the key parameters highlighted in table 8 will not change much in such extensions because the underlying mechanisms they represent are unchanged. A few modifications in the resources that we have provided in the online appendix would suffice for the re-calibration of the model. After estimating all parameters, the model could be reclosed and used for diverse application.

6. Discussion

This study reviewed the recent HPA axis models, replicated five of them, and compared them by using 24-hour observations of 17 healthy subjects and the partial predication method. Our study showed that the average errors between the models’ outputs and the actual data are large. We calibrated the best-performing model from the literature (27) and improved the MAPE of cortisol by more than 71% using parameter estimation and individual level circadian terms. In addition, we found that adding the feedback of cortisol on CRH through the hippocampal GR and MR reduced the MAPE of ACTH by 48.3 percentage points. The partial calibration of cortisol, despite the existence of a circadian rhythm in ACTH data, required further exogenous stimulation in cortisol production. Therefore, we conclude that the circadian cycle drives the HPA axis oscillations through changing the baseline cortisol production as well as changes to ACTH. This is consistent with the fact that SCN projects the circadian rhythm through both the PVN of the hypothalamus and adrenal gland (9).

Based on our analysis, the circadian and ultradian cycles of the hormones cannot be created endogenously by the HPA axis feedbacks, which is in agreement with (27) and (24). We reached this conclusion from two steps. First, we showed that much of the oscillations in cortisol could be best explained by an exogenous function (i.e., the individual level time-dependent terms), because an exogenous circadian rhythm added to the cortisol stimulation improves the fit. Second, we showed that with correctly estimated parameters, the HPA axis model will have no endogenous oscillations. It is also consistent with the literature of the circadian clock (9) which claims that the circadian cycles is regulated by neural signals from the SCN to the PVN of the hypothalamus and by SCN projection to the adrenal gland through the autonomic nervous system. Sources of ultradian oscillation remain elusive at present. Some of the models that create the ultradian oscillation use physiologically unrealistic parameters or their ACTH level deviates substantially from the data. Accurately estimated models offer no endogenous oscillation consistent with ultradian cycle. So, it is speculated that multiple mechanisms may create the rhythm, and the role of the HPA axis in creating the rhythm endogenously will at best be marginal.

The resulting calibrated model can be applied to diverse applications including studies on depression, PTSD, post infection fatigue, and chronic fatigue syndrome. Improving the quality of the fit between fully endogenous models and healthy human data may not be easy because much of the unexplained variation is due to individual level differences in environmental and genetic variables, which fall outside of the boundary of HPA axis models. Nevertheless, the model could be estimated to data from patients suffering from different conditions such as Cushing disease and depression in which changes in the HPA axis are a potential contributor. Such estimation can provide an indirect method to identify the specific causal mechanisms that have been altered in those patients and pinpoint the corresponding biological processes that can benefit from further empirical research. Individualized estimation of the model based on data collected from a patient can also inform the identification of key variations between an individual and those of the general population, offering a pathway to diagnose potential alterations in the HPA axis in an individual. In turn, implementing such changes when modeling the HPA axis may offer a new path forward for applications on a host of health concerns.

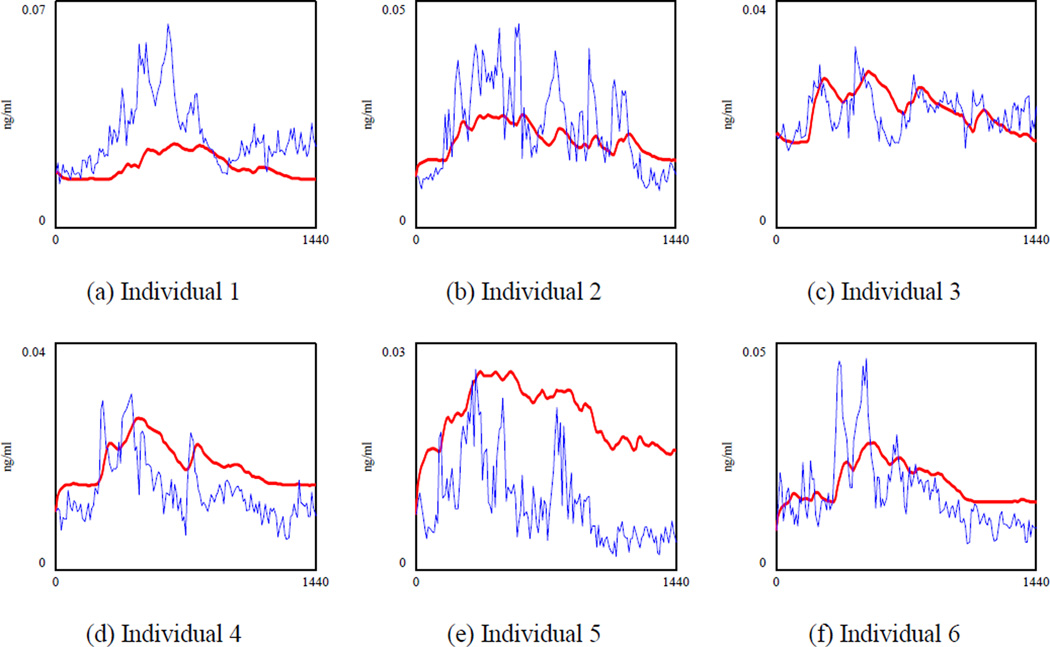
Figure 7.

The simulated ACTH (the bold line) and the actual ACTH for 17 healthy individuals.

Highlights.

• We review the recent models of the HPA axis and replicate five of them.

• We use a dataset of 17 healthy individuals to determine the best performing model.

• We calibrate and extend the best model by using the partial prediction method.

• We reduce the mean error between the cortisol data and model output by 71 %.

• The oscillations are not created by the endogenous dynamics of the HPA axis.