Sensitivity to imputation models and assumptions in receiver operating characteristic analysis with incomplete data

Abstract

Modern statistical methods using incomplete data have been increasingly applied in a wide variety of substantive problems. Similarly, receiver operating characteristic (ROC) analysis, a method used in evaluating diagnostic tests or biomarkers in medical research, has also been increasingly popular problem in both its development and application. While missing-data methods have been applied in ROC analysis, the impact of model mis-specification and/or assumptions (e.g. missing at random) underlying the missing data has not been thoroughly studied. In this work, we study the performance of multiple imputation (MI) inference in ROC analysis. Particularly, we investigate parametric and non-parametric techniques for MI inference under common missingness mechanisms. Depending on the coherency of the imputation model with the underlying data generation mechanism, our results show that MI generally leads to well-calibrated inferences under ignorable missingness mechanisms.

1. Introduction

Receiver operating characteristic (ROC) analysis is a quite efficient and popular method used in evaluating diagnostic tests or biomarkers in medical research. While a ROC curve provides visual evidence used to distinguish diseased subjects from healthy ones, ROC analysis can also be used to provide a summary measure by computing the area under the curve (AUC) for the assessment of performance of a given diagnostic test or biomarker. Using test results, the ROC curve plots sensitivity (probability of a test detecting disease when the subject has the disease) against 1-specificity (specificity is the probability of a negative test given the subject is healthy). Assuming that larger test results (or scores) indicate evidence in favour of disease, for a randomly chosen healthy and diseased subject and AUC essentially results in the estimate of P(Y > X) (where Y denotes the test result for a sick patient and X is the result of a healthy patient). The larger area indicates a better performance of a diagnostic test. For example, if the area is close to 1, then the underlying diagnostic test has a nearly perfect classification. On the other hand, if the AUC is around 0.5, then the diagnostic test is uninformative and has the same performance of a completely random decision as flipping a fair coin.

In medical studies on the performance of a diagnostic test, negative results from a test may not be investigated further for verification (gold standard test). There are several reasons for this. Obtaining a gold standard might be expensive or it might require a risky invasive operation on the patient. In a study of diagnostic test performance, if the targeted population is evaluated based on only those whose true status is known, then AUC of ROC is typically estimated with bias. This is known as verification bias. The problem of verification bias can actually be thought of as a missing-data problem as the gold standard measurement for a diagnostic test for some patient might be missing. Almost always, this added complexity is exacerbated by the arbitrary missingness in biomarkers. As documented by many researchers, analyses that fail to take sensible action on missing data have potentially undesirable inferential properties including bias and distorted estimates on the uncertainty measures.[1] An increasingly popular method to accomplish this is multiple imputation (MI).[2] Briefly, MI is a simulation-based inferential tool operating on M > 1 ‘completed’ data sets, where the missing values are replaced by random draws from their respective predictive distributions (e.g. posterior predictive distribution of missing data). These M versions of completed data are then analysed by standard complete-data methods and the results are combined into a single inferential statement using rules to yield estimates, standard errors and p-values that formally incorporate the missing-data uncertainty into the modelling process.[3] The key ideas and the advantages of MI are given by Rubin [3] and Schafer.[4]

Our work aims to assess the performance of commonly used parametric and non-parametric MI methods as well as their sensitivity to the key assumptions made on the mechanisms underlying the way in which missing values occur. The remainder of this paper is organized as follows. In the next section, we review previous work on missing data in ROC analysis. Section 3 introduces notation, assumptions and MI methodology to be evaluated in Section 4 via a simulation study, which mimics a typical scenario described earlier. Section 5 provides a discussion of the strengths and weaknesses of MI as well as our current and future work.

2. Missing data in ROC analysis

Similar to any study involving data, ROC studies are often subject to missing data. Any form of case deletion (list wise or record deletion) is arguably one of the most used methods to handle missing data. Unless the underlying mechanism of missingness is missing completely at random (MCAR), it almost invariably leads to bias in any respect of the statistical inference. Further, regardless of the missingness mechanism, it often deletes unacceptable rates of data records leading to inefficiency.[1] Alternatively, practice of imputation which is to fill missing data with plausible values is also used. There are several single imputation methods in practice including mean imputation, hot-deck, cold-deck or regression imputation. While these methods can be more efficient than case deletion, they often fail to incorporate missing-data uncertainty into the final inferences. This is a serious drawback as the inferences are artificially precise.

The more principled approach within the framework of ROC analysis in the presence of verification bias was developed by Gray et al.[5] This work pertains to the development of unbiased estimation of specificity and sensitivity in the presence of verification bias. However, important limitations in this work relate to distributional assumption of normality, potential selection bias occurring in the selection of patients for verification and disallowance of arbitrary missing data in covariates. Missing data were only allowed in the gold standard disease status (some of the patients with diagnostic test results may not have verified disease status).

Acknowledging these serious problems and limitations, the more recent literature on ROC analysis with missing data has focused on more principled methods designed to implicitly or explicitly incorporate the uncertainty due to arbitrary missing data. Overall, there are two general approaches. The first approach is based on the idea of maximizing observed-data likelihood, which essentially integrates out the missing data, and hence can be viewed as ‘averaging’ over all possible values of missing data.[1] This can be viewed as incorporating missingness uncertainty implicitly as the end results will not distinguish the sampling variability from missing-data uncertainty. Zhou [6] formulates the verification bias problem as a missing-data problem where the decision to verify a patient depends only on the test result. Zhou [6] then derives a maximum-likelihood (ML) estimation for the ROC curve area. More recently, Long et al. [7] proposed a robust estimation of AUC using MI paradigm.

The second approach uses a MI framework. While MI was originally developed to handle item nonresponse in surveys, it has been increasingly used in a wide variety of statistical problems, including ROC analysis verification bias. For example, Harel and Zhou [8] assess performance of imputation procedures for drawing inferences on sensitivity and specificity in the presence of missing data in the gold standard disease status. De groot et al. [9] also perform a similar assessment of MI performance under alternative imputation models variable-by-variable imputation and predictive mean matching. Long et al. [10] proposed a MI inference for ROC analysis for applications where a gold standard data might be missing under a mechanism called missing at random (MAR).[2]

As evidenced by these numerous applications of the popular MI inference, there does not exist any unified approach to creating MIs. Then, how should a practitioner proceed with the ROC analysis with missing values? What are the inferential consequences of choosing a particular analytic tool for sampling from the underlying posterior predictive distribution of missing data (i.e. forming of the imputations)? Finally, what are the inferential prices to be paid by the investigators when the models for missingness and/or data generation mechanisms are mis-specified? These are all standard questions casting doubt on the analysis with missing values regardless of the method of choice. Our work aims to unravel direct inferential consequences of the choices made on such questions.

3. Notation and assumptions

Below, we state notation commonly used in the missing-data literature as well as assumptions pertaining to both mechanisms creating the missing data and models used to impute them.

3.1. Common missing-data mechanisms

Statistical methods adopted to deal with missing values ranging from case-deletion to model-based MI assume a certain missingness mechanism. This is also the case in ROC analyses as the studies designed to investigate efficiency of a diagnostic test may contain incomplete data. Mechanism underlying these missing values may be determined completely partially at random. Partially random mechanisms are the mechanisms where missingness probabilities could depend on other diagnostics test results. For example, patients whose fasting plasma glucose levels are higher than certain values are further required to be measured their oral glucose tolerance level (OGTL). Therefore, the missingness mechanism for OGTL can be deemed to depend on the fasting plasma glucose level.

Some statistical techniques explicitly state these mechanisms while others state them implicitly. Most current methods such as those implemented in R package pan and MlWin mimacro [11–13]; or others for cross-sectional data such as [14,15] and PROC MI [16] assume that missing values are MAR.[2] Below, we generically describe missingness mechanisms (for more details see [2,4]) and provide discussion in their applications.

First, let R denote a matrix of indicator variables whose elements are 0 or 1; identifying whether elements of a data matrix Y are missing or observed. Note that R is always observed and its dimension is the same as Y. Furthermore, suppose that Y_obs and Y_mis denote the observed and missing partitions of Y, respectively. Finally, let X denote a matrix of covariates that are fully observed (e.g. auxiliary variables).

The missing values are said to be MAR if P(R|Y_obs, Y_mis, X, θ) = P(R = r|Y_obs = y_obs, X, θ) holds for all θ, where θ contains all unknowns of the assumed model. This assumption states that the probability distribution of the missingness indicators may depend on the observed data but not on the missing values. This mechanism is typically applicable when completely observing the gold standard variable is almost impossible due to factors such as cost, risky or require invasive operation.

A special case of MAR is MCAR in which P(R|Y_obs = y_obs, Y_mis, X, θ) = P(R|θ), for all θ. In MCAR, the probability distribution of missingness is independent of both the observed and missing data. This mechanism can be applied in ROC analyses in situations including lost patient records, exclusion from the study or drop-out, etc.

Finally, if MAR is violated, the probability distribution depends on the missing values and the missingness mechanism is said to be missing not at random (MNAR). In the case of MNAR, a joint probability model must be assumed for the complete data as well as the R, the missingness indicators. In ROC analyses, MNAR typically underlies the missingness mechanism for gold standard test results. Gold standard test is typically sought for those whose diagnostic test result is abnormal. If this result does not warrant further attempt to obtain the gold standard test result, then we can view the underlying missingness mechanism as MNAR.

Another important concept is ‘ignorability’ of the missingness mechanism and it is often seen an implied condition once MAR is assumed. Ignorability of missing-data mechanism occurs when the mechanism is MAR and the parameters γ and θ are distinct: f (Y_obs, R|θ, γ) = f (Y_obs|θ) f (R|γ). As named by Rubin [2] and discussed extensively by Little and Rubin,[1] the rough meaning of ignorability is that the missing-data mechanism can be ignored in the statistical analyses. More detailed explanation and conditions under which ignoring missing-data mechanism is valid for inferences about θ are given by Rubin,[2] and for more practical description see [17].

This paper is concerned with the performance of the current missing-data methods under a varying range of MAR, MCAR and MNAR assumptions as stated earlier. This performance is investigated under an ignorable missingness mechanism as defined by Rubin [2]; that is, the missing data are MAR and the parameters of missingness distribution and the complete-data distribution are distinct (see more detailed discussion in [2,4]). The ‘ignorability’ merely means that missingness mechanism can be ignored when performing statistical analyses, in other words, no harm is done working with the observed data. This should not be understood as to discard any missing datum: It should be understood that working with the observed likelihood L(θ|Y_obs, X)=∫ L(θ|Y_obs, Y_mis, X) dY_mis is the same as the full likelihood for θ.

3.2. Inference via MI

The key feature of MI over the other methods that are either parametric (e.g. likelihood-based) or non-parametric (e.g. weighting-based) is its versatility in the post-imputation phase as MI can serve multiple analytical goals using the same multiply-imputed data sets. Regardless of the nature of the post-imputation phase, MI inference treats missing data as an explicit source of random variability and the uncertainty induced by this is explicitly incorporated into the overall uncertainty measures of the underlying inferential process. This is accomplished by repeating the same complete-data analysis on the imputed data, and combining the estimates and standard errors under rules defined by Rubin,[3] including an explicit estimate of the degree of uncertainty due to the missing-data methodology.

To produce the imputations, some assumptions about the data (typically a parametric model) and the mechanism producing missing data need to be made. The assumed data model should be plausible and should be somewhat related to the analyst's investigation.[18] This model forms the basis to approximate the distribution in which the missing data conditional on observed data (i.e. predictive distribution of missing data). Our work focuses on limited but widely used imputation techniques and their performance in ROC analyses. These techniques are implementations of three distinct computational algorithms and imputation models that aim to simulate the predictive distribution of missing data.

The first approach jointly models variables subject to missingness, thus jointly samples from the underlying predictive distribution. Considering the nature of our data, which is a mixture of continuous and categorical data, we adopt a general location model as an imputation model.[4] The R [11] package called mix [19] has been used for drawing imputations. The second approach has been an alternative to this method. It approximates the joint modelling approach with a potentially incoherent variable-by-variable approach.[20] While ‘incoherence’ has been a subject of debate, this method has been quite successfully applied in many survey settings where the joint approach is essentially not applicable. The final approach pertains to a re-sampling-based algorithm using bootstrap for which we used R package called mi.[21]

4. Simulation study

The ultimate goal of our work was to assess the impact of the particular choice of imputation methodology and assumptions on the overall inference. To do this, we conducted a pseudo-random experiment where typical data from medical decision problems were simulated and assessed with respect to the frequentist benchmarks in a repetitive sampling environment (e.g. coverage rates, standardized biases, etc.) We investigated the performance of multiple imputation method using joint, variable-by-variable and non-parametric re-sampling (i.e. bootstrap) approaches under alternative missingness mechanisms (i.e. MCAR, MAR and MNAR).

Our simulation experiment consisted of the following steps: we first simulated gold standard test results $(Y_i^{\ast })$ from a binomial distribution with 0.5 success probability (e.g. prevalence of a disease in a population) for i = 1, 2, …, n. Sample size, n, was varied between 100, 300 and 500. Data on diagnostic test results were then simulated from a normal distribution conditional on $Y_i^{\ast }$ (i.e. disease versus non-disease):

$$\begin{array}{c}{Y}_i|Y_i^{\ast }=1~N(120,{\sigma }_Y^2),\\ Y_i|Y_i^{\ast }=0~N(110,{\sigma }_Y^2),\\ Y_i^{\ast }~\text{Bin}(n,0.5)\end{array}$$

Particular specification on the means for the distribution of Y and Y* was motivated by the diagnosis process of a condition known as diabetes mellitus. To make a gold standard (i.e. error-free) diagnosis on such a condition, oral glucose tolerance test is used, and for error-prone diagnosis, plasma glucose (FPG measured by mg/dl) is used. In the simulation experiment, for example, 120 and 110 can be thought as fasting plasma glucose level as commonly seen in diabetes studies (Standards of Medical Care in Diabates, 2012). Standard deviation (σ_Y) are chosen arbitrarily to be 10, 20, 30 and 40 to reflect possible variations in the underlying groups. Our simulation experiment also considers other glucose levels, specifically, 130 and 110 (underlying AUC is 0.75), 140 and 110 (underlying AUC is 0.85) to study performance under differing AUC values.

Missing values on the observed (or simulated) values on Y and Y* were imposed under three different missingness mechanisms. First, we imposed MCAR where the missingness indicator (r_Yi or $r_{Y_i^{\ast }}$) was drawn from a binomial distribution whose success probability was made independent from all the variables observed or missing:

$$\begin{array}{c}{r}_{Y_i}~\text{Bin}(n,p(r_{Y_i})=0.3),\\ r_{Y_i^{\ast }}~\text{Bin}(n,p(r_{Y_i^{\ast }})=0.3).\end{array}$$

The MAR mechanism on these variables was determined so that the missingness probabilities on Y depended on Y*:

$$r_{Y_i^{\ast }}|Y_i~\text{Bin}(n,p(r_{Y_i^{\ast }}=1|Y_i)=\frac{1}{1+e^{{\beta }_1+{\beta }_2{Y}_i}}),$$

where β₁ = −15.3, β₂ = 0.125 were set to obtain rates of missingness around 10%, 30% and 40% on either variables. Note that, in some scenarios, we set the missingness rate on diagnostic test result Y variable to 0% as it might be the case in clinical practice where an imperfect test result is observed for all units unlike the gold standard variable Y*. Finally, missing values on both Y and Y* were imposed under MNAR according to a cut point. Specifically, for the scenarios pertaining to AUC = 0.64, Y values were set to missing if they were higher than 125, and Y* values were set to missing with a probability of 0.3:

$$\begin{array}{c}P(r_{Y_i}=1|Y_i,Y_i^{\ast })=1\text{if}{Y}_i>125,\\ Pr(r_{Y_i^{\ast }}=1|Y_i,Y_i^{\ast })=0.3\forall i,\end{array}$$

and, for the AUC values 0.75 and 0.85, these cut-off values were set to 140 and 150, respectively.

Next, we created multiply imputed data sets on Y, Y * using joint, variable-by-variable and re-sampling (i.e. bootstrap) approaches as described in Section 3.2. We then employed inference by MI [3] to draw inferences on AUC using estimation routines developed by Hanley et al.,[22] particularly the method for computing standard error of AUC estimate. The number of imputations was set to 10. A higher number of imputations led to similar results. The steps of incomplete data generation under MCAR, MAR, MNAR, creating MI, estimation and combining the estimates and standard errors via MI were repeated 1000 times. This process allowed us to simulate the sampling distribution behaviour of MI inference for AUC estimation using the four distinct but widely used methods for missing data. The summary measures of this sampling distribution are then investigated to gauge the performance of each of the three methods of missing data. These measures are given below:

• Coverage rate (CR): The percentage of times that the true parameter value is covered in the 95% confidence interval. Here, the true parameter value is the average parameter estimate across the simulations before the missing values are imposed. If a procedure is working well, the actual coverage should be close to the nominal rate of 95% in our study. However, it is important to evaluate coverage with the other measures because high variances can lead to higher CRs. The performance of the procedure is regarded to be poor if its coverage drops below 90%.[23] If the procedure results in CRs that are close to 100% or below 85%, extra caution should be taken when using that procedure.

• Average width of confidence interval (AW): The distance between the average lower and upper confidence interval limits across 1000 confidence intervals. A high CR along with narrow, calibrated confidence intervals translates into greater accuracy and higher power.

• Root-mean-square error (RMSE): Because nonresponse or missing values have undesirable effect on the variances, it is important to evaluate this adverse effect. An integrated measure of bias and variance is used, evaluating θ̂ in terms of combined accuracy and precision. RMSE(θ̂) is defined as $\sqrt{E{(\widehat{\theta }-\theta )}^2}$

The simulation results focusing on the performance of the various methods of MI as well as case deletion are summarized in Tables 1–3. Table 1 provides summary of our simulation experiment under a sample size of 100 and Tables 2 and 3 are for sample sizes of 300 and 500. Each of these tables' simulation experiment assessed the performance and sensitivity to the imputation model and method in variations with respect to prevalence (π_Y* which is also varied between the values of 0.5, 0.35, 0.25), AUC value (approximately set to be 0.6, 0.75, 0.85), and standard deviation for Y, taking values of 10, 20, 30 and 40.

Table 1.

Performance of AUC estimation using MI methods as well as case deletion under MAR, MCAR and MNAR.

			% miss.		Case deletion			Joint imputation				Sequential imputation				Re-sampling (bootstrap)
MM	TV	CD(SE)	Y*	Y	CR	AW	RMSE	AUC (SE)	CR	AW	RMSE	AUC (SE)	CR	AW	RMSE	AUC (SE)	CR	AW	RMSE
Scenario 1: {n = 100 πY* = 0.5 σY = 10}
MCAR	0.64	0.64 (0.04)	0.30	0.30	0.84	0.10	0.03	0.64 (0.03)	0.91	0.13	0.03	0.64 (0.04)	0.93	0.15	0.03	0.64 (0.04)	0.95	0.15	0.03
MAR	0.64	0.61 (0.03)	0.27		0.90	0.10	0.03	0.64 (0.03)	0.90	0.12	0.02	0.63 (0.04)	0.88	0.16	0.04	0.63 (0.04)	0.95	0.14	0.02
MNAR	0.64	0.60 (0.04)	0.31	0.30	0.76	0.12	0.06	0.61 (0.03)	0.71	0.13	0.06	0.62 (0.08)	0.99	0.36	0.05	0.62 (0.05)	0.92	0.20	0.05
Scenario 2:{n = 100 πY* = 0.5 σY = 30}
MCAR	0.60	0.61 (0.08)	0.30	0.30	0.78	0.18	0.003	0.62 (0.07)	0.91	0.28	0.004	0.61 (0.08)	0.96	0.32	0.003	0.61 (0.08)	0.96	0.31	0.003
MAR	0.60	0.58 (0.07)	0.32		0.88	0.18	0.003	0.58 (0.07)	0.97	0.27	0.006	0.62 (0.08)	0.96	0.33	0.006	0.61 (0.08)	0.98	0.33	0.003
MNAR	0.64	0.62 (0.09)	0.36	0.30	0.83	0.18	0.007	0.63 (0.09)	0.94	0.34	0.008	0.68 (0.13)	0.97	0.43	0.008	0.64 (0.11)	0.99	0.43	0.006
Scenario 3:{n = 100 πY* = 0.5 σY = 40}
MCAR	0.58	0.59 (0.08)	0.30	0.30	0.80	0.19	0.003	0.61 (0.07)	0.91	0.28	0.004	0.59 (0.08)	0.97	0.32	0.003	0.60 (0.08)	0.97	0.31	0.003
MAR	0.58	0.57 (0.07)	0.31		0.91	0.19	0.002	0.57 (0.07)	0.98	0.27	0.004	0.61 (0.09)	0.97	0.33	0.005	0.60 (0.08)	0.98	0.32	0.003
MNAR	0.58	0.58 (0.08)	0.33	0.30	0.86	0.21	0.004	0.61 (0.07)	0.92	0.29	0.007	0.64 (0.11)	0.99	0.48	0.009	0.61 (0.09)	0.98	0.37	0.005
Scenario 4:{n = 100 πY* =0.5 σY = 20}
MCAR	0.64	0.64 (0.06)	0.10	0.10	0.74	0.13	0.001	0.64 (0.06)	0.95	0.239	0.001	0.64 (0.06)	0.96	0.25	0.001	0.64 (0.06)	0.96	0.25	0.001
MAR	0.64	0.63 (0.06)	0.09		0.75	0.13	0.001	0.63 (0.06)	0.94	0.237	0.001	0.64 (0.06)	0.95	0.25	0.001	0.64 (0.06)	0.96	0.24	0.001
MNAR	0.64	0.62 (0.06)	0.11	0.10	0.80	0.15	0.002	0.65 (0.06)	0.93	0.291	0.002	0.63 (0.07)	0.97	0.29	0.003	0.64 (0.07)	0.97	0.27	0.002
Scenario 5:{n = 100 πY* = 0.5 σY = 20}
MCAR	0.64	0.64 (0.09)	0.40	0.40	0.73	0.16	0.005	0.6 (0.07)	0.92	0.30	0.006	0.64 (0.09)	0.96	0.37	0.004	0.65 (0.09)	0.97	0.36	0.004
MAR	0.64	0.62 (0.08)	0.42		0.76	0.16	0.004	0.61 (0.07)	0.96	0.28	0.007	0.64 (0.09)	0.98	0.35	0.006	0.64 (0.09)	0.98	0.35	0.003
MNAR	0.64	0.61 (0.10)	0.39	0.40	0.85	0.19	0.006	0.64 (0.07)	0.91	0.29	0.008	0.66 (0.12)	1.00	0.52	0.007	0.64 (0.10)	0.99	0.41	0.006
Scenario 6:{n = 100 πY* = 0.25 σY = 20}
MCAR	0.64	0.65 (0.09)	0.30	0.30	0.72	0.15	0.004	0.64 (0.09)	0.96	0.35	0.004	0.64 (0.10)	0.96	0.385	0.004	0.65 (0.10)	0.98	0.38	0.003
MAR	0.64	0.62 (0.07)	0.30		0.81	0.16	0.003	0.63 (0.08)	0.94	0.32	0.006	0.65 (0.09)	0.95	0.373	0.005	0.63 (0.09)	0.98	0.36	0.003
MNAR	0.64	0.61 (0.09)	0.36	0.30	0.85	0.18	0.006	0.64 (0.09)	0.94	0.35	0.009	0.68 (0.13)	0.97	0.525	0.008	0.64 (0.11)	0.99	0.44	0.005
Scenario 7:{n = 100 πY* = 0.35 σY = 20}
MCAR	0.64	0.64 (0.08)	0.30	0.30	0.74	0.15	0.004	0.64 (0.08)	0.94	0.31	0.004	0.64 (0.09)	0.96	0.34	0.004	0.64 (0.09)	0.97	0.34	0.003
MAR	0.64	0.62 (0.07)	0.29	-	0.79	0.15	0.003	0.63 (0.07)	0.97	0.29	0.004	0.64 (0.08)	0.95	0.33	0.005	0.63 (0.08)	0.97	0.32	0.003
MNAR	0.64	0.61 (0.09)	0.36	0.30	0.85	0.18	0.007	0.63 (0.09)	0.94	0.34	0.009	0.68 (0.13)	0.97	0.53	0.008	0.64 (0.11)	0.98	0.43	0.006
Scenario 8:{n = 100 πY* = 0.50 σY = 20}
MAR	0.64	0.62 (0.06)	0.27		0.82	0.15	0.05	0.60 (0.06)	0.93	0.27	0.08	0.63 (0.07)	0.96	0.31	0.06	0.64 (0.08)	0.97	0.31	0.05
MCAR	0.64	0.64 (0.08)	0.30	0.30	0.72	0.15	0.06	0.65 (0.07)	0.92	0.29	0.06	0.63 (0.08)	0.96	0.34	0.06	0.64 (0.08)	0.97	0.33	0.06
MNAR	0.64	0.61 (0.08)	0.32	0.30	0.86	0.18	0.07	0.64 (0.07)	0.94	0.30	0.08	0.63 (0.10)	0.98	0.47	0.08	0.64 (0.09)	0.98	0.41	0.07
Scenario 9:{n = 100 πY* = 0.25 σY = 20}
MAR	0.75	0.71 (0.07)	0.42		0.34	0.09	0.07	0.73 (0.08)	0.86	0.32	0.09	0.73 (0.09)	0.84	0.36	0.09	0.73 (0.10)	0.96	0.40	0.07
MCAR	0.76	0.77 (0.07)	0.30	0.30	0.30	0.07	0.06	0.75 (0.08)	0.92	0.33	0.06	0.75 (0.09)	0.93	0.37	0.07	0.75 (0.09)	0.97	0.38	0.06
MNAR	0.76	0.72 (0.07)	0.22	0.30	0.28	0.09	0.07	0.72 (0.08)	0.85	0.31	0.09	0.73 (0.10)	0.92	0.46	0.08	0.74 (0.09)	0.94	0.39	0.07
Scenario 10:{n = 100 πY* = 0.50 σY = 20}
MAR	0.76	0.71 (0.07)	0.35		0.33	0.09	0.07	0.69 (0.07)	0.78	0.26	0.10	0.72 (0.07)	0.85	0.30	0.08	0.74 (0.08)	0.95	0.32	0.05
MCAR	0.76	0.76 (0.07)	0.30	0.30	0.36	0.07	0.05	0.76 (0.06)	0.89	0.26	0.06	0.75 (0.07)	0.92	0.30	0.06	0.75 (0.07)	0.94	0.31	0.05
MNAR	0.76	0.72 (0.07)	0.17	0.30	0.32	0.09	0.07	0.74 (0.06)	0.85	0.26	0.07	0.72 (0.09)	0.90	0.39	0.08	0.74 (0.07)	0.92	0.32	0.06
Scenario 11:{n = 100 πY* = 0.25 σY = 20}
MAR	0.85	0.80 (0.07)	0.54		0.08	0.05	0.08	0.81 (0.07)	0.85	0.28	0.10	0.82 (0.07)	0.74	0.31	0.11	0.81 (0.09)	0.10	0.40	0.08
MCAR	0.85	0.85 (0.06)	0.30	0.30	0.13	0.03	0.05	0.83 (0.07)	0.93	0.27	0.05	0.85 (0.07)	0.93	0.30	0.05	0.84 (0.08)	0.97	0.32	0.05
MNAR	0.85	0.81 (0.06)	0.24	0.30	0.09	0.04	0.06	0.83 (0.06)	0.88	0.26	0.08	0.81 (0.10)	0.95	0.44	0.09	0.83 (0.08)	0.96	0.32	0.06
Scenario 12:{n = 100 πY* = 0.50 σY = 20}
MAR	0.86	0.80 (0.07)	0.42		0.11	0.05	0.08	0.79 (0.06)	0.77	0.23	0.10	0.79 (0.06)	0.74	0.27	0.10	0.82 (0.07)	0.96	0.32	0.06
MCAR	0.86	0.86 (0.06)	0.30	0.30	0.13	0.02	0.04	0.85 (0.05)	0.88	0.21	0.04	0.85 (0.06)	0.91	0.23	0.04	0.85 (0.06)	0.94	0.25	0.04
MNAR	0.86	0.81 (0.06)	0.17	0.30	0.13	0.04	0.06	0.84 (0.05)	0.86	0.20	0.05	0.81 (0.07)	0.90	0.34	0.08	0.84 (0.06)	0.94	0.26	0.05

Notes: MM (missingness mechanism), TV (true value), CD (case deletion), SE (standard error), CR (coverage rate), AW (average width of confidence intervals), RMSE (root-mean-square error). CR and AW are based on 95% nominal confidence rate. CD(SE) column contains AUC estimate and estimate of its standard error under case deletion.

Table 3.

Performance of AUC estimation using MI methods as well as case deletion under MAR, MCAR and MNAR.

			% miss.		Case deletion			Joint imputation				Sequential imputation				Re-sampling (bootstrap)
MM	TV	CD(SE)	Y*	Y	CR	AW	RMSE	AUC (SE)	CR	AW	RMSE	AUC (SE)	CR	AW	RMSE	AUC (SE)	CR	AW	RMSE
Scenario 18:{n = 500 πY* = 0.25 σY = 20}
MAR	0.76	0.71 (0.03)	0.42		0.19	0.06	0.05	0.75 (0.04)	0.93	0.15	0.03	0.75 (0.04)	0.78	0.17	0.06	0.75 (0.04)	0.97	0.17	0.030
MCAR	0.76	0.76 (0.03)	0.30	0.30	0.43	0.04	0.03	0.76 (0.04)	0.94	0.15	0.03	0.76 (0.04)	0.95	0.16	0.03	0.76 (0.04)	0.97	0.17	0.028
MNAR	0.76	0.72 (0.03)	0.22	0.30	0.27	0.06	0.05	0.75 (0.03)	0.88	0.13	0.04	0.69 (0.08)	0.96	0.41	0.09	0.75 (0.04)	0.97	0.17	0.030
Scenario 19:{n = 500 πY* = 0.50 σY = 20}
MAR	0.76	0.71 (0.03)	0.35		0.20	0.06	0.05	0.77 (0.03)	0.87	0.11	0.03	0.75 (0.03)	0.75	0.14	0.05	0.76 (0.03)	0.95	0.14	0.03
MCAR	0.76	0.76 (0.03)	0.30	0.30	0.50	0.04	0.02	0.76 (0.03)	0.92	0.11	0.02	0.76 (0.03)	0.94	0.13	0.02	0.76 (0.03)	0.96	0.14	0.02
MNAR	0.76	0.72 (0.03)	0.16	0.30	0.21	0.06	0.05	0.75 (0.03)	0.87	0.11	0.03	0.69 (0.07)	0.91	0.34	0.09	0.75 (0.03)	0.94	0.14	0.03
Scenario 20:{n = 500 πY* = 0.5 σY = 20}
MCAR	0.64	0.64 (0.04)	0.3	0.30	0.84	0.10	0.03	0.64 (0.03)	0.91	0.13	0.03	0.64 (0.04)	0.94	0.15	0.03	0.64 (0.04)	0.95	0.147	0.03
MAR	0.64	0.61 (0.03)	0.27		0.90	0.10	0.03	0.64 (0.03)	0.89	0.12	0.02	0.63 (0.04)	0.88	0.16	0.04	0.63 (0.04)	0.95	0.141	0.02
MNAR	0.64	0.60 (0.04)	0.31	0.30	0.76	0.12	0.06	0.61 (0.03)	0.71	0.13	0.06	0.62 (0.08)	0.99	0.36	0.05	0.62 (0.04)	0.91	0.196	0.05
Scenario 21:{n = 500 πY* = 0.25 σY = 20}
MCAR	0.638	0.64 (0.04)	0.30	0.30	0.80	0.10	0.001	0.64 (0.04)	0.92	0.16	0.001	0.64 (0.05)	0.97	0.182	0.001	0.64 (0.05)	0.97	0.18	0.001
MAR	0.639	0.62 (0.03)	0.30	-	0.84	0.10	0.001	0.63 (0.04)	0.94	0.16	0.001	0.64 (0.05)	0.89	0.199	0.002	0.64 (0.04)	0.97	0.17	0.001
MNAR	0.637	0.59 (0.04)	0.36	0.30	0.76	0.13	0.003	0.59 (0.04)	0.64	0.16	0.005	0.64 (0.10)	0.99	0.434	0.002	0.62 (0.05)	0.94	0.23	0.003
Scenario 22:{n = 500 πY* = 0.25 σY = 20}
MAR	0.85	0.80 (0.03)	0.54		0.03	0.03	0.07	0.85 (0.03)	0.94	0.11	0.03	0.85 (0.03)	0.68	0.14	0.06	0.85 (0.04)	0.97	0.16	0.03
MCAR	0.85	0.85 (0.02)	0.30	0.30	0.17	0.01	0.02	0.85 (0.03)	0.96	0.11	0.02	0.85 (0.03)	0.97	0.13	0.02	0.85 (0.03)	0.98	0.13	0.02
MNAR	0.85	0.81 (0.02)	0.24	0.30	0.06	0.02	0.05	0.85 (0.03)	0.93	0.11	0.02	0.73 (0.09)	0.88	0.47	0.14	0.85 (0.03)	0.97	0.13	0.02
Scenario 23:{n = 500 πY* = 0.50 σY = 20}
MAR	0.85	0.80 (0.03)	0.43		0.02	0.03	0.07	0.85 (0.02)	0.88	0.08	0.02	0.83 (0.02)	0.67	0.12	0.06	0.85 (0.03)	0.95	0.13	0.02
MCAR	0.85	0.85 (0.02)	0.30	0.30	0.22	0.01	0.02	0.86 (0.02)	0.94	0.09	0.02	0.86 (0.02)	0.94	0.10	0.02	0.85 (0.03)	0.96	0.11	0.02
MNAR	0.85	0.81 (0.03)	0.17	0.30	0.06	0.02	0.05	0.85 (0.02)	0.88	0.08	0.02	0.75 (0.07)	0.83	0.35	0.11	0.85 (0.02)	0.93	0.10	0.02

Notes: MM (missingness mechanism), TV (true value), CD (case deletion), SE (standard error), CR (coverage rate), AW (average width of confidence intervals), RMSE (root-mean-square error). CR and AW are based on 95% nominal confidence rate. CD(SE) column contains AUC estimate and estimate of its standard error under case deletion.

Table 2.

Performance of AUC estimation using MI methods as well as case deletion under MAR, MCAR and MNAR.

			% miss.		Case deletion			Joint imputation				Sequential imputation				Re-sampling (bootstrap)
MM	TV	CD(SE)	Y*	Y	CR	AW	RMSE	AUC(SE)	CR	AW	RMSE	AUC(SE)	CR	AW	RMSE	AUC(SE)	CR	AW	RMSE
Scenario 13:{n = 300 πY* = 0.25 σY = 20}
MAR	0.64	0.62 (0.04)	0.30		0.82	0.12	0.04	0.65 (0.05)	0.93	0.20	0.04	0.64 (0.06)	0.88	0.25	0.06	0.63 (0.06)	0.96	0.23	0.04
MCAR	0.64	0.64 (0.05)	0.30	0.30	0.75	0.12	0.04	0.64 (0.05)	0.91	0.21	0.04	0.64 (0.06)	0.95	0.25	0.04	0.64 (0.06)	0.97	0.24	0.04
MNAR	0.64	0.60 (0.05)	0.36	0.30	0.75	0.15	0.06	0.65 (0.05)	0.84	0.22	0.07	0.64 (0.10)	0.98	0.50	0.06	0.62 (0.07)	0.94	0.31	0.06
Scenario 14:{n = 300 πY* = 0.25 σY = 20}
MAR	0.76	0.71 (0.04)	0.42		0.24	0.07	0.06	0.77 (0.04)	0.93	0.17	0.03	0.75 (0.05)	0.81	0.22	0.07	0.75 (0.05)	0.96	0.23	0.04
MCAR	0.76	0.76 (0.04)	0.30	0.30	0.41	0.05	0.03	0.75 (0.05)	0.93	0.19	0.03	0.76 (0.05)	0.96	0.21	0.04	0.76 (0.05)	0.96	0.22	0.03
MNAR	0.76	0.72 (0.04)	0.22	0.30	0.28	0.07	0.05	0.75 (0.05)	0.91	0.18	0.04	0.71 (0.09)	0.97	0.44	0.08	0.75 (0.05)	0.95	0.22	0.04
Scenario 15:{n = 300 πY* = 0.50 σY = 20}
MAR	0.75	0.71 (0.04)	0.35		0.25	0.07	0.05	0.78 (0.03)	0.84	0.13	0.04	0.74 (0.04)	0.80	0.18	0.06	0.75 (0.04)	0.96	0.18	0.03
MCAR	0.75	0.76 (0.04)	0.30	0.30	0.44	0.05	0.03	0.76 (0.04)	0.90	0.15	0.03	0.76 (0.04)	0.94	0.17	0.03	0.76 (0.04)	0.95	0.18	0.03
MNAR	0.76	0.72 (0.04)	0.17	0.30	0.27	0.06	0.05	0.75 (0.04)	0.85	0.14	0.04	0.70 (0.07)	0.94	0.37	0.08	0.75 (0.04)	0.92	0.19	0.04
Scenario 16:{n = 300 πY* = 0.25 σY = 20}
MAR	0.85	0.80 (0.04)	0.54		0.04	0.03	0.07	0.86 (0.04)	0.95	0.15	0.03	0.83 (0.04)	0.66	0.18	0.08	0.84 (0.05)	0.98	0.21	0.03
MCAR	0.85	0.85 (0.03)	0.30	0.30	0.15	0.02	0.03	0.85 (0.04)	0.96	0.16	0.02	0.85 (0.04)	0.95	0.16	0.03	0.85 (0.04)	0.97	0.17	0.03
MNAR	0.85	0.81 (0.03)	0.23	0.30	0.09	0.03	0.05	0.85 (0.04)	0.95	0.15	0.03	0.76 (0.10)	0.95	0.52	0.12	0.85 (0.04)	0.97	0.17	0.03
Scenario 17:{n = 300 πY* = 0.50 σY = 20}
MAR	0.86	0.80 (0.04)	0.43		0.05	0.03	0.07	0.87 (0.03)	0.81	0.10	0.03	0.830 (0.04)	0.70	0.15	0.07	0.85 (0.04)	0.96	0.16	0.03
MCAR	0.86	0.86 (0.03)	0.30	0.30	0.19	0.01	0.02	0.85 (0.03)	0.92	0.12	0.02	0.85 (0.03)	0.94	0.13	0.02	0.85 (0.03)	0.96	0.14	0.02
MNAR	0.86	0.81 (0.03)	0.16	0.30	0.08	0.03	0.05	0.85 (0.03)	0.88	0.11	0.02	0.78 (0.08)	0.93	0.38	0.10	0.85 (0.03)	0.94	0.14	0.02

Notes: MM (missingness mechanism), TV (true value), CD (case deletion), SE (standard error), CR (coverage rate), AW (average width of confidence intervals), RMSE (root-mean-square error). CR and AW are based on 95% nominal confidence rate. CD(SE) column contains AUC estimate and estimate of its standard error under case deletion.

Across the scenarios underlying MAR and MCAR mechanisms, regardless of the imputation methodology, the MI inferences lead to acceptable parameter estimation and coverage, indicating a good performance. We specifically observe estimates with minimal biases and CIs with excellent coverage rates, even when the sample sizes are small and large variances for the underlying error-prone variable Y. Furthermore, our results clearly note that the performance of the MI is far more superior than the unprincipled method of simple case deletion, which leads to significant biases as well as dismal coverage rates even under MCAR. It is also noted that in some conditions the performance of the MI procedure is not as satisfactory. When the true missingness mechanism is MNAR, the performance of MI is often not acceptable with respect to bias, coverage rates or RMSE regardless of the sample size, variance of the error-prone variable (Y) or prevalence of a disease in a population (π_Y*).

As repeatedly shown in the missing-data literature, case deletion performs worst with respect to all criteria. When the underlying missingness mechanism is MCAR, as expected, AUC estimates under case deletion lead to unbiased estimates (see column #3, named CD(SE)). This result is drawn from comparing the third column which contains the estimate after case deletion averaged across the 1000 simulation repetitions and the second column which contains the true value () of AUC as computed as the average AUC estimate across the 1000 simulation repetitions. The most striking observation with case deletion is the unacceptably low nominal coverage rates as the AUC values increase along with the prevalence. Unlike the general thinking, case-deletion performance is quite poor compared to more principled MI methods even when the missingness mechanism is MCAR. This poor performance is most noticeable with respect to criteria on coverage rates which are as low as 2% for a nominal 95%. When the missingness mechanism is not ignorable (i.e. the MNAR rows) coverage rates are seemingly improved, however, with a closer we realize that these improved rates are always with the price of wider confidence intervals and higher RMSE. This is an important point as the MNAR missingness mechanism induces more selection causing higher magnitude of biases as well as increased standard errors associated with these estimates contrary to a common intuition.

Figure 1 provides a graphical illustration of the performance of each of the four methods (case deletion, joint imputation, sequential imputation and re-sampling-based imputation) with respect to bias across the three missingness mechanisms. Specifically, a matrix scatter plot of the true AUC values and estimated AUC values across several simulation scenarios is given in Figure 1. Top panel depicts the relationship under MCAR across the four methods, middle and lower panel provide the same for MAR and MNAR. We clearly see that as the missingness mechanism become more dependent on the observed and missing data, increasingly larger biases are observed (i.e. deviations from a 45-degree line are more obvious).

Figure 1.

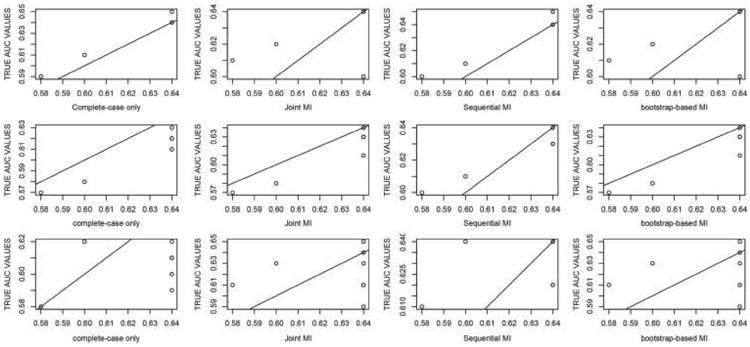
Bias performance of case deletion, joint, sequential and bootstrap-based MI across MCAR (top panel), MAR (middle panel) and MNAR (bottom panel).

MI estimation appears to produce an acceptable performance in most scenarios. Regardless of the imputation method of choice, MI outperforms case deletion under MCAR. This should be noted by practitioners who prefer case deletion because the missingness mechanism in MCAR as even under MCAR, the case deletion could lead substantial inefficiency in multivariate analyses.

Under MAR mechanism, MI inference leads to well-calibrated inferences. Joint imputation methods generally result in more efficient results (i.e. lower RMSE, see ‘Joint Imputation’ column and RMSE sub-column). Performance criteria of RMSE as well as AW are somewhat stable: lower RMSEs and smaller AWs are observed for higher variances (σ_Y), different missingness mechanisms and prevalence of disease.

We also noted that higher but mostly negligible biases in the AUC estimation occur under joint imputation in smaller sample sizes (under MAR, n = 100). These biases completely disappear as the sample size increases. This contrast shows that when the joint aspects of the distribution are not well estimated (e.g. correlation), the MI performance potentially leads to bias. When the underlying mechanism is MNAR, selection bias induced by MNAR adversely impacts on the CRs as well as RMSE. Note that with lower sample sizes (e.g. n = 100), impact of selection bias is most observable in MI under parametric modelling. Re-sampling-based MI techniques (e.g. bootstrap) outperforms parametric competitors under MNAR as seen in the last rows of each panel in Table 1. Larger biases, wider confidence intervals thus much higher-than-nominal coverage rates are observed consistently across the simulation scenarios. Overall, under MAR sequential methods of imputation outperforms joint approach especially smaller sample sizes. Under MNAR, however, regardless of the choice of imputation methodology, poor performance is seen across all simulation scenarios. If such a mechanism is suspected, practitioners are strongly recommended avoiding methods that makes ignorability assumption.[1] If this is not possible, it would help improve the poor performance adding variables that are either predictive of missing variables or help explain missingness as suggested by Collins et al.[23]

5. Discussion

The overall goal of our work was to assess the impact of the model and missingness mechanism assumptions on the MI-based inferences in ROC analysis. Regardless of how the missing values occur, case deletion is seen to be dangerous in ROC analyses. Its application would undoubtedly lead to biases in medical diagnostic test performances, which could have a direct, adverse effect on patients' care. It is clearly advisable to adopt any of the MI techniques regardless of its particular analytical form. Under MCAR and MAR, the joint modelling approach appears to be preferable.

Our work considered a simple ROC analyses with arbitrary missingness and did not consider covariate information. It explicitly targeted performance of a diagnostic test. We would like to extend our current work to problems with covariate information. This is a useful extension not only because of its common occurrence but also because of its typical inclusion as covariates in the missing-data models. While we note that MI methods that operate under MAR/MCAR are not really suitable for MNAR, it may be possible to improve the performance by including informational covariates in the imputation models.[23] It is also known that richer imputation models improve the performance of MI inference. We note that the joint models can be sensitive to estimation problems originating from data scarcity underlying the estimation of joint aspects.

It is also valuable to study the MI performance in covariate-adjusted ROC analyses and three-way ROC analyses. We believe that our simulation study serves as a starting point and extensions require a careful imputation model selection. Both these considerations require multivariate models but care has to be taken as increases in dimension typically leads to adversities in the imputations. Our results indicate that variable-by-variable imputation techniques have promise in such applications whereas joint models seem to be problematic in cases where the joint aspects might be poorly estimated.

Finally, we plan to examine how study design or data structure influence the performance of MI inference in ROC analyses. It is known that ignoring design features such as the longitudinal or clustered nature of data lead to strong inferential drawbacks such as understated standard errors or biased estimates. This problem can easily be exacerbated with missing data. The imputation models in such situations must account for variation in data structures. For example, if the design is longitudinal, then the imputation model must reflect possible variations among the coefficients of the imputation model across the study subjects to avoid the potential underestimation of uncertainty measures in ROC analyses (e.g. AUC and its standard error). Finally, we believe that the most important direction is the dissemination of such methods by means of statistical software as when there are no statistical software available to the practitioners, methods that lead to invalid inferences (e.g. case deletion) are typically preferred.